摘要:松散体结构松散, 是崩塌、滑坡等地质灾害的主要物源, 其致灾范围受含石量和坡度等因素影响较大. 传统的对松散体滑动堆积特性的研究多为宏观或定性分析, 对细观的内在运动机理研究较少. 本文采用离散元方法定量分析了含石量和坡度变化对松散颗粒滑动后的冲程、堆积宽度、最大厚度、堆积面积、堆积轮廓形状、堆积区体积、静堆积角和累积质量等堆积特征值的影响, 并从颗粒的能量和接触力角度探讨了松散体灾变过程中的运动和堆积特征, 以揭示颗粒之间的相互作用机理. 研究结果表明: 含石量在0—70%范围增加时, 冲程、堆积宽度和堆积面积均先增大后递减, 最终累积质量减小; 坡度在30°—65°范围增大时, 冲程、堆积宽度、堆积面积和累积质量均会增大, 最大厚度近似线性减小, 静堆积角近似二次函数减小. 此外, 粗、细颗粒在堆积区的体积占额存在一个临界距离L_c, 当距坡脚线距离L < L_c时, 细颗粒大于粗颗粒所占体积; 当L > L_c时, 细颗粒小于粗颗粒所占体积.
关键词: 松散体/
堆积特性/
非球形颗粒/
离散元

English Abstract

全文HTML

--> --> -->

松散体是由大量的松散颗粒组成, 在自然界广泛存在, 具有结构松散、孔隙度大、粒间结合力差和易变形等特点, 还衍生着诸多的动力学行为和物理力学特性; 因结构构成的特殊性, 往往在自重或其他外界因素的影响下失稳破坏, 造成河流堵塞、道路阻断及房屋掩埋等危害^[1-5]. 当前, 对于松散体滑动后的堆积范围很难科学预测及易损性评估, 已成为国际上的研究热点.
****们在研究松散体滑动后的堆积特性时, 主要考虑初始松散体的体积、颗粒粒径、坡高、启动区坡度、坡角、摩擦系数和地震荷载等因素对松散颗粒变形过程和滑动后的堆积形态、冲程、平均粒径分布、固相分数及分选系数等指标的影响规律^[6-10]. 堆积形态与颗粒运动过程及速度密切相关, 通过物理模型试验和理论分析提出了滑坡冲程与速度的预测方法^[11]、落石运动速度与距离的数学公式^[12]、松散体运动中的障碍物与冲程的动态关系模型^[13]. 可见, 模型试验和理论分析为其他方法研究松散颗粒滑动堆积特性提供了前提, 但缺乏滑动过程的实测数据去解释松散颗粒滑动堆积特性的内在机理. 此外, 在现场调研中发现坡度对松散体滑动堆积范围分布各异, 松散体中的含石量大小与滑后堆积特性之间的内在关系仍需进一步定量研究.
离散元方法(discrete element method, DEM)最早由Cundall^[14-16]教授1971年提出, 当前正广泛用于研究非连续介质颗粒运动等问题^[6,17]. 由于现实的颗粒运动体量太大, 这会大幅度降低DEM的计算效率; ****们通常借鉴物理模型试验中的缩尺滑槽试验, 并采用DEM研究松散颗粒的变形失稳过程及滑动后的颗粒分布特性^[6]、坡高和坡角对滑后堰塞体的内部结构和堆积性质的影响规律^[8]. 颗粒间和颗粒与滑动边界间的摩擦系数对颗粒堆积特性的影响显著, 摩擦系数对颗粒堆积角的影响较大^[18,19]. 前述离散元研究都有一个共同点, 均是基于球形颗粒开展研究, 而自然界中的球形物质实际上很少; 近年来****们开始研究非球形颗粒, 这就使得研究更加贴近现实. 滚动摩擦系数对非球形颗粒堆积角和颗粒堆内外边界间隙ζ的影响较大^[17].
松散体滑动后堆积特性的内在机理与运动中的颗粒能量及动力学关系密切. 根据牛顿第二定律及颗粒相互作用时的接触力关系, 可从颗粒流分析法和能量交换方面分析颗粒整个运动过程^[20,21]. 颗粒间的动势能转化与颗粒的摩擦联系紧密, 可用土力学方法分析颗粒在运动中的能量衰减^[22,23]. 从上述研究中可以看出, 颗粒间的能量及接触力为解释松散颗粒滑动堆积特性提供了切入点.
因此, 本文采用DEM构建了松散体滑动堆积三维模型, 对非球形颗粒滑动堆积过程进行了数值模拟, 研究了含石量和坡度变化对松散体滑动堆积特性的影响规律, 分析了颗粒滑动堆积过程中的能量交换和接触作用力, 为深入理解和进一步揭示松散颗粒堆积特性的内在机理提供参考.

2

-->

2.1.DEM的计算原理^[14-16,24]

DEM认为颗粒单元间的运动是相互独立的, 只有颗粒单元间发生相互作用时, 才会在接触点处产生作用力. 根据力与位移关系, 由位移得到颗粒受到的作用力, 再由牛顿第二定律得出颗粒i的运动方程

$\left\{ \begin{aligned} &{m_i}\mathop {{u_i}}\limits^{..} = \sum F \\& {I_i}\mathop {{\theta _i}}\limits^{..} = \sum M ,\end{aligned} \right.$

式中, ${\mathop u\limits^{..} {_i}}$、$\mathop {{\theta _i}}\limits^{..} $、${m_i}$、${I_i}$分别为颗粒i的加速度、角加速度、质量和转动惯性; $\displaystyle\sum F $、$\displaystyle\sum M $分别是颗粒在质心处受到的合外力和合外力距.
利用中心差分法对(1)式进行积分, 得到以两次迭代时间步长的中间点表示的更新速度表达式为

$\left\{ \begin{aligned} &{({{\mathop u\limits^{.}} _i})_{N + \textstyle\frac{1}{2}}} = {({{\mathop u\limits^{.}} _i})_{N - \textstyle\frac{1}{2}}} + {\left[ {\sum {F/{m_i}} } \right]_N}\Delta t, \\ &{({{\mathop \theta \limits^{.}} _i})_{N + \textstyle\frac{1}{2}}} = {({{\mathop \theta \limits^{.}} _i})_{N - \textstyle\frac{1}{2}}} + {\left[ {\sum {M/{I_i}} } \right]_N}\Delta t,\end{aligned} \right.$

式中, $\Delta t$是时间步长; N对应时间t.
对(2)式进行积分, 可得到关于位移的等式表述为

$\left. \begin{aligned} {({{\mathop u\limits^{}} _i})_{N + 1}} = {({{\mathop u\limits^{}} _i})_N} + {({{\mathop u\limits^{.}} _i})_{N + \textstyle\frac{1}{2}}}\Delta t \\ {({\theta _i})_{N + 1}} = {({{\mathop \theta \limits^{}} _i})_N} + {({{\mathop \theta \limits^{.}} _i})_{N + \textstyle\frac{1}{2}}}\Delta t\end{aligned} \right\},$

进而得到颗粒单元新的位移值, 并将该新位移代入力与位移关系计算新的作用力, 循环反复就可实时跟踪每个颗粒单元在任意时刻的运动, 如图1所示.
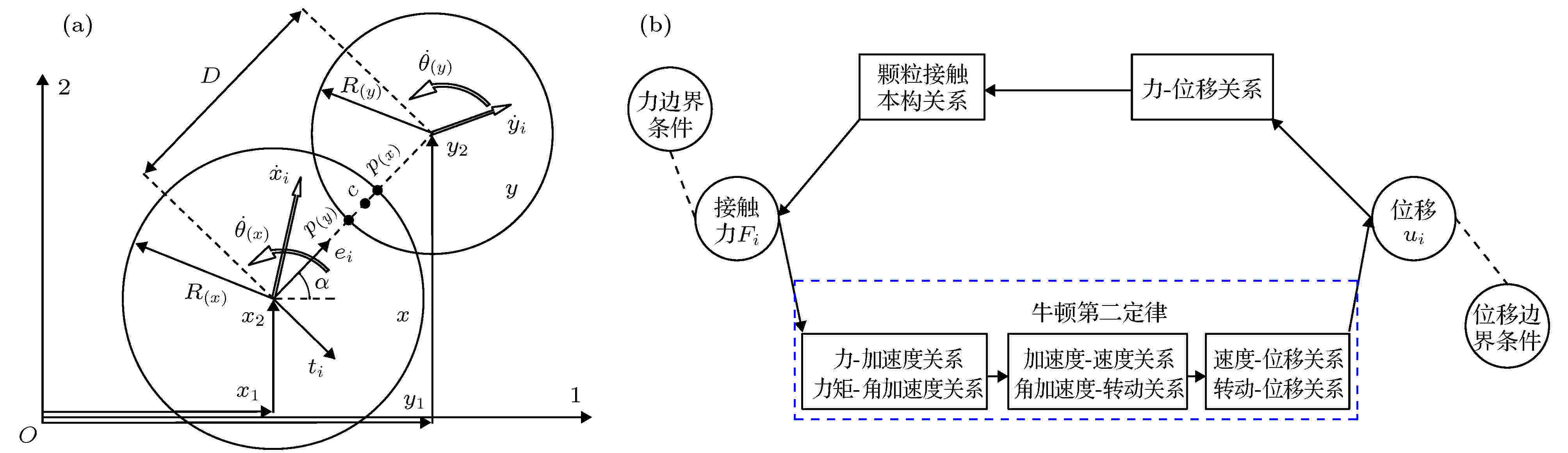图 1 颗粒计算迭代示意图　(a) 力与位移关系; (b) 理论计算
Figure1. Granular computing iteration diagram: (a) Relationship between force and displacement; (b) theoretical computing.

2 -->

2.2.Hertz-Mindlin(no slip)接触模型^[14-16,25]

当颗粒与颗粒发生相互作用时, 会产生相应的接触法向力F_n和切向力F_t, 如图2所示.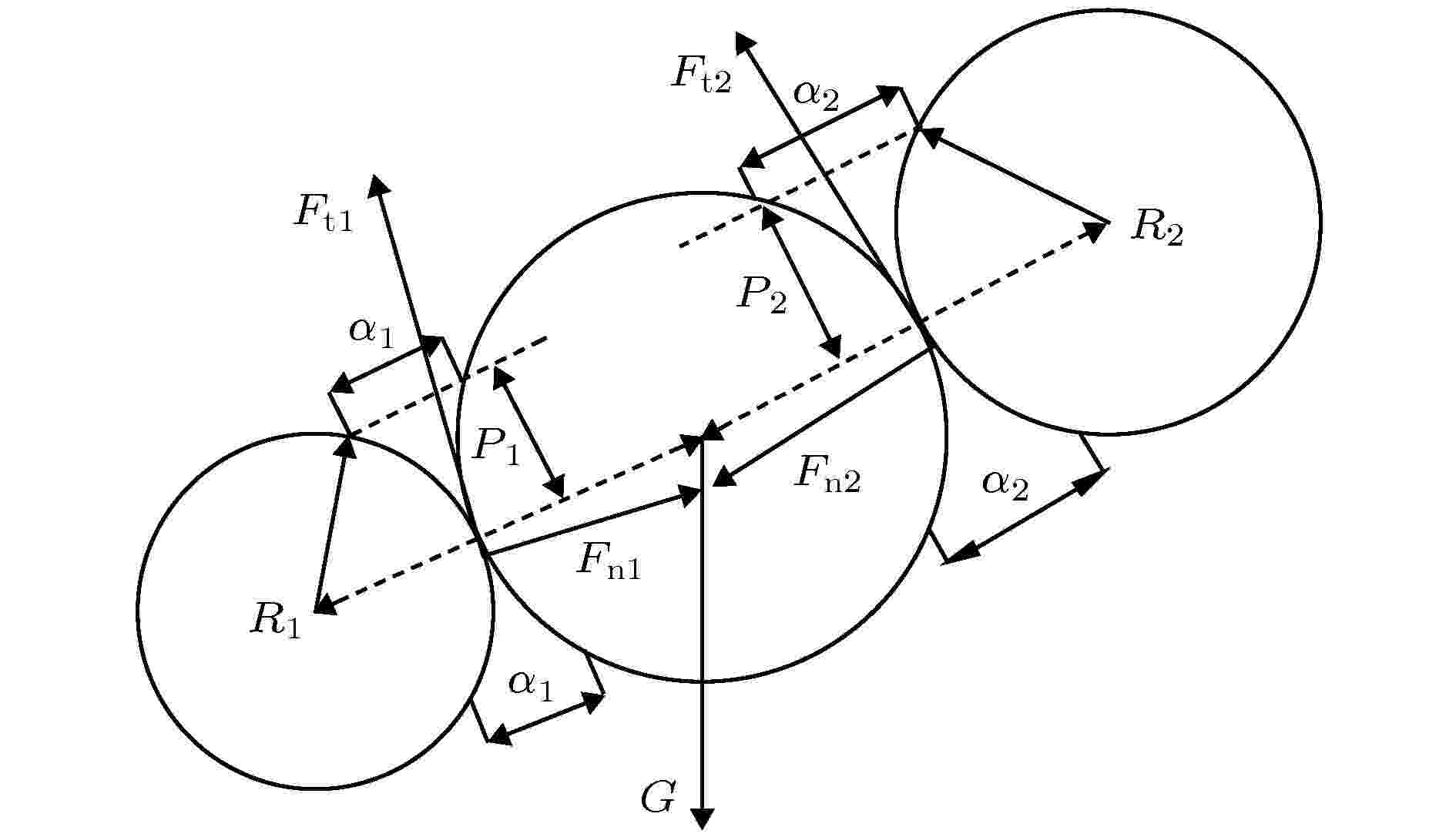
图 2 颗粒相互作用时的受力
Figure2. The forces by particles interacting.

图3为颗粒法向力示意图, F_n表达式为
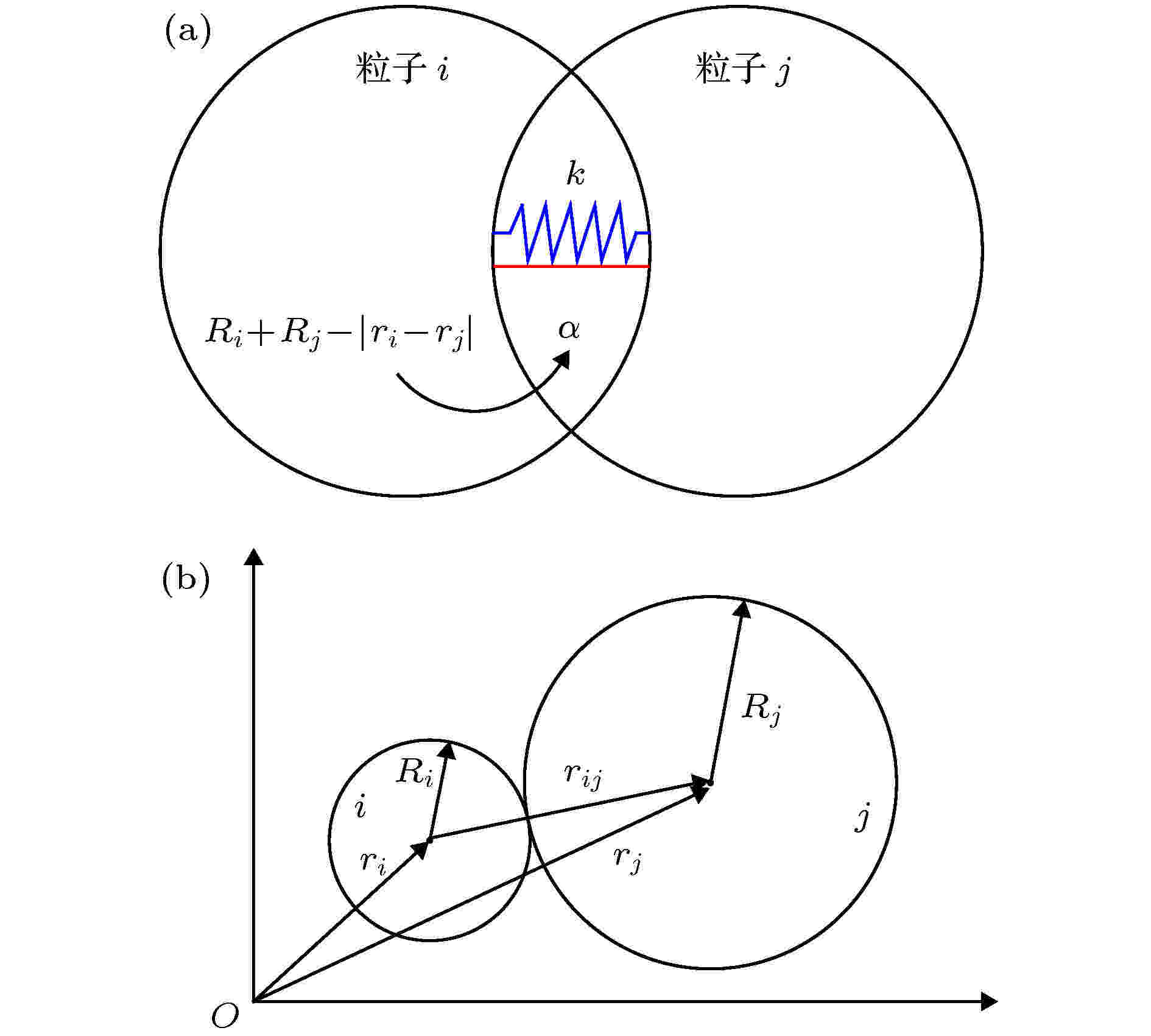图 3 颗粒法向力示意图　(a) 法向重叠量; (b) 位置关系
Figure3. Diagram of normal force of granular: (a) Normal overlap; (b) position relations.

${F_{\rm{n}}} = \frac{4}{3}{E^ * }{\left( {{R^ * }} \right)^{1/2}}{\alpha ^{3/2}},$

其中, E^*为等效弹性模量, 由颗粒的弹性模量E和泊松比v求得; R^*为等效颗粒半径, 由颗粒的半径R求得, 其表达式为

$\frac{1}{{{E^ * }}} = \frac{{1 - \nu _1^2}}{{{E_1}}} + \frac{{1 - \nu _2^2}}{{{E_2}}},$

$\frac{1}{{{R^ * }}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}.$

颗粒间发生作用的法向重叠量α由颗粒半径R和颗粒的球心位置矢量r求得, 即

$\alpha = {R_1} + {R_2} - \left| {{r_1} - {r_2}} \right|,$

$a = \sqrt {\alpha {R^ * }} ,$

式中, a为颗粒间接触面为圆形时的接触半径.
颗粒发生接触时法向阻尼力$F_{\rm{n}}^{\rm{d}}$的表达式为

$F_{\rm{n}}^{\rm{d}} = - 2\sqrt {\frac{5}{6}} \beta \sqrt {{S_{\rm{n}}}{m^ * }} \nu _{\rm{n}}^{{\rm{rel}}},$

其中, β为法向阻尼力系数, 由颗粒间相互作用时的弹性恢复系数e求出; S_n为法向刚度, 由颗粒的等效模量、等效颗粒半径和颗粒的法向重叠量求出; m^*为等效质量, 由颗粒的质量m求出; 即

$\beta = \frac{{\ln e}}{{\sqrt {{{\ln }^2}e + {{\rm{\pi }}^2}} }},$

${S_{\rm{n}}} = 2{E^ * }\sqrt {{R^ * }\alpha } ,$

${m^ * } = \frac{{{m_1}{m_2}}}{{{m_1} + {m_2}}},$

$\nu _{\rm{n}}^{{\rm{rel}}}$为颗粒间相对速度的法向分量值, 由颗粒的泊松比v和颗粒间碰撞时的法向单位矢量n计算得出, 其表达式为

$\nu _{\rm{n}}^{{\rm{rel}}} = \left( {{\nu _1} - {\nu _2}} \right) \cdot n,$

$n = \frac{{{r_1} - {r_2}}}{{\left| {{r_1} - {r_2}} \right|}},$

在颗粒接触的切线方向上, 其切向接触力F_t, 切向阻尼力$F_{\rm{t}}^{\rm{d}}$的表达式为

${F_{\rm{t}}} = - {S_{\rm{t}}}\delta ,$

${S_{\rm{t}}} = 8{G^{_ * }}\sqrt {{R^ * }\alpha } ,$

${G^ * } = \frac{{2 - \nu _1^2}}{{{G_1}}} + \frac{{2 - \nu _2^2}}{{{G_2}}},$

$F_{\rm{t}}^{\rm{d}} = - 2\sqrt {\frac{5}{6}} \beta \sqrt {{S_{\rm{t}}}{m^ * }} \nu _{\rm{t}}^{{\rm{ret}}},$

式中, G^*为等效切向模量; 切向力F_t由切向重叠量δ和切向刚度S_t确定; $\nu _{\rm{t}}^{{\rm{rel}}}$为切向相对速度.
2 -->

2.3.数值模拟计算方案

为探讨松散体滑动后的堆积特性, 以堆积体中的含石量σ (%)和滑床坡度θ (°)为变量参数开展数值模拟. 含石量σ的取值分别为0, 30, 50, 70; 坡度θ的取值分别为30, 45, 65. 本研究共开展12组模拟, 每组模拟三次取平均值作为该组的模拟结果.
本次数值模拟的主要目的是针对松散体滑动后堆积特性的规律及机理研究. 因此, 借鉴碎屑流滑槽物理模型试验^[26,27], 基于相似比原理开展数值模拟, 底板模拟堆积区, 初始堆积体由黄色粗颗粒和蓝色细颗粒在模拟软件EDEM 2.7^[17]中自动生成并自然堆积, 如图4所示. 需要指出的是, 本文数值模型的边界条件在处理时参照了文献[6]和文献[8]中的研究思路, 将料箱和底板沿滑床中轴线设置, 滑床和底板均为全约束并保持静止状态; 在松散体颗粒整个滑动堆积过程中, 滑床和底板的弹性形变忽略不计, 只考虑颗粒与滑床间以及颗粒与底板间的相互摩擦和碰撞作用. 此外, 颗粒流为固相运动, 仅在重力作用下滑动, 忽略外力(如风力等)的干扰.
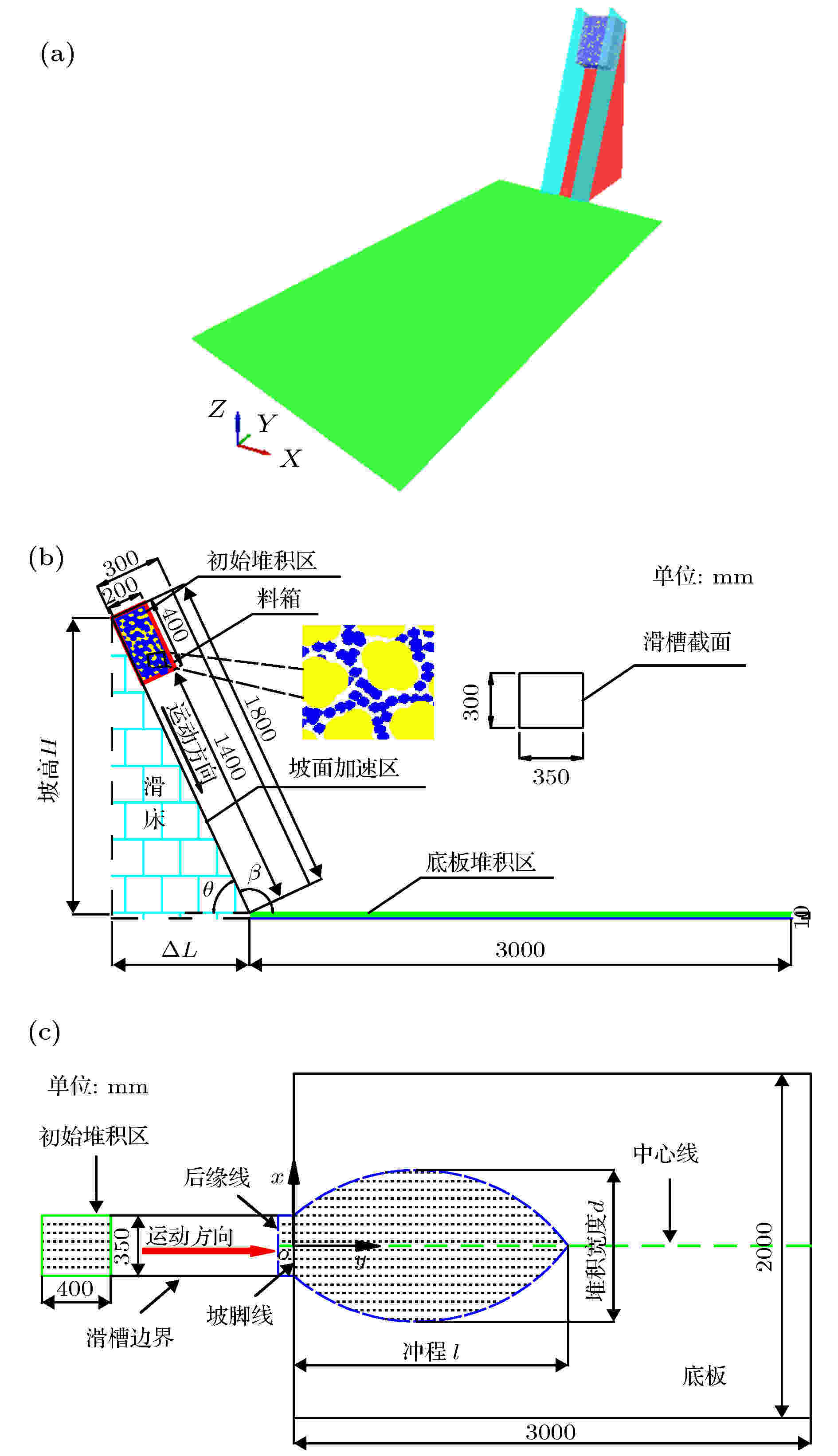图 4 松散体滑动堆积模型示意图　(a) 三维数值模型; (b) 侧视图; (c) 俯视图
Figure4. Diagram of sliding accumulation model of loose accumulation body: (a) Three-dimensional numerical model; (b) side of view; (c) vertical view.

依据现场典型地质灾害点的松散堆积体现场取样, 通过室内的土工试验, 对松散体中的块石与碎石土粒径及其体积范围进行统计, 并参照文献[28]中对松散体中颗粒粒径及其分形理论的研究结论, 最后结合模拟实际计算效率综合确定粗颗粒体积约为细颗粒体积的46.9倍, 满足现场调查及相关研究的范围要求. 其中, 模拟的大粒径块石和碎石土单个颗粒均由4个球形基础颗粒组成, 如图5所示. 通过野外调研和土工试验, 确定了模拟材料的本征参数和弹性恢复系数, 颗粒与滑槽间的摩擦系数通过物理试验确定^[29], 主要计算参数见表1.

参数	符号	单位	数值		参数	符号	单位	数值
细颗粒基础球粒径	d	mm	4.00		静摩擦系数	μps	—	0.44
粗颗粒基础球粒径	d	mm	14.00		滚动摩擦系数	μpr	—	0.05
颗粒密度	ρ	kg/m3	2100.00		堆积体质量	M	kg	30.00
剪切模量	E	MPa	1000.00		时间步长	dt	s	6.26616 × 10–5
泊松比	v	—	0.26		滑槽尺寸	L × W × H	mm	1800 × 350 × 300
恢复系数	e	—	0.40		底板尺寸	L × W × H	mm	3000 × 2000 × 10
摩擦系数	μpp	—	0.42		料箱尺寸	l × w × h	mm	400 × 350 × 200

表1松散颗粒堆积离散元模拟的主要计算参数
Table1.Main computational parameters of discrete element simulation for loose granular accumulation.

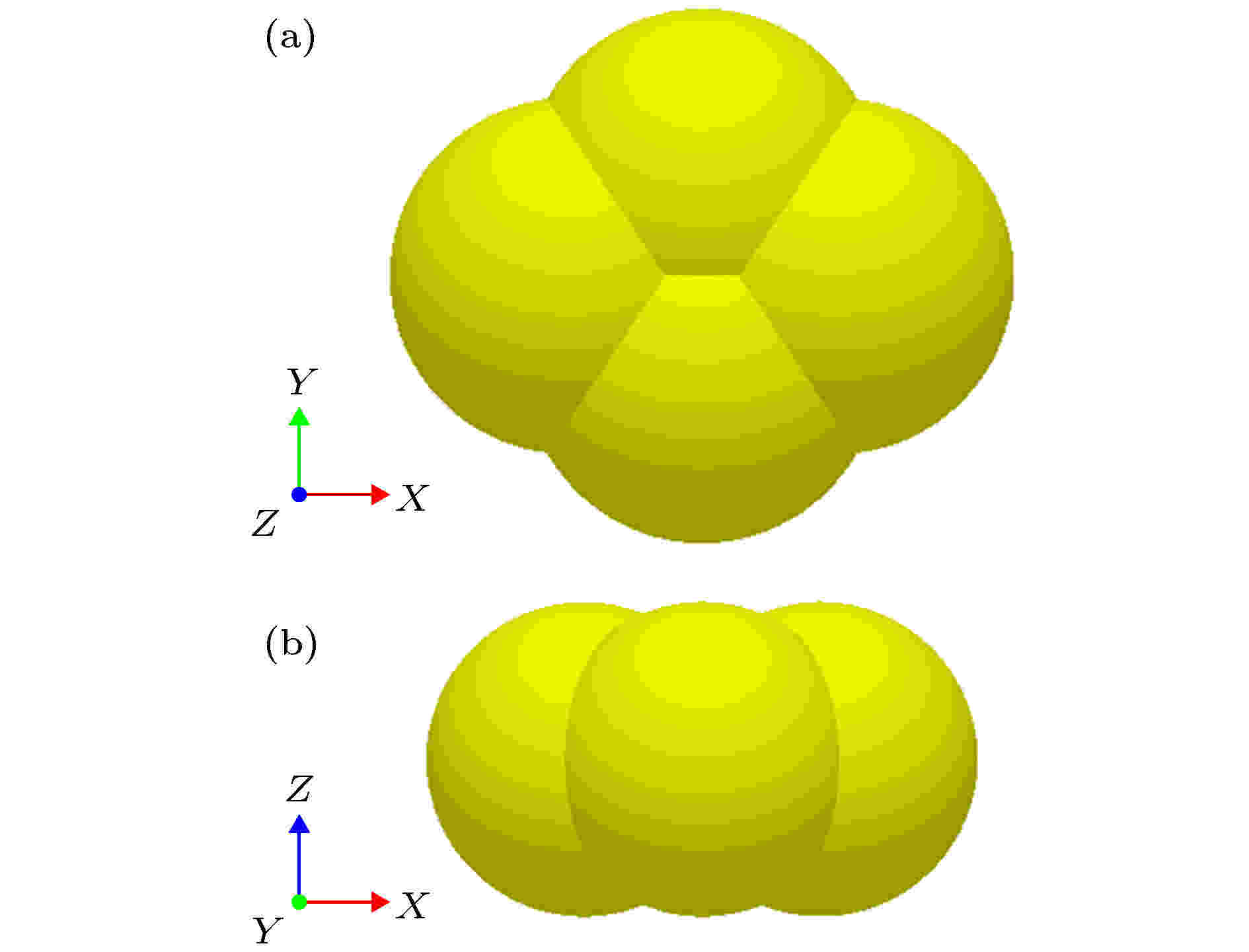图 5 单个颗粒大样图　(a) –Z视角; (b) +Y视角
Figure5. Diagram large sample of single particle: (a) –Z of view; (b) +Y of view.

2 -->

2.4.颗粒滑动堆积过程的试验对比验证

为了验证本文数值计算的准确性与稳定性, 首先对参数为坡度为38°, 体积为0.015 m³, 颗粒粒径为5—20 mm, 单个颗粒形状如图5所示, 其他参数见表1的松散体滑动过程进行了数值模拟计算, 并与文献[30]中的物理模型试验结果进行对比, 如图6所示. 可知, DEM计算结果累积体积开始的时间略早, 最后达到稳定阶段的累积体积较试验结果稍小, 可能是因为试验中滑槽的摩擦系数偏小, 但总体变化的规律与试验结果吻合良好, 说明颗粒形状对累积体积的影响较小, 同时反映了本文DEM数值模型可以较好地模拟松散体的滑动过程.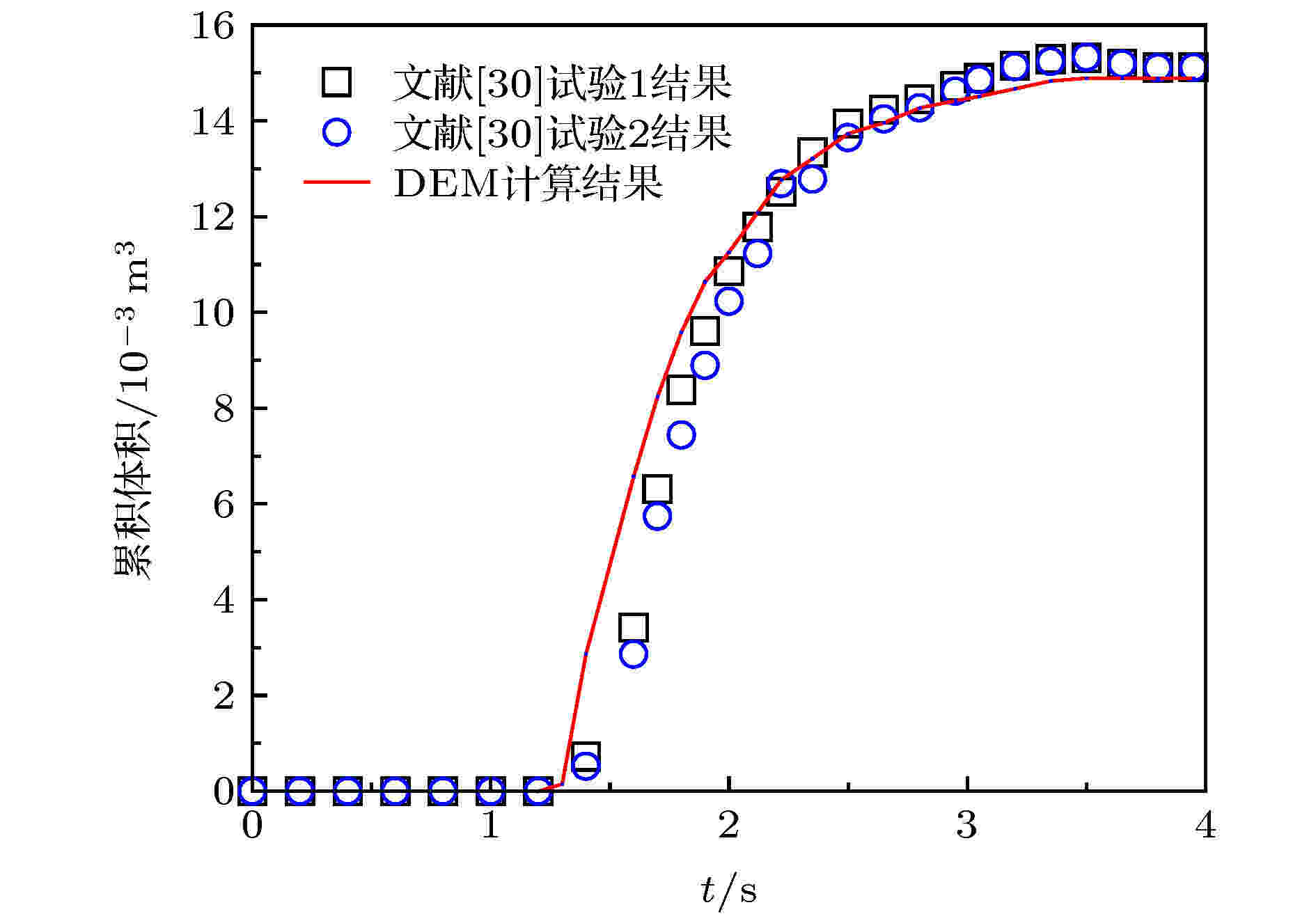
图 6 颗粒滑动后累积体积试验值^[30]与DEM计算值比较
Figure6. Comparison of cumulative volume between experiment results^[30] and DEM simulation results of granular after sliding.

2

-->

3.1.堆积过程与速度分布

图7为坡度为65°、含石量为50% 的松散体滑动堆积过程与速度分布. t = 400 ms时, 初始堆积体在重力下呈倾覆式变形, 前端和表层颗粒的启动速度较内部和底层大. t = 600 ms时, 因颗粒流头部受约束较小, 所以颗粒速度较大, 少量颗粒脱离颗粒流运动. t = 860 ms时, 颗粒流长度延伸最大, 而厚度越扁平, 平均速度达到最大, 最早接触底板时易发生弹跳. t = 1000 ms时, 由于底板限制了颗粒流的运动方向, 部分颗粒到达坡底便开始减速堆积, 颗粒流长度变短的同时其厚度短暂增大; 速度出现明显分层, 底层最小, 中间层次之, 顶层最大. t = 1 200 ms时, 颗粒流长度再次延展, 相反的厚度逐渐减小; 头部速度最大, 中部次之, 尾部最小. 随着时间的推移, 颗粒渐渐准静态堆积, 呈蓝色状态, 堆积结束.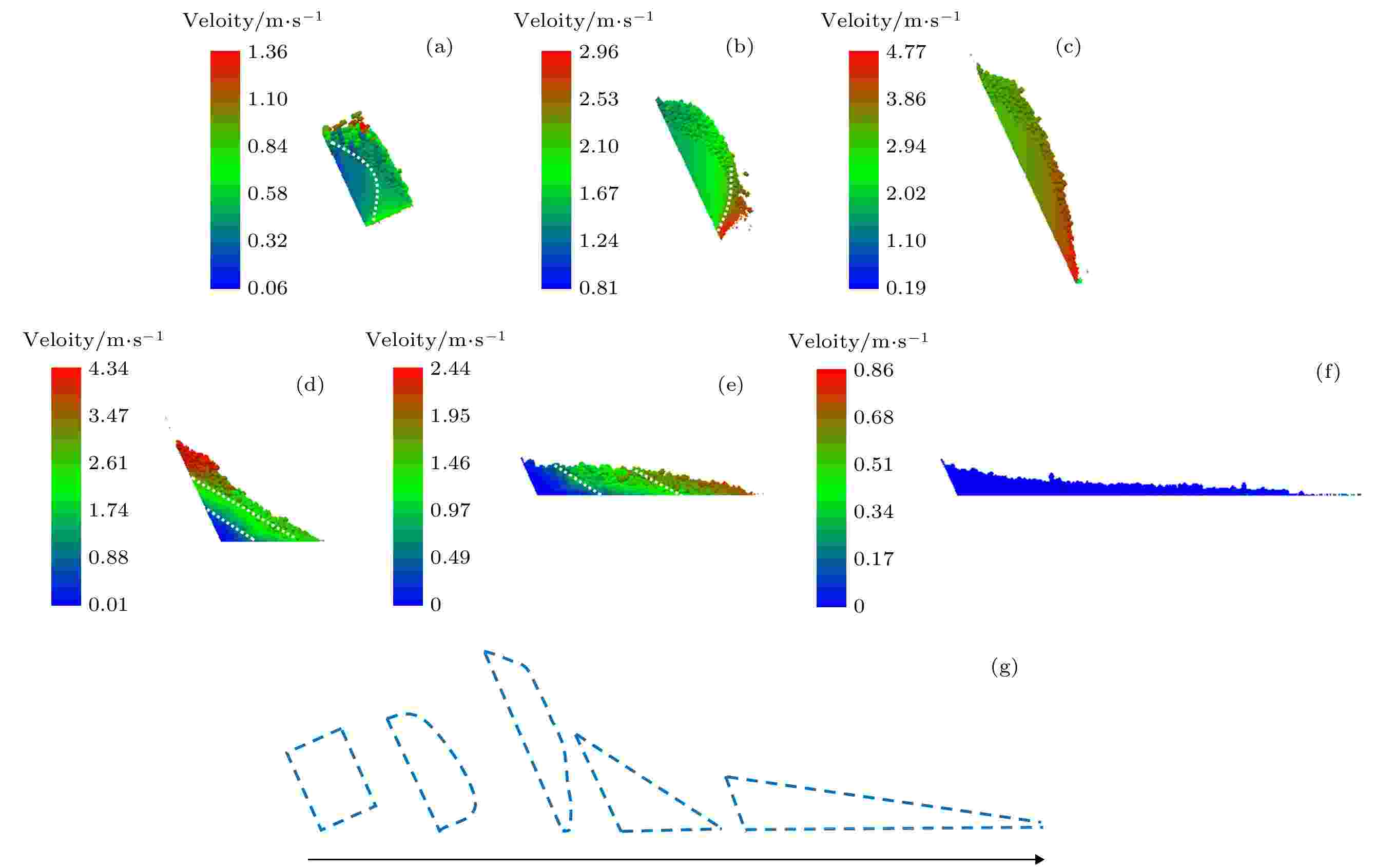
图 7 松散体滑动堆积全过程(+X视角)　(a) t = 400 ms; (b) t = 600 ms; (c) t = 860 ms; (d) t = 1 000 ms; (e) t = 1 200 ms; (f) t = 2 000 ms; (g) 堆积过程形状变化
Figure7. Loose materials the whole process of sliding accumulation(+X view): (a) t = 400 ms; (b) t = 600 ms; (c) t = 860 ms; (d) t = 1 000 ms; (e) t = 1 200 ms; (f) t = 2 000 ms; (g) accumulation process changes shape.

综上, 松散体滑动堆积大体可划分为启程变形加速, 近程高速滑动, 中程减速滑动, 远程准静态堆积四个阶段; 这里只是定性的分析松散体堆积过程中长度、厚度、形状及速度的变化, 接下来将对堆积结果进行定量分析.
2 -->

3.2.含石量对堆积特性的影响

本文主要分析含石量和坡度变化对松散体滑动后堆积特性的影响规律, 最终得到12组不同的颗粒堆. 通过提取颗粒堆中与底板接触的颗粒位置坐标, 导入Origin 2018软件中, 采用网格划分法, 选取特殊交点可得到平面堆积区域的简化计算示意图, 进一步获取堆积特征值(冲程l, 堆积宽度d, 最大厚度h, 平面堆积面积S ), 如图8所示. 其中, 冲程l是指松散体滑动后沿坡脚线至主堆积区最前缘的距离, 是地质灾害防治和预测的常用指标; 堆积宽度d是指在堆积区中与冲程方向垂直的最大距离; 最大厚度h为堆积区竖直方向上底层至表层的最大距离; 平面堆积面积S则是松散体地质灾害范围预测、评估和保护区搬迁范围的重要参考指标.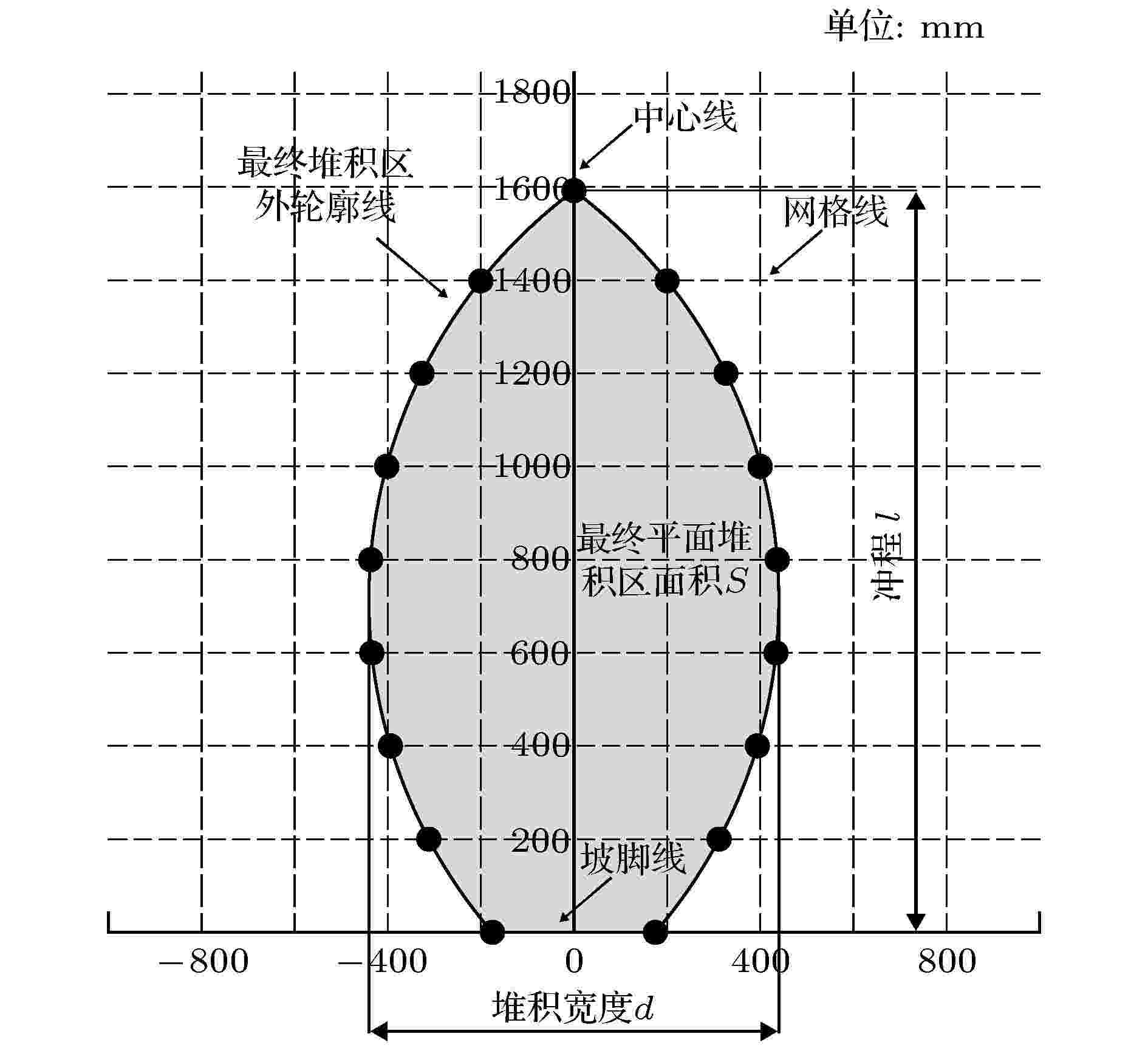
图 8 最终平面堆积形态示意图
Figure8. The final diagram of plane accumulation form.

图9给出的是含石量对最终堆积特征值的影响. 分析可知, 随着含石量增大, 颗粒堆的冲程、堆积宽度、堆积面积均先增大后递减, 而最大厚度呈先减小后递增趋势. 主要是因为运动中细颗粒的减少, 使得粗颗粒间的空隙及粗颗粒与滑槽间的摩擦都相对变大, 粗颗粒相互碰撞作用增强, 能量耗散较大.
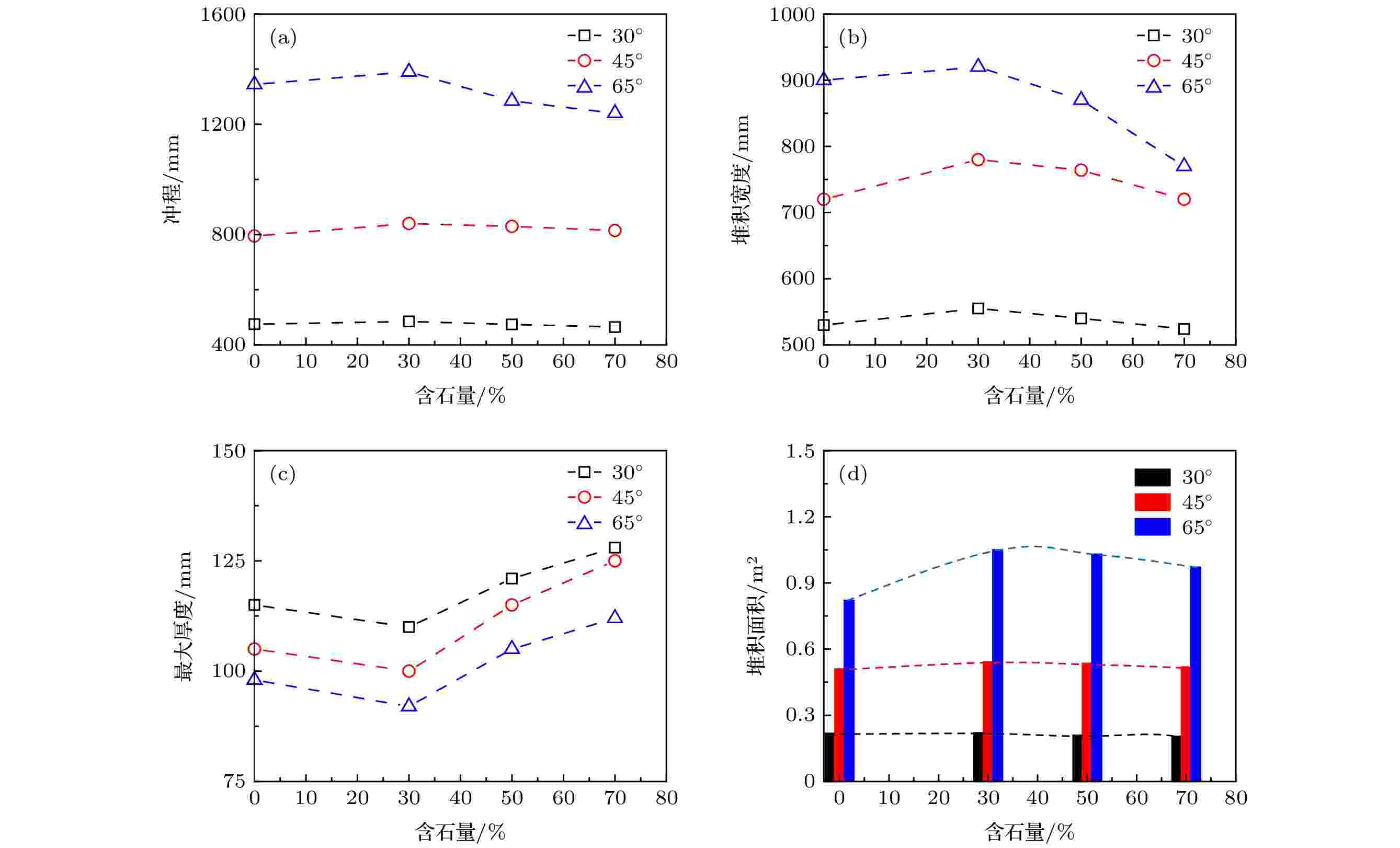图 9 含石量对堆积形态的影响　(a) 冲程; (b) 堆积宽度; (c) 最大厚度; (d) 堆积面积
Figure9. Influence of stone content on the accumulation form: (a) Stroke; (b) accumulation width; (c) maximum thickness; (d) accumulation area.

静堆积角γ是指底平面保持静止时松散颗粒在重力下堆积后的自然坡度表面与水平面间的夹角, 它是研究散体颗粒材料基本物理堆积特性的常用测量参数^[25]. 为了定量分析不同计算条件下静堆积角的变化规律, 同时为了静堆积角的测量精确, 对颗粒堆X轴正方向和X轴负方向采用Origin 2018图像数字化技术获得颗粒堆的边界轮廓线, 并对边界轮廓线做线性拟合, 进一步获取拟合方程及其斜率k. 如图10所示. 最终测定静堆积角的表达式为
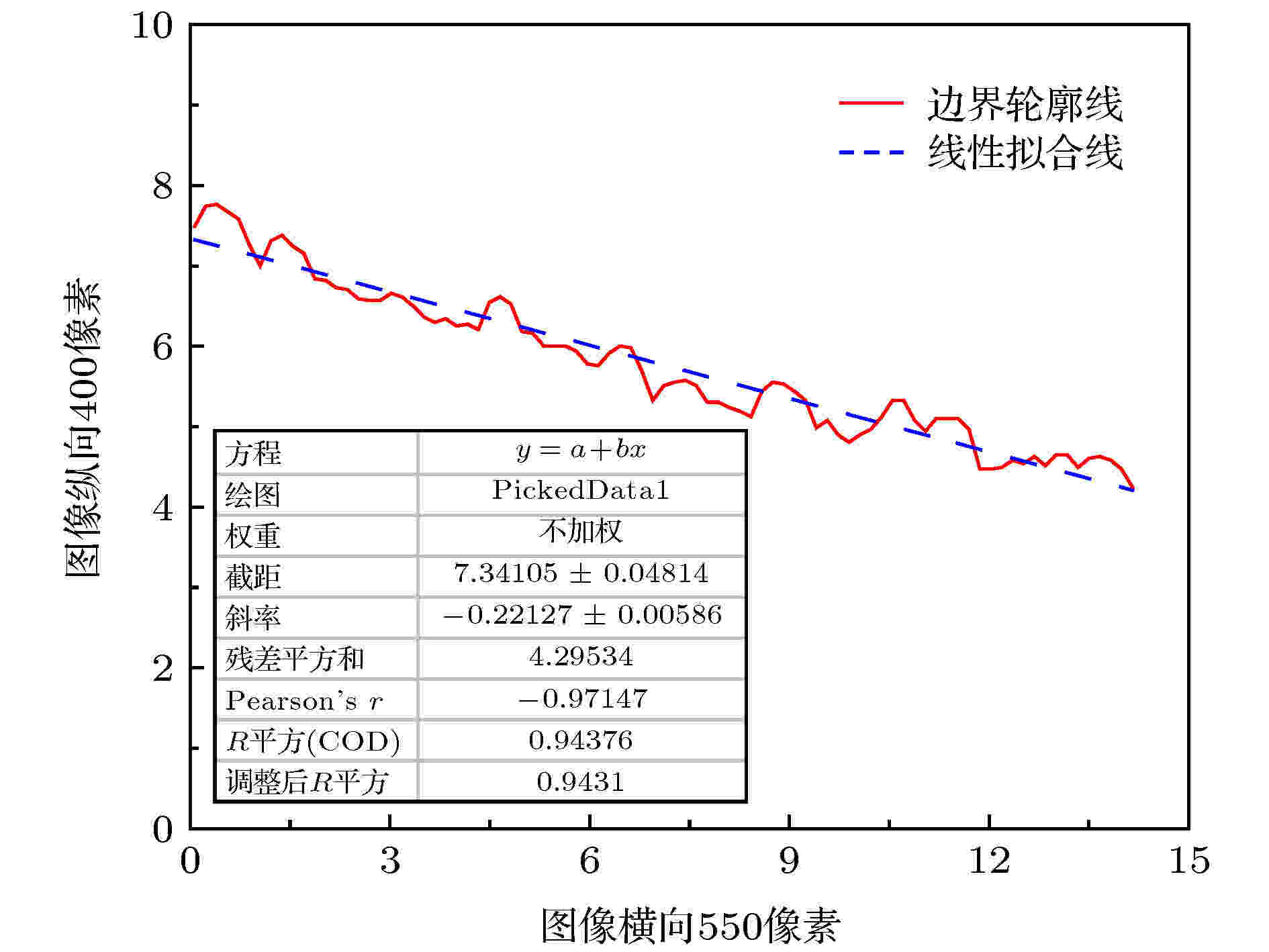图 10 静堆积角边界轮廓提取
Figure10. Static accumulation angle boundary contour acquire.

$\gamma = ({{\arctan |k|}}/{{\text{π}}}) \times 180^{\circ} ,$

由表2分析可知, 随着含石量增大, 在一定坡度时, 静堆积角会出现小幅度减小, 而超过一定坡度时, 静堆积角会小幅度增大. 由于静堆积角与松散颗粒的流动性密切相关, 从而反映了松散体中含石量值的大小对颗粒流动性有不同程度的影响, 坡度较小时颗粒流动性有增强的趋势, 而坡度较大时颗粒流动性则有所减弱; 主要是因为含石量变化会使得颗粒滑动过程中的碰撞强度、摩擦及接触形式在一定程度上改变颗粒的流动性, 除此之外影响颗粒流动性的因素还有很多, 如黏聚力、内摩擦力和初始堆积体密度等, 所以未来的工作会针对这一点进一步研究. 另外, 相比于含石量, 坡度对静堆积角值的影响显著; 换句话说, 坡度对颗粒流动性的影响关系更加密切, 至于坡度是如何影响静堆积角和颗粒流动性的, 以及二者的关系模型在后文会进一步分析.

计算条件	+X方向γ /(°)	-X方向γ /(°)	均值γ /(°)
30° 0%	13.58	13.46	13.52
30° 30%	12.94	13.13	13.40
30° 50%	12.48	13.32	12.90
30° 70%	12.03	11.27	11.65
45° 0%	8.25	8.21	8.23
45° 30%	6.85	7.31	7.08
45° 50%	7.28	6.92	7.10
45° 70%	7.78	7.24	7.51
65° 0%	4.17	4.28	2.23
65° 30%	4.25	4.59	2.42
65° 50%	4.26	4.89	2.58
65° 70%	4.96	4.74	2.85

表2不同计算条件下静堆积角测量值
Table2.Measured value of static accumulation angle under different computing conditions.

为了进一步建立含石量与松散体滑动后静堆积角的关系模型, 同时考虑到坡度在一定程度上对含石量的影响效应, 在其他参数不变的条件下, 对表2中的静堆积角γ均值与含石量σ值进行关系式拟合, 得到拟合关系模型方程式为

$\left. \begin{array}{l} \gamma = - 0.0006{\sigma ^2} + 0.0173\sigma + 13.505,\;\;{R^2} = 0.9946,\theta = 30 \\ \gamma = 0.0007{\sigma ^2} - 0.0569\sigma + 8.2212 ,\;\;{R^2} = 0.9955,\theta = 45 \\ \gamma = 7 \times {10^{ - 5}}{\sigma ^2} + 0.0036\sigma + 2.2331 ,\;\;{R^2} = 0.9977,\theta = 65\end{array} \right\},$

在建立的静堆积角γ均值与含石量σ值的关系模型((20)式)可以看出, 二者之间的关系近似二次抛物线, 相关性系数R²趋近于1, 说明静堆积角与含石量的相关性拟合很好; 也即是说, 在一定条件下, 这种关系模型可以从散体颗粒流动性的基本物理特性角度出发为该类松散体滑动后的静堆积角对含石量的响应提供预测模型.
为研究含石量对堆积区颗粒稀疏程度的影响, 这里以坡度65°、含石量50%的松散体滑动堆积区为例. 在模拟软件中, 以坡脚线为基线沿颗粒主流运动方向每隔150 mm划分一个区域, 并自动获取每个区域的颗粒体积, 进而分析A1～A10的颗粒稀疏程度, 体积计算平面示意如图11所示.
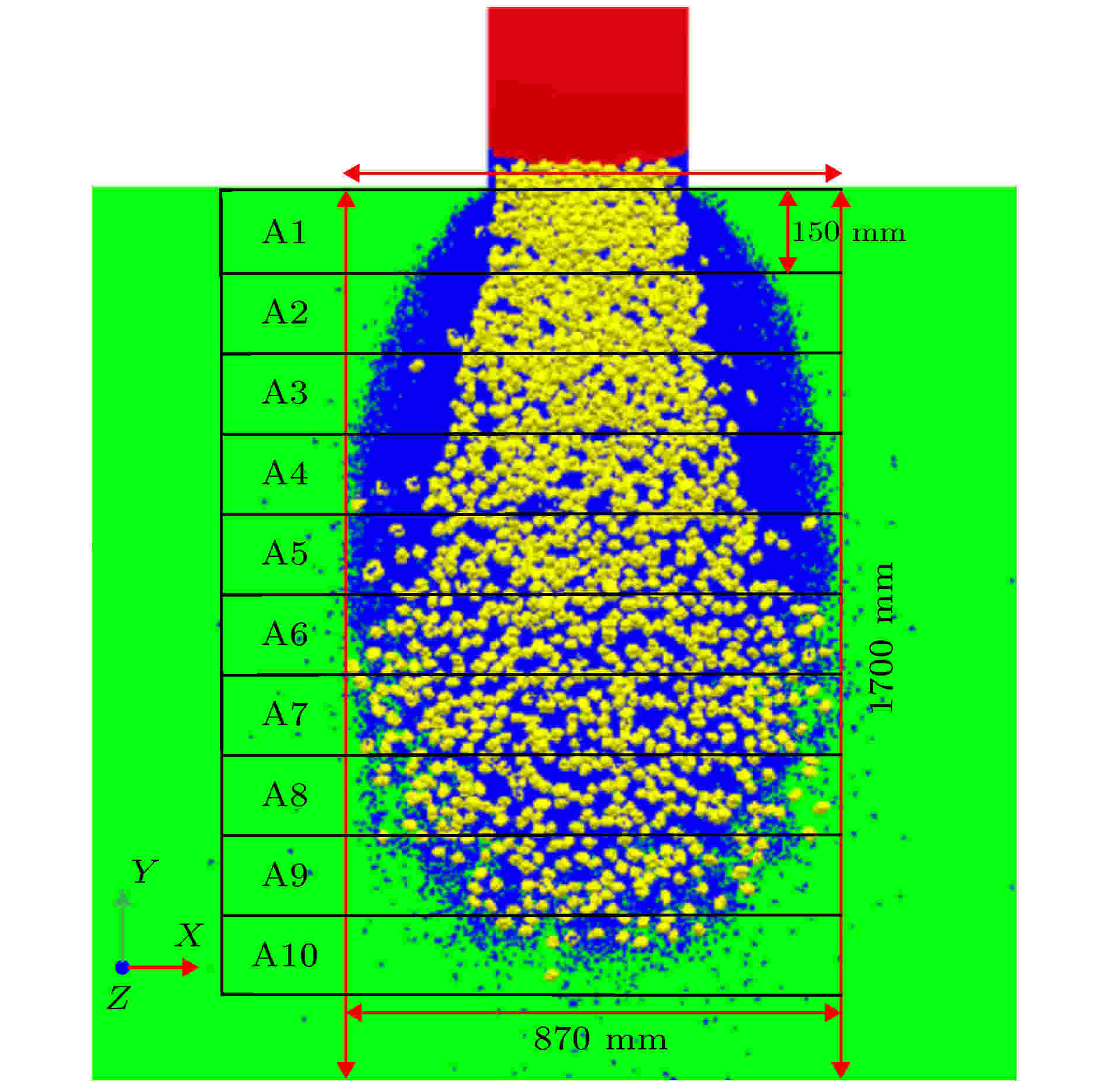图 11 堆积区体积计算平面示意图
Figure11. Schematic diagram of volume calculation of accumulation area.

由图12分析可知, 距离坡脚线越远, 颗粒堆体积逐渐减小, 颗粒越稀疏. 随着含石量增大, 堆积区体积有所下降, 但差异不明显; 其中含石量70%的体积最小, 下降速度最快. 主要原因是粗颗粒间的相互碰撞及粗颗粒与滑面的摩擦变化.
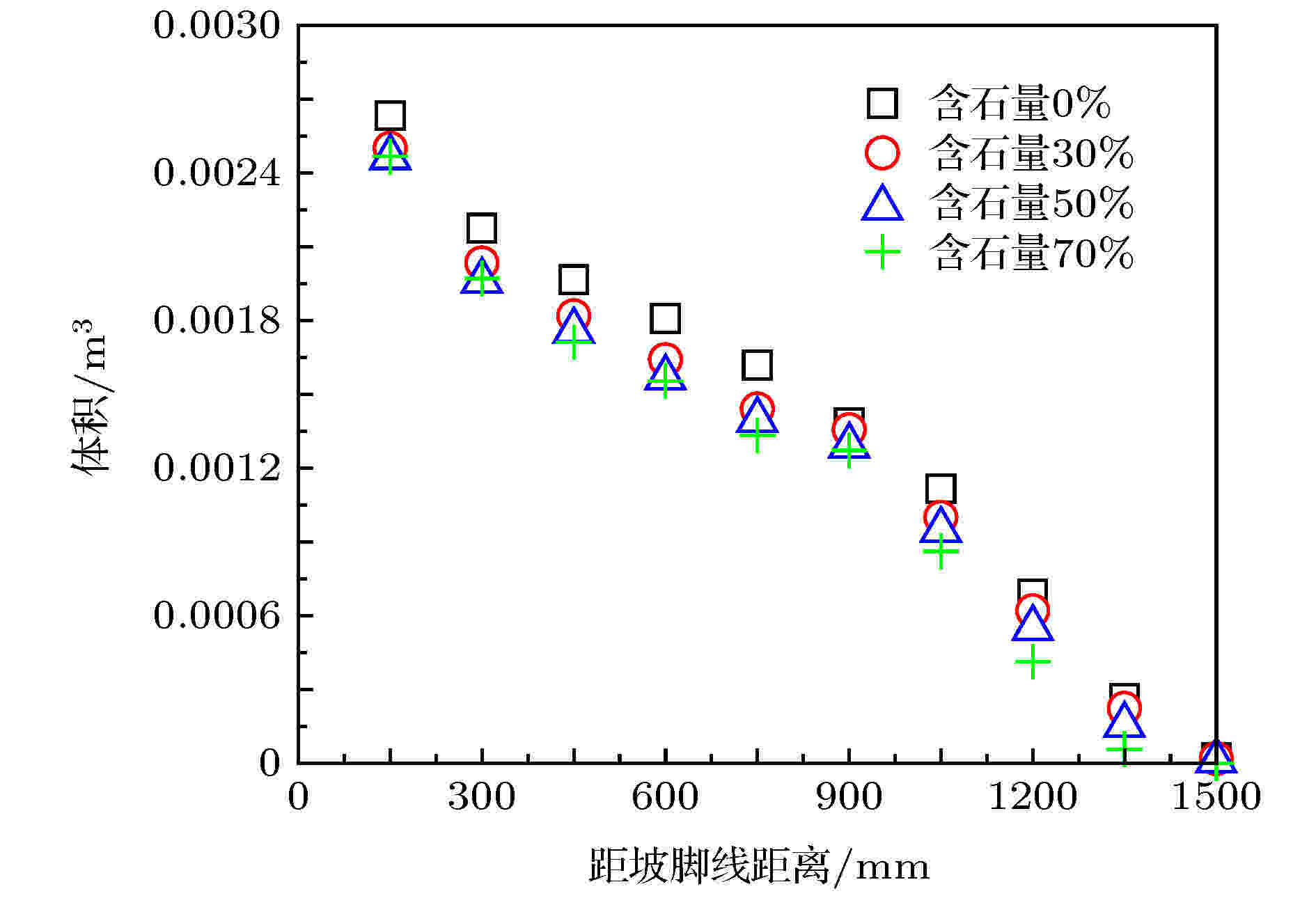图 12 坡度65°时不同含石量对堆积体积的影响
Figure12. Influence of different stone contents on the accumulation volume at a slope of 65°.

2 -->

3.3.坡度对堆积特性的影响

图13给出的是坡度对最终堆积特征值的影响. 由图13分析可知, 虽然坡长相同代表滑槽的滑动距离相同, 但颗粒的势能随坡度的增大而增大, 重力势能转化为更大的动能. 这就使得相应的冲程, 堆积宽度, 堆积面积都有不同程度的增大, 而最大厚度呈减小趋势; 这一结论与文献[7]中的相关结论基本相符, 同时也说明了颗粒形状相较于坡度对堆积特性的影响较小. 其中, 冲程和堆积面积呈线性增大; 堆积宽度随坡度增大, 增长趋势变缓. 坡度影响堆积特性的主要原因是: 坡度越小时, 坡高越小, 颗粒作用在滑面上的自重力及受到滑面的摩阻力相对增大, 导致颗粒能量损失增大; 此外, 坡度越小的颗粒运动速度和冲击能力较小, 即是说后缘颗粒无法推动或跃过前缘颗粒向前运动.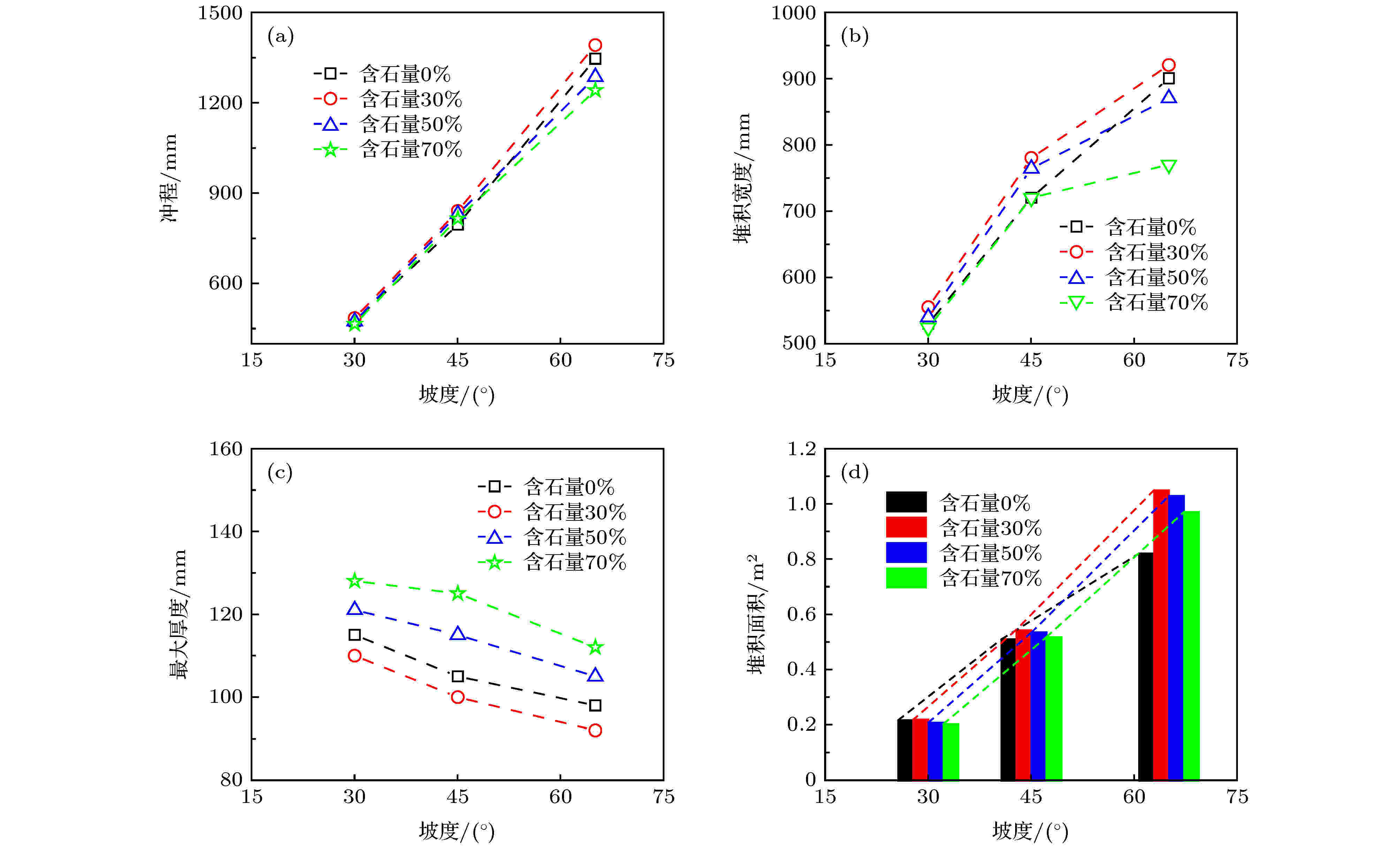
图 13 坡度对堆积形态的影响　(a) 冲程; (b) 堆积宽度; (c) 最大厚度; (d) 堆积面积
Figure13. Influence of slope on the accumulation form: (a) Stroke; (b) accumulation width; (c) maximum thickness; (d) accumulation area.

在以上关于含石量变化对静堆积角以及颗粒流动性的分析时, 发现坡度变化对静堆积角的影响显著, 且随着坡度增大, 静堆积角呈递减趋势; 这就反映了坡度越大的散体颗粒流动性越好. 为了深入研究坡度因素与静堆积角的相关关系, 在其他参数不变的情况下, 对表2中的静堆积角γ均值与坡度θ进行多项式拟合, 得到如下关系式

$\left.\!\!\begin{array}{l} \gamma = 0.0015{\theta ^2} - 0.4655\theta + 26.131,\;\;{R^2} = 1,\sigma = 0\\ \gamma = 0.0054{\theta ^2} - 0.8249\theta + 33.304,\;\; {R^2} = 1,\sigma = 30 \\ \gamma = 0.0046{\theta ^2} - 0.731\theta + 30.697 ,\;\; {R^2} = 1,\sigma = 50 \\ \gamma = 0.0012{\theta ^2} - 0.3681\theta + 21.589 ,\;\; {R^2} = 1,\sigma = 70\end{array}\!\!\right\}.$

从建立的静堆积角γ均值与坡度θ值的关系模型((21)式)可以看出, 采用二次函数拟合时, 得到的相关性系数R²均为1, 说明静堆积角与坡度的相关性关系程度极强, 几乎不受含石量变化的影响; 同样, 在一定条件下, 这种关系模型可以从散体颗粒流动性的基本物理特性角度出发为该类松散体滑动后的静堆积角对坡度的响应提供预测模型.
图14表明, 随着坡度增大, 堆积轮廓平面形状由近似圆状趋于近似椭圆状, 主要是因为颗粒堆冲程的延伸性较堆积宽度显著. 同时也说明坡度比含石量对堆积轮廓平面形状影响明显.
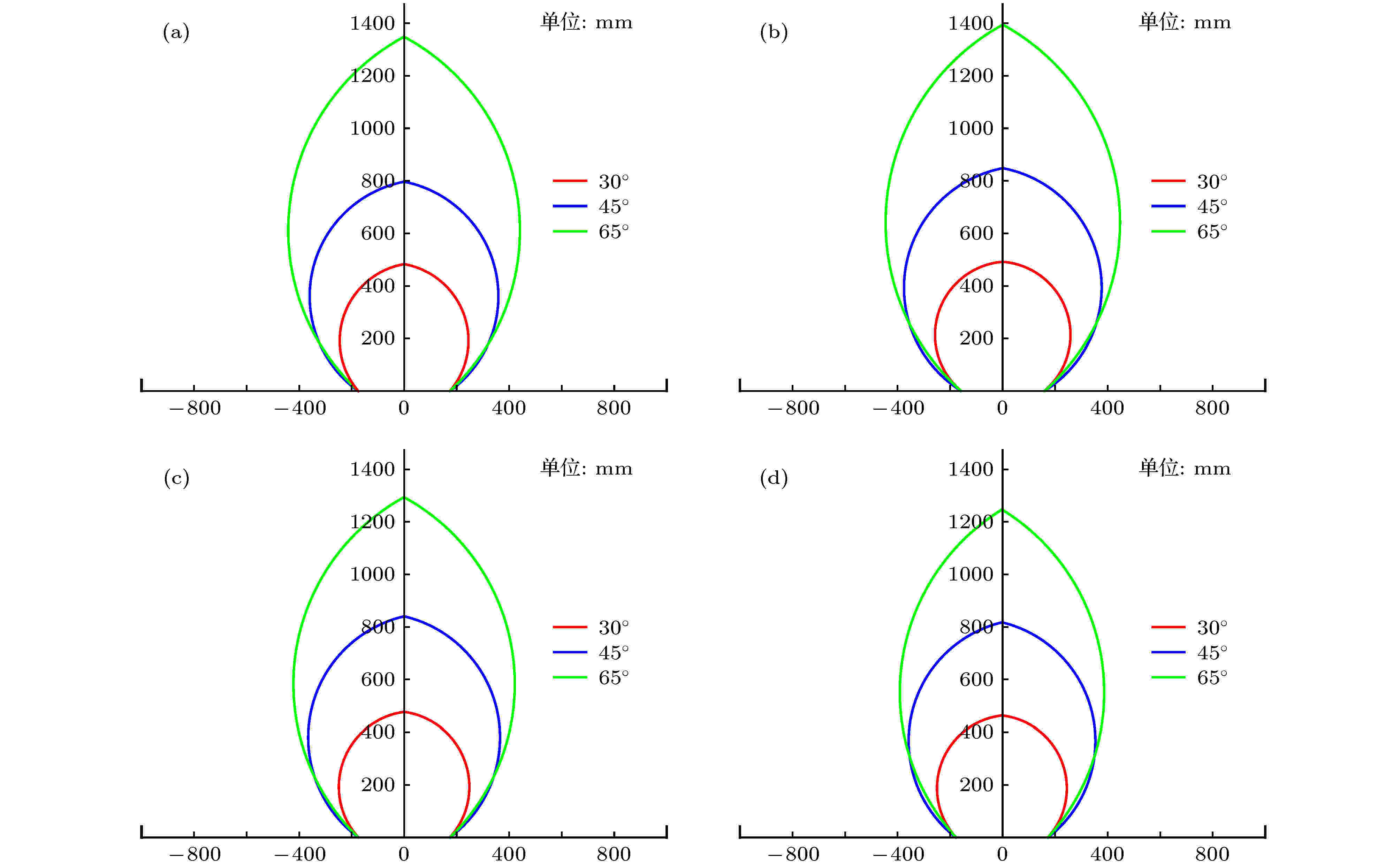图 14 不同坡度下的堆积轮廓平面形状　(a) 含石量0%; (b) 含石量30%; (c) 含石量50%; (d) 含石量70%
Figure14. Plane accumulation morphology under different slope: (a) Stone content 0%; (b) stone content 30%; (c) stone content 50%; (d) stone content 70%.

由图15可以观察到, 无论何种坡度下, 堆积区颗粒的稀疏程度由后缘往前缘逐渐增大; 随着坡度增大, 颗粒的稀疏程度更加明显. 其中, 细、粗颗粒在堆积区中的分布各异, 坡度较小时, 粗颗粒大部分均匀分布在细颗粒表层; 随着坡度增大, 粗颗粒的分布路径趋于冲积扇, 这一现象与现实中的沟谷碎屑流堆积相似. 说明粗颗粒较细颗粒的运动更加活跃, 平均冲击与携带能力更强.
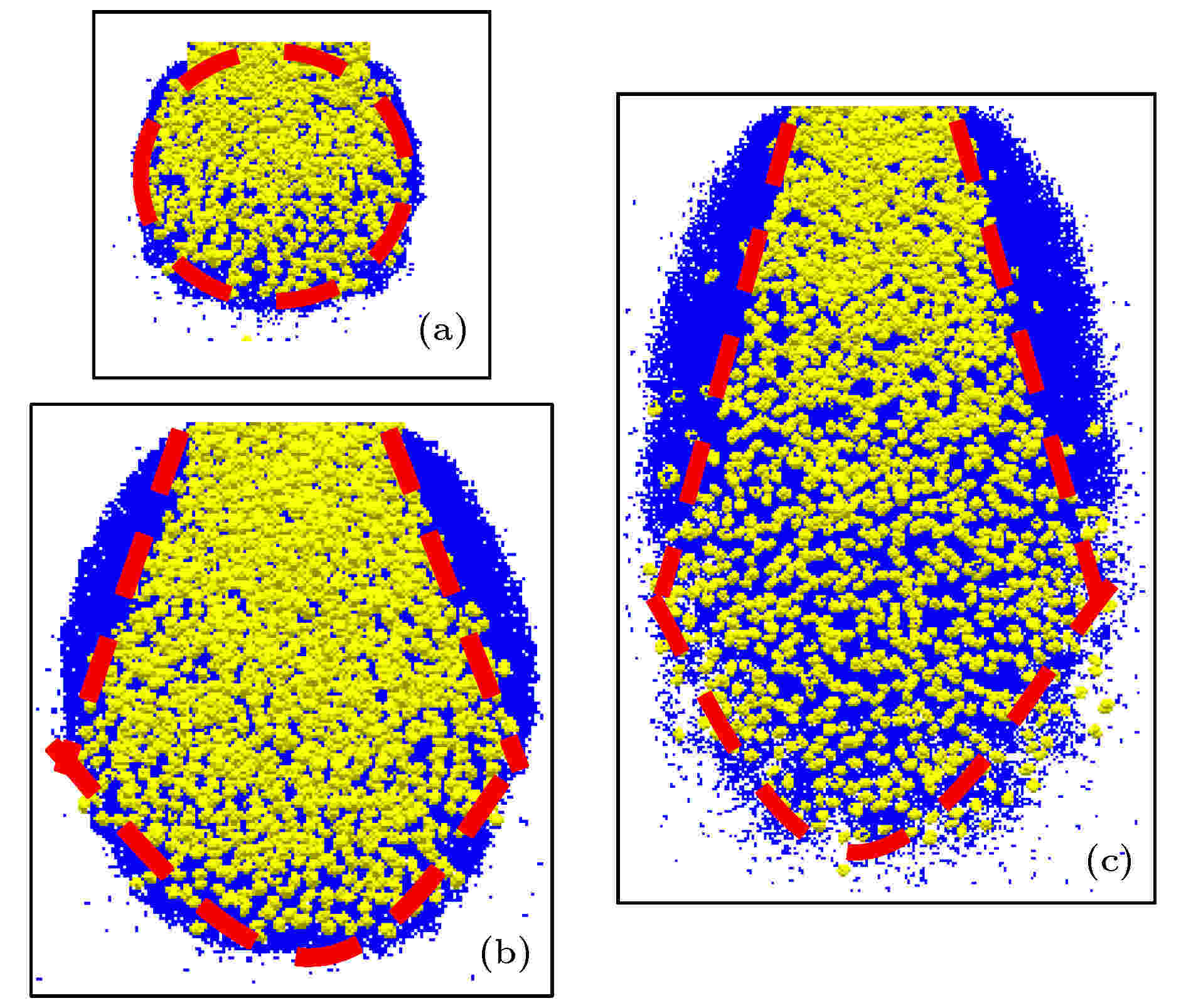图 15 含石量50%时不同坡度松散颗粒滑动堆积模拟结果　(a) 30°; (b) 45°; (c) 65°
Figure15. The results of the sliding accumulation simulation of stone content 50% loose granular with different slopes: (a) 30°; (b) 45°; (c) 65°.

图16为含石量50%的松散体在不同坡度下滑动后的体积计算结果. 分析可知, 当坡度为30°和65°时, 距离坡脚线越远, 颗粒堆体积逐渐减小, 颗粒越稀疏; 坡度45°时, 颗粒堆体积在坡脚线附近形成隆起区, 当距离持续增大, 颗粒堆体积依然逐渐减小.
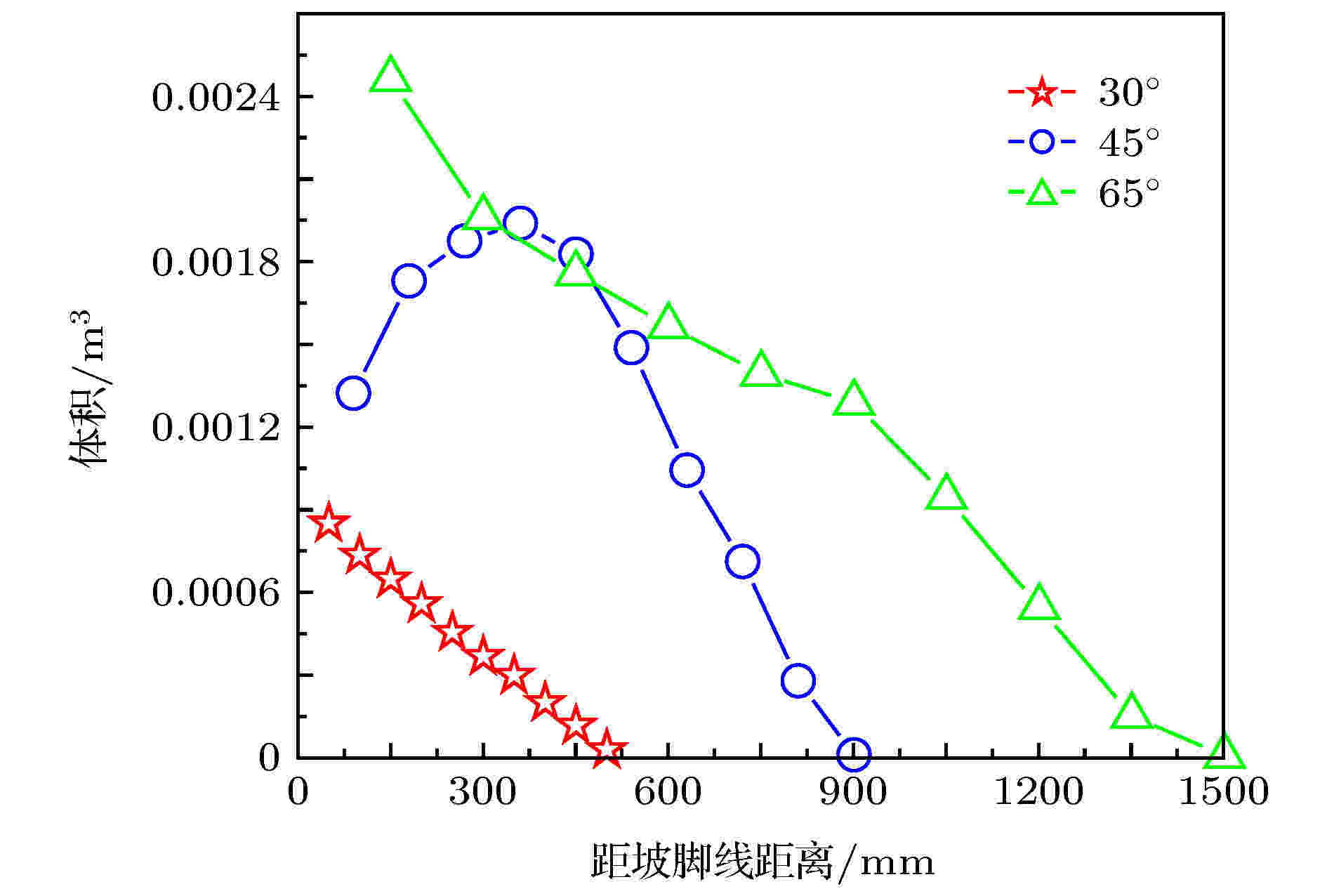图 16 含石量50%时不同坡度对堆积体积的影响
Figure16. Influence of different slope of 50% stone content on the accumulation volume.

进一步分析初始松散体中相同比重的粗、细颗粒分别在堆积区体积中的占额, 如图17所示. 可以观察到, 粗、细颗粒的体积占额均出现一个临界距离L_c, 当距坡脚线距离L < L_c时, 细颗粒大于粗颗粒所占体积; 当L > L_c时, 粗颗粒反而较细颗粒体积大; 坡度越大, L_c值越大, 即距离坡脚线越远. 说明粗颗粒的平均位移能力较细颗粒大, 换句话说, 粗颗粒较细颗粒平均运动距离更远. 此外, 由于实际的松散体滑动堆积形式和运动过程十分复杂, 与颗粒的能量耗散和接触力等因素, 以及颗粒材质、粒径和堆积体密集度等因素联系紧密; 因此, 不同边界计算条件下的临界距离存在差异.
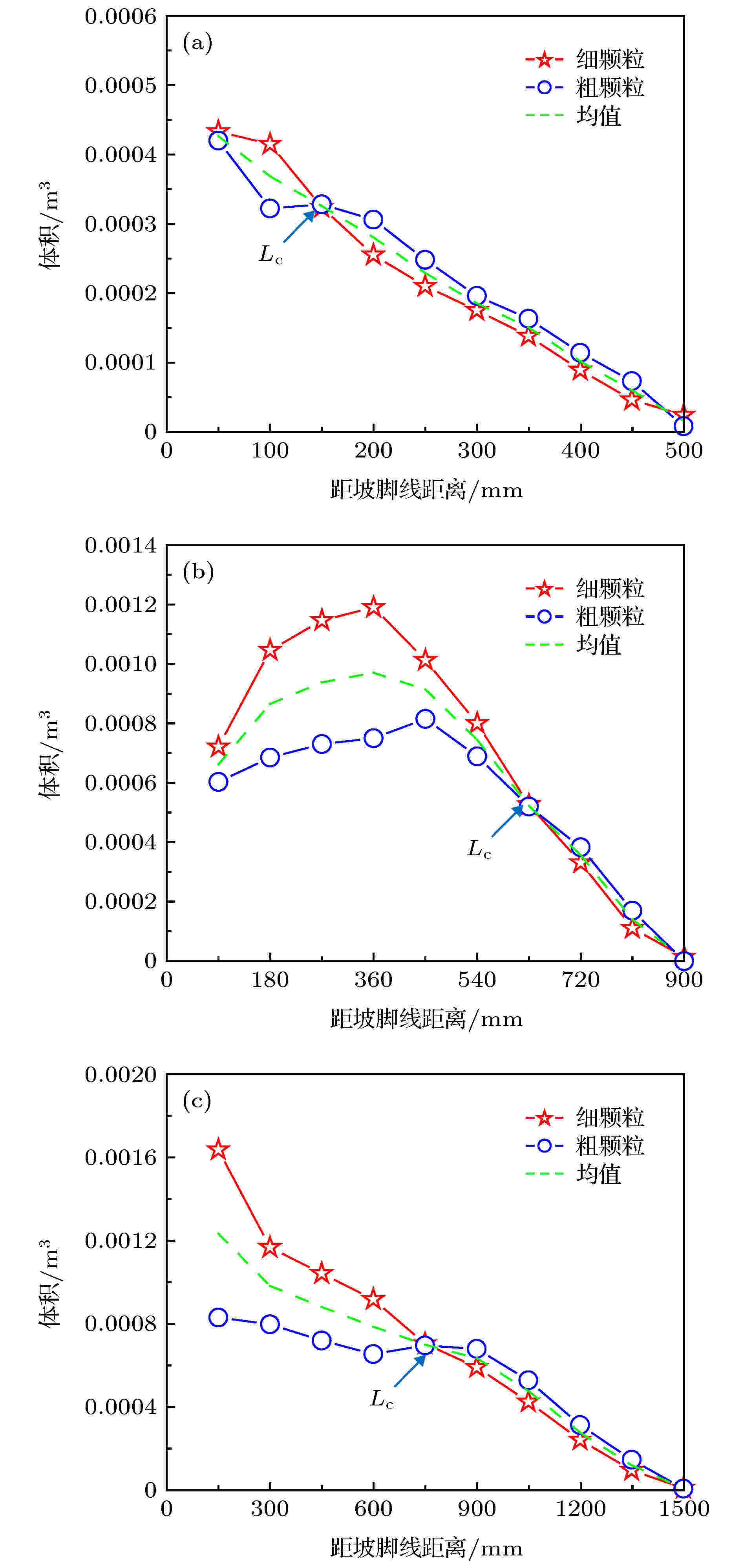图 17 含石量50%时不同坡度颗粒体积对比　(a) 30°; (b) 45°; (c) 65°
Figure17. The volume comparison of granular with different slopes with 50% stone content: (a) 30°; (b) 45°; (c) 65°.

2 -->

3.4.含石量和坡度对堆积区颗粒质量补给的影响

累积质量或累积体积常用于表征松散体滑动后对河流堵塞程度或公路掩埋等的影响^[6,30]. 图18给出的是同一坡度下, 不同含石量的松散体对堆积区颗粒累积质量供应时程曲线. 分析可知, 含石量为30%, 50%和70%时, 松散体几乎同一时间开始对堆积区进行颗粒质量供给, 累积质量曲线增长速度基本一致; 在达到稳定值时, 含石量越大, 堆积区的颗粒累积质量越小.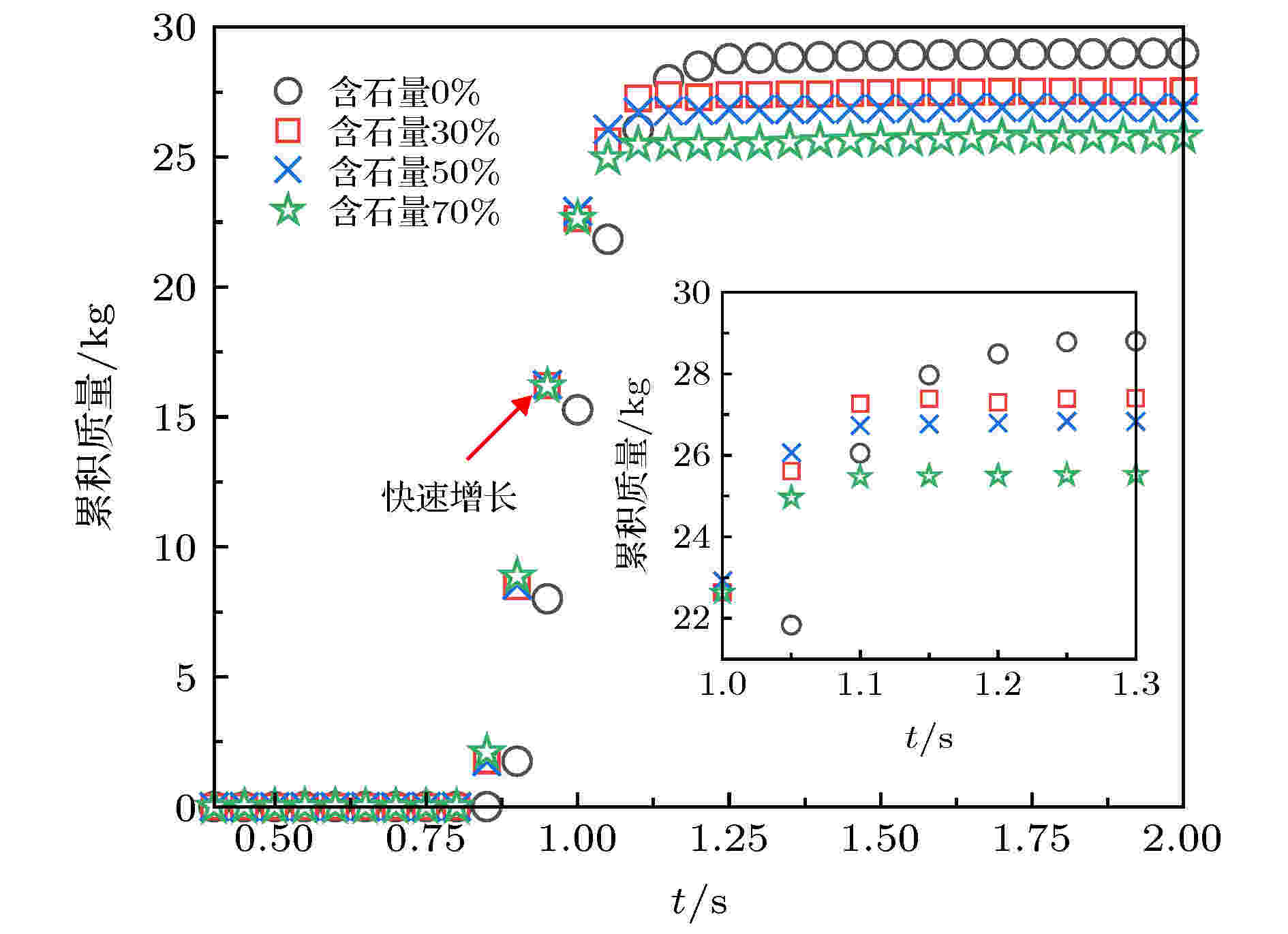
图 18 坡度65°时不同含石量对累积质量的影响
Figure18. Influence of different stone contents on cumulative mass at slope of 65°.

图19给出的是同一含石量下, 不同坡度的松散体对堆积区颗粒累积质量供应时程曲线. 分析可知, 坡度越小的松散体对堆积区的颗粒质量供给开始时间越晚, 且供给持续时间越长; 随着坡度增大, 累积质量曲线的增长率越大. 在达到稳定值时, 坡度越大, 堆积区的颗粒累积质量越大; 其中, 坡度为30°—45°的颗粒累积质量增幅十分显著, 当坡度持续增大时, 增幅趋于平缓.
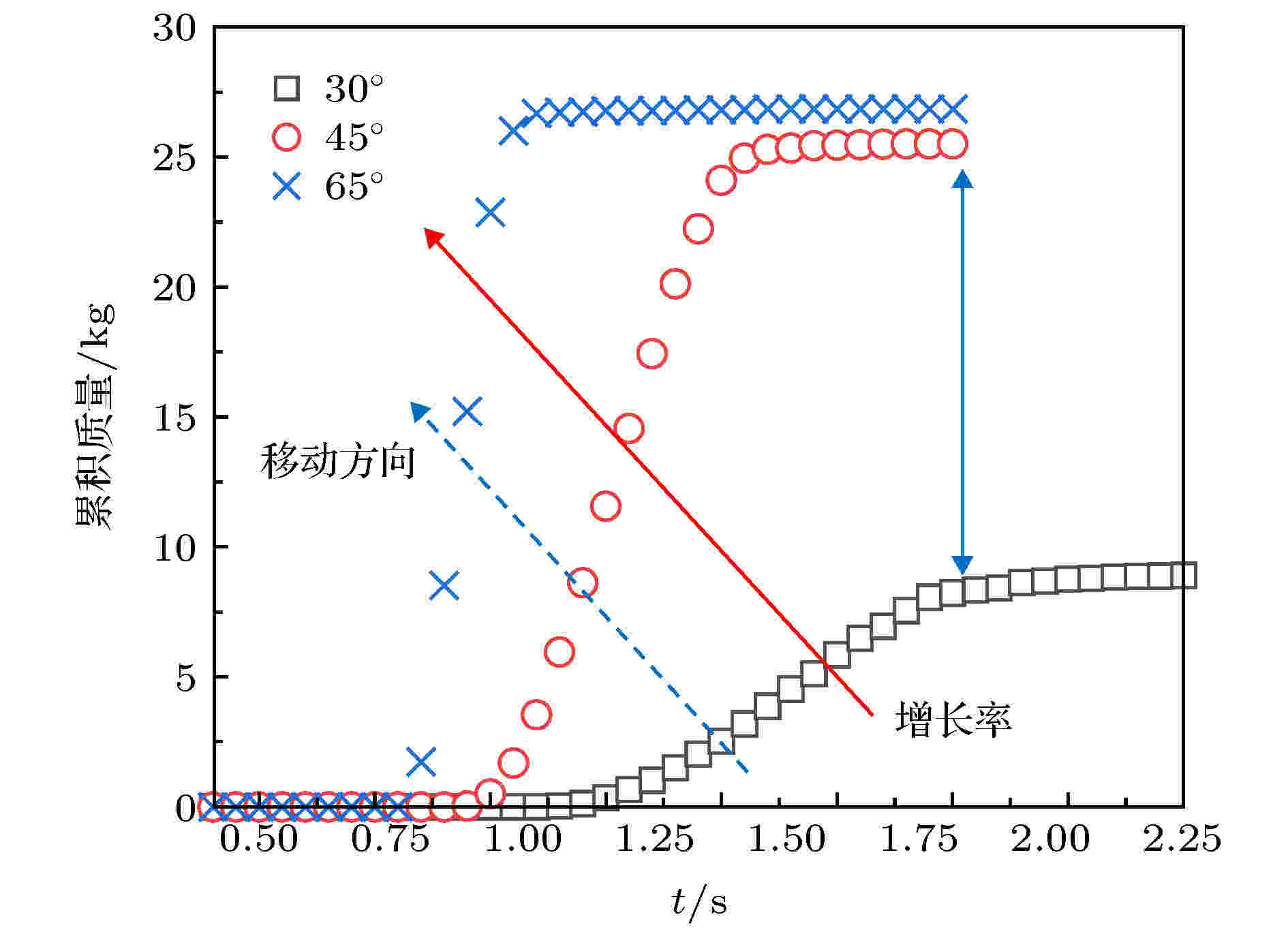图 19 含石量50%时不同坡度对累积质量的影响
Figure19. Influence of different slope on cumulative mass at stone content of 50%.

进一步分析松散体中相同比重的粗、细颗粒分别在堆积区颗粒累积质量供给中的占额, 如图20所示. 这里定义粗、细颗粒的累积质量差值最早大于0.5 kg的时间点作为二者累积质量占额的分异点. 图20表明, 当坡度为30°时, 粗、细颗粒在堆积区的颗粒累积质量供给差异很小, 无分异点; 随着坡度增大, 粗、细颗粒的分异点出现时间越早; 达到稳定值时, 细颗粒的累积质量供给大于粗颗粒, 但随坡度增大, 二者间的差距有缩小趋势. 主要是由于细颗粒摩擦力较小, 整体滑动性好; 而粗颗粒运动十分活跃, 除了消耗自身能量, 也会使得细颗粒获得一部分能量.
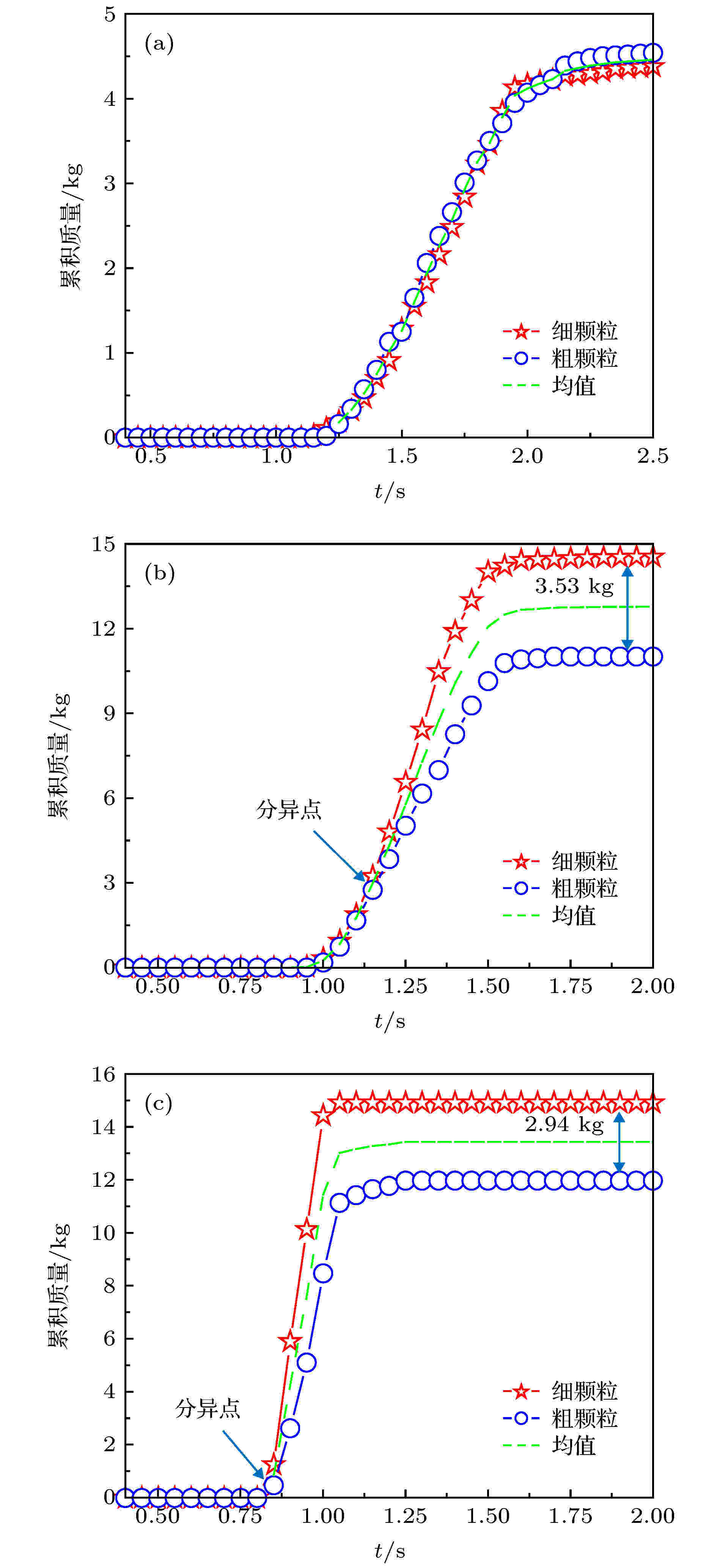图 20 含石量50%时各坡度颗粒累积质量对比　(a) 30°; (b) 45°; (c) 65°
Figure20. The cumulative mass comparison of granular with different slopes with 50% stone content: (a) 30°; (b) 45°; (c) 65°.

2 -->

3.5.颗粒堆积过程的动能与接触力分布特性

为探究松散体滑动堆积特性的内在机理, 以坡度为65°、含石量为50%的松散体为例, 分析颗粒滑动过程中的动能与接触力分布特性, 如图21—图25所示. 颗粒平均动能与平均接触力的均值见表3. 需要指出的是, 本文模拟的非球形(复合几何体)颗粒是由四个球形颗粒组成, 在文献[31]和文献[32]中的研究结论中, 认为基于球形的接触模型及其动能和接触力的统计方法可以用于对复合几何体颗粒的研究.

参量	细颗粒	粗颗粒	细颗粒与粗颗粒
平均平动动能Et/10–4 J	2.41	169.28	—
平均转动动能Er/10–7 J	4.66	26.03	—
平均法向力Fn/10–6 N	19.04	155.37	31.77
平均切向力Ft/10–3 N	6.84	55.37	11.36
平均法向重叠量/ 10–2 mm	4.01	10.13	4.77
平均切向重叠量/ 10–2 mm	1.05	2.87	1.27

表3滑动堆积过程中颗粒的平均动能和接触力均值
Table3.Average kinetic energy and contact force of granular in the process of sliding accumulation.

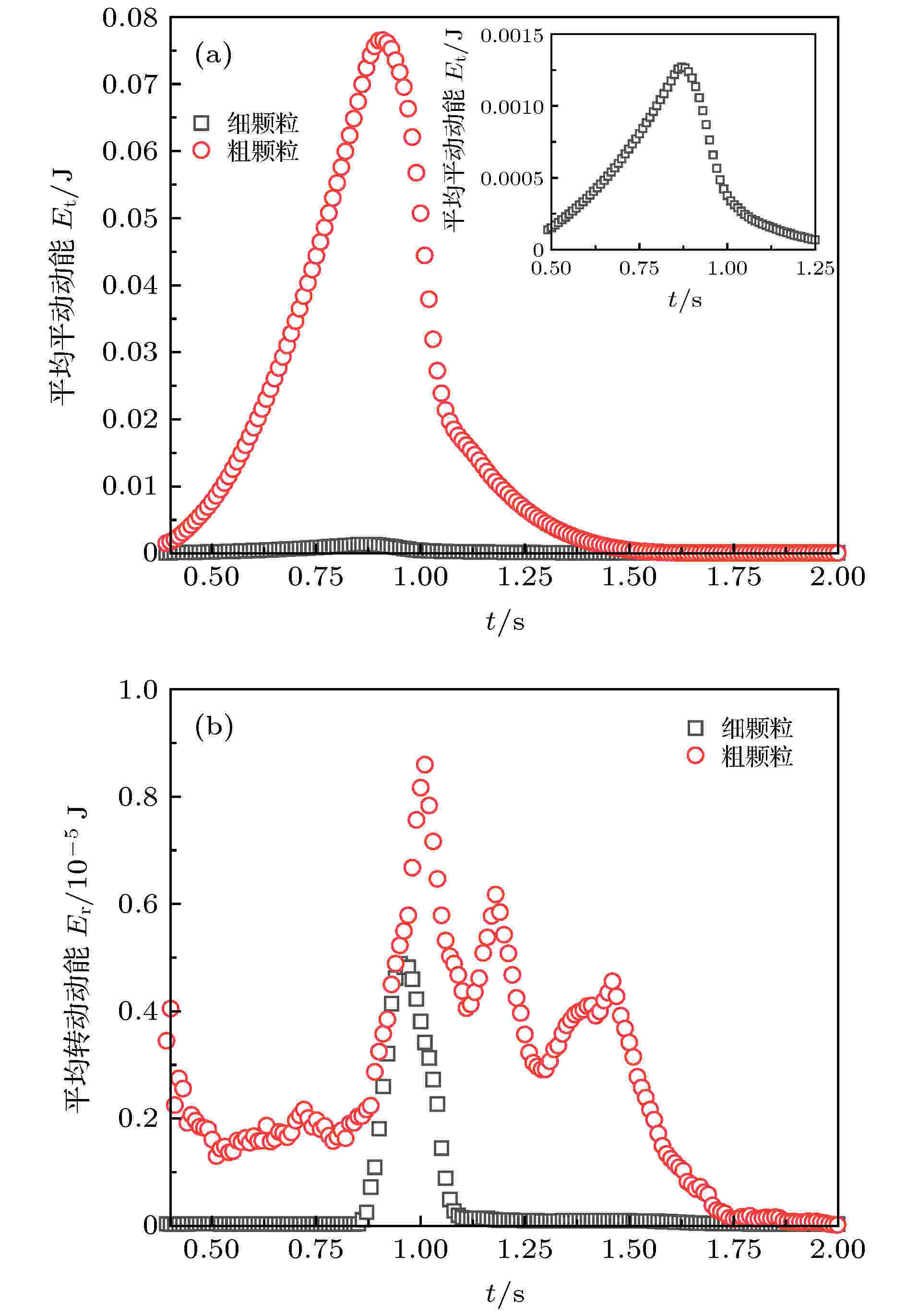图 21 颗粒平均动能分布特性　(a) 平动动能; (b) 转动动能
Figure21. Granular average kinetic energy distribution characteristics: (a)Translational kinetic energy; (b) rotational kinetic energy.

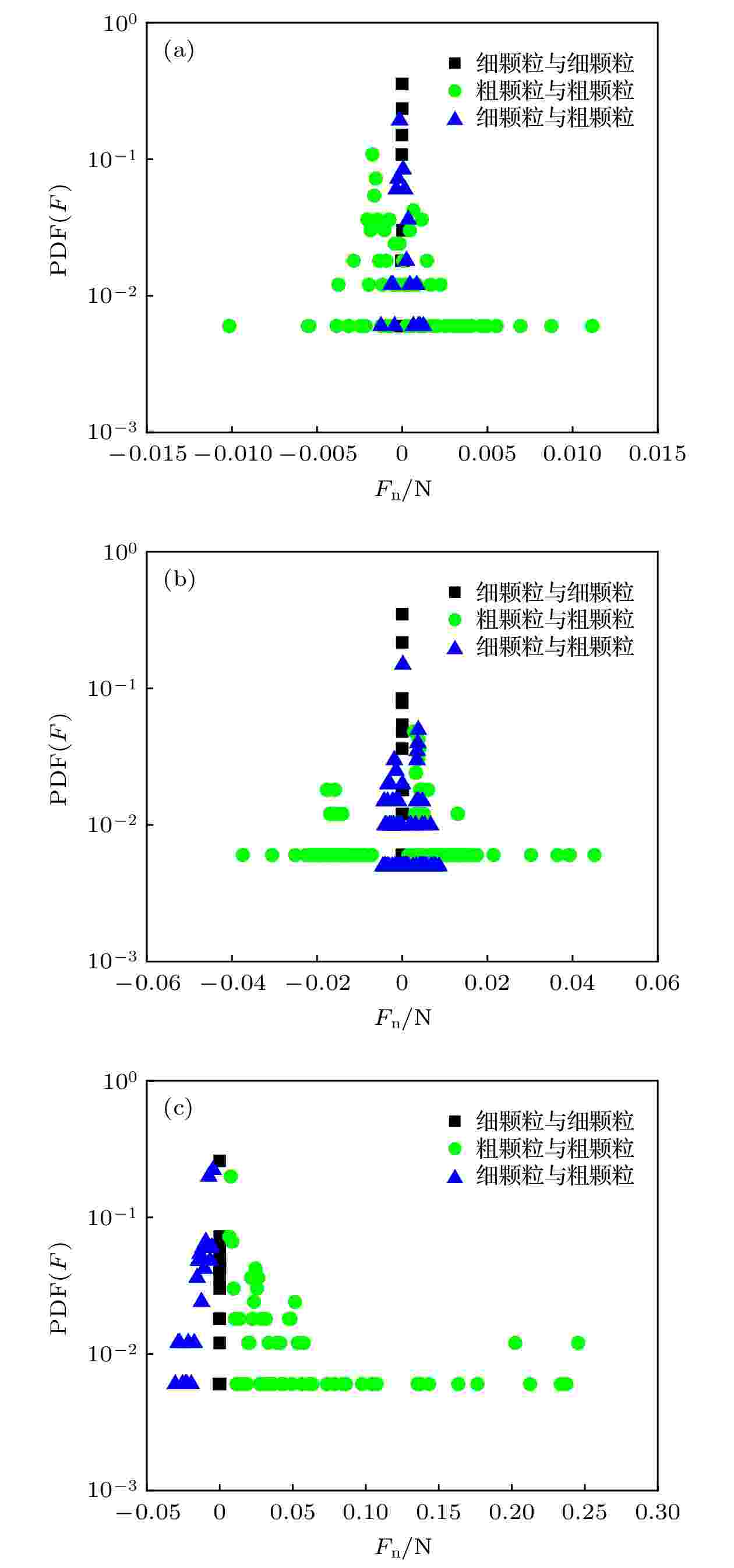图 25 颗粒间平均法向接触力概率密度函数(PDF)分布　(a) x方向; (b) y方向; (c) z方向
Figure25. Probability density functions (PDF) of average normal contact force between granulars: (a) x direction; (b) y direction; (c) z direction.

结合图21与表3可以看出, 粗颗粒的平均动能波动幅度最大, 说明粗颗粒的运动十分活跃, 从而为细颗粒的下渗提供足够的间隙, 当细颗粒相对位移后, 粗颗粒就变得更容易发生滚动或滑动. 颗粒的平动动能远远大于转动动能, 并且粗颗粒的平均动能及变化幅度均大于细颗粒的平均动能. 其中, 粗颗粒的平均平动动能均值最大, 达到了细颗粒的70.2倍, 粗颗粒的平均转动动能均值达到了细颗粒的5.6倍. 这就从能量角度解释了粗颗粒在堆积运动中较细颗粒更活跃的原因, 粗颗粒较细颗粒具有更大的能量, 动能衰减时间更长.
图22、图23给出的分别是颗粒相互作用时的平均法向接触力与平均切向接触力时程曲线. 结合表3分析可知, 颗粒间的法向力均为切向力的两倍多, z方向的法向力与切向力最大, y方向次之, x方向最小; 这符合颗粒运动主要沿水平和竖直运动, 同时也说明颗粒的横向运动不显著. 可以观察到, 粗颗粒间的接触力波动最剧烈, 其平均接触力均值约为细颗粒与粗颗粒间平均接触力均值的4.8倍, 约为细颗粒间平均接触力均值的8.1倍. 说明粗颗粒间的相互碰撞作用更明显, 滚动和转动运动十分活跃, 使得接触力及能量消耗较大. 细颗粒与粗颗粒的碰撞接触力主要是来自二者的相对位移运动, 而它们的接触力变化及力的传递形式较为复杂, 还有待进一步研究. 细颗粒间的接触力最稳定, 这就反映了细颗粒在整个运动中以滑动为主.
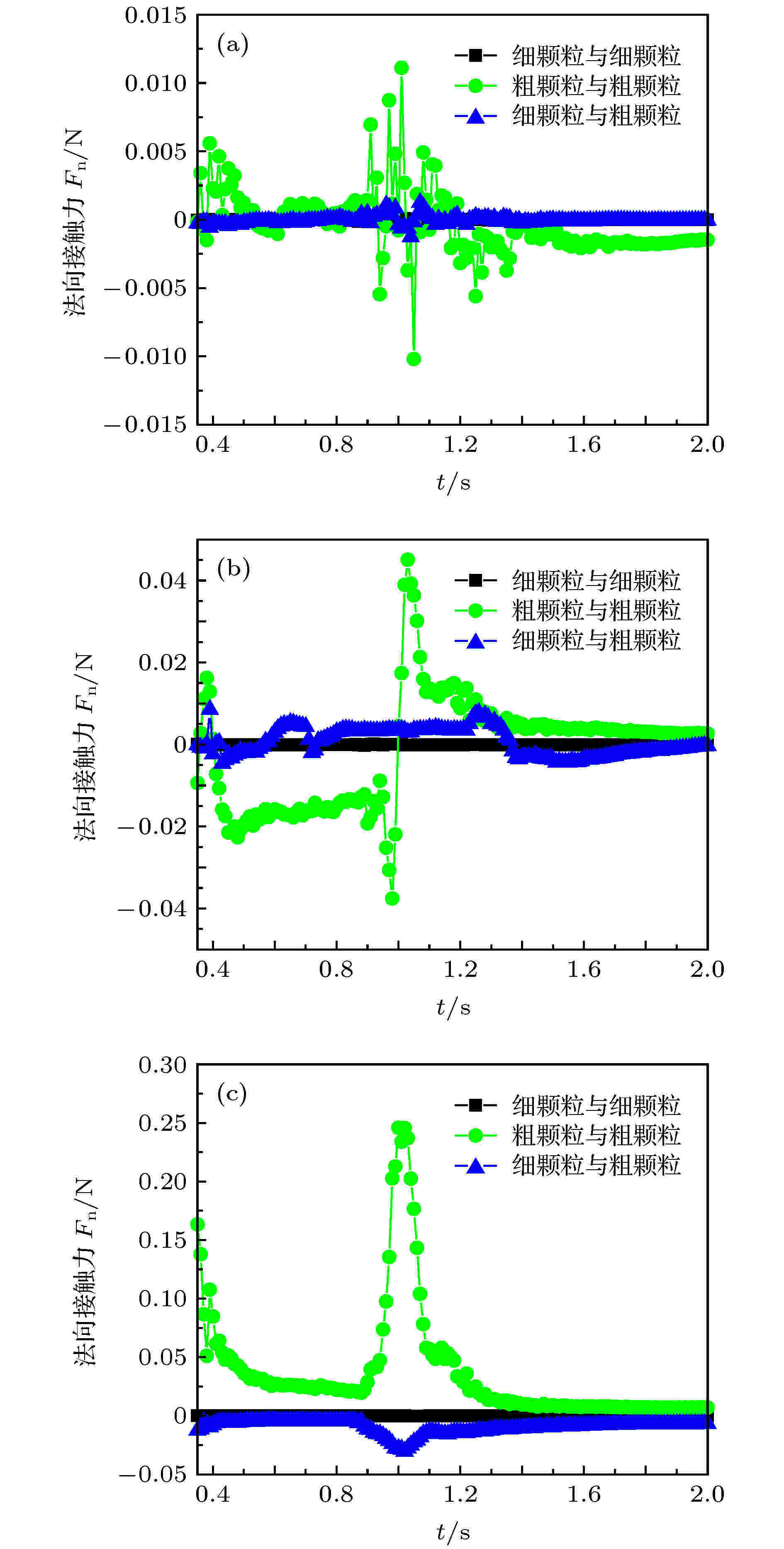图 22 颗粒间平均法向接触力时程曲线　(a) x方向; (b) y方向; (c) z方向
Figure22. Time-history curve of average normal contact force between granulars: (a) x direction; (b) y direction; (c) z direction.

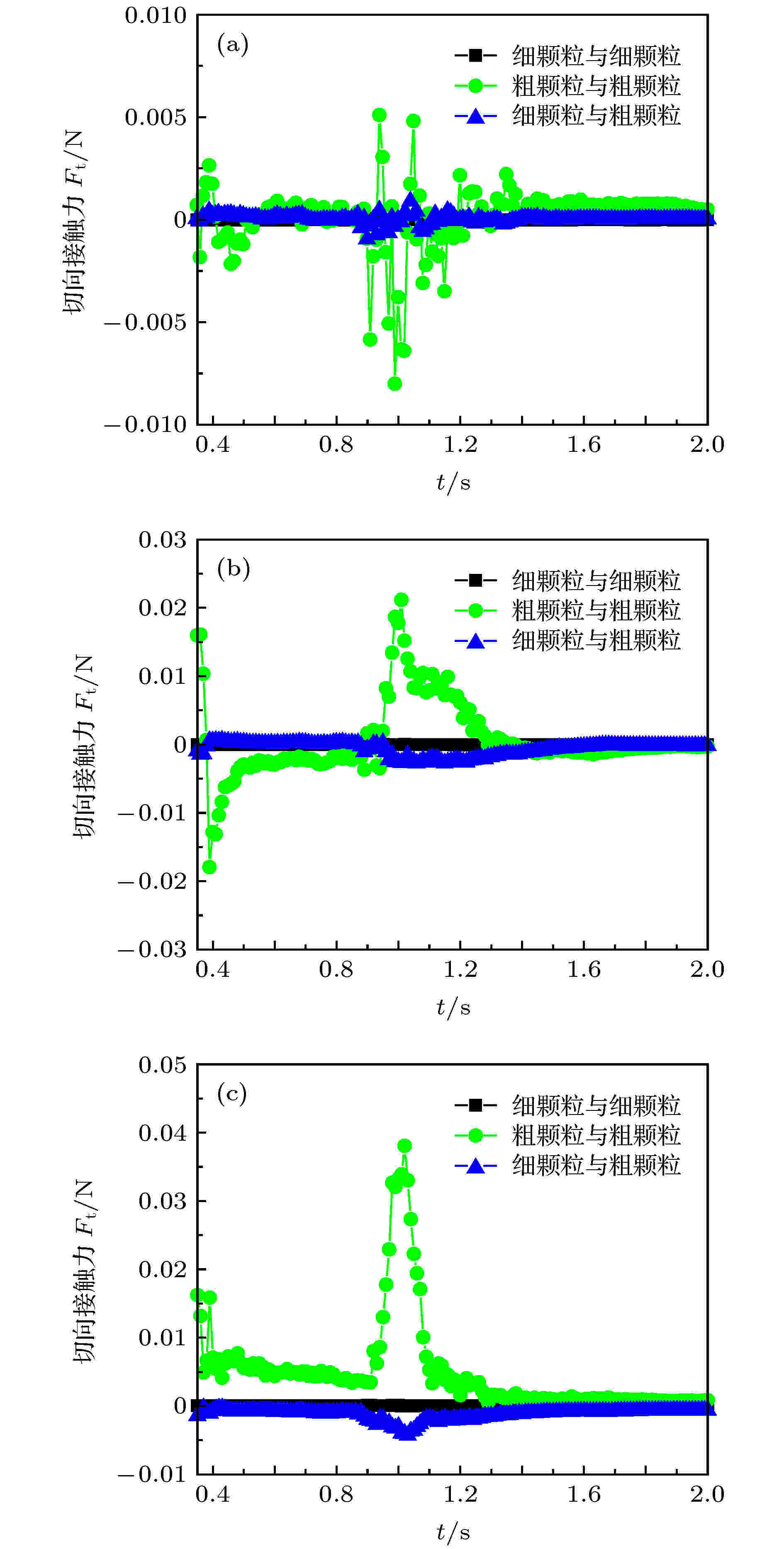图 23 颗粒间平均切向接触力时程曲线　(a) x方向; (b) y方向; (c) z方向
Figure23. Time-history curve of average tangential contact force between granulars: (a) x direction; (b) y direction; (c) z direction.

图24给出的是颗粒间平均法向接触力重叠量与平均切向接触力重叠量时程曲线. 可以观察到, 粗颗粒间的重叠量最大, 细颗粒与粗颗粒次之, 细颗粒间最小; 根据(4)式, 颗粒间的接触力随接触力重叠量α的增大而增大. 当大部分颗粒到达底板时, 接触重叠量达到最大, 法向重叠量约为切向重叠量的三倍多; 粗颗粒间的接触重叠量均为细颗粒间、细颗粒与粗颗粒间的两倍多; 说明颗粒的位移运动主要来自颗粒间接触的法向力. 最后稳定阶段粗颗粒间的接触重叠量最大, 验证了图17的结论, 粗颗粒较细颗粒的平均位移能力更强.
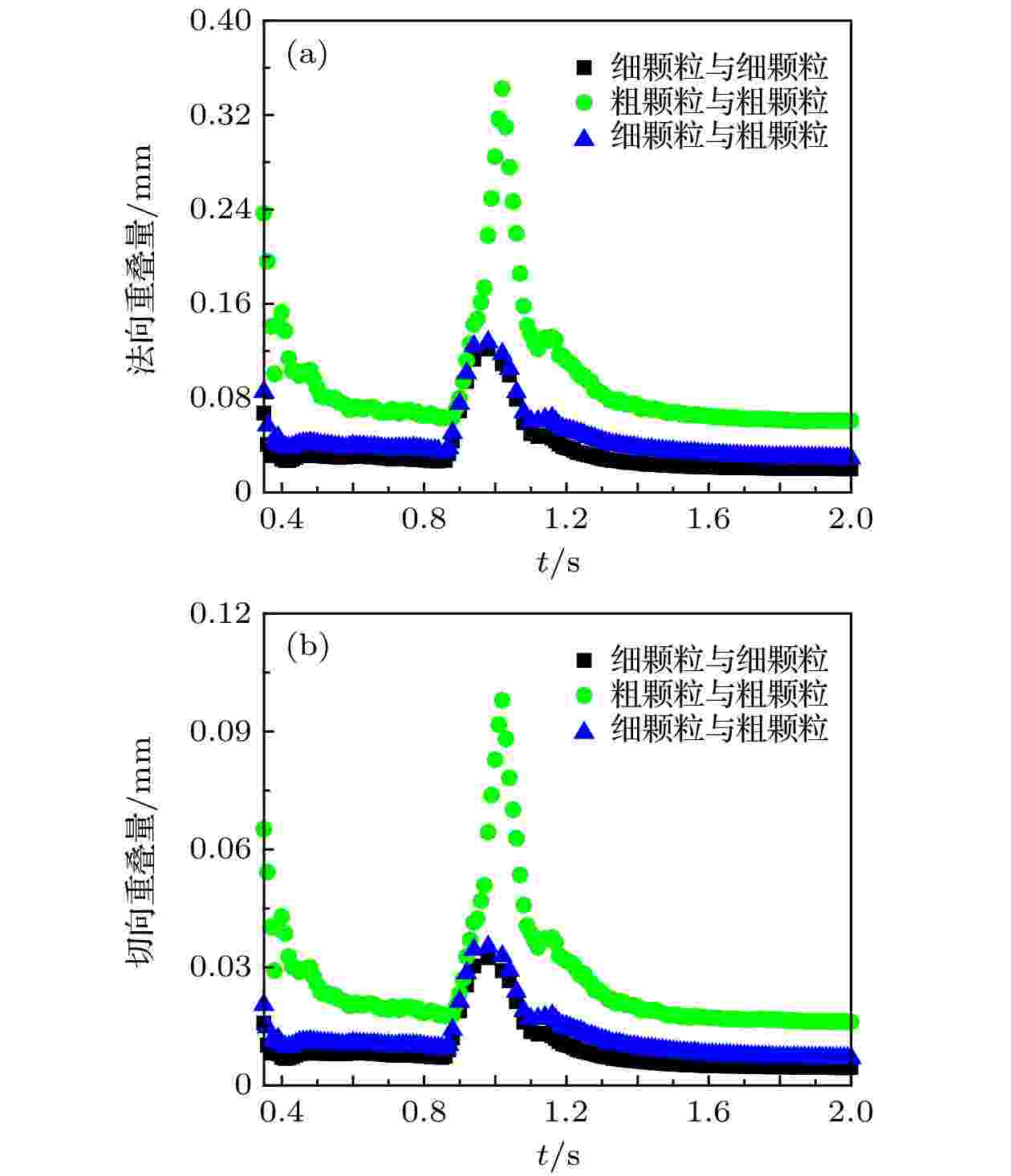图 24 颗粒间平均接触力重叠量时程曲线　(a) 法向; (b) 切向
Figure24. Time-history curve of average contact force overlap between granulars: (a) Normal; (b) tangential.

为了进一步从颗粒不同方向相互作用的细观接触力分布特性角度出发, 深入分析散体颗粒的滑动堆积特性, 故采用概率密度函数(probability density function, PDF)进行定量研究. 由于颗粒的切向接触力与法向接触力变化规律基本一致, 因此这里以分析法向接触力为主. 由图25分析可知, 法向接触力越大或越小时, 概率密度越小, 而在0附近的接触力概率密度越大; 可以观察到, 相比于粗颗粒间的作用力, 细颗粒与粗颗粒间、细颗粒间的接触力概率密度逐渐增大, 但力的分布宽度逐渐减小. 此外, 从接触力概率分布的复杂程度来看, 细颗粒间的概率密度分布比较稳定, x方向和y方向的粗颗粒间、细颗粒与粗颗粒间的概率密度分别在0附近对称分布; 而z方向则表现出粗颗粒间的概率密度均分布在0的右侧, 且随着接触力值的增大, 概率密度越小, 细颗粒与粗颗粒间的概率密度均分布在0的左侧, 随着接触力的减小, 概率密度越小. 上述数据分析表明了一个有趣的可能, 在更大的松散颗粒体系滑动运动中, 细颗粒间的接触力长度较短或趋于点状并位于颗粒流底层; 细颗粒与粗颗粒间的接触力形式变化复杂, 可能存在耦合作用, 使得一定的细颗粒作用在粗颗粒周围; 在z方向上的粗颗粒间接触力或许存在一个临界值, 接触力小于临界值的概率密度呈指数函数分布, 接触力大于临界值的概率密度则呈幂函数分布.
2 -->

3.6.小　结

将上述含石量和坡度对松散体滑动后堆积特性的影响规律汇总, 见表4.

模拟变量	模拟结果
	冲程	堆积宽度	最大厚度	堆积面积	累积质量	静堆积角
含石量	↗↘	↗↘	↘↗	↗↘	↘(较小)	↘(较小)或↗(较小)
坡度	↗↗	↗	↘	↗↗	↗↗	↘↘
注: 1. 表中所考虑的均是模拟变量数值增大对模拟结果的影响; 其中, 含石量σ (%)的取值分别为0, 30, 50, 70; 坡度θ (°)的取值分别为30, 45, 65. 2. “↗”表示模拟结果持续增大, “↘”表示模拟结果持续减小; “↗ ↘”表示模拟结果先增大后持续减小, “↘ ↗”表示模拟结果先减小后持续增大, “↗ ↗”表示模拟结果增大明显, “↘ ↘”表示模拟结果减小明显, “↘(较小)”表示模拟结果小幅度减小, “↗(较小)”表示模拟结果小幅度增大.

表4模拟结果汇总表
Table4.Summary table of simulation results.

本文基于DEM, 探究了不同含石量和坡度对松散体滑动后堆积特性的影响, 主要结论如下:
1)相同坡度, 随着含石量增加, 松散体最终堆积区的冲程、堆积宽度和堆积面积均表现为先增大后减小, 而最大厚度则是先减小后增大. 含石量对堆积区轮廓平面形状的影响较小, 最终累积质量随含石量的增加而减小.
2)相同含石量, 随着坡度增大, 松散体最终堆积区的冲程、堆积宽度、堆积面积和累积质量均会变大, 而最大厚度近似线性减小. 坡度对冲程、堆积面积和平面堆积轮廓形状的影响显著, 平面堆积轮廓由近似圆状趋于近似椭圆状.
3)相比于含石量, 坡度对静堆积角的影响更加显著, 且随坡度的增大而减小, 颗粒的流动性越佳. 含石量、坡度与静堆积角的拟合关系模型表明, 在一定条件下, 可为静堆积角对含石量、坡度的响应提供预测模型.
4)堆积区体积计算中, 粗、细颗粒的体积占额存在一个临界距离L_c, 当距坡脚线距离L < L_c时, 细颗粒大于粗颗粒所占体积; 当L > L_c时, 粗颗粒反而较细颗粒体积大; 坡度越大, L_c值越大. 堆积区累积质量计算中, 坡度越大, 粗、细颗粒累积质量占额分异点出现越早.
5)最后, 对颗粒滑动与堆积过程的平动动能和转动动能进行了讨论, 详细分析了颗粒间不同方向、不同颗粒间的接触力及其概率密度分布特性; 从而在细观尺度上探讨了松散颗粒滑动与堆积运动的内在机理.
本文的研究结论是在组合球模拟非球形颗粒的基础上所得出的. 由于研究重点主要是含石量和坡度变化对松散颗粒物理堆积特性的影响, 因此并未深入考虑颗粒形状因素对研究结果的影响. 颗粒形状特别是研究复杂颗粒对其物理堆积特性、动力学行为及接触力学的影响, 一直是作者研究的重点方向之一, 更多的研究工作正在进行中, 以期研究结论更具普适性, 进而为颗粒的物理机制揭示工程地质行为提供更为现实的参考价值.