全文HTML
--> --> -->在电场分布极不均匀的空间发生的局部自持放电现象为电晕放电. 对于电晕放电早在1938年Trichel[6]就进行了研究, 分析了其放电机理, 并发现其放电电流为脉冲电流, 且此脉冲只存在于电负性气体中, 并随着负离子的产生与消散不断建立. 2012年, Liao等[7]基于流体动力学方程对电晕放电过程进行分析, 研究了重离子对放电的影响, 指出负离子对放电起抑制作用. 2013年, Zheng等[8]就放电过程中带电离子的时空行为规律及空间电场的发展规律进一步对电晕放电进行了研究. 目前, 国内外文献描述电晕放电微观过程的理论较为成熟, 但其反应空间最小为毫米级, 对本文微尺度下反应空间的使用价值有待进一步验证; 且本课题组[9-11]长期研究微纳电离式气体传感技术, 探索了以N2为背景气体下此传感器对NO和CH4等气体的放电特性与敏感机理, 但其在仿真时使用的是一维简化放电模型[11], 忽略了离子的横向漂移与扩散和分子的横向扩散, 对此本文建立二维空间放电模型进行分析. 就电离式气体传感器而言, 旨在通过宏观参数即电压和电流曲线来判断气体种类与浓度, 但此类传感器存在输出电流较小, 容易受到干扰信号影响的缺陷, 因此研究空间电流的形成过程、并通过改变其形成过程的影响因素来提高器件的输出电流, 这对电离式气体传感器的优化具有非常重要的现实意义.
为此, 本文以国内外文献中纳米管的参数为参考依据[12,13], 基于流体-化学动力学混合方法建立了二维微纳级棒-板电晕放电模型, 并以常温常压下大气中N2-O2混合气体为背景进行仿真计算. 并且由于本文针对的是击穿之前的局部自持放电, 即放电强度较为微弱, 且放电间隙较大, 因此忽略了场致发射[14]和光电离效应对放电过程的影响, 重点研究放电过程中的电离反应, 重离子反应以二次电子发射等物理过程. 以国内外现有的分析方法与结论为基础[15—27]分析了空间电子输运机制、放电电流密度、正负离子分布以及空间电场畸变程度的相互耦合关系, 阐明了微米间隙、纳米尖端下空间放电的动态发展过程, 并为了提高传感器输出性能进一步研究了不同极间距对放电电流密度的影响.
2.1.控制方程
本文在传统流体动力学模型中加入了等离子体的化学反应模型对气体放电空间进行仿真, 在仿真中考虑到电子碰撞反应、电离反应、重离子反应和二次电子发射的微观过程. 因此本文采用的控制方程为电子连续控制性方程为
电子动量方程为
电子能量守恒方程为[28]
重粒子(正负离子、中性粒子)连续控制性方程为
Poisson方程为
2
2.2.化学反应类型
以空气作为空间电离的主要气体, 由于空气中N2比例为78%, O2为21%, 因此背景气体及其比例为
| 类型 | 序号 | 反应式 | 反应速率 | 参考文献 |
| 电子碰撞反应 | R1 | ${\rm{e}} + {{\rm{N}}_{\rm{2}}} \to {\rm{e}} +{\rm{ e}} +{\rm{ N}}_{\rm{2}}^{{ + }} $ | f (ε) | [29] |
| R2 | ${\rm{e}} + {{\rm{O}}_2} \to {\rm{e}} + {\rm{e}} + {\rm{O}}_2^ + $ | f (ε) | [29] | |
| R3 | ${\rm{e}} + {\rm{O}}_4^ + \to 2{{\rm{O}}_2}$ | 1.4 × 10–42(300/Te)0.5 mol·s–1 | [29] | |
| R4 | ${\rm{e}} + {\rm{O}}_2^ + \to 2{\rm{O}}$ | 2.0 × 10–13(300/Te) mol·s–1 | [29] | |
| R5 | ${\rm{e}} + 2{{\rm{O}}_2} \to {{\rm{O}}_2} + {\rm{O}}_2^ - $ | 2.0 × 10–41(300/Te) mol·s–1·m–6 | [29] | |
| 重粒子反应 | R6 | ${\rm{O}}_{\rm{2}}^{{ + }}{{ + }}{{\rm{O}}_{\rm{2}}}{{ + }}{{\rm{N}}_{\rm{2}}} \to {\rm{O}}_{\rm{4}}^{{ + }}{{ + }}{{\rm{N}}_2}$ | 2.4 × 10–42 mol·s–1·m–6 | [29] |
| R7 | ${{\rm{N}}_{\rm{2}}}{\rm{O}}_{\rm{2}}^{{ + }}{{ + }}{{\rm{O}}_{\rm{2}}} \to {\rm{O}}_{\rm{4}}^{{ + }}{{ + }}{{\rm{N}}_2}$ | 1.0 × 10–15 mol·s–1·m–3 | [29] | |
| R8 | ${{\rm{N}}_{\rm{2}}}{\rm{O}}_{\rm{2}}^{{ + }}{{ + }}{{\rm{N}}_{\rm{2}}} \to {\rm{O}}_2^{{ + }}{{ + 2}}{{\rm{N}}_{\rm{2}}}$ | 4.3 × 10–10 mol·s–1·m–3 | [29] | |
| R9 | ${\rm{O}}_{\rm{2}}^{{ + }}{{ + 2}}{{\rm{N}}_{\rm{2}}} \to {{\rm{N}}_{\rm{2}}}{\rm{O}}_{\rm{2}}^{{ + }}{{ + }}{{\rm{N}}_{\rm{2}}}$ | 9.0 × 10–43 mol·s–1·m–6 | [29] | |
| R10 | ${{\rm{O}}_{\rm{2}}} +{\rm{ N}}_{\rm{2}}^{{ + }} \to {{\rm{N}}_{\rm{2}}} +{\rm{ O}}_{\rm{2}}^{{ + }}$ | 6.0 × 10–17 mol·s–1·m–3 | [29] | |
| R11 | ${\rm{N}}_{\rm{2}}^{{ + }}{{ + }}{{\rm{N}}_{\rm{2}}}{{ + }}{{\rm{O}}_{\rm{2}}} \to {{\rm{O}}_{\rm{2}}} + {\rm{N}}_{\rm{4}}^{{ + }}$ | 5.0 × 10–41 mol·s–1·m–6 | [29] | |
| R12 | ${{\rm{O}}_{\rm{2}}}+ {\rm{ N}}_{\rm{4}}^{{ + }} \to {\rm{2}}{{\rm{N}}_{\rm{2}}}+ {\rm{ O}}_{\rm{2}}^{{ + }}$ | 2.5 × 10–16 mol·s–1·m–3 | [29] | |
| R13 | ${\rm{2}}{{\rm{N}}_{\rm{2}}}+ {\rm{ N}}_{\rm{2}}^{{ + }} \to {{\rm{N}}_{\rm{2}}}+ {\rm{ N}}_{\rm{4}}^{{ + }}$ | 5.0 × 10–41 mol·s–1·m–6 | [29] | |
| R14 | ${\rm{O}}_{\rm{2}}^{{ + }}+ {\rm{ 2}}{{\rm{O}}_{\rm{2}}} \to {\rm{O}}_{\rm{4}}^{{ + }}{{ + }}{{\rm{O}}_{\rm{2}}}$ | 2.4 × 10–42 mol·s–1·m–6 | [29] | |
| R15 | ${\rm{O}}_{\rm{4}}^{{ + }}+ {\rm{ O}}_{\rm{2}}^ - \to {\rm{3}}{{\rm{O}}_{\rm{2}}}$ | 1.0 × 10–13 mol·s–1·m–3 | [29] | |
| R16 | ${\rm{O}}_{\rm{4}}^{{ + }}+ {\rm{ O}}_{\rm{2}}^ - {{ + }}{{\rm{N}}_2} \to {\rm{3}}{{\rm{O}}_{\rm{2}}} + {{\rm{N}}_{\rm{2}}}$ | 2.0 × 10–17 mol·s–1·m–6 | [29] | |
| R17 | ${\rm{O}}_{\rm{4}}^{{ + }}+ {\rm{ O}}_{\rm{2}}^ - {{ + }}{{\rm{O}}_{\rm{2}}} \to {\rm{3}}{{\rm{O}}_{\rm{2}}}{{ + }}{{\rm{O}}_{\rm{2}}}$ | 2.0 × 10–17 mol·s–1·m–6 | [29] | |
| R18 | ${\rm{O}}_{\rm{2}}^{{ + }}+ {\rm{ O}}_{\rm{2}}^ - {{ + }}{{\rm{O}}_{\rm{2}}} \to {\rm{2}}{{\rm{O}}_{\rm{2}}}{{ + }}{{\rm{O}}_{\rm{2}}}$2 | 2.0 × 10–17 mol·s–1·m–6 | [29] | |
| R19 | ${\rm{O}}_{\rm{2}}^{{ + }}+ {\rm{ O}}_{\rm{2}}^ - {{ + }}{{\rm{N}}_{\rm{2}}} \to {\rm{2}}{{\rm{O}}_{\rm{2}}}{{ + }}{{\rm{N}}_{\rm{2}}}$ | 2.0 × 10–17 mol·s–1·m–6 | [29] |
表1N2-O2等离子体化学反应
Table1.N2-O2 plasma chemical reactions.
上述反应中R1, R2的电离能Δε分别为15.6 eV和12.06 eV.
对于初始离子的数密度主要遵循电中性原则, 离子分布采用的是混合物平均模型. 具体参数为电子初始数密度为1 × 1013 m–3, O2–初始数密度1 × 1012 m–3, N2+初始数密度6 × 1012 m–3, N4+初始数密度1 × 1012 m–3, O2+初始数密度2 × 1012 m–3, O4+初始数密度1 × 1012 m–3, N2O2+初始数密度1 × 1012 m–3.
2
2.3.边界条件的设置
气体放电的原理图如图1所示, 分别为带有纳米管的极板、平板电极以及放电过程中的保护电路. 其中纳米管的长度为H = 20 μm、直径为R = 0.1 μm, 极间距为D = 100 μm, 极板半径为L = 150 μm, 电压为V0 = 300 V, 电阻为R1 = 1000 Ω, 电容为C = 1 pF, 由于研究的是常温常压下的气体放电, 所以将气体放电时的环境温度设置为293.1 K, 背景压强设置为1 atm.
图 1 放电原理图Figure1. Discharge schematic diagram.
由于离子会撞击边界而发生表面反应, 并且当正离子轰击阴极纳米管会产生二次电子发射现象, 通常情况下表面二次发射系数取值范围在0.001—0.5[30], 其平均初始电子能量通常取值范围在1—5 eV[30], 二次发射系数和平均电子能量通量分别取值为0.05和4 eV, 具体边界表面反应式如表2所列.
| 序号 | 反应式 | 针电极(阴极) | 板电极(阳极) | |||
| γ | εi/eV | γ | εi/eV | |||
| R20 | ${\rm{e}} + {\rm{N}}_{\rm{2}}^{{ + }} \to {{\rm{N}}_{\rm{2}}}$ | 0.05 | 4 | 0 | 0 | |
| R21 | ${\rm{e }}+{{\rm{N}}_{\rm{2}}}{\rm{O}}_{\rm{2}}^{{ + }} \to {{\rm{N}}_{\rm{2}}}{{ + }}{{\rm{O}}_{\rm{2}}}$ | 0.05 | 4 | 0 | 0 | |
| R22 | ${\rm{e}} + {\rm{N}}_{\rm{4}}^{{ + }} \to {\rm{2}}{{\rm{N}}_{\rm{2}}}$ | 0.05 | 4 | 0 | 0 | |
| R23 | ${\rm{e}} + {\rm{O}}_{\rm{2}}^{{ + }} \to {{\rm{O}}_{\rm{2}}}$ | 0.05 | 4 | 0 | 0 | |
| R24 | ${\rm{e}} +{\rm{ O}}_{\rm{4}}^{{ + }} \to 2{{\rm{O}}_{\rm{2}}}$ | 0.05 | 4 | 0 | 0 | |
| R25 | ${\rm{e}} +{\rm{ O}}_{\rm{2}}^{{ - }} \to {{\rm{O}}_{\rm{2}}}$ | 0 | 0 | 0 | 0 | |
表2表面反应
Table2.Surface reactions.
电子通量在阴极和阳极边界条件为
本文是通过定义COMSOL软件中的PDE(偏微分方程)模块实现仿真, 模型计算方法采用有限元法, 方程的求解采用基于向后微分时间步进算法, 求解时间步长遵循自适应原则, 其最大约束步长为10–6 s, 最小约束步长为10–13 s. 其中电子迁移率和电子碰撞反应速率分别通过求解玻尔兹曼方程和麦克斯韦方程式得到. 在进行网格剖分时整个反应区域选用三角形网络进行网格划分, 具体尺寸为: 最大单元尺寸为1.13 μm, 最小单元尺寸为0.3 μm, 最大单元增长率为1.1, 曲率因子为0.2, 狭窄区域分辨率为1. 并且由于针电极(纳米管)的尺寸较小, 因此再对针极边界进行剖分(遵循最小单元尺寸小于最窄宽度的十分之一的原则, 本模型中最窄宽度为纳米管半径r = 0.05 μm), 其具体剖分参数为: 最大单元尺寸为0.05 μm, 最小单元尺寸为0.003 μm.
3.1.电子密度分布
微纳电离式气体传感器的内部放电机理, 主要体现在放电期间电子的动态发展过程上, 因此研究了不同时刻电子密度的空间分布情况. 随着放电的发展电子团向阳极运动其密度先减小如图2(a)和图2(b)所示, 后不断增加如图2(b)—(d)所示, 之后其最大值又不断向阴极推进并保持稳定如图2(e)和图2(f)所示. 造成此种现象的原因是: 通电起初, 由于RC电路的作用使得电压缓慢上升, 此时空间内的电场强度较小使得电子碰撞气体分子而发生电离的概率过小, 所以主要表现为电子整体向阳极迁移, 并被阳极复合而消失, 从而使得空间中的电子密度减小, 如图2(a)和图2(b)所示; 随着电压不断的升高, 尖端处的电场强度随之增加, 正离子运动到尖端发生表面反应并产生二次电子发射, 为尖端处的电离反应R1, R2提供了种子电子, 进而造成尖端处的电子密度不断增加, 如图2(b)和图2(c)所示; 随着时间的推移, 尖端处的电子在电场的加速下获得能量, 在运动的过程中不断地与气体分子发生碰撞电离, 而碰撞电离出的电子又在运动的过程中获得能量, 并碰撞其他气体分子发生电离反应, 如此不断循环, 使电子得以增值. 当电子团到达阳极时被复合而消失, 但由于空间电离还在不断地产生电子且速率不断加强(电离产生的正离子不断向阴极移动, 使得其与阴极之间的电场不断加强), 进而使得不断汇集至阳极处的电子数量大于被阳极吸收而消失的电子数量, 因此会看到电子团在阳极附近保持了一段时间且数密度不断增加, 如图2(d)所示; 后因电离产生的正离子不断累积且不断向纳米管运动使其之间的场加强作用不断增加, 使得空间的电离反应速率不断增强且正离子撞击纳米尖端产生的二次电子发射数量不断增加, 并且导致放电过程由空间电离主导演化为二次电子发射主导, 从而阴极附近电子密度不断增加, 加之由电子附着反应产生的负离子不断累积使得其与阳极之间的场加强作用增强, 造成电子在阳极因复合而消失的速率不断增强, 其二者共同作用造成空间的电子密度不断增加, 阳极处的电子密度相对减小, 进而表现出电子密度最大值不断向纳米管推进, 如图2(e)所示; 直至运动到阴极上方某一位置处时, 正负离子的产生与消耗达到动态平衡, 即空间电场不在发生变化时, 使得电子的产生与消耗速率也达到平衡, 因此会看到最终电子密度与其峰值位置基本保持不变如图2(f)所示.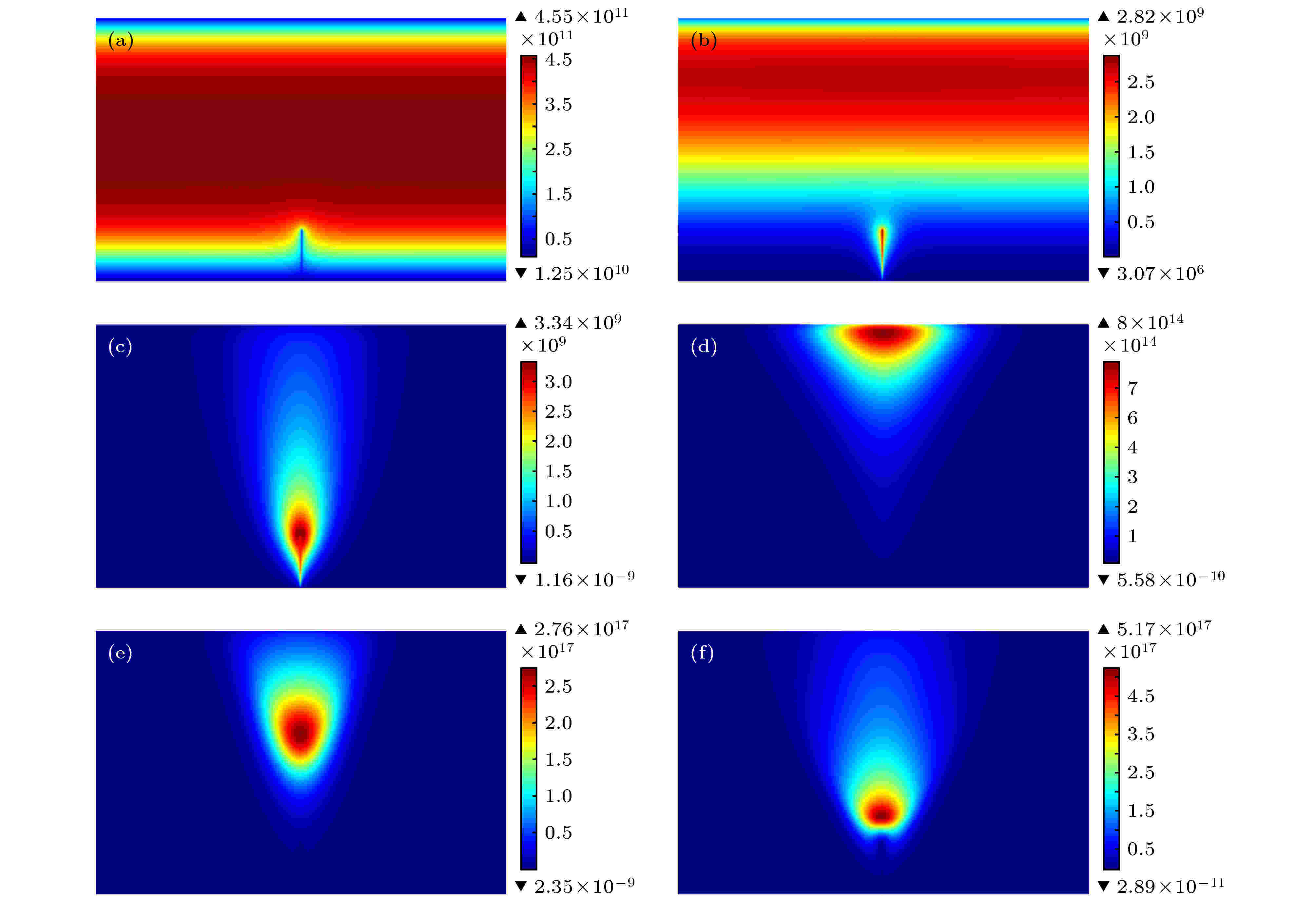
图 2 不同时刻的电子密度分布图 (a) t1 = 0.1 ns; (b) t2 = 0.3 ns; (c) t3 = 1 ns; (d) t4 = 100 ns; (e) t5 = 150 ns; (f) t6 = 200 nsFigure2. Electron density maps at different times: (a) t1 = 0.1 ns; (b) t2 = 0.3 ns; (c) t3 = 1 ns; (d) t4 = 100 ns; (e) t5 = 150 ns; (f) t6 = 200 ns.
2
3.2.放电电场的时空分布
在一定条件下空间中的电场强度是影响其气体电离过程的最主要因素. 如图3为中轴线上不同位置处的电场强度随时间的变化曲线. 起初极板间的电场强度随着外加电压的升高而增加, 当t = 4 ns时, 其电压达到最大(如图4所示), 此时极板间的电场强度也达到最大, 并且由于棒极曲率半径较小, 造成其附近的场强相对板级较大. 随后所有点处的场强都在一段时间内保持相对恒值, 造成这种现象的原因是由于外加电压达到最大且保持稳定, 加之正负离子虽然在电子向阳极运动的过程中有所增加, 但其量级较小所以产生的内部电场相对于外加电压产生的电场基本可以忽略不计, 如图3所示表现为所有点处的电场强度为一条相对平稳的直线. 且在t1 = 100 ns时刻之后, 由于正离子N2+, N4+, O2+, O4+, N2O2+与负离子O2–数密度不断积累对空间电场产生畸变. 整体表现为正离子对阴极的场加强作用, 负离子对阳极的场加强作用, 正负离子之间的场削弱作用, 即正负离子会对空间电场产生畸变, 此结论与文献[15]中的结果一致. 以对称轴上X = 50 μm与X = 80 μm点处电场强度的变化为例, t1 = 100 ns时刻两点处的场强都逐渐开始减小, 由图5(a)可以看出, 此时正离子对于阳极之间的电场减小作用大于负离子对于阳极之间的场加强作用, 因此总体呈现出电场减小. 后在t2 = 140 ns时刻X = 80 μm点处的电场强度又开始增加, 由图5(b)可以看出此时负离子的数密度不断增加至与正离子相等(峰值), 并且在点X = 80 μm点处负离子为主要的空间电荷, 因此在此时刻开始负离子的作用相对不断加强, 直至t4 = 200 ns时刻以后主要表现为负离子的加强作用(体现在总电场强度大于由外加电压产生的电场强度), 并且由于之后空间内正负离子数密度保持基本恒定, 导致电场强度值也保持不变. X = 50 μm点处在大约t3 = 150 ns时刻电场强度开始反向增加, 由图5(c)可以看出此时在此点附近负离子数密度不断增加, 使得正离子的对电场的减弱作用减小, 由于此时刻之后此点附近的正负离子数密度大致相等如图5(d)所示, 因此, 此点的电场强度畸变主要体现阴极附近的净空间电荷(正离子)与阳极附近的净空间电荷(负离子)之间形成的反向电场, 后同X = 80 μm点处一致, 即在t4 = 200 ns时刻以后正负离子的分布及其数密度保持基本恒定, 电场强度为一条平稳的直线.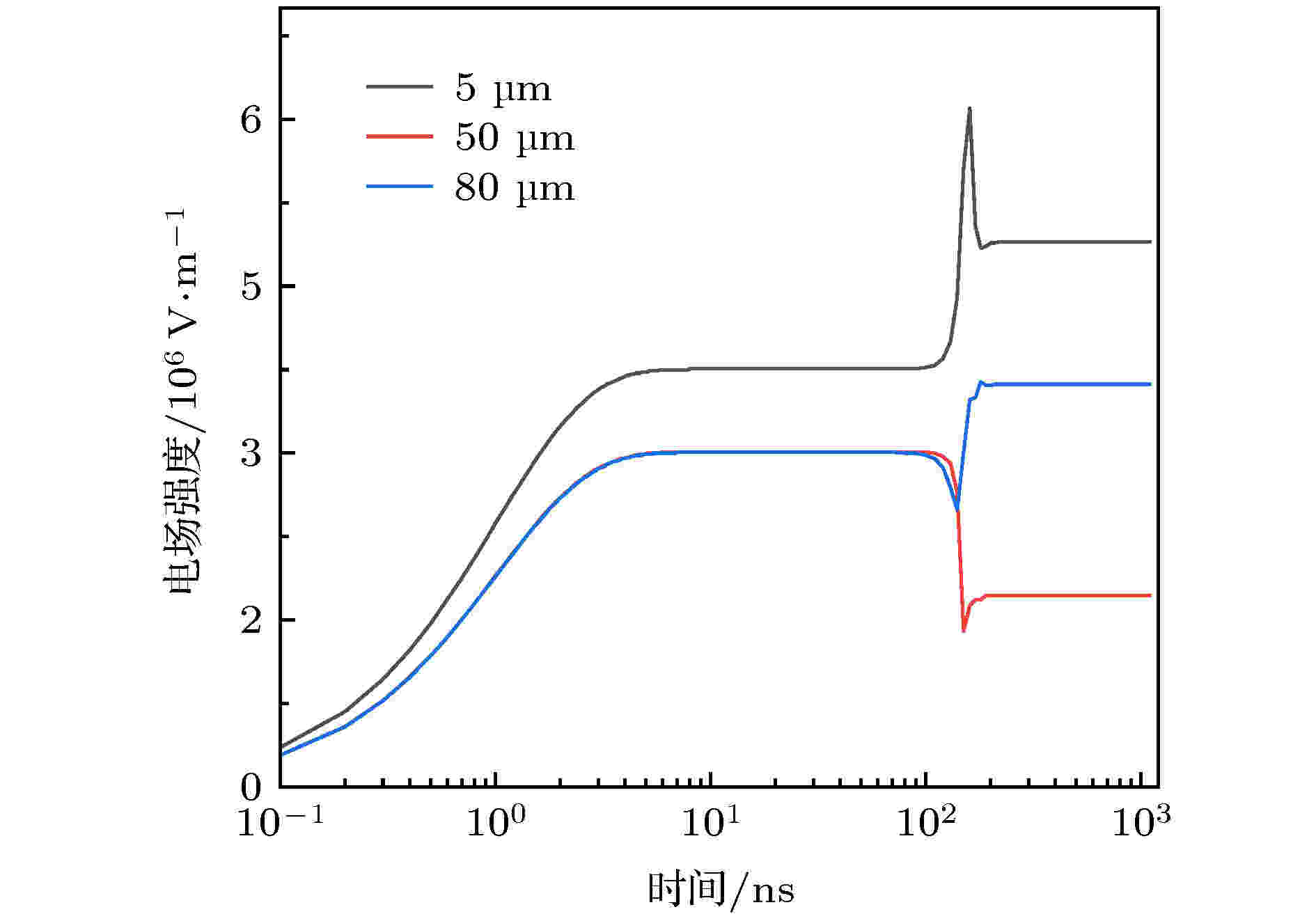
图 3 中轴线上不同位置处电场强度随时间的变化曲线Figure3. Curves of electric field strength with time at different positions on the central axis.
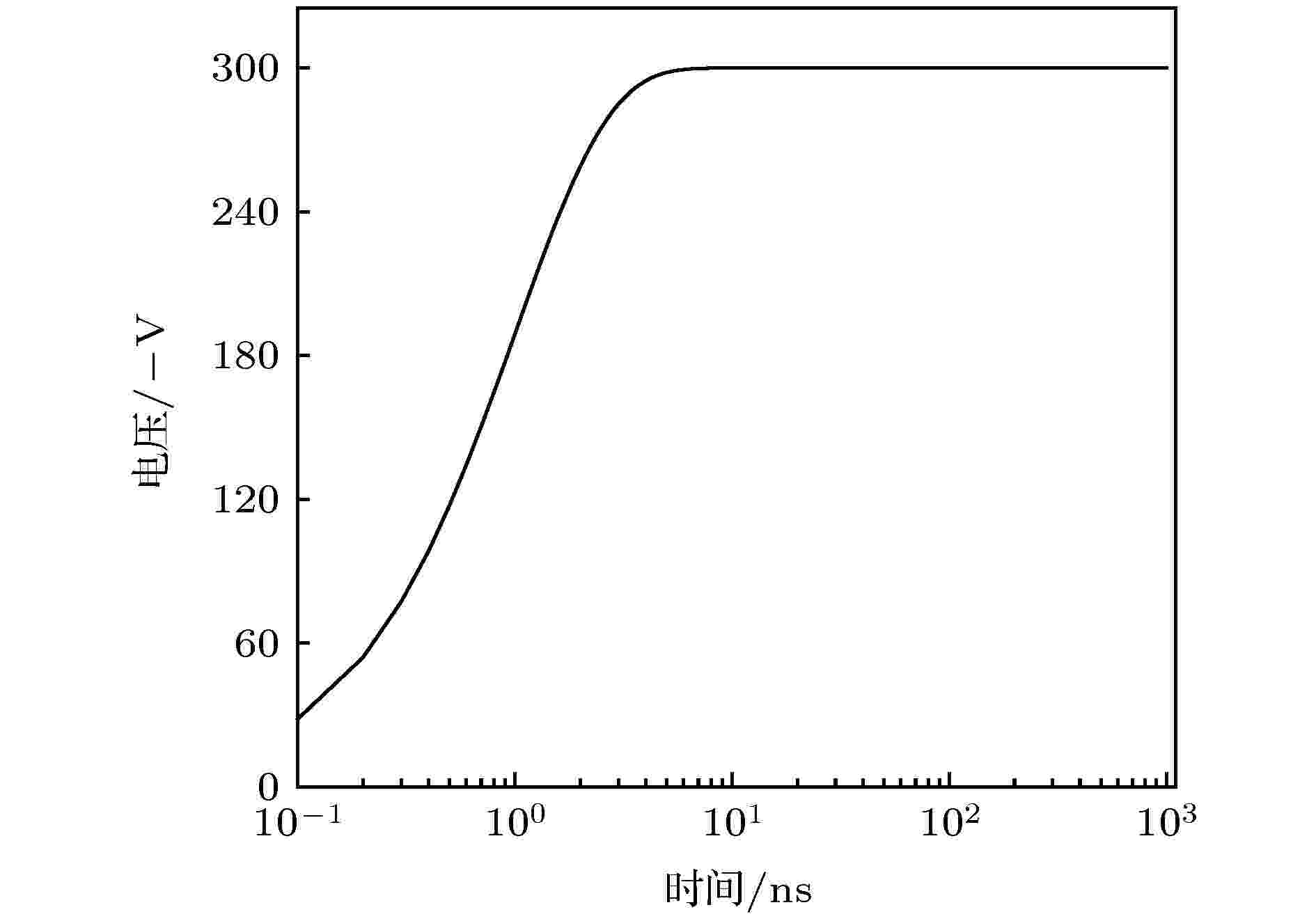图 4 负极板上外加电压随时间的变化曲线Figure4. Time-varying curve of applied voltage on the negative plate.
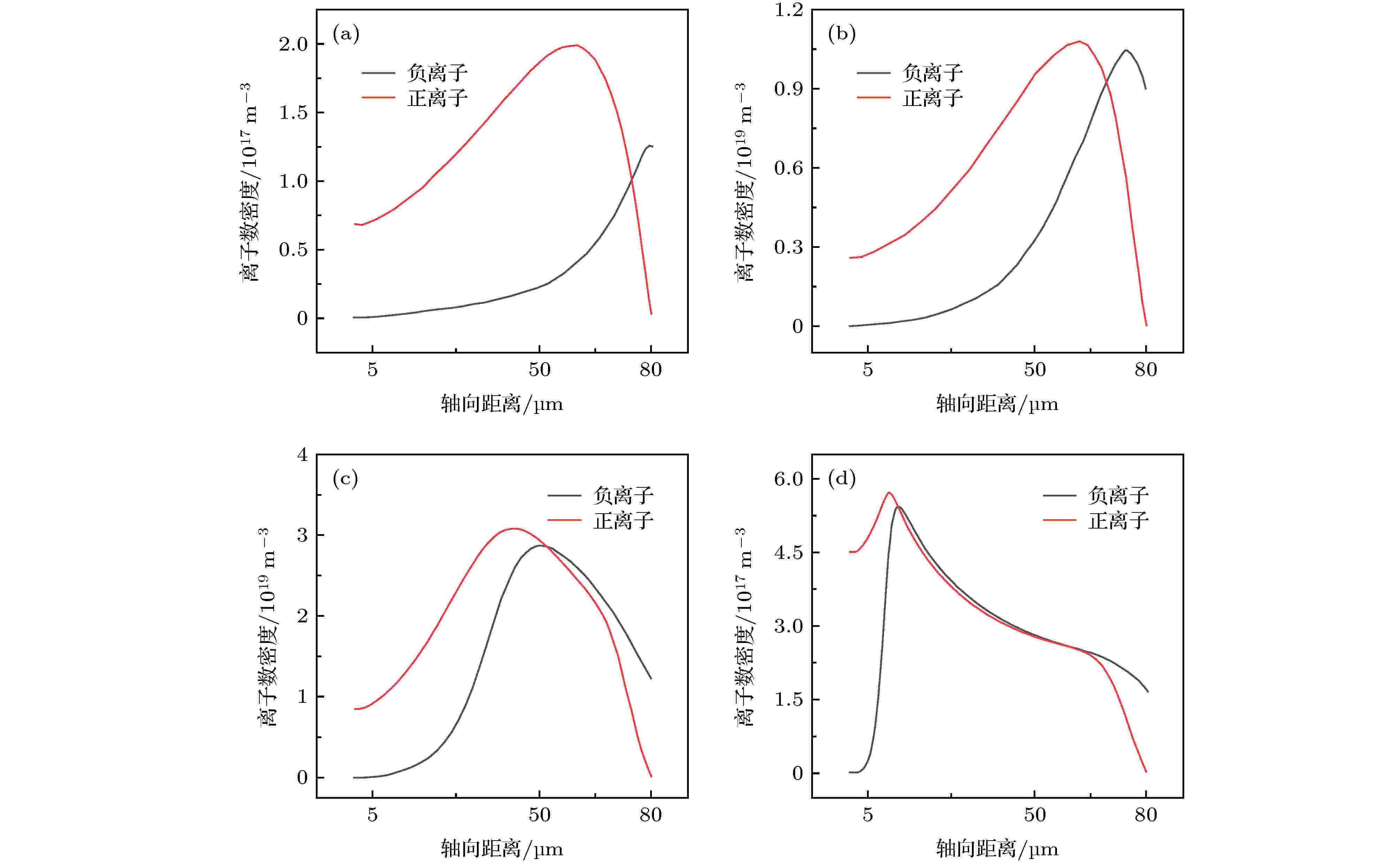图 5 不同时刻正负离子密度轴向分布 (a) t1 = 100 ns; (b) t2 = 140 ns; (c) t3 = 150 ns; (d) t4 = 200 nsFigure5. Axial distributions of positive and negative ion density at different times: (a) t1 = 100 ns; (b) t2 = 140 ns; (c) t3 = 150 ns; (d) t4 = 200 ns
2
3.3.放电电流密度的发展
放电期间电流密度随时间的变化曲线呈现出, 电子电流密度与离子电流密度的变化趋势一致, 即通电一段时间后电流密度突然增大而最终保持稳定, 如图6所示. 以离子电流密度变化为例进行分析, 即随着时间的推移电压不断升高, 纳米管尖端处的电场随之增加, 但其强度相对较弱造成电离反应速率较小因此产生的正离子数较少, 因此使得放电起初电流密度几乎为零; 后因正离子的不断累积对纳米管与其之间的场加强作用使得电离速率加剧, 产生大量的正离子且不断向纳米管运动, 造成纳米管与正离子间的电场不断增强, 如图7所示, 进而电离反应也更加剧烈并产生更多的正离子, 形成一个正反馈过程, 并且纳米管上方电场强度的增大也会使得正离子以更快的速度运动到纳米管表面并发生表面反应, 进而放电电流密度迅速增大; 当正离子在纳米管尖端发生表面反应而消失的速率大于电离产生的速率时, 使得正离子数密度减小, 从而对纳米管尖端的场加强作用相对减弱, 并导致正离子的表面反应R20, R21, R22, R23和R24的反应速率减小, 从而放电电流出现相对减弱的状态; 随后当电离产生的正离子速率与发生表面反应而消失的正离子速率保持平衡时, 即正离子的产生与消耗达到动态平衡, 导致其对纳米管的场加强作用也随之保持平衡, 最终为一条平稳的直线, 使得正离子在纳米管处发生的表面反应速率也保持恒定, 进而电流密度最终保持稳定, 即放电得以维持.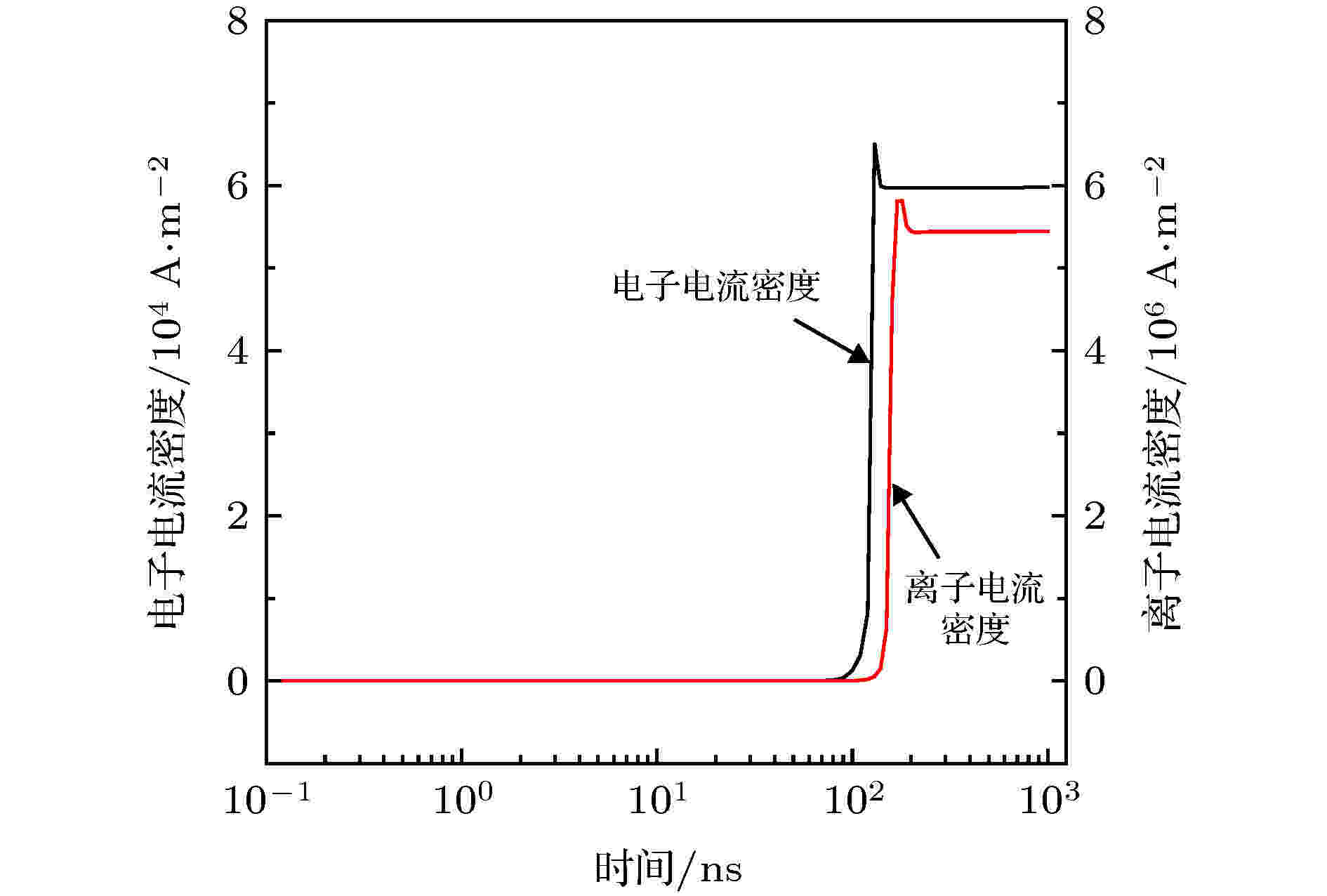
图 6 放电电流密度随时间的变化曲线Figure6. Curve of discharge current density with time.
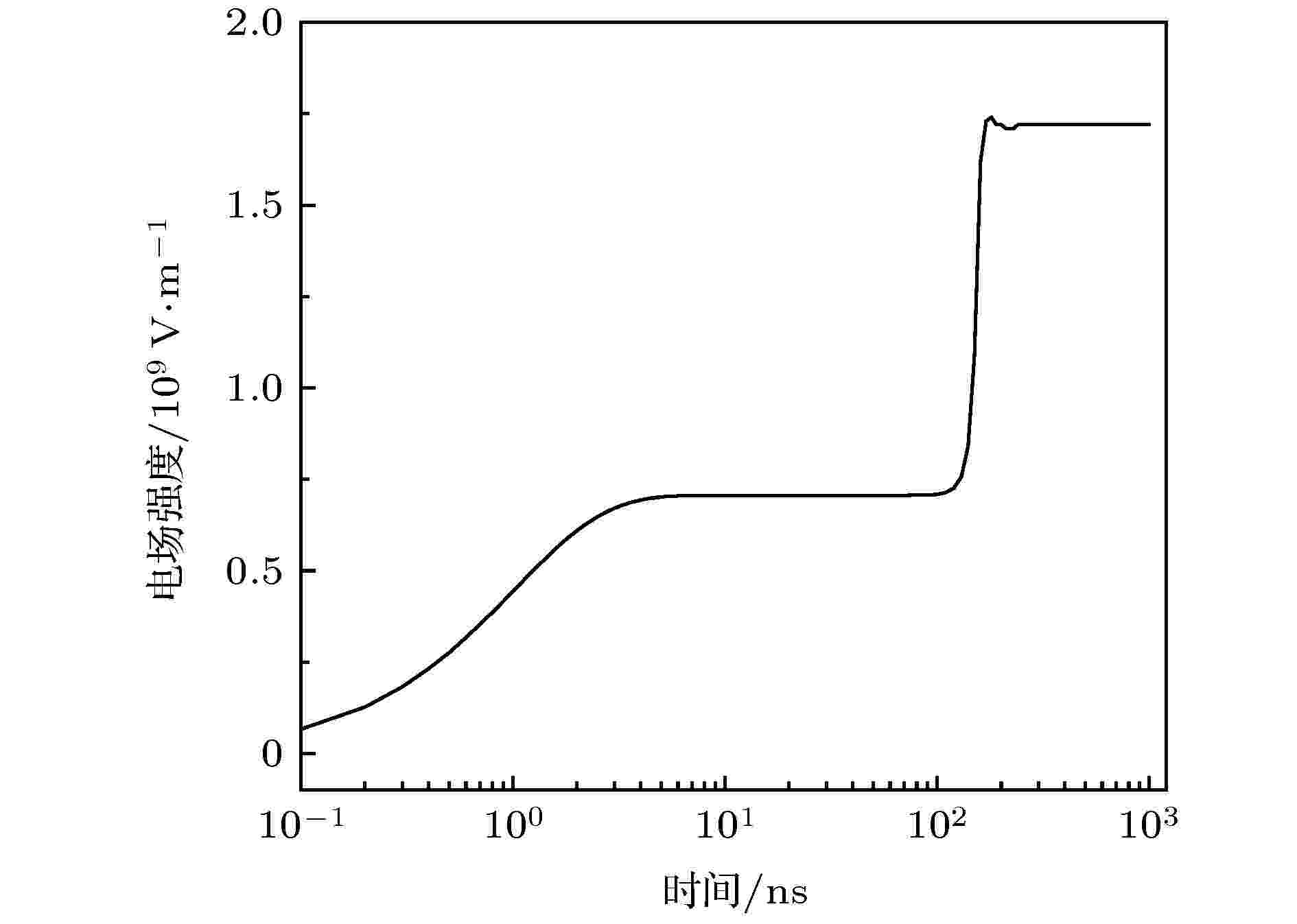图 7 尖端处的电场强度随时间的变化曲线Figure7. Curve of the electric field strength at the tip with time.
而电子电流与离子电流的变化趋势一致, 是由于除去初始电子, 在碰撞电离过程中电子和离子成对出现; 在离子轰击阴极的二次电子发射过程中, 进入阴极极板的离子与发射出的电子数量存在一定比例关系; 在复合湮灭反应(R3, R4)过程中离子和电子会成对消失, 因此出现电子电流密度与离子电流密度变化趋势一致. 但由于离子与电子存在质量差异, 使得在扩散迁移过程中电子的速度大于离子的速度, 进而出现电子电流密度出现时间较早. 并且由于离子轰击阴极的二次电子发射过程中, 进入阴极极板的离子与发射出的电子数量存在的比例关系, 即一个正离子撞击阴极, 发射出0.05(二次电子发射系数)个电子, 导致在放电过程中电极极板的离子电流密度数量级大于电子电流密度.
2
3.4.极间距对电流密度的影响
由3.3节可知在极间距一定的情况下空间电场强度的强弱直接影响着放电电流密度的大小, 且表现出场强越强, 放电越剧烈从而电流密度越大. 而对于所述的放电结构, 增加空间场强的方法为增大外加电压或缩小极间距. 由于以尽量减小放电功耗、并提高输出电流(便于检测)为原则, 因此研究了同一电压不同极间距下的放电电流.分别对极间距为45, 47, 50, 60, 80和100 μm进行了建模仿真, 如图8所示. 由图8不同极间距下尖端处的电场强度可以看出, 起初极间距越小电场强度越大, 使得开始发生电离反应的时间越早, 并表现出正离子对尖端的场加强作用开始的时间越早, 即电流开始增大的时间也越早, 如图9(a)所示, 体现出电场强度对电子增值起主导作用, 致使电离反应速率增大, 正离子造成尖端处的场强增量增大(图10), 电流密度增大. 当极间距D = 50 μm时达到最佳, 即表现出此时由正离子造成的场强增量最大, 电流密度最大, 如图9(b)所示, 而后再减小极间距虽然起初极板间的场强增强, 但电子增值过程中的发展距离减小, 致使电离程度相对减弱, 正离子的场加强作用减小, 即由正离子造成的尖端处的场强增量减小, 进而放电电流密度也随之减小.
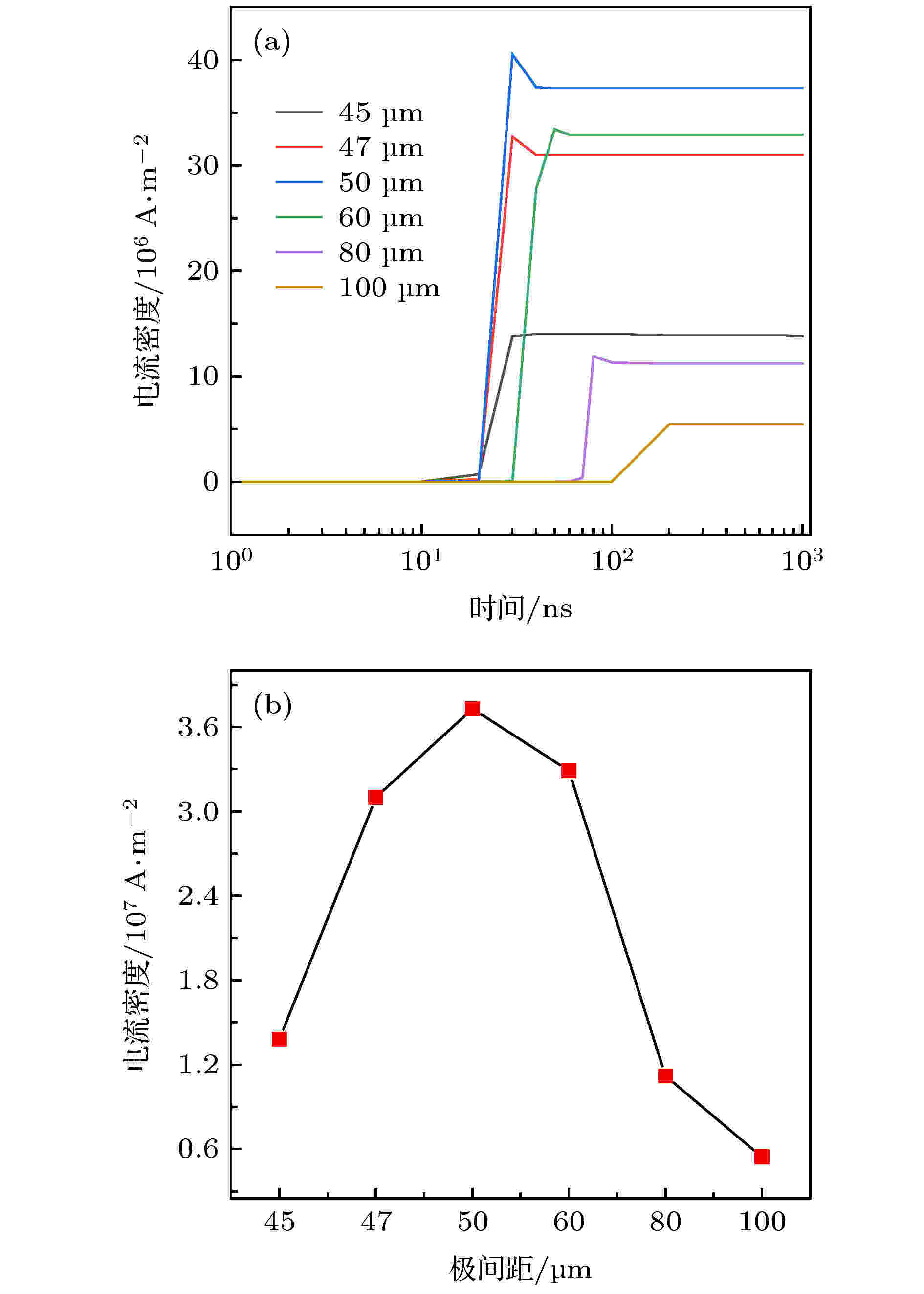图 9 不同极间距下的放电电流密度 (a) 所有时间; (b) 稳定时刻Figure9. The intensity of the electric field at the different poles: (a) All the time; (b) stable time.
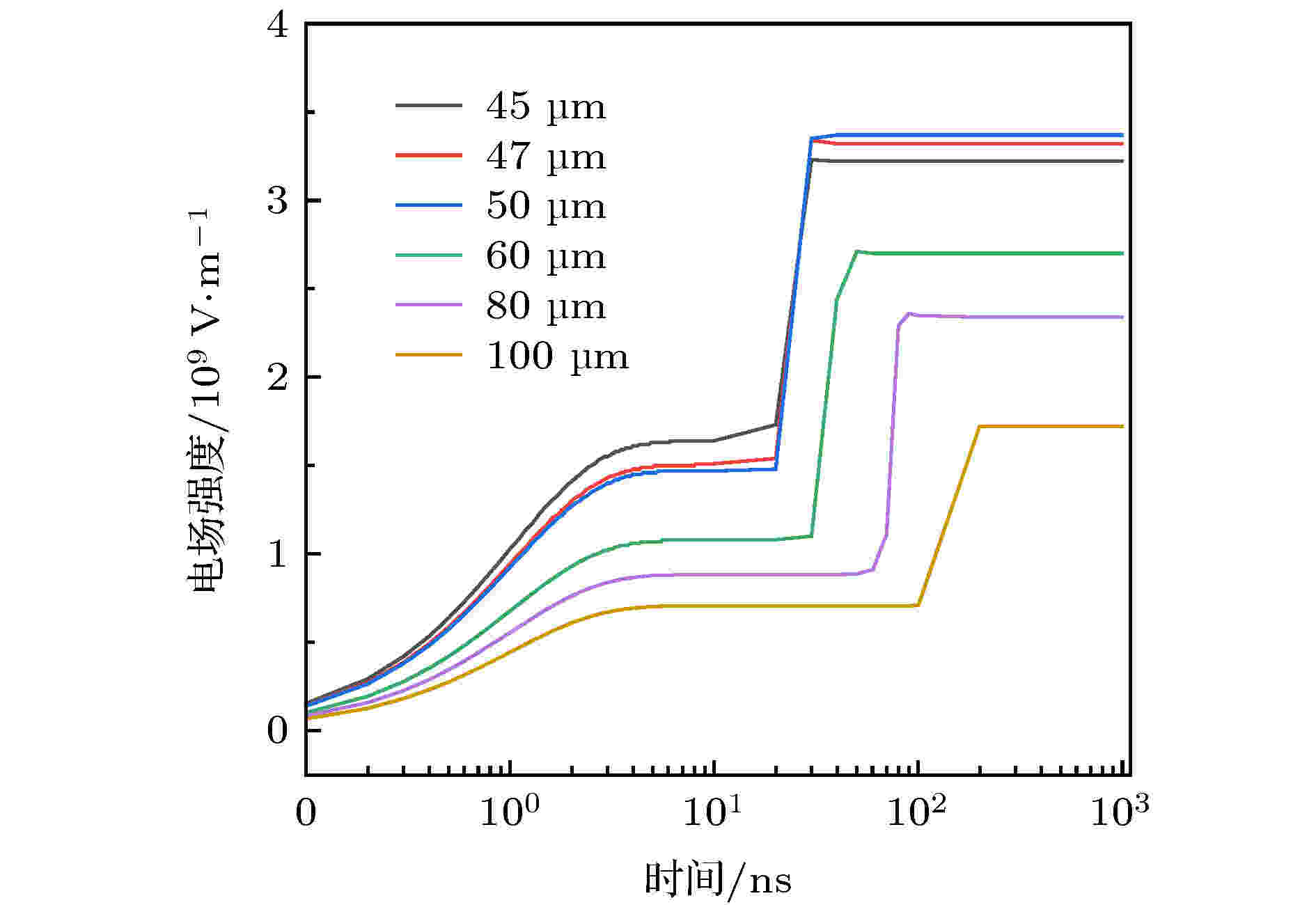图 8 不同极间距下尖端处电场强度随时间的变化曲线Figure8. Variation curve of electric field strength with time at the tip under different pole spacing.
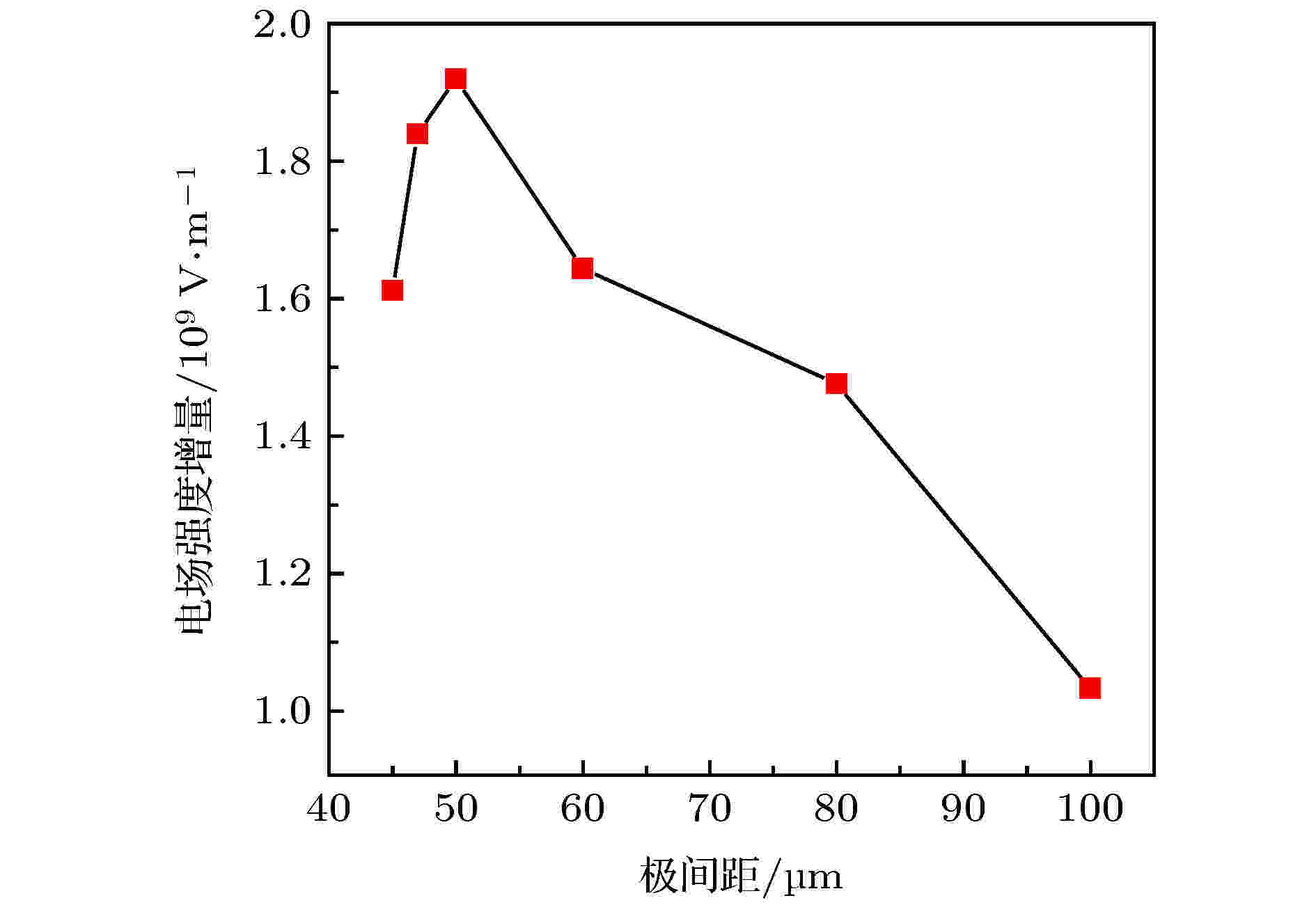图 10 不同极间距下尖端处的场强增量Figure10. The increment of field strength at the tips of different pole spaces.
1)此微纳级放电空间的放电电流密度的变化曲线随着正负离子的产生与消耗达到动态平衡, 而保持稳定即放电得以维持, 并且此电流密度曲线特性有利于电离式气体传感器对电流的检测;
2)放电过程中产生的正负离子会对电场产生畸变, 整体表现为正离子团相对阴极板的场加强作用, 负离子团相对于阳极板的场加强作用以及正负离子团之间的场减弱作用, 并由于正负离子数密度不断趋于恒定, 使得空间电场保持不变;
3)随着极间距的减小, 空间中的电场强度不断加强, 但放电稳定时刻的电流密度却呈现出先增大后减小的趋势, 这说明放电的激烈程度不仅与电场强度有关, 而且还与电子增值过程中的发展距离有关.
