摘要:铁电负电容场效应晶体管可以突破传统金属氧化物半导体场效应晶体管中的玻尔兹曼限制, 将亚阈值摆幅降低到60 mV/dec以下, 极大地改善了晶体管的开关电流比和短沟道效应, 有效地降低了器件的功耗, 为实现晶体管特征尺寸的减小和摩尔定律的延续提供了选择. 本文分析总结了国内外近年来关于铁电负电容场效应晶体管代表性的研究进展, 为进一步研究提供参考. 首先介绍了铁电负电容场效应晶体管的研究背景及其意义; 然后总结了铁电材料的基本性质和种类, 并对铁电材料负电容的物理机制和铁电负电容场效应晶体管的工作原理进行了讨论; 接下来从器件沟道材料维度的角度, 分别总结了最近几年基于三维沟道材料和二维沟道材料且与氧化铪基铁电体结合的铁电负电容场效应晶体管的研究成果, 并对器件的亚阈值摆幅、开关电流比、回滞电压和漏电流等性能的改善进行了分析概述; 最后对铁电负电容场效应晶体管目前存在的问题和未来的发展方向作了总结与展望.
关键词: 铁电负电容场效应晶体管/
氧化铪基铁电体/
三维沟道材料/
二维沟道材料

English Abstract

全文HTML

--> --> -->

1965年, Moore^[1]提出摩尔定律, 即每过18个月, 集成电路芯片上集成的晶体管数量增长一倍, 晶体管的特征尺寸减小为上一代的0.7倍. 半个世纪以来, 随着半导体技术的快速发展, 晶体管的特征尺寸大幅度减小. 2002年, 金属-氧化物半导体场效应晶体管(metal-oxide-semiconductor field-effect transistors, MOSFETs)的尺寸进入了100 nm节点^[2], 但仅仅通过缩小沟道尺寸带来的性能提升已经不能满足市场对MOSFETs的要求, 因此需要引入新的材料和结构来提升MOSFETs的性能. 在90 nm节点的时候引入了应力硅技术^[3], 使得沟道中载流子的迁移率得到了提高. 为了抑制SiO₂氧化介质层减薄导致的漏电流, 在45 nm节点引入了高k介质层以及金属栅工艺, MOSFETs的性能得到了极大的提升. 但随着MOSFETs尺寸达到22 nm节点, 传统体硅平面结构MOSFETs的问题变得严重, 短沟道效应导致的漏电流和亚阈值摆幅(subthreshold swing, SS)退化现象使得器件的功耗急剧上升, 因此人们开始考虑采用新型结构器件. 其中, 绝缘体上硅^[4] (silicon on insulator, SOI)、超薄绝缘体上硅^[5] (ultra thin body-SOI, UTB-SOI)和三栅鳍式晶体管^[6] (FinFET)等结构的利用在很大程度上缓解了由于短沟道效应带来的诸多问题. 文献[7]中指出, 在3 nm节点, MOSFETs采用环栅结构(gate all around, GAA)以提高栅对沟道的控制能力, 其性能相较于目前主流的FinFET将提高30%以上.
但随着晶体管特征尺寸进入10 nm以内, 由于短沟道效应和漏致势垒降低(drain induced barrier lowering, DIBL)效应造成的亚阈值区性能退化现象已变得不可忽略, 器件的SS增大, 因而其阈值电压${V_{{\rm{th}}}}$和工作电压${V_{{\rm{DD}}}}$不能等比例减小, 这导致器件的静态功耗急剧增大, 成为阻止器件尺寸进一步缩小的主要因素. 2017年的国际器件与系统路线图(international roadmap for devices and systems, IRDS) (图1)^[8]指出, 由于对高集成度低功耗器件的需求, 到2033年, 晶体管的特征尺寸将缩小到2 nm, 其SS也将降低到40 mV/dec. 而对于传统MOSFETs, 由于载流子玻尔兹曼分布的^[9]限制, 室温下的SS无法降低到60 mV/dec以下, 因此探寻降低晶体管的SS的方法, 对于促进晶体管特征尺寸的进一步减小具有重要的意义.
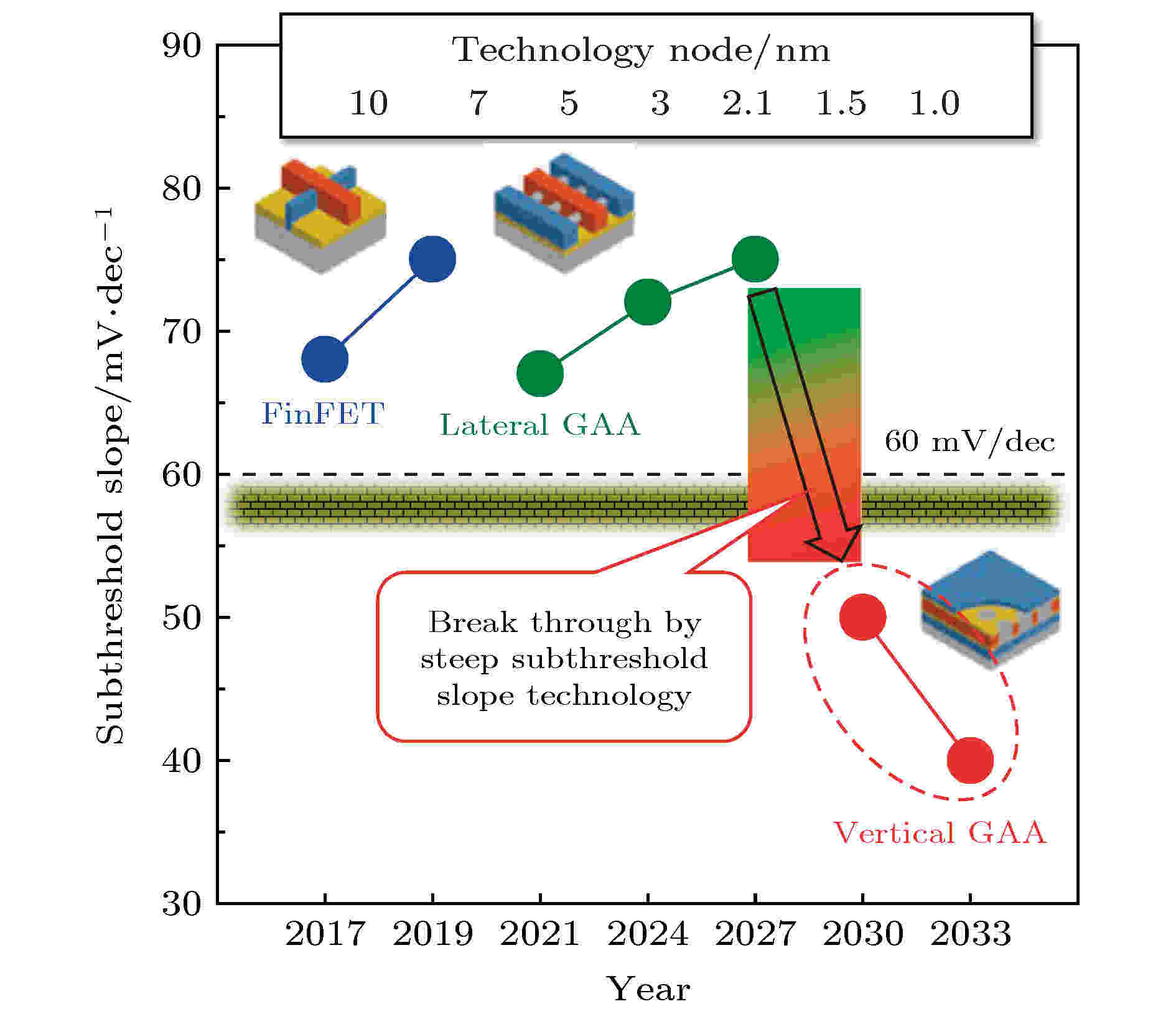图 1 IRDS提出的SS路线图^[8]
Figure1. Roadmap of subthreshold swing (SS) proposed by IRDS^[8].

目前一类器件是通过改变器件载流子的运输机制来降低SS, 主要包括隧穿晶体管^[10-13]、雪崩晶体管^[14]和纳机电原理晶体管^[15-17]等. 这一类器件都可以将SS降低到60 mV/dec以下, 但是都面临着相应的技术上的问题. 其中隧穿晶体管的电子隧穿概率低导致器件工作电流小和源漏之间的非对称工作特性是其面临的主要问题^[18]; 雪崩晶体管的雪崩击穿电压高, 不利于器件系统的稳定性^[19]; 纳机电原理晶体管的制作工艺复杂, 开关速度慢^[20], 因此这一类器件目前仍停留在实验室研究阶段. 另外一类器件是通过调节栅介质层电容和沟道电容的电容匹配来降低SS, 如超薄体硅SOI晶体管^[21]、无结纳米线晶体管^[22,23], 但这类器件本质上还是传统MOSFETs, 其室温SS仍然无法突破60 mV/dec的物理限制.
铁电负电容场效应晶体管(ferroelectric negative capacitance field effect transistors, Fe-NCFETs)一种新兴的晶体管, 其概念最早由Salahuddin和Datta^[24]于2008年提出, 他们提出将传统MOSFETs的栅极氧化介质层替换成铁电材料介质层, 放大栅压对沟道的作用效果, 降低栅电容与沟道电容的比值, 原理上可以把晶体管的SS降低到60 mV/dec以下, 这种现象他们称之为负电容(negative capacitance, NC)效应. 与其他降低晶体管SS的方法相比, Fe-NCFETs有着明显的优势. 由于Fe-NCFETs仅是在MOSFETs栅介质层中引入了铁电材料, 其总电容等效为NC, 本质上并没有改变金属-氧化物半导体(metal oxide semiconductor, MOS)器件的工作机制, 晶体管结构上也没有太大的变化, 因此Fe-NCFETs保持了传统MOS器件高驱动电流的优点, 而且还具有与互补金属氧化物半导体(complementary metal oxide semiconductor, CMOS)工艺兼容、对称的源漏工作机制、低功耗和负DIBL效应等优点^[25,26], 使Fe-NCFETs成为未来小尺寸、低功耗MOS器件中极具潜力的一种选择. 研究人员也因此对Fe-NCFETs进行了广泛的研究, 各种新材料^[27-30]、新结构^[31-34]和新技术^[35-38]不断被提出, Fe-NCFETs的性能也得到了极大提升.
本文从器件沟道材料维度的角度, 总结国内外最近几年关于Fe-NCFETs理论和实验的重要研究进展, 并对器件的SS、开关电流比、回滞电压和漏电流等性能的改善进行分析概述. 第二部分首先介绍铁电材料的基本性质, 然后对铁电材料的种类进行总结. 其中氧化铪基铁电材料的发明, 解决了传统铁电材料与CMOS工艺的兼容问题, 使得Fe-NCFETs的性能进一步提高. 第三部分首先对MFS、MFIS和MFMIS结构Fe-NCFETs的优缺点作简要总结; 然后从原子微观受力出发, 推导出铁电材料的“S”关系曲线, 并结合吉布斯自由能公式和Landau-Khalatnikov (L-K)方程, 得到铁电材料自由能曲线中的本征NC区域, 接下来从概念和电路特点方面分别讨论铁电电容中稳态NC和瞬态NC; 最后讨论NC Fe-NCFETs的工作区域. 第四部分从三维沟道材料和二维沟道材料角度总结近几年来采用氧化铪基铁电体的Fe-NCFETs的重要研究成果. 其中采用硅、锗基材料、III-V族化合物和碳纳米管等三维沟道材料的Fe-NCFETs与传统CMOS工艺的兼容性高, 沟道与铁电层之间界面性能好, 电学性能稳定. 但是, 也存在一些问题, 比如硅材料的载流子有效迁移率低限制了晶体管开态电流的大小, 锗基材料的带隙较小导致开关电流比小, III-V族化合物材料与介质层之间的界面性能差以及碳纳米管Fe-NCFETs的工作机理尚未探索清楚等. 而与过渡金属硫族化物、石墨烯和黑磷等二维材料相结合的Fe-NCFETs为晶体管特征尺寸进入3 nm提供了可能, 二维材料一些独特的物理效应也极具应用潜力. 但是二维材料与栅介质层的界面性能较差, 沟道表面缺陷态较多, 而且二维材料与传统CMOS工艺兼容性较差. 因此, 需要寻找新型材料和新的设计方案, 以在这些条件之间寻找一个平衡, 来满足未来器件对沟道材料的要求. 最后对Fe-NCFETs目前存在的问题和未来的发展方向作总结与展望.

2

-->

2.1.铁电材料基本性质

在一定温度范围内, 某些晶体会在特定方向上产生自发极化, 使晶胞中的正负电荷中心沿该方向产生相对位移, 形成电偶极矩, 且自发极化的大小和方向会随着外界电场的大小和方向的改变而改变, 具有这种特性的晶体称为铁电体(ferroelectrics). 其中, 极化方向与晶体的其他任何方向都不是对称等效的, 也就是在晶体所属点群的任何对称操作下都保持不动的方向, 称这个方向为特殊极性方向. 而在32个晶体学点群中, 只有1(C₁)、2(C₂)、m(C₃)、mm2(C_2v)、3(C₃)、3m(C_3v)、4(C₄)、4mm(C_4v)、6(C₆)和6mm(C_6v)这10个点群具有特殊极性方向^[39]. 即只有属于这10个点群的晶体, 才有可能发生自发极化, 也才有可能是铁电体, 图2给出了32个晶体学点群所包含的电介质材料所属点群之间的关系^[39,40].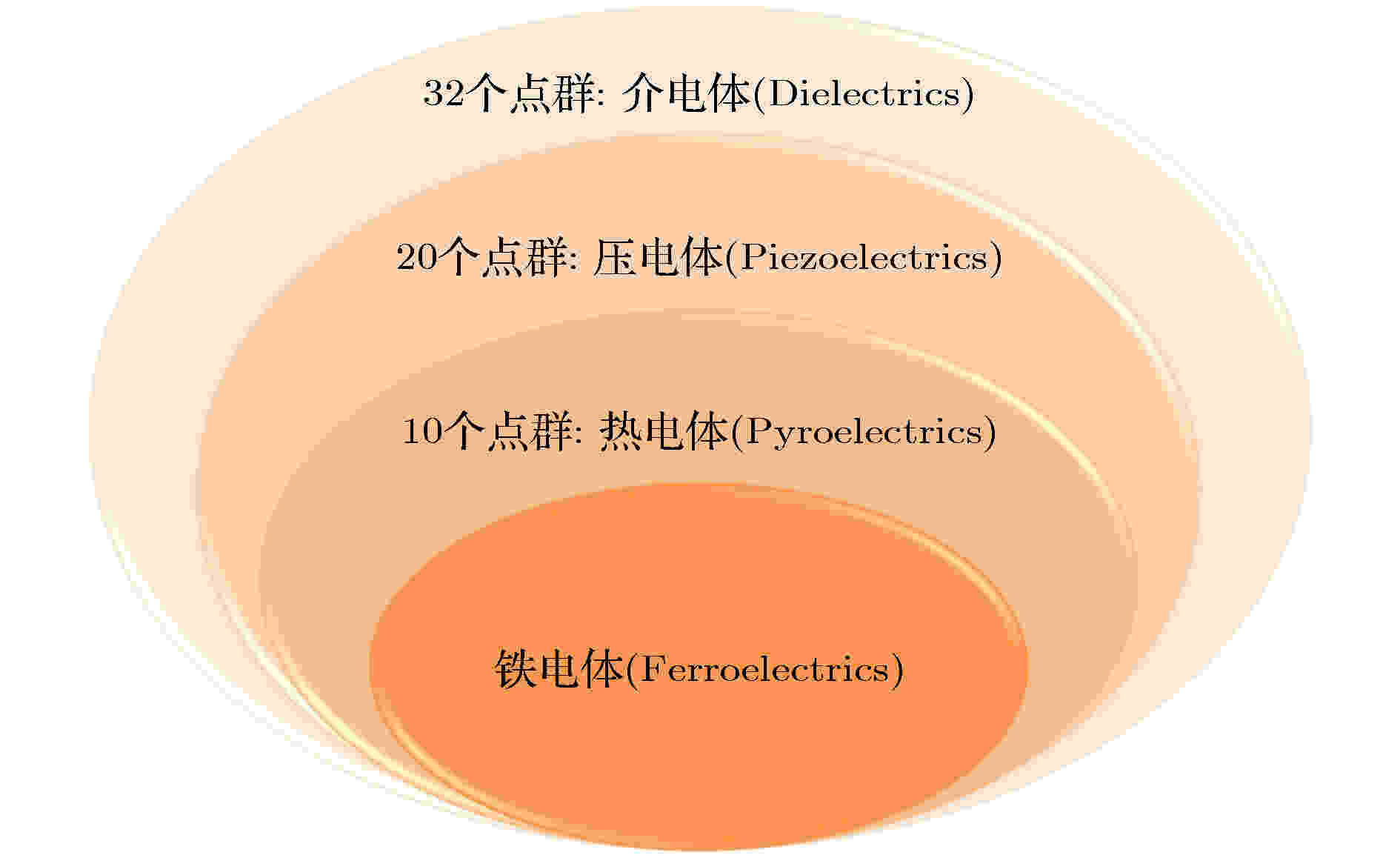
图 2 介电体分类示意图
Figure2. The schematic diagram of the classification of dielectrics.

铁电材料在宏观上具有居里温度和电滞回线两个主要特征. 图3为铁电材料极化强度P和外加电场E之间的典型关系图, 即电滞回线^[41]. 其中, ${P_{\rm{r}}}$为剩余极化强度, 表示撤去外电场时材料剩余的极化强度; ${E_{\rm{c}}}$为矫顽电场, 表示使极化强度为零时的电场强度. 当铁电体位于初始状态时, 内部的电偶极矩方向随机排列, 铁电体的净极化强度为零(点1). 当施加外加电场时, 电偶极矩开始沿着电场方向排列(点1到点3). 当全部的电偶极矩方向与电场方向一致时, 铁电体的极化强度达到最大值. 随后撤去外电场, 由于电偶极矩之间的相互耦合, 铁电体内部存在剩余极化, 极化强度为${P_{\rm{r}}}$(点4). 当施加反向电场时, 电偶极矩开始反转. 当施加电场强度达到$ - {E_{\rm{c}}}$时, 铁电体内部的电偶极矩方向随机排列, 此时净极化强度为零(点5). 继续增大电场强度, 极化强度将在反方向上达到最大值(点6).
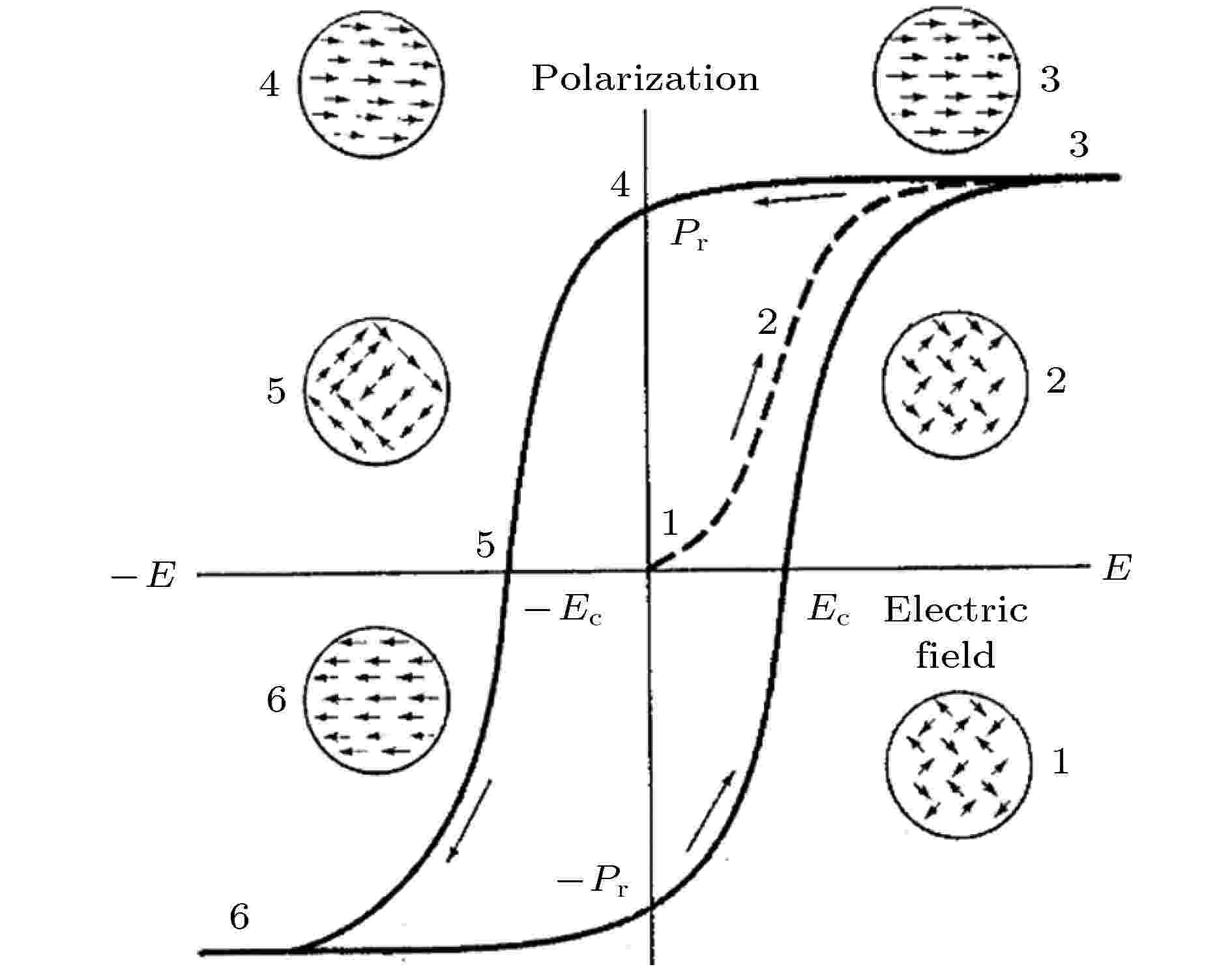图 3 铁电电滞回线^[41]
Figure3. Ferroelectric hysteresis loop^[41].

因为晶体的构型是温度的函数, 所以晶体的极化状态将随温度的变化而变化^[42]. 对于铁电体来说, 存在一个临界温度T_c, 当温度低于T_c时, 晶体结构为有自发极化的铁电体结构; 当温度高于T_c时, 晶体结构转变为没有自发极化的顺电体(paraelectrics)结构, 称T_c为居里温度. 以BaTiO₃为例, 其居里温度T_c为130 ℃, 当温度T > 130 ℃时, 晶格结构为立方晶系(m3m), 此时晶体是顺电体, 不具有自发极化; 当0 < T < 130 ℃时, 晶格结构为四方晶系(4 mm), 此时的自发极化方向为 [001]; 当–90 ℃ < T < 0时, 晶格结构为正交晶系(mm2), 自发极化方向为 [110]; 当T < –90 ℃时, 晶格结构为三角晶系(3 m), 自发极化方向为 [111]^[43-45].
2 -->

2.2.铁电材料分类

自1921年Valasek^[46]发现罗息盐(酒石酸钾钠, NaKC₄H₄O₆·4 H₂O)晶体具有铁电电滞回线以来, 到目前为止, 人们已经发现1000多种具有铁电性的材料, 按照材料组成大致可分为传统无机铁电材料、有机铁电材料、范德华类层状二维铁电材料和氧化铪基铁电材料四类.
3 -->

2.2.1.传统无机铁电材料

传统无机铁电材料包括: 钙钛矿型铁电体如BaTiO₃、PbTiO₃、PbTiZrO₃和KNbO₃等, 酸锂型铁电体如LiNbO₃、LiTaO₃和BiFeO₃等, 青铜矿型铁电体如PbTa₂O₆、PbNb₂O₆和Ba₂Sr₃Nb₁₀O₃₀等, 铋层状钙钛矿结构铁电体如SrBi₂Ta₂O₉, 其铁电性来源于晶格结构的不对称性. 这一类材料具有居里温度点高、抗疲劳特性优异和自发极化强度大等优点, 所以最开始被应用于基于极化反转特性的铁电存储器研究领域, 但是其薄膜沉积温度高(一般大于800 ℃)、电滞回线矩形度差以及与CMOS工艺兼容性差等缺点也阻碍了其商业化进程^[39].
3 -->

2.2.2.有机铁电材料

有机铁电材料包括聚偏氟乙烯(Polyvinylidene fluoride, PVDF)及其衍生物^[47-50]、奇数尼龙^[39] (如尼龙–11、尼龙–9等)、金属-有机混合物铁电材料^[51,52]和铁电液晶(癸氧基苄叉对氨二甲丁基肉硅酸盐^[39]、溴化胆固醇及其衍生物^[53]等)等, 其铁电性的物理机制是材料含有的手性有机物分子基团导致了材料分子的不对称性, 从而表现出自发极化的特性. 有机铁电材料的沉积温度低(一般在200—300 ℃左右), 与衬底无化学反应, 因此可以在各种半导体材料上兼容生长, 而且还具有延展性好、生物兼容、去极化场小、稳定性高、光化学响应速度快和衍生物种类丰富等优点^[28], 因此吸引了研究人员的广泛关注, 并对有机铁电材料在存储器^[49]、晶体管^[50,54]和电光显示等^[55]方面的应用以及新型有机铁电材料的开发^[56,57]进行了大量的研究, 而提高自发极化强度和居里温度是目前有机铁电材料主要研究方向.
文献[56]中报道了新型有机钙钛矿铁电材料, 如图4所示, 采用手性有机分子基团、NH⁴⁺离子和卤族负离子(Cl^–, Br^–, I^–)分别替代了传统钙钛ABO₃中的A³⁺离子, B³⁺离子和O^2–离子, 合成了结构式为A(NH₄)X₃的一大类共计23种全有机新型钙钛矿材料. 其中共有17种材料显示出了良好的铁电性, 尤其是发现的MDABCO-NH₄I₃, 其自发极化强度(P_s)为22 μC/cm², 已接近无机钙钛矿铁电体BaTiO₃的极化强度(26 μC/cm²), 其居里温度T_c高达175 ℃, 比BaTiO₃的居里温度(117 ℃)高出50 ℃以上, 在新一代柔性可穿戴器件和生物电子学方面具有极高的应用潜力.
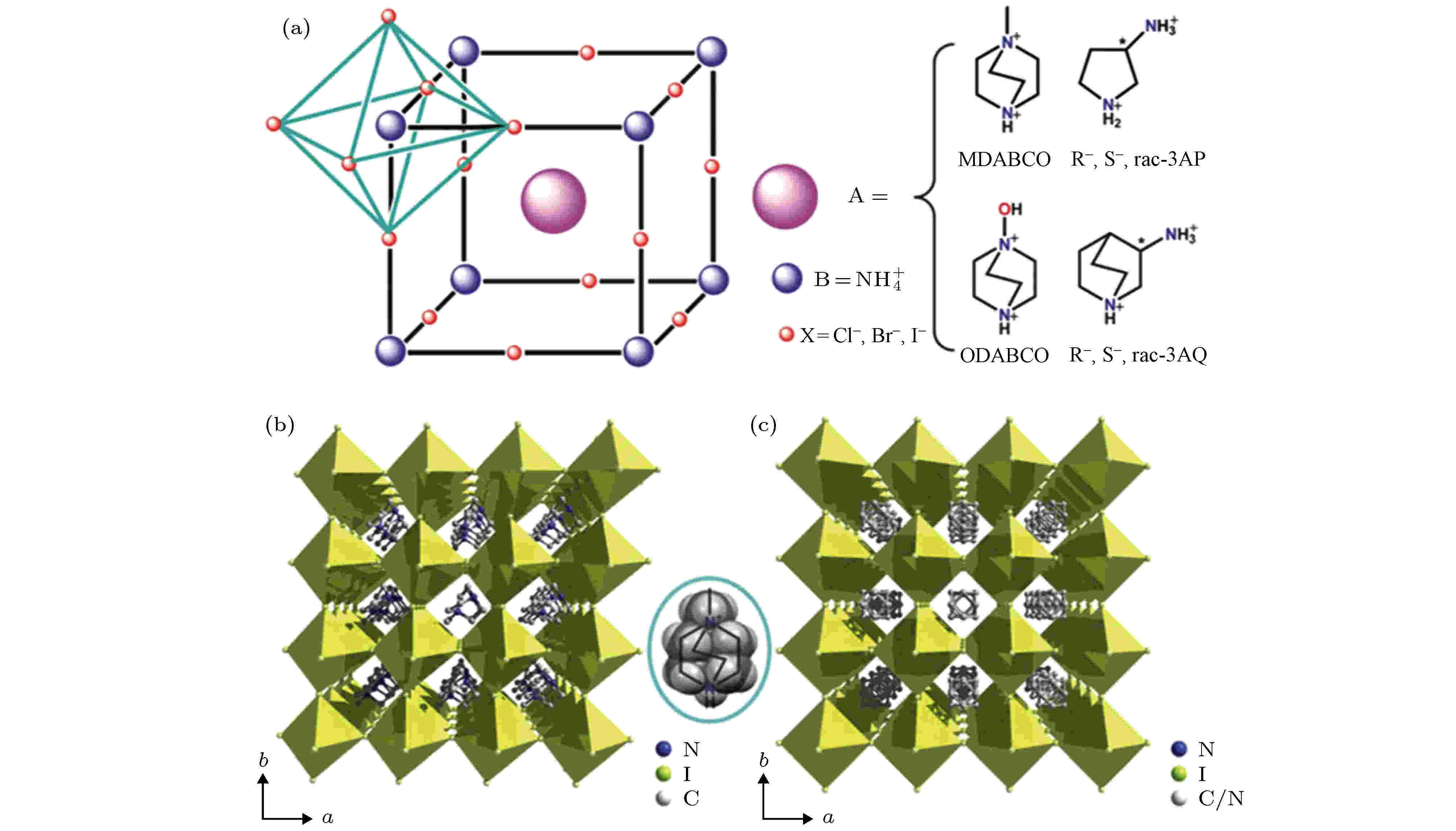图 4 有机钙钛矿A(NH₄)X₃家族化学和晶格结构^[56]　(a) 有机钙钛矿铁电体的三维化学结构组成图; (b) 铁电相MDABCO-NH₄I₃在293 K时的晶胞结构图, 右侧椭圆中为有机正离子的空间结构示意图, 其对称性接近于球体; (c) 铁电相MDABCO-NH₄I₃在463 K时的晶胞结构图
Figure4. Chemical and crystal structures of the metal-free A(NH₄) X₃ family^[56]: (a) Chemical structures of constituents of the metal-free 3D perovskite ferroelectrics; (b) the packing diagram of MDABCO–NH₄I₃ in the ferroelectric phase at 293 K. The oval to the right contains the space-fill diagram of the organic cation, showing the cationic geometry to be close to a ball; (c) the packing diagram of MDABCO–NH₄I₃ in the paraelectric phase at 463 K.

3 -->

2.2.3.范德华类层状二维铁电材料

近几年来, 人们发现范德华类层状二维材料具有铁电性. Li和Wu^[58]通过第一性原理计算, 证明二维AB型层状堆叠材料(BN、AlN、ZnO、MoS₂、GaSe等)由于层间的电子转移导致其在垂直方向上具有铁电性. Ding等^[59]也通过第一性原理计算从理论上证明了二维In₂Se₃具有水平方向和垂直方向的自发极化, 而且其自发极化方向可以通过外部电场调控^[60], 为调控铁电材料的极化方向提供了新方法. Liu等^[61]通过在硅上沉积了一层厚度为4 nm的范德华类二维CuInP₂S₆薄膜制备了二极管, 在50 ℃下观察到了材料的铁电性能, 而且器件的开关电流比约为100, 表现出了较好的存储性能. 这一类材料由于只需要几个分子薄层就能表现出铁电性能, 对于实现铁电器件尺寸的进一步缩小是很有吸引力的. 但是其居里温度低, 而且铁电性的物理机制尚未研究清楚, 关于材料铁电性的实验证明也相对较少, 所以这一类材料仍需要进行大量的研究工作^[62].
3 -->

2.2.4.氧化铪基铁电材料

氧化铪基铁电材料是一类新型的铁电材料, 自2011年B?scke等^[63]发现Si掺杂的HfO₂薄膜具有铁电性以来, 人们又陆续发现掺杂Al^[64]、Y^[65,66]、Gd^[67]、La^[67]、Sr^[68]等元素的HfO₂也显示出了显著的铁电性, 而且, B?scke等^[63]还发现在HfO₂中掺入ZrO₂形成的薄膜表现出了优异的铁电性能^[69,70]. 本征HfO₂常见的三种晶体结构^[71]分别是: 单斜相-c (T < 1727 ℃)、非极性四方相-nmc (1717 ℃ < T < 2597 ℃)和立方相-m3m (2597 ℃ < T < 2845 ℃), 这三个晶体结构都不具有特殊极性方向, 所以本征HfO₂是不具有铁电性的. Müller等^[70]认为在HfO₂中加入杂质元素之后, 将温度升高至四方相温度区间, 然后降温, 在降温过程中可形成具有特殊极性方向的正交相-mm2, 因此掺杂后的HfO₂表现出了铁电性. 氧化铪基铁电材料具有剩余极化强度(P_r)高、居里温度高(T_c > 200 ℃)、与CMOS工艺兼容性高、与半导体材料界面性能好和介电常数高等优点^[72], 因此被认为是Fe-NCFETs中很有应用潜力的一种介质层材料.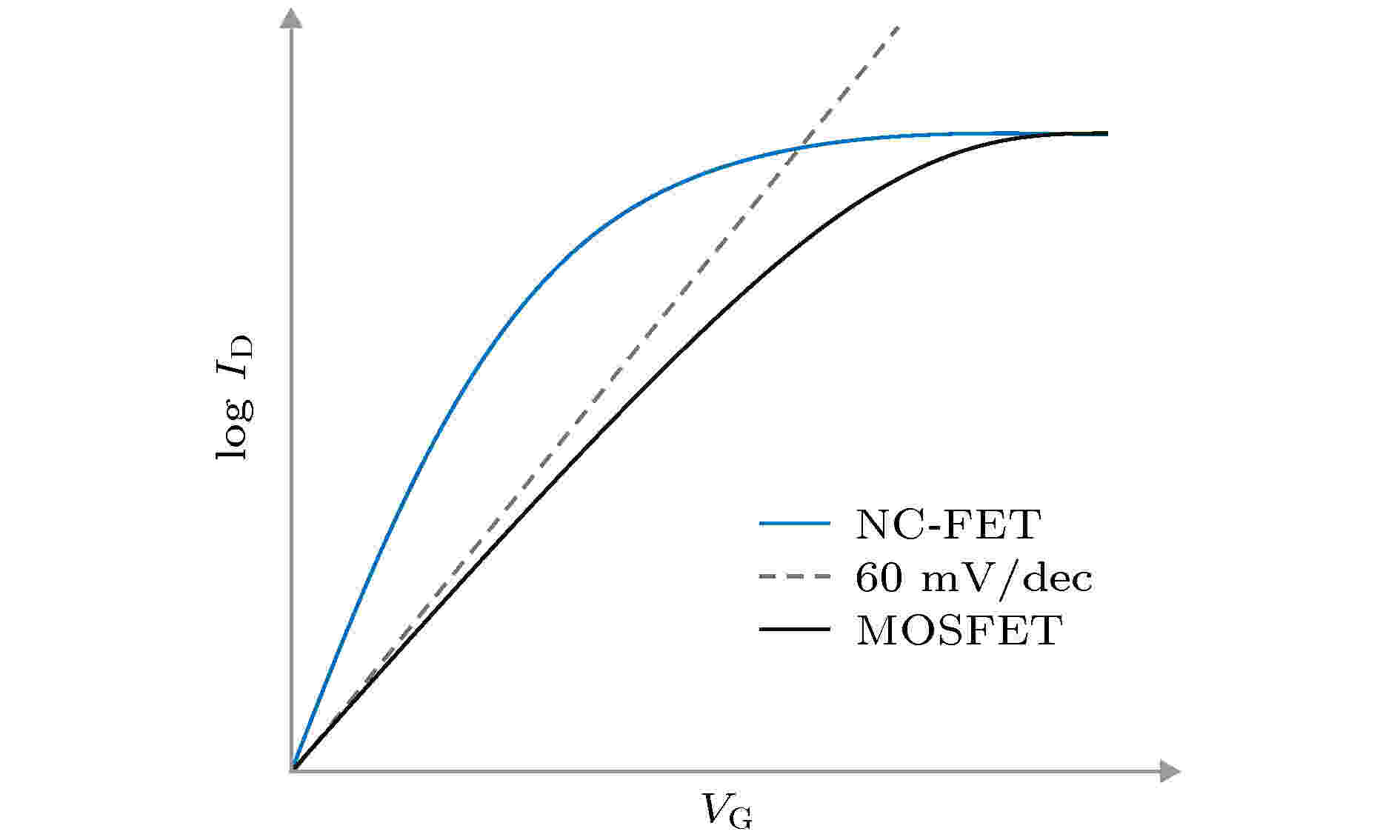

Fe-NCFETs作为一种新型低功耗器件, 通过在传统的MOSFETs栅介质层中引入铁电材料将SS降低到60 mV/dec以下(图5). SS是描述器件开关性能的重要参数, 定义为源漏电流每改变一个数量级所带来的栅压改变量. SS数值越小, 表示栅对沟道的控制能力越强, 即器件的开关性能越好, 同时可以在较小的栅压下得到相同的电流, 降低器件的功耗. SS的表达式为
图 5 场效应晶体管转移特性曲线
Figure5. The transfer characteristic curve of field effect transistors.

${\rm{SS}} = \frac{{\partial {V_{\rm{G}}}}}{{\partial {{\log }_{10}}{I_{\rm{D}}}}} = \frac{{\partial {V_{\rm{G}}}}}{{\partial {\psi _{\rm{S}}}}}\frac{{\partial {\psi _{\rm{S}}}}}{{\partial {{\log }_{10}}{I_{\rm{D}}}}} = m \times n,$

其中${V_{\rm{G}}}$为栅压, ${I_{\rm{D}}}$为源漏电流, ${\psi _{\rm{S}}}$为沟道表面电势; $m = {{\partial {V_{\rm{G}}}} / {\partial {\psi _{\rm{S}}}}}$ 称为体因子, 表示栅压对沟道表面电势的控制能力, 取决于沟道电容与栅介质层电容的比值大小; $n = {{\partial {\psi _{\rm{S}}}} / {\partial {{\log }_{10}}{I_{\rm{D}}}}}$称为传输因子, 表示沟道表面电势对源漏电流的控制能力, 取决于载流子的传输机制.
传统MOSFETs的器件结构图和电容模型如图6所示^[24], 利用图中的等效电容模型, 可以将m表示为

$m = \frac{{\partial {V_{\rm{G}}}}}{{\partial {\psi _{\rm{S}}}}} = \left( {1 + \frac{{{C_{\rm{s}}}}}{{{C_{{\rm{ins}}}}}}} \right),$

其中${C_{{\rm{ins}}}}$为介质层电容, ${C_{\rm{s}}}$为沟道电容. 对于常规MOS器件来说, ${C_{{\rm{ins}}}}$和${C_{\rm{s}}}$均为正值, 所以m取值总是大于1. 另一方面, 由于MOS器件沟道中载流子的输运机制是漂移扩散原理, 会受到载流子玻尔兹曼分布的限制, 导致n存在一个理论最小值, 即

$n \geqslant \frac{{\ln 10 \cdot {k_{\rm{B}}}T}}{q},$

其中${k_{\rm{B}}}$为玻尔兹曼常数, T为温度, q为单位电荷.
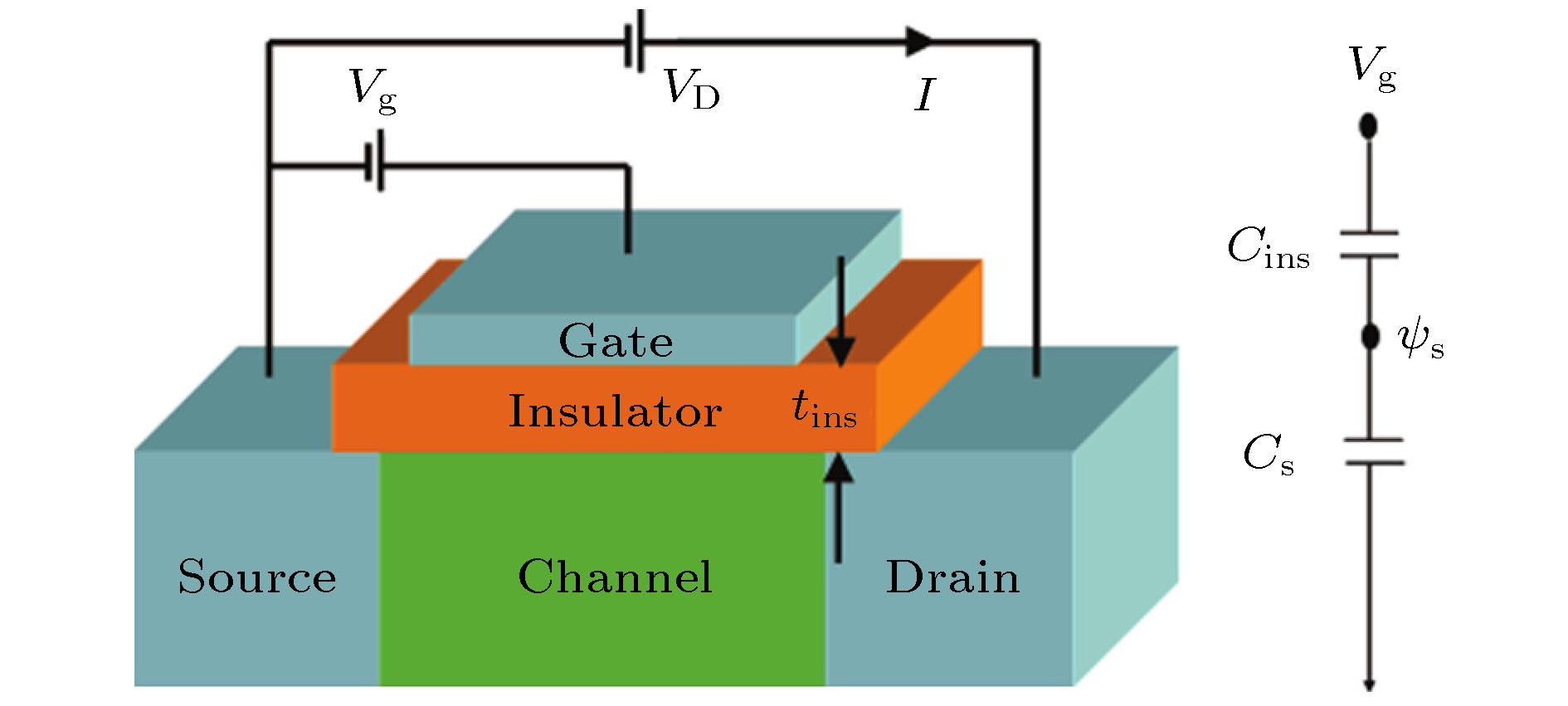图 6 标准场效应晶体管结构示意图与其等效电容电路^[73]
Figure6. The schematic diagram of a standard field effect transistors.structure and its eauivalent circuit of capacitance^[73].

因此传统MOSFETs室温(T = 300 K)下的SS的理论最小值为60 mV/dec, 而对于Fe-NCFETs来说, 由于栅介质层中的铁电材料具有NC效应, 因此栅介质层电容可以为负值, 即

${C_{{\rm{ins}}}} < 0,$

所以m的数值可以小于1, 则SS可以突破60 mV/dec的限制, 但同时为了保证器件运行的稳定性, 需要满足m > 0, 即

$\left| {{C_{{\rm{ins}}}}} \right| < {C_{\rm{s}}}.$

因此, 通过合理设计器件的电容, 可以实现SS低且稳定性好的低功耗高性能Fe-NCFETs器件, 而且由于栅介质层电容与漏端电容的耦合作用, 器件具有负DIBL和负微分电阻(negative differential resistance, NDR)效应^[25], 改善了短沟道效应, 对于晶体管尺寸的减小是很有利的.
对MFS、MFIS和MFMIS结构Fe-NCFETs的优缺点作简要总结; 然后从原子微观受力出发, 推导出铁电材料的“S”关系曲线, 并结合吉布斯自由能公式和L-K方程, 得到铁电材料自由能曲线中的本征NC区域; 接下来从概念和电路特点方面分别讨论铁电电容中稳态NC和瞬态NC; 最后讨论NC Fe-NCFETs的工作区域.
2

-->

3.1.不同栅介质层结构的Fe-NCFETs

2008年, Salahuddin 和Datta^[24]首先提出利用铁电材料替换传统晶体管的栅介质材料, 可以将器件的栅电压放大, 从而理论上可以降低器件的SS, 这种器件结构称为MFS(图7(a)), 具有结构简单的优点, 但是铁电层与沟道之间的界面不兼容性问题严重, 器件的界面性能差. 随后人们提出在铁电层和沟道之间加入一层传统栅介质层, 即MFIS结构(图7(b)), 这种结构很好地解决了铁电层与沟道之间的界面问题, 但由于沟道的表面电势在源漏之间有变化, 而铁电层上表面电势分布是均匀的, 从而导致铁电材料在沟道方向上电压放大效果不一样^[74-79]. 因此, 有人提出在栅介质层和铁电层之间加入一层金属, 即MFMIS结构(图7(c)), 以此来均匀铁电层在沟道方向上的电势放大效果, 但内部金属栅电极的存在极大地增加了器件的制造难度, 对于器件尺寸的进一步减小是不利的, 而且会导致栅极漏电流的增加, 降低了器件的稳定性能^[80-82]. 相比于MFMIS结构, MFIS结构Fe-NCFETs的电容匹配更稳定, 将更适用于高频逻辑应用^[83].
图 7 器件结构图　(a) 传统MOSFETs; (b) MFIS; (c) MFMIS
Figure7. Device structure diagram: (a) Traditional MOSFETs; (b) MFIS; (c) MFMIS.

因此, MFIS结构仍是未来Fe-NCFETs的主要选择, 而且随着氧化铪基铁电材料的提出, 通过热氧即可在氧化铪和硅之间形成一层薄氧化硅介质层, 改善了MFIS结构中铁电层与沟道的界面性能差的问题, 同时还引入高k材料介质层的优点^[84], 进一步优化了器件的性能.
2 -->

3.2.铁电材料NC效应的微观本质

3 -->

3.2.1.稳态NC

铁电材料NC来源于晶格不对称性导致的自发极化, 之前人们采用吉布斯自由能理论, 结合铁电材料的电滞回线和相关物理参数, 分析证明了铁电材料NC现象, 但是缺少对铁电材料电滞回线来源的理论分析^[24]. 之后, Wong和Salahuddin^[85]从晶格出发, 结合晶格中原子受到的各种微观力, 分析得到了铁电材料极化强度P与电场强度E 的“S”曲线关系图的物理机制. 其中, “S”曲线的负斜率区域内是热力学不稳定的, 而且P具有多值的特点, 因此, 随着电压正、反扫描过程中, 在相同电压下, 铁电层处于不同的极化状态, 因此P-E关系曲线表现出回滞的特点, 即“电滞回线”. 因此, 结合多种理论, 以钙钛矿型铁电材料为例, 从原子微观受力出发, 推导出P与E的“S”关系曲线; 然后结合电位移矢量连续方程, 得到材料所带电荷量Q与电压V的“S”关系曲线, 从宏观角度(${C_{{\rm{FE}}}} = \partial {Q_{{\rm{FE}}}}/\partial {V_{{\rm{FE}}}}$)证明NC的存在; 接着采用吉布斯自由能公式, 得到系统能量U与所带电荷Q的“双势阱”关系曲线, 又从微观角度(${C_{{\rm{FE}}}} = {\left( {{\partial ^2}{U_{{\rm{FE}}}}/\partial Q_{{\rm{FE}}}^2} \right)^{ - 1}}$)证明NC的存在, 系统性地介绍铁电材料NC现象的物理机制来源.
图8是钙钛矿型(ABO₃)铁电体的晶胞结构图和极化电场分布图, 图中B离子所受的力可以分解为由于离子与周围价电子之间的位移所导致的局域有效原子力${{{F}}_{{\rm{ion}}}}$、由于偶极子电场导致的极化力${{{F}}_{\rm{p}}}$和外界电场施加的电场外力${{{F}}_{{\rm{ext}}}}$.
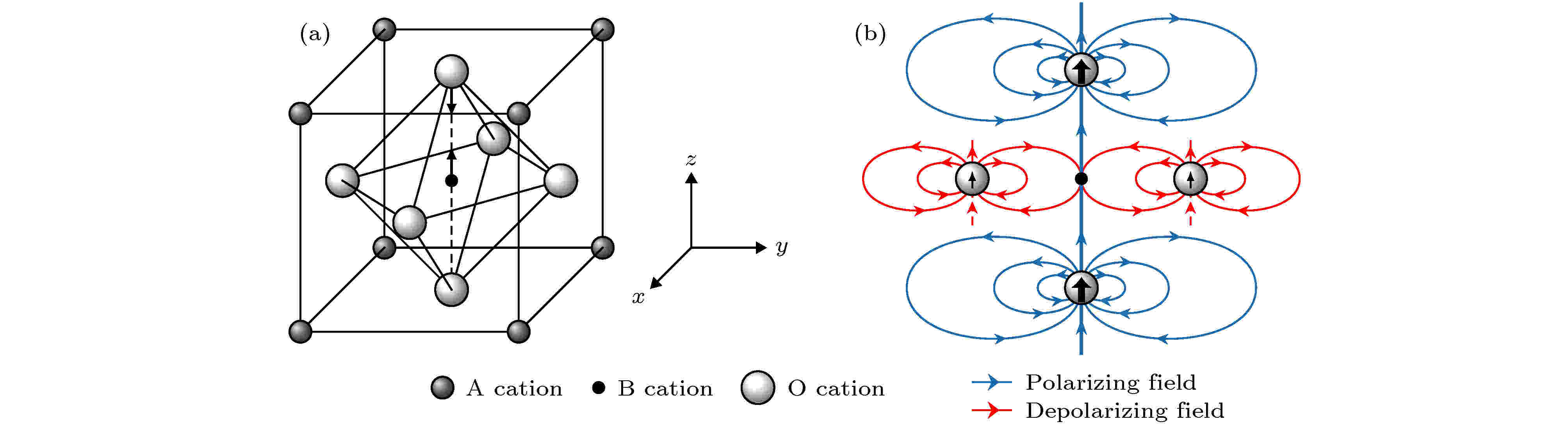图 8 (a) 钙钛矿型(ABO₃)铁电体的晶胞结构图^[85]; (b) (200)晶面的极化场分布图^[85]
Figure8. (a) Conventional unit cell of an FE perovskite (ABO₃)^[85]; (b) schematic of the dipole fields in the (200) plane^[85].

B离子的局域有效原子力可表示为

${{F}}_{{\rm{ion}}}^{\rm{B}} = - \nabla {V_{\rm{B}}}\left( {{{{u}}_{\rm{B}}}} \right),$

其中${V_{\rm{B}}}$为B离子的局域有效电势能, ${{{u}}_{\rm{B}}}$为B离子与其周围价电子的相对位移. 为了简化, 假设相对位移沿着z方向, 把${{{u}}_{\rm{B}}}$写为${{{z}}_{\rm{B}}}$, 然后${V_{\rm{B}}}\left( {{{{z}}_{\rm{B}}}} \right)$展开为

${V_{\rm{B}}}({{{z}}_{\rm{B}}}) \approx \;\,\underbrace {\frac{1}{2}{{\left. {\frac{{{\partial ^2}{V_{\rm{B}}}}}{{\partial {z_{\rm{B}}}^2}}} \right|}_{\rm{0}}}}_{{a_{\rm{B}}}}{{z}}_{\rm{B}}^2 + \,\underbrace {\frac{1}{{4!}}{{\left. {\frac{{{\partial ^4}{V_{\rm{B}}}}}{{\partial {z_B}^4}}} \right|}_{\rm{0}}}}_{{b_{\rm{B}}}}{{z}}_{\rm{B}}^4,$

这里有${V_{\rm{B}}}\left( 0 \right) = 0$, 而且由于晶格对称性的原因奇数项也为零, 为了简化, 省略了高阶项. 其中${a_{\rm{B}}}$和${b_{\rm{B}}}$可通过第一性原理计算得到, 为了简化, 设${a_{\rm{B}}} > 0{\rm{, }}{b_{\rm{B}}} > 0$. 将(7)式代入(6)式中, 得到

${{F}}_{{\rm{ion}}}^{\rm{B}}\left( {{{{z}}_B}} \right) \approx - \left( {2{a_{\rm{B}}}{z_{\rm{B}}} + 4{b_{\rm{B}}}z_{\rm{B}}^{\rm{3}}} \right){\hat {{z}}}.$

B离子除了受有效局域原子力之外, 还会和周围的离子发生库仑相互作用. 当离子i振动时, 会产生一个赝偶极矩${{{p}}_i}$, 这个赝偶极子在位置r处会产生一个偶极子电场, 其表示式为

${{E}}_{{\rm{dipole}}}^{\left( i \right)}\left( {{r}} \right) = \frac{{3\left[ {{{{p}}_i} \cdot \left( {r - {{{R}}_i}} \right)} \right]\left( {r - {{{R}}_i}} \right) - {{{p}}_i}{{\left| {r - {{{R}}_i}} \right|}^{\rm{2}}}}}{{{\rm{4\pi }}{\varepsilon _{\rm{0}}}{{\left| {r - {{{R}}_i}} \right|}^5}}},$

其中${{{R}}_i}$是离子i的平衡位置, $ {\varepsilon }_{0} $时真空介电常数. 将晶胞中各离子在r处产生电场叠加后可得到r处的总偶极子电场

${{{E}}_{\rm{p}}} = {\sum \nolimits_i}{{E}}_{{\rm{dipole}}}^i\left( {{r}} \right).$

采用Luttinger和Tisza^[86]的偶极子叠加理论, 可得到B离子处的偶极子电场为

$\begin{split}{{{E}}_{\rm{p}}}({{{R}}_{\rm{B}}}) \approx\;& \frac{{\left\langle {{{{p}}_{\rm{A}}}} \right\rangle }}{{4{\text{π}}{\varepsilon _0}{v_{{\rm{cell}}}}}}\left( { - 4{\text{π}} + \frac{{4{\text{π}}}}{3}} \right) \\ & + \frac{{\left\langle {{{{p}}_{\rm{B}}}} \right\rangle }}{{4{\text{π}}{\varepsilon _0}{v_{{\rm{cell}}}}}}\left( { - 4{\text{π}} + \frac{{4{\text{π}}}}{3}} \right)\\&+ \frac{{\left\langle p_{\rm O /\!/} \right\rangle }}{{4{\text{π}}{\varepsilon _0}{v_{{\rm{cell}}}}}}\left( { - 4{\text{π}} + \frac{{4{\text{π}}}}{3} + {\rm{30}}} \right)\\& + \frac{{\left\langle {{{{p}}_{\rm{O}}}_ \bot } \right\rangle }}{{4{\text{π}}{\varepsilon _0}{v_{{\rm{cell}}}}}}\left( { - 4{\text{π}} + \frac{{4{\text{π}}}}{3} - {\rm{15}}} \right),\end{split}$

其中$\left\langle {{{{p}}_{\rm{A}}}} \right\rangle $, $\left\langle {{{{p}}_{\rm{B}}}} \right\rangle $, $\left\langle p_{\rm O/\!/} \right\rangle$和$\left\langle {{{{p}}_{\rm{O}}}_ \bot } \right\rangle $分别表示A离子、B离子、${{\rm{O}}_{/\!/} }$离子和${{\rm{O}}_ \bot }$离子的平均偶极矩; ${v_{{\rm{cell}}}}$是晶胞体积. ${{\rm{O}}_{/\!/} }$离子表示在B离子位移方向上的两个O离子, ${{\rm{O}}_ \bot }$离子为在于B离子位移方向垂直平面上的4个O离子. 由于钙钛矿中B离子的位移主要受${O_{/\!/} }$离子影响^[87], 因此可假设$\left\langle {{{{p}}_{\rm{A}}}} \right\rangle \approx \left\langle {{{{p}}_{\rm{B}}}} \right\rangle \approx {\rm{0}}$, 则可以将偶极子电场简化为

$\begin{split}{{{E}}_{\rm{p}}}\left( {{{{R}}_{\rm{B}}}} \right) \approx\; & \frac{{\left\langle {{{{p}}_{\rm{B}}}} \right\rangle }}{{4{\text{π}}{\varepsilon _0}{v_{{\rm{cell}}}}}}\left( { - 4{\text{π}} + \frac{{4{\text{π}}}}{3}} \right) \\ &+ \frac{{\left\langle {{{{p}}_{{{\rm{O /\!/}} }}}} \right\rangle }}{{4{\text{π}}{\varepsilon _0}{v_{{\rm{cell}}}}}}\left( { - 4{\text{π}} + \frac{{4{\text{π}}}}{3} + 30} \right).\end{split}$

为了进一步简化, 假设$\left\langle {{{{p}}_{\rm{B}}}} \right\rangle = \left\langle {{{{p}}_{{{\rm{O}}_ \bot }}}} \right\rangle = {{{p}}_0}$, 则可以得到宏观极化强度P的表达式

${{P}} = \frac{{2{{{p}}_0}}}{{{v_{{\rm{cell}}}}}},$

将其代入(11)式中可得

${{{E}}_{\rm{p}}}\left( {{{{R}}_{\rm{B}}}} \right) \approx - \frac{{{p}}}{{{\varepsilon _0}}} + \frac{{{p}}}{{3{\varepsilon _0}}} + \frac{{15{{p}}}}{{4{\text{π}}{\varepsilon _0}}},$

则B离子受到的极化电场极化力为

$\begin{split}& {{{F}}_{\rm{p}}}\left( {{{{R}}_{\rm{B}}}} \right) = {q_{\rm{B}}} \cdot {{{E}}_{\rm{p}}}\left( {{{{R}}_{\rm{B}}}} \right) \\={}& {q_{\rm{B}}}\left( { - \frac{{{p}}}{{{\varepsilon _0}}} + \frac{{{p}}}{{3{\varepsilon _0}}} + \frac{{15{{p}}}}{{4{\text{π}}{\varepsilon _0}}}} \right),\end{split}$

其中${q_{\rm{B}}}$为B离子的有效电荷量.
到此为止, 已经得到了B离子所受到全部内部微观力: 局域有效原子力${{F}}_{{\rm{ion}}}^{\rm{B}}\left( {{z_{\rm{B}}}} \right)$和极化力${{{F}}_{\rm{p}}}\left( {{{{R}}_{\rm{B}}}} \right)$, 接下来推导外部电场E时对B离子所产生的电场外力${{{F}}_{{\rm{ext}}}}$. 由电位移矢量方程${{D}} = {\varepsilon _0} \cdot {{E}} + {{P}}$可得到电场E与极化极化强度P的关系, 其中P为电位移矢量, 表示外部电场与内部偶极子相互作用后在材料表面所产生的净电荷. 因此可以得到施加外部电场后对B离子所产生的电场力为

${{{F}}_{{\rm{ext}}}} = {q_{\rm{B}}}\frac{{{D}}}{{{\varepsilon _0}}} = {q_{\rm{B}}}\left( {{{E}} + \frac{{{P}}}{{{\varepsilon _0}}}} \right),$

则由(8)式、(15)式和(16)式可以得到B离子所受的合力为

$\begin{split} {{{F}}_{{\rm{all}}}} =\;& {{F}}_{{\rm{ion}}}^{\rm{B}} + {{{F}}_{\rm{p}}} + {{{F}}_{{\rm{ext}}}} \\ =\;&- (2{a_{\rm{B}}}{z_{\rm{B}}} + 4{b_{\rm{B}}}z_{\rm{B}}^{\rm{3}}){ {{z}}} \\ &+ {q_{\rm{B}}}\left( { - \frac{{{P}}}{{{\varepsilon _0}}} + \frac{{{P}}}{{3{\varepsilon _0}}} + \frac{{15{{P}}}}{{4{\text{π}}{\varepsilon _0}}}} \right) \\ &+ {q_{\rm{B}}}\Big({{E}} + \frac{{{P}}}{{{\varepsilon _0}}}\Big) \\ =\;& - (2{a_{\rm{B}}}{z_{\rm{B}}} + 4{b_{\rm{B}}}z_{\rm{B}}^3){ {{z}}} \\ &+ {q_{\rm{B}}}\left( {\frac{{{P}}}{{3{\varepsilon _0}}} + \frac{{15{{P}}}}{{4{\text{π}}{\varepsilon _0}}}} \right) + {q_{\rm{B}}}{{E}} .\end{split} $

之前假设$\left\langle {{{{p}}_{\rm{B}}}} \right\rangle = \left\langle {{{{p}}_{{{\rm{O}}_ \bot }}}} \right\rangle $, 则可通过${{P}} = 2{q_{\rm{B}}}{z_{\rm{B}}}{{z}}/ {v_{{\rm{cell}}}}$将B离子的位移矢量${z_{\rm{B}}}{{z}}$与极化强度P联系起来. 当处于平衡态时, ${{{F}}_{{\rm{all}}}} = 0$, 得到如下关系式

$\begin{split}{{E}} ={}& \left( {\frac{{{a_{\rm{B}}}{v_{{\rm{cell}}}}}}{{q_{\rm{B}}^{\rm{2}}}} - \frac{1}{{3{\varepsilon _0}}} - \frac{{15}}{{4{\text{π}}{\varepsilon _0}}}} \right){{P}} \\& + \left( {\frac{{{b_{\rm{B}}}v_{{\rm{cell}}}^3}}{{q_{\rm{B}}^4}}} \right){{{P}}^3}, \end{split}$

其关系曲线如图9(a)所示, 即P-E关系的“S”曲线. 但是当改变外加电场, 测量铁电材料的极化强度, 得到图9(b)中的电滞回线, 而不是图9(a)中的“S”曲线, 这是因为在图9(b)中的蓝色虚线区域, P具有多值特点, 而且宏观NC现象是热力学不稳定的, 所以表现出滞回曲线的特点. 图中红色虚线为铁电体处于初始状态时的扫描曲线, 蓝色曲线为经过一个扫描周期后的扫描曲线.
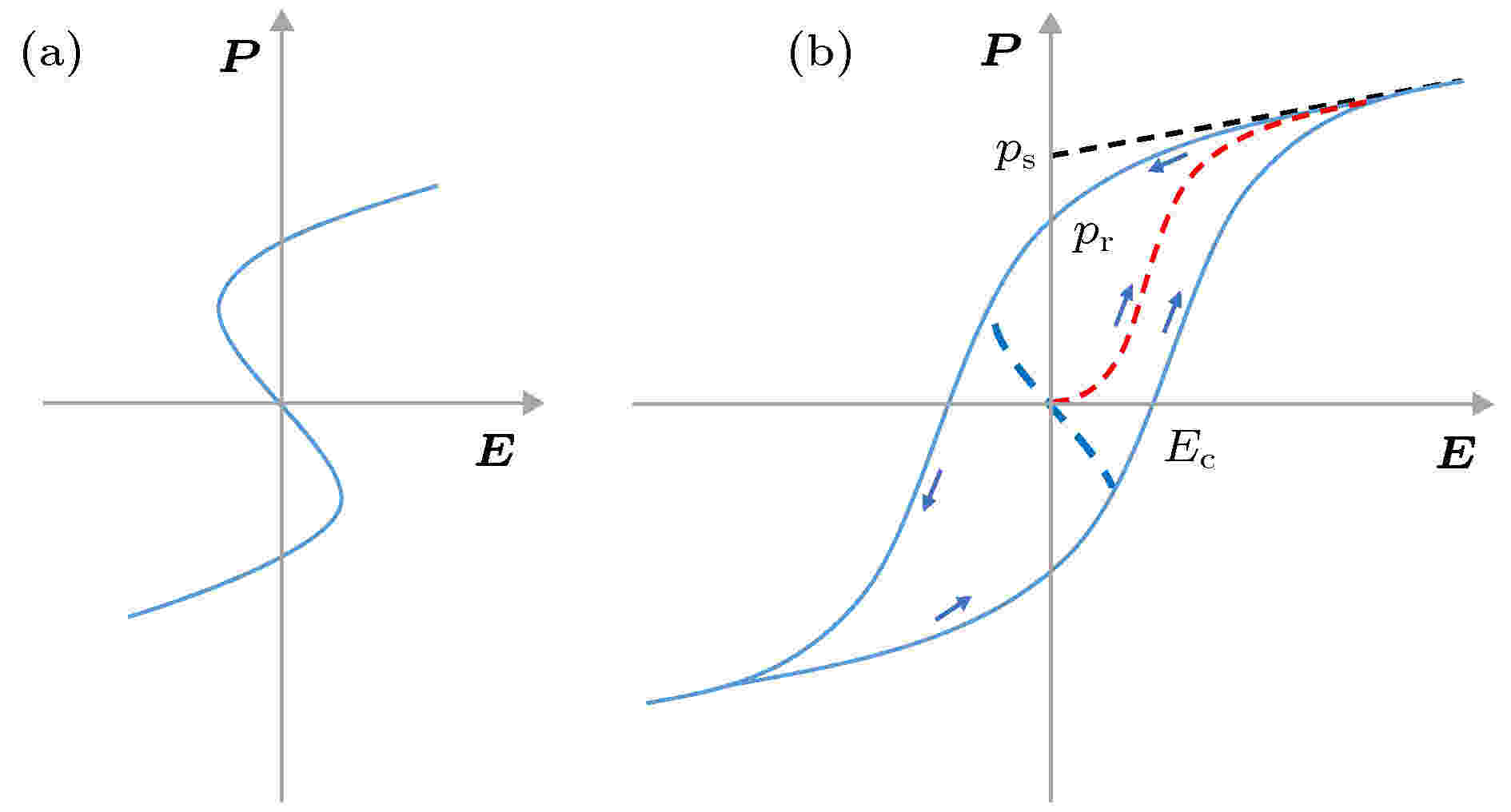图 9 铁电体极化强度P和电场E之间的关系　(a) P-E关系图; (b) 电滞回线图
Figure9. The relationship between polarization P and electric field E of ferroelectrics: (a) P vs. E; (b) hysteresis diagram.

前面提到, 材料表面净电荷${{{Q}}_{{\rm{FE}}}}$即为电位移矢量, 即

${{{Q}}_{{\rm{FE}}}} = {\varepsilon _0} \cdot {{E}} + {{P}},$

而对于铁电材料, 可假设认为${{P}} \gg {\varepsilon _0} \cdot {{E}}$^[88], 则${{{Q}}_{{\rm{FE}}}} \approx {{P}}$. 根据电场强度定义式${{E}} = {{{V}}_{{\rm{FE}}}}/{t_{{\rm{FE}}}}$其中${t_{{\rm{FE}}}}$为铁电材料的厚度, 可得到表面净电荷${{{Q}}_{{\rm{FE}}}}$与电压${{{V}}_{{\rm{FE}}}}$的关系

$\begin{split}{{{V}}_{{\rm{FE}}}} =\; & {t_{{\rm{FE}}}}\left( {\frac{{{a_{\rm{B}}}{v_{{\rm{cell}}}}}}{{q_{\rm{B}}^{\rm{2}}}} - \frac{1}{{3{\varepsilon _0}}} - \frac{{15}}{{4{\text{π}}{\varepsilon _0}}}} \right){{{Q}}_{{\rm{FE}}}}\\ & + {t_{{\rm{FE}}}}\left( {\frac{{{b_{\rm{B}}}v_{{\rm{cell}}}^{\rm{3}}}}{{q_{\rm{B}}^4}}} \right){{Q}}_{{\rm{FE}}}^3,\end{split}$

其关系曲线如图10(a)所示, 根据宏观电容定义式${C_{{\rm{FE}}}} = \partial {Q_{{\rm{FE}}}}/\partial {V_{{\rm{FE}}}}$, 可以看到图10(a)中红色虚线框区域为NC区域.
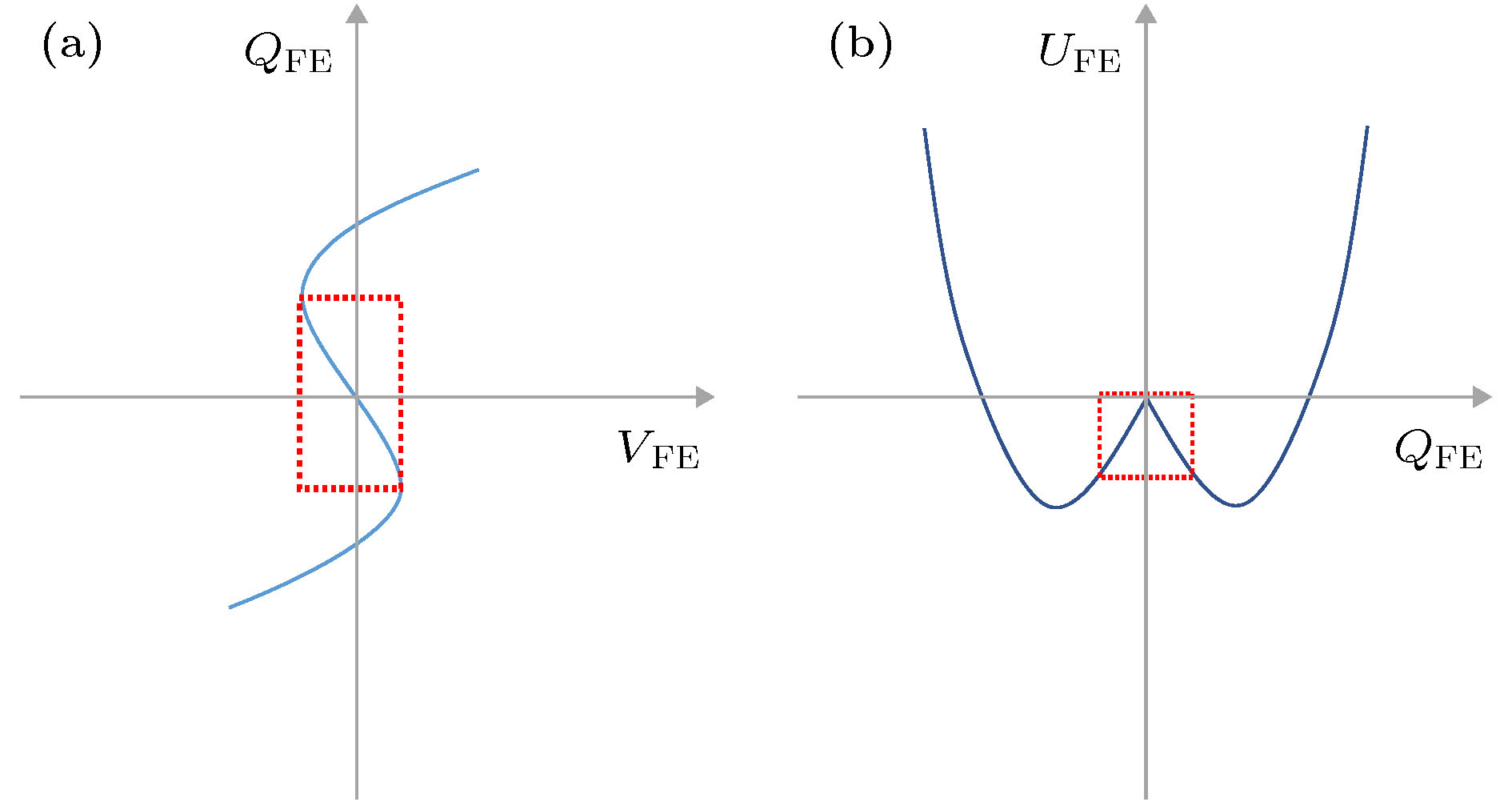图 10 (a) 铁电体的Q_FE-V_FE关系图; (b)铁电体的U_FE-Q_FE关系图
Figure10. (a) Q_FE vs. V_FE of ferroelectrics; (b) U_FE vs. Q_FE of ferroelectrics.

对于铁电材料, 其吉布斯自由能公式为

$U = \alpha {{{P}}^2} + \beta {{{P}}^4} + \lambda {{{P}}^6} - {{E}} \cdot {{P}},$

其中$\alpha $, $\beta $和$\lambda $为材料的常量参数, 而且铁电材料的$\alpha $为负值^[89]. 可得到能量${U_{{\rm{FE}}}}$与电荷${{{Q}}_{{\rm{FE}}}}$的关系

$\begin{split}{U_{{\rm{FE}}}} =\;& \left( {\alpha - \frac{{{a_{\rm{B}}}{v_{{\rm{cell}}}}}}{{q_{\rm{B}}^2}} + \frac{1}{{3{\varepsilon _0}}} + \frac{{15}}{{4{\text{π}}{\varepsilon _0}}}} \right){{Q}}_{{\rm{FE}}}^2 \\ &+ \left( {\beta - \frac{{{b_{\rm{B}}}v_{{\rm{cell}}}^{\rm{3}}}}{{q_{\rm{B}}^{\rm{4}}}}} \right){{Q}}_{{\rm{FE}}}^4 + \lambda {{Q}}_{{\rm{FE}}}^{\rm{6}},\end{split}$

其关系曲线如图10(b)所示, 根据微观电容定义式${C_{{\rm{FE}}}} = {\left( {{\partial ^2}{U_{{\rm{FE}}}}/\partial Q_{{\rm{FE}}}^2} \right)^{ - 1}}$, 可以看到图10(b)中红色虚线框区域为NC区域.
通过上述分析, 得到了铁电材料的本征NC区域, 但是由于NC在宏观上是热力学不稳定的, 因此, 需要串联一个线性的介质层电容(C_DE), 通过介质层中退极化场的作用^[88], 将铁电层的电容(C_FE)稳定在NC区域. 不同电容系统自由能和极化强度的关系曲线如图11所示, 可以看到, 在串联了一个合适大小的C_DE之后, 系统自由能的最低点位于铁电电容的NC区域, 因此铁电层的NC得到了稳定^[90].
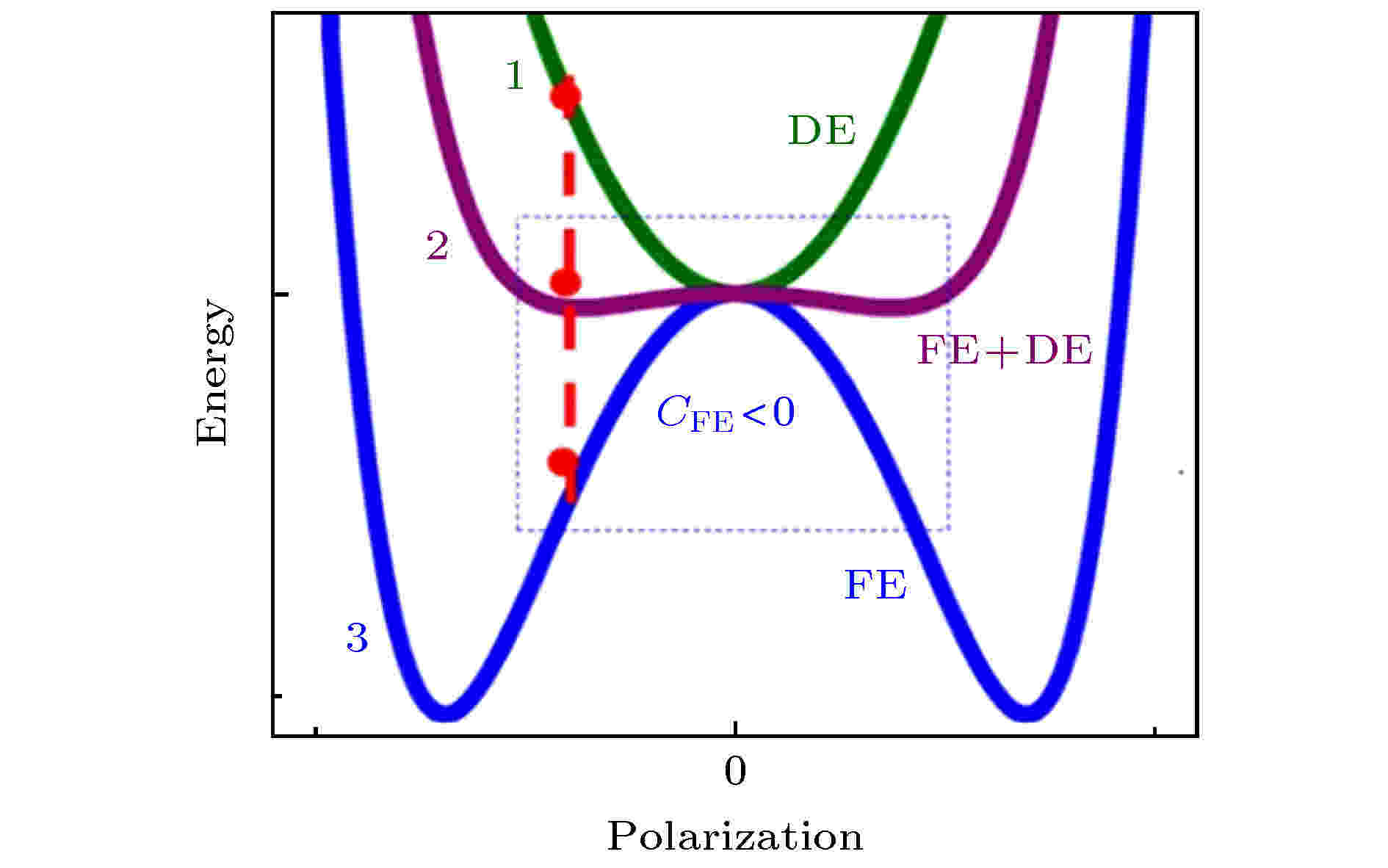图 11 不同电容系统的自由能曲线形貌^[90]
Figure11. Energy landscapes of C_FE, C_DE and their series combination^[90].

由于热力学不稳定性, 不能直接在电路中观察到NC现象, 只能通过对比串联后系统电容的增大来间接证明铁电层中NC的存在. 其测量电路如图12(a)所示, 测量模式称为小信号测量, 被认为是一种准静态的测量模式, 因为在测量过程中没有发生极化翻转^[91]. Gao等^[90]制备了图12(b)所示的LaAlO₃/Ba_0.8Sr_0.2TiO₃超晶格结构, 其中LaAlO₃为介质层, Ba_0.8Sr_0.2TiO₃为铁电层, 超晶格结构的电容和相同厚度LaAlO₃介质层的电容与电压的关系如图12(c)所示, 可以看到, 与相同厚度的LaAlO₃介质层相比, 超晶格结构的电容增大了, 这说明Ba_0.8Sr_0.2TiO₃铁电层的电容为负值.
图 12 小信号测量模式测量铁电体NC　(a) 等效电路图^[91]; (b) LAO/BSTO超晶格结构示意图^[90]; (c) 电容与电压的关系^[90]
Figure12. Ferroelectric NC measured by small-signal measurement mode: (a) Equivalent circuit diagram^[91]; (b) schematic diagram of a LAO/BSTO superlattice stack^[90]; (c) capacitance dependence on voltage^[90].

上述的测量结果是在单电畴近似下得到的, 在多电畴铁电材料Hf_xZr_1–xO₂(HZO)电容与介质层电容串联结构中没有发现这种直流增强效应^[92], 因此人们认为目前HZO中的NC是瞬态NC^[93], 即接下来要讨论的内容.
3 -->

3.2.2.瞬态NC

到目前为止, 得到了铁电材料的自由能曲线中的本征NC区域, 并通过串联一个介质层电容, 通过介质层中能够退极化场的作用, 将铁电层的电容稳定在NC区域, 称为稳态NC. 在铁电材料中还存在另外一种NC, 即瞬态NC, 是指在R-C_FE串联电路(图13)中, 当施加一个正(负)脉冲电压时, 在短时间内C_FE上的电压与电荷的变化相反, 即C_FE上的电荷增加(减少)而电压下降(增加). 关于铁电材料瞬态NC的实验现象已有大量的文献报道^[94-97], 其中, Khan等^[94]首次在R-C_FE串联电路中观察到了瞬态NC现象, 认为当施加的脉冲电压超过铁电材料的矫顽电压时, 铁电体发生极化翻转, 极化状态从一个稳定态转换到另外一个稳定态, 会经过NC区域, 从而表现出了短暂的NC效应, 因此, 瞬态NC效应可以看成是铁电体极化翻转过程中在自由能曲线中存在负曲率区域的一种表征. 之后人们指出导致瞬态NC的直接原因是铁电材料极化强度的变化速度比金属极板上自由电荷的变化速度快, 而且这个差值越大, 瞬态NC现象越明显^[98].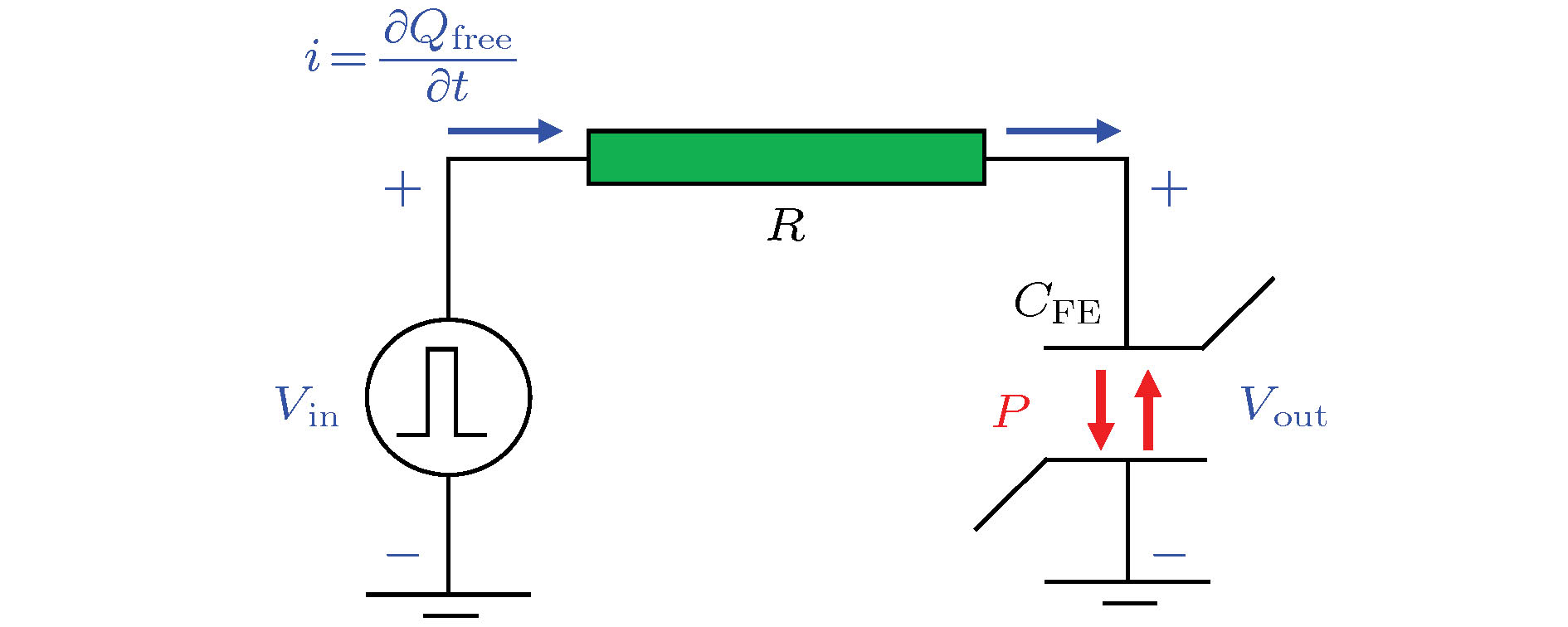
图 13 测量铁电体瞬态NC的R-C_FE等效电路图^[99]
Figure13. The schematic of a R-C_FE circuit for studying the transient NC in ferroelectrics^[99].

2018年, Chang等^[99]结合基尔霍夫电路定律和朗道自由能理论对瞬态NC的物理机制进行了分析. 考虑图13所示的电路, 根据基尔霍夫定律, 电极板电荷${Q_{{\rm{free}}}}$与时间t的关系为

$\frac{{\partial {Q_{{\rm{free}}}}}}{{\partial t}} = \frac{{{V_{{\rm{in}}}} - {V_{{\rm{out}}}}}}{{R \cdot A}} = \frac{{{V_{{\rm{in}}}} - {V_{{\rm{FE}}}}}}{{R \cdot A}},$

其中$\partial {Q_{{\rm{free}}}}/\partial t$为电流密度, ${V_{{\rm{in}}}}$为输入电压, ${V_{{\rm{out}}}} = {V_{{\rm{FE}}}}$为铁电材料电容电压, R为串联电阻电阻值, A为铁电电容的表面积. 根据电位移矢量方程, 可将自由电荷${Q_{{\rm{free}}}}$写为

${Q_{{\rm{free}}}} = {\varepsilon _0}{E_{{\rm{FE}}}} + P,$

其中${E_{{\rm{FE}}}}$表示穿过铁电层的电场, ${\varepsilon _0}$为真空介电常数, P为铁电层的平均极化强度, 其与时间的微分方程可根据L-K方程^[100]写为

$\gamma \frac{{\partial P}}{{\partial t}} = \left( { - 2{\alpha _1} + \frac{{{t_{{\rm{dep}}}}}}{{{\varepsilon _0}{t_{{\rm{FE}}}}}}} \right)P - 4{\alpha _{11}}{P^3} - 6{\alpha _{111}}{P^5} + {E_{{\rm{FE}}}},$

其中$\gamma $为铁电材料的粘度系数, ${\alpha _1}$、${\alpha _{11}}$和${\alpha _{111}}$是铁电材料的热膨胀系数, ${t_{{\rm{FE}}}}$和${t_{{\rm{dep}}}}$分别是铁电层的厚度和有效退极化场厚度.
结合(23)式—(25)式中可得

$R \cdot A\frac{{\partial {Q_{{\rm{free}}}}}}{{\partial t}} = {V_{{\rm{in}}}} - \frac{{{t_{{\rm{FE}}}}\left( {{Q_{{\rm{free}}}} - P} \right)}}{{{\varepsilon _0}}}.$

对(24)式两边取时间的微分可得

$\frac{{\partial {V_{{\rm{FE}}}}}}{{\partial t}} = \frac{{{t_{{\rm{FE}}}}}}{{{\varepsilon _0}}}\left( {\frac{{\partial {Q_{{\rm{free}}}}}}{{\partial t}} - \frac{{\partial P}}{{\partial t}}} \right).$

由(25)式与(26)式可以看到, 自由电荷和极化强度之间通过${E_{{\rm{FE}}}}$耦合. 同时, 自由电荷和极化强度对时间的响应速度分别被R和$\gamma $所限制. 通过欧拉方法对(25)式和(26)式进行模拟, 并且在模拟之前, 先输入一个负电压, 使得铁电层中的初始极化方向为负. 模拟结果如图14和图15所示. 图14(a)展示了R-C_FE电路对脉冲输入信号的响应, 可以看到, 有两个区域中铁电电容上自由电荷增加(减少)但是电压降低(升高), 也就是$\partial {Q_{{\rm{free}}}}/\partial V < 0$. 从图14(b)中可以看到, NC仅发生于铁电层中极化翻转时, 而且自由电荷和极化强度与随时间的变化基本一样. 但对其取时间微分, 结果如图14(c)所示, 自由电荷和极化强度对时间的微分总是存在一个差距, 而且在第一个NC发生时有$\partial P/\partial t > \partial {Q_{{\rm{free}}}}/\partial t$. 从(27)式可以看到, 铁电电容电压随时间的变化速度与自由电荷和极化强度随时间的变化速率之间的差值线性相关. 对比图14(a)和(d)可看到, 在NC刚开始出现时, $\partial {V_{{\rm{FE}}}}/\partial t$变为负值, 而当在施加负向脉冲电压区间内的的NC发生时, $\partial {V_{{\rm{FE}}}}/\partial t$变为正值, 此时自由电荷和极化强度减小, 但$\left| {\partial P/\partial t} \right| > \left| {\partial {Q_{{\rm{free}}}}/\partial t} \right|$. 因此在NC发生时, 极化强度的变化速率总是快于自由电荷的变化速率的.
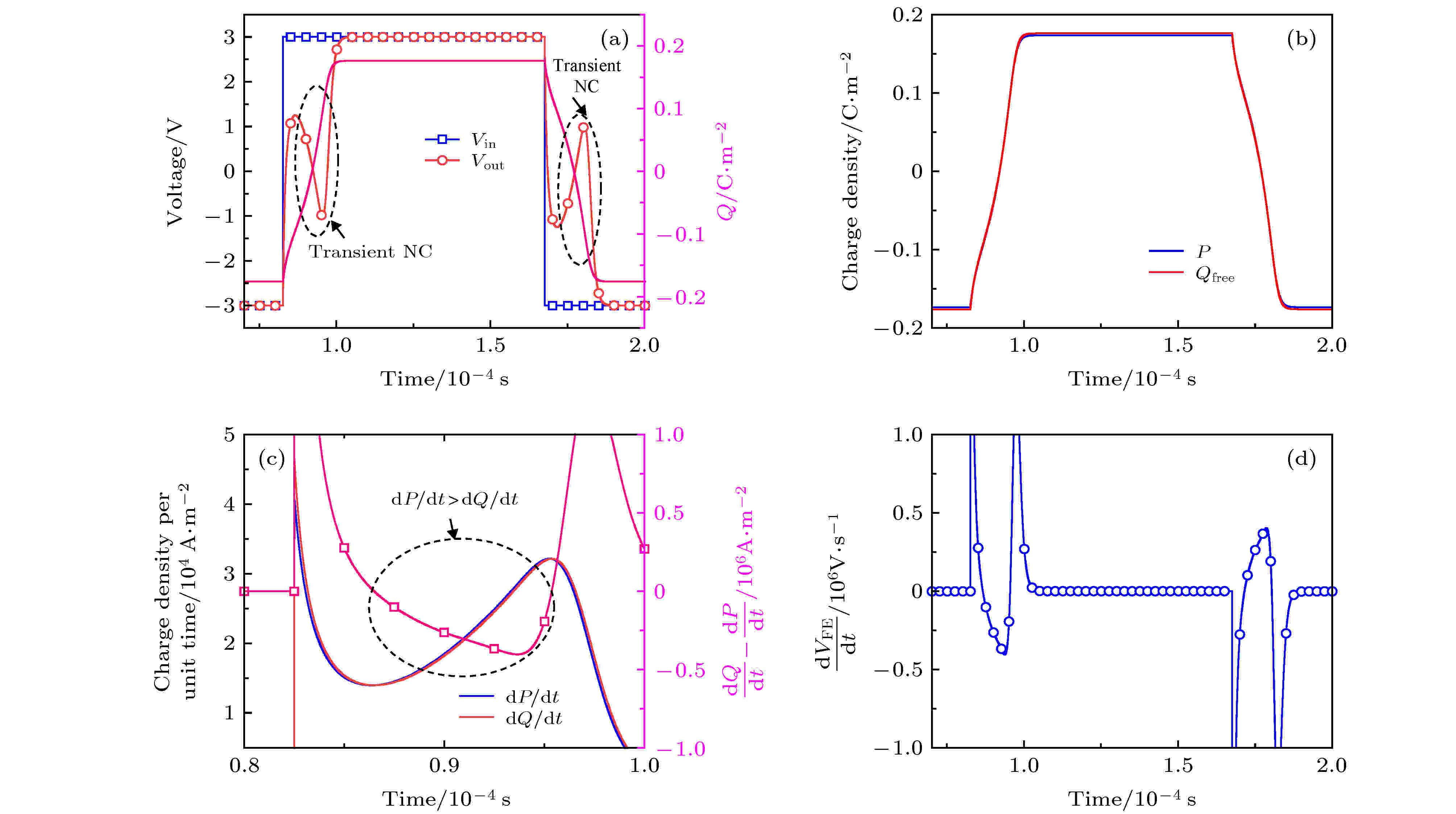图 14 瞬态NC模拟结果^[99]　(a) 输入电压, 输出电压和铁电电容上自由电荷与时间的关系图; (b) 极化强度和自由电荷与时间的关系图; (c) 极化强度和自由电荷对时间的微分结果及其差值随时间的变化曲线; (d) 铁电电容电压的变化速度随时间的变化曲线
Figure14. The simulation results of transient NC^[99]: (a) Input voltage, output voltage, and free charge on a ferroelectric capacitor as functions of time; (b) polarization and free charge as functions of time; (c) charge density per unit time for free charge and polarization and the difference between them; (d) change in the voltage across a ferroelectric capacitor per unit time as a function of time.

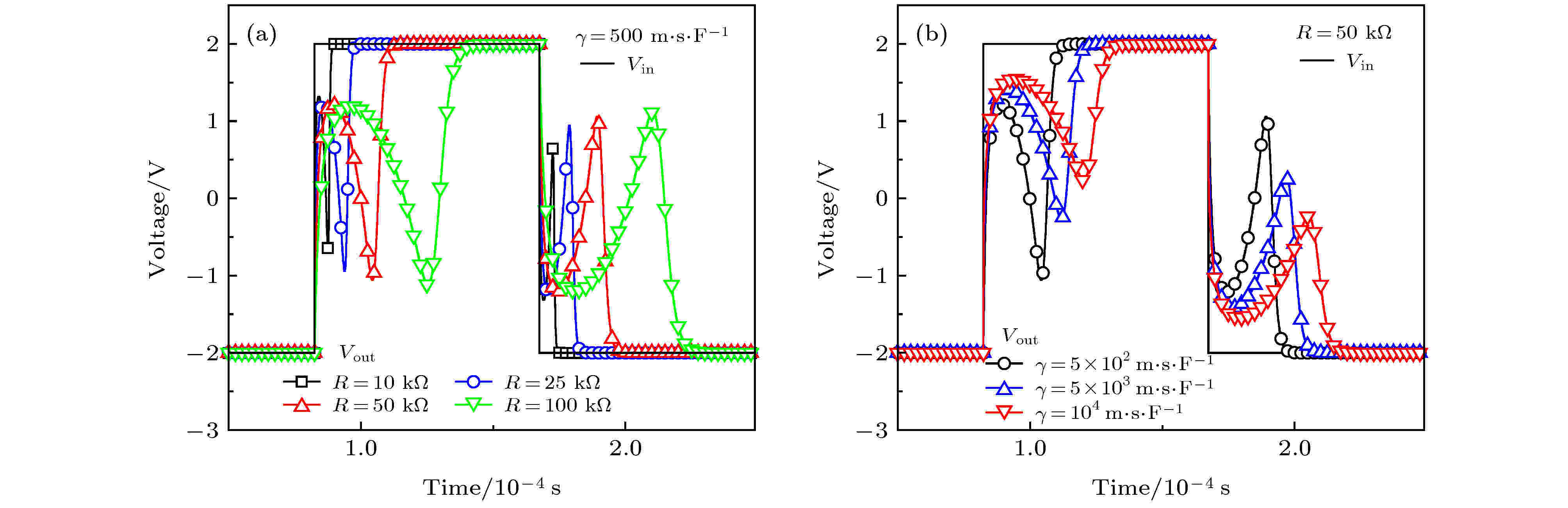图 15 (a) 外电阻对R-C_FE电路中瞬态NC的影响; (b) 粘度系数对R-C_FE电路中瞬态NC的影响^[99]
Figure15. (a) The effect of the external resistance on transient NC in a R-C_FE circuit; (b)the effect of the viscosity coefficient on transient NC in a R-C_FE circuit^[99].

由上述分析可得, R-C_FE中的瞬态NC与自由电荷和和极化强度随时间的变化速率之间的差值相关, 因此由(25)式和(26)式可得, 外部电阻和粘度系数对瞬态NC会产生影响, 其模拟结果如图15所示. 由图15(a)可以看到, 随着外部电阻的增大, 极化翻转速度变慢, 瞬态NC持续的时间也变长, 这是因为自由电荷需要更多的时间在铁电电容中建立电场. 而且瞬态NC现象也随着外部电阻的增大而变得更明显, 这是因为随着R的增大, $\partial {Q_{{\rm{free}}}}/\partial {\rm{t}}$将变小, (27)式中的差值将增大, 因此瞬态NC现象将变得更明显. 同样地, 随着粘度系数的增大, 极化翻转速度变慢, $\partial P/\partial {\rm{t}}$将变小, 因此瞬态NC持续的时间增长, 而(27)式中的差值将减小, 瞬态NC现象也变得更不明显. Hoffmann等^[101]从铁电畴翻转动力学角度分析得到了R-C_FE电路中瞬态NC的持续时间$\Delta T$与外部电阻和粘度系数的关系式

$\Delta T = \left| {{C_{{\rm{FE}}}}} \right|\left( {RA + {t_{{\rm{FE}}}}\gamma } \right)\exp \left( {{{{E_{\rm{a}}}}}/{{{E_{{\rm{FE}}}}}}} \right),$

其中, ${C_{{\rm{FE}}}}$为铁电层单位面积电容, ${t_{{\rm{FE}}}}$为铁电层厚度, ${E_{\rm{a}}}$为铁电畴翻转的激活电场^[102], ${E_{{\rm{FE}}}}$为铁电层的内部电场. 可以看到, 瞬态NC的持续时间与随外部电阻和粘度系数的增大而增大, 与图15中的结果相符合.
瞬态NC效应并不能在无滞回Fe-NCFETs中导致瞬时电流增强效应, 这是因为瞬态NC的发生伴随着铁电体的极化翻转, 而无滞回Fe-NCFETs没有发生极化翻转^[103]. 因此由于瞬态NC导致也能观察到SS的下降的Fe-NCFETs, 但由于自由电荷迟滞现象的存在, 器件往往伴随着较大的回滞电压^[104], 对于低功耗逻辑晶体管的实现是不利的, 因此仍需要进行更深入的研究.
2 -->

3.3.NC器件的工作区域

通过以上分析得到了铁电材料NC的物理来源, 但是由于NC区域多值特性导致的热力学不稳定性, 因此单独的铁电材料存在滞回曲线, 并不能稳定在NC区域工作, 需要串联一个合适的常规正电容, 才能将铁电材料稳定在NC区域工作.
考虑如图12所示的电容模型, 采用稳态NC理论, 则各电容器上的电荷量分别为

${Q_{{\rm{FE}}}} = {V_{{\rm{FE}}}}{C_{{\rm{FE}}}},$

${Q_{\rm{S}}} = {\psi _{\rm{S}}}{C_{\rm{S}}} = \left( {{V_{\rm{G}}} - {V_{{\rm{FE}}}}} \right){C_{\rm{S}}},$

由串联电容的带电荷量相等可得

${Q_{{\rm{FE}}}} = \left( {{V_{\rm{G}}} - {V_{{\rm{FE}}}}} \right){C_{\rm{S}}},$

则(20)式与(31)式曲线的交点即为器件的工作点^[26], 如图16(b)和(c)所示, 图中红色实线为${V_{\rm{G}}} = 0$时的沟道电容电荷量与铁电层电压的关系曲线, 红色虚线为${V_{\rm{G}}} > 0$时的沟道电容电荷量与铁电层电压的关系曲线. 可以看到, 当${C_{\rm{S}}} < \left| {{C_{{\rm{FE}}}}} \right|$时, 两条曲线只有一个交点, 如图16(b)所示, 此时器件的转移特性曲线无回滞现象, 称之为Fe-FETs^[91](图16(d)). 而当${C_{\rm{S}}} > \left| {{C_{{\rm{FE}}}}} \right|$时, 两条曲线在NC区域有多个交点, 如图16(c)所示, 此时器件的转移特性曲线有回滞现象, 称之为Fe-NCFETs(图16(e)). 而且可以看到, 当${C_{\rm{S}}}$增大时, SS低, 但同时回滞现象也变严重了, 从(2)式中也可看到这个趋势.
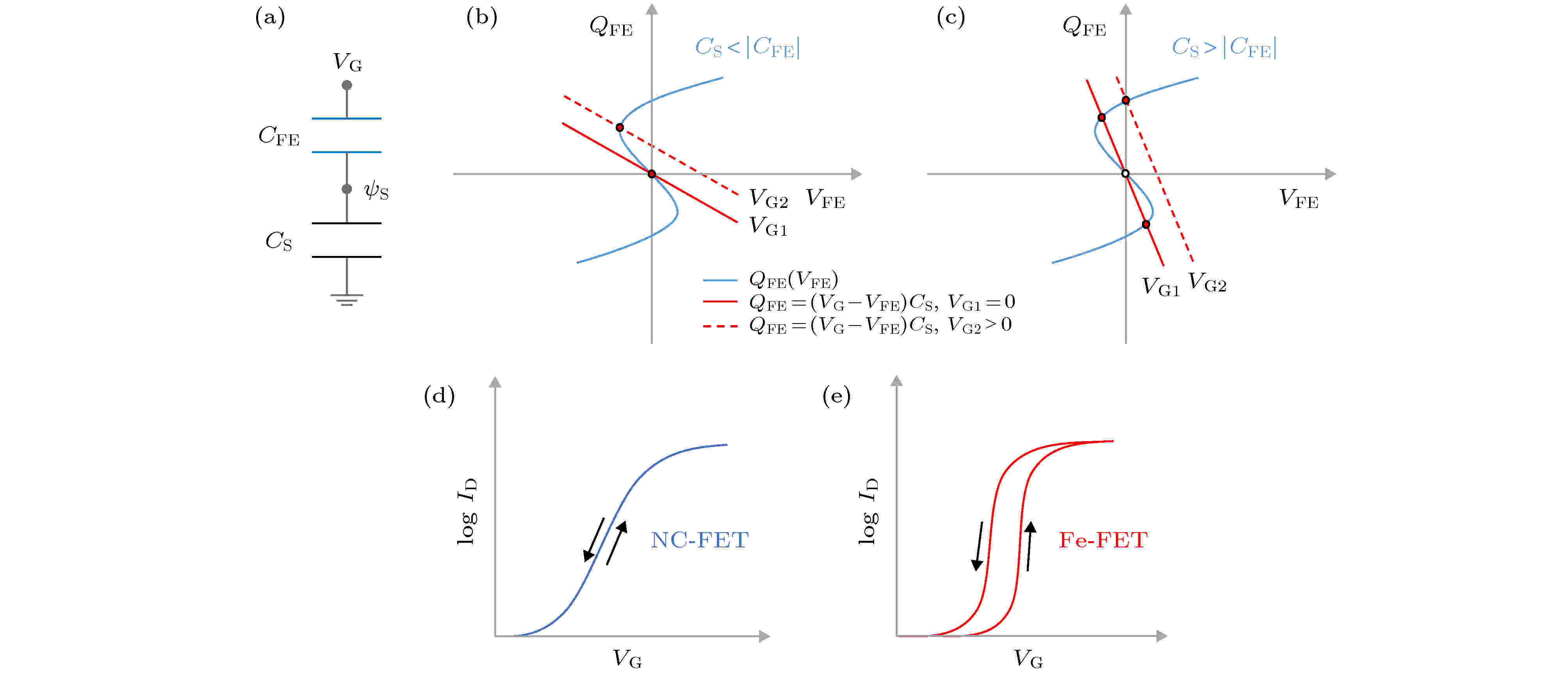图 16 器件电容电荷量与电压的关系　(a) 电容模型; (b) ${C_{\rm{S}}} < \left| {{C_{{\rm{FE}}}}} \right|$; (c) ${C_{\rm{S}}} < \left| {{C_{{\rm{FE}}}}} \right|$; (d) Fe-NCFETs^[91]; (e) Fe-FET^[91]
Figure16. The relationship between capacitive charge and voltage of the device: (a) Capacitance model; (b) ${C_{\rm{S}}} < \left| {{C_{{\rm{FE}}}}} \right|$; (c) ${C_{\rm{S}}} < \left| {{C_{{\rm{FE}}}}} \right|$ (d) Fe-NCFETs^[91]; (e) Fe-FETs^[91].

所以器件的SS与回滞现象之间存在一个本质上的矛盾关系, 即不能同时减小SS和回滞现象, Wang等^[105]结合Kolmogorov-Avrami-Ishibashi(KAI)方程^[106], 从多电畴动态反转的角度解释了器件SS与回滞现象之间存在矛盾关系的物理机制.
对于逻辑器件的应用, 回滞现象是要避免的, 可以通过调节${C_{\rm{S}}}$与${C_{{\rm{FE}}}}$之间的比例, 从而调制器件的SS与回滞电压, 即所谓的电容匹配(capacitance matching)工程, 研究人员也对此进行了大量的研究^[107-112]. Si等^[113]制作了以Hf_0.5Zr_0.5O₂/Al₂O₃为介质层的二维MoS₂沟道器件, 其中2 nm厚的Al₂O₃作为掩蔽层和电容匹配层, 器件的SS降低到47 mV/dec, 而且消除了回滞现象, 为低功耗逻辑器件的实现提供了选择.

沟道的形状和材料种类对于器件的性能有着很大的影响. 近十年来, 为了提高器件性能, 延续摩尔定律, 各种新技术和新沟道材料被应用于Fe-NCFETs上, 也就是所谓的沟道工程, 研究人员对这个方向开展了大量的研究工作. 而氧化铪基铁电材料因具有高介电常数和与CMOS技术兼容性高等优点被人们广泛应用于Fe-NCFETs研究. 以下从沟道的形状和材料种类出发, 分别从三维沟道材料和二维沟道材料的角度总结了近几年来采用氧化铪基铁电体的Fe-NCFETs的重要研究成果, 并对器件的SS、开关电流比、回滞电压和漏电流等性能的改善进行了分析概述, 对于Fe-NCFETs的设计与制造具有指导意义.
2

-->

4.1.三维沟道

采用硅、锗基材料、III-V族化合物和碳纳米管等三维材料作为沟道的Fe-NCFETs有诸多优点, 如与传统CMOS工艺的兼容性高、沟道与铁电层之间界面性能好、在三维尺度上的可控性高、电学性能稳定. 因此, 三维沟道Fe-NCFETs被认为是下一代MOS晶体管的主要选择之一^[114].
3 -->

4.1.1.硅沟道

氧化铪基铁电材料的出现, 使得利用传统CMOS技术集成硅和铁电材料成为了可能, 自2014年Cheng和Chin^[115]首次报道了SS小于60 mV/dec的采用氧化铪基铁电体(HfZrO, HZO)的硅基Fe-NCFETs以来, 人们对硅基Fe-NCFETs进行了广泛的研究, 器件的结构也从最开始的平面型(planar)发展到现在的FinFET型和GAA纳米线型.
Fan等^[116]制备了铁电层为10 nm-HfAlO (Al: 6%) 的planar型硅基Fe-NCFETs, 如图17(a)所示, 器件的性能优异, 其开关电流比大于10⁸, 正扫和反扫SS均低于25 mV/dec, 而且回滞电压仅为20 mV, 成功实现了无回滞且低SS的Fe-NCFETs. 他们采用了TaN作为栅电极, 栅电极会对HfAlO铁电层施加应力, 这个应力会导致HfAlO由顺电性的单斜晶相向具有铁电性的正交晶相转变^[117], 而且由于铁电体具有压电性质, 应力的存在还会增大铁电体的极化强度, 因此随着TaN中的N含量的增加, TaN的应力逐渐增大, HfAlO的剩余极化强度增大, 如图17(b)所示. 而且他们还采用了CF₄等离子体对器件进行钝化处理以消除界面处的氧离子缺陷, 从而减小了界面陷阱电荷对铁电层极化作用的抑制作用, 增大了铁电层对沟道表面电势的放大作用, 如图17(c)所示. 由图17(d)可以看到, 在经过栅电极应力和F离子钝化作用后, 不仅器件的SS大大降低了, 而且回滞现象也得到了抑制. 他们通过测量恒压应力和相对应力诱导漏电流的方法研究了F离子钝化作用对铁电层NC的影响, 进一步证明界面处的陷阱电荷和氧离子空位在经过F离子钝化作用后被消除了^[118].
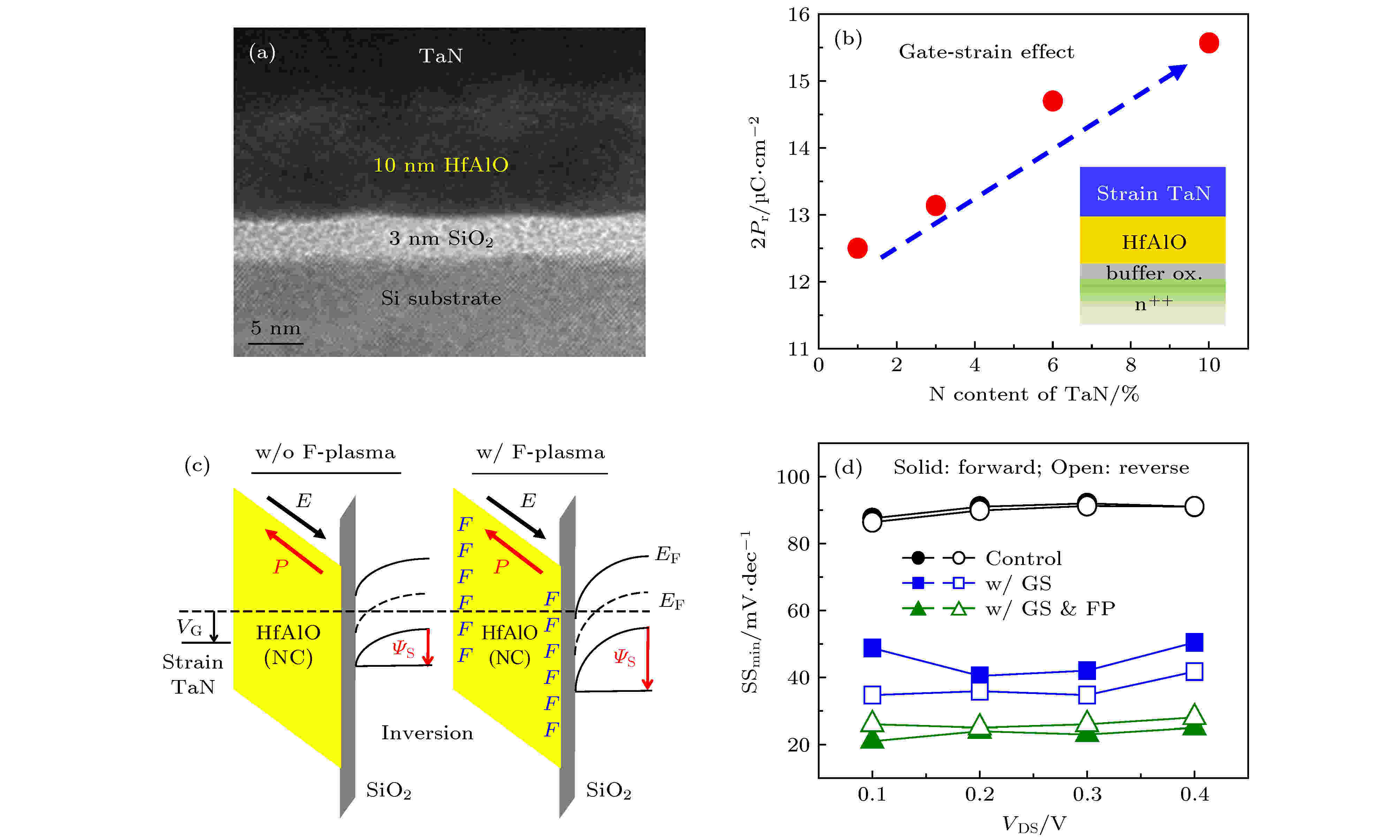图 17 平面型硅基- HfAlO Fe-NCFETs^[116]　(a) 器件截面透射电子显微镜(transmission electron microscope, TEM)图; (b) 剩余极化强度与TaN中N含量的关系曲线; (c) F离子钝化作用对铁电层能带影响的示意图; (d) 不同处理作用后器件的SS与源漏电压的关系
Figure17. Planar Silicon based HfAlO Fe-NCFETs^[116]: (a) HR TEM cross-section image; (b) polarization as a function of nitrogen content of TaN; (c) schematic band diagram of HfAlO before and after F-passivation; (d) SS as a function of V_DS after different treatments.

Cheng等^[119]研究了Hf_1–xZr_xO₂中Zr含量对planar型硅基Fe-NCFETs性能的影响, 发现随着Zr含量的增大, Hf_1-xZr_xO₂中正交相的占比增大, 铁电层的极化强度增大, 即铁电性增强, 器件的SS减小. 但当Zr的含量超过50%时, Zr离子的漂移作用会导致介质层漏电流的增大, 从而降低了铁电层电容与沟道电容的匹配度, 导致SS退化, 最后通过实验确定当Zr含量为25%时, 器件的SS和介质层漏电流都较小. 其他研究人员也对planar型硅基Fe-NCFETs中栅电极种类^[120]、铁电层退火温度与电压扫描范围^[121]和ZrO₂籽晶层^[122]对器件性能的影响进行了研究. 由于结构本身的限制因素, planar型硅基Fe-NCFETs和传统MOSFETs相比, 其亚阈值区性能改善并不理想, 维持SS低于60 mV/dec的电流区间往往小于三个数量级, 因此人们对其他结构如FinFET和GAA结构硅基Fe-NCFETs进行了研究.
Li等^[123]报道了首个硅基铁电NC FinFET, 他们采用5 nm Hf_0.42Zr_0.58O₂作为铁电体, 其结构如图18(a)所示, 沟道宽度约为30 nm, 栅介质层为MFMIS双TiN栅结构. 图18(b)是不同栅压下铁电层对栅压的放大系数曲线, 可以看到, 栅压放大系数最大为1.4左右. 而由图18(c)可以看到, 铁电NC FinFET的SS为58 mV/dec, 比传统FinFET的SS(88 mV/dec)下降了1.5倍, 与图18(b)中的测量结果相符合. 2018年Zhou等^[25]采用全耗尽SOI为衬底, 制作了铁电层为4 nm Hf_0.5Zr_0.5O₂的硅基铁电NC FinFET, 不仅将器件SS降低到54.5 mV/dec, 而且还消除了回滞现象, 使其回滞电压仅为3 mV. 除此之外, 他们还首次在硅基Fe-NCFETs中发现了由于铁电层NC和漏端电容耦合作用导致的负DIBL和NDR效应, 对于抑制短沟效应和实现器件尺寸的进一步减小是很有利的.
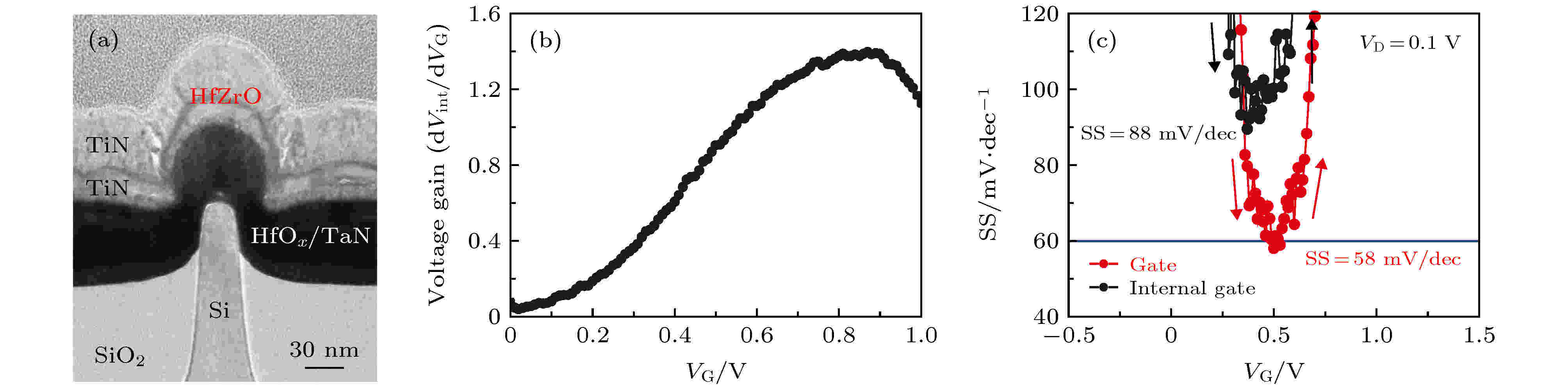图 18 硅基NCFinFET^[123]　(a) 器件截面TEM图; (b) 铁电NCFinFET的栅压放大系数与栅压的关系曲线; (c) 常规FinFET和铁电NCFinFET的SS与栅压的关系曲线
Figure18. Silicon based NC-FinFET^[123]: (a) TEM cross-sectional image of NC-FinFET with TiN internal gate, HfZrO FE film and TiN gate; (b) the gate amplification coefficient as a function of V_G for NC-FinFET; (c) SS as a function of V_G for conventional FinFET and NC-FinFET.

Zhang等^[124]在超薄SOI衬底制备了如图19(a)所示的硅基铁电NC p-FinFET, 其栅介质层结构为Hf_0.42Zr_0.58O₂/TiN/TaN/TiN/W, 这种多层栅电极结构可以在降低铁电层和栅电极之间界面态密度的同时增强对铁电层的栅控能力, 同时在铁电层与沟道之间沉积了一层1 nm厚的HfO₂界面层, 改善了铁电层与沟道之间的界面性能. 而且多栅结构会对Fin沟道施加应力, 增强了沟道载流子迁移率. 图19(b)是传统FinFET和NC-FinFET在不同栅长下的I_DS数值, 可以看到, NC-FinFET的I_DS比传统FinFET的I_DS提高了250%以上, 这得益于NC-FinFET较低的界面态密度和较高的载流子迁移率. 在这个器件中, HZO铁电薄膜的厚度已经达到了3 nm, 为实现5 nm及以下节点高性能和低功耗晶体管性能需求提供了技术支持. Chen等^[125]也对具有不同栅长和沟道宽度的硅基HZO NC FinFET进行了研究, 发现当栅长是沟道宽度的十倍以上时, 器件的SS大都能低于60 mV/dec, 这是因为栅长变大时, 铁电层对栅压的放大作用增强, 从而增强了栅电极对沟道的控制能力, 改善了SS. 可以看到, 在结合了铁电材料之后, FinFET型器件的电流性能提升(~250%)比planar型器件的电流性能提升(~50%)更明显, 这得益于FinFET结构器件具有更强的栅控能力.
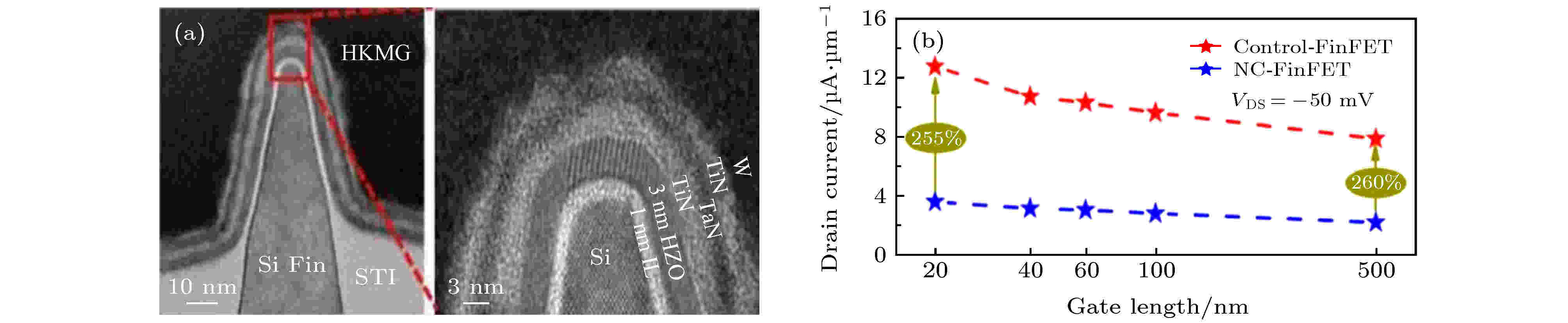图 19 (a)硅基铁电NCp-FinFET截面TEM图^[124]; (b) 源漏电流与栅长关系曲线^[124]
Figure19. (a) TEM cross-sectional image of silicon based NC-p-FinFET^[124]; (b) I_DS as a function of gate length^[124].

Lee等^[126]首次报道了GAA双层堆叠硅纳米线结构Fe-NCFETs, 器件采用10 nm HZO为铁电层, 表现出了优异的电学性能, 其开关电流比超过10⁸, 平均SS为43.85 mV/dec, 回滞电压仅为2.77 mV. 器件结构如图20(a)所示, 共栅堆叠纳米线结构可以有效增强栅对沟道的控制能力, 而且在保持器件特征尺寸不变的情况下增加了沟道的有效宽度, 因此增大了器件的跨导和沟道电流, 但是和单层沟道器件相比, 其电流增幅小于两倍, 这是因为双层沟道器件引入了更多的寄生电阻^[127]. 他们还在HZO下面淀积了一层2 nm厚的ZrO₂籽晶(图20(b)), 由HZO的X射线衍射(X-ray diffraction, XRD)曲线(图20(c))可看到, 与没有ZrO₂籽晶层(灰色曲线), 有ZrO₂籽晶层(红色曲线)HZO正交相的衍射强度增强了, 因为ZrO₂籽晶层可在HZO沉积的时候诱导正交相HZO的生成, 提高了HZO的结晶性. 这种采用ZrO₂籽晶层诱导正交相HZO生成的方法省去了传统HZO生长工艺中高温结晶退火步骤, 大大提高了器件的热稳定性.
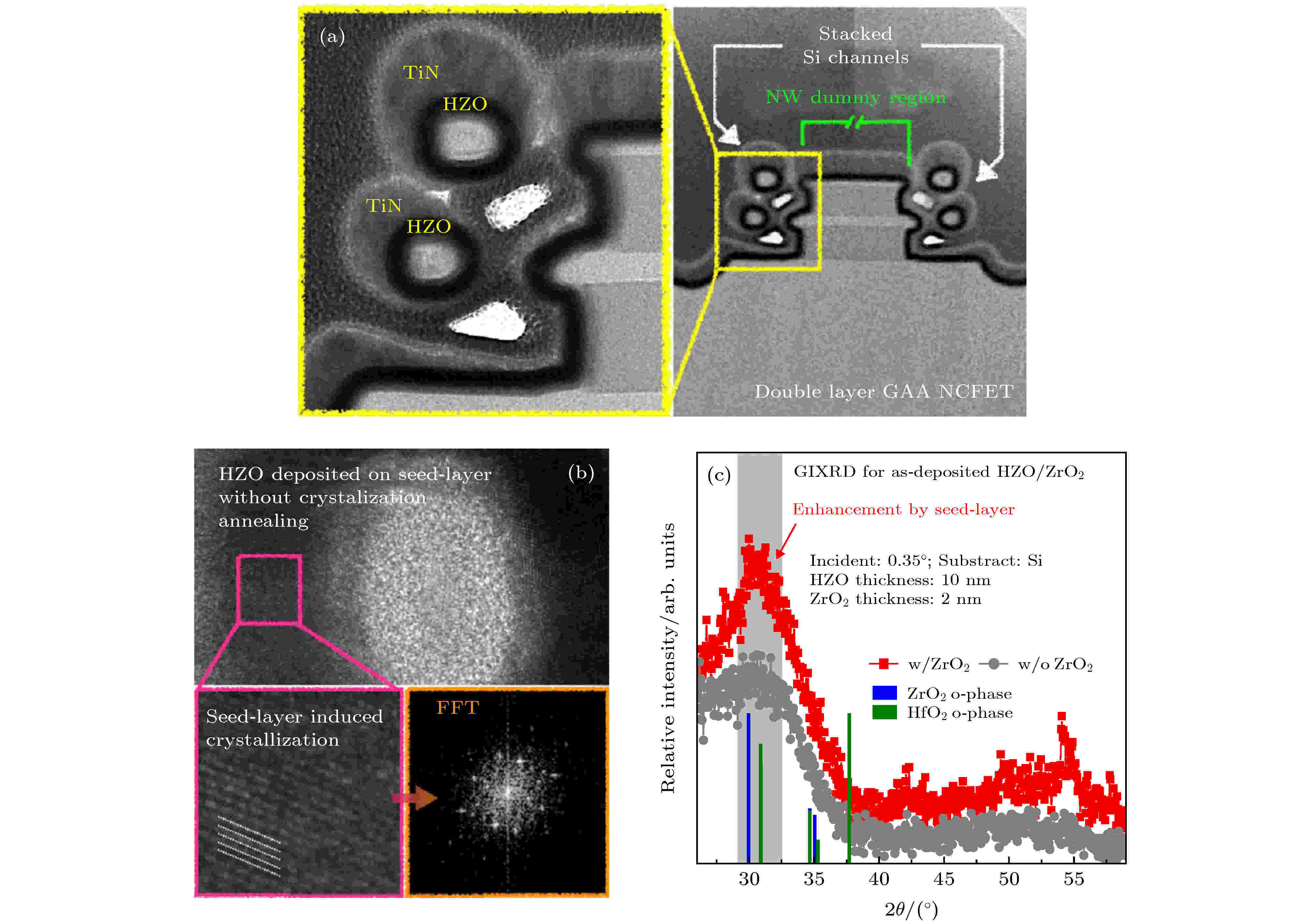图 20 双层堆叠硅纳米线GAA结构Fe-NCFETs^[126]　(a) 器件截面TEM图; (b) 沟道部分高分辨率TEM图; (c) HZO层的掠入角XRD曲线
Figure20. Two-layer stacked silicon nanowire GAA Fe-NCFETs^[126] : (a) TEM cross-sectional image of the device; (b) HRTEM of a portion of the channel; (c) the GIXRD spectrum for the as-deposited HZO layer.

硅基Fe-NCFETs具有与CMOS工艺兼容性高和工艺成熟等优势, 器件也表现出了SS低、开关电流比大和性能稳定等优点, 但是硅材料的载流子有效迁移率低, 限制了晶体管开态电流的大小, 所以人们对采用其他三维沟道材料的Fe-NCFETs进行了研究.
3 -->

4.1.2.锗基材料沟道

锗基材料具有很多优点, 如锗(Ge)的空穴迁移率为1900 cm²·V^–1·s^–1, 是硅的空穴迁移率(430 cm²·V^–1·s^–1)的5倍左右^[128], 而且还可以通过掺入锡(Sn)引入应力从而进一步提高空穴迁移率, 因此人们对Ge基NC-pFET进行了广泛的研究.
Zhou等^[129]报道了第一个SS小于60 mV/dec的Ge基NC-pFET, 他们采用HZO作为铁电层分别制备Ge沟道NC-pFET和Ge_0.96Sn_0.04沟道NC-pFET, 其结构示意图分别为图21(a)和21(b), HZO层的厚度为6.5 nm. 但是器件的性能并不理想, 图21(c)和(d)分别是Ge沟道NC-pFET和Ge_0.96Sn_0.04沟道NC-pFET的转移特性曲线图, 可以看到, 器件的回滞电压分别为2.3 V和0.4 V, 平均SS也仅为60 mV/dec左右, 器件的开关电流比也仅为10³左右, 导致器件的静态功耗大大增加, 这是由于Ge带隙较小(E_{g, Ge} = 0.66 eV), 结间漏电流和带间隧穿漏电流增大, 因此器件的关态漏电流增大. 而且与常规pFET相比, 在V_DD等于1 V时的源漏电流仅提高了20%, NC效应不明显.
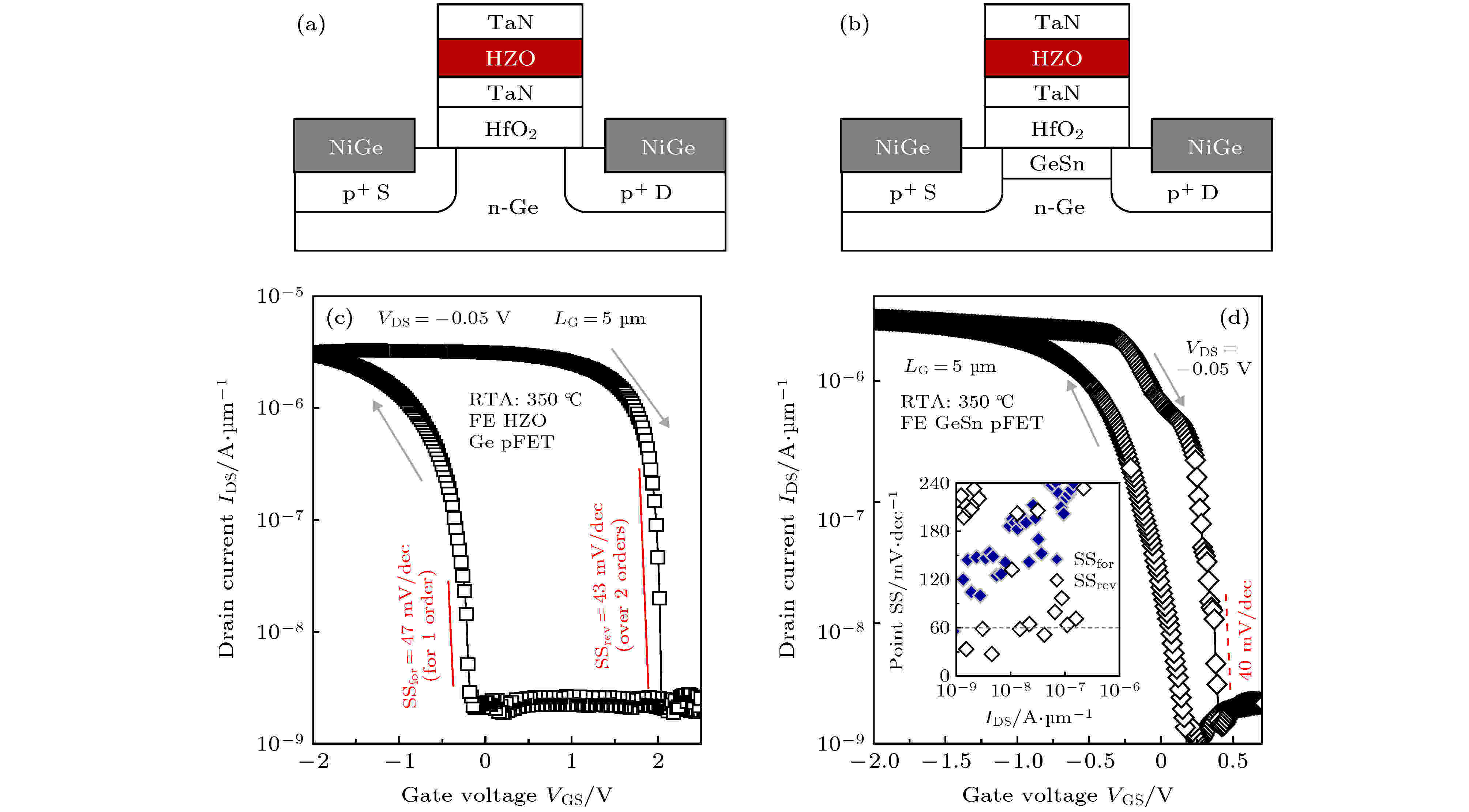图 21 Ge基- HZO NCP型晶体管^[129]　(a) Ge沟道器件结构示意图; (b) Ge-Sn沟道器件结构示意图; (c) Ge沟道器件转移特性曲线; (d) Ge-Sn沟道器件转移特性曲线
Figure21. Germanium based HZO NC-pFET^[129]: (a) Schematic diagram of the device with Ge channel; (b) schematic diagram of the device with Ge-Sn channel; (c) transfer characteristic curve of the device with Ge channel; (d) transfer characteristic curve of the device with Ge-Sn channel.

Zhou等^[130]将Ge_0.96Sn_0.04沟道NC-pFET中HZO的退火结晶温度从400 ℃增大到500 ℃, 改善了铁电相HZO的结晶质量, 提高了其${P_{\rm{r}}}/{E_{\rm{c}}}$比值, 在将SS降低到20 mV/dec以下的同时也将回滞电压也降低到了100 mV以下, 而且与常规pFET相比, 沟道电流改善比例提高到了30%. 随后, 他们研究了Ge沟道NC-pFET中栅电容C_G与跨导G_m的关系^[131], 发现C_G-V_G和G_m-V_G曲线在相同的栅压位置都出现了峰值, 而且SS-I_DS曲线有一个下降台阶, 对应的V_GS与C_G-V_G峰值栅压是一样的, 而且峰值越大, 下降台阶越明显, 进一步证明HZO介质层的NC效应可以有效改善器件的性能. 但文献[131]中只是对器件的性能改善做了表征, 缺少对铁电材料内在结构的研究, 如果能将铁电材料结构的改变及其相关机理研究清楚, 将可以更好地指导器件的设计.
Zhou等^[132]对Ge基NC-pFET中铁电层电容C_FE和沟道电容C_MOS之间的匹配进行了研究, 在Ge沟道器件中发现了NDR效应, NDR效应来源于栅介质层电容与漏端电容的耦合, 其耦合因子${\eta _{{\rm{GD}}}}$的表达式为: ${\eta _{{\rm{GD}}}} = {{{C_{{\rm{GD}}}}} / {\left( {\left| {{C_{{\rm{FE}}}}} \right| - {C_{{\rm{MOS}}}}} \right)}}$, 其中${C_{{\rm{GD}}}}$表示栅与沟道的耦合电容. 当器件没有回滞时, 即$\left| {{C_{{\rm{FE}}}}} \right| > {C_{{\rm{MOS}}}}$, 此时随着铁电层厚度${t_{{\rm{FE}}}}$和栅压${V_{{\rm{GS}}}}$的增大, ${\eta _{{\rm{GD}}}}$增大, NDR效应变明显; 当器件有回滞时, 即$\left| {{C_{{\rm{FE}}}}} \right| < {C_{{\rm{MOS}}}}$, 此时仅在小${V_{{\rm{GS}}}}$下可以观察到NDR效应, 这是因为随着${V_{{\rm{GS}}}}$的增大, ${\eta _{{\rm{GD}}}}$变小, 导致NDR效应消失. 他们首次研究了栅压扫描范围对器件性能的影响^[133], 发现当栅压扫描范围减小时, 器件的回滞现象变明显, 这是因为随着栅压扫描范围的减小, ${P_{\rm{r}}}/{E_{\rm{c}}}$比值减小, $\left| {{C_{{\rm{FE}}}}} \right|$减小, 与CMOS的匹配性变差, 从而导致器件回滞电压增大. Peng等^[134]和Zhang等^[124]分别对钝化时间长短和Hf_1–xZr_xO₂中Zr含量的变化对器件性能的影响进行了研究, 结果表明当钝化时间为40 min和Zr含量为33% 时器件具有较小的SS和较高的I_DS.
Alghamdi等^[135]研究了栅压扫描速度和扫描范围对Ge纳米线NC-pFET的SS和I_DS的影响. 当栅压扫描范围为 ±5 V时, 只有在扫描时间超过25 μs的情况下才能在转移特性曲线中观察到回滞现象, 而当扫描时间超过25 μs时, 随着扫描时间的延长, 回滞电压反而变小, 如图22(a)和(b)所示. 这是因为铁电体中极化子的反转速度较慢, 当栅压扫描速度过快时, 极化子在栅压扫描过程中没有完成一个完整的反转过程, 所以观察不到明显回滞现象; 而当扫描时间超过极化子的反转所需的最小时间时, 随着扫描时间的延长, 极化子能充分跟上扫描电压的变化速度, 所以回滞电压减小. 随着栅压扫描范围的减小, I_DS减小, 而且出现回滞现象的最小扫描时间变长(图22(c)), 他们认为这可能是因为随着最大栅压减小, 极化子的反转速度变慢, 因此导致极化子反转所需最短时间变长, 但是更明确的物理机制需进一步的理论和实验分析.
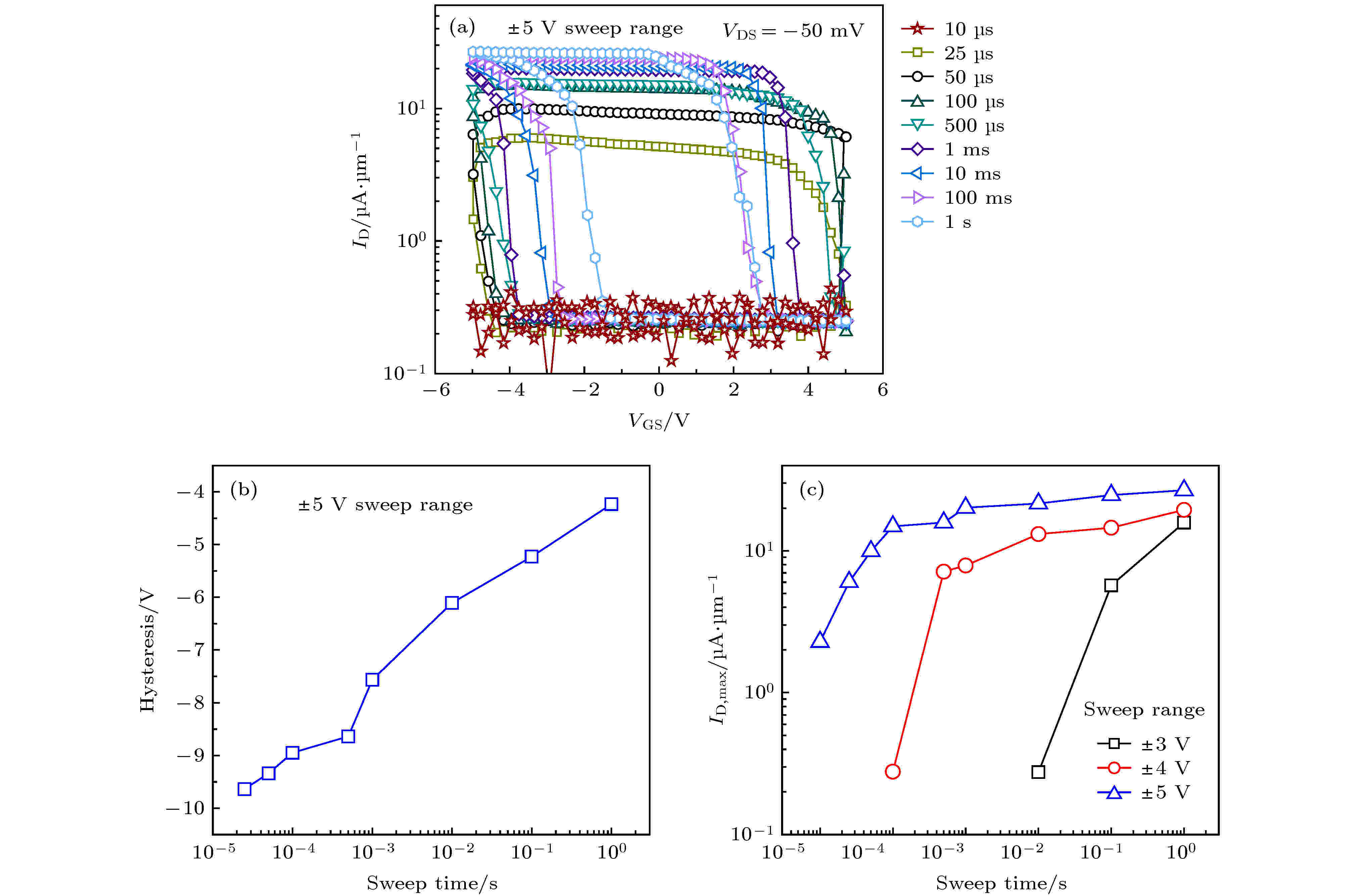图 22 锗纳米线Fe-NCFETs^[135]　(a) 栅压扫描范围为 ±5 V时在不同扫描时间下的转移特性曲线; (b) 栅压扫描范围为 ±5 V时的回滞电压与扫描时间关系曲线; (c) 不同栅压扫描范围下的I_{D, Max}与扫描时间关系曲线
Figure22. Germanium nanowire NC-pFET^[135]: (a) The transfer characteristic curve at different sweep times for ±5 V sweep range; (b) hysteresis versus sweep time for ±5 V sweep range; (c) maximum drain current versus sweep time for different sweep ranges.

Ge基材料由于具有较高的空穴迁移率, 因此被广泛应用于NC-pFET, 但是目前仍然存在一些关键问题, 比如高频下滞回现象明显、由于Ge材料带隙较小导致开关电流比小、Ge_xSn_y沟道中难以实现Sn元素的高浓度掺杂以及与CMOS技术的兼容性问题等.
3 -->

4.1.3.III-V族化合物沟道

III-V族化合物材料, 包括GaAs、InAs、InGaAs和InSb等, 具有较高的电子迁移率(如: μ_{n, InAs} = 42000 cm²·V^–1·s^–1), 是Si电子迁移率(1600 cm²·V^–1·s^–1)的十倍以上, 因此被认为是nMOS沟道材料极具潜力的选择^[128].
Luc等^[136]报道了第一个SS小于60 mV/dec的平面型In_0.53Ga_0.47As沟道Fe-NCFETs, 其结构示意图如图23(a)所示, 采用8 nm HZO作为铁电层, 在HZO与沟道之间有1 nm的Al₂O₃介质层, 衬底为InP. 他们研究了不同退火温度和退火时间下的器件性能, 发现当退火温度为500 ℃以及退火时间为30 s时, 器件的性能最好, 此时器件的转移特性曲线如图23(c)所示, 可以看到, 当V_DS为0.05 V时, 器件的最小SS达到11 mV/dec, 回滞电压为0.7 V, 开关电流比为10⁵左右. 2019年, Chang等^[137]报道了第一个Fin结构In_0.53Ga_0.47As沟道Fe-NCFETs, 其结构示意图如图23(b)所示, 器件的物理参数和之前报道的平面型器件类似. 其转移特性曲线如图23(d)所示, 当V_DS为0.05 V时, 最小SS为23 mV/dec, 回滞电压为0.2 V, 传输性能与平面型器件相比有所改善, 但是其开关电流比小于10⁵, 低于平面型器件, 这可能是由于FinFET器件的表面态较多导致漏电流增大, 从而降低了开关电流比, 还需要深入研究以探明其内在机理, 进一步提高III-V族沟道Fe-NCFETs的性能.
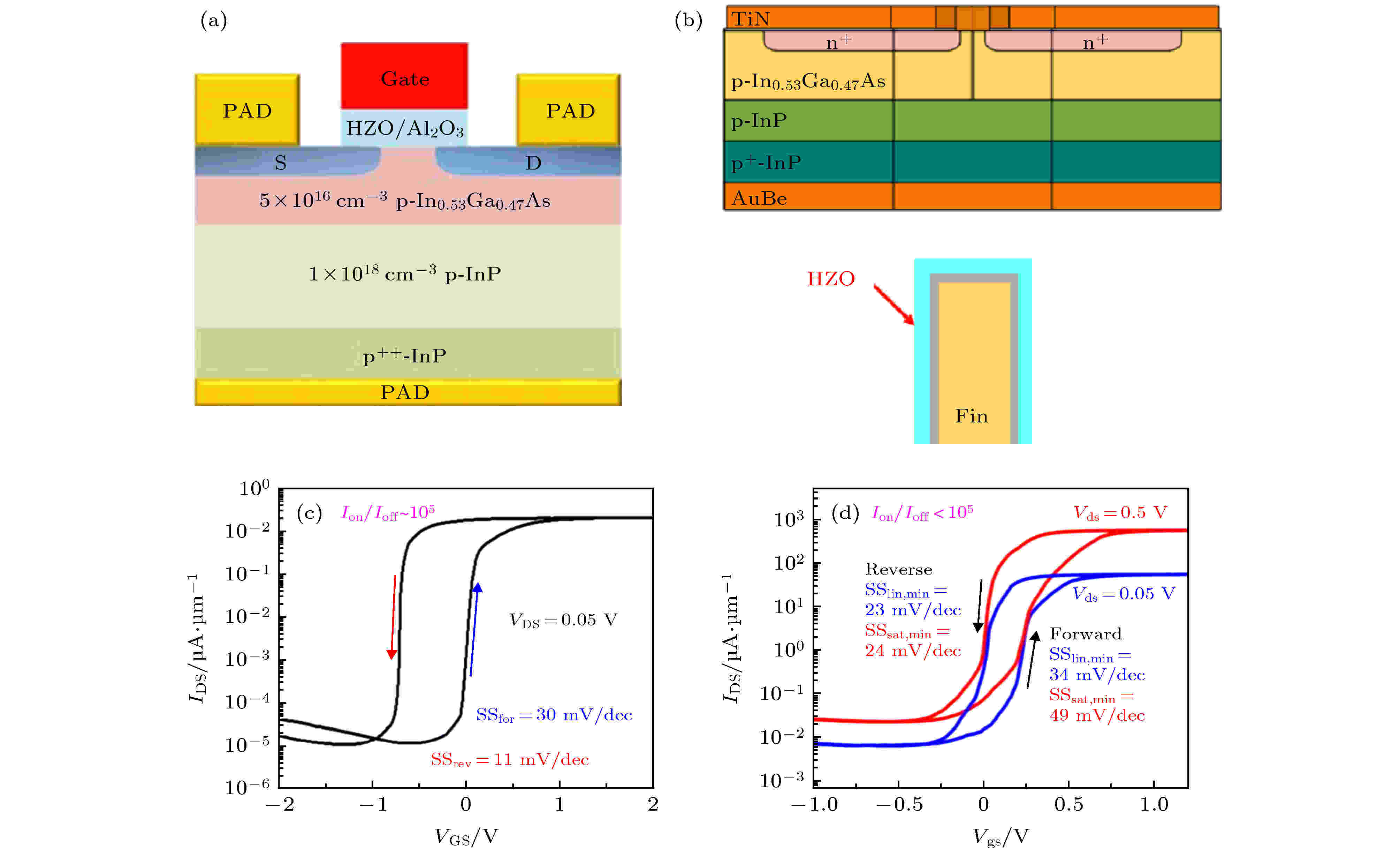图 23 In_0.53Ga_0.47As沟道Fe-NCFETs　(a) 平面型器件的结构示意图^[136]; (b) Fin结构器件的结构示意图平^[137]; (c) 平面型器件的转移特性曲线^[136]; (d) Fin结构器件的转移特性曲线^[137]
Figure23. In_0.53Ga_0.47As channel Fe-NCFETs: (a) Schematic diagram^[136] and (c) transfer characteristic curve of planar device^[136]; (b) schematic diagram^[137] and (d) transfer characteristic curve of Fin device^[137].

III-V族化合物由于具有极高的电子迁移率, 有望替代Si成为nMOS器件的沟道材料, 因此也被用于n型Fe-NCFETs的研究, 但是III-V族化合物与介质层之间的界面性能差和难以实现高浓度掺杂是目前存在的主要问题.
3 -->

4.1.4.碳纳米管沟道

首个碳纳米管Fe-NCFETs由Srimani等^[138]报道, 器件结构如图24(a)所示, 采用MFMIS结构, 其中铁电层为10 nm HfAlO. 与碳纳米管MOSFETs(蓝色曲线)相比, 碳纳米管Fe-NCFETs(红色曲线)的电学性能更优异, 图24(c)为器件的转移特性曲线, 可以看到, 加了HfAlO铁电层之后, 晶体管的SS有所提高, 其中Fe-NCFETs的平均SS为55 mV/dec, 而且栅极漏电流也减小了(图24(d)). 但是由图24(b)中的电滞回线可以看到, HfAlO层的电滞回线不像铁电体的电滞回线, 反而更像由于内部金属栅充放电导致的回滞现象. 由于他们没有对HfAlO的晶相结构进行研究, 因此由于HfAlO的铁电性而导致器件性能改善的说法需要进行进一步的实验验证. 目前关于碳纳米管Fe-NCFETs的实验报道相对较少, 其工作机理也尚未明确, 仍需要进行更多的理论和实验研究.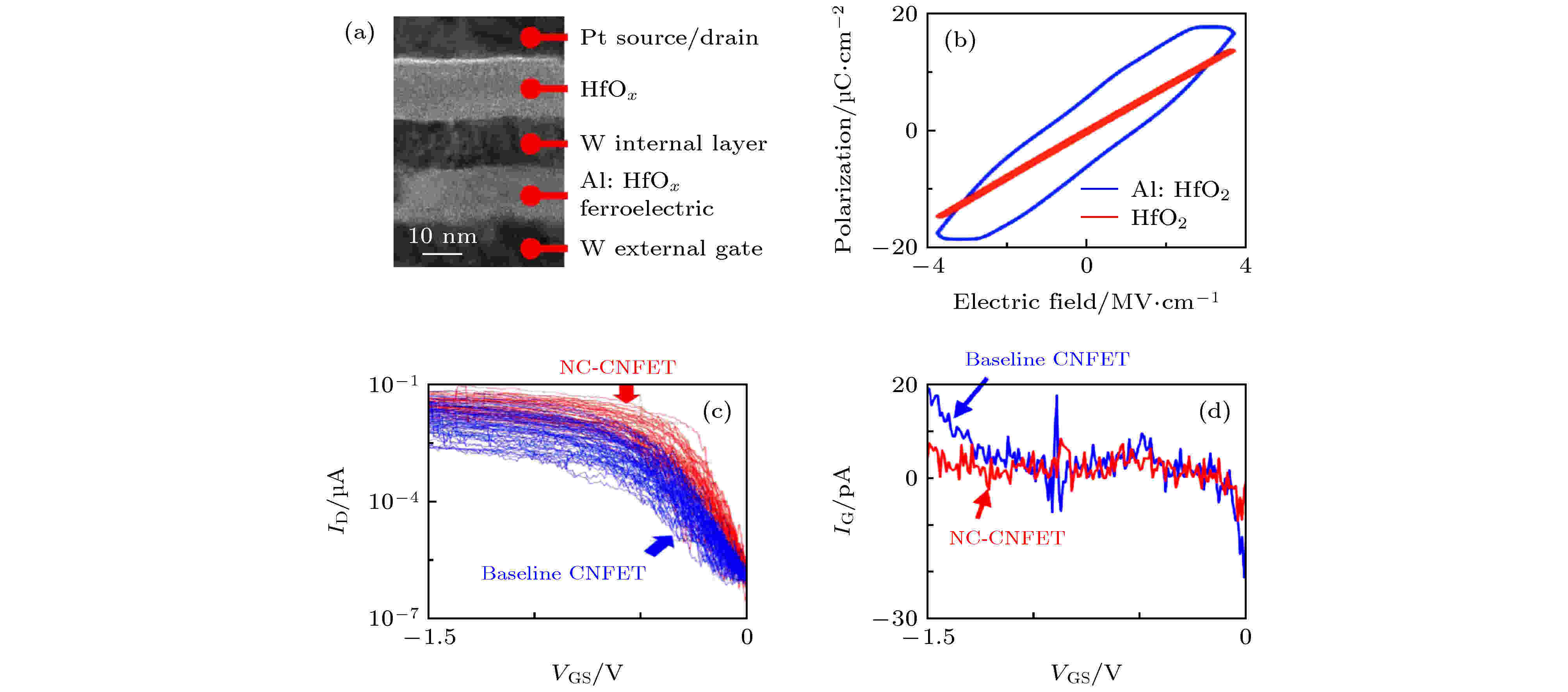
图 24 碳纳米管Fe-NCFETs^[138]　(a) 器件横截面TEM图; (b) 电滞回线; (c) 转移特性曲线; (d) 栅电流和栅压的关系曲线
Figure24. Carbon nanotube Fe-NCFETs^[138]: (a) TEM cross-sectional image; (b) P_r vs. E; (c) the transfer characteristic curve; (d) I_GS as a function of V_GS.

2 -->

4.2.二维材料沟道

二维材料如过渡金属硫族化物、烯类材料和黑磷等具有丰富的界面效应、高的电子迁移率、可调控的光电性能和低的光散射损失等优点^[139]. 而且二维材料的厚度非常小(原子尺度), 所以对于使用二维沟道材料器件, 其理论特征长度非常小, 可以有效地抑制短沟道效应从而获得非常低的关断电流, 对于低功耗晶体管的实现是很有利的. 因此二维材料被广泛应用于Fe-NCFETs^[140-143], 器件也表现出低SS (6.07 mV/dec)^[33]和大开关电流比(> 10⁹)^[144]等优异的电学性能.
3 -->

4.2.1.过渡金属硫族化物材料

Nourbakhsh等^[108]于2017年首次报道了以MoS₂作为沟道的Fe-NCFETs, 器件采用Al掺杂HfO₂作为铁电层. 他们对不同Al掺杂剂量和铁电层厚度做了研究, 发现当采用10 nm厚7.3% Al: HfO₂的铁电层时, 器件表现出较好的电学性能, SS降低到55 mV/dec, 回滞电压为17 mV, 与仅用HfO₂作为介质层的FET相比, 其电压放大了1.25倍, SS下降了10 mV/dec, I_DS增大了两倍左右. 但是SS < 60 mV/dec只能维持1个电流数量级, 这可能是热噪声导致的, 而且他们没有排除内部金属栅的充放电效应对于SS的影响, 因此提到的稳态NC导致SS降低是有待讨论的.
Yap等^[145]报道了相同结构的Fe-NCFETs, 如图25(a)所示. 他们指出, 当扫描电压为 ±7 V时, 转移特性曲线表现出顺时针回滞曲线(图25(b)), 这是由于MoS₂/Si₃N₄界面层陷阱电荷充放电导致的; 当扫描电压增大到10 V时, 转移特性曲线表现出逆时针回滞曲线(图25(c)), 这是由于扫描过程中极化子的反转导致的. 当对器件施加脉冲电压时也发现了同样的情况, 与瞬态电容理论模型分析得到的结果一致.
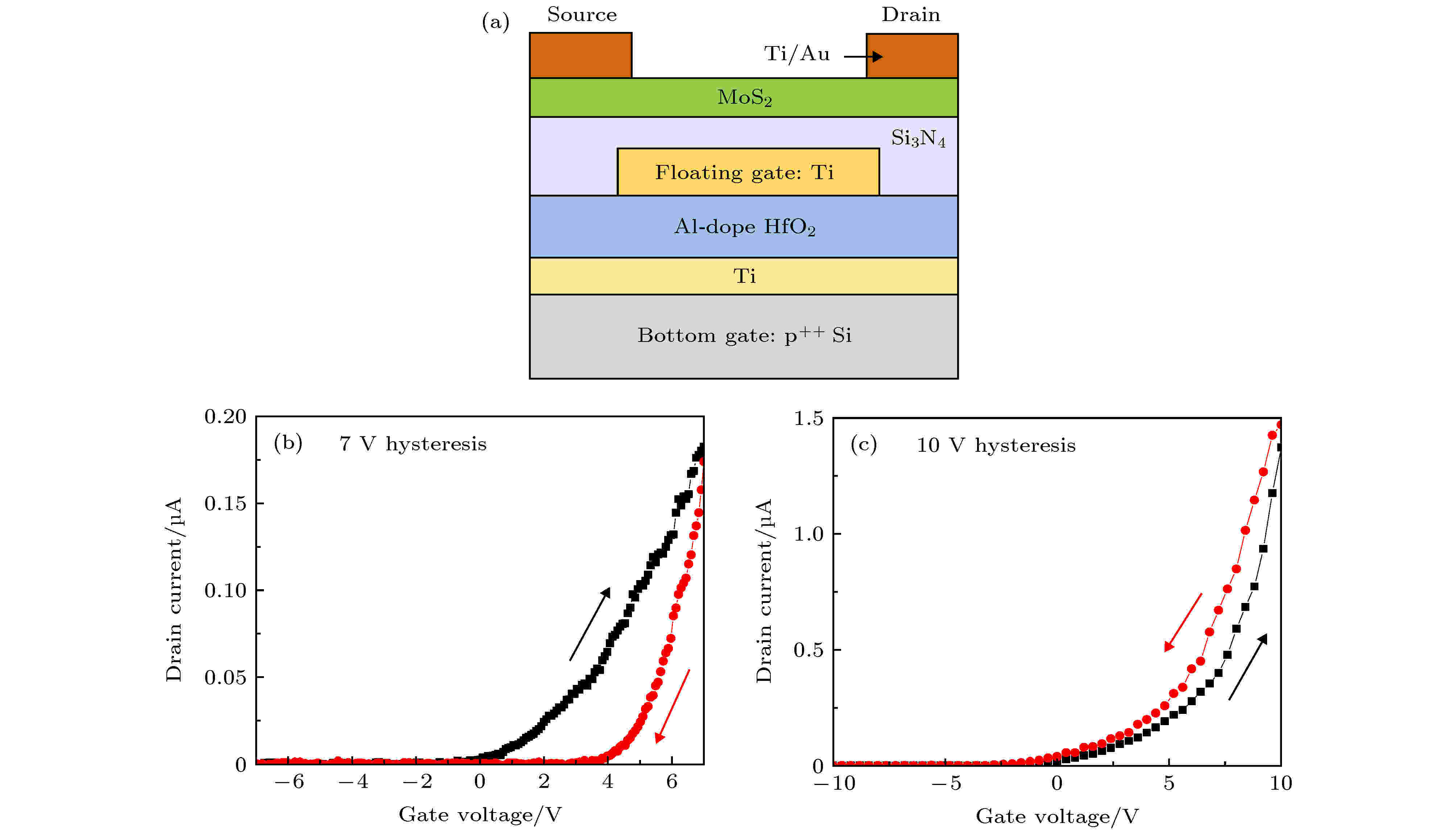图 25 MoS₂铁电NC体晶体管^[145]　(a) 器件结构图; (b) V_G = ± 7 V的转移特性曲线; (c) V_G = ± 10 V时的转移特性曲线
Figure25. MoS₂ Fe-NCFETs^[145]: (a) Structure of the device; (b)transfer characteristic curve of V_G = ± 7 V; (c)transfer characteristic curve of V_G = ± 10 V.

McGuire等^[33]采用15 nm厚的Hf_0.5Zr_0.5O₂作为铁电层, 制备了内部TiN金属栅结构的MoS₂ Fe-NCFETs, SS最小为6.07 mV/dec, 比常规MoS₂ FET的SS(161 mV/dec)下降了2个数量级, 而且在4个电流数量级内的平均SS为8.03 mV/dec. 当改变介质层厚度、铁电层厚度和源漏电压时, 都可以看到明显的SS降低现象. 但是由于内部金属栅的存在, 在所有扫描过程中都存在回滞现象, 而且回滞电压随着测量频率的增大而变大, 表明导致器件SS降低的原因为瞬态NC, 而不是稳态NC. 人们也研究了背栅电压模式^[30]、栅介质层材料^[144]、栅长^[146]和低频噪声影响^[147]等对MoS₂ Fe-NCFETs的影响, 发现器件均能表现出较低的SS, 说明MoS₂在Fe-NCFETs方面有极大的潜力.
除了MoS₂之外, WSe₂也被用作Fe-NCFETs沟道材料^{[140,148,149]}, 其中Si等^[140]分别制备了以Hf_0.5Zr_0.5O₂作为铁电层的MFIS型和MFMIS型WSe₂ Fe-NCFETs, 如图26(a)和(b)所示. 图26(c)为MFIS型Fe-NCFETs转移特性曲线, 可以看到, 当源漏电压为0.1 V时, 正向扫描亚阈值摆幅SS_For为57.5 mV/dec, 反向扫描亚阈值摆幅SS_Rev为40.2 mV/dec, 导致SS_Rev小于SS_For的原因是由于在反向扫描过程中, 极化子的反转会给栅极带来一个额外的电压降, 从而进一步降低了器件的SS. 图26(d)为MFMIS型Fe-NCFETs转移特性曲线, 当源漏电压为0.1 V时, SS_For和SS_Rev分别为41.2 mV/dec和14.4 mV/dec, 由于内部金属栅对铁电层电压放大作用均匀化, 因此MFMIS型Fe-NCFETs的SS要比MFIS型Fe-NCFETs的SS低, 但同时内金属栅的充放电效应也导致其回滞电压的增大.
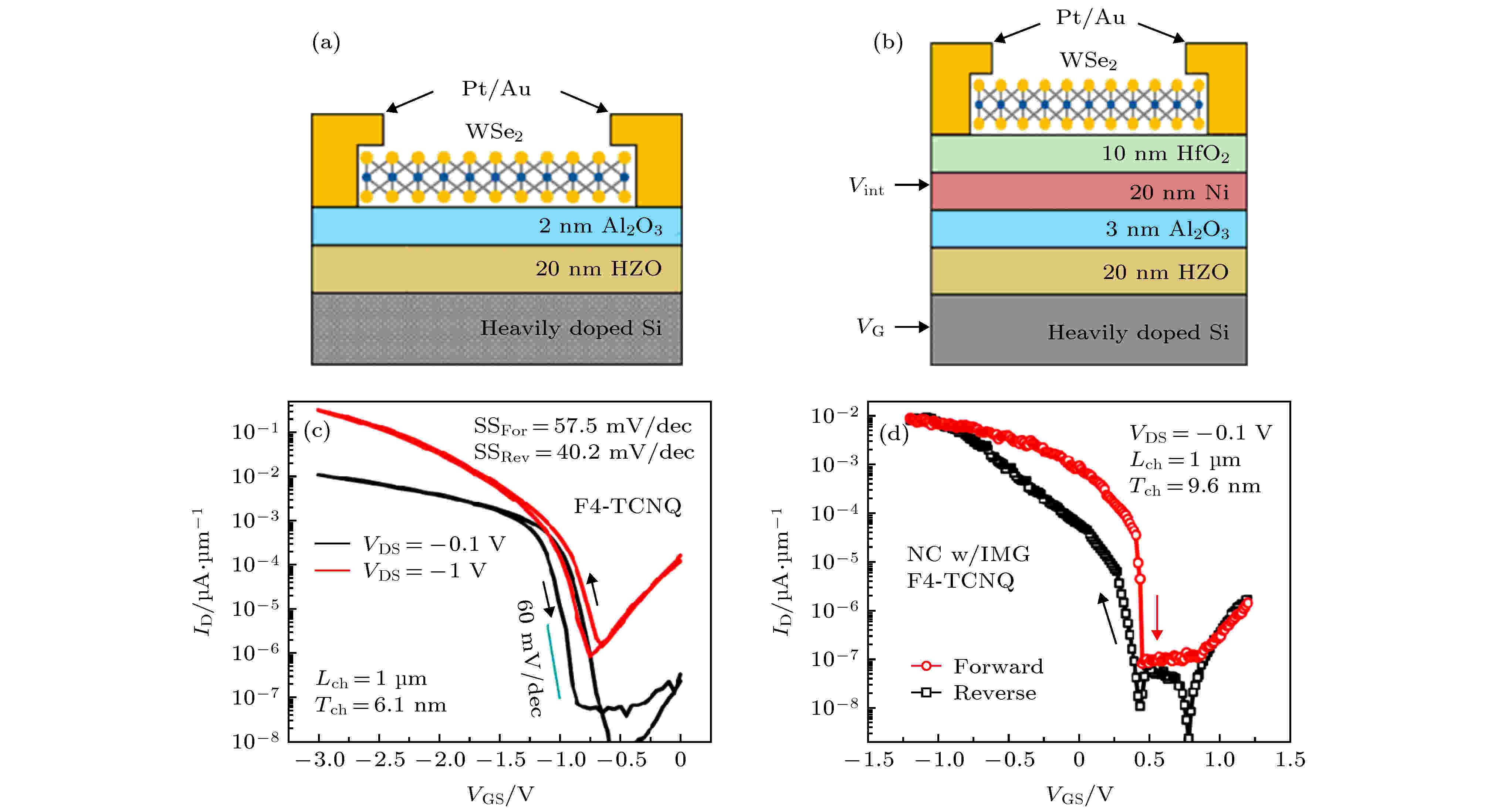图 26 WSe₂铁电NC体晶^[140]　(a) MFIS型器件结构图; (b) MFMIS型器件结构图; (c) MFIS型器件的转移特性曲线; (d) MFMIS型器件的转移特性曲线
Figure26. WSe₂ Fe-NCFETs^[140]: (a) Structure of MFIS device; (b) structure of MFMIS device; (c) transfer characteristic curve of MFIS device; (d) transfer characteristic curve of MFMIS device.

3 -->

4.2.2.石墨烯和黑磷

以石墨烯或黑磷作为沟道的Fe-NCFETs主要采用如P(VDF-TrFE)^[141,142]、SrBi₂NbO₉^[150]、PMN-PT^[151,152]和PbZrO₃^[153]等传统铁电材料, 随着材料制备工艺的改进, 采用氧化铪基铁电体的二维石墨烯/黑磷Fe-NCFETs近来已有报道.
Lee等^[154]通过pALD在单层石墨烯上生长了5 nm厚的介孔结构Hf_xAl_yO₂, 并研究了不同Al组分下的相关性能参数, 如图27所示. 由图27(b)可以看到, 当Al组分为9.5%时, Hf_xAl_yO₂材料的相对介电常数达到最高值 (ε = 25), 是纯净HfO₂的相对介电常数(ε = 17)的1.5倍, 他们认为这是因为在这个组分下, Hf_xAl_yO₂的晶胞结构主要为四方相, 而四方相Hf_xAl_yO₂的介电常数比单斜相和立方相Hf_xAl_yO₂的介电常数高. 所以他们采用密度泛函理论分析了不同组分下Hf_xAl_yO₂的三个相之间的能量差值, 如图27(c)所示, 当Al组分为7.9%—9.3%时, 晶体结构为四方相, 与实验结果中的9.5%一致. 然后, 他们测试了以Hf_xAl_yO₂ (9.5% Al) 作为铁电层的FET的转移特性曲线, 如图27(d)所示, 可以看到, 由于石墨烯材料独特的带隙结构, 器件的开关电流比很小, 仅为2.75, 这对于低功耗晶体管是不利的. 而且氧化铪基材料只有在正交相下才能体现出铁电性能, 他们提到了四方相Hf_xAl_yO₂是不具有铁电性的, 因此这里的Hf_xAl_yO₂只是作为普通的介质层, 而不具备铁电体的效应, 所以以氧化铪基材料为铁电介质层的石墨烯Fe-NCFETs仍需进一步研究.
图 27 石墨烯- Hf_xAl_yO₂晶体管^[154]　(a) 在石墨烯/二氧化硅衬底上沉积的Hf_xAl_yO₂薄膜; (b) Hf_xAl_yO₂的相对介电常数; (c) 不同Al组分下Hf_xAl_yO₂三个相的能量差; (d) 转移特性曲线(9.5% Al)
Figure27. Graphene-Hf_xAl_yO₂ transistor^[154]: (a) Hf_xAl_yo₂ films deposited on graphene/SiO₂ substrates; (b) relative dielectric constant of Hf_xAl_yO₂; (c) energy difference among three phases in Hf_xAl_yO₂ with different Al concentrations; (d) transfer characteristic curve.

Tian等^[155]于2019年首次报道了氧化铪基黑磷Fe-NCFETs, 其结构如图28(a)所示, 采用内部Al金属背栅电极以增强栅对沟道的控制能力, 黑磷和Al金属栅电极之间为5 nm厚的Al₂O₃介质层, 然后在Al金属栅上串联一个HfZrO₂厚度为20 nm的电容. 图28(b)为器件的转移特性曲线, 紫色曲线表示串联了HfZrO₂电容的Fe-NCFETs, 红色曲线表示没有HfZrO₂电容的传统FET, 可以看到传统FET的曲线表现出回滞现象, 这是由于黑磷和Al₂O₃界面层陷阱电荷的充放电导致的. 与传统FET相比, Fe-NCFETs由于NC效应的引入, 亚阈值区域更陡峭, 但由于铁电回滞效应的影响, 其回滞现象更明显. 从图28(c)可以看到, Fe-NCFETs的SS虽然比传统FET小, 但由于黑磷和Al₂O₃界面层缺陷电荷较多, 导致其SS不能低于60 mV/dec, 而且随着测试次数的增加, SS也逐渐退化, 器件性能的保持度较差.
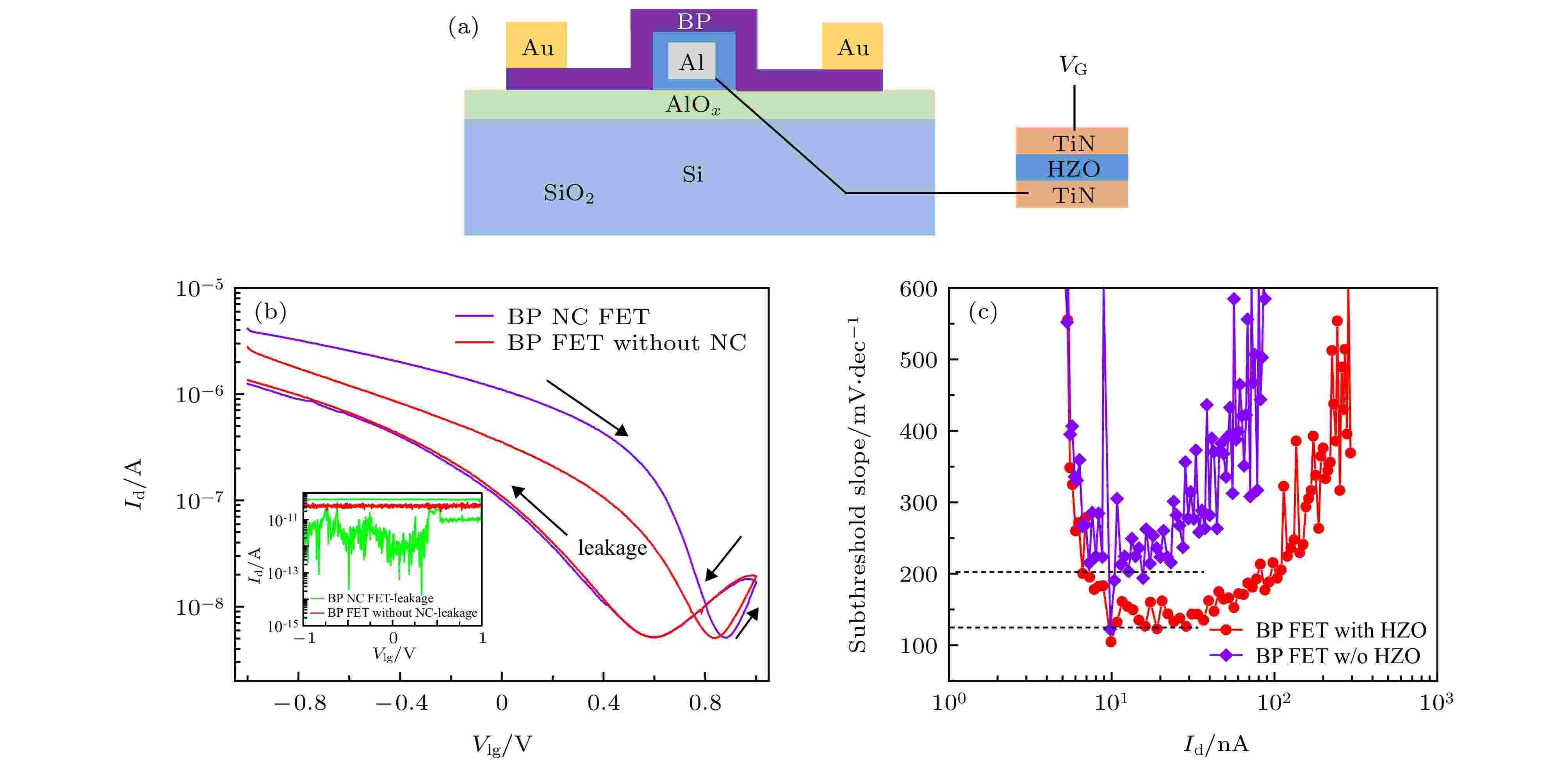图 28 黑磷铁电NC体晶体管^[155]　(a) 器件结构图; (b) 转移特性曲线; (c) 不同I_d下的SS
Figure28. Black phosphorus Fe-NCFETs^[155]: (a) Structure of the device; (b) transfer characteristic curve; (c) SS in different I_d.

石墨烯和黑磷在理论上预测可作为Fe-NCFETs理想的二维沟道材料, 但是实验上的解释仍不清晰, 而且与过渡金属硫族化合物Fe-NCFETs相比, 其界面性能较差, SS不能降低到60 mV/dec以下, 电流开关比很小(< 10⁴), 关于其实验方面的报道也较少. 因此, 在实现性能优异的石墨烯和黑磷Fe-NCFETs之前, 需要克服很多理论上和实验上的困难.
与过渡金属硫族化物、石墨烯和黑磷等二维材料相结合的Fe-NCFETs表现出了优异的电学性能, 二维材料原子级别的厚度也为晶体管特征尺寸进入3 nm提供了可能. 但是二维材料与栅介质层的界面性能较差, 沟道表面缺陷态较多, 在升高器件SS的同时也加重了回滞现象, 这导致器件的功耗急剧增大, 而且二维材料与传统CMOS工艺兼容性较差. 所以为了实现二维材料沟道Fe-NCFETs的商业应用仍需进行大量的实验研究, 目前主要有3个研究方向: (1)降低高k介质和二维材料的界面密度, 以保持固有的高载流子迁移率; (2)实现源/漏区的高浓度掺杂以降低接触电阻; (3)提高器件性能的稳定性.
表1是近几年发表的采用氧化铪基铁电体的Fe-NCFETs的性能参数表, 按照器件结构和沟道材料分类, 列举了器件的SS_min、Hysteresis、Orders of I_DS、V_D和I_on/I_off等参数, 其中Hysteresis表示回滞电压, Orders of I_DS表示SS小于60 mV/dec的源漏电流数量级跨度, I_on/I_off表示开关电流比. 不同器件SS_min和Hysteresis之间的关系如图29所示, 为了实现器件在低功耗逻辑电路中的应用, 须保持SS小于60 mV/dec以及Hysteresis小于0.01 V, 可以看到, 只有一部分硅基Fe-NCFETs可以满足此条件, 所以硅基Fe-NCFETs是目前最有可能替代传统MOSFETs成为下一代低功耗晶体管的选择.

MOS structure	Channel materials	Gate structure	Ferroelectric materials	tFE/nm	SSmin/ (mV·dec–1)	Hysteresis/V	Orders of IDS	VD/V	ION/IOFF	Year	Ref.
Planar	p-Si	MFIS	Hf0.65Zr0.35O2	30	5	—	—	–0.5	104	2014	[115]
Planar	n-Si	MFIS	HfAlO (Al: 6%)	10	Sub-25	0.02	4	0.2	108	2017	[116]
Planar	n-Si	MFIS	Hf0.75Zr0.25O2	10	40	Free	1	0.2	107	2018	[119]
Planar	n-Si	MFIS	Hf0.53Zr0.47O2	5	~40	~0.1	2	0.2	107	2019	[121]
Planar	n-Si	MFIS	HfAlO (Al: 4%)	10	Sub-30	0.02	4	0.2	108	2019	[118]
FinFET	n-Si	MFIS	Hf0.5Zr0.5O2	4	Sub-30	0.003	2	0.05	107	2018	[25]
FinFET	n-Si	MFMIS	Hf0.42Zr0.58O2	5	58	0.003	1	0.1	105	2015	[123]
FinFET	n-Si	MFIS	Hf0.5Zr0.5O2	5	Sub-60	Free	—	0.1	107	2019	[125]
FinFET	p-Si	MFMIS	Hf0.42Zr0.58O2	3	34.5	0.009	2	–0.05	104	2019	[124]
FinFET	n-Si	MFIS	Hf0.5Zr0.5O2	5	Sub-60	Free	—	0.1	107	2019	[125]
GAA	poly n-Si	MFIS	Hf0.5Zr0.5O2	10	26.84	0.003	4	0.1	108	2019	[126]
Planar	p-Ge	MFMIS	Hf0.5Zr0.5O2	6.5	43	2.34	1	–0.05	103	2016	[129]
Planar	p-GeSn	MFMIS	Hf0.5Zr0.5O2	6.5	40	0.41	2	–0.05	103	2016	[129]
Planar	p-GeSn	MFMIS	Hf0.5Zr0.5O2	6	Sub-20	< 0.01	2	–0.05	104	2017	[130]
Planar	p-Ge	MFMIS	Hf0.5Zr0.5O2	4.5	~87.5	Free	—	–0.05	103	2019	[156]
Planar	p-Ge	MFIS	Hf0.67Zr0.33O2	7	~125	~0.105	—	–0.5	104	2019	[134]
Planar	n-InGaAs	MFIS	Hf0.5Zr0.5O2	8	23	~0.2	3	0.05	105	2018	[136]
FinFET	n-InGaAs	MFIS	Hf0.5Zr0.5O2	5	23	0.2	1	0.05	103	2019	[137]
GAA	nanotube	MFMIS	HfAlO(Al: 7%)	10	~45	—	—	0.05	104	2018	[138]
2D-FET	MoS2	MFMIS	Hf1-xZrxO2	15	Sub-60	1.2	3	0.5	105	2017	[146]
2D-FET	MoS2	MFMIS	Hf0.5Zr0.5O2	15	6.07	0.5	4	0.5	105	2017	[33]
2D-FET	MoS2	MFMIS	HfAlO(Al:7.3%)	10	57	0.5	4	0.5	105	2017	[108]
2D-FET	MoS2	MFMIS	HfZrOx	15	47	2.5	1	0.1	106	2018	[30]
2D-FET	MoS2	MFIS	Hf0.5Zr0.5O2	20	Sub-60	< 0.005	4	0.5	106	2018	[147]
2D-FET	MoS2	MFIS	Hf0.5Zr0.5O2	20	23	0.077	6	0.1	109	2017	[144]
2D-FET	WSe2	MFMIS	Hf0.5Zr0.5O2	20	14.4	0.12	2	–0.1	105	2018	[140]
2D-FET	WSe2	MFIS	Hf0.5Zr0.5O2	10	18.2	0.02	4	–0.1	104	2018	[148]
2D-FET	Graphene	MFS	HfAlO(Al:9.5%)	5	—	—	—	0.1	2.75	2016	[154]
2D-FET	BP	MFMIS	Hf0.5Zr0.5O2	20	104	0.5	—	0.1	102	2019	[155]

表1实验报道的Fe-NCFETs的性能参数对比
Table1.Performance comparison of the reported Fe-NCFETs.

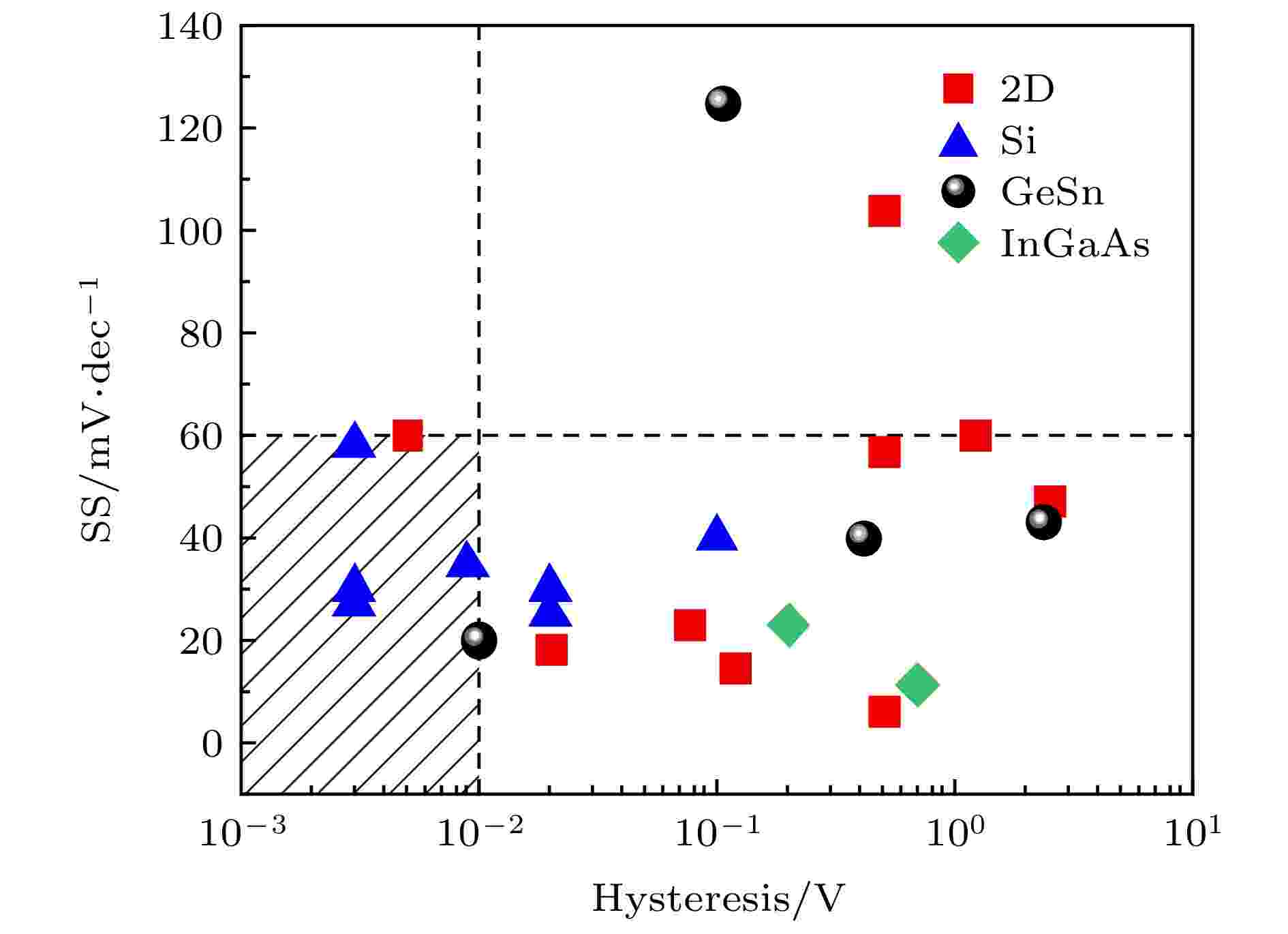图 29 实验报道的Fe-NCFETs的SS与Hysteresis关系图 (2D^{[30,33,108,140,144,146-148,155]}, Si^{[25,116,118,119,121,123-126]}, GeSn^{[129,130,134,156]}, InGaAs^[136,137])
Figure29. SS versus Hysteresis of the reported Fe-NCFETs (2D^{[30,33,108,140,144,146-148,155]}, Si^{[25,116,118,119,121,123-126]}, GeSn^{[129,130,134,156]}, InGaAs^[136,137]).

作为未来CMOS理想的沟道材料需要满足一些条件, 比如具有合适的带隙、低的缺陷态密度、高的载流子迁移率、与介质层的界面性能好、与CMOS技术兼容性高和成本低等, 目前没有任何一种材料满足以上所有条件. 因此, 传统CMOS技术正在进入一个新的阶段, 需要寻找新型材料和新的设计方案, 以在这些条件之间寻找一个平衡, 来满足未来器件对沟道材料的要求.

随着晶体管特征尺寸进入10 nm, 功耗增加变得不可忽视, 与传统MOSFETs相比, Fe-NCFETs具有SS低、负DIBL等优点, 提高了晶体管的开关电流比, 极大程度地降低了器件的功耗, 为实现晶体管尺寸的进一步缩小和摩尔定律的延续提供了选择. 其中, 掺杂氧化铪基铁电材料的发现改善了传统铁电材料与CMOS工艺兼容问题, 使得Fe-NCFETs的性能大大提高, 因此近几年来采用掺杂氧化铪基铁电材料的Fe-NCFETs被广泛研究, 器件的性能也大大提升. 目前Fe-NCFETs的应用主要集中于存储器方面^{[145,157,158]}, 其原理是基于铁电材料处于两个极化状态时晶体管具有不同的电流数值, 而铁电层极化反转导致晶体管表层处于不同状态的特性, 在新一代显示屏——有源矩阵有机发光二极管中也具有应用潜力^[139,159].
但是在Fe-NCFETs大规模投入商业应用之前, 仍需要解决以下几个关键问题.
第一, Fe-NCFETs中的滞回现象. 滞回现象的存在阻碍了逻辑晶体管的应用, 而铁电材料本身存在滞回的特性, 因而在设计Fe-NCFETs时可以考虑从减小铁电材料厚度、增大沟道的掺杂浓度以减小沟道电容、减小${V_{{\rm{DD}}}}$和${V_{\rm{G}}}$扫描上限和调节铁电材料的参数等方面入手. 但是要注意的是, 由于在滞回电压和SS之间存在权衡关系, 因此在降低滞回电压的时候将会增大SS.
第二, 内部金属电极引入的问题. 采用内部金属电极结构可以均匀铁电层在沟道方向上的电势放大效果, 但极大地增加了器件的制造难度, 对于器件尺寸的进一步减小是不利的, 而且会导致栅极漏电流的增加, 降低了器件的稳定性能. 可以从栅电极结构的设计、栅电极材料的选择以及制作工艺等几个方面改进这个问题.
第三, 纳米尺度下面临的一些问题. 随着晶体管特征尺寸进入10 nm, 铁电层的厚度也减小到了3 nm以下, Lee等^[160]指出将1 nm厚的HZO铁电薄膜集成在Fe-NCFETs上以获得陡峭的SS是可行的. 但是如何在纳米尺度下有效地控制铁电层的界面态密度是需要认真考虑的, 小尺度下氧化铪基铁电体的电畴结构也需要进一步研究. 而且, 随着器件尺寸的减小, 量子效应变得不可忽略, 如沟道电流的量子输运现象^[161-163], 需要探明其微观机制并结合利用, 以指导材料和器件的设计, 进一步发掘Fe-NCFETs的应用潜力.
Fe-NCFETs作为一种新型低功耗器件, 虽然目前在材料和工艺上仍然存在很多技术问题, 但是随着研究的深入, 将成为下一代CMOS最具潜力的器件之一.