摘要:钙钛矿铁电压电材料具有高介电压电常数和高机电耦合系数等特点, 在工业、消费电子和军事等领域具有广泛的应用, 其压电性能起源的机理及与材料多尺度结构之间的关系一直是凝聚态物理和材料科学领域的研究热点. 铁电材料的压电效应主要来源于本征的场致晶格畸变以及非本征的畴翻转和畴壁运动, 理解并区分这两种压电效应的贡献机制对研究材料压电性能的起源具有重要意义. 本文综述了近年来通过电场原位X射线衍射技术分析电场作用下材料晶格结构和畴结构变化的技术手段和研究方法, 重点介绍了自第三代同步辐射光源和高速探测器获得长足发展以来, 通过时间分辨衍射技术、单双峰拟合、全谱拟合、质心计算等方法开展压电材料本征和非本征贡献, 以及电场诱导相变对其宏观性能影响的研究进展, 期望通过对各类方法的介绍和回顾为多种压电材料的机理分析提供研究方法和技术支持.
关键词: 压电性/
X射线衍射/
本征贡献/
非本征贡献

English Abstract

全文HTML

--> --> -->

在铁电压电材料领域, 传统无机钙钛矿材料由于优异的压电性能和机电耦合系数, 在生产生活中得到广泛应用, 在商业上获得了巨大成功^[1–4]. 以锆钛酸铅(Pb(Zr,Ti)O₃, PZT)陶瓷和铌镁酸铅-钛酸铅(Pb(Mg_1/3Nb_2/3)O₃-PbTiO₃, PMN-PT)单晶为代表的高压电系数含铅材料^[5–9]和以铌酸钾钠((K, Na)NbO₃, KNN)基固溶体^[10–14]及钛酸铋钠-钛酸钡((Na_1/2Bi_1/2)TiO₃-BaTiO₃, NBT-BT)^[15,16]等为代表的环境友好无铅材料多年来一直是学术界基础研究和应用研究的热点. 在机理研究方面, 关于特定结构特征, 如准同型相界结构^[17–20]或局部非均质结构^[21]等, 与高压电性能关联的研究近年来引起了学术界的广泛关注, 但仍然需要系统性的直接实验验证. 值得注意的是, 逆压电效应表现为, 在外加电场作用下材料产生应变, 除了可测量的宏观应变, 还包括材料微观/介观尺度的应变, 后者可以通过对晶格结构和畴结构的表征以及对其在外加电场作用下变化的追踪实现测量. 这类研究的好处在于, 能够在晶格尺度将材料的结构与性能建立直接联系, 从而从机理角度实现对材料压电性能来源及贡献的定量分析.
自1913年布拉格父子通过分析X射线衍射图谱建立氯化钠结构以来, X射线衍射已成为晶体学领域应用最为广泛的结构研究工具^[22]. 通过对X射线或中子衍射图谱中布拉格衍射峰的位置、强度和劈裂情况进行分析、建模和精修, 可以得到较为准确的材料晶格结构^[23–25]. 在施加电场的情况下, 晶格结构在某方向的畸变可通过衍射谱的变化得到反映. 此外, 由于铁电材料具有畴结构, 即具有一定相干长度的区域内有相同序参量(如极化矢量方向)的有序结构^[26], 电场作用下的畴壁运动和畴重排也常常对特定方向的宏观应变产生较大作用^[27]. 因此, 利用衍射技术进行多畴结构的识别和表征也是压电响应定量分析的重要组成部分. 具体来说, 压电效应的主要贡献包括两部分: 第一部分是“本征贡献”, 它是由场致晶格畸变引起的^[5,9], 场致逆压电效应、残余晶格应力以及可能存在的极化矢量旋转效应^[18]导致了晶格形变, 从而产生晶格参数的变化, 在衍射图谱中反映为布拉格衍射峰位置的变化; 另一部分是“非本征贡献”(或称为“外部贡献”), 来自电场作用下的畴翻转和畴壁运动^[27,28]. 由于近邻铁电和铁弹畴中具有方向不同的极化矢量, 极化矢量受外加电场诱导, 使得部分畴沿电场矢量方向翻转, 这在衍射图谱中反映为布拉格衍射峰强度的增强或减弱, 甚至可能发生代表不同畴方向的多个衍射峰强度发生互换. 然而, 受限于普遍存在于钙钛矿材料, 尤其是高性能钙钛矿材料中的复杂结构, 包括较小的晶格畸变、低对称性晶格或多相共存结构、以及复杂的畴结构等, 用传统衍射方法将“本征”和“非本征”机制分开仍然具有一定的挑战性. 近年来, 随着高能量同步辐射技术^[29]及高速二维探测器的开发^[30], 以及相关分析方法的开展和成熟, 通过原位X射线衍射技术表征和分析电场作用下的多尺度应变成为可能, 使得学术界涌现出了一系列具有代表性的工作, 试图针对不同钙钛矿压电材料, 运用多种方法, 开展“本征”和“非本征”压电起源的讨论. 本文综述了对样品施加电场情况下的高能同步辐射衍射实验, 并结合时间分辨衍射技术、单双峰拟合、全谱拟合、质心计算、以及相变研究等方式来研究样品本征和非本征贡献对其宏观性能的影响, 并结合不同的例子介绍了不同体系压电材料中宏观压电性能的主要来源.

在X射线衍射和中子衍射中, 时间分辨的衍射测量技术能够有效地实现同步分析样品在随时间快速变化的外部刺激(电场、磁场、温度等)下微观/介观结构(晶体结构、畴结构等)的变化情况^[31–33]. 时间分辨衍射测量随时间同步收集材料对应时间点的衍射谱; 而在不同时间点, 材料所受外部刺激情况也不同(如随时间变化的交变电场). 通过这种方式, 就能获得不同外部刺激下材料的衍射谱.
而另一方面, 铁电体是一种非常适用于时间分辨研究的理想材料:
1)一般情况下, 在多次电场循环中, 相同电场下铁电体的衍射谱是可以重复叠加的^[34];
2)铁电体晶体结构变化和畴翻转过程对外加电场的响应时间在皮秒尺度^[35–38], 其响应可以被实时观测到.
2

-->

2.1.频闪技术

在目前较为通用的X射线衍射实验中, 由于光子能量有限, 在所测陶瓷或单晶材料厚度较厚或包含铅、铋等重原子的情况下, 大量光子被样品吸收, 一次衍射过程不足以收集到信噪比好的衍射谱. 所以研究者往往对相同条件下的衍射谱进行多次叠加, 从而获得总衍射谱. 通常有两种测量策略: 单次测量与频闪测量^[34].
单次测量实验通过连续等间隔测量序列来收集数据. 单次测量的时间分辨率受到每次测量时间的限制, 所以需要在给定时间内尽可能提高测量次数来保证最高分辨率. 通常单次测量实验适用于材料演变过程随外部刺激不可重复的情况, 如外部刺激为温度^[32,34].
频闪测量则是通过控制外部刺激的周期性变化来收集数据, 适用于材料演变过程随外部刺激可重复的情况, 如外部刺激为电场、磁场. 在该情况下, 循环周期会被分为若干个时间通道. 每个循环周期的时间通道中收集到的数据都会加总到下一个循环周期中对应的时间通道中去, 直到满足统计精度为止, 其原理^[32,34,39]如图1所示, Q为倒空间矢量, 单位是r. l. u. (reciprocal lattice unit); t为时间.
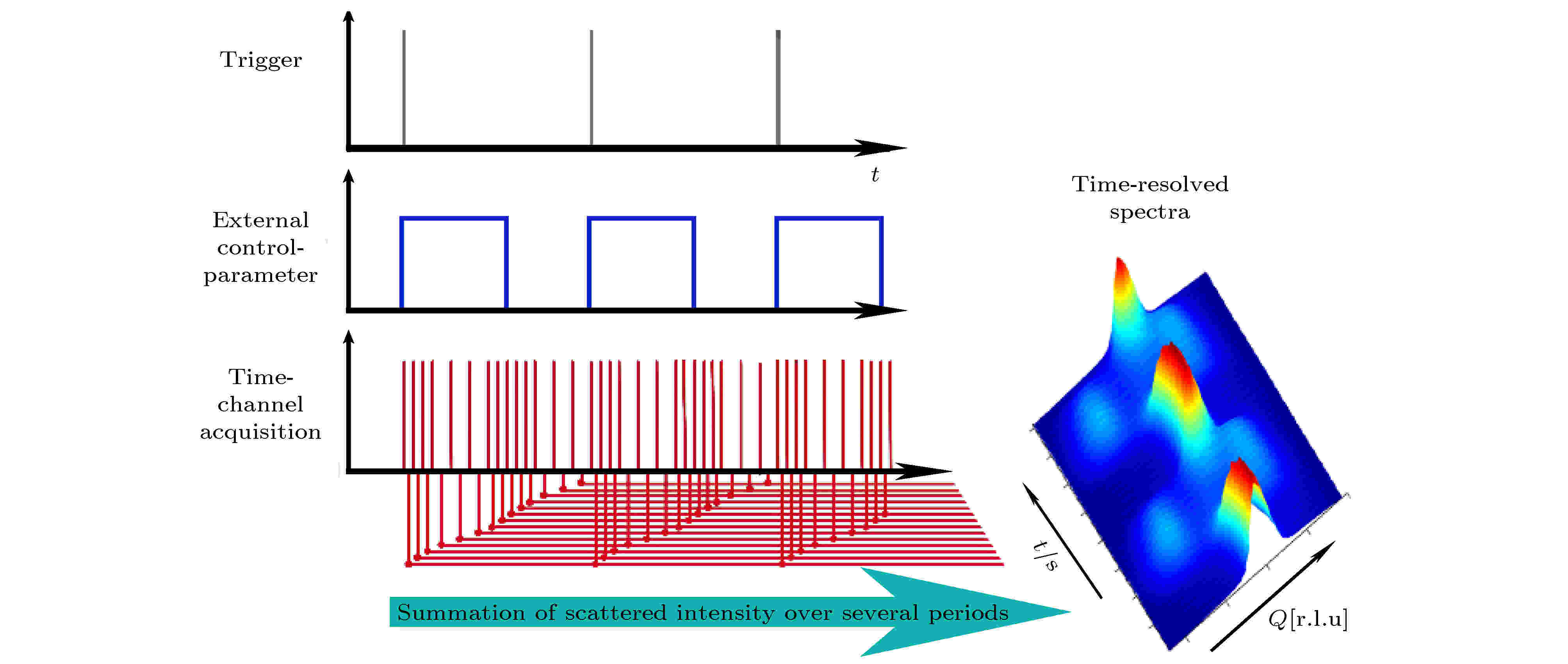图 1 频闪数据收集原理
Figure1. Principle of stroboscopic data-acquisition

2 -->

2.2.数据采集与控制信号的同步

由于时间分辨衍射测量需要反映材料结构与外部刺激间的关系, 采集衍射数据的设备(如探测器)触发信号与控制外部刺激的控制信号间必须要保持同步^[39]. 如在施加交变电场的时间分辨测量中, 各个时间点的衍射谱必须对应该时间点的准确电压, 而不是错误匹配到其他时间点的电压上.
对于数据获取与控制信号的同步, 不同研究者往往有着不同的数据获取方案. Choe等^[40]的数据采集系统如图2(a)所示, 系统的信号同步过程如图2(b)所示. 该系统可以收集不同电压条件下样品的二维衍射谱. 系统保持同步的思路是:
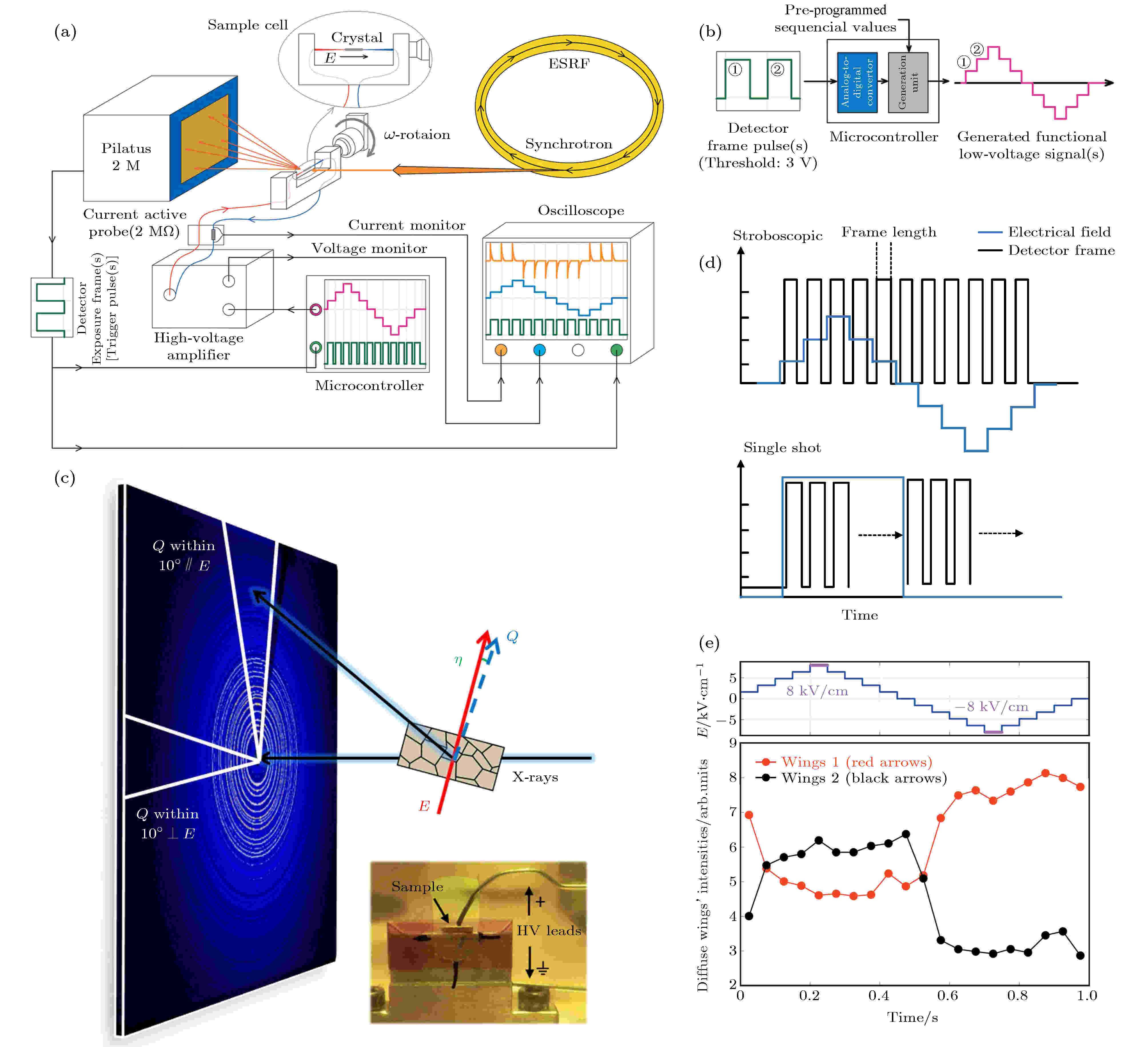图 2 (a) Choe等^[40]的数据采集系统; (b) Choe等^[40]的系统中信号同步过程; (c) Daniels等^[41]的数据采集系统; (d) Daniels等的系统中数据采集的时间序列; (e)频闪技术中样品所施加电场与时间的关系, 以及相关衍射强度随电场变化趋势^[40]
Figure2. (a) Data acquisition system by Choe et al.^[40]; (b) signal synchronization process in the system of Choe et al.^[40]; (c) data acquisition system by Daniels et al.^[41]; (d) timing sequences for data acquisition processes in the system of Daniels et al.; (e) time dependence of the AC electric field and the collected intensity of diffraction wings, showing the field-induced intensity exchange between the two wings^[40]. (a) (b) (e) Copyright ? 2017 International Union of Crystallography. Reproduced with permission of the International Union of Crystallography.

1)探测器每次发出的信号都标志着一个独立的衍射数据采集帧, 即在该帧时间内系统可以生成一个二维衍射谱.
2)探测器信号的上升沿被微控制器检测到后, 微控制器通过高压放大器改变样品所加电压值. 这样就能保证在一个数据采集帧的时间里, 样品处于相同电场下.
3)在一个数据采集帧完成后, 新的探测器信号通过微控制器再次改变样品所加电压.
而Daniels等^[32,41]的数据采集系统(如图2(c)所示)采取了另一种保持同步的思路:
1)系统中函数发生器产生所需的电场波形, 通过高压放大器施加到样品上;
2)同时函数发生器产生触发脉冲信号, 通过延迟发生器的延迟后传输到探测器上, 探测器开始进行单次数据采集或者频闪数据采集, 如图2(d)所示.
两个测量系统的区别在于: Choe等^[40]的系统中, 初始信号从探测器产生, 由微控制器调控电压; Daniels等^[32,41]的系统中, 初始信号从函数发生器中产生, 需分别调控样品电压和探测器来完成数据采集.
另一方面, 不同衍射数据采集系统也存在相同点. 首先, 时间分辨衍射测量系统的时间分辨率均取决于探测器的最小采集帧时间. 在Choe等^[40]的系统中, 探测器PILATUS-2M的最小帧时间约为33 ms. 在Daniels等^[32]的系统中, 探测器Pixium 4700的最大帧率为7.5 Hz. 其次, 时间分辨衍射测量实验是一种准动态的测量. 如在施加不同电场的测量中, 为了保证在数据采集时间内样品电场不变, 所施加的电场是随时间逐步阶跃式改变的, 如图2(e)所示.

传统上, 以采集一维粉末衍射数据为主要目的衍射实验主要使用点探测器, 其具有可校准、衍射峰位置精确等优势, 但同时具有测量耗时长, 不同2θ角度无法做到同时收集等缺点. 相比于使用点探测器的X射线衍射技术, 使用二维面探测器能够在采集一帧数据的短时间内收集到更完整的倒易空间信息, 是原位衍射实验更为通用的选择^[42].
具体来说, 在研究晶体结构随电场变化的实验中, 使用二维面探测器开展衍射实验能够实现:
1)对于陶瓷样品来说, 能同步地收集到样品与电场不同夹角下的二维衍射图像, 即德拜-谢勒环 (Debye-Scherrer rings), 如图2(c)所示.
2)对于单晶样品, 能够在二维衍射图像中特定的衍射光斑附近观察到样品中不同取向畴的存在^[33,43]. 如在钛酸铋钠((Na_1/2Bi_1/2)TiO₃, NBT)单晶{002}衍射峰的ω-2θ二维图中, 可观察到两个布拉格衍射峰在ω和2θ方向上均处于不同的位置, 分别对应单晶中(002)和(200)两种不同的铁弹畴, 如图3(a)所示. 通过分析两种衍射峰的相对位置, 可获取关于畴的强度分布以及畴壁方向等信息.
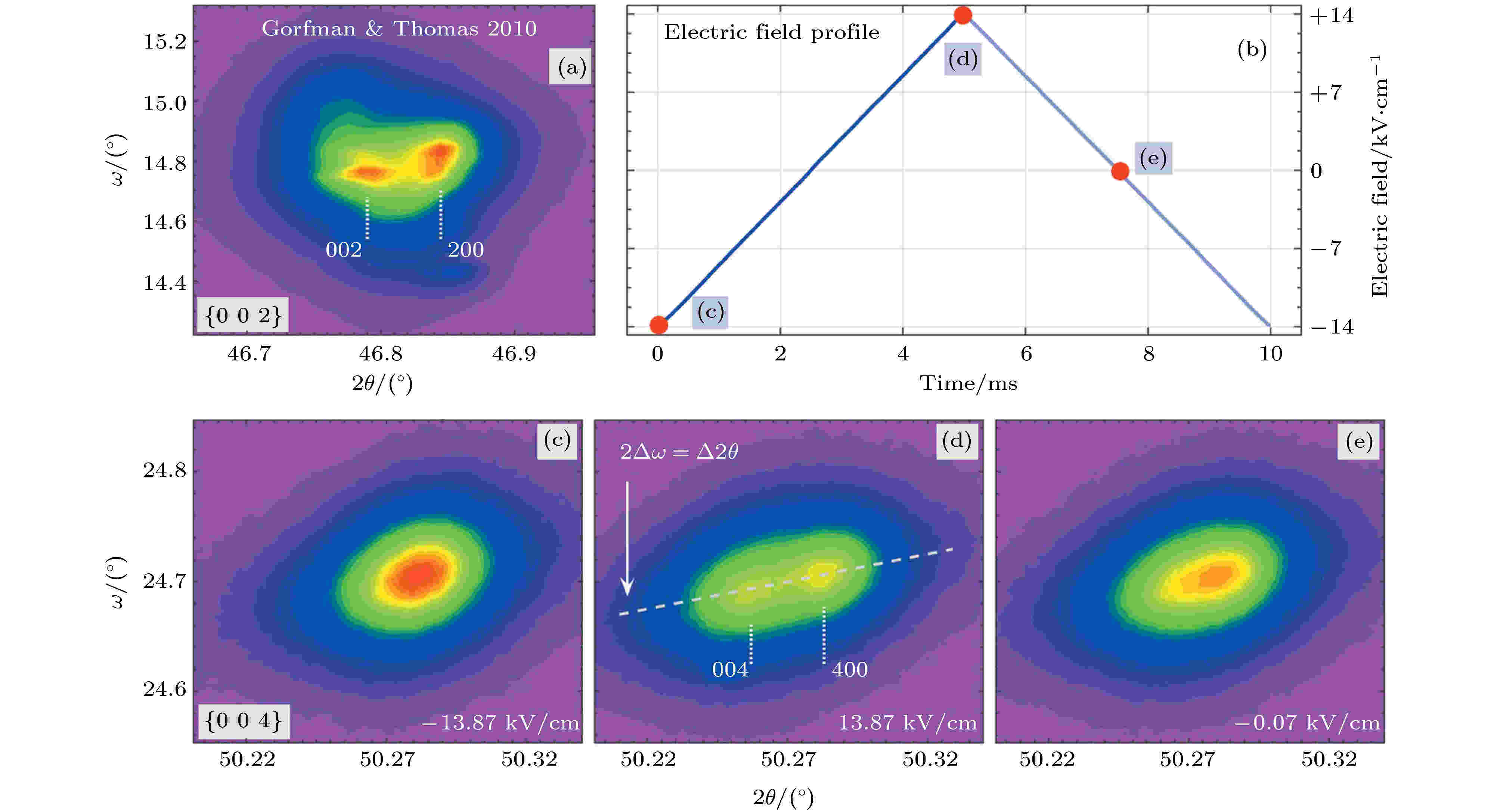图 3 NBT单晶{00h}衍射峰X-ray衍射峰强度　(a) {002}衍射峰的静态ω-2θ二维衍射图像; (b)外加电场(沿[001]方向)与时间的关系; (c)?(e)使用频闪技术收集到的{004}衍射峰的ω-2θ二维衍射图像, 分别对应不同的时间通道与电场^[33]
Figure3. Diffraction intensity of the X-ray around the {00h} family of reflections of NBT single crystal: (a) Static ω versus 2θ mesh of the {002} reflections family; (b) the time-dependence of the applied external electric field (along [001]); (c)?(e) stroboscopically collected versus 2θ meshes of the {004} family of reflections, corresponding to different time channels and electric fields^[33]

3)对于在施加电场的同时同步收集数据的单晶样品, 能直观地观察到样品中不同畴随电场变化的演变过程^[33,44]. 如在电场由–13.87 kV/cm逐渐增大的过程中, {004}衍射峰劈裂程度增大, 当电场回落至–0.07 kV/cm, {004}衍射峰的劈裂程度下降, 表明了电场方向和强度变化对由极化矢量旋转导致的近邻铁弹畴的影响, 如图3(b)—(e)所示.
结合二维衍射图像, 文献[42, 45–47]提出了一种高分辨率单晶衍射开展结构分析的方法: 在倒易空间二维图中, 通过$ 2\theta $方向上衍射峰的分峰数量以及处于不同位置的衍射峰之间的距离来确定晶体对称性并拟合计算晶格参数. 以NBT为例, 在中子衍射和X射线粉末衍射实验测量中, NBT一般被认为是三方相结构^[15]. 但在高分辨率单晶X射线衍射实验中发现, $\omega\text{-}2\theta$二维衍射图中的分峰情况更接近单斜相, 如图4所示; 而对$ 2\theta $方向上的衍射峰距离的拟合结果显示, 空间群为C_c的单斜相得到的拟合误差是最小的^[46]. 对样品施加电场的情况下, 利用该方法可以更准确地分析晶体结构随电场的演变过程.
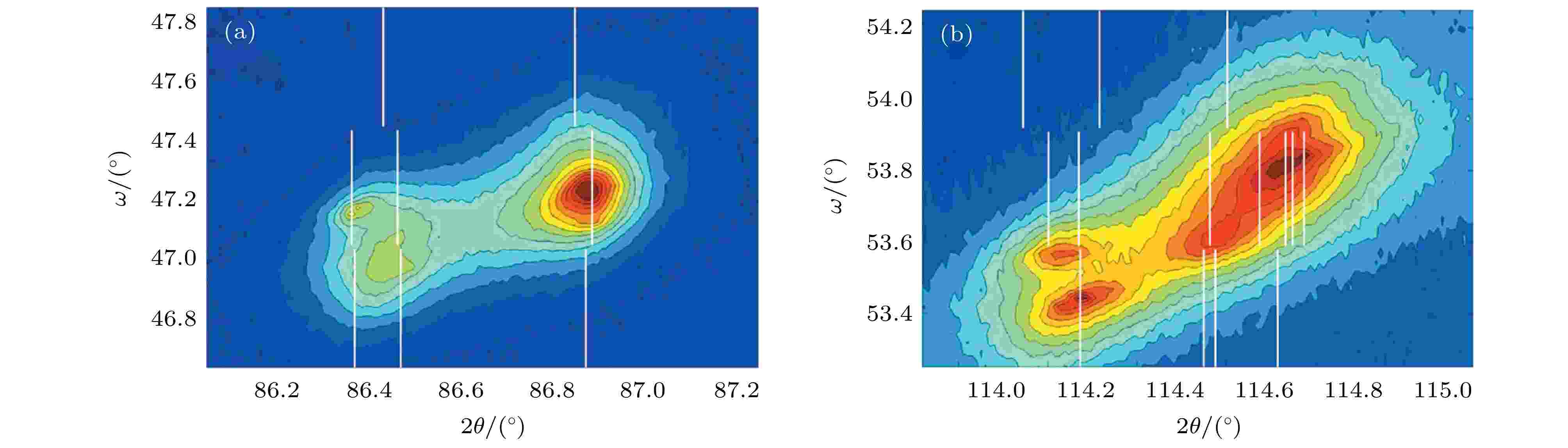图 4 NBT单晶中不同{hkl}_pc衍射峰的ω-2θ二维衍射图像, 其中从上到下的白线表示三方相, 单斜相C_c和三方-四方混合相可能的分峰$ 2\theta $位置　 (a) {222}; (b) {114}^[46]
Figure4. Two ω versus 2θ maps for different {hkl}_pc of NBT single crystal collected on the high-resolution diffractometer. The lines indicate the simulated position of the scattering angle: from top to bottom, rhombohedral, monoclinic, and a combination of rhombohedral and tetragonal: (a) {222}; (b) {114}^[46] (Copyright ? 2010 International Union of Crystallography. Reproduced with permission of the International Union of Crystallography)

压电效应的主要贡献包括: 由场致晶格畸变引起的本征贡献与来自畴翻转和畴壁运动的非本征贡献. 为了更深入地理解这两种机制对压电效应的贡献, 研究者们结合X射线衍射技术做了大量的工作, 提出了包括单双峰拟合、全谱拟合等多种计算方法.
2

-->

4.1.单双峰拟合

在陶瓷样品衍射数据的分析过程中, 为了表征在施加循环电场期间压电陶瓷的结构变化, 首先需要收集多个(hkl )衍射峰强度和2θ位置. 在定量或半定量分析中, 通过单独选取1—2个(hkl )衍射峰, 使用合适的轮廓形状函数对其进行拟合, 可以获得分别代表不同畴方向或不同相组成的衍射峰位置和强度随电场变化的信息, 从而在一定程度上重建出相关相结构或畴结构出现、重组以及消失的过程.
3 -->

4.1.1.晶格应变(本征贡献)

通过X射线衍射或中子衍射技术, 多晶陶瓷材料在电场诱导下产生的应变可以通过单双峰拟合方法被定量计算. Daymond ^[48]提出, 平均应力$ \bar \varepsilon $可以通过对不同晶面族的晶格应变$ {\varepsilon }_{hkl} $进行加权平均得到:

$\bar \varepsilon = \frac{{\sum\nolimits_{hkl} {{\alpha _{hkl}}} {\varepsilon _{hkl}}}}{{\sum\nolimits_{hkl} {{\alpha _{hkl}}} }},$

其中$ {\alpha }_{hkl} $为权重因子, 表达式为

${\alpha _{hkl}} = \dfrac{{{t_{hkl}}{m_{hkl}}{E_{hkl}}}}{{\bar E}},$

其中$ {t}_{hkl} $为取向因子, $ {m}_{hkl} $为多重性因数, $ {E}_{hkl} $为{hkl}方向的杨氏模量, $ \bar{E} $为样品平均杨氏模量. $ {t}_{hkl} $反映了多晶材料中不同晶粒的取向分布, 其具体数值需要对衍射数据进行计算才能得到. $ {m}_{hkl} $取决于材料对称性和{hkl}晶面间距大小. 在立方相结构中, $ \left\{111\right\} $晶面族包含有8个方向不同而晶面间距相同的晶面, 所以$ {m}_{111}=8 $; 而在四方相中, 晶面间距$ {d}_{200}\!=\!{d}_{020}\ne {d}_{002} $, 所以$ {m}_{200}\!=\!4, {m}_{002}\!=\!2 $.
基于这一原理, Pramanick等^[49]结合二维衍射图像, 对交变电场下镧/铁掺杂的PZT陶瓷的晶格应变进行了量化计算, 他们的实验装置见图5.
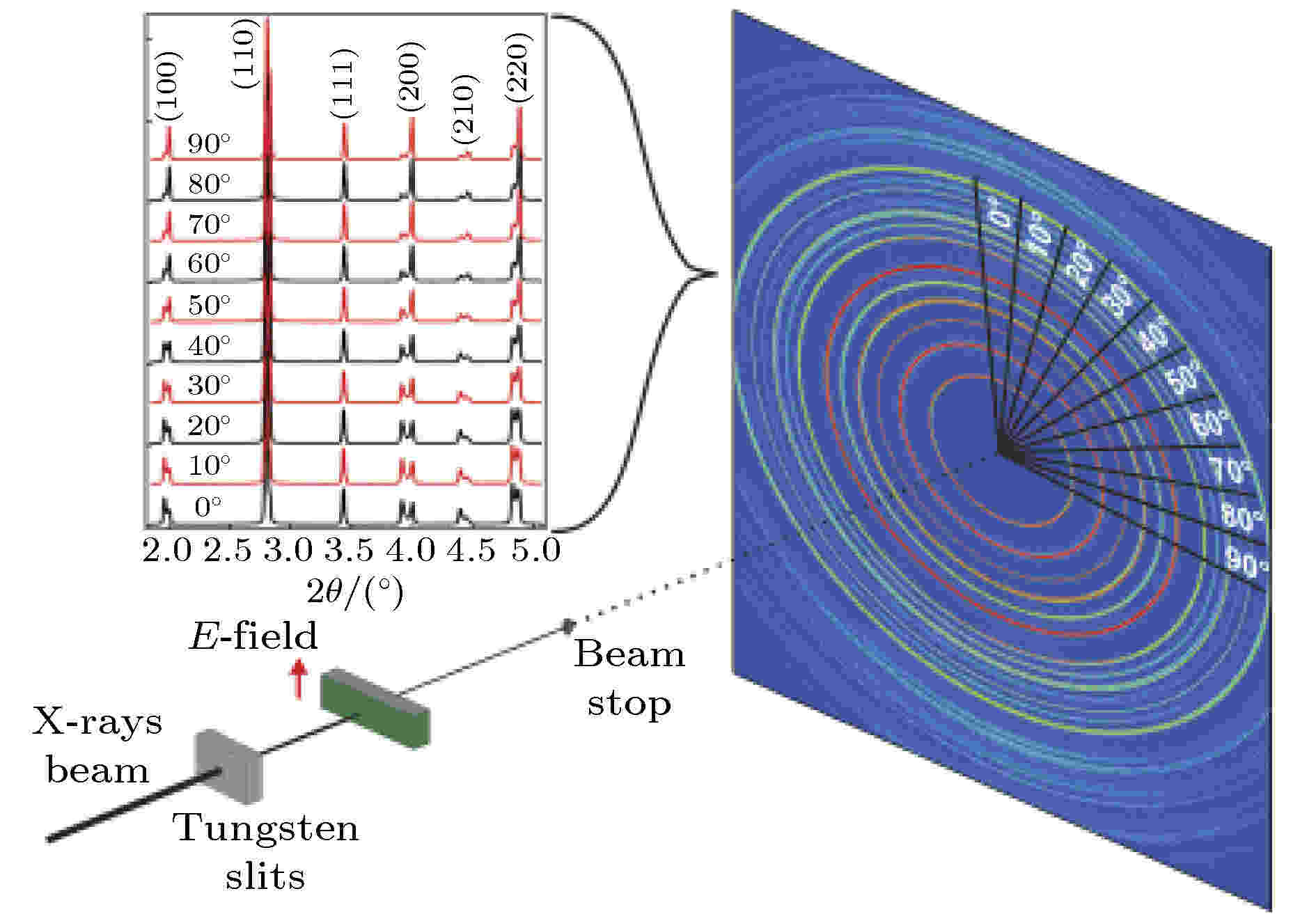图 5 时间分辨高能X射线衍射装置以及德拜环不同区域分别对应晶粒方向与电场不同夹角的衍射图谱^[49]
Figure5. Experimental set-up for time-resolved high-energy X-ray diffraction. Different sections in the Debye ring correspond to grains with specific angles respect to the applied E field^[49] (Copyright ? 2011 John Wiley and Sons).

在幅度为$ {E}_{0} $的双极性交变方波电场下(即施加电压范围为$ {+E}_{0} $至$-{E}_{0}$), 不同晶面族的晶格应变$ {\varepsilon }_{hkl} $为^[49]

${\varepsilon _{hkl}} = ({{d_{hkl}^ + - d_{hkl}^ - }})/{{d_{hkl}^ - }},$

其中$ {d}_{hkl}^{+} $和${d}_{hkl}^{-}$分别对应最大电场$ {+E}_{0} $与最小电场$ -{E}_{0} $下的$ \left(hkl\right) $晶面间距.
在Daymond^[48]方法的基础上, 考虑到材料的取向特性, 在电场下的材料晶格应变$ \bar{\varepsilon } $被化简为^[31,49]

$\left\langle {{\varepsilon _{hkl}}} \right\rangle = \frac{{ \sum \nolimits_{hkl} {t_{hkl}}{m_{hkl}}{\varepsilon _{hkl}}}}{{ \sum \nolimits_{hkl} {t_{hkl}}{m_{hkl}}}},$

而在X射线二维衍射谱中, 无晶体取向陶瓷中的晶格应变为

$\begin{split}{\varepsilon _{{\rm{lattice}}}} \;&= \frac{{ \sum \nolimits_{hkl} {t_{hkl}}\left( 0 \right){m_{hkl}}{\varepsilon _{hkl}}\left( 0 \right)}}{{ \sum \nolimits_{hkl} {t_{hkl}}\left( 0 \right){m_{hkl}}}} \\ &= \frac{{ \sum \nolimits_{hkl} {f_{hkl}}\left( 0 \right){m_{hkl}}{\varepsilon _{hkl}}\left( 0 \right)}}{{ \sum \nolimits_{hkl} {f_{hkl}}\left( 0 \right){m_{hkl}}}},\end{split}$

其中$ {t}_{hkl}\left(0\right) $表示平行于电场方向的取向因子. 在陶瓷样品中, 取向因子$ {t}_{hkl}\left(0\right) $由畴取向$ {f}_{hkl}\left(0\right) $确定^[50,51].
3 -->

4.1.2.畴壁运动引起的应变(非本征贡献)

在铁电材料中, 非180°畴壁运动对宏观应变的贡献主要来自于畴体积分数变化导致特定晶体学方向上的宏观应变.
以四方相的镧掺杂PZT陶瓷为例, 在二维衍射谱中, 对德拜-谢勒环特定角度上的衍射强度进行积分, 可以得到与电场具有不同夹角的陶瓷晶粒的一维衍射谱. 从图6可以看出, 与电场不同夹角的一维衍射谱中(002)衍射峰与(200)衍射峰的衍射强度不同, 即反映了四方相PZT陶瓷中002畴与200畴的体积分数不同. 通过单双峰拟合的方式, 可以得到这两个衍射峰的衍射强度$ {I}_{002} $和${I}_{200}$, 则002畴的体积分数为
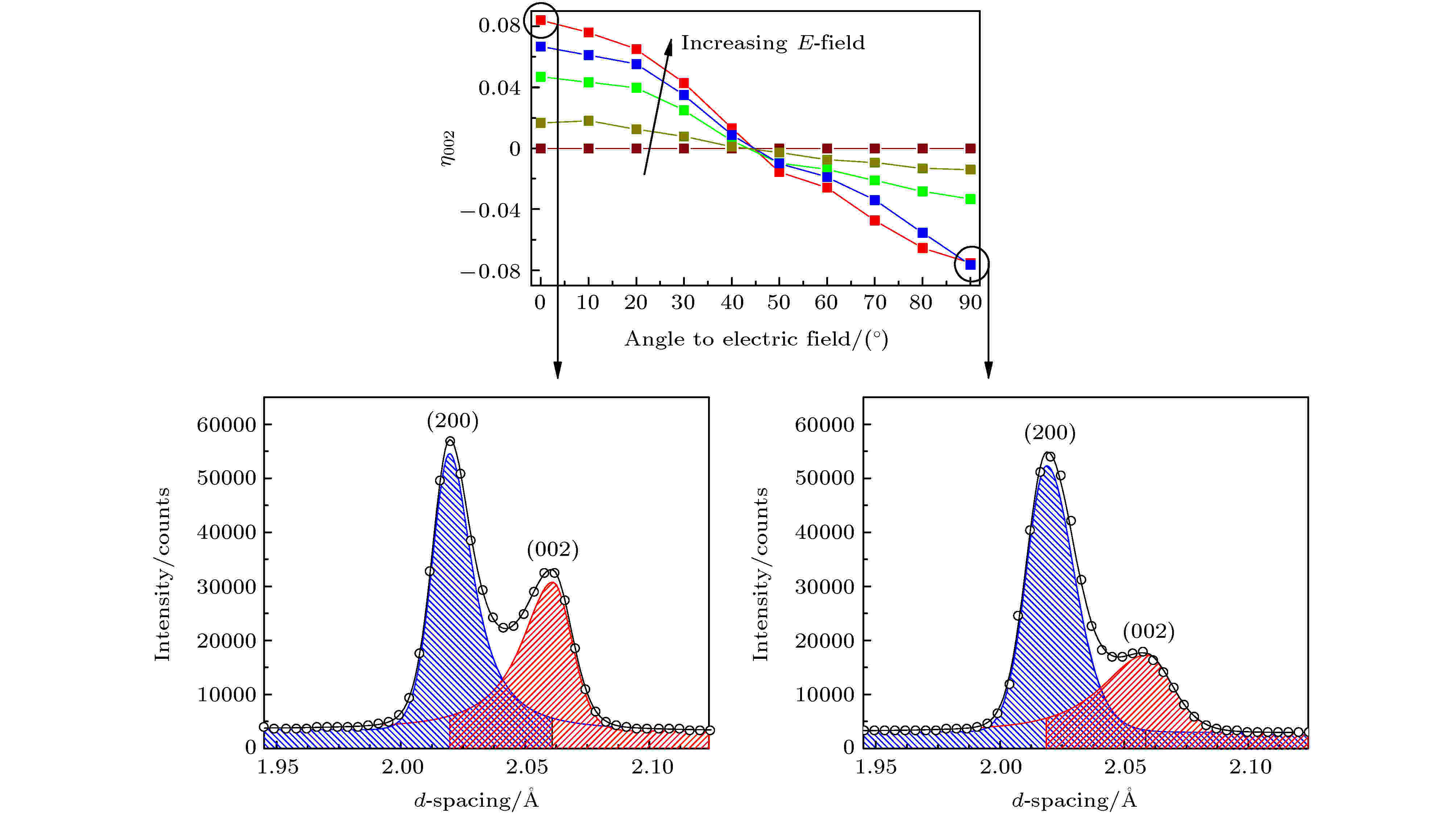图 6 La掺杂PZT陶瓷中002畴体积分数与电场不同夹角的关系(底图分别显示与电场呈0°与90°条件下(002)与(200)衍射峰体积分数的变化)^[49]
Figure6. η₀₀₂ as a function of the field amplitude as well as orientation with respect to the direction of applied field, for an unpoled La-doped tetragonal PZT ceramic under the application of static electric fields. The measured and fitted (002)-type diffraction peaks corresponding to the particular values of η₀₀₂ (marked by circles and indicated by arrows) are shown in the bottom section of the figure. For the fitted diffraction patterns, the deconvoluted (200) and (002) peaks are shown in black solid lines. The integration of individual (002) and (200) peaks are terminated beyond the peak position of the adjacent peak, as indicated by the color-shaded areas^[49] (Copyright ? 2011 John Wiley and Sons).

${v_{002}} = \frac{{\dfrac{{{I_{002}}}}{{{I'_{002}}}}}}{{\dfrac{{{I_{002}}}}{{{I'_{002}}}} + 2\left( {\dfrac{{{I_{200}}}}{{{I'_{200}}}}} \right)}}.$

考虑到在畴随机分布的四方相样品中, $ {v}_{002}= 1/3 $, 所以在电场诱导下重新取向的畴体积分数为

${\eta _{002}} = {v_{002}} - {1}/{3}.$

通过结合二维衍射谱数据与单双峰拟合方法, Jones等^[52]给出非180°畴壁运动引起的应变为

$\left\langle {{\varepsilon _{{\rm{non}} - 180^\circ }}} \right\rangle = \varepsilon \int_0^{\frac{{\text{π}}}{2}} \left[ {\left( {m\Delta\eta \left( \alpha \right){{\cos }^2}\alpha } \right)} \right]\sin \alpha {\rm{d}}\alpha ,$

其中, $ \varepsilon $为晶体的自发应变, 四方相陶瓷中$\varepsilon = \dfrac{{d}_{00 h}-{d}_{h00}}{{d}_{h00}},\; m = 4$, 三方相陶瓷$ \varepsilon =\dfrac{{d}_{kkk}-{d}_{kk\bar{k}}}{{d}_{kk\bar{k}}}$, m = 3; 而$m\Delta\eta,\; \sin\alpha$表示不同取向晶粒对应变的加权项, $ \alpha $为与电场的夹角(如图5所示), $ \Delta\eta $反映双极性交变方波电场作用下重新取向的非180°畴体积分数的变化.
通过结合二维衍射谱数据, 单双峰拟合这种方法可以分别计算样品在电场作用下的本征晶格应变与非本征的非180°畴壁运动引起的应变, 由此能进一步确定在电场作用下本征贡献与非本征贡献的占比.
3 -->

4.1.3.宏观应变测量和同步辐射X射线衍射实验相结合的方法

除了上述计算本征应变与非本征应变的方法外, Kungl等^[53]还提出了一种将宏观应变测量和同步辐射X射线数据分析相结合来估算晶格应变与畴翻转机制对总应变贡献的半经验方法. 该方法以准同型相界(morphotropic phase boundary, MPB)处组分的PZT陶瓷为样品, 并认为该组分PZT的相结构为三方相与四方相的两相共存.
该方法首先需要确定三方相畴与四方相畴的体积分数, 通过X射线衍射数据并应用单双峰拟合的方法可以计算得到

${f_{\rm{t}}} = {{{I_{{\rm{t}}\left( {200} \right)}}}}/({{{I_{{\rm{t}}\left( {002} \right)}} + {I_{{\rm{t}}\left( {200} \right)}}}}),\tag{9a}$

${f_{\rm{r}}} = {{{I_{\rm{r}}}\left( {111} \right)}}/({{{I_{{\rm{r}}\left( {111} \right)}} + {I_{{\rm{r}}\left( { - 111} \right)}}}}),\tag{9b}$

那么样品极化前后的三方相与四方相畴体积分数的变化为

$\Delta{f_{{\rm{t}},{\rm{rem}}}} = {f_{{\rm{t}},{\rm{po}}}} - {f_{{\rm{t}},{\rm{unp}}}},\tag{10a}$

$\Delta{f_{{\rm{r}},{\rm{rem}}}} = {f_{{\rm{r}},{\rm{po}}}} - {f_{{\rm{r}},{\rm{unp}}}}.\tag{10b}$

由于极化后陶瓷样品中畴发生了重新取向, 伴随产生了剩余应变$ {\varepsilon }_{\rm{rem}} $, 其值由极化前后的畴体积分数差值给出:

${\varepsilon _{{\rm{rem}}}} = g \cdot \Delta{f_{{\rm{rem}}}},$

其中$ g $为应变效率系数. 那么通过宏观应变测量的电场-应变曲线首先可以确定$ {\varepsilon }_{\rm{rem}} $, 再通过X射线衍射数据确定$ \Delta{f}_{\rm{rem}} $, 从而可以计算得到$ g $.
假设在极化过程和电场作用这两个过程中, 畴翻转与应力-应变相互关系的影响相同. 根据这个假设, 电场作用下畴体积分数变化$ \Delta{f}_{E} $产生的畴翻转应变$ {\varepsilon }_{\rm{switch}} $与剩余应变$ {\varepsilon }_{\rm{rem}} $具有相同的应变效率系数$ g $. 由此畴翻转应变$ {\varepsilon }_{\rm{switch}} $可以通过X射线衍射数据来计算:

${\varepsilon _{{\rm{switch}}}} = g \cdot \Delta{f_E}.$

已知宏观应变测量的总应变$ {\varepsilon }_{E} $主要由本征的晶格应变$ {\varepsilon }_{\rm{piezo}} $与非本征的畴翻转应变$ {\varepsilon }_{\rm{switch}} $两部分构成. 所以本征的晶格应变为总应变与畴翻转应变之差:

${\varepsilon _{{\rm{piezo}}}} = {\varepsilon _E} - {\varepsilon _{{\rm{switch}}}}.$

通过该种方法, Kungl等^[53]得到了六种不同MPB组分PZT陶瓷(x = 52.5—55)的剩余应变, 本征晶格应变与非本征的畴翻转应变. 他们发现在经过2 kV/mm的电场极化后, 陶瓷样品中剩余应变$ {\varepsilon }_{\rm{rem}} $的范围为0.18%—0.28%, 畴翻转应变$ {\varepsilon }_{\rm{switch}} $的范围为0.04%—0.07%, 晶格应变$ {\varepsilon }_{\rm{piezo}} $的范围为0.07%—0.10%. 在该范围组分内, 随着陶瓷中Zr的含量增加, 畴翻转应变$ {\varepsilon }_{\rm{switch}} $随之逐渐减小.
总的来说, 该方法结合了宏观应变测量和同步辐射X射线衍射数据, 计算思路相对简洁, 能通过半经验的方式得到剩余应变、本征应变和非本征应变. 但是该方法没有直接计算本征的晶格应变, 而是通过总应变与畴翻转应变相减得到. 这种处理方式可能将样品中缺陷、晶粒间相互作用等因素的影响归入晶格应变中, 并且总应变与畴翻转应变这两种应变也是由不同的测量技术得到. 所以该方法得到的本征应变和非本征应变可能存在着一定的计算误差.
2 -->

4.2.全谱拟合

单双峰拟合方法具有诸多优点, 但是仍有一定的局限性. 该方法不能完整描述电场作用下晶体结构和畴结构的变化, 且当多相共存时, 对晶体结构的分析更加复杂, 全谱拟合方法因此具有一定的优势. 常用的全谱拟合如Rietveld refinement方法^[23], 是通过计算特定结构模型在不同(hkl)位置的结构因子, 对所测量的多个衍射峰的强度和位置进行最小二乘法拟合. 这一方法对衍射数据尤其是2θ分辨率和衍射强度的准确性要求较高, 一般要求所收集衍射数据来自于方向分布随机、应力均匀的样品. 但是, 施加电场的情况下, 非180°畴翻转^[48]以及晶粒间应变^[54]会导致特定(hkl)衍射峰强度受到取向分布的强烈影响, 使得依赖于衍射强度进行结构分析的准确性大为下降, 如对不同结构模型及空间群进行区分或对原子位置进行拟合等, 由于以上原因均不适宜在施加电场的情况下开展.
由于使用二维探测器收集电场作用下的德拜衍射环, 并将其划分为等间隔的不同扇形区域进行衍射强度积分, 能够大致区分不同晶粒取向与电场方向的相对关系, 这可以在一定程度上规避上述提到的问题. 例如Fan等^[55]选取受织构影响最小的45°角区域, 对PbZr_0.535Ti_0.465O₃ (PZT53.5)陶瓷在外加电场作用下的高能同步辐射数据进行了全谱拟合, 认为单斜相本征晶格应变是PZT53.5产生较大宏观应变的主要原因.
Hinterstein等^[56]采用了一种在Rietveld refinement中引入应变、织构等取向表征参数的综合方法STRAP (strain, texture, and rietveld analysis for piezoceramics), 来分析在电场作用下失去随机取向的压电陶瓷粉末衍射数据. 该精修方法基于Rietveld扩展组合分析程序MAUD (materials analysis using diffraction)^[57], 能够得到表征电场诱导相变的各相占比, 并通过织构模型分析畴翻转, 通过应变模型分析晶格应变, 最终将应力和取向导致的衍射峰强度变化与晶体结构建模相结合, 从而计算出电场作用下具有复杂组成的样品中畴翻转、畴壁运动和晶格畸变导致的整体应变^[58]. 相比于选取特定德拜环区域衍射强度积分并开展普通结构精修的方法, STRAP方法将取向对衍射强度的影响引入精修过程, 得到的结构模型和原子位置更为精确, 同时获得更为全面的多种应变信息.
Hinterstein等^[59]和Khansur等^[60]采用这种方法, 通过调整结构参数, 对比PZT, NBT-BT等体系的实验数据和拟合所得图谱, 确立了能够准确描述衍射图谱的结构模型, 如图7所示. 在分析过程中, 他们将该材料的平均结构视为三方相和四方相的两相共存, 并分别分析这两个相在电场作用下的结构变化. 在计算从各个相到宏观应变的应变贡献过程中, 也考虑了相的占比问题:
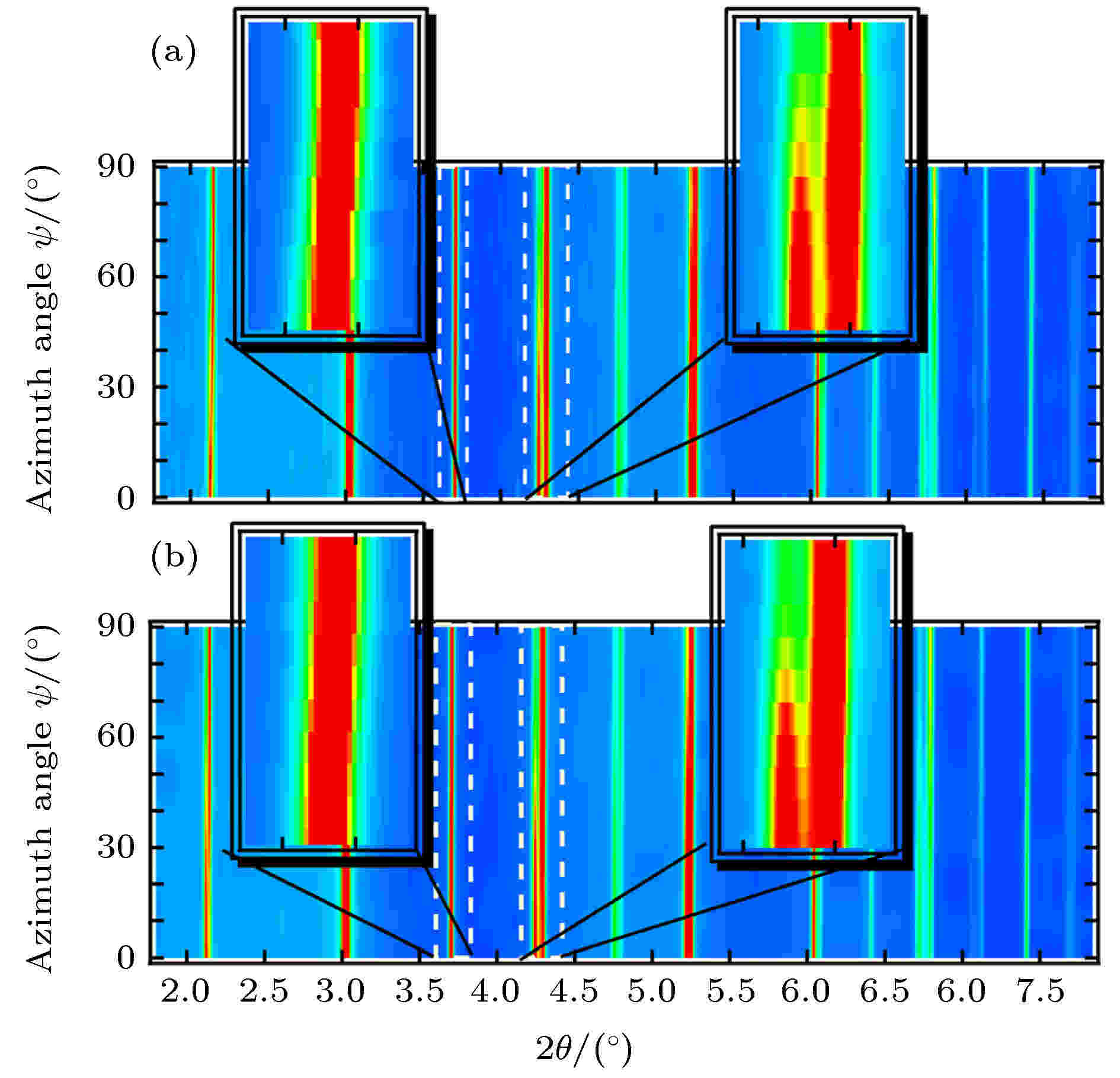图 7 NBT-BT陶瓷在施加最大电场E_max = 4 kV/mm下的实验(a)和模拟(b)所得的取向相关衍射图样^[60]
Figure7. Measured (a) and modelled (b) orientation dependent diffraction patterns of NBT-BT at maximum field E_max = 4 kV/mm^[60] (Copyright ? 2015 AIP Publishing).

${\varepsilon _{\rm{L}}} = {{\rm{\% }}_{\rm{T}}}\cdot{\varepsilon _{\left( {{\rm{L}},{\rm{T}}} \right)}} + {{\rm{\% }}_{\rm{R}}}\cdot{\varepsilon _{\left( {{\rm{L}},\rm{R}} \right)}},\tag{14a}$

${{\rm{\varepsilon }}_{\rm{D}}} = {{\rm{\% }}_{\rm{T}}}\cdot{\varepsilon _{\left( {{\rm{D}},{\rm{T}}} \right)}} + {{\rm{\% }}_{\rm{R}}}\cdot{\varepsilon _{\left( {{\rm{D}},{\rm{R}}} \right)}},\tag{14b}$

其中, %_T和%_R分别是四方相和三方相的占比, $ {\varepsilon }_{\left({\rm{L}}, {\rm{T}}\right)} $和$ {\varepsilon }_{\left({\rm{L}}, {\rm{R}}\right)} $分别指四方相和三方相的晶格应变, $ {\varepsilon }_{\left({\rm{D}}, {\rm{T}}\right)} $和$ {\varepsilon }_{\left({\rm{D}}, {\rm{R}}\right)} $分别对应四方相和三方相的畴翻转应变. 然后考虑畴翻转过程中可能导致的{hkl}随机取向翻倍(multiples of a random distribution, MRD)^[51]得到翻转畴应变$ {\varepsilon }_{{\rm{D}}} $的大小:

${\varepsilon _{\rm{D}}} \!=\! {\rm{\eta }}\frac{1}{{2{\text{π}}}}\int_{\alpha = 0}^{\frac{{\text{π}}}{2}} \left[ {\Delta {\rm{MR}}{{\rm{D}}_{hkl}}\left( \alpha \right) {{\cos }^2}\alpha } \right] {\sin \alpha } {\rm{d}}\alpha ,$

其中$\eta $表示晶格畸变, ?MRD表示随机分布的极轴的方向和施加电场的角度. 四方相和三方相的晶格畸变分别用${\rm{\eta }}_{{\rm{T}}}= {{c}_{{\rm{T}}}}/{{a}_{{\rm{T}}}}-1$和${\rm{\eta }}_{{\rm{R}}}= {{\sqrt{2}c}_{\rm{H}}}/{{\sqrt{3}a}_{\rm{H}}}-1$表示, 结合相成分占比分数加权和织构参数计算得出从不加电场至外加电场状态下的宏观形变. 最终获得在电场作用下, 畴翻转和晶格应变的贡献.
2 -->

4.3.具有代表性的多晶压电体系中本征贡献与非本征贡献的计算

根据本征贡献与非本征贡献的计算方法, 研究者们对于包括含铅压电体、无铅压电体和弛豫铁电体等在内的多晶压电体系中具有代表性的材料进行了探索与分析.
在传统含铅压电材料中, PZT由于发现年代较早、性能优越、应用广泛, 成为多种新型实验方法首选的研究对象. Pramanick等^[49]对不同组分镧/铁掺杂的PZT陶瓷进行了原位、高能、时间分辨的X射线衍射测试, 分别得到了不同电场强度下晶格应变与畴壁运动对压电常数$ {d}_{33} $的贡献, 如图8所示. Zhao等^[61]报道了MPB组分范围的Nb掺杂的PZT陶瓷中电场诱导的本征应变与非本征应变对宏观应变都有着较大贡献, 在靠近MPB组分的陶瓷中本征应变的贡献更高, 而远离MPB组分的陶瓷中非本征应变的贡献更高.
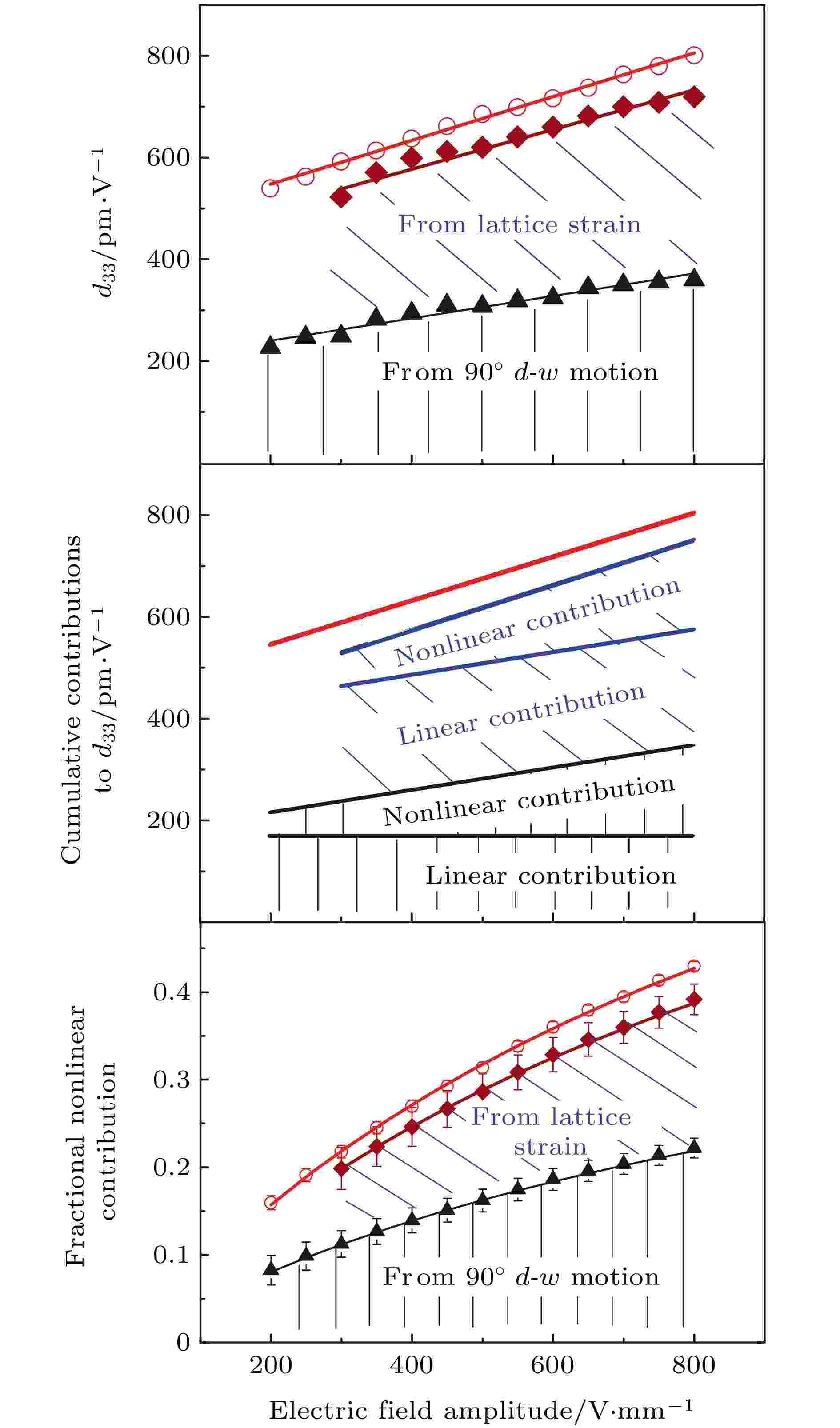图 8 La掺杂的PbZr_0.52Ti_0.48O₃陶瓷中晶格应变与畴壁运动对宏观压电常数及非线性压电常数的贡献^[49]
Figure8. Contributions of lattice strain and domain wall motion to macroscopic piezoelectric coefficient and non-linear piezoelectric coefficient in La-doped PbZr_0.52Ti_0.48O₃ ceramics^[49] (Copyright ? 2011 John Wiley and Sons)

在无铅压电材料中, KNN基材料因其较高的压电系数与优异的温度性, 具有广阔的研究前景. Fu等^[62]报道了 (K_0.48–xNa_0.52)(Nb_0.92–xSb_0.08)O₃-xLiTaO₃陶瓷在多晶型相界(polymorphic phase boundary, PPB), 即正交相-四方相相界附近组分的压电响应来源, 材料富正交相组分中的应变以本征晶格应变为主, 而在富四方相组分中以非本征的可逆畴翻转应变为主. 同时非本征应变的贡献不仅取决于晶格畸变, 还取决于极化取向、PPB组分的相比例和畴类型. Ochoa等^[63]报道了KNN基四方相(K_0.44Na_0.52Li_0.04)-(Nb_0.86Ta_0.10Sb_0.04)O₃ (KNL-NTS)陶瓷中, 非180°畴壁运动对电场诱导宏观应变的贡献极大, 占到了宏观应变的约80%.
Zheng等^[64]报道了一种KNN基压电陶瓷$(1\!-\!x)({\rm K}_{1-y}{\rm Na}_y)({\rm Nb}_{1-z}{\rm Sb}_z){\rm O}_3 \text{-}x{\rm Bi}_{0.5}({\rm Na}_{1-w}{\rm K}_w)_{0.5}$HfO₃ 的新相界(三方-四方相相界). 在施加电场过程中, 陶瓷的(100)和(220)衍射峰的峰强度比发生了明显变化, 而这则与极化矢量在三方相-四方相之间的翻转密切相关, 如图9所示.
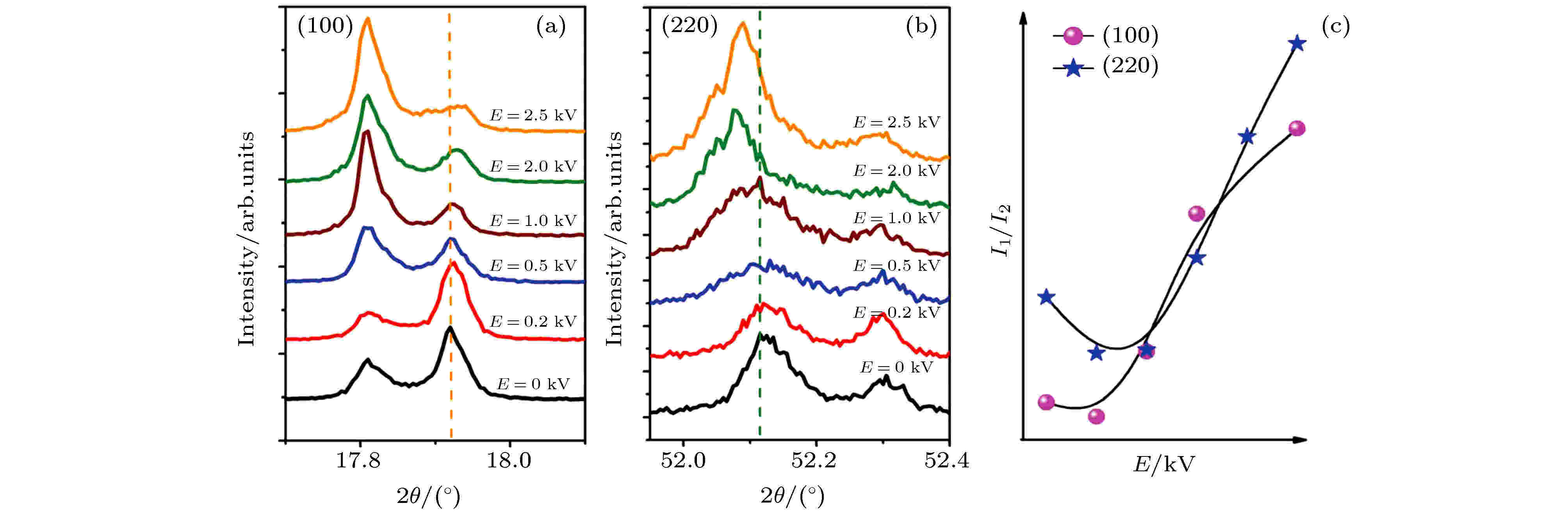图 9 (1–x)(K_1–yNa_y)(Nb_1–zSb_z)O₃-xBi_0.5(Na_1–wK_w)_0.5HfO₃ (x = 0.035, y = 0.52, z = 0.05, w = 0.18)陶瓷　(a), (b) (100)和(220)衍射峰随电场的演变过程; (c) (100)和(220)衍射峰中低角度衍射峰与高角度衍射峰的强度之比(I₁/I₂)随电场的变化^[64]
Figure9. (1–x)(K_1–yNa_y)(Nb_1–zSb_z)O₃-xBi_0.5(Na_1–wK_w)_0.5HfO₃ ceramic with x = 0.035, y = 0.52, z = 0.05 and w = 0.18: (a), (b) Evolution of the (100) and (220) pseudocubic reflections as a function of the electric field; (c) ratio of low angle peak intensity to high angle intensity (I₁/I₂) for (100) and (220) pseudocubic reflections as a function of the electric field^[64] (Copyright ? 2017 The Royal Society of Chemistry)

在其他无铅压电材料方面, Ba(Zr, Ti)O₃-(Ba, Ca)TiO₃ (BZT-BCT)也表现出了能与PZT相媲美的压电性能. Tutuncu等^[65]对材料MPB附近组分的陶瓷进行了电场原位X射线衍射分析. 他们报道了在机电耦合响应中宏观应变主要由90°畴壁运动贡献导致; 随着组分越靠近MPB边界, 90°畴壁运动对宏观应变的贡献越大, 从而压电系数$ {d}_{33} $也随之增大.
在BiFeO₃体系中, Khansur等^[66]报道了三方相BiFeO₃陶瓷中电场诱导应变主要来自非180°畴翻转, 并且观察到了非180°畴翻转的强弛豫行为. Li等^[67]发现非遍历性(non-ergodic, NR)弛豫铁电体 0.57BiFeO₃-0.21(K_0.5Bi_0.5)TiO₃-0.22PbTiO₃ (BF-KBF-PT)在电场诱导下会不可逆地从非遍历性赝立方相$ Pm\bar{3}m $转变为三方铁电相$ R3 c $. 在交变电场下, BF-KBF-PT陶瓷中本征应变对宏观应变$ {\varepsilon }_{33} $的贡献明显大于非本征应变.
在NaNbO₃-BaTiO₃ (NN-BT)体系中, Zuo等通过同步辐射X射线衍射、X射线吸收精细结构谱、拉曼光谱研究了NN-BT弛豫铁电体在外场作用下的结构变化^[68]. 图10(a)—(g)显示了样品在外加电场的作用下, 极性纳米微区(polar nanoregions, PNRs)逐渐演化成铁电微畴, 且当电场大于0.8 kV/mm时, 观察到畴翻转现象. 电场诱导的PNR生长过程主导了场致应变的最快增长和最大应变滞后的形成, 而不是随后的畴翻转. 如图10(h)所示, 当外加电场释放时, 所有的变化又都被完全恢复, 表明电场强迫PNR生长和畴翻转的过程是可逆的.
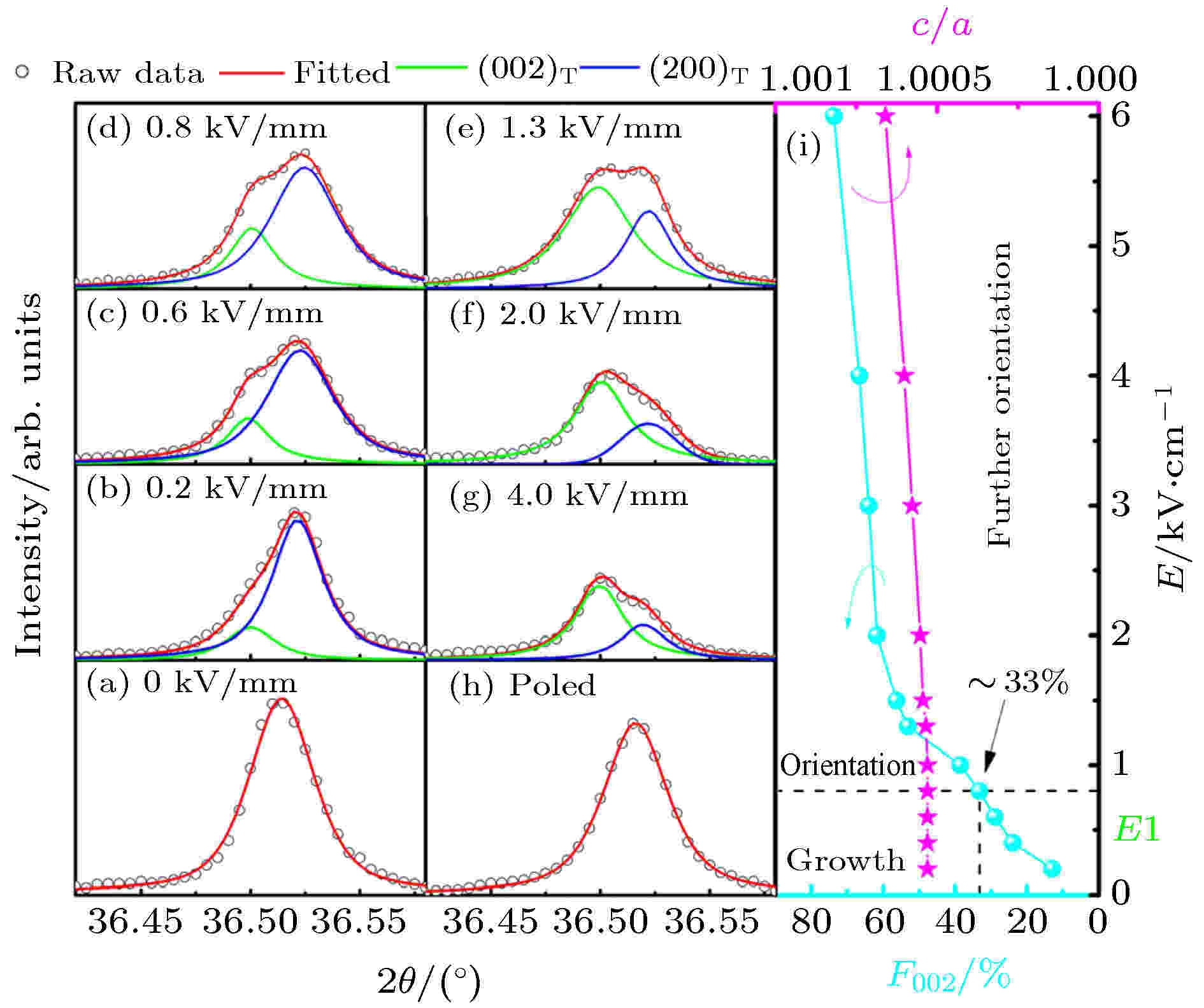图 10 NN-BT陶瓷{200}衍射峰在电场作用下的重新分布现象^[68]
Figure10. {200} reflections and their redistributions under electric field for NN-BT^[68] (Copyright ? 2017 AIP Publishing)

2 -->

4.4.原位单晶衍射

相对于陶瓷, 单晶纯度高、缺陷少、不存在晶界、机电性能更好. 同时, 单晶X射线衍射能够将倒易空间中的三维方向进行区分, 避免了同一族{hkl}衍射峰的相互重叠, 从而能够得到具有不同取向畴结构所生成的衍射强度分布. 受限于分辨率, 陶瓷衍射实验多针对具有较高对称性(如三方相和四方相)的材料进行分析, 或将MPB结构简单等同于三方和四方的两相共存结构, 然而高分辨单晶衍射数据可清晰区分低对称性结构(如单斜相)中的较小衍射峰分峰, 具有更大的通用性.
Choe等^[33]通过时间分辨原位单晶X衍射实验研究了NBT单晶在电场作用下的极化矢量旋转现象. 未施加电场时(004)和(400)衍射峰不重合, 显示材料为单斜相, 施加正向电场时, (004)和(400)峰在散射矢量方向上的距离加大, 随着电场逐步减小, 两峰间距进一步减小, 在施加最小电场–14 kV/cm下, 两峰距离最近, 但仍不重合. 通过对(004)和(400)峰三维倒易空间坐标随电场的变化进行分析和拟合, 他们还原了该材料在电场诱导下, 极化矢量在{110}镜面上的旋转过程.
Hu等^[69]生长出了具有超高电致应变的KNN单晶, 并通过原位单晶同步辐射X射线衍射实验观察到施加1.2 kV/mm电场时, {302}和{310}峰处产生新的衍射斑点, 显示了新的铁弹畴的产生, 同时表明该单晶的高电致应变主要来源于畴的重新分布.
Zhang等^[70]提出了一种通过高分辨单晶X射线衍射实验收集三维倒易空间衍射强度随交变电场变化, 从而分离MPB组分PZT单晶压电效应中本征贡献与非本征贡献的方法. 该实验中可观察到一个衍射峰中往往包含着多个独立衍射强度分布, 分别代表一类铁电/铁弹畴. 在数据分析过程中, 将三维衍射强度的坐标系规定为: X平行于散射矢量方向, Y和Z分别为选定的垂直于X的一个方向; 每个衍射峰的分量在YZ二维衍射强度分布图(沿X方向积分)中用一个YZ Box标记出来, 如图11(b)和图11(c)所示. 假设两组布拉格衍射峰的质心位置分别为$ {X}_{1}, {X}_{2} $, 对应曲线下的面积为$ {I}_{1}, {I}_{2} $, 同时假设两个衍射峰组的强度互换主要是由于畴翻转导致, 即$ \Delta{I}_{1}\approx -\Delta{I}_{2} $, 则电场诱导下的质心位置偏移可以表达为
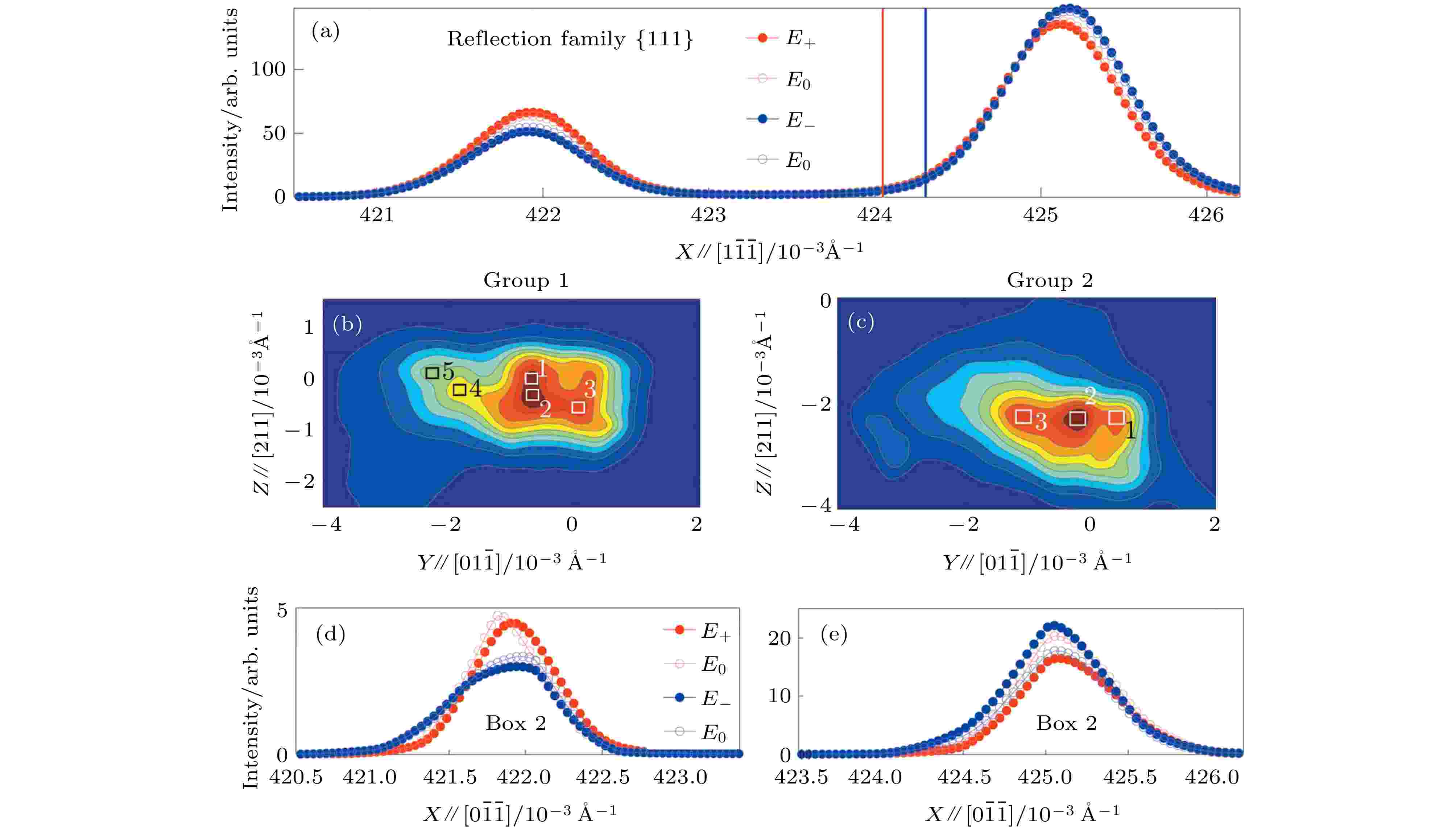图 11 (a) {111}衍射峰的衍射强度(沿YZ方向积分)与X的关系曲线, 垂直的红蓝线分别对应$ {E}_{+}\backslash {E}_{-} $状态下的质心位置; (b), (c)沿不同X范围积分的二维衍射强度分布图, 分别对应图(a)中的Group 1和Group 2; (d), (e)一个YZ Box范围内积分的衍射强度与X的关系曲线, 其中(d), (e)分别对应Group 1中的Box 2和Group 2中的Box 2 ^[70]
Figure11. (a) The X dependence of the diffraction intensity around {111} reflections, integrated within the full YZ range. The vertical red and blue lines mark the center of mass positions corresponding to the E₊ and ${E_ - } $ states. (b), (c) YZ dependence of the diffraction intensity integrated within two ranges of X, corresponding to Group 1 and Group 2 in panel (a). Several boxes are marked to show the positions of Bragg peak sub-components. (d), (e) Integrated intensities within one YZ box against X under four states of field. (d) Corresponds to Box 2 in Group 1 and (e) to Box 2 in Group 2^[70] (Copyright ? 2018 International Union of Crystallography. Reproduced with permission of the International Union of Crystallography)

$\Delta X = \frac{{\Delta{I_1}\left( {{X_1} - {X_2}} \right)}}{{{I_1} + {I_2}}} + \frac{{{I_1}\Delta{X_1} + {I_2}\Delta{X_2}}}{{{I_1} + {I_2}}},$

式中第一部分取决于衍射强度的改变($ \Delta{I}_{1} $), 这反映了畴壁运动导致的各类畴比例的变化, 这属于非本征效应; 第二部分取决于两个衍射峰组分别的质心位移($ \Delta{X}_{1}, \Delta{X}_{2} $), 这是每一组中各分量的累计值, 对应各个畴独立的本征响应. 这种计算方法可以得到各个YZ Box的尺寸与压电常数的关系以及累加本征效应与非本征效应对压电常数的贡献, 在实验考察的PZT单晶中, 非本征效应占据80%以上的贡献. 值得注意的是, 在单晶实验得到的压电贡献中, 非本征贡献的比例远远高于多晶材料中测得的非本征贡献比例^[49,55], 这一方面是由于在多晶实验中, 受限于三维空间信息的缺失和分辨率的限制, 一部分低对称性畴重排引起的分峰强度变化无法被观察到, 极易被混淆为本征贡献; 另一方面, 陶瓷材料中由于晶粒及晶粒间应力的存在, 可能导致畴翻转过程被“钉扎效应”阻碍, 因此畴翻转的活跃程度小于单晶材料.

在电场诱导的相变过程中, 铁电体的宏观应变除了来自于晶格应变和畴翻转应变的贡献外, 还有来自于相变应变的贡献. 在这一过程中, 铁电体中可能出现对称性变化、氧八面体扭转^[71]、可逆畴结构形成^[72]等晶体结构变化, 因此晶格应变、畴翻转应变与相变应变^[59,73]对宏观压电效应共同产生影响.
在早期对经典含铅压电材料如PZT^[59], PMN-PT^[36]和Pb(Zn_1/3Nb_2/3)O₃-PbTiO₃ (PZN-PT)^[74]等的研究过程中, 单斜相在MPB区域被陆续发现; 由于单斜M_A/M_B结构中, 极化矢量可在连接三方相和四方相的{110}镜面或连接正交相和三方相的{110}镜面上自由旋转, 因而电场诱导的结构相变常常伴随着极化矢量旋转的过程^[18]. 在MPB区域, 不同相结构的自由能较为相近, 较小的外场刺激就可能导致较大的极化旋转, 被认为是压电效应本征贡献的重要组成部分^[75].
例如在针对PZT的早期研究中, Guo等^[9]报道了MPB组分PZT陶瓷极化后, 其晶胞压电伸长并不沿三方相或四方相的极化矢量方向, 而是向单斜M_A结构的方向伸长. 换言之, MPB组分的PZT陶瓷在极化过程中, 其极化矢量在连接三方相和四方相的镜面上旋转, 即图12中的a-g-f-e (R-T)路径. 值得一提的是, Fu和Cohen^[18]通过第一性原理计算了钙钛矿结构BaTiO₃的三方相-四方相相变中所需的自由能, 这条a-g-f-e路径是其中所需自由能最少的路径.
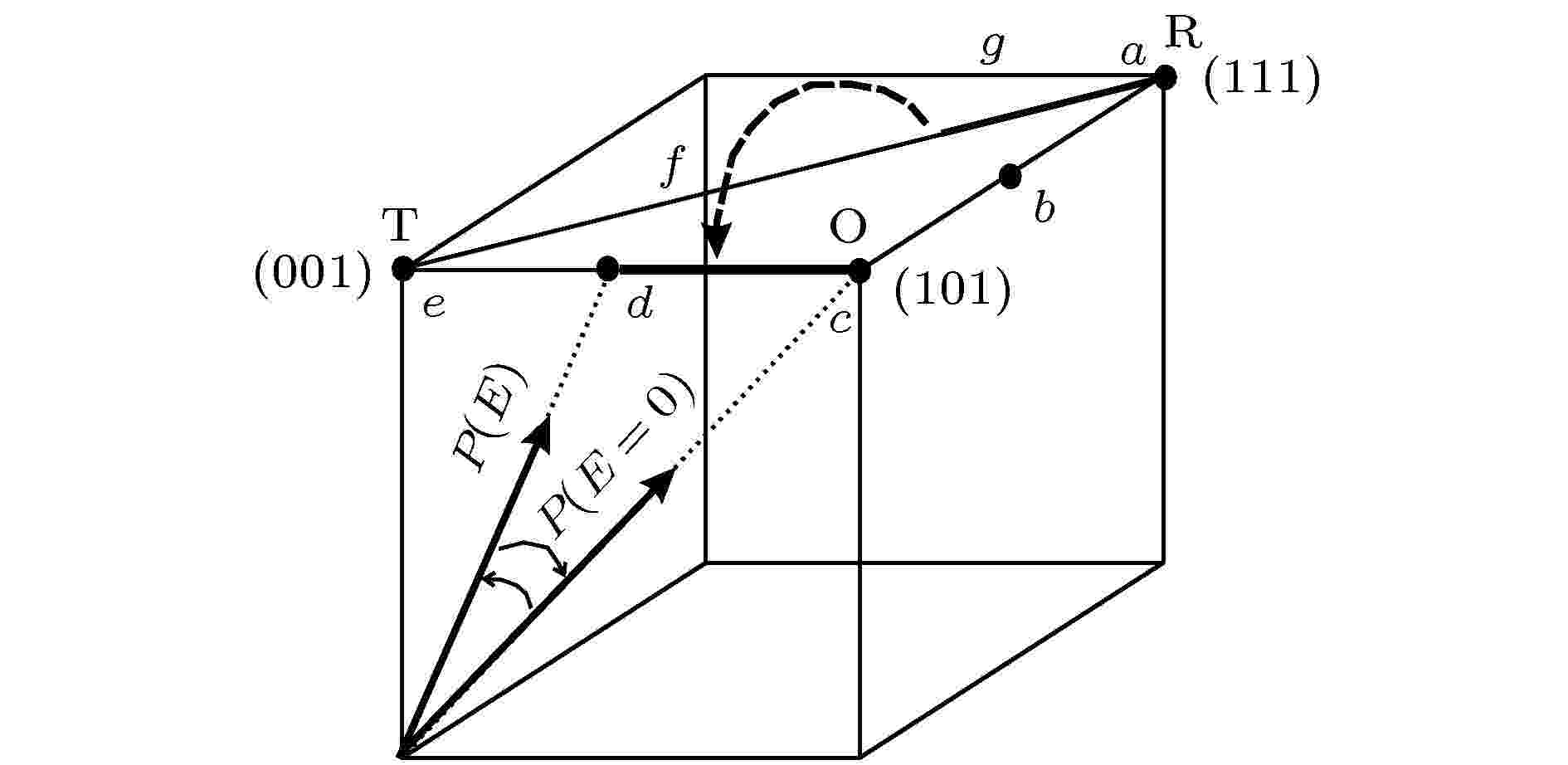图 12 三方相-四方相相变中可能的极化矢量旋转路径^[18,76]
Figure12. The two possible paths for the polarization direction to change from [111] in the rhombohedral (R) phase to [001] in the tetragonal (T) phase^[18,76] (Copyright ? 2001 American Physical Society)

在PZN-PT中, Noheda等^[76]报道了PZN-8%PT单晶在电场诱导下的极化矢量旋转路径. 在极化过程中, PZN-8%PT单晶会不可逆地从三方相结构转变为单斜相, 其极化矢量的旋转路径为图12中的a-c-d-e路径. 即极化矢量首先沿着a-g路径(R-T)旋转, 然后不可逆地转跳到另一条c-d-e (O-T)路径. 他们认为相比于PZT, PZN-PT单晶存在的两条旋转路径很有可能是其压电响应高于PZT的原因.
在无铅压电材料中也发现了类似的极化矢量旋转现象. 如Fu等^[77]报道了位于三方-正交相相界处组分的KNN基陶瓷(Na_0.52K_0.48)(Nb_1–ySb_y)O₃在极化过程中, 正交相会不可逆转地转变为单斜相, 其极化矢量会沿着极化旋转路径(三方相-单斜相-正交相, R-M-O)来进行旋转, 如图13所示; 而三方-单斜相变则为可逆相变, 从而带来了相的不稳定性. Li等^[78]通过织构化工艺制备出了超高压电性能的高织构度KNN基压电陶瓷. 他们发现对织构化样品KNN-3T (3 mol% NaNbO₃模板)施加一定电场时三方相转变为了中间相单斜相, 而当电场继续加大后, 单斜相则继续转变为了正交相. 一方面, 陶瓷高压电性能的重要来源之一就是电场诱导的高晶格畸变; 另一方面, 极化过程中中间相的出现有利于整个极化过程的实现. 以上KNN基陶瓷的研究表明: 在极化过程中, 单斜相作为中间相有助于实现两相之间极化矢量的旋转, 从而增强了KNN基陶瓷的压电响应.
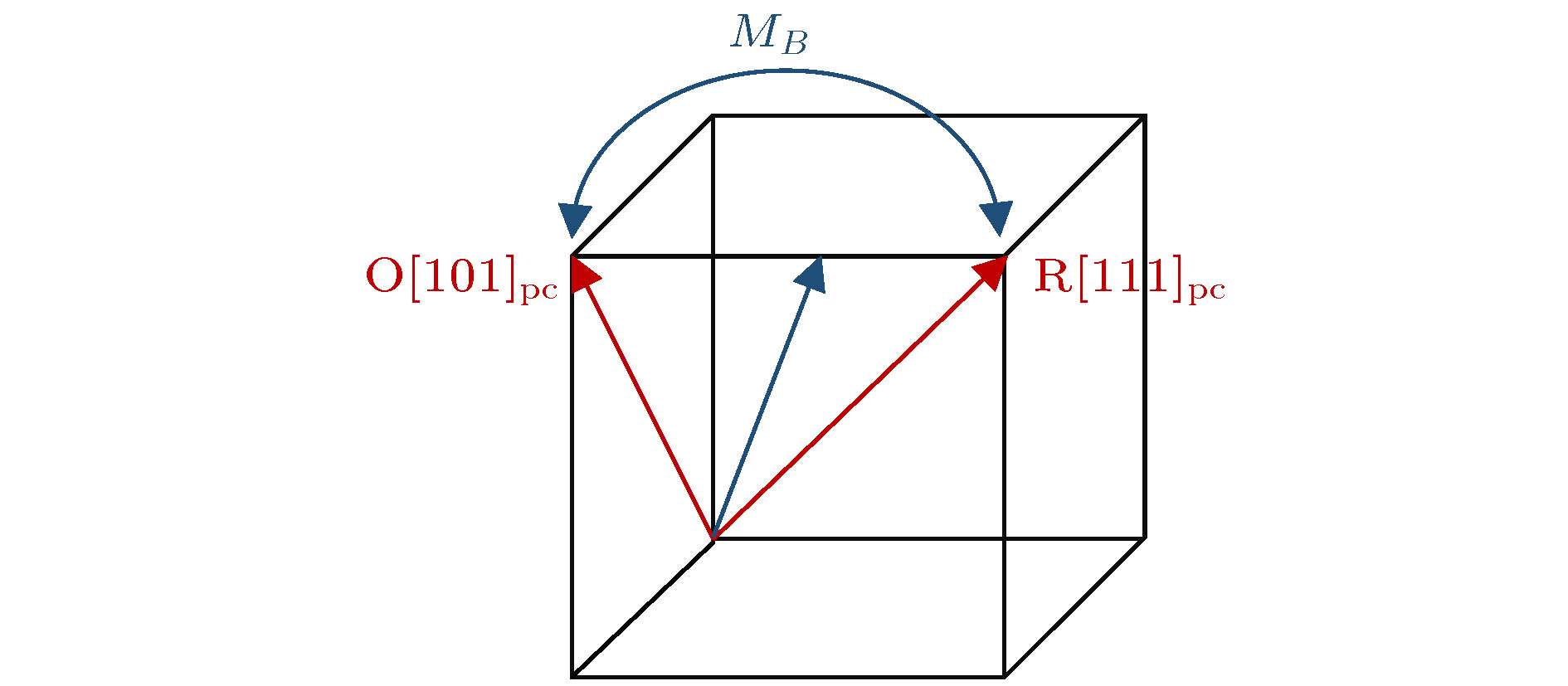图 13 KNN基陶瓷中的三方相-单斜相-正交相的极化旋转路径
Figure13. Polarization rotation path of rhombohedral-monoclinic-orthorhombic phase in KNN-based ceramic

此外, Yao等^[79]报道了CaZrO₃掺杂的KNN陶瓷在电场作用下的另一种相变可能, 即正交相与四方相的相互转化. 未加电场时PPB附近组分存在正交和四方的两相共存, 电场诱导下的晶格体积增大促进了四方相大量转化为正交相, 从而进一步增强了电致应变.
NBT基无铅固溶体为代表的一类具有弛豫特性的钙钛矿材料中, 发现了可恢复电致相变现象, 与传统压电材料不同的是, 这类材料平均结构十分接近立方相, 但局部结构较为复杂, 因而可能在电场作用下诱导出非中心对称结构以及各相异性的大应变效应. 以0.93NBT-0.07BT陶瓷材料为例^[60], 在电场作用下, 可能出现赝立方相至具有较大畸变的三方相和四方相的相变. 结合高能原位X射线衍射谱分析得到, 0.93NBT-0.07BT陶瓷在极化过程中晶格应变、畴翻转应变和相变应变分别占总应变的24%, 44%和32%. Simons等^[80]报道了0.94NBT-0.06BT陶瓷在高温下(T > 75 ℃)表现出的可恢复的大应变现象, 如图14所示. 通过原位中子衍射实验, 他们发现在高温下0.94NBT-0.06BT中出现大的可恢复应变的主要原因为电场诱导下可逆相变引起的体积变化. 类似的现象也在(Na_0.5Bi_0.5)TiO₃-BaTiO₃-0.03AgNO₃ (NBTBT-3AN)中被观察到^[81].
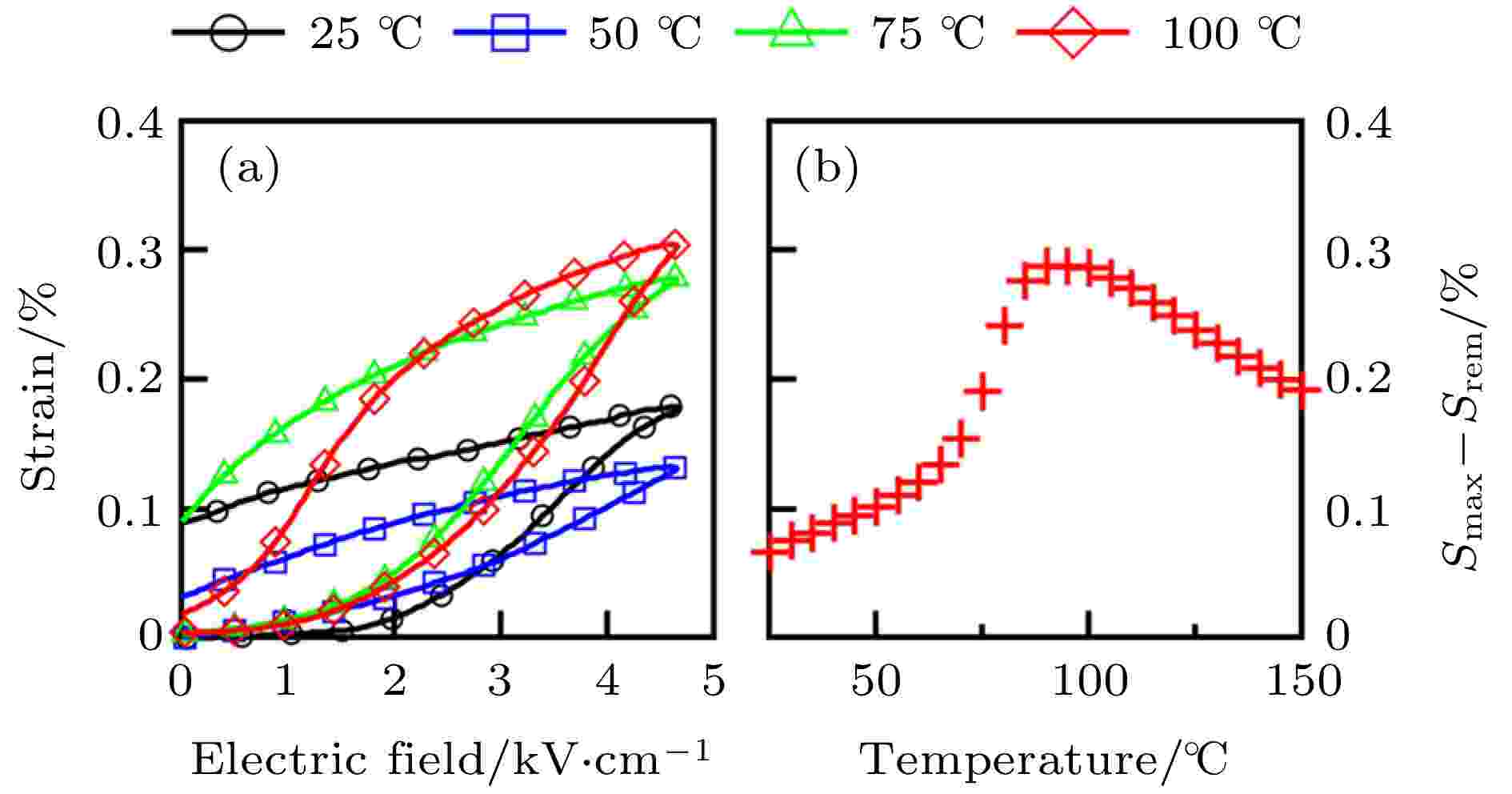图 14 对于0.94NBT-0.06BT陶瓷　(a) 在25, 50, 75和100 ℃下的单极电场-应变曲线; (b) 可恢复应变(S_max – S_rem)的温度依赖关系 ^[80]
Figure14. For 0.94NBT-0.06BT ceramic, (a) unipolar strain hysteresis at 25, 50, 75, and 100 ℃; (b) temperature-dependence of recoverable strain (S_max – S_rem)^[80] (Copyright ? 2013 AIP Publishing)

在KNN掺杂的NBT基无铅固溶体(1–x – y)NBT-xBT-yKNN的研究中, Hinterstein等^[71]报道了0.92NBT-0.06BT-0.02KNN陶瓷在电场的作用下, 会从具有赝立方晶格结构的、几乎无极性的四方相转变为具有明显晶格畸变的、铁电性的三方相. Daniels等^[73]报道了0.93NBT-0.07BT和0.86NBT-0.14KNN两个端元组分间的NBT-BT-KNN陶瓷的电场-应变行为. 在电场作用下, BT含量更高的陶瓷会从赝立方结构转变为四方相结构. 而陶瓷中KNN含量越高, 该电致相变过程发生时所需的电场也就越高. 当KNN含量到达端元组分0.86NBT-0.14KNN时, 陶瓷在5.5 kV/mm的电场下, 依然观察不到电致相变现象, 其宏观应变主要是来自于晶格应变. 而另一个端元组分的0.93NBT-0.07BT陶瓷中, 其0.4%的宏观应变(在5.5 kV/mm的电场下)则分别是来自于相变应变(0.11%)、畴翻转应变(0.08 %)和晶格应变. 考虑到表征技术以及三元陶瓷体系中组分的微小差别等原因, NBT-BT-KNN陶瓷电致相变是从赝立方结构转变为三方相结构还是转变为四方相结构, 目前学界没有统一的结论, 仍有待进一步的探究.
Wang等^[82]采用同步辐射和Rietveld精修对大应变和高击穿强度的BiFeO₃-BaTiO₃-xNd(Li_0.5Nb_0.5)O₃ (BF-BT-NLN) 进行了研究. 图15为不同电场条件下, 0.67BF-0.33BT和0.6BF-0.3BT-0.1BiO₃同步辐射X射线衍射图谱, 施加电场之前、期间和之后, 晶体结构均为赝立方, 即便以最初施加电场的2—3倍(150 kV/cm)进行原位极化, 仍未观察到峰的劈裂. 因此, 他们认为该材料大应变的产生不是从传统的弛豫态到电场诱导的长程铁电相变导致的, 而是提出了一种场诱导的伪对称模型, 在赝立方晶体中存在多个非中心对称纳米畴, 导致局部区域在施加电场的方向上产生畸变. 该模型不仅解释了这些高活性固溶体中的大应变, 还解释了应变的各向异性.
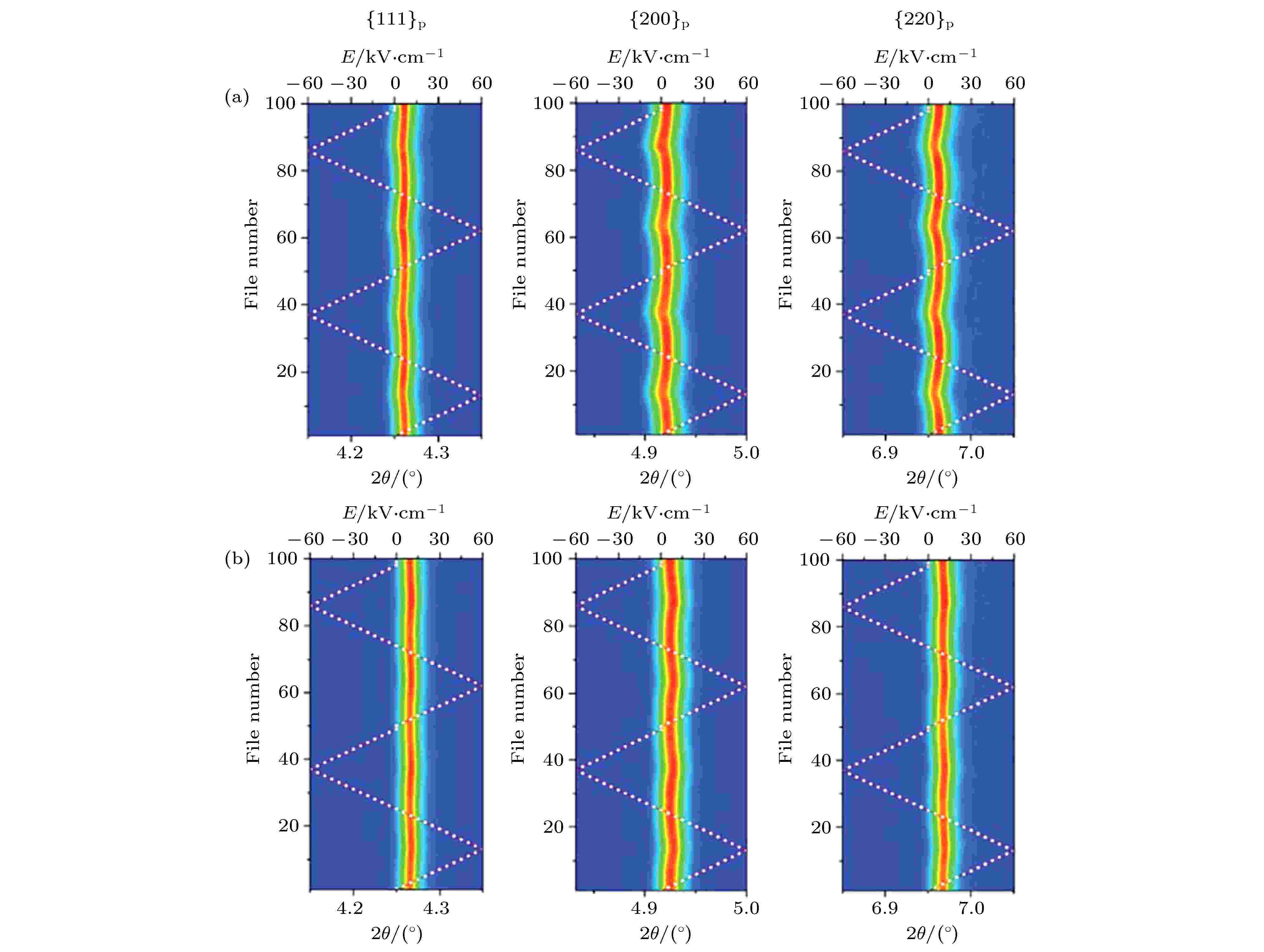图 15 对BF-0.3 BT-0.03 NLN陶瓷在 ± 60 kV/cm的电场下进行了两个电场循环观察到的{111}, {200}和{220}峰的等高线图 (a)平行电场方向; (b)垂直电场方向^[82]
Figure15. Contour plots of the {111}, {200} and {220} peak profiles for (a) $ \beta $ = 0° and (b) $ \beta $ = 90° obtained from the in situ X-ray diffraction experiment for BF-0.3 BT-0.03 NLN, with two cycles of electric field poling under ± 60 kV/cm^[82] (Copyright ? 2019 The Royal Society of Chemistry)

综合含铅压电材料与无铅压电材料的电场诱导相变情况, PZT和KNN基陶瓷等材料中, 相变过程多为两个铁电相之间的相互转变, 通常伴随极化矢量旋转, 属于经典的压电现象; 而对于NBT基等伴有弛豫现象的体系来说, 其相变过程为接近立方结构的弛豫相在电场作用下转化为平均结构尺度或局部结构尺度的铁电相, 由于这一相转变过程, 这类材料中的电致应变可能很大, 但由于相变可恢复, 通常准静态压电系数不高, 因而应用范围与PZT等传统压电材料有所区别. 通过原位电场衍射实验, 可以较为方便地区分这两类电场诱导电致相变现象, 尤其对判断新材料体系的电致应变本质有较大帮助.
另一个值得讨论的问题是, 这两类电场诱导相变都导致了晶格的形变或体积变化, 从而涉及到电致应变的本征贡献. 然而在实际材料中, 相变现象不可避免地伴随着畴的产生、消失和重新分布; 同时, 第二类相变中也有部分可以理解为由局部尺度畴结构的变化导致, 因而, 电致相变无法被简单地归类为本征或非本征贡献, 而是多种效应综合贡献的结果.

弛豫铁电体, 如PMN-PT和PZN-PT, 是当前压电性能极为优异的无机铁电材料. 研究者们普遍认为, 弛豫铁电体的高压电介电系数与其独特的极性纳米微区密切相关. 但是极性纳米微区的起源与它随电场的演变过程尚不明确, 这也激发了研究者们的讨论与研究^[83–88].
弛豫铁电体中极性纳米微区的局部结构通常与它的平均晶体结构不同, 如$ x $值较小的情况下PMN-xPT和PZN-xPT中极性纳米微区表现为具有极短程相关性的$\left\langle {110} \right\rangle $极化矢量, 而该组分的宏观平均结构却为三方相^[84,89]. 在单晶衍射实验中, 尖锐的布拉格衍射峰以下仍然存在具有特定形状的较低衍射强度, 被称为漫散射. 漫散射强度来自于材料内部长程有序结构的被打破^[90], 因此能够提供材料的局部结构信息, 是研究极性纳米微区的有力工具.
2006年, Xu等^[83]报道了铌锌酸铅(Pb(Zn_1/3Nb_2/3)O₃, PZN)单晶在电场诱导下极性纳米微区的重新分布行为. 在同步辐射X射线漫散射实验中, 沿[111]方向的外加电场使得PZN单晶的三维漫散射谱的分布形状发生了显著改变, 即极性纳米微区在电场的作用下进行了重新分布. [111]方向的电场增强了[110], [101]和[011]方向的漫散射形状, 分别对应着极化方向沿$ \left[1\bar{1}0\right], \left[10\bar{1}\right], \left[01\bar{1}\right] $的极性纳米微区的增长. 该结果表明极性纳米微区趋向于一个与周围晶格的极化方向相垂直的方向生长, 这很有可能是极性纳米微区避免融入铁电相的一个关键因素.
2008年, Xu等^[84] 通过不同电场温度条件的中子非弹性散射实验, 进一步验证了弛豫铁电单晶PZN-4.5%PT中的极性纳米微区在电场作用下的重新分布现象, 同时证明在这一过程中, 极性纳米微区通过与横声学模声子的相互作用显著地影响了弛豫体系的晶格稳定性, 而这种结构不稳定性有可能是弛豫铁电体超高压电性能的成因之一.
限于漫散射强度较低、数据收集时间较长、许多单晶难于获得等原因, 目前学界针对弛豫铁电体局部结构随电场变化的原位漫散射实验开展不多, 数据分析方法尚未成熟. 在针对弛豫体局部不均匀结构与极性纳米微区对压电性能可能具有显著影响的讨论背景下, 开展此类实验仍然具有较大的必要性, 可能是铁电压电材料结构与性能关系研究的一个发展方向.

随着衍射技术的不断发展, 包括中子衍射、X射线衍射、X射线散射在内的时间分辨、高能原位衍射/散射技术已经成为了目前压电研究领域的重要研究工具. 这些衍射/散射技术能够更为完整充分地描述电场作用下压电材料的微观结构变化, 如电场作用下本征的晶格畸变、畴壁运动和电致相变等, 有助于科研工作者开展对压电响应起源的深入研究.
而在实验数据的处理上, 科研工作者们提出了多种研究分析方法, 采用了加权计算、单双峰拟合、STRAP、质心计算等方式, 对压电效应中晶格畸变、畴壁运动的贡献进行了计算, 取得了显著的研究成果.
时间分辨、高能原位衍射/散射技术和新的研究分析方法不仅将压电材料的研究领域极大拓展, 同时也会进一步促进衍射/散射技术的发展与研究分析方法的创新.