摘要:NiAl纳米颗粒具有较高的能量密度和良好的高温力学性能, 铝吸附原子在不同镍基表面上的扩散行为与不同扩散机制对铝在镍基表面沉积生长的影响有待进一步阐明. 本文通过采用肘弹性带和分子动力学结合嵌入原子势的方法, 系统地研究了单个铝吸附原子在镍基表面的扩散行为和纳米颗粒团簇在十面体(DEC)、立方八面体(CUB)和二十面体(ICO)结构上的生长. 研究结果表明: Al吸附原子在三种Ni基底上表面扩散的交换与跳跃两种机制, 最低的Ehrlich-Schwoebel(ES)势垒为0.38 eV (交换CUB{111} → 100})、0.52 eV (交换DEC{111} → 100})和0.52 e V (跳跃ICO{111} → 111}), 从{111}面扩散到{100}面主要以交换机制为主, 而相邻两个{111}面之间的扩散则以跳跃机制为主. 沉积的铝原子首先倾向于扩散到台阶边缘和顶点附近. 随着Al原子数量的增加, 沉积的Al原子开始聚集. 对于Ni团簇上的Al原子, 在较低温度下在镍基底表面沉积Al原子, 可以获得良好的Ni核/Al壳结构. 对于二十面体结构基底, 其对应的核壳团簇的缺陷数最小, 随后为十面体结构和八面体结构. 随着生长温度的增加NiAl纳米粒子的表面逐渐开始合金化.
关键词: Ni基衬底/
表面扩散/
纳米粒子生长/
核壳结构/
嵌入原子势(EAM)

English Abstract

全文HTML

--> --> -->

纳米粒子指粒子的直径在1—100 nm之间. 纳米粒子由于其独一无二的物理化学性能, 在催化、光学、生物诊断等方面有着潜在的应用^[1,2], 由于金属之间具有协同作用, 双金属纳米粒子对比单金属纳米粒子, 一些特定的性能得到了很好地提升^[2], 双金属纳米粒子一直吸引着材料科学家广泛的兴趣. 通常来说, 纳米合金的性能可以通过改变其尺寸大小、组成成份、原子排布顺序等方面进行调节^[3,4]. 双金属纳米合金的结构类型主要有混合结构、偏析结构、核壳结构和类洋葱三层结构, 最近开展的实验和理论研究表明, 一些双金属系统的团簇优先呈现核-壳结构, 即金属A的核被金属B的薄壳包裹^[5-8].
因为有利于系统能量的降低确保稳定结构形成, 一般而言, 原子半径大的、表面能小的金属原子倾向于占据纳米粒子的表面. 在理论上, 当前主要采用静态的理论方法研究, 如蒙特卡罗^[9,10]和全局优化方法^[11]. 在实验上, 通过透射电子显微镜观察到了三层的核壳结构Au-Pd体系^[7], Henglein^[12]采用氢还原和辐射分解方法分别合成了Au核/Pt壳和Pt核/Au壳的纳米团簇. 通过原子沉积生长理论模拟获得了Mg核/Al壳、Fe核/Al壳和Pd核/Ag壳纳米团簇^[2,13,14].
Ni是过渡金属基催化剂中应用最广泛的元素, 与其他金属形成双金属体系的能力最强, 因此研究人员对双金属镍催化剂进行了大量的研究^[15]. 尽管在纳米合金的生长方面已经进行很多的理论数值研究^[5,16-18], 但是关于基底结构对生长影响的研究却非常有限. 与Al原子相比, 金属Ni原子具有更小的原子半径和更大的表面能. 原子半径小的占据有利于释放团簇内部的应力, 从而增强纳米粒子的稳定性^[19]. 从偏析的理论角度, Al原子应该倾向于纳米粒子的表面, 形成Ni-核/Al-壳结构. 因此本文选择NiAl双金属体系作为研究对象, 探究不同的Ni基底构型对Al原子在Ni团簇表面的生长影响. 得到NiAl的形成热为一个负值, 表明NiAl应该倾向于形成混合的合金结构, 因此探究不同的基底构型对生长的影响是非常有必要的. 在纳米尺寸范围内, 对于FCC晶体含有原子数为923, 正二十面体(Icosahedra, ICO₉₂₃)、截角十面体(Decahedra, DEC₉₂₃)和截角八面体(Cuboctahedra, CUB₉₂₃)这三种几何结构是能够稳定存在的结构. 由于这三种结构具有相同的原子数, 但是却拥有截然不同的几何结构, 并且通过本文所采用的EAM势^[20], 采用共轭梯度法对三种基底结构进行能量最小化, 计算得出系统的总能量也较为接近(ICO₉₂₃, –4.14 eV/atom; DEC₉₂₃, –4.12 eV/atom; CUB₉₂₃, –4.12 eV/atom), 因此适合用来进行比较研究. 首先通过对单个Al吸附原子在ICO₉₂₃, DEC₉₂₃和CUB₉₂₃结构的Ni基底表面的扩散行为进行对比研究, 随后从原子的角度分析了不同基底结构对生长的影响. 研究结果能够为实验上控制和合成特定结构的纳米合金提供一定的理论依据.

采用了Purja Pun和Mishin^[20]开发的嵌入原子势模型并结合分子动力学^[21-23]的方法进行了金属Al原子在不同的Ni基底上的生长模拟. 利用该势能模型能够精确再现NiAl和Ni₃Al相的很多物理性质, 并且通过该势能模型计算NiAl整个相图的稳定性, 与第一性原理计算和实验得到的结果有很好的一致性. 使用该势能模型能够很好地描述金属Al原子在Ni基底上的生长行为, 关于该势能模型的详细细节请参考文献[20]. Wu等^[24]利用该势能进行了NiAl薄膜在Ni衬底上沉积和退火的分子动力学模拟.
为了去研究Al吸附原子在不同Ni基底构型上的扩散行为, 单个金属Al吸附原子被放在结构分别为ICO₉₂₃, DEC₉₂₃和CUB₉₂₃的Ni基底表面. 然后在正则系综下(canonical ensemble, NVT), 对整个体系逐渐升温并追踪Al吸附原子的运动轨迹, 随后使用肘弹性带方法(nudged elastic band, NEB), 计算出对应扩散路径的能量势垒. NEB方法是求解给定初始状态和最终状态之间过渡的最小能量路径的有效方法. 在NEB方法中, 在初态和末态之间线性地插入中间图像链, 每一幅图像对应着原子从初始位置到最终位置特定的几何形状, 这些图像通过弹性弹簧相互连接, 同时进行优化, 其中初始位置和最终位置保持不变^[4,25]. 在当前的模拟中, 分子动力学(MD)模拟采用LAMMPS程序^[26]中的NEB方法计算最小能量路径上的扩散势垒, 在NEB中使用了二十个中间图像. 在扩散过程中, 能量最高的图像对应系统的鞍点E_sad, 系统的扩散势垒E_a可以被定义为E_a = E_sad – E_min, 这里的E_min表示系统初态或者末态的能量.
对于单个Al原子在Ni基底(CUB₉₂₃, DEC₉₂₃和ICO₉₂₃结构)上的生长注入模拟是在Lammps软件中^[26]进行的. 在生长过程中原子的注入方式是Al原子随机沉积到Ni基底的表面, 其中注入原子的速率为100 ps/atom, 所选取的系综是NVT系综. 系统的运动方程遵循牛顿定律, 原子运动的数值积分算法采用的是具有时间反演对称的Verlet算法, 时间步长?t = 1 fs, 这与原子振动的时间尺度是相同的, CUB, DEC和ICO结构的壳层数与原子数之间的关系如下^[27]:

$ {N}_{l}=\frac{10}{3}{l}^{3}+5{l}^{2}+\frac{11}{3}l+1, $

其中l表示结构的壳层数, N_l 表示的是该结构所包含的总原子数. 图1中显示了三种不同的基底构型图, 即CUB₉₂₃, DEC₉₂₃和ICO₉₂₃. 图1(a)显示CUB结构由八个{111}面和六个{100}面构成, 而图1(b)中的DEC结构由十个{111}面和四个{100}面构成, 图1(c)中的ICO结构仅由二十个{111}面构成. 对于三种结构, 总原子数和表面原子数所占的比例与壳层数的函数关系如图2所示, 随着层数的增加, 系统的总原子数呈指数增加, 然而表面原子所占的比例却逐渐降低. 作为例子, 选取壳层大小l = 6包含923个原子的Ni基底作为研究对象. 在生长模拟过程中, 对于壳层数l = 7时可知包含的原子数为1415, 因此当注入的Al原子数达到500的时候停止注入.
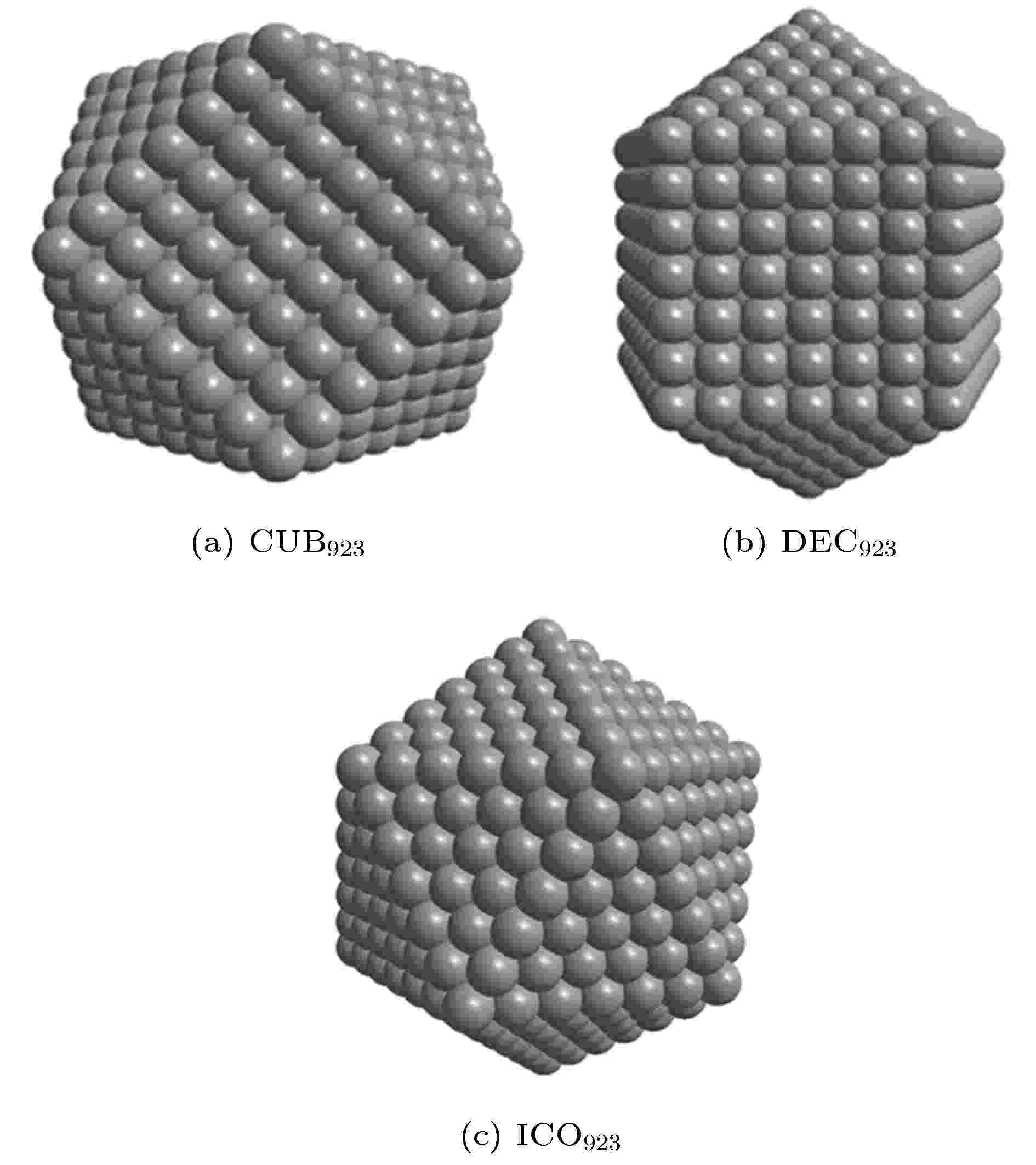图 1 含有923个原子的CUB (a), DEC (b)和ICO (c)结构示意图, 三种结构是以壳层组成的非晶结构, 其中DEC和CUB由{111}和{100}面组成, 而ICO仅由{111}面组成
Figure1. CUB (a), DEC (b) and ICO (c) microstructure with 923 atoms. The three clusters are a non-crystalline structure organized in shells. The DEC and CUB consist of {111} and {100} facets, and the ICO has only {111} facets.

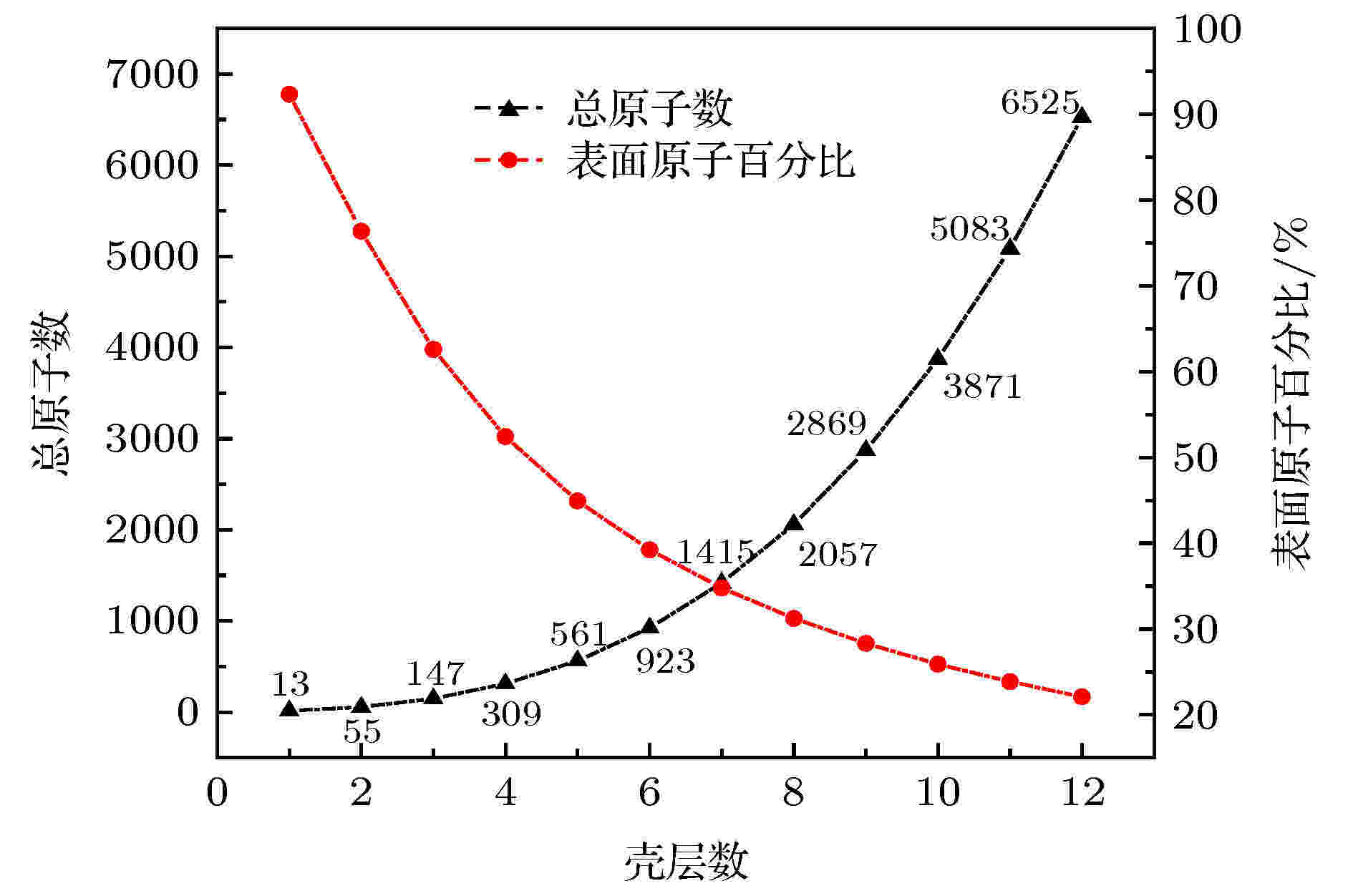图 2 对于ICO, DEC和CUB结构, 总原子数和表面原子数所占的比例与壳层数的函数关系
Figure2. For the ICO, DEC and CUB structures, the total atomic number and percent of the surface atoms as a function of the shell number.

2

-->

3.1.表面能和形成热

表面能(E_surf)定义为一个特定的晶体平面单位面积上的表面多余自由能, 是表面物理的基本物理量之一, 它决定了晶体的平衡形态, 对晶体的形成、粗化和生长起着重要的作用, 其计算表达式如下^[28,29]:

${E_{{\rm{surf}}}} = \frac{1}{S}\left( {{E_{\rm{A}}} - {E_{{\rm{bulk}}}}} \right)$

其中E_A是系统为自由表面时的总能量, S是体系自由表面的表面积, E_bulk表示在周期性条件下系统的总能量. 在表1中列出了金属Ni和金属Al不同晶面的表面能大小以及第一性原理计算的数据, 本工作计算的结果与第一性原理的结果进行对比有很好的一致性. 金属Ni的表面能远高于金属Al的表面能, 从能量的角度来看, 对于NiAl合金, Al原子偏析于表面是有利的. 同时计算发现两种金属不同晶面的表面能顺序为$ {\gamma }_{111}<{\gamma }_{100}<{\gamma }_{110} $. 一般情况下, 某个表面原子排布得越密集则表面能越小. 对FCC结构金属, 其(111)面是密排面, 而(110)面的原子排布最稀疏, 因此(111)面的表面能最低.

元素	晶体结构	Esurf/mJ·m–2
		晶面	本工作	FP[25]
Ni	FCC	(111)	1875	2011
		(100)	1964	2426
		(110)	2148	2368
Al	FCC	(111)	933	939
		(100)	994	1081
		(110)	1063	1090

表1金属Ni和金属Al的表面能(E_surf). 列出了对应的第一性原理(FP)^[28]数据
Table1.The surface energy (E_surf) for the two different material of Ni and Al. For comparison, the first principle (FP) calculations^[28] are listed.

表2中列出了NiAl体系形成B2结构和L12结构的金属化合物的形成热, 与对应的实验数据和第一性原理计算结果有很好的一致性, 说明我们使用的势函数能够应用于不同浓度比例的NiAl合金, 其形成热$\left( {\Delta H} \right)$的计算公式如下^[30,31]:

化合物	结构	?H/eV·atom–1
		本工作	FP	EMP	EXP
NiAl	B2	–0.61	–0.67		–0.67
NiAl3	L12	–0.26
Ni3Al	L12	–0.45	–0.44	–0.46, -0.48	–0.49, -0.43

表2NiAl不同化合物的形成热(?H). 为了对比列出了对应的第一性原理^[32](FP)和其他理论方法^[33] (EMP)以及对应实验结果^[34-36] (EXP)
Table2.The calculated heat of formation (?H), structural of NiAl in varying crystal structures. For comparison, the first-principle (FP)^[32] and other calculations with empirical methods (EMP)^[33] and available experimental values (EXP)^[34-36] are also listed.

$\Delta H = \left[ {E\left( {{A_n}{B_m}} \right) - \left( {n{E_A} + m{E_B}} \right)} \right]/\left( {n + m} \right),$

这里的n和m分别表示A类原子和B类原子的数目, $ E\left({A}_{n}{B}_{m}\right) $表示化合物$ {A}_{n}{B}_{m} $的总能量, 其中$ {E}_{A} $和$ {E}_{B} $分别为金属A和B的每原子的能量. 通常来说, 如果系统的形成热是一个负值, 则体系更容易合金化.
2 -->

3.2.单个Al原子在Ni团簇的表面扩散

金属原子的扩散机制主要分为两类, 一类是跳跃机制, 即吸附原子从一个平衡位置跨过能量势垒进入另外一个新的平衡位置进行扩散; 另一类则是交换机制, 当吸附原子到达台阶边缘, 它会推出台阶边缘原子然后占据其留下的空位, 随后边界原子成为新的吸附原子在邻面上进行扩散^[37].
为研究单个金属Al原子在Ni基底(即CUB₉₂₃, DEC₉₂₃和ICO₉₂₃)表面的扩散行为, 将单个Al原子添加到Ni基底的{111}面的中心作为扩散的起始点, 如图3所示, 我们给出了Al原子在不同Ni基底表面的扩散路径.
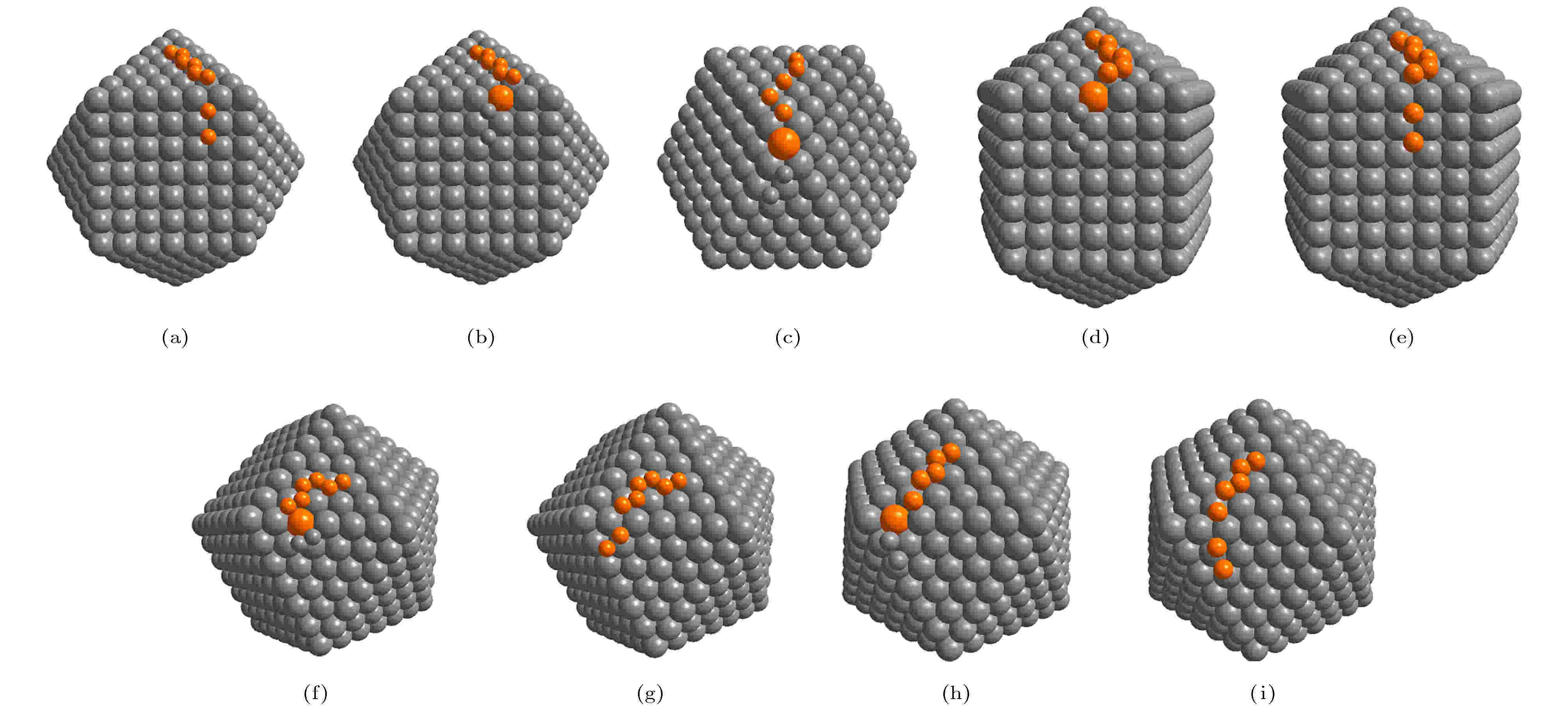图 3 对于Al 吸附原子在CUB₉₂₃, DEC₉₂₃和ICO₉₂₃结构的Ni基底表面上, 通过跳跃和交换机制, 吸附原子从{111}面向{100}面或向{111}面扩散的路径　(a) Hopping CUB_{{111} → {100}}; (b) Exchange CUB_{{111} → {100}}; (c) Exchange CUB_{{111} → {111}}; (d) Exchange DEC_{{111} → {100}}; (e) Hopping DEC_{{111} → {100}}; (f) Exchange DEC_{{111} → {111}}; (g) Hoping DEC_{{111} → {111}}; (h) Exchange ICO_{{111} → {111}}; (i) Hoping ICO_{{111} → {111}}. 橙色的球表示铝原子, 灰色的球表示镍原子
Figure3. For the Al adatoms on the surfaces of the Ni CUB₉₂₃, DEC₉₂₃, and ICO₉₂₃, the diffusion path of the adatom from the {111} facet to the {100} facet or to the {111} facet via the hopping and exchange mechanisms: (a) Hopping CUB_{{111} → {100}}; (b) Exchange CUB_{{111} → {100}}; (c) Exchange CUB_{{111} → {111}}; (d) Exchange DEC_{{111} → {100}}; (e) Hopping DEC_{{111} → {100}}; (f) Exchange DEC_{{111} → {111}}; (g) Hoping DEC_{{111} → {111}}; (h) Exchange ICO_{{111} → {111}}; (i) Hoping ICO_{{111} → {111}}. The orange balls show the Al adatoms and the gray balls show the Ni atoms.

3 -->

3.2.1.Al原子在Ni CUB₉₂₃表面的扩散行为

在CUB₉₂₃的表面, Al吸附原子能够通过交换机制或者跳跃机制从{111}面扩散到{100}面, 然而对于Al吸附原子从{111}面扩散到相邻的{111}面上仅能通过交换机制, 这三种类型的扩散路径如图3(a)—图3(c)所示.
Al吸附原子在Ni CUB₉₂₃基底两个相邻表面之间有三种可能的扩散路径, 对应扩散路径上的能量势垒如图4(a)和图4(b)所示, 图中的横坐标已经进行了归一化处理, 其中0.0和1.0分别对应于吸附原子扩散中的初始位置和最终位置, 扩散路径上系统能量的最低点被定义为0. 对比于在平面上的扩散, 其中一个额外的势垒在台阶的边缘存在, 即Ehrlich-Schwoebel(ES)势垒^[34]. 对于吸附原子从{111}面扩散到{100}面通过跳跃和交换机制对应的ES势垒分别为0.79和0.38 eV. 对比可知, 跳跃机制的ES势垒^[38]远高于交换机制, 因此吸附原子从{111}面扩散到{100}面应该优先发生交换, 当吸附原子从{111}面通过交换机制扩散到相邻的{111}面时存在一个巨大的ES势垒^[38] (1.26 eV), 表明吸附原子从{111}面扩散到相邻的{111}面只可能在高温下发生.
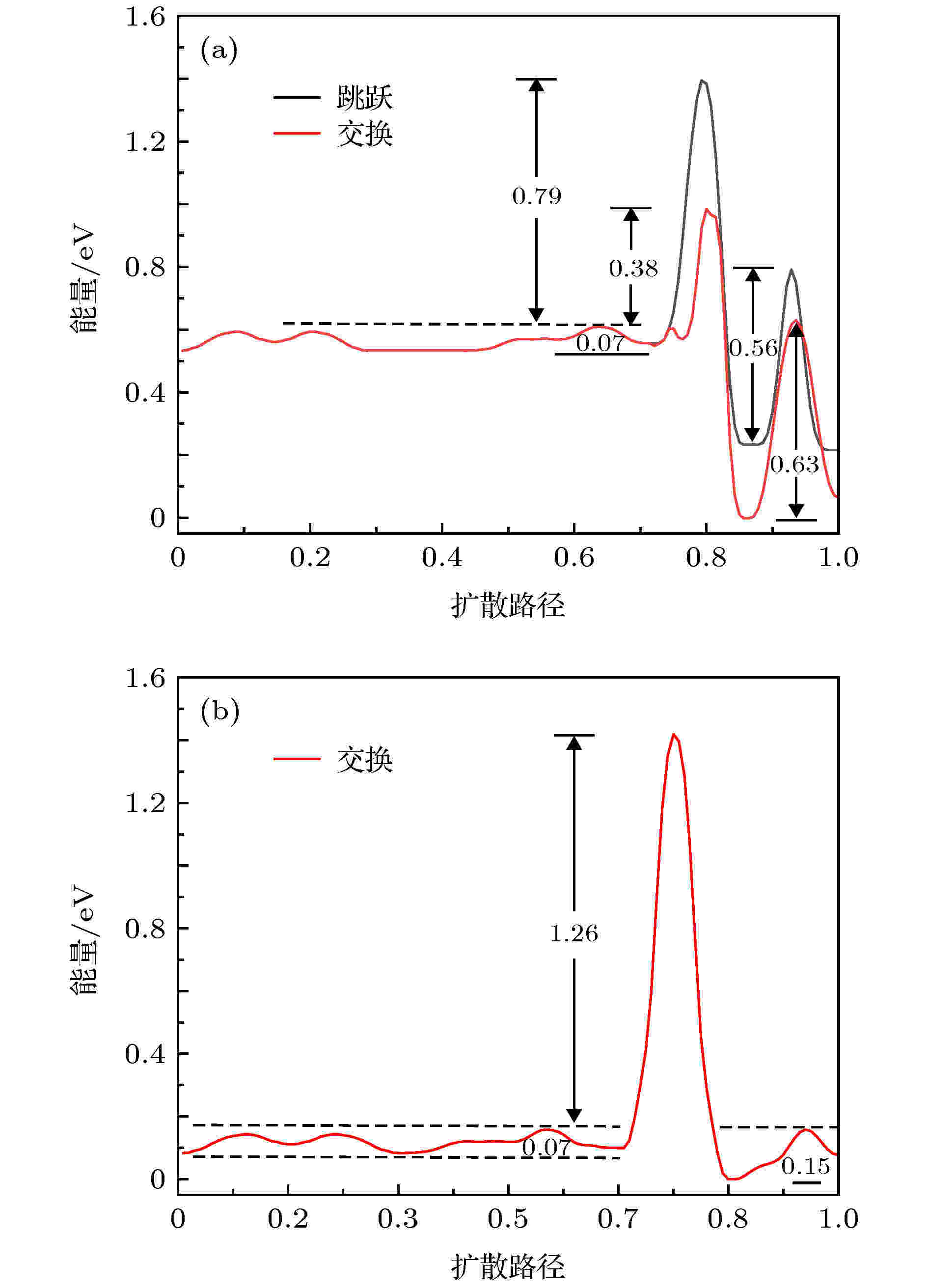图 4 Al吸附原子在Ni CUB₉₂₃基底表面扩散对应的能量势垒曲线　(a) {111} → {100}; (b) {111} → {111}. 扩散路径如图3(a)—图3(c)所示
Figure4. For the Al adatom on the surface of the Ni CUB₉₂₃, the system energies as a function of reaction coordinate corresponding to the diffusion path shown in Fig.3(a)-Fig.3(c): (a) {111} → {100}; (b) {111} → {111}.

3 -->

3.2.2.Al原子在Ni DEC₉₂₃表面的扩散行为

如图3(d)—图3(g)所示, Al吸附原子在Ni DEC₉₂₃基底两个相邻表面之间有四种可能的扩散路径, 其对应系统的能量作为扩散路径的函数已经在图5中给出. 如图5所示, 吸附原子在台阶边缘从{111}面扩散到{100}面, 对于交换和跳跃机制, 其ES势垒分别为0.52 和0.78 eV, 结果与在CUB₉₂₃表面扩散行为类似, 即跳跃的能量势垒高于交换势垒, 应当优先发生交换. 然而, 对于吸附原子在{111}面与相邻{111}面之间扩散, 交换的势垒(0.87 eV)高于跳跃的势垒(0.54 eV). 这主要与不同面之间的几何结构有关, 在扩散过程中台阶越平滑则跳跃势垒越小^[4]. 对于DEC结构, 两个相邻{111}面之间的二面角大于{111}与{100}面之间的二面角, 通过几何结构之间的关系能够解释上述所观察到的现象.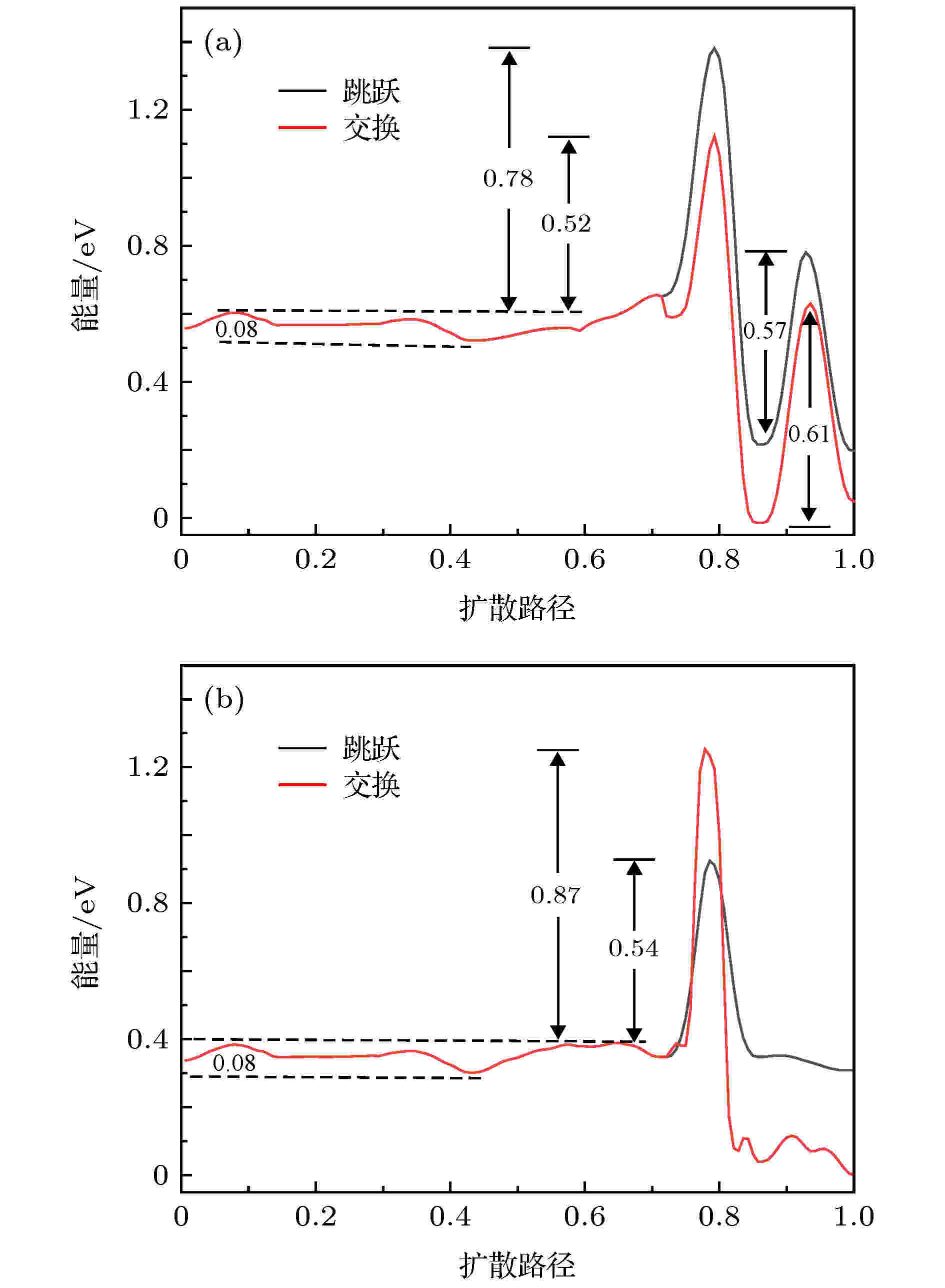
图 5 Al吸附原子在Ni DEC₉₂₃基底表面扩散对应的能量势垒曲线　(a) {111} → {100}; (b) {111} → {111}. 扩散路径如图3(d)—图3(g)所示
Figure5. For the Al adatom on the surface of the NiDEC₉₂₃, the system energies as a function of reaction coordinate corresponding to the diffusion path shown in Fig.3(d)-Fig.3(g): (a) {111} → {100}; (b) {111} → {111}.

3 -->

3.2.3.Al原子在Ni ICO₉₂₃表面的扩散行为

由于ICO结构仅由二十个{111}面组成, 因此吸附原子只会在相邻的两个{111}面之间扩散, 如图3(h)和图3(i)所示. 对应系统的能量作为扩散路径的函数, 如图6所示. 对于跳跃机制, 通过计算得到的ES势垒为0.52 eV, 然而对于交换机制, 其ES势垒为0.73 eV. 如上所述, 对于ICO结构, 由于相邻的{111}面之间的台阶相对比较平滑, 因此吸附原子在基底表面扩散通过跳跃机制更加有利.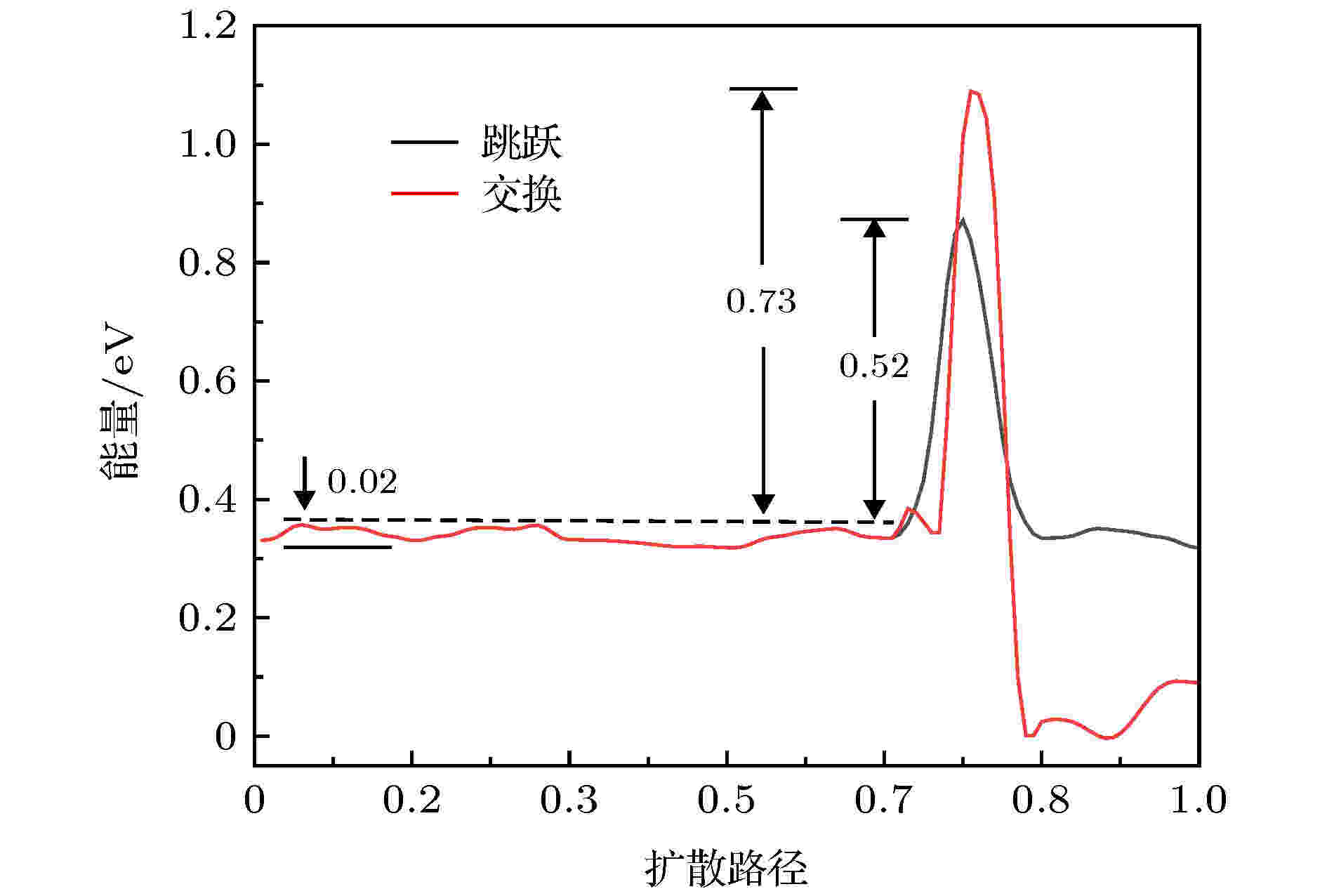
图 6 Al吸附原子在Ni ICO₉₂₃基底表面扩散对应的能量势垒曲线, 扩散路径如图3(h)和图3(i)所示
Figure6. For the Al adatom on the surface of the Ni ICO₉₂₃, the system energies as a function of reaction coordinate corresponding to the diffusion path shown in Fig. 3(h) and Fig.3(i).

3 -->

3.2.4.扩散行为差异的原因

如上所述, Al吸附原子通过交换或跳跃两种机制分别在三种不同Ni基底上表面扩散, 最低的ES势垒分别为0.38 eV (Exchange CUB_{{111}→{100}}), 0.52 eV (Exchange DEC_{{111}→{100}})和0.52 eV (Hoping ICO_{{111}→{111}}). 由此可知, 对于CUB和DEC两种基底, Al吸附原子的最低ES势垒所对应的机制为交换机制, 这将不利于Ni核Al壳的形成. 通过对比三种结构的面间扩散势垒可知, 当Al吸附原子从{111}面扩散到{100}面时, 对应的交换势垒小于跳跃势垒, 当在两个相邻的{111}面间扩散时, 其对应的交换势垒大于跳跃势垒. 这种行为的差异除了上述提到的几何结构原因, 还有另外一个重要的原因, 即在台阶边缘处的原子配位数大小. 其中对于{111}面和{100}面之间, 台阶边缘上的原子配位数为7, 而对于两个相邻的{111}面之间, 台阶边缘上的原子配位数为8. 扩散势垒的大小通常由打破吸附原子与基底原子间的成键所需要耗费的能量决定^[39]. 当吸附原子在两个相邻的{111}面之间进行交换扩散, 则需要打破更多的键, 因此需要更多的能量.
吸附原子在{100}面上的扩散势垒远大于在{111}面上的扩散势垒. 最主要的原因是, 对于FCC金属, {111}面相比于{100}面排布得更紧凑, 因此{111}面更加平滑, 对应的跳跃势垒更低. 通过计算吸附原子在不同的基底表面扩散的能量势垒的差异, 可以预测相比于CUB和DEC基底, 在ICO结构基底的表面沉积Al原子将获得最好的核壳结构.
2 -->

3.3.Al吸附原子在Ni基衬底的聚集生长

3 -->

3.3.1.基底结构对生长的影响

系统地研究了金属Al原子在不同Ni基底表面的扩散机制, 进一步分析在不同Ni基底的团簇生长情况是非常必要的. 由于在台阶边缘处有一个较大的ES势垒^[38], 为进一步研究不同Ni基底Al原子团簇的生长情况, 我们选取的生长的模拟温度为室温, 即300 K. 根据Baletto等^[8]的描述, 利用纳米颗粒表面原子数($ N_{A}^{\rm surf} $)和内部原子数($N_B^{\rm bulk}$)定量描述了双金属纳米颗粒结构的生长, 其中A和B分别表示基底原子和注入原子. $ N_{A}^{\rm surf} $和$ N_B^{\rm bulk} $的交叉点定义为核壳团簇的缺陷数(N_def), 通常来说, N_def越小形成的核壳结构越好^[5].
如图7所示, 对于三种不同的基底结构生长, $ N_{\rm Al}^{\rm bulk} $和$N_{\rm Ni}^{\rm surf}$作为沉积原子数的函数. 从图可知在堆积的开始阶段, $ N_{\rm Ni}^{\rm surf} $随着注入原子数的增加线性减少, 而$ N_{\rm Al}^{\rm bulk} $的大小基本为0, 随着堆积的Al原子数进一步增加, $ N_{\rm Al}^{\rm bulk} $开始缓慢增加. 增加的原因主要来自两个方面, 首先, 随后注入的Al原子堆积在已存在的Al壳上, 使得原本的Al表面原子变为体原子; 其次来自于金属表面能与合金化能力之间的竞争, 从表2可以得知NiAl复合物的形成热为一个负值, 从能量的角度上, NiAl易于形成合金. 随着注入的Al原子逐渐增加, 一部分Al原子进入Ni基底内与Ni原子成键, 增加其异质配位数, 降低系统的能量. 对于CUB₉₂₃基底, $ N_{\rm Al}^{\rm bulk} $增加的速率最快, 随后为DEC₉₂₃和ICO₉₂₃基底. 其对应的交叉点N_def大小分别约为100, 80和30. 在生长注入过程中, 当吸附原子在基底的面间进行扩散, 如果交换势垒低于跳跃势垒, 则说明吸附原子进行面间扩散时优先与Ni的边上原子交换而成为新的边上原子(如图3的交换机制), 因此会导致$ N_{\rm Al}^{\rm bulk} $的速率增加. 这一结果与之前的Al吸附原子在Ni基底团簇表面扩散行为差异是一致的, 即在ICO基底上跳跃机制占优势, 而在DEC和CUB基底上交换机制占优势.
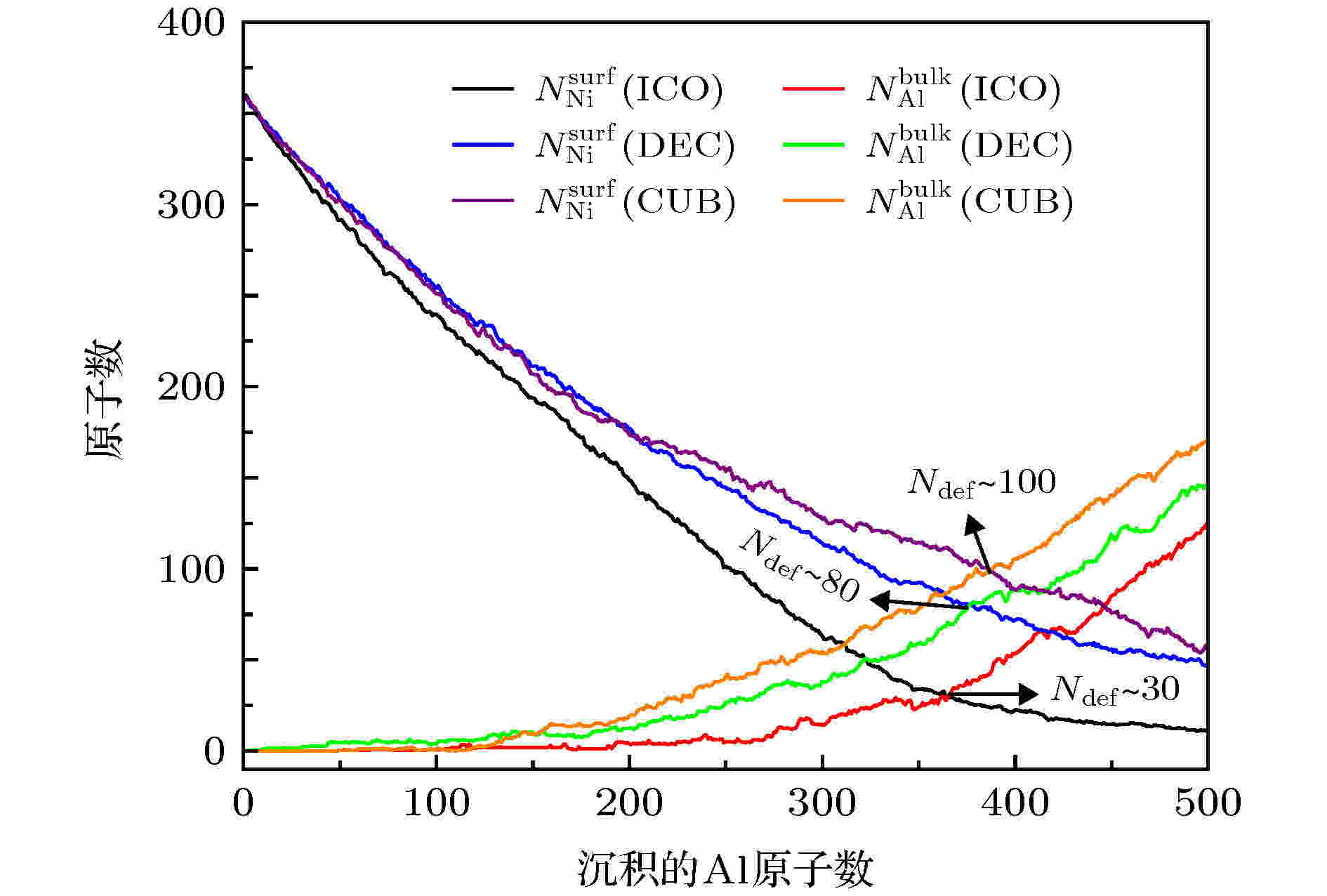图 7 T = 300 K, 在不同的Ni基底表面生长, $ N_{\rm Ni}^{\rm surf} $和$ N_{\rm Al}^{\rm bulk} $与沉积的Al原子数的函数关系
Figure7. On the different substrates of Ni core, the $ N_{\rm Ni}^{\rm surf} $ and $ N_{\rm Al}^{\rm bulk} $ as functions of the deposited Al atoms at T = 300 K.

为了更加清楚地看到这一生长过程, Al原子在ICO结构的Ni基底表面生长序列如图8所示. 从图8(a)—图8(e), 对应沉积Al原子的数量分别为100, 200, 300, 400和500. 从图可知, 沉积的Al原子倾向于占据台阶边缘和顶角位置, 随着沉积的Al原子数(N_dep)增加, 然后开始聚集成岛. 这一现象的主要原因是Al原子在扩散过程中相遇, 随后相互成键, 以此降低系统的能量. 随着注入的Al原子数超过400, 最终得到一个ICO结构的Ni-核/Al-壳纳米团簇, 如图8(d)所示.
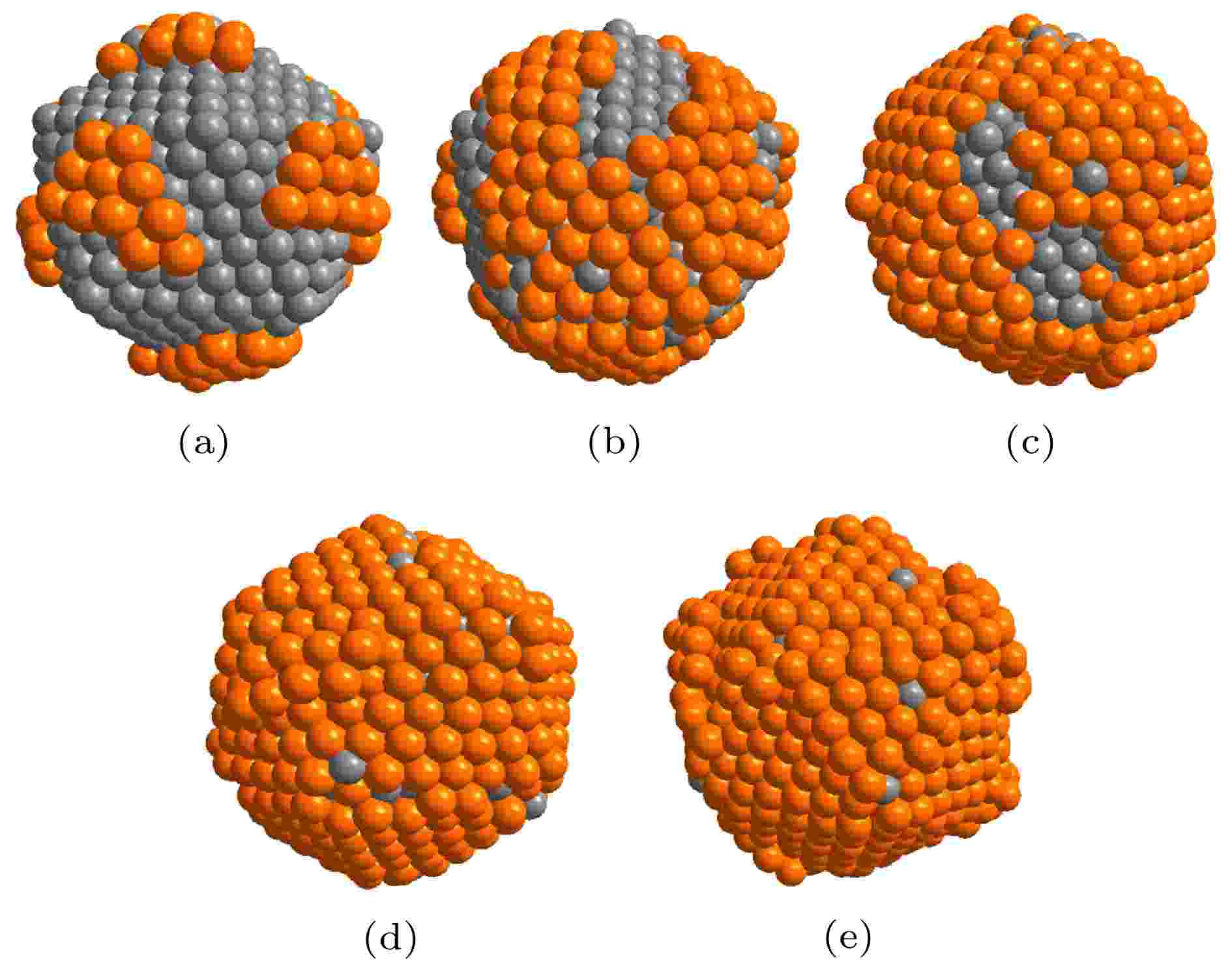图 8 T = 300 k, Al原子在Ni ICO₉₂₃基底上的生长序列　(a) N_dep = 100; (b) N_dep = 200; (c) N_dep = 300; (d) N_dep = 400; (e) N_dep = 500. 橙色和灰色的球分别表示Al原子和Ni原子
Figure8. Growth sequence of Al atoms growth on the ICO₉₂₃ of Fe at T = 300 k: (a) N_dep = 100; (b) N_dep = 200; (c) N_dep = 300; (d) N_dep = 400; (e) N_dep = 500. The orange and gray balls show the Al atoms and the Ni atoms, respectively.

3 -->

3.3.2.温度对生长的影响

为进一步探究温度对生长的影响, 选取NiICO₉₂₃作为生长的基底, 在300, 500, 700和900 K下, 通过沉积Al原子在Ni基底的表面, 如图9所示. $N_{\rm Al}^{\rm bulk}$和$N_{\rm Ni}^{\rm surf}$作为沉积原子数的函数, 随着沉积原子数的增加, 对应的$ N_{\rm Ni}^{\rm surf} $逐渐线性地减少而$ N_{\rm Al}^{\rm bulk} $逐渐增加, 最终注入到一定的原子数, 二者进行交叉. 随着生长温度的增加, N_Ni^surf下降的速率也逐渐增加, 同时$ N_{\rm Ni}^{\rm surf} $和$ N_{\rm Al}^{\rm bulk} $交叉点大小, 即缺陷数N_def也随着增加.
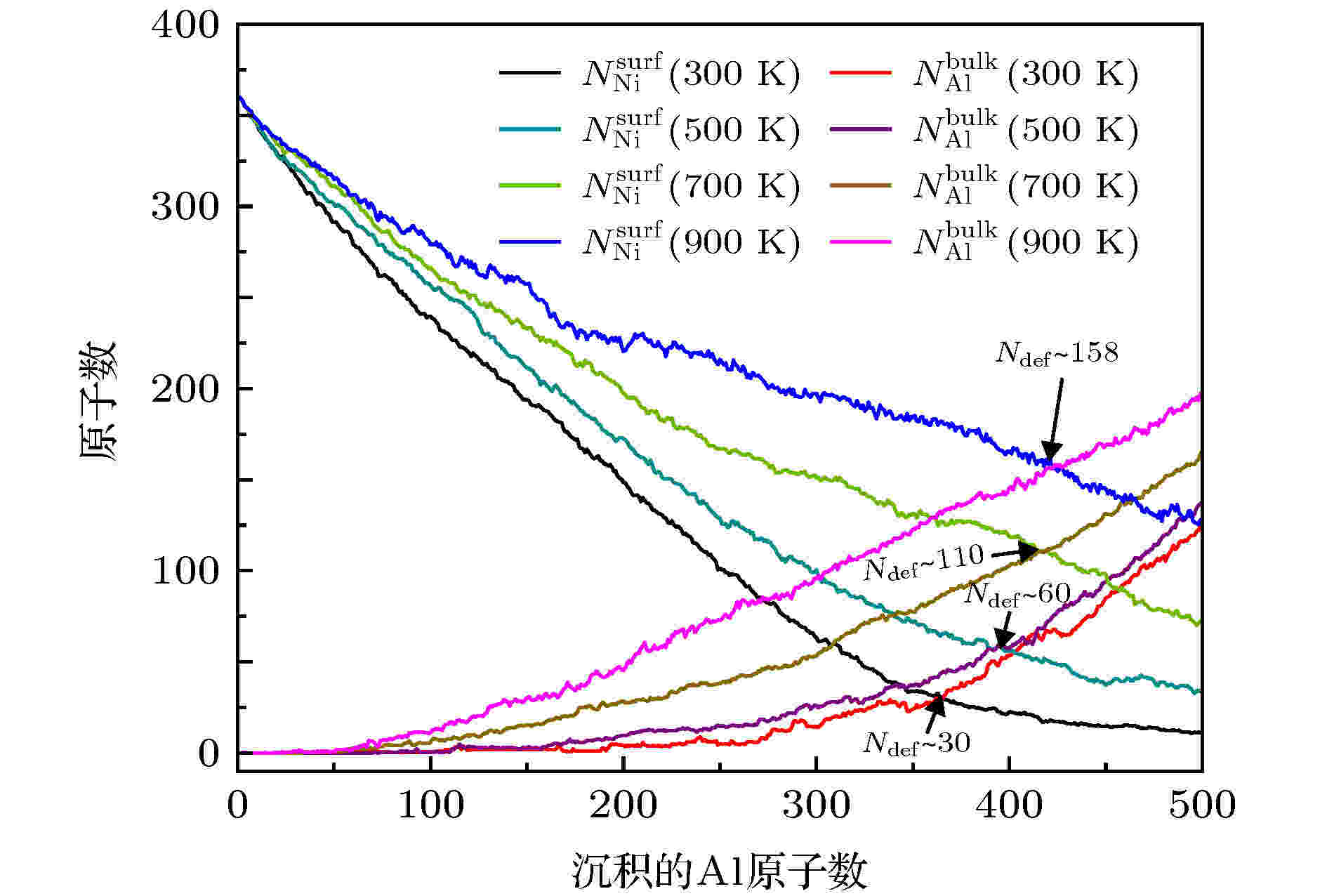图 9 在T = 300, 500, 700和900 K, Al原子在Ni ICO₉₂₃基底表面生长, $ N_{\rm Ni}^{\rm surf} $和$ N_{\rm Al}^{\rm bulk} $作为沉积的Al原子数的函数
Figure9. At T = 300, 500, 700 and 900 K, for the growth of Al atoms on the ICO₉₂₃ of Ni, the $ N_{\rm Ni}^{\rm surf} $ and $ N_{\rm Al}^{\rm bulk} $ as functions of the deposited Al atoms.

如图9所示, 生长温度为300, 500, 700和900 K时, 对应的缺陷数N_def分别是30, 60, 110和158. 说明当生长的温度逐渐升高, Al吸附原子拥有更高的能量, 更加容易进入Ni核里面与金属Ni原子成键, 而不是与自身成键. 与之前计算NiAl的形成热为负值一致.
通过计算NiAl原子的异质配位数N_Al-Ni的大小来表征NiAl合金化的程度^[40], 如图10所示. 随着温度的升高, N_Al-Ni逐渐增加, 表明合金化程度越强, NiAl键的数量越来越多, 插图对应于不同生长温度下NiAl纳米粒子的最终构型. 随着温度的升高, NiAl纳米粒子的表面逐渐开始合金化. 然而, 值得注意的是, NiAl纳米粒子的核内部仍然是纯Ni原子, 如图10中对应的截面图.
图 10 异质配位数(N_Al-Ni)随温度的变化, 插图对应于每个生长温度下最终构型. 橙色的球表示Al原子, 灰色的球表示Ni原子
Figure10. The variation of hetero-coordination number (N_Al-Ni) with temperature, and the inset correspond to the final configuration at each growth temperature. The orange and gray balls show the Al atoms and the Ni atoms, respectively.

本文从扩散与纳米团簇生长动力学的角度, 采用肘弹性带和分子动力学结合嵌入原子势的方法, 系统地研究了单个铝吸附原子在镍基表面的扩散行为和纳米颗粒团簇在十面体(DEC)、立方八面体(CUB)和二十面体(ICO)结构上的生长. 研究结果表明: Al吸附原子在三种Ni基底上的表面扩散的交换或跳跃机制, 扩散势垒的大小与台阶边缘的光滑度和基底的原子配位数有关. 最低的Ehrlich-Schwoebel (ES)势垒为0.38 eV (交换CUB{111} → 100}), 0.52 eV (交换DEC{111}→100})和0.52 eV (跳跃ICO{111} → 111}). 从{111}面扩散到{100}面主要以交换机制为主, 而相邻两个{111}面之间的扩散则以跳跃机制为主, 沉积的铝原子首先倾向于扩散到台阶边缘和顶点附近.
随着Al原子数量的增加, 沉积的Al原子开始聚集. 对于Ni团簇上的Al原子, 在较低温度下在Ni基底表面沉积Al原子, 可以获得良好的Ni核/Al壳结构. 相对于CUB和DEC基底, ICO基底对应的核壳团簇缺陷数较小. 随着生长温度的升高, NiAl双金属表面逐渐合金化.