摘要:即将开展的“嫦娥5号”探月任务, 将使我国在月球上首次实现无人钻井取样. 考虑到实际探测活动与探测区域的光照和温度有关, 有必要对研究区域的光照和温度特征进行分析, 为此, 本文利用SPICE系统对“嫦娥5号”候选登陆区Mons Rümker高原的实时光照进行计算. 发现求解的相对光强度分布与日本SELENE卫星提供的早晨光照影像一致, 验证了光照算法及计算程序的合理性. 以此为基础, 利用1维热传导模型, 对候选登陆区风化层不同深度的温度进行仿真分析. 结果表明风化层温度在近表面区域受光照的影响较大, 随着深度的增加, 光照影响逐渐减弱. 到达0.57 m深度时, 风化层温度不再变化. 为确保钻井任务的开展, 实际钻井作业应考虑风化层内外温度差异引起的应力不均. 考虑“嫦娥5号”的实际钻井深度远大于0.57 m, 应能测量到常温层的热流值, 后续探月任务可考虑搭载热流探测设备, 以促进月球科学研究的发展.
关键词: 嫦娥5号/
Mons Rümker/
实时光照/
温度分布

English Abstract

全文HTML

--> --> -->

根据我国探月工程计划, 继“嫦娥”1号、2号、3号和4号的成功实施, 我国即将开展探月工程第三期“回”^[1-3]. 该阶段计划发射“嫦娥5号”月球车, 在月表进行软着陆, 对月表风化层进行钻井, 提取相关岩石样品并返回地球, 届时, 我国将成为继苏联和美国之后, 全球第3个实现月球采样并返回的国家^[4]. 有关“嫦娥5号”登陆区的选择, 文献[5]认为风暴洋(oceanus procellarum)北面的Rümker区域, 曾经拥有较长的火山活动, 形成了多重地质单元, 具有不同的元素组成, 采集该区域的岩石样本具有重要的地质和科学意义. 该区域的Mons Rümker位于风暴洋北部, 中心坐标为(40oN, 58oW), 拥有古火山活动时遗留的月溪、穹隆和熔岩流管道. 其地形起伏在1000—2000 m之间, 文献[6—8]认为它属于火山中心, 文献[9]认为它属于大型盾型火山. 文献[10]对Mons Rümker的地形地貌, 以及地质特征进行分析, 提出将该区域作为“嫦娥5号”登陆候选区, 采集该区域的岩石样品, 有助于理解月球火山作用特征及其演化历史.
文献[11]对Mons Rümker高原的累积光照条件进行研究, 发现3年时间拥有30%至53%的光照率, 且地基观测系统的通信条件较好. 优良的光照条件可以快速地提升月表温度, 但由于月表风化层具有良好的绝热特性, 使得光照对风化层内部温度的贡献有限^[12-15]. 尽管文献[12—15]对风化层温度分布进行了估算, 但太阳光照方向主要依据理论公式求得, 与现实情况存在一定的偏差. 另外, 他们在估算光照引起的温度分布时, 并没有考虑地形对太阳光的遮挡, 而地形遮挡效应对实际探测活动至关重要. 为此, 本文利用美国NASA (National Aeronautics and Space Administration)开发的SPICE(Spacecraft, Planet, Instrument, Camera-matrix, Events)系统, 精确确定不同时刻的太阳光照方向. 结合文献[16,17]提供的高分辨率月球数字地形模型DTM (digital terrain model), 估算顾及地形遮挡的实时太阳光照. 同时, 考虑月球内部热流, 对Mons Rümker高原风化层的温度分布进行计算, 以期为“嫦娥5号”钻井采样活动, 以及后继探月活动的开展提供一定程度的参考.

Mons Rümker高原的平均面积约为4000 km², 地形图如图1白色方框区域所示. 本文采用的数字地形模型, 来自LRO (lunar reconnaissance orbiter)的激光测高数据LOLA (lunar orbiter laser altimeter). LRO自2009年发射以来, 其激光测距载荷LOLA取得了高精度的月球全球地形数据, 促进了月表永久阴影区及水冰的研究, 同时也确保了月球全球高精度大地参考框架的建立, 为后续载人登月提供了安全保障^[18]. LRO目前仍处于在轨状态, 尽管后期拓展任务阶段因调轨操作, 无法采集月球北半球地形数据, 但激光测距载荷LOLA仍然在不断地更新数据, 地形格网数据已更新至2019年(https://pds-geosciences.wustl.edu/missions/lro/lola.htm). 本文采用的地形模型, 来自LOLA的格网数据LDEM_512_00N_45N_270_ 360 (1/512o × 1/512o), 其分辨率约为59.2 m × 59.2 m. 其中, 黑色方块表示文献[10]建议的“嫦娥5号”候选登陆点(303.34oE, 40.11oN).
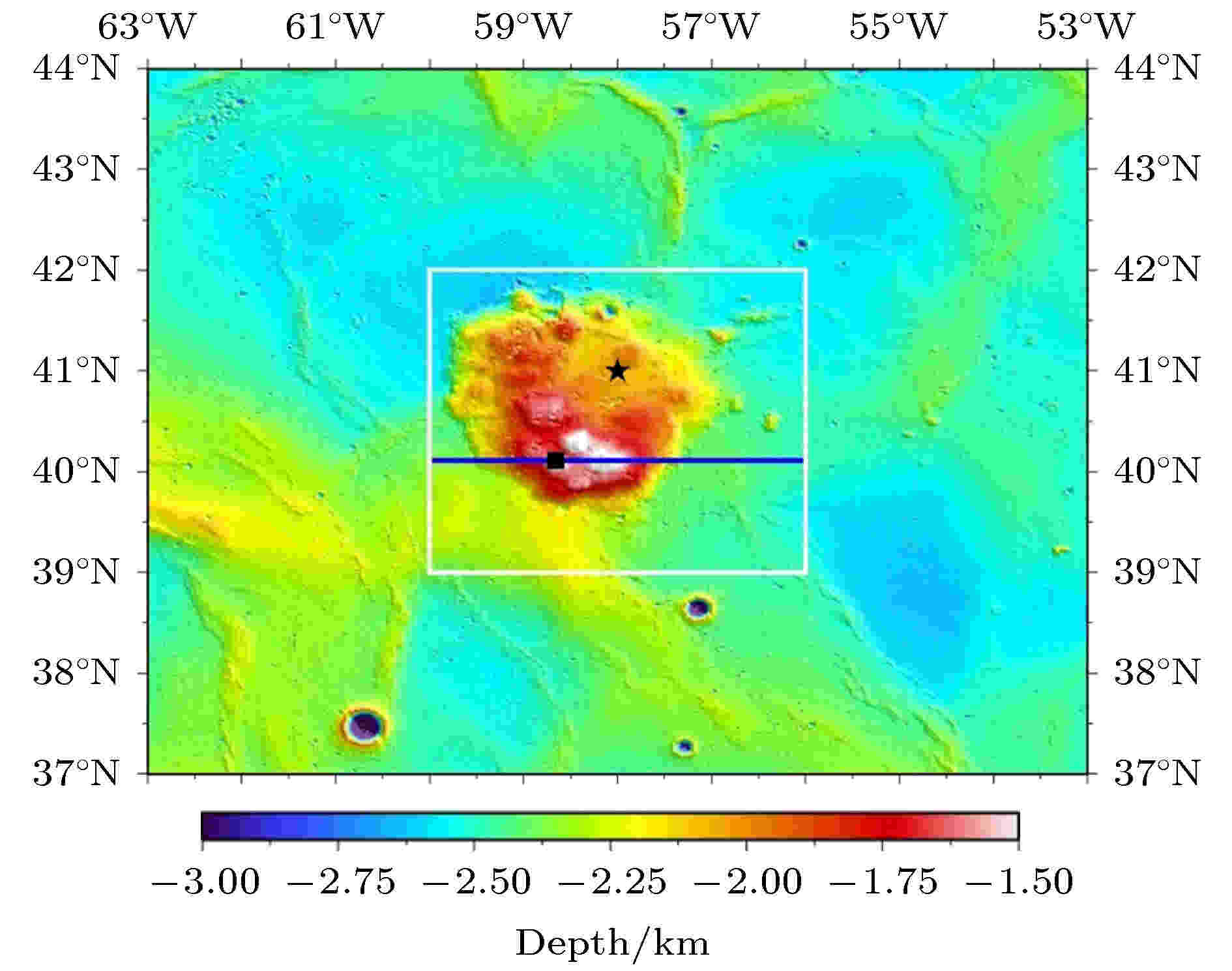图 1 Mons Rümker区域地形图, 如白色方框所示, 其中黑色方块表示文献[10]建议的“嫦娥5号”登陆点(303.34oE, 40.11oN)
Figure1. Topography around Mons Rümker region, which is figured out with a white box. The black box indicates the candidate landing site of CE-5 proposed by reference [10], and this site is centered at (303.34oE, 40.11oN)

如图2所示, 为了判断目标点A是否有太阳光照射, 以及判断A点是否被邻区地形点B遮挡, 可以通过点A的太阳高度角, 以及比较BC和DC的大小来判断. 过点A作等效球面(圆弧型虚线所示), 与OB相交于点C, 点A和点B间的中心角为θ. 假定点A的太阳高度角为α, 它表示太阳入射光线与目标点水平地面间的夹角. 若α ≤ 0, 文献[11]的研究表明, 对于高海拔区域, 太阳光有可能照射至目标点A. 如图1所示, 本文研究区域Mons Rümker高原, 其最大高程不超过–1.5 km, 不属于高海拔区域, 因此, 本文不考虑文献[11]的高海拔特殊情况, 认为α ≤ 0时, 太阳光不能照射至目标点A. 当α > 0时, 若DC < BC, 则目标点A被邻区地形点B遮挡, 太阳光无法到达点A; 当DC≥BC时, 则不受点B的地形遮挡. 考虑月球表面地形高低的最大落差, 文献[11]表明最大中心角θ = 8o, 通过不断地减小中心角, 可以依次判断距离目标点A远近不同的地形遮挡效应. BC的大小可以根据数字地形模型求得, 依据文献[11], 可得
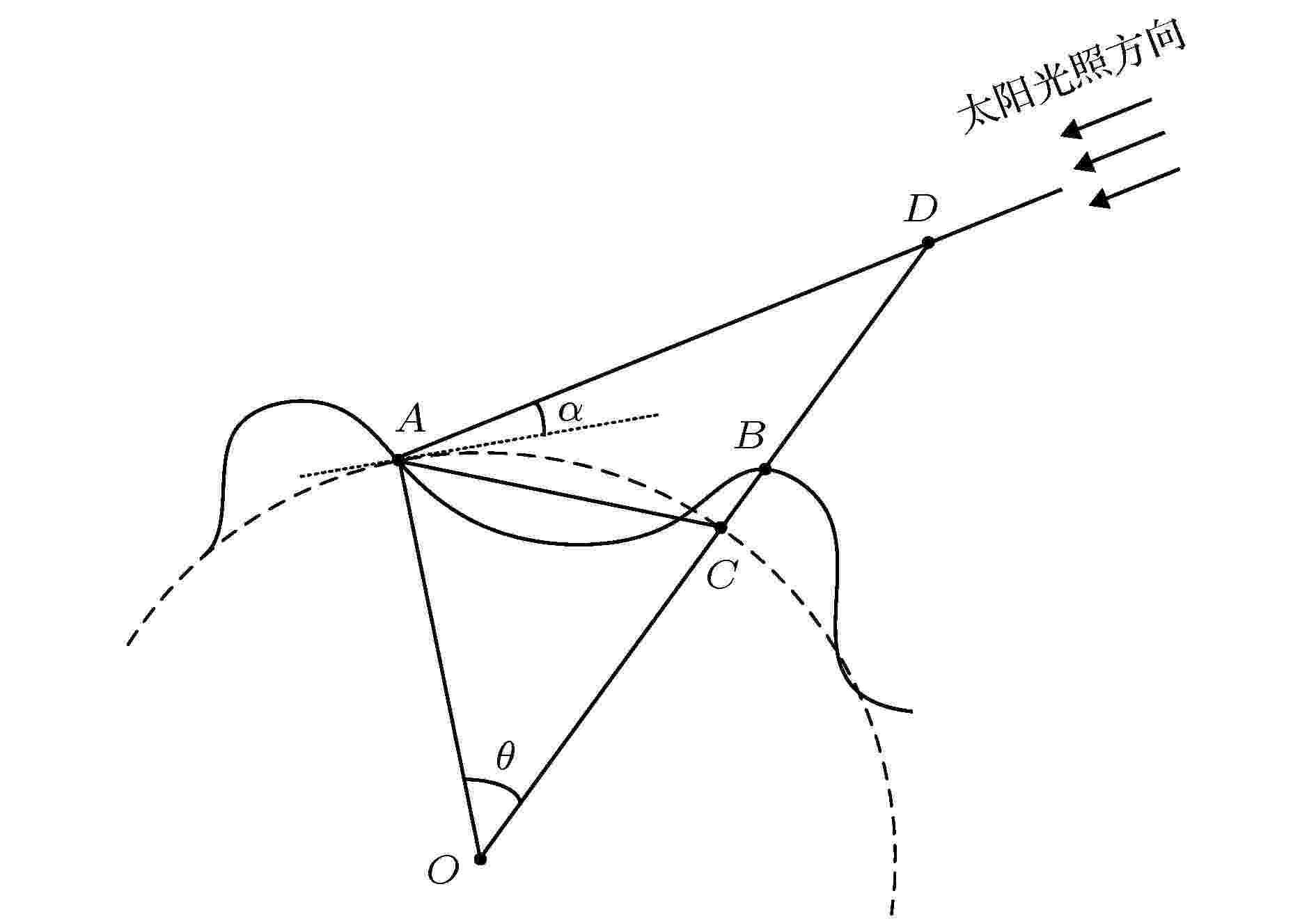图 2 太阳光照条件示意图
Figure2. Schematic of illumination condition

$ DC = \frac{{AC{\rm{sin}}\left( {\dfrac{\theta }{2} + \alpha } \right)}}{{{\rm{cos}}\left( {\theta + \alpha } \right)}}, $

其中AC可以根据中心角θ和OA求得; OA可以根据数字地形模型DTM求得; α为实时太阳光高度角, 可以根据SPICE系统由行星历表求得.

已知光照强度, 根据热传导方程, 可以估算风化层的温度变化. 月表风化层的厚度, 就整个研究区域而言相对较小, 因此, 通常采用一维热传导模型来计算温度分布^[12-15]. 就温度T和风化层深度z而言, 一维模型的控制方程为

$\rho {c_p}\frac{{\partial T}}{{\partial t}} = \frac{{\partial T}}{{\partial z}}\left( {k\frac{{\partial T}}{{\partial z}}} \right),$

其中, ρ和c_p分别表示风化层的密度和比热容, k表示热传导系数, 这些参数通常与风化层的深度和温度分布有关. 根据文献[13,14,19—21], 有

$\rho {\rm{ = }}{\rho _{\rm{d}}} - \left( {{\rho _{\rm{d}}} - {\rho _{\rm{s}}}} \right){\rm{exp}}\left( { - \frac{z}{H}} \right),$

$k = \left[ {{k_{\rm{d}}} - \left( {{k_{\rm{d}}} - {k_{\rm{s}}}} \right)\frac{{{\rho _{\rm{d}}} - \rho }}{{{\rho _{\rm{d}}} - {\rho _{\rm{s}}}}}} \right]\left[ {1 + x{{\left( {\frac{T}{{350}}} \right)}^3}} \right],$

${c_p} = {c_0} + {c_1}T + {c_2}{T^2} + {c_3}{T^3} + {c_4}{T^4},$

式中相关参数的取值如表1所列.

序号	参数	取值
1	密度ρs和ρd [14]	ρs = 1100 kg·m–3, ρd = 1800 kg·m–3
2	热传导系数ks和kd [14]	ks = 7.4 × 10–4 W·m–1·K–1, kd = 3.4 × 10–3 W·m–1·K–1
3	比热容拟合系数[14] c0, c1, c2, c3, c4	c0 = –3.6125 J·kg–1·K–1, c1 = 2.7431 J·kg–1·K–2, c2 = 2.3616 × 10–3 J·kg–1·K–3, c3 = –1.234 × 10–5 J·kg–1·K–4, c4 = 8.9093 × 10–9 J·kg–1·K–5
4	参数H和x [13,14]	H = 0.06 m, x = 2.7

表1相关参数取值
Table1.Values of parameters used in study

为了求解(2)式, 需要指定两个边界条件, 一个在月表, 另一个在风化层底部. 月表边界取决于太阳光照及月表红外辐射, 风化层底部取决于月球内部热流分布. 对于深度为z_b的底部边界z = z_b, 有如下关系^[14]:

${\left. {\frac{{\partial T}}{{\partial z}}} \right|_{z = {z_{\rm{b}}}}} = \frac{Q}{k},$

其中, Q表示风化层底部的热流值, 根据Apollo任务测量值^[22], 取Q = 0.018 W·m^–2.
对于月表边界温度T_s, 假定太阳光照加热率为Q_s, 考虑红外辐射后的月表温度梯度有^[13-15]:

$k{\left. {\frac{{\partial T}}{{\partial z}}} \right|_{z = 0}} + {Q_{\rm{s}}} = \overline \varepsilon \sigma T_{\rm{s}}^4,$

其中, $ \overline \varepsilon $为辐射系数, σ为斯特藩-玻尔兹曼常数. 参考文献[23], 取辐射系数$ \overline \varepsilon= $ $ 0.95, $ σ = 5.67 × 10^–8 W·m^–2·K^–4. 假定太阳实时入射角为β, 相应的入射流为F_sun, 太阳光照加热率有如下关系^[13,24]:

${Q_{\rm{s}}} = \Big[ {1 - {A_0} - a{{\Big( {\frac{{4\beta }}{\text{π}}} \Big)}^3} - b{{\Big( {\frac{{2\beta }}{\text{π}}} \Big)}^8}} \Big]{F_{{\rm{sun}}}},$

其中a, b为系数, 参考文献[13], 取a = 0.06, b = 0.25; A₀表示月球表面的邦德反照率(又称球面反照率), 该参数用于描述太阳于正中天, 太阳光垂直入射时, 天体表面的反射系数, 参考文献[12], 本文取A₀ = 0.12. 太阳实时入射流F_sun和入射角β通常与月表计算点和太阳之间的实时距离r有关, 该距离可以通过SPICE系统精确求得. 假定地球与太阳间的平均距离为r₀, 对应的太阳常数为S, 则入射流F_sun为

${F_{{\rm{sun}}}}{\rm{ = }}\frac{{Sr_0^2}}{{{r^2}}}{\rm{cos}}\beta {\rm{,}}$

其中, r₀为日-地平均间距. 参考文献[25], 取r₀ = 1.49598261 × 10¹¹ m, S = 1361 W·m^–2. 由(8)式和(9)式可知, 求取太阳光照加热率, 关键在于入射角β的求取. 参考文献[26], 入射角β与研究点的坡度λ、方位角γ、太阳天顶距θ_z、太阳方位角γ_s有关, 关系为

${\rm{cos}}\beta {\rm{ = cos}}{\theta _{\rm{z}}}{\rm{cos}}\lambda {\rm{ + sin}}{\theta _{\rm{z}}}{\rm{sin}}\lambda {\rm{cos}}\left( {\gamma - {\gamma _{\rm{s}}}} \right),$

其中, 方位角γ可由研究点的坡向求出; 太阳天顶距θ_z及其方位角γ_s可由SPICE系统提供的实时太阳星下点坐标以及文献[26]的方法求出; 研究点的坡度λ可由文献[17,18]提供的月球全球坡度分布图求出.

为了测试算法与程序的合理性, 图3给出了Mons Rümker高原的早晨光照分布. 该图对应月球地方时t_m = 06:30:30, Mons Rümker高原在早晨相应时刻, 地表对太阳光反射的相对光强度分布. 其中图3(a)来自日本SELENE卫星提供的早晨光照影像(http://darts.isas.jaxa.jp/planet/pdap/selene/), 由影像TCO_MAPm04_N42E300N39E303SC和TCO_MAPm04_N42E303N39E306SC拼接得到, 其中白色和黑色分别代表光照强度最强和最弱, 其他颜色表示光照强度在两者间的变化. 图3(a)表明太阳光自东向西, 东边光照强度强, 西边光照弱; 迎光方向出现光亮区域, 而背光方向则由于地形遮挡出现阴暗区域. 采用与图3(a)相同的光照时刻, 图3(b)表示基于LOLA地形模型、(1)式和(10)式求解的相对光强度RII(relative intensity of illumination). 图3(b)中等高线表示Mons Rümker高原, 相对半径为1737.151 km的参考球面的地形高. 由图3(b)可知: 1)东边相对光强度强, 西边相对光强度弱; 2)东边迎光方向部分区域, 由于坡向正对太阳光, 相对光强度较强, 呈现出白色; 3)西边背光方向部分区域, 由于地形遮挡, 相对光强度接近于零, 呈现出黑色. 对比图3(a)和图3(b), 可以发现除少部分小区域外, 两者光照强度的分布总体上一致. 部分小区域出现偏差, 主要是由于光照计算采用的LOLA地形模型的分辨率, 低于日本SELENE卫星提供的早晨光照影像所致. 本文计算的光强度分布, 在总体上与观测结果一致, 说明整个算法及计算程序具有一定的合理性, 可以进一步应用于Mons Rümker高原风化层温度的估算.
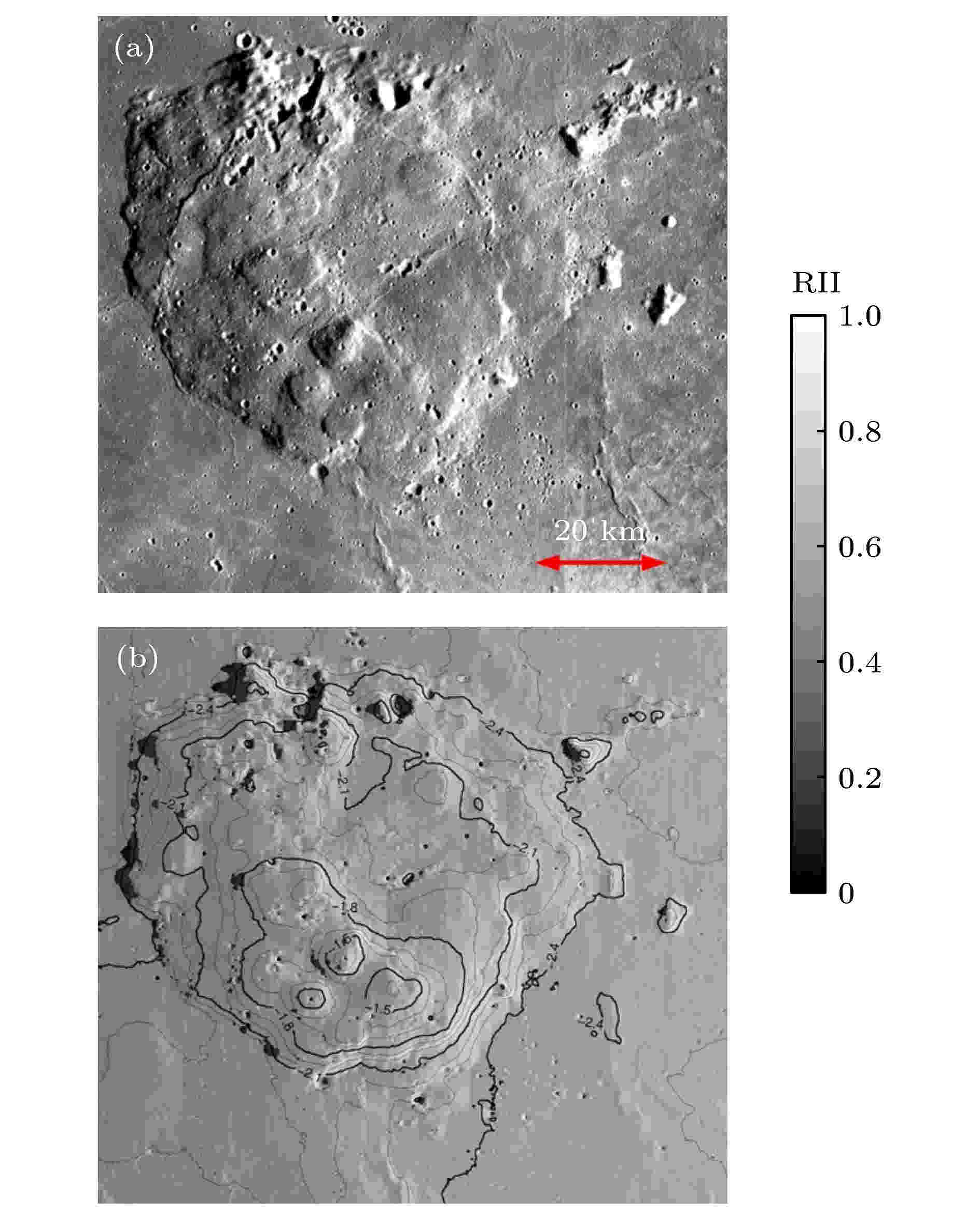图 3 Mons Rümker区域早晨光照图, 对应月球地方时t_m = 06:30:30　(a)日本SELENE卫星提供的早晨光照图; (b)本文计算的与图3(a)相同时刻的实时光照图
Figure3. Morning map of illumination over Mons Rümker at the lunar local time t_m = 06:30:30: (a) Japan’s SELENE morning map of illumination; (b) our estimated relative intensity of illumination at the same time of Fig. 3(a)

利用本文计算的实时光照强度, 根据(2)— (7)式, 可以求出Mons Rümker高原风化层的实时温度分布. 为了计算风化层不同深度处的温度, 利用文献[14]提供的标准化有限差分方法对(2)式进行数值计算. 图4给出了Mons Rümker高原不同时刻的表面温度, 其中图4(a)对应协调世界时UTC(universal time coordinated): 2020年10月28日11点30分00秒, 简写为UTC 2020-10-28T 11:30:00, 后文所有时间依此格式表述. 此时, 由于没有太阳光照, 大部分区域的温度在80 K左右. 至图4(b)时(UTC 2020-10-29T 06:45:00), 随着太阳光的到来, 东边温度逐渐升高, 特别是坡向正对太阳光的区域, 温度一度接近200 K, 西边由于背光, 温度维持在120 K左右. 随着太阳高度角的增大, 类似情况也出现在图4(c)中, 大部分区域的温度升至200 K左右, 高温区域一度接近280 K, 该图对应的时刻为UTC 2020-10-30T 06:45:00. 到达正午时分(如图4(d)所示, 对应时刻为UTC 2020-11-02T 04:45:00), 大部区域的温度升至360 K左右, 少部分区域接近或超过400 K. 至图4(e)时, 由于太阳高度角的下降, 光照减少, 表面温度也逐渐下降. 此时, Mons Rümker高原处于月球地方时的下午时分, 太阳光照至西向东, 西边迎光方向光照强, 东边背光方向光照弱, 对应时刻为UTC 2020-11-12T 02:45:00. 如图4(f)所示(对应时刻为UTC 2020-11-12T 17:00:00), 随着太阳高度角的进一步降低, 大部分区域的温度降至120 K左右, 西边迎光方向部分区域的温度维持在200 K左右. 尽管温度下降, 部分背光区域的温度一度高于200 K, 这些区域恰好对应图4(b)—(d)中的高温区域. 在表面光照强时, 这些高温区域的热量不断地向风化层底部传递, 至图4(f)时, 尽管表面光照减弱, 已传递至风化层内部的热量反向传递至风化层表面, 使得表面温度升高. 由于这些区域内部温度高于其他区域, 至图4(f)时, 尽管光照减弱, 得到内部热量的补充, 表面温度仍然高于其他区域.
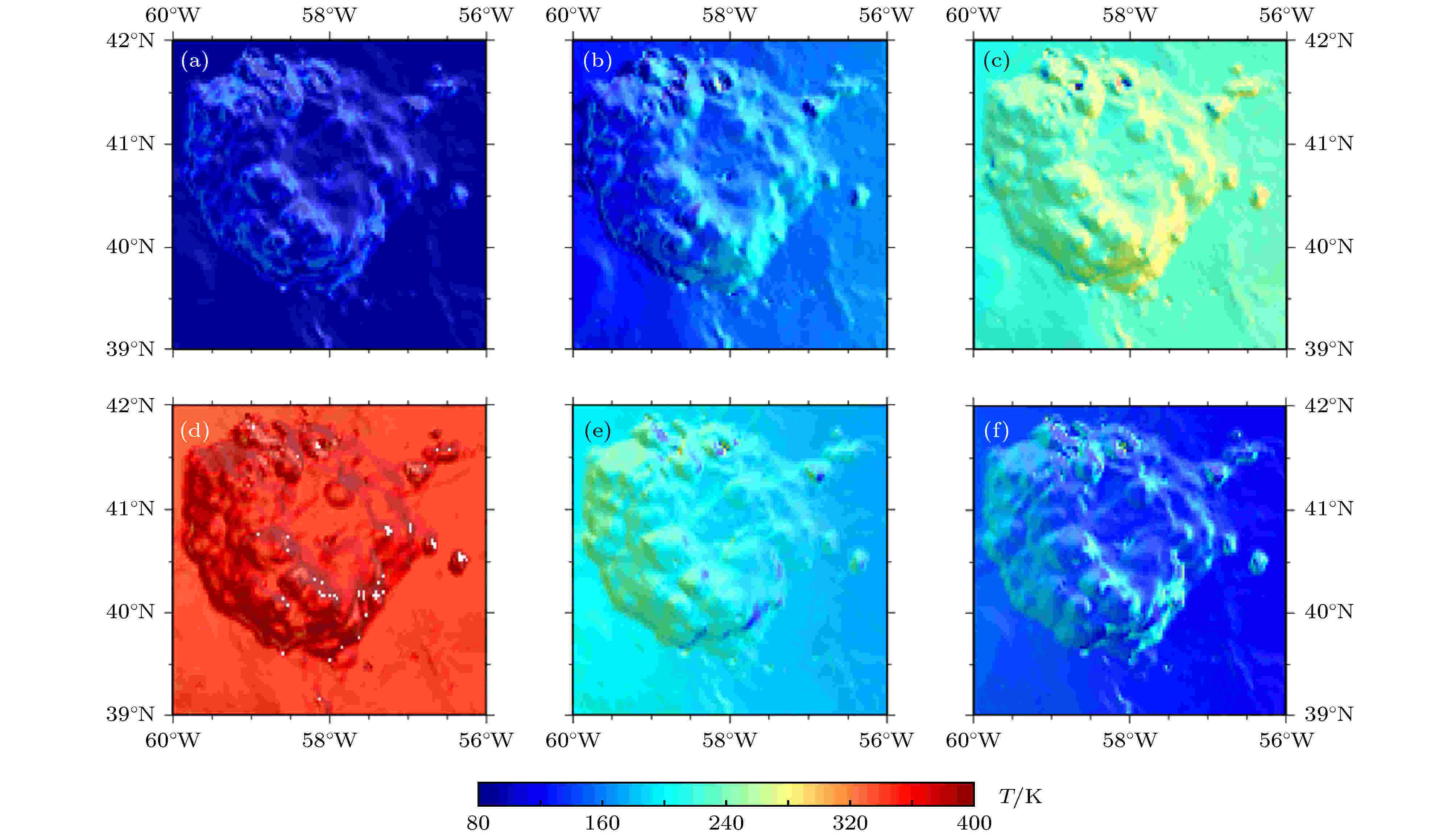图 4 Mons Rümker区域表面温度分布图　(a)对应时刻为UTC 2020-10-28T 11:30:00; (b)对应时刻为UTC 2020-10-29T 06:45:00; (c)对应时刻为UTC 2020-10-30T 06:45:00; (d)对应时刻为UTC 2020-11-02T 04:45:00; (e)对应时刻为UTC 2020-11-12T 02:45:00; (f)对应时刻为UTC 2020-11-12T 17:00:00
Figure4. Surface temperature distribution with time over Mons Rümker plateau: (a) Time at UTC 2020-10-28T 11:30:00; (b) time at UTC 2020-10-29T 06:45:00; (c) time at UTC 2020-10-30T 06:45:00; (d) time at UTC 2020-11-02T 04:45:00; (e) time at UTC 2020-11-12T 02:45:00; (f) time at UTC 2020-11-12T 17:00:00

这种结论也可以由图5得到佐证. 图5表示Mons Rümker高原风化层5 cm深度的温度分布, 对应时刻与图4各分图一致. 由图5(a)—5(c)可知, 随着太阳光照增加, 尽管表面温度在升高(如图4(a)—4(c)所示), 但风化层5 cm深度处的温度始终维持在200 K左右, 至正午时分图5(d)时, 底部温度才有所升高. 这说明月球风化层的导热能力较弱, 具有一定的绝热性能, 该结果与文献[14,15]的一致. 随着下午时分太阳光照的减弱, 尽管表面温度下降至120 K左右(如图4(e)和图4(f)所示), 但5 cm深度的温度始终维持在260 K左右, 部分区域甚至达到300 K. 此时, 随着表面温度下降, 内部温度高于月表温度, 热量由内向外传递, 使得图4(f)部分背光区域的温度高于邻近区域.
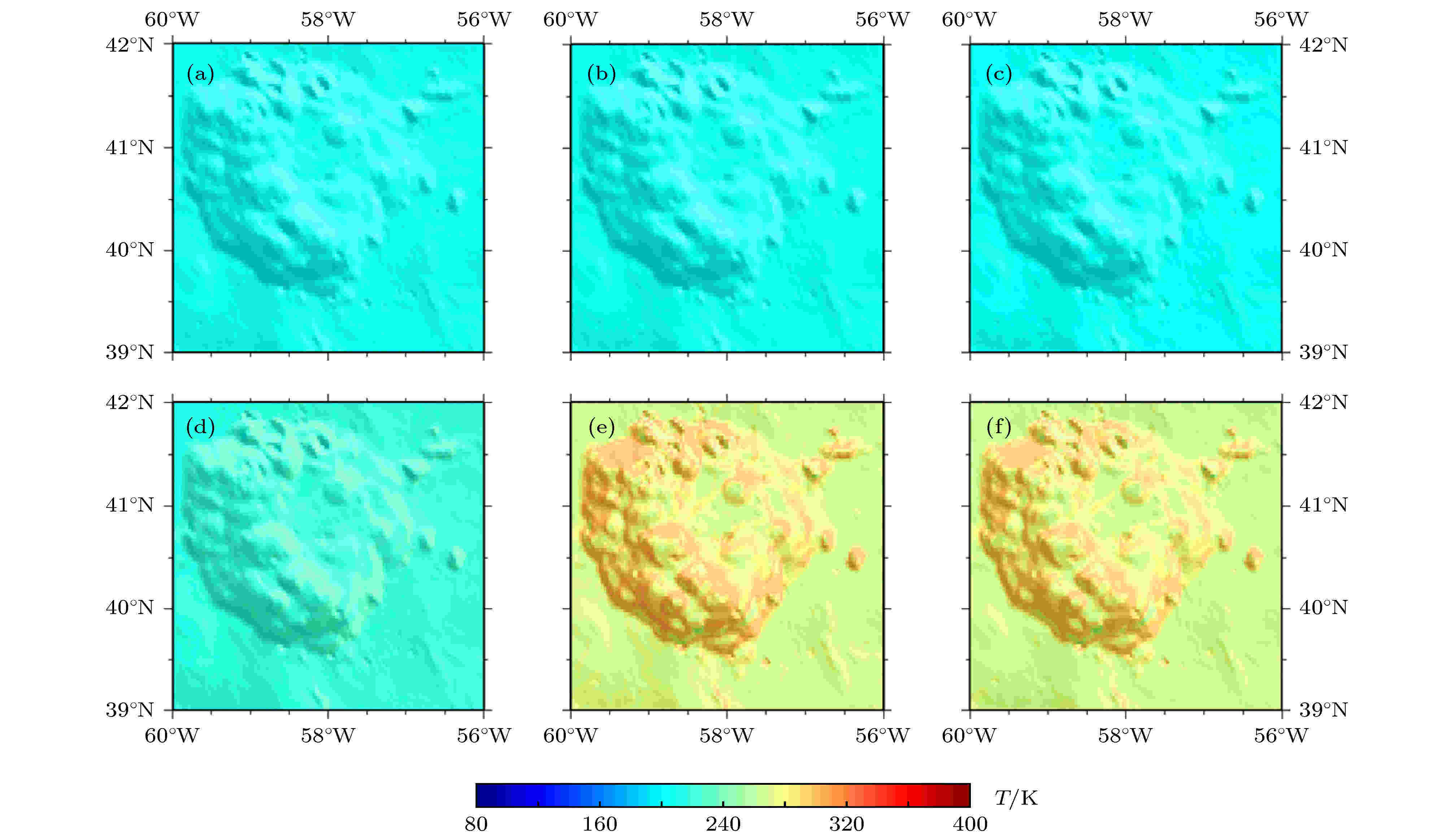图 5 Mons Rümker区域底部5 cm深度的温度分布图　(a)对应时刻为UTC 2020-10-28T 11:30:00; (b)对应时刻为UTC 2020-10-29T 06:45:00; (c)对应时刻为UTC 2020-10-30T 06:45:00; (d)对应时刻为UTC 2020-11-02T 04:45:00; (e)对应时刻为UTC 2020-11-12T 02:45:00; (f)对应时刻为UTC 2020-11-12T 17:00:00
Figure5. Subsurface temperature distribution at the depth of 5 cm over Mons Rümker plateau: (a) Time at UTC 2020-10-28T 11:30:00; (b) time at UTC 2020-10-29T 06:45:00; (c) time at UTC 2020-10-30T 06:45:00; (d) time at UTC 2020-11-02T 04:45:00; (e) time at UTC 2020-11-12T 02:45:00; (f) time at UTC 2020-11-12T 17:00:00

为了进一步探究风化层的温度变化, 图6给出了温度随深度变化的剖面图, 剖面方向沿图1蓝色直线的方向, 横轴表示经度, 纵轴表示深度, 对应时刻与图4和图5一致. 由图6(a)—(c)可知, 随着太阳光照的增加, 风化层5 cm深度以内的温度不断地增加, 5 cm以下的温度变化较弱, 这与图5(a)—(c)的结果一致. 至正午时刻图6(d)时, 表面温度升至最大值, 热量向风化层内部传递, 内部温度不断升高. 图6(d)中黑色曲线表示沿剖面方向的表面地形轮廓, 其幅度表示地形的相对变化, 其大小与图6纵轴刻度范围无关, 该图表明温度的变化与地形有关. 至图6(e)和图6(f)时, 内部储存的热量向表面传递, 使得表面对应区域的温度高于邻近区域.
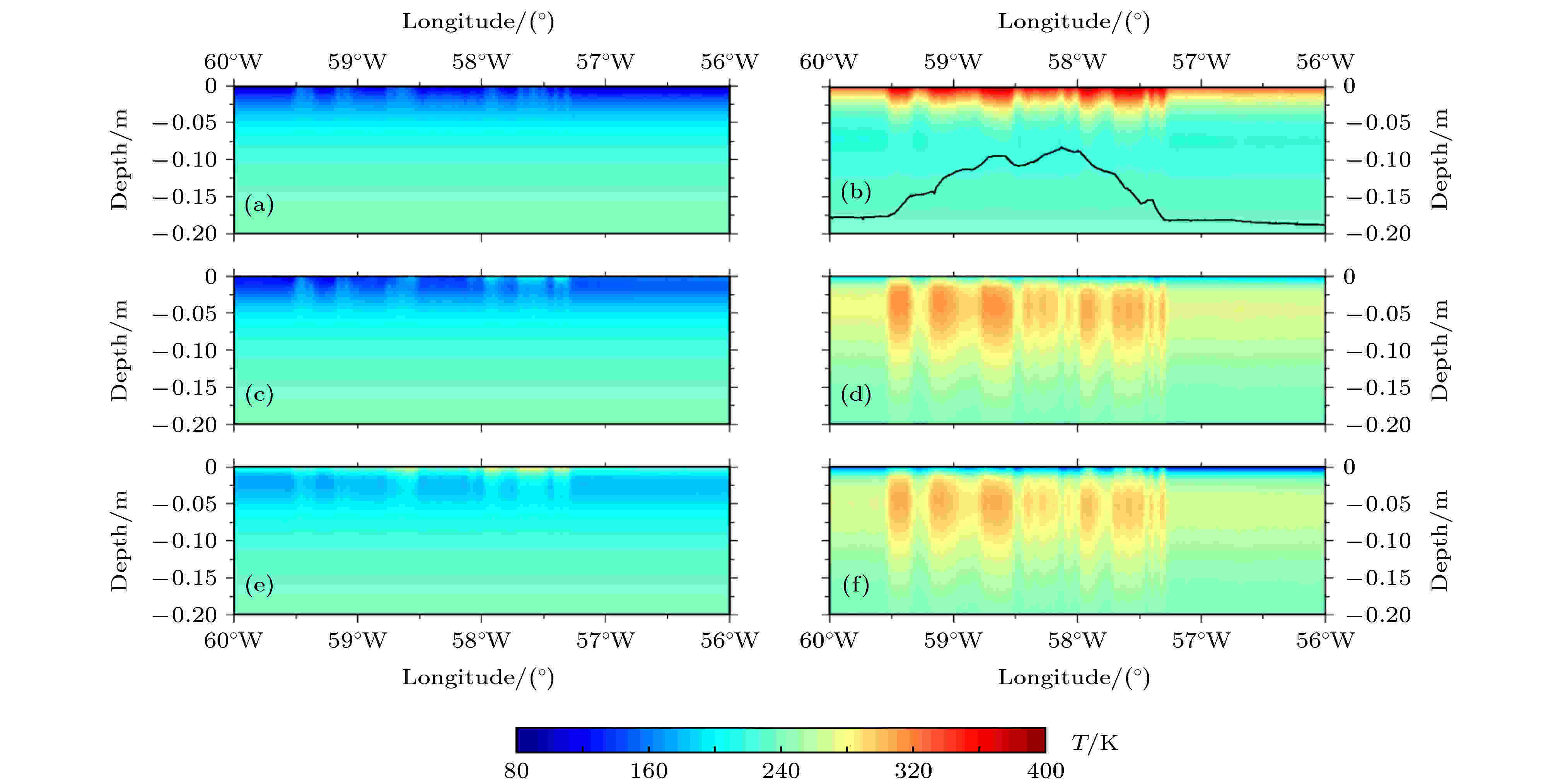图 6 剖面温度沿图1所示经度方向的分布　(a)对应时刻为UTC 2020-10-28T 11:30:00; (b)对应时刻为UTC 2020-10-29T 06:45:00; (c)对应时刻为UTC 2020-10-30T 06:45:00; (d)对应时刻为UTC 2020-11-02T 04:45:00; (e)对应时刻为UTC 2020-11-12T 02:45:00; (f)对应时刻为UTC 2020-11-12T 17:00:00. 图6(d)所示黑色曲线表示图1蓝线方向的表面地形轮廓
Figure6. Temperature variation along the longitude direction shown in Fig.1: (a) Time at UTC 2020-10-28T 11:30:00; (b) time at UTC 2020-10-29T 06:45:00; (c) time at UTC 2020-10-30T 06:45:00; (d) time at UTC 2020-11-02T 04:45:00; (e) time at UTC 2020-11-12T 02:45:00; (f) time at UTC 2020-11-12T 17:00:00. The black carves in Fig. 6(d) represents the surface topography along the same blue line direction displayed in Fig. 1

为了进一步研究0.2 m深度以下的温度变化, 图7给出了两个参考点不同深度处温度随时间的变化关系. 其中, 图7(a)表示“嫦娥5号”候选登陆点(图1所示黑色方块)的温度变化, 图7(b)表示另一参考点(图1所示黑色五角星)的温度变化. 由图7可知, 两个参考点的温度在0.27 m深度的温度最小值在239 K左右. 温度变化幅度随着深度的降低逐渐减小, 到达0.57 m深度时, 温度几乎不再变化, 保持在241.5 K左右. 结合图4—图7, 保守估计风化层的常温层深度在0.6 m. 参考文献[4], “嫦娥5号”的钻井深度接近2 m, 在进行钻井作业及仿真分析时, 有必要考虑风化层内外温度的差异; 另外, 考虑到常温层深度在0.6 m左右, “嫦娥5号”的钻井深度达2 m, 能探测到常温层的热流. 结合“嫦娥5号”的钻井经验, 后期探月工程可考虑搭载探测月球内部热流值的载荷, 以促进月球内部结构及热演化研究的发展.
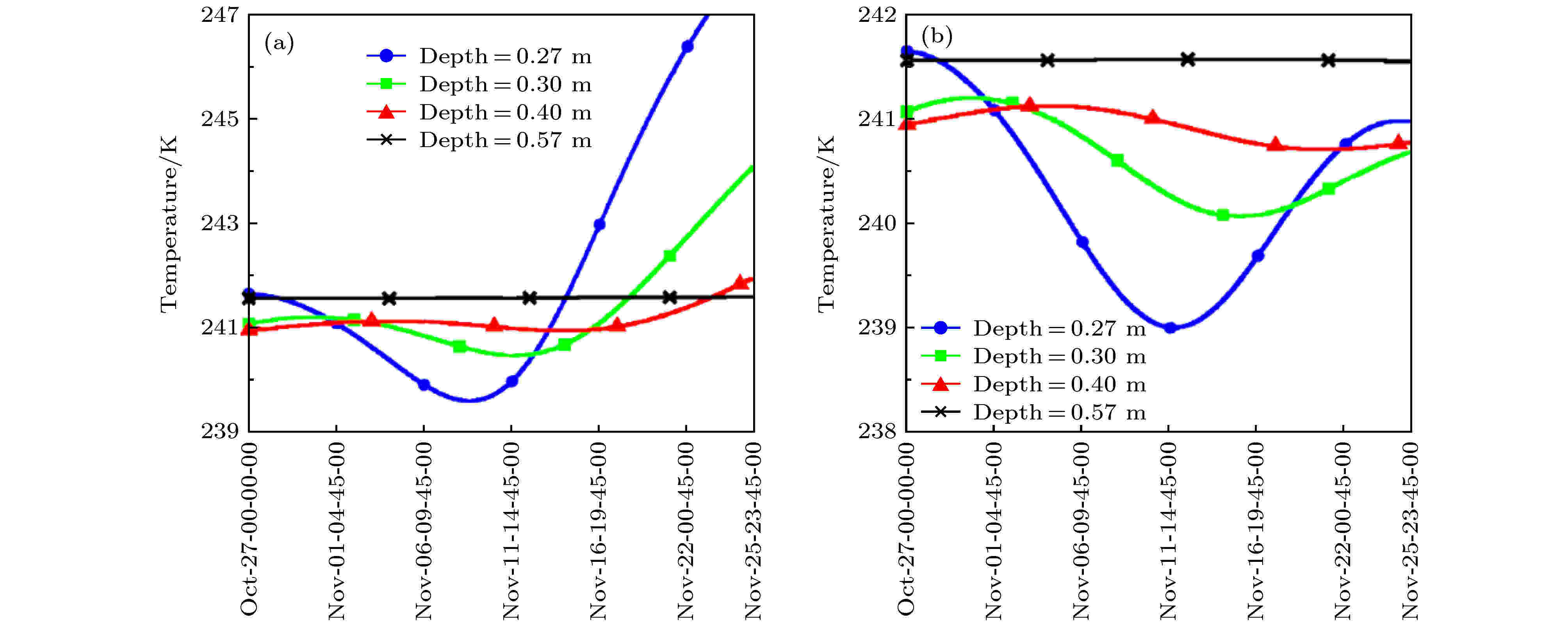图 7 底部温度随时间的变化　(a)“嫦娥5号”候选登陆点的底部分温度变化; (b)图1中黑色五角星所示参考点的底部温度变化
Figure7. Subsurface temperature variations: (a) Variations for the point of CE-5 candidate landing site; (b) variations for the black star in Fig. 1

前文在估算Mons Rümker高原风化层的温度分布时, 控制风化层密度分布的H参数取值为0.06 m, 热流值Q选用的是Apollo 15号和Apollo 17号测量的平均值(Q = 0.018 W·m^–2), 不同参数取值有可能引起温度波动, 为此, 有必要讨论相关参数的适用性. 参考文献[14], 相关参数如热传导系数、风化层密度和比热容等参数主要受H参数的调控, 因此, 仅讨论H参数对温度的影响. 参考文献[14], H参数的最小值为0.02 m, 最大值为0.09 m. 参考文献[22], 热流测量的最大值在Apollo 15号登陆点, 约为0.021 W·m^–2. 文献[27]利用数值方法, 估算的全球热流值约为0.012 W·m^–2, 小于Apollo任务的测量值. 为了直观方便, 图8和表2给出了H参数和热流值Q取极值时, 参考点(如图1黑色五角星所示)温度随深度的变化. 其中黑色实线和红色虚线, 表示Q = 0.018 W·m^–2, H参数分别取0.02 m和0.09 m时, 参考点温度随深度的变化; 绿色和蓝色虚线表示H = 0.06 m, 热流值分别取Q = 0.012 W·m^–2和Q = 0.021 W·m^–2时的温度分布. 图8(a)—8(c)分别对应月球地方时t_m = 06:30:30, t_m = 12:30:30和t_m = 18:30:30, 对应参考点的早晨、正午和傍晚时刻. 1)由图8(a)—8(c)可知, H参数和热流值Q取值的不同, 对温度的变化只有细微的影响, 绝对误差不超过10 K; 2)如图8(c)以及表2所示, H参数对温度的影响超过热流值Q, H参数主要对风化层0.2 m以内区域产生较大的影响, 对底层温度的影响较弱; 3)如表2所列, 热流值Q取值的不同, 主要对风化层基底温度产生较小的影响, 绝对误差不超过1 K. 综上所述, 同时考虑实际钻进深度超过1 m, H参数和热流值Q的差异, 对温度分布的影响可以忽略不计, 因此, 本文计算结果具有一定的参考价值.

深度/m	tm = 06:30:30					tm = 12:30:30					tm = 18:30:30
	H = 0.02 m	H = 0.09 m	Q = 0.012 W·m–2	Q = 0.021 W·m–2		H = 0.02 m	H = 0.09 m	Q = 0.012 W·m–2	Q = 0.021 W·m–2		H = 0.02 m	H = 0.09 m	Q = 0.012 W·m–2	Q = 0.021 W·m–2
0	170.0	169.6	169.7	169.7		348.1	351.7	350.9	350.9		122.3	110.7	112.9	112.9
0.0136	158.5	149.4	152.3	152.3		322.5	325.7	324.4	324.4		213.6	205.6	207.1	207.1
0.0526	192.4	194.5	194.4	194.4		270.6	261.1	263.2	263.2		260.9	260.7	260.1	260.1
0.1000	221.3	223.8	223.2	223.2		237.9	231.9	233.6	233.6		260.3	253.9	255.3	255.3
0.1822	239.3	239.6	239.5	239.5		234.0	235.1	234.7	234.7		243.0	239.5	240.4	240.4
0.3240	241.2	241.2	241.2	241.2		240.8	240.9	240.8	240.8		240.0	240.2	240.1	240.1
0.4721	241.2	241.2	241.2	241.2		241.3	241.3	241.3	241.3		241.2	241.3	241.3	241.3
0.8250	242.4	242.4	242.4	242.4		242.4	242.4	242.4	242.4		242.4	242.4	242.4	242.4
1.0000	242.9	242.9	242.7	243.1		242.9	242.9	242.7	243.1		242.9	242.9	242.7	243.1

表2参考点(图1中黑色五角星)温度(单位为K)在不同时刻随深度的变化
Table2.Temperature (in K) variations with depth for the point of black star in Fig. 1 at various lunar local time

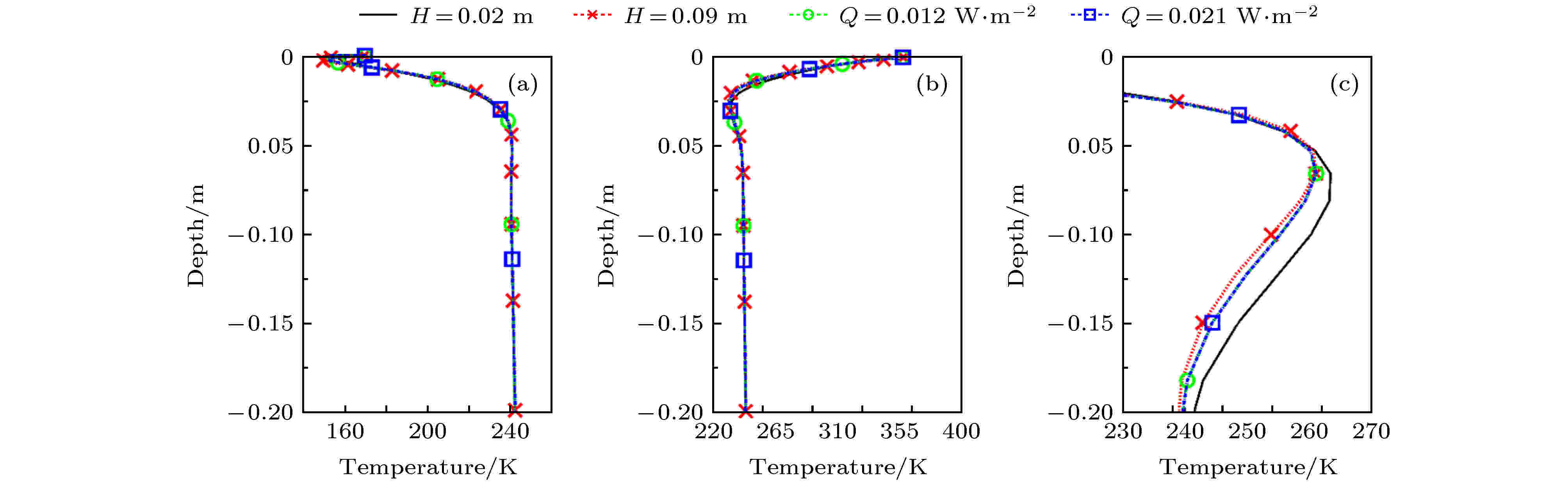图 8 参考点(图1中黑色五角星)温度随深度的变化　(a)对应月球地方时t_m = 06:30:30; (b)对应月球地方时t_m = 12:30:30; (c)对应月球地方时t_m = 18:30:30
Figure8. Subsurface temperature variations with depth for the point of black star in Fig. 1: (a) Temperature variations at the lunar local time t_m = 06:30:30; (b) temperature variations at the lunar local time t_m = 12:30:30; (c) temperature variations at the lunar local time t_m = 18:30:30

针对“嫦娥5号”候选登陆区Mons Rümker高原风化层的温度变化, 利用SPICE系统对实时光照进行计算, 在此基础上, 结合1维热传导模型对风化层的温度进行仿真分析. 结果表明: 1)本文计算的实时相对光照强度分布与日本SELENE卫星提供的早晨光照影像总体一致, 说明本文的算法及计算程序具有一定的合理性; 2)依据求解的光照作为边界条件, 发现0.5 cm深度以内的风化层温度, 受表面光照的影响较大, 随着深度的增加, 光照影响逐渐减弱; 3)风化层底部0.57 m深度以下的温度不随时间变化, 保守估计常温层的深度在0.6 m左右; 4)决定风化层物理特征的H参数, 其大小的改变并不会引起温度的大幅波动, 对常温层产生的影响较弱; 5)热流值Q的不同, 仅对基底边界温度产生较小的影响, 实际应用中可以不考虑热流值Q选取的差异.