摘要: 针对双基地电磁矢量传感器多输入多输出(electromagnetic vector sensors multiple-input multiple-output, EMVS-MIMO)雷达参数估计精度以及角度参数配对问题, 通过设计一种新的稀疏阵列和采用自动参数配对算法来实现高分辨的角度参数和极化参数联合估计. 首先, 通过设计稀疏的发射阵列和接收阵列来实现对EMVS-MIMO雷达阵列孔径的扩展; 然后, 提出平行因子-三线性分解算法对接收数据的三阶张量模型进行求解. 所提出的平行因子-三线性分解算法能够实现二维发射角、二维接收角、极化相位角和极化相位差的联合参数自动配对; 且针对估计得到的发射导向矢量矩阵和接收导向矢量矩阵, 根据旋转不变特性可以实现高精度的发射俯仰角和接收俯仰角测量. 在得到精确的发射俯仰角和接收俯仰角之后, 相应的发射和接收方位角、极化角和极化相位差可以通过矢量叉积算法来进行估计. 相比于现有算法, 所提出的算法能够避免高维数据奇异值分解以及额外的参数配对过程; 且通过稀疏阵列设计, 角度参数估计精度能够进一步地提升, 仿真结果表明所提出的算法具有优良的角度参数估计性能.
关键词: 稀疏阵列 /
双基地电磁矢量传感器多输入多输出雷达 /
平行因子-三线性分解 /
联合参数估计 English Abstract Efficient angle and polarization parameter estimaiton for electromagnetic vector sensors multiple-input multiple-output radar by using sparse array Xie Qian-Peng Pan Xiao-Yi Chen Ji-Yuan Xiao Shun-Ping State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System, National University of Defense Technology, Changsha 410073, China Received Date: 15 December 2019Accepted Date: 02 February 2020Published Online: 05 April 2020Abstract: In this paper, a new sparse transmitting and receiving array is designed to improve the joint angle and polarization parameter estimation performance for bistatic electromagnetic vector sensors Multiple-Input Multiple-Output radar. Firstly, large array aperture can be obtained with the aid of the sparse transmitting and receiving array. Then, an effective third-order tensor model is constructed in order to make full use of the multidimensional space-time characteristics of output data after matching filtering. And, the Parallel Factor trilinear alternating least square algorithm is proposed to deal with the constructed third-order tensor model, which can yield closed-form automatically paired two dimensional Direction of Departure and two dimensional Direction of Departure estimation without additional angle pair matching process. Furthermore, two sets of high accuracy rotation invariance relationships corresponding to transmit elevation angle and receive elevation angle can be achieved by using the estimated transmit steering vector matrix and receive steering vector matrix. After the accuracy transmit elevation angle and receive angle are obtained, the corresponding transmitting and receiving azimuth angle, polarization angle and polarization phase difference can be accurately estimated by using the vector-cross-product algorithm. Compared with existing algorithms, the proposed algorithm can avoid high dimensional eigenvalue decomposition and additional parameter matching process. Moreover, the high estimation performance of the proposed can be further guaranteed by using the designed sparse array. Finally, simulation results demonstrate the effectiveness and superiority of the proposed method in terms of estimation accuracy and angle resolution.Keywords: sparse array /bistatic electromagnetic vector sensors multiple-input multiple-output radar /parallel factor trilinear alternating least square /joint parameter estimation 全文HTML --> --> --> 1.引 言 多输入多输出(multiple-input multiple-output, MIMO)雷达参数估计是当前研究的一个热点问题, 相比于使用相关波形的常规相控阵雷达, 其通过发射相互正交的信号波形能够实现高的角度分辨率、灵活可控的波形设计以及阵列自由度的提升升[1 -3 ] . 根据阵列的配置方式, MIMO雷达可分为利用空间多样性的统计MIMO雷达和利用波形多样性的集中式MIMO雷达[4 ] . 并且, 集中式MIMO雷达可以进一步地划分为单基地MIMO雷达和双基地MIMO雷达. 其中, 单基地MIMO雷达由于发射阵和接收阵距离较近, 相应的发射角(direction-of-departure, DOD)和接收角(direction-of-arrival, DOA)是相同的; 而双基地MIMO雷达由于发射阵和接收阵相距较远, 其DOD和DOA是不同的. 本文主要针对双基地MIMO雷达的角度参数估计展开研究.5 ,6 ]中, 谱峰搜索类算法二维Capon估计器和二维MUSIC估计器被提出. 但是, 为了确保DOD和DOA的估计精度, 二维谱峰搜索类算法由于需要较小的搜索间隔, 具有较高的计算复杂度. 为了降低计算代价, 相应的降维Capon和降维MUSIC算法在文献[5 ,6 ]中也被提出. 相比于二维谱峰搜索类算法, 降维类算法仅需要一维谱峰搜索过程. 并且, 降维类算法在降低计算复杂度的同时也能保持良好的估计精度. 为了避免谱峰搜索过程, 文献[7 ]利用旋转不变技术 (estimated signal parameters via rotational invariance technique, ESPRIT) 来实现对双基地MIMO雷达DOD和DOA的联合估计. 但是, 文献[7 ]所提的算法需要额外的角度参数配对过程. 在文献[8 ]中, 一种修正的自动参数配对ESPRIT算法被提出. 文献[9 ]提出多项式求根MUSIC算法来实现对DOD和DOA的角度参数估计. 文献[10 ,11 ]提出联合对角化算法来实现对双基地MIMO雷达的角度参数的自动配对, 并且所提出的算法相比于ESPRIT算法具有更高的估计精度. 为了充分利用匹配滤波之后阵列接收数据的多维特性, 文献[12 ]提出三阶张量方法. 文献[13 ]利用高斯色噪声的空时非相关特性, 通过构建延时相关的四阶张量矩阵来实现对双基地MIMO雷达中色噪声的抑制. 为了进一步地利用发射相关增益来提高角度参数估计精度, 文献[14 ]利用波束空间变化技术来实现对发射波形进行约束, 从而把发射信号的能量和接收信号的能量集中到DOD和DOA所在的区域. 针对冲击噪声背景下宽带双基地MIMO雷达的角度参数估计问题, 文献[15 ]利用Sigmoid变化来实现对联合DOD和DOA角度参数估计性能的提升. 针对双基地MIMO雷达发射阵列以及接收阵列阵元损坏背景下的DOD和DOA估计问题, 文献[16 ,17 ]利用图像熵和低秩块Hankel矩阵补全技术来实现对丢失数据的恢复.[18 ] . 为了实现对双基地EMVS-MIMO雷达的角度参数估计, 文献[19 ]从发射EMVS阵列和接收EMVS阵列中提取出旋转不变特性来实现对2D-DOD和2D-DOA的估计. 但是, 文献[19 ]提出的ESPRIT-Like算法需要进行高维矩阵的奇异值分解. 为了避免高维奇异值分解的计算复杂度, 文献[20 ]利用传播算子(propagator method, PM) 来实现对信号子空间的近似. 文献[21 ]进一步考虑利用EMVS-MIMO雷达阵列接收数据的多维特性, 提出基于协方差高阶奇异值分解的2D-DOD和2D-DOA联合估计算法. 在文献[19 -21 ]中, 面临的共性问题在于为了实现2D-DOD和2D-DOA的参数配对, 需要进行构建额外的配对优化函数, 并且, 在进行发射俯仰角和接收俯仰角参数估计的时候, 需要进行合适的参数选择来实现旋转不变关系的构建. 如果不能选择合适的旋转不变参数, 那么估计得到的角度信息将会产生较大的误差或者导致参数估计算法失效. 因此, 为了进一步提升双基地EMVS-MIMO的角度参数和极化参数的估计性能, 本文通过设计新型的稀疏发射EMVS阵列和稀疏接收EMVS阵列来实现对阵列孔径的提升. 同时为了避免2D-DOD和2D-DOA角度参数配对和额外旋转不变参数的选择, 本文提出利用平行因子-三线性分解 (PARAFAC-TALS) 算法来实现对角度参数和极化参数的估计. 所提出的算法既能够充分利用匹配滤波之后接收阵列数据的多维特性, 同时又能够避免高维数据的奇异值分解. 仿真实验证明, 针对双基地EMVS-MIMO雷达的角度参数和极化参数联合估计, 所提出的算法具有较高的参数估计精度以及较低的计算复杂度.2.信号模型 如图1 所示, 考虑一个包含M 个稀疏EMVS发射阵列和N 个稀疏EMVS接收阵列的双基地EMVS-MIMO雷达系统, 其中发射稀疏阵列和接收稀疏阵列均包含两个稀疏子阵. 对于发射稀疏阵列, 第一个稀疏子阵的阵列个数为${M_1}$ 且阵元间距为${M_1}\lambda $ , 第二个稀疏子阵的阵列个数为${M_2}$ 且阵元间距为${M_2}\lambda $ , 其中λ 表示发射信号的波长. 第一个发射子阵和第二个发射子阵的阵元间距为${M_1}\lambda $ . 对于接收稀疏阵列, 第一个稀疏子阵的阵列个数为${N_1}$ 且阵元间距为${N_1}\lambda $ , 第二个稀疏子阵的阵列个数为${N_2}$ 且阵元间距为${N_2}\lambda $ . 第一个接收子阵和第二个接收子阵的阵元间距为${N_1}\lambda $ . 因此, 发射稀疏阵列和接收稀疏阵列的阵元位置可以表示为图 1 稀疏阵列EMVS-MIMO雷达系统Figure1. EMVS-MIMO radar system with sparse linear array.K , 则稀疏EMVS发射导向矢量和稀疏EMVS接收导向矢量为${{{q}}_{{t_k}}} \!=\! {\left[ {1, {{\rm{e}}^{ - {\rm{j}}2{\text{π}}{d_{t2}}{{\sin {\theta _{{t_k}}}} / \lambda }}}, \cdot \cdot \cdot, {{\rm{e}}^{ - {\rm{j}}2{\text{π}}{d_{tM}}{{\sin {\theta _{{t_k}}}} / \lambda }}}} \right]^{\rm{T}}}$ 对应发射俯仰角的导向矢量矩阵,${{{c}}_{{t_k}}}({\theta _{{t_k}}}, {\phi _{{t_k}}}, $ ${\gamma _{{t_k}}}, {\eta _{{t_k}}})$ 和${{{c}}_{{r_k}}}\left( {{\theta _{{r_k}}}, {\phi _{{r_k}}}, {\gamma _{{r_k}}}, {\eta _{{r_k}}}} \right)$ 表示对应于发射阵列和接收阵列的电磁矢量传感器的空间响应.${{{F}}_{{t_k}}}\left( {{\theta _{{t_k}}}, {\phi _{{t_k}}}} \right)$ 和${{{F}}_{{r_k}}}\left( {{\theta _{{r_k}}}, {\phi _{{r_k}}}} \right)$ 表示维度为$6 \times 2$ 的空间角度位置矩阵, ${\theta _{{t_k}}}, {\theta _{{r_k}}} \in \left[ {0, {\text{π}}} \right)$ 表示俯仰角, ${\phi _{{t_k}}}, {\phi _{{r_k}}} \in \left[ {0, 2{\text{π}}} \right)$ 表示方位角; ${{{g}}_{{t_k}}}\left( {{\gamma _{{t_k}}}, {\eta _{{t_k}}}} \right)$ 和${{{g}}_{{r_k}}}\left( {{\gamma _{{r_k}}}, {\eta _{{r_k}}}} \right)$ 表示维度为$2 \times 1$ 的极化状态矢量, ${\gamma _{{t_k}}}, {\gamma _{{r_k}}} \in \left[ {0, {{\text{π}} / 2}} \right)$ 表示极化角, ${\eta _{{t_k}}}, {\eta _{{r_k}}} \in \left[ { - {\text{π}}, {\text{π}}} \right)$ 表示极化相位差. 发射EMVS和接收EMVS的空间角度位置矩阵和极化状态矢量可以表示为11 )和(12 )可以看出, 如果能够得到归一化波印廷矢量, 那么就可以对发射俯仰角、发射方位角、接收俯仰角和接收方位角的角度参数进行提取. 并且, 从极化状态矢量中可以提取相应的极化状态角和极化相位差.[19 ] ${{{A}}_t} = \left[ {{{{a}}_{t1}}, {{{a}}_{t2}}, \cdot \cdot \cdot, {{{a}}_{tK}}} \right]$ 和${{{A}}_r} =[{{{a}}_{r1}}, {{{a}}_{r2}}, \cdots,$ $ {{{a}}_{rK}}]$ 分别表示发射导向矢量矩阵和接收导向矢量矩阵, ${\bf{n}}(t)$ 表示加性高斯白噪声矢量. 对于L 个采样快拍, 总的阵列接收数据可以表示为14 )可以看出, 双基地EMVS-MIMO雷达的阵列接收数据满足多维张量结构, 如果直接对公式(14 )进行协方差矩阵的求解, 则会破坏接收数据的空时特性. 因此, 为了充分考虑发射阵列、接收阵列和采样快拍之间的内在联系, 这里采用张量结构来对阵列接收数据进行处理.3.基于张量结构的PARAFAC算法 23.1.角度参数和极化参数联合估计 3.1.角度参数和极化参数联合估计 为了实现对阵列接收数据的张量求解, 这里首先给出PARAFAC分解的定义[22 ] :定义1[PARAFAC分解] 一个维度为M × N × L 的三阶张量X F 表示核数; ${a_{i, f}}$ , ${b_{j, f}}$ 和${c_{k, f}}$ 分别表示加载矩阵${{A}} \in {{\mathbb{C}}^{M \times F}}$ , ${{B}} \in {{\mathbb{C}}^{N \times F}}$ 和${{C}} \in {{\mathbb{C}}^{K \times F}}$ 的第$\left( {i, f} \right)$ , $\left( {j, f} \right)$ 和$\left( {k, f} \right)$ 个元素. 并且, 根据公式(15 ), 对应于三阶张量X ${{{D}}_j}\left( {{B}} \right)$ , ${{{D}}_k}\left( {{C}} \right)$ 和${{{D}}_i}\left( {{A}} \right)$ 表示对角矩阵, 其对角线上的元素分别为加载矩阵A B C i , j 和k 行的元素.14 )的阵列接收数据可以进一步地重新表示为${{{A}}_t}$ 和${{{A}}_r}$ 的联立方程可以表示为${{{A}}_t}$ , 接收导向矢量矩阵${{{A}}_r}$ 和信号矩阵S 17 ), (18 )和(19 ), 关于${{{A}}_t}$ , ${{{A}}_r}$ 和S ${{\tilde{ A}}_r}$ , ${{\tilde{ A}}_t}$ 和${\tilde{ S}}$ 分别表示估计得到的加载矩阵, 则Y ${{\tilde{ A}}_t}$ 和${{\tilde{ A}}_r}$ , 利用最小二乘拟合求解${\tilde{ S}}$ ; 对于给定的${{{Y}}_t}$ , ${\tilde{ S}}$ 和${{\tilde{ A}}_r}$ , 利用最小二乘拟合求解${{\tilde{ A}}_t}$ ; 对于给定的${{{Y}}_r}$ , ${\tilde{ S}}$ 和${{\tilde{ A}}_t}$ , 利用最小二乘拟合求解${{\tilde{ A}}_r}$ . 经过多次迭代求解, 能够得到最优的${\tilde{ S}}$ , ${{\tilde{ A}}_t}$ 和${{\tilde{ A}}_r}$ . 在本文仿真中, 三线性迭代最小二乘的停止准则为达到所设置的迭代收敛次数或估计误差小于门限值, 迭代次数和门限值分别设置为200和${10^{ - 6}}$ .${\tilde{ S}}$ , ${{\tilde{ A}}_t}$ 和${{\tilde{ A}}_r}$ , 其中的发射导向矢量矩阵和接收导向矢量矩阵是一一对应的. 这种一一对应关系意味着包含在${{\tilde{ A}}_t}$ 和${{\tilde{\bf A}}_r}$ 中的2D-DOD和2D-DOA是自动配对的, 其自动参数配对特性是PARAFAC算法的固有特性. 因此, 本文所提的算法相比于文献[19 -21 ]中的算法不需要进行构建额外的配对优化函数. 下面分别针对估计得到的发射导向矢量矩阵和接收导向矢量矩阵进行发射俯仰角、发射方位角、发射极化角、发射极化相位差和接收俯仰角、接收方位角、接收极化角、接收极化相位差的估计.${{\tilde{ A}}_t}$ , 首先可以利用选择矩阵来实现对发射俯仰角${\theta _{{t_k}}},\; k = $ $1, 2, \cdots, K$ 的高精度参数估计. 定义如下的选择矩阵:${\theta _{{t_k}}}, k = 1, 2, \cdot \cdot \cdot, K$ 满足如下的旋转不变特性${{{\varPhi }}_{t1}}\left( {{\theta _t}} \right)$ 和${{{\varPhi }}_{t2}}\left( {{\theta _t}} \right)$ 的估计可以表示为28 )和(29 )可以看出, 由于发射稀疏子阵的阵元间距大于半个波长, 所以以上估计得到的发射俯仰角是高精度周期模糊的. 根据模糊周期与阵元间距的对应关系, 稀疏发射子阵1和稀疏发射子阵2的所有高精度稀疏模糊值可以表示为$\left( {\tilde m{}_1, \tilde m{}_2} \right)$ :$\left( {\tilde m{}_1, \tilde m{}_2} \right)$ , 最终的无模糊发射俯仰角的正弦值可以表示为${{\tilde{ A}}_t}$ 进行极化参数矩阵的提取. 于是, 发射的电磁矢量传感器阵列的空间响应${{\tilde{ C}}_t}\left( {{\theta _t}, {\phi _t}, {\gamma _t}, {\eta _t}} \right)$ 可以表示为${{\tilde{ A}}_t}\left( {6 m - 5:6 m, :} \right)$ 表示${{\tilde{ A}}_t}$ 的第$6 m - 5$ 到6m 行的元素,11 ), 发射EMVS阵列的归一化波印廷矢量可以表示为${{\tilde \phi} _{{t_k}}}$ 可以表示为$\left( {{\tilde \theta} _{{t_k}}^{{\rm{fine}}}, {{{\tilde \phi} }_{{t_k}}}} \right), k = 1, 2, \cdot \cdot \cdot, K$ 之后, 极化状态矢量可以通过如下方程得到$\left( {{{\tilde \gamma }_{{t_K}}}, {{\tilde \eta }_{{t_K}}}} \right)$ , $k = 1, 2, \cdots, K $ 可以表示为${{\tilde{ A}}_r}$ 进行处理. 首先, 为了得到高精度的接收俯仰角${\theta _{{r_k}}}, k = 1, 2, \cdot \cdot \cdot, K$ , 定义如下的选择矩阵:${\theta _{{r_k}}}, k = 1, 2, \cdot \cdot \cdot, K$ .${{{\varPhi }}_{r1}}\left( {{\theta _r}} \right)$ 和${{{\varPhi }}_{r2}}\left( {{\theta _r}} \right)$ 的估计可以被表示为46 )和(47 )得到的高精度发射俯仰角满足周期模糊特性, 且针对稀疏子阵1和稀疏子阵2的所有的高精度稀疏模糊值可以表示为$\left( {\tilde n{}_1, \tilde n{}_2} \right)$ :$\left( {\tilde n{}_1, \tilde n{}_2} \right)$ , 高精度无模糊的接收俯仰角的正弦值可以表示为${{\tilde{ C}}_r}\left( {{\theta _r}, {\phi _r}, {\gamma _r}, {\eta _r}} \right)$ 可以表示为${{\tilde{ A}}_r}\left( {6 n - 5:6 n, :} \right)$ 表示${{\tilde{ A}}_r}$ 的第$6 n - 5$ 到6n 行的元素, ${{\tilde{ \varPhi }}_r}\left( {{\theta _r}} \right) = {\rm{diag}}\left[ {{{{\tilde{ \varPhi }}}_{r1}}\left( {{\tilde \theta} _r^{{\rm{fine}}}} \right), {{{\tilde{ \varPhi }}}_{r2}}\left( {{\tilde \theta} _r^{{\rm{fine}}}} \right)} \right]$ 对应于已估计得到的接收稀疏阵列的旋转不变因子. 根据公式(12 ), 接收EMVS阵列的归一化波印廷矢量可以表示为${{\tilde \phi} _{{r_k}}}$ 可以表示为$\left( {{\tilde \theta} _{{r_k}}^{{\rm{fine}}}, {{{\tilde \phi} }_{{r_k}}}} \right), k = 1, 2, \cdot \cdot \cdot, K$ 之后, 接收阵列的极化状态矢量可以通过如下方程得到:$\left( {{{\tilde \gamma }_{{r_K}}}, {{\tilde \eta }_{{r_K}}}} \right), k = 1, 2, \cdot \cdot \cdot, K$ 可以表示为3.2.克拉美罗界(Cramer-Rao Bound)以及计算复杂度分析 -->3.2.克拉美罗界(Cramer-Rao Bound)以及计算复杂度分析 为了实现对所提算法性能的评价, 这里给出相应的CRB下界限以及所提算法的计算复杂度. CRB表示参数无偏估计的下界, 在衡量参数估计性能中具有重要的意义. 对应于发射阵列和接收阵列需要估计的四维参数分别为$\left( {{\theta _t}, {\phi _t}, {\gamma _t}, {\eta _t}} \right)$ 和$\left( {{\theta _r}, {\phi _r}, {\gamma _r}, {\eta _r}} \right)$ , 根据文献[23 ], 关于四维发射参数和四维接收参数的随机CRB可以表示为${{A}} = \left( {{{{A}}_t} \odot {{{A}}_r}} \right)$ 表示双基地EMVS-MIMO雷达的联合发射接收矩阵, $\Pi _{{A}}^ \bot = {{{I}}_{36 MN}} - {{A}}{{{A}}^{\dagger} }$ 表示矩阵A $ \oplus $ 表示Hadamard乘积, ${{{R}}_s}$ 表示多快拍信号协方差矩阵, ${{\bf{1}}_{8 \times 8}}$ 表示维度为$8 \times 8$ 的全1矩阵. D A $\left( {{\theta _t}, {\phi _t}, {\gamma _t}, {\eta _t}} \right)$ 和四维接收参数$({\theta _r}, {\phi _r},$ $ {\gamma _r}, {\eta _r})$ 的联合导数矢量矩阵, 其具体形式如下:表1 所示. 同时为了对比, 表1 中也列出了文献[19 ]中的ESPRIT-Like算法、文献[20 ]中的PM-Like算法和文献[21 ]中Tensor子空间算法的计算复杂度. 四种算法的仿真软件平台为MATLAB R2018a, 硬件平台为Lenovo ThinkPad X1 Carbon笔记本, 其处理器为Intel Core i7-6500U, CPU为2.5 GHz, 电脑内存为8 GB. 在进行时间统计时, 信噪比设置为$10\;{\rm{dB}}$ , 快拍数为100. 运行时间能够实现对各算法计算复杂度的直观对比. 从表1 中给出的各算法的平均运行时间可以看出, 相比于其他算法, 本文算法具有较低的计算复杂度. 如图2 所示, 进一步考虑10元发射阵列和10元接收阵列条件下, 目标数$K = 3$ 时, 各种不同算法的计算复杂度随快拍数L 的变化关系. 从图2 也可以看出, 所提算法相比于ESPRIT-Like算法、PM-Like算法和Tensor子空间算法具有较低的计算复杂度. Tensor子空间算法由于需要对四维矩阵进行奇异值分解, 因此在四种算法中具有最高的计算复杂度.算法类型 计算复杂度 计算时间/s ESPRIT-Like算法 [19 ] $\begin{aligned}& o((6 M)^2(6N)^2L + (6 M)^3(6 N)^3 + 2K^26(N + M - 2) + 6{K^3} \\ & + 7(M + N){K^2} + 12 K + 36 MN(36 MN - K) + (36 MN - K){K^2}) \end{aligned} $ 28.332 PM-Like算法 [20 ] $\begin{aligned}& o((6M)^2(6N)^2L + 72MN{K^2} + 2{K^2}6 (N + M - 2) + 6{K^3} \\& + 7( {M + N} ) {K^2} + 12K + 36MN({36MN - K}) + (36MN - K){K^2})\end{aligned} $ 2.0698 Tensor子空间算法 [21 ] $\begin{aligned} & o((6 M)^2(6N)^2L + 4(6M)^3(6N)^3 + 2K^2 6(N + M - 2) + 6{K^3} \\& + 7( {M + N} ) K^2 + 12 K + 36 MN( {36 MN - K} ) + (36 MN - K)K^2) \end{aligned} $ 109.880 所提算法 $\begin{aligned}& o(\kappa ( 3K^3+ 108 MNKL + 3K^2) + \kappa (3K^2(36 MN + 6 NL + 6 ML)) \\ & + 2{K^2}6({N + M - 2} ) + 6{K^3} + 7(M + N){K^2} + 12K) \end{aligned} $ 0.5684
表1 不同算法的计算复杂度对比Table1. Computational complexity comparison of different methods.图 2 不同算法的计算复杂度随快拍数的变化Figure2. Comparison of computational complexity versus different snapshots number.4.仿真实验 为了验证所提算法的有效性, 下面通过不同的仿真实验来开展所提算法与文献[19 ]中的ESPRIT-Like算法、文献[20 ]中的PM-Like算法和文献[21 ]中Tensor子空间算法的性能对比. 如图1 所示, 发射阵列和接收阵列均采用稀疏EMVS阵列. 其中, 发射阵元个数$M = 10\left( {{M_1} = 3, {M_2} = 7} \right)$ , 接收阵元个数$N = 10\left( {{N_1} = 3, {N_2} = 7} \right)$ . 并且, 为了实现算法的有效对比, 利用ESPRIT-Like算法、PM-Like算法和Tensor子空间算法进行参数估计时仍然采用文献[19 -21 ]中使用的均匀半波长EMVS阵列, 并设置相同的发射阵元数和接收阵元数. 假设入射目标的个数$K = 3$ , 并且各个信号之间相互独立, 相应的发射俯仰角、发射方位角、发射极化角、发射极化相位差和接收俯仰角、接收方位角、接收极化角、接收极化相位差如表2 所示. 其中表2 中的第一个参数对应发射EMVS阵列, 第二个参数对应接收EMVS阵列. 噪声设置为相互独立的零均值加性高斯白噪声, 并且信号和噪声之间相互独立.目标 方位角θ /(°) 俯仰角? /(°) 极化角γ /(°) 极化相位差η /(°) 1 $40/24$ $15/21$ $10/42$ $38/17$ 2 $20/38$ $25/32$ $22/33$ $48/27$ 3 $30/16$ $35/55$ $45/60$ $56/39$
表2 目标回波参数表Table2. Parameters of target signals.4.1.算法的角度参数自动配对特性 4.1.算法的角度参数自动配对特性 首先, 通过星座图来验证所提算法的角度参数自动配对的有效性. 在仿真中, 快拍数L 设置为200, 信噪比设置为$10\;{\rm{dB}}$ . 利用100次蒙特卡洛仿真实验结果来绘制如图3 所示的星座图. 从图3(a) 和图3(b) 可以看出, 所提出的PARAFAC-TALS算法能够实现2D-DOD和2D-DOA的自动参数配对; 从图3(c) 到图3(f) 可以看出, 所提出的PARAFAC-TALS算法也能够实现发射阵列四维参数和接收阵列四维参数的自动角度配对. 因此, 所提算法的自动参数配对性能得到了有效的验证.图 3 所提算法角度参数和极化参数估计星座图 (a) 发射俯仰角和接收俯仰角; (b) 发射方位角和接收方位角; (c) 发射俯仰角和发射方位角; (d) 发射极化角和极化相位差; (e) 接收俯仰角和接收方位角; (f) 接收极化角和极化相位差Figure3. Scatter plot of the angle parameters and polarization parameters by using the proposed method: (a) Scatter plot of the transmit elevation angle and receive elevation angle; (b) scatter plot of the transmit azimuth angle and receive azimuth angle; (c) scatter plot of the transmit elevation angle and azimuth angle; (d) scatter plot of the transmit polarization angle and polarization phase difference; (e) scatter plot of the receive elevation angle and azimuth angle; (f) scatter plot of the receive polarization angle and polarization phase difference.4.2.信噪比对算法的影响 -->4.2.信噪比对算法的影响 下面进一步验证信噪比对算法性能的影响, 其入射信号个数和快拍数与第一个实验相同. 信噪比的变化范围为$- 10\;{\rm{dB}}$ 到$30\;{\rm{dB}}$ , 变化的步长为$5\;{\rm{dB}}$ . 在每个信噪比条件下蒙特卡洛仿真实验次数为200. 均方误差的定义为${\rm{RMSE}} = \sqrt {\dfrac{1}{{KI}}\displaystyle\sum\limits_{i = 1}^I {{{\left\| {\tilde \vartheta - \vartheta } \right\|}^2}} } $ , 其中$\tilde \vartheta $ 表示估计得到的角度或极化参数, $\vartheta $ 表示真实的角度或极化参数, I 表示蒙特卡洛仿真实验次数. 同时, 也给出了相应的检测成功概率曲线. 本文中检测成功概率的准则和文献[20 ,21 ]中给出的准则一致. 从图4(a) 可以看出, 相比于ESPRIT-Like算法、PM-Like算法和Tensor子空间算法, 所提算法具有最好的均方误差估计性能, 其中的下标d 表示角度参数, 下标p 表示极化参数. 从图4(b) 可以看出, 所提算法的角度参数检测成功概率和极化参数检测成功概率均好于其他三种算法, 且检测概率基本上接近于1.图 4 信噪比对算法的影响 (a) 均方误差随信噪比的变化; (b) 检测概率随信噪比的变化Figure4. The effect of the SNR for different methods: (a) Curves of RMSE versus SNR; (b) curves of PSD versus SNR.4.3.快拍数对算法的影响 -->4.3.快拍数对算法的影响 为了评价采样快拍数对所提算法性能的影响, 入射信号个数和信噪比与第一个仿真实验相同. 快拍数的变化范围为$100-1000$ , 变化的步长为100. 在每个信噪比条件下蒙特卡洛仿真实验次数为200. 同时检测成功概率随快拍数的变化如图5(b) 所示. 从图5 可以看出, 本文所提算法的性能随快拍数的增加表现出优良的估计精度和检测概率. 并且在快拍数比较小的情况下, 所提出的算法仍然能够得到满意的估计性能.图 5 快拍数对算法的影响 (a) 均方误差随快拍数的变化; (b) 检测概率随快拍数的变化Figure5. The effect of the snapshot for different methods: (a) Curves of RMSE versus snapshot; (b) curves of PSD versus snapshot.4.4.角度分辨率分析 -->4.4.角度分辨率分析 为了进一步验证所提算法的角度分辨率性能, 这里考虑两个相邻目标. 第一个目标的发射四维参数和接收四维参数分别为$\left( {{\theta _{{t_1}}}, {\phi _{{t_1}}}, {\gamma _{{t_1}}}, {\eta _{{t_1}}}} \right) = $ (40°, 15°, 10°, 36°)和$\left( {{\theta _{{r_1}}}, {\phi _{{r_1}}}, {\gamma _{{r_1}}}, {\eta _{{r_1}}}} \right) = $ (24°, 21°, 42°, 17°), 第二个目标的发射四维参数和接收四维参数分别为$({\theta _{{t_2}}}, {\phi _{{t_2}}}, {\gamma _{{t_2}}}, {\eta _{{t_2}}}) = ({{40}^ {\circ} } + \varDelta, {{15}^ {\circ} } + \varDelta, {{10}^ {\circ} } + $ $\varDelta, {{36}^ {\circ} } + \varDelta) $ 和$\left( {{\theta _{{r_2}}}, {\phi _{{r_2}}}, {\gamma _{{r_2}}}, {\eta _{{r_2}}}} \right) = ({{24}^ {\circ} } \!+\! \varDelta, {{21}^ {\circ} } \!+ \!\varDelta, $ ${{42}^ {\circ} } + \varDelta, {{17}^ {\circ} } + \varDelta)$ . 其中Δ的变化范围为1°—10° , 步长为1°. 快拍数为200, 信噪比为$10\;{\rm{ dB}}$ , 每次角度间隔下的蒙特卡洛仿真实验次数为200. 从图6 可以看出, 本文所提算法具有较好的角度分辨性能. 因此, 对于相邻目标也能实现精确估计.图 6 不同算法的目标分辨力比较 (a) 均方误差随角度间隔的变化; (b) 检测概率随角度间隔的变化Figure6. Comparison of target resolution ability of different methods: (a) curves of RMSE versus angular separation; (b) curves of PSD versus angular separation.5.结 论 本文的主要工作在于提出了一种新型稀疏双基地EMVS-MIMO雷达系统, 有效地解决了双基地EMVS-MIMO雷达的阵列孔径扩展问题. 同时利用平行因子-三线性分解算法解决了当前双基地EMVS-MIMO雷达所面临的2D-DOD和2D-DOA的角度参数配对问题. 本文利用稀疏发射EMVS阵列和稀疏接收EMVS阵列来构建针对于发射俯仰角和接收俯仰角的旋转不变关系, 从而实现了高精度的角度参数求解. 同时利用估计得到的发射导向矢量矩阵和接收导向矢量矩阵, 使得相应的方位角, 极化角和极化相位差可以通过归一化波印廷矢量来求解. 相比于ESPRIT-Like算法、PM-Like算法和Tensor子空间算法, 所提出的算法能够避免高维矩阵奇异值的分解以及角度参数配对过程中的高维谱峰搜索过程, 因此, 所提算法具有较低的计算复杂度. 且通过仿真实验可以发现, 本文所提算法在降低计算复杂度的同时能够实现较高的参数估计精度和角度分辨率. 在接下来的研究中, 为了进一步提升双基地EMVS-MIMO雷达的角度参数和极化参数估计性能, 将主要围绕设计灵活的稀疏发射EMVS阵列和稀疏接收EMVS阵列来展开. 













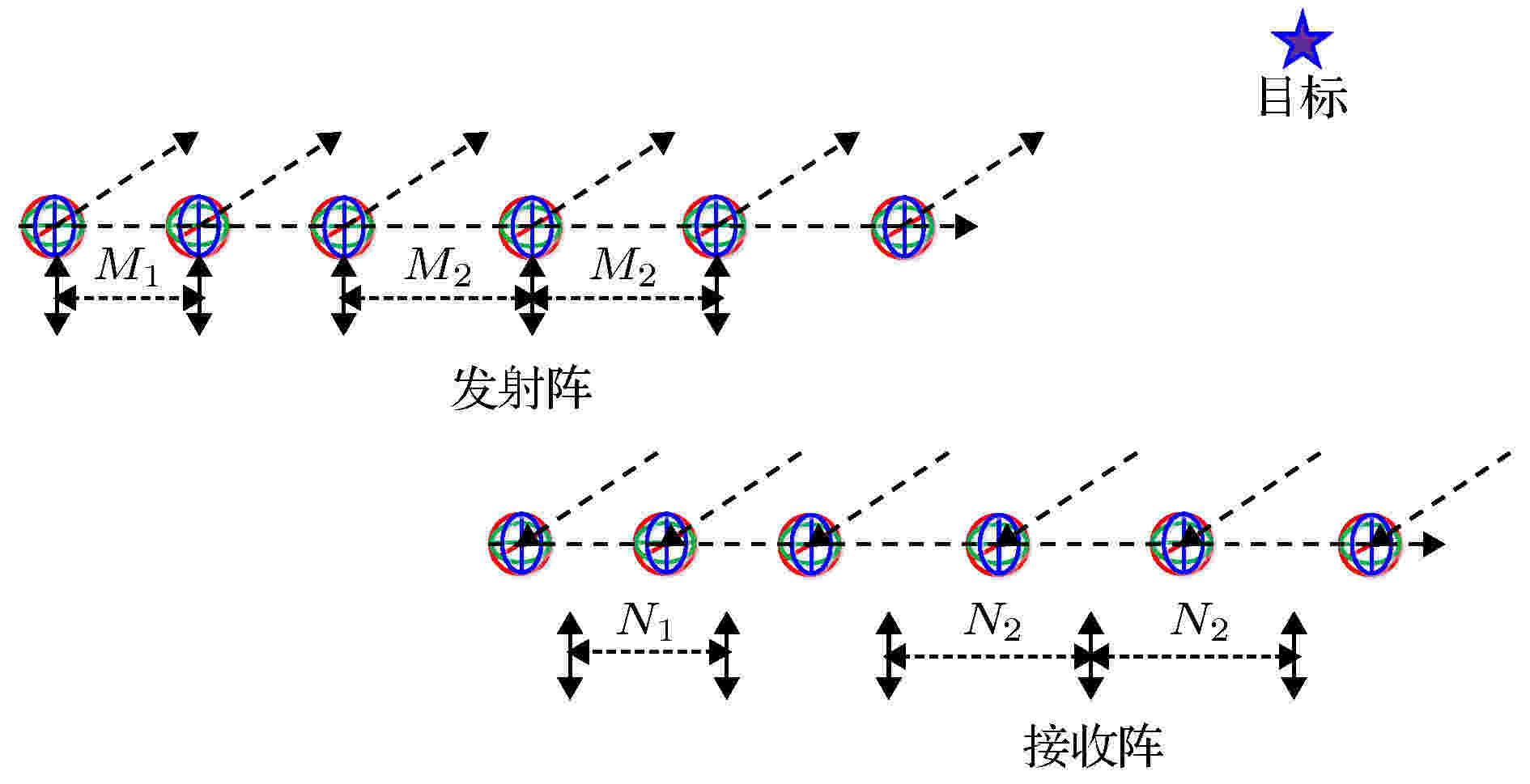 图 1 稀疏阵列EMVS-MIMO雷达系统
图 1 稀疏阵列EMVS-MIMO雷达系统

















































































































































 图 2 不同算法的计算复杂度随快拍数的变化
图 2 不同算法的计算复杂度随快拍数的变化



 图 3 所提算法角度参数和极化参数估计星座图 (a) 发射俯仰角和接收俯仰角; (b) 发射方位角和接收方位角; (c) 发射俯仰角和发射方位角; (d) 发射极化角和极化相位差; (e) 接收俯仰角和接收方位角; (f) 接收极化角和极化相位差
图 3 所提算法角度参数和极化参数估计星座图 (a) 发射俯仰角和接收俯仰角; (b) 发射方位角和接收方位角; (c) 发射俯仰角和发射方位角; (d) 发射极化角和极化相位差; (e) 接收俯仰角和接收方位角; (f) 接收极化角和极化相位差





 图 4 信噪比对算法的影响 (a) 均方误差随信噪比的变化; (b) 检测概率随信噪比的变化
图 4 信噪比对算法的影响 (a) 均方误差随信噪比的变化; (b) 检测概率随信噪比的变化
 图 5 快拍数对算法的影响 (a) 均方误差随快拍数的变化; (b) 检测概率随快拍数的变化
图 5 快拍数对算法的影响 (a) 均方误差随快拍数的变化; (b) 检测概率随快拍数的变化






 图 6 不同算法的目标分辨力比较 (a) 均方误差随角度间隔的变化; (b) 检测概率随角度间隔的变化
图 6 不同算法的目标分辨力比较 (a) 均方误差随角度间隔的变化; (b) 检测概率随角度间隔的变化