摘要: 从物理学的视角看, 群体观点演化实质可以看作是观点粒子状态变化的集体效应. 本文考察在双稳态势中噪声诱导观点粒子的状态转变, 利用加权拉盖尔完备正交函数法计算了时间关联函数和描述驱动-响应关系的弛豫时间. 理论计算结果表明, 噪声诱导作用存在一个临界值
D c , 若噪声强度高于临界值, 时间关联函数随关联时间呈指数型增加. 结果还显示, 存在弛豫时间随势垒纵横比/噪声强度变化取值趋于无穷的双奇异点现象. 奇异点处无法实现观点粒子状态的转变. 弛豫时间与势垒纵横比之间存在线性关系, 预示着在双稳态势场中观点粒子受噪声驱动呈现类似牛顿第二定律的驱动-响应关系, 而弛豫时间在这个关系中充当表征惯性质量的角色.
关键词: 观点空间 /
拉盖尔函数 /
弛豫时间 /
驱动-响应关系 English Abstract Theoretical studies on the drive-response relationship for opinion particles in a bistable potential field Wang Peng 1 ,Pan Feng-Chun 1 ,Guo Jing-Jing 1 ,Li Ting-Ting 1 ,Wang Xu-Ming 1,2 1.School of Physics and Electronic-Electrical Engineering, Ningxia University, Yinchuan 750021, China Received Date: 08 October 2019Accepted Date: 19 December 2019Published Online: 20 March 2020Abstract: From the perspective of physics, evolution of group opinion can be regarded as the collective effect of the state change of opinion particles. It is similar to a material particle system that there is usually a dynamic criticality in the opinion state transition of a group, and is dominated by a scaling law. To exhibit this phenomenon, a bistable potential field is introduced to mimic the opinion transition by the jump from one stable state to the other. In this investigation, we will focus on the state change of the opinion particles induced by the noise. The time correlation function and the relaxation time describing drive-response relationship are calculated, by using of the generalized Laguerre weight complete set of orthogonal functions method, to reveal the regularity and the relative mechanism governing the state change of the opinion particle confined by the bistable potential and affected by the noise. The results indicate that there is a critical value D c for noise intensity. When the noise intensity is greater than D c , the time correlation function will increase exponentially with correlation time τ . There also are two points at which the dependence of the relaxation time on the noise intensity/aspect ratio of the energy barrier are divergent. The divergence implies that the state transition of opinion particles cannot be achieved. It is worth noting that there is a linear relationship between the relaxation time and the aspect ratio of energy barrier. This relation means that there is a drive-response relationship for opinion particles in the bistable potential field just like the Newton’s second law, in which the time relaxation plays the role of quasi-inertia. This result also implies another important conclusion that the energy and information may be equated due to the fact that the opinion particle transiting from one stable state to the other needs obtaining energy to climb over the barrier, and from another point of view, the transition can be regarded as the opinion particle having been obtaining information via the noise correlation. These investigations may provide us with new understandings to the evolution of group opinion.Keywords: opinion space /Laguerre function /relaxation time /drive-response relationship 全文HTML --> --> --> 1.引 言 现实社会中, 一些事件会引发广泛关注和深刻讨论, 导致观点一致或分化等强烈变化[1 -3 ] . 事件发展的动力学机制是什么? 如何刻画? 目前, 基于伊辛模型的基本思想, 建立了观点动力学[4 -6 ] 、人文动力学[7 ] 、语言动力学[8 ] 、动物的集群行为[9 ] 、人类迁移动力学[10 -13 ] 等模型定量描述了人类行为规律, 探索了人类行为的特征量或属性量. 德国物理学家Helbing[14 -16 ] 引入社会力, 提出类惯性的属性量, 依据牛顿第二定律考察人类空间行走和人群应急出逃的路径选择等行为, 为将人类社会行为研究纳入经典物理学理论框架进行了有益探索. 观点演化等人类信念传播过程中, 个体的“状态”变化亦可能受普适物理学规律的支配, 类惯性等属性应当存在于驱动-响应关系中, 但如何表达应该是一个非常大的挑战.[17 -23 ] . 一些物理学家基于伊辛模型以及相关的统计理论, 发现随机涨落会诱导双稳态间的翻转[24 ,25 ] . Sznajd-Weron和Sznajd[21 ] 模拟了噪声诱导一维观点粒子的自发翻转. 同时, 观点传播被理解为舆论在对称双稳态有效势场中的运动, 揭示了观点粒子在双稳态间自发翻转的最大等待时间与系统尺寸间呈幂指数关系[25 ] . de la Lama等[26 ] 依据Sznajd模型的个体观点变化递归关系, 以概率p 实现观点转变, 则以概率$ (1-p) $ 保持观点不变, 结果表明若$ p>{p_{\rm{c}}} $ (这里${p_{\rm{c}}}$ 是个体状态转变的阈值)时, 个体观点会自发地形成双稳态, 相反则形成单稳态或无序态.2.观点转变的随机动力学模型 舆情的形成、观点传播等社会群体行为, 其实质是每个个体状态的转变. 与实物粒子系统类似, 群体状态转变通常存在一个动力学临界, 表现为一种标度规律. 为了清晰地展示这种群体状态的转变, 将观点粒子的状态转变抽象为双稳态势中的粒子从一个稳态跳跃至另一个稳态的动力学行为. 基于物理系统中对双稳态势的选取[27 ] , 取V (x ) = $ -\alpha x^2+x^4 $ , 这里x 表示观点空间, $ \alpha $ 是调整双稳态场势垒高度的参数, 双稳态对应的观点位置分别为${x_{{\rm{st}}}} = \pm \sqrt \alpha $ , 势垒高度为$ \Delta V = {\alpha ^2}/{2} $ , 如图1 所示. 势垒高度描述粒子跃迁所需的最小能量, 可以刻画观点粒子实现转变的困难程度. 为了考虑势垒宽度对状态转变的影响, 将其与势垒高度的影响归并, 从而引入势垒的高宽比即纵横比$ \gamma = {\sqrt {\alpha ^3} }/{4} $ . 从纵横比的表达形式可知, 纵横比越大($ \alpha $ 越大, 即势垒高度$ \Delta V $ 越大), 观点粒子维持状态的能力越强, 实现翻转需要注入的能量越多, 反之则相反. 对于开放的社会系统, 观点粒子状态的变化不仅受确定势场的作用, 同时还会受由社会环境施加的不确定作用, 即随机作用(突发事件、突然的关注等不确定的作用)的影响. 因此, 应由Langevin方程描述观点粒子的动力学, 则有图 1 不同势垒高度下的双稳态广义势Figure1. Bistable generalized potential with different barrier heights.$ -\nabla V(x) $ 表示观点粒子受势场的负梯度力; $ \xi(t) $ 表示由社会环境不确定因素引发的随机力, 服从高斯白噪声, 其统计特征满足:1 )转变为概率演化方程[11 -13 ,27 ] , 即Fokker-Planck方程$ {{L}} = -\dfrac{\partial }{{\partial x}}\left( {\nabla V(x)} \right) + 2 D\dfrac{{{\partial ^2}}}{{\partial {x^2}}} $ 表示空间的微分算符. 在自然边界条件下, 方程(3 )的稳态解为$ N_0 $ 是归一化常数.[28 ] , Huber和Tsimring[29 ] , Lett等[30 ] 对关联函数的定义, 考察变量$ \Delta x(\tau ) = x(\tau ) - \left\langle x \right\rangle $ 时间关联函数$ \left\langle \cdot \right\rangle $ 表示变量的统计平均. 从关联函数的定义形式可知, $ {K_{\Delta x}}(\tau ) $ 表示观点粒子从$ {t_0} = 0 $ 时刻至$ t_1 $ 时刻(且$ \tau = {t_1} - {t_0} $ ) 变化强度的统计关联, 可写成积分形式为$ P(x, \tau ;{x_0}, 0) $ 表示初始条件为$ x(0) = x_0 $ , 经历时间$ \tau $ 出现在位置$ x(\tau) $ 的概率. 由于观点粒子状态的变化是一个随机过程, 因此, 从状态$ x_0 $ 经过时间间隔$ \tau $ 转变为状态x 的概率可以通过转移概率密度$ P(x, \tau |{x_0}, 0) $ 获得, 即3 )中微分算符的时间独立性, 可以推出转移概率的广义形式为7 )和方程(8 )代入方程(6 ), 得时间关联函数$ \tau \geqslant 0 $ 的情形下, 方程(9 )关于$ x_0 $ 空间积分可得$ {{\rm{e}}^{{{L}}\tau }}\Delta x{P_{\rm st}}(x) = P(x, \tau) $ , 并对其求时间导数, 则有3 )), 即此函数是Fokker-Planck方程的一种含时解, 且初始条件满足10 ), 则时间关联函数的形式转变为$ P(x, \tau) $ 在完备正交函数空间$ \{{\text{φ} _n}(x)\} $ 展开, 即$ c_n(\tau) $ 是展开系数, $ {{\text{φ}}_n}(x) $ 表示加权广义拉盖尔多项式, 其形式为$ {{\rm L}}_{n}^{m}(x) $ 是广义拉盖尔多项式, 且满足递归关系[31 ] 对时间关联函数的标准化定义, 则有$ {K_{\Delta x}}(0) = \left\langle {{x^2}} \right\rangle - {\left\langle x \right\rangle ^2} $ .14 )代入方程(17 ), 则15 )和方程(16 )代入方程(18 ), 则$ A_n $ 分别为21 )代入方程(18 ), 可得$ {\varPhi _x}(\tau) $ , 只需要计算含时系数$ c_0(\tau) $ 和$ c_1(\tau) $ .14 )代入方程(11 ), 借助加权广义拉盖尔多项式的正交性和递归关系得附录A .23 ), 引入含时系数$ c_n(\tau) $ 的矢量形式23 )转变为三角矢量递归关系[27 ] , 其形式为$ { S}_n^{-} $ , $ { S}_n $ 和$ { S}_n^{+} $ 是系数矩阵, 且分别满足25 )做Laplace变换, 则有I ${{d}_0}(0)$ 是稳态展开系数. 根据加权广义拉盖尔展开系数的定义式$ y = \dfrac{{2 D}}{\alpha }{x^2} $ .28 )可知稳态概率的拉盖尔级数展开系数为27 ), 引入非奇异关联矩阵${{Q}_n}$ , 将${{\tilde d}_{n + 1}}(s)$ 和${{\tilde d}_n}(s)$ 关联起来27 )两边同时除以${{\tilde d}_n}(s)$ , 并将方程(31 )代入, 则32 )两边同时除以${{\tilde d}_{n + 1}}(s)$ , 可推出关联矩阵的递归关系33 )的下角标$ n-1 $ 改为n , 同时将方程(27 )代入, 即得27 )式进行连续迭代, 从而建立了关联矩阵的连分数形式$ N $ 次递归迭代, 且$ N \to \infty $ , 若连分数的极限存在, 则关联矩阵将趋于常矩阵, 方程(32 )便可转变为36 )可以看作是Q [27 ] , 即39 )代入方程(27 ), 可得26 ), (27 ), (30 )和(38 )代入方程(40 ), 计算得A , B , $ \psi $ , $ \phi $ 和$ \varTheta $ 分别为$ {\tilde c_0}(s) $ 和$ {\tilde c_1}(s) $ 分别为43 )进行Laplace逆变换, 则有$ \kappa $ 和$ \varepsilon $ 是一元二次方程($ A - Bs + {s^2} = 0 $ )的解, 即44 )和方程(45 )代入方程(22 ) 即得时间关联函数3.结果分析 通过上述理论解析, 获得了刻画双稳态观点粒子状态转变的时间关联函数和弛豫时间. 图2 展示了时间关联函数对关联长度的依赖关系, 噪声强度D 的差异将时间关联函数划分为两种不同的变化方式: 若$ D < {D_{\rm{c}}} \buildrel .\over = 0.158 $ , 时间关联函数呈单峰形式, 如图2(a) 所示, 递增意味着噪声诱导群体状态转变的有序性随着关联时间长度的增加而增加, 从而促进状态转变的有序性, 但当关联时间长度达到某阈值(时间关联函数增减转折点${\tau _{\rm{c}}} = 1.8$ )时, 噪声诱导状态转变的关联强度开始减小, 即有序性开始降低. 形成此结果主要是由于随着关联时间的增加, 观点粒子的独立性增强[12 ] , 而噪声作用却增强了观点粒子的局部关联性[13 ] , 二者形成一种竞争关系, 在关联时间长度$\tau \to {\tau _{\rm{c}}}$ 时, 噪声作用引起群体局部关联性达到最强, 诱导观点粒子相变的有序性达到最高, 因此形成了时间关联函数的单峰形式. 当$ D>{D_{\rm{c}}} $ , 时间关联函数随时间呈指数形式递增, 如图2(b) 所示. 指数随着噪声作用的增强而变大($ D = 0.20 \to 0.25 $ 对应指数从$ k_{\rm e} = 0.14$ $\to 0.32 $ ), 标志着强噪声作用强到完全压制关联函数随时间衰减的程度, 噪声诱导群体状态转变的有序性随之提高.图 2 在确定势垒高度的纵横比($\gamma =0.2$ )情形下, 时间关联函数对关联时间长度的依赖关系 (a) 若噪声强度$D < {D_{\rm{c}}}$ , 关联函数呈单峰形式, 当$D\to D_c$ , 时间关联函数至时间关联长度$\tau =2.4$ 时达到确定值$ {\varPhi _x}(\tau \geqslant 2.4) \to 1.3$ ; (b) 若噪声强度$D>{D_{\rm{c}}}$ , 时间关联函数对关联时间长度呈指数关系, $ {\varPhi _x}(\tau ) \propto {{\rm{e}}^{ - {k_{\rm{e}}}\tau }} $ Figure2. Time correlation function with different aspect ratios of energy barrier: (a) When $D<{D_{\rm{c}}}$ , the correlation function presents single peak; when $D \to {D_{\rm{c}}}$ and time correlation length $\tau=2.4$ , the time correlation function tends to 1.3; (b) when $D>{D_{\rm{c}}}$ , time correlation function increases with time correlation length exponentially, ${\varPhi _x}(\tau ) \propto {{\rm{e}}^{ - {k_{\rm{e}}}\tau }}$ .图3 展示了观点粒子状态转变的弛豫时间. 弛豫时间随势垒纵横比呈现出衰减趋势且存在两个不连续的奇异点, 如图3(a) 所示. 衰减变化表明势垒越高, 两态转变的弛豫时间越短. 这可从相反的情形得到理解, 即势垒越低, 观点粒子虽然越容易跨过势垒到达另一状态, 但越难稳定于此状态, 即弛豫时间越长. 图3(b) 刻画了弛豫时间与噪声强度间的依赖关系, 同样呈现出双奇异点现象. 弛豫时间对纵横比和噪声强度的双奇异点, 从方程(48 )的表达形式可知产生奇异的两种情形, $ 8 D-6\alpha \to 0 $ 和$ K_{\Delta x}(0)\to 0 $ . 这两种情形分别对应图3 中的第一个和第二个不连续奇异点, 前者表示噪声强度与势垒纵横比间竞争的临界关系, 后者描述了群体系统位移的均方差趋于0, 即观点粒子分布趋于空间均匀. 第一个奇异点的参数${D_{\rm{s}}} = 0.75\alpha $ 和与之对应的势垒纵横比图 3 (a) 在不同的噪声强度情形下, 弛豫时间对势垒深度纵横比的依赖关系; (b) 在不同纵横比情形下, 弛豫时间对噪声强度的依赖关系Figure3. (a) Dependence of relaxation time on aspect ratio of energy barrier under different noise intensities; (b) dependence of relaxation time on noise intensity under different aspect ratios of energy barrier.$\{ {D_{\rm{s}}}, {\gamma _{\rm{s}}}\} $ 以及第二个奇异点的条件$\{ {D_{\rm{s}}}, {\gamma _{\rm{s}}}\} $ 如图4 所示.图 4 蓝色点连成的线为$\left\{ {{{\left. {({D_{\rm{s}}}, {\gamma _{\rm{s}}})} \right|}_{{\gamma _{\rm{s}}} = \frac{2}{3}\sqrt {D_{\rm{s}}^3/3} }}} \right\}$ , 红色圈连成的线表示临界条件$\left\{ {{{\left. {({D_{\rm{s}}}, {\gamma _{\rm{s}}})} \right|}_{\langle {{x^2}} \rangle - {{\langle x \rangle }^2} = 0}}} \right\}$ Figure4. Dotted blue line shows the critical condition of $\left\{ {{{\left. {({D_{\rm{s}}}, {\gamma _{\rm{s}}})} \right|}_{{\gamma _{\rm{s}}} = \frac{2}{3}\sqrt {D_{\rm{s}}^3/3} }}} \right\}$ , red circle line presents the critical condition $\left\{ {{{\left. {({D_{\rm{s}}}, {\gamma _{\rm{s}}})} \right|}_{\langle {{x^2}} \rangle - {{\langle x \rangle }^2} = 0}}} \right\}$ .49 ))时观点粒子无法实现状态转变. 第二个奇异点是系统整体趋于无序的均匀状态, 亦无法实现观点粒子的状态翻转.图5(a) 展示了弛豫时间(过程特征)与噪声强度(驱动)间呈线性相关, 即图 5 (a) 弛豫时间与噪声强度间呈线性依赖关系; (b) 关联系数与纵横比间呈线性依赖关系$ Figure5. (a) Relaxation time depends linearly on noise intensity; (b) correlation coefficient depends linearly on aspect ratio of energy barrier.$ {1}/{C} $ 是关联系数. 图5(b) 展示了噪声强度与势垒纵横比间呈线性关系, 因此方程(51 ) 可变形为k 是C 与势垒纵横比的比例系数.52 )来描述观点粒子状态转变的驱动-响应关系. 在这个关系中D 是驱动力, $ C = k\gamma $ 代表观点粒子状态变化的难度, 一定程度上反映两个态之间的差异程度, 对应相变时的状态变化量, 度量系统对驱动的响应; T 描述观点粒子从一个态变到且稳定于另一个态的“瞬态”时长, 在这个驱动响应关系中, 具有表征惯性的“质量”的意义, 称之为“类惯性”.4.结 论 通过理论计算时间关联函数以及弛豫时间, 考察观点粒子状态转变过程的细节特征. 时间关联函数的变化规律显示: 在确定的纵横比下, 噪声诱导观点粒子状态转变存在一个临界值${D_{\rm{c}}}$ , 若$ D<{D_{\rm{c}}} $ , 噪声诱导群体状态转变的有序性先增强后减弱, 若$ D>{D_{\rm{c}}} $ , 诱导群体状态转变的时间关联函数呈指数型递增, 表明噪声作用引起群体的局部关联与时间关联长度间形成竞争. 噪声诱导作用强, 群体状态转变行为显著且有序性高. 弛豫时间与纵横比/噪声强度间的双奇异点现象揭示了: 1)当系统处于均匀的空间分布状态时, 噪声无法诱导观点粒子状态的转变; 2)噪声诱导作用与观点粒子状态转变困难程度的竞争处于平衡时, 即处于参数曲线$\left\{ {{{\left. {({D_{\rm{s}}}, {\gamma _{\rm{s}}})} \right|}_{{\gamma _{\rm{s}}} = \frac{2}{3}\sqrt {D_{\rm{s}}^3/3} }}} \right\}$ 时, 同样无法实现观点粒子状态的转变. 弛豫时间随势垒纵横比的衰减关系表明, 观点状态转变的难度越高, 群体系统对噪声的响应时间越短. 弛豫时间与噪声强度以及C 与势垒纵横比间的线性关系, 实际体现了群体系统的驱动-响应关系, 即$ D = CT $ . 其中D 是驱动强度, C 是系统的响应, T 则度量系统的类惯性大小. 这个关系可以看作是支配观点演化的“牛顿第二定律”.[32 -34 ] 一致的经典领域的结果.附录A 含时系数的计算 为了计算含时系数, 将方程(14 )代入方程(11 ), 则A1 )右边第一项记为A1 )右边第二项化简得A2 )—(A4 )以及拉盖尔函数$ \small {\rm L}_0(x) = 1 $ 代入方程(A1 ), 即A5 )进行递归关系变换, 即做如下的递归变换:$ {{\rm L}}_n^m(x) $ , 然后对x 空间的积分, 则方程(A5 )左边为A5 )右边的项分别为A7 )—(A14 )代入方程(A5 ), 化简得A15 )中的系数分别为 











 图 1 不同势垒高度下的双稳态广义势
图 1 不同势垒高度下的双稳态广义势




























































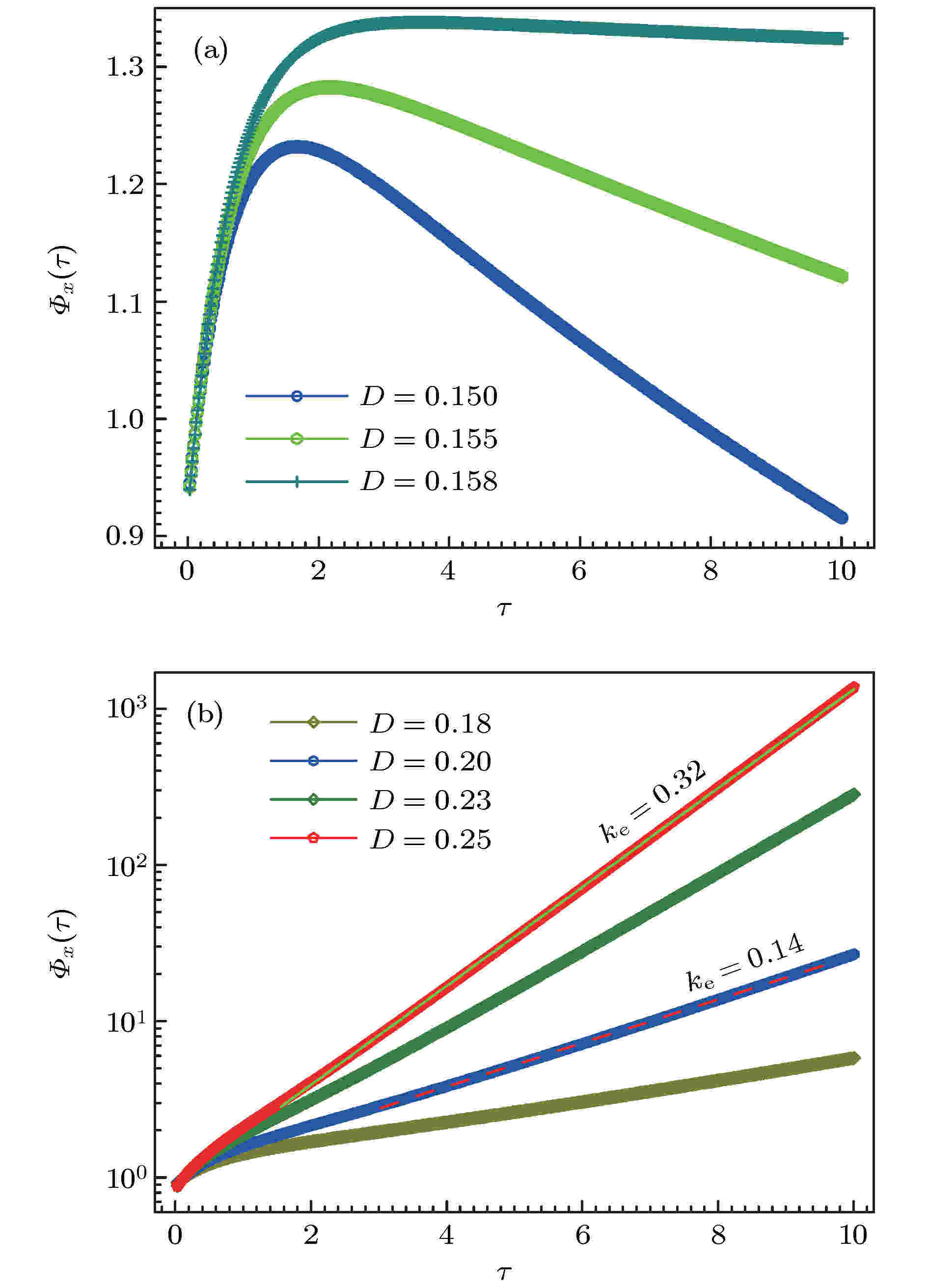 图 2 在确定势垒高度的纵横比(
图 2 在确定势垒高度的纵横比(














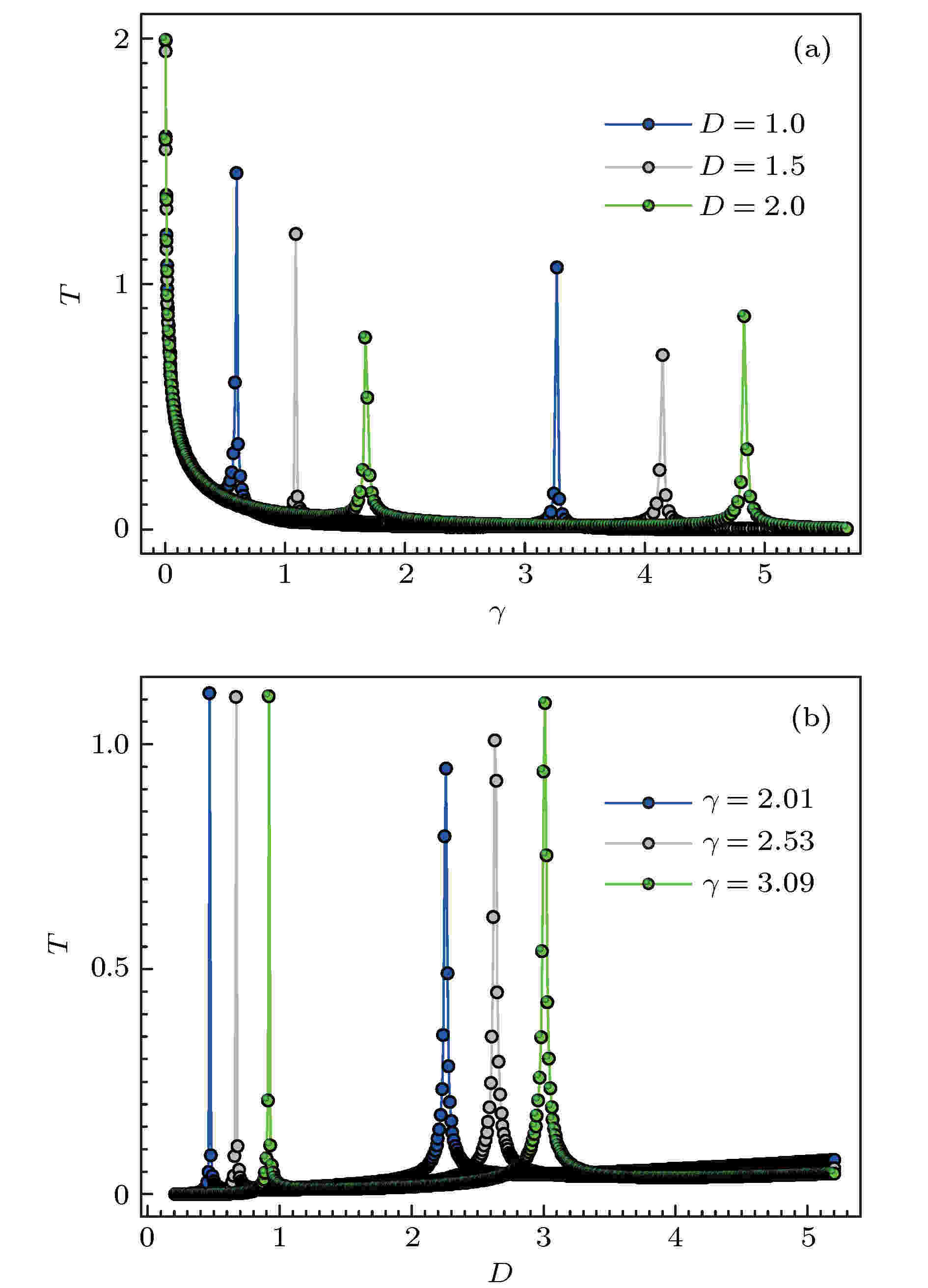 图 3 (a) 在不同的噪声强度情形下, 弛豫时间对势垒深度纵横比的依赖关系; (b) 在不同纵横比情形下, 弛豫时间对噪声强度的依赖关系
图 3 (a) 在不同的噪声强度情形下, 弛豫时间对势垒深度纵横比的依赖关系; (b) 在不同纵横比情形下, 弛豫时间对噪声强度的依赖关系

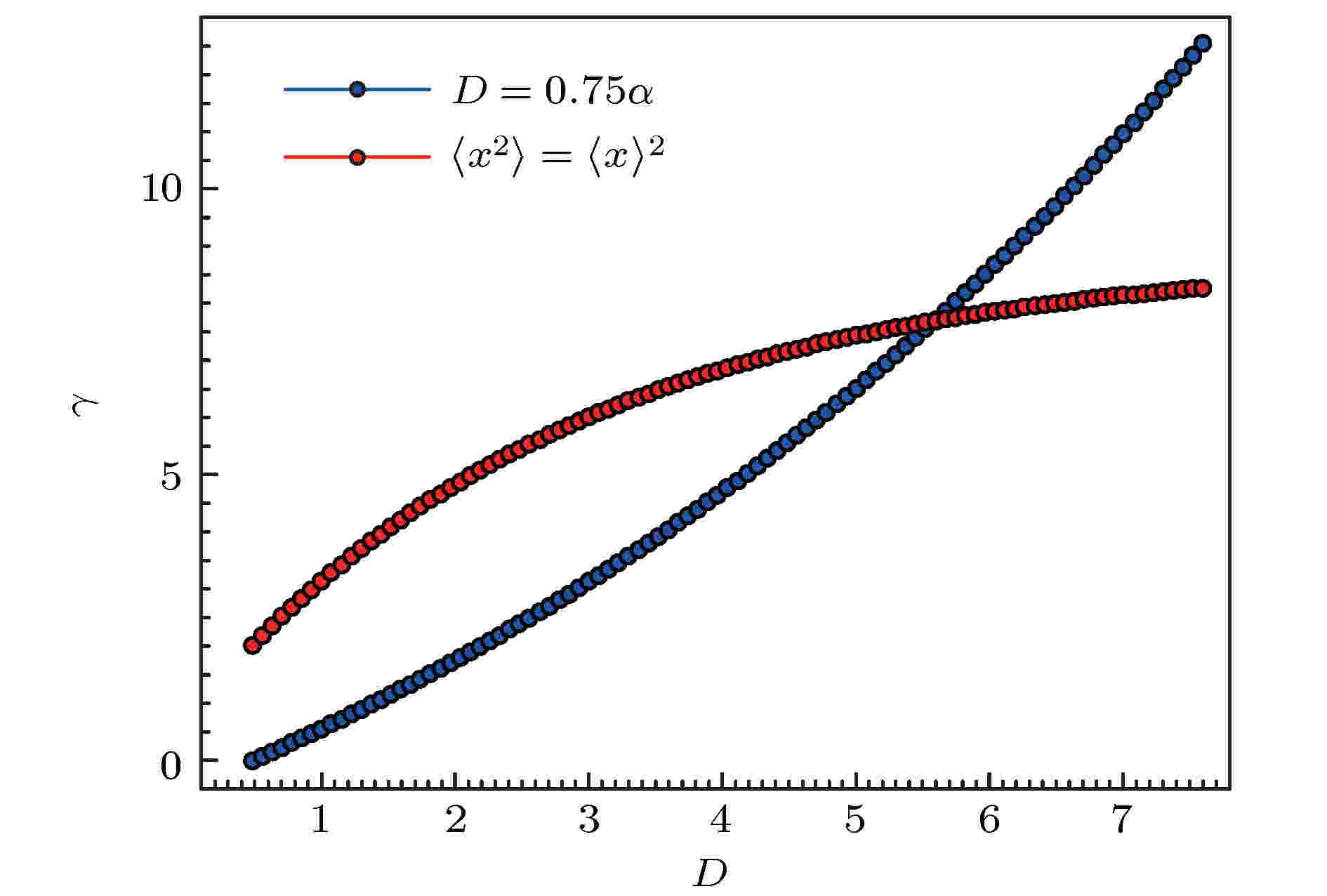 图 4 蓝色点连成的线为
图 4 蓝色点连成的线为



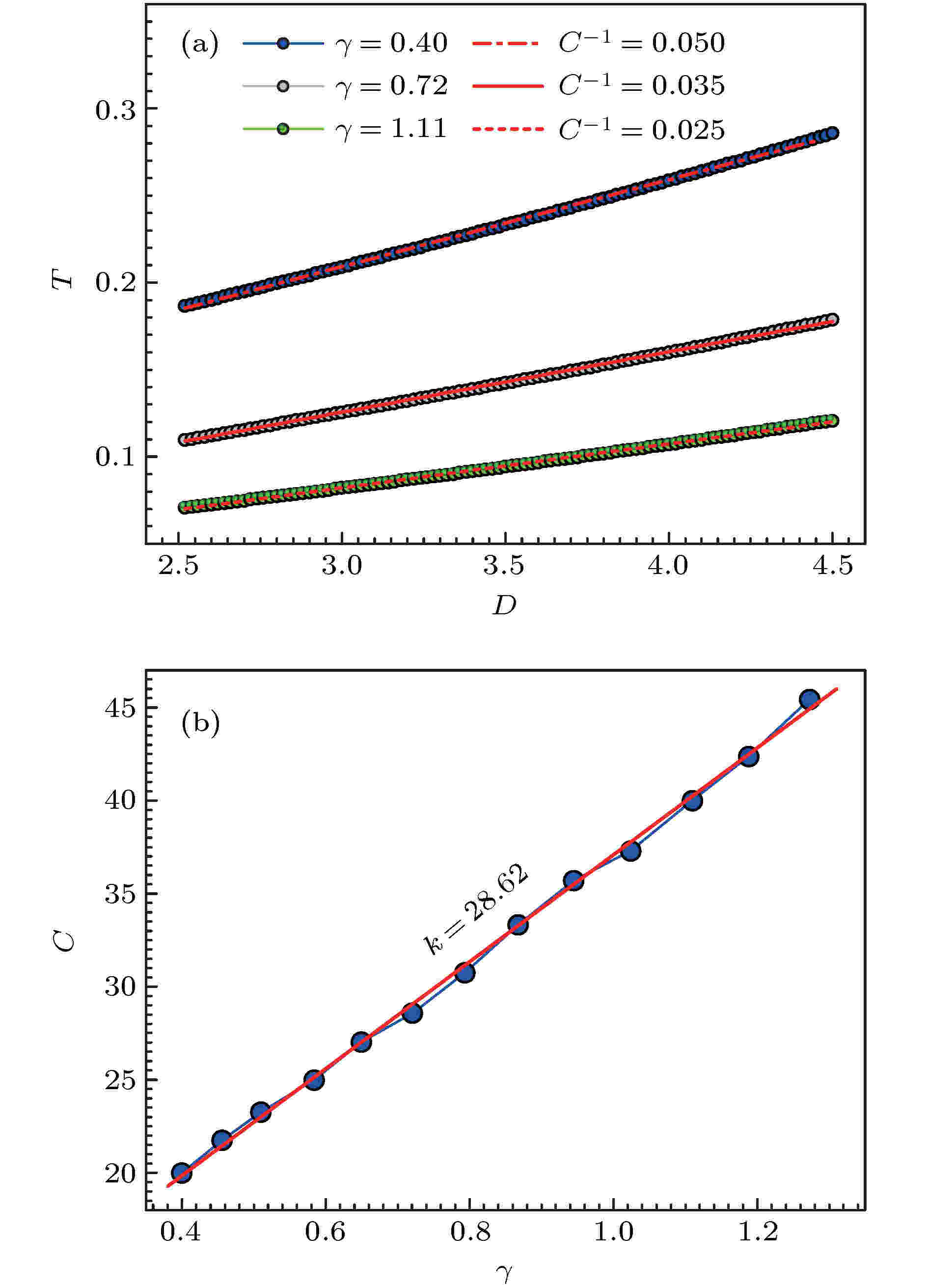 图 5 (a) 弛豫时间与噪声强度间呈线性依赖关系; (b) 关联系数与纵横比间呈线性依赖关系
图 5 (a) 弛豫时间与噪声强度间呈线性依赖关系; (b) 关联系数与纵横比间呈线性依赖关系









