摘要: 传统的载流细导体段模型是分析导体闭合回路磁场的基本模型, 尽管不满足电流连续性定律, 但适用于导体闭合回路的磁场分析. 然而, 对于工程中只关注导体闭合回路中某一局部的多分支导体段并联的电流分配问题, 传统模型将不能完整地反映各分支导体段之间磁场的相互作用. 为此, 现有文献提出的位移电流模型, 满足了电流连续性定律, 较好地解决了上述问题, 但是, 仍然存在理论不完整、不自洽以及计算公式复杂等问题. 本文提出载流细导体段的传导电流模型, 确保了载流细导体段在段内、段端及段外的电流连续性. 推导出物理内涵更加深刻的总磁场微分方程和矢量磁位计算公式. 提出载流细导体段传导电流模型磁场能量和电感的计算公式, 极大地降低了计算复杂度, 弥补了现有文献的不足. 本文算例从模型、公式、计算等方面验证了本文理论和计算公式的正确性.
关键词: 细导体段 /
电流连续性 /
磁场 /
电感 English Abstract Magnetic field and inductance of filament conductor segment model with current continuity Cui Xiang State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Beijing 102206, China Received Date: 09 August 2019Accepted Date: 30 October 2019Published Online: 05 February 2020Abstract: Traditional current-carrying model of filament conductor segment is the basic model for analyzing the magnetic field in a closed conductor loop. Although it does not satisfy the law of current continuity, it is still suitable for analyzing the magnetic field in the closed conductor loop. However, for the current distribution problem of some local multi-branch parallel-connection conductor segments in a closed conductor loop, the traditional model cannot fully reflect the interaction between magnetic fields of the local multi-branch parallel-connection conductor segments. For this reason, the displacement current model proposed in the existing literature satisfies the law of current continuity and solves the above problem well. But, there remain some problems to be solved, such as incomplete theory, inconsistency and complex formulae in the existing literature. In this paper, a conductive current-carrying model of filament conductor segment is proposed, which ensures current continuity inside, outside, and on two terminals of the filament conductor segment. The differential equation of total magnetic field with more profound physical connotation and the formulae of vector magnetic potential are derived in detail. Further, the formulae for calculating magnetic field energy and inductance of the conductive current-carrying model of filament conductor segment are proposed, which greatly reduces the computational complexity and makes up for the shortcoming of model in the existing literature. An example given in this paper verifies the correctness of the above theory and formulae.Keywords: filament conductor segment /current continuity /magnetic field /inductance 全文HTML --> --> --> 1.引 言 传统的载流细导体段模型如图1 所示, 它是分析单个或多个导体闭合回路磁场问题的基本模型[1 ] . 尽管图1 模型不满足电流连续性定律, 但将这些足够短的模型依次首尾相接, 便可组成满足电流连续性定律的导体闭合回路. 因此, 图1 模型的磁感应强度及电感的计算方法, 在导体闭合回路的研究中获得了广泛的应用. 例如, 采用图1 模型, 可以推导出不同形状的单个细导体段的自电感、不同形状及方位的两个细导体段的互电感等计算公式[2 ,3 ] , 这些计算公式已被大量地编入各类手册中[4 -6 ] , 并被广泛使用.图 1 传统的载流细导体段模型 (a) 单个载流细导体段; (b) 两个载流细导体段Figure1. Classical current models of filament conductor segments: (a) One filament conductor segment; (b) two filament conductor segments.图2(a) 所示的多分支导体段并联[7 ] 和图2(b) 所示的压接型绝缘栅双极型晶体管(insulated gate bipolar transistor, IGBT)器件内部多凸台芯片并联[8 ] 等问题. 此时, 要么因这一局部的多分支导体段在整个导体闭合回路的占比极小, 要么不知其所在导体闭合回路的全部几何参数, 如压接型IGBT器件制造商根本不知道用户的导体闭合回路情况等. 对于这类问题, 一般不再考虑导体闭合回路、而只考虑这一局部多分支导体段的磁场问题. 例如, 通过提取各分支导体段的自电感和互电感, 建立图2(c) 所示的并联支路等效电路, 以研究器件在导通或关断瞬间总电流在各个并联支路的分配规律等.图 2 多导体段并联及其等效电路 (a) 三导体段并联[7 ] ; (b) 压接型IGBT器件内部多凸台芯片并联[8 ] ; (c) 多导体段并联的等效电路Figure2. Multiconductor parallel connection and its equivalent circuit: (a) Three conductors in parallel connection[7 ] ; (b) multi-protrusion chips parallel connection in Press-Pack IGBTs[8 ] ; (c) equivalent circuit for multiconductor parallel connection.[9 ] 和Holloway等[10 ] 结合导体闭合回路的电感定义, 基于采用矢量磁位表示的磁链法, 将导体闭合回路的电感计算公式进行分段表示, 通过引入部分电感的概念, 定义了部分电感模型. 随后, 该模型在高速电子电路、微波电路、电磁兼容等领域被广泛采用, 开发了部分电感参数的高效提取方法和软件[11 ,12 ] . 部分电感的概念还被推广应用于频变情况[13 ,14 ] . 此外, 针对高速电路印制线的矩形截面导体, 美国****Holloway和Kuester[15 ] 推导出内电感的近似解, 意大利****Antonini等[16 ] 研究后指出, Wheeler规则不适用矩形截面导体的内阻抗计算.图1 模型推导的自电感和互电感计算公式, 将不能完整地反映各分支导体段之间磁场的相互作用[17 ] . 例如, 采用毕奥-萨伐尔定律推导出来的磁感应强度计算公式, 与采用安培环路定律推导出来的结果是不相同的[18 ] . 又如, 采用能量法推导出来的电感计算公式, 与采用磁链法推导出来的结果也是不相同的[19 ] . 导致它们不相同的根本原因在于图1 所示的载流细导体段模型不满足电流连续性定律.[18 ] 认为, 在载流直细导体段的两个段端上, 应该有电荷积累并在空间产生位移电流, 且位移电流应该等于载流直细导体段中的传导电流, 以确保满足电流连续性定律. 据此, Kalhor[18 ,20 ] 分别采用毕奥-萨伐尔定律与安培环路定律, 推导出来的磁感应强度计算公式是相同的, 从而解决了这个问题.[19 ,21 ] 对图1 模型进行了修改, 提出了载流细导体段的位移电流模型, 即在载流细导体段的两个段端添加了积累的等值但极性相反的点电荷, 并使其产生的位移电流等于载流细导体段中的传导电流. 在此基础上, 倪筹帷等[19 ,21 ] 推导出位移电流对应的矢量磁位计算公式, 论证了矢量磁位的主要性质, 进而推导出载流细导体段的自电感与互电感计算公式, 修正了现有文献中载流细导体段的自电感与互电感计算公式的错误. 为了进一步论证结果的正确性, 倪筹帷等[17 ] 利用法拉第电磁感应定律, 又提出了基于感应电压的载流细导体段自电感与互电感计算公式的推导方法. 从库仑规范和洛伦兹规范两个方面, 分析了产生矢量磁位计算出现差异的原因[19 ] . 倪筹帷等的工作在理论上解决了采用能量法与磁链法分别计算载流细导体段自电感与互电感的不一致问题.2.载流细导体段的传导电流模型 本文提出的载流细导体段的传导电流模型如图3 所示, 即假设在无限大空间中充满均匀导电媒质, i 为细导体段中的传导电流, l 为细导体段的曲线段, ${{{r}}^ + }$ 为细导体段中i 终止端的位置矢量, ${{{r}}^ - }$ 为起始端的位置矢量, 细导体段两端之间的距离矢量为${{d}} = {{{r}}^ + } - {{{r}}^ - }$ . 假设传导电流i 随时间变化缓慢, 其涡流效应可以忽略不计. 为了分析方便, 将图3 无限大空间分为细导体段内部空间V c 和外部空间V d . J c 为V c 中的传导电流密度, 满足电流连续性定律, 即图 3 载流细导体段的传导电流模型Figure3. Conductive current model of filament conductor segment.J d 为V d 中的电流密度, 也满足电流连续性定律, 即S c , 有e n $S_{\rm{c}}^ + $ 和$S_{\rm{c}}^ - $ 上, 分别有图3 所示细导体段内部V c 中的传导电流i , 一方面从细导体段的段端${{{r}}^ + }$ 流入细导体段外部V d , 另一方面又通过细导体段的段端${{{r}}^ - }$ 流入到细导体段内部V c . 对于细导体段外部V d 而言, 从细导体段两个段端流出和流入的电流可以被假设为两个幅值相等、流向相反的点电流源. 考虑到细导体段的直径非常小, 进一步假设点电流源的电流密度对该点是球对称均匀分布的. 由叠加定理, 细导体段外部V d 中的电流密度J d 为图3 所示的这个传导电流模型, 即在充满均匀导电媒质的无限大空间中, 放置了一根被绝缘材料包覆的细导体段, 在细导体段内部有一个电流为i 的理想电流源, 并通过细导体段的两端向无限大空间供电. 因此, 相对于现有文献的位移电流模型而言[19 ,21 ] , 这个传导电流模型的物理图像更加清晰, 容易被物理实现, 且适用于直流情况.3.磁感应强度 23.1.J c 产生的磁感应强度 3.1.J c 产生的磁感应强度 由毕奥-萨伐尔定律, 细导体段内部V c 中电流密度J c 在场点r B c 为μ 为磁导率; ${{{e}}_R}$ 为矢量${{r}} - {{r}}'$ 的单位矢量, 且$R = |{{r}} - {{r}}'|$ . 对于图3 的载流细导体段, (6a )式为3.2.J d 产生的磁感应强度 -->3.2.J d 产生的磁感应强度 亦由毕奥-萨伐尔定律, 细导体段外部V d 中电流密度J d 在场点r B d 为5 )式代入上式, 得${{{B}}_{\rm{d}}}$ , 做如下分解:${{{B}}_{{\rm{d}} + }}({{r}})$ . 为计算方便, 不妨令${{{r}}^ + } = 0$ , 即让球坐标系的原点落在图3 所示载流细导体段电流的流出端点上, 此时, (9a )式变为${{r}}'$ 和r ${{r}}' \times {{r}}$ 运算后的矢量只有${{{e}}_{\phi} }$ 和${{{e}}_{\theta} }$ 分量. 又由于上式积分的球对称性, 在积分过程中${{{e}}_{\phi} }$ 和${{{e}}_{\theta} }$ 分量将被抵消. 所以, 可以推断, ${{{B}}_{{\rm{d}} + }}({{r}}) = 0$ . 可见, 尽管点电流源在无限大空间中形成传导电流, 但不产生磁场.${{{B}}_{{\rm{d}} - }}({{r}}) = 0$ . 所以, 由(8 )式得10 )式表明, 细导体段外部V d 中的传导电流不产生磁场.3.3.总磁感应强度 -->3.3.总磁感应强度 利用叠加定理, 细导体段内部电流密度J c 和外部电流密度J d 在空间中产生的总磁感应强度B 6a )式代入(11 )式, 得3.4.B 的散度与旋度 -->3.4.B 的散度与旋度 利用矢量恒等式12 )式可以被转换为$\nabla \times (\varphi {{D}}) = (\nabla \varphi ) \times {{D}} + \varphi \nabla \times$ D ${{{J}}_{\rm{c}}}({{r}}')$ 只是源点${{r}}'$ 的函数, 与场点r r $\nabla $ ”可以移到积分号外面. 因此, 上式变为$\nabla \cdot (\nabla \times {{D}}) = 0$ , 对(14 )式求散度, 得14 )式求旋度, 得$\nabla \times \nabla \times {{D}} = \nabla (\nabla \cdot {{D}}) - {\nabla ^2}{{D}}$ , 上式被转化为16 )式等号右边两项积分中的被积分项.$\nabla \cdot (\varphi {{D}}) = (\nabla \varphi ) \cdot {{D}} +$ $ \varphi \nabla \cdot {{D}} $ , (16 )式等号右边的第一项中的被积分项可以写为13 )式和矢量恒等式$\nabla \cdot (\varphi {{D}}) = (\nabla \varphi ) \cdot $ $ {{D}} + \varphi \nabla \cdot {{D}}$ , 上式可以被写为16 )式等号右边的第二项中的被积分项, 容易证明17 )和(18 )式代入(16 )式, 并利用散度定理, 得${S_{\rm{c}}}+S_{\rm{c}}^++S_{\rm{c}}^ - $ 为细导体段${V_{\rm{c}}}$ 的闭合曲面. 将(1a ), (2 ), (3a )和(3b )式代入上式, 得${{B}}({{r}}) = \mu {{H}}({{r}})$ 和(5 )式, 上式也可以写为H 15 )式正是磁通连续性定律的微分形式, (19 )式正是安培环路定律的微分形式. (19 )式表明, 总磁场强度的旋度源由两部分构成, 第一部分是细导体段内部V c 中的电流密度${{{J}}_{\rm{c}}}$ , 第二部分是为了满足电流连续性定律而从细导体段两个段端流出与流入的细导体段外部V d 的电流密度${{{J}}_{\rm{d}}}$ .${{{J}}_{\rm{d}}}$ 作为总磁场强度的旋度源之一已经体现在(19 )式中了, 但正如(10 )和(11 )式指出的, 它并不产生磁场, 总磁场仅由细导体段内部V c 中电流密度J c 产生, 并可以直接采用毕奥-萨伐尔定律, 通过(12 )式进行计算. 这与美国****Kalhor[18 ,20 ] 采用位移电流假设获得的结果是类似的. 但是, Kalhor的工作是对载流直细导体段通过直接积分获得的结果, 没有如本文上述工作, 通过散度和旋度分析, 获得了有更加深刻物理内涵的微分方程.${{{J}}_{\rm{d}}}$ 不产生磁场, 但它仍将产生矢量磁位. 这一点在后面的磁场能量和电感的计算中是非常必要的.4.矢量磁位 24.1.矢量磁位及其散度 4.1.矢量磁位及其散度 由(15 )式, 引入矢量磁位A ${{B}}({{r}}) = \nabla \times $ ${{A}}({{r}}) $ , 对A 19 )式用矢量磁位A $\nabla \times \nabla \times {{D}} = \nabla (\nabla \cdot {{D}}) - {\nabla ^2}{{D}}$ 和(20 )式, 上式变为A c 和A d 分别为电流密度J c 和J d 产生的矢量磁位. 将(21 )式中的矢量磁位A 23a )式中${{{A}}_{\rm{c}}}$ 的积分解为23b )式中${{{A}}_{\rm{d}}}$ 的积分解, 首先求(24 )式的散度, 即17 )式代入上式, 并由(1a )式以及散度定理, 得20 )和(22 )式得${{{A}}_{\rm{d}}}$ 做如下分解:${{{A}}_{{\rm{d}} + }}({{r}})\! $ , 以${{{r}}^ + }\! $ 为球心做半径为$a \! = \! |{{r}}\! -\! {{{r}}^ + }|$ 的球体. 显然, ${{{A}}_{{\rm{d}} + }}({{r}})$ 在以${{{r}}^ + }$ 为球心的球体上具有球对称性, 且${{{A}}_{{\rm{d}} + }}({{r}})$ 是${{{e}}_{{{r}} - {{{r}}^ + }}}$ 方向的矢量. 在该球体内对(28a )式进行体积分, 得29 )式等号左边的体积分可以被转化为29 )式比较, 得28b )式的解为30a )和(30b )式代入(27 )式, 得22 )以及(24 )和(31 )式, 得矢量磁位A 图3 的载流细导体段, (32a )式为4.2.矢量磁位的旋度 -->4.2.矢量磁位的旋度 首先, 求${{{B}}_{\rm{c}}}({{r}}) = \nabla \times {{{A}}_{\rm{c}}}({{r}})$ , 对(24 )式两边取旋度得到33 )式正是(6a )式给出的毕奥-萨伐尔定律.${{{B}}_{\rm{d}}}({{r}}) = \nabla \times {{{A}}_{\rm{d}}}({{r}})$ , 对(31 )式两边取旋度, 得34 )式等号右边括号内的第一项为$\nabla \times {{r}} = 0$ , 上式变为35a )和(35b )式代入(34 )式, 得36 )式再次验证了(10 )式, 即细导体段外部V d 中的传导电流只产生(31 )式中的矢量磁位${{{A}}_{\rm{d}}}$ , 而不产生磁场.4.3.无限远渐近式 -->4.3.无限远渐近式 为了后面讨论需要, 现推导当$r \to \infty $ 时矢量磁位及其散度和旋度的渐近式. 设细导体段两个端点之间的距离为d ($d \ll r$ ), 且距离的中点是直角坐标系或球坐标系的原点, 两个端点均在直角坐标系的z 轴上. 因此, 有θ 为球坐标的纬度坐标. 由(24 )和(33 )式, 当$r \to \infty $ 时, 有37 )和(38 )式分别代入(31 )和(26 )式, 当$r \to \infty $ 时, 有7 , 19 ]中因错误地认为$\nabla \cdot {{{A}}_{\rm{c}}}({{r}}) = {\rm{0}}$ , 故导致了规范不自洽问题, 且矢量磁位的数学推导非常繁复. 而本文(20 )和(25 )式与(26 )式是自洽的, (31 )式中${{{A}}_{\rm{d}}}({{r}})$ 的推导非常简单.5.磁场能量与电感 25.1.磁场能量 5.1.磁场能量 磁场能量既可以采用能量法也可以采用磁链法进行计算. 特别是对于无限大空间的磁场问题, 磁链法由于只需要对载流导体区域进行体积分, 因此计算量远低于能量法. 然而, 对于本文提出的载流细导体段的传导电流模型而言, 电流充满了整个无限大空间, 那么磁链法还有这种优势吗?现讨论如下.图3 所示载流细导体段的磁场能量, 即43 )式的能量法, 推导磁链法.${{B}}({{r}}) \!=\! \mu {{H}}({{r}})$ 和${{B}} \!=\! \nabla \!\times\! {{A}} \!=\! \nabla \!\times\! {{{A}}_{\rm{c}}}$ , (43 )式被写为$\nabla \cdot ({{C}} \times {{D}}) = (\nabla \times {{C}}) \cdot {{D}} - {{C}} \cdot $ $(\nabla \times {{D}}) $ 和$\nabla \times \nabla \times {{D}} = \nabla (\nabla \cdot {{D}}) - {\nabla ^2}{{D}}$ , (44 )式中的被积分项可以写为26 )和(23a )式以及矢量恒等式$\nabla\!\cdot\! (\varphi {{D}}) \!= $ $ (\nabla \varphi ) \cdot {{D}}\! + \!\varphi \nabla \cdot {{D}}$ 和$\nabla \!\times \!\nabla \times {{D}}\! =\! \nabla (\nabla \cdot {{D}})\! -\! {\nabla ^2}{{D}}$ , 上式可以被转化为$\nabla \cdot ({{C}} \times {{D}}) = (\nabla \times {{C}}) \cdot $ ${{D}} - {{C}} \cdot (\nabla \times {{D}})$ , 且由(36 )式, 上式被写为44 )式, 并利用散度定理, 得39 )—(42 )式知, 当$r \to \infty $ 时, 上式等号右边的第二项面积分中的被积分项反比于${r^3}$ , 而${S_{\infty} }$ 正比于${r^2}$ , 因此该项面积分为零. 因此, 上式变为45 )式就是本文提出的计算磁场能量的磁链法. 与现有文献的磁链法被积分项仅含矢量磁位${{{A}}_{\rm{c}}}$ 不同的是, 在本文(45 )式中的被积分项中, 还含有矢量磁位${{{A}}_{\rm{d}}}$ . 正是因为现有文献的磁链法中没有这一项, 从而导致了现有文献中细导体段的电感计算公式是不完整的.45 )式计算磁场能量时, 只需要对细导体段进行体积分, 不需要像(43 )式中的能量法那样, 需要对无限大空间进行体积分. 显然, (45 )式极大地简化了细导体段的磁场能量以及电感的计算复杂度.5.2.细导体段的电感 -->5.2.细导体段的电感 设图4 所示的无限大空间中有两根载流细导体段, 其中${l_1}$ 和${l_2}$ 分别表示沿两根细导体段的表面路径, ${l'_1}$ 和${l'_2}$ 分别表示沿两根细导体段的中心路径. 下面讨论电感计算问题, 包括自电感与互电感. 对于载流细导体而言, 有${{{J}}_{\rm{c}}}({{r}}'){\rm{d}}V' = i{\rm{d}}{{l}}'$ , 由(45 )式的磁链法, 并利用(32b )式, 得磁场能量为图 4 两根细导体段Figure4. Two filament conductor segments.46 )式, 先讨论(46 )式等号右边第三项和第六项的线积分, 即${{{A}}_{m{\rm{d}} + }}$ 和${{{A}}_{m{\rm{d}} - }}$ 分别为第m 根细导体段流出端和流入端对应的点电流源产生的矢量磁位.47 )式中${{{A}}_{m{\rm{d}} + }}$ 对应的线积分, 由(30a )式有${\rm{d}}{{{l}}_k} = {\rm{d}}{{{r}}_k}$ , 因此(48 )式中的线积分为${{a}} \cdot {\rm{d}}{{a}} = 0.5{\rm{d(}}{a^2}) = a{\rm{d}}a$ , 上式可以写为48 )式, 得47 )式中${{{A}}_{m{\rm{d}} - }}$ 对应的线积分为49a )和(49b )式代入(47 )式, 得图5 所示, 设第1根和第2根细导体段的截面半径分别为${a_1}$ 和${a_2}$ , 各自流出端与流入端之间的距离分别为${d_1}$ 和${d_2}$ ; 第1根和第2根细导体段流出端与流入端之间的距离分别为$d_{12}^{ + + }$ , $d_{12}^{ - - }$ , $d_{12}^{ + - }$ , $d_{12}^{ - + }$ .图 5 两根细导体段不同端点之间的距离Figure5. Distances between different terminals of two filament conductor segments.50 )式中, ${{r}}_1^ + $ , ${{r}}_1^ - $ , ${{r}}_2^ + $ 和${{r}}_2^ - $ 分别表示细导体段l 1 和l 2 的段端中心的位置矢量, ${{r}}_1^{\prime+} $ , ${{r}}_1^ {\prime- }$ , ${{r}}_2^ {\prime+ }$ 和${{r}}_2^ {\prime- }$ 分别表示细导体段l 1 和l 2 的段端边缘的位置矢量. 由图5 , 有50 )式代入(46 )式, 并由(51 )式, 得磁场能量为52 )式又可以写为53 )式与(52 )式进行对比, 得两根细导体段的自电感与互电感分别为图5 知, $d_{12}^{ + + } = d_{21}^{ + + }$ , $d_{12}^{ - - } = d_{21}^{ - - }$ , $d_{12}^{ + - } = d_{21}^{ - + }$ 和$d_{12}^{ - + } = d_{21}^{ + - }$ , 所以, 从(54b )和(54c )式可以看出, 两根细导体段的互电感是对称的, 即54 )式和(55 )式推广到无限大空间中具有n 根细导体段的传导电流模型, 可以得出, 第k 根细导体段的自电感为k 根细导体段与第m 根细导体段的互电感为${L_{km}} = {L_{mk}}$ .[3 -6 ] , 可以发现本文的电感计算公式(56a )和(56b )中, 分别多出了等号右边带方框的第二项, 即[19 ,21 ] 提出的电感计算公式相比, 在本文(56 )式的自电感与互电感计算公式中, 等号右边的第二项已不再是线积分, 而是由细导体段的端点几何参数表示的解析表达式, 且极为简单. 同时, 本文(56b )式也自然地揭示了互电感的对称性.6.算 例 为了说明本文提出的模型及电感计算公式的正确性, 下面引用文献[19 ]的一个算例.图6 为空气中两根半径相同、长度相同的圆柱形平行细导体段. 细导体段半径为r , 长度为l , 轴心距离为d , 且$ d \!= \! 10r $ . 由(56a )和(56b )式, 得细导体段的自电感(含内电感)和互电感分别为图 6 两根半径相同的圆柱截面的平行细导体段[19 ] Figure6. Two parallel filament conductor segments with same length and radius[19 ] .图7(a) 和图7(b) 分别给出了图6 所示细导体段的单位长度自电感和单位长度互电感随长度与半径之比(l /r )的变化曲线. 图中蓝色实线显示的L kk -CL km -CL kk -BL km -B43 )式的能量法进行电感计算的, 即先利用毕奥-萨伐尔定律计算无限大空间的磁场, 再进行(43 )式中的无限大空间积分, 最后再计算电感; 绿色带点实线显示的Lkk 和Lkm 是按本文(57a )和(57b )式进行计算的. 从图7 可以看出, 对于细导体段而言, 无论是单位长度自电感还是单位长度互电感, 采用本文提出的电感计算公式获得的结果与能量法的计算结果是一致的, 而现有文献的计算结果因缺少(57a )和(57b )式等号右边的两个方框项而存在很大的误差.图 7 两根平行细导体段自电感与互电感[19 ] (a) 单位长度自电感; (b) 单位长度互电感Figure7. Inductances of two parallel filament conductor segments[19 ] : (a) Unit-length self-inductance; (b) unit-length mutual-inductance.7.结 论 本文系统地研究了细导体段的电流连续性问题, 对磁感应强度、矢量磁位及其规范、磁场能量与电感等进行了深入的理论研究. 本文提出的载流细导体段的传导电流模型及其磁场理论, 体系完整, 电感计算公式简单, 解决了现有文献存在的理论与计算等方面的不足, 主要结论如下.V d 中的传导电流密度J d 认为是位移电流密度, 只要保证细导体段两个段端上的电流连续性即可.  图 1 传统的载流细导体段模型 (a) 单个载流细导体段; (b) 两个载流细导体段
图 1 传统的载流细导体段模型 (a) 单个载流细导体段; (b) 两个载流细导体段 图 2 多导体段并联及其等效电路 (a) 三导体段并联[7]; (b) 压接型IGBT器件内部多凸台芯片并联[8]; (c) 多导体段并联的等效电路
图 2 多导体段并联及其等效电路 (a) 三导体段并联[7]; (b) 压接型IGBT器件内部多凸台芯片并联[8]; (c) 多导体段并联的等效电路


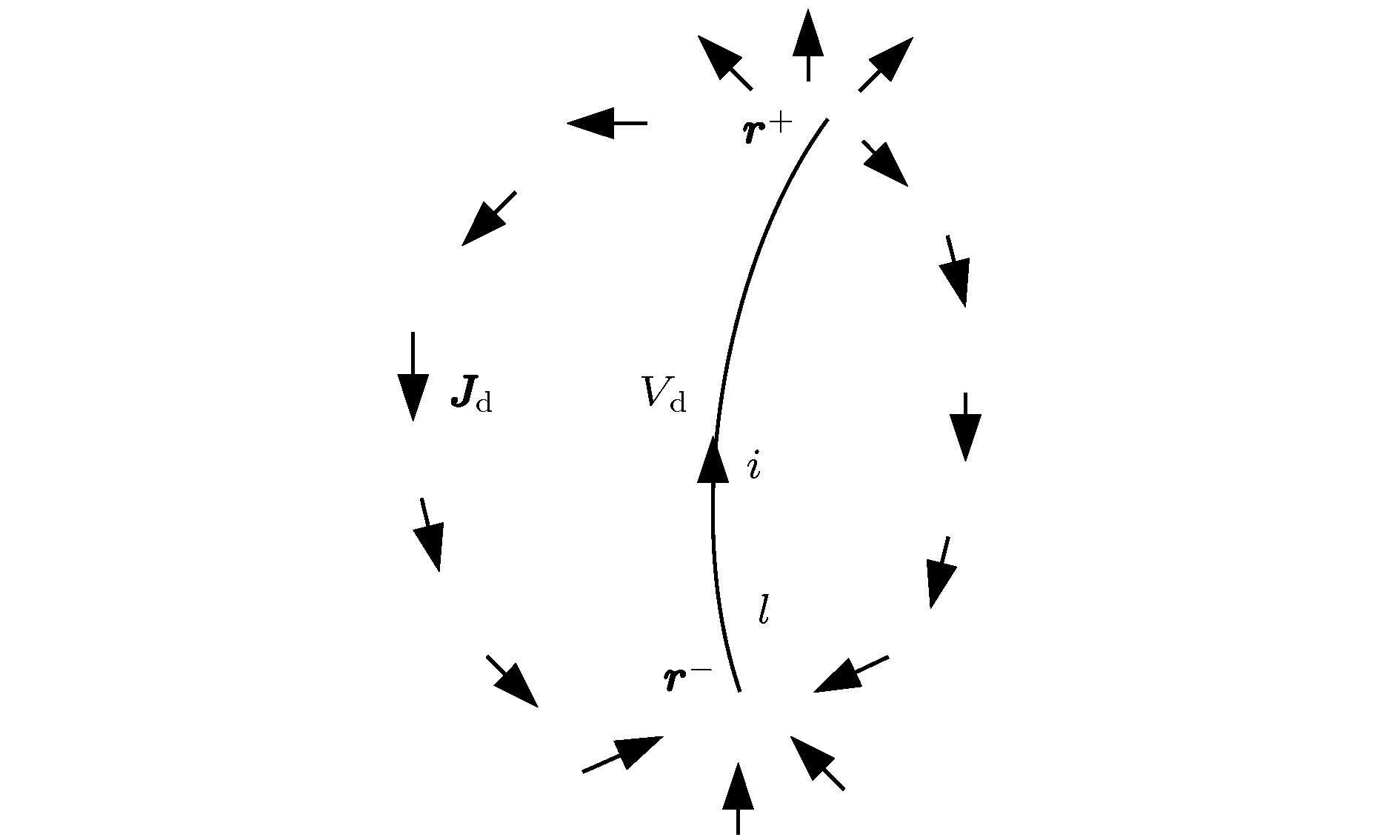 图 3 载流细导体段的传导电流模型
图 3 载流细导体段的传导电流模型




















































































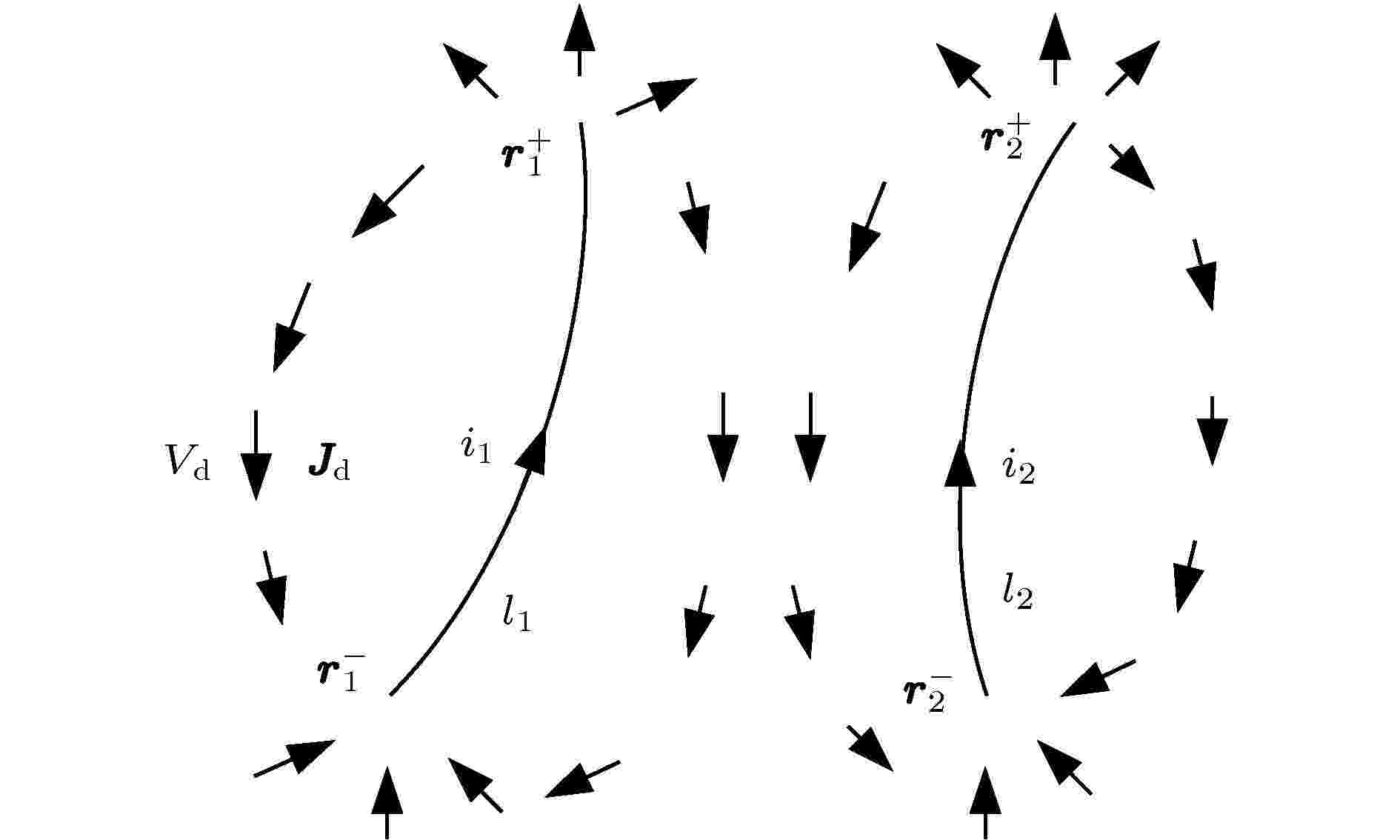 图 4 两根细导体段
图 4 两根细导体段













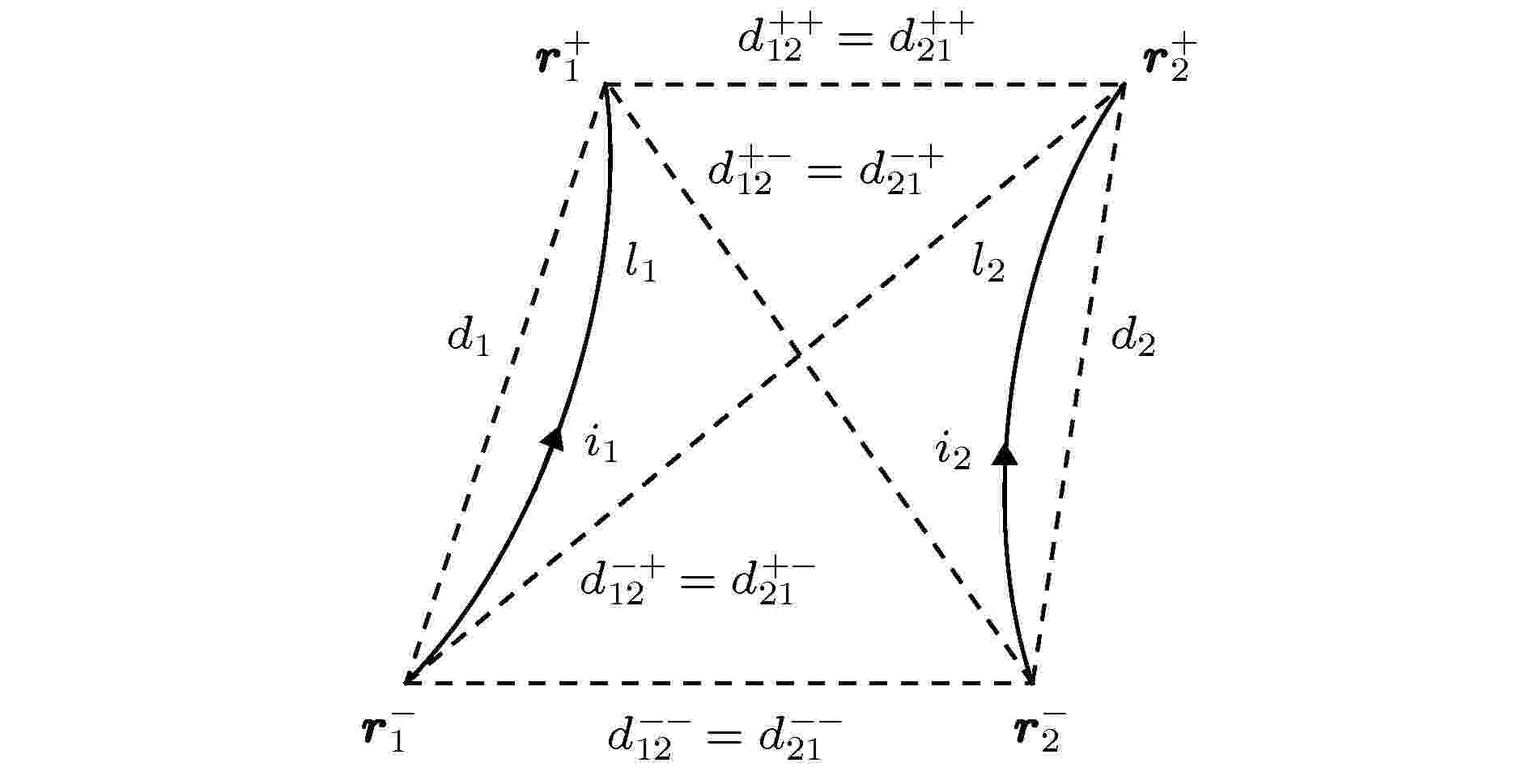 图 5 两根细导体段不同端点之间的距离
图 5 两根细导体段不同端点之间的距离













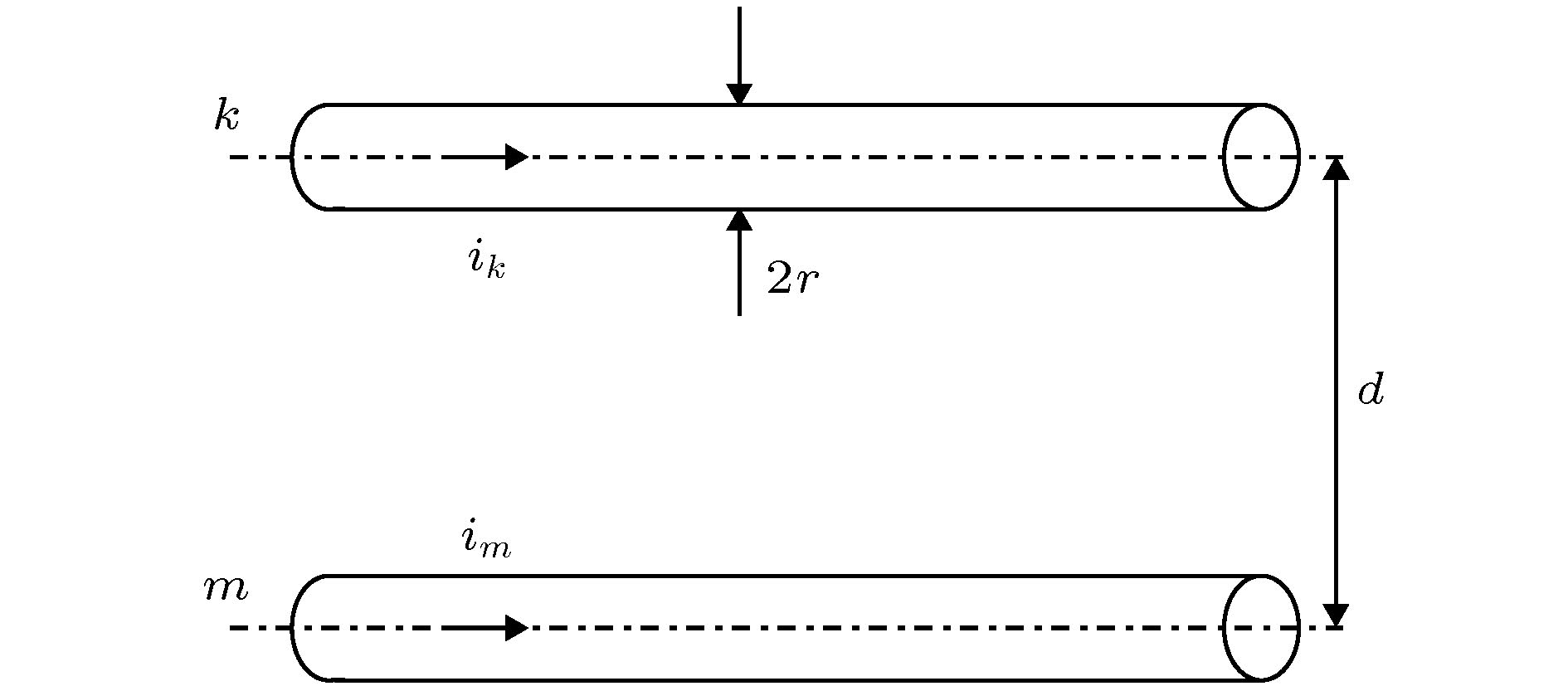 图 6 两根半径相同的圆柱截面的平行细导体段[19]
图 6 两根半径相同的圆柱截面的平行细导体段[19]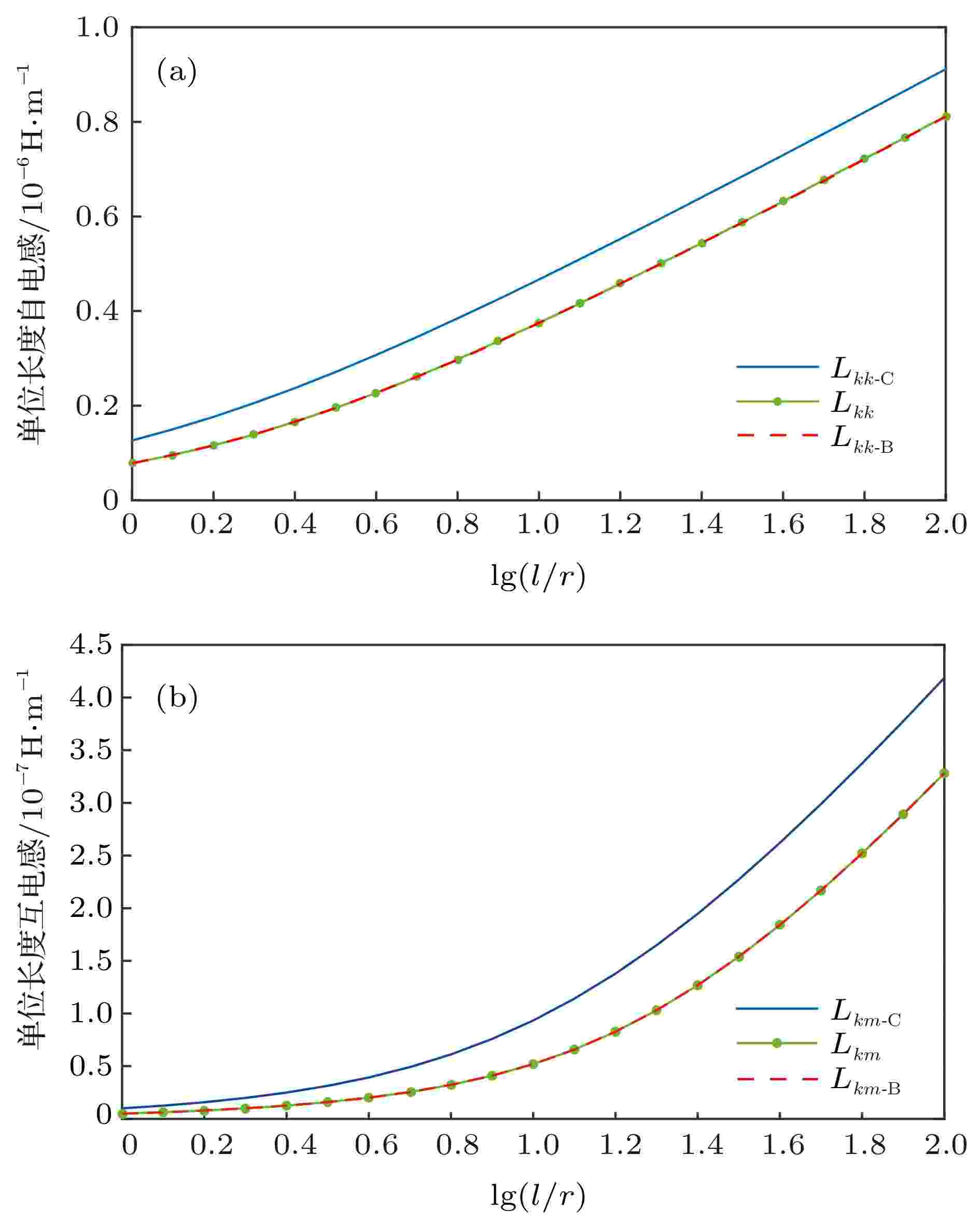 图 7 两根平行细导体段自电感与互电感[19] (a) 单位长度自电感; (b) 单位长度互电感
图 7 两根平行细导体段自电感与互电感[19] (a) 单位长度自电感; (b) 单位长度互电感