摘要:提出了一种锥形靶层裂实验新方法, 开展非一维应变冲击条件下高纯铜初始层裂行为实验研究, 讨论了锥形靶内部损伤分布特征及其与自由面速度典型特征之间的内禀关系. 结果显示: 1)初始层裂的锥形靶内部出现了连续损伤区, 损伤区扩展方向与锥面平行, 从锥底到锥顶呈现了不同的损伤状态, 从微孔洞独立长大到局部聚集, 最后形成宏观裂纹, 这种损伤状态分布特征归因于锥形靶内部拉伸应力幅值和持续时间的空间演化; 2)通过锥形靶横截面损伤度定量统计分析, 揭示损伤演化早期的微孔洞成核与早期长大过程是随机的, 而损伤演化后期的微孔洞聚集过程具有显著的局域化特征; 3)不同位置处实测的自由面法向粒子速度剖面呈现出典型的层裂Pull-back信号, 但是通过与内部损伤分布特征对比, 揭示基于Pull-back速度获得高纯铜层裂强度本质是微孔洞成核阈值应力, Pull-back回跳速度斜率反映了损伤演化速率, Pull-back回跳幅值与损伤度引起的应力松弛密切相关.
关键词: 锥形靶/
初始层裂/
损伤演化/
自由面速度

English Abstract

全文HTML

--> --> -->

在稀疏波相互作用引起的动态拉伸载荷下, 延性金属可能以层裂的形式失效, 涉及到微孔洞成核、长大和聚集的复杂过程^[1-3]. 有关延性金属层裂研究主要采用一维应变平面靶层裂实验技术, 重点关注加载应变率^[4-6]、加载应力幅值^[7-9]及材料微观结构^[10-12]等因素对损伤演化和层裂特性的影响. 同时, 基于一维应变平面靶层裂实验结果, 研究人员建立了许多的损伤演化物理模型和层裂准则^[13-16], 再通过计算结果与实验结果的对比来验证模型适用性. 事实上, 这些模型在描述和预测非一维应变冲击下材料损伤演化与层裂行为问题的适用性还有待进一步考证.
在实际工程中, 延性金属层裂破坏往往是在非一维应变冲击条件下产生的, 例如碎甲弹, 它是通过塑性炸药在装甲板外侧面上爆炸, 爆炸冲击波传到装甲板内侧反射成稀疏波, 该稀疏波与冲击波波阵面后的稀疏波在装甲板内相遇, 从而产生拉伸应力, 在该拉伸应力作用下装甲板发生层裂, 崩落的层裂碎片可以杀伤车内人员和毁伤设备. 非一维应变冲击下延性金属层裂实验技术难度相对较大, 实验数据测量和分析也比较复杂, 文献报道有限. 少量研究工作关注了炸药爆轰载荷下延性金属的层裂特性^[17,18]. 与一维应变平板撞击加载相比, 炸药爆轰可产生复杂的冲击波加载条件, 特别是滑移爆轰波加载, 但载荷参数难以精确控制和调整; 另外, 炸药爆轰产生的加载脉冲峰值应力较高, 往往使得试样发生完全层裂破坏, 不利于对试样进行软回收, 研究试样初始层裂时内禀损伤演化和微介观机理.
本文提出了一种锥形靶层裂实验新方法, 用于研究非一维应变冲击加载下延性金属的损伤演化和层裂特性. 通过轴对称二维波系图定性分析了锥形靶层裂实验中波系复杂的相互作用及层裂基本原理. 基于一级轻气炮加载系统, 开展铝合金平板飞片撞击高纯铜锥形靶层裂实验. 通过控制飞片的撞击速度, 在高纯铜锥形靶内产生了初始层裂状态. 实验中, 采用多通道激光位移干涉诊断技术测量了锥形靶表面不同位置点的自由表面法向速度剖面, 讨论了自由面速度剖面典型特性与内部损伤演化之间的内禀关系. 基于高纯铜锥形靶内损伤分布的显微观测, 获得了损伤演化的时空分布特征及定量统计信息, 为构建损伤演化物理模型以及物理模型验证提供了丰富的实验数据.

2

-->

2.1.基本原理

为了阐述锥形靶层裂实验的基本原理, 这里采用x-y-t二维轴对称波系图来分析锥形靶中波系传播及复杂的相互作用, 讨论锥形靶中拉伸应力的形成机制与演化, 如图1所示. 当平板飞片撞击锥形靶时, 定义为t = 0时刻, 在碰撞界面产生两束压缩冲击波, 分别在飞片和锥形靶中传播. 一束压缩冲击波到达飞片自由面后反射为稀疏波, 该反射稀疏波传入锥形靶中(见图1中蓝色虚线所示); 锥形靶中另一束压缩冲击波首先会在圆锥自由面上反射成稀疏波(见图1中紫色虚线所示), 这里选取一个典型时刻t = t₁时, 两束稀疏波在锥形靶中相遇(见图1中A点所示), 从而在A点附近形成拉伸应力区. 如果拉伸应力幅值超过材料的损伤阈值应力, 将在材料产生损伤, 甚至层裂破坏. 随着压缩冲击波(见图1红线表示)继续向前传播, 紧随其后的两束稀疏波持续相互作用, 从而在锥形靶内产生从锥底到锥顶滑移拉伸应力区以及复杂的应力状态. 在典型时刻t = t₂时, 拉伸应力波从A点滑移至B点, AB连线周围区域是主要的拉伸应力区, 会产生连续的损伤演化区/层裂面, 方向与锥面平行, 这一点得到了后面的实验结果验证. 上述简要的波系图分析可知, 平板飞片撞击锥形靶后, 由于波系之间复杂的相互作用在锥形靶产生了非一维应变的滑移拉伸应力状态, 这与炸药滑移爆轰加载条件是非常类似的. 但是, 在锥形靶层裂实验中, 可以通过调整平板飞片厚度和撞击速度来对滑移冲击波加载条件进行比较精确的调控, 这一点比炸药滑移爆轰加载条件更有优势.
图 1 平板飞片撞击锥形靶实验中x-y-t波系相互作用示意图
Figure1. Schematic diagram of x-y-t wave interactions in the experiment of flat flyer impacting conical target.

2 -->

2.2.实验方案

利用直径为57 mm的一级轻气炮加载系统开展平板飞片撞击锥形靶层裂实验, 实验装置示意图如图2所示. 平板飞片安装在铝合金弹托上, 在高压气体驱动下沿着炮管加速, 通过调整驱动气体的压力来控制飞片撞击速度, 由炮口测速探针来测量飞片击靶速度. 实验中, 采用多通道激光位移干涉诊断技术实时监测锥形靶自由表面不同位置处的法向粒子速度剖面, 一个激光探头布置在锥面中点, 另两个探头分别布置在上下两部分的中点, 如图2所示. 实验中, 飞片材料选取铝合金材料, 直径为53 mm, 厚度为3 mm. 锥形靶选取高纯铜材料, 直径为53 mm, 顶角为90o. 实验前, 对高纯铜靶板材料的微观结构进行了电子背散射衍射(electron backscattered diffraction, EBSD)表征, 如图3所示, 晶粒基本接近与等轴晶, 平均晶粒尺度约为25 μm. 实验中, 通过设计合理的回收装置来实现锥形靶体的软回收. 采用光学和扫描电子显微镜对软回收的初始层裂锥形靶进行损伤显微观察和定量统计分析, 讨论损伤分布特征及微介观机理, 为建立损伤演化物理模型提供宝贵的基础数据.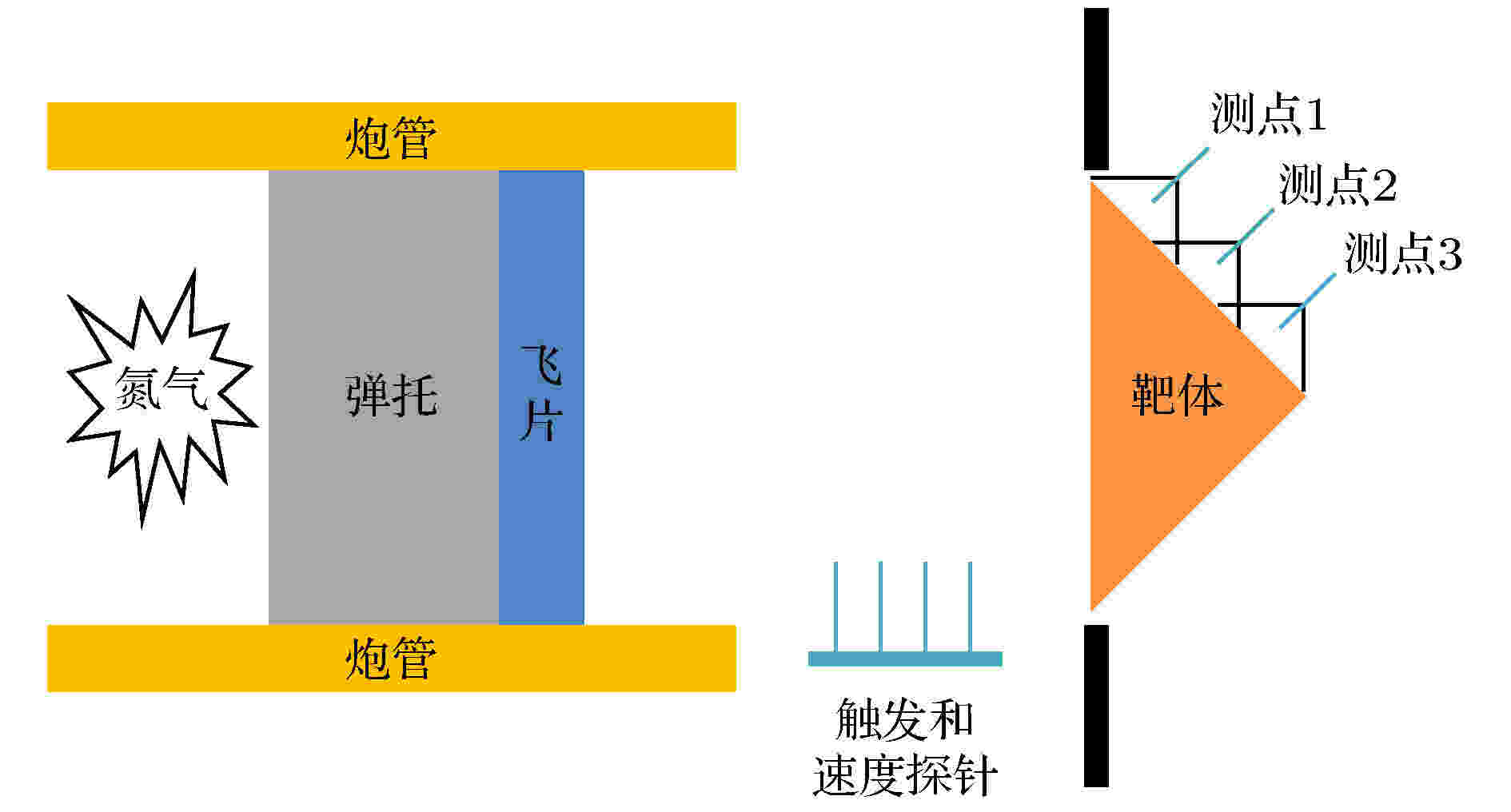
图 2 锥形靶层裂实验装置示意图
Figure2. Schematic diagram of conical target experiment.

图 3 高纯铜样品微观结构EBSD表征照片
Figure3. Microstructure image of high-purity spallation copper by using EBSD.

2

-->

3.1.损伤分布特征

为了研究高纯铜锥形靶层裂过程中微损伤演化特征, 采用波阻抗较低的铝合金飞片低速撞击高纯铜锥形靶, 在靶中产生初始层裂状态, 软回收的高纯铜锥形靶样品如图4所示, 锥形靶外表面保持完整, 没有发生完全层裂和飞片二次碰撞的痕迹. 采用线切割方式将锥形靶样品沿着对称面切割为四份, 取其中四分之一块体进行表面研磨和抛光后, 利用光学显微镜来观察锥形靶样品横截面上损伤分布特征, 如图5所示, 清晰地观察到沿着与外锥面平行方向出现了连续微损伤分布区域, 从锥底角附近向锥顶扩展, 从而在锥形靶内形成了锥形分布损伤区, 该损伤区沿着x方向分布宽度约为1 mm. 图5显示的损伤分布区域与2.1节讨论的拉伸应力区域是一致的, 验证了简化波系分析合理性. 值得注意的是, 在锥形靶锥顶附近会出现来自锥形靶自由面反射的稀疏波相互作用, 导致该区域拉伸应力分布更为复杂, 损伤相对比较严重一些, 并向锥体内部延伸.
图 4 软回收的锥形靶样品图
Figure4. Soft-recovered conical copper target.

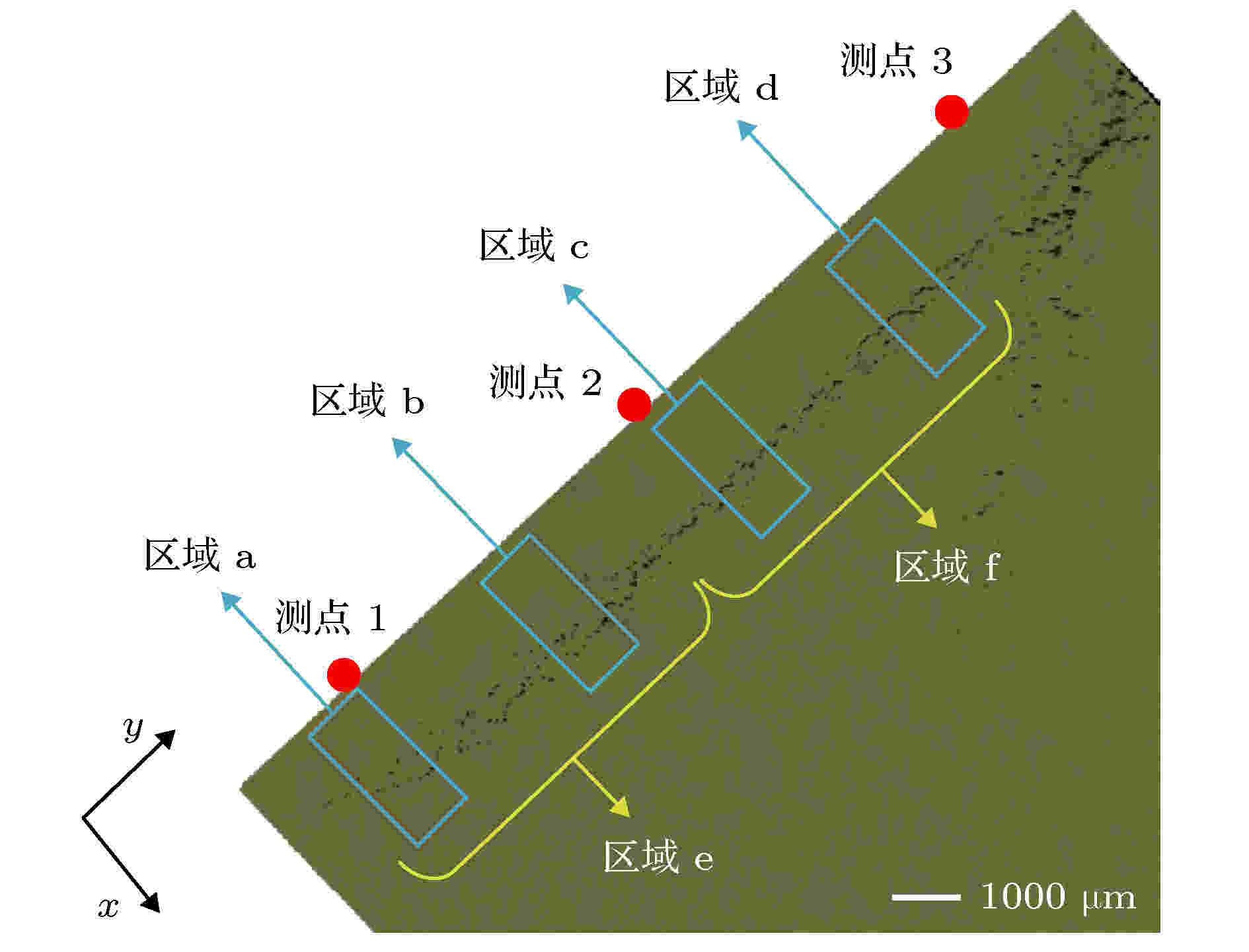图 5 锥形靶内部微损伤分布特征光学显微照片
Figure5. Optical micrograph of micro-damage distribution in the conical copper target.

在图5中沿着Y方向选取4个微损伤分布典型区域(宽为1 mm, 长为1.4 mm)进行局部放大, 如图6所示, 分别代表了损伤演化的不同阶段. 锥底附近区域a中观察到微孔洞基本上处于成核与独立长大阶段, 微孔洞尺寸大小和分布区域都比较分散, 如图6(a)所示; 在图6(b)中可以观察到少数微孔洞之间发生了聚集行为, 而在图6(c)中则观察到比较严重的微孔洞聚集行为, 这种聚集行为具有局域化特征, 最后微孔洞之间不断聚集形成了贯通的断裂带, 如图6(d)所示. 由此可见, 锥形靶内损伤分布特征具有显著的空间依赖性, 其内在机制是与锥形靶内拉伸应力分布、幅值及持续时间密切相关. 遗憾的是, 目前没有任何测试技术可以实时测量材料内部应力时空分布, 这里只能借助数值仿真手段来获取不考虑损伤条件下锥形靶内的应力分布特征, 来定性说明损伤与载荷之间的关系. 根据实验条件, 建立铝合金飞片撞击高纯铜锥形靶二维轴对称计算模型, 如图7(a)所示. 铝合金采用理想流体弹塑性本构关系, 具体表达式及计算参数见文献[14], 高纯铜采用Johnson-Cook (J-C)本构关系, 具体表达式及参数见文献[19]. 压力计算采用Mie-Grüneisen 状态方程, 参数来源于文献[20]. 图7(b) 给出了数值仿真得到的4个典型区域中心处单元应力时程曲线, 可以观察锥形靶内拉伸应力幅值和持续时间随着空间在不断演化, 锥底附近的区域a处拉伸应力幅值低, 且持续时间短, 必然导致其在锥形靶内产生的损伤比较弱; 从区域a到区域d, 拉伸应力幅值逐渐增大和持续时间逐渐增长, 必然导致锥形靶内呈现越来越严重的损伤状态.
图 6 锥形靶内4个典型区域的微损伤分布光学显微照片　(a)区域a; (b)区域b; (c)区域c; (d)区域d
Figure6. Optical micrographs of micro-damage distribution in four typical regions of the conical target: (a) Region a; (b) region b; (c) region c; (d) region d.

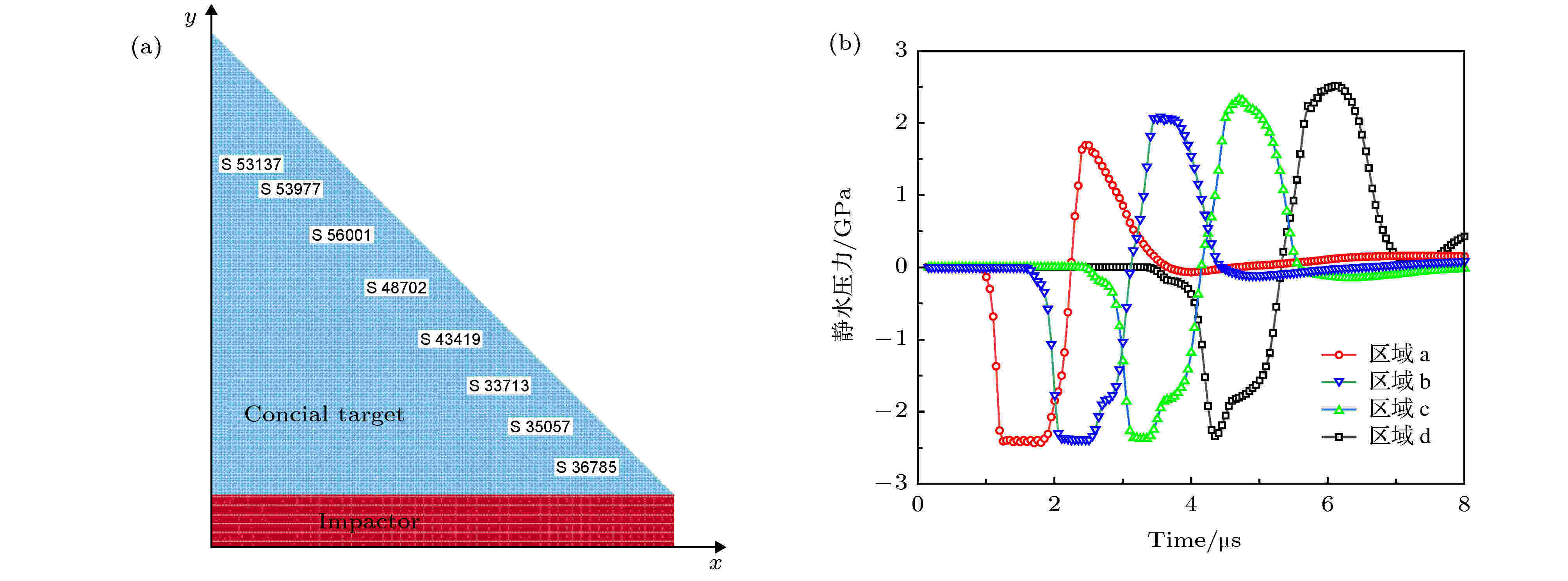图 7 平板撞击锥形靶轴对称二维有限元计算模型及4个典型区域中心单元应力时程曲线　(a)有限元计算模型; (b)应力时程曲线
Figure7. Two-dimensional axial symmetric finite element method model of conical target impacted by planar impactor and stress profiles of central element in four typical regions: (a) Finite element method model; (b) stress profiles.

材料内部出现损伤必然影响材料的宏观力学响应, 在损伤力学框架下, 通常引进损伤内变量来架设起损伤与力学响应之间的桥梁, 从而建立损伤演化方程及含损伤内变量的本构方程. 在层裂研究中, 通常定义横截面上微孔洞的面积与基体面积之比作为损伤变量, 简称为损伤度. 下面对锥形靶内的损伤度进行定量统计^[21], 为构建损伤演化方程提供重要的实验数据. 首先将图6沿着x方向切割成一定数量的小区域, 再通过图像灰度对比来自动识别和统计微孔洞尺寸及空间分布, 由此得到损伤度沿着x方向的分布曲线, 如图8所示, 图中显示: 区域a微孔洞成核、长大阶段损伤度分布是随机的, 损伤度基本呈现多峰分布; 从区域b至区域d, 损伤度逐渐增大, 其分布特征也在变化, 从“多峰”到“双峰”, 再到逐渐变为“单峰”分布, 这表明了微孔洞从长大到聚集的演化过程具有局域化特征. 正是这种微孔洞局域化聚集行为导致损伤演化速率显著增大, 从而诱发宏观的灾变式断裂. 为了获得损伤沿着锥面y方向分布特征, 把图5中损伤区域分两段(区域e和区域f)进行局部放大, 如图9所示, 再采用上述相同的方法, 定量统计损伤度沿着y方向分布, 如图10所示, 图中显示: 初始阶段损伤度沿y方向呈线性增加, 随后损伤度基本维持恒定, 最后锥顶附近损伤度迅速增大, 这也归因于锥形靶内复杂的拉伸应力分布特征. 但是, 在实验上确定内部损伤演化与拉伸应力状态之间的定量关系是非常困难的, 目前还没有任何测试手段可以监测材料内容损伤演化和应力状态变化.
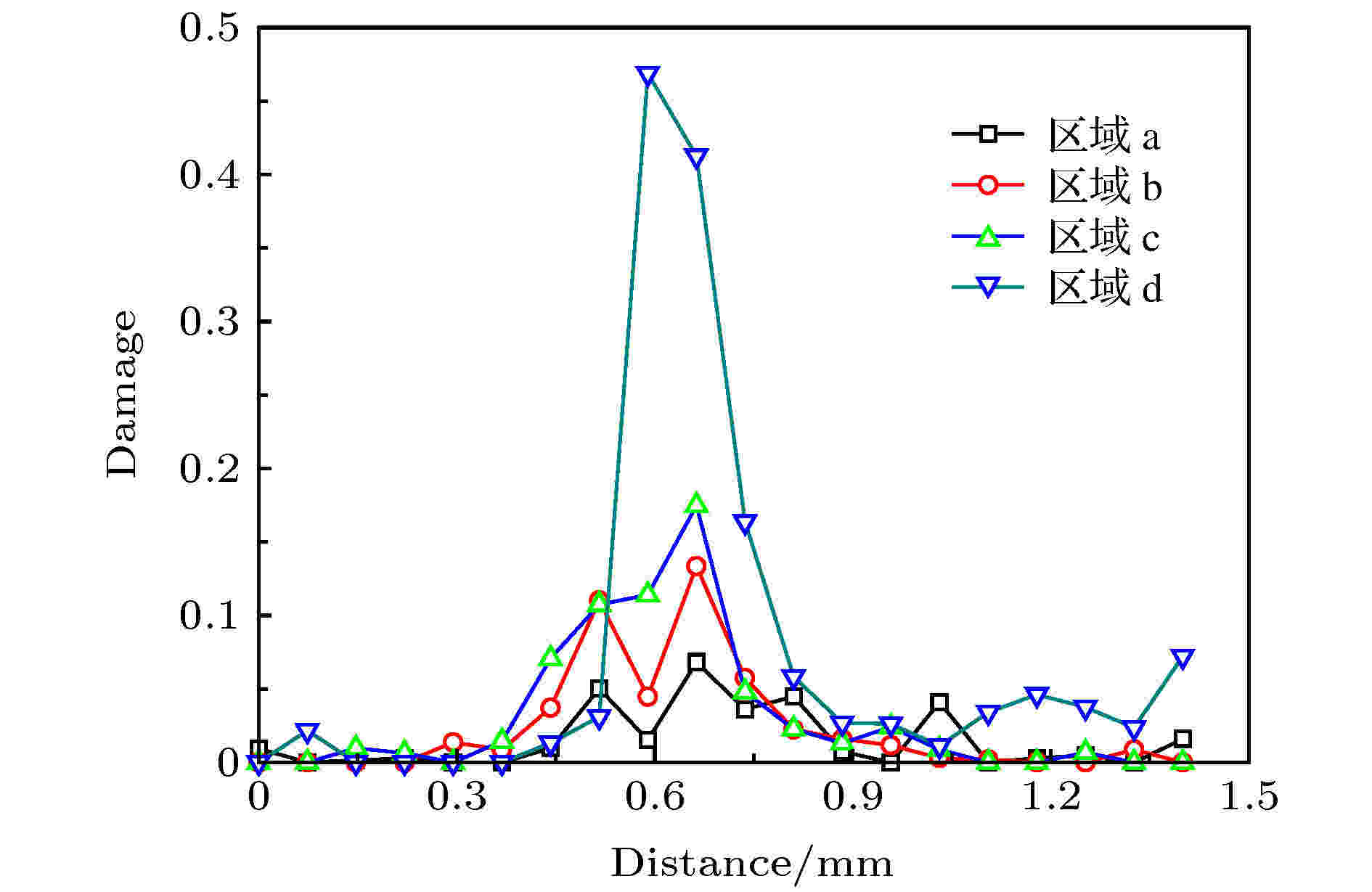图 8 锥形靶内4个典型位置处沿x方向的损伤度统计结果
Figure8. Damage distribution along the x direction in four typical regions of the conical target.

图 9 锥形靶内沿着y方向微损伤分布的光学显微照片 (a)区域e; (b)区域f
Figure9. Optical micrographs of micro-damage distribution along y direction in the conical target: (a) Region e; (b) region f.

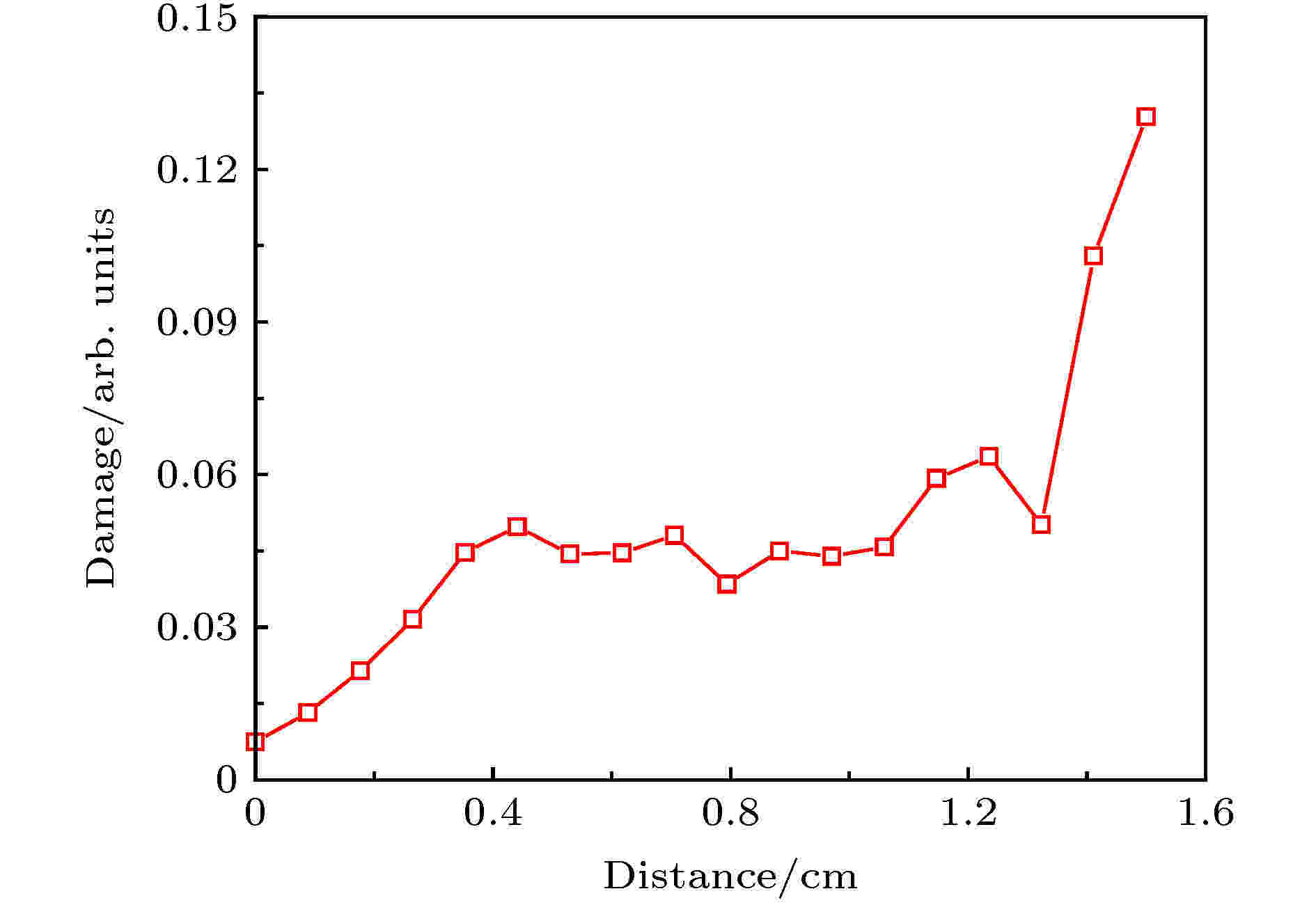图 10 锥形靶内沿y方向的损伤度定量统计分布
Figure10. Damage distribution along the y direction in the conical copper target

为了进一步揭示微孔洞长大和聚集的微观机理, 图11给出了不同损伤度条件下锥形靶横截面损伤分布EBSD表征照片, 可以观察到绝大多数微孔洞在晶界处成核并长大, 尺寸小的孔洞沿着晶界以直接贯穿方式聚集形成较大尺寸孔洞, 较大尺寸孔洞之间继续相互聚集贯通形成宏观的断裂面, 这表明微孔洞聚集行为具有局域性和多层次特性, 在损伤演化过程中占据重要地位, 在构建损伤演化理论模型时需要重点考虑. 另外, 对比图3和图11, 发现回收高纯铜晶粒尺寸有所减小, 平均晶粒尺寸从25 μm降低到20 μm, 具体的统计分布结果如图12所示. 众所周知, 在层裂实验中, 样品总是先受到冲击压缩, 然后自由表面反射的稀疏波相互作用形成冲击拉伸. 目前, 关于冲击压缩对材料微观结构影响的研究还很少. 关于晶粒尺寸对材料损伤特性的影响已做了大量的研究工作, 但这些研究基本都忽略了冲击压缩对材料微观结构的影响.
图 11 不同损伤阶段横截面损伤分布的EBSD表征 (a)微孔洞长大; (b)微孔洞聚集
Figure11. EBSD orientation maps of cross section damage at different damage stages: (a) Microvoid growth; (b) microvoid coalescence.

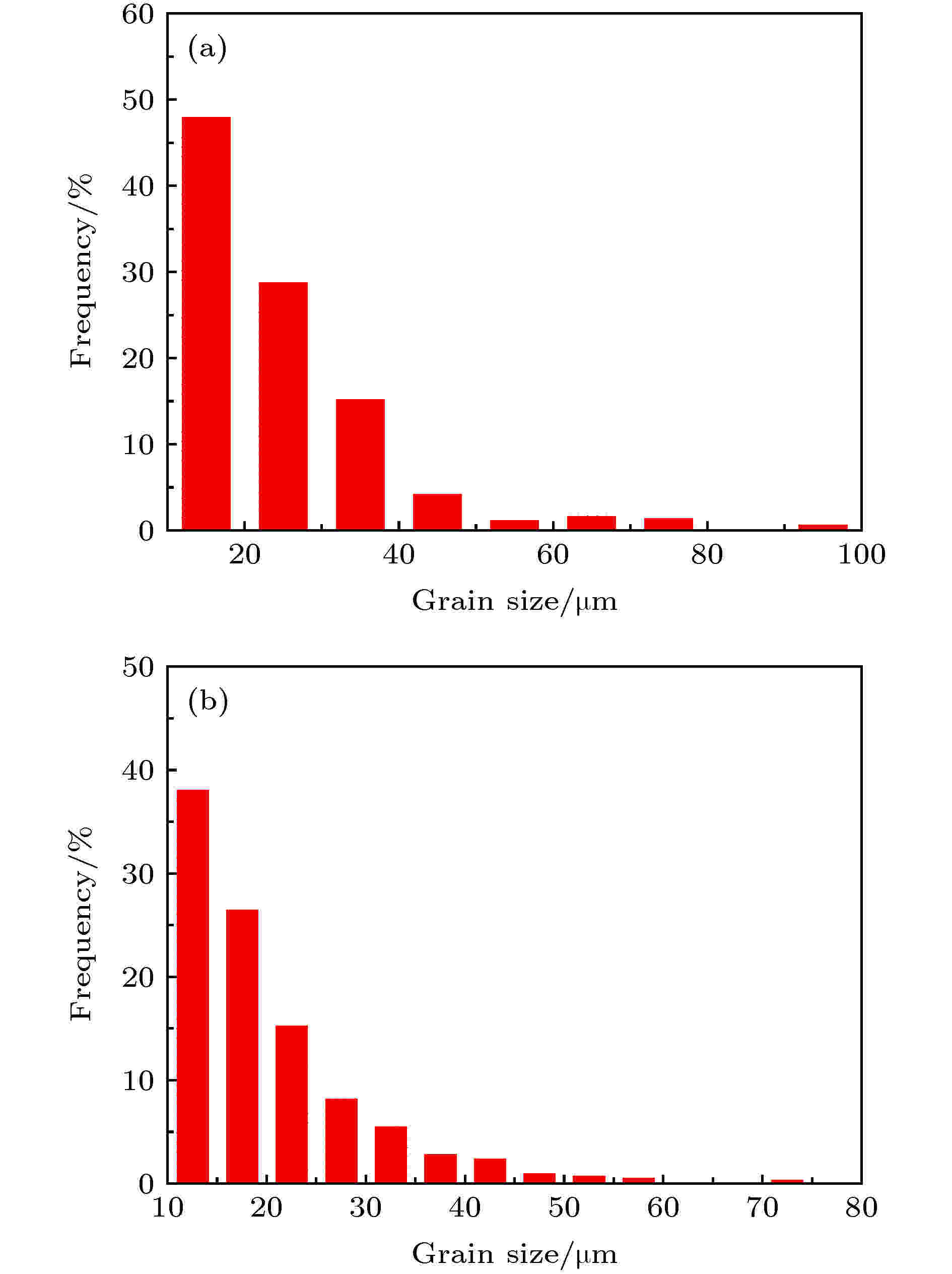图 12 原始态和冲击态高纯铜晶粒尺寸分布对比　(a)原始态; (b)冲击态
Figure12. Comparison of grain size distributions of the high-purity copper in cross section: (a) Original; (b) shock compressed.

2 -->

3.2.自由面速度

通过全光纤激光干涉测速仪(displacement interferometer system for any reflector, DISAR)获取的自由面速度时程曲线包含了丰富的波传播及波系相互作用信息, 可以间接反映材料内部发生的微损伤演化动力学过程. 图13给出了锥形靶自由表面3个测点处的法向粒子速度时程曲线, 从中首先观察到不同测点的加载波形发生了明显变化, 从开始类矩形波逐渐向三角形波转变, 这是由于飞片自由面反射形成的稀疏波对前驱压缩加载波形成追赶卸载效应.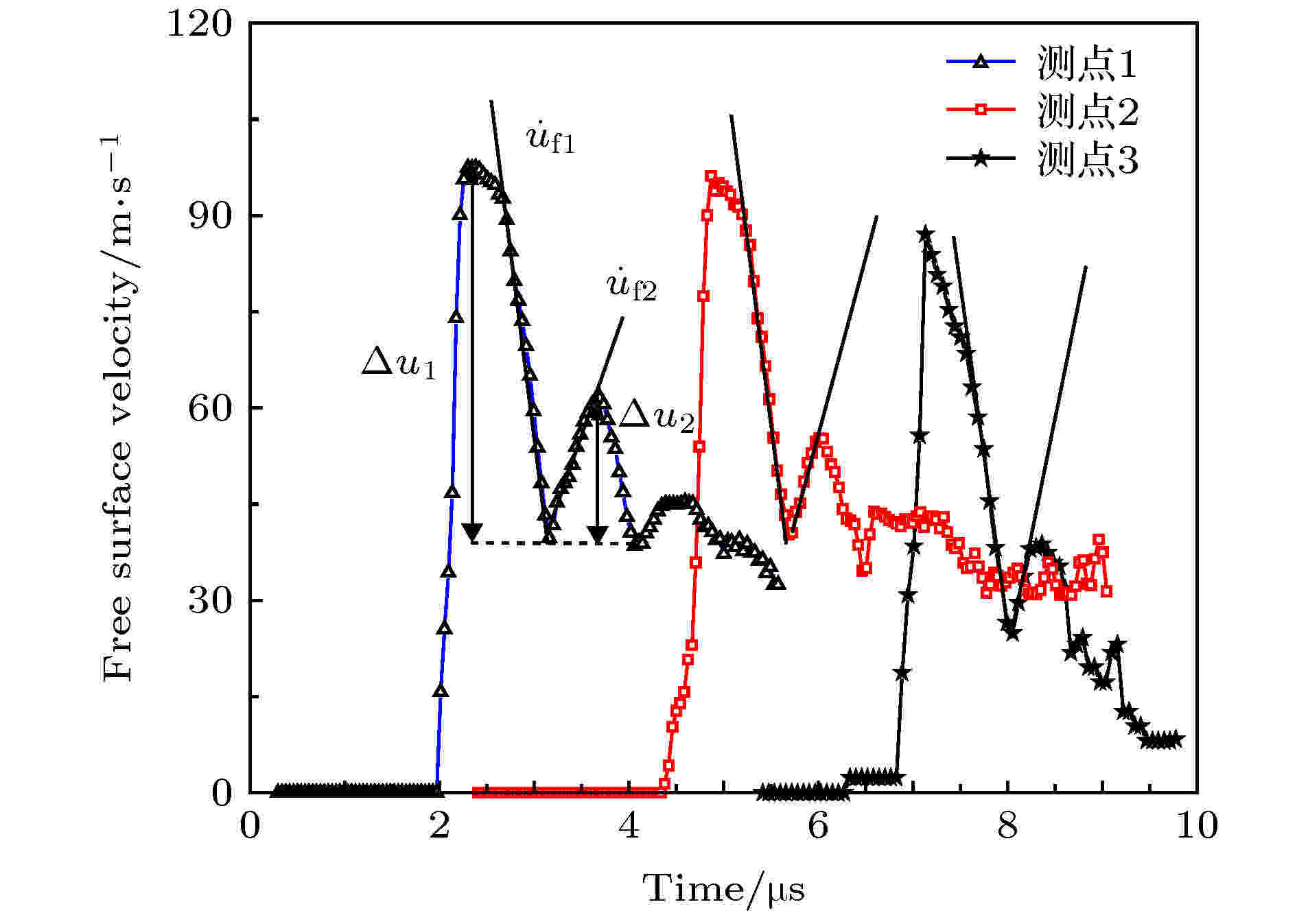
图 13 锥形靶3个测点处的自由面速度时程曲线
Figure13. Free surface velocity profiles measured from different points of conical target.

为了详细讨论自由面速度波形的典型特征及其与内部损伤演化之间内禀关系, 这里以测点1速度时程曲线为例, 定义了一些特征参数. 首先关注Pull-back速度Δu₁, 定义为自由面速度最大值与信号第一次反弹时自由面速度之差. 从图13可以看到, 3个测点的自由面速度剖面上都出现了明显的Pull-back信号, 测量的Pull-back速度Δu₁列于表1, 结果显示基本恒定, 不依赖于测点位置. 在声学近似条件下, Novikov^[22]提出了一维应变加载条件下利用Δu₁来计算材料的层裂强度${\sigma _{{\rm{spall}}}}$公式, 即

编号	Δu1/m·s–1	${\sigma _{{\rm{spall}}}}$/GPa	Δu2/m·s–1	$\dot \varepsilon $/104s–1	${\dot u_{{\rm{f}}2}}$/107m·s–2
测点1	57.76	1.34	21.84	1.34	4.34
测点2	55.85	1.31	14.80	1.33	6.67
测点3	61.11	1.32	13.05	1.31	7.08

表1三个测点的自由面速度参数
Table1.Free surface velocity parameters measured from different points of conical target

${\sigma _{{\rm{spall}}}} = \frac{1}{2}{\rho _0}{c_0}\Delta {u_1}, $

这里ρ₀是材料密度, c₀是材料的体积声速. Chen等^[23]采用特征线方法推导了该公式. 锥形靶层裂实验是非一维应变稀疏波以一定角度斜碰, (1)式是否适用值得讨论. Rybakov^[24]研究平板样品在滑移爆轰加载下非一维冲击层裂问题, 当滑移爆轰波向前传播时, 向平板样品中斜入射冲击波, 该冲击波到自由面反射成稀疏波, 与加载稀疏波相遇产生拉伸应力, 从而引起层裂. 采用特征线方法, Rybakov^[24]推导了非一维加载条件下层裂强度的计算公式, 即:

${\sigma _{{\rm{spall}}}} = \frac{1}{2}{{{\rho _0}{c_0}\Delta {u_1}} / {\cos \alpha }}, $

这里α为斜入射角. 通过平板飞片撞击锥形靶, 在锥形靶中也产生了非一维滑移冲击波加载状态, 与滑移爆轰波加载条件是非常类似的. 如图1所示, 以锥体自由面为参考平面, 冲击波与锥体自由面之间就是斜入射问题, 容易确定斜入射角α为45o. 基于Pull-back 速度, 采用(2)式计算得到的层裂强度列于表1, 结果显示高纯铜层裂强度约为1.3 GPa, 这与一维应变冲击加载下高纯铜层裂强度是非常接近的^[25].
事实上, 对Pull-back速度信息的解读存在诸多争议. 传统观点一直把Pull-back信号用来判断层裂是否发生的一个重要依据. 下面结合锥形靶内部损伤分布特征(如图5和图6所示)和波传播理论, 来讨论层裂强度的物理本质. 图5和图6中已清晰地显示, 测点1、测点2及测点3所对应锥形靶内部位置处的出现了损伤, 没有出现完全断裂面, 由此可以推断: Pull-back 信号出现并不意味着材料发生完全断裂, 层裂强度本质上不能代表材料最大拉伸强度. 另一方面, 测点1、测点2及测点3所对应的损伤度是逐渐增大, 但是层裂强度却是不依赖于材料内部的损伤度, 那么层裂强度的物理本质是什么? 根据应力波传播理论可知, 波在介质中传播时, 一旦遇到波阻抗不同的界面就会发生反射和透射. 在层裂实验中, 一旦材料内部出现损伤成核, 则该区域的波阻抗就会减小, 自由面反射的稀疏波遇到该低阻抗区域时会发生反射, 从而形成压缩波, 此压缩波传播到自由面时就会导致自由面速度开始回跳, 在实测自由面速度剖面即出现Pull-back信号. 因此, 从宏观上来说, 层裂强度反映了微损伤成核临界应力; 而从图11可以观察到高纯铜中微损伤首先成核于晶界, 从细观来说, 层裂强度反映了晶界强度. 大量实验结果显示层裂强度强烈依赖于拉伸应变率^[4-6], 其内在本质是拉伸应变率会对微孔洞成核产生重要的影响. 在本文提出的锥形靶实验中, 可以根据图12自由面速度曲线下降段的斜率来估算拉伸应变率, 计算公式为

$\dot \varepsilon = \frac{{{{\dot u}_{{\rm{f}}1}}}}{{{\rm{2}}{c_{\rm{b}}}}}, $

式中, ${\dot u_{{\rm{f}}1}}$为卸载段的自由面速度变化率, ${c_{\rm{b}}}$为体波声速, 计算结果也列于表1, 结果显示: 拉伸应变率不依赖空间位置, 保持恒定, 从而导致了层裂强度恒定性.
如3.1节讨论, 锥形靶内损伤度强烈依赖于拉伸应力幅值, 而这里讨论的层裂强度却不依赖损伤度, 由此推断层裂强度不依赖拉伸应力幅值, 这与许多实验结果是一致的. 层裂强度反映了损伤成核特性, 损伤长大及聚集过程在自由面速度时程曲线也必然有所表现. 重新仔细观察图13, 发现不同测点的Pull-back回跳速度斜率${\dot u_{{\rm{f}}2}}$和回跳幅值Δu₂有显著变化, 且依赖于空间位置, 从测点1到测点3, Pull-back速度的回跳斜率逐渐增大, 回跳幅值Δu₂逐渐减小. Pull-back回跳速度斜率与内部的损伤演化速率之间是强关联的^[26], 基于特征线方法, Kanel等^[27]建立了Pull-back回跳速度斜率${\dot u_{{\rm{f}}2}}$和材料损伤演化速率${{\dot V}_\nu }$的关系, 具体形式如下:

${\dot u_{{\rm{f}}2}} = A\left( {{{\dot V}_\nu } - B} \right), $

式中A和B为材料参数. 损伤演化速率${{\dot V}_\nu }$强烈依赖于拉伸应力幅值^[8], 而图7给出的数值模拟结果显示从测点1到测点3锥形靶内拉伸应力幅值逐渐增大, 损伤则演化速率${{\dot V}_\nu }$逐渐增大, 从而导致Pull-back回跳速度斜率逐渐增大. Pull-back速度回跳幅值Δu₂与损伤引起应力松弛行为是密切相关的, 而损伤引起应力松弛行为显然是强烈依赖于损伤度, 图10显示从测点1到测点3对应的内部损伤度逐渐增大, 引起的应力松弛行为也愈严重, 从而导致从测点1到测点3 Pull-back回跳速度幅值Δu₂逐渐减小.

发展了一种锥形靶层裂实验方法, 研究了非一维应变加载下高纯铜初始层裂行为. 基于“软回收”锥形靶内部损伤显微分析, 阐明了锥形靶内损伤空间分布主要特征, 发现损伤区扩展方向与锥面平行, 呈现了微孔洞成核、随机独立长大、局域化聚集及形成宏观裂纹整个损伤演化过程; 从损伤度定量统计数据中观测到损伤演化初期的微孔洞成核与长大具有一定的随机性, 而后期的微孔洞聚集具有明显的局域性. 基于实测的锥形靶自由面法向粒子速度剖面, 讨论了层裂强度、Pull-back回跳速度斜率和回跳幅值等特征量与损伤演化之间内禀关联性, 阐明层裂强度物理本质是微孔洞成核阈值应力, 而Pull-back回跳速度斜率和回跳幅值与损伤演化速率和损伤程度之间是强关联性的.