全文HTML
--> --> -->实验方面, 1998年美国麻省理工学院(MIT)的Stamper-Kurn研究组[16]在沿磁势阱的中心轴射入红外线光束形成的光偶极阱中, 首次实现了金属23Na原子系统的BEC, 通过这一突破性进展把在磁势阱中冻结的自旋自由度解放出来, 在冷原子物理领域中开辟了旋量BEC研究的崭新领域. 实验采用光势阱捕获和冷却钠原子, 当温度达到1—2 μK, 原子密度数约为1 × 1014 cm–3时, 转移到磁势阱中经由射频诱导蒸发进一步冷却, 在 F = 1, mF = –1的电子基态上产生含有(5—10) × 106个原子的凝聚体. 随着红外线激光束能量的提升, 在稳定的磁势阱中控制凝聚体进入光势阱, 然后关闭磁势阱, 让凝聚体处于全光阱中. 图1为光势阱中F = 1旋量BEC所有精细态上钠原子的分布, 从图1(b)可以清晰地看到凝聚体分布在三个超精细态上, 金属钠原子的自旋自由度被充分释放.
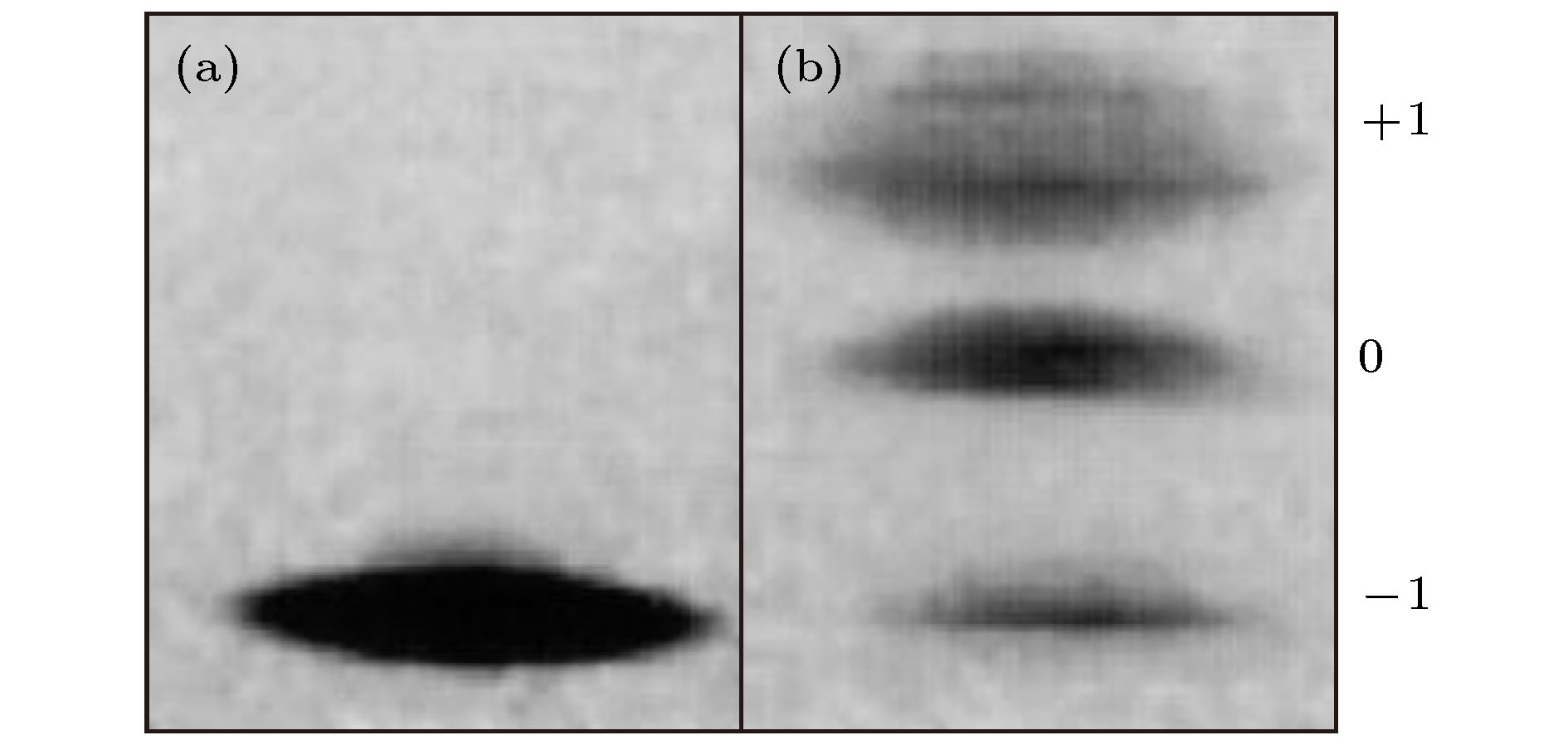 图 1 光势阱中F = 1 23Na凝聚体的超精细态[16]. (a) 250 ms时光势阱中钠原子的吸收图像; (b) 340 ms时光势阱中钠原子的吸收图像
图 1 光势阱中F = 1 23Na凝聚体的超精细态[16]. (a) 250 ms时光势阱中钠原子的吸收图像; (b) 340 ms时光势阱中钠原子的吸收图像Figure1. Optical trapping of 23Na condensates in all F = 1 hyperfine states: shown are absorption images after (a) 250 ms and (b) 340 ms of optical confinement.
2001年, Barrett等[17]在两束CO2激光束(功率为12 W, 波长为10.6 μm)交叉会聚形成的全光阱中得到了F = 1的87Rb原子的旋量BEC. 实验中首先将低速的铷原子装载到磁光阱中, 接着逐步降低光强, 关闭磁场, 然后把原子抽运到F = 1, mF = 1态, 最后打开CO2激光束, 使原子装载到光势阱中. 整个过程中是通过在2 s时间内逐步降低光强, 即减少阱深来实现蒸发冷却的. 图2为实验得到的Stern-Gerlach梯度磁场中自由膨胀10 ms后的原子吸收图像, 从下到上分别是F = 1, mF = –1, 0, 1凝聚体的三个分量.
 图 2 铷原子云在Stern-Gerlach梯度磁场中自由膨胀10 ms后的吸收图像[17]. 从下到上分别是F = 1, mF = (–1, 0, 1)凝聚体的三个分量
图 2 铷原子云在Stern-Gerlach梯度磁场中自由膨胀10 ms后的吸收图像[17]. 从下到上分别是F = 1, mF = (–1, 0, 1)凝聚体的三个分量Figure2. Absorptive image of Rb atomic cloud after 10 ms free expansion in a Stern-Gerlach magnetic field gradient. Three distinct components are observed corresponding to F = 1, mF = (–1, 0, 1) spin projections from bottom to top, respectively.
2003年, Gustavson等[18]研究了F = 2的23Na旋量BEC, 观察到了数秒寿命的精细态(F = 2, mF = –2), 且原子密度数为每立方厘米1014 . Chang[19]、Schmaljohann[20]、Kuwamoto[21]等观察到了F = 2的87Rb旋量BEC, 并研究了其动力学性质. 2012年, Pasquiou等[22]也从实验上观察到了F = 3的52Cr旋量BEC, 并研究了其热力学性质, 表明在极低磁场下, 当自旋自由度被热激活时, 凝聚体的临界温度会降低.
特别地, 在2011年, 美国国家标准与技术研究院的Spielman[23]研究组在87Rb旋量BEC中两个内部自旋态之间通过双光子拉曼过程实现了等效的自旋-轨道耦合, 这是人类历史上首次通过人工合成磁场实现了BEC的自旋-轨道耦合效应, 成为近年来冷原子物理中的一个研究热点[24-27]. 2012年, 中国科技大学潘建伟[28]研究组也实现了BEC中的一维自旋-轨道耦合. 此外, 山西大学[29]和麻省理工[30]的研究组, 分别用40K和6Li实现了费米冷原子气体中的自旋-轨道耦合. 量子气体中自旋-轨道耦合的实现, 开辟了研究冷原子物理的新方向, 如光与原子相互作用对旋量BEC拓扑结构的影响, 自旋涡旋阵列的产生, 以及各种新奇拓扑缺陷的产生. 科研工作者不仅详细研究了自旋-轨道耦合的BEC的性质[31-34], 还在实验上成功模拟了Zitterbewegung(狄拉克颤动)[35,36]、自旋霍尔效应[37]等现象, 并提出了研究量子霍尔效应[38]、反常量子自旋霍尔效应[39]、费米气体中的拓扑量子相变[40]等物理问题的方案.
理论方面, 1998年Ho[41]和Ohmi[42]独立进行了旋量BEC的理论研究. 他们推广了Gross-Pitaevskii方程, 在平均场理论下研究了自旋F = 1的BEC的基态结构和拓扑缺陷的性质. 同年, Law等[43]利用量子光学中的代数方法研究了其自旋混合动力学行为. 接着, Koashi[44,45]、Ciobanu[46]和Semenoff[47]等研究了F = 2的旋量BEC的基态结构、自旋相关、磁效应、激发谱及相位等一系列理论性质. Santos[48]、Diener[49]、Makela[50]等对F = 3的旋量BEC也进行了理论研究. 2007年, Yip[51]研究了自旋F ≤ 4的旋量BEC的基态及其对称性.
BEC作为一种新颖的物质形态, 是物理学前沿的研究热点之一, 特别是实验上实现了旋量BEC、分子的BEC、费米凝聚体、自旋-轨道耦合的超冷原子气体以来, 又掀起了新一轮的研究热潮. 本文综述了旋量BEC的实验和理论研究, 旋量BEC中产生的拓扑缺陷的种类, 如自旋畴壁、涡旋、磁单极子、skymions、扭结, 并结合我们的工作着重介绍了两分量和三分量旋量BEC中拓扑缺陷的研究进展.
2.1.旋量玻色-爱因斯坦凝聚体的哈密顿量表示
自旋为f的BEC的序参量在旋转下有2f + 1个分量, 且这些分量是随着时间空间变化的, 携带关于超流和磁性的信息, 能形成自旋流及质量流, 产生丰富的自旋结构[52].考虑自旋f的全同玻色子体系, 取







2
2.2.旋量玻色-爱因斯坦凝聚体的拓扑荷
对于各种形式的拓扑缺陷主要通过计算拓扑荷来判定. 线缺陷形式的涡旋可通过观察相位图中的奇异点和缠绕数来识别, 对于点缺陷, 如磁单极子, 可以通过计算拓扑荷来确定是整数磁单极子还是分数磁单极子[53]. 在两分量BEC系统中, 原子可以是两种不同的元素[54], 也可以是同种元素的两种同位素[55], 或者是同种原子的不同超精细态[56], 该体系可用贋自旋
贋自旋


| πn | 缺陷 | 孤子 |
| π0 | 磁畴壁 | 暗孤子 |
| π1 | 涡旋 | 非奇异磁畴壁 |
| π2 | 磁单极 | 二维skyrmions |
| π3 | skyrmions, 扭结 | |
| π4 | 瞬子 |
表1同伦群描述的拓扑缺陷结构
Table1.Topological defect structures described by homotopy groups.
2
3.1.自旋畴壁
畴壁可由零阶同伦群




 图 3 赝自旋密度Sz, Sx, Sy的空间分布[73] (a)?(c)表示旋转角频率为0; (d)自旋纹理投影到x-y平面内的矢量表示
图 3 赝自旋密度Sz, Sx, Sy的空间分布[73] (a)?(c)表示旋转角频率为0; (d)自旋纹理投影到x-y平面内的矢量表示Figure3. The pseudospin density distribution for (a) Sz, (b) Sx and (c) Sy for Ω = 0; (d) the vectorial representation of the spin texture projected onto the x-y plane.
2
3.2.涡 旋
涡旋可由一阶同伦群





对于自旋1的铁磁BEC, 序参量流形为SO(3), 其基本群为



另一种涡旋结构为极核涡旋, 对应序参量为
对于涡旋而言, 相位的改变量是量子化的, 应是2π的整数倍[75]. 在两分量BEC系统中, 通过光学方法可以实现半量子化涡旋(half-quantized vortice), 描述两分量系统中, 组分一涡旋的相位改变量是2π, 组分二相位改变量为0的情况. 相对于整个系统, 每个组分的相位改变量为π, 因此称之为半量子化涡旋或Alice涡旋[76]. 2017年Liu C F和Liu W M[77]利用变分方法, 得到了自旋-轨道耦合和外磁场联合作用下自旋1BEC中无核半量子涡旋可能的稳定解. 计算表明, 各向同性自旋-轨道耦合提供了稳定无核半量子涡旋和相应的奇异半量子自旋纹理激发的局部能量最小. 各向同性自旋-轨道耦合和垂直磁场的联合约束是获得这种激发的关键因素, 研究还提供了半量子涡旋的稳定相图和最可能的尺寸. 图4为自旋1BEC中半量子涡旋近似解和相应的奇异自旋纹理. 在自旋2BEC的单轴向列相和四面体循环相中还存在非阿贝尔涡旋, 其迷向群都是阿贝尔群[78]. 非阿贝尔涡旋的特点在于其涡旋的生成元是不能互换的, 因此当两个涡旋碰撞时, 它们不能合并或者通过对方, 而是形成一个rung涡旋粘在一起.
 图 4 自旋1 BEC中半量子涡旋的近似解和相应的奇异自旋纹理[77] (a)和(b)对应
图 4 自旋1 BEC中半量子涡旋的近似解和相应的奇异自旋纹理[77] (a)和(b)对应


Figure4. Approximate half-quantum vortex solution in the spin-1 BEC and the corresponding singular spin texture: (a) and (b) are the densities of the



2
3.3.磁单极子
磁单极子可由二阶同伦群
 图 5 两种常见的二维skyrmions的矢量场构型[79] (a) 豪猪型skyrmion; (b) 螺旋型skyrmion
图 5 两种常见的二维skyrmions的矢量场构型[79] (a) 豪猪型skyrmion; (b) 螺旋型skyrmionFigure5. Two common vector field configurations of two-dimensional skyrmions: (a) The hedgehog type skyrmion; (b) the spiral type skyrmion.
自1931年狄拉克磁单极子被首次提出以来, 便受到了广泛关注, 尽管到目前为止仍然没有探测到真实的磁单极子, 科研工作者在不同领域也取得了较大的进展, 例如固态物理中的自旋冰材料, 便提供了一种人造磁单极子环境. 最具有突破性进展的是研究者在铁磁BEC中实验上实现了人造磁单极子[80,81].
2
3.4.三维skyrimion
三维skyrimion可由三阶同伦群




Skyrmion在凝聚态的许多体系中发挥了作用, 例如液氦、量子霍尔体系、液晶以及螺旋铁磁系统, 目前在旋量BEC中的skyrimon已经成为研究热点. 图6是研究者在两分量BEC中通过非阿贝尔规范场诱导观察到的三维skyrmions[82,83].
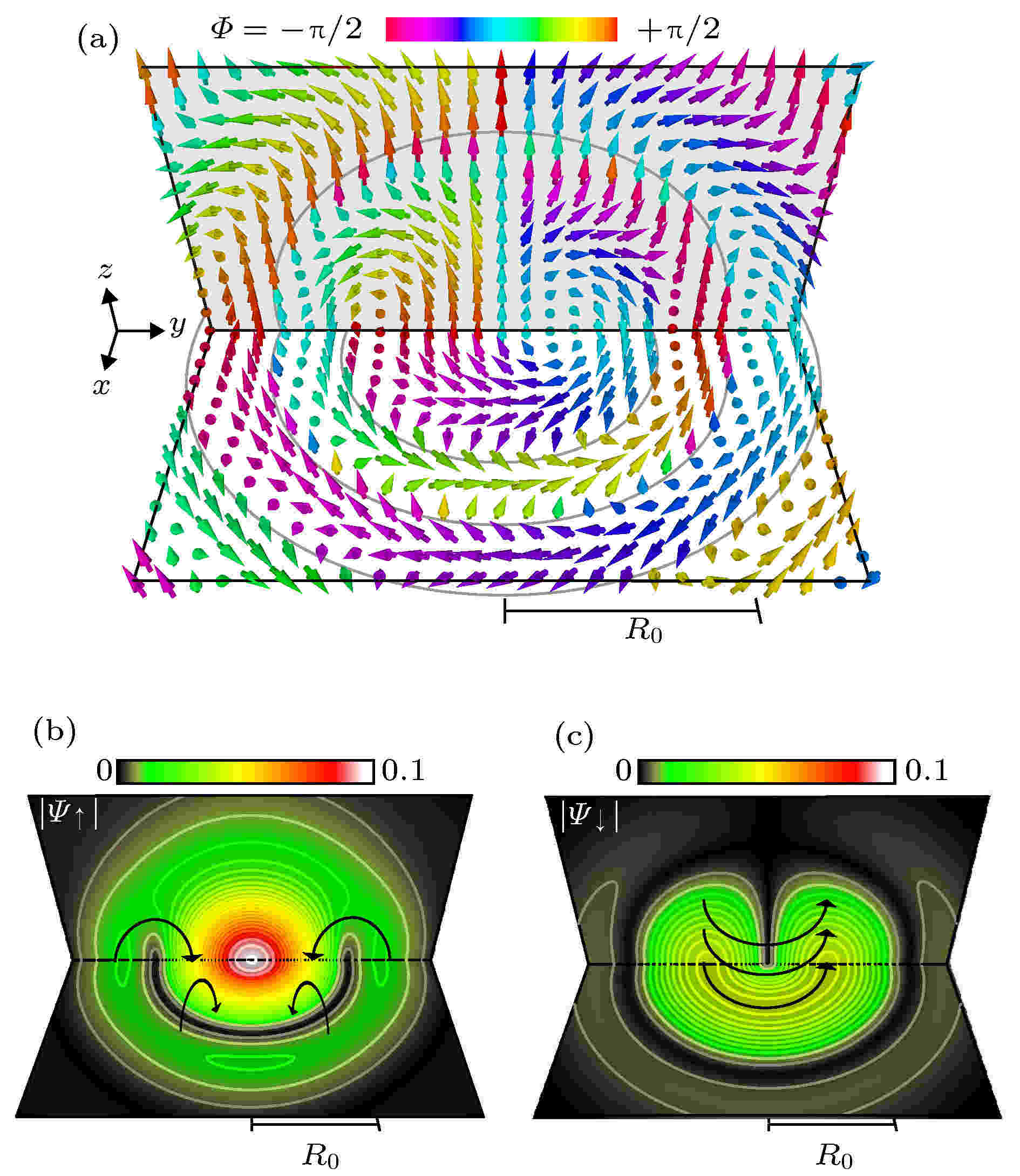 图 6 稳定的三维skyrmions在x-y和z-x平面的空间分布[83] (a)中的箭头和颜色分别表示贋自旋方向和OP的U(1)相分布. 彩图(b)和(c)分别表示
图 6 稳定的三维skyrmions在x-y和z-x平面的空间分布[83] (a)中的箭头和颜色分别表示贋自旋方向和OP的U(1)相分布. 彩图(b)和(c)分别表示

Figure6. The spatial profile of the stable 3D skyrmions in the x-y and z-x planes: The arrows and their colors in (a) indicate the pseudospin direction and the U(1) phase of the OP, respectively; the color maps of (b) and (c) give the amplitudes


2
3.5.扭 结
扭结也可由三阶同伦群




通过操纵外部磁场, 可以在自旋1BEC中形成扭结. 在外部磁场存在时, 线性塞曼效应引起

























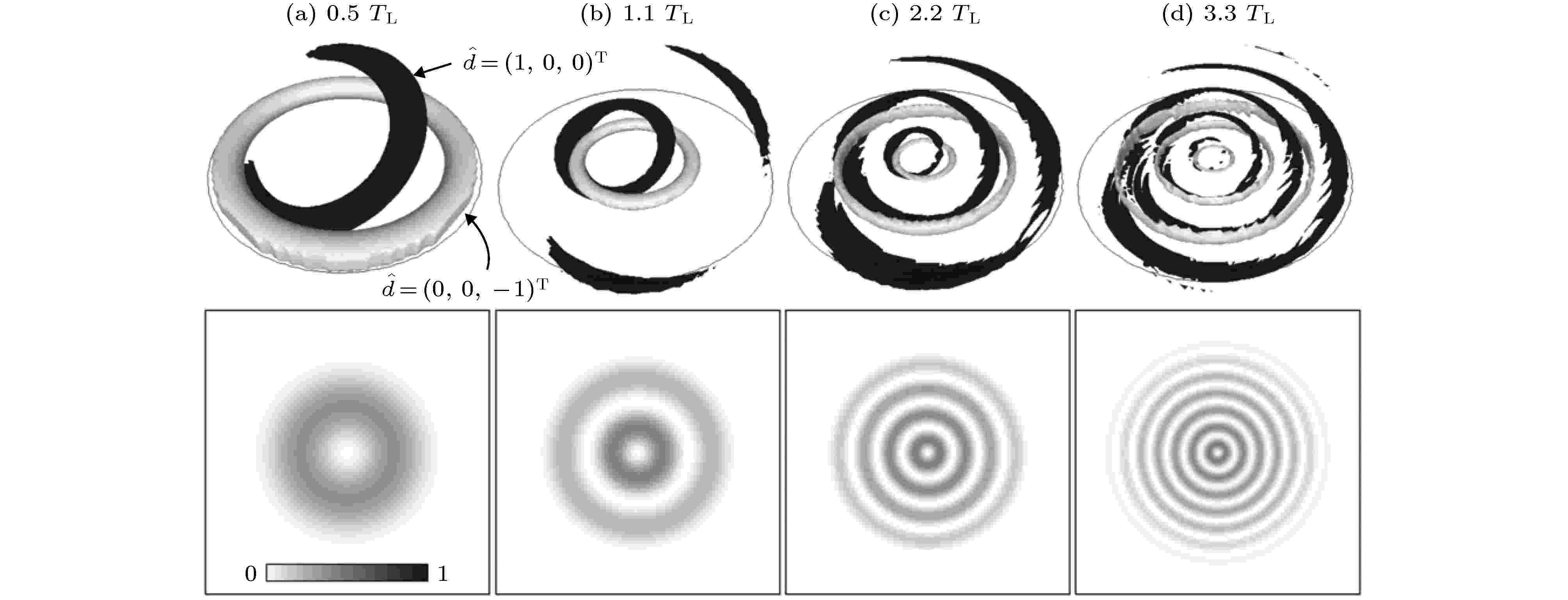 图 7 四极场作用下球形光势阱中扭结产生的动力学过程[85]. 上一行表示
图 7 四极场作用下球形光势阱中扭结产生的动力学过程[85]. 上一行表示

Figure7. Dynamics of the creation of knots in a spherical optical trap under a quadrupole magnetic field. Snapshots of the preimages of




4.1.两分量旋量玻色-爱因斯坦凝聚体中的拓扑缺陷研究
对于两分量BEC[86], 由于组分内相互作用与组分间相互作用两者的竞争导致体系出现丰富而有趣的拓扑结构, 如上文介绍的涡旋、skyrmion、磁单极子和量子扭结等, 现已成为实验研究的理想平台. 实验方面, 1999年Matthews等[87]在两分量BEC中产生了量子涡旋. 2001年Anderson等[88]采用两束正交的探测光观察到双组分的BEC中暗孤子受动力学不稳定的影响衰变为涡旋环. 2016年Hall等[89]演示了在旋量BEC中扭结孤子的实验创建和检测, 所观察到的扭结纹理对应于三阶同伦群, 如图8.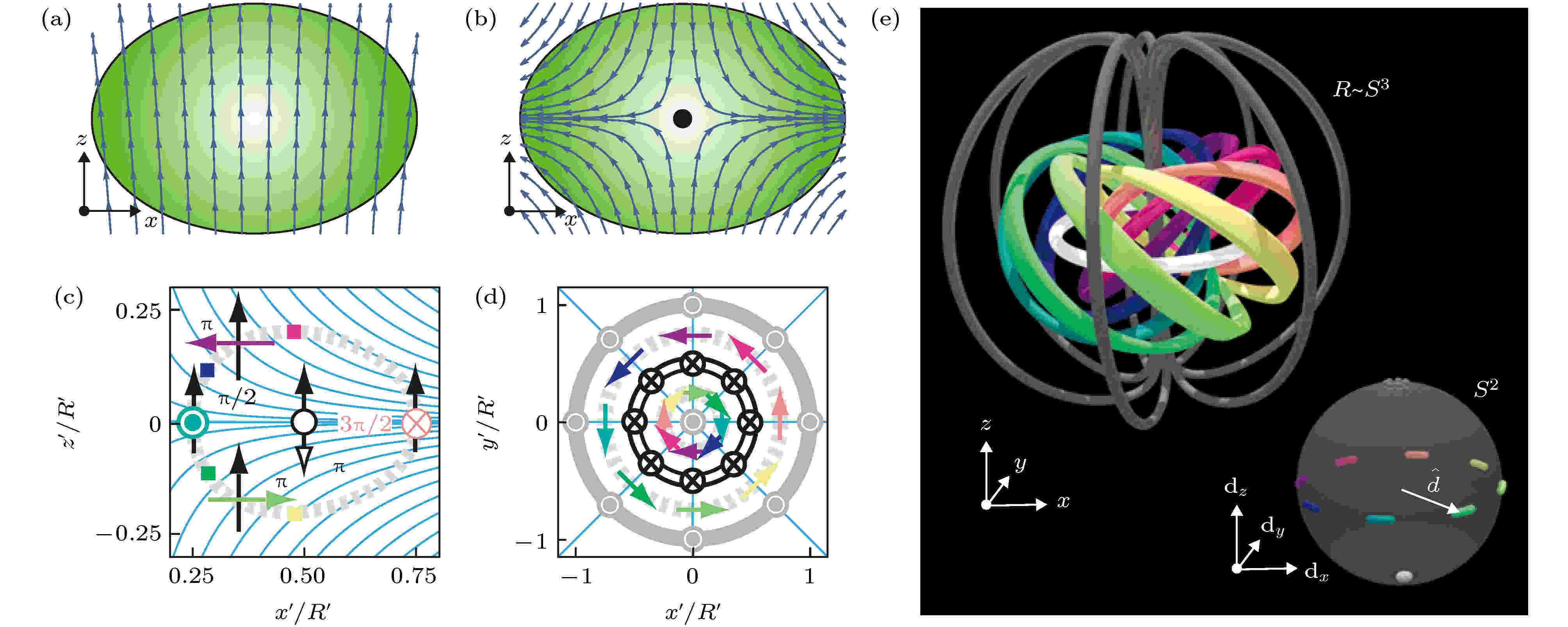 图 8 扭结孤子的结构及其产生方法[89] (a)和(b)为扭结形成之前和形成过程中磁感应线的示意图, 绿色椭圆为对应的凝聚体; (c)和(d)显示扭结形成时, 最初的z方向的向列相矢量(黑色箭头)沿着局部磁场(青色线)的方向进动, 以实现最终的结构(彩色箭头). 灰色虚线表示dz = 0, 白线表示孤子核(dz = –1), 深灰色线表示体积V (dz = 1)的边界; (e)表示实空间中扭结孤子的构型及其与S2中向列矢量
图 8 扭结孤子的结构及其产生方法[89] (a)和(b)为扭结形成之前和形成过程中磁感应线的示意图, 绿色椭圆为对应的凝聚体; (c)和(d)显示扭结形成时, 最初的z方向的向列相矢量(黑色箭头)沿着局部磁场(青色线)的方向进动, 以实现最终的结构(彩色箭头). 灰色虚线表示dz = 0, 白线表示孤子核(dz = –1), 深灰色线表示体积V (dz = 1)的边界; (e)表示实空间中扭结孤子的构型及其与S2中向列矢量
Figure8. Structure of the knot soliton and the method of its creation: Schematic magnetic field lines before (a) and during (b) the knot formation, with respect to the condensate (green ellipse); (c), (d) as the knot is tied, the initially z-pointing nematic vector (black arrows) precesses about the direction of the local magnetic field (cyan lines) to achieve the final configuration (coloured arrows); the dashed grey line shows where dz = 0, the white line indicates the soliton core (dz = –1), and the dark grey line defines the boundary of the volume V (dz= 1); (e) the knot soliton configuration in real space and its relation to the nematic vector

理论方面, 1999年Williams和Holland[90]展示了在BEC中选择性地产生具有不同角动量超流涡旋的方法, 包括求解具有强耦合原子态的双组分凝聚体的时间相关运动方程. 2002年Battye等[91]证实了在两分量BEC中存在稳定的skyrmion结构. 同年Martikainen等[92]理论研究了在两分量BEC中产生磁单极子的方法, 并证明磁单极子的产生并不局限于反铁磁自旋凝聚, 同时研究了这种磁单极子的膨胀探测, 以及势阱中位移磁单极子的动力学. 2004年Kasamatsu和Tsubota[93]通过数值积分耦合的Gross-Pitaevskii方程, 研究了双组分BEC在轴对称势阱中由调制不稳定性引起的多畴壁形成动力学. 2010年Wang等[94]在无外势的自旋-轨道耦合两分量BEC中发现了平面波相和条纹相, 在考虑外势的情况下, 体系将出现新的量子态, 如分数涡旋和涡旋格子[95]以及skyrmion格子[96].
接着, 人们研究了旋转势下自旋-轨道耦合两分量BEC的基态性质. 2011年Xu和Han[97]在旋转势下自旋-轨道耦合两分量BEC体系中发现了对称排列的涡旋列和中心伴有巨skyrmion的三角涡旋格子. 2011年Zhou等[98]探讨了具有旋转和自旋-轨道耦合两分量BEC的基态性质, 发现了半量子数涡旋格子结构. 2012年Liu等[99]总结了skyrmions的类型, 并通过研究自旋-轨道耦合的两分量BEC的随机投影Gross-Pitaevskii方程, 发现自旋-轨道耦合能够诱导系统产生具有两个Sz极值的环形-双曲状的skyrmions. 图9为总结的skyrmions类型.
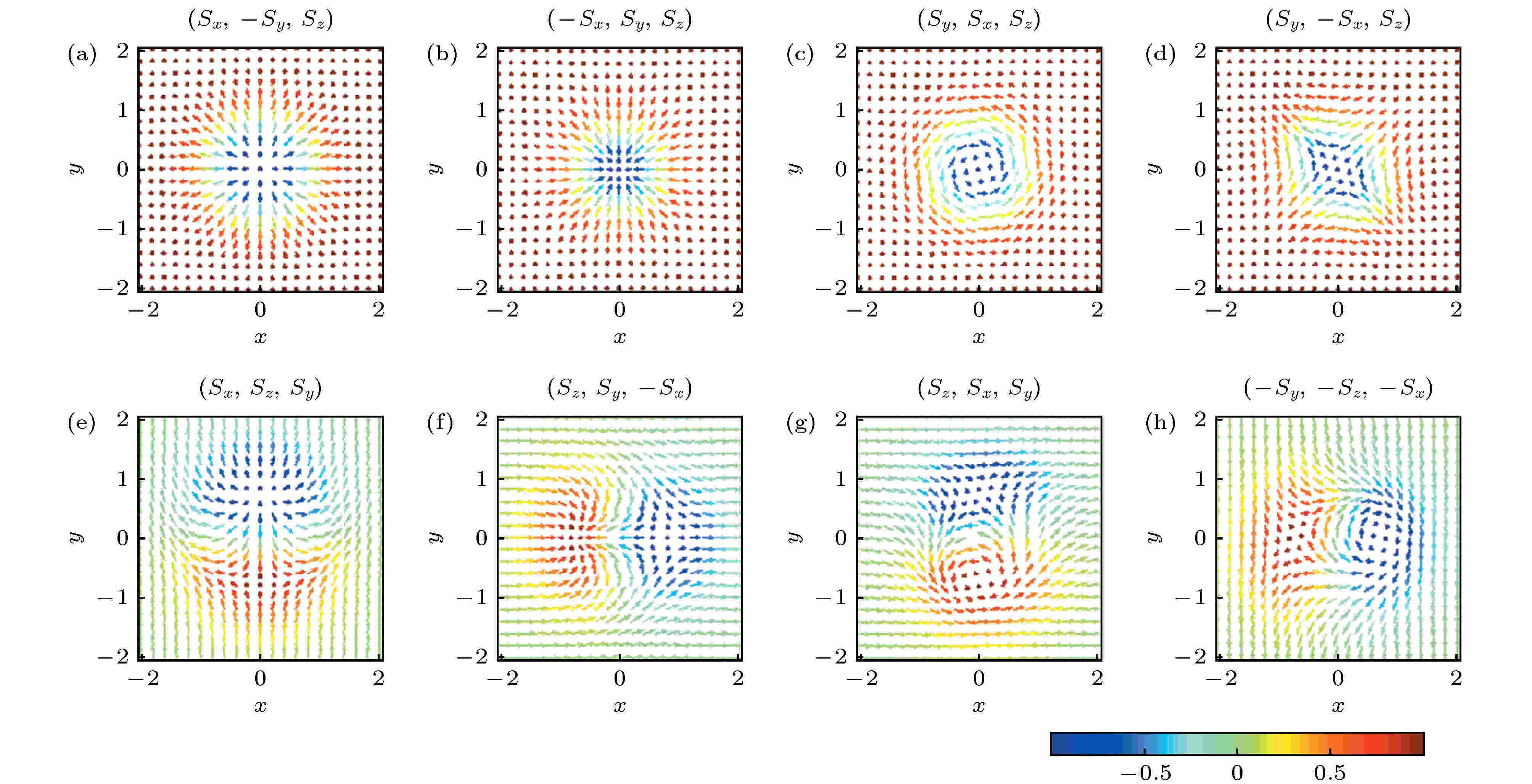 图 9 Skyrmions的类型(λ = 0.5)[99] (a)?(h)表示自旋矢量的模式: (a)径向-向外skyrmion, (b)径向-向内skyrmion, (c)环形skyrmion, (d)双曲skyrmion, (e)双曲-径向向外skyrmion, (f)双曲-径向向内skyrmion, (g)环形-双曲skyrmion-I, (h)环形-双曲skyrmion-II
图 9 Skyrmions的类型(λ = 0.5)[99] (a)?(h)表示自旋矢量的模式: (a)径向-向外skyrmion, (b)径向-向内skyrmion, (c)环形skyrmion, (d)双曲skyrmion, (e)双曲-径向向外skyrmion, (f)双曲-径向向内skyrmion, (g)环形-双曲skyrmion-I, (h)环形-双曲skyrmion-IIFigure9. Configuration of the skyrmion where λ = 0.5: The (a)?(h) figures indicate the mode of the spin vectors: (a) radial-out skyrmion, (b) radial-in skyrmion, (c) circular skyrmion, (d) hyperbolic skyrmion, (e) hyperbolic-radial(out) skyrmion, (f) hyperbolic-radial (in) skyrmion, (g) circular-hyperbolic skyrmion-I, and (h) circular-hyperbolic skyrmion-II[99].
2014年Wang等[100]研究了准二维旋转双分量BEC在改变自旋-轨道耦合和旋转频率强度的情况下呈现出的各种丰富的基态结构, 表明各向异性自旋-轨道耦合引起的不同基态相之间的转变明显不同于各向同性的情况. Fetter[101]用时间相关的拉格朗日形式和变分函数研究了自旋-轨道耦合的BEC中双组分涡旋的动力学. 2016年Sakaguchi和Umeda[102]通过数值模拟和变分方法, 研究了Rashba型自旋-轨道耦合的双组分BEC的Gross-Pitaevskii方程. 发现当不存在相互作用时, 多量子涡旋态成为谐波势中的基态. 当引力相互作用较强时, 多量子涡旋态在方位角方向呈现调制不稳定性, 出现孤子态. 当排斥相互作用较强时, 形成中心为多量子涡旋的涡旋晶格态, 且涡旋晶格态近似于多量子涡旋态的线性组合.
2017年Sakaguchi[103]通过数值分析研究了双组分BEC中自旋-轨道耦合条纹和半涡旋物质波孤子在组分间线性混合(Rabi耦合)作用下, 以耦合结构振荡和穿梭运动形式产生宏观量子效应的可能性. 研究得到在一维系统中, 本征振荡表现为条纹孤子在空间上的偶数分量和奇数分量之间的翻转, 而在二维系统中则表现为半涡旋孤子的零涡旋和涡旋分量之间的周期性跃迁. 同年, Wang等[104]研究了环形势阱中自旋-轨道耦合两分量BEC的旋涡态和自旋纹理, 系统地讨论了旋转、自旋-轨道耦合和原子间相互作用对系统基态涡旋结构和自旋纹理的影响. 特别是当旋转频率固定在临界值以上时, 各向同性自旋-轨道耦合的增强使每个分量中有一个可见的涡旋链, 在中心区域伴随着一个隐藏的巨涡旋和一个(或几个)隐藏的涡旋链. Kato等[105]研究了具有Rashba自旋-轨道耦合双组分BEC中涡旋-反涡旋对的动力学性质, 并且发现旋涡-反涡旋对的速度远小于无自旋-轨道耦合的速度且存在稳态, 而两个具有相同环流的涡旋相互移动或联合会形成一个静止状态.
2018年Shi等[106]研究了旋转非对称势阱中具有Dreselhaus自旋-轨道耦合(DSOC)的两分量BEC中的拓扑缺陷和自旋纹理. 结果表明, 对于不含自旋-轨道耦合的初始混合凝聚体, 旋转频率的增强可导致系统的结构相变. 在各向同性DSOC存在的情况下, 该系统维持涡流对、Anderson-Toulouse无核涡流、圆形涡旋片和组合涡旋结构. 特别地, 当旋转频率固定在径向势阱频率之上时, 强DSOC导致了由多层可见涡旋链、隐藏涡旋链和隐藏巨涡旋流组成的特殊拓扑结构. Li和Liu[107]利用Gross-Pitaevskii方程研究了自旋-轨道耦合作用和梯度磁场对旋转两分量BEC基态的影响. 研究结果表明, 在梯度磁场中, 随着自旋-轨道耦合强度增大, 基态结构由skyrmion格子逐渐过渡为沿着对角线方向排列的skyrmion列. 当自旋-轨道耦合强度和旋转频率都小的情况, 磁场梯度的增强可导致基态由平面波相转变为half-skyrmion; 当自旋-轨道耦合强度和旋转频率都大的情况, 梯度磁场可诱导hidden涡旋的产生. 图10为不同自旋-轨道耦合强度下梯度磁场中两分量87RbBEC基态粒子数密度分布和相位分布.
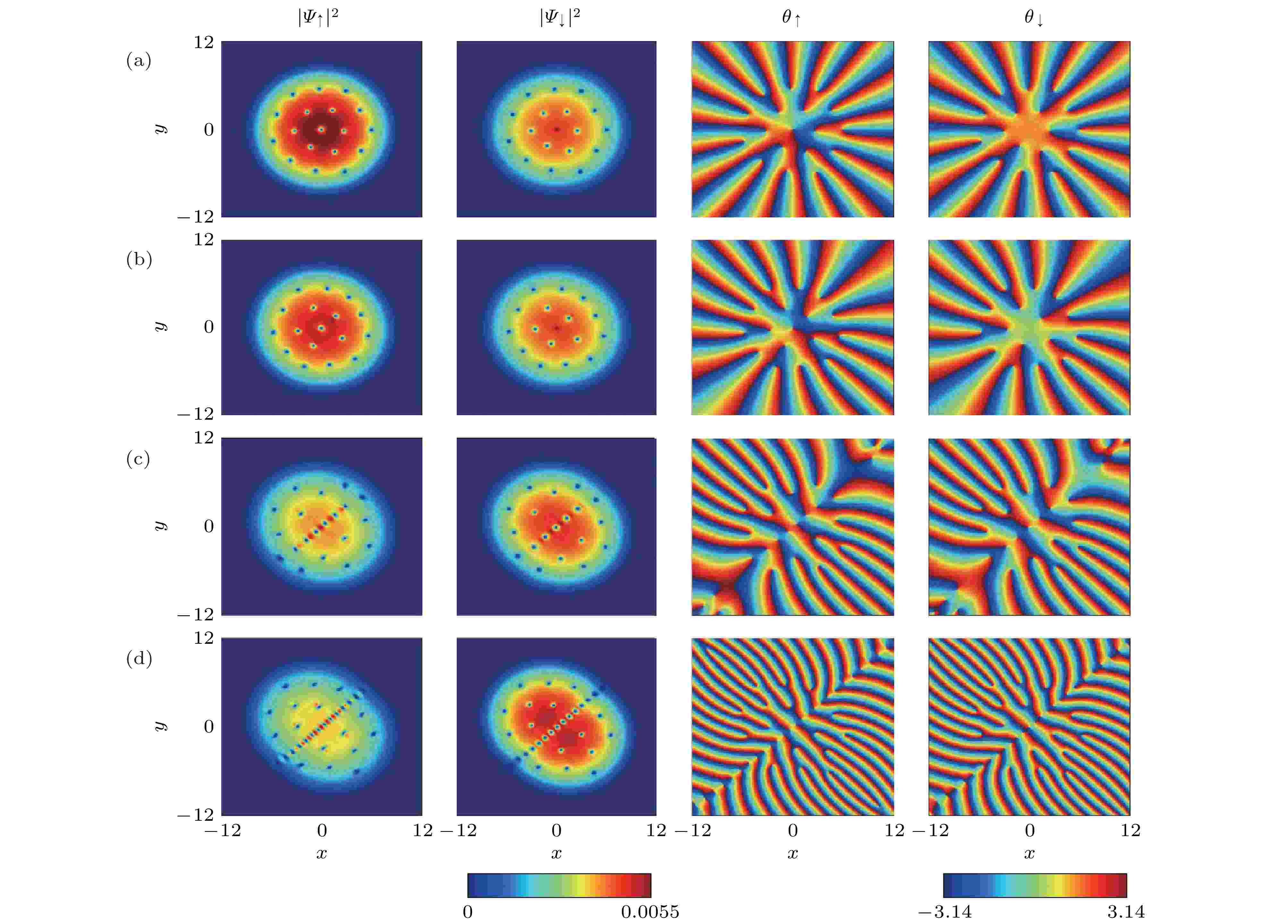 图 10 不同自旋-轨道耦合强度下梯度磁场中两分量87RbBEC基态粒子数密度分布(第1、2列)和相位分布(第3、4列)[107] (a)?(d)的
图 10 不同自旋-轨道耦合强度下梯度磁场中两分量87RbBEC基态粒子数密度分布(第1、2列)和相位分布(第3、4列)[107] (a)?(d)的
Figure10. Particle number densities (the first and second columns) and phase distributions (the third and fourth columns) of ground state of the two-component BEC of 87Rb for the different spin-orbit coupling strengths: the parameters of

2
4.2.三分量旋量玻色-爱因斯坦凝聚体中的拓扑缺陷研究
对于自旋F = 1的旋量三分量BEC, 原子可能占据的塞曼态有


实验上2001年Raghavan等[108]通过静态直流磁场在三分量旋量BEC中产生了暗孤子和涡旋结构. 2002年Ogawa等[109]采用四极磁场将自旋1BEC限制在Ioffe-Pritchard势阱中, 发现在凝聚体中产生了涡旋. 2006年Itin等[110]研究了自旋1BEC在一对载流线和偏置磁场控制的双磁阱中产生涡旋的几种机制, 图11为凝聚体快速分裂过程中涡旋的动力学形成, 显示动态涡旋存在于凝聚体的所有分量中, 在ψ–1分量中占99%以上, 在ψ0分量中动态涡旋和拓扑涡旋共存. 2014年, Ray等[80,81]在自旋1BEC中借助梯度磁场, 观察到了狄拉克磁单极子, 图12为狄拉克磁单极子的实验产生过程, 显示了凝聚体中不同自旋组分中的粒子密度随BZ, f的减小而减小.
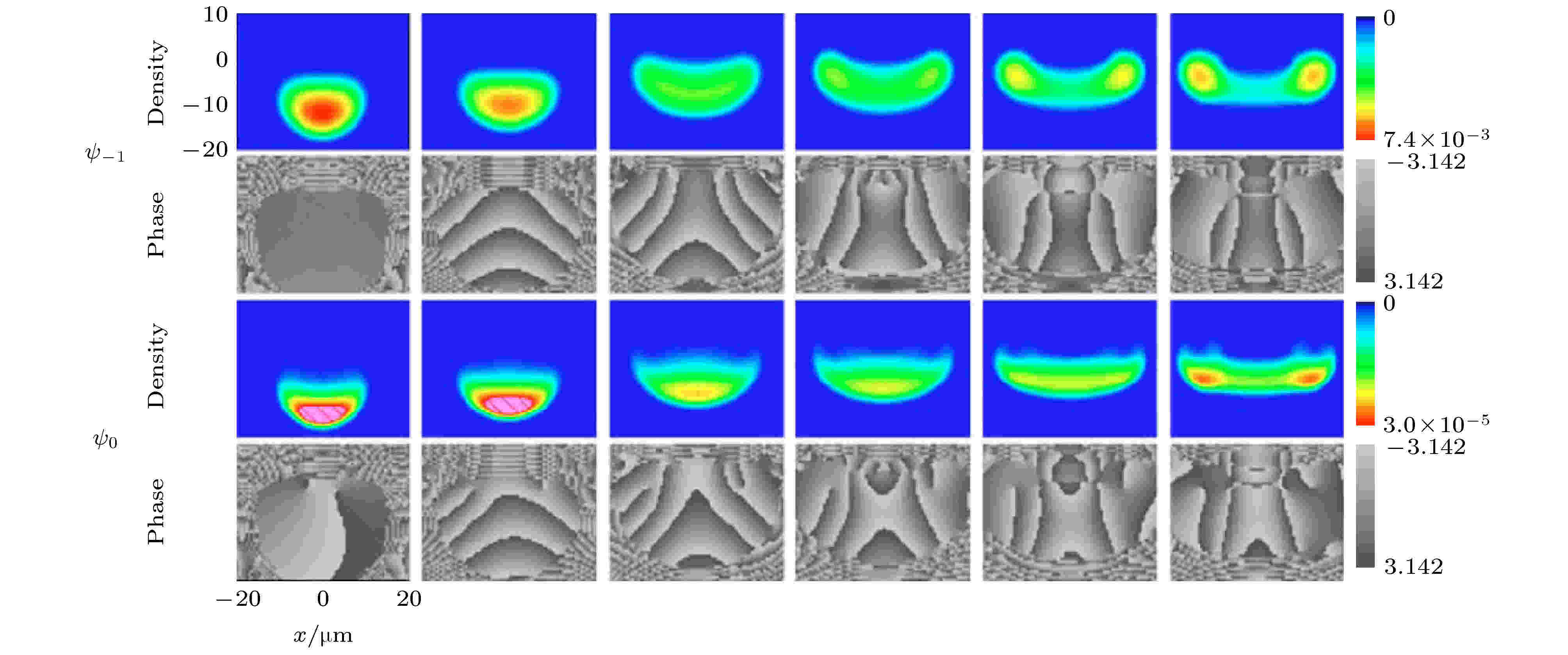 图 11 涡旋的动力学形成[110]. 涡旋形成于凝聚体的所有分量中, 在ψ–1分量中占99%以上, 在ψ0分量中动态涡旋和拓扑涡旋共存
图 11 涡旋的动力学形成[110]. 涡旋形成于凝聚体的所有分量中, 在ψ–1分量中占99%以上, 在ψ0分量中动态涡旋和拓扑涡旋共存Figure11. Dynamical formation of vortices: vortices are formed in all components, more than 99% of total population is in ψ–1 component. In the ψ0 component, dynamical and topological vortices coexist[110].
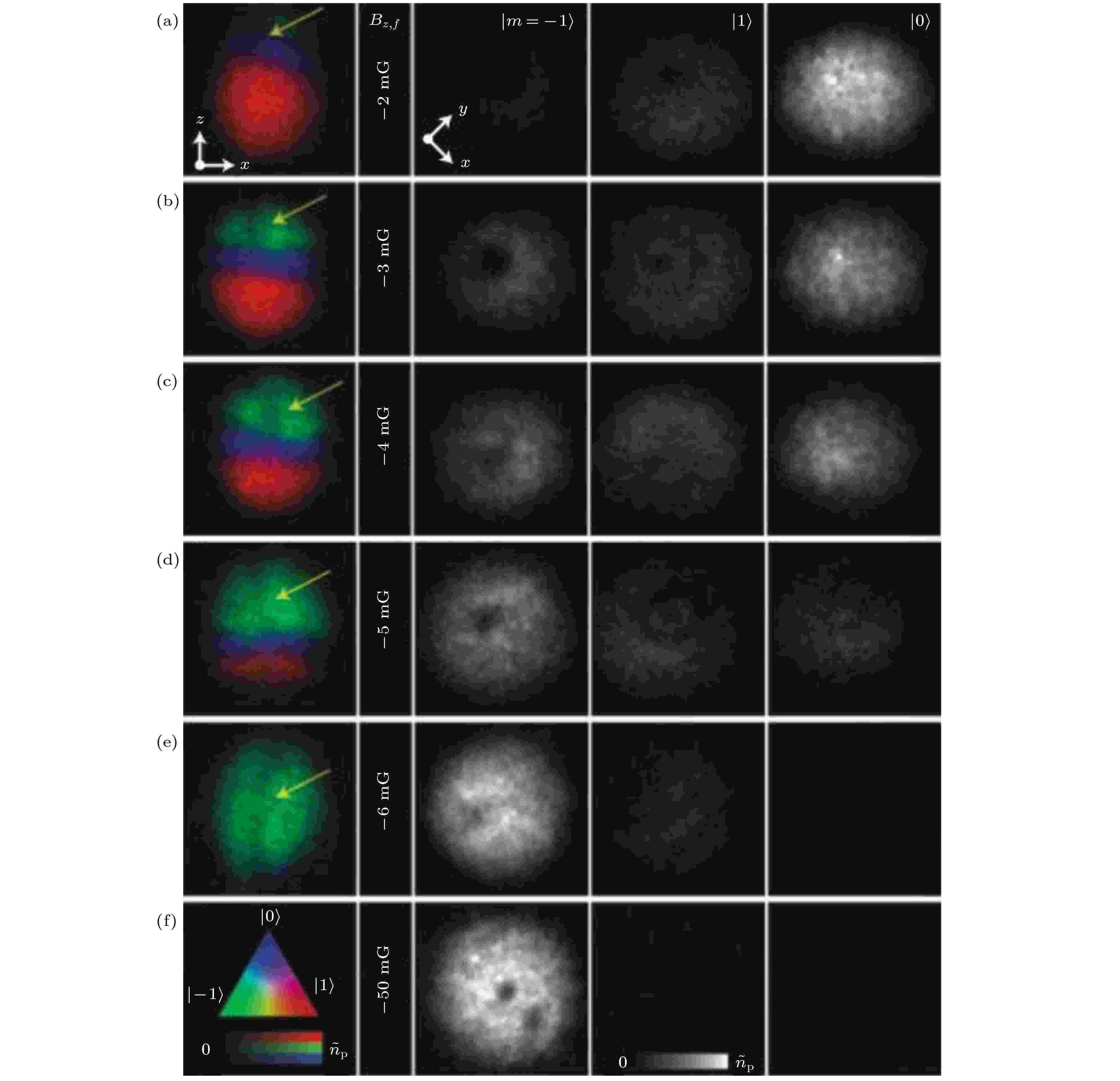 图 12 狄拉克磁单极子的实验产生[80] (a)?(f)每一行都包含单个凝聚体的图像. 最左边的列显示了三种自旋状态
图 12 狄拉克磁单极子的实验产生[80] (a)?(f)每一行都包含单个凝聚体的图像. 最左边的列显示了三种自旋状态
Figure12. Experimental creation of Dirac monopoles. Each row (a)?(f) contains images of an individual condensate. The leftmost column shows colour composite images of the column densities taken along the horizontal axis for the three spin states

理论上2002年Isoshima和Machida[111]在旋转外势下, 采用推广的Bogoliubov理论研究了自旋1BEC中各种轴对称涡旋的稳定结构. 同年Mizushima等[112]通过求解广义Gross-Pitaevskii方程研究了旋转条件下铁磁自旋1BEC中的Mermin-Ho和Anderson-Toulouse无核涡旋, 得到在铁磁情况下, Mermin-Ho涡旋是稳定的. 2006年Saito等[113,114], 以及2009年Turner[115]研究了铁磁自旋1BEC中的极核涡旋, 发现系统核心由mF = 0原子填充, 围绕涡旋有mF = 1分量的质量流, 以及mF = –1分量的相等但自旋相反的质量流, 这就产生了净自旋流, 但没有净质量流. 2007年Mottonen等[116]研究了非旋转条件下在三维抛物势与Ioffe-Pritchard场中的自旋1铁磁态旋量BEC中无核涡旋的能量和动力学稳定性.
2008年Ji等[117]研究了自旋1钠原子BEC中半量子涡旋的动态生成. 模拟结果表明, 在外加脉冲磁捕获势的情况下, 旋转光势阱中可以同时产生独立的半量子涡旋和涡旋晶格, 同时还发现, 一个明显的周期调制的自旋密度波空间结构总是嵌入在方形半量子涡旋晶格中. 2012年Liu和Liu[118]研究了旋转和快速淬火的自旋1BEC中由自旋-轨道耦合引起的半skyrmion激发, 给出了描述半skyrmion自旋矢量的三个表达式. 结果表明, 半skyrmion激发依赖于自旋-轨道耦合和旋转的结合, 当自旋-轨道耦合强度和旋转频率均大于某些临界值时, 半skyrmion由一个或几个圆包围中心, 形成径向晶格, 即使在强铁磁(或反铁磁)凝聚体中也会发生. 图13为旋转频率对23Na旋量BEC自旋纹理的影响.
 图 13 旋转频率对23Na旋量BEC的影响[118], 其中
图 13 旋转频率对23Na旋量BEC的影响[118], 其中


Figure13. The effect of rotation frequency for spinor BEC of 23Na with



2013年Liu等[119]利用阻尼映射Gross-Pitaevkii方程, 研究了二维体系中自旋-轨道耦合的23Na自旋1BEC中的涡旋斑图, 研究发现较弱的自旋-轨道耦合可以完全破坏不考虑自旋-轨道耦合情况下出现的周期性涡旋晶格; 在自旋-轨道耦合较强的情况下, 各自旋态的涡旋易形成涡旋组, 并绕凝聚体中心形成花瓣状涡旋斑图. 2014年Song等[120]利用精确对角化和平均场理论研究了弱相互作用的自旋-轨道耦合自旋1玻色气体在外谐波势阱中的碎裂问题, 研究发现这种碎裂倾向源于总角动量守恒, 且受自旋-轨道耦合强度和自旋相关相互作用的影响. Lovegrove等[121]将铁磁态无核涡旋通过相位植入法, 在极化态凝聚体中得到了混合态下稳定的无核涡旋. 2015年Zhao等[122]在自旋1BEC中解析得到了两种不均匀的自旋畴构型, 它们分别由正二次塞曼效应和负二次塞曼效应所致. 分析表明, 二次塞曼效应可以诱导自旋畴的动态相变, 其符号可以影响自旋模式的拓扑结构. 2016年, Gautam和Adhikari[123]对零磁化强度的自旋1和自旋2旋量BEC中的分数涡旋进行分类, 并利用精确的数值解和拉格朗日变分近似研究了准二维旋量BEC中涡旋的静力学和动力学性质.
2017年Liu等[124]通过虚实演化方法研究了具有面内四极磁场自旋1的旋量BEC的基态结构. 研究发现, 面内四极磁场和旋转双重作用可导致中央Mermin-Ho涡旋的产生; 随着磁场梯度增强, Mermin-Ho涡旋周围环绕的涡旋趋向对称化排布; 在四极磁场下, 密度相互作用和自旋交换相互作用作为体系的调控参数, 可以控制Mermin-Ho涡旋周围的涡旋数目. Li等[125]研究了铁磁自旋1BEC中由自旋-轨道耦合引起具有极核旋涡的狄拉克磁单极子, 随着自旋-轨道耦合强度的增加, 具有极核涡旋的狄拉克磁单极子可以转化为正方形晶格. 在自旋-轨道耦合确定的情况下, 增大相互作用强度可引起从具有极核涡旋的狄拉克磁单极子向具有Mermin-Ho涡旋的循环相变. 图14显示了具有Mermin-Ho涡旋的磁单极子的形成.
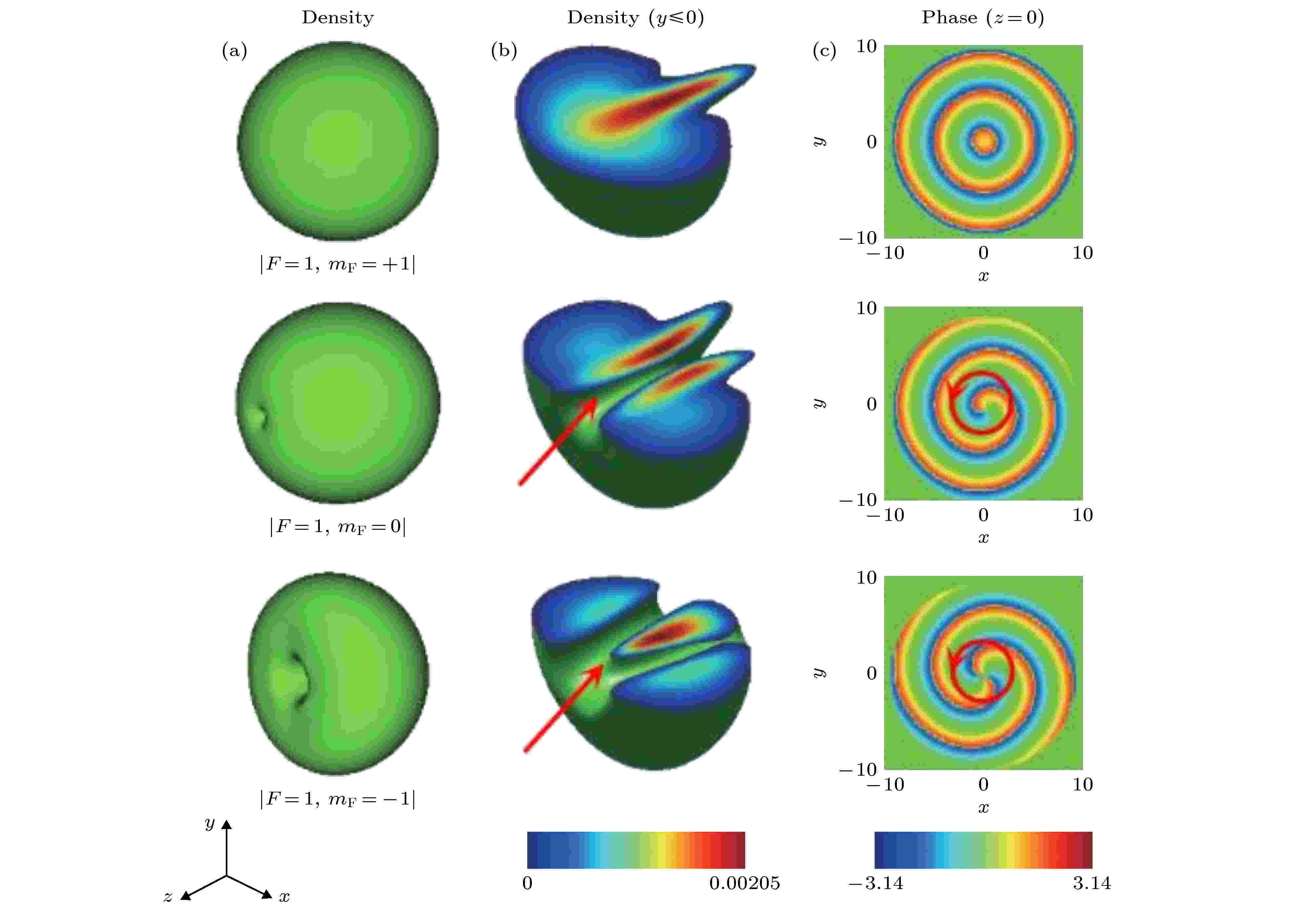 图 14 具有Mermin-Ho涡旋的磁单极子[125] (a)等值面的粒子数密度; (b)粒子数密度等深线段(y ≤ 0), 节点线(Dirac线)的位置用红色箭头突出显示; (c) z=0平面上的位相分布. 单涡旋(mF = 0)和双涡旋(mF = –1)具有相同的环流, 由红圈突出显示
图 14 具有Mermin-Ho涡旋的磁单极子[125] (a)等值面的粒子数密度; (b)粒子数密度等深线段(y ≤ 0), 节点线(Dirac线)的位置用红色箭头突出显示; (c) z=0平面上的位相分布. 单涡旋(mF = 0)和双涡旋(mF = –1)具有相同的环流, 由红圈突出显示Figure14. The monopoles with the Mermin-Ho vortex: (a) Isosurface of particle densities; (b) segments of isosurface of particle densities (y ≤ 0). the position of the nodal line (Dirac string) is highlighted by the red arrow; (c) phase distributions in the z = 0 planes. the single vortex (mF = 0) and double vortex (mF = –1) have the same circulations, as highlighted by the red circles[125].
