摘要:在就地γ谱仪搜索扫描测量“热粒子”、“放射性汇集点”、“放射性汇集区”过程中, 只能给出污染源的大概位置, 不能给出源的污染深度等边界参数. 本文主要对虚拟技术在就地γ谱仪搜索扫描测量细化污染源边界中的应用进行了研究. 将就地γ谱仪测量对象简化成衰减层 + 放射性热区(测量目标源) + 衰减层 + 干扰源的四层理论模型, 运用虚拟技术将源项层虚拟成点源, 进一步简化了理论模型, 使用蒙特卡罗方法模拟计算探测效率与峰谷比等参数, 最后使用最小二乘法使模拟计算结果反演逼近源项实际参数, 从而建立了源边界参数反演计算的理论方法及步骤. 理论研究和实验结果一致, 验证了所建立的计算模型和技术方法是正确可靠的. 目前, 对于均匀分布的放射性核素, 该技术已经能够准确确定污染区域深度分布等边界参数, 从而在治理时达到废物处置减容的目的. 同时, 该技术对于禁核试核查目标核弹头惰层厚度参数的确定也具有重大的参考价值.
关键词: 虚拟点源/
参数表征/
蒙特卡罗模拟/
源边界

English Abstract

全文HTML

--> --> -->

“热粒子”、“放射性汇集点”、“放射性汇集区”的监测是目前国际上核辐射探测领域重点关注的参数, 其中放射性源边界是最为关键的参数. 目前国内外现有的就地γ谱仪搜索扫描测量及伽玛相机成像技术, 只能给出污染源的大概位置, 而对于源边界参数的确定目前研究较少, 尤其是无法给出核素深度方向的参数; 通过出壳γ谱反推核弹头结构材料厚度是一件比较复杂和难度较大的工作, 需要的参数多, 解的不确定性大^[1]. 因此, 亟待发展新的测量方法和实验技术来解决这些问题. 放射性源边界测量的准确性最为关键的是探测效率因子这个参数的准确刻度^[2,3], 而国内外针对这个问题开展的研究也非常多, 在蒙特卡罗模拟刻度中主要使用点源实验表征晶体参数^[4-10], 提高了测量的准确性; 在虚拟刻度方面, 国内外开展了虚拟点探测器理论研究^[11-15], 虚拟点探测器模型由Noteal^[15]最早提出, 在处理探测器效率刻度问题中该模型被许多研究者使用并进行了大量的实验验证. 在测量源与探测器之间存在一定距离时可用虚拟的点探测器来等效大体积的探测器, 此时探测器峰效率将较精确地满足平方反比定律, 这样, 对于一确定尺寸的探头, 虚拟点探测器位置仅随光子能量的变化而变化. 根据平方反比定律, 可求得空间任意一点处点源的峰效率, 然后可对点源效率积分求解得到体源的探测效率, 即使用点源完成了复杂体源的刻度, 简化和方便了仪器刻度工作. 本文反向使用蒙特卡罗模拟表征晶体参数的技术, 结合虚拟点探测器理论及虚拟源刻度方法等^[16,17], 根据测量能谱分析, 就可以确定放射性污染区域深度方向分布参数, 同时对反解核弹头惰层厚度具有参考意义.

HPGe探测器晶体一般为圆柱状, 射线与晶体的作用可以认为是射线与晶体内一虚拟点探测器作用, 即将晶体等效为一个虚拟的点. 这个虚拟的点位置可能不止一个, 但是为了简化模型和计算方便, 一般是在探测器中心对称轴线找到一个且唯一一个代表性的点(代表点), 该点距离晶体上表面的距离又称有效作用深度. 虚拟点探测器: 对于辐射探测器, 在探测器中心对称轴线上存在有一个唯一的代表点位置, 其点探测器对参考点位置点源的探测效率与探测器对点源的探测效率相等且满足平方反比定律, 即该点探测器叫探测器的虚拟点探测器. 虚拟点探测器刻度方法首先用于点源探测效率的刻度, 主要借用参考点位置的标准点源探测效率值通过平方反比定律来计算空间不同位置处点源的探测效率.
根据虚拟点探测器的理论, 将探测器测量对象也进行虚拟化, 定义虚拟点源概念. 虚拟点源: 对于辐射探测器测量对象为单个体源或单个面源的情况下, 在探测器中心对称轴线上有一个唯一的代表点位置, 该位置的放射性点源全能峰探测效率与所对应的放射性体源或面源的探测效率相等, 该点源叫做体源或面源的虚拟点源. 在多数情况下, 测量对象可能不止一个源, 有可能是多个源(体源、面源和点源)组成, 为了区分单个源的情况, 在这里引入等效虚拟点源. 等效虚拟点源: 对于辐射探测器测量对象为混合源(多个体源、面源和点源组成)情况下, 在探测器中心对称轴线上有一个唯一的代表点位置, 该位置的放射性点源全能峰探测效率与混合源探测效率相等, 该点源叫作混合源的等效虚拟点源. 它和虚拟点源的区别是测量对象为多个源, 其他定义都一致.
在无源效率刻度中, 蒙特卡罗模拟表征晶体参数的研究工作非常多, 技术方法也非常成熟. 其基本原理是: 通过标准点源或体源(源的形状大小、材料和活度参数等完全已知)固定位置实验, 获取探测器的实验效率刻度值, 再使用蒙特卡罗方法建立理论计算模型, 调整理论计算模型中的晶体参数使其计算效率值和实验值一致, 从而达到表征晶体参数的目的. 在这一表征的过程中测量对象源的参数是已知的, 测量仪器晶体参数是未知的, 但在实际测量中经常会遇到大量测量对象未知的情况. 针对这种情况, 本文采用逆向思维, 提出源边界参数表征技术, 即晶体参数已知, 源边界参数未知. 其基本原理和晶体参数表征技术类似: 即首先通过实验方法获得测量对象的峰谷比及全能峰探测效率的实验值, 再通过蒙特卡罗方法建立理论计算模型, 为了优化理论计算模型, 使用虚拟技术将测量对象虚拟成点源, 计算调整理论模型中的源边界参数并借助最小二乘方法使计算得到的峰谷比及效率值不断逼近实验值. 具体过程是: 污染沙土的放射性源项层可能会很复杂, 可能有很多各种各样的源组成, 各个源之间又有沙土衰减层, 但不管怎么复杂, 都将它们统一简化成如图1所示的四层理论模型.
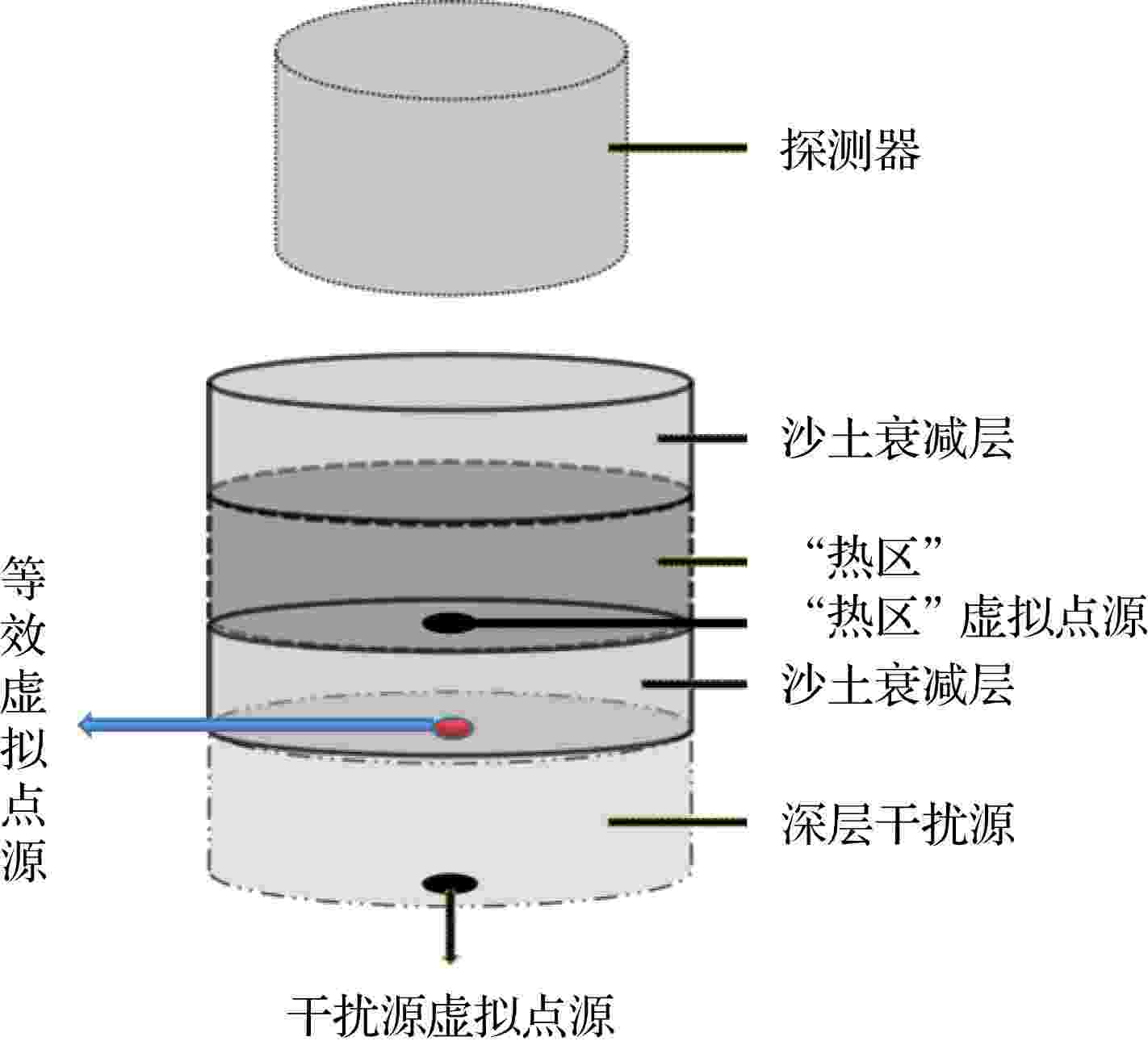图 1 源边界参数反演理论模型
Figure1. The inversion theory model of source boundary parameters.

关心的测量对象目标源一般为体源(目标体源), 又称放射性“热区”, 若直接裸露于地表, 就没有图1中最上一层沙土衰减层. 同时, 热区下方可能存在其他放射源, 我们称之为干扰源, 干扰源是一个相对概念, 当关心它的参数时, 也可以定为目标源. 热区和干扰源之间有衰减层, 干扰源在一些源项简单的测量中可能就不存在. 本文的目标就是在有干扰源存在的情况下反演出热区位置及厚度参数. 具体分三步反演.
第一步: 等效虚拟点位置的实验反演计算. 使用虚拟技术将热区和深层干扰源虚拟成一个等效虚拟点源, 该虚拟点源包含了所有源项的辐射信息. 对于钚污染土, ²⁴¹Am和²³⁹Pu的单位体积活度比一般为常数, 设为$Q ={{{A_{239}}}}/{{{A_{241}}}}$, 其中A表示活度(Bq), 其与探测效率的关系推导为:

${A_{241}} = \frac{{{N_{241}}}}{{t \times {\varepsilon _{241}} \times {P_{{\rm{\gamma }}241}}}},$

${A_{239}} = \frac{{{N_{239}}}}{{t \times {\varepsilon _{239}} \times {P_{{\rm{\gamma }}239}}}},$

$Q = \frac{{{\varepsilon _{241}}}}{{{\varepsilon _{239}}}} \times \frac{{{P_{{\rm{\gamma }}241}} \times {N_{239}}}}{{{P_{{\rm{\gamma }}239}} \times {N_{241}}}},$

其中t为测量时长(s), N表示特征射线全能峰计数, ε表示探测效率, 241表示²⁴¹Am, 239表示²³⁹Pu, ${P_{\rm{\gamma }}}$表示射线分支比. ²⁴¹Am核素的59.54 keV (分支比0.359, 26.4 keV分支比0.024)和²³⁹Pu核素的51.62 keV (分支比0.000271, 129 keV分支比0.000062)射线全能峰计数一般通过实际测量能谱得到, 分支比也是常数, 因此从(3)式可以看出活度比和探测效率比是一一对应的, 因此, 在图1中对称轴上(使用MCNP程序模拟计算对称轴上不同位置处点源探测效率)总能找到一个等效虚拟点位置, 该处的射线全能峰探测效率比算得的²³⁹Pu/²⁴¹Am活度比应与给出的一致. 该步反演除了得到等效虚拟点位置外还得到三个参数: 实测59.54 keV射线的峰谷比以及等效虚拟点处59.54 keV和26.4 keV或129 keV射线全能峰探测效率, 这些参数是下一步反演计算的基础. 其中59.54 keV射线的峰谷比设为X₁, 59.54 keV射线全能峰探测效率参数设为X₂, 26.4 keV或129 keV射线全能峰探测效率参数设为X₃, E表示根据实验获得的数学期望值, 则它们的数学期望分别表示为:

$\frac{{{N_{\rm m}}}}{{{N_{\rm {vm}}}}} = E({X_1}),$

$\varepsilon ({h_{\rm{e}}}) = E({X_2}),$

$\varepsilon {({h_{\rm{e}}})^*} = E({X_3}),$

v表示谷区, 对于59.54 keV射线一般取54—57 keV这个区间, h表示虚拟点位置(虚拟点位置一般在源对称轴线上变化), m表示实测谱值, e表示等效虚拟点, 上标^*用于区分虚拟点位置处不同能量射线全能峰探测效率. (5)和(6)式左边的虚拟点源位置h_e处的探测效率值是通过核素活度比值(3)式定出, 峰谷比通过能谱获得.
第二步: 热区和深层干扰源的虚拟点源位置反演计算. 将热区和深层干扰源分别虚拟成其虚拟点源, 如图1中所示, 用a表示图1中上虚拟点位置(热区虚拟点位置), b表示下虚拟点位置(深层干扰源虚拟点位置), 等效虚拟点是由这两个虚拟点按不同的权重组合而成的. 设59.54 keV和26.4 keV或129 keV射线在对称轴上不同位置按不同权重组合模拟计算结果设为X_i, 表示为:

$\frac{N}{{{N_{\rm v}}}}({h_{\rm{a}}}){w_{\rm{a}}} + \frac{N}{{{N_{\rm v}}}}({h_{\rm{b}}})(1 - {w_{\rm{a}}}) = {X_1},$

$\varepsilon ({h_{\rm{a}}}){w_{\rm{a}}} + \varepsilon ({h_{\rm{b}}})(1 - {w_{\rm{a}}}) = {X_2},$

$\varepsilon {({h_{\rm{a}}})^*}{w_{\rm{a}}} + \varepsilon {({h_{\rm{b}}})^*}(1 - {w_{\rm{a}}}) = {X_3},$

w表示权重因子; 然后结合第一步获取的E(X_i)参数使用最小二乘法计算均方偏差$\sigma (X)$, 如(10)式所示, 找出均方偏差$\sigma (X)$最小的组合(其对应的热区和深层干扰源的虚拟点源位置就是所求)即可.

$\sigma (X) = \sqrt {\frac{1}{3}\sum\limits_{i = 1}^3 {{{\big[({X_i} - E({X_i}))/E({X_i})\big]}^2}} } .$

该步反演结果是分别得到热区和深层干扰源的虚拟点源位置以及它们的射线全能峰探测效率及峰谷比信息.
第三步: 根据第二反演得到热区虚拟点源位置反演计算热区参数. 使用MCNP程序模拟计算热区源项不同参数组合下(不同衰减层厚、不同源厚两两组合)的射线全能峰探测效率和能谱的峰谷比参数, 利用(10)式计算, 找出均方偏差ó最小的组合(其对应的衰减层厚度和热区厚度就是所求)即可.

根据图1的理论计算模型, 设计了两种实验探测模式. 探测模式1: 75 mm × 25 mm ²³⁹Pu体源下方放置1.6 cm厚沙土衰减层然后放置在距离平板型高纯锗探测器铍窗0.953 cm位置处, 源与衰减层密度都为1.34 g/cm³, 如图2所示.
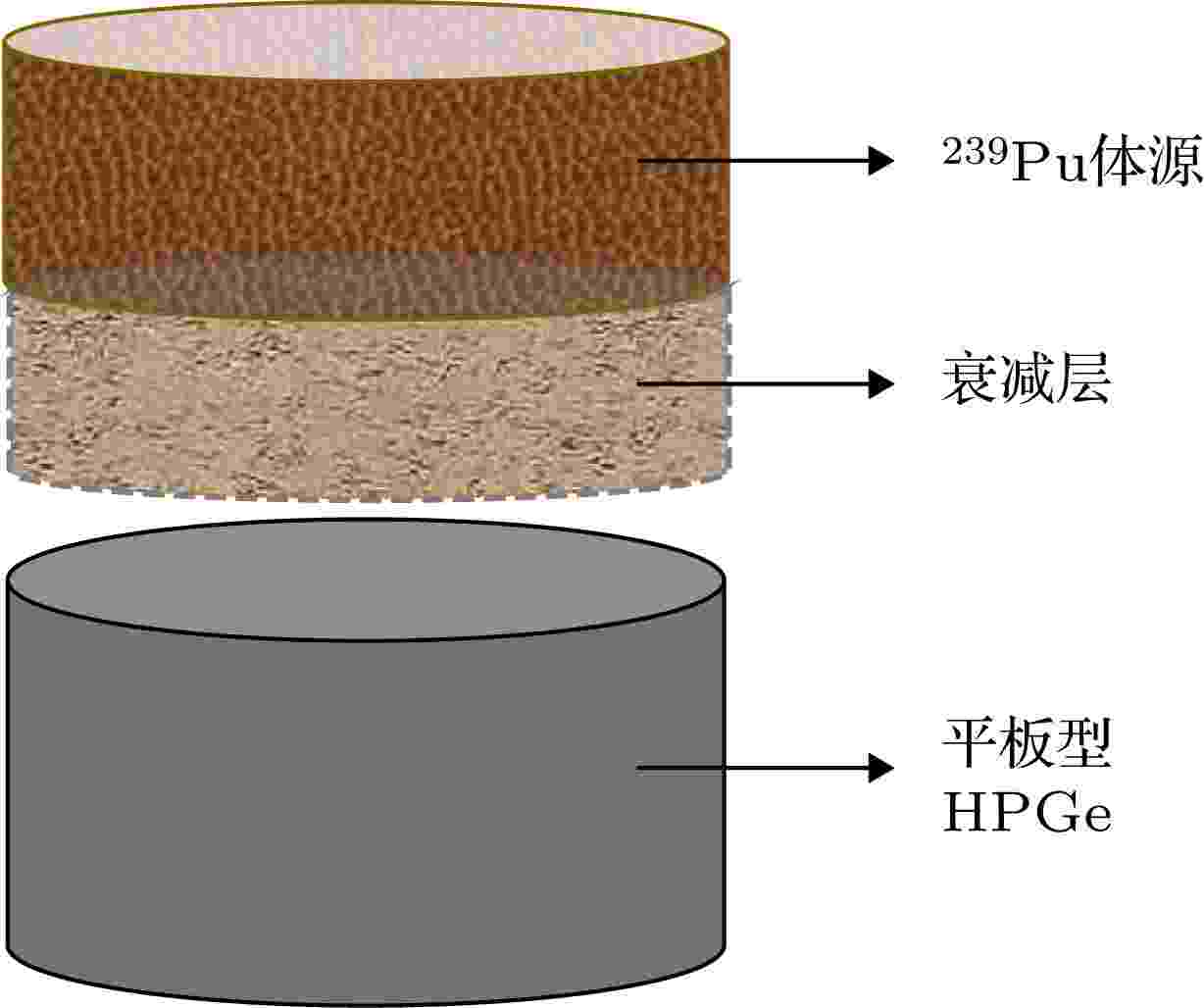图 2 探测模式1
Figure2. The detection mode 1.

探测模式2: ²⁴¹Am点源通过支架放置在距离2.0 cm处的0.5 cm厚沙土衰减层上再将其放置在75 mm × 25 mm厚²⁴¹Am体源上, 然后将它们整个放置在平板型高纯锗探测器铍窗进行放射性测量, 源与沙土地密度都为1.43, 如图3所示.
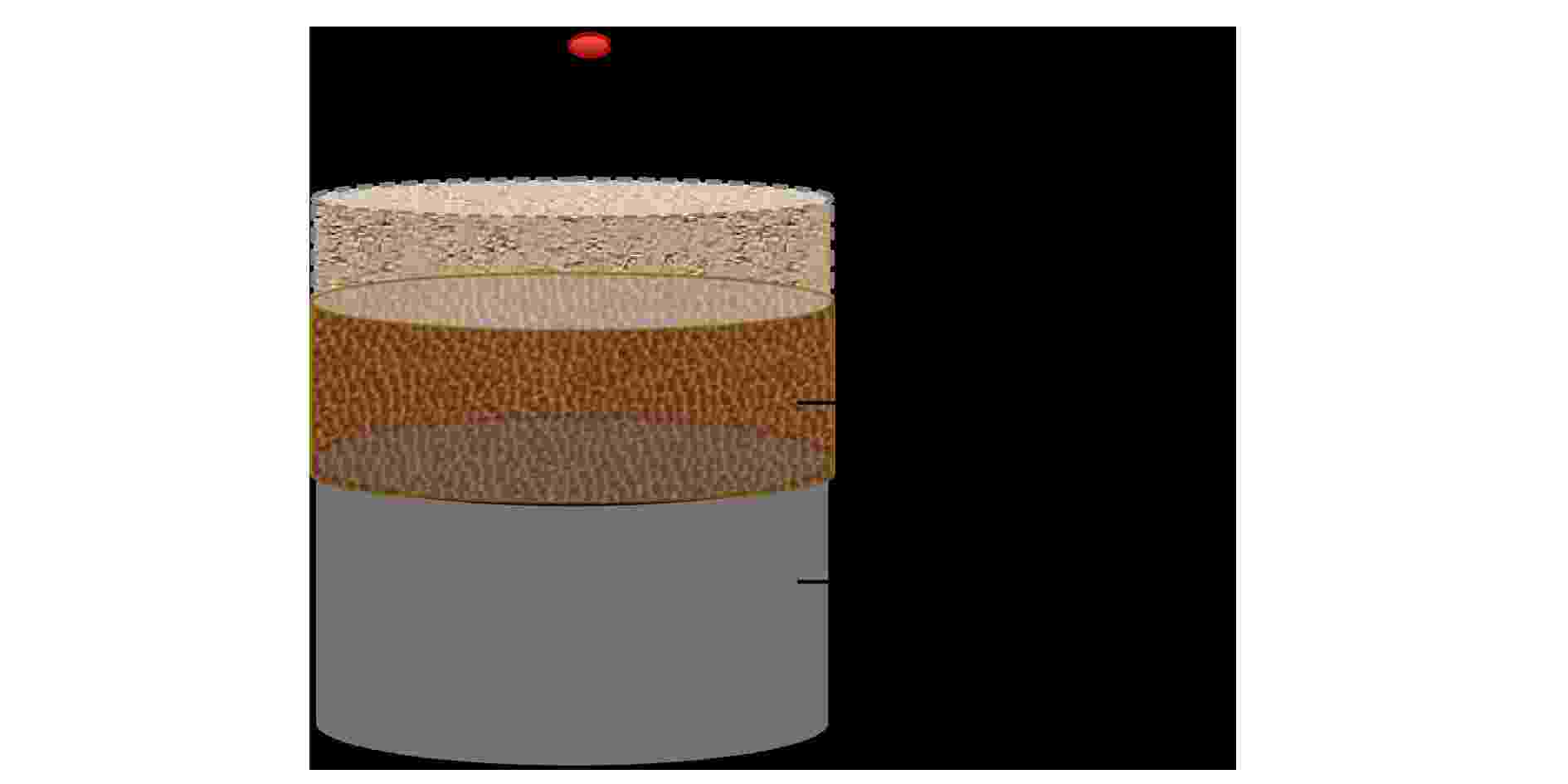图 3 探测模式2
Figure3. The detection mode 2.

谱获取时间足够长, 保证使其统计涨落控制在1.0%以内, 实验数据见表1和表2 (表1和表2中分别给出了体源和点源单独测量数据, 只是为了获得两种探测模式的实验参数, 因此不涉及计算参数的数据, 在此未提供).

测量对象	测量时长t/105 s	N241 (54—57 keV)	N241 (59.54 keV)	N239 (51.62, 129 keV)	A/104 Bq
					241Am	239Pu
探测模式1	3.16	4325136	25339979	—	—	—
239Pu体源	2.00	—	75248200	239711, 52717	4.56	18.7

表1探测模式1实验能谱峰计数及处理结果
Table1.Energy peak count of experimental spectrum and process results for detection mode 1.

测量对象	测量时长 t/105 s	N241 (26.4 keV)	N241 (54—57 keV)	N241 (59.54 keV)	A/× 104 Bq
					26.4 keV	59.54 keV
探测模式2	4.00	240050	9531180	65964536	8.16	8.91
241Am点源	0.565	4160024	—	65331456	7.74	8.38
241Am体源	0.800	45346	—	2745773	0.423	0.532

表2探测模式2实验能谱峰计数及处理结果
Table2.Energy peak count of experimental spectrum and process results for detection mode 2.

将计数通过计算转化为活度, 活度计算结果见表1, 其中探测效率数据是由蒙特卡罗模拟计算给出. 体源效率: 51.62 keV为2.03 × 10^–2, 59.54 keV为2.3 × 10^–2, 129 keV为2.72 × 10^–2, 其中活度计算结果18.7 × 10⁴ Bq是取了²³⁹Pu核素两条射线计算结果的平均值, A₂₃₉/A₂₄₁ = 18.7/4.56 = 4.1 (对于未知源项目标该比值一般是通过取样测量得到, 或根据已有资料查询得到). ²⁴¹Am源谷区选择54—57 keV能区, 探测模式1下峰谷比为25339979/4325136 = 5.9.
表2中, ²⁴¹Am点源效率26.4 keV为3.66 × 10^–2, 59.54 keV为4.16 × 10^–2; ²⁴¹Am体源效率26.4 keV为4.44 × 10^–3, 59.54 keV为2.26 × 10^–2. 在探测模式2下, 通过²⁴¹Am两个射线能量计算其活度, 其总活度为点源活度加体源活度, 如26.4 keV射线能量计算总活度为8.16 × 10⁴ (Bq) = (7.74 + 0.423) × 10⁴ (Bq), 59.54 keV射线能量计算总活度结果为8.91 × 10⁴ (Bq) = (8.38 + 0.532) × 10⁴ (Bq), 且A₂₄₁ (26.4 keV)/A₂₄₁ (59.54 keV)比值理论上应该是1.0, 但由于存在系统误差, ²⁴¹Am (26.4 keV)/²⁴¹Am (59.54 keV)比值计算结果为8.16/8.91 = 0.92, 对于这个系统误差可以不用校正, 因为后面计算都采用该比值. 探测模式2下, 峰谷比为65964536/9531180 = 6.9.

根据实验设计及探测器参数, 建立了如图4和图5所示的蒙特卡罗计算模型(图中的数字及位置坐标表示尺寸参数). 探测器参数: 晶体角死层被两个球及一个圆柱所切得到, 球心在Z轴上坐标分别为1.90和3.44, 球半径分别为1.90和2.06. 图中单位为cm. 铍窗密度1.85, 沙土成分由下列元素(符号)组成: O(52.2%), Si(30.6%), Al(5.49%), Fe(2.21%), Ca(8.04%), Mg(1.40%), 括号内为质量分数.
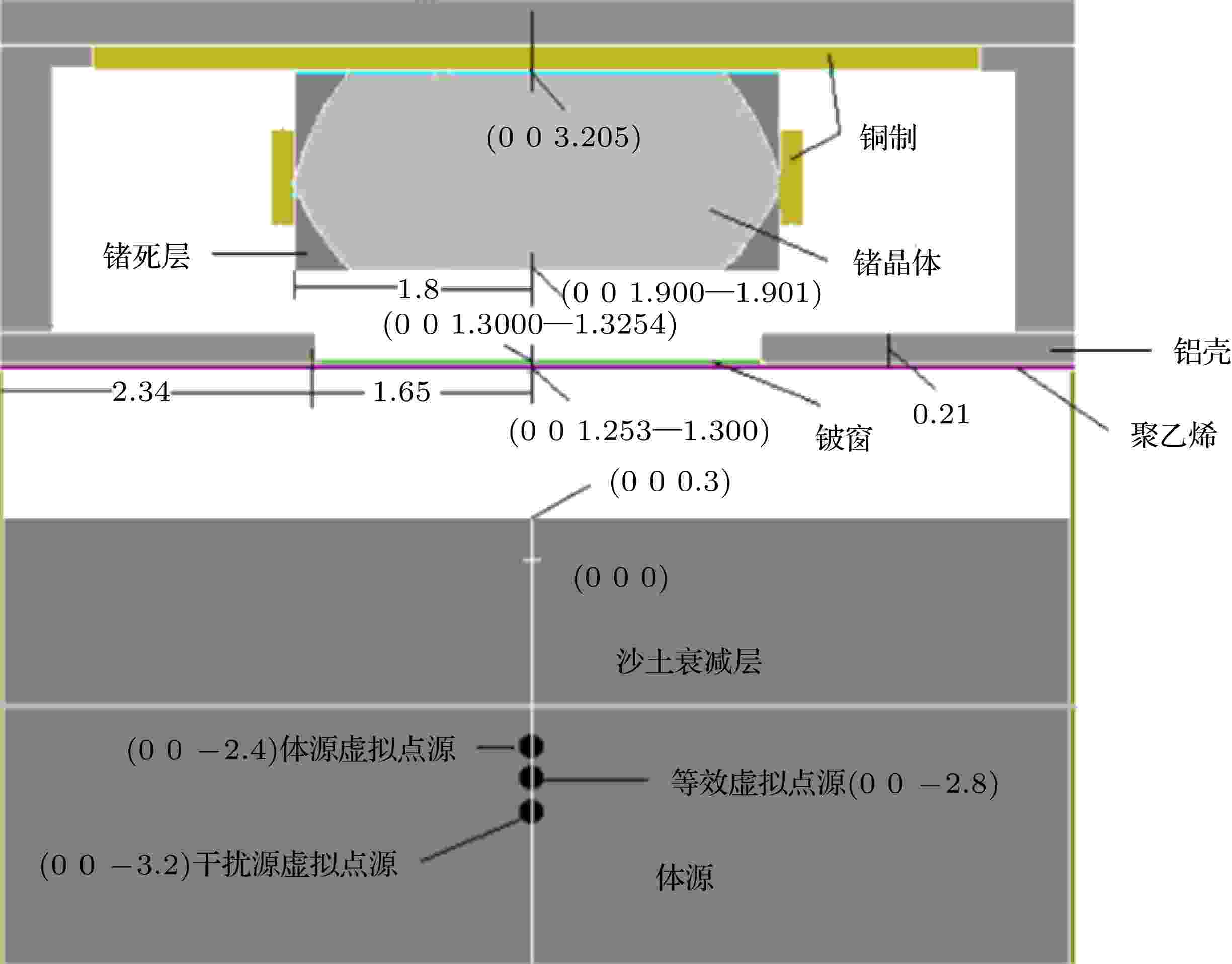图 4 探测模式1的MCNP程序计算模型
Figure4. Calculation model of MCNP procedure for detection mode 1.

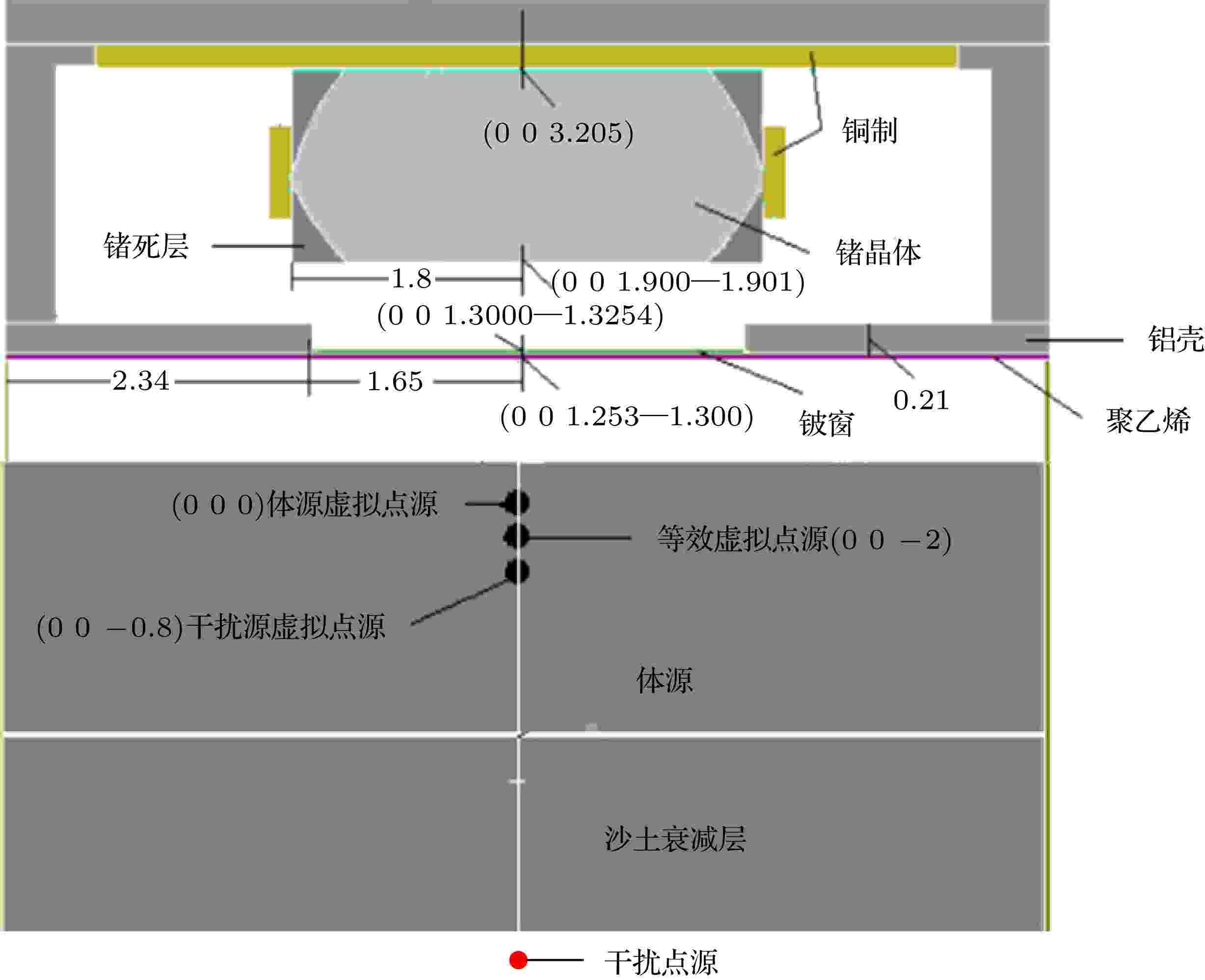图 5 探测模式2的MCNP程序计算模型
Figure5. Calculation model of MCNP procedure for detection mode 2.

对于探测器模式1, 只有图1中沙土衰减层和体源, 没有干扰源的存在. 但模拟的过程中都是假设有干扰源存在的, 下面介绍其模拟计算过程.
2

-->

4.1.等效虚拟点源

在对称轴上, 计算不同位置处点源探测效率, ²⁴¹Am主要计算其59.54 keV射线探测效率, ²³⁹Pu主要计算其129 keV射线探测效率, 其计算结果如表3中数据所示.

h/cm	${\varepsilon _{241}}(h)$/10–3	${\varepsilon _{239}}(h)$/10–3	A241/104 Bq	A239/105 Bq	Q	${N}/{ { {N_{\rm v}} } }(h)$
–1.25	24.3	24.6	0.921	0.497	5.4	8.05
–1.60	17.9	19.5	1.24	0.629	5.0	6.99
–2.00	12.9	15.1	1.73	0.810	4.7	6.12
–2.40	9.45	11.9	2.36	1.03	4.4	5.44
–2.80	7.00	9.45	3.19	1.30	4.1	4.92
–3.20	5.24	7.60	4.26	1.61	3.8	4.51
–3.60	3.97	6.16	5.62	1.98	3.5	4.18
–3.80	3.47	5.56	6.45	2.20	3.4	4.04
–4.00	3.03	5.04	7.37	2.43	3.3	3.90

表3等效虚拟点源探测效率及峰谷比
Table3.The detection efficiency and peak/valley of equivalent virtual point source.

根据表3中探测效率值, 结合表1中探测模式1的能峰数据计算不同位置坐标处的Q活度比值, 可以看出, 在坐标为–2.80处时Q比值为4.1, 和表1中活度比值一致, 因此, 可以认为等效虚拟点源(如图4中)的位置坐标为(0 0 –2.80). 等效虚拟点源包含了两部分的等效, 一部分是测量对象体源的贡献, 一部分是干扰源的贡献(干扰源可以是点源、面源和体源, 统一将其转化成虚拟点源), 将这两部分各自虚拟成点源, 可以认为等效虚拟点源由体源虚拟点源和干扰源虚拟点源按不同的权重组合而成, 因此下一步的目标就是找出这个权重和体源的虚拟点源位置坐标.
2 -->

4.2.体源虚拟点源

等效虚拟点源的探测效率值7.0 × 10^–3和9.45 × 10^–3即为(5)式和(6)式的数学期望值, 峰谷比5.9为(4)式的数学期望值. 根据表3中不同点位置处的探测效率, 计算不同虚拟点位置和不同权重组合下的等效探测效率及等效峰谷比, 计算结果见表4. 根据这些值按(7)—(9)式计算其理论值X_i, 最后按理论计算公式(10)计算均方偏差, 如表4所列.

w	h/cm	$\varepsilon (h)$/10–3	${\varepsilon ^*}(h)$/10–3	${N}/{ { {N_{\rm v}} } }(h)$	X2/10–3	X3/10–3	X1	$\sigma (X)$
0.10	–1.25	24.3	24.6	8.05	—	—	—	—
0.90	–3.20	5.24	7.60	4.51	7.15	9.30	4.87	0.177
0.90	–3.60	3.97	6.16	4.18	6.00	8.01	4.56	0.308
0.90	–3.80	3.47	5.56	4.04	5.55	7.47	4.44	0.385
0.90	–4.00	3.03	5.04	3.90	5.16	6.99	4.31	0.458
0.10	–1.60	17.9	19.5	6.99	—	—	—	—
0.90	–3.20	5.24	7.60	4.51	6.51	8.79	4.76	0.217
0.90	–3.60	3.97	6.16	4.18	5.36	7.50	4.46	0.396
0.90	–3.80	3.47	5.56	4.04	4.91	6.96	4.33	0.479
0.90	–4.00	3.03	5.04	3.90	4.52	6.48	4.21	0.554
0.10	–2.00	12.9	15.1	6.12	—	—	—	—
0.90	–3.20	5.24	7.60	4.51	6.01	8.35	4.67	0.277
0.90	–3.60	3.97	6.16	4.18	4.86	7.06	4.37	0.474
0.90	–3.80	3.47	5.56	4.04	4.41	6.52	4.24	0.559
0.90	–4.00	3.03	5.04	3.90	4.02	6.04	4.12	0.635
0.10	–2.40	9.45	11.9	5.44	—	—	—	—
0.90	–3.20	5.24	7.60	4.51	5.66	8.03	4.61	0.327
0.90	–3.60	3.97	6.16	4.18	4.52	6.74	4.30	0.530
0.90	–3.80	3.47	5.56	4.04	4.06	6.20	4.18	0.616
0.90	–4.00	3.03	5.04	3.90	3.67	5.72	4.05	0.693

表4不同组合下等效虚拟点的均方偏差计算数据
Table4.The mean square deviation calculation data of equivalent virtual point at different combination.

表4中热区虚拟点源位置坐标为–1.25, –1.60, –2.00和–2.40 cm, 干扰源的虚拟点源位置坐标为–3.20, –3.60, –3.80和–4.00 cm. 省去中间过程, 直接计算得到虚拟点坐标、权重及均方偏差的一一对应的表5.

h/cm	w	$\sigma (X)$	w	$\sigma (X)$	w	$\sigma (X)$	w	$\sigma (X)$	w	$\sigma (X)$
–1.25	0.10	—	0.20	—	0.30	—	0.40	—	0.50	—
–3.20	0.90	0.177	0.80	0.355	0.70	0.664	0.60	0.988	0.50	1.32
–3.60	0.90	0.308	0.80	0.223	0.70	0.508	0.60	0.848	0.50	1.20
–3.80	0.90	0.385	0.80	0.201	0.70	0.448	0.60	0.792	0.50	1.15
–4.00	0.90	0.458	0.80	0.210	0.70	0.399	0.60	0.744	0.50	1.11
–1.60	0.10	—	0.20	—	0.30	—	0.40	—	0.50	—
–3.20	0.90	0.217	0.80	0.195	0.70	0.360	0.60	0.568	0.50	0.784
–3.60	0.90	0.396	0.80	0.210	0.70	0.234	0.60	0.435	0.50	0.669
–3.80	0.90	0.479	0.80	0.262	0.70	0.203	0.60	0.384	0.50	0.622
–4.00	0.90	0.554	0.80	0.318	0.70	0.196	0.60	0.343	0.50	0.583
–2.00	0.10	—	0.20	—	0.30	—	0.40	—	0.50	—
–3.20	0.90	0.277	0.80	0.187	0.70	0.177	0.60	0.256	0.50	0.371
–3.60	0.90	0.474	0.80	0.328	0.70	0.210	0.60	0.181	0.50	0.272
–3.80	0.90	0.559	0.80	0.399	0.70	0.257	0.60	0.178	0.50	0.238
–4.00	0.90	0.635	0.80	0.465	0.70	0.307	0.60	0.193	0.50	0.215
–2.40	0.10	—	0.20	—	0.30	—	0.40	—	0.50	—
–3.20	0.90	0.327	0.80	0.264	0.70	0.209	0.60	0.173	0.50	0.167
–3.60	0.90	0.530	0.80	0.435	0.70	0.344	0.60	0.261	0.50	0.195
–3.80	0.90	0.616	0.80	0.510	0.70	0.407	0.60	0.309	0.50	0.225
–4.00	0.90	0.693	0.80	0.577	0.70	0.464	0.60	0.356	0.50	0.257

表5不同组合下等效虚拟点的均方偏差计算数据
Table5.The mean square deviation calculation data of equivalent virtual point at different combination.

h/cm	w	$\sigma (X)$	w	$\sigma (X)$	w	$\sigma (X)$	w	$\sigma (X)$
–1.25	0.60	—	0.70	—	0.80	—	0.9	—
–3.20	0.40	1.65	0.30	1.98	0.20	2.31	0.10	2.64
–3.60	0.40	1.55	0.30	1.90	0.20	2.26	0.10	2.61
–3.80	0.40	1.51	0.30	1.88	0.20	2.24	0.10	2.60
–4.00	0.40	1.48	0.30	1.85	0.20	2.22	0.10	2.60
–1.60	0.60	—	0.70	—	0.80	—	0.90	—
–3.20	0.40	1.00	0.30	1.23	0.20	1.45	0.10	1.67
–3.60	0.40	0.910	0.30	1.16	0.20	1.40	0.10	1.65
–3.80	0.40	0.872	0.30	1.13	0.20	1.38	0.10	1.64
–4.00	0.40	0.839	0.30	1.10	0.20	1.37	0.10	1.63
–2.00	0.60	—	0.70	—	0.80	—	0.90	—
–3.20	0.40	0.498	0.30	0.630	0.20	0.763	0.10	0.898
–3.60	0.40	0.410	0.30	0.561	0.20	0.716	0.10	0.875
–3.80	0.40	0.375	0.30	0.533	0.20	0.698	0.10	0.865
–4.00	0.40	0.347	0.30	0.509	0.20	0.681	0.10	0.857
–2.40	0.60	—	0.70	—	0.80	—	0.90	—
–3.20	0.40	0.194	0.30	0.244	0.20	0.305	0.10	0.372
–3.60	0.40	0.169	0.30	0.199	0.20	0.267	0.10	0.351
–3.80	0.40	0.174	0.30	0.186	0.20	0.252	0.10	0.342
–4.00	0.40	0.186	0.30	0.178	0.20	0.240	0.10	0.335

从表5中可以看出, 均方偏差最小的值为0.167, 其对应的体源虚拟点位置坐标为–2.40, 干扰源对应的虚拟点位置坐标–3.20, 而其对应的权重都为0.50. 由于两个点位置很近权重又一样, 因此, 可以认为没有干扰源的存在, 实际上等效虚拟点位置坐标就是体源的虚拟点位置坐标.
2 -->

4.3.体源参数反演

将表3中坐标–2.80对应的探测效率及峰谷比作为(4)—(6)式的数学期望值, 然后计算不同体源中心坐标不同体源厚度下的探测效率及峰谷比值, 将这些值作为理论计算值, 并计算其与数学期望之间的均方偏差, 计算结果如表6所列.

hV/cm	体源厚度/cm	$\varepsilon ({h_{\rm{V}}})$ /10–3	${\varepsilon ^*}({h_{\rm{V}}})$ /10–2	${N}/{ { {N_{\rm v}} } }({h_{\rm{V} } })$	$\sigma (X)$
–2.80	0.80	4.54	0.689	4.69	0.444
–2.80	1.2	4.60	0.696	4.74	0.431
–2.80	1.6	4.70	0.705	4.81	0.414
–2.45	0.80	5.68	0.818	5.03	0.231
–2.45	1.2	5.76	0.826	5.07	0.217
–2.45	1.6	5.89	0.837	5.16	0.200
–2.45	2.0	6.05	0.851	5.26	0.181
–2.45	2.5	6.31	0.874	5.41	0.159
–2.45	3.0	6.65	0.903	5.63	0.163
–2.45	4.0	7.57	0.981	6.24	0.289
–2.45	4.9	8.78	1.08	7.12	0.539
–2.00	0.80	7.62	1.03	5.58	0.188
–2.00	1.2	7.75	1.04	5.64	0.212
–2.00	1.6	7.93	1.05	5.75	0.248
–2.00	2.0	8.17	1.07	5.88	0.295
–2.00	2.5	8.55	1.10	6.11	0.373
–2.00	3.0	9.03	1.14	6.41	0.474
–2.00	4.0	10.4	1.25	7.35	0.769
–1.50	0.80	10.7	1.33	6.43	0.744
–1.50	1.2	10.9	1.35	6.54	0.781
–1.50	1.6	11.2	1.37	6.68	0.834
–1.50	2.0	11.5	1.40	6.90	0.905
–1.50	3.0	12.9	1.50	7.79	1.18
–0.50	0.80	22.0	2.34	10.1	2.81

表6体源参数的反演计算数据
Table6.The inversion data of volume source parameters.

体源中心坐标用h_V表示. 从表6中可以看出, 均方偏差最小的为0.159, 其对应的体源中心坐标为–2.45, 体源厚度为2.5 cm, 和实际情况完全一致, 充分说明了该技术方法的可行性和准确性. 对于探测模式2, 探测器参数和探测模式1一致, 但是沙土密度变为1.43, 整个测量是贴近探测器进行的, 129 keV射线能量变成26.4 keV. 其计算过程如表7—表9所列.

h/cm	${\varepsilon _{26.4\;{\rm{keV}}}}(h)$/10–3	${\varepsilon _{59.54\;{\rm{keV}}}}(h)$/10–2	A26.4 keV/104 Bq	A59.54 keV/104 Bq	A59.54 keV/A26.4 keV	${N}/{ { {N_{\rm v}} } }(h)$
0.80	48.200	14.4	0.0519	0.318	6.10	17.0
0.40	13.500	8.79	0.1850	0.523	2.80	12.0
0	4.060	5.56	0.6150	0.826	1.30	9.3
–0.20	2.260	4.48	1.1100	1.030	0.90	8.4
–0.40	1.270	3.64	1.9700	1.260	0.60	7.7
–0.60	0.717	2.98	3.4900	1.540	0.40	7.1
–0.80	0.409	2.45	6.1200	1.880	0.30	6.6

表7等效虚拟点源探测效率、峰谷比及活度比
Table7.The detection efficiency, peak/valley and acvitiy ratio of equivalent virtual point source.

hV/cm	体源 厚度/cm	${\varepsilon ^*}({h_{\rm{V}}})$/ 10–2	$\varepsilon ({h_{\rm{V}}})$/ 10–3	${N}/{ { {N_{\rm v}} } }({h_{\rm{V} } })$	$\sigma (X)$		hV/cm	体源 厚度/cm	${\varepsilon ^*}({h_{\rm{V}}})$/ 10–2	$\varepsilon ({h_{\rm{V}}})$/ 10–3	${N}/{ { {N_{\rm v}} } }({h_{\rm{V} } })$	$\sigma (X)$
0.75	1.00	3.54	10.4	11.90	1.5900		0.15	2.20	2.45	5.00	9.34	0.2310
0.75	0.60	3.47	8.06	11.40	1.0100		0.15	1.60	2.31	2.69	8.54	0.3470
0.75	0.30	3.44	7.23	11.20	0.8060		0.15	1.00	2.21	1.72	8.07	0.5920
0.25	2.00	2.59	5.49	9.61	0.3530		0.15	0.40	2.17	1.32	7.86	0.6920
0.25	1.90	2.56	4.91	9.44	0.2110		0	2.50	2.26	4.40	9.00	0.0900
0.25	1.80	2.54	4.42	9.29	0.0890		0	2.45	2.24	4.14	8.90	0.0470
0.25	1.70	2.51	4.00	9.14	0.0220		0	2.40	2.23	3.90	8.83	0.0640
0.25	1.60	2.49	3.63	9.03	0.1090		0	2.00	2.13	2.52	8.30	0.3950
0.25	1.50	2.47	3.32	8.92	0.1870		0	1.50	2.04	1.60	7.83	0.6260
0.25	1.30	2.43	2.81	8.72	0.3130		0	1.00	1.97	1.13	7.54	0.7470
0.25	0.80	2.37	2.04	8.38	0.5080		–0.25	1.10	1.65	0.602	6.86	0.8910
							–0.25	0.50	1.61	0.457	6.70	0.9300

表9体源参数的反演计算数据
Table9.The inversion data of volume source parameters.

表8中热区虚拟点源位置坐标为0.80, 0.40, 和0 cm, 干扰源的虚拟点源位置坐标为–0.40, –0.60和–0.80 cm. 从表8中可以看出, 均方偏差最小是0.112, 其对应的上下虚拟点源权重都为0.50, 上下虚拟点源坐标分别为0和–0.8 cm, 等效虚拟点源坐标为–0.20 cm, 比较靠近上虚拟点位置, 两虚拟点位置较远, 权重也占了一半, 因此, 可以认为有一个强的干扰源的存在. 干扰源只需证明它存在或者不存在即可, 它的存在及其设置只是为了更为准确地解出体源边界参数, 在本文中它的边界参数是不必求解的.

h/cm	w	$\sigma (X)$	w	$\sigma (X)$	w	$\sigma (X)$	w	$\sigma (X)$	w	$\sigma (X)$
0.80	0.10	—	0.20	—	0.30	—	0.40	—	0.50	—
–0.40	0.90	2.414	0.80	1.783	0.70	2.807	0.60	3.832	0.50	4.86
–0.60	0.90	2.115	0.80	1.512	0.70	2.569	0.60	3.627	0.50	4.69
–0.80	0.90	1.951	0.80	1.362	0.70	2.433	0.60	3.510	0.50	4.59
0.40	0.10	—	0.20	—	0.30	—	0.40	—	0.50	—
–0.40	0.90	0.466	0.80	0.291	0.70	0.529	0.60	0.780	0.50	1.03
–0.60	0.90	0.177	0.80	0.119	0.70	0.286	0.60	0.567	0.50	0.857
–0.80	0.90	0.185	0.80	0.245	0.70	0.175	0.60	0.447	0.50	0.753
0	0.10	—	0.20	—	0.30	—	0.40	—	0.50	—
–0.40	0.90	0.190	0.80	0.160	0.70	0.168	0.60	0.235	0.50	0.327
–0.60	0.90	0.431	0.80	0.346	0.70	0.214	0.60	0.123	0.50	0.165
–0.80	0.90	0.620	0.80	0.512	0.70	0.350	0.60	0.197	0.50	0.112

表8不同组合下等效虚拟点的均方偏差计算数据
Table8.The mean square deviation calculation data of equivalent virtual point at different combination.

h/cm	w	$\sigma (X)$	w	$\sigma (X)$	w	$\sigma (X)$	w	$\sigma (X)$
0.80	0.60	—	0.70	—	0.80	–	0.90	—
–0.40	0.40	5.88	0.30	6.91	0.20	7.93	0.10	8.96
–0.60	0.40	5.75	0.30	6.81	0.20	7.87	0.10	8.92
–0.80	0.40	5.67	0.30	6.75	0.20	7.83	0.10	8.90
0.40	0.60	–	0.70	—	0.80	–	0.90	—
–0.40	0.40	1.29	0.30	1.55	0.20	1.80	0.10	2.06
–0.60	0.40	1.15	0.30	1.44	0.20	1.73	0.10	2.03
–0.80	0.40	1.06	0.30	1.38	0.20	1.69	0.10	2.01
0	0.60	—	0.70	—	0.80	—	0.90	—
–0.40	0.40	0.427	0.30	0.532	0.20	0.639	0.10	0.747
–0.60	0.40	0.287	0.30	0.425	0.20	0.567	0.10	0.711
–0.80	0.40	0.207	0.30	0.361	0.20	0.523	0.10	0.689

表9中, 均方偏差的计算只用了26.4 keV射线能量探测效率和59.54 keV射线峰谷比这两项, 没有使用59.54 keV射线能量探测效率. 从表9中可以看出, 最小均方偏差为0.0220, 其对应的体源中心坐标为0.25 cm, 体源厚度为1.7 cm, 计算得沙土衰减层厚度为1.53 mm, 由于这一值相对体源厚度太小, 在表层不可能存在这么薄的沙土衰减层, 因此可以将其直接忽略, 并入体源厚度, 可认为体源厚度为2.0 cm, 相对真实值2.5 cm, 大概有20.0%左右的相对偏差, 其偏差稍微偏大的原因是干扰点源使用低能26.4 keV射线穿透3.0 cm左右沙土衰减层后在探测器晶体内产生的有效计数太少, 统计涨落过大, 造成了计算误差也大. 因此, 不能选用能量过低的低能射线, 比如本文选用的26.4 keV能量射线就有些偏低, 会造成结果一定的偏差.

本文提供一种确定放射性可疑区源边界参数的虚拟点源方法, 解决了现有探测方法无法准确判定放射性污染区深度边界参数的技术问题. 该技术方法可应用于多种核素或发射多条特征能量射线核素的源项目标, 其过程是: 首先根据核素活度浓度比值(一种核素该比值可认为是1.0, 但要测量其两条及以上特征能量射线)找出等效虚拟点源, 该虚拟点源特点是由该点算出的活度浓度比值与给出的一致, 它包含了目标体源及其他干扰源的信息; 其次再将该等效虚拟点按一定的权重分成上下两个虚拟点源, 若上下两个虚拟点源与等效虚拟点源距离过近且权重相等, 则不需要将等效虚拟点源分成上下两个虚拟点源, 它本身就是体源的虚拟点源, 不存在干扰源, 若上下两个虚拟点源距离等效点源距离较远或权重不一致, 则可认为上虚拟点源就是目标体源的虚拟点源, 该虚拟点源的探测效率及峰谷比和目标体源的一致; 最后就是根据目标体源的虚拟点源的探测效率及峰谷比计算并反演得到体源边界参数. 该技术的优点是: 1)利用虚拟点探测器理论及虚拟点源技术, 成功地解决了方程组法遇到深层干扰源情况下存在病态或不确定大的难题, 使就地及航测γ谱仪发展为一项更为有效的探测手段; 2)使用了新原理及测量方式, 不增加新的物理探测设备, 大大减少了经费开支, 减少了工作量及时间.