摘要: 经验模态分解一类的递归算法所产生的模态混淆和端点效应将导致所获物理信息失真, 变分模态分解可改善这些问题. 但因其需预设参数, 对信号分解精度影响显著, 为此, 提出采用目标信号功率谱峰值所对应的频率以初始化变分模态分解所需中心频率, 借鉴经验模态分解递归模型, 基于能量截止法将变分模态分解改进为递归模式算法, 并采用粒子群优化算法对具有带宽约束能力的惩罚因子进行最优取值, 构成优化递归变分模态分解. 通过对比分析经验模态分解, 集成经验模态分解及优化递归变分模态分解在分解信号时的计算精度; 研究传统变分模态分解与优化递归变分模态分解在处理实际振动信号时计算速率. 结果表明: 优化递归变分模态分解在处理目标信号时精度最高, 与原分量相关性达99.9%; 与集成经验模态分解对比, 可由低至高将信号分解至不同频段, 物理意义更加清晰且不产生虚假模态; 处理实际非线性信号时, 优化递归变分模态分解无需预设分解模态个数, 相比于传统变分模态分解, 计算速率高12.5%—18.5%.
关键词: 变分模态分解 /
非线性 /
信号处理 English Abstract Application of the proposed optimized recursive variational mode decomposition in nonlinear decomposition Xu Zi-Fei 1,2 ,Yue Min-Nan 1 ,Li Chun 1,2 1.University of Shanghai for Science and Technology, Energy and Power Engineering Institute, Shanghai 200093, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 51976131, 51676131), the Funds for International Cooperation and Exchange of the National Natural Science Foundation of China (Grant No. 51811530315), and the Shanghai Committee of Science and Technology, China (Grant No. 19060502200)Received Date: 30 June 2019Accepted Date: 11 September 2019Available Online: 26 November 2019Published Online: 05 December 2019Abstract: Variational mode decomposition can improve traditional recursive algorithms, such as empirical mode decomposition, resulting modal aliasing and endpoint effects, but it has a significant influence on signal decomposition accuracy due to its pre-set parameters. The frequency corresponding to the peak value of the target signal power spectrum is proposed to initialize the center frequency required for the variational mode decomposition. The empirical mode decomposition and recursive model is used to improve the variational mode decomposition into the recursive mode algorithm based on the energy cutoff method. The group optimization algorithm optimally takes the penalty factor with bandwidth constraint ability to form an optimized recursive variational mode decomposition. By comparing with and analyzing empirical mode decomposition, integrating empirical mode decomposition and optimizing the computational accuracy of recursive variational mode decomposition in decomposing signals; studying traditional variational mode decomposition and optimizing recursive variational mode decomposition in dealing with actual vibration signals calculating rate, the results are obtained, showing that the optimized recursive variational mode decomposition has the highest accuracy when dealing with the target signal, and the correlation with the original component is 99.9%. Comparing with the integrated empirical mode decomposition, the signal can be decomposed into different frequency bands from low to high, and the physical meaning is clearer. No false modality is generated. When the actual nonlinear signal is processed, the optimized recursive variational mode decomposition does not need to preset the number of decomposition modes, and the calculation rate is 12.5%–18.5% higher than thay of the traditional variational mode decomposition.Keywords: variational mode decomposition /nonlinear /signal process 全文HTML --> --> --> 1.引 言 非平稳信号具有随机性强、稳定性差与物理信息混叠等特点[1 ] . 为探寻非稳定信号中所含信息, 在结构分析、故障诊断乃至医学领域[2 -5 ] , 相关****对信号(时间序列)分解技术已展开诸多研究. 其中, 应用较为广泛的有小波分解(wavelet transform, WT)、经验模态分解(empirical mode decomposition, EMD)、集合经验模态分解(ensemble empirical mode decomposition, EEMD)和局部均值分解(local mean decomposition, LMD)等[6 -9 ] . WT方法采用缩放、平移窗函数将原信号分解为若干小波叠加的形式, 但易产生无物理意义的虚假谐波, 影响结果分析[10 ] . EMD与EEMD均属于递归模式分解, EEMD在处理信号时, 通过对信号加入高斯噪声以抑制EMD处理信号时易产生的模态混淆的问题, 可有效处理非线性、非平稳信号分解; 但在EEMD迭代过程中, 由于包络线估计误差的叠加, 导致引发端点效应及模态混淆[11 ] . LMD作为递归算法, 可自适应分解无规则信号至多个含物理意义的乘积函数分量, 较小波分析有更好的自适应性, 但无法分离频率相近的信号. 以上方法因求解本质属于递归分解, 均存在包络线估计误差随迭代而累计, 从而导致模态混淆及端点效应, 影响对物理信息的提取及分析.[12 ] 提出基于Hilbert变换、Wiener滤波及频率混合等概念的新型分解方法—变分模态分解(viriational mode decomposition, VMD), 该方法因具有完备的数学理论基础, 通过求解约束变分模型代替原有的递归模式, 从而抑制模态混淆、避免端点效应及解决相近频率难分离的问题[13 ] .α 与模态分解数K 对信号分解精度影响最为显著[14 ] . 已有****针对惩罚因子α 与模态分解数K 的何种取值对分解效果如何影响做了相关研究. 文献[15 ]以VMD分解所获分量间的相关系数作为约束, 从而确定模态分解数K 的取值, 并将改进VMD与深度置信网络相结合, 实现故障预警. 文献[16 ]以包络熵作为VMD参数优化的目标函数进行寻优取值, 结果具有良好的分解精度, 并将其应用于滚动轴承故障诊断中. 文献[17 ]将VMD与多尺度排列熵相结合, 在生物组织变性识别中获得较优的聚类效果与分类性能. Baldini等[18 ] 比较VMD与EMD在分解无线电信号的准确性, 并采用机器学习对信号进行分类, 得出基于VMD分解的信号具有更高的准确性. Chen等[19 ] 分别采用VMD与EMD对轴承振动信号进行分解, 以能量熵作为特征值构建特征向量, 并采用支持向量机对特征向量进行分类, 结果表明以VMD-能量熵构建的特征样本, 使得分类结果具有更高的准确性, 但未考虑VMD分解时预设参数对VMD分解精度的影响. 为此, Cui等[20 ] 基于目标信号瞬时频率, 对VMD算法K 值设定进行改进, 指出该方法可提升VMD分解精度, 并成功用于智能负载建模与去噪, 但忽略了VMD分解时以约束带宽的参数—惩罚因子对结果的影响.α 与模态分解数K , 且α 与K 取值组合对分解精度有显著影响的问题, 提出一种优化递归VMD算法(optimized recursive variational mode decomposition, ORVMD), 该算法借鉴EMD递归分解时可自适应获取模态分解数K 的优点, 以目标信号功率谱最大值对应的频率作为初始频率, 并基于能量差追踪法将传统VMD改进为递归VMD, 并采用粒子群优化算法获取惩罚因子α 的最优取值, 得到最佳α , K 组合, 以保证分解所得分量具有更多的物理信息. 对比EMD, EEMD及ORVMD在分解信号时的精确性, 分析EEMD与ORVMD在处理非线性调制信号时的可靠性, 研究传统VMD与ORVMD解决实际振动信号时的时效性, 发现ORVMD具有更高的计算精度与效率, 亦可保留更多的物理信息, 以期为信号处理、结构分析及故障诊断等方面奠定理论基础, 提供处理方法.2.VMD算法 VMD算法是基于Wiener滤波、Hilbert变换与外差解调所形成的一种分解算法, 因其具有完备的数学基础, 采用VMD处理信号时可有效避免EMD类算法导致的模态混淆及端点效应. 与属递归性质的EMD类算法不同, VMD属约束变分性问题, 通过假设模态分量的中心频率, 将约束模态带宽的过程转化为约束变分问题, 求解变分模型以实现模态分解. VMD算法中涉及的约束变分模型为$\{ {u_k}\} \!=\! \{{u_1}, {u_2}, \cdots\!, {u_k}\}$ 与$\{ {\omega _k}\} \!=\! \{{\omega _1}, {\omega _2}, \cdots\!, {\omega _k}\}$ 分别为第k 个模态分量及其相应中心频率, 共K 个模态; $\delta (t)$ 为单位脉冲函数; j表示虚数单位; * 表示卷积运算; ${\partial _t}$ 为偏导运算; f 为目标信号.α 和Lagrange乘子λ 以求解变分约束问题. 所得增广Lagrange表达式如下:2 )式的鞍点, 在频域内迭代更新${u_k}$ , ${\omega _k}$ 及λ .K 个模态分量, 步骤如下:$\{{\hat u^1}\}$ , $\{{\hat \omega ^1}\}$ , ${\hat \lambda ^1}$ 和n 为零;${u_k}$ 和${\omega _k}$ 分别由(3 )式和(4 )式迭代更新,τ 为保真系数; $ \wedge $ 表示傅里叶变换; n 为迭代次数;5 )式更新λ ,6 )式给出,ε 为判别精度, 且$\varepsilon > 0$ ; 上标n 为迭代步数, 下标k 表示当前模态数;K 个模态分量.3.优化递归VMD算法 与EMD等递归分解算法相比, VMD具有较高的准确性与稳定性. 但VMD算法需给出预设模态分解数K , 且K 的取值影响分解精度. 因此, 借鉴EMD递归思想, 提出一种递归VMD算法. 借鉴能量差追踪法以设定停止条件, 实现递归VMD算法. 该方法既拥有VMD算法中可抑制求解包络线迭达误差而导致失真的优点, 也可实现自适应分解, 无需预设模态分解数K .3.1.递归算法 3.1.递归算法 33.1.1.改进变分模型 -->3.1.1.改进变分模型 基于传统VMD算法, 给定初始模态分解数$K = 1$ 的约束变分模型, 获得有限带宽本征模态函数(bandwidth intrinsic mode function, BIMF), 将(1 )式转化为(7 )式.α 和Lagrange乘子λ 后, (2 )式将变为(8 )式, (5 )式和(6 )式被转换为(9 )式和(10 )式, 其余步骤与传统VMD算法相同.${\omega _k}$ 需预计算. 而Dragomiretskiy等[12 ] 所提出三种初始化中心频率的方法(分别为: 赋予初值零、线性化及随机初值化)均有一定的局限性. 其中线性化以获取初值具有较好的准确性与稳定性, 但当$K = 1$ 时, 中心频率${\omega _k}=0$ , 与赋予初值零情况相同, 从而导致线性化失败. 因此, 提出以目标信号功率密度谱(power density spectrum, PSD)最大值所对应的频率作为${\omega _k}$ 初值.3.1.2.停止准则 -->3.1.2.停止准则 Huang等[21 ] 与Damerval等[22 ] 所提出的停止准则均不适用于VMD算法, 故采用Cheng等[23 ] 所提出的能量差追踪法应用于本文所提出的改进变分模型. 基于能量差追踪法的VMD停止准则如下.$f(t)$ 分解后所得BIMF分量${u_k}(t)$ 具有正交性, 由(11 )式给出, 其总能量表达式由(12 )式给出.E 为原信号能量.12 )式可表示为${E_1} + {E_2} + \cdots + {E_n}$ 为各BIMF分量的能量.${E_{{\rm{total}}}}$ 应与原信号能量E 相等,${E_{{\rm{total}}}}$ 与E 之间存在误差${E_{{\rm{err}}}}$ ,${E_{{\rm{err}}}}$ 越接近零, 表明分解效果越好, 与原分量符合度更高, 所得模态分量颇含物理意义. 因此, 令${E_{{\rm{err}}}}$ 的绝对值$\left| {{E_{{\rm{err}}}}} \right|$ 为停止准则, 当$\left| {{E_{{\rm{err}}}}} \right|$ 小于收敛阈值时停止迭代, 以获取最佳模态分解数K .3.1.3.递归VMD算法 -->3.1.3.递归VMD算法 基于以上提出的改进变分模型, 结合能量差追踪法确定收敛条件, 递归VMD算法流程图如图1 所示, 具体计算步骤如下:图 1 递归VMD流程Figure1. The recursive VMD diagram.${\omega _{{\rm{initial }}}}$ ;$K = 1$ , 获取(7 )式的变分模型, 通过(9 )式和(10 )式分别获取${u_k}$ 与${\omega _k}$ ;${u_k}$ 作为BIMF分量, 将$f - {u_k}$ 作为新目标信号并重复步骤1与2;15 )式计算能量误差$\left| {{E_{{\rm{err}}}}} \right|$ , 当$\left| {{E_{{\rm{err}}}}} \right|$ 小于收敛阈值时停止分解并获取全部BIMF分量. 根据计算经验, 采用$\left| {{E_{\rm err}}} \right| \leqslant [\left( {0.7 \sim 2.0} \right)E]/100$ 为收敛阈值;3.2.PSO算法 -->3.2.PSO算法 粒子群优化算法(particle swarm optimization, PSO)是由Kennedy 和Eberhart[24 ] 受鸟群觅食行为启发所提出的. 在PSO算法中, 每个粒子具有相应的速度与位置以调整自身的状态, 粒子的位置代表待优化问题的潜在解. PSO算法的数学描述如下.D 维空间中, 存在由m 个粒子组成的种群, 第i 个粒子在D 维空间中的位置向量为${{ X}_i} = {({x_{i1}}, {x_{i2}}, \cdots, {x_{iD}})^{\rm{T}}}$ , 其速度向量为${{ V}_i} = $ ${({v_{i1}}, {v_{i2}}, \cdots, {v_{iD}})^{\rm{T}}}$ , 第i 个粒子的最佳位置由向量${{ P}_i} = {({p_{i1}}, {p_{i2}}, \cdots, {p_{iD}})^{\rm{T}}}$ 表示, 种群最佳位置由向量${{ P}_g} = {({p_{g1}}, {p_{g2}}, \cdots, {p_{g{\rm{D}}}})^{\rm{T}}}$ 表示, 速度与位置的更新由(16 )式和(17 )式所示.$i = 1, 2, \cdots, m$ ; $d = 1, 2, \cdots, {{D}}$ ; k 为当前进化代数; ${c_1}$ 与${c_2}$ 为学习因子; ω 为惯性权重; η 为[0, 1]内随机数.3.3.ORVMD算法 -->3.3.ORVMD算法 以上所提出的递归VMD方法虽可自适应获取分解模态数K , 但惩罚因子α 作为约束带宽的参数, 其取值也严重影响了信号处理的准确性. 带宽的变化影响分解所获各模态能量的变化, 从而进一步影响递归模态分解数K 或信号分解失效[25 ] . 因此, 以能量误差$\left| {{E_{{\rm{err}}}}} \right|$ 为寻优过程的适应度函数, 将适应度函数最小取值作为寻优目标, 基于PSO算法对改进递归VMD算法进行参数寻优, 获取最佳分解参数组合, 其流程如图2 所示.图 2 基于PSO优化改进递归VMD参数流程Figure2. The process of using PSO to optimize recursive VMD parameter.$\left| {{E_{{\rm{err}}}}} \right|$ , 以惩罚因子α 及模态分解数K 作为粒子位置, 并随机初始化粒子移动速度;$\left| {{E_{{\rm{err}}}}} \right|$ , 以此作为对应粒子的适应度函数;$\left| {{E_{{\rm{err}}}}} \right|$ 小于当前最小适应度函数, 则对粒子进行更新;16 )式与(17 )式更新粒子属性;$[\alpha, K]$ .α 以约束带宽, 并自动获得分解模态个数K , 确定最佳参数组合$[\alpha, K]$ .4.ORVMD算法验证 为验证ORVMD分解信号的可靠性及有效性, 以两个低频信号与间断高频冲击信号组成仿真复合信号. 仿真复合信号$f(t)$ 与其分量表达式由(18 )式所示:图3 所示. 为验证算法ORVMD的有效性, 分别采用EMD, EEMD及ORVMD对信号$f(t)$ 进行分解, 对比其结果.图 3 合成信号及其分量 (a) 分量s 1 ; (b) 分量s 2 ; (c) 分量s 3 ; (d) 合成信号f Figure3. Analog signal and its component waveform: (a) s 1 ; (b) s 2 ; (c) s 3 ; (d) f .图4 所示. 由图4 可知, EMD将信号分解为5个IMF分量及1个残余分量, 分解效果较差, IMF1与IMF2均出现模态混淆现象, IMF3勉强具有一定的物理意义.图 4 EMD分解结果 (a) IMF1; (b) IMF2; (c) IMF3; (d) IMF4; (e) IMF5; (f) resFigure4. The results of EMD: (a) IMF1; (b) IMF2; (c) IMF3; (d) IMF4; (e) IMF5; (f) res.图5 所示.图 5 EEMD分解结果 (a) IMF1; (b) IMF2; (c) IMF3; (d) IMF4; (e) IMF5; (f) IMF6; (g) IMF7; (h) resFigure5. The results of EEMD: (a) IMF1; (b) IMF2; (c) IMF3; (d) IMF4; (e) IMF5; (f) IMF6; (g) IMF7; (h) res.图5 可知, EEMD分解出7个IMF分量及1个残余分量. 其中IMF1, IMF3与IMF4分别为原信号中的间断高频信号及两个低频信号, 与原信号分量的相关系数分别为0.981, 0.942和0.944, 表明EEMD对分解信号的物理意义还原性较好, 较EMD具有更好的准确性, 但仍产生许多虚假模态不具有物理性.$K = 3, \;\alpha =500$ , 分解结果如图6 所示.图 6 ORVMD分解结果 (a) IMF1; (b) IMF2; (c) IMF3Figure6. The results of ORVMD: (a) IMF1; (b) IMF2; (c) IMF3.图6 所示, 原信号3个分量被较好地还原至3个IMF分量, 其中IMF3为间断高频信号, 两个低频信号分别为IMF1与IMF2. 各IMF分量与对应原分量的相关系数分别为0.998, 0.991与0.999, 较EEMD具有更高的精度, 可获取更具物理意义的信号分量.5.非线性信号分解 处理实际信号时, 目标信号多为调制信号, 故为验证ORVMD在处理实际信号也具有高效性与准确性, 以如下数学模型模拟滚动轴承早期局部损伤信号$x(t)$ [26 ] :$s(t)$ 为周期性冲击信号. 信号衰减指数$C = 1000$ , 系统共振频率${f_n}=4000\;{\rm{Hz}}$ . ${\tau _k}$ 表示第k 次冲击相对于特征周期的小波动, 该随机波动服从均值为零, 标准差为0.5%转频的正态分布. 特征频率${f_{\rm{r}}}=140\;{\rm{Hz}}$ . $U({t_k})$ 为单位阶跃函数. 加入高斯噪声信号后得信噪比为–5 dB的仿真信号. 采样频率为16000 Hz, 采样点N = 4096. 信号时域及频谱如图7 所示.图 7 早期轴承内圈故障信号 (a) 时域; (b) 频谱Figure7. Early inner race fault diagnosis signal.5.1.EEMD分解 5.1.EEMD分解 采用EEMD对信号$x(t)$ 进行分解, 其分解所得时域与频域如图8 所示, 共11个IMF分量及1个残余分量.图 8 故障信号EEMD分解结果 (a) IMF1; (b) IMF2; (c) IMF3; (d) IMF4; (e) IMF5; (f) IMF6; (g) IMF7; (h) IMF8; (i) IMF9; (j) IMF10; (k) IMF11; (l) IMF12Figure8. The results of EEMD for fault signal: (a) IMF1; (b) IMF2; (c) IMF3; (d) IMF4; (e) IMF5; (f) IMF6; (g) IMF7; (h) IMF8; (i) IMF9; (j) IMF10; (k) IMF11; (l) IMF12.图8 所示, IMF1—IMF6五个分解分量包含良好的物理信息, 将重叠在全频段的信号分解在不同频段, 但低频信号仍互相重叠, 无法体现轴承损伤的物理信息. 且IMF7—IMF11基本属于无效信息, 蕴含的物理信息较少, 这说明EEMD对非线性信号的分解效果不佳.5.2.VMD分解 -->5.2.VMD分解 采用所提出的ORVMD方法对信号进行处理, 其中模态分解数$K = 9$ , 优化惩罚因子$\alpha =$ 16100, 所得结果如图9 所示.图 9 故障信号ORVMD分解结果 (a) IMF1; (b) IMF2; (c) IMF3; (d) IMF4; (e) IMF5; (f) IMF6; (g) IMF7; (h) IMF8; (i) IMF9Figure9. The results of ORVMD for fault diagnosis: (a) IMF1; (b) IMF2; (c) IMF3; (d) IMF4; (e) IMF5; (f) IMF6; (g) IMF7; (h) IMF8; (i) IMF9.图9 可知, 每一阶IMF都包含一定的物理意义, 原本冗杂在各个频段的信号已从低频至高频准确区分, 且未出现过分解或者虚假模态. IMF1中蕴含内圈损伤特征频率, IMF5因损伤导致轴承系统发生共振, 主频与谐波之间的频段间隔清晰可见, 包含一定的物理信息. 相比于EEMD, ORVMD具有更高的精度, 不存在虚假模态, 且未分解出不具物理意义的IMF分量以干扰对信号的分析.5.3.ORVMD与传统VMD对比 -->5.3.ORVMD与传统VMD对比 因采用VMD分解时, 已有研究表明模态分解数K 与惩罚因子α 对分解结果及精度有显著影响, 在此不做分析. 除模态分解数K 可自适应获得外, 配合PSO优化算法获取最佳参数组合, 较之于传统VMD, 本文所提出的ORVMD因改变模态分量的初始中心频率获取方式, 以PSD最大值对应的频率作为初始中心频率, 代替传统VMD线性初始化的方法, 可减少迭代次数以提升计算速度.[27 ] , 对风扇端轴承内圈故障的25组信号分别进行ORVMD以及传统VMD进行分解, 其中实验台转速为1730 rmp, 采样频率12000 Hz, 负载为3 Hp. 为保证对比有意义, 采用与ORVMD分解时所需参数$[\alpha, K]$ 组合作为传统VMD分解时的输入参数.α 及K 组合, 采用PSO算法时, 惩罚因子α 寻优的取值范围为[5000, 20000], 取值步长为100. ORVMD参数组合如表1 所列.编号 K , α 编号 K , α 1 12, 12100 14 12, 12400 2 12, 12900 15 12, 12000 3 12, 11800 16 12, 12000 4 12, 11900 17 13, 11900 5 12, 11800 18 12, 11900 6 12, 12700 19 12, 11400 7 12, 12100 20 12, 11900 8 12, 13100 21 13, 11900 9 12, 12100 22 12, 11900 10 12, 12000 23 12, 12000 11 11, 12000 24 12, 12000 12 11, 12000 25 11, 12100 13 12, 13200 — —
表1 ORVMD参数组合Table1. Parameter set of ORVMD.表1 可得, 80%的模态分解数均为12, 故选取模态分解数$K = 12$ 为传统VMD分解时的模态预设定. 惩罚因子看似毫无规律, 但对应实验数据采样频率可知, 惩罚因子作为约束带宽的参数, 均在12000附近波动, 与采样频率相近(12000 Hz), ORVMD获取的25个最优惩罚因子均值为12600, 但其中7次为12000, 6次为11900. 因此, 确定α = 12000为传统VMD分解时的惩罚因子.$\alpha =12000, \;K = 12$ 作为传统VMD分解预设参数, 分别采用传统VMD与ORVMD对上述25组实验振动信号进行分解, 两种方法分解信号耗时如图10 所示.图 10 VMD与ORVMD计算耗时Figure10. The duration of calculation for VMD and ORVMD.图10 可知, 改进的ORVMD算法在计算时间上比传统VMD所需时间少, 虽然平均耗时仅减少12.5%—18.5%, 但由于ORVMD在处理信号时调用PSO算法以获取最优惩罚因子的过程占用较大计算资源, 因此, 认为ORVMD比传统VMD具有更高分解精度与计算效率.6.结 论 对于传统VMD算法需预设分解个数及惩罚因子, 提出ORVMD算法, 该算法可对目标信号递归并获取确定模态分解数K , 并基于PSO算法对惩罚因子α 进行寻优取值, 获取最佳预设参数组合. 同时, 对比分析EMD, EEMD, VMD与ORVMD对非线性信号分解, 表明所提出的ORVMD较EMD, EEMD具有更高的精准性. 该方法可将物理信息分解至不同频段, 且不产生虚假模态, 保证了信号分解的有效性及准确性. 并且, 与传统VMD方法相比, ORVMD具有更高的计算效率, 效率升幅在12.5%—18.5%之间. 此外, 还可开展以复信号、分布式信号[28 -31 ] 为研究对象的变分模态分解处理效果研究. 

































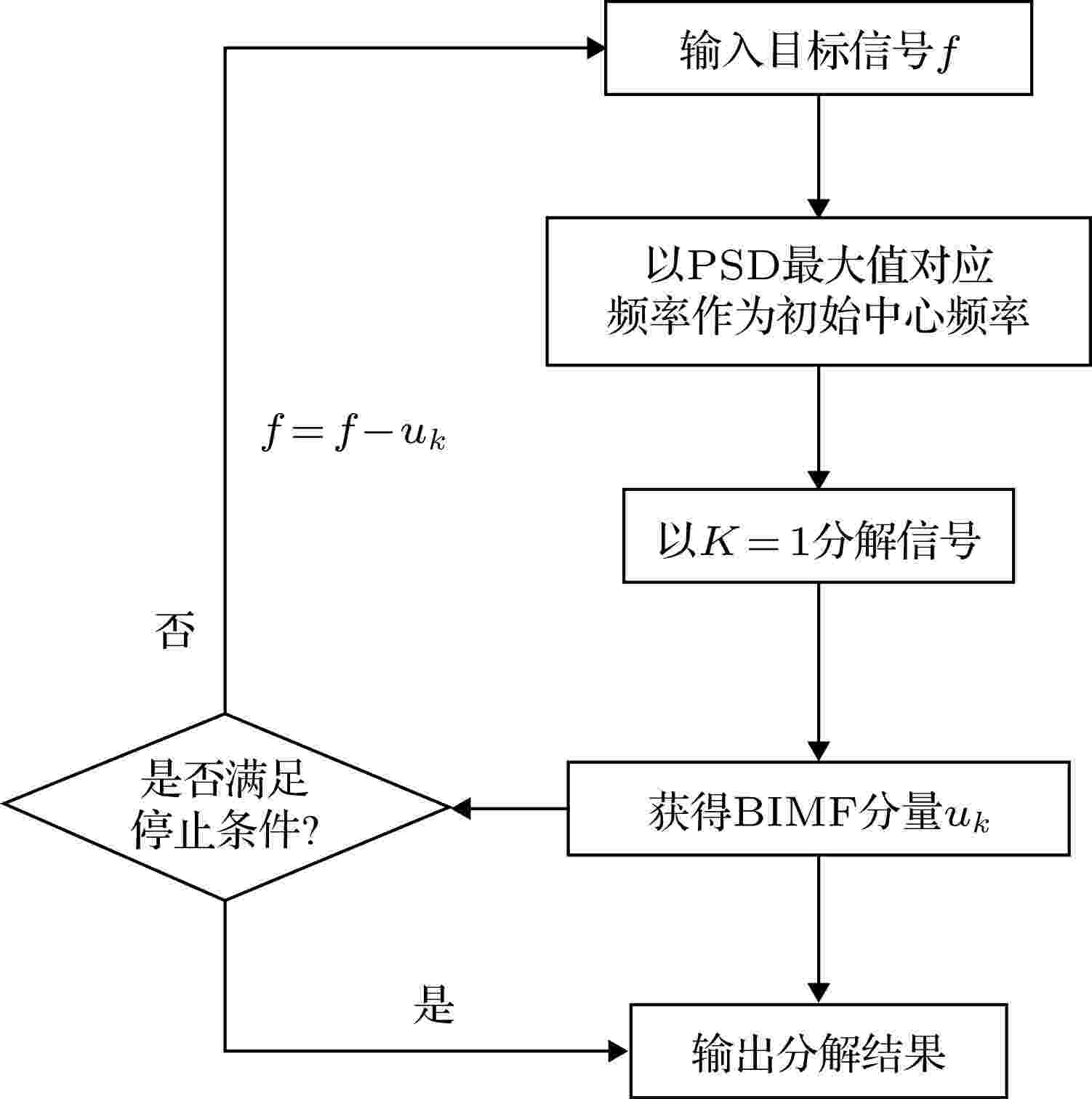 图 1 递归VMD流程
图 1 递归VMD流程




















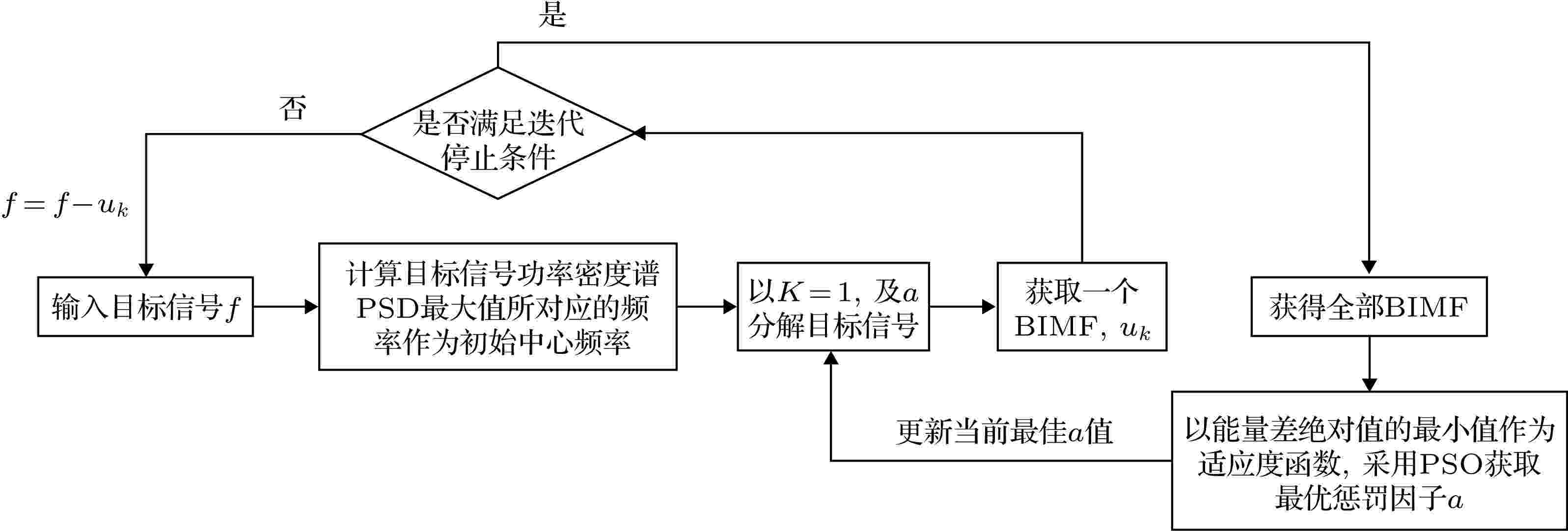 图 2 基于PSO优化改进递归VMD参数流程
图 2 基于PSO优化改进递归VMD参数流程






 图 3 合成信号及其分量 (a) 分量s1; (b) 分量s2; (c) 分量s3; (d) 合成信号f
图 3 合成信号及其分量 (a) 分量s1; (b) 分量s2; (c) 分量s3; (d) 合成信号f 图 4 EMD分解结果 (a) IMF1; (b) IMF2; (c) IMF3; (d) IMF4; (e) IMF5; (f) res
图 4 EMD分解结果 (a) IMF1; (b) IMF2; (c) IMF3; (d) IMF4; (e) IMF5; (f) res 图 5 EEMD分解结果 (a) IMF1; (b) IMF2; (c) IMF3; (d) IMF4; (e) IMF5; (f) IMF6; (g) IMF7; (h) res
图 5 EEMD分解结果 (a) IMF1; (b) IMF2; (c) IMF3; (d) IMF4; (e) IMF5; (f) IMF6; (g) IMF7; (h) res
 图 6 ORVMD分解结果 (a) IMF1; (b) IMF2; (c) IMF3
图 6 ORVMD分解结果 (a) IMF1; (b) IMF2; (c) IMF3






 图 7 早期轴承内圈故障信号 (a) 时域; (b) 频谱
图 7 早期轴承内圈故障信号 (a) 时域; (b) 频谱
 图 8 故障信号EEMD分解结果 (a) IMF1; (b) IMF2; (c) IMF3; (d) IMF4; (e) IMF5; (f) IMF6; (g) IMF7; (h) IMF8; (i) IMF9; (j) IMF10; (k) IMF11; (l) IMF12
图 8 故障信号EEMD分解结果 (a) IMF1; (b) IMF2; (c) IMF3; (d) IMF4; (e) IMF5; (f) IMF6; (g) IMF7; (h) IMF8; (i) IMF9; (j) IMF10; (k) IMF11; (l) IMF12

 图 9 故障信号ORVMD分解结果 (a) IMF1; (b) IMF2; (c) IMF3; (d) IMF4; (e) IMF5; (f) IMF6; (g) IMF7; (h) IMF8; (i) IMF9
图 9 故障信号ORVMD分解结果 (a) IMF1; (b) IMF2; (c) IMF3; (d) IMF4; (e) IMF5; (f) IMF6; (g) IMF7; (h) IMF8; (i) IMF9


 图 10 VMD与ORVMD计算耗时
图 10 VMD与ORVMD计算耗时