摘要:铁电材料由铁电相转化为顺电相的临界温度被称为居里温度, 是铁电材料的一个关键指标. 本文使用固溶体组成元素的基本物理性质等特征对不同组分和配比的铅基钙钛矿铁电固溶体进行了统一的描述, 采用岭回归、支持向量回归、极端随机森林回归等机器学习方法对铅基钙钛矿铁电固溶体的居里温度进行了学习. 使用交叉验证的方法对学习效果进行验证, 得到上述机器学习方法对材料居里温度的预测值与实验值之间的平均误差分别为14.4, 14.7, 16.1 K, 集成三种回归方法优化的模型在交叉验证中测得的平均误差为13.9 K. 在此基础上对超过20万种铅基钙钛矿的居里温度进行了预测, 给出了两种可能具有高居里温度的铁电材料.
关键词: 机器学习/
铁电/
居里温度/
钙钛矿

English Abstract

全文HTML

--> --> -->

近年来, 具有优秀压电和热电性质的弛豫铁电体受到了广泛关注. 其中以固溶体Pb(Mg_1/3Nb_2/3)O₃-PbTiO₃ (PMN-PT)为代表的铅基钙钛矿铁电体由于其高压电系数而备受关注. 然而PMN-PT的居里温度较低(～130—170 ℃), 限制了它在高温场景下的应用. 因此, 为了解决这类铁电体高温应用的难题, 研究者们在实验中尝试将Pb(In_1/2Nb_1/2)O₃, Pb(Lu_1/2Nb_1/2)O₃, Pb(Yb_1/2Nb_1/2)O₃ (PIN, PLN, PYN)等不同的简单钙钛矿与PbTiO₃结合在一起来形成二元或三元的铅基钙钛矿固溶体来提高铅基钙钛矿铁电体的热稳定性.
Liu等^[1]研究者制备了一系列PLN-PT二元固溶体材料, 其测得的居里温度范围为145—365 ℃. Wu等^[2]研究者制备了一系列PIN-PMN-PT三元固溶体, 测得的居里温度范围为188—231 ℃.
在实验上类似的尝试还有很多. 然而将十几种简单铅基钙钛矿与PbTiO₃组合成二元或三元固溶体拥有超过100种可能的组合, 再考虑到其中各组分比例的变化, 可以看出该类体系的搜索空间是巨大的, 通过实验的方法穷尽所有可能的组合来寻找高温铁电体是非常困难的. 在实验方法之外, 第一性原理计算的方法可以对材料的诸多电学性质进行模拟计算^[3-5], 然而目前该方法尚不能用来计算材料的居里温度.
近年来, 机器学习方法在物理、材料领域发挥了越来越重要的作用. 在机器学习方法的指引下, 人们可以快速地探索、挖掘出具有目标性质的材料^[6-9]. 在本研究之前, 就有研究者曾使用机器学习方法探索钙钛矿铁电材料的居里温度. 例如Balachandran等^[10]针对(1–x)Pb(B₁,B₂)O₃-xPbTiO₃体系从117种不同组分的数据中训练得到机器学习模型, 用以预测该体系的居里温度, 他们使用交叉验证的方法进行模型评估, 发现其最优模型的预测值与实验值之间的平均绝对误差(mean average error, MAE)为30.2 K; Zhai等^[11]从47种钙钛矿材料数据中训练得到了多个预测钙钛矿居里温度机器学习模型, 其表现最优的模型为支持向量回归(support vector regression, SVR)模型, 交叉验证得到预测模型的MAE为21.2 K, 预测值与实验值之间相关系数为0.85.
为了进一步得到适用于铅基钙钛矿铁电晶体的、具有更高预测准确度和更具有鲁棒性的居里温度预测模型, 本文通过利用元素属性构建特征, 从205种不同铅基钙钛矿固溶体的数据中学习, 得到三种预测居里温度的机器学习模型. 并且通过模型集成的方法对习得的模型进行集成, 得到预测误差更小的机器学习模型. 据此对大量复杂铅基钙钛矿的居里温度进行了预测, 以供实验研究者参考.

本文构建机器学习模型来预测复杂铅基钙钛矿的居里温度主要包含以下3个步骤:
1)获取训练数据, 构建用来预测居里温度的特征;
2)通过交叉验证的方法选取合适的机器学习模型并进行其超参数的调整; 将多个模型进行集成, 构建最终的机器学习模型;
3)使用机器学习模型学习训练数据, 对未知的复杂铅基钙钛矿材料的居里温度进行预测.
本工作使用了python库scikit-learn^[12]来进行模型的训练和评估.
2

-->

2.1.数据集及构建特征

我们从十余篇已发表的实验论文中收集了205种不同的铅基钙钛矿的居里温度数据^[1,2,13-28]. 其居里温度的范围为–120—490 ℃. 其中涉及到18种简单铅基钙钛矿和45种前者组合而成的复杂钙钛矿. 在这些铅基钙钛矿中, 钙钛矿结构的A位离子都为Pb离子, X位离子都为O离子, 其居里温度的差异是由B位离子的差异所导致的. 在我们收集的训练数据中既有结构较简单的PbTiO₃, PbZrO₃等B位仅有一种离子的钙钛矿, 也有PMN-PFN-PZT等B位有5种离子的复杂钙钛矿, 这保证了学习得到的模型对于不同复杂程度的钙钛矿固溶体均有良好的泛化能力.
由于本研究的体系之间的差异仅在于钙钛矿的B位离子的不同, 因此针对铅基钙钛矿铁电体的B位离子构建了以下特征来描述不同的材料: 1)材料中不同种类B位离子所对应的化学计量占比、不同离子种类数目; 2)对于材料中的B位元素, 引入其离子半径、电离能等39种的物理化学性质, 该数据取自Balachandran等^[10]的研究, 针对材料中各元素的属性及配比计算材料中B位元素化学计量占比加权平均得到的平均属性和各种属性的方差; 3)采用第一性原理计算和机器学习方法得到的钙钛矿中B位离子偏移氧八面体中心的距离, 取自文献[29, 30], 计算其加权平均及方差. 根据上述元素级别性质, 对每种材料构建了86项特征用来描述不同材料之间的差异, 并提供给机器学习模型用作建模的依据. 所有特征的数值都进行了缩放, 将特征数值缩放到均值为0、方差为1的范围内, 这样可以确保所有的特征数值在相同的尺度上, 从而避免由于特征尺度不同而对机器学习模型带来误导. 得到特征向量x, 作为后续不同机器学习模型的输入. 本文中采用的具体特征指标及取值在补充文件(online)中给出.
2 -->

2.2.机器学习模型

如果仅研究某种特定组分的钙钛矿固溶体不同构成比例的材料的居里温度, 可以通过开展一系列实验, 制备出若干组分占比不同的材料, 然后通过线性回归等简单方法进行拟合, 并分析该组分的钙钛矿固溶体的居里温度随配比的变化. 这种不依赖于额外物理知识和物理规律的统计方法难以推广至各种不同组分的钙钛矿固溶体. 仅能分析特定组分固溶体的居里温度与配比的关系, 而无法触类旁通得对其他组分的材料居里温度进行判断.
为了克服这一缺点, 发挥机器的“智能”来解决这一难题, 构建了上述特征来对铅基钙钛矿铁电晶体进行描述, 使用机器学习的方法从其基本的物理性质出发挖掘不同材料之间深层的相似性, 将不同种类固溶体的知识纳入统一的模型, 达到“触类旁通”的效果. 基于这些基本物理性质和学到的不同固溶体居里温度的知识, 对完全未知的材料的居里温度做出预言.
本文尝试了多种机器学习模型来对该问题进行建模, 其中效果较好的模型为: SVR^[31]、极端随机森林回归(extremely randomized trees regression, ETR)^[32]、岭回归(kernel ridge regression, KRR) (使用径向基函数(radial basis function, rbf)核)^[33].
3 -->

2.2.1.KRR (使用rbf核)^[33,34]

KRR是线性回归模型的拓展. 线性回归模型基于一系列的假设, 例如: 目标值与特征之间呈现线性关系; 特征之间应该相互独立等.
为了将线性回归推广至更一般的场景, 引入了KRR: 通过在线性回归的损失函数中添加L2正则项来解决潜在的特征共线性的问题; 引入了核技巧来使得模型可以拟合目标变量与特征之间的非线性关系. 使用核技巧的KRR模型具有如下数学形式和损失函数^[34]:

$y = {{{w}}^{\rm{T}}}{{\varPhi}} ({{x}}),$

$C = \frac{1}{2}\sum\limits_i {{{\left( {{y_i} - {{{w}}^{\rm{T}}}{{\varPhi}} ({{{x}}_i})} \right)}^2}} + \frac{1}{2}\lambda ||{{w}}|{|^2},$

其中x为输入的特征向量; $\lambda $为正则项的权重, 是为了平衡结构风险与经验风险而预先设定的超参数; ${{\varPhi}} ({{x}})$为将特征向量映射到高维希尔伯特空间的映射函数, 其映射方法取决于核函数. 本文采用的核函数K为机器学习中较为常用的rbf核, 其对应了特征从原始空间到无穷维空间映射, 核函数中的$\gamma $为预先设定的超参数^[35].

$K\left( {{{{x}}_i},{{x}}} \right) = \exp \left( { - \gamma \left\| {{{{x}}_i} - {{x}}} \right\|_2^2} \right),$

${{\phi}} (x) = {{\rm e}^{ - \gamma {x^2}}}{\left[ {1,\sqrt {\frac{{2\gamma }}{{1!}}} x,\sqrt {\frac{{{{(2\gamma )}^2}}}{{2!}}} {x^2},\sqrt {\frac{{{{(2\gamma )}^3}}}{{3!}}} {x^3}, \cdots } \right]^{\rm{T}}}.$

模型在映射空间中使用线性模型进行数据建模, 线性模型的权重w通过优化损失函数而得到. 据此推导出使得损失函数最小的w:

${{w}} = {\left( {\lambda {{{I}}_{\rm{d}}} + {{\varPhi}}{{{\varPhi}}^{\rm{T}}}} \right)^{ - 1}}{{\varPhi y}} = {{\varPhi}}{\left( {{{{\varPhi}}^{\rm{T}}}{{\varPhi}} + \lambda {{{I}}_{\rm{n}}}} \right)^{ - 1}}{{y}},$

式中定义${{\varPhi}} = {{{\varPhi}}_{{\rm{ai}}}}$为数据集映射到高维空间后的特征矩阵, ${{y}} = {{{y}}_{\rm{i}}}$为目标向量. 将该w代回(1)式中, 并使用核函数代替高维向量的内积, 得到

$\begin{split} y \, &= {{{w}}^{\rm{T}}}{{\varPhi}}({{x}}) = {{y}}{\left( {{{{\varPhi}}^{\rm T}}{{\varPhi}} + \lambda {{{I}}_{\rm{n}}}} \right)^{ - 1}}{{{\varPhi}}^{\rm{T}}}{{\varPhi}} ({{x}}) \\ &= {{y}}{\left( {{{K}} + \lambda {{{I}}_{\rm{n}}}} \right)^{ - 1}}\kappa ({{x}}), \end{split}$

其中${{{K}}_{ij}} ={{\varPhi}} {\left( {{{{x}}_i}} \right)^{\rm{T}}}{{\varPhi}} \left( {{{{x}}_j}} \right)$, $\kappa ({{x}}) ={{K}}\left( {{{{x}}_i}, {{x}}} \right)$. 如果将核函数${{K}}\left( {{{{x}}_i}, {{x}}} \right)$视为计算新样本x与训练样本${{{x}}_i}$之间的相似度, 那么可以认为使用核函数的KRR的预测结果是基于计算新样本与训练样本之间的相似度的方法得到的. 与训练样本相似的新样本具有与之相似的元素级别特征, 因而也会根据实验已知的结论给出相似的预测结果. 而与训练数据较不同的样本, 则通过全局考察其相似性, 来给出合理的预测值.
3 -->

2.2.2.SVR^[31]

SVR与KRR类似, 具有线性模型的回归形式. 在SVR模型中, 同样采用核函数的方法为模型引入非线性拟合能力. 而该方法与KRR不同的是, SVR对权重w进行优化时容许预测值与实验值之间有ε的偏差, 因此它不需要模型完美地满足所有的数据点, 可以减少模型过拟合的风险. 具体地, 它的损失函数如下^[31]:

${\min _{{{w}},b}}\frac{1}{2}||{{w}}|{|^2} + \;C\sum\limits_{i = 1}^m {{{\ell }_\varepsilon }} \left( {f\left( {{{{x}}_i}} \right) - {{{y}}_i}} \right),$

${\ell _\varepsilon }(z) = \left\{{\begin{array}{*{20}{l}}{0,}& |z| \leqslant \varepsilon, \\{|z| - \varepsilon,}&{{\rm{ otherwise }}},\end{array}} \right.$

其中C为权衡结构风险与经验风险的超参数; ${{\ell }_\varepsilon }$为ε-不敏感函数, 用以忽略数据与模型之间的较小偏差. 在本研究中SVR的核函数选为径向核函数. 为了使得其损失函数最小化, 通过构造拉格朗日函数并解其对偶问题, 最终可以将SVR模型表示为

$f({{x}}) = \sum\limits_{i = 1}^m {\left( {{{\hat \alpha }_i} - {\alpha _i}} \right)} \kappa \left( {{{x}},{{{x}}_i}} \right) + b.$

SVR与KRR具有类似的形式, 但是在SVR中只有对应的${\hat \alpha _i} - {\alpha _i}$不为0的训练样本才被用来预测未知的铁电体, 而这些样本就被称为“支持向量”. SVR的思想与实验科学非常切合, 研究者在实验测得的居里温度本身就存在一定的随机误差, 在损失函数中引入ε-不敏感函数可以在一定程度上防止将这种随机误差纳入模型. 此外使用该方法可以防止对训练样本的过拟合, 同时还可以使模型更快地进行预测.
3 -->

2.2.3.ETR模型^[32]

为了尝试使机器学习模型获得更好的可解释性, 还使用了ETR模型对复杂铅基钙钛矿的居里温度进行建模. ETR将若干个分类与回归树(classification and regression trees, CART)集成在一起. 其中每棵CART在构建时采用随机挑选属性和分裂值的分裂方法, 从而构建出若干个完全随机的树. 在ETR模型中, 通过控制每棵树的最大深度“depth”、划分节点时最少的样本数“min_samples”来限制树的规模, 通过控制总共集成树的数量“n”来调节模型的拟合能力.
2 -->

2.3.模型超参数的优化

3 -->

2.3.1.交叉验证策略

为了调整模型的超参数和检验模型的泛化效果, 采用5次10折交叉验证的策略. 在一次10折交叉验证中, 将样本集随机划分为10等份, 轮流使用其中的1份作为测试集而其余9份作为训练集. 机器学习训练集的数据而对测试集中的样本的居里温度进行预测, 通过比较测试样本居里温度的实验值与预测值之间的MAE、均方跟误差(root-mean-square error, RMSE)来衡量模型对于未知样本的预测能力. 为了减少单次随机划分样本集带来的偶然性, 以上过程重复5次, 取结果的均值作为最终的评价依据.
由于本文研究对象分为简单铅基钙钛矿和复杂铅基钙钛矿两种, 而简单铅基钙钛矿的种类有限且研究较为详尽, 同时本研究的主要目标—复杂铅基钙钛矿种类繁多, 相对而言已研究确认的材料较少, 因此在交叉验证的过程中将数据集中B位元素种类小于3的24项简单钙钛矿的数据作为“教师”, 只出现在训练集中用来模型训练, 不出现在测试集中参加模型性能的评估.
3 -->

2.3.2.超参数的优化

模型的超参数直接影响了模型的拟合能力和拟合策略, 选取一组合适的超参数对模型的构建非常重要. 在定义了交叉验证的策略之后, 在一定的超参数区间内通过随机搜索^[36]和网格搜索的方式选取若干组超参数并使用该超参数构建模型. 通过之前定义的交叉验证策略对模型效果进行检验, 最终选取使得交叉验证结果最理想的一组超参数作为模型最终的超参数.
例如, 当优化SVR中的超参数ε时, 在0—10的取值范围内以0.5为步长对ε进行网格搜索. 如图1所示, 对比了ε取不同值时模型的测试误差, 同时将该参数模型应用于全部数据集时的支持向量数目也一并列出, 以作参考. 当ε取值小于4时模型的误差较低; 当ε取值进一步增大时模型的误差出现快速上升. 另一方面随着ε取值的增大, 模型中的支持向量的数目也在减少. 在泛化能力相似的情况下, 倾向于选择较简单的模型以避免过拟合, 因此ε的值最终取为4. 此时, 模型经过完整地学习训练集中所有205项数据后, 其模型中的支持向量数目为147项, 也就是说模型仅使用其中147项材料的数据对未知材料进行预测.
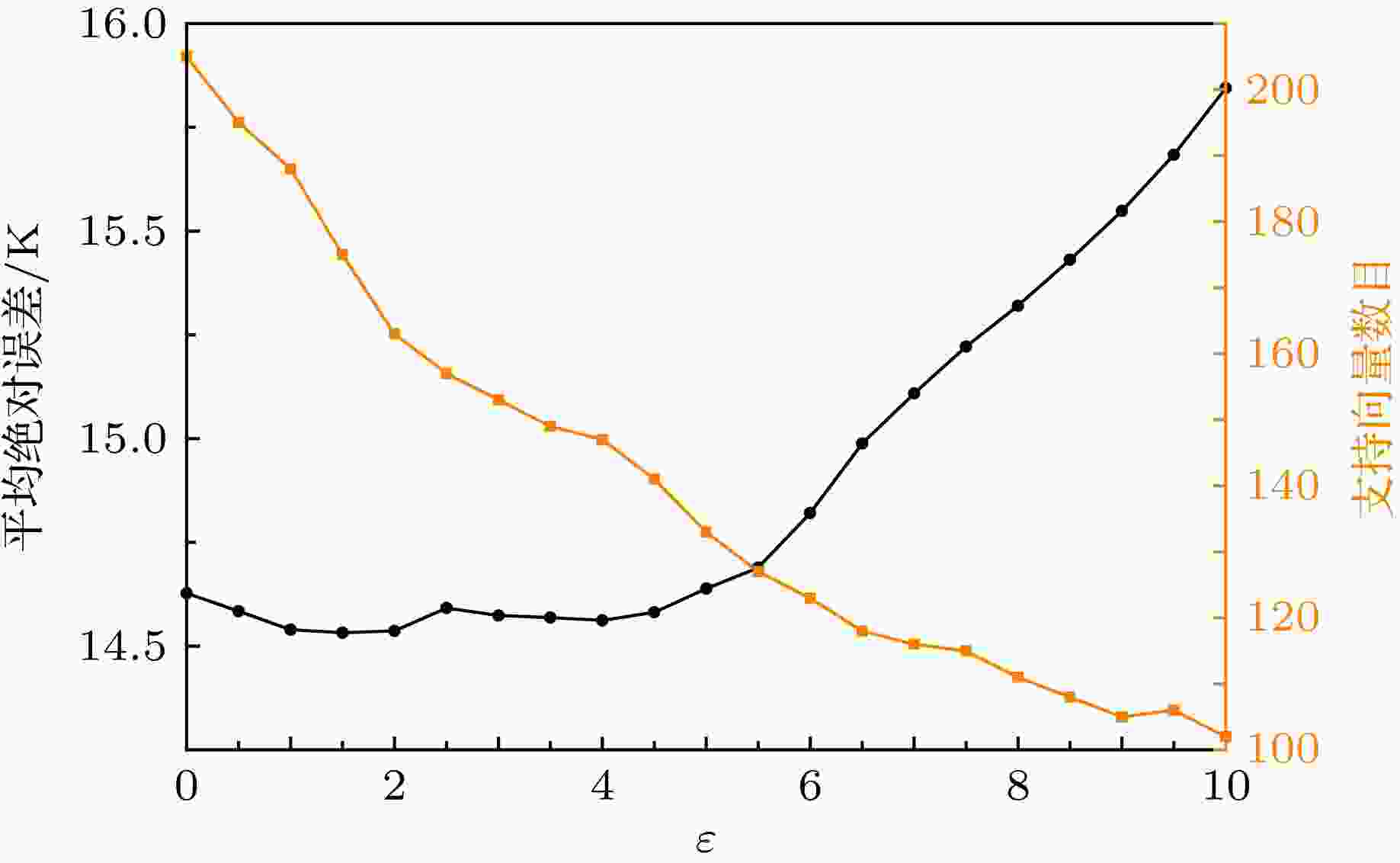图 1 支持向量回归中的超参数ε的优化及支持向量数目分析
Figure1. Optimization of hyperparameters in support vector regression and the analysis of the number of support vectors

依据上述方法, 同样对其他超参数做了类似的搜索和优化, 最终得到的超参数如表1所列.

模型	超参数
KRR	$\lambda $ = 0.001, $\gamma $ = 0.005
SVR	$\gamma $ = 0.02, ε = 4, C = 900
ETR	n = 108, depth = 20, min_samples = 2

表1本文三种机器学习方法所采用的超参数
Table1.Hyperparameters of the three machine learning methods in this study.

2 -->

2.4.模型的集成

上述三种模型, 从不同的角度出发对钙钛矿铁电材料的居里温度进行了学习, 均取得了良好的成效. 为了进一步提高预测的准确度, 通过集成的方法, 将上述三种回归模型融合为一个统一的模型. 集成模型同时训练上述三种机器学习模型, 并使用三种模型分别对居里温度进行预测. 将三种机器学习模型的预测均值作为最终的输出.
为了检验集成的效果, 也对集成模型使用交叉验证的方法进行了评估. 另外, 也尝试了赋予三个模型其他合理的权重, 如图2所示, 当将三种模型融合在一起时, 往往可以得到比最优单模型更好的效果. 测得的最优融合比例为0.6∶0.2∶0.2 (KRR∶SVR∶ETR), 其MAE为13.7 K. 等权重模型融合测得的MAE为13.9 K (图2中的红色点). 出于保持模型简单性的考虑, 直接采用了等权重的方法对模型进行融合.
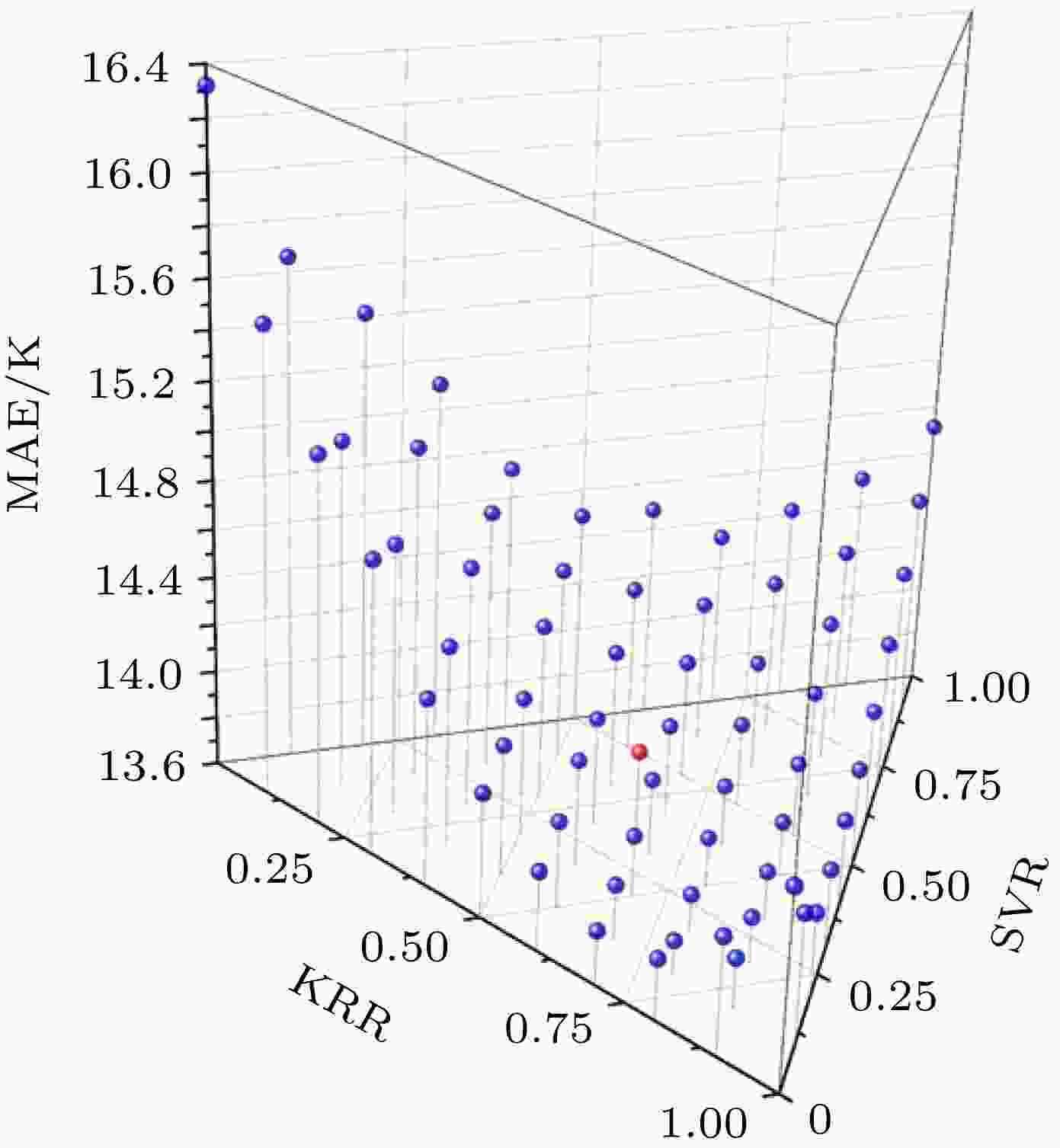图 2 不同模型权重的融合实验结果
Figure2. Performance of ensembled model with different base model weight.

2 -->

2.5.使用机器学习方法对未知材料探索

对数据集中出现的20种不同组分的简单铅基钙钛矿相互组合, 得到了大量的包含PbTiO₃组分的二元或三元的复杂钙钛矿固溶体, 共有190种可能的组合方式, 而在这些复杂钙钛矿固溶体中, 使其中简单钙钛矿组分从2%开始, 以2%为步长变化, 从而研究不同组分的复杂铅基钙钛矿. 至此, 得到了超过20万种铅基钙钛矿材料. 使用上文中的方法对它们构建特征, 并使用机器学习的方法对其中所有材料的居里温度进行预测.

2

-->

3.1.模型效果验证

在5轮的交叉验证中, 使用了MAE, RMSE和相关系数三项指标对三种机器学习模型和集成后模型的预测结果进行了评估. 评估结果列于表2, 在三种学习模型中KRR给出了最低的MAE, 为14.4 K, 同时RMSE为最低的22.5 K. 所有模型的在交叉验证中对于未学习过的材料的预测值与材料的实验值之间均有较大的相关系数. 而将三种机器学习模型进行集成后, 集成模型的表现比三种机器学习模型更为优秀. 同时在表2中也将本文机器学习模型与其他使用机器学习方法研究钙钛矿居里温度的工作中的最优模型进行了比较.

	模型					对比
	KRR	SVR	ETR	集成 模型		文献[10]	文献[11]
MAE/K	14.4	14.7	16.1	13.9		30.2	21.2
RMSE/K	22.5	23.4	23.8	21.4		—	28.7
相关系数	0.96	0.96	0.96	0.97		—	0.85

表2本文所使用的机器学习方法的评估及与其他研究者工作的对比
Table2.Evaluation of machine learning methods in this paper and the comparison with other works.

为了给读者更直观地展示各种机器学习模型对于未知材料居里温度的预测效果, 给出了5轮交叉验证过程中不同材料的预测均值与实验值, 如图3所示. 图3中不同的橘色点对应不同的材料, 其纵坐标为该材料的居里温度实验值, 横坐标为本文机器学习模型对该材料居里温度的预测均值. 蓝色点划线y = x代表着预测值与实验值完全吻合的理想情况. 从图3可以看出在交叉验证过程中对于大部分未学习的铅基钙钛矿, 机器学习模型对其居里温度的预测值都落在其实验值的附近, 预测值与实验值之间具有较强的相关性.
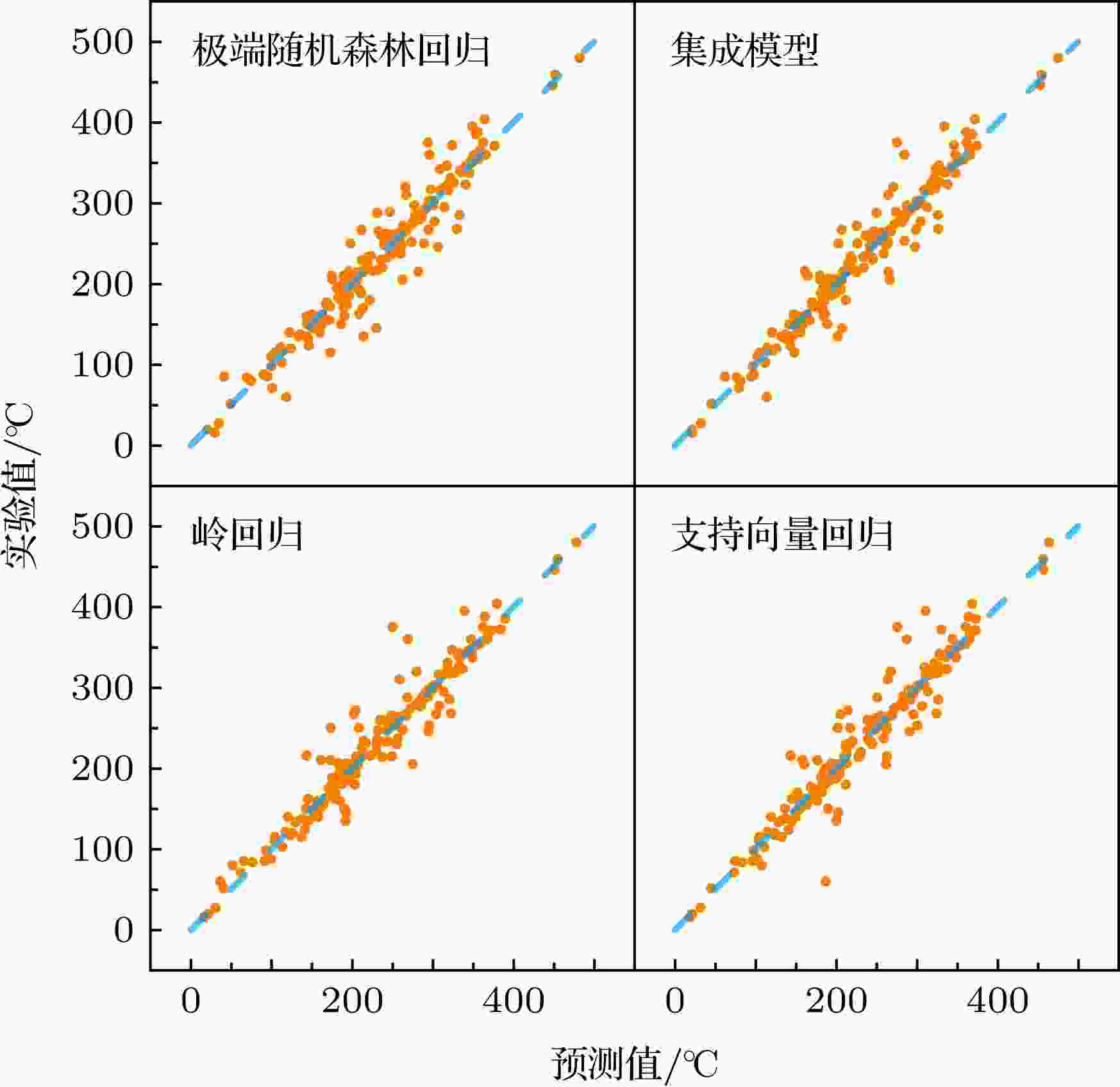图 3 三种机器学习模型及其集成模型对材料的预测值与实验值的比较
Figure3. Comparison of prediction and experimental values of three machine learning models and their ensemble models.

此外, 在图3中对比三种机器学习模型不难看出, 这三种机器学习模型一致得给出了不错的预测成绩, 但是其对于特定材料的预测结果却不尽相同, 这是由模型之间的差异所导致的. 如上文所述, KRR模型与SVR模型具有相同的广义线性回归形式, 相同的核函数形式. 但是其不同的损失函数赋予了两种模型不同的“价值观”, 在学习过程中它们遵从各自的“价值观”各自寻找其最优参数, 最后得到的结果必然是不同的. ETR模型基于CART, 与前两种模型形式显著不同, 在交叉验证中, 其MAE与RMSE也略逊于前两种模型, 但是其树的形式更利于人类理解. 同时如图2所示, 融合更多的模型也有助于提高模型的预测能力, 因此将这三种模型融合在一起, 相互取长补短, 得到了预测能力更优的集成模型. 例如支持向量模型对于实验值50 K附近的某材料的预测值发生了明显的偏差, 经过模型融合之后, 该偏差得到了有效的缓解.
2 -->

3.2.模型成果

本文的产出主要分为两方面: 本研究中整理的铅基钙钛矿的居里温度数据和本文中构建的机器学习模型; 对超过20万种铅基钙钛矿材料的居里温度进行了预测, 并挑选了两种可能具有高居里温度的材料以供实验研究人员参考.
3 -->

3.2.1.数据与模型

在本研究中收集的包含205种铅基钙钛矿的居里温度数据集在补充文件(online)中给出, 可以供其他相关领域的理论或实验研究者参考和使用. 利用该数据集, 本文构建了三种机器学习模型: KRR, SVR, ETR. 与多数研究者不同的是, 还将这三种机器学习模型集成为一个模型.
为了检验单个机器学习模型和集成机器学习模型的可靠性, 本文通过交叉验证的方法对模型进行测试. 在交叉验证的过程中KRR, SVR, ETR单模型的MAE分别为14.4 K, 14.7 K, 16.1 K. 集成后的机器学习模型在交叉验证中的MAE为13.9 K. 而在其他研究者对钙钛矿铁电体的居里温度进行预测的而建立的模型, 其交叉验证的MAE为30.2 K^[10]和21.2 K^[11]. 该交叉验证误差的差异可能来源于模型构建过程中特征构建的方式不同等因素, 因此本文中使用元素属性的均值和方差构建特征的方法拥有一定的泛化意义.
此外, 使用ETR模型学习后, 可以根据CART在不同特征上进行分裂时的方差变化来量化不同特征对于材料居里温度的重要性. 具体而言, ETR模型是多棵CART的总和, CART在其每个节点中以某个特征的取值作为分割点将节点中的样本分割至两个子节点(一个节点中的样本对应特征取值均大于等于该值, 另一个节点中的样本对应特征取值均小于该值). 本文采用节点中样本居里温度的方差来刻画节点中样本的离散性, 采用分裂前后的加权方差变化来刻画该分裂带来的聚合增益. 如果依据某特征值将样本分为两类时带来了较大的聚合增益, 也就是说依据样本该特征的值可以将节点中具有较高居里温度的样本和居里温度较低的样本更好地区分开来, 那么该特征的取值对于判断居里温度显然是重要的. 将所有节点上采用某特征的取值作为分割条件时的方差变化以其节点中的样本数量作为权重加权求和, 得到该特征对于预测材料居里温度的重要性. 该指标表示了在使用ETR模型预测居里温度时该特征的重要程度^[37].
将所有特征重要性进行了归一化, 并将重要性最大的五种特征表示在图4中. 图4所示为B位元素(或该元素最常见单质)的热导率均值、电导率均值、比热容方差、元素序数均值、钙钛矿中离子偏移均值, 五种特征在使用ETR模型预测材料的居里温度中起到了最重要的作用.
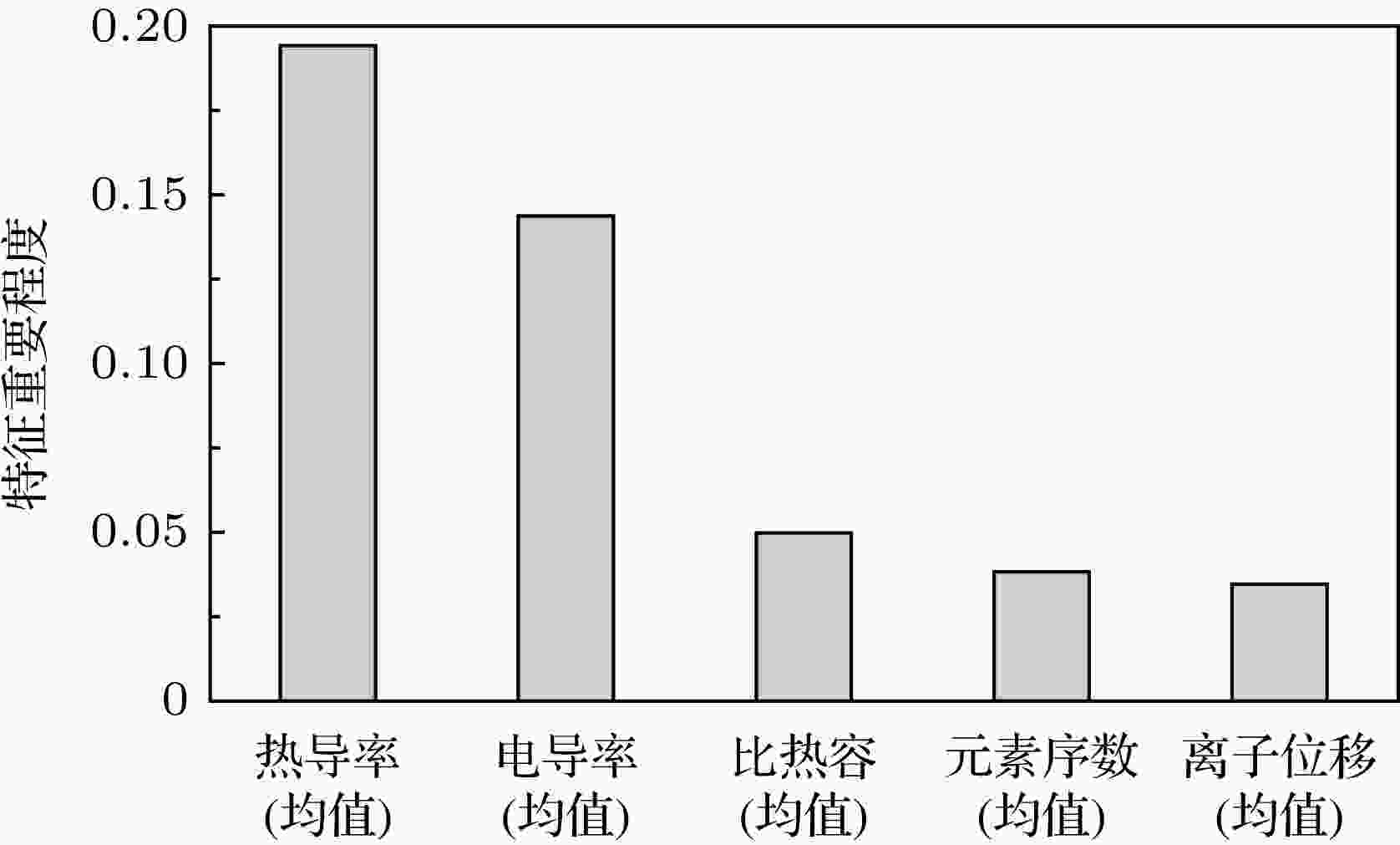图 4 ETR模型中最重要的5项特征
Figure4. Five most important features in ETR.

3 -->

3.2.2.使用机器学习寻找高温铅基铁电体

使用集成的机器学习模型, 对数据集以外的超过20万种铅基钙钛矿材料的居里温度进行了预测, 并挑选出了0.02PbMn_1/2Nb_1/2O₃-0.98PbTi O₃ (0.02PMN-0.98PT), 0.02PbGa_1/2Nb_1/2-0.02Pb Mn_1/2Nb_1/2O₃-0.96PbTiO₃ (0.02PGN-0.02PMN-0.96PT)两种具有较高居里温度的铅基钙钛矿固溶体, 其对应的居里温度分别为481 ℃和466 ℃. 集成机器学习模型对于PGN-PMN-PT体系中不同组分权重所形成的一系列固溶体进行的预测结果如图5所示.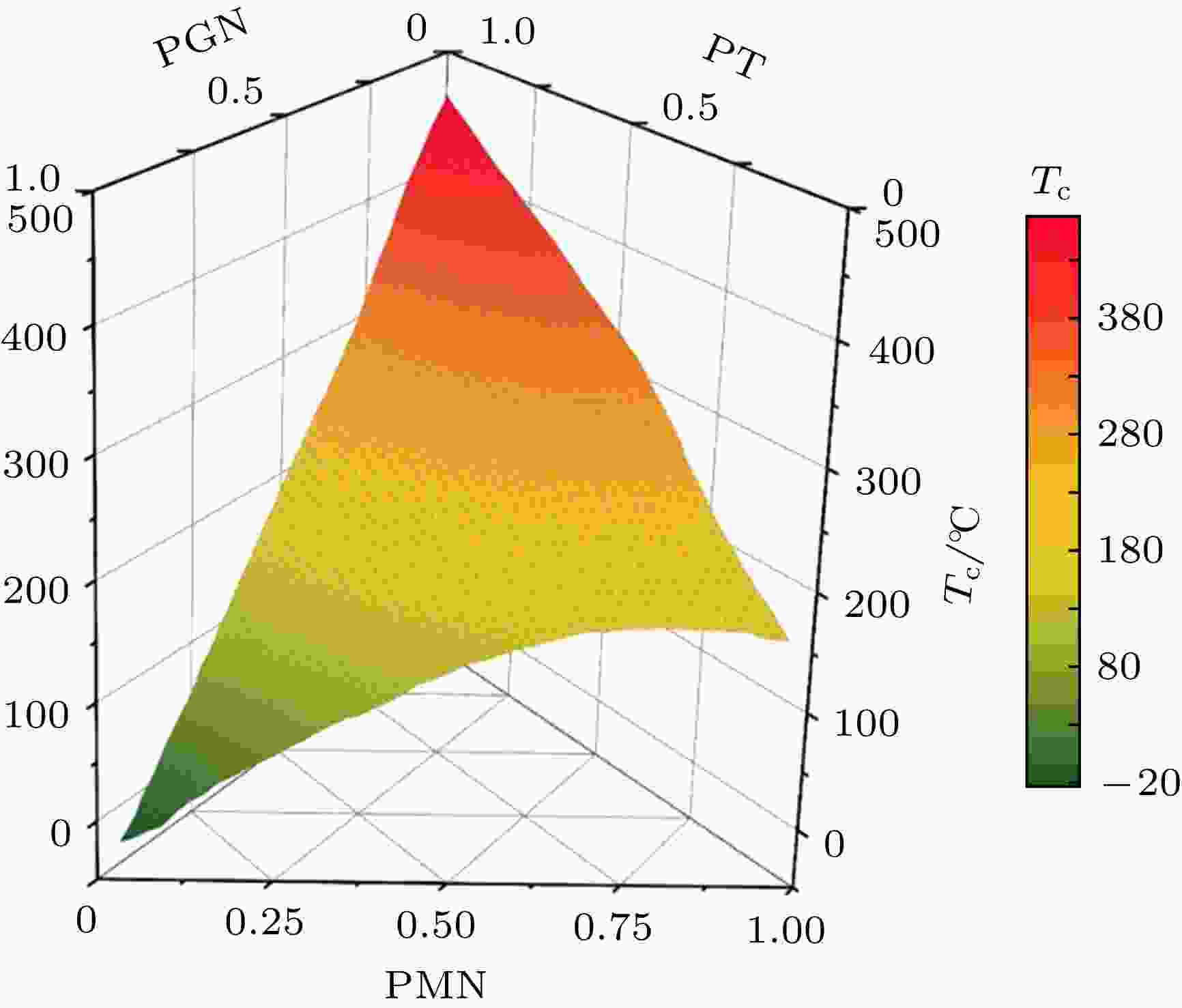
图 5 集成机器学习模型对PGN-PMN-PT固溶体的居里温度的预测
Figure5. Prediction of Curie temperature of PGN-PMN-PT solid solution by ensemble machine learning model

此外, 在补充材料(online)中还提供了全部20余万种钙钛矿固溶体的居里温度预测数据来为实验研究提供更详尽的参考.

本文在不同组分和配比的铅基钙钛矿铁电晶体所形成的庞大搜索空间中寻找具有高居里温度的铁电体, 利用元素基本物理性质等信息构建了一系列特征, 得以对各种不同组分的铅基钙钛矿铁电晶体进行统一的描述, 从而使得机器可以从基本物理性质出发对固溶体的居里温度进行建模和预测. 分别使用了KRR, SVR, ETR三种机器学习方法对铅基钙钛矿铁电固溶体的居里温度进行了学习, 并使用了等比例融合的方法构建了集成学习模型.
采用交叉验证的方法对模型的可靠性进行了评估, 其中集成机器学习模型在交叉验证中测得MAE为13.9 K. 使用该方法对超过20万种铅基钙钛矿铁电体的居里温度进行了预测, 并挑选出了两种具有潜在高居里温度的铅基钙钛矿铁电晶体: 0.02PMN-0.98PT, 0.02PGN-0.02PMN-0.96PT.