摘要: 高频天波探测设备在执行早期预警和海态遥感等任务时必须依靠电离层作为传播媒质, 而电离层具有时变、不稳定的特性, 会改变经过它传播的高频电磁波的特征, 导致回波频谱展宽, 严重影响了对目标的探测和海态参数的反演. 从色散效应、相位污染和多模传播等方面详细分析了回波谱展宽的原因和机理, 利用多层准抛物线电离层模型讨论了避免多模传播的选频措施. 针对在实际中较难解决的相位污染问题, 提出了一种不用估计回波瞬时频率的污染校正方法. 该方法利用了信号子空间与信号导频矢量张成空间的一致性原理, 能够较准确地估计出相位污染项, 实测数据处理表明新方法能够使展宽的回波谱得到有效锐化.
关键词: 电离层 /
多层准抛物线模型 /
高频射线 /
多模传播 /
相位污染校正 English Abstract Analysis of broadening mechanism of ionospheric echo spectrum and spectrum sharpening method Luo Huan 1,2 ,Xiao Hui 2 1.Air Force 95519 Army of PLA, Zunyi 563000, China Fund Project: Project supported by the Young Scientists Fund of the National Natural Science Foundation of China (Grant No. 51309232)Received Date: 09 June 2019Accepted Date: 07 August 2019Available Online: 01 November 2019Published Online: 05 November 2019Abstract: High-frequency sky wave detection equipment must rely on the ionosphere as the propagation medium in the early warning and sea state remote sensing tasks. The ionosphere is time-varying and unstable, which will change the characteristics of the high-frequency electromagnetic wave propagating through it, resulting in the broadening of the echo spectrum, thus seriously affecting the detection of targets and the inversion of sea state parameters. The reason and mechanism of the echo spectrum expansion are analyzed in detail from the dispersion effect, phase contamination and multimode propagation. The bandwidth of the dispersion effect is different from that of the high frequency detection equipment. When the bandwidth of the sky wave equipment is 3–30 MHz, the bandwidths of the dispersion effect are 41.6–57.4 kHz and 0.17–10.8 MHz. The multi-quasi-parabolic ionospheric model is used to discuss the frequency selection measures to avoid multimode propagation. The modulation process of ionospheric contamination to echo is studied theoretically. It is shown that the non-linear phase contamination will cause the energy of echo to diffuse in frequency domain and to be unable to accumulate. To solve the problem of phase contamination which is difficult to solve in practice, a contamination correction method without estimating the instantaneous frequency of the echo is proposed. In the method the consistency principle of signal subspace and signal frequency vector expansion space is used, and therefore the phase contamination term can be well estimated. Based on the real data, the contamination correction results from the proposed method, phase gradient autofocus method, maximum entropy spectral analysis method and time-frequency processing method are given. The results show that the new method is a better method and can effectively sharpen the broadened echo spectrum.Keywords: ionosphere /multi-quasi-parabolic model /high frequency ray /multimode propagation /phase contamination correction 全文HTML --> --> --> 1.引 言 高频天波探测设备依靠电离层对电磁波的反射和折射作用, 可对视距外数千公里的广袤范围进行监控和探测, 在军事领域可对威胁目标实现早期预警[1 ,2 ] , 在民用领域可进行海态遥感, 实时监测海洋表面风速、风向和浪高等[3 ] . 电离层是高频天波设备必不可少的传播信道, 其特性对探测设备的性能有很大影响. 电离层是时变、不稳定的, 当高频电磁波经过电离层时, 电离层色散效应会破坏不同时刻电磁波之间的相位相关性, 使得电磁波的相位发生随机变化, 导致回波谱展宽. 电离层的高度范围为60 km至几千公里, 具有分层的结构特性, 从下往上一般分为E层、F1层和F2层[4 ,5 ] , 且每层的物理结构特性均不相同. 多层的电离层结构是高频电波发生多模传播的直接原因, 一旦出现多模传播现象, 处于不同地面距离的目标或者杂波将会在同一时刻进入接收机, 经过脉冲压缩和匹配滤波处理后, 它们会出现在同一距离单元内, 引起频谱展宽, 造成测量误差或者目标误判.[6 ] ; 2)最大熵谱估计(MESA)法[7 ] ; 3)多项式拟合法[8 ] . 这些方法要求相位污染缓慢变化, 当其变化过快或者幅度过大时, 性能将下降. 时频分析工具[9 ] 和最大似然估计[10 ] 也被应用于相位调制校正领域, 时频级联法[11 ] 不需要提取标校信号, 直接可获得回波的瞬时频率, 可应对大幅度的相位污染, 但是缺点是污染去除不够彻底, 需要与其他方法进行级联.2.高频天波回波谱展宽的机理分析 22.1.基于多层准抛物线的电离层模型 2.1.基于多层准抛物线的电离层模型 为从理论上研究天波回波谱的展宽机理, 需要用到电磁波的空间斜距、地面距离和射线群路径等参数信息, 这些参数需要建立一个合理的电离层模型进行确定. 目前, 多层准抛物线(multi-quasi-parabolic, MQP)模型和国际参考电离层(international reference ionosphere, IRI)模型[12 ,13 ] 是描述电离层电子浓度剖面的主要模型, 但IRI依赖大量的历史数据[2 ] , 而MQP模型计算量小且对电离层分层结构具有优良的模拟效果, 被大量应用于高频射线传播中[2 ,14 ] . 根据MQP模型, 单层电离层的电子浓度表示为[14 ] ${N_{\rm{e}}}(r)$ 代表电子浓度; r 为该层电离层的高度; ${N_{\rm{m}}}$ 是单层电离层的电子浓度最大值; ${q_{\rm{m}}}$ 是层厚度; ${r_0}$ 是地球半径, 地心到电离层的距离为${r_{\rm{m}}}$ , 若电离层与地面相距${h_{\rm{m}}}$ , 则满足${r_{\rm{m}}} = {h_{\rm{m}}} + {r_0}$ ; ${r_{\rm{b}}}$ 是电离层底部与地心的距离, 满足${r_{\rm{b}}} = {r_{\rm{m}}} - {q_{\rm{m}}}$ .D 、射线群路径G 均不相同. 由(1 )式可得D 和G 的解析式[15 ] :$F \!=\! {f}/{{{f_{\rm{c}}}}},{f_{\rm{c}}} \!=\! \sqrt {80.6{N_{\rm{m}}}}$ 为单层电离层的截止频率; $\gamma = {\cos ^{ - 1}}\left[ {\left( {{{{r_0}} / {{r_{\rm{b}}}}}} \right)\cos {\beta _0}} \right]$ ; $B = {{ - 2{r_{\rm m}}r_{\rm{b}}^2} / {q_{\rm m}^2}}$ , U = ${B^2} - 4AC$ , $A \!=\! {F^2} - 1 + {\left( {{{{r_{\rm{b}}}} /{{q_{\rm m}}}}} \right)^2}$ , $C \!=\! {\left( {{{{r_{\rm{b}}}{r_{\rm m}}} / {{q_{\rm m}}}}} \right)^2} - $ ${F^2}r_0^2{\cos ^2}{\beta _0} $ , $V = 2A{r_{\rm{b}}} + B + 2{r_{\rm{b}}}F{A^{{1 / 2}}}\sin \gamma $ ; ${\beta _0}$ 表示高频电磁波发射的初始仰角.2.2.电离层色散效应对回波的影响 -->2.2.电离层色散效应对回波的影响 电离层的相对介电系数是电磁波频率的函数, 所以电离层是一种色散的媒质. 当已调制的高频探测电磁波(例如频率调制信号、相位编码信号)经过电离层传播时, 由于传播信号中存在不同的频率成分, 它们的传播速度不同, 当探测电磁波返回后, 各频率分量之间的相对包络和相对相位都产生了变化, 导致波形起伏畸变, 即出现了色散效应[16 ] .[15 ] $\Delta \tau $ 是色散系数, 它的倒数为色散带宽; c 是光速; 由(3 )式可见, ${{{\rm{d}}G} / {{\rm{d}}f}}$ 越大, 电离层色散带宽越小. ${{{\rm{d}}G} / {{\rm{d}}f}}$ 的计算式为${{{\rm{d}}{\beta _0}} / {{\rm{d}}f \!= \!}} - \!({{{{\partial D} / {\partial f}}}) / ({{{\partial D} / {\partial {\beta _0}}}}})$ . 将(4 )式代入(3 )式, 可得${{\partial G} / {\partial f}}$ , ${{\partial G} /{\partial {\beta _0}}}$ , ${{\partial D} / {\partial f}}$ 和${{\partial D} / {\partial {\beta _0}}}$ 可通过对(2 )式进行求导来计算. 根据(5 )式, 考虑天波探测设备的工作频率为3—30 MHz, 设定电离层参数为: E层, f cE = 4.0 MHz, r bE = 86 km, q mE = 18 km; F1层, f cF1 = 6.1 MHz, r bF1 = 128 km, q mF1 = 60 km; F2层, f cF2 = 10.8 MHz, r bF2 = 205 km, q mF2 = 118 km. 电离层各层的色散系数与探测设备工作频率的关系见图1 , 可见: 1)不同的分层电离层的色散系数(带宽)不同, 具体来说, E层的色散带宽最大, F1层次之, F2层最小; 2)最大、最小色散系数分别对应于最小、最大的色散带宽, 当$\Delta \tau = {\rm{2}}{\rm{.4}} \times {\rm{1}}{{\rm{0}}^{ - {\rm{5}}}}$ 时, 对应最小的色散带宽41.6 kHz, 当$\Delta \tau = {\rm{9}}{\rm{.2}} \times {\rm{1}}{{\rm{0}}^{ - {\rm{8}}}}$ 时, 对应最大的色散带宽10.8 MHz. 一般的天波探测设备工作带宽为十几到几十千赫兹[17 ] , 所以电离层色散效应对高频电磁波的影响很小. 若色散效应对回波产生了影响, 则可通过改变工作带宽或工作频率加以避免.图 1 色散系数与探测频率的关系Figure1. Relationship between dispersion coefficient and detection frequency.2.3.相位污染对回波的影响 -->2.3.相位污染对回波的影响 引起高频回波相位污染的直接原因是回波相位路径发生非线性改变, 而回波相位路径的非线性改变与电离层电子浓度的不均匀变化密切相关. 下面利用电离层MQP模型(三层电离层+两层连接层)[2 ] 分析电子浓度改变与回波相位污染的关系. 设定${t_1}$ 时刻的电离层参数为: E层, ${f_{{\rm{cE}}}}=$ 3.0 MHz, ${r_{{\rm{bE}}}}=$ 120 km, ${q_{{\rm{mE}}}}=$ 20 km; F1层, ${f_{{\rm{cF1}}}}=$ 4.2 MHz, ${r_{{\rm{bF}}1}}=$ 209 km, ${q_{{\rm{mF}}1}}=$ 87 km; F2层, ${f_{{\rm{cF}}2}}=$ 6 MHz, ${r_{{\rm{bF}}2}}=$ 320 km, ${q_{{\rm{mF}}2}}=$ 100 km. ${t_2}$ 时刻的电离层参数为: E层, ${f_{{\rm{cE}}}}=$ 3.2 MHz, ${r_{{\rm{bE}}}}=$ 122 km, ${q_{{\rm{mE}}}}=$ 20 km; F1层, ${f_{{\rm{cF1}}}}=$ 4.0 MHz, ${r_{{\rm{bF}}1}}=$ 209 km, ${q_{{\rm{mF1}}}}=$ 88 km; F2层, ${f_{{\rm{cF2}}}}=$ 6.8 MHz, ${r_{{\rm{bF2}}}}=$ 320 km, ${q_{{\rm{mF}}2}}=$ 101 km. 之所以将${t_1}$ 和${t_2}$ 时刻的电离层参数设置为不同, 是为了模拟不同时刻对应于不同的电子浓度, ${t_1}$ 和${t_2}$ 时刻的电子浓度随高度的变化如图2 所示. 从图2 可见, 由于电离层结构不稳定导致不同时刻的电子浓度曲线存在差异(该差异无规律), 以200 km高度为例, 在此高度${t_1}$ 和${t_2}$ 时刻的电子浓度不同, 将会使先后经过该层反射的回波的相位产生调制, 而该调制方式无规律可循, 属于非线性调制, 相位的相关性遭到破坏, 其结果是多个回波脉冲在积累后无法完成能量聚集.图 2 不同时刻的电离层电子浓度曲线Figure2. Ionospheric electron concentration curves at different times.$u\left( t \right) = \left\{ {\begin{aligned} & {1,\;\;0 \leqslant t < T}, \\ & {0,\;\;\;\;\;{\rm{otherwise}}}, \end{aligned}} \right.$ ${f_0}$ 是发射频率(工作频率), T 是扫频周期, $\alpha = {{{B_{\rm{w}}}} / T}$ 是调频率, ${B_{\rm{w}}}$ 是发射带宽, ${\varphi _0}$ 是初相位. 经过电离层折射、反射后的返回电磁波为${a_{\rm{R}}}$ 为回波幅度; ${\tau _{\rm{r}}} = {{2R} / c}$ 为电磁波的返回时延, R 是目标或杂波到探测设备的距离; $\varepsilon (t)$ 为电离层电子不均匀分布导致的非线性污染项. 假设目标或杂波的径向速度为v , 则${\tau _{\rm{r}}}$ 可以另写为${R_0}$ 是探测初始时刻目标/杂波到探测设备的距离, ${\tau _0} = {{2{R_0}} /c}$ , 可见时延${\tau _{\rm{r}}}$ 与时间t 呈线性关系. 将(8 )式代入(7 )式, 则${s_{\rm{R}}}(t)$ 的相位为${R_0}\gg vt$ 且$\alpha {\tau _0} \gg {{2v{f_0}} / c}$ [18 ] , 则(9 )式可进一步简化为10 )式可以看出, 中括号中的前三项为常数, 第四项为t 的线性函数, 第五项为常数, $\varepsilon (t)$ 是t 的非线性函数. 正是$\varepsilon (t)$ 的存在使得$\varphi (t)$ 也变为非线性函数, 直接导致不同时刻的脉冲在压缩处理时无法聚集目标/杂波的能量, 引起谱峰在频域扩展.$\varepsilon (t)$ 是t 的线性函数时, 各次回波的相位$\varphi (t)$ 也是t 的线性函数, 不同时刻的回波相位之间具有相同的“斜率”, 它们的相关性未被破坏, 所以频谱不会扩展, 只是目标/杂波的谱线发生了偏移. 图3 利用直达波回波信号仿真了相位线性污染和非线性污染的回波谱, 可见, 非线性相位污染引起回波谱展宽, 而线性相位污染只是造成频谱偏移, 不会改变频谱形状和特性, 通过频移校正后, 不会对目标检测和海态遥感产生影响.图 3 线性和非线性相位污染的回波谱比较Figure3. Comparison of echo spectra contaminated by the linear and nonlinear phases.2.4.多模传播对回波的影响 -->2.4.多模传播对回波的影响 除了色散效应和相位污染, 多模传播是导致天波回波谱展宽的另一个重要原因. 与相位污染的机理不同, 电离层多模传播是指不同地面距离的返回电磁波经过不同的分层电离层折射、反射后, 落入了同一个距离单元内, 即具有不同传播路径的杂波/目标信号, 由于具有相同的返回时延, 在进入接收设备后, 它们会“挤入”相同的距离单元, 在频域表现为频谱扩展, 多模传播的路径示意图见图4 . 图4 中位于不同地面距离的飞机和舰船经过不同路径传播后, 在同一时刻到达接收机, 产生了多模传播现象.图 4 多模传播的路径示意图Figure4. Path schematic of the multimode propagation.6 )式的发射信号返回后变为${a_{{\rm{R}}i}}$ 和${\varphi _{0i}}$ 分别为第i 个多模信号的幅度和初相位. I 个多模信号具有相同的时延${\tau _{\rm{r}}}$ , 但各个多模信号中的目标/杂波的初始距离${R_{0i}}$ 和速度${v_i}$ 都不相同, 即对第i 个多模信号的时延${\tau _{\rm{r}}}$ 有${\tau _{\rm{r}}}$ 相同而${R_{0i}}$ 不同, 则${v_i}$ 必然不同, 其多普勒频率${f_{{\rm{d}}i}} = {{2{f_0}{v_i}}/ c}$ 也不相同, 在回波频谱中表现为具有不同多普勒频率${f_{{\rm{d}}i}}$ 的多模信号叠加在一起, 谱峰区域明显扩大.1 )和(2 )式, 可以得到射线群距离G 与探测设备工作频率之间的关系, 电离层参数与2.2 节相同, D = 2000 km, 结果如图5 所示. 需要说明的是, 图5 中的曲线为各层的最小时延线所对应的射线距离线${G_{\min }}(f)$ , 简称为${G_{\min }}(f)$ 线. 具有一定波束宽度的电磁波以某频率返回时, 由于散射传播, 使得返回的回波不止1条, 不同的返回射线对应着不同的仰角和不同的群时延, 其中群时延最短的这条线就被称为最小时延线, 又称为“回波前沿”[17 ] . 从图5 可见: 1)当射线群距离大于2180 km时, 只有F2模式可用, 即只能选择F2层作为电磁波的传输信道, 此时可避免多模传播; 2)图中曲线只是显示的${G_{\min }}(f)$ 线, 实际上在${G_{\min }}(f)$ 线的上方一定区域内还有很多群距离线(中国电波传播研究所的很多实测返回散射电离图均显示了该特性[17 ,19 —21 ] ); 以F1层和F2层的交叠区域(图中灰色椭圆区域)为例, 该部分既位于F1-${G_{\min }}(f)$ 线上方, 也位于F2-${G_{\min }}(f)$ 线的上方, 那么该区域属于F1和F2模式的交叠区域, 该区域内的某个群距离(如2110 km)对应的回波既可能是F1层的回波, 也可能是F2层的回波, 或者二者皆有, 此时就出现了模式模糊, 产生多模传播, 造成频谱交叠展宽. 在执行探测或遥感任务时, 工作频率只要避开存在模式模糊的区域, 就可以避免多模传播, 其他区域也可以做类似分析; 3)当工作频率为3—20 MHz时, 电磁波在E模式、F1模式和F2模式下都能传播, 此时很容易出现同一个目标经过不同传播模式的电磁波散射返回的情况, 由于返回射线群距离不同, 时延也不同, 它们最终会出现在不同距离段的回波中, 造成一个目标/杂波被误判为多个目标/杂波, 增大了探测设备的虚警率, 该问题不会引起回波谱展宽, 但也可以通过合理选择工作频率加以避免.图 5 射线群距离与探测频率的关系Figure5. Relationship between radiation group distance and detection frequency.3.相位污染回波谱的锐化方法 通过第2 节的分析, 色散效应、多模传播和电离层相位污染都会引起天波回波谱展宽, 色散效应对天波探测设备影响很小, 多模传播可以通过合理选频进行克服, 只有非稳定电离层造成的相位污染问题具有较大的解决难度. 本节主要研究回波相位污染去除和频谱锐化的解决方法.7 )式的回波经过常规脉冲压缩和匹配滤波后, 进行数字化采样, 可得离散化的海面回波信号${a_ + }$ 和${a_ - }$ 分别是正负Bragg峰(一阶海杂波峰)的幅度; ${f_{\rm{b}}}$ 是Bragg峰频率; $m = 1,2, \cdots,M$ , M 是采样点数; $\Delta t$ 是采样间隔; $\varepsilon (m)$ 是$\varepsilon (t)$ 的离散值, 即$\varepsilon (m)$ 是第m 个采样点的相位污染; $v(m)$ 是噪声. 目前, 几乎所有的相位污染校正方法均需要提取出能量较强的标校信号[6 —8 ,22 ] , 而海杂波幅度大, 是天然优良的标校信号, 则提取出的标校信号(假设正的一阶海杂波能量占优)为${s_{{\rm{R}} + }}(m)$ 用向量表示为${{\zeta}} = {\rm{diag}}\left[{{\rm{e}}^{{\rm{j}}\varepsilon (1)}},\quad {{\rm{e}}^{{\rm{j}}\varepsilon (2)}},\cdots,{{{\rm{e}}^{{\rm{j}}\varepsilon (M)}}}\right]$ , ${{a}}(f) = $ $ \left[ {1,}\quad {{\rm{e}}^{{\rm{j}}2{\text{π}}f \cdot 1 \cdot \Delta t}},\quad {{\rm{e}}^{{\rm{j}}2{\text{π}}f \cdot 2 \cdot \Delta t}},\cdots, {{\rm{e}}^{{\rm{j}}2{\text{π}}f \cdot (M - 1) \cdot \Delta t}} \right]^{\rm{T}}$ , k 是常数(与${a_ + }$ 有关). 计算${{{s}}_{{\rm{R + }}}}$ 的自相关矩阵${{{a}}_\zeta }(f) = {{\zeta}} {{a}}(f)$ , 对${{{R}}_ + }$ 进行特征值分解, 有${{\varSigma}} = {\rm{diag}}\left[ {{\lambda _1},}~{{\lambda _2},}~{ \cdots,}~{{\lambda _M}} \right]$ 是特征值矩阵, ${\lambda _1} > {\lambda _2} > \cdots > {\lambda _m} = \cdots = {\lambda _M} = {\sigma ^2}$ , ${\sigma ^2}$ 为噪声功率; ${{U}}$ 是特征矢量矩阵. 由于${{{s}}_{{\rm{R}} + }}$ 只含有一个杂波信号, 故${\lambda _1}$ (对应于杂波)绝对占优, ${\lambda _1}$ 远远大于其他特征值(对应于噪声), 则${{{R}}_ + }$ 可由信号和噪声子空间重构:${{{U}}_{\rm s}} = {\left[ {\begin{array}{*{20}{c}} {{u_1},}&{{u_2},}&{ \cdots,}&{{u_M}} \end{array}} \right]^{\rm{T}}}$ 是杂波子空间(或称信号子空间), 是一个M × 1的列矢量; ${{{U}}_{\rm v}}$ 是噪声子空间. 根据信号处理理论[23 ] , 信号子空间${{{U}}_{\rm s}}$ 与信号导频矢量张成的空间${{{a}}_\zeta }(f)$ 是同一个空间, 即p , 使得${{{U}}_{\rm s}}$ 和${{{a}}_\zeta }(f)$ 均为M × 1的列矢量, ${{a}}(f)$ 中的f 是已知的, 等于一阶海杂波频率${f_{\rm{b}}}$ , ${f_{\rm{b}}}$ 可通过${\hat f_{\rm{b}}} = 0.102\sqrt {{f_0}} $ 进行计算[17 ] , ${f_0}$ 为工作频率, 单位为MHz. 取出(20 )式中的第1行求解p , 有${a_1}({f_{\rm{b}}})$ 是${{a}}({f_{\rm{b}}})$ 的第1个元素. 不失一般性, 可认为${{\rm{e}}^{{\rm{j}}\varepsilon (1)}} = 1$ , 即以第1个采样数据为参考, 所有的采样序列数据只是残留了一个相同的固定相位, 这并不影响频谱的质量和形状[24 ] , 且因为${a_1}({f_{\rm{b}}}) = 1$ , 则(21 )式为${u_1}p = 1$ , 所以$p = {1 / {{u_1}}}$ .20 )式, 要得到${{\zeta}}$ 的估计值, 需要构造代价函数${F_\zeta }$ , 并使其达到最小$\left\| \cdot \right\|_F^2$ 是Frobenius范数运算. 根据(22 )式, ${{\zeta}}$ 的最小二乘估计为${\rm pinv}\left\{ \cdot \right\}$ 是求矢量的伪逆矩阵. 得到${\hat{{ \zeta }}}$ 后, 即可对${s_{\rm{R}}}(m)$ 进行相位污染校正${{\tilde{{ s}}}_{\rm{R}}}$ 是校正后的回波矢量, “*”是共轭运算. 经过(24 )式补偿后, 回波频谱得到锐化.${f_{\rm{b}}}$ , 但受电离层上下运动的影响, 实际的${f_{\rm{b}}}$ 与理论值常常存在偏差, 若${f_{\rm{b}}}$ 估计不准, ${\hat{{ \zeta }}}$ 也会存在很大误差, 导致频谱锐化质量下降. 针对该问题, 可通过最小熵搜索法使频谱达到最佳的锐化效果. 对相位校正后的回波${\tilde s_{\rm{R}}}(m)$ 进行傅里叶变换, 得到频域形式${\tilde S_{\rm{R}}}(m)$ , 对${\tilde S_{\rm{R}}}(m)$ 进行归一化处理${f_{\rm b}} \in $ $\left[ {{{\hat f}_{\rm{b}}} - \Delta f,{{\hat f}_{\rm{b}}} + \Delta f} \right]$ , 该范围内有I 个均匀分布的频率值, ${\hat f_{\rm{b}}}$ 是理论计算出的值, $\Delta f$ 为频移偏量, 对频率搜索区间的第i 个频率值${f_{{\rm{b}}i}}$ , 根据(20 )—(24 )式, 可得到对应的校正回波, 再根据(26 )式可计算出对应的信息熵${H_i}$ . 重复以上操作, 可获得I 个信息熵, 其中最小的信息熵对应校正回波即是我们需要的回波, 其相位污染去除得最彻底, 频谱的锐化效果最佳.4.实测数据处理分析 24.1.相位污染校正方法的性能比较 4.1.相位污染校正方法的性能比较 在一批实测的海面回波数据中选择某个未被污染的距离单元作为分析对象, 对该距离单元回波添加相位污染, 以此来分析不同方法的污染校正性能, 这也是****们普遍采用的分析方法[6 —9 ] . 该批实测数据的参数为: 探测频率为14.5 MHz, 工作于探海模式, 脉冲重复间隔为58 ms, 积累的脉冲数为512个, 相干积累时间为29.696 s. 对第400个距离单元的数据添加非线性相位污染函数: ${\rm{3}}\sin \left( {{\rm{2{\text{π}} }} \cdot 0.2t} \right)$ [6 —9 ] , 属于快变污染, 图6 给出了相位污染前后的频谱图. 从图6 可见, 受到电离层污染前, 回波谱中的正负海杂波谱线能量集中、清晰锐利, 多普勒频率为0.71 Hz的舰船目标可以准确地从海杂波背景中区分出来; 当回波被电离层污染后, 其频谱发生扩展, 原本锐利的谱峰严重展宽, 遮盖了0.71 Hz处的舰船目标, 导致目标检测失败.图 6 相位污染前后的实测频谱Figure6. Real spectrum before and after phase contamination.${\hat{{ \zeta }}}$ . 处理方式为: 利用带通滤波器提取展宽的负一阶海杂波峰作为标校信号, MESA法和时频级联法将长数据序列划分为16个短的子数据序列, 以保证在子数据段内污染是线性的. 为了比较各种方法的性能, 定义相位污染的估计误差为: $E(m) = \left| {{{\zeta}}(m) - {\hat{{ \zeta }}}(m)} \right|$ , 图7 给出了四种方法的污染估计误差曲线. 由图7 可见: 1) PGA法的污染估计误差最大, MESA法次之, 时频级联法和本文方法的估计误差基本相当, 具体而言, 在512个脉冲时间内, PGA、MESA、时频级联法和本文方法的平均估计误差分别为2.08, 0.602, 0.203和0.212; 本文方法和时频级联法的效果相差很小, 比MESA法和PGA法的平均估计误差分别小0.39和1.869; 2) PGA法和MESA法效果较差的主要原因是PGA法在将谱峰移至零多普勒频率处时, 由于展宽后的谱峰最值并不是真正的Bragg峰, 导致相位梯度误差不断积累; MESA法虽然将长数据进行了切割划分, 但每个子段并不能完全保证污染呈线性变化, 另外由于子段的数据点少, 在估计频率时会因为多普勒分辨率下降而导致频率估计不准; 3)虽然本文方法和时频级联法的效果基本相当, 但本文方法的复杂度和计算量要小于时频级联法, 时频级联法的效果与时频窗的长度选择有关, 窗长度过长或过短都会降低方法的污染估计效果. 图7 给出了在最佳窗长度条件下得到的时频级联法的误差曲线, 若该方法未选择最佳长度的时频窗, 则方法的效果会差于本文所提方法.图 7 相位污染的估计误差Figure7. Estimation error of the phase contamination.4.2.实测数据校正结果分析 -->4.2.实测数据校正结果分析 图8(a) 是已经发生了电离层相位污染的实测回波的距离-多普勒谱图, 图8(b) 是采用本文所提方法校正后的结果, 其中横坐标表示多普勒频率, 纵坐标表示距离. 从图8 可以看出, 由于电离层污染的存在, 正负海杂波(包括地杂波)谱发生了严重展宽, 若海杂波谱线附近存在慢速舰船目标, 则将被扩展的杂波遮盖; 经过污染校正后的杂波谱得到了较好的锐化, 以正的海杂波谱线为例, 锐化前后的海杂波峰的多普勒宽度相差0.5 Hz.图 8 相位污染校正前后的距离-多普勒谱(颜色条表示归一化功率, 单位是dB)Figure8. Range-Doppler spectra before and after phase contamination correction (color bar represents normalized power, and the unit is dB).5.讨论与结论 本文研究了造成天波回波谱展宽的机理, 详细分析了电离层色散效应、相位污染和多模传播等物理现象, 针对回波的相位污染问题提出了一种新的频谱锐化方法. 主要结论为: 





























 图 1 色散系数与探测频率的关系
图 1 色散系数与探测频率的关系





























































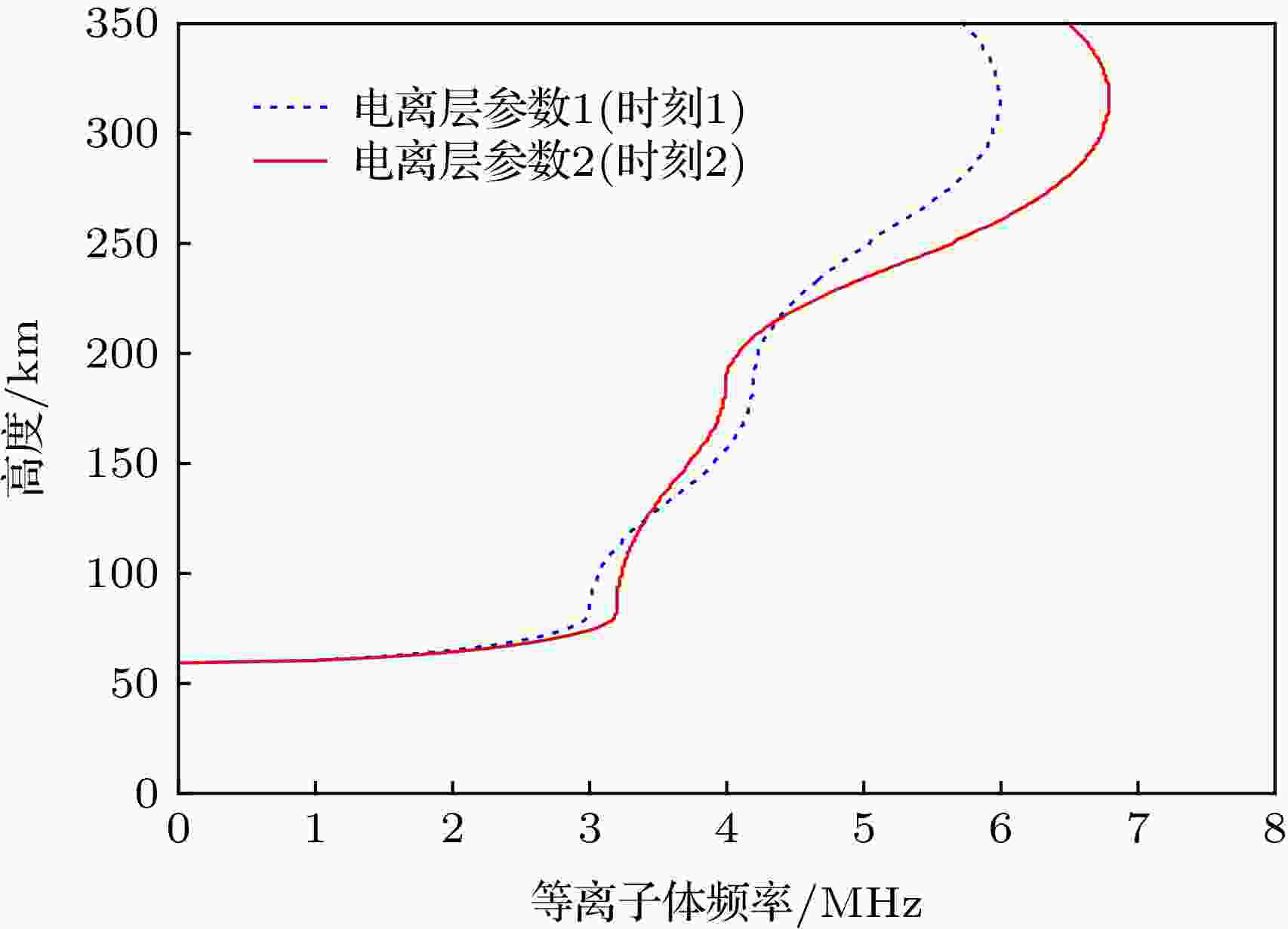 图 2 不同时刻的电离层电子浓度曲线
图 2 不同时刻的电离层电子浓度曲线





















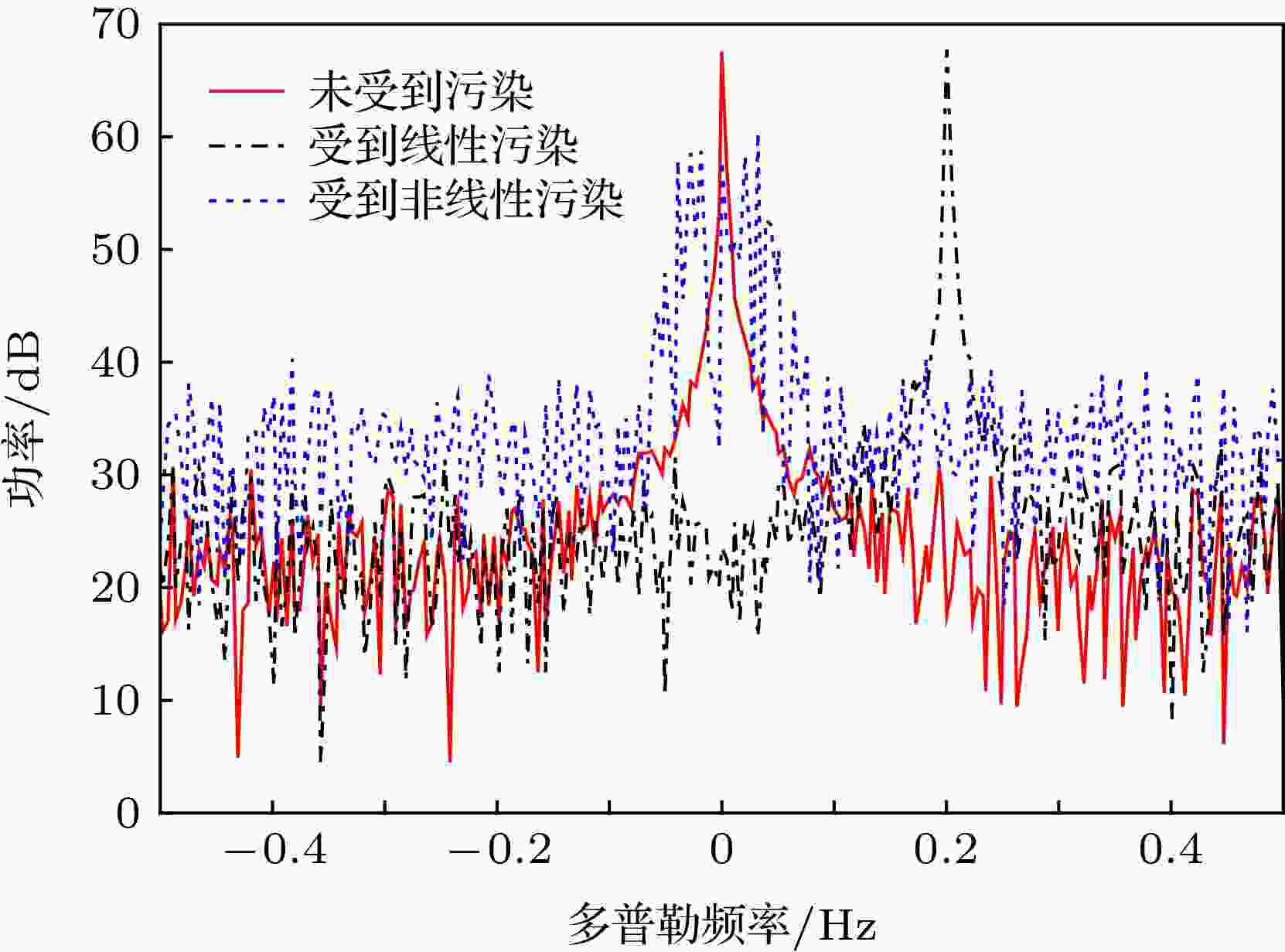 图 3 线性和非线性相位污染的回波谱比较
图 3 线性和非线性相位污染的回波谱比较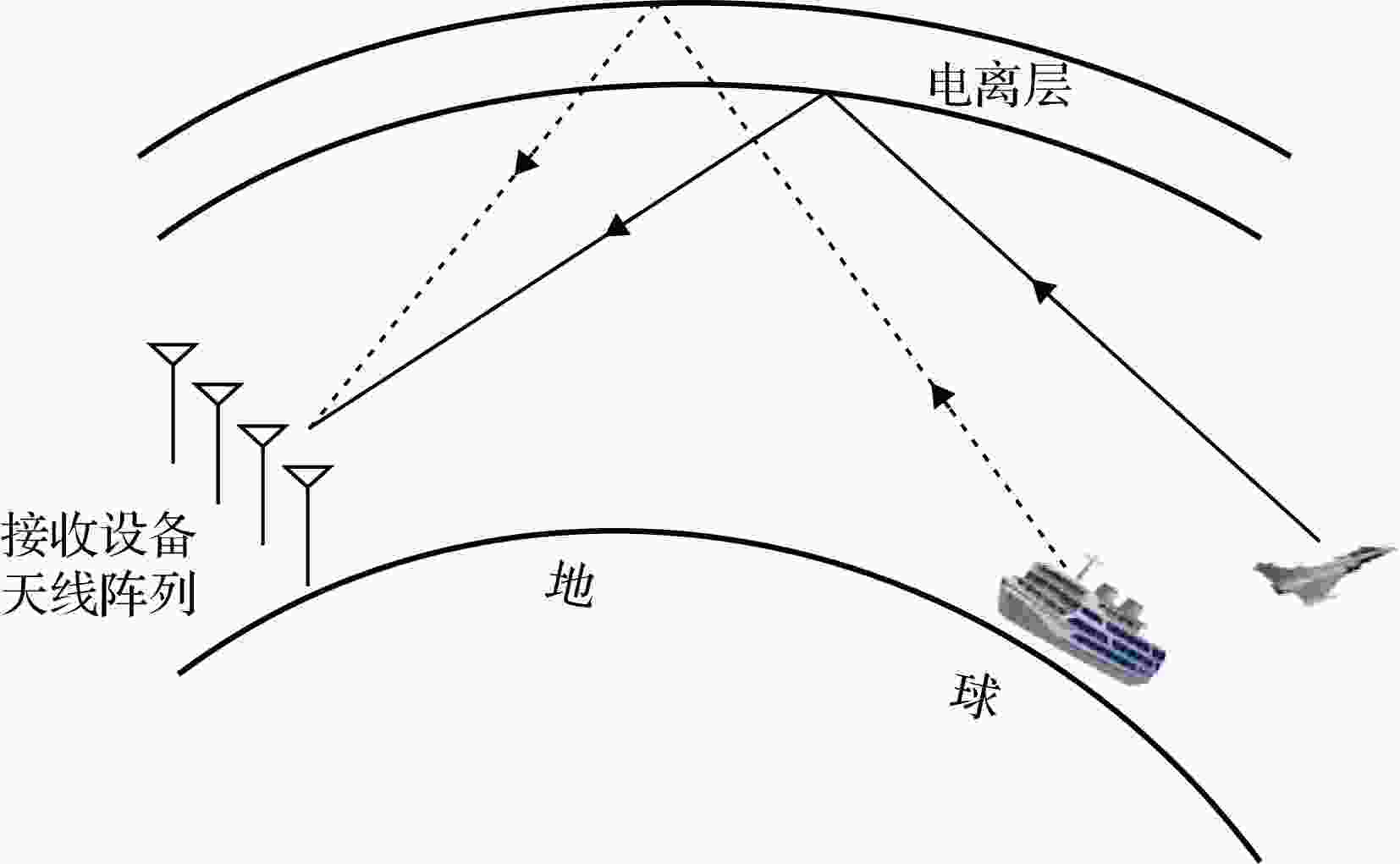 图 4 多模传播的路径示意图
图 4 多模传播的路径示意图
















































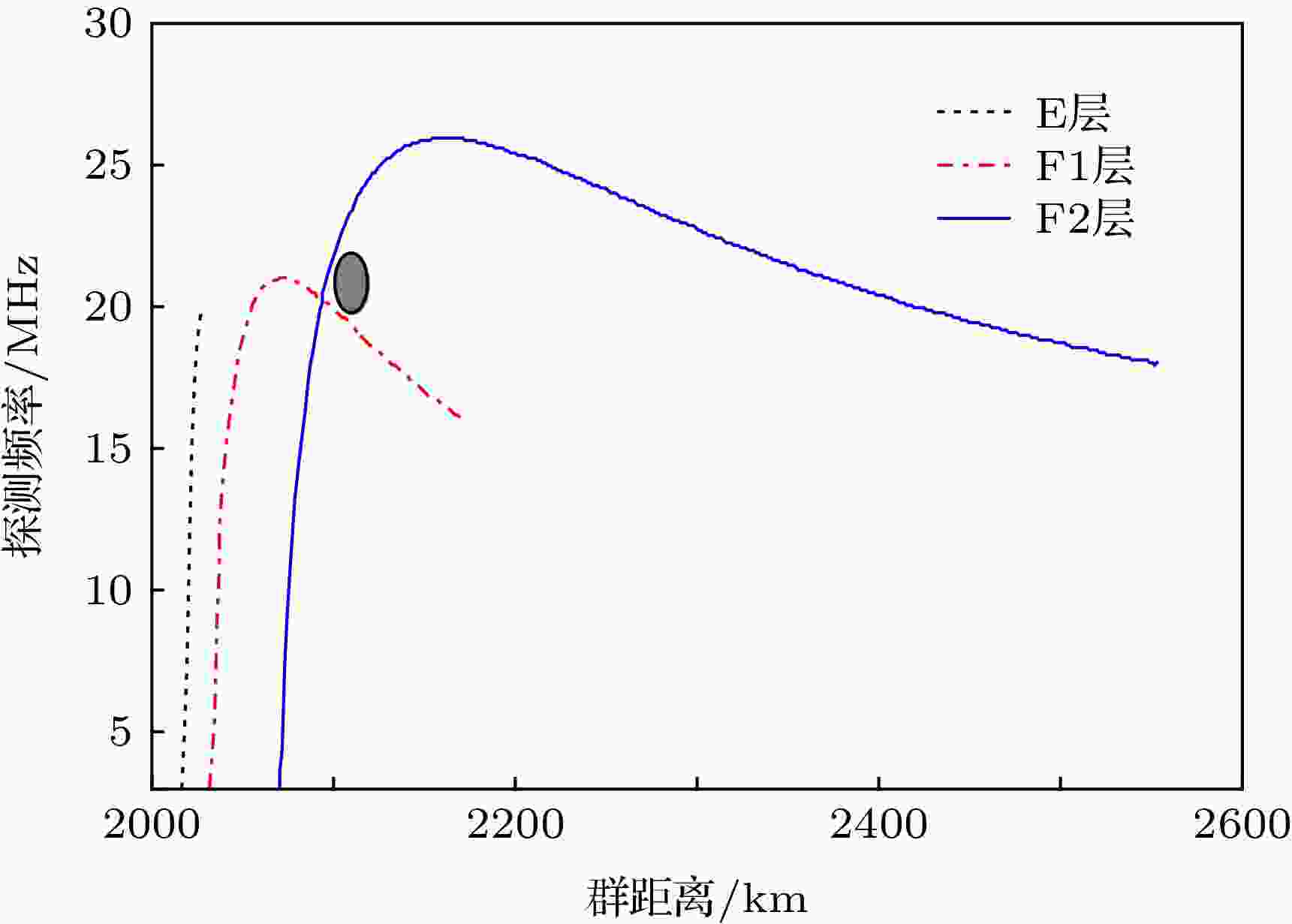 图 5 射线群距离与探测频率的关系
图 5 射线群距离与探测频率的关系













































































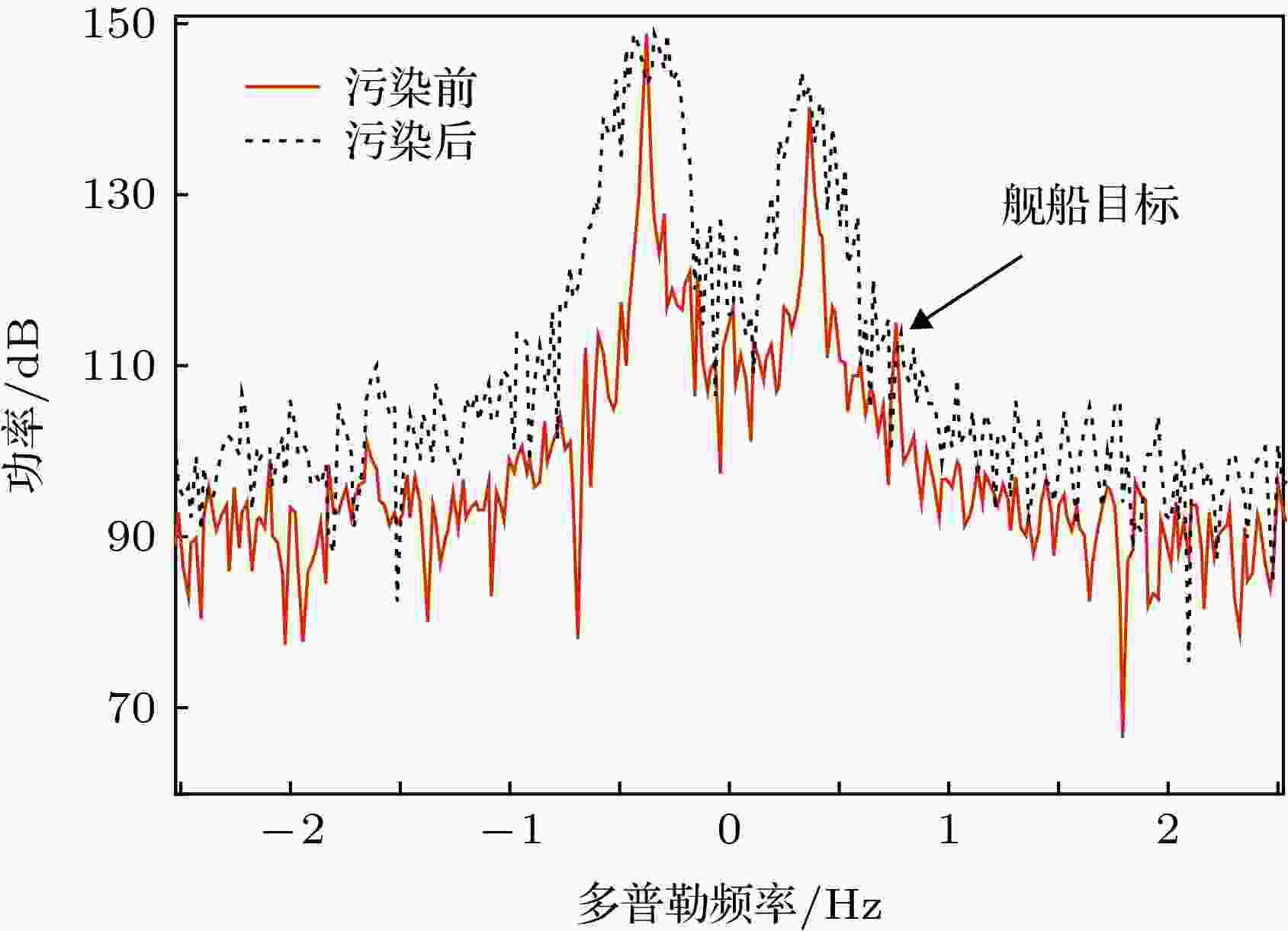 图 6 相位污染前后的实测频谱
图 6 相位污染前后的实测频谱

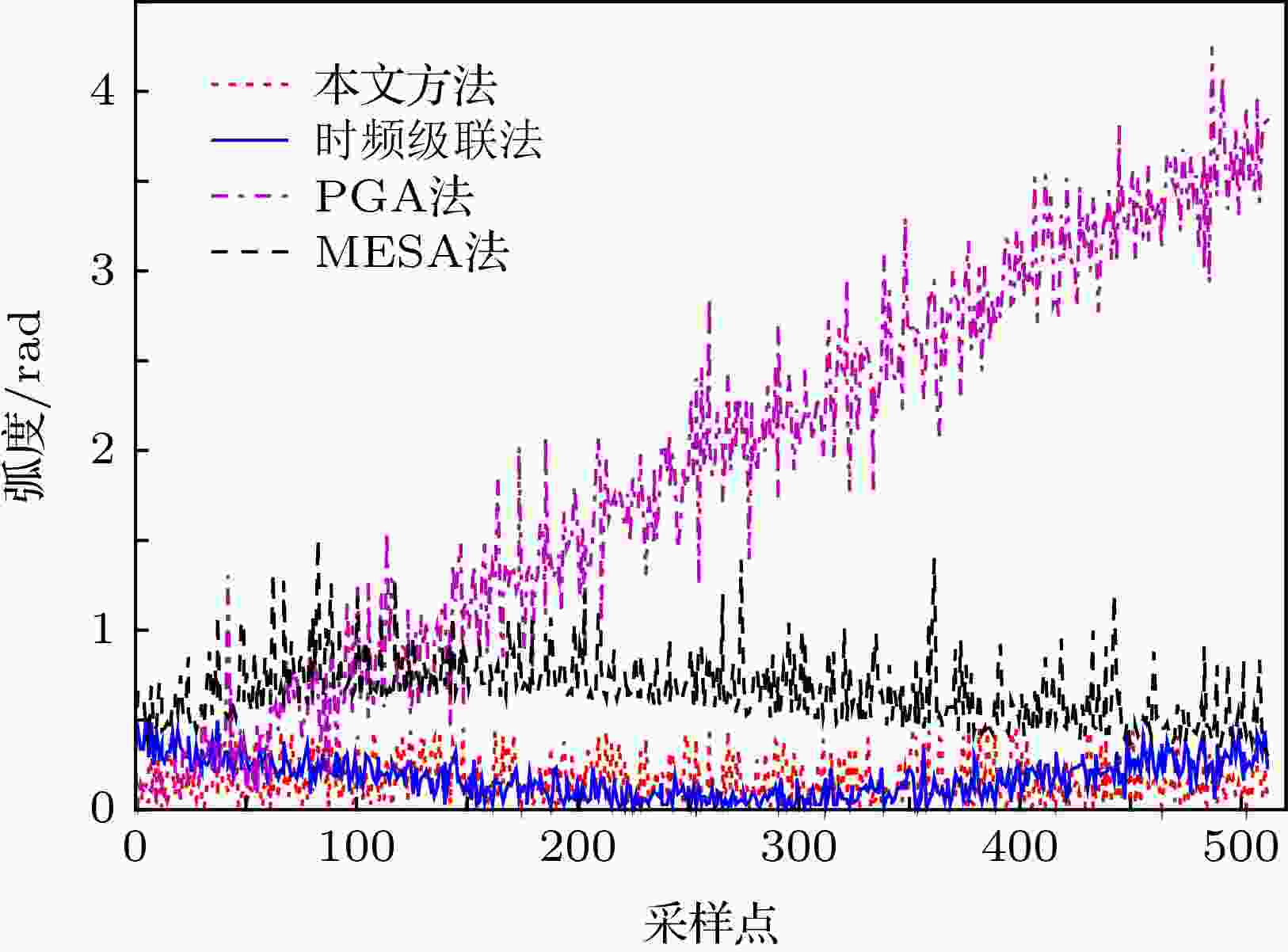 图 7 相位污染的估计误差
图 7 相位污染的估计误差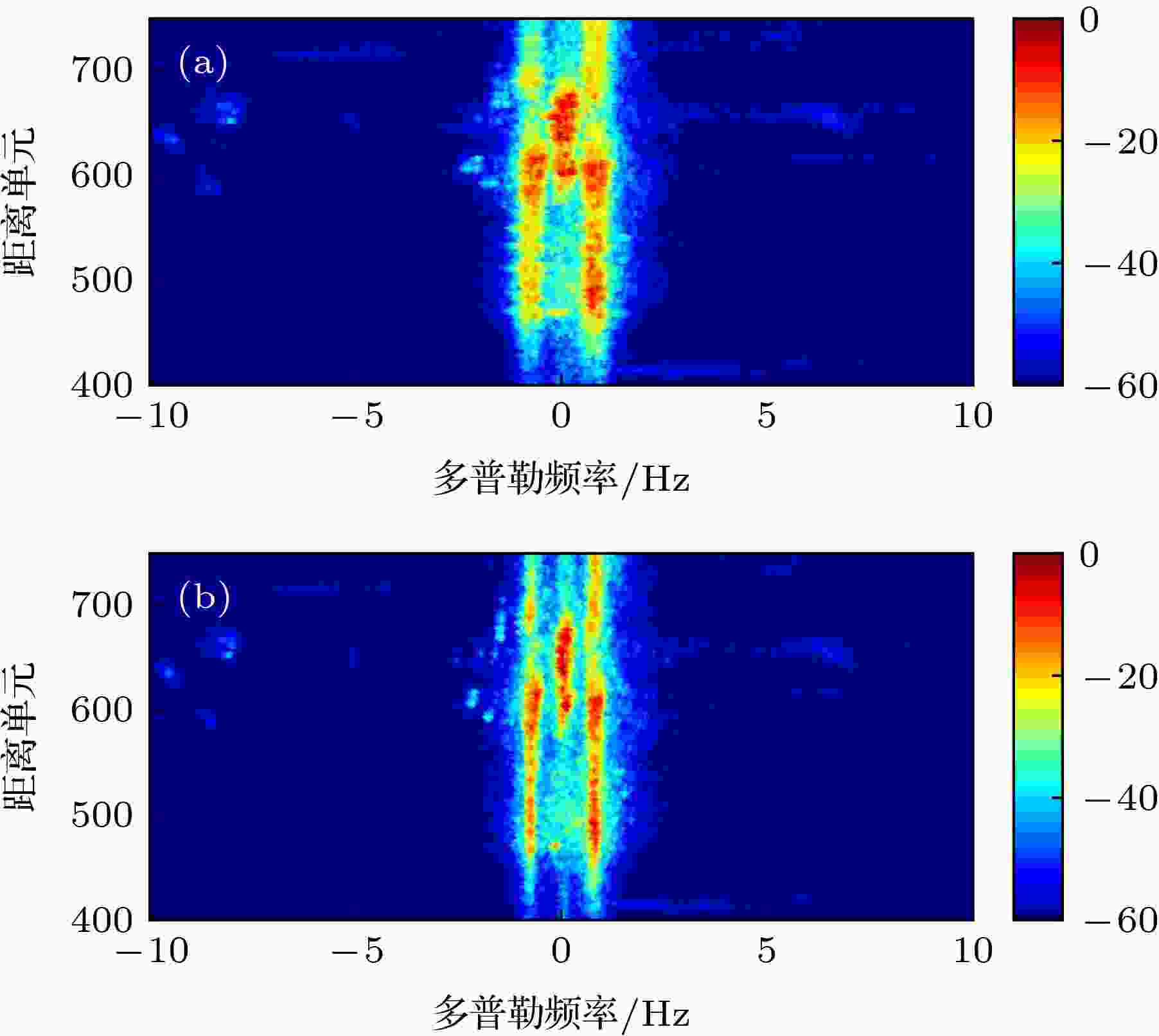 图 8 相位污染校正前后的距离-多普勒谱(颜色条表示归一化功率, 单位是dB)
图 8 相位污染校正前后的距离-多普勒谱(颜色条表示归一化功率, 单位是dB)