摘要: 以往有关忆阻器模型及其应用研究主要集中于忆阻器基本概念构建并分析忆阻器模型及其等效电路模型, 而基于市场上商用忆阻器件的研究则很少. 本文根据忆感器与忆阻器之间的理论关系, 基于全球首款商用忆阻器芯片: Knowm忆阻器, 结合第二代电流传输器和跨导运算放大器, 构建了一种新型忆感器模型. 通过调节输入信号的频率和幅值以及运算跨导放大器的跨导增益, 可有效地在电路中实现忆感器忆感值的连续调节. 设计了新型忆感器的LTspice电路模型和硬件实验电路, 以电路仿真结果和硬件电路实验结果验证了新型忆感器模型的有效性和设计方法的正确性.
关键词: Knowm忆阻器 /
跨导 /
忆感器 English Abstract Design and analysis of new meminductor model based on Knowm memristor Zhu Lei-Jie Wang Fa-Qiang State Key Laboratory of Electrical Insulation and Power Equipment, School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 51377124) and the New Star of Youth Science and Technology of Shaanxi Province, China (Grant No. 2016KJXX-40)Received Date: 24 May 2019Accepted Date: 03 July 2019Available Online: 01 October 2019Published Online: 05 October 2019Abstract: In the past, the memristor model and its application research have mainly focused on constructing and analyzing the memristor model and its equivalent circuit model based on the basic concept of memristor, while the research based on commercial memristive devices in the market has been rare. According to the theoretical relationship between meminductor and memristor, a new model of meminductor is constructed based on Knowm memristor, the first commercial memristor chip in the world, combined with the second-generation current conveyor and transconductance operational amplifier. By adjusting the frequency and the amplitude of the input voltage and the transconductance gain of the transconductance operational amplifier, the continuous adjustment of the meminductance can be effectively achieved in the circuit. The LTspice circuit model and hardware experimental circuit of the proposed meminductor are designed. The validity of the new meminductor model and the correctness of the design method are verified by LTspice simulations and circuit experiments.Keywords: Knowm memristor /transconductance /meminductor 全文HTML --> --> --> 1.引 言 在1971年, Chua教授[1 ] 根据电路的完备性原理提出了区别于传统双端无源元件的第四种基本电路元件—忆阻器的概念. 而在2008年, HP实验室Strukov团队[2 ] 在《Nature》杂志上首次报道: 在实验室中成功制造了基于纳米级TiO2 的固态忆阻器件. 由此以后, 国际国内掀起了研究忆阻器及忆阻系统的热潮, 并取得了一定的研究成果[3 -8 ] . 2009年, 在研究忆阻器的基础上, Ventra等[9 ] 又定义了忆容器和忆感器的概念. 与忆阻器类似, 忆容器与忆感器分别具有电荷和电压平面以及电流和磁通平面上的捏滞回线, 且在周期信号的激励下, 捏滞回线的面积与信号的频率成反比, 而在高频下退化为一条直线. 但是, 忆容器和忆感器是储能元件, 这与忆阻器有着本质区别. 忆感器的出现, 以其特有的“记忆”特性, 使得研究者找到了不同于传统的电路工作模式, 打开了一个全新的研究领域. 而一直以来, 研究者一方面致力于忆感器器件的物理实现. 例如, 2014年, 清华大学Han团队[10 ] 提出利用自旋霍尔效应在纳米级的薄膜上能够物理实现忆感器. 但是由于忆感器的制备相当困难, 还没有实际的物理器件出现, 难以对其进行更深入的研究. 因此, 另一方面, 根据忆感器的本构关系和电学特性, 研究者构建它的等效电路模型, 且在这方面已有大量的文献进行报道. 例如, Biolek等[11 ] 提出了忆感器的Spice模型, 通过Spice模型对忆感器的捏滞回线进行模拟. 也有文献提出忆感器的Matlab模型以及通过忆阻器转换为忆感器的Spice模型[12 -15 ] . 而在文献[1 ]中, Chua教授展示了使用非线性元件通过二端口线性变换得到忆阻器的思路. 在此基础上, Biolek等[16 ] 提出了基于忆阻器变换得到忆感器的方法. 而Pershin 和Ventra [17 ] 则按照这个思路构建了基于忆阻器的忆感系统, 其忆阻仿真器由数字电位器实现, 并通过微控制器连续调节电阻值, 且在2011年, Pershin 和Ventra[18 ] 提出了两种基于忆阻器的忆感器模型, 一种模型使用了第二代电流传输器(second generation current conveyor, CCII), 另一种模型则使用了两个双输出CCII. Yu等[19 ] 提出了一种新的忆阻器模型, 并通过忆阻器模型实现了浮地忆感器模型, 完成了忆阻器和忆感器两个元件之间互相转换的通用模型[20 ] . Sah等[21 ] 提出了一种忆感值可以通过外部电流源改变的忆感器模型. Wang等[22 ] 在研究HP忆阻器模型的基础上, 提出了一种类似于HP忆阻器的忆感器模型, 此模型更适合忆感器的未来物理实现. 李志军等[23 ] 采用两个差动差分电流传输器(differential difference current conveyor, DVCC)构建了一种忆感器模拟电路. Yunus[24 ] 提出了一种基于跨导运算放大器(operational transconductance amplifier, OTA)的忆感器仿真模型, 此模型不需要通过忆阻器来转换. 提出了一种根据HP忆阻器的关系式使用乘法器构建忆感器的方法[25 ] . 然而, 上述忆感器模型使用的均是等效电路模型, 而基于材料构成且体现忆阻器特性的Knowm忆阻器构建忆感器模型的研究, 至今未见公开报道. 相比于其他模型, 以Knowm忆阻器构建的忆感器模型更为简单和真实.$f$ 和幅值${V_{\rm{m}}}$ 外, 还通过改变OTA的输入偏置电流, 以有效地实现忆感值的连续调节, 并通过电路仿真和电路实验验证了模型的有效性.2.Knowm忆阻器及其数学模型 Knowm忆阻器是全球第一款商用忆阻器芯片. 该芯片使用多层硫系化合物材料取代传统的氧空位迁移来改变器件电阻, 电气性能的稳定性得到了显著的提高, 它的符号如图1 所示.图 1 Knowm忆阻器符号Figure1. Symbol of Knowm memristor.[26 ] 模型进行精确模拟. MSS模型中, 忆阻器表示为在不同电阻状态之间切换的导电通道的集合, 通过施加外部电压, 使通道在导电状态和非导电状态之间切换, 从而实现对忆阻器忆阻值的改变. 每个通道可以视为一个MSS, MSS有两种状态, A状态和B状态, 由势垒分开, 每个状态都有其固有电导${G_{\rm{a}}}$ 和${G_{\rm{b}}}$ , 单位为西门子S, 如图2 所示. 设势垒为参考电位$V = 0{\rm{ V}}$ , ${P_{\rm a}}$ 为MSS从B状态切换到A状态的概率, ${P_{\rm{b}}}$ 为MSS从A状态切换到B状态的概率, 其表达式为图 2 Knowm忆阻器的理论模型Figure2. Theoretical model of Knowm memristor.$\beta = \dfrac{q}{{kT}} = {\left( {{V_T}} \right)^{ - 1}}$ , 这里${V_T}$ 是热电压在热力学温度$T = 300\;{\rm{K}}$ 时值, 约等于$26\;{\rm{m}}{{\rm{V}}^{ - 1}}$ , $\alpha = {{\Delta t}}/{{{t_{\rm{c}}}}}$ 是步长周期$\Delta t$ 与忆阻器的特征时间尺度${t_{\rm{c}}}$ 的比值, $V$ 是忆阻器两端的电压, ${V_{\rm{a}}}$ 是A状态的切换阈值电压, ${V_{\rm{b}}}$ 是B状态的切换阈值电压.$N$ 个MSS的集合, 忆阻器的总电导可以表示为${N_{\rm{a}}}$ 是A状态MSS的数目, ${N_{\rm{b}}}$ 是B状态MSS的数目, 且$N = {N_{\rm{a}}} + {N_{\rm{b}}}$ .3.忆感器模型的设计与LTspice仿真分析 对于磁通控制型忆感器, 通过忆感器端子的磁通量$\varphi $ 与内部电流$i$ 之间的非线性本构关系可以表示为${L_{\rm{m}}}(\varphi )$ 是忆感器忆感值.图3 所示. 注意, U5为OTA, 且OTA的跨导参数${g_{\rm{m}}}$ 与流过其偏置电流端子的电流${I_{\rm{b}}}$ 成比例. U4为电压反馈运算放大器, U1, U2和U3均为电流反馈运算放大器. 根据电流反馈运算放大器的端口特性可知图3 中的端口特性关系为图 3 忆感器模拟电路图Figure3. Emulator circuit for meminductor.$ \left| {{X_C}} \right| \ll {R_{\rm{3}}} $ 时, 其电压可以近似表示为$\varphi (t) = \int {{v_{{\rm{pn}}}}(\tau )} {\rm{d}}\tau $ , 则(7 )式可以写成$L_{\rm{m}}^{ - 1}$ 是忆感模拟电路忆感值的倒数.13 )式可见, 忆感器的忆感值与忆阻值、电阻值、电容值以及跨导增益${g_{\rm{m}}}$ 有关, 而跨导增益${g_{\rm{m}}}$ 可通过OTA外部直流电压源调节, 故而, 可通过调节OTA外部直流电压源有效地实现忆感器忆感值的连续调节.图3 设计LTspice电路仿真模型. 注意, OTA、电流反馈放大器、运算放大器分别采用LM13700, AD844和LF356的LTspice模型实现, LTspice仿真中使用的电路参数在表1 中给出.元件 参数值 ${V_{{\rm{dd}}}}$/V $ \pm {\rm{10 }}$ ${V_{\rm{m}}}$/mV 60 ${R_{\rm{1}}}$/kΩ 56 ${R_2}$/kΩ 56 ${R_6}$/kΩ 51 ${R_7}$/kΩ 200 $C$ $100\;{\rm{ nF}}-{R_3} = {R_4} = 43\;{\rm{k}}\Omega,{R_5} = 22\;{\rm{k}}\Omega $ ${\rm{47\;nF}}-{R_3} = {R_4}={\rm{80\;k}}\Omega,{R_5}={\rm{40\;k}}\Omega $ $10\;{\rm{ nF}}-{R_3} = {R_4} = 100\;{\rm{ k}}\Omega,{R_5} = 50\;{\rm{ k}}\Omega $
表1 LTspice仿真电路中使用的元件参数值Table1. Component parameter values used in LTspice simulation circuits.${V_{\rm{m}}}$ 为60 mV的正弦电压波驱动仿真电路, 根据(10 )式和(11 )式, U4的输出端电压${v_{\rm{o}}}(t)$ 对应通过忆感器模型的磁通量的变化规律, U2的输出端电流${i_{z - }}(t)$ 对应流过忆感器模型的电流. 分别以不同的频率和不同的电容器值进行仿真, 得到图4 的仿真结果. 图4(a) 显示了在电容值为100 nF、频率在100—140 Hz时的仿真波形. 图4(b) 显示了在电容值为47 nF、频率在240—400 Hz时的仿真波形. 而图4(c) 显示了在电容值为10 nF、频率在500—1400 Hz时的仿真波形. 它们的跨导增益${g_{\rm{m}}}$ 都是1.62 mA/V. 从图4(a) —图4(c) 仿真结果可以看出, 为了在较高频率下保持捏滞回线, 必须减小电容器值, 电阻${R_3}$ , ${R_4}$ 和${R_5}$ 也要做相应的改变, 如电容值为10 nF时, 电阻${R_3}$ 和${R_4}$ 为100 kΩ,${R_5}$ 为50 kΩ, 以确保电阻${R_3}$ 消除电容积分器输出电压偏移的有效性, 不同的电容值对应的每个频率范围内的捏滞回线的变化规律是不同的. 当电容器电容值较大时, 忆感器模型对频率的变化敏感, 捏滞回线频率变化范围很小, 而当电容器值较小时, 忆感器模型的工作频率变化范围会增大. 不同电容值匹配的忆感器模型在其工作频率范围下, 忆感器模型的捏滞回线面积会随着频率的增加而逐渐减小, 逐渐趋近于一条直线, 这是由于Knowm忆阻器的内部运动机制是由离子迁移改变阻值, 在一个工作频率范围内, 当频率逐渐增大, Knowm忆阻器离子迁移率开始滞后于端口电压的变化率, 离子尚未由一个端口全部迁移到另一个端口时, 器件的电压已经反向, 离子又开始反向迁移, 当频率足够大时, 造成了忆阻值基本没有变化, 因此, 当频率较高时, 忆阻值的变化规律表现为图4(a) —图4(c) 中面积最小的近似为一条直线的图形. 图4(d) 分析了在忆感器模型输入幅值${V_{\rm{m}}}$ 、频率$f$ 和电容值$C$ 不变的情况下, 通过改变OTA的偏置电流${I_{\rm{a}}}$ , 从而控制跨导增益${g_{\rm{m}}}$ 以达到调节忆感器模型忆感值大小的目的. 从图4(d) 可看出, 跨导增益${g_{\rm{m}}}$ 的大小对忆感器模型的忆感值同样具有调节作用, 对于更大的${g_{\rm{m}}}$ 参数, 压缩磁滞回线的面积增加, 反之亦然, 这种情况证实了(12 )式. 由以上分析可以得知, 忆感器模型的捏滞回线由Knowm忆阻器提供, 因此, Knowm忆阻器本身的状态调节也会对忆感器模型有影响. 采用幅值${V_{\rm{m}}}$ 为60 mV、频率为100 Hz的正弦电压波驱动仿真电路, 电容为100 nF, 跨导增益为1.62 mA/V, 调节Knowm忆阻器的状态进行仿真得到图5 的仿真结果, 其中图5(a) 为在不同的A,B状态切换阈值电压${V_{\rm{a}}}$ 和${V_{\rm{b}}}$ 下的仿真结果, 图5(b) 为在不同的A,B状态固有电导${G_{\rm{a}}}$ 和${G_{\rm{b}}}$ 下的仿真结果. 由结果可知, 忆阻器的离子迁移运动机制导致其忆阻值大小由器件两端的固有电导以及切换阈值电压调节, 而且, 忆感器模型的忆感值的变化会跟随忆阻器忆阻值的变化而变化.图 4 不同参数情况下的$\varphi - i$ 关系图 (a) $f$ = 100—140 Hz,${g_{\rm{m}}}$ = 1.62 mA/V; (b) $f$ = 240—400 Hz, ${g_{\rm{m}}}$ = 1.62 mA/V; (c) $f$ = 500—1400 Hz,${g_{\rm{m}}}$ = 1.62 mA/V; (d) $f$ = 120 Hz,${g_{\rm{m}}}$ = 1.49—1.97 mA/VFigure4. $\varphi - i$ relationship diagram under different parameters: (a) $f$ = 100—140 Hz,${g_{\rm{m}}}$ = 1.62 mA/V; 11. (b) $f$ = 240—400 Hz, ${g_{\rm{m}}}$ = 1.62 mA/V; (c) $f$ = 500—1400 Hz,${g_{\rm{m}}}$ = 1.62 mA/V; (d) $f$ = 120 Hz,${g_{\rm{m}}}$ =1.49—1.97 mA/V.图 5 不同Knowm忆阻器参数情况下的$\varphi - i$ 关系图 (a) ${V_a}$ , ${V_{\rm{b}}}$ ; (b) ${G_{\rm{a}}}$ , ${G_{\rm{b}}}$ Figure5. $\varphi - i$ relationship diagram under different Knowm memristor parameters: (a) ${V_a}$ ,${V_{\rm{b}}}$ ; (b) ${G_{\rm{a}}}$ ,${G_{\rm{b}}}$ .4.电路实验 为了验证所提忆感器模型以及LTspice仿真结果的正确性, 设计硬件实验电路, 如图6 所示, 相应参数如表1 所列. 注意, Knowm忆阻器在首次使用时, 需要先激活, 激活方法为给忆阻器串联51 kΩ的限流电阻, 施加100 Hz的正弦波, 正弦波的幅值从0.25 V慢慢增大且不能大于3 V, 直到观测到捏滞回线, 再次使用时, 需要串联限流电阻, 忆阻器的工作电压通常在1 V以下. 采用幅值为60 mV的正弦波电压驱动此实验电路, 为了测量忆感器模型的$\varphi - i$ 特性, 端口电流转换为${R_2}$ 上的电压${v_{\rm{1}}}(t)$ , 由示波器的第二通道进行测量, 通过端口的磁通量转换为LF356的输出电压${v_{\rm{o}}}(t)$ , 由示波器的第一通道进行测量, 得到忆感器模型磁通量与电流的捏滞回线如图7 所示. 图7(a) 是输入信号为100 Hz、跨导增益${g_{\rm{m}}}$ 为1.62 mA/V时模型的捏滞回线, 图7(b) 是输入信号为120 Hz、跨导增益${g_{\rm{m}}}$ 为1.62 mA/V时模型的捏滞回线, 图7(c) 是输入信号为140 Hz、跨导增益${g_{\rm{m}}}$ 为1.62 mA/V时模型的捏滞回线. 从图7 可以看出, 捏滞回线的面积高度依赖频率的变化, 与理论分析和仿真结果一致. 当输入信号为120 Hz, OTA的跨导增益${g_{\rm{m}}}$ 由1.62 mA/V减小为$ {\rm{1}}{\rm{.49 mA/V}} $ 时, 忆感器模型磁通量与电流的捏滞回线如图7(d) 所示, 与图7(b) 相比, 忆感器模型的忆感值大小明显不同, 说明控制输入偏置电流的大小可以有效地实现忆感值的连续调节, 以适应不同的工作环境.图 6 实验接线图Figure6. Wiring diagram for the experiment.图 7 不同参数作用下的$\varphi - i$ 关系图, 其中第一通道为${v_{\rm{o}}}(t)/{\rm{V}}$ , 第二通道为${v_{\rm{1}}}(t)/{\rm{V}}$ (a) $f$ = 100 Hz,${g_{\rm{m}}}$ = 1.62 mA/V; (b) $f$ = 120 Hz,${g_{\rm{m}}}$ = 1.62 mA/V; (c) $f$ = 140 Hz, ${g_{\rm{m}}}$ = 1.62 mA/V; (d) $f$ = 120 Hz,${g_{\rm{m}}}$ = 1.49 mA/VFigure7. $\varphi - i$ relationship diagram under different parameters. The first channel is ${v_{\rm{o}}}(t)/{\rm{V}}$ , and the second channel is$ {v_{{1}}}(t)/{\rm{V}} $ : (a) $f$ = 100 Hz,${g_{\rm{m}}}$ = 1.62 mA/V; (b) $f$ = 120 Hz,${g_{\rm{m}}}$ = 1.62 mA/V; (c) $f$ = 140 Hz,${g_{\rm{m}}}$ = 1.62 mA/V; (d) $f$ = 120 Hz,${g_{\rm{m}}}$ = 1.49 mA/V.5.结 论 基于电流反馈运算放大器、电压反馈运算放大器、OTA以及电阻和电容等电路元器件, 首次以商用Knowm忆阻器构建了新型磁通控制忆感器模型. 该模型的主要特征是通过改变OTA的输入偏置电流, 即改变跨导参数${g_{\rm{m}}}$ , 可实现对忆感器忆感值的有效调节, 其电路仿真和电路实验结果验证了模型的有效性. 

 图 1 Knowm忆阻器符号
图 1 Knowm忆阻器符号




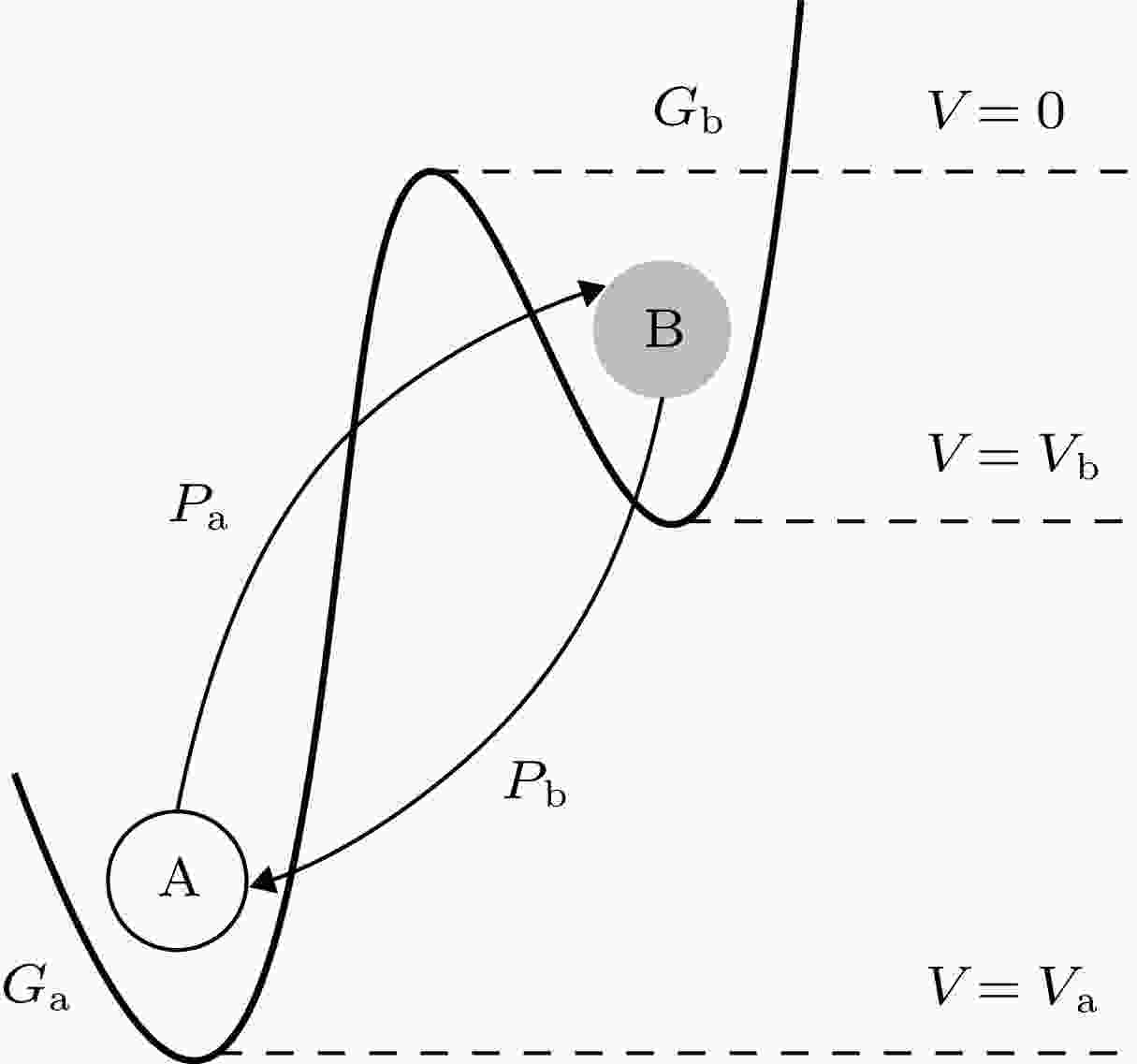 图 2 Knowm忆阻器的理论模型
图 2 Knowm忆阻器的理论模型


















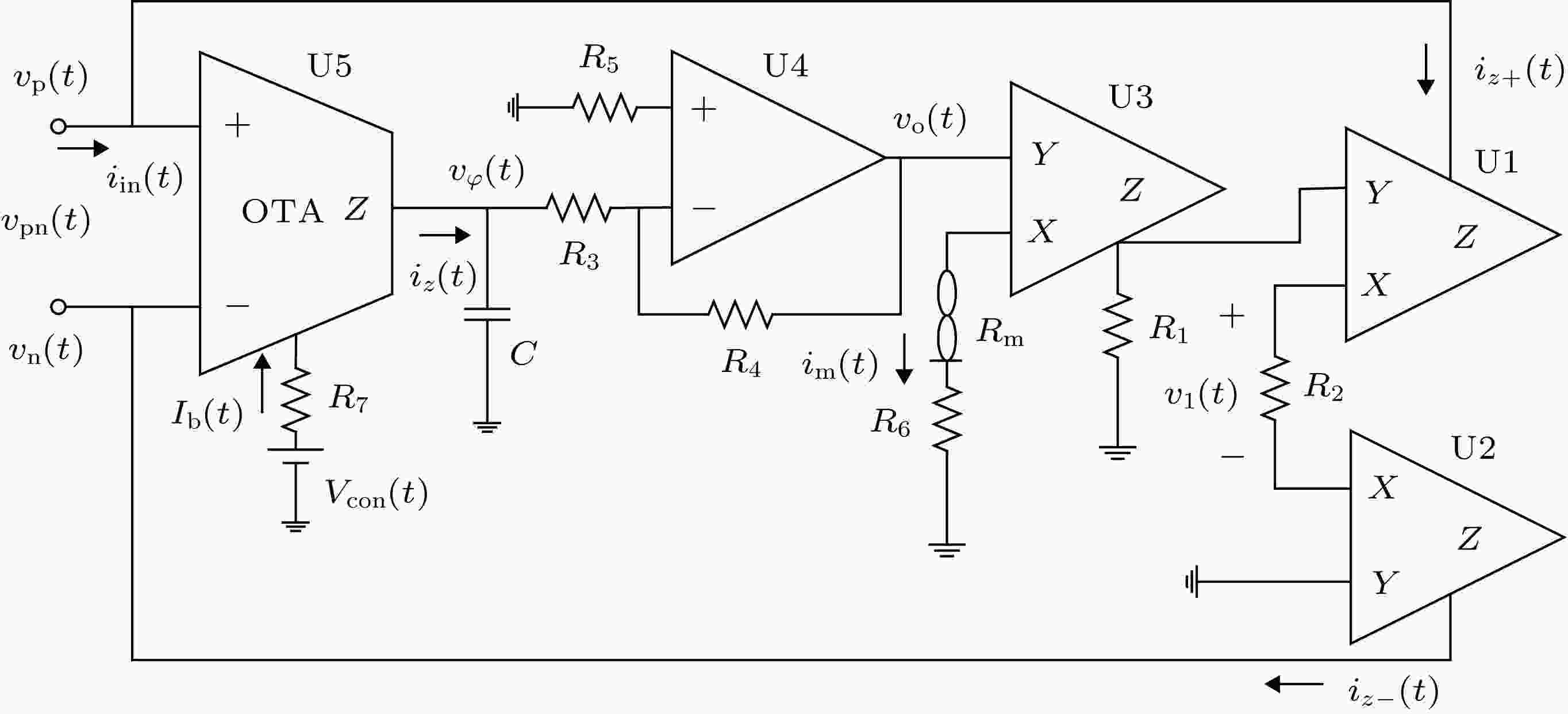 图 3 忆感器模拟电路图
图 3 忆感器模拟电路图

























































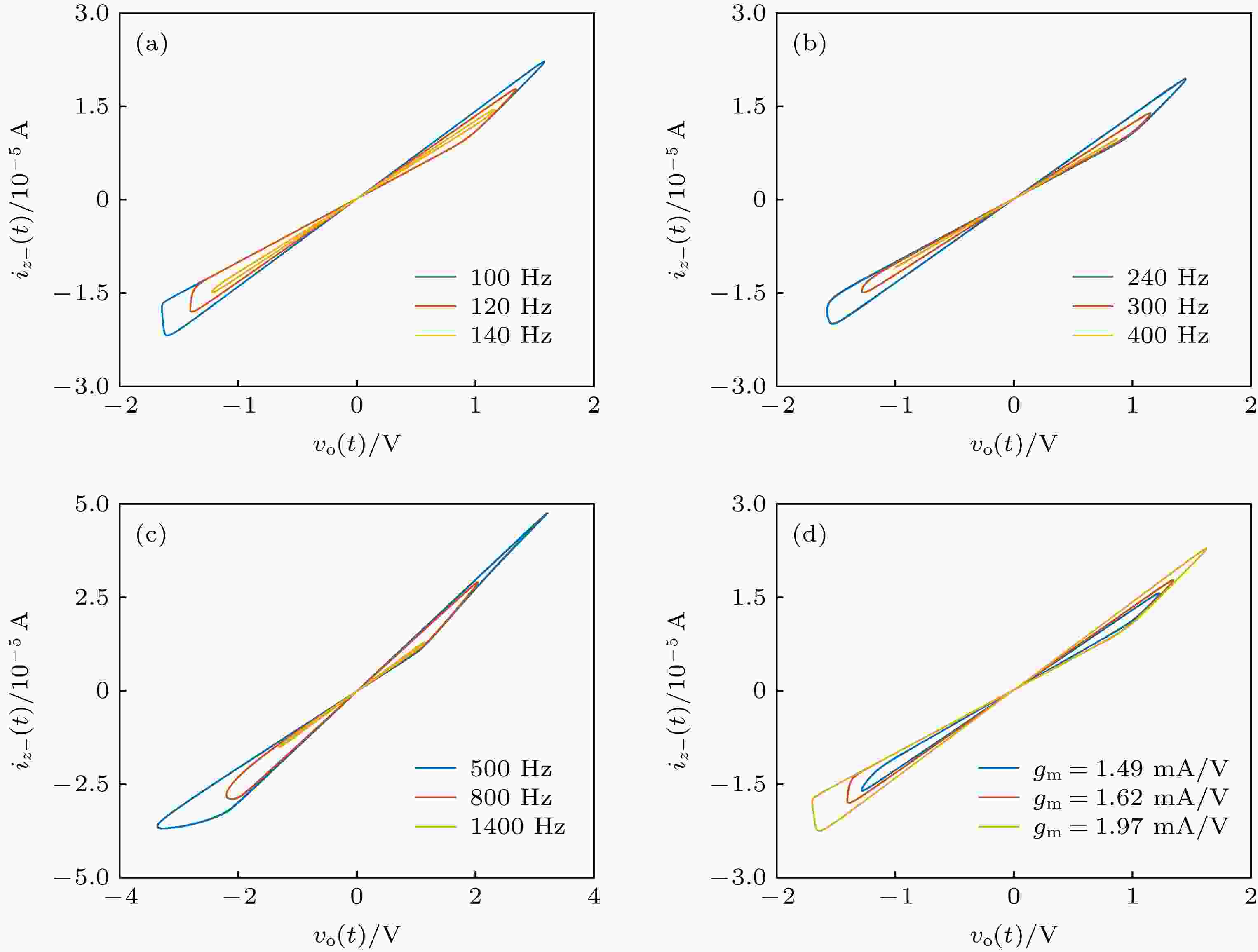 图 4 不同参数情况下的
图 4 不同参数情况下的

































































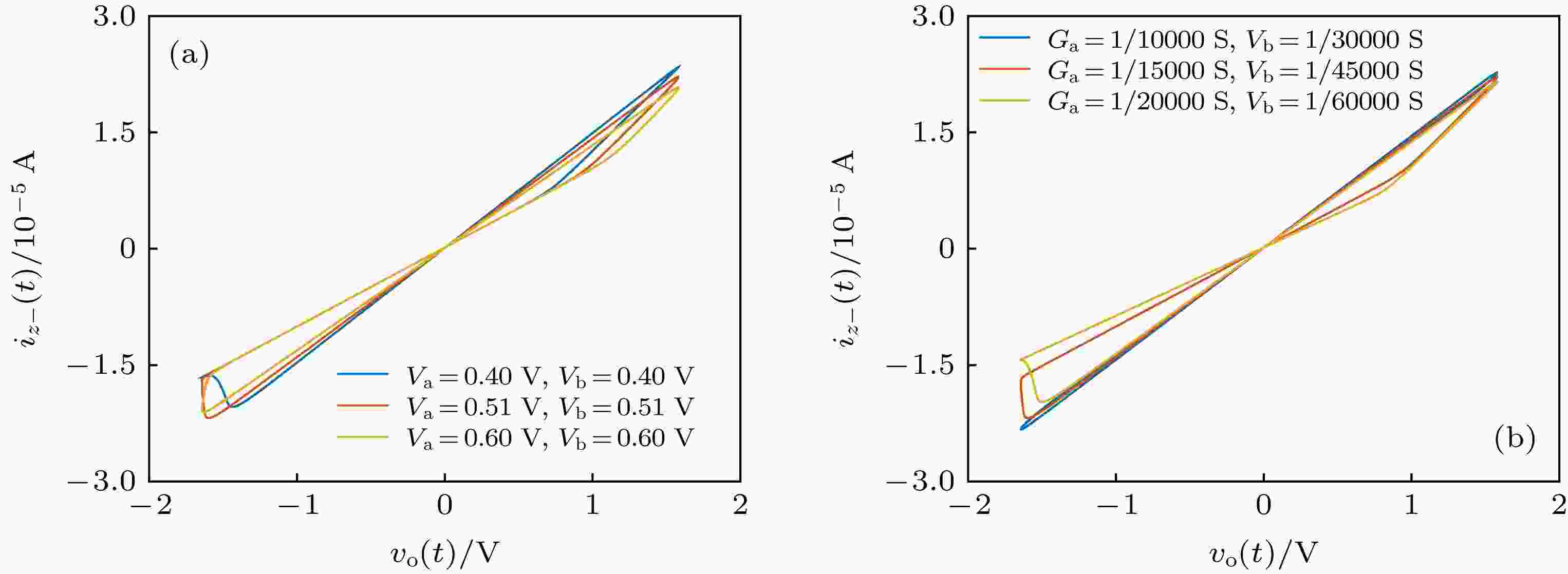 图 5 不同Knowm忆阻器参数情况下的
图 5 不同Knowm忆阻器参数情况下的






























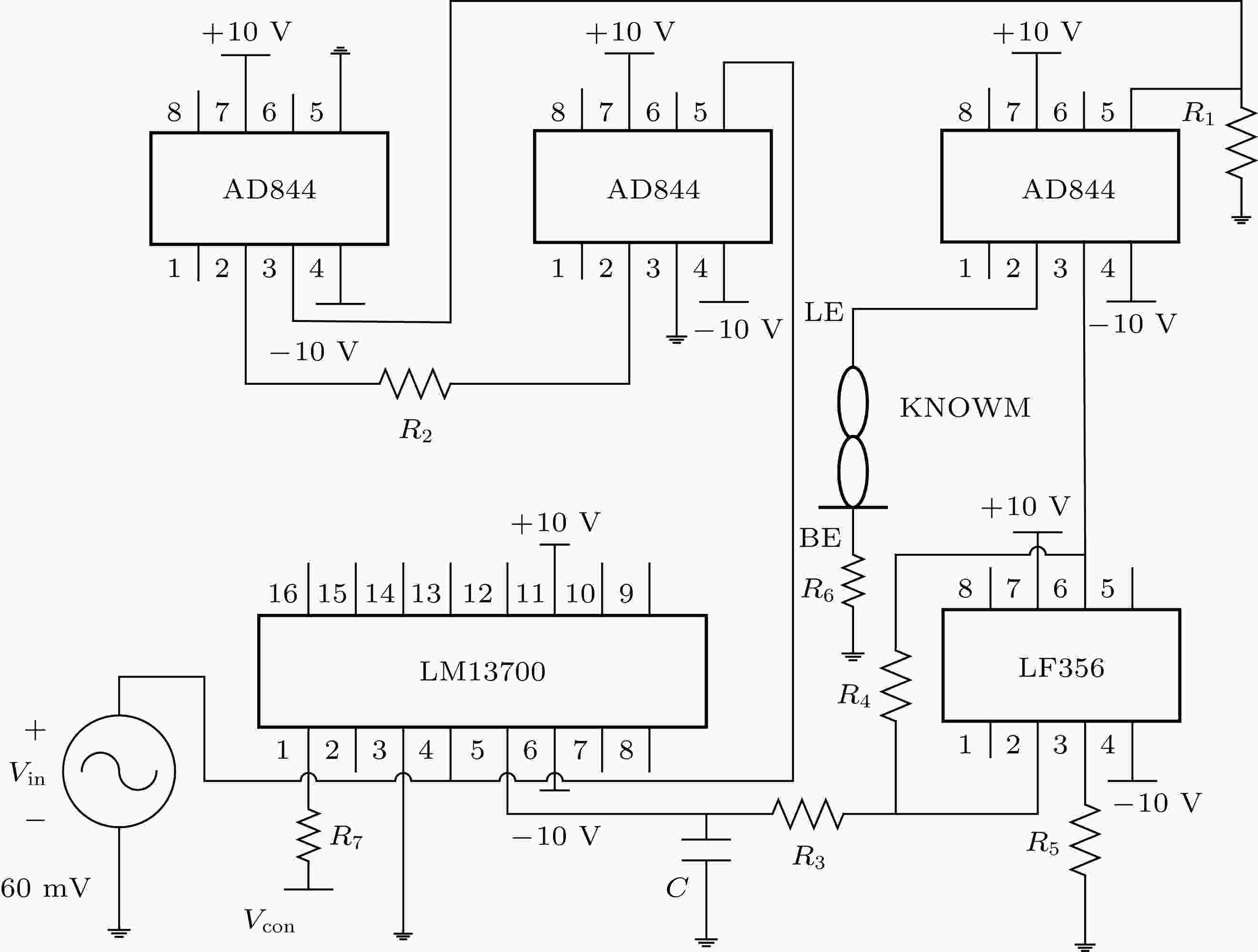 图 6 实验接线图
图 6 实验接线图 图 7 不同参数作用下的
图 7 不同参数作用下的






































































