摘要: 将含绝对值项的磁控忆阻器引入改进型蔡氏电路, 构建新型磁控忆阻混沌电路, 通过分岔图与Lyapunov指数谱创新性地观察到系统的对称分岔行为, 揭示系统双参数平面内运动状态分布的对称性. 同时, 基于忆阻电路参数-初值平面的系统运动分布图, 分析对称吸引域内系统的多稳态特性, 相图的绘制进一步证明电路多稳态现象的存在性. 此外, 应用现场可编程逻辑门阵列完成电路实验, 在数字示波器上捕捉实验结果, 证明所构磁控忆阻电路的物理可实现性.
关键词: 磁控忆阻系统 /
对称动力学行为 /
多稳态特性 /
现场可编程逻辑门阵列 English Abstract Dynamic analysis of symmetric behavior in flux-controlled memristor circuit based on field programmable gate array Lü Yan-Min Min Fu-Hong School of Electrical and Automation Engineering, Nanjing Normal University, Nanjing 210023, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 61871230).Received Date: 29 March 2019Accepted Date: 16 April 2019Available Online: 01 July 2019Published Online: 05 July 2019Abstract: The lack of the relationship between flux and charge has been made up for by the memristor which is suitable to constructing chaotic circuits as a nonlinear element. Commonly, the memristor-based chaotic systems are constructed by introducing the model of memristor into various classical nonlinear circuits, and more special and abundant dynamic behaviors are existent in these memristive systems. With the deepening of research, several novel nonlinear phenomena of memristor circuits have been found, such as hidden attractors, self-excited attractors and anti-monotonic characteristic. Meanwhile, multistability of a memristor-based circuit explained by the coexistence of multiple attractors with different topological structures is a typical phenomenon in a nonlinear system, and it is also one of the hotspots in this field. In addition, the chaotic sequences generated by the memristive circuits are used as additional signals for information transmission or image encryption. Therefore, the study of modeling memristor systems and analyzing various nonlinear behaviors is of certain valuable. In this paper, a four-dimensional flux-controlled memeristive circuit is constructed by introducing an active memristor with absolute value into an improved Chua’s circuit, and the special dynamic behaviors are observed. Through the bifurcation diagrams and Lyapunov exponent spectra, the symmetric bifurcations are shown, and the symmetric system states in parameter mappings are found. Besides, the distribution maps of memristive circuit are used to analyze the multistability in a symmetrical attraction domain, and the corresponding phase diagrams are depicted to confirm the existence of multistability. Furthermore, the circuit experiments of the flux-controlled memeristive circuit are implemented by the field programmable gate array simulation, and the experimental results are obtained on a digital oscilloscope, which proves the physical implementability of the memristor-based system. Keywords: flux-controlled memristor circuit /symmetrical dynamic behaviors /multistability /field programmable gate array 全文HTML --> --> --> 1.引 言 忆阻器是一种具有记忆功能的非线性元件, 它的提出弥补了磁通与电荷间关系的缺失[1 ] , 其作为一种非线性二端口元件, 适用于构建混沌振荡电路并产生复杂的非线性现象. 但是, 从1971年蔡少棠教授提出忆阻这一概念以来, 忆阻器就因其物理工艺难度大、制造成本高等缺点, 不适用于作为实用电路中的分立元件[2 ] . 因此, 关于建立各类忆阻器等效电路或替代模型, 构建忆阻混沌电路的研究相继广泛开展[3 —7 ] . 忆阻模型的建立主要有两种思路, 其一是基于惠普实验室的一类忆阻模型, 研究最为广泛的是HP TiO2 线性参杂漂移模型[3 ] 和HP TiO2 非线性窗函数忆阻模型[4 ] ; 其二是根据忆阻原始定义构建的二次非线性模型[5 ] 、分段线性模型[6 ] 、三次非线性模型[7 ] 等. 而将第二类忆阻器引入各类经典混沌系统, 如蔡氏电路[8 ] 、Loren系统[9 ] 、Jerk电路[10 ] 和文氏桥振荡器[11 ] 等, 是构建忆阻混沌系统最常见的方法之一.[12 —17 ] . 近年来, 随着研究的深入, ****们也提出并定义了一些忆阻电路所特有的新的非线性现象, 如隐藏吸引子[12 ] 、自激吸引子[13 ] 及反单调特性[14 ] 等. 其中, 文献[12 ]构造了一个新型超混沌四维忆阻电路, 针对该电路中存在的无限隐藏多吸引子共存现象进行分析. 为了区别于隐藏吸引子的概念, 文献[13 ]将传统连续混沌系统中由不稳定鞍焦点产生的吸引子定义为自激吸引子. 文献[14 ]基于忆阻自激振荡的jerk电路, 观察到一些新的特殊非线性现象, 即反单调特性、周期窗与混沌危机. 当然, 多稳态是许多非线性系统中的典型现象[18 —21 ] , 也是近年来研究的热点之一. 它解释了系统中多吸引子的共存现象, 表现为在相同系统参数下改变不同的初值, 系统拥有多个不同拓扑结构吸引子, 如左右混沌/超混沌、极限环或小周期等共存现象[18 ] . 当这种共存吸引子的数量趋于无穷时便被认为是无穷多吸引子的共存, 研究者们将这种现象称之为超级多稳态[19 ] . 同时, 忆阻系统中的多稳定性可被作为信息应用工程的外加信号源[22 ] , 或用于图像加密处理[23 ] , 因此研究此类忆阻混沌系统的实现方法和多稳态现象具有理论意义与工程价值.[24 ] , 构建新型四维忆阻系统, 观察到忆阻电路中的对称动力学行为, 这一行为在之前极少被报道. 文献[25 ,26 ]根据忆阻系统对称性出现时的极性平衡需求, 提出极性调整与偏置控制的方法来构建更为多样的对称忆阻系统及繁殖吸引子. 因此, 对系统自身存在的对称行为进行分析是具有物理意义的, 也可为后续控制与应用打下基础. 本文提出的忆阻电路模型简单且规整, 通过分岔图与Lyapunov指数谱等非线性分析手段, 观察到特定系统参数下特殊的对称分岔行为. 随后, 通过双参数映射图进一步探讨这种特殊对称行为的存在性. 对称域内多吸引子共存的多稳态现象则通过对应参数-初值平面内的运动状态分布图展现, 并使用混沌与周期的相轨迹图验证. 最后, 利用现场可编程逻辑门阵列(field programmable gate array, FPGA)实现所构四维忆阻系统. 结合“Modelsim”与“ISE Design Suite”软件, 完成数字电路实验, 其结果也验证数值仿真的正确性.2.电路模型 以改进型蔡氏系统[24 ] 为基础, 构建一个基于绝对值忆阻模型的新型磁控忆阻混沌电路, 整体电路方案如图1(a) 所示. 图1(b) 是磁控忆阻模型的等效电路原理图[27 ] , 其端口的对外特性与二次非线性的有源磁控忆阻器等效.图 1 电路模型 (a)磁控忆阻电路; (b)磁控忆阻等效电路Figure1. Circuit schematic: (a) Flux-controlled memristor circuit; (b) equivalent Circuit of flux-controlled memristor.参数 数值 参数 数值 $a$ 1 $\xi $ 0.12 $b$ 3.5 $\alpha $ 0.3 $c$ 1 $\beta $ 0.8 $\gamma $ 0.86
表1 系统参数Table1. The valueof system parameters图1(a) 中, 改进型磁控忆阻电路由四个一阶非线性微分方程表示, 其对应的四个状态变量分别为电压${v_1}$ 、电压${v_2}$ 、电流i 和磁通$\varphi $ , 这四个变量代表四个电路元件C 1 , C 2 , L 和忆阻器$W\left( \varphi \right)$ 的电压-电流或磁通-电荷关系. 根据基尔霍夫定律, 图1(a) 所对应的状态方程如下1 )式中磁控忆阻器的忆导方程如(2 )式, 其中$\alpha $ 和$\beta $ 为两个正忆阻参数值.3 )式中给出:1 )式对应的电路状态方程, 可得到(4 )式描述的数学模型, 其中$W(w) = - \alpha + \beta \left| w \right|$ 是忆阻器的归一化模型.4 )式所描述的数学模型为基础, 系统参数设置如表1 . 初值设置为(10–9 , 0, 0, 0), 图2(a) 为y -z 平面上双涡卷混沌吸引子相图. 图2(b) 展现y -z 平面上对应的Poincaré截面图, 呈现的曲线是连续的, 证明该系统是混沌的.图 2 $y-z$ 平面上典型混沌吸引子的相图与Poincaré截面图 (a)相图; (b) Poincaré截面图Figure2. Phase portrait and Poincaré map of typical chaotic attractor in $y-z$ plane: (a) Phase portrait; (b) Poincaré map3.动力学行为分析 23.1.对称共存分岔 3.1.对称共存分岔 为了讨论不同参数下系统(4)的动力学机理, 随参数$\gamma $ , c 变化的分岔图与Lyapunov指数谱分别在图3 和图4 中给出, 其他系统参数的选择如表1 所示. 将仿真初值设置为接近于原点的$( \pm {10^{ - 9}},$ $0,0,0)$ , 可最大程度地降低初值对系统动力学行为的影响. 图3(a) 与图4(a) 中两重叠的分岔轨迹展现的是状态变量${x_{\max }}$ 随参数$\gamma $ , c 的变化趋势, 其中蓝红两色点分别对应初值$({10^{ - 9}},0,0,0)$ 及$( - {10^{ - 9}},$ 0,0,0). 其次, 由于取相反初值时Lyapunov指数谱是大致相同的, 因此图3(b) 和图4(b) 仅给出正初值$({10^{ - 9}},0,0,0)$ 对应的Lyapunov指数谱.图 3 随参数$\gamma $ 变化的分岔图与Lyapunov指数谱 (a)分岔图; (b)Lyapunov指数谱Figure3. Bifurcation and Lyapunov exponent spectrum with parameter $\gamma $ : (a) Bifurcation diagram; (b) Lyapunov exponent spectrum图 4 随参数c 变化的分岔图与Lyapunov指数谱 (a)分岔图; (b) Lyapunov指数谱Figure4. Bifurcation and Lyapunov exponent spectrum with parameter $c$ : (a) Bifurcation diagram; (b) Lyapunov exponent spectrum.图3(a) 可知, 参数$\gamma $ 在(0.704, 0.808)范围内变化时, 系统(4)处在周期态. 当参数$\gamma \in$ $ ({0.808,0.829)} \cup {(0.845,0.9)}$ , 四阶忆阻系统(4)产生混沌吸引子, 而且图3(b) 中对应的最大Lyapunov指数大于零. 随后, 观察图4(b) 的Lyapunov指数谱发现$0.9 \leqslant c \leqslant 1.13$ 时大部分最大Lyapunov指数均大于0, 即系统处在混沌态, 同时运动过程中有多个周期窗出现. 参数c 在(1.13, 1.41)或(1.41, 1.5)区间内增加时, 系统分别产生周期轨迹与稳定不动点, 两区间内相应的Lyapunov指数如图4(b) 所示, 分别为零值与小于零的值. 系统动力学状态与具体区间分布如表2 所列. 总体而言, 随参数$\gamma $ 在0.66到0.9内增加, 新型忆阻系统从稳定不动点过渡到周期态, 后又通过多个倍周期分岔进入混沌态. 值得注意的是, 在参数c 的变化范围内, 系统所呈现的动力学行为与参数$\gamma $ 变化时大致相反. 换言之, 随这两种不同参数变化时, 系统分岔行为呈现对称性. 当参数c 从0.9开始增加时, 系统最先处在混沌状态, 随后经过反向倍周期分岔进入周期, 最后系统运动变为稳定不动点.参数$\gamma $ 运动状态 Lyapunov指数 $(0.6{\rm{6}},0.{\rm{704}})$ 稳定不动点 $( -, -, -, - )$ $(0.{\rm{704}},0.8{\rm{08}}) \cup (0.{\rm{829}},0.{\rm{845}})$ 周期运动 $( + , -, -, - )$ ${\rm{(0}}{\rm{.808,}}\,{\rm{0}}{\rm{.829)}} \cup {\rm{(0}}{\rm{.845,}}\,{\rm{0}}{\rm{.9)}}$ 复杂运动(混沌, 多周期) $( +,0, -, - )$ 参数c 运动状态 Lyapunov指数 ${\rm{(0}}{\rm{.9,}}\,{\rm{1}}{\rm{.02)}} \cup {\rm{(1}}{\rm{.07,1}}{\rm{.13)}}$ 复杂运动(混沌, 多周期) $( +,0, -, - )$ ${\rm{(1}}{\rm{.02,}}\,{\rm{1}}{\rm{.07)}} \cup {\rm{(1}}{\rm{.13,}}\,{\rm{1}}{\rm{.41)}}$ 周期运动 $( + , -, -, - )$ $({\rm{1}}{\rm{.41,1}}{\rm{.5}})$ 稳定不动点 $( -, -, -, - )$
表2 参数$\gamma $ , c 变化时系统运动状态与对应的Lyapunov指数Table2. The dynamic behavior and Lyapunov exponent with parameter $\gamma $ and $c$ 3.2.双参数平面的运动分布 -->3.2.双参数平面的运动分布 通过双参数吸引盆讨论系统参数对运动状态分布对称性的影响. 系统(4)初值固定在$\left( {{{10}^{ - 9}},0,0,0} \right)$ , 相关系统参数取值依据表1 , 可得到图5 的双参数吸引盆. 参数组合$\gamma -b$ , $c-b$ , $\gamma -\xi $ 与$c-\xi $ 所对应的运动状态分布分别在图5(a) —(d) 中展现, 各种系统动力学行为用不同颜色标注, 紫色为稳定不动点, 蓝色为周期1, 绿色描述周期2, 黄色代表周期3, 红色为复杂运动, 具体内容见表3 . 值得指出的是, 被命名为“复杂运动”的红色区域, 包含大于周期3的多周期与混沌运动.图 5 双参数吸引盆 (a)参数$\gamma -b$ ; (b)参数$c-b$ ; (c)参数$\gamma -\xi $ ; (d)参数$c-\xi $ Figure5. Parameter mappings: (a) Parameter $\gamma $ and $b$ ; (b) parameter $c$ and $b$ ; (c) parameter $\gamma $ and $\xi $ ; (d) parameter $c$ and $\xi $ 颜色 系统运动 紫色 稳定不动点 蓝色 周期1 绿色 周期2 黄色 周期3 红色 复杂运动(混沌, 多周期)
表3 不同颜色所对应的系统运动状态Table3. Colors and the corresponding system states图5 可知, 系统(4)拥有丰富的动力学行为和典型的非线性电路运动特征, 即稳定不动点、周期态与混沌态. 为了方便分析与讨论, 将图5(a) 、图5(b) 与图5(c) 、图5(d) 分为两组, 分别命名为组Ⅰ和组Ⅱ, 发现同组中的吸引盆是对称的. 当参数$\gamma \in \left( {0.6{\rm{6}},0.{\rm{86}}} \right)$ , 不论另一变化参数取值如何, 系统总是依次历经不动点、周期与混沌三种运动. 而参数c 从1.0增加到1.5的过程中, 吸引域分布从混沌到周期, 再过渡到稳定不动点. 这意味着双参数平面内运动分布的对称性依然是由于参数$\gamma $ , c 下系统演变趋势的相反性, 同时其他系统参数的取值对这种对称性影响甚微. 若将两组吸引盆进行组间比较会发现, 组Ⅱ的系统运动分布呈现类带状, 而组Ⅰ的吸引域分布是不规则的, 这种不规则态在混沌与周期交叠区域更为明显. 结合图1(a) 所示电路模型可知, 组Ⅰ内的另一变化参数b 代表电路中电容C 2 , 组Ⅱ参数$\xi $ 则表示电阻R 的值. 这表明, 当选择不同参数变量时, 系统的运动状态分布会呈现出明显的差异性. 另外, 组Ⅱ稳定不动点的区域更多, 占到总体的2/3左右, 但组Ⅰ中的不动点区域仅占总体的1/4. 组Ⅰ内更大的绿色及黄色范围也说明, 系统在参数$\gamma -b$ 或$c-b$ 组合下, 出现以周期2, 3为代表的小周期运动的可能性更高. 综上, 系统运动的对称性不会被其他参数变化破坏, 但是吸引域的分布特性会受另一参数变量选择的影响.图5 所呈现的双参数吸引盆在红黄两色区域中的重叠散点也是值得注意的. 由于分布对称性的存在, 参数$\gamma \in \left( {0.{\rm{81}},{\rm{0}}{\rm{.86}}} \right)$ 且$b \in \left( {{\rm{6}},9} \right)$ 或参数$c \in \left( {1,1.1} \right)$ 且$b \in \left( {6,9} \right)$ 时, 散点尤为明显. 这表明这两块区域内, 该忆阻系统的运动切换更为频繁, 且吸引子结构稳定性差. 然而, 图5(c) 和图5(d) 内的散点较少, 系统会出现完整且稳定的红色区块. 这意味着参数$\gamma -\xi $ 及$c-\xi $ 组合下, 该忆阻系统具有更好的混沌特性及鲁棒性, 并且混沌吸引子结构更为稳定. 如果选择所提出的系统(4)作为随机信号发生器或用来产生信息加密的密钥, 在参数范围$\gamma \in \left( {0.{\rm{81}},{\rm{0}}{\rm{.86}}} \right) \cup \xi \in \left( { - 0.1,{\rm{0}}{\rm{.13}}} \right)$ 或$c \in \left( {1,1.1} \right) \cup\xi \in$ $ \left( { - {\rm{0}}{\rm{.1}},{\rm{0}}{\rm{.13}}} \right)$ 内选择参数值可得到更好的应用效果.3.3.对称域内的多稳态特性 -->3.3.对称域内的多稳态特性 这里主要讨论特定参数下对称多稳态现象的存在性, 以及依赖于初值的多吸引子共存现象. 随$\gamma - x\left( 0 \right)$ 与$c - x\left( 0 \right)$ 变化的吸引子分布分别在图6(a) 和图6(b) 中给出, 初始条件设置为$\left( {x\left( 0 \right),0,0,0} \right)$ , 其中$x\left( {\rm{0}} \right)$ 为非忆阻初值. 当然, 忆阻系统(4)对于忆阻初值的变化十分敏感, 因此在图7 中给出$\gamma {\rm{ - }}w\left( 0 \right)$ 及$c{\rm{ - }}w\left( 0 \right)$ 平面上的吸引盆,$w\left( 0 \right)$ 为忆阻初值, 其中图7(a) 和图7(b) 初值为$( - {{10}^{ - 9}},\,0,$ $\,0,w\left( 0 \right))$ . 之后, 为了分析的完整性, 图7(c) 和图7(d) 选择相反初值$\left( {{{10}^{ - 9}},0,0,w\left( 0 \right)} \right)$ . 不同颜色区域描述多种形态的共存吸引子, 包括紫色描述的点吸引子、浅蓝与深蓝标注的左右共存周期1、绿色与青色表示的左右周期2、黄色与草绿描述的左右共存周期3及红橙两色标注的左右共存复杂运动, 具体内容如表4 . 需要指出的是, 图中仅有9种颜色, 即9种状态被区分. 事实上, 在不同初始条件下, 系统中存在多种不同拓扑结构的吸引子, 这意味着该忆阻系统中存在多稳态或极端多稳态现象.颜色 浅蓝 绿色 黄色 红色 紫色 共存类型 左侧周期1 左侧周期2 左侧周期3 左侧复杂运动(左侧多周期, 混沌) 稳定不动点 颜色 深蓝 青色 草绿 橙色 共存类型 右侧周期1 右侧周期2 右侧周期3 右侧复杂运动(右侧多周期, 混沌)
表4 运动状态与色标的对应表Table4. Different colors and the corresponding dynamical state图 6 不同变量组合下的共存吸引盆 (a) $\gamma -x\left(0\right)$ 平面, 初始条件为$\left(x\left(0\right),0,0,0\right)$ ; (b)$c-x\left(0\right)$ 平面, 初始条件为$\left(x\left(0\right),0,0,0\right)$ Figure6. Attraction basins of coexistence in different planes: (a) $\gamma -x\left(0\right)$ plane, with initial value of $\left(x\left( 0 \right),0,0,0\right)$ ; (b) $c-x\left(0\right)$ plane, with initial value of $\left(x\left(0\right),0,0,0\right)$ 图 7 不同变量组合下系统状态分布图 (a) $\gamma -w(0)$ 平面, 初始条件为$( - {10^{ - 9}},0,0,w(0))$ ; (b)$c-w(0)$ 平面, 初始条件为$( - {10^{ - 9}},0,0,w(0))$ ; (c)$\gamma -w(0)$ 平面, 初始条件为$({10^{ - 9}},0,0,w(0))$ ; (d)$c-w(0)$ 平面, 初始条件为$({10^{ - 9}},0,0,w(0))$ Figure7. Attraction basins of coexistence in different planes: (a) $\gamma -w(0)$ plane, with initial value of $( - {10^{ - 9}},0,0,w(0))$ ; (b) $c-w(0)$ plane, with initial value of $( - {10^{ - 9}},0,0,w(0))$ ; (c) $\gamma -w(0)$ plane, with initial value of $({10^{ - 9}},0,0,w(0))$ ; (d) $c-w(0)$ plane, with initial value of $({10^{ - 9}},0,0,w(0))$ 图6 和图7 所展示的吸引盆, 发现两种类型的对称特性. 其一, 系统运动分布关于相反初值存在对称性. 其二, 在参数$\gamma $ , c 的相应变化范围内, 系统共存吸引子的分布域也是大致对称的. 图6(a) , 图7(a) 和图7(c) 所展现的均是随参数$\gamma $ 变化的多吸引子共存现象, 系统总体运动呈现周期到混沌的趋势. 由于特殊参数下的对称性, 系统随参数c 的运动行为与参数$\gamma $ 变化时相反, 如图6(b) , 图7(b) 和图7(d) 所示, 这与图3 、图4 中单参数变化情况一致. 当$0.{\rm{708}} \leqslant \gamma \leqslant 0.{\rm{82}}$ 时, 可以找到九种不同结构的共存吸引子. 同样地, 在$1.048 \leqslant c \leqslant 1.37$ 范围内, 系统也出现9种吸引子共存现象. 通过共存相图进一步验证这种多稳态现象的存在性, 按照上述吸引盆所呈现的运动状态分布, 选择特殊参数下的不同初值绘制出具有多种拓扑结构的共存吸引子. 图8 和图9 展示的相轨迹图分别与吸引盆图6(a) 、图7(a) 和图7(c) 对应, 图10 、图11 则对应吸引盆图6(b) 、图7(b) 及图7(d) , 相应的初值设置见表5 . 其中, 图8 与图10 固定参数$\gamma = 0.74$ , 其他参数按表1 设置, 得到不同结构的吸引子类型. 特殊的是, 图10 完整展现吸引盆所区分的9种共存吸引子类型, 包括稳定不动点及左右共存周期1、周期2、周期3和混沌, 其对应的初值分别为$\left( { \pm {{10}^{ - 9}},0,0, \mp 0.{\rm{45}}} \right)$ , $\left( \pm {10^{ - 9}},0,0,0\right)$ , $\left( \pm {10^{ - 9}},0,0 \pm 0.4{\rm{5}}\right)$ , $( \pm {10^{ - 9}},0,0 \pm$ $ 0.{\rm{5}})$ 及$\left( \pm {10^{ - 9}},0,{\rm{0,}} \pm {\rm{0}}{\rm{.9}}\right)$ . 此外, 取参数$c = 1.274$ , 选取初值$\left( \pm {\rm{0}}{\rm{.45}},0,0,{\rm{0}}\right)$ , $\left( \pm {\rm{0}}{\rm{.8}},0,0,{\rm{0}}\right)$ 及$( \pm {\rm{0}}{\rm{.1}},$ 0, 0, 0)可得到图9 所呈现的周期3, 混沌与周期1吸引子相图; 相图11 所展示的左右点吸引子, 左 右周期1, 与左右混沌对应的初值分别为$( \pm {10^{ - 9}},$ $0,0, \mp 0.{\rm{45}})$ , $\left( \pm {10^{ - 9}},0,0,0\right)$ 及$( \pm {10^{ - 9}},0,{\rm{0,}}$ $ \pm {\rm{0}}{\rm{.9}})$ . 由于该忆阻系统吸引域分布对称性的存在, 图9 及图11 两张图所展现的吸引子运动相轨迹与图8 、图10 相一致, 但其呈现形态又因初值的微小差别而不同. 需要指出的是, 从吸引盆的分布情况看出, 选择的两种固定参数下周期2的状态较少, 因此仅在图10(b) 中展现, 表明在忆阻系统(4)中此状态确实存在.图 8 参数$\gamma {\rm{ = 0}}{\rm{.74}}$ , $x-z$ 平面上不同初值下的多种共存吸引子 (a)左右共存周期3; (b)左右共存混沌与左右共存周期1Figure8. For different initial value, phase diagram of coexisting attractors in $x-z$ planes when $\gamma {\rm{ = 0}}{\rm{.74}}$ : (a) Coexisting attractors of period-3; (b) coexisting attractors of chaos and period-1图 9 参数$c = 1.274$ , $x-z$ 平面上不同初值下的多种共存吸引子 (a)左右共存周期3; (b)左右共存混沌与左右共存周期1Figure9. For different initial value, phase diagram of coexisting attractors in $x-z$ planes when $c = 1.274$ : (a) Coexisting attractors of period-3; (b) coexisting attractors of chaos and period-1.图 10 参数$\gamma {\rm{ = 0}}{\rm{.74}}$ , $x-z$ 平面上不同初值下的多种共存吸引子 (a)左右共存周期3、左右共存周期1与稳定不动点; (b)左右共存混沌与左右共存周期2Figure10. For different initial value, phase diagram of coexisting attractors in $x-z$ planes when $\gamma {\rm{ = 0}}{\rm{.74}}$ : (a) Coexisting attractors of period-3, period-1 and fixed point; (b) coexisting attractors of chaos and period-2图 11 参数$c = 1.274$ , $x-z$ 平面上不同初值下的多种共存吸引子 (a)左右共存周期3与稳定不动点; (b)左右共存混沌与左右共存周期1Figure11. For different initial value, phase diagram of coexisting attractors in $x-z$ planes when $c = 1.274$ : (a) Coexisting attractors of period-3 and fixed point; (b) coexisting attractors of chaos and period-1参数 吸引子类型 初始条件 $\gamma = 0.{\rm{74}}$ 左右共存点吸引子 $\left( \pm {10^{ - 9}},0,0, \mp 0.{\rm{45}}\right)$ 左右共存周期1 $\left( \pm 0.1,0,0,0\right)$,$\left( \pm {10^{ - 9}},0,0, \pm {\rm{0}}{\rm{.45}}\right)$ 左右共存周期2, 左右共存周期3 $\left( \pm {\rm{1}}{{\rm{0}}^{ - {\rm{9}}}},0,0, \pm {\rm{0}}{\rm{.45}}\right)$, $ \left( \pm 0.{\rm{4}},0,0,0\right) $, $\left( \pm {10^{ - 9}},0,0 \pm 0.{\rm{5}}\right)$ 左右共存混沌 $\left( \pm 0.{\rm{8}},0,0,0\right)$, $\left( \pm {10^{ - 9}},0,0, \pm 0.9\right)$ $c = 1.274$ 左右共存点吸引子 $\left( \pm {10^{ - 9}},0,0, \mp 0.{\rm{45}}\right)$ 左右共存周期1 $\left( \pm 0.1,0,0,0\right)$, $\left( \pm {10^{ - 9}},0,0,0\right)$ 左右共存周期3 $\left( \pm 0.45,0,0,0\right)$, $\left( \pm {10^{ - 9}},0,0 \pm 0.4{\rm{5}}\right)$ 左右共存混沌 $\left( \pm 0.{\rm{8}},0,0,0\right)$, $\left( \pm {10^{ - 9}},0,0, \pm 0.9\right)$
表5 不同初值对应的共存多吸引子类型Table5. Coexisting multiple attractor with different initial condition4.基于FPGA的忆阻数字电路实现 为了拓展此类记忆元件的应用, 将系统(4)进行离散化并用FPGA数字平台进行实现. FPGA是可重复编写的硅芯片, 与定制电路最大的不同就是其内部有事先建立的逻辑块及可被重新编写的布线资源, 其功能的实现依赖于用户的编程. 因此, 这样的数字电路实现平台在更改系统参数或初值等设置上更为方便精准, 适用于实现忆阻混沌电路. 本次使用四阶龙格-库塔法离散忆阻系统(4), 该算法与其他常用离散化算法, 如Euler法或二阶龙格-库塔法相比较, 拥有稳定性高、精度好等一系列优点. 之后, 得到离散化方程(5 ), 其中$i = 1,2,$ $3,4$ , 分别对应方程(4 )中$x,y,z,w$ 四项, 相应的参数取值如表1 所示. 同时, 考虑到DA转换的$ \pm {\rm{5}}V$ 范围, 需要添加一个缩放系数E , 结合相图中各项范围, 给定E 为0.5, 迭代步长$h$ 设置为0.0001.图12 . 从图12 看出, 按顺序调用module_K4与module_XB两模块便可实现四阶龙格-库塔算法. 此外, 另一底层模块module_DA服务于高速DA转换器, 此次采用的数模转换芯片为AD9767, 其功能是将浮点数转换为定点数, 并赋值给输出通道, 最终在示波器上捕捉到相应时序图与相图.图 12 顶层模块控制流程图Figure12. The flow chart of calling order图13 所示, 其中图13(b) 为$y-z$ 平面上的双涡卷混沌吸引子相图, 该混沌相图与数值仿真所展示的图2(a) 相对应. 图13(c) 分别展示y , z 两项时序图, 并用蓝色与黄色线条表示. 此外, 为了证实所构忆阻系统存在对称共存的多稳态现象, 在图14 中展现固定参数$a = 1,b =$ $ 3.5,c = 1.274,\gamma = 0.86$ $\xi = 0.12$ , 选取不同初值时y -z 平面上的共存吸引子. 这组共存吸引子与图11 所示的数值仿真结果对应, 图14(a) 和图14(d) 为左右共存的周期1吸引子, 此时初值设定为$( \pm {10^{ - 9}},$ $0,0,0)$ ; 图14(b) 和图14(e) 呈现初值为$( \pm {10^{ - 9}},0,$ $0, \pm 0.45)$ 时的共存周期3吸引子, 与图11(a) 一致. 共存单涡卷混沌吸引子由图14(c) 和图14(f) 给出, 初值选择为$({10^{ - 9}},0,0,0.9)$ 和$( - {10^{ - 9}},0,0, - 0.9)$ . 通过FPGA数字电路实验, 证实所构忆阻系统(4)的物理可实现性. 数值仿真结果与电路实验结果的一致性, 也证明该系统确实存在多吸引子共存的多稳态现象.图 13 FPGA实物连接图与实现结果 (a)实物连接图; (b)y -z 平面相图; (c)y , z 两项时序图Figure13. The hardware connection diagram and the result of implementation: (a) The hardware connection diagram; (b) phase diagram in y -z plane; (c) timing diagram of the term y and z 图 14 固定参数$c = 1.274$ 时x -z 平面内不同初值条件下的共存, Ch 1 = 500 MV, Ch 2 = 500 MV (a)初值为$\left( {{\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,0}}} \right)$ , 左侧周期1; (b)初值为$\left( {{\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,0}}{\rm{.45}}} \right)$ , 左侧周期3; (c)初值为$\left( {{\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,0}}{\rm{.9}}} \right)$ , 左侧混沌; (d)初值为$\left( { - {\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,0}}} \right)$ , 右侧周期1; (e)初值为$\left( { - {\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,}} - {\rm{0}}{\rm{.45}}} \right)$ 右侧周期3; (f)初值为$\left( { - {\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,}} - {\rm{0}}{\rm{.9}}} \right)$ , 右侧混沌Figure14. The phase diagram of coexistence attractors with different initial conditions at $c = 1.274$ in x -z plane, Ch 1 = 500 MV, Ch 2 = 500 MV: (a) The initial value as $\left( {{\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,0}}} \right)$ , left period-1; (b) the initial value as $\left( {{\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,0}}{\rm{.45}}} \right)$ , left period-3; (c) the initial value as $\left( {{\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,0}}{\rm{.9}}} \right)$ , left period-3; (d) the initial value as $\left( { - {\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,0}}} \right)$ , right chaos; (e) the initial value as $\left( { - {\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,}} - {\rm{0}}{\rm{.45}}} \right)$ , right period-3; (f) the initial value as $\left( { - {\rm{1}}{{\rm{0}}^{ - {\rm{9}}}}{\rm{,0,0,}} - {\rm{0}}{\rm{.9}}} \right)$ , right chaos5.结 论 本文基于新型四维磁控忆阻电路, 观察特定系统参数的分岔图与Lyapunov指数谱, 发现该忆阻电路中对称分岔行为的存在性. 通过双参数吸引盆再次验证系统运动状态的对称性是真实存在的, 分析该忆阻系统在对称吸引域内的多稳态特性. 同时, 基于FPGA技术的电路实验平台, 完成该忆阻系统的数字电路实现, 在示波器上捕捉到双涡卷混沌吸引子与多种状态的共存. 实验结果表明数值仿真的有效性, 以及新型四维磁控忆阻电路的物理可实现性. 当然, 目前所构忆阻电路中的对称动力学行为还无法从理论角度来解释. 系统的动力学行为会受到平衡点位置的影响, 考虑到无法准确定位该忆阻系统的平衡点, 之后会进行更多的工作并探索新的方法来解决这一问题, 从理论出发更易找出这种特殊对称行为存在原因与规律. 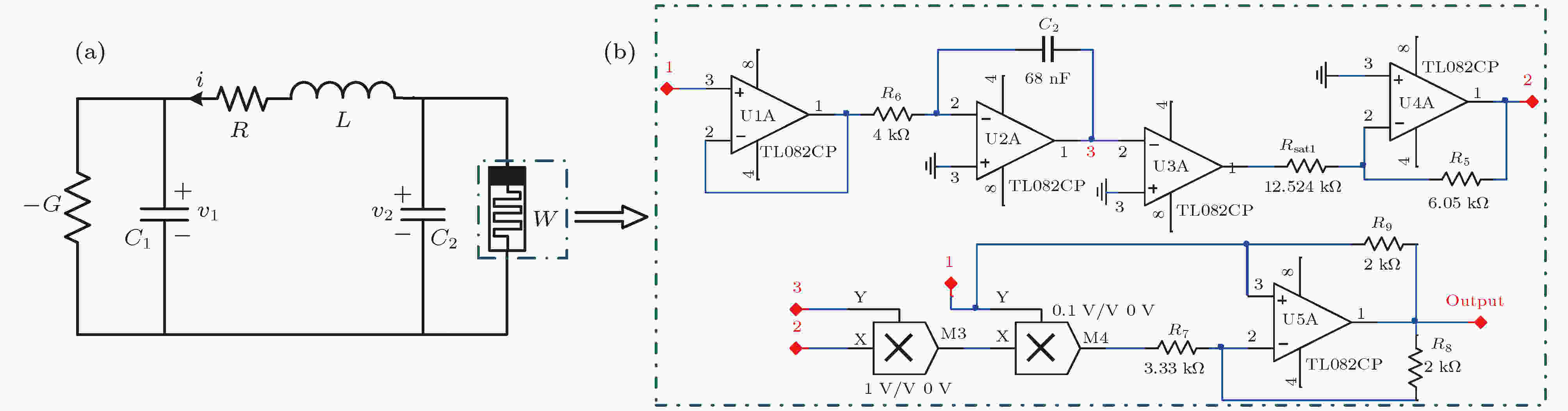 图 1 电路模型 (a)磁控忆阻电路; (b)磁控忆阻等效电路
图 1 电路模型 (a)磁控忆阻电路; (b)磁控忆阻等效电路






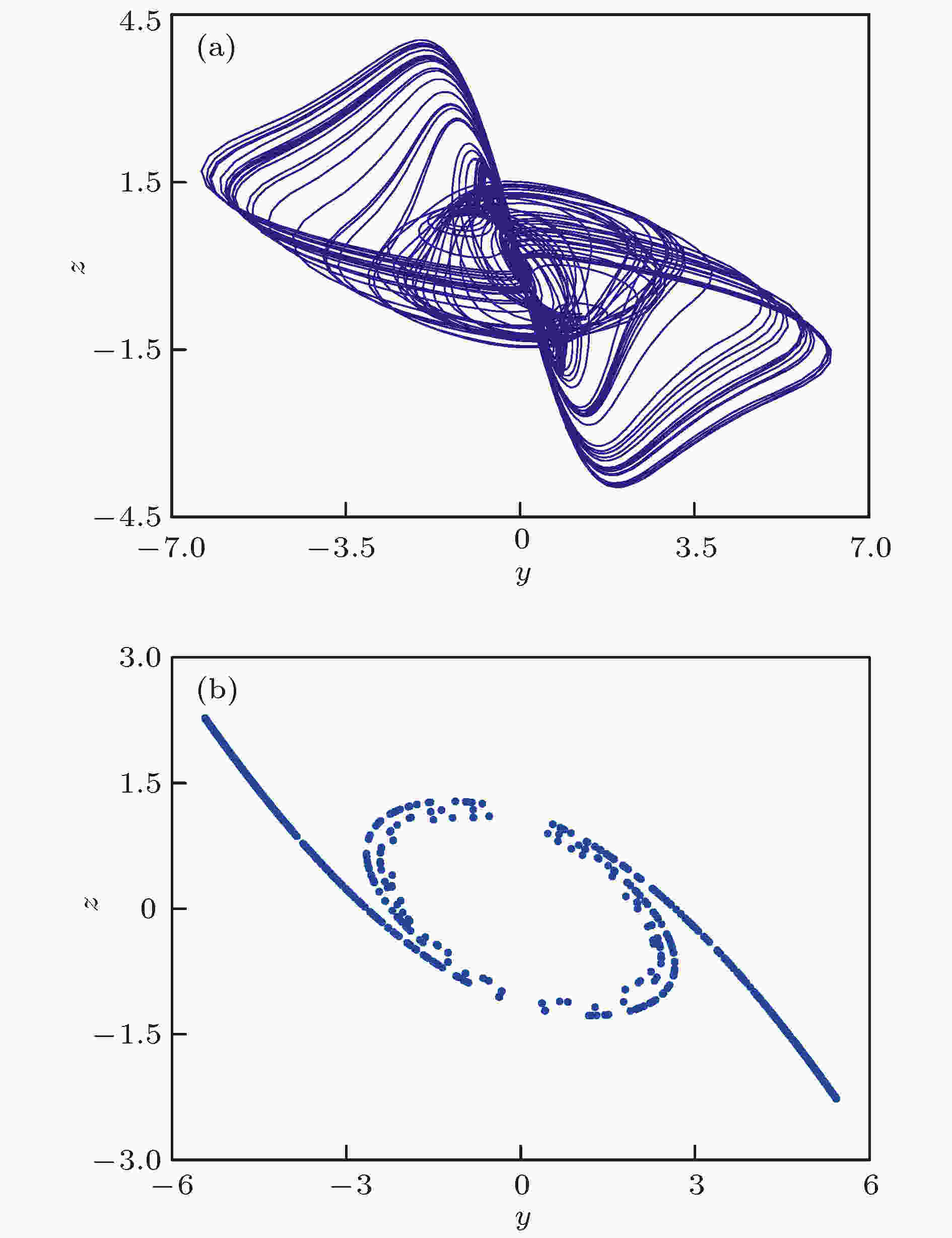 图 2
图 2 













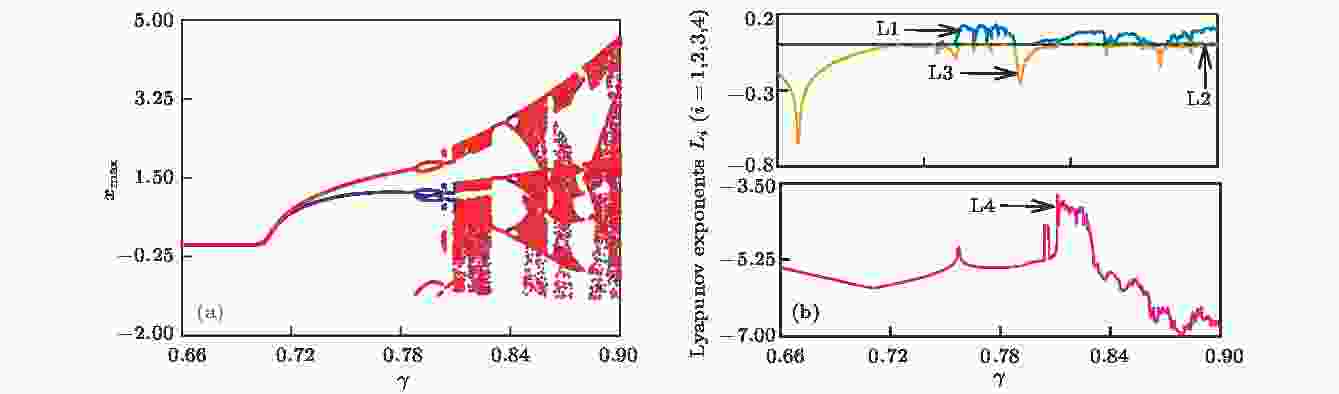 图 3 随参数
图 3 随参数

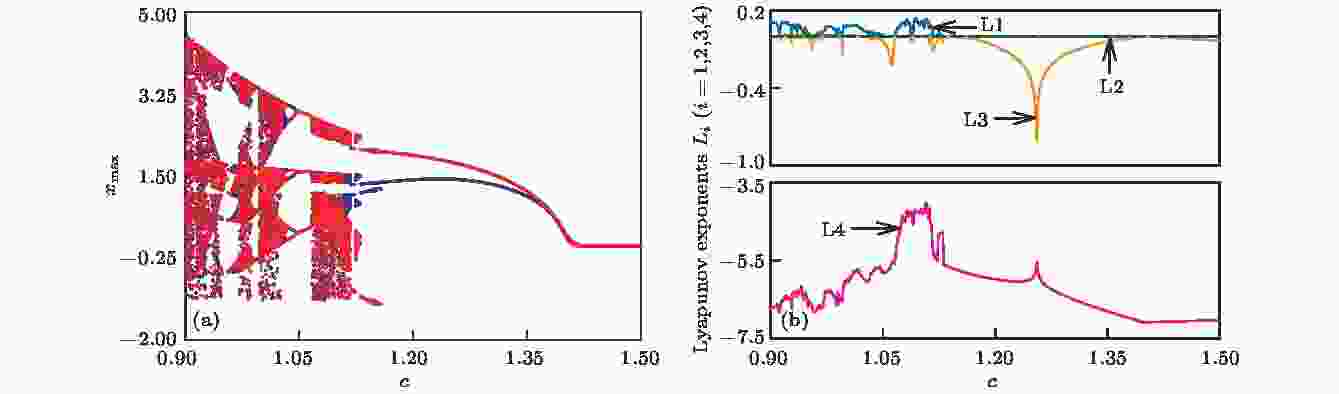 图 4 随参数c变化的分岔图与Lyapunov指数谱 (a)分岔图; (b) Lyapunov指数谱
图 4 随参数c变化的分岔图与Lyapunov指数谱 (a)分岔图; (b) Lyapunov指数谱




















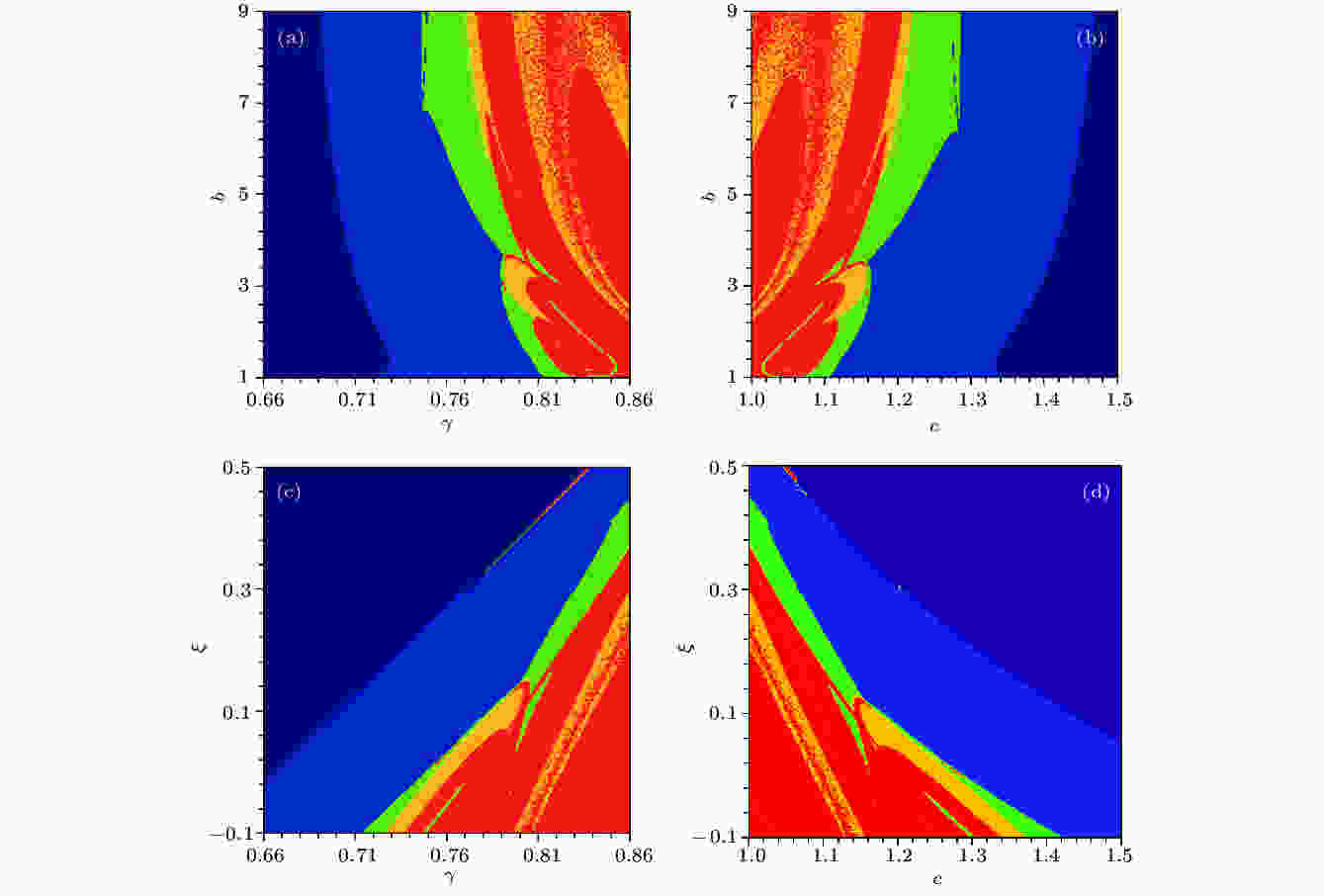 图 5 双参数吸引盆 (a)参数
图 5 双参数吸引盆 (a)参数




















































 图 6 不同变量组合下的共存吸引盆 (a)
图 6 不同变量组合下的共存吸引盆 (a) 









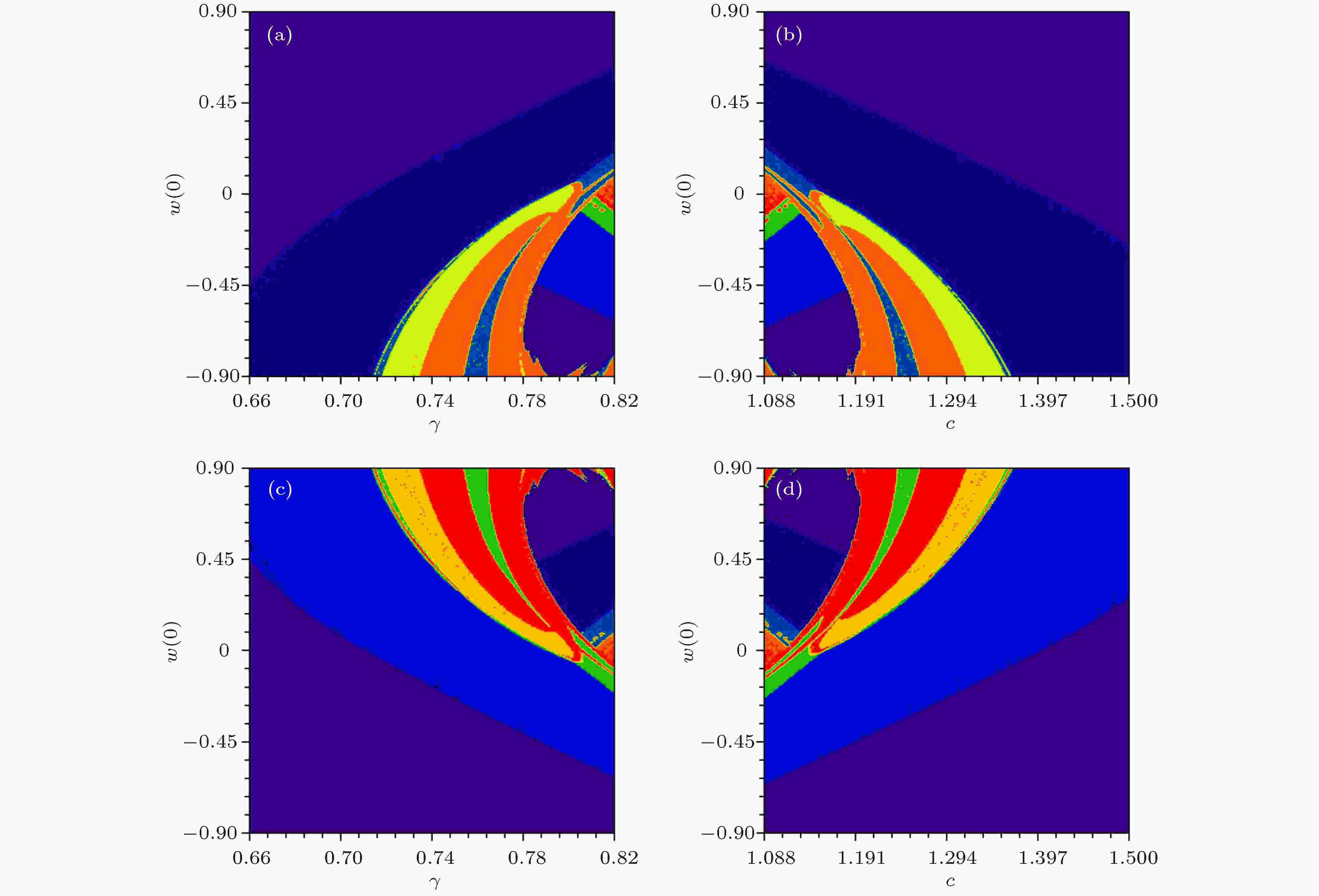 图 7 不同变量组合下系统状态分布图 (a)
图 7 不同变量组合下系统状态分布图 (a) 




























































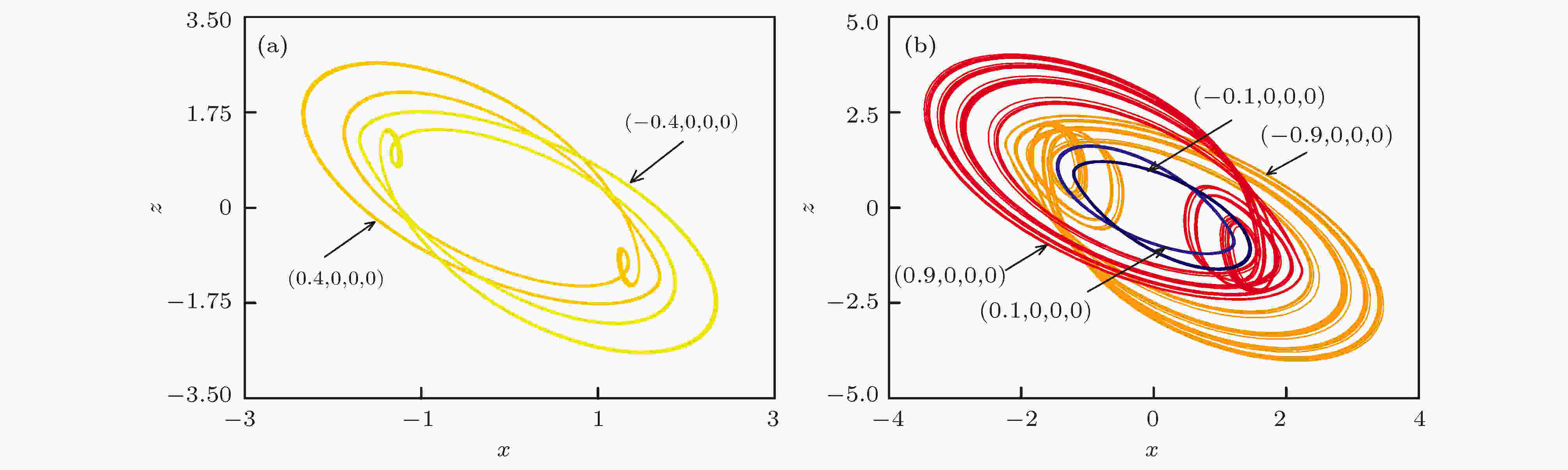 图 8 参数
图 8 参数



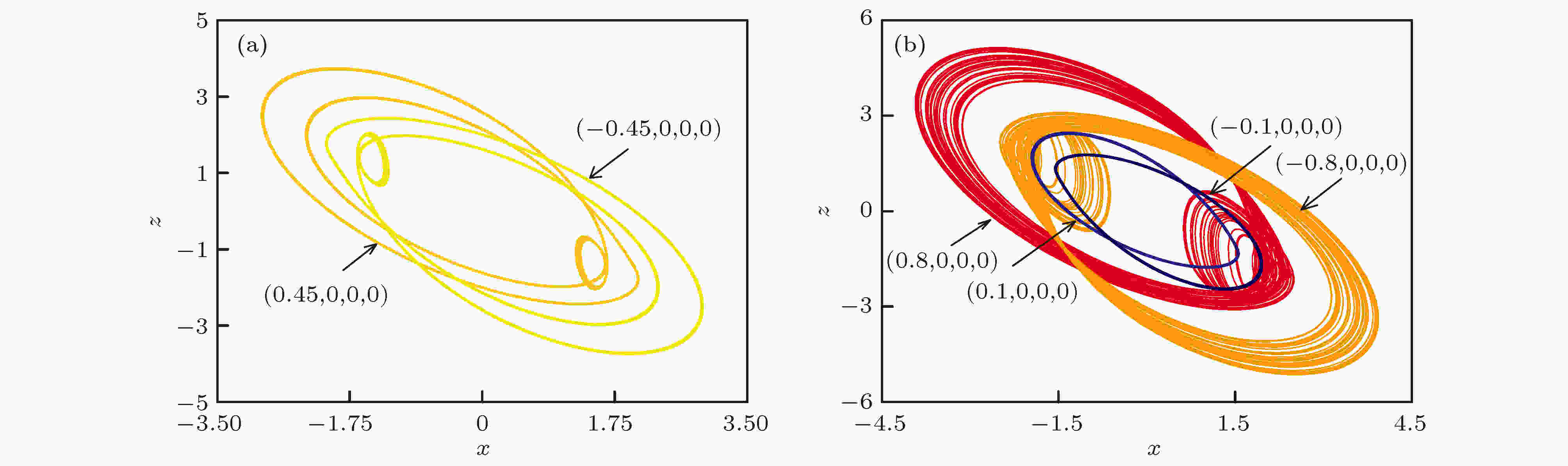 图 9 参数
图 9 参数



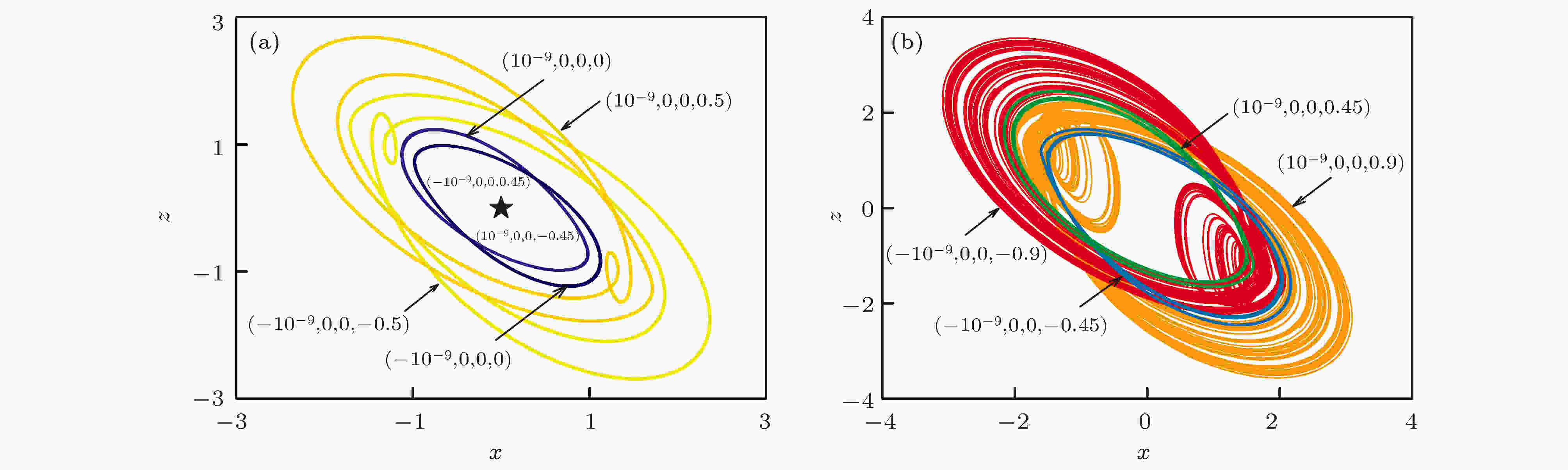 图 10 参数
图 10 参数



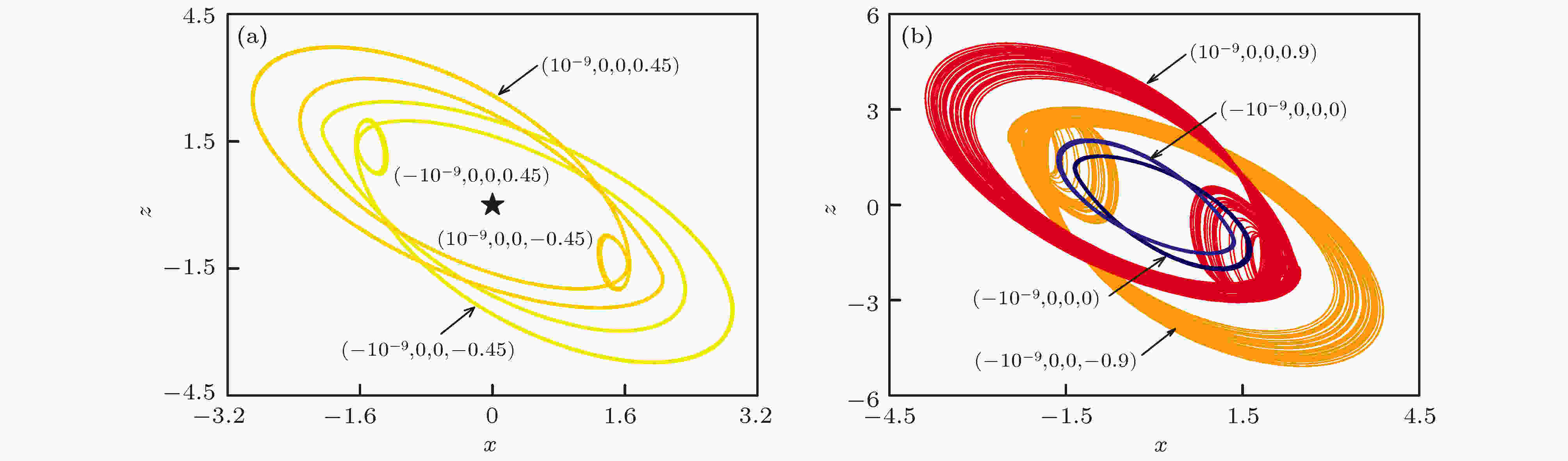 图 11 参数
图 11 参数








 图 12 顶层模块控制流程图
图 12 顶层模块控制流程图









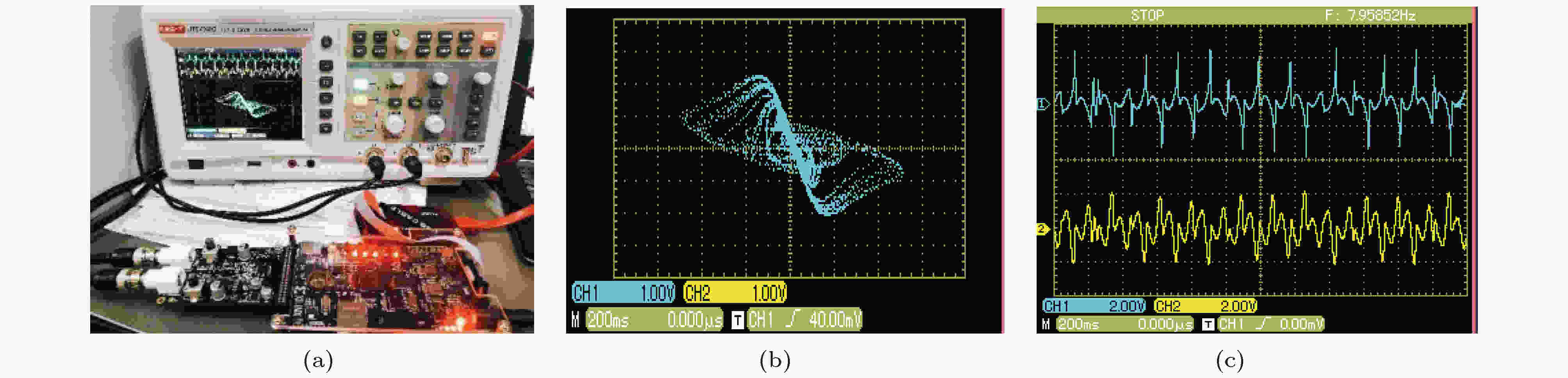 图 13 FPGA实物连接图与实现结果 (a)实物连接图; (b)y-z平面相图; (c)y, z两项时序图
图 13 FPGA实物连接图与实现结果 (a)实物连接图; (b)y-z平面相图; (c)y, z两项时序图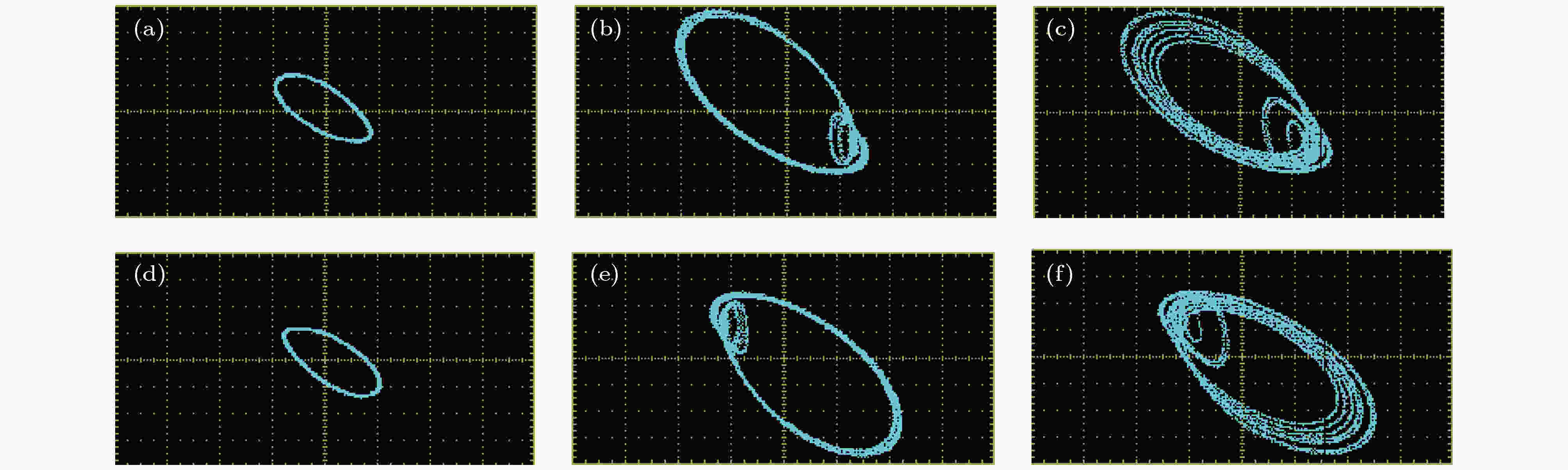 图 14 固定参数
图 14 固定参数













