摘要: Jiles-Atherton (J-A)模型和Zheng Xiao-Jing-Liu Xing-En (Z-L)模型在分析应力对铁磁材料磁化的影响方面应用十分广泛. 目前, J-A模型中的磁致伸缩应变与应力和磁化强度的关系式采用Jiles给出的经典拟合公式, 该拟合公式中磁化强度的二次项和四次项系数与应力均为线性关系, 不能准确描述铁磁材料磁致伸缩系数随应力、磁化强度的非线性变化规律; Z-L模型中磁致伸缩应变与应力和磁化强度的关系式采用了双曲正切函数tanh(
x ), 更好地描述了铁磁材料磁致伸缩应变和磁化强度随应力的非线性变化规律, 但Z-L模型却没有考虑Weiss分子场、钉扎效应的作用, 且由于采用了基于弹性能的接近定理, 只能描述弹性应力对磁化过程的影响. 针对上述问题, 本文结合Z-L模型中的非线性磁致伸缩应变关系式以及J-A模型中的磁滞理论, 考虑弹性应力、塑性变形对模型参数的影响, 建立了能够反映弹-塑性阶段应力与塑性变形对铁磁材料磁化曲线影响的修正磁化模型, 分析了弹性拉、压应力及塑性拉、压变形对磁化曲线、矫顽力和剩余磁化强度的影响规律. 通过与试验结果及原有模型的计算结果进行对比, 发现修正模型能够更好地反映单次磁化、循环磁化过程中应力、塑性变形对磁化曲线的影响规律, 理论预测结果与试验结果之间的相关系数均在0.98以上, 可为分析力磁耦合效应对铁磁材料磁化影响规律提供更准确的理论模型.
关键词: 力磁耦合 /
磁致伸缩 /
磁滞回线 /
Jiles-Atherton模型 /
Zheng Xiao-Jing-Liu Xing-En模型 English Abstract A modified model of magneto-mechanical effect on magnetization in ferromagnetic materials Luo Xu 1 ,Zhu Hai-Yan 2 ,Ding Ya-Ping 3 1.School of Mechatronic Engineering of Southwest Petroleum University, Chengdu 610500, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 51874253) and the Young Scientists Fund of the National Natural Science Foundation of China (Grant No. 51604232)Received Date: 20 May 2019Accepted Date: 02 July 2019Available Online: 01 September 2019Published Online: 20 September 2019Abstract: The prevailing Jiles-Atherton (J-A) model and Zheng Xiao-Jing-Liu Xing-En (Z-L) model are extensively used in modeling the magneto-mechanical effect on magnetization in ferromagnetic materials. In the J-A model, a fitting formula of magnetostrictive strain interms of stress and magnetization is adopted to model the stress effect on magnetostriction. However, the fitting formula is not in good accordance with the experimental results obtained by Kuruzar and Culllity. In order to solve this problem, a transcendental function tanh(x ) is appropriately selected to describe the nonlinear magnetostrictive strain in the Z-L model, and it is found that the general formula of magnetostrictive strain is more effective to describe the nonlinear relation of magnetostrictive strain with stress and magnetization. Then, the modified law proposed by Jiles and Li is adopted to modify the Z-L model by Shi Pengpeng to describe the hysteretic behavior; nevertheless, the effect of Weiss molecular field, pinning energy and plastic deformation on magnetization are not taken into account, and the modified Z-L model can only describe the elastic stress effect on magnetization. In order to solve these problems above, a modified magneto-mechanical model is established by combining the magnetostrictive constitutive relationships of Z-L model with the modified energy conservation equation of J-A model, as well as taking the effect of elastic stress and plastic strain on the model parameters into account simultaneously. It is found that the predictions of proposed model here are in better accordance with the initial magnetization curves given by Jiles and Atherton and the hysteresis loops obtained by Makar and Tanner under different stresses and plastic deformation than those calculated by the J-A model and Z-L model. The correlation coefficients between experimental data and theoretical results calculated by the modified model are all over 0.98, which indicates that the modified model here is more effective than the existing model. A detailed study also performed to reveal the effects of the elastic tensile and compressive stress and plastic tensile and compressive strain on hysteresis loops, coercivity and remanence. The proposed model reveals that the area of hysteresis loop and coercivity increase nonlinearly with the stress and plastic deformation increasing, while the remanence decreases significantly; the effects of compressive stress and compressive plastic deformation on magnetization characteristic parameters above are more significant than those of tensile stress and tensile plastic deformation, which is consistent with the experimental trend. The proposed model can be used to quantitatively analyze the magneto-mechanical effect on the magnetization of ferromagnetism.Keywords: magneto-mechanical effect /magnetostriction /hysteresis loops /Jiles-Atherton model /Zheng Xiao-Jing-Liu Xing-En model 全文HTML --> --> --> 1.引 言 应力-应变对铁磁材料磁化过程的影响规律, 即力磁耦合效应, 一直是国内外****的研究热点[1 —9 ] . 随着应力-应变的改变, 特别是应力集中或塑性变形的出现, 铁磁材料内部的磁畴结构和钉扎点密度等会发生显著变化, 从而影响材料的磁化曲线、矫顽力、剩余磁化强度等磁化特性[10 —14 ] . 基于上述现象, 发展出多种磁无损检测技术, 如: 金属磁记忆检测技术、巴克豪森磁噪声技术、磁声发射技术. 建立准确的磁化模型来描述应力、塑性变形对铁磁材料磁化的影响规律, 是利用上述磁无损检测技术实现应力集中、塑性变形检测与反演的基础.[15 ,16 ] 根据接近定理, 将磁化强度分为可逆磁化和不可逆磁化两部分, 建立了著名的J-A模型; 在该模型的基础上, Sablik等[6 ] 将应力等效为附加磁场, 建立了反映均匀弹性应力对磁化过程影响的Jiles-Atherton-Sablik (J-A-S)模型; 初期, Sablik等[6 ,17 ] 认为磁致伸缩系数只与磁化强度的二次项有关, 并给出了三种不同形式的磁致伸缩应变关系式; 此后, Sablik等[7 ,18 ] 基于磁畴理论和能内定理, 建立了新的磁致伸缩应变关系式; 由于实际材料中磁畴结构很难提前预知, Jiles[8 ] 提出利用经验公式来拟合磁致伸缩应变与磁化强度之间的变化关系, 并将其Taylor展开式简化为只包含磁化强度二次项和四次项的式子, 由此形成了J-A模型的中经典磁致伸缩应变关系式; 此后, 文献[19 —21 ]针对原磁致伸缩系数关系式不能很好反映低应力条件下磁致伸缩系数的变化规律, 提出利用神经网络来拟合磁致伸缩系数与磁化强度关系. 为描述拉应力和压应力对磁化特性影响的非对称性, Li和Xu [22 ] 以及 Sablik[23 ] 在原有模型基础上引入退磁项, 并基于Gaussian方程建立了饱和磁致伸缩系数与应力的变化关系; Li和Jiles [24 ] 则利用Rayleigh定理对J-A模型中的接近定理进行了修正; 针对循环应力作用下零应力附近的磁化强度不符合逐渐趋于稳定状态的问题, Sablik等[25 ] 提出了两种方法对接近定理进行改进. 为实现利用J-A模型描述塑性变形对材料磁化的影响, 文献[3 , 26 —33 ]分析了塑性变形对材料位错密度的影响, 建立了钉扎系数、Weiss分子场耦合系数、形状系数等与晶粒尺寸、位错密度之间的关系, 推导了基于J-A模型的不同形式的塑性磁化模型.[34 ,35 ] 通过在Zheng Xiao-Jing-Liu Xing-En (Z-L)模型中的磁致伸缩应变关系中引入磁化强度四次项, 更好地反映了铁磁材料磁致伸缩应变随应力、磁化强度的非线性变化规律; 但是, 周浩淼等改进的磁化模型中没有考虑Weiss分子场、退磁场和磁滞效应的影响, 不能反映循环磁化过程中的磁滞现象. Shi等[36 ,37 ] 在考虑退磁场和磁滞效应的基础上, 对Z-L模型进行了改进, 但仍未考虑Weiss分子场作用, 同时由于采用了基于弹性能的接近定理, 无法描述塑性变形对磁化曲线的影响.2.非线性力磁耦合模型 22.1.非磁滞条件下的力磁耦合模型 2.1.非磁滞条件下的力磁耦合模型 当铁磁材料所受应力方向与外加磁场方向同轴时, 根据热力学第一定律, 材料单位体积内能$U\left( {\sigma,{M_{{\rm{an}}}},T} \right)$ 满足[35 ] $Q$ 为材料从外部吸收的热能; $W$ 为外力对材料做所的功; T 为外界温度; $S$ 为体积熵的变化量; $\sigma $ 为应力; $\varepsilon $ 为应变; ${\mu _0}$ 为真空磁导率, ${\mu _0} = 4{\text{π}} \times {10^{ - 7}}$ ; $H$ 为外磁场强度; ${M_{{\rm{an}}}}$ 为非磁滞磁化强度.${G_{\rm{m}}}\left( {\sigma,{M_{{\rm{an}}}},T} \right)$ 可表示为[36 ] $\alpha $ 为Weiss分子场耦合系数, ${N_{\rm{d}}}$ 为退磁系数. 则${G_{\rm{m}}}\left( {\sigma,{M_{{\rm{an}}}},T} \right)$ 的全微分可写为${\rm{d}}T = 0$ , 则可得到只包含应力$\sigma $ 与非磁滞磁化强度${M_{{\rm{an}}}}$ 的Gibbs自由能${G_{\rm{m}}}\left( {\sigma,{M_{{\rm{an}}}}} \right)$ 全微分表达式, 即$\varepsilon \left( {\sigma,{M_{{\rm{an}}}}} \right)$ 和有效场${H_{\rm{e}}}\left( {\sigma,{M_{{\rm{an}}}}} \right)$ 关系为[34 —36 ] ${G_{\rm{m}}}\left( {\sigma,{M_{{\rm{an}}}}} \right)$ 在$\left( {\sigma,\;{M_{{\rm{an}}}}} \right) = \left( {0,\;0} \right)$ 进行泰勒展开, 并根据试验现象对泰勒展开式进行简化. 根据Kurzar和Cullity[38 ] , Yamasaki等[39 ] 的试验结果及Jiles、周浩淼等的理论分析, 铁磁材料的磁致伸缩曲线是关于$y$ 轴对称的偶函数, 因此磁致伸缩应变$\varepsilon \left( {\sigma,{M_{{\rm{an}}}}} \right)$ 中的耦合项只保留含有$M_{\rm{an}}^2$ 和$M_{\rm{an}}^4$ 项, 则${E_{\rm{s}}}$ 为材料固有弹性模量; ${\lambda _0}\left( \sigma \right)$ 为应力单独作用下磁畴移动导致的磁致伸缩应变量; ${\lambda _{\max }}\left( \sigma \right)$ 为应力单独作用时由于磁畴移动导致的最大磁致伸缩应变量; ${M_{{\rm{ws}}}}$ 为无应力时的饱和壁移磁化强度; ${\lambda _{{\rm{ws}}}}$ 为无应力条件下材料的饱和磁致伸缩应变; ${M_0}\left( \sigma \right)$ 为应力作用时的饱和壁移磁化强度; $\vartheta $ 为阶跃函数, 当${M_{{\rm{an}}}} < {M_0}\left( \sigma \right)$ 时, $\vartheta = 0$ , 当${M_{{\rm{an}}}} \geqslant {M_0}\left( \sigma \right)$ 时, $\vartheta = n$ , 以保证只有当磁化强度${M_{{\rm{an}}}}$ 超过${M_0}\left( \sigma \right)$ 后, 磁化强度的四次项${M_{{\rm{an}}}}^4$ 才对磁致伸缩应变产生影响. 在文献[35 , 36 ]理论分析的基础上, 结合文献[32 , 33 ]对J-A模型的讨论, ${M_{{\rm{an}}}}$ , ${M_0}\left( \sigma \right)$ , ${\lambda _0}\left( \sigma \right)$ 和${\lambda _{\max }}\left( \sigma \right)$ 可表示为${M_{\rm{s}}}$ 为饱和磁化强度; $a$ 为形状系数; ${\rm{tanh}}\left( x \right)$ 是双曲正切函数; ${\sigma _0}$ 表示将${\lambda _0}\left( \sigma \right)$ 在原点附近线性化为斜率为${1 / {{E'}}}$ 的直线时, 使${\lambda _0}\left( \sigma \right) = {\lambda _{{\rm{ws}}}}$ 时的应力值, ${1 / {{E'}}} = {1 / {{E_0}}} - {1 / {{E_{\rm{s}}}}}$ , ${E_0}$ 为初始弹性模量; $\beta $ 为比例系数, 影响曲线斜率. 周浩淼改进的Z-L模型采用了分段函数来表示压应力和拉应力对${\lambda _0}\left( \sigma \right)$ 的不同影响, 为简化公式, 本文通过平移变换, 将Z-L模型中${\lambda _0}\left( \sigma \right)$ 的表达式变为了连续函数, 其中$ - \rm{arctanh} \left( {{1 / 3}} \right)$ 的引入是为保证当应力$\sigma = $ 0 MPa时, ${\lambda _0}\left( \sigma \right) = 0$ .8 )式代入(7 )式中, 即可得到非磁滞条件下材料磁致伸缩应变和磁化强度随应力、磁场的变化规律.2.2.磁滞效应对磁化强度的影响 -->2.2.磁滞效应对磁化强度的影响 实际磁化过程中, 材料内部不可避免地存在缺陷、位错、晶格滑移等钉扎点, 从而阻碍磁畴运动. 钉扎效应的存在, 导致材料在磁化过程中不可避免地存在能量损耗. 因此, 根据能量守恒原理, 实际磁化过程中的磁化能量等于无磁滞磁化能减去钉扎点造成的磁滞损耗[33 ] , 即$M$ 为实际磁化强度, $M = {M_{{\rm{rev}}}} + {M_{{\rm{irr}}}}$ , ${M_{{\rm{irr}}}}$ 为不可逆磁化强度, ${M_{{\rm{rev}}}}$ 为可逆磁化强度; ${k_{{\rm{eff}}}}$ 为有效钉扎系数; $\delta $ 为方向系数, 当${{{\rm{d}}{H_{\rm{e}}}\left( M \right)} / {{\rm{d}}t}} > 0$ 时, $\delta = 1$ , 当${{{\rm{d}}{H_{\rm{e}}}\left( M \right)} / {{\rm{d}}t}} < 0$ 时, $\delta = - 1$ , 以保证钉扎点的作用总是阻碍磁场的变化; ${B_{\rm{e}}}\left( M \right)$ 表示实际磁感应强度, ${B_{\rm{e}}}\left( M \right) = {\mu _0}{H_{\rm{e}}}\left( M \right)$ ; ${H_{\rm{e}}}\left( M \right)$ 为实际磁化强度条件下的等效磁场强度, ${H_{\rm{e}}}\left( M \right)$ 可将(7 )式中的${M_{{\rm{an}}}}$ 换成$M$ 得到, 即9 )式可得$M = {M_{\rm rev}} + {M_{\rm irr}}$ , ${M_{{\rm{rev}}}} = c\left( {{M_{{\rm{an}}}} - {M_{{\rm{irr}}}}} \right)$ 可得12 )式对外磁场强度$H$ 取微分可得10 )式对外磁场强度$H$ 取微分可得11 ), (13 )和(14 )式, 并整理可得${{{\rm{d}}{M_{{\rm{an}}}}} / {{\rm{d}}H}}$ 可联立(7 )和(8 )式得到, 即15 )和(16 )式即可计算不同应力条件下磁化强度$M$ 随外磁场$H$ 的变化规律.2.3.应力-应变对模型参数的影响 -->2.3.应力-应变对模型参数的影响 在应力、应变, 特别是塑性变形作用下, 材料内部磁畴结构的形状和尺寸以及钉扎点密度都会发生改变, 从而改变Weiss分子场耦合系数$\alpha $ 、有效钉扎系数${k_{{\rm{eff}}}}$ 以及形状系数$a$ 的取值.${\sigma _{\rm{F}}}$ 与塑性应变${\varepsilon _{\rm{r}}}$ 之间的关系可根据Ludwik定律得到[40 ] :$A$ 为常数; $m$ 为Ludwik指数, 与材料性质有关.${\zeta _{\rm{d}}}$ 与材料的应变硬化应力${\sigma _{\rm{F}}}$ 呈比例关系[28 ] :${\zeta _{{\rm{d}}0}}$ 为无应力时材料初始位错密度; $G$ 为剪切模量, 其与固有弹性模量${E_{\rm{s}}}$ 和泊松比$\upsilon $ 之间的关系为$G = {{{E_{\rm{s}}}} / {2\left( {1 + \upsilon } \right)}}$ ; $ b$ 为柏氏矢量, 是描述位错实质的物理量; ${\alpha _k}$ 为常数, 取0.76.[28 ,29 ] 的试验结果表明: 拉应力使钉扎密度减小, 压应力使钉扎密度增大; 而位错会以钉扎的形式阻碍畴壁运动. 因此, 有效钉扎系数${k_{{\rm{eff}}}}$ 和形状系数$a$ 与应力和位错密度之间的关系可表示为[30 ] $\left[ {{G_1} + {{{G_2}} / d}} \right]\zeta _{\rm{d}}^{{1 / 2}}{k_0}$ 表示塑性变形对钉扎系数的改变量, $ - {{3\eta {\lambda _{{\rm{ws}}}}\sigma } / 2}$ 表示$\sigma $ 对${k_{{\rm{eff}}}}$ 的改变量; ${\zeta _{\rm{d}}}$ 为错密度, ${k_0}$ 为初始钉扎系数; ${G_1}$ , ${G_2}$ , ${G_3}$ , ${G_4}$ , $\eta $ 为拟合常数, 一般取${G_1} = {G_3}$ , ${G_2} = {G_4}$ ; ${a_0}$ 为初始形状系数; $d$ 为材料晶粒尺寸. 在弹性阶段, 材料内部位错密度不会发生改变, 取$\left[ {{G_1} \!+\! {{{G_2}} / d}} \right]\zeta _{{{\rm{d}_{\rm{0}}}}}^{{1 / 2}}\!=\! 1$ , $\left( {{G_3} + {{{G_4}} / d}} \right)\zeta _{{{\rm{d}}_0}}^{{1 / 2}} = 1$ .$\alpha $ 会随着应力-应变的增加而发生变化, 其与应力-应变的关系为[23 ,31 ,41 ] ${\alpha _0}$ 为初始Weiss分子场耦合系数; ${q_1}\ln \left( {{q_2}{\varepsilon _{\rm{r}}} + {q_3}} \right)$ 表示塑性变形对$\alpha $ 改变量;$\alpha $ 改变量; ${q_1}$ , ${q_2}$ , ${q_3}$ 均为拟合常数.3.模型理论计算结果与试验结果对比 23.1.单次磁化过程中应力对磁化曲线的影响 3.1.单次磁化过程中应力对磁化曲线的影响 为说明修正模型相对于Z-L模型、J-A模型的改进情况, 利用Jiles等[8 ] 进行的–200, –100, 0, 100和200 MPa五组不同预应力条件下的磁化测试结果进行验证, 试验结果如文献[8 ]图3虚线所示. Jiles模型中参数与文献[8 ]中的图2一致; Z-L模型中相关参数取值与文献[35 ]中图9一致; 修正模型中$\beta = 1.4$ , $\vartheta = 0.75$ , ${\alpha _0} = 1.44 \times {10^{ - 3}}$ , 其他参数与Z-L模型参数取值一致, 不同应力条件下不同模型计算结果与试验结果对比如图1 所示.图 1 单次磁化条件下不同模型计算得到的${B_{\rm{e}}}$ -$H$ 曲线对比 (a)修正模型计算结果; (b) J-A模型计算结果; (c) Z-L模型计算结果; (d)不同模型计算结果与试验结果相关系数对比Figure1. Comparison of initial${B_{\rm{e}}}$ -$H$ curves calculated by different models: (a) Our theoretical model; (b) J-A model; (c) Z-L model; (d) correlation coefficients of different models${R^2}$ 作为模型拟合度优劣的评价标准, 其计算公式为${P_i}$ 为试验结果, ${\hat P_i}$ 为模型计算结果, $i$ 表示测试数据编号; $n$ 为数据点数量. ${R^2}$ 值越接近1, 则表明模型拟合度越高. 不同模型计算结果的相关系数${R^2}$ 如表1 和图1(d) 所示.模型类型 应力值/MPa –200 –100 0 100 200 修正模型${R^2}$ 0.9904 0.9947 0.9973 0.9859 0.9724 Z-L模型${R^2}$ 0.9421 0.9290 0.9333 0.9300 0.8956 J-A模型${R^2}$ 0.6289 0.0394 –0.0289 0.2688 0.6440
表1 不同模型的相关系数${R^2}$ 比较Table1. Correlation coefficients ${R^2}$ of initial magnetization curve predicated by different models.${R^2}$ 远远高于J-A模型的计算结果, 这种准确性的提高主要源于Z-L模型和本文修正模型都采用了更好的非线性磁致伸缩应变关系式; 同时, 相对于Z-L模型, 本文修正模型的准确性更好, 不同应力条件下预测结果与试验结果之间的相关系数比Z-L模型的相关系数要高0.05以上.3.2.加载条件下应力对磁滞回线的影响 -->3.2.加载条件下应力对磁滞回线的影响 利用Makar等[13 ] 在不同含碳量的碳钢棒材试件上进行的试验进一步验证修正模型的改进情况. 由于, Makar等进行的试验包含了弹-塑性两个阶段, 而原Z-L模型只能描述弹性阶段应力的影响, 本节中只将修正模型、J-A模型计算结果与Makar等的试验结果进行对比. 选择含碳量为0.003%和0.15%两种碳钢棒材试件的测试结果进行验证, 修正模型及J-A模型的部分参数可根据参考文献[13 ]中的试验数据直接得到, 如: 含碳量为0.003%试件的屈服强度${\sigma _{\rm{s}}} = $ 90 MPa, 平均晶粒直径$d = 1.25 \times\! {10^{ - 3}}$ m, ${\lambda _{{\rm{ws}}}} = 3.85 \times \!{\rm{1}}{{\rm{0}}^{ - 6}}$ m, ${M_{{\rm{ws}}}} = $ $ 1.25 \times {10^6}$ A·m–1 , $-{M_{\rm{s}}} = 1.45 \times {10^6} $ A·m–1 , 所受应力分别为0, 33和160 MPa; 含碳量为0.15%试件的屈服强度${\sigma _{\rm{s}}} = $ 122 MPa, 平均晶粒直径$ d = $ $ 1.9 \times {10^{ - 4}}$ m, ${\lambda _{{\rm{ws}}}} = 4.17 \times {\rm{1}}{{\rm{0}}^{ - 6}}$ m, ${M_{{\rm{ws}}}} = 1.35 \;\times$ 106 A·m–1 , ${M_{\rm{s}}} = 1.6 \times {10^6}$ A·m–1 , 所受应力分别为0, 36和182 MPa; 修正模型其他参数则需要根据磁化曲线通过拟合得到, 如: 当含碳量为0.003%时,$c = 0.25$ , ${k_0} = 4.522\; \times $ $ {10^{ - 3}}\;{\rm{ A}}\cdot{{\rm{m}}^{{\rm{ - 1}}}}$ , 其他参数与含碳量为0.003%时相同. J-A模型中磁致伸缩系数关系式中的参数可根据参考文献[13 ]中给出的磁致伸缩应变曲线拟合得到: 当含碳量为0.003%时,13 ]中的图3的试验结果进行对比, 结果如图2 所示.图 2 不同应力条件下修正模型和J-A模型磁滞回线计算结果的对比 (a)含碳量为0.003%时修正模型计算结果; (b)含碳量为0.003%时J-A模型计算结果; (c)含碳量为0.15%时修正模型计算结果; (d)含碳量为0.15%时J-A模型计算结果Figure2. Hysteresis loops predicated by modified model and J-A model under different loading stresses: (a) Our modified model for 0.003 wt% C sample; (b) J-A model for 0.003 wt% C sample; (c) our modified model for 0.15 wt% C sample; (d) J-A model for 0.15 wt% C sample图2 结果表明: 随着应力的增大, 磁滞回线均会产生顺时针转动, 且塑性应力对磁滞回线的影响更为显著; 随着含碳量的增大, 磁滞损耗增大, 磁滞回线面积增大; 此外, 在弹性应力(0.003 wt% C, 33 MPa; 0.15 wt% C, 36 MPa)作用下, 铁磁材料的饱和磁化强度变化很小, 而塑性应力(0.003 wt% C, 160 MPa; 0.15 wt% C, 182 MPa)作用下, 铁磁材料的饱和磁化强度却显著降低, 其原因在于当材料发生塑性变形时, 材料内部的位错、晶格滑移增大, 钉扎点数量急剧增多, 使得材料磁化过程中的磁滞损耗显著增大. 对比不同模型计算结果和试验结果可知: 在弹性应力范围内, J-A模型能够较好地反映应力对磁滞回线的影响趋势, 但当进入塑性阶段后, J-A模型计算结果与试验结果存在明显差距; 而修正模型能够同时反映弹性阶段和塑性阶段应力对不同含碳量试件磁滞回线的影响规律, 不同应力条件下理论计算得到的磁滞回线与试验测试得到的磁滞回线基本重合.${R^2}$ , 结果如表2 所列.模型类型 试件含碳量0.003 wt% 试件含碳量0.15 wt% 0 MPa 33 MPa 160 MPa 0 MPa 36 MPa 182 MPa 修正模型${R^2}$ 0.9845 0.9894 0.9898 0.9840 0.9808 0.9937 J-A模型${R^2}$ 0.9133 0.9188 0.8984 0.9485 0.9496 0.9153
表2 加载条件下不同模型计算得到的磁滞回线与试验曲线相关系数${R^2}$ 比较Table2. Correlation coefficients ${R^2}$ of hysteresis loops predicated by different models under loading condition.表2 的对比可知: 在加载条件下, 修正模型计算得到的磁滞回线与试验结果相关系数均在0.98以上, 明显高于J-A模型的相关系数, 能够更准确地预测弹性阶段和塑性阶段不同应力条件下的磁滞回线.3.3.卸载条件下残余塑性变形对磁滞回线的影响 -->3.3.卸载条件下残余塑性变形对磁滞回线的影响 在上述试验基础上, Makar和Tanner [14 ] 进一步分析了在塑性载荷卸载后碳钢棒材试件存在的残余塑性变形对磁滞回线的影响, 同样选择含碳量为0.003%和0.15%两种试件的分别加载至160 MPa和182 MPa再卸载后测试得到的磁滞回线进行验证, 结果如图3 所示.图 3 不同残余塑性变形条件下修正模型和J-A模型磁滞回线计算结果的对比 (a)含碳量0.003%时修正模型计算结果; (b)含碳量0.003%时J-A模型计算结果; (c)含碳量0.15%时修正模型计算结果; (d)含碳量0.15%时J-A模型计算结果Figure3. Hysteresis loops predicated by modified model and J-A model under different residual plastic deformation: (a) Our modified model for 0.003 wt% C sample; (b) J-A model for 0.003 wt% C sample; (c) our modified model for 0.15 wt% C sample; (d) J-A model for 0.15 wt% C sample图3 试验结果可知: 当不存在残余塑性变形时, 即$\sigma = 0$ MPa, 不同含碳量试件的磁滞回线均为标准的“S”型; 当存在残余塑性变形时, 为保证材料内部晶粒间的总体应力平衡, 试件内部将产生残余压应力, 从而使得磁滞回线的形状显著改变: 磁滞回线发生顺时针旋转, 磁滞回线面积增大, 饱和磁化强度明显降低, 低磁场条件下磁滞回线的斜率显著减小, 说明残余塑性变形增加了磁化难度, 使得试件更难磁化. 对比理论计算结果和试验数据可知: 与J-A模型相比, 修正模型的计算结果与试验结果更为吻合, 能够更好地反映残余塑性变形对材料磁滞回线的影响. 计算不同模型预测的磁滞回线与试验曲线的相关系数, 结果如表3 所列.模型类型 试件含碳量0.003 wt% 试件含碳量0.153 wt% 0 MPa 160 MPa 0 MPa 182 MPa 修正模型${R^2}$ 0.9845 0.9943 0.9840 0.9858 J-A模型${R^2}$ 0.9133 0.9826 0.9485 0.9765
表3 卸载条件下不同模型计算得到的磁滞回线与试验曲线相关系数${R^2}$ 比较Table3. Correlation coefficients ${R^2}$ of hysteresis loops predicated by different models under different residual plastic deformation.表3 数据表明: 卸载后, 修正模型计算得到的磁滞回线与试验测试得到的磁滞回线都吻合得非常好, 相关系数均在0.98以上, 明显高于J-A模型计算得到的相关系数.4.应力、塑性变形对磁滞回线的影响 由第3节的分析可知, 在弹性变形和塑性变形阶段, 磁滞曲线形状将发生显著改变.为更好地掌握弹性拉、压应力和塑性拉、压应变对材料磁化过程的不同影响, 本节进一步进行具体讨论.4.1.弹性应力对磁滞回线的影响 4.1.弹性应力对磁滞回线的影响 在弹性应阶段, 拉伸应力取$\sigma = $ 0, 50, 100, 150和200 MPa, 压应力取$\sigma = $ –50, –100, –150和–200 MPa, 不同应力条件下磁滞回线、矫顽力${H_{\rm{c}}}$ 和剩余磁感应强度${B_{\rm{r}}}$ 随外磁场的变化规律如图4 所示.图 4 弹性应力对磁滞回线、矫顽力及剩余磁感应强度的影响 (a)弹性拉应力对磁滞回线的影响; (b)弹性压应力对磁滞回线的影响; (c)弹性拉、压应力对矫顽力的影响; (d)弹性拉、压应力对剩余磁感应强度的影响Figure4. Effects of elastic stress on hysteresis loops, coercivity and remanence: (a) Effect of elastic tensile stress on hysteresis loop; (b) effect of elastic compressive stress on hysteresis loop; (c) effect of elastic tensile and compressive stress on coercivity; (d) effect of elastic tensile and compressive stress on remanence图4(a) 和图4(b) 可知: 在弹性阶段, 随着拉、压应力的增大, 初始磁化曲线斜率降低, 磁滞回线发生顺时针旋转, 饱和磁化强度将发生极小幅度的衰减, 磁滞回线所包围的面积增大, 说明应力增大了材料磁化的难度; 相比于拉应力, 压应力条件下的上述变化更为明显, 说明压应力对材料磁化的阻碍作用更强. 由图4(c) 和图4(d) 可知: ${H_{\rm{c}}}$ 随着拉应力的增大呈非线性增大, 而随着压应力的增大呈线性增大, 相同幅值条件下拉应力对应的${H_{\rm{c}}}$ 远远小于压应力; ${B_{\rm{r}}}$ 随拉应力的增大先小幅增大后迅速减小, 而随压应力的增大则是呈非线性减小趋势. 需要指出的是, ${H_{\rm{c}}}$ 和${B_{\rm{r}}}$ 随弹性拉应力的上述变化规律与文献[13 ]中图5、图6中试验得到的变化规律是一致的.4.2.塑性应变对磁滞回线的影响 -->4.2.塑性应变对磁滞回线的影响 当存在塑性变形时, 拉伸塑性变形分别取${\varepsilon _{\rm{r}}} = 0$ , $0.001$ , $0.002$ , $0.003$ 和$0.004$ , 压缩塑性变形分别取${\varepsilon _{\rm{r}}} = - 0.001$ , $ - 0.002$ , $ - 0.003$ 和$ - 0.004$ , 不同塑性变形条件下, 磁滞回线、矫顽力${H_{\rm{c}}}$ 和剩余磁感应强度${B_{\rm{r}}}$ 随外磁场的变化如图5 所示.图 5 塑性应变对磁滞回线、矫顽力及剩余磁化强度的影响 (a)拉伸塑性应变对磁滞回线的影响; (b)压缩塑性变形对磁滞回线的影响; (c)塑性变形对矫顽力的影响; (d)塑性变形对剩余磁感应强度的影响Figure5. Effects of plastic deformation on hysteresis loops, coercivity and remanence: (a) Effect of plastic tensile deformation on hysteresis loop; (b) effect of plastic compressive deformation on hysteresis loop; (c) effect of plastic tensile and compressive deformation on coercivity; (d) effect of plastic tensile and compressive deformation on remanence图5(a) 和图5(b) 可知: 当发生塑性变形时, 材料内部的位错、晶格滑移增大, 钉扎点数量急剧增多, 增大了材料磁化的阻力, 导致初始磁化曲线的斜率大幅降低, 磁滞回线形状将发生显著改变且沿顺时针旋转; 随着塑性变形的增大, 磁滞回线面积增大, 饱和磁化强度显著降低; 相比于拉伸塑性变形, 压缩塑性变形条件下的上述变化更为明显, 说明压缩塑性变形对材料磁化的阻碍作用更强; 此外, 较小的塑性变形都将极大地改变磁化曲线形状, 这也与文献[31 ]得到的结论相符. 由图5(c) 和图5(d) 可知: ${H_{\rm{c}}}$ 随着塑性变形的增大呈非线性而增大, 而${B_{\rm{r}}}$ 随着塑性变形的增大呈非线性减小, 且压缩塑性变形条件下${H_{\rm{c}}}$ 和${B_{\rm{r}}}$ 的变化幅度明显大于拉伸塑性变形. 需要特别指出的是: 参考文献[28 ]中改进的J-A模型计算分析结果显示${H_{\rm{c}}}$ 和${B_{\rm{r}}}$ 均是随塑性变形的增大而增大; 而对比Makar等[13 ,14 ] 的试验结果可以看出: 在塑性变形条件下, 矫顽力随塑性变形的增大呈线性增大趋势, 而剩余磁化强度随塑性的增大呈非线性减小的趋势. 因此, 文献[28 ]改进的J-A模型计算得到的剩余磁化强度随塑性变形的变化规律与Makar等的试验结果相比存在偏差, 而本文修正模型所反映的${H_{\rm{c}}}$ 和${B_{\rm{r}}}$ 随塑性变形的变化趋势更符合试验结果.5.结 论 本文针对J-A模型和Z-L的不足, 在结合两种模型各自优势的基础上, 建立了能够更好反映弹-塑性应力/应变对铁磁材料磁化曲线影响的修正磁化模型, 通过与试验结果及原有模型计算结果进行对比, 验证了本文修正磁化模型的有效性、准确性; 在此基础上, 进一步分析了弹性拉、压应力及塑性拉、压应变对磁化曲线、矫顽力和剩余磁化强度的影响规律.${H_{\rm{c}}}$ 和${B_{\rm{r}}}$ 的影响更为明显, 说明压应力和压缩塑性变形对材料磁化的阻碍作用更强; 此外, 相对于弹性变形, 塑性变形对磁化的影响更大, 较小的塑性变形都将显著改变磁化曲线形状、${H_{\rm{c}}}$ 和${B_{\rm{r}}}$ , 这为利用${H_{\rm{c}}}$ 和${B_{\rm{r}}}$ 检测塑性变形提供了理论基础. 





















































































































































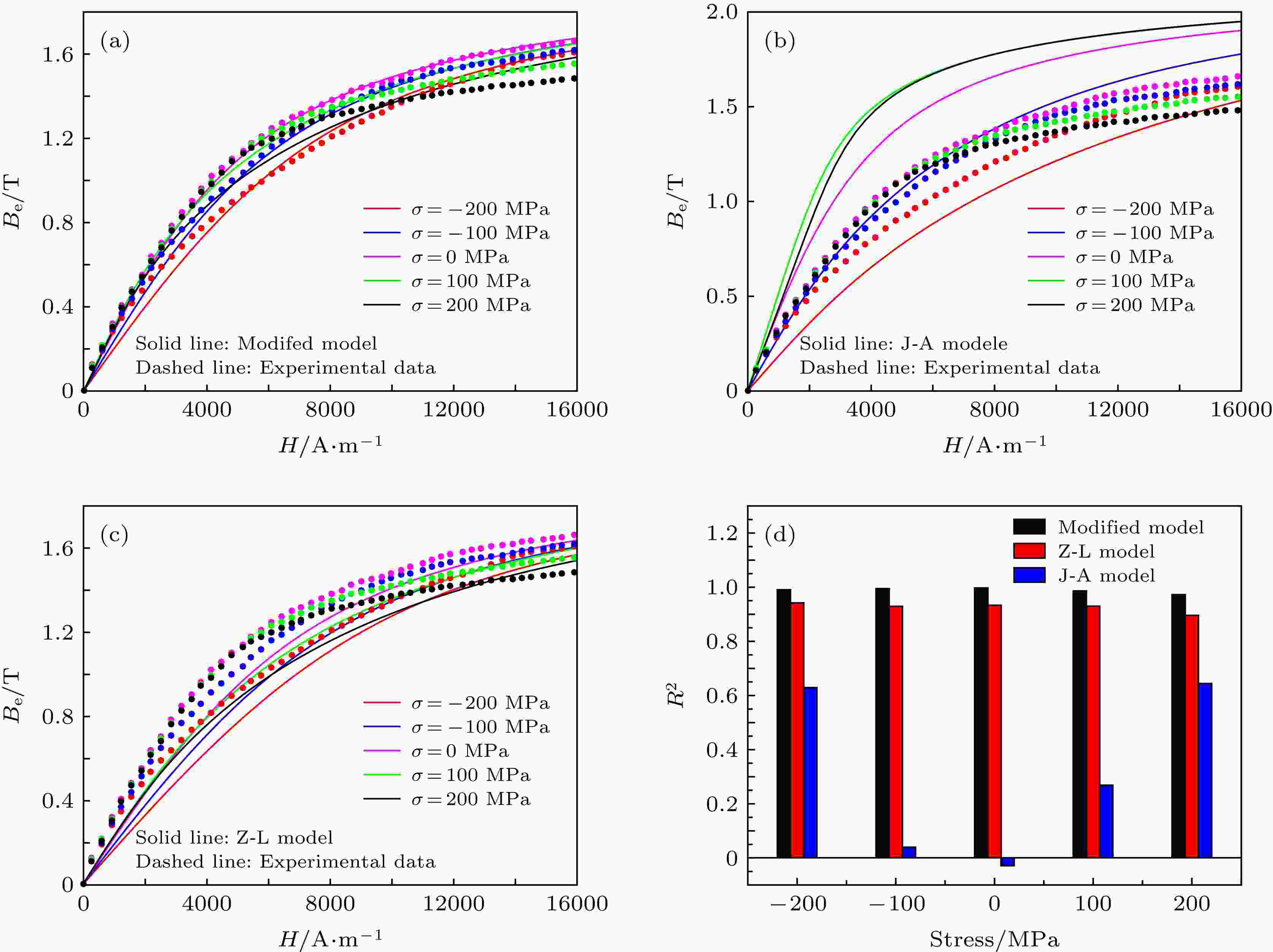 图 1 单次磁化条件下不同模型计算得到的
图 1 单次磁化条件下不同模型计算得到的
































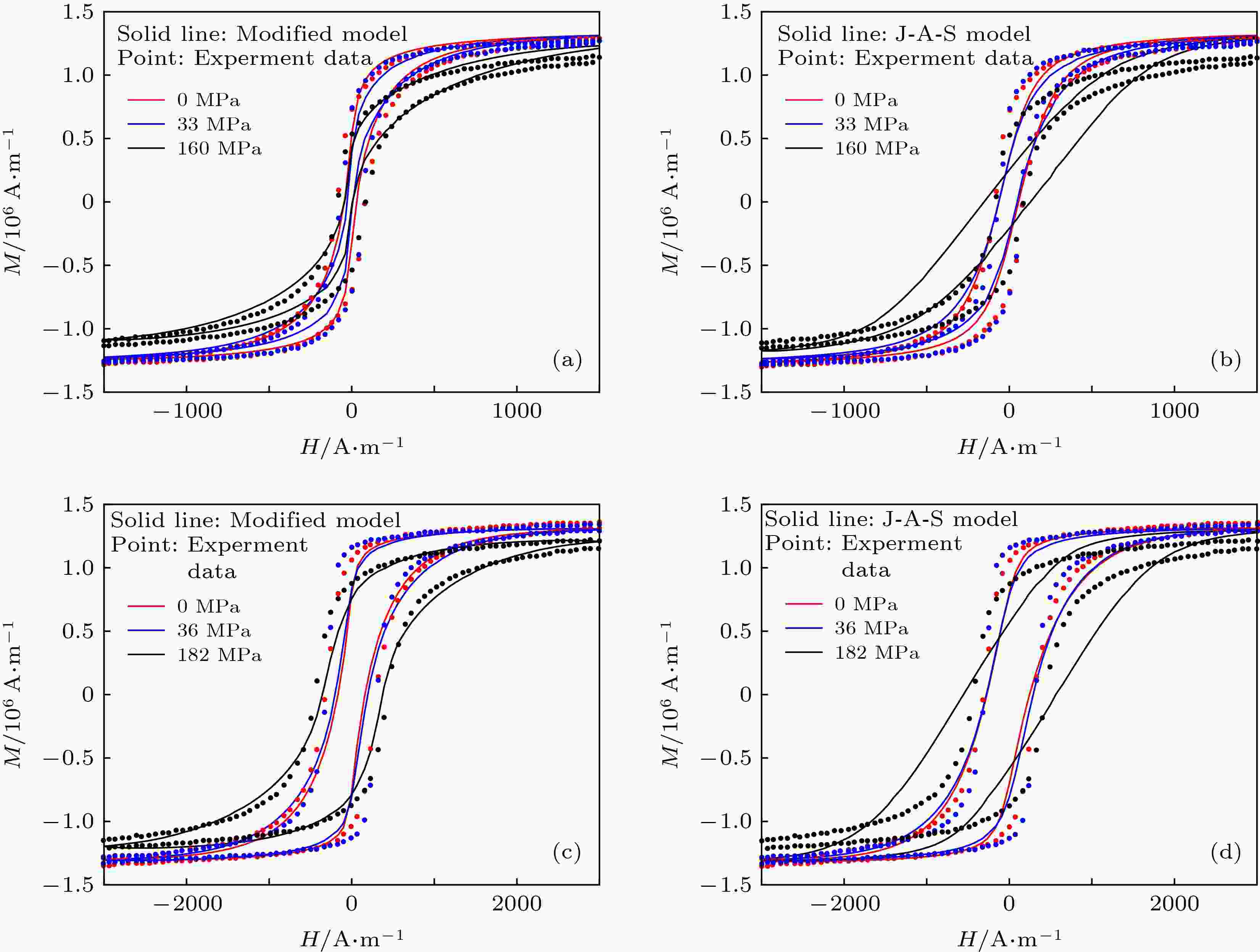 图 2 不同应力条件下修正模型和J-A模型磁滞回线计算结果的对比 (a)含碳量为0.003%时修正模型计算结果; (b)含碳量为0.003%时J-A模型计算结果; (c)含碳量为0.15%时修正模型计算结果; (d)含碳量为0.15%时J-A模型计算结果
图 2 不同应力条件下修正模型和J-A模型磁滞回线计算结果的对比 (a)含碳量为0.003%时修正模型计算结果; (b)含碳量为0.003%时J-A模型计算结果; (c)含碳量为0.15%时修正模型计算结果; (d)含碳量为0.15%时J-A模型计算结果


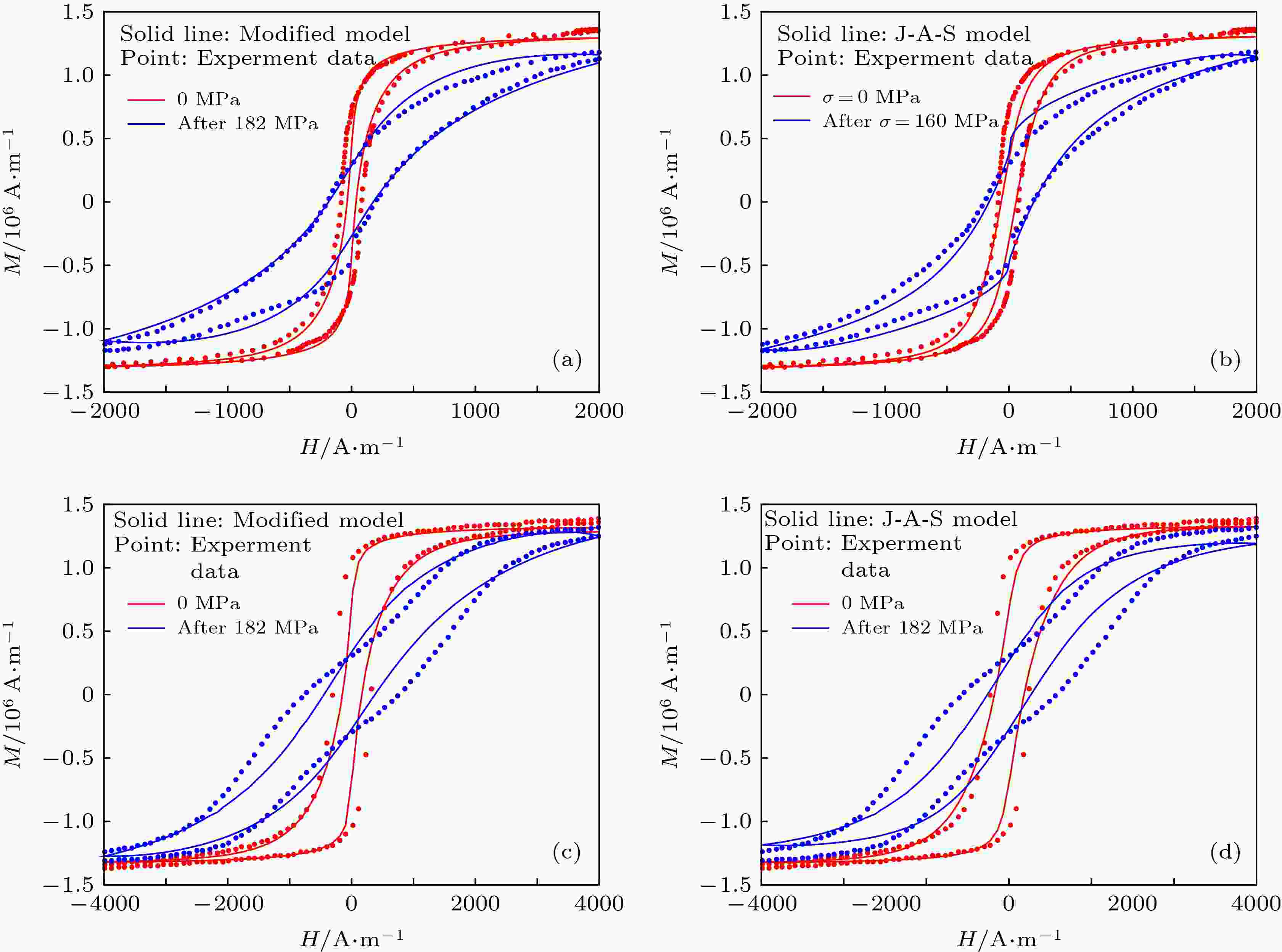 图 3 不同残余塑性变形条件下修正模型和J-A模型磁滞回线计算结果的对比 (a)含碳量0.003%时修正模型计算结果; (b)含碳量0.003%时J-A模型计算结果; (c)含碳量0.15%时修正模型计算结果; (d)含碳量0.15%时J-A模型计算结果
图 3 不同残余塑性变形条件下修正模型和J-A模型磁滞回线计算结果的对比 (a)含碳量0.003%时修正模型计算结果; (b)含碳量0.003%时J-A模型计算结果; (c)含碳量0.15%时修正模型计算结果; (d)含碳量0.15%时J-A模型计算结果








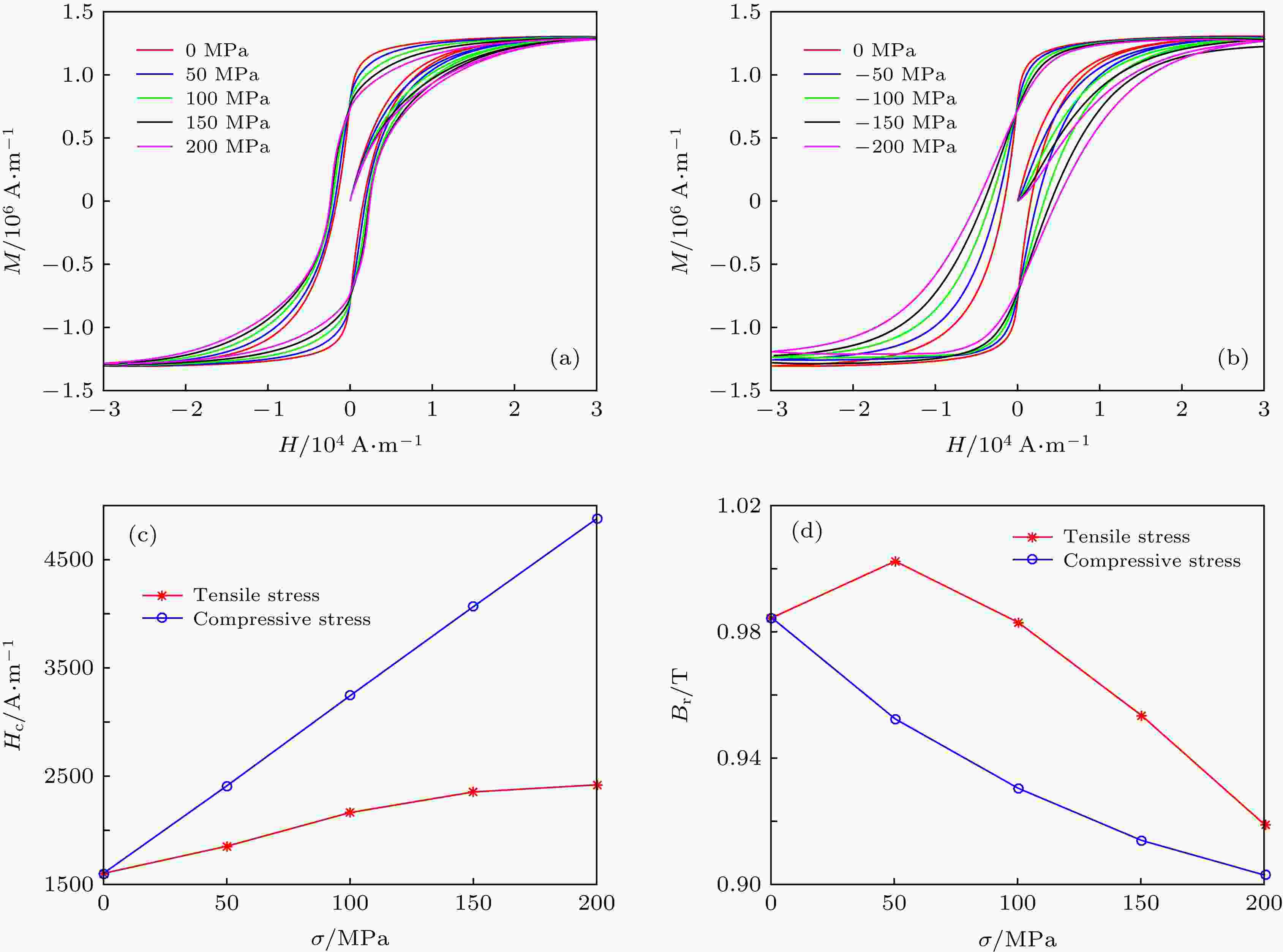 图 4 弹性应力对磁滞回线、矫顽力及剩余磁感应强度的影响 (a)弹性拉应力对磁滞回线的影响; (b)弹性压应力对磁滞回线的影响; (c)弹性拉、压应力对矫顽力的影响; (d)弹性拉、压应力对剩余磁感应强度的影响
图 4 弹性应力对磁滞回线、矫顽力及剩余磁感应强度的影响 (a)弹性拉应力对磁滞回线的影响; (b)弹性压应力对磁滞回线的影响; (c)弹性拉、压应力对矫顽力的影响; (d)弹性拉、压应力对剩余磁感应强度的影响























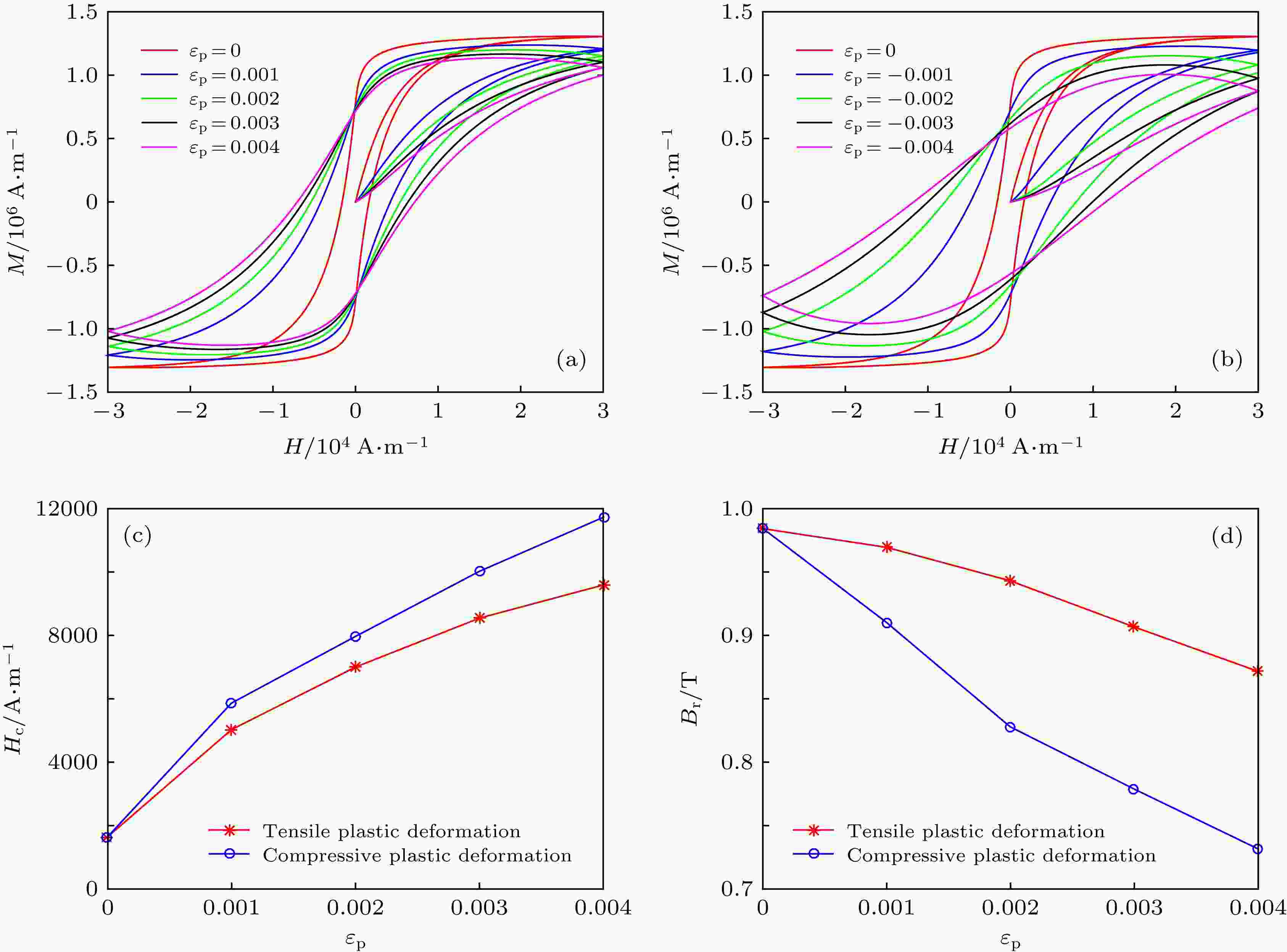 图 5 塑性应变对磁滞回线、矫顽力及剩余磁化强度的影响 (a)拉伸塑性应变对磁滞回线的影响; (b)压缩塑性变形对磁滞回线的影响; (c)塑性变形对矫顽力的影响; (d)塑性变形对剩余磁感应强度的影响
图 5 塑性应变对磁滞回线、矫顽力及剩余磁化强度的影响 (a)拉伸塑性应变对磁滞回线的影响; (b)压缩塑性变形对磁滞回线的影响; (c)塑性变形对矫顽力的影响; (d)塑性变形对剩余磁感应强度的影响

















































