摘要: 针对特征基函数法在分析电大目标电磁散射特性时存在缩减矩阵方程迭代求解收敛慢的问题, 提出一种新型缩减矩阵构造方法提高特征基函数法的迭代求解效率. 首先, 应用奇异值分解技术压缩激励源, 求解出新激励源下各子域的特征基函数; 其次, 将新激励源和特征基函数作为构造缩减矩阵的检验函数和基函数, 新方法构造的缩减矩阵的对角子矩阵均为单位矩阵, 缩减矩阵条件数得到了优化. 与传统方法相比, 新方法构造的缩减矩阵方程迭代求解效率得到了显著提高; 另外, 由于矩阵方程求解次数减少, 特征基函数的构造效率也得到了提高, 数值结果证明了新方法的精确性和有效性.
关键词: 特征基函数法 /
缩减矩阵 /
奇异值分解 /
特征基函数 English Abstract New reduced matrix construction accelerated iterative solution of characteristic basis function method Wang Zhong-Gen 1 ,Mu Jun-Wen 1 ,Lin Han 1 ,Nie Wen-Yan 2 1.College of Electrical and Information Engineering, Anhui University of Science and Technology, Huainan 232001, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 61401003), the Natural Science Foundation of Anhui Province, China (Grant Nos. 1808085MF166, 1808085QF197), the Postdoctoral Science Foundation of Anhui Province, China (Grant No. 2017B214), and the Outstanding Young Talents of Anhui Province, China (Grant No. gxgwfx2018025).Received Date: 18 April 2019Accepted Date: 06 June 2019Available Online: 01 September 2019Published Online: 05 September 2019Abstract: The characteristic basis function method is known as an effective method to solve the electromagnetic scattering problems, but the convergence of the iterative solution of the reduced matrix equation is slow when the characteristic basis function method is used to analyze the electromagnetic scattering characteristics of the electrically large target. In order to mitigate this problem, a new reduced matrix construction method is proposed to improve the iterative solution efficiency of characteristic basis function method in this paper. Firstly, the singular value decomposition technique is used to compress the incident excitations, and the characteristic basis functions of each sub-domain under the new excitations are solved. Then, the new excitations and the characteristic basis functions are defied as the testing and basis functions to construct the reduced matrix. The diagonal sub-matrices of the reduced matrix constructed by the new testing and basis functions are all identity matrices, thereby improving the condition of reduced matrix. Thus, the total number of iterations to achieve reasonable results is significantly reduced. Numerical simulations are conducted to validate the performance of the proposed method. The results demonstrate that the efficiency of the iterative solution of the reduced matrix equation constructed by the new method is significantly improved. Furthermore, the characteristic basis functions’ generation time required by the proposed method is noticeably less than that by the traditional characteristic basis function method due to the reduced number of matrix equation solutions.Keywords: characteristic basis function method /reduced matrix /singular value decomposition /characteristic basis functions 全文HTML --> --> --> 1.引 言 矩量法[1 ] 是求解频域积分方程的一种有效数值方法, 被广泛应用于目标雷达散射截面计算、天线设计与分析、电磁环境预估、电磁兼容设计等领域. 但矩量法需要对目标精细剖分, 随着目标电尺寸的增大, 计算复杂度以及内存需求都会急剧增大. 为解决这个问题, 一些快速有效的矩量法被提出来, 如快速多极子法(fast multipole method, FMM)[2 ] 、多层快速多极子法(multilevel fast multipole method, MLFMM)[3 ,4 ] 、预修正-快速傅立叶变换法(precorrected fast Fourier transform, P-FFT)[5 ] 、自适应积分法(adaptive integral method, AIM)[6 ] 等, 这些方法可以降低矩阵向量积计算复杂度, 但不能减少未知数的数目. 为降低未知数的数目, 有****提出将宏基函数引入到矩量法中, 如子全域基函数法[7 ] 、复合基函数法[8 ] 、子域多层法[9 ] 、特征模法[10 ,11 ] 以及特征基函数法(characteristic basis function method, CBFM)[12 -14 ] , 其中CBFM因考虑到各子域间的耦合作用而备受关注. 为提高CBFM计算效率, 文献[15 ]提出应用物理光学法生成特征基函数(characteristic basis functions, CBFs), 但精确度不高; 文献[16 ,17 ]分别应用自适应交叉近似-LU分解技术、自适应交叉近似-奇异值分解来高效生成CBFs; 文献[18 ,19 ]提出一种CBFs融合构造方法, 提高了CBFM的计算精度; 文献[20 -23 ]应用自适应交叉近似(adaptive cross approximation, ACA)算法、快速偶极子法加快矩阵向量积运算, 提高缩减矩阵构造效率; 文献[24 -26 ]将CBFM与MLFMM, AIM, P-FFT相结合, 通过迭代法求解缩减矩阵方程, 提高了CBFM分析电大目标电磁散射问题的能力, 但是随着目标电尺寸的增大, CBFs数目不断增加, 缩减矩阵维数会变得越来越大, 矩阵条件数变差, 迭代求解缩减矩阵方程效率降低[27 ] .2.特征基函数法 CBFM首先将目标划分为$M$ 个邻接的子域, 再将每个子域剖分成${N_i}$ 个单元(i = 1, 2, ..., M ). 为获得一组包含多角度电流信息的CBFs, CBFM采用不同入射方向和极化的激励照射每个子域, 假设总的激励数为${N_{{\rm{pws}}}} = 2{N_\theta }{N_\phi }$ , ${N_\theta }$ , ${N_\phi }$ 分别表示在$\theta $ , $\phi $ 方向上的激励数目, 于是子域$i$ 上的主要特征基函数(primary characteristic basis functions, PCBFs)即可通过下式求得:${{E}}_i^{}$ 表示扩展子域$i$ 的激励矩阵, 维数为$N_i^{{\rm{be}}} \times {N_{{\rm{pws}}}}$ ; ${{Z}}_{ii}^{}$ 表示扩展子域$i$ 的自阻抗矩阵, 维数为$N_i^{{\rm{be}}} \times N_i^{{\rm{be}}}$ ; ${{J}}_i^{\rm{P}}$ 为扩展子域$i$ 的电流系数矩阵, 维数为$N_i^{{\rm{be}}} \times {N_{{\rm{pws}}}}$ , $N_i^{{\rm{be}}}$ 为扩展子域$i$ 的未知数数目. 通过直接求解(1 )式, 得到扩展子域$i$ 的${{J}}_i^{\rm{P}}$ . 由于采用多角度激励源得到的${{J}}_i^{\rm{P}}$ 必然含有冗余信息, 故通过奇异值分解(singular value decomposition, SVD)压缩${{J}}_i^{\rm{P}}$ 矩阵去除冗余信息, 即${{{U}}_i}$ 和${{{V}}_i}$ 均为酉矩阵, 维数分别为$N_i^{{\rm{be}}} \times N_i^{{\rm{be}}}$ 和${N_{{\rm{pws}}}} \times {N_{{\rm{pws}}}}$ ; ${{{W}}_i}$ 为对角阵, 维数为$N_i^{{\rm{be}}} \times {N_{{\rm{pws}}}}$ . 通过设置合适的门限$\tau $ , 保留${{{U}}_i}$ 中大于门限的前${K_{\rm{i}}}$ 个列向量并去除扩展部分作为子域$i$ 的最终CBFs. 假设子域$i$ 经过SVD后得到${K_i}$ 个CBFs, 则子域$i$ 的表面电流可由这${K_i}$ 个CBFs线性组合表示:$\alpha _i^k$ 为待求的CBFs系数, ${ J}_i^k$ 为子域$i$ 上的第k 个CBFs. 为求解出$\alpha _i^k$ , 应用伽略金法得到一个关于$a_i^k$ 降阶的缩减矩阵方程:${{{Z}}^{\rm{R}}}$ 表示所有子域CBFs之间的相互作用, 维数为$\sum\limits_{i = 1}^M {{K_i}} \times \sum\limits_{i = 1}^M {{K_i}} $ ; ${{{E}}^{\rm{R}}}$ 是激励向量; ${{\alpha }}$ 为待求CBFs系数. 缩减矩阵方程构造原理与矩量法构造阻抗矩阵方程相似, 子域$i$ 上的第$m$ 个CBFs与子域$j$ 上第$n$ 个CBFs之间的相互作用表示为${{{F}}_{i,m}}$ , ${{{F}}_{j,n}}$ 分别表示子域$i$ 和$j$ 上的第$m$ , n 个CBFs; ${{{f}}_{i,p}}\left( {{r}} \right)$ , ${{{f}}_{j,q}}\left( {{r}} \right)$ 分别为子域$i$ 和$j$ 上的第$p$ , $q$ 个Rao-Wilton-Glisson (RWG)基函数. ${{{Z}}_{ij}}\left( {p,q} \right) = {Z_{pq}} = \left\langle {{{{f}}_{i,p}}{\rm{(}}{{r}}{\rm{),}}L\left( {{{{f}}_{j,q}}{\rm{(}}{{r}}{\rm{)}}} \right)} \right\rangle $ , ${{{Z}}_{ij}}$ 表示子域$i$ 和$j$ 上所有RWG基函数之间的相互作用, ${Z_{pq}}$ 是第$p$ 个RWG基函数和第$q$ 个RWG基函数之间的相互作用. ${{{J}}_i}{\rm{(}}p,m{\rm{)}}$ 为联系子域$i$ 中第$m$ 个CBFs和子域$i$ 中第$p$ 个RWG的线性标出系数, 这些系数构造矩阵${{{J}}_i}$ 中的每一列对应一个 CBFs; ${{{J}}_j}{\rm{(}}q,n{\rm{)}}$ 为联系子域$j$ 中第$n$ 个CBFs和子域$j$ 中第$q$ 个RWG的线性标出系数, ${N_i}$ 和${N_j}$ 分别表示子域$i$ 和$j$ 所包含的RWG基函数的数目. 因此子域$i$ 和$j$ 所有CBFs之间的相互作用可以表示为${{Z}}_{ij}^{\rm{R}}$ 的维数为${K_i} \times {K_j}$ , ${K_i}$ 、${K_j}$ 分别为子域$i$ 和$j$ 的CBFs数目; ${{Z}}_{ij}^{\rm{R}}$ 为${{{Z}}^{\rm{R}}}$ 的子矩阵; ${{J}}_i^{\rm{H}}$ 为${{{J}}_i}$ 的共轭转置矩阵. 同理, 子域$i$ 所有CBFs对应的激励向量${{E}}_i^{\rm{R}}$ 可表示为6 )式和(7 )式可以看出, 运用伽略金方法构造缩减矩阵时, 使用${{{J}}_i}$ 的共轭转置同乘方程两边, 检验函数和基函数均采用CBFs(${{{J}}_i}$ ). 由(6 )式和(7 )式可得整个缩减矩阵方程的表达式为8 )式即可得到系数矩阵${{\alpha }}$ , 通常求解(8 )式可以选择直接法求解, 但在分析电大复杂目标时, 缩减矩阵维数增大, 缩减矩阵方程需要通过迭代法求解.3.新型缩减矩阵构造 为提高缩减矩阵方程迭代求解效率, 本文提出一种新型缩减矩阵构造方法, 首先应用SVD对激励矩阵进行压缩:$\tau $ 去除${{{U}}_i}$ 中具有线性相关性的分量并将其表示为${{E}}_i^{{\rm{new}}}$ , 并将${{E}}_i^{{\rm{new}}}$ 定义为激励基函数. 假设每个子域经过SVD后包含${L_i}$ 个激励矢量, 将新的激励源${{E}}_i^{{\rm{new}}}$ 代入到(1 )式, 求解出每个子域的CBFs:${L_i} \ll {N_{{\rm{pws}}}}$ , 可以显著减少方程求解次数. 通过求解(10 )式, 每个子域可得到${L_i}$ 个CBFs(${{J}}_i^{{\rm{new}}}$ ). 将${{E}}_i^{{\rm{new}}}$ 和${{J}}_i^{{\rm{new}}}$ 分别作为构建缩减矩阵的检验函数和基函数, 则缩减矩阵子矩阵${{Z}}_{ij}^{{{\rm{R}}^{{\rm{new}}}}}$ 可以表示为${{E}}_i^{{\rm{new}}}$ 是酉矩阵, 所以${\left( {{{E}}_i^{{\rm{new}}}} \right)^{\rm{H}}}{{E}}_i^{{\rm{new}}} = $ I I 11 )式可以看出, 当$i = j$ 时, ${{Z}}{_{ii}^{{\rm{R}}^{{\rm{new}}}}} = {{I}}$ , (8 )式可以重新写成${{E}}_i^{{{\rm{R}}^{{\rm{new}}}}} = {\left( {{{E}}_i^{^{{\rm{new}}}}} \right)^{\rm{H}}}{{E}}_i^{^{{\rm{new}}}}$ . 新的缩减矩阵构造方法将缩减矩阵${{{Z}}^{\rm{R}}}$ 的对角子矩阵均简化为单位矩阵, 优化了缩减矩阵条件数, 主对角元素对应的CBFs系数可以精确快速地计算出来, 这将加快缩减矩阵方程迭代求解的收敛速度.4.数值算例 为验证本文方法(novel characteristic basis function method, NCBFM)的有效性和精确性, 分别对导体球、锥球带缝体的双站RCS以及杏仁体的单站RCS进行了计算. 所有算例均在Intel(R) Core(TM) i5-6200U 2.30 GHz, 48 GB RAM 的PC 机上完成, 编译器采用Visual studio 2013, BiCGStab迭代误差为0.001, 为了验证NCBFM计算精度, 定义电流系数均方根误差为$I_i^{{\rm{CBF}}{{\rm{M}}_x}}$ 为应用NCBFM和CBFM计算出的电流系数, $I_i^{{\rm{FEKO}}}$ 为应用商业软件FEKO(采用MLFMM求解)计算得到的电流系数.算例1 计算一个半径为$\lambda $ 导体球的双站RCS, 入射频率为300 MHz, 入射角度$\theta = {0^ \circ },$ $\phi = {0^ \circ }$ . 应用三角单元剖分球表面, 未知数为17278, 目标划为8个子域. NCBFM和CBFM均为每个子域构造800个激励, 图1(a) 给出了2种方法在不同SVD门限下的电流误差以及CBFs数目. 从图1(a) 可以看出, 采用SVD压缩激励源, 电流误差收敛速度更快; 另外, CBFM在分析电大复杂目标时, 激励数目往往根据经验设定, 存在大量冗余计算, 而应用SVD对激励源进行压缩, 只需设置合适的SVD门限, 就可以在保证精度的情况下减少冗余计算. 根据电流误差分析, CBFM和NCBFM的门限$\tau $ 分别取0.005和0.008, 图1(b) 给出了左半球面4个子域SVD后奇异值的分布曲线. 从图1(b) 可以看出, 2种方法在每个子域奇异值数目为80时即可达到门限设置要求, CBFM得到653个CBFs, 缩减矩阵维数为$653 \times 653$ , 矩阵条件数为5282, 采用BiCGStab迭代法求解缩减矩阵方程, 迭代26次即可收敛. NCBFM共得到649个CBFs, 缩减矩阵维数为$649 \times 649$ , 矩阵条件数为1785, 缩减矩阵方程迭代17次即可收敛, 计算效率提高了34.6%. 分别应用CBFM和NCBFM计算了导体球HH极化双站RCS, 计算结果如图1(c) 所示, 从图1(c) 可以看出, NCBFM与CBFM计算结果吻合较好, 计算精度较高.图 1 (a)不同SVD门限下2种方法的计算误差及CBFs数目; (b)左半球面4个子域的奇异值分布曲线; (c)导体球双站RCSFigure1. (a) Calculation error and numbers of CBFs under different SVD thresholds of two methods; (b) singular value distribution curve in four sub-domains of the left hemisphere; (c) bistatic RCS of PEC sphere.算例2 计算一个锥球带缝体的双站RCS, 其几何外形定义见文献[28 ], 入射频率为6 GHz, 入射角度$\theta = {270^ \circ },\;\phi = {0^ \circ }$ . 应用三角单元剖分目标表面, 得到124685个未知数, 目标被划为48个子域. 2种方法在每个子域上均设置1600个激励, CBFM的SVD门限为0.001, 共得到7829个CBFs, 若采用直接法(LU分解)求解缩减矩阵方程需要耗时1239.6 s, 而采用迭代法求解缩减矩阵方程, 迭代86次即可收敛, 耗时104.5 s. NCBFM的SVD门限为0.002, 共得到7775个基函数, 缩减矩阵方程迭代求解45次即可收敛, 耗时57.3 s, 计算效率提高了45.2%. 2种方法计算的HH极化双站RCS如图2 所示, 从图2 可以看出NCBFM计算的结果与CBFM和FEKO吻合较好.图 2 锥球带缝体双站RCSFigure2. Bistatic RCS of cone-sphere with gap.算例3 计算一个252.3744 mm杏仁体的单站RCS, 入射频率为20 GHz, 入射角为$\theta = 90^ \circ , $ $\varphi = {0^ \circ }$ —$180^ \circ $ . 用三角单元对目标表面进行剖分, 共得到153690个未知数, 目标划为52个子域. 2种方法设置的激励数均为1600, CBFM和NCBFM的SVD门限分别为0.001和0.002, 分别得到11410和11362个CBFs, 若采用直接法求解缩减矩阵方程, 需要耗时5387.3 s. 应用CBFM求解缩减矩阵方程, 迭代次数平均为128.2, 单次缩减矩阵方程求解平均耗时237.8 s; NCBFM迭代次数平均为63.5, 迭代次数减少了50.4%, 单次缩减矩阵方程求解平均耗时121.2 s. 图3 给出了2种方法计算的HH极化单站RCS, 从图3 可以看出, NCBFM的计算结果与FEKO吻合较好, 具有较高的计算精度.图 3 杏仁体HH极化单站RCSFigure3. Monostatic RCS in HH polarization of NASA almond.表1 给出了CBFM和NCBFM在阻抗矩阵填充、基函数构造、缩减矩阵构造以及缩减矩阵方程时的求解时间. 从表1 可以看出, NCBFM在基函数构造方面计算效率有了小幅提高, 在缩减矩阵方程迭代求解方面计算效率都得到了显著提高.目标及未知量个数 方法 阻抗矩阵填充/s 基函数构造/s 缩减矩阵构造/s 缩减矩阵方程求解/s 计算时间/s 导体球(17278) CBFM 239.9 1081.4 41.7 0.44 1375.6 NCBFM 239.1 979.4 40.8 0.31 1267.9 锥球带缝体(124685) CBFM 3297.5 27736.4 1535.7 104.5 32740.1 NCBFM 3289.2 26985.1 1506.6 57.3 31889.7 杏仁体(153690) CBFM 4097.8 33173.5 3553.7 237.8 83936.8 NCBFM 4098.4 31832.3 3524.1 121.2 61437.9
表1 计算时间比较Table1. Comparison of computation time.5.结 论 本文给出了一种新型缩减矩阵构造方法, 该方法应用奇异值分解技术压缩激励源, 并在新激励源下求解出各子域的特征基函数, 减少了冗余计算; 在构造缩减矩阵时, 选择激励基函数和特征基函数作为检验函数和基函数, 将缩减矩阵的对角子矩阵优化为单位矩阵, 提高了缩减矩阵方程的迭代求解效率. 数值结果证明了本文方法在保证精度的前提下, 有效地提高了缩减矩阵方程的迭代求解效率. 本文方法提高了缩减矩阵方程的迭代求解效率, 但在迭代过程中存在大量的矩阵向量积运算, 今后会进一步研究将多层快速多极子法、自适应积分法、预修正-快速傅里叶变换法、快速偶极子法等算法引入到该方法中, 加快矩阵向量积运算, 以提高特征基函数法分析电大目标电磁散射特性的效率. 



























































































































































































































































































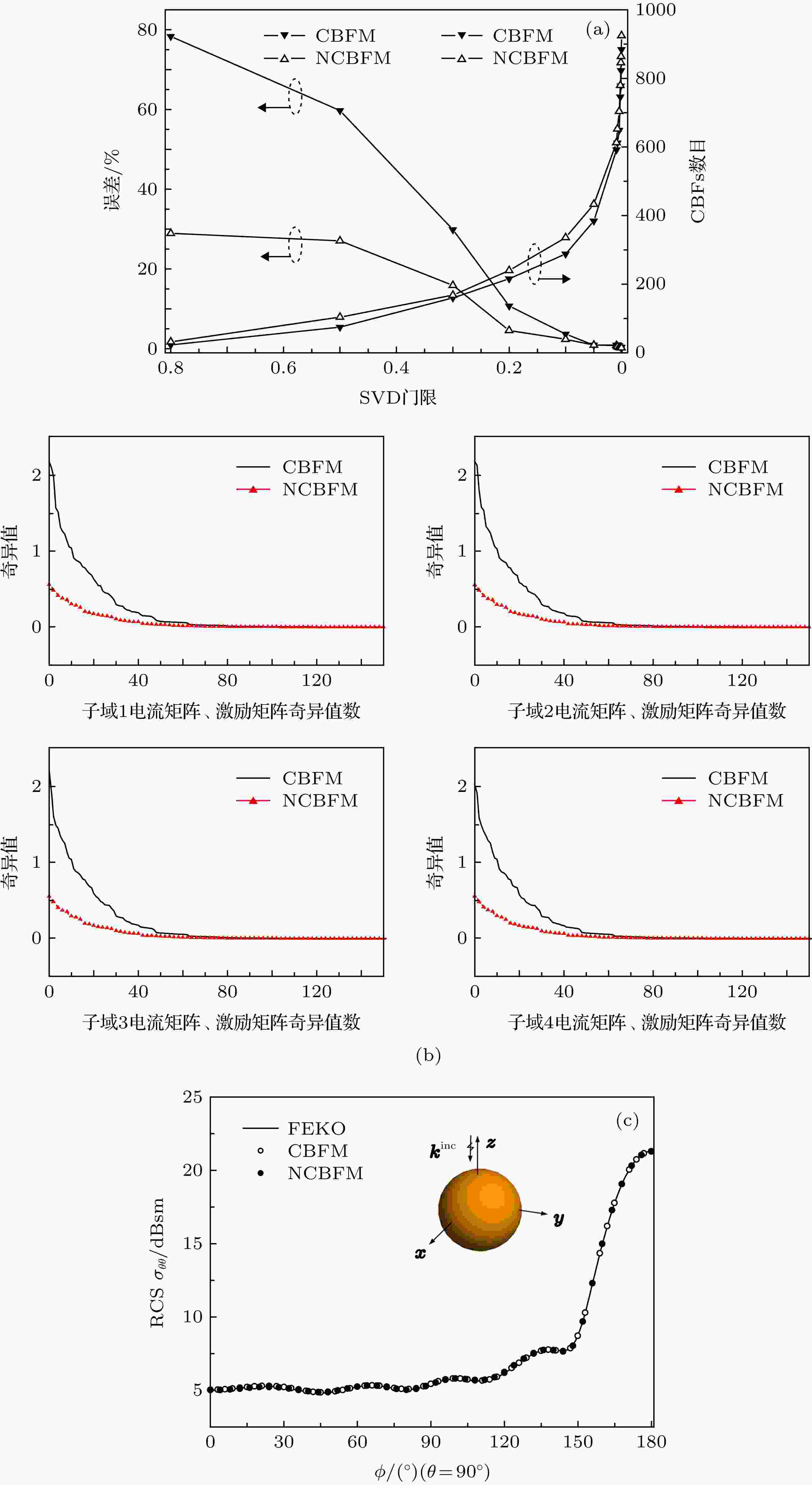 图 1 (a)不同SVD门限下2种方法的计算误差及CBFs数目; (b)左半球面4个子域的奇异值分布曲线; (c)导体球双站RCS
图 1 (a)不同SVD门限下2种方法的计算误差及CBFs数目; (b)左半球面4个子域的奇异值分布曲线; (c)导体球双站RCS
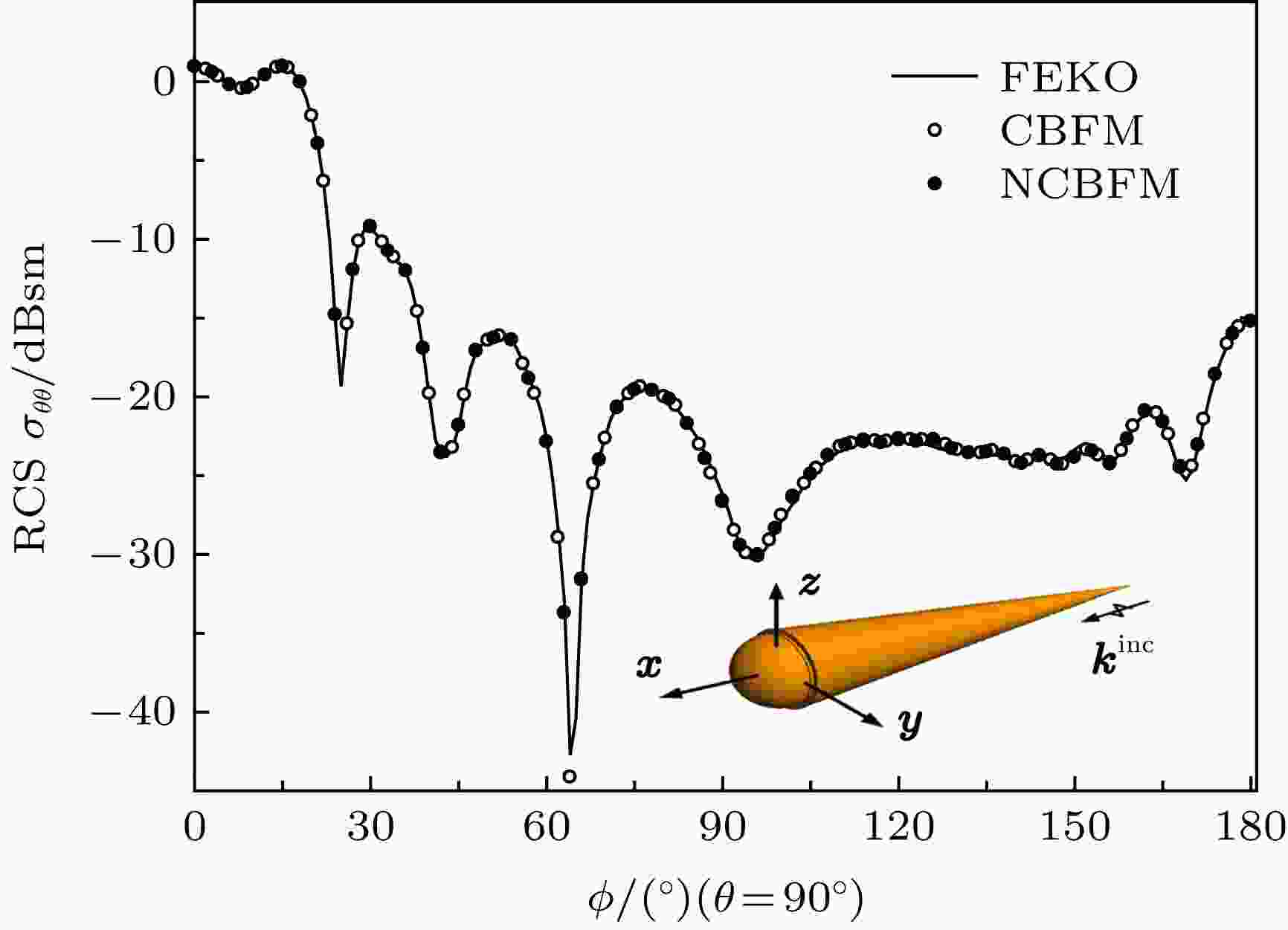 图 2 锥球带缝体双站RCS
图 2 锥球带缝体双站RCS


 图 3 杏仁体HH极化单站RCS
图 3 杏仁体HH极化单站RCS