摘要: 密度矩阵重正化群方法(DMRG)在求解一维强关联格点模型的基态时可以获得较高的精度, 在应用于二维或准二维问题时, 要达到类似的精度通常需要较大的计算量与存储空间. 本文提出一种新的 DMRG异构并行策略, 可以同时发挥计算机中央处理器(CPU)和图形处理器(GPU)的计算性能. 针对最耗时的哈密顿量对角化部分, 实现了数据的分布式存储, 并且给出了CPU和GPU之间的负载平衡策略. 以费米Hubbard模型为例, 测试了异构并行程序在不同DMRG保留状态数下的运行表现, 并给出了相应的性能基准. 应用于4腿梯子时, 观测到了高温超导中常见的电荷密度条纹, 此时保留状态数达到10
4 , 使用的GPU显存小于12 GB.
关键词: 密度矩阵重正化群 /
强关联格点模型 /
异构并行 English Abstract Hybrid parallel optimization of density matrix renormalization group method Chen Fu-Zhou 1 ,Cheng Chen 1,2 ,Luo Hong-Gang 1,2 1.School of Physical Science and Technology, Lanzhou University, Lanzhou 730000, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11674139, 11834005) and the Program for Changjiang Scholars and Innovative Research Team in University, China (Grant No. IRT-16R35).Received Date: 22 April 2019Accepted Date: 16 May 2019Available Online: 01 June 2019Published Online: 20 June 2019Abstract: Density matrix renormalization group (DMRG), as a numerical method of solving the ground state of one-dimensional strongly-correlated lattice model with very high accuracy, requires expensive computational and memory cost when applied to two- and quasi-two-dimensional problems. The number of DMRG kept states is generally very large to achieve a reliable accuracy for these applications, which results in numerous matrix and vector operations and unbearably consuming time in the absence of the proper parallelization. However, due to its sequential nature, the parallelization of DMRG algorithm is usually not straightforward. In this work, we propose a new hybrid parallelization strategy for the DMRG method. It takes advantage of the computing capability of both central processing unit (CPU) and graphics processing unit (GPU) of the computer. In order to achieve as many as DMRG kept states within a limited GPU memory, we adopt the four-block formulation of the Hamiltonian rather than the two-block formulation. The later consumes much more memories, which has been used in another pioneer work on the hybrid parallelization of the DMRG algorithm, and only a small number of DMRG kept states are available. Our parallel strategy focuses on the diagonalization of the Hamiltonian, which is the most time-consuming part of the whole DMRG procedure. A hybrid parallelization strategy of diagonalization method is implemented, in which the required data for diagonalization are distributed on both the host and GPU memory, and the data exchange between them is negligible in our data partitioning scheme. The matrix operations are also shared on both CPU and GPU when the Hamiltonian acts on a wave function, while the distribution of these operations is determined by a load balancing strategy. Taking fermionic Hubbard model for example, we examine the running performance of the hybrid parallelization strategy with different DMRG kept states and provide corresponding performance benchmark. On a 4-leg ladder, we employ the conserved quantities with U (1) symmetry of the model and a good-quantum number based task scheduling to further reduce the GPU memory cost. We manage to obtain a moderate speedup of the hybrid parallelization for a wide range of DMRG kept states. In our example, the ground state energy with high accuracy is obtained by the extrapolation of the results, with different numbers of states kept, and we show charge stripes which are usually experimentally observed in high-temperature superconductors. In this case, we keep 104 DMRG states and the GPU memory cost is less than 12 Gigabytes.Keywords: density matrix renormalization group /strongly correlated lattice model /hybrid parallelization 全文HTML --> --> --> 1.引 言 密度矩阵重正化群方法(DMRG)[1 ,2 ] 是研究相互作用量子系统最重要的多体数值方法之一. 众所周知, 多体量子系统的复杂度随着系统尺寸指数增长, 给数值计算带来了极大的困难. 而DMRG给出了一种非常有效的截断希尔伯特空间的方法, 保留有限个状态并通过扫描即可得到变分收敛的基态或低激发性质. 应用于自旋1的海森伯链时, 该方法仅保留数百状态并通过数次扫描即可得到相对误差$10^{-9}$ 左右的基态能量, 而所需的计算量仅随格点尺寸线性增长[3 ,4 ] . 作为求解一维格点模型基态的成熟方法, DMRG也不断被应用于其他各类问题并取得了一定的成功, 如动量空间中的哈密顿量[5 ] 与量子化学问题[6 -8 ] 、量子系统的时间演化问题[9 -11 ] 、准二维以及二维量子格点模型[12 -14 ] 等. 这些尝试极大扩展了DMRG的应用, 但同时也对该数值算法的优化提出了更高的要求. 以二维相互作用电子系统为例, 该系统包含非常丰富的物理, 例如高温超导条纹相[15 -17 ] 、量子自旋液体[18 ,19 ] 等. 然而, 在面对二维或者准二维格点模型时, DMRG所需的保留状态数大致随格点宽度指数增长, 得到收敛结果所需的扫描次数也大大增加. 此时, DMRG所需的计算量和存储量较大, 使用各种方法优化算法显得十分必要.[20 ,21 ] , 使用动态保留状态数节约计算资源[22 ,23 ] , 使用好的初始预测波函数减少对角化方法迭代次数[24 ] , 使用单格点DMRG方法减少计算量与内存[25 ,26 ] 等. 另一方面, 人们结合DMRG算法的特性, 发挥高性能计算机的并行计算能力进一步缩短计算时间, 包括实空间并行[27 ] 、共享存储的多核行[28 ] 、分布式存储的多节点行[29 ] 以及CPU-GPU异构并行[30 ] 等.[31 ] 、量子蒙特卡罗方法[32 ] 以及张量乘积态方法[33 ] 等)都实现了基于GPU的并行优化. 在CPU-GPU异构并行环境中, 异构并行算法可以同时发挥CPU和GPU的计算性能, 并且可以实现内存和GPU显存的分布式存储, 在一定程度上减小了GPU显存容量对计算规模的限制. 最近, Nemes 等[30 ] 提出了DMRG方法的一种CPU-GPU异构并行实现, 并将其应用到一维格点模型的基态能量计算. 在保留状态较多时, 最耗时的哈密顿量对角化部分在GPU中获得了接近峰值的运算性能. 在对角化过程中, 对占用存储空间较多的Davidson方法实现了内存和GPU显存的分布式存储, 减小了GPU显存的容量限制. 然而与此同时, Davidson方法在计算中内存和GPU显存之间需要通信向量数据, 其性能会受到通信带宽的限制. 另一方面, 该方案中哈密顿量和波函数基于两子块表示, 其子块算符需要的存储量大致相当于目前流行的四子块表示的$d^2$ 倍(d 为单格点希尔伯特空间维数), 在实际应用中存在很大的局限性.2 节回顾了有限DMRG算法, 基于四个子块表示的DMRG实现, 介绍了该工作采用的基准模型, 并得到了在CPU执行时各个部分的计算时间占总时间的比例; 第3 节针对DMRG中最耗时的哈密顿量对角化部分给出了异构并行优化方法; 第4 节以计算4腿Hubbard模型基态为例, 对比了异构并行优化方法与单个CPU中MKL并行的性能; 最后给出本文的总结.2.有限DMRG方法和基准模型 有限尺寸格点模型的DMRG计算分为两部分: 首先执行无限DMRG方法, 这可为后面的计算提供较好的初始波函数; 然后执行有限DMRG扫描, 其中每一步有限DMRG扫描会优化系统块的状态, 直到收敛至基态. 在准二维梯子模型的计算中, 有限DMRG部分需要多次扫描, 且保留很多的状态才能收敛, 几乎占用整个DMRG计算的全部时间, 因此本文主要考虑该部分的并行优化. 有限DMRG计算中向左扫描和向右扫描非常相似, 本文以向右扫描为例介绍有限DMRG方法. 每一步优化的过程中整个格点系统由四个部分构成(图1 ): S , $s1$ , $e1$ 和E , 其中S 和$s1$ 构成系统块, E 和$e1$ 构成环境块, 系统块和环境块构成超块. 基于四个子块, 波函数有如下形式:图 1 超块中的四个子块Figure1. 4 Sub-blocks of super-block$\left|s \right \rangle$ , $\left|e \right\rangle$ , $\left|\sigma_{s1} \right\rangle$ 和$\left|\sigma_{e1} \right\rangle$ 分别为子块S , E , $s1$ 和$e1$ 上的状态. 同样, 基于四个子块, 一般形式的哈密顿量H 可以表示为$O^{S}$ , $O^{E}$ , $O^{s1}$ 和$O^{e1}$ 分别为子块S , E , $s1$ 和$e1$ 上的算符. 以求解系统的基态为例, 给出基于四子块表示的DMRG一步优化过程, 如算法1所示. 重复执行DMRG的一步优化过程, 进行多次实空间扫描, 即可得到收敛的结果. 在算法1中, 对角化超块哈密顿量最为耗时, 通常人们采用稀疏矩阵对角化方法(Lanczos方法、Davidson方法等). 此时, 不需要超块哈密顿量的矩阵表示, 仅需要算符在四个子块中的矩阵表示, 并迭代执行$\left|\phi\right\rangle = H\left| \psi \right\rangle$ , 文献[4 ]中给出了该操作的高效算法, 具体过程如算法2. 在后面的描述中, 我们称算法2中第2, 5和8行对应的循环分别为step1, step2和step3. 可以看到该算法step1和step3中为矩阵乘法, 对应的计算量为$O\left( {D^{3}} \right)$ , 其中D 为DMRG保留状态数. step2中仅包含向量操作, 对应的计算量为$O\left( {D^{2}} \right)$ . 在保留状态较多时, 哈密顿量作用在波函数的计算量主要由step1和step3决定. 而对角化哈密顿量的总时间线性依赖于对角化方法的迭代次数, 本文实现的有限DMRG中通过上一步优化波函数给出一个较好的初始迭代波函数, 可以有效地加快对角化方法的收敛[24 ] .算法1 有限DMRG向右扫描一步$H\left| \psi \right\rangle = E\left|\psi \right\rangle$ , 得到当前表示下哈密顿量的最小本征值E 和相应的本征矢$\left| \psi \right\rangle =\sum\limits_{s, \sigma_{s1}, \sigma_{e1}, e}\psi_{s\sigma_{s1}, \sigma_{e1}e} $ $\cdot\left|s\right\rangle \left|\sigma_{s1}\right\rangle\left|\sigma_{e1}\right\rangle\left|e \right\rangle$ ;${{\rho}}^{S, s1}$ , 其中${{\rho}}^{S, s1}_{s\sigma_{s1}, s^\prime \sigma^\prime_{s1}}=\sum\limits_{\sigma_{e1}, e}\psi_{s\sigma_{s1}, \sigma_{e1}e}\psi^{\dagger}_{\sigma_{e1}e, s^\prime\sigma_{s1}^\prime}$ ;${{\rho}}^{S, s1}$ 较大本征值对应的态;算法2 $\left| \phi \right\rangle =H\left|\psi \right\rangle$ Input: $\left|\psi \right\rangle$ Output: $\left|\phi \right\rangle$ for s in system-block do for $\sigma_{s1}$ , $\sigma_{e1}$ , e and j do ${\text{ }}{\text{ }}\; \Big|\tilde{\psi}^{[ {s, \sigma_{s1}, \sigma_{e1}, e^\prime}]}_j \Big\rangle = O^{E}_j\left|\psi^{\left[ {s, \sigma_{s1}, \sigma_{e1}, e} \right]} \right\rangle$ end for for $\sigma_{s1}, \sigma_{e1}$ , $e^\prime$ and i do ${\text{ }}{\text{ }} \Big|\hat{\psi}^{[ {s, \sigma^\prime_{s1}, \sigma^\prime_{e1}, e^\prime}]}_i \Big\rangle = \Big|\hat{\psi}^{[ {s, \sigma^\prime_{s1}, \sigma^\prime_{e1}, e^\prime} ]}_i \Big\rangle $ ${\text{ }}{\text{ }} {\text{ }} + \sum_{j, k, l}W_{ijkl}{O^{s1}_kO^{e1}_l}\Big|\tilde{\psi}^{[ {s, \sigma_{s1}, \sigma_{e1}, e^\prime}]}_j \Big\rangle$ end for for $\sigma_{s1}^\prime, \sigma_{e1}^\prime$ , $e^\prime$ and i do ${\text{ }}{\text{ }}\left|\phi^{\left[ {s^\prime, \sigma_{s1}^\prime, \sigma_{e1}^\prime, e^\prime} \right]}\right\rangle = \Big|\phi^{[ {s^\prime, \sigma_{s1}^\prime, \sigma_{e1}^\prime, e^\prime} ]}\Big\rangle $ ${\text{ }}{\text{ }}{\text{ }}{\text{ }} +O^{S}_i\Big|\hat{\psi}^{[{s, \sigma_{s1}^\prime, \sigma_{e1}^\prime, e^\prime} ]} \Big\rangle$ end for end for t 为两个格点之间的电子跃迁能, U 为单个格点上的电子在位库仑排斥能, $\hat{c}_{i, \sigma}^{\dagger}\left( {\hat{c}_{i, \sigma}} \right)$ 为格点i 上自旋σ 的费米子产生(湮灭)算符, $\hat{n}_{i, \sigma}$ 为自旋σ 的粒子数算符, 其中$\sigma\in\left\{ {\uparrow, \downarrow} \right\}$ . 在梯子模型中, 格点i 包含$x, y$ 两个方向的分量, 以x 标记梯子长边坐标, y 标记梯子短边坐标. 在后面的测试计算中, 选取$t = 1$ 为能量单位, 沿着长边和短边方向分别使用开边界和周期边界条件, 梯子长度为16. 对于其他参数, 取相互作用$U = 8$ , 总电荷密度0.875, 即$1/8$ 空穴掺杂, 这是在其他数值工作中观测到条纹相的典型参数[13 ,34 ] . 另外本文的实现利用了该模型的总粒子数和总自旋在z 方向投影两个好量子数, 每个子块的希尔伯特空间可以被划分为多个子空间, 每个子空间中的状态对应于相同的量子数. 此时模型(1)中算符的矩阵表示为分块矩阵, 相应地, 超块的希尔伯特空间可以用其四个子块的好量子数划分为多个子空间.[35 ,36 ] 对角化该哈密顿量. Davidson方法是一种使用预条件技术的子空间迭代方法, 算法3给出了该方法每一步迭代的具体操作. 可以看到, 每一步迭代都需要作用哈密顿量到波函数, 并且包含多个向量操作. 其中向量操作的计算量和存储量均线性依赖于Davidson方法子空间中向量的个数和向量的维数. 在性能测试中, 使用7次有限DMRG扫描收敛到基态, Davidson方法子空间中向量个数最大为11.算法3 一步Davidson迭代Input: ${\hat{{H}}}$ 为哈密顿算符的矩阵表示; ${{\psi}}^{\left( {0} \right)},$ $ {{\psi}}^{\left( {1} \right)}, \cdots, {{\psi}}^{\left( {i} \right)}$ 和${{\phi}}^{\left( {0} \right)}, {{\phi}}^{\left( {1} \right)}, \cdots, {{\phi}}^{\left( {i-1} \right)}$ 为之前迭代得到的向量${{\phi}}^{\left( {i} \right)}={\hat{{H}}}{{\psi}}^{\left( {i} \right)}$ $B_{kl}={{{\phi}}^{\left( {k} \right)}}^{\rm T} {{\psi}}^{\left( {l} \right)},\; 0\leqslant k, l \leqslant i$ B λ 和相应的本征矢x ${{v}}=\sum_{k=0}^{i}x_k{{\psi}}^{\left( {k} \right)}$ ${{r}}={\hat{{H}}}{{v}}-\lambda {{v}}$ λ 和v ${\hat{{H}}}$ 的最小本征值和本征矢, 然后退出r u $t_k={{{\psi}}^{\left( {k} \right)}}^{\rm T} {{u}},\; 0\leqslant k \leqslant i$ ${{u}}={{u}}-\sum_{k=0}^{i}t_k{{\psi}}^{\left( {k} \right)}$ ${{\psi}}^{\left( {i+1} \right)}=\displaystyle\frac{{{u}}}{\sqrt{{{u}}^T{{u}}}}$ 图2(a) . 可以看出, 当矩阵尺寸较大(大于400)时, 矩阵乘法的性能较高, 并随着矩阵尺寸增大而增大. 对于DMRG算法, 图2(b) 中的结果表明, 保留状态数越大并行计算性能越高, 并逐渐接近峰值性能. 另外也测试了对角化哈密顿量以及哈密顿量作用于波函数部分占总计算时间的比例, 如图3 所示. 在我们所关心的保留状态数范围内, 对角化哈密顿量的耗时比例超过总计算时间的90%, 其中作用哈密顿量到波函数占总时间比例超过80%. 因此, 我们的工作主要针对该部分进行异构并行优化.图 2 CPU中作用哈密顿量在波函数上的性能 (a)矩阵乘法的浮点性能; (b)作用哈密顿量于波函数的性能, 及矩阵乘法中的最大矩阵尺寸Figure2. Performance of acting the Hamiltonian on the wave function in CPU: (a) The matrix multiplication performance; (b) the performance of acting the Hamiltonian on the wave function, and the maximum matrix size of the matrix multiplications.图 3 对角化哈密顿量和作用哈密顿量到波函数操作占总计算时间的比例Figure3. Time ratio of diagonalization of the Hamiltonian and acting the Hamiltonian on the wave function to the total time cost.3.DMRG的异构并行实现 主要考虑DMRG方法在准二维模型中的应用, 并且针对有限DMRG中计算量较大的哈密顿量对角化部分进行并行优化. 对于准二维问题, DMRG方法达到较高精度通常需要保留较多的状态, 相应地, 对角化哈密顿量时会执行一些大尺寸矩阵操作. 类似于CPU, 矩阵乘法的性能在GPU中随着矩阵尺寸增大而增大; 同时, GPU的浮点运算能力一般远大于单个CPU. 因此, 在异构并行优化中, 我们倾向于尽可能在GPU中执行大尺寸的矩阵操作. 从存储方面考虑, 为了避免GPU显存和内存之间频繁的数据通信, 多次参与GPU计算的数据需要存储在GPU显存中, 主要包括Davidson方法中的向量、算符数据和临时数据(算法2中$\left|\tilde{\psi} \right\rangle$ 和$\left|\hat{\psi} \right\rangle$ ). 但同时, 保留较多的状态也导致计算中需要的存储容量较大; 考虑到当前GPU显存容量较小, 在异构并行方法中需要合理分配各个部分的存储利用.S 中的好量子数分为多个组, 此时各个组中的运算可以独立进行, 仅在求和计算$\left|\phi \right\rangle$ (即算法2中step3)时需要通信. 此时波函数$\left|\psi \right\rangle$ 也按$S$ 中好量子数划分为两个部分, 其中一部分仅在GPU中计算(记为$\left|\psi_{\rm{GPU}} \right\rangle$ ), 另一部分仅在CPU中计算(记为$\left|\psi_{\rm{CPU}} \right\rangle$ ).S 中每个好量子数对应分组的计算量在执行运算前可以比较准确地估计. 通常, GPU的浮点运算能力强于CPU, 适合处理大尺寸矩阵乘法运算, 因此在这一步尽量将大矩阵运算分配至GPU, 将相对较小的矩阵运算分配至CPU执行. 为了实现这一目标, 在具体操作中, 我们将矩阵乘法平均运算量较大的组分配到GPU中执行, 这里平均运算量为组内矩阵乘法总计算量与矩阵乘法个数的比值. 进一步, 可根据GPU中计算量占的比例$P_{\rm GPU}$ 将相互独立的分组计算分配给GPU, 剩余组的计算分配给CPU执行.$P_{\rm GPU}$ 以尽可能实现负载均衡. 在具体操作中, 将每一步迭代优化比例所处的区间记为$\left( {P^{0}, \ P^{1}} \right)$ . 设定初始区间$P^{0} = 0,$ $P^{1} = 1$ , 然后进入Davidson方法迭代过程. 令GPU中计算量比例$P_{\rm GPU} = \left( {P^0+P^1} \right)/2$ , 执行一步Davidison迭代, 可以获得此时作用哈密顿量到波函数的CPU和GPU计算时间, 分别记为$T_{\rm CPU}$ 和$T_{\rm GPU}$ . 以此为依据更新下一步迭代区间, 使得S 分组后各个组的操作依次执行. 这种情况下, 仅需要分配一段存储空间, 使其同时满足任意一个组中的所有操作即可. 在图4 中, 给出了对角化哈密顿量部分运算的存储需求, 并给出了与两子块表示所需存储的对比. 可以明显看出其总体的显存需求远远小于两子块表示. 因此, 相比于参考文献[30 ]中的异构并行, 本文方案可以处理需要更大DMRG保留状态数的问题.图 4 存储临时数据, 子块算符需要的GPU显存Figure4. The GPU memory cost of temporary data and sub-block operators.$\left| {{\phi _{{\rm{GPU}}}}} \right\rangle =$ $ H\left| {{\psi _{{\rm{GPU}}}}} \right\rangle $ 和$\left| {{\phi _{{\rm{CPU}}}}} \right\rangle = H\left| {{\psi _{{\rm{CPU}}}}} \right\rangle $ 时, 首先需要将$\left| {{\psi _{{\rm{GPU}}}}} \right\rangle $ 和$\left| {{\psi _{{\rm{CPU}}}}} \right\rangle $ 分别拷贝到GPU显存和内存中. 由于GPU中各个组依次计算, 为了获得较高的性能, 我们在执行其中一个组对应矩阵乘法操作时, 同时进行另一个组的数据通信. 对于CPU部分, $\left| {{\phi _{{\rm{CPU}}}}} \right\rangle = H\left| {{\psi _{{\rm{CPU}}}}} \right\rangle $ 包含的的矩阵向量操作基于IntelMKL库中的矩阵向量操作子程序并行执行; 而对于GPU部分, $\left| {{\phi _{{\rm{GPU}}}}} \right\rangle = H\left| {{\psi _{{\rm{GPU}}}}} \right\rangle $ 中的矩阵向量操作基于CUBLAS. 在算法2中, 由于每个组的操作中step2的计算依赖于step1的结果, 而step3的计算依赖于step2的结果, 因此本文依次执行step1, step2和step3. 进一步可以看到step1中所有矩阵乘法操作相互独立, 因此被分配到多个CUDA流(stream)中, 这样使得多个矩阵乘法可以在GPU中同时计算, 较充分地利用GPU的并行计算能力. step2和step3中输出结果为多个操作求和得到, 因此相同好量子数标记的输出结果相关的矩阵向量操作被分配到同一个CUDA流执行, 这样使得多个不同好量子数标记的输出结果相关的操作尽可能同时被GPU执行. 可以看到算法3中$\left|\phi \right\rangle$ 进一步将参与Davidson方法中的向量操作, 因此需要被分布式存储在内存和GPU显存中, 为了实现异构并行计算$\left|\phi\right\rangle = \left|\phi_{\rm{CPU}}\right\rangle+\left|\phi_{\rm{GPU}} \right\rangle$ , 需要将$\left|\phi_{\rm{GPU}} \right\rangle$ 中参与CPU计算的数据从GPU显存中拷贝到内存中, 并将$\left|\phi_{\rm{CPU}} \right\rangle$ 中参与GPU计算的数据从内存中拷贝到GPU显存中. 每个由好量子数标记的输出计算完成则可以开始内存和GPU显存之间的数据通信, 因此该部分的实现中数据通信与计算是并行执行的, 有利于实现较高的总性能.4.数值结果 为了说明本文优化方法的有效性, 我们分别保留4096, 6144, 8192, 10240个状态计算4腿Hubbard梯子的基态能量, 并得到了相应的性能基准. 图5(a) 给出了DMRG优化中各个部分相对于单个CPU的加速比(单个CPU计算时间与单个GPU计算时间的比值), 可以看到作用哈密顿量在波函数部分获得加速比最大, 其加速比在保留状态数大于4096后较为接近(不低于3.8). 当保留状态数较大时, 由于GPU显存总量的限制(如图5(b) 所示), 大部分向量操作由CPU完成, 这导致Davidson方法的加速比在保留状态数较大时有所下降. 然而, Davidson方法中向量操作占哈密顿量对角化的时间比例较少, 因此对哈密顿量对角化部分加速比影响较小(不低于3.5). 本文哈密顿量对角化之外的其他操作计算时间占总时间比例约10% (如图3 ), 该部分的GPU并行优化还没有被考虑, 因此总并行加速比低于哈密顿量对角化部分的加速比, 这里保留最大10240个状态获得的加速比为2.85. 图5(c) 中给出了异构并行实现中CPU和GPU分别贡献的浮点性能, 可以看到随着保留状态数的增大, CPU和GPU中执行的大尺寸矩阵增多, 两者贡献的浮点性能随之增大. 虽然本文数值计算保留状态数较大, 但是其中矩阵尺寸为两子块表示时的$1/d$ (Hubbard模型中$d=4$ ), 目前获得的性能仍明显小于GPU可以达到的峰值性能(1200 GFLOPS). 对$16\times4$ 的梯子, 根据不同保留状态数(4096, 6144, 8192, 10240)得到的基态能量外推得到模型(1)在$U=8. 0$ 时的格点平均能量$ E_g=-0. 75114(2) $ , 与文献[34 ]结果一致, 见图6 . 进一步给出基态的电荷密度分布, 如图7 所示, 可以观察到明显的电荷密度条纹, 这是铜氧化物高温超导体中经常被观测到的现象之一[13 ,14 ,37 ,38 ] .图 5 异构并行的性能 (a)加速比; (b) Davidson方法中的向量占用GPU显存; (c)作用哈密顿量到波函数部分的性能Figure5. Performance of hybrid parallel strategy: (a) The speedup; (b) the GPU memory cost of vectors in Davidson; (c) the performance of $H\left|{\psi}\right\rangle$ 图 6 基态能量关于截断误差的函数(直线表示对基态能量的线性外推, 直至截断误差为0)Figure6. Groundstate energy as a function of truncation error. The straight line gives a linear extrapolation of the ground energy until 0 truncation-error.图 7 对于16 × 4 Hubbard模型, U = 8.0时的基态电荷密度分布(可以观察到明显的电荷密度条纹)Figure7. Ground state density profile for the 16 × 4 Hubbard ladder with U = 8.0. Charge density stripes can be clearly observed.5.结 论 本文主要考虑DMRG方法在准二维格点模型中的应用, 针对其中最耗时的哈密顿量对角化部分实现了CPU-GPU异构并行优化, 并且给出了负载平衡方法. 为了减小准二维格点模型计算中GPU显存的限制, 本文的实现中哈密顿量与波函数基于四子块表示, 其对角化时需要的GPU显存占用远小于两子块表示, 使得本文的异构并行方法可以应用于更多模型、更多问题的研究. 将该方法应用到4腿Hubbard梯子模型的求解中, 得到了不同保留状态数时DMRG中各个部分的加速比. 数值结果表明, 本文的异构并行方法适用于保留状态数较大的准二维模型计算, 并且总性能随着保留状态数增大而增大. 目前, 强关联物理问题很大程度上依赖于多体数值计算, 一些复杂问题通常进一步受制于计算方法的计算量与计算时间. 在多体算法本身出现革命性发展之前, 合理利用计算机技术的发展提升算法的效率能为研究强关联系统提供很大的帮助. 我们希望该并行方法可以在更多的复杂格点模型、更多问题中得到应用, 并能够进一步引起强关联领域对于以GPU为代表的新技术的关注和重视. 









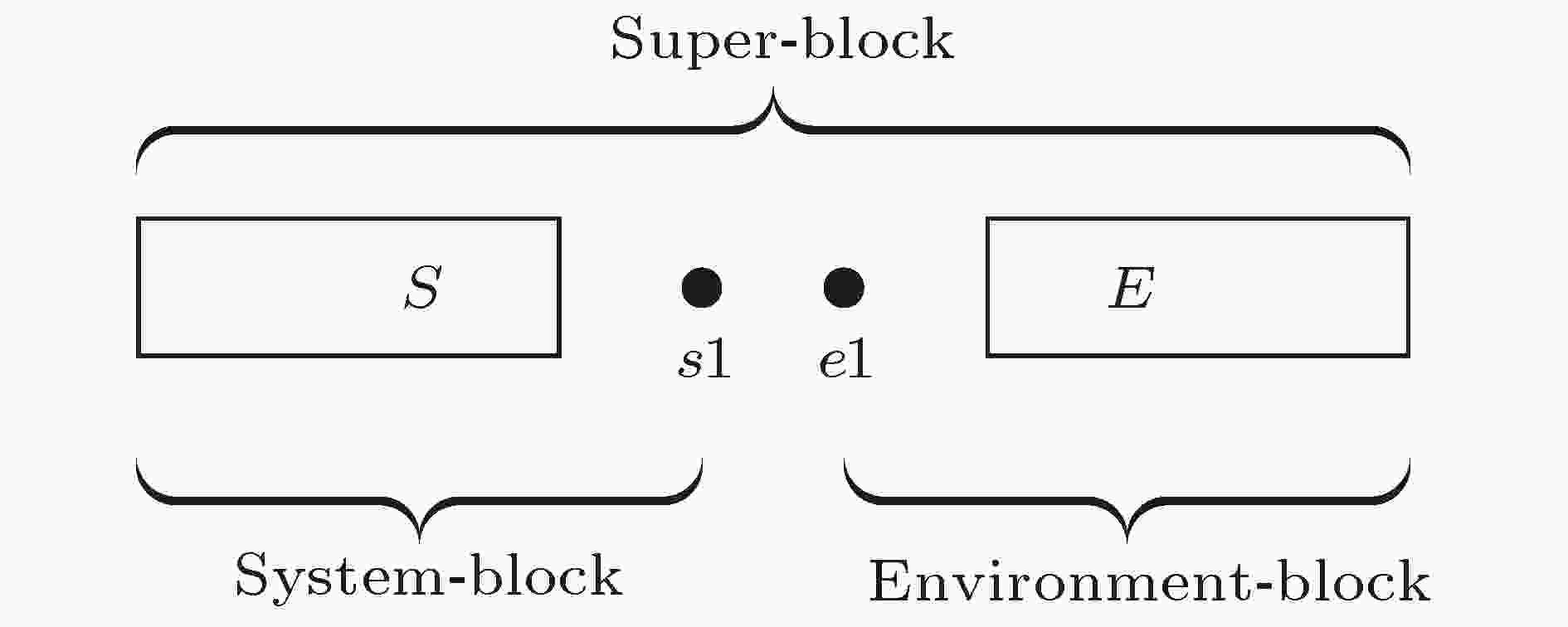 图 1 超块中的四个子块
图 1 超块中的四个子块





















































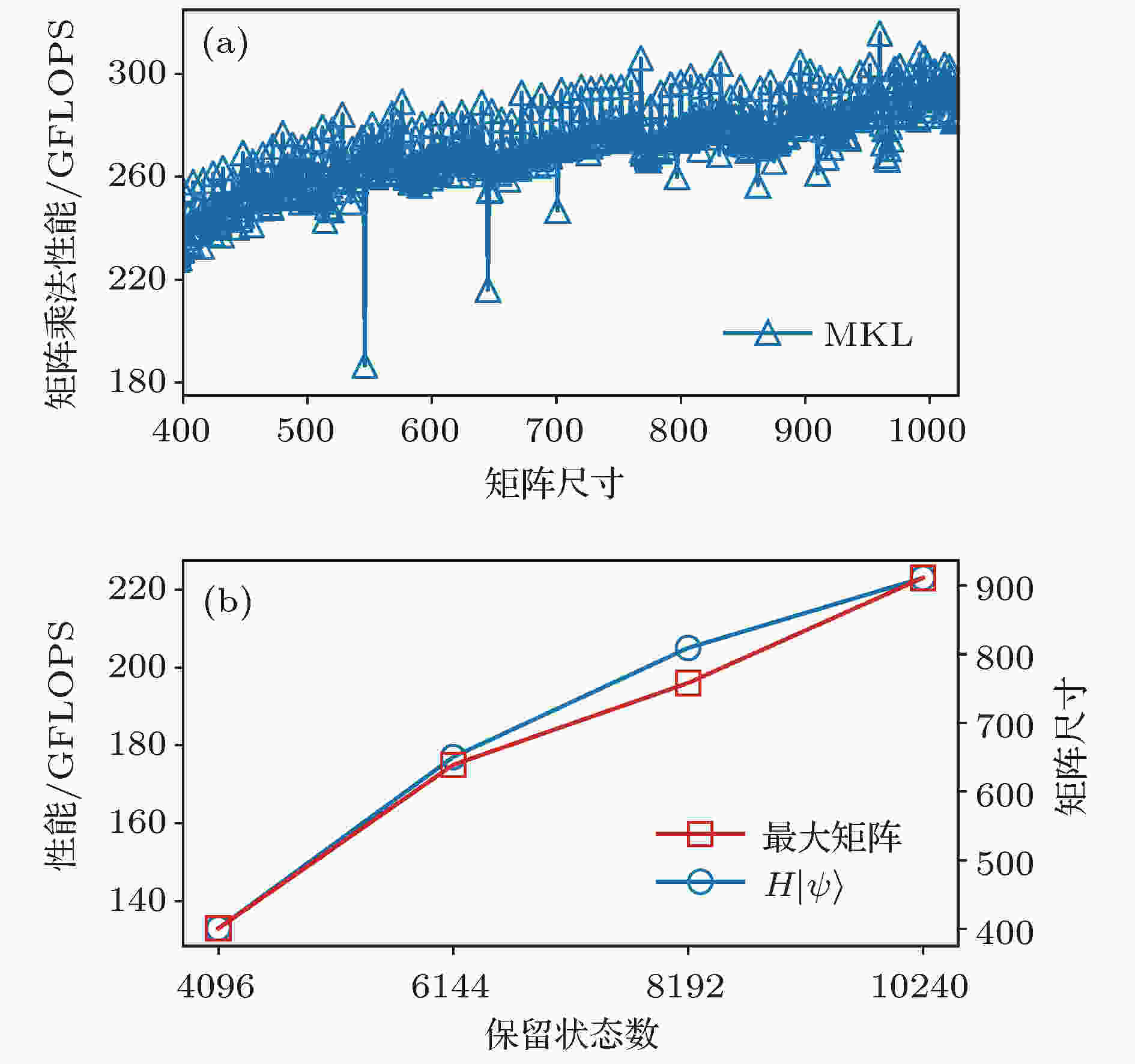 图 2 CPU中作用哈密顿量在波函数上的性能 (a)矩阵乘法的浮点性能; (b)作用哈密顿量于波函数的性能, 及矩阵乘法中的最大矩阵尺寸
图 2 CPU中作用哈密顿量在波函数上的性能 (a)矩阵乘法的浮点性能; (b)作用哈密顿量于波函数的性能, 及矩阵乘法中的最大矩阵尺寸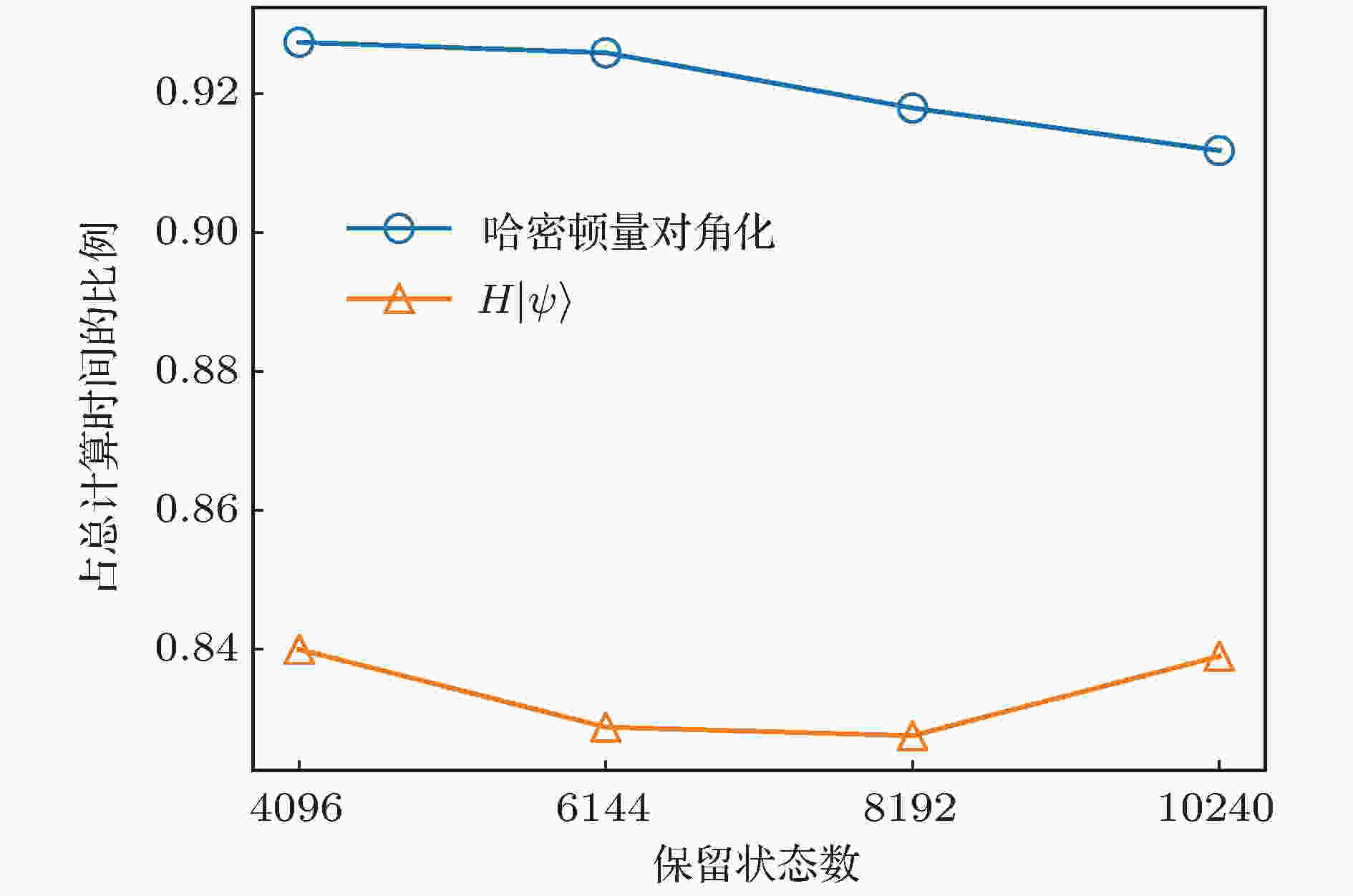 图 3 对角化哈密顿量和作用哈密顿量到波函数操作占总计算时间的比例
图 3 对角化哈密顿量和作用哈密顿量到波函数操作占总计算时间的比例














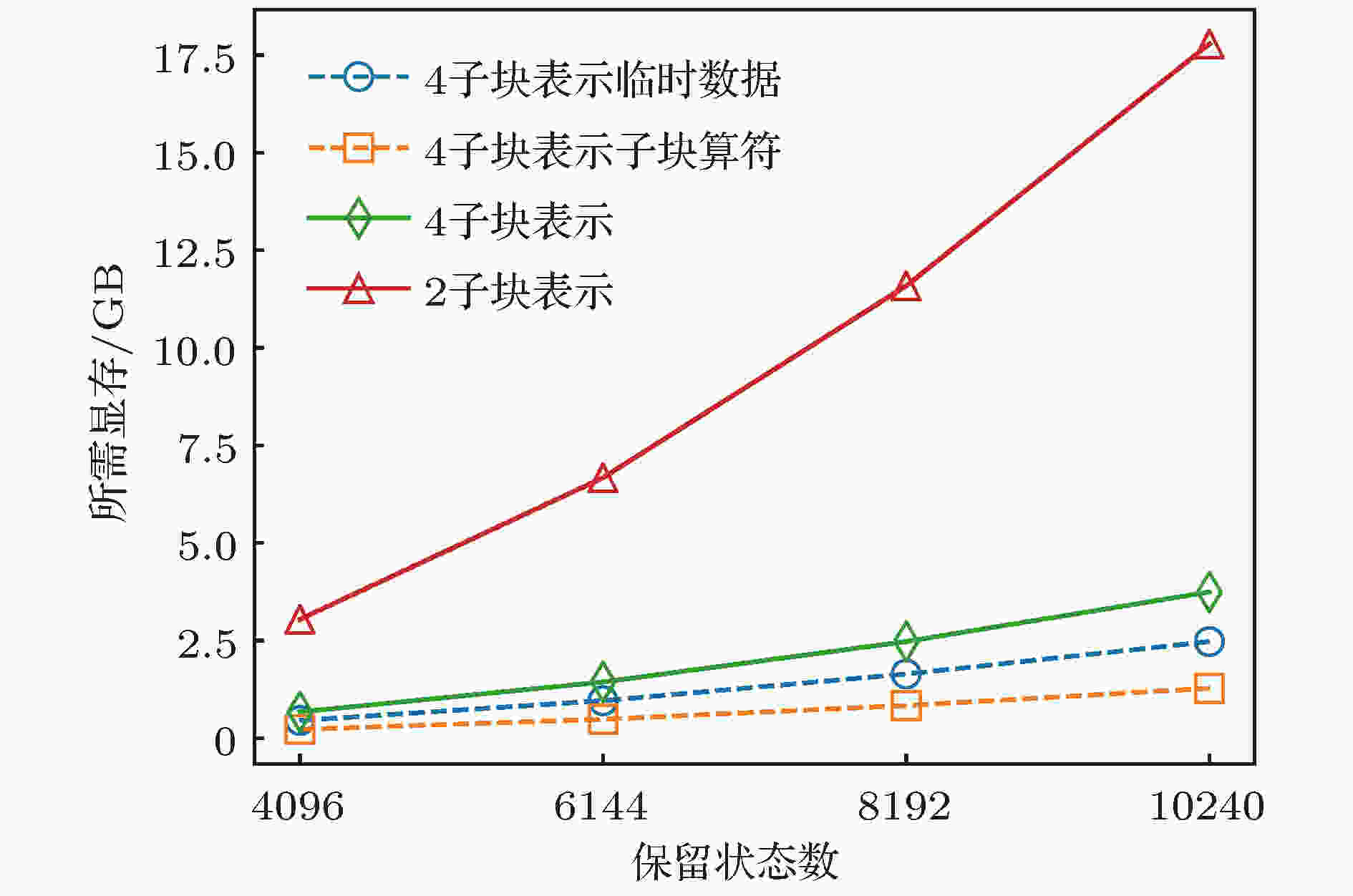 图 4 存储临时数据, 子块算符需要的GPU显存
图 4 存储临时数据, 子块算符需要的GPU显存

















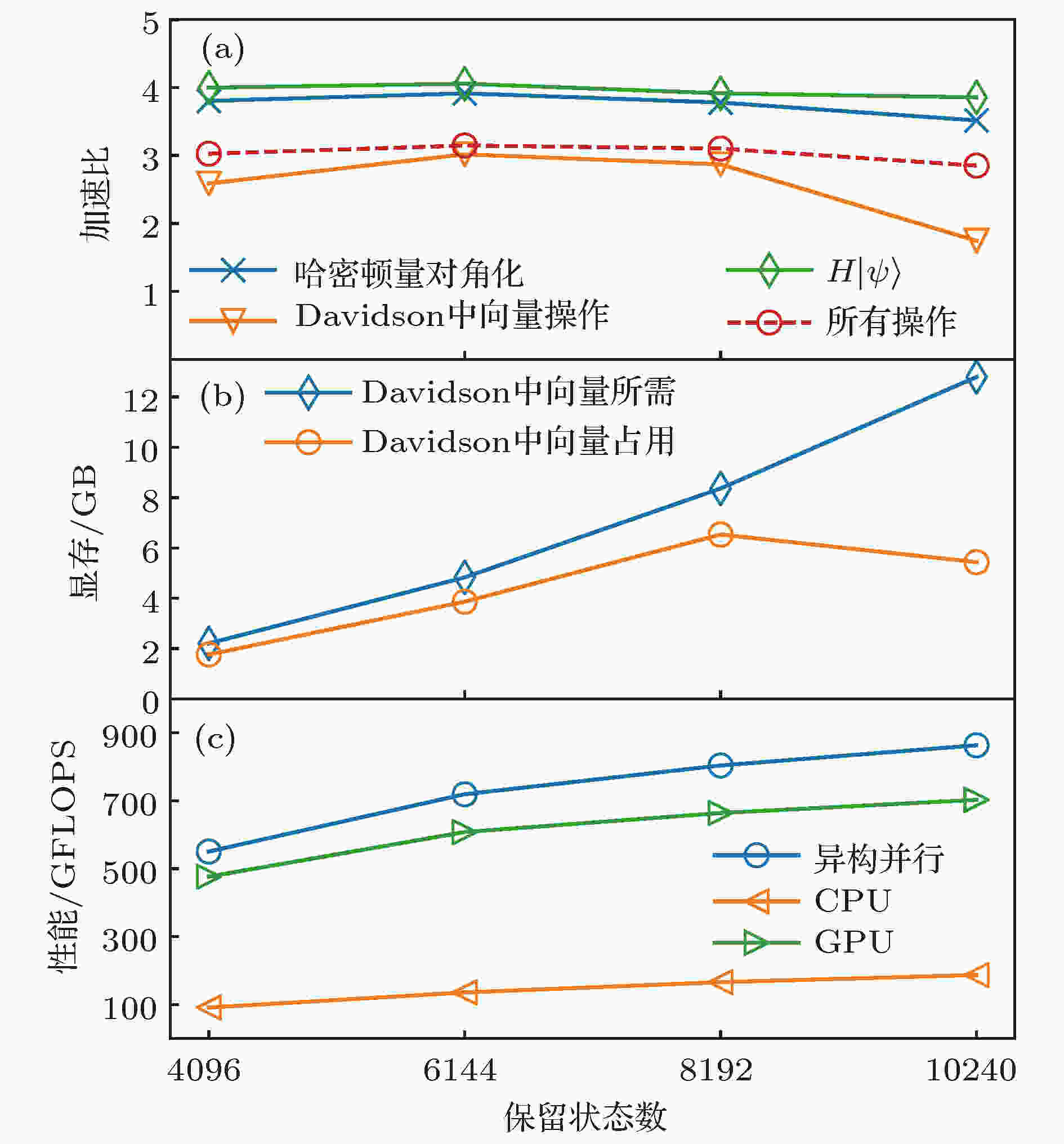 图 5 异构并行的性能 (a)加速比; (b) Davidson方法中的向量占用GPU显存; (c)作用哈密顿量到波函数部分的性能
图 5 异构并行的性能 (a)加速比; (b) Davidson方法中的向量占用GPU显存; (c)作用哈密顿量到波函数部分的性能
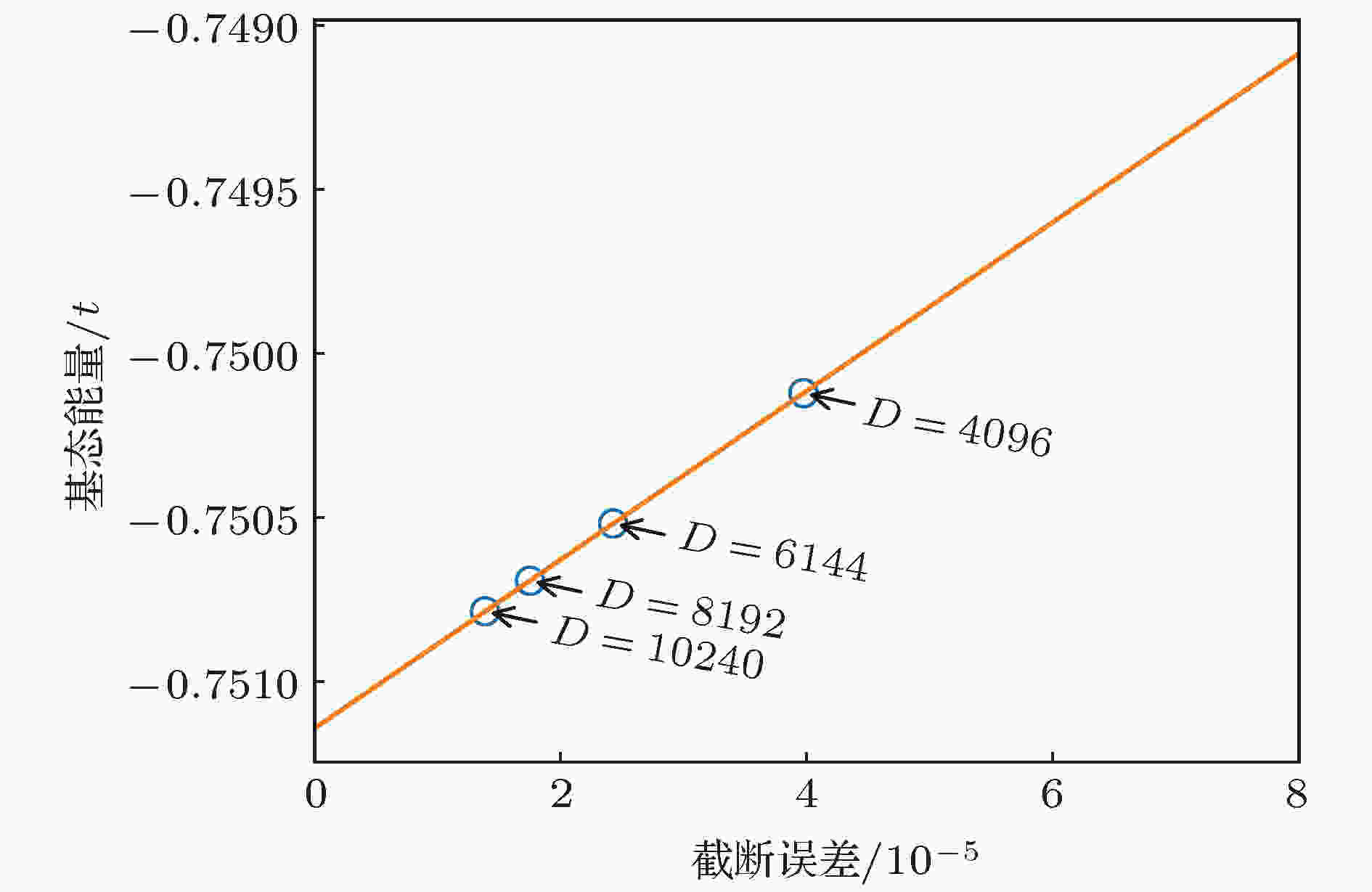 图 6 基态能量关于截断误差的函数(直线表示对基态能量的线性外推, 直至截断误差为0)
图 6 基态能量关于截断误差的函数(直线表示对基态能量的线性外推, 直至截断误差为0)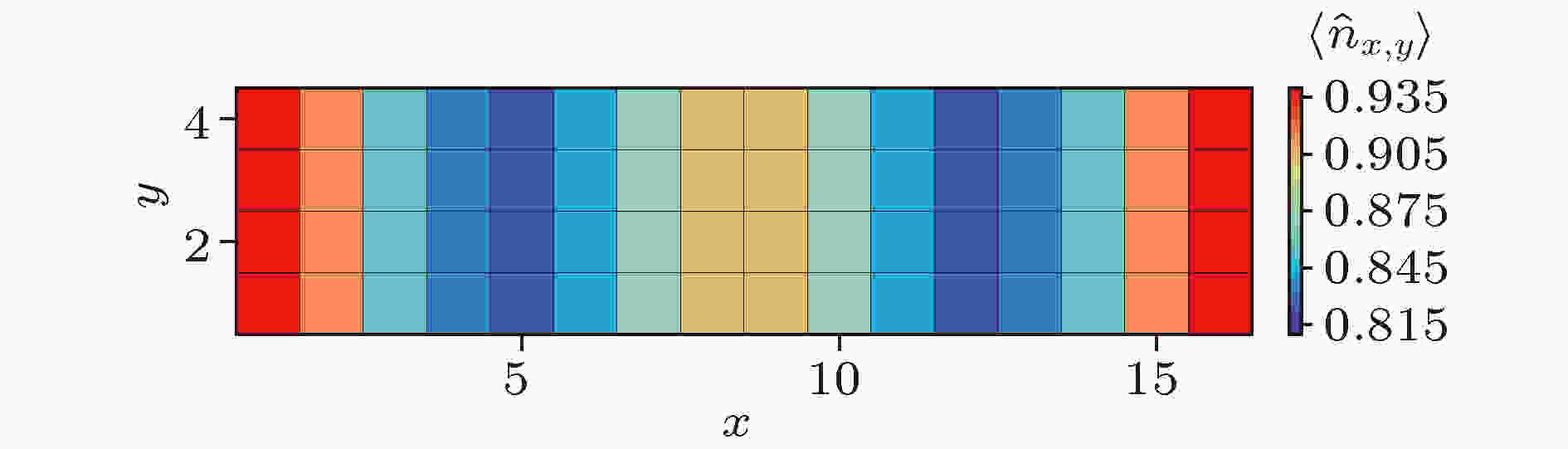 图 7 对于16 × 4 Hubbard模型, U = 8.0时的基态电荷密度分布(可以观察到明显的电荷密度条纹)
图 7 对于16 × 4 Hubbard模型, U = 8.0时的基态电荷密度分布(可以观察到明显的电荷密度条纹)