摘要:采用多组态鞍点变分方法计算了类硼S离子K壳层激发共振态1s2s²2p², 1s2s2p³, 1s2p^{4 2, 4}L (L = S, P, D) 的非相对论能量和波函数, 利用截断变分方法饱和波函数空间, 改进体系的非相对论能量. 利用微扰理论计算了相对论修正和质量极化效应, 利用屏蔽的类氢公式计算了QED (quantum electrodynamics) 效应和高阶相对论修正. 进一步, 考虑闭通道和开通道相互作用, 计算了由俄歇共振效应引起的能级移动, 从而得到了共振态的精确相对论能级. 利用优化的波函数, 计算了类硼S离子K壳层激发共振态的电偶极辐射跃迁的线强度、振子强度、跃迁率和跃迁波长. 计算的振子强度和辐射跃迁率均给出了长度规范、速度规范、加速度规范的结果. 三种规范结果的一致性表明了本文计算的波函数是足够精确的. 利用鞍点复数转动方法计算了类硼S离子K壳层激发共振态的俄歇跃迁率、俄歇分支率和俄歇电子能量. 本文的计算结果与其他文献数据符合较好.
关键词: K壳层激发共振态/
辐射跃迁/
俄歇跃迁/
俄歇电子

English Abstract

全文HTML

--> --> -->

多电子原子内壳激发共振态的研究有助于考察原子的结构, 分析离子(电子)与原子(分子)的碰撞过程, 探究原子高激发态的退激发机制. S作为天体物理中的重要的元素之一, 其离子高激发态研究研究与天体物理、等离子体物理、化学物理以及X射线物理等学科都密切相关^[1,2]. 类硼S离子的K壳层激发共振态, 其K壳层的1s电子被激发, 存在着“空洞”, 能级较高并位于多重离化阈之上, 可以通过辐射跃迁或俄歇跃迁进行退激发衰变. 在辐射跃迁过程中产生X射线波段的光谱, 在俄歇跃迁过程中, 能够释放出俄歇电子, 具有 “指纹” 特性, 其研究对等离子诊断、光谱线鉴定、软X射线激光器设计、元素鉴定和成分分析具有重要的应用价值^[3,4].
近年来, 理论和实验工作者对类硼离子K壳层激发共振态的辐射跃迁光谱和俄歇电子谱开展了系列研究. 实验方面, 实验物理学家利用高能离子碰撞实验和束箔碰撞实验技术对B原子^[5], C^+[5,6], O^3+[7], Ne^5+[7—9]离子俄歇电子谱进行了测量, 报道了精确测量的俄歇电子谱线. 在K壳层激发态的辐射跃迁光谱实验中, Armour等^[10,11]利用束箔实验技术测量了高离化Mg, Al, Si离子的X射线谱. Faenov^[12]利用CO₂激光等离子体实验测量了Mg, Al, Si, P, S离子的伴线波长, 其中部分谱线来源于类硼离子的K壳层激发共振态的辐射跃迁. 利用合并光子-离子束技术, Schlachter等^[13]利用1s→2p内壳层光激发实验测量C⁺离子K壳层激发态(1s2s²2p²、1s2s(³S)2p³)^2,4L的线宽度和能级寿命. Gharaibeh等^[14]测量了N²⁺离子K壳层激发光电离截面. Müller等^[15,16]研究了C⁺离子K壳层电离区域附近的自电离过程, 分析了其单电子俄歇、双电子俄歇、三电子俄歇的自电离机制.
理论方面, Chen和Crasemann^[17,18]利用MCDF-AL(multiconfiguration Dirac-Fock with average-level)方法系统计算了类硼等电子序列(Z = 6－54)离子K壳激发共振态1s2s²2p², 1s2s2p³, 1s2p^{4 2, 4}L的俄歇电子能量、俄歇跃迁率、X射线波长和跃迁强度. Safronova和Shlyaptseva^[19]利用1/Z微扰理论计算了类硼等电子序列(Z = 6—54) K壳层激发态ls2s²2pⁿ, ls2s2pⁿ, ls2pⁿ (n = 1—3)的能级和自电离跃迁率. Zhou等^[20]利用微扰理论计算了C⁺离子K壳层激发共振态1s2s²2p^{2 2}D, ²P的单电子俄歇、双电子俄歇和三电子俄歇跃迁率. 利用SCUNC (screening constant by unit nuclear charge) 模型, Sako等^[21]计算了类B等电子序列 (Z = 5—18) 的K壳层激发共振态1s2p⁴ (²S, ^2,4P, ²D)的X射线波长和俄歇电子能量. 目前, 人们对类硼离子的K壳层高激发共振态的能级、辐射跃迁和俄歇过程开展了相关研究, 得到了一些精确的理论和实验数据结果. 然而, 与类硼S离子K壳层激发共振态的相关报道还甚少. 理论上主要有MCDF方法^[17,18]和1/Z微扰理论^[19]对类硼S离子的K壳层激发共振态的能级、辐射光谱和俄歇跃迁数据进行了计算. 然而受限于早期的计算条件, 这些计算仅考虑了很少组态相互作用, 数据的精确度不够高.
在前期的工作中^[22,23], 我们利用鞍点变分方法和鞍点复数转动方法对类硼离子K壳层激发共振态的辐射跃迁和俄歇跃迁开展了相关计算, 得到了较为精确的理论结果. 本文采用该方法对类硼S离子K壳层激发共振态1s2s²2p², 1s2s2p³, 1s2p^{4 2, 4}L (L = S, P, D) 进行研究, 在本文计算过程中, 进一步考虑了QED(quantum electrodynamics)效应和高阶相对论的修正, 得到了精确的理论数据. 利用鞍点变分方法计算类硼S离子K壳层激发共振态的能级和波函数. 利用优化的波函数计算这些K壳层激发共振态的电偶极辐射跃迁线强度、振子强度、辐射跃迁率、跃迁波长. 利用鞍点复数转动方法计算这些K壳层激发共振态的俄歇跃迁率、俄歇分支率及俄歇电子能量. 本文计算结果与相关的实验理论数据进行对比, 符合较好.

在LS表象下, 类硼五电子体系的非相对论哈密顿算符为

${{H}_{0}}=\sum\limits_{i=1}^{5}{\left[ -\frac{1}{2}\nabla _{i}^{2}-\frac{Z}{{{r}_{i}}} \right]}+\sum\limits_{\begin{smallmatrix} i,j=1 \\ i < j \end{smallmatrix}}^{5}{\frac{1}{{{r}_{ij}}}}.$

内壳层激发共振态的波函数可写成如下形式:

$\begin{split} & {\psi _b}(1,2, \cdots,5)\\ = & A\sum\limits_i^n {{C_i}[1 - {P_j}]{\phi _{n(i),l(i)}}(R)Y_{l(i)}^{{\rm{LM}}}(\varOmega ){\chi _{s{s_z}}}},\end{split}$

式中, A为反对称算符, ${C_i}$为线性参数, ${\phi _{n(i),l(i)}}$代表径向波函数, $Y_{l(i)}^{{\rm{LM}}}$代表轨道角动量波函数, ${\chi _{s{s_z}}}$为自旋波函数. 径向部分采用Slater基函数进行展开,

${\phi _{n(i),l(i)}} = \prod\limits_{j = 1}^5 {{r_j}^{{n_j}}\exp ( - {\alpha _j}{r_j})},$

${\alpha _j}$为每个电子对应的非线性参数; 五个电子对应的非线性参数$\{{\alpha _1},{\alpha _2},{\alpha _3},{\alpha _4},{\alpha _5}\}$构成非线性参数集; ${l_i}$表示一组${l_1},{l_2},{l_3},{l_4},{l_5}$; ${n_i}$为对应的一组主量子数. 角向部分的波函数为

$\begin{split} & {Y_{{\rm{LM}}}}(\varOmega ) \\ = & \sum\limits_{{m_j}} {\left\langle {{l_1}{l_2}{m_1}{m_2}|{l_{12}}{m_{12}}} \right\rangle } \\ & \times\left\langle {{l_{12}}{l_3}{m_1}_2{m_3}|{l_{123}}{m_{123}}} \right\rangle \\ & \times \left\langle {{l_{123}}{l_4}{m_1}_{23}{m_4}|{l_{1234}}{m_{1234}}} \right\rangle \\ & \times \left\langle {{l_{1234}}{l_5}{m_1}_{234}{m_5}|{l_{12345}}{m_{12345}}} \right\rangle \prod\limits_{j = 1}^5 {{Y_{{l_j}{m_j}}}({\varOmega _j})}, \end{split} $

展开系数
$\left\langle {{l_1}{l_2}{m_1}{m_2}|{l_{12}}{m_{12}}} \right\rangle,\left\langle {{l_{12}}{l_3}{m_1}_2{m_3}|{l_{123}}{m_{123}}} \right\rangle \cdots $$\left\langle {{l_{1234}}{l_5}{m_1}_{234}{m_5}|{l_{12345}}{m_{12345}}} \right\rangle $为C.G.系数. 为简便表示, 将角动量波函数表示为

$l(i) = [(({l_1},{l_2}){l_{12}},{l_3}){l_{123}},{l_4}]{l_{1234}},{l_5};$

自旋部分波函数表示为

${\chi _{s{s_z}}} = [(({s_1},{s_2}){s_{12}},{s_3}){s_{123}},{s_4}]{s_{1234}},{s_5}.$

对于K壳层激发共振态, 由于能级高, 在计算过程中很容易产生变分崩溃. 因此, 在波函数中引入空轨道, 在(2)式中, 投影算符表示为

${P_j} = \left| {{\phi _o}({r_j})} \right\rangle \left\langle {{\phi _o}({r_j})} \right|,$

空轨道可表示为

${\phi _o}(r) = N{{\rm{e}}^{ - qr}},$

q为空轨道的有效核电荷数, N为归一化常数. 在鞍点变分计算过程中, 首先对非线性参数集$\{{\alpha _1},{\alpha _2},{\alpha _3},{\alpha _4},{\alpha _5}\}$以及线性参数${C_i}$变分优化能量极小, 之后再对q参数优化能量极大, 从而在鞍点处求得共振态最佳的非相对论能量值${E_b}$. 如在本文变分优化过程中, 在1s轨道位置加入空轨道, 排除了1s(2)$nln'l'n''l''$的组态, 从而防止2s轨道坍缩到1s轨道引起变分崩溃^[24]. 对于K壳层激发态, 空轨道的非线性参数q值接近Z-0.5, 这里初始值定为15.5. 当试探波函数非线性参数全部优化完毕后, 再对空轨道的q参数优化能量极大, 最大值的能量即为K壳层激发共振态的能量.
在计算过程中, 为了防止遗漏重要的组态相互作用波函数, 本文利用截断变分方法计算了非相对论能量的修正值$\Delta {E_{{\rm{RV}}}}$, 从而得到共振态的非相对论能量${E_b} + \Delta {E_{{\rm{RV}}}}$. 对于截断变分方法的相关理论, 文献[23]有详细描述, 这里不再赘述. 利用微扰理论, 本文还考虑相对论修正$\Delta {E_{{\rm{rel}}}}$和质量极化效应的修正$\Delta {E_{{\rm{mp}}}}$. 微扰算符包括质量极化项、动能修正项、达尔文项、电子和电子相互作用项以及轨道和轨道相互作用项. 这些算符的在文献[22]中有详细描述, 这里不再展开.
随着核电荷数Z的增加, QED效应和高阶相对论效应修正变得愈发重要, 因此为了得到精确的能级数据, 本文利用屏蔽的类氢公式^[25—27], 计算了类硼S¹¹⁺离子K壳层激发共振态的QED效应和高阶相对论修正. 在QED效应计算中, 仅考虑了主要部分自能修正和真空极化修正效应. 对于ns电子, QED效应修正公式为

$\begin{split}\Delta {E_{{\rm{QED}}}}(n,0) = & \frac{{4Z_{{\rm{eff}}}^{\rm{4}}{\alpha ^3}}}{{3{\text{π}}{n^3}}}\left\{ \frac{{19}}{{30}} - 2\ln (\alpha {Z_{{\rm{eff}}}})\right.\\& - \ln [K(n,0)] + 7.214\alpha {Z_{{\rm{eff}}}}\\ & - {({Z_{{\rm{eff}}}}\alpha )^2}[3{\ln ^2}({Z_{{\rm{eff}}}}\alpha )\\ & \bigg. + 8.695\ln ({Z_{{\rm{eff}}}}\alpha )]\bigg\} .\end{split}$

对于其他的nl电子,

$\begin{split}\Delta {E_{{\rm{QED}}}}(n,l) = &\frac{{4Z_{{\rm{eff}}}^{\rm{4}}{\alpha ^3}}}{{3{\text{π}}{n^3}}}\left\{ \frac{{3{c_{l,j}}}}{{8(2l + 1)}}\right.\\& - \ln K(n,l) + {(\alpha {Z_{{\rm{eff}}}})^2}\ln {(\alpha {Z_{{\rm{eff}}}})^{ - 2}}\\ &\times \left[(1 - \frac{1}{{{n^2}}})(\frac{1}{{10}} + \frac{1}{4}{\delta _{j,\frac{1}{2}}}){\delta _{l,1}}\right.\\ &+ \left.\frac{{8(3 - l(l + 1)/{n^2})}}{{(2l - 1)(2l)(2l + 1)(2l + 2)(2l + 3)}}\right]\\&\bigg. + \frac{{3\alpha }}{{4{\rm{\pi }}}}( - 0.3285){c_{l,j}}/(2l + 1)\bigg\} ,\end{split}$

其中

${c_{l,j}} = \left\{ {\begin{aligned}&{l/(l + 1)}\quad{j = l + 1/2,}\\& - 1/l \quad\quad {j = l - 1/2.}\end{aligned}} \right.$

$\ln K(n,l)$的值来自于文献[28], 有效核电荷数${Z_{{\rm{eff}}}}$的值由文献[27]中计算方法求得. 对单电子狄拉克方程的能量本征值为

${E_{{\rm{Dirac}}}}(Z) \!=\! \frac{1}{{{\alpha ^2}}}{\left\{ {1 \!+\! {{\left[ {\frac{{\alpha Z}}{{n \!-\! k + \sqrt {{k^2}\! -\! {\alpha ^2}{Z^2}} }}} \right]}^2}} \right\}^{ - \textstyle\frac{1}{2}}}\! - \!\frac{1}{{{\alpha ^2}}},$

其中$k = j + 1/2$($j$是电子的总轨道角动量). 对(11)式进行泰勒展开, 如果仅考虑到${\alpha ^2}{Z^4}$阶, ${E_{{\rm{Dirac}}}}(Z)$可简写为

${E^{(1)}}(Z) = - \frac{{{Z^2}}}{{2{n^2}}}\left\{ {1 + \frac{{{\alpha ^2}{Z^2}}}{n}\left[ {\frac{1}{k} - \frac{3}{{4n}}} \right]} \right\}.$

nl电子的高阶相对论为

$\Delta {E_{{\rm{HO}}}}(nl) = {E_{{\rm{Dirac}}}}({Z_{{\rm{eff}}}}) - {E}^{(1)}({Z_{{\rm{eff}}}}).$

通过依次求得每个电子的QED效应修正和高阶相对论修正, 求和得到体系的总QED效应和高阶相对论效应为

$\Delta {E_{{\rm{QED}}}} = \sum\limits_{i = 1}^5 {\Delta {E_{{\rm{QED}}}}} ({n_i}{l_i}{j_i},LSJ),$

$\Delta {E_{{\rm{HO}}}} = \sum\limits_{i = 1}^5 {\Delta {E_{{\rm{HO}}}}} ({n_i}{l_i}{j_i},LSJ).$

K壳层激发共振态的宽度和能量位移, 是共振态波函数中连续通道与束缚通道之间相互作用的结果. 共振态束缚通道波函数${\psi _{\rm{b}}}({R_N},{\varOmega _N})$, 加上连续通道波函数构成体系的总波函数. ${R_N}$表示N个电子的径向坐标, ${\varOmega _N}$代表N个电子的角向坐标. 在LS耦合表象下的实空间, 共振态的总波函数表示为

$\begin{split}\varPsi ({R_N},{\varOmega _N}) =\, &{\psi _{\rm{b}}}({R_N},{\varOmega _N}) \\ &+ A\sum\limits_{i,k} {{d_{ik}}{\phi _i}} ({R_{N - 1}},{\varOmega _{N - 1}}){U_k}({{{r}}_N}),\end{split}$

式中, A为是反对称算符, ${d_{ik}}$为线性参数, ${\phi _i}({R_{N - 1}},{\varOmega _{N - 1}})$是四电子靶态的波函数, ${U_k}$$({{{r}}_N})$为出射电子波函数, 可写为

${U_k}({{{r}}_N}) = {r^k}{{\rm{e}}^{ - \alpha r}},$

$\alpha $为电子的非线性参数, ${U_k}$构成一维的完备基, 在计算过程中, 非线性参数是可选择的. 利用复数转动方法^[29,30], 哈密顿算符经转动变为

$H = H({R_N}{{\rm{e}}^{{\rm{i}}\theta }},{\varOmega _N}),$

其中, ${R_N}{{\rm{e}}^{{\rm{i}}\theta }}$表示每个径向坐标${r_j}$变换为${r_j} \to {r_j}{{\rm{e}}^{{\rm{i}}\theta }}$, $\theta $为相位角, 为了保证体系本征值更好的收敛性, 鞍点复数转动方法采用基组的复旋转代替哈密顿量的旋转. 基组经旋转变为

${\varphi _j} = {\varphi _j}({R_N}{{\rm{e}}^{{\rm{i}}\theta }},{\varOmega _N}).$

于是, 共振态的波函数(16)式可写为

$\begin{split} & \varPsi ({R_N}{{\rm{e}}^{{\rm{i}}\theta }},{\varOmega _N}) \\ =\, & {\psi _{\rm{b}}}({R_N}{{\rm{e}}^{{\rm{i}}\theta }},{\varOmega _N}) \\ & + A\sum\limits_{i,k} {{d_{ik}}{\phi _i}} ({R_{N - 1}}{{\rm{e}}^{{\rm{i}}\theta }},{\varOmega _{N - 1}}){U_k}({{{r}}_N}),\end{split}$

在复平面内, 共振态的波函数是平方可积的. 利用转动后的波函数$\varPsi $, 共振态的能级和宽度可通过求解久期方程求得:

$\delta \frac{{\langle \varPsi |{H_0}|\varPsi \rangle }}{{\langle \varPsi |\varPsi \rangle }} = 0.$

求得本征值$E - {\rm{i}}\varGamma /2$, 其中, 实部E为能级位置, 虚部Γ为能级的宽度. $\Delta {E_{\rm{S}}} = E - {E_{\rm{b}}}$, 表示考虑了闭通道与连续态相互作用引起的能级位移. 通过文献[29, 30]可知, 在鞍点复数转动计算中, 转角$\theta $在$0.3-0.6$范围内, 俄歇共振能级位移和能级宽度数值呈现出良好的稳定性和收敛性. 当$\theta = 0.5$时, 出射电子的非线性参数$\alpha $的变化引起的共振能级位移和能级宽度变化最小, 收敛性最好. 因此, 本文的鞍点复数转动计算中, 取$\theta = 0.5$. 于是, 共振态的总能量为

$\begin{split}{E_{{\rm{total}}}} =\, & {E_{\rm{b}}} + \Delta {E_{{\rm{RV}}}} + \Delta {E_{\rm{mp}}} + \Delta {E_{{\rm{rel}}}} \\ &+ \Delta {E_{{\rm{QED}}}} + \Delta {E_{{\rm{HO}}}} + \Delta {E_{\rm{S}}}.\end{split}$

能级宽度和俄歇跃迁率的关系为

${{ A}_{{\rm{au}}}} = \varGamma /\hbar .$

本文采用多组态鞍点变分方法计算了类硼S离子K壳层激发共振态1s2s²2p², 1s2s2p³, 1s2p^{4 2, 4}L (L = S, P, D)的能级和波函数. 在LS耦合框架下, 为得到精确的理论计算结果, 需要充分考虑电子关联效应及各种修正效应. 在计算过程中, 根据组态相互作用定则选取重要的轨道-自旋角动量分波来考虑电子关联效应. 为了方便表示计算过程中所考虑的组态波函数, 本文利用每个电子的轨道角动量量子数组合$[{l_1},{l_2},{l_3},{l_4},{l_5}]$来表示所添加的组态, 称为轨道角动量分波, 其中每个电子对应的主量子数是可变的, 增大主量子数可增加每个分波中的term数目, 扩展更多的组态. 每个轨道角动量分波可能包含多种轨道角动量耦合方式, 如对于[0, 0, 1, 1, 1]分波耦合到总轨道角动量L = P态, 具有三种可能的耦合方式: $[(((0,0)0,1)1,1)0,1]1$, $[(((0,0)0,1)1,1)1,1]1$, $[(((0,0)0,1)1,1)2,1]1$. 在计算中, 本文考虑到所有可能的轨道角动量耦合方式. 对于K壳层激发四重态, 自旋角动量耦合方式有四种, 对于K壳层激发二重态, 自旋角动量耦合方式多达五种. 不同耦合方式的轨道角动量和自旋角动量的组合称为轨道-自旋角动量分波. 对于偶宇称结构(1s2s²2p², 1s2p⁴), 重要的轨道角动量分波系列$[{l_1},{l_2},{l_3},{l_4},{l_5}]$为$[0,0,0,l,l]$, $[0,0,0,l,l + 2]$, $[0,0,1,l,l + 1]$, $[0,0,1,l,l + 3]$, $[0,1,1,l,l]$, $[0,1,1,l,l + 2]$, $[0,0,2,l,l]$, $[1,1,1,l,l + 1]$等; 对于奇宇称结构(1s2s2p³), 重要的轨道角动量分波系列$[{l_1},{l_2},{l_3},{l_4},{l_5}]$为$[0,0,1,l,l]$, $[0,0,1,l,l + 2]$, $[0,0,0,l,l + 1]$, $[0,1,1,l,l + 1]$, $[0,1,1,l,l + 3]$, $[0,0,2,l,l + 1]$, $[1,1,1,l,l]$等. 在构建波函数过程中, 轨道角动量量子数$l$的取值范围为0到8, 当$l > 8$时, 组态分波对体系的能量贡献很小, 可以忽略. 在计算过程中, 随着$l$的增加, 分波能量的贡献呈现收敛趋势. 对于每个轨道-自旋角动量分波, 当增加电子的主量子数n所引起的能量贡献小10^–6 a.u.时, 停止增加n. 在本文计算中, 轨道-自旋角动量组态分波的数目达到148, 波函数term的总数达到4500项. 通过对构建的试探波函数的非线性参数集变分优化极小, 而后再对空轨道参数q优化能量极大, 从而得到组态的最佳波函数和对应的非相对论能量${E_{\rm{b}}}$. 为了防止遗漏的重要的角动量-自旋组态分波和考虑高l系列分波的能量贡献, 本文利用截断变分方法计算了非相对能量改进$\Delta {E_{{\rm{RV}}}}$, 于是得到共振态的非相对能量${E_{\rm{b}}} + \Delta {E_{{\rm{RV}}}}$.
为了得到精确的相对论能量, 本文利用微扰理论, 计算了质量极化和相对论效应修正$\Delta {E_{{\rm{rel}}}} + \Delta {E_{{\rm{mp}}}}$. 其中相对论微扰算符包括动能项、达尔文项、电子与电子相互作用项和轨道与轨道的相互作用项. 同时利用屏蔽的类氢公式本文还考虑了QED效应修正$\Delta {E_{{\rm{QED}}}}$和高阶相对论修正$\Delta {E_{{\rm{HO}}}}$, 于是总的修正能量$\Delta {E_{{\rm{corr}}}} = \Delta {E_{{\rm{mp}}}} + \Delta {E_{{\rm{rel}}}} + \Delta {E_{{\rm{QED}}}} + \Delta {E_{{\rm{HO}}}}$. K壳层激发共振态位于多重离化阈之上, 镶嵌在连续态内, 这些K壳层激发共振态的原子存在一定的概率自电离, 导致K壳层激发态的寿命变短, 能级加宽. 同时由于相互作用能级间的“相互排斥”, 即来源于束缚空间和连续空间的相互作用, 这些K壳层激发态的能级将发生一定的能级移动$\Delta {E_{\rm{S}}}$. 因此, 类硼S离子K壳层激发态的总能量为${E_{{\rm{total}}}} = $$ {E_{\rm{b}}} + \Delta {E_{{\rm{RV}}}} + \Delta {E_{{\rm{corr}}}} + \Delta {E_{\rm{S}}}$.
表1列出了本文计算的类硼S离子的K壳层激发共振态权重中心的能级. 为便于对比, 表1还列出了这些K壳层激发共振态能量的绝对值(–E_total, 单位eV). 对比文献[21]的SCUNC理论计算结果, 可以发现, 对于1s2p^{4 2, 4}L激发态, 本文的理论计算结果与SCUNC理论值的均方根误差约为5.01 eV. 考虑电子自旋与轨道、自旋与其他轨道、自旋与自旋相互作用, 表2列出了类硼S离子K壳层激发共振态的精细结构劈裂能级. 对比文献[19]利用1/Z微扰理论的计算数据, 本文的计算结果与1/Z微扰理论的均方根误差约为3.28 eV. 相比SCUNC理论和1/Z微扰理论方法, 本文在计算过程中考虑了更多的组态相互作用和能量修正, 如QED和高阶相对论修正. 目前, 没有更多类硼S离子的K壳层激发共振态的能级数据可以对比, 因此需要更加精确的实验或理论数据来验证. 在研究类硼S离子K壳层激发共振态的辐射跃迁和俄歇跃迁中, 需要S¹¹⁺离子低位激发态和S¹²⁺离子低位激发态的能级和波函数. 本文采用多组态Rayleigh-Ritz变分方法对它们进行了计算, 结果列于表2. 表2还列出了NIST (National Institute of Standards and Technology) 数据库^[31]的实验数据, 对比发现, 本文的计算数据和NIST实验数据的均方根偏差仅为0.15 eV, 符合得非常好.

共振态	${E_{{\rm{nonrel}}}}/{\rm{a.u.}}$			${E_{{\rm{total}}}}/{\rm{a.u.}}$	$ - {E_{{\rm{total}}}}/{\rm{eV}}$
	${E_{\rm{b}}} + \Delta {E_{{\rm{RV}}}}$	$\Delta {E_{{\rm{corr}}}}$	$\Delta {E_{\rm{S}}}$		本文	SCUNC[21]
1s2s22p2 4P	–229.35389	–0.64011	–0.00245	–229.99645	6258.52
1s2s22p2 2S	–228.66774	–0.66777	–0.00174	–229.33725	6240.58
1s2s22p2 2P	–228.81110	–0.66633	–0.00089	–229.47832	6244.42
1s2s22p2 2D	–228.91613	–0.67942	0.00322	–229.59233	6247.52
1s2s(3S)2p3 4So	–227.40768	–0.60823	0.00018	–228.01573	6204.62
1s2s(1S)2p3 4So	–228.21123	–0.62298	0.00151	–228.83270	6226.85
1s2s(3S)2p3 4Po	–228.00558	–0.62215	0.00106	–228.62667	6221.25
1s2s(3S)2p3 4Do	–228.30315	–0.62288	–0.00017	–228.92620	6229.40
1s2s(3S)2p3 2So	–226.86291	–0.62586	0.00070	–227.48807	6190.26
1s2s(3S)2p3 2Po	–226.91669	–0.61114	0.00193	–227.52590	6191.29
1s2s(1S)2p3 2Po	–227.28245	–0.61646	0.00620	–227.89271	6201.28
1s2s(3S)2p3 2Do	–227.21472	–0.61330	0.00204	–227.82598	6199.46
1s2s(1S)2p3 2Do	–227.56290	–0.62041	0.00280	–228.18051	6209.11
1s2p4 4P	–226.53817	–0.55727	–0.00249	–227.09793	6179.65	6173.07
1s2p4 2S	–225.47488	–0.56220	0.00072	–226.03636	6150.76	6145.67
1s2p4 2P	–225.94003	–0.56493	0.00251	–226.50245	6163.44	6159.02
1s2p4 2D	–226.07283	–0.56074	0.00279	–226.63078	6166.94	6163.51

表1类硼S离子K壳层激发共振态1s2s²2p², 1s2s2p³, 1s2p^{4 2, 4}L (L = S, P, D)的权重中心能级(单位a.u.), 能量转化关系:1 a.u = 27.21138 eV
Table1.Center of gravity levels of 1s2s²2p², 1s2s2p³, 1s2p^{4 2, 4}L (L = S, P, D) of K-shell excited resonance states in boron-like sulfur ion (unit: a.u.). The energy conversion relationship: 1 a.u = 27.21138 eV.

偶宇称			奇宇称
S11+离子K壳层激发态共振态
共振态	本文	文献[19]	共振态	本文	文献[19]
1s2s22p2 4P1/2	6259.50	6265.62	1s2s(3S)2p3 4S3/2	6204.62	6207.16
1s2s22p2 4P3/2	6258.83	6264.85	1s2s(1S)2p3 4S3/2	6226.85	6229.68
1s2s22p2 4P5/2	6257.99	6264.05	1s2s(3S)2p3 4P1/2	6221.05	6223.62
1s2s22p2 2S1/2	6240.58	6243.03	1s2s(3S)2p3 4P3/2	6221.24	6223.52
1s2s22p2 2P1/2	6245.72	6248.94	1s2s(3S)2p3 4P5/2	6221.32	6223.54
1s2s22p2 2P3/2	6243.77	6247.23	1s2s(3S)2p3 4D1/2	6229.21	6231.96
1s2s22p2 2D3/2	6247.38	6251.29	1s2s(3S)2p3 4D3/2	6229.21	6232.01
1s2s22p2 2D5/2	6247.62	6251.38	1s2s(3S)2p3 4D5/2	6229.30	6232.00
1s2p4 4P1/2	6178.53	6180.77	1s2s(3S)2p3 4D7/2	6229.61	6231.85
1s2p4 4P3/2	6179.12	6181.26	1s2s(3S)2p3 2S1/2	6190.26	6192.27
1s2p4 4P5/2	6180.37	6182.44	1s2s(3S)2p3 2P1/2	6191.17	6193.98
1s2p4 2S1/2	6150.76	6152.75	1s2s(3S)2p3 2P3/2	6191.36	6193.65
1s2p4 2P1/2	6163.28	6165.34	1s2s(1S)2p3 2P1/2	6201.72	6204.18
1s2p4 2P3/2	6163.52	6166.42	1s2s(1S)2p3 2P3/2	6201.05	6206.82
1s2p4 2D3/2	6166.83	6169.56	1s2s(3S)2p3 2D3/2	6199.29	6199.03
1s2p4 2D5/2	6167.00	6169.69	1s2s(3S)2p3 2D5/2	6199.57	6202.14
			1s2s(1S)2p3 2D3/2	6209.23	6212.93
			1s2s(1S)2p3 2D5/2	6209.03	6212.33
S11+离子低位激发态
激发态	本文	NIST[31]	激发态	本文	NIST[31]
1s22s2p2 4P1/2	8617.38	8617.29	1s22s22p 2P1/2	8641.58	8641.33
1s22s2p2 4P3/2	8616.83	8616.70	1s22s22p 2P3/2	8639.78	8639.70
1s22s2p2 4P5/2	8615.98	8615.86	1s22p3 4S3/2	8565.71	8565.69
1s22s2p2 2S1/2	8586.78	8586.83	1s22p3 2P1/2	8545.44	8545.36
1s22s2p2 2P1/2	8584.06	8583.71	1s22p3 2P3/2	8545.42	8545.14
1s22s2p2 2P3/2	8582.99	8582.88	1s22p3 2D3/2	8555.97	8555.79
1s22s2p2 2D3/2	8598.49	8598.35	1s22p3 2D5/2	8555.74	8555.72
1s22s2p2 2D5/2	8598.39	8598.31
S12+离子低位激发态
激发态	本文	NIST[31]	激发态	本文	NIST[31]
1s22s2 1S0	8076.99	8076.93	1s22s2p 1P1	8028.74	8028.63
1s22p2 1S0	7987.61	7987.44	1s22s2p 3P0	8052.36	8052.23
1s22p2 1D2	8004.12	8003.85	1s22s2p 3P1	8051.81	8051.70
1s22p2 3P0	8012.11	8012.06	1s22s2p 3P2	8050.64	8050.50
1s22p2 3P1	8011.53	8011.37
1s22p2 3P2	8010.43	8010.37

表2S¹¹⁺离子K壳层激发共振态, S¹¹⁺, S¹²⁺离子低位激发态的精细结构能级($ - E$, 单位eV)
Table2.Fine-structure energy levels of the K-shell excited resonance states in S¹¹⁺ ion, and low-excited states in S¹¹⁺, S¹²⁺ ion ($ - E$, unit eV).

表3给出了类硼S离子的K壳层激发共振态1s2s²2p², 1s2s2p³, 1s2p^{4 2, 4}L(L = S, P, D)的电偶极辐射跃迁线强度S, 辐射跃迁率${A_{ik}}$, 振子强度${f_{ki}}$和跃迁波长$\lambda $. 对于辐射跃迁振子强度和辐射跃迁率, 表3均列出了三种规范的计算结果: 长度规范, 速度规范, 加速度规范. 三种规范的一致性可反映理论计算的波函数精确程度. 图1给出了电偶极辐射跃迁振子强度长度规范${f_{\rm{l}}}$和速度规范${f_{\rm{v}}}$, 长度规范${f_{\rm{l}}}$和加速度规范${f_{\rm{a}}}$的对比图. 从图1可以看出, 大多数$\lg ({f_{\rm{l}}}/{f_{\rm{v}}})$和$\lg ({f_{\rm{l}}}/{f_{\rm{a}}})$取值位于[–0.025, 0.025]范围. 随着线强度的增大, 三种规范的结果符合得越来越好. ${f_{\rm{l}}}$和${f_{\rm{v}}}$的符合程度要好于${f_{\rm{l}}}$和${f_{\rm{a}}}$符合程度. 整体上, 三种规范结果显示出良好的一致性, 从而表明了本文计算的波函数是足够精确的. 本文计算的电偶极辐射跃迁率与MCDF理论^[17]计算的辐射跃迁率的对比见图2. 可以发现, 本文的计算的辐射跃迁率和MCDF理论计算值符合得较好, 大部分误差在20% 以内. 唯一误差较大的跃迁为1s2s(³S)2p^{3 2}P^o→1s²2s2p^{2 2}D, 本文计算的辐射跃迁率为4.95 × 10¹² (s^–1), 比MCDF^[17]理论值3.38 × 10¹² (s^–1)大约46%. 表3的最后两列还给出了MCDF ^[17]和SCUNC^[21]的理论波长. 本文计算的波长和MCDF理论波长符合得更好, 均方根偏差约为0.003 ?. 类硼S离子K壳层激发态的辐射跃迁波长位于X射线波段范围, 彼此十分靠近, 本文精确计算的理论值将为相关实验的光谱谱线鉴定提供有价值的理论参考数据.

初态	末态	S/a.u.	${A_{ik}}/{\rm{s}}^{-1}$					${f_{ki}}$				λ/?
			${A_{\rm{l}}}$	${A_{\rm{v}}}$	${A_{\rm{a}}}$	文献[17]		${f_{\rm{l}}}$	${f_{\rm{v}}}$	${f_{\rm{a}}}$		本文	文献[17]	文献[21]
1s2s22p2 4P	1s22p3 4So	5.06[–4]	5.48[11]	5.32[11]	5.31[11]	5.09[11]		7.14[–3]	6.94[–3]	6.92[–3]		5.374	5.379
1s2p4 4P	1s22p3 4So	2.14[–2]	2.55[13]	2.65[13]	2.67[13]	2.57[13]		3.12[–1]	3.23 [–1]	3.26[–1]		5.196	5.193	5.203
1s2s22p2 2S	1s22s22p 2Po	3.81[–3]	2.78[13]	2.82[13]	2.80[13]	2.93[13]		3.72[–2]	3.78[–2]	3.76[–2]		5.166	5.176	5.167
	1s22p3 2Po	1.78[–4]	1.15[12]	1.15[12]	1.02[12]	9.87[11]		1.68[–3]	1.67[–3]	1.48[–3]		5.379	5.383
1s2s22p2 2P	1s22s22p 2Po	3.26[–2]	7.88[13]	7.87[13]	7.84[13]	7.53[13]		3.18[–1]	3.18[–1]	3.17[–1]		5.175	5.176
	1s22p3 2Po	1.80[–4]	3.87[11]	3.88[11]	3.99[12]	3.20[11]		1.69[–3]	1.69[–3]	1.74[–3]		5.388	5.392
	1s22p3 2Do	6.30[–4]	1.37[12]	1.39[12]	1.40[12]	1.23[12]		3.56[–3]	3.61[–3]	3.64[–3]		5.364	5.368
1s2s22p2 2D	1s22s22p2Po	1.92[–2]	2.77[13]	2.67[13]	2.64[13]	2.71[13]		1.87[–1]	1.80[–1]	1.78[–1]		5.181	5.183
	1s22p3 2Po	1.01[–4]	1.29[11]	1.28[11]	1.45[11]	1.35[11]		9.43[–4]	9.34[–4]	1.06[–3]		5.396	5.401
	1s22p3 2Do	3.68[–4]	7.98[11]	8.18[11]	8.25[11]	7.74[11]		3.46[–3]	3.55[–3]	3.59[–3]		5.371	5.375
1s2p4 2S	1s22p3 2Po	7.14[–3]	5.17[13]	5.26[13]	5.28[13]	5.13[13]		6.96[–2]	7.08[–2]	7.11[–2]		5.178	5.175	5.191
1s2p4 2P	1s22p3 2Po	1.75[–2]	4.17[13]	4.26[13]	4.26[13]	3.97[13]		1.70[–1]	1.74[–1]	1.73[–1]		5.205	5.205	5.217
	1s22p3 2Do	2.89[–2]	6.97[13]	6.80[13]	6.71[13]	6.17[13]		1.69[–1]	1.65[–1]	1.63[–1]		5.182	5.182	5.191
1s2p4 2D	1s22s22p 2Po	2.58[–4]	4.09[11]	4.42[11]	4.14[11]			2.59[–3]	2.80[–3]	2.62[–3]		5.013
	1s22p3 2Po	9.20[–3]	1.30[13]	1.32[13]	1.33[13]	1.32[13]		8.91[–2]	9.04[–2]	9.11[–2]		5.213	5.212	5.220
	1s22p3 2Do	2.74[–2]	3.93[13]	4.10[13]	4.13[13]	4.02[13]		1.60[–1]	1.67[–1]	1.68[–1]		5.190	5.189	5.198
1s2s(1S)2p3 4So	1s22s2p2 4P	3.08[–2]	1.11[14]	1.09[14]	1.09[14]	1.09[14]		1.50[–1]	1.48[–1]	1.47[–1]		5.188	5.189
1s2s(3S)2p3 4So	1s22s2p2 4P	7.57[–4]	2.80[12]	2.90[12]	2.99[12]	2.28[12]		3.72[–3]	3.85[–3]	3.97[–3]		5.141	5.135
1s2s(3S)2p3 4Po	1s22s2p2 4P	2.33[–2]	2.81[13]	2.79[13]	2.80[13]	2.67[13]		1.14[–1]	1.13[–1]	1.13 [–1]		5.176	5.174
1s2s(3S)2p3 4Do	1s22s2p2 4P	3.89[–2]	2.79[13]	2.78[13]	2.77[13]	2.63[13]		1.89[–1]	1.88[–1]	1.88[–1]		5.194	5.192
1s2s(3S)2p3 2So	1s22s2p2 2P	1.57[–2]	1.13[14]	1.13[14]	1.13[14]	8.54[13]		1.53[–1]	1.52[–1]	1.52[–1]		5.181	5.180
1s2s(1S)2p3 2Po	1s22s2p2 2P	1.05[–3]	2.50[12]	2.78[12]	2.74[12]	2.53[12]		1.02[–2]	1.13[–2]	1.12[–2]		5.205	5.208
	1s22s2p2 2D	1.71[–2]	4.14[13]	4.17[13]	4.14[13]	3.92[13]		1.00[–1]	1.01[–1]	1.00[–1]		5.172	5.173
1s2s(3S)2p3 2Po	1s22s2p2 2S	1.59[–3]	3.85[12]	3.93[12]	3.50[12]	3.55[12]		4.66[–2]	4.76[–2]	4.24[–2]		5.176	5.174
	1s22s2p2 2P	1.00[–2]	2.42[13]	2.42[13]	2.30[13]	3.01[13]		9.79[–2]	9.79[–2]	9.31[–2]		5.183	5.183
	1s22s2p2 2D	2.01[–3]	4.95[12]	4.92[12]	5.19[12]	3.38[12]		1.18[–2]	1.19[–2]	1.25[–2]		5.151	5.149
1s2s(1S)2p3 2Do	1s22s2p2 2P	1.85[–3]	2.60[12]	2.64[12]	2.64[12]	2.19[12]		1.79[–2]	1.81[–2]	1.81[–2]		5.222	5.225
	1s22s2p2 2D	5.21[–2]	7.49[13]	7.54[13]	7.55[13]	7.13[13]		3.04[–1]	3.06[–1]	3.07[–1]		5.189	5.191
1s2s(3S)2p3 2Do	1s22s2p2 2P	1.70[–2]	2.43[13]	2.49[13]	2.50[13]	2.40[13]		1.65[–1]	1.69[–1]	1.70[–1]		5.201	5.201
	1s22s2p2 2D	5.16[–3]	7.51[12]	7.72[12]	7.83[12]	7.84[12]		3.02[–2]	3.11[–2]	3.15[–2]		5.168	5.166

表3类硼S离子的K壳层激发共振态1s2s²2p², 1s2s2p³, 1s2p^{4 2, 4}L(L = S, P, D)的电偶极辐射跃迁线强度S (a.u.)、辐射跃迁率${A_{ik}}$(s^–1) (长度规范${A_{\rm{l}}}$, 速度规范${A_{\rm{v}}}$, 加速度规范${A_{\rm{a}}}$), 跃迁振子强度${f_{ki}}$(长度规范${f_{\rm{l}}}$, 速度规范${f_{\rm{v}}}$, 加速度规范${f_{\rm{a}}}$), 和跃迁波长$\lambda $(?), 方括号的数代表10的幂次方
Table3.Line strengths S (a.u.), radiative transition probabilities ${A_{ik}}$ (length gauge ${A_{\rm{l}}}$, velocity gauge${A_{\rm{v}}}$, acceleration gauge ${A_{\rm{a}}}$) (s^–1), transition oscillator strengths ${f_{ki}}$ (length gauge ${f_{\rm{l}}}$, velocity gauge ${f_{\rm{v}}}$, and acceleration gauge ${f_{\rm{a}}}$), and transition wavelengths $\lambda $ (?) of electric dipole transitions of the K-shell excited resonance states 1s2s²2p², 1s2s2p³, 1s2p^{4 2, 4}L (L = S, P, D) in boron-like sulfur ion. The numbers in square brackets represent the power of 10.

图 1 本文计算的电偶极跃迁振子强度的长度规范值分别与速度规范值及加速度规范值的对比
Figure1. Comparison diagram of the calculated electrical dipole transition oscillator strength values in length gauge with the velocity gauge and acceleration gauge.

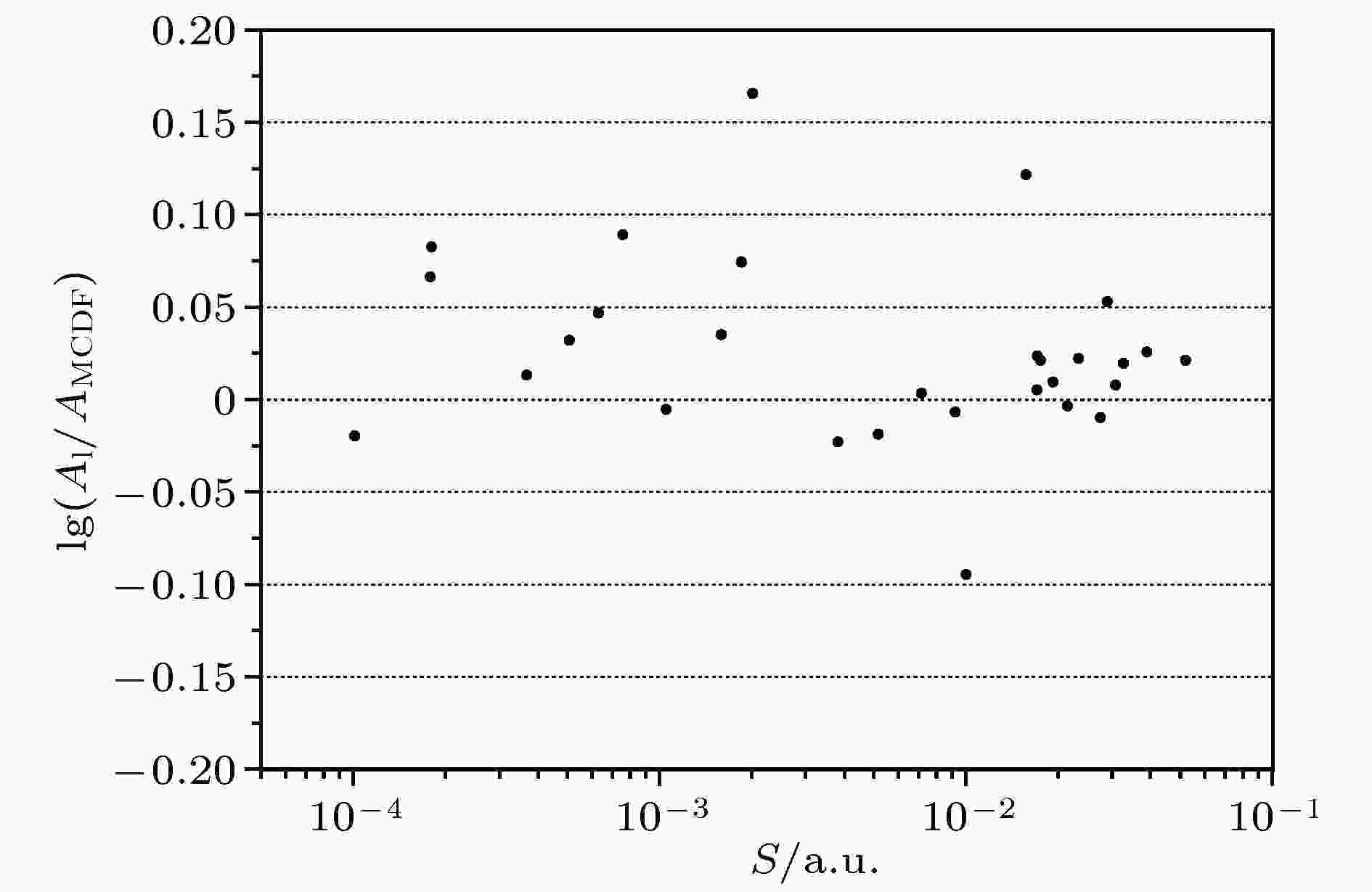图 2 本文计算的长度规范的电偶极辐射跃迁率与MCDF理论计算的跃迁率的对比
Figure2. Comparison diagram of calculated radiative transition rates in length gauge with the theoretical data from MCDF calculations.

俄歇跃迁过程起源于两个激发电子的库仑相互作用, 在类硼S离子K壳层激发共振态的俄歇跃迁过程中, 一个电子去填充K壳层的1s空位, 并且把多余的能量传递给另外一个电子, 通常情况下能量足够把电子离化, 因此接收能量的电子逃逸出系统成为自由电子, 剩余的系统为S¹²⁺离子低位激发态. 利用鞍点复数转动方法, 我们计算了类硼S离子的K壳层激发态1s2s²2p², 1s2s2p³, 1s2p^{4 2, 4}L(L = S, P, D)的俄歇跃迁率和俄歇分支率, 结果列于表4. 计算中主要考虑了以下六个末态: 1s²2s^{2 1}S, 1s²2p^{2 1}S, 1s²2p^{2 1}D, 1s²2p^{2 3}P, 1s²2s2p ¹P, 1s²2s2p ³P, 其对应的能级列于表2. 对比表4中列出的MCDF理论^[17]计算的俄歇跃迁率, 除1s2p⁴共振态外, 本文的计算结果与MCDF的理论计算数值符合的较好. 表5给出了计算的俄歇电子能量. 本文的计算结果与MCDF方法的理论值^[17]约为1.97 eV, 整体上符合得较好. 在俄歇跃迁计算中, MCDF方法对于初态和末态仅采用了35个组态波函数和10个组态波函数. 在本文计算中, 对于初态和末态, 分别采用了4500和300个组态波函数. 由于考虑了更多的组态相互作用, 计算结果更为精确. 目前, 由于缺乏足够的实验和理论数据, 我们无法作出进一步的对比. 通过的俄歇分支率和俄歇电子能量可以更加清晰的了解类硼S离子K壳层激发共振态的俄歇跃迁过程, 综合利用这两者能够很好地对实验中的俄歇电子谱进行标定, 研究实验的动态反应过程. 本文的理论数据可为相关的实验提供有价值的理论数据.

俄歇跃迁通道		俄歇跃迁率/s–1		BR/%	俄歇跃迁通道		俄歇跃迁率/s–1		BR(%)
		本文	文献[17]				本文	文献[17]
1s2s22p2	2S →1s22s2 1S	5.05[13]	8.33[13]	23.3	1s2s(1S)2p3	2Po→1s22s2 1S	6.63[11]	2.33[11]	0.3
	2S →1s22s2p 1Po	6.35[13]	6.02[13]	29.3		2Po→1s22s2p 1Po	1.18[12]	1.46[13]	0.5
	2S →1s22s2p 3Po	1.61[13]	2.06[13]	7.4		2Po→1s22s2p 3Po	1.29[14]	1.22[14]	59.6
	2S →1s22p2 1S	7.10[13]	7.85[13]	32.8		2Po→1s22p2 1S	6.50[12]	5.20[12]	3.0
	2S →1s22p2 1D	1.53[13]	1.48[13]	7.1		2Po→1s22p2 1D	5.25[12]	9.54[12]	2.4
	2P→1s22s2p 1Po	1.82[13]	2.55[13]	14.7		2Po→1s22p2 3P	7.40[13]	7.54[13]	34.2
	2P→1s22s2p 3Po	1.05[13]	7.34[12]	8.5		2Do→1s22s2p 1Po	7.30[12]	8.82[12]	2.8
	2P→1s22p2 1D2	1.97[10]	7.42[12]	0		2Do→1s22s2p 3Po	1.74[14]	1.74[14]	66.1
	2P→1s22p2 3P	9.50[13]	8.68[13]	76.8		2Do→1s22p2 1D	9.55[12]	1.40[13]	3.6
	2D→1s22s2 1S	1.24[14]	1.14[14]	40.3		2Do→1s22p2 3P	7.25[13]	7.66[13]	27.5
	2D→1s22s2p 1Po	6.80[13]	6.42[13]	22.1		4So→1s22p2 3P	3.85[13]	3.88[13]	100
	2D→1s22s2p 3Po	1.72[13]	2.26[13]	5.6	1s2s(3S)2p3	2So→1s22p2 3P	6.55[13]	4.35[13]	100
	2D→1s22p2 1S	3.43[12]	2.82[12]	1.1		2Po→1s22s2 1S	4.33[12]	2.67[12]	1.6
	2D→1s22p2 1D	9.15[13]	9.22[13]	29.8		2Po→1s22s2p 1Po	1.28[14]	1.18[14]	46.9
	2D→1s22p2 3P	3.37[12]	4.47[12]	1.1		2Po→1s22s2p 3Po	5.40[12]	7.38[12]	2.0
	4P→1s22s2p 3Po	1.10[14]	1.18[14]	54.3		2Po→1s22p2 1S	4.54[13]	4.68[13]	16.6
	4P→1s22p2 3P	9.25[13]	9.48[13]	45.7		2Po→1s22p2 1D	6.40[13]	6.23[13]	23.4
1s2p4	2S →1s22s2 1S	2.75[12]	3.04[11]	0.6		2Po→1s22p2 3P	2.58[13]	3.47[13]	9.5
	2S →1s22s2p 1Po	4.15[12]	4.73[12]	1.0		2Do→1s22s2p 1Po	1.76[14]	1.71[14]	54.5
	2S →1s22s2p 3Po	8.57[11]	1.48[12]	0.2		2Do→1s22s2p 3Po	6.85[12]	1.16[13]	2.1
	2S →1s22p2 1S	2.43[14]	3.66[13]	56.3		2Do→1s22p2 1D	1.18[14]	1.19[14]	36.5
	2S →1s22p2 1D	1.81[14]	1.87[14]	41.9		2Do→1s22p2 3P	2.22[13]	1.99[13]	6.9
	2P→1s22s2p 1Po	2.73[11]	5.19[11]	0.1		4So →1s22p2 3P	1.92[14]	2.02[14]	100
	2P→1s22s2p 3Po	2.38[11]	1.86[11]	0.1		4Po→1s22s2p 3Po	1.35[14]	1.38[14]	88.9
	2P→1s22p2 1D2	6.95[10]	2.06[13]	0		4Po→1s22p2 3P	1.68[13]	1.45[13]	11.1
	2P→1s22p2 3P	2.15[14]	1.90[14]	99.8		4Do→1s22s2p 3Po	1.84[14]	1.84[14]	90.4
	2D→1s22s2 1S	2.95[12]	7.35[9]	1.0		4Do→1s22p2 3P	1.96[13]	1.41[13]	9.6
	2D→1s22s2p 1Po	1.35[12]	1.38[12]	0.5
	2D→1s22s2p 3Po	2.73[11]	4.54[11]	0.1
	2D→1s22p2 1S	1.25[13]	4.09[13]	4.2
	2D→1s22p2 1D	2.68[14]	2.74[14]	90.6
	2D→1s22p2 3P	1.05[13]	1.26[13]	3.6
	4P→1s22s2p 3Po	1.96[12]	2.50[12]	0.9
	4P→1s22p2 3P	2.08[14]	2.09[14]	99.1

表4类硼S离子K壳层激发态1s2s²2p², 1s2s2p³, 1s2p^{4 2, 4}L(L = S, P, D)的俄歇跃迁率(s^–1) 和俄歇分支率(BR), 方括号的数表示10的幂次方
Table4.The Auger rates (s^–1) and branching ratios (BR) of the K-shell excited resonance states 1s2s²2p², 1s2s2p³, 1s2p^{4 2, 4}L (L=S, P, D) in boron-like sulfur ion. The numbers in square brackets represent the power of 10.

跃迁通道		本文	文献[17]	跃迁通道		本文	文献[17]
1s2s22p2 2S1/2	1s22s2 1S0	1836.41	1837.80	1s2s(3S)2p3 2S1/2	1s22p2 3P0	1821.85	1825.18
	1s22s2p 1P1	1788.16	1787.75		1s22p2 3P1	1821.27	1824.50
	1s22s2p 3P0	1811.78	1812.97		1s22p2 3P2	1820.17	1823.49
	1s22s2p 3P1	1811.23	1812.44	1s2s(3S)2p3 2P1/2	1s22s2 1S0	1885.82	1888.35
	1s22s2p 3P2	1810.06	1811.23		1s22s2p 1P0	1837.57	1838.30
	1s22p2 1S0	1747.03	1746.35		1s22s2p 3P1	1861.19	1863.52
	1s22p2 1D2	1763.54	1763.33		1s22s2p 3P2	1860.64	1862.99
1s2s22p2 2P1/2	1s22s2p 1P1	1783.02	1782.25		1s22s2p 3P3	1859.47	1861.78
	1s22s2p 3P0	1806.64	1807.47		1s22p2 1S0	1796.44	1796.90
	1s22s2p 3P1	1806.09	1806.94		1s22p2 1D2	1812.95	1813.88
	1s22s2p 3P2	1804.92	1805.74		1s22p2 3P0	1820.94	1823.09
	1s22p2 1D2	1758.40	1757.84		1s22p2 3P1	1820.36	1822.41
	1s22p2 3P0	1766.39	1767.05		1s22p2 3P2	1819.26	1821.40
	1s22p2 3P1	1765.81	1766.37	1s2s(3S)2p3 2P3/2	1s22s2 1S0	1885.63	1888.87
	1s22p2 3P2	1764.71	1765.36		1s22s2p 1P0	1837.38	1838.83
1s2s22p2 2P3/2	1s22s2p 1P1	1784.97	1784.03		1s22s2p 3P1	1861.00	1864.05
	1s22s2p 3P0	1808.59	1809.25		1s22s2p 3P2	1860.45	1863.51
	1s22s2p 3P1	1808.04	1808.72		1s22s2p 3P3	1859.28	1862.31
	1s22s2p 3P2	1806.87	1807.52		1s22p2 1S0	1796.25	1797.43
	1s22p2 1D2	1760.35	1759.62		1s22p2 1D2	1812.76	1814.41
	1s22p2 3P0	1768.34	1768.83		1s22p2 3P0	1820.75	1823.62
	1s22p2 3P1	1767.76	1768.15		1s22p2 3P1	1820.17	1822.94
	1s22p2 3P2	1766.66	1767.14		1s22p2 3P2	1819.07	1821.93
1s2s22p2 2D3/2	1s22s2 1S0	1829.61	1830.38	1s2s(1S)2p3 2P1/2	1s22s2 1S0	1875.27	1877.33
	1s22s2p 1P1	1781.36	1780.34		1s22s2p 1P0	1827.02	1827.28
	1s22s2p 3P0	1804.98	1805.56		1s22s2p 3P1	1850.64	1852.50
	1s22s2p 3P1	1804.43	1805.02		1s22s2p 3P2	1850.09	1851.97
	1s22s2p 3P2	1803.26	1803.82		1s22s2p 3P3	1848.92	1850.77
	1s22p2 1S0	1740.23	1738.94		1s22p2 1S0	1785.89	1785.88
	1s22p2 1D2	1756.74	1755.92		1s22p2 1D2	1802.40	1802.87
	1s22p2 3P0	1764.73	1765.13		1s22p2 3P0	1810.39	1812.08
	1s22p2 3P1	1764.15	1764.45		1s22p2 3P1	1809.81	1811.40
	1s22p2 3P2	1763.05	1763.44		1s22p2 3P2	1808.71	1810.39
1s2s22p2 2D5/2	1s22s2 1S0	1829.37	1830.33	1s2s(1S)2p3 2P3/2	1s22s2 1S0	1875.94	1877.26
	1s22s2p 1P1	1781.12	1780.29		1s22s2p 1P0	1827.69	1827.21
	1s22s2p 3P0	1804.74	1805.51		1s22s2p 3P1	1851.31	1852.43
	1s22s2p 3P1	1804.19	1804.97		1s22s2p 3P2	1850.76	1851.90
	1s22s2p 3P2	1803.02	1803.77		1s22s2p 3P3	1849.59	1850.70
	1s22p2 1S0	1739.99	1738.89		1s22p2 1S0	1786.56	1785.81
	1s22p2 1D2	1756.50	1755.87		1s22p2 1D2	1803.07	1802.80
	1s22p2 3P0	1764.49	1765.08		1s22p2 3P0	1811.06	1812.01
	1s22p2 3P1	1763.91	1764.40		1s22p2 3P1	1810.48	1811.33
	1s22p2 3P2	1762.81	1763.39		1s22p2 3P2	1809.38	1810.32
1s2p4 2S1/2	1s22s2 1S0	1926.23	1930.57	1s2s(3S)2p3 2D3/2	1s22s2p 1P0	1829.45	1831.14
	1s22s2p 1P1	1877.98	1880.52		1s22s2p 3P0	1853.07	1856.36
	1s22s2p 3P0	1901.60	1905.75		1s22s2p 3P1	1852.52	1855.83
	1s22s2p 3P1	1901.05	1905.21		1s22s2p 3P2	1851.35	1854.62
	1s22s2p 3P2	1899.88	1904.01		1s22p2 1D2	1804.83	1806.72
	1s22p2 1S0	1836.85	1839.13		1s22p2 3P0	1812.82	1815.93
	1s22p2 1D2	1853.36	1856.11		1s22p2 3P1	1812.24	1815.25
1s2p4 2P1/2	1s22s2p 1P1	1865.46	1867.17		1s22p2 3P2	1811.14	1814.24
	1s22s2p 3P0	1889.08	1892.39	1s2s(3S)2p3 2D5/2	1s22s2p 1P0	1829.17	1830.60
	1s22s2p 3P1	1888.53	1891.86		1s22s2p 3P0	1852.79	1855.82
	1s22s2p 3P2	1887.36	1890.66		1s22s2p 3P1	1852.24	1855.28
	1s22p2 1D2	1840.84	1842.76		1s22s2p 3P2	1851.07	1854.08
	1s22p2 3P0	1848.83	1851.97		1s22p2 1D2	1804.55	1806.18
	1s22p2 3P1	1848.25	1851.29		1s22p2 3P0	1812.54	1815.39
	1s22p2 3P2	1847.15	1850.28		1s22p2 3P1	1811.96	1814.71
1s2p4 2P3/2	1s22s2p 1P1	1865.22	1866.27		1s22p2 3P2	1810.86	1813.70
	1s22s2p 3P0	1888.84	1891.50	1s2s(1S)2p3 2D3/2	1s22s2p 1P0	1819.51	1819.23
	1s22s2p 3P1	1888.29	1890.96		1s22s2p 3P0	1843.13	1844.45
	1s22s2p 3P2	1887.12	1889.76		1s22s2p 3P1	1842.58	1843.92
	1s22p2 1D2	1840.60	1841.86		1s22s2p 3P2	1841.41	1842.71
	1s22p2 3P0	1848.59	1851.07		1s22p2 1D2	1794.89	1794.81
	1s22p2 3P1	1848.01	1850.39		1s22p2 3P0	1802.88	1804.02
	1s22p2 3P2	1846.91	1849.38		1s22p2 3P1	1802.30	1803.35
1s2p4 2D3/2	1s22s2 1S0	1910.16	1913.47		1s22p2 3P2	1801.20	1802.33
	1s22s2p 1P1	1861.91	1863.42	1s2s(1S)2p3 2D5/2	1s22s2p 1P0	1819.71	1819.38
	1s22s2p 3P0	1885.53	1888.64		1s22s2p 3P0	1843.33	1844.60
	1s22s2p 3P1	1884.98	1888.11		1s22s2p 3P1	1842.78	1844.07
	1s22s2p 3P2	1883.81	1886.91		1s22s2p 3P2	1841.61	1842.86
	1s22p2 1S0	1820.78	1822.02		1s22p2 1D2	1795.09	1794.96
	1s22p2 1D2	1837.29	1839.01		1s22p2 3P0	1803.08	1804.17
	1s22p2 3P0	1845.28	1848.22		1s22p2 3P1	1802.50	1803.50
	1s22p2 3P1	1844.70	1847.54		1s22p2 3P2	1801.40	1802.49
	1s22p2 3P2	1843.60	1846.53	1s2s(3S)2p3 4S3/2	1s22p2 3P0	1807.49	1810.50
1s2p4 2D5/2	1s22s2 1S0	1909.99	1913.40		1s22p2 3P1	1806.91	1809.82
	1s22s2p 1P1	1861.74	1863.35		1s22p2 3P2	1805.81	1808.81
	1s22s2p 3P0	1885.36	1888.57	1s2s(1S)2p3 4S3/2	1s22p2 3P0	1785.26	1785.14
	1s22s2p 3P1	1884.81	1888.04		1s22p2 3P1	1784.68	1784.46
	1s22s2p 3P2	1883.64	1886.84		1s22p2 3P2	1783.58	1783.45
	1s22p2 1S0	1820.61	1821.95	1s2s(3S)2p 3 4P1/2	1s22s2p 3P0	1831.31	1832.66
	1s22p2 1D2	1837.12	1838.94		1s22s2p 3P1	1830.76	1832.13
	1s22p2 3P0	1845.11	1848.15		1s22s2p 3P2	1829.59	1830.93
	1s22p2 3P1	1844.53	1847.47		1s22p2 3P0	1791.06	1792.24
	1s22p2 3P2	1843.43	1846.46		1s22p2 3P1	1790.48	1791.56
1s2s22p2 4P1/2	1s22s2p 3P0	1792.86	1791.05		1s22p2 3P2	1789.38	1790.55
	1s22s2p 3P1	1792.31	1790.51	1s2s(3S)2p3 4P3/2	1s22s2p 3P0	1831.12	1832.56
	1s22s2p 3P2	1791.14	1789.31		1s22s2p 3P1	1830.57	1832.03
	1s22p2 3P0	1752.61	1750.62		1s22s2p 3P2	1829.40	1830.83
	1s22p2 3P1	1752.03	1749.94		1s22p2 3P0	1790.87	1792.14
	1s22p2 3P2	1750.93	1748.93		1s22p2 3P1	1790.29	1791.46
1s2s22p2 4P3/2	1s22s2p 3P0	1793.53	1791.83		1s22p2 3P2	1789.19	1790.45
	1s22s2p 3P1	1792.98	1791.30	1s2s(3S)2p3 4P5/2	1s22s2p 3P0	1831.04	1832.48
	1s22s2p 3P2	1791.81	1790.09		1s22s2p 3P1	1830.49	1831.95
	1s22p2 3P0	1753.28	1751.40		1s22s2p 3P2	1829.32	1830.75
	1s22p2 3P1	1752.70	1750.72		1s22p2 3P0	1790.79	1792.06
	1s22p2 3P2	1751.60	1749.71		1s22p2 3P1	1790.21	1791.38
1s2s22p2 4P5/2	1s22s2p 3P0	1794.37	1792.66		1s22p2 3P2	1789.11	1790.37
	1s22s2p 3P1	1793.82	1792.13	1s2s(3S)2p3 4D1/2	1s22s2p 3P0	1823.15	1824.54
	1s22s2p 3P2	1792.65	1790.92		1s22s2p 3P1	1822.60	1824.01
	1s22p2 3P0	1754.12	1752.23		1s22s2p 3P2	1821.43	1822.80
	1s22p2 3P1	1753.54	1751.55		1s22p2 3P0	1782.90	1784.11
	1s22p2 3P2	1752.44	1750.54		1s22p2 3P1	1782.32	1783.43
1s2p4 4P1/2	1s22s2p 3P0	1873.83	1876.31		1s22p2 3P2	1781.22	1782.42
	1s22s2p 3P1	1873.28	1875.78	1s2s(3S)2p3 4D3/2	1s22s2p 3P0	1823.15	1824.49
	1s22s2p 3P2	1872.11	1874.57		1s22s2p 3P1	1822.60	1823.96
	1s22p2 3P0	1833.58	1835.88		1s22s2p 3P2	1821.43	1822.75
	1s22p2 3P1	1833.00	1835.20		1s22p2 3P0	1782.90	1784.06
	1s22p2 3P2	1831.90	1834.19		1s22p2 3P1	1782.32	1783.39
1s2p4 4P3/2	1s22s2p 3P0	1873.24	1875.77		1s22p2 3P2	1781.22	1782.38
	1s22s2p 3P1	1872.69	1875.24	1s2s(3S)2p3 4D5/2	1s22s2p 3P0	1823.06	1824.41
	1s22s2p 3P2	1871.52	1874.03		1s22s2p 3P1	1822.51	1823.88
	1s22p2 3P0	1832.99	1835.34		1s22s2p 3P2	1821.34	1822.67
	1s22p2 3P1	1832.41	1834.66		1s22p2 3P0	1782.81	1783.98
	1s22p2 3P2	1831.31	1833.65		1s22p2 3P1	1782.23	1783.30
1s2p4 4P5/2	1s22s2p 3P0	1871.99	1874.50		1s22p2 3P2	1781.13	1782.29
	1s22s2p 3P1	1871.44	1873.96	1s2s(3S)2p3 4D7/2	1s22s2p 3P1	1822.20	1823.70
	1s22s2p 3P2	1870.27	1872.76		1s22s2p 3P2	1821.03	1822.50
	1s22p2 3P0	1831.74	1834.07		1s22p2 3P1	1781.92	1783.13
	1s22p2 3P1	1831.16	1833.39		1s22p2 3P2	1780.82	1782.12
	1s22p2 3P2	1830.06	1832.38

表5类硼S离子K壳层激发态1s2s²2p², 1s2s2p³, 1s2p^{4 2, 4}L(L = S, P, D)的俄歇电子能量(单位: eV)
Table5.The Auger electron energies of the K-shell excited resonance states 1s2s²2p², 1s2s2p³, 1s2p^{4 2, 4}L (L = S, P, D) in boron-like sulfur ion (unit: eV).

本文采用多组态鞍点变分方法, 在考虑相对论修正、质量极化效应、QED效应、共振能级移动的基础上, 充分考虑组态相互作用, 计算了类硼S离子K壳层激发共振态能级. 利用精确计算的波函数, 对这些K壳层激发共振态重要的电偶极辐射跃迁的线强度、振子强度、跃迁率、跃迁波长数据进行了系统计算, 得到了与其他文献符合较好的结果. 本文计算的电偶极跃迁振子强度的长度规范、速度规范、加速度规范结果总体显示出良好的一致性, 从而证明本文计算的波函数是足够精确的. 利用鞍点复数转动方法, 对这些K壳层激发共振态的俄歇跃迁率、俄歇分支率、俄歇电子能量进行了计算, 并与其他理论结果进行了对比. 本文的理论计算结果可为将来相关的实验光谱和俄歇电子谱线标定提供有价值的理论参考数据.