摘要: 为构造一类扰动Kadomtsev-Petviashvili (KP)方程的级数解, 利用同伦近似对称法求出三种情形下具有通式形式的相似解以及相应的相似方程. 而且, 对于第三种情形下的前几个相似方程, 雅可比椭圆函数解亦遵循共同的表达式, 这可以产生形式紧凑的级数解, 从而为收敛性的探讨提供便利: 首先, 对于扰动KP方程的微扰项, 给定
$u$ 关于变量
$y$ 的导数阶数
$n$ , 若
$n\leqslant 1$ (
$n\geqslant 3$ ), 则减小(增大)
$|a/b|$ 致使收敛性改善; 其次, 减小
$\varepsilon$ ,
$|\theta-1|$ 以及
$|c|$ 均有助于改进收敛性. 在更一般情形下, 仅当微扰项的导数阶数为偶数时, 扰动KP方程才存在雅可比椭圆函数解.
关键词: 同伦近似对称法 /
扰动Kadomtsev-Petviashvili方程 /
级数解 /
收敛性 English Abstract Convergence for Jacobi elliptic function series solutions to one kind of perturbed Kadomtsev-Petviashvili equations Jiao Xiao-Yu 1 ,Jia Man 2 ,An Hong-Li 3 1.School of Applied Mathematics, Nanjing University of Finance and Economics, Nanjing 210023, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11505094, 11775116) and the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20150984).Received Date: 09 March 2019Accepted Date: 12 May 2019Available Online: 01 July 2019Published Online: 20 July 2019Abstract: This paper is devoted to constructing series solutions to one kind of perturbed Kadomtsev-Petviashvili (KP) equations, of which the perturbation terms are of all six-order derivatives of space variable $x$ and $y$ . First, by making the series solutions expansion with respect to the homotopy parameter $q$ , the homotopy model of the perturbed KP equations can be decomposed into infinite number of approximate equations of the general form. Second, Lie symmetry method is applied to these approximate equations to achieve similarity solutions and the related similarity equations with common formulae in three cases. Third, for the first few similarity equations in the third case, Jacobi elliptic function solutions are constructed through a step-by-step procedure and are also subject to common formulae for each equation of the whole kind of perturbed KP equations. Finally, one kind of compact series solutions for the original perturbed KP equations is obtained from these Jacobi elliptic function solutions. The convergence of these series solution is dependent on perturbation parameter $\epsilon$ , auxiliary parameter $\theta$ and arbitrary constants $\{a, b, c\}$ , among which the most prominent is decreasing arbitrary constant $c$ or perturbation parameter $\varepsilon$ . For the perturbation term in perturbed KP equations, given the derivative order $n$ of $u$ with respect to $y$ , smaller (greater) $|a/b|$ causes the improved convergence provided $n\leqslant 1$ ($n\geqslant 3$ ). Nonetheless, the decrease of arbitrary constant $|c|$ or $|a/b|$ leads to the enlargement of period in a certain direction and thus should be specified appropriately. This paper also considers the perturbed KP equations with more general perturbation terms. Only if the derivative order of the perturbation term is an even number, do Jacobi elliptic function series solutions exist for perturbed KP equations. The existence of series solutions can serve as a criterion of solvability for perturbed equations.Keywords: approximate homotopy symmetry method /perturbed Kadomtsev-Petviashvili equation /series solutions /convergence 全文HTML --> --> --> 1.引 言 对于源于现实问题中各种现象的非线性方程, 人们通常研究其数值解. 除去数值解之外, 近似解析解也有助于非线性方程的研究. 非线性方程附加了微扰项则变成扰动非线性方程, 这类方程的近似解析解可以利用扰动理论[1 ,2 ] 结合精确求解方法进行构造.[3 ,4 ] 中的经典或非经典李群法[5 ] 、李对称方法与直接法[6 ] 进行求解. 这些方法通过减少自变量的个数实现偏微分方程的化简. 作为直接法的一种修正, 改进的直接法[7 ,8 ] 貌似与李群理论无关, 但是却可以重构李对称群甚至离散变换群.[9 ] 而产生, 这套方案引领了诸如孤立子、cnoidal周期波与Painlevé波等不同类型非线性波之间相互作用的研究[10 ,11 ] .[12 ] 提出的近似对称法实际上是对称群的近似, 因为对称群生成元推广至扰动形式; 而Fushchich等[13 ] 提出的近似对称法则是基于扰动方程近似子方程的精确对称. 文献[14 ,15 ]对两种方法进行了比较, 说明第二种方法优于第一种方法. 文献[16 ,17 ]进一步推广了第二种近似对称法, 得到了通式形式的约化方程. 第二种近似对称法甚至可以求出扰动非线性方程的级数解[18 ] . 近似直接法[16 ] 改为利用直接法求解这些子方程, 则可以得到与近似对称法相同的约化结果.[19 -21 ] , 该方法通过将非线性方程分解为无穷多线性子方程实现非线性方程的化简与求解. 此方法适用于非扰动方程, 因而较扰动理论优越, 甚至能够求出扰动方法、人工参数法[22 ] 、$ \delta $ 扰动展开法[23 ] 以及Adomian分解法[24 ] 求解的级数解.[25 ] 与同伦分析法的主要区别在于, 同伦近似对称法将非线性方程分解为无穷多非线性子方程. 类似地, 同伦结合近似直接法可以得到同伦近似直接法[26 ] .2 节, 对于具有相似微扰项的一类扰动Kadomtsev-Petviashvili (KP)方程, 根据同伦近似对称法, 无穷多约化方程以及约化解的通式形式得以构造. 前几个约化方程的雅可比椭圆函数解亦具有通式形式. 第3 节主要涉及级数解的收敛性的讨论. 第4 节是结论部分, 针对更加广泛的微扰项, 讨论了扰动KP方程雅可比椭圆函数级数解的存在性.2.扰动KP方程的同伦近似对称 扰动KP方程形如[27 ] 添加微扰项$ \varepsilon E\left( u \right) $ 而产生的:$ u_{x^3} = u_{xxx} $ 的记号.q 由0变到1时, 逐渐由KP方程转变为扰动KP方程, 这体现了由简单到复杂的渐变过程. 其中, $ \theta\neq1 $ 是辅助参数. 暂取定一类特殊微扰项$\varepsilon E\left( u \right) = \varepsilon {u_{{x^{6 - n}}{y^n}}},\;\left( {n = 0,\;1,\; \cdots,\;6} \right)$ , 即因变量关于空间变量$\left\{ {x,y} \right\}$ 的所有六阶导数. 关于同伦参数q 的级数展开$ u_{-1} = 0 $ . 本文所有负指标量均取0. 这些近似子方程的线性化方程为$ \left\{ {X,\;Y,\;T,\;{U_k}\;\left( {k = 0,\;1,\; \cdots } \right)} \right\}$ 的变量为$ \left\{ {x,\;y,\;t,\;{u_k}\;\left( {k = 0,\;1,\; \cdots } \right)} \right\} $ .5 )式—(7 )式联立用于决定$\{X,\;Y,$ $T,\;{U_k}\} $ $\left( {k = 0,\;1,\; \cdots } \right) $ . 取定n , 将(7 )式代入(6 )式, 利用(5 )式消去$ u_{k,xt} $ , 并且将$ u_k $ 的所有导数系数取0, 得到关于$ \left\{ {X,\;Y,\;T,\;{U_k}\;\left( {k = 0,\;1,\; \cdots } \right)} \right\} $ 的无数方程组成的决定方程组. 为简化求解, 仅考虑(5 )式的前几个方程. 例如限定(5 )式中的k 的范围$ k\in\{0, 1, 2\} $ . 易知$ \{X,\ Y,\ T,\ U_0,\ U_1,\ U_2\} $ 的变量减少为$ \{x,\ y,\ t,\ u_0,\ u_1,\ u_2\} $ , 尝试不同的n 的取值, 反复求解决定方程组, 可以推断决定方程组的解形如C 1 ，C 2 都是任意常数; f (t )是关于t 的任意函数. 满足$ \delta_{0,0} = 1 $ 以及$ \delta_{k,0} = 0,\ (k\neq0) $ 的记号$ \delta_{i,j} $ 亦适用于下文. 令(7 )式中的所有$ \sigma_k $ 取0, 求解相应的特征方程, 则可以确定(5 )式的相似解.情形1: 当$ C_1\neq0 $ 时, 不失一般性, 做变换$ C_2\mapsto C_1a $ , $ C_3\mapsto C_1b $ , $ f(t)\mapsto C_1f(t) $ , 使得如下的相似解不会出现$ C_1 $ 5 )式约化为统一形式情形2: 当$ C_1 = 0 $ , $ C_2\neq0 $ 时, 不失一般性, 做变换$ C_3\mapsto C_2a $ , $ f(t)\mapsto C_2f(t) $ , 求解特征方程, 可以得出相似解5 )式约化为统一形式情形3: 当$ C_1 = 0 $ , $ C_2 = 0 $ , $ C_3\neq0 $ 时, 将$ C_3 $ 改写为a , 可得相似解5 )式约化为统一形式$ k $ 给定, 且$ \{P_0,\ P_1,\ \cdots,\ P_{k-1}\} $ 已知, 以上三种情况的相似方程显然是关于$ P_k $ 的四阶偏微分方程.14 )式中约化方程的诸如雅可比椭圆函数形式的特解, 做出假设$ \{f_{k,i},\ g\} $ 是关于所含变量的待定函数. 所有$ f_{k,i} $ 都不是$ \{{\rm sn}^i(g(\xi,t),m),\ i = 0,\ 1,\ 2,\ \cdots\} $ 的线性组合. 由于(14 )式中的系数包含$ f(t) $ 及其导数, 所以这些系数的化简可以通过假设$ f(t) $ 为一个常数b 实现. 此时, 这些系数退化为常数.18 ]中关于各阶约化方程的求解过程, (15 )式中$ P_k $ 的确定也是通过分步求解过程实现的. 在第k 步中, 将已知解$ \{P_0,\ P_1,\ \cdots,\ P_{k-1}\}$ 以及未知解$ P_k $ 代入(14 )式中的k 阶方程, 再取所有含有$\left\{ {{\rm{sn}}\left( {g\left( {\xi ,t} \right),m} \right),\;{\rm{cn}}\left( {g\left( {\xi ,t} \right),m} \right),{\rm{dn}}\left( {g\left( {\xi ,t} \right),m} \right)} \right\} $ 的各项系数为0, 则可以得到(15 )式中各项系数${f_{k,i}}\left( {\xi ,t} \right) $ 的方程组. 通过求解这些方程组, 再回代入(15 )式, 即可得到约化方程(14 )中的前几个方程的雅可比椭圆函数解(见附录 ).14 )式中的约化方程, 则可以求出$ \{P_4,\ P_5,\ P_6, \cdots\} $ 等更多的解. 易知每个$ P_k $ 都是k 项$\left\{ {{\rm{s}}{{\rm{n}}^l}\left( {c\xi + h,m} \right),l = 0,\;2,\;4,\; \cdots ,\;2\left( {k + 1} \right)} \right\}$ 的线性组合. 当k 增加时, $ P_k $ 表达式中的线性组合系数的复杂程度迅速增加.3.扰动KP方程的级数解 在$ q = 1 $ 条件下, 将(13 )式以及附录 中的雅可比椭圆函数解代入(4 )式, 提取关于$ {\rm sn}(c\xi+h,m) $ 的不同幂次的系数, 可以将级数解重新表示为如下紧凑形式$ a_{k,i} $ 与$ b_{k,i} $ 只包含常数m . 容易验证, 若$ \theta = 0 $ , 该级数解一定是近似对称法所得级数解.$ [-1,\ 1] $ , 所以, 为了确保(16 )式的收敛性, 须满足$ \lim\limits_{k\rightarrow\infty}|A_k| = 0 $ . 显而易见, 当k 增加时, 减小$ \epsilon $ , $ |\theta-1| $ 或者$ |c| $ 有助于减小$ |A_k| $ . 任意常数a 和b 对于收敛性的影响需另当别论. 尤其需要注意$ A_k $ 之中${\left[ {a}/{{{(6b)}}} \right]^{\left[ {\left( {2 - n} \right)i + n} \right]}}$ 的幂次$\left[ {\left( {2 - n} \right)i + n} \right]$ . 当$ n\geqslant 3 $ 时, 对于$ i\geqslant k $ 有$ (2-n)i < 0 $ , 仅当$ |a/(6b)| > 1 $ 时, $\mathop {\lim }\limits_{i \to \infty } {\left[ a/(6b) \right]^{\left[ {\left( {2 - n} \right)i + n} \right]}} = 0$ 成立, 此时增大$ |a/b| $ 可改善收敛性; 当$ n = 2 $ 时, $ (2-n)i+n = 2 $ . 任意常数a 和b 与收敛性之间没有明显关系; 当$ n \!\leqslant 1\! $ 时, $ (2-n)i \! >\! 0 $ . 仅当$ |a/6b| \!<\! 1 $ 时, $\mathop {\lim}\limits_{i \to \infty } {\left( {{a}/{{6b}}} \right)^{\left[ {\left( {2 - n} \right)i + n} \right]}} $ = 0成立. 此时, 减小$ |a/b| $ 改善收敛性.$ t = 0 $ 且$ y = 0 $ 时, 取$ \alpha = 1,$ h (t ) = t , m = 0.5, c = 1以及$\varepsilon = 0.1$ , 在图1 —图4 中对截断级数解关于变量x 做图, 这些图可以说明辅助参数$ \theta $ 与比值$ |a/b| $ 如何影响级数解的收敛性. 实线、虚线、点线、点划线分别表示k 取值$ \{0,\ 1,\ 2,\ 3\} $ 情形下的级数解$ \sum_{i = 0}^ku_k $ . 在这些截线图中, 相邻曲线之间相对距离的变化趋势可用于研究级数解的收敛性. 当k 增加时, 若相邻曲线之间的相对距离显著减少, 则收敛性得以保证, 相应区域可视为收敛域. 从这些截线图容易看出, 相邻曲线之间最大相对距离的区域恰好是波峰与波谷区域. 发散区域可以从波峰与波谷区域中寻找.图 1 当n = 1, α = 1, h (t ) = t , m = 0.5, c = 1, ε = 0.1, a = 2b 并且t = 0, y = 0时, 截断级数解$\sum\nolimits_{i = 0}^k {{u_k}\left( {k = 0,1,2,3} \right)} $ 的截线图Figure1. Transversals of truncated series solution $\sum\nolimits_{i = 0}^k {{u_k}} $ for $\left( {k = 0,1,2,3} \right)$ when n = 1, α = 1, h (t ) = t , m = 0.5, c = 1, ε = 0.1, a = 2b and t = 0, y = 0图 4 当n = 3, α = 1, h (t ) = t , m = 0.5, c = 1, ε = 0.1, a = b /2并且t = 0, y = 0时, 截断级数解$\sum\nolimits_{i = 0}^k {{u_k}\left( {k = 0,1,2,3} \right)}$ 的截线图Figure4. Transversals of truncated series solution $\sum\nolimits_{i = 0}^k {{u_k}}$ for $\left( {k = 0,1,2,3} \right)$ when n = 3, α = 1, h (t ) = t , m = 0.5, c = 1, ε = 0.1, a = b /2 and t = 0, y = 0图1 —图4 中的每个子图(a), (b), (c), (d)分别对应参数$ \theta $ 取值0.90, 0.99, 1.01, 1.10. 图1 和图2 取值$ n = 1 $ , 而图3 和图4 取值$ n = 3 $ . 图1 和图3 取定$ a = 2b $ , 而图2 和图4 取定$ a = b/2 $ . 从每个图的各个子图之间的比较易知, $ \theta = 0.99 $ 以及$ \theta = 1.01 $ 两种情形的级数解的收敛性明显强于$ \theta = 0.90 $ 以及 $ \theta = 1.10 $ 两种情形. 于是, 辅助参数愈接近1, 级数解的收敛性愈好.图 2 当n = 1, α = 1, h (t ) = t , m = 0.5, c = 1, ε = 0.1, a = b /2并且t = 0, y = 0时, 截断级数解$\sum\nolimits_{i = 0}^k {{u_k}\left( {k = 0,1,2,3} \right)} $ 的截线图Figure2. Transversals of truncated series solution $\sum\nolimits_{i = 0}^k {{u_k}}$ for $\left( {k = 0,1,2,3} \right)$ when n = 1, α = 1, h (t ) = t , m = 0.5, c = 1, ε = 0.1, a = b /2 and t = 0, y = 0图 3 当n = 3, α = 1, h (t ) = t , m = 0.5, c = 1, ε = 0.1, a = 2b 并且t = 0, y = 0时, 截断级数解$\sum\nolimits_{i = 0}^k {{u_k}\left( {k = 0,1,2,3} \right)}$ 的截线图Figure3. Transversals of truncated series solution $\sum\nolimits_{i = 0}^k {{u_k}}$ for $\left( {k = 0,1,2,3} \right)$ when n = 3, α = 1, h (t ) = t , m = 0.5, c = 1, ε = 0.1, a = 2b and t = 0, y = 0图1 和图2 的唯一区别是常数a 和b . 比较图1 和图2 的对应图形可得, $ a = b/2 $ 情形的收敛性强于$ a = 2b $ 情形. 同样方式, 图3 和图4 的唯一区别也是常数a 和b . 比较图3 和图4 的对应图形可得, $ a = 2b $ 情形的收敛性强于$ a = b/2 $ 情形. 由于图1 和图2 区别于图3 和图4 之处仅是微扰项中n 关于变量y 的导数阶数n , 这也可以说明, 若$ n\leqslant 1 $ , $ |a/b| $ 取值越小收敛性越好; 若$ n\geqslant 3 $ , $ |a/b| $ 取值越大收敛性越好.16 )的表达式, $ A_k $ 中的${\left[ {{c^2}\varepsilon \left( {\theta - 1} \right)} \right]^{i - 1}}$ 表明, 满足$\left| {{c^2}\varepsilon \left( {\theta - 1} \right)} \right| < 1$ 且减小$\left| {{c^2}\varepsilon \left( {\theta - 1} \right)} \right|$ 可以改善级数解的收敛性. 减小$ c^2 $ , $\varepsilon $ , $\left| {\theta - 1} \right|$ 对收敛性的改善效果基本相同, 但是三者应区分对待. 首先, 扰动参数$\varepsilon $ 是小参数, 表明实际问题中微扰因素的强弱, 具体取值取决于实际问题. 其次, 在同伦模型(3 )式中, $ \theta $ 越接近1, 该模型越接近KP方程而不是扰动KP方程, 从而级数解(16 )式更好地刻划KP方程而不是扰动KP方程. 最后, 减小$ |c| $ 有利于改善收敛性, 但是, $ |c| $ 并不是越小越好, 顾及(13 )式中的相似变量$\xi = y - \dfrac{{ax}}{{6f\left( t \right)}}$ 和$ f(t) = b $ , 级数解(16 )式可以化为c 的取值对级数解的形态有很大影响: 第一, 减小$ |c| $ 致使级数解的周期变大, 波动愈加平缓; 第二, 减小$ |c| $ 时, $ (b/a)(h_t/c)$ 会使级数解急剧增加或减小, 级数项的系数$ c^2 $ 会使级数解急剧减小. 所以, 减小$ |c| $ 也应适度. 此外, 此级数解也表明: 减小$ |a/b| $ 致使x 轴方向周期变大.4.总结与讨论 总之, 对于微扰项为$\varepsilon E\left( u \right) = \varepsilon {u_{{x^{6 - n}}{y^n}}},$ $\left( {n = 0,\;1,\; \cdots ,\;6} \right) $ 的一类扰动KP方程, 同伦近似对称法可以求出无穷多相似方程和对应相似解的通式. 通过分步求解的方法可以求解前几个相似方程的雅可比椭圆函数解, 值得注意的是, 这些雅可比椭圆函数解亦具有通式形式.$\varepsilon E\left( u \right) = \varepsilon {u_{{x^{p - n}}{y^n}}},$ $\left( {p \geqslant 6,\;n = 0,\;1,\; \cdots ,\;p} \right)$ , 同伦近似对称法亦适用. 通过关于p 以及n 不同取值的反复计算, 可以发现, 相似解(11 )式和(13 )式仍然有效. 而且, 近似方程、相似方程以及相应的相似解都具有通式形式. 然而, 仅当p 为偶数时, 才可以解出约化方程的雅可比椭圆函数解. 并且, 这些雅可比椭圆函数解亦具有类似附录中雅可比椭圆函数解的通式形式, 从而得出原扰动KP方程的级数解. 所以, p 为偶数时扰动KP方程(1 )的可解性强于p 为奇数时的情况. 在某种程度上, 扰动非线性方程是否有雅可比椭圆函数(或双曲正切函数)形式的级数解可用于可解性优劣的判定, 从而确立为原扰动方程可解性的一个判断依据. 关于可解性的全面的讨论见文献[28 ].$ \{a,\ b,\ c\} $ , 扰动参数$\varepsilon $ 以及辅助参数$ \theta $ . 然而, 任意常数$ \{a,\ b,\ c\} $ 的调整会导致级数解的周期随之显著变化. 所以, 减小扰动参数$\varepsilon $ 是改进收敛性最便捷最有效的手段. 不同于任意常数$ \{a,\ b,\ c\} $ , 调整扰动参数不会显著影响级数解的形态.附录 (14 )式的雅可比椭圆函数解 c 为任意常数. 
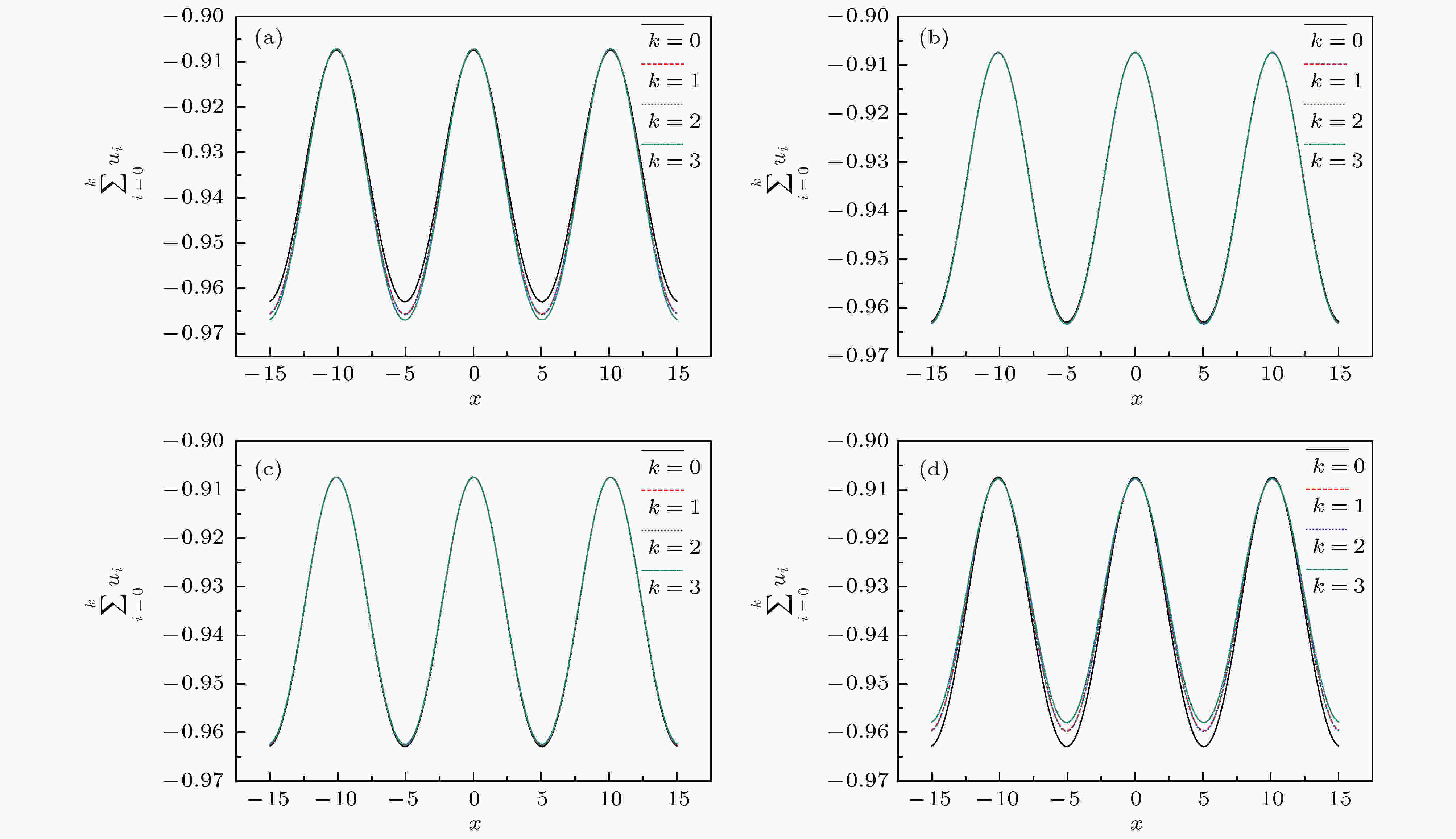图 1 当n = 1, α = 1, h(t) = t, m = 0.5, c = 1, ε = 0.1, a = 2b并且t = 0, y = 0时, 截断级数解
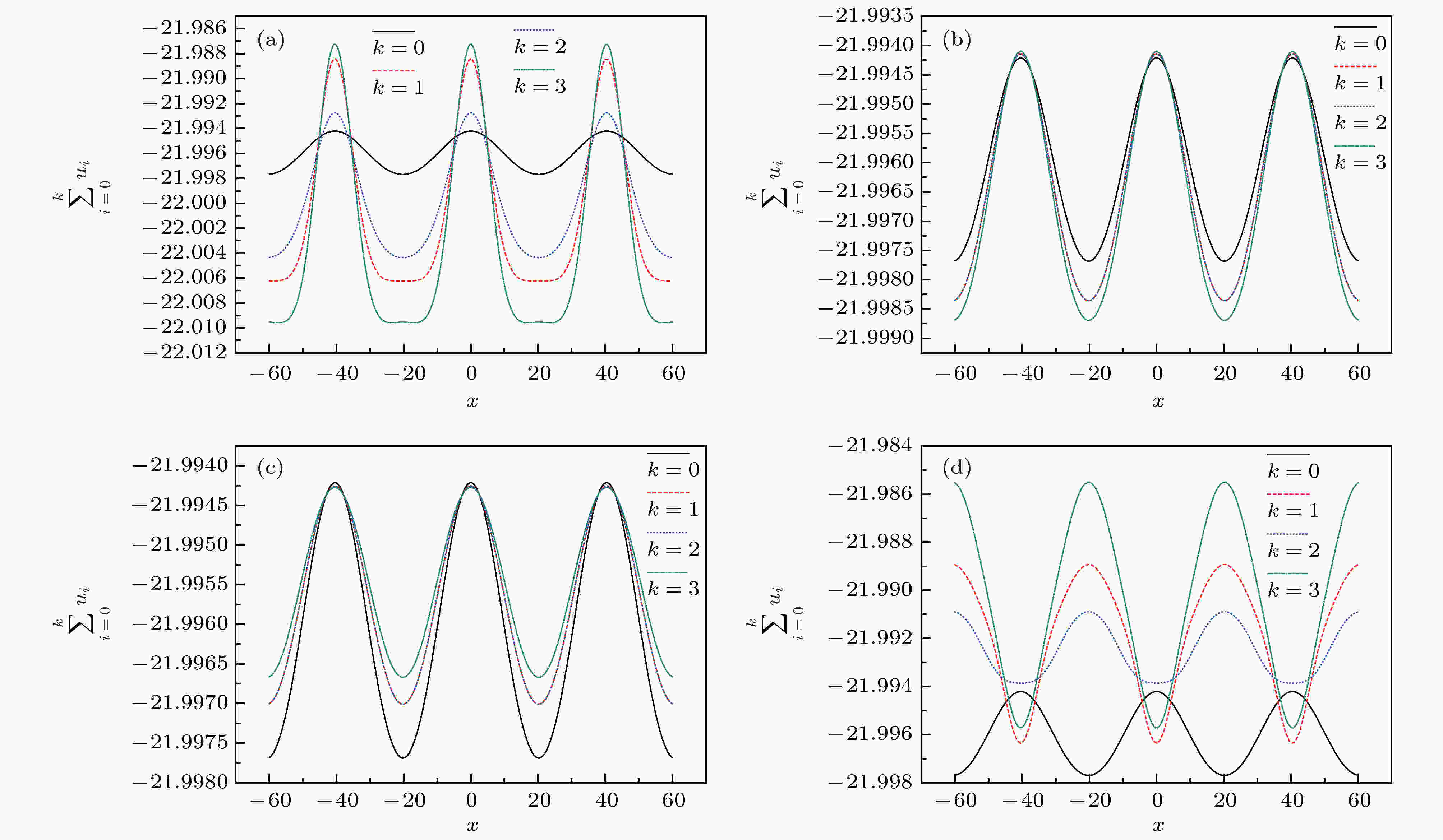图 4 当n = 3, α = 1, h(t) = t, m = 0.5, c = 1, ε = 0.1, a = b/2并且t = 0, y = 0时, 截断级数解
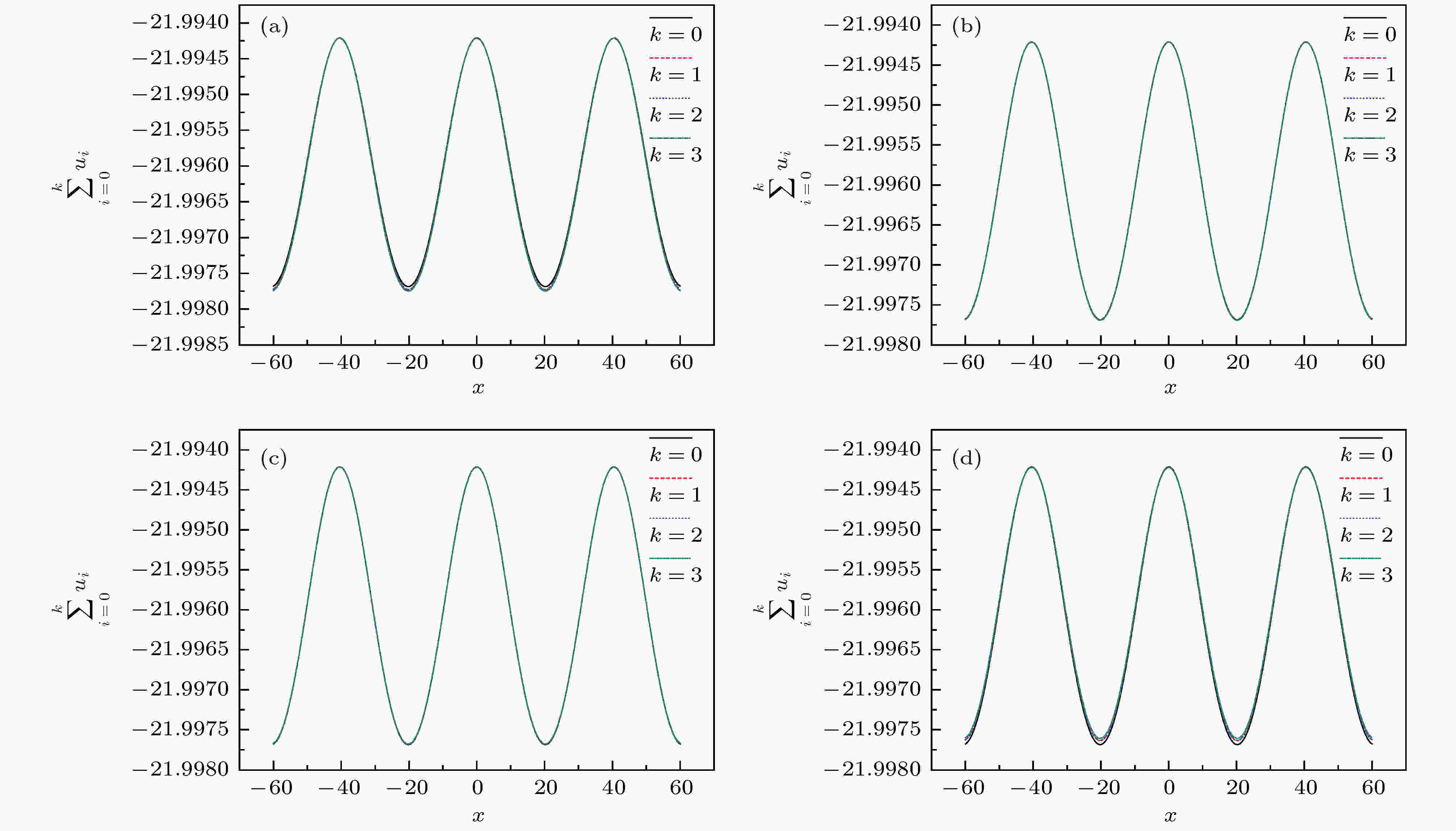图 2 当n = 1, α = 1, h(t) = t, m = 0.5, c = 1, ε = 0.1, a = b/2并且t = 0, y = 0时, 截断级数解
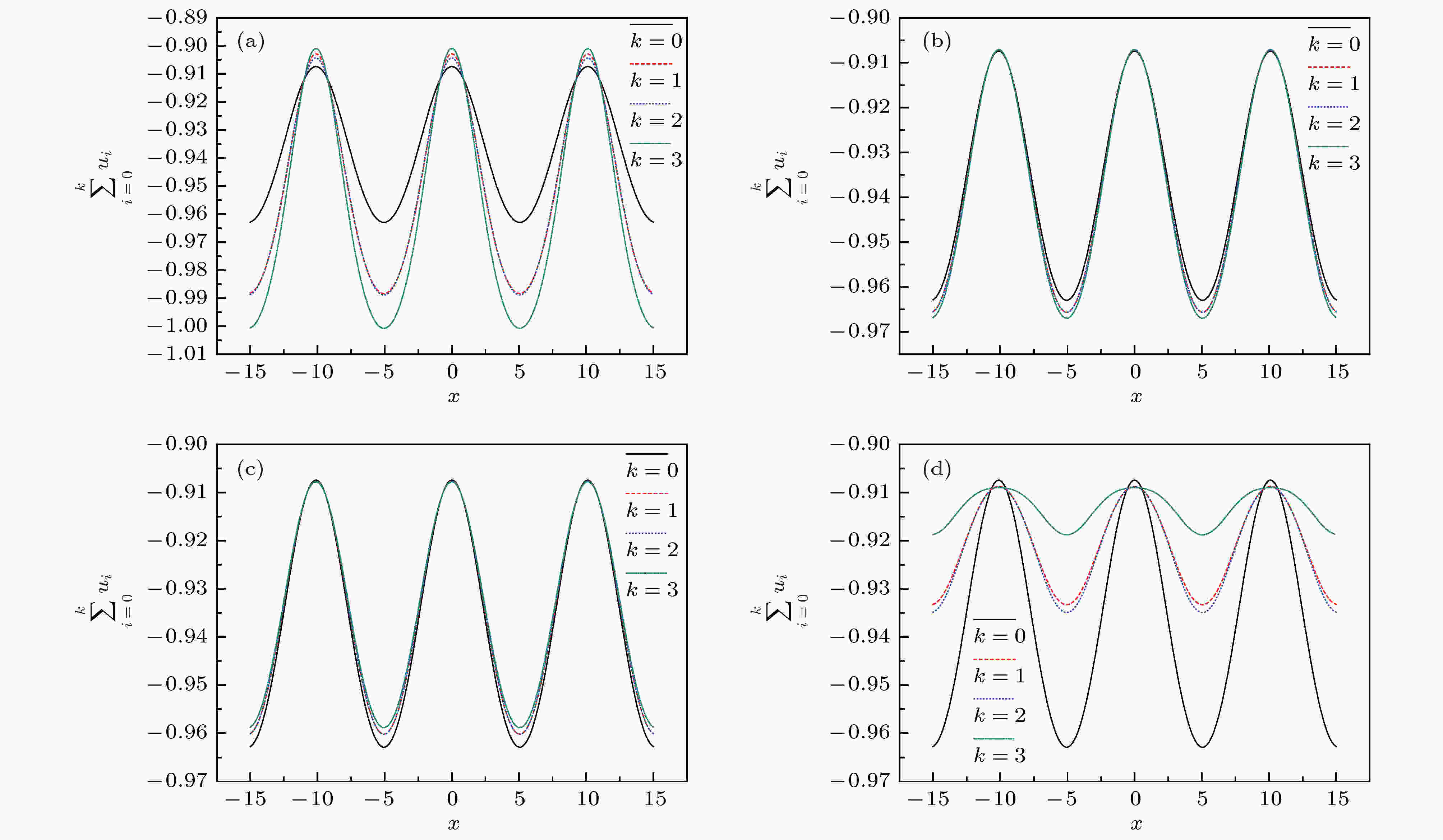图 3 当n = 3, α = 1, h(t) = t, m = 0.5, c = 1, ε = 0.1, a = 2b并且t = 0, y = 0时, 截断级数解
