摘要:井筒电磁法作为一种高效的地球物理勘探技术特别适合我国地形复杂地区(沙漠、高山等)的油气资源勘探. 地形起伏区域对井筒电磁响应的观测具有严重影响, 但到目前为止人们对三维井筒电磁地形效应特征的研究十分有限. 本文提出基于区域划分的积分方程法模拟带地形频率域井筒电磁系统响应, 与基于偏微分方程的有限差分、有限单元法相比, 该方法能更高效地模拟地形响应. 首先根据地形起伏情况定义感应数, 将地形条件下目标体的井筒电磁场模拟区域划分为参考模型、背景介质及目标体介质分布子区域, 针对各子区域的模拟计算特点, 配置Anderson算法、稳定型双共轭梯度-快速傅里叶积分方程算法, 从而获得三维地形频率域井筒电磁场响应. 通过将计算结果与半空间模型的Anderson算法解析解、带山谷地形模型的其他已发表的三维边界积分方程结果进行对比, 检验了本文算法的精度及高效性. 最后, 系统分析了山谷地形对井筒电磁地井观测系统电磁场响应的影响特征. 本文研究结果对三维井筒电磁地形效应的识别和校正具有指导意义.
关键词: 区域积分方程/
三维地形响应/
井筒电磁/
地井观测

English Abstract

全文HTML

--> --> -->

我国油气资源短缺已经成为国民经济发展的瓶颈, 但现有油气储量的采收率仍然不高, 大量剩余油气资源难以发现和采出. 发展地球物理新技术对于剩余油气储层的发现、油气动态开采过程的监测及采收率的提高具有重要意义. 与常规的重力法、磁法及地震法等方法相比, 电磁法由于在探测油气介质时电阻率、极化率等参数变化相对波速、密度等参数更敏感, 而成为油气储层探测最重要的手段之一. 对地面电磁勘探方法而言, 发射源和接收器均布置于地面之上, 地表电磁噪声及围岩介质的滤波作用, 使得地面电磁接收数据的信噪比较低. 随着研究的深入, 油气储层电磁探测研究的方向逐渐转入地下^[1]. 井筒电磁法的独特优点在于将接收或发射装置或者二者均放置于井中特定深度, 因而对于井中发射而言, 可对目标层位形成最直接的激发; 而对于井中接收来说, 由于井中电磁噪音平静, 所以目标体异常信号几乎不被背景介质滤波衰减, 从而具有较高信噪比^[2].
在复杂介质(如起伏地形)电磁场正演模拟方法中, 基于非结构化网格、无网格及自适应网格有限元法开展的数值模拟研究是当前的主流^[3-4], 采用有限差分法^[5]及派生的有限体积法^[6]开展复杂介质电磁场模拟的研究亦不断涌现. 微分方程法模拟复杂介质的、电磁响应需谨慎处理边界截断、误差积累、场源奇异性等问题. 对带金属套管的地井电磁模拟而言, 微分方程法还需特别解决包含井孔在内的特殊边界和网格剖分问题, 这在当前仍属于一项艰巨的任务^[7,8]. 而积分方程法模拟仅需要局部空间离散, 求解精度高, 相较于微分方程法无需考虑金属井孔电磁模拟问题, 在三维井筒电磁场模拟中, 这一优势更为明显^[9-13].
尽管积分方程法在涉及井筒的大尺度电磁场模拟过程中比微分方程有优势, 但数值求解积分方程比求解微分方程需处理更为困难的数学问题. 针对电性多面体问题, Tiberi等^[13]提出解析微分特征基函数的谱域积分方程法, Nie等^[14]采用预校正的快速傅里叶变换法开展随钻测井电磁场模拟, Chobanyan等^[15]提出双高阶大范围的广义体-面积分方程法. 目前, 国内外开展积分方程法模拟带地形频率域电磁场响应的研究工作还很少见. 针对二维地电模型模拟问题, 国内外****多数采用矩形单元及不同阶数的积分方程法开展数值模拟, 对复杂模型的剖分通常采用加密网格方法以获取高精度数值模拟结果. 但矩形单元很难精确模拟复杂地形和复杂地下目标体, 而加密网格则导致计算量及存储量增大^[16].
为此, Zhdanov等^[17]提出基于分离模拟技术的体积分方程法, 尝试高效地解决同时存在三维大尺度盐丘体与二维大尺度薄层目标体的电磁场模拟问题, 但其采用规则六面体网格剖分且未考虑地形起伏问题, 模拟的目标体也仅局限于规则形体. 有限元模拟中广泛采用的非线性结构、自适应四面体网格及自适应矩形网格, 可有效模拟复杂地形及地下目标体, 其理论发展与实际应用已渐趋成熟, 但涉及较大计算量及存储量^[18]. 积分方程区域分解是另外一种提高模拟井筒电磁多尺度目标能力的方法, 其在工程、通讯领域电磁模拟方面具有较好的应用, 但由于要求每个子区域具有相同的大小和结构, 使得对井筒电磁非周期或者复杂目标的电磁建模有一定的局限性^[19].
综上所述, 尽管电磁法的数值模拟理论及算法已取得了长足发展, 但对于多源多频率井筒电磁法, 利用高效高精度正演模拟技术, 研究地形响应对井筒电磁场异常的影响规律和提出相应的校正方法, 仍是当前该方法走向实用化亟待解决的两个重要方面. 本文基于深井井旁目标体二次电磁场响应与地形响应弱耦合的前提, 引入区域分解理论对研究区域采用分离模拟技术, 结合高斯滤波半解析算法, 开展区域体积分方程法研究, 实现起伏地形和复杂储层的频率域井筒电磁响应的高效、高精度模拟, 并利用多方位Walkaround观测系统实现三维频率域地井电磁正演模拟算例分析, 为推进该方法的实用化提供了技术基础.

2

-->

2.1.积分方程

理论上积分方程模拟电磁场求解的过程为: 在电性参数有别于背景介质的异常区域的网格剖分基础上, 推导满足勘探问题的可控源电磁三维体积分方程, 采用稳定型双共轭梯度法求解目标区域离散化后的大型线性方程组. 三维积分方程正演模拟问题的实质为均匀半空间介质或水平层状背景介质中异常区域的三维地面可控源电磁场模拟问题的转化. 即拟采用地面发射源激发一次场, 在电磁场远区定义范围之外面积性观测异常电磁场.
考虑多方位Walkaround地井电磁观测系统(图1), 第n层的节点处总电场可表示为该点入射场与散射场之和^[11]:
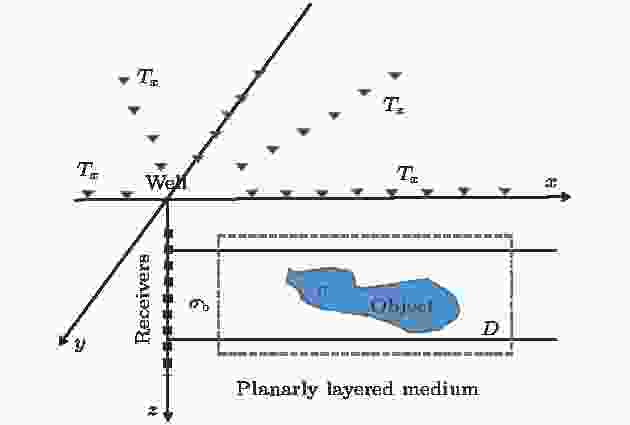图 1 积分方程模拟三维地井电磁场观测系统示意图(未显示地形)
Figure1. Sketch of 3D (three-dimensional) SBEM (surface to borehole electromagnetic) measurement system using IE (integral equation) without topography.

${{E}}_n({{r}}) = {{E}}_n^{\rm{i}}({{r}}) + {{E}}_n^{\rm{s}}({{r}}),$

其中${{E}}_n({{r}})$为总电场, ${{E}}_n^{\rm{i}}({{r}})$为层状介质中入射场, ${{E}}_n^{\rm{s}}({{r}})$为异常体散射场; $r = \sqrt {{x^2} + {y^2} + {z^2}} $为三维空间位置. 由感应电流引起的散射场为

${{E}}_n^{\rm{s}}({{r}}) = \int_D {{\bar{\rm G}}({{r}},{{r}}') \cdot {{J}}({{r}}')} {\rm{d}}{{r}}',$

式中D为六面体网格剖分区域, ${\bar{\rm G}}({{r}},{{r}}')$为三维均匀层状介质电场的并矢格林函数, $J(r') $为外加电流密度矢量. 由于考虑层状背景介质, 包含目标异常体在内的剖分区域D由对比度函数$\chi ({{r}}) = \sigma /{\sigma _{\rm{b}}} - 1$定义, 其中, $\sigma $及${\sigma _{\rm{b}}}$为目标区域及其所位于的背景层介质的电导率, 三维电场体积分方程为

$\begin{split}{{E}}(r) = &\; {{{E}}^{\rm{i}}}({{r}}) + {\rm{j}}\omega \left(\bar {{I}} + \frac{{\nabla \nabla \cdot }}{{k^2}}\right)\\&\times\int_D {{\bar{\rm G}}({{r}},{{r}}') \cdot \chi ({{r}}')} \cdot {{E}}({{r}}'){\rm{d}}{{r}}',\end{split}$

其中$\omega $为角频率, $\bar {{I}}$为单位矩阵, k为波数;

${\bar{\rm G}}({{r}},{{r}}') = \dfrac{{k_{\rm{b}}^2}}{{k^2}}(k^2\bar {{I}} + \nabla \nabla \cdot ){{{G}}_A}({{r}},{{r}}'),$

式中${{{G}}_A}({{r}},{{r}}')$为单位电偶极子源产生的磁矢量函数. 网格剖分区域D内电场同样满足(3)式, 即$r \in D$, 利用稳定型双共轭梯度法求解^[20], 可得到散射体内任一点的总场, 根据(3)式可求散射体外任意一点的散射场.
注意到, 求解格林函数过程涉及巨大的计算量及存储量, 本文将正演过程中的并矢格林函数分解, 结合积分方程核, 运用快速傅里叶变换 (FFT)加速计算. 将整体研究区域网格剖分, 离散体积分方程为矩阵方程组, 结合稳定型双共轭梯度法求解方程; 层状背景介质电导率只在z方向变化, 对积分核中的电场并矢格林函数做如下处理:

$\begin{split}{\bar{ G}}({{r}},{{r}}')= & \;{{{G}}_{\rm{c}}}(|{r_{xy}} - {r_{xy}}^\prime |,z - z') \\& +{{{G}}_{{\rm{cr}}}}(|{r_{xy}} - {r_{xy}}^\prime |,z + z'),\end{split}$

式中$\bar {{{\rm G}}}(r,r')$定义为三维水平层状介质电场的并矢格林函数; ${r_{xy}} = \sqrt {{x^2} + {y^2}} $为目标体外平面空间位置, $r'$为目标体内空间位置; ${{{G}}_{\rm{c}}}(|{r_{xy}} - {r_{xy}}^\prime |,\;z - z')$在坐标轴三方向具有空间平移不变性, 可在各自方向使用卷积运算; ${{{G}}_{{\rm{c}}r}}(|{r_{xy}} - {r_{xy}}^\prime |,\;z + z')$是$z + z'$的函数, 在平面方向具有空间平移不变性, 可使用卷积运算和在z方向使用相关运算. 由此, 积分核的计算通过使用FFT得到了加速, 以期将计算复杂度由传统矩量法的${O}({N^3})$降低为${O}(N\log N)$.
2 -->

2.2.区域划分

电磁场响应的数值模拟方法可应用于实际工程问题, 但往往涉及求解大型矩阵方程组. 对应的计算区域往往是多尺度且其形态可能很不规则, 如三维地形、巨型盐丘与局部异常目标体, 会给模拟计算带来很大的困难. 此外, 值得注意的是, 针对网格剖分尺度, 数值方法对长波现象具有较好模拟精度. 若为了提高分辨率而加密网格剖分密度, 亟待解决的问题将是求解过程的计算量和速度的限制. 本文将区域分解理论引入多尺度电磁场响应的积分方程模拟问题, 即引入参考模型, 将三维地形、巨型盐丘与局部异常目标体等视为不同子区域, 子区域应尽可能规则, 从而将原问题的求解转化为在多个子域上的求解. 由于上述操作有别于精确定义的区域分解方法, 故称之为“区域划分”. 对于区域划分原则, 本文采用感应数作为区域划分的标准.
假定地形起伏的剧烈程度为${L_{\rm{p}}}$(定义为研究区域最大高程变化与水平距离的比值), 感应几何尺寸由趋肤深度度量:

${\delta _{\rm{p}}} = {\left[ {{\rm{Re}}({k_{\rm{p}}})} \right]^{ - 1}},\;{k_{\rm{p}}} = {({\rm{i}}\omega {\mu _0}{\sigma _{\rm{p}}})^{1/2}},$

式中Re为取实部, ${k_{\rm{p}}}$为波数, ${\rm{i}} = \sqrt { - 1} $. 根据电磁散射理论, 感应数可以表示为

${M_{\rm{p}}} = {L_{\rm{p}}}/{\delta _{\rm{p}}}.$

目前对大、小感应数的界定并无定论, 本文取${M_{\rm{p}}} \ll 1$为小感应数, 相反为大感应数.
以井筒电磁地井观测系统为例, 针对大尺度电磁场模拟问题(图2(a)), 大感应数情况下, 地下深处异常体对地形的影响忽略不计, 先设置参考背景模型, 求解纯地形(缺失油气储层目标体的情况)引起的频率域地井电磁场响应, 将其作为新的背景一次场, 再求解油气储层目标体异常响应. 对于小尺度电磁场模拟问题(图2(b)), 在小感应数情况下, 地形和地下深处异常体之间的电磁场相互耦合很小, 可以忽略, 可以将地形与地下油气储层目标体作为统一“目标体区域”, 先求解参考背景模型一次场, 再求解这一“目标体区域”引起的综合电磁场响应. 通过采用上述场“划分”模拟, 实现考虑起伏地形、复杂油气储层目标体三维频率域地井电磁场的快速正演模拟.
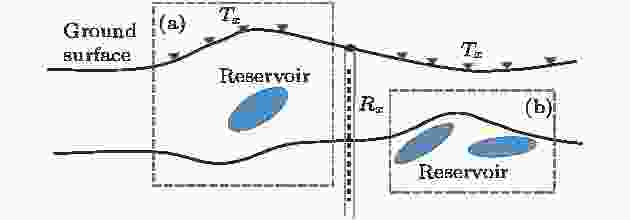图 2 区域划分示意图(剖面图)
Figure2. Sketch of domain decomposition in profile.

2 -->

2.3.区域积分方程模拟

考虑包含目标异常体在内的整个研究区域(目标剖分区域D), 采用三维多方位地井电磁观测系统, 如图3(a)所示, 研究范围内具有三维地形、不规则起伏层状背景介质及油气目标体分布. 按区域划分步骤, 引入参考模型, 如图3(b)所示, 电导率为${\sigma _{\rm{h}}}$, 可设置为均匀半空间介质或层状介质; 假设不规则起伏层状背景介质与三维地形之间满足区域划分标准的小感应数范畴, 将上述二者划分为复杂地质构造背景介质${\sigma _{\rm{b}}}$(图3(c)); 假设三维地形、不规则起伏层状背景介质内油气目标体满足区域划分标准的大感应数范畴, 则可将三维地形、不规则起伏层状背景介质电磁响应作为求解油气目标体$\sigma $的电磁场响应的入射场(图3(d)).
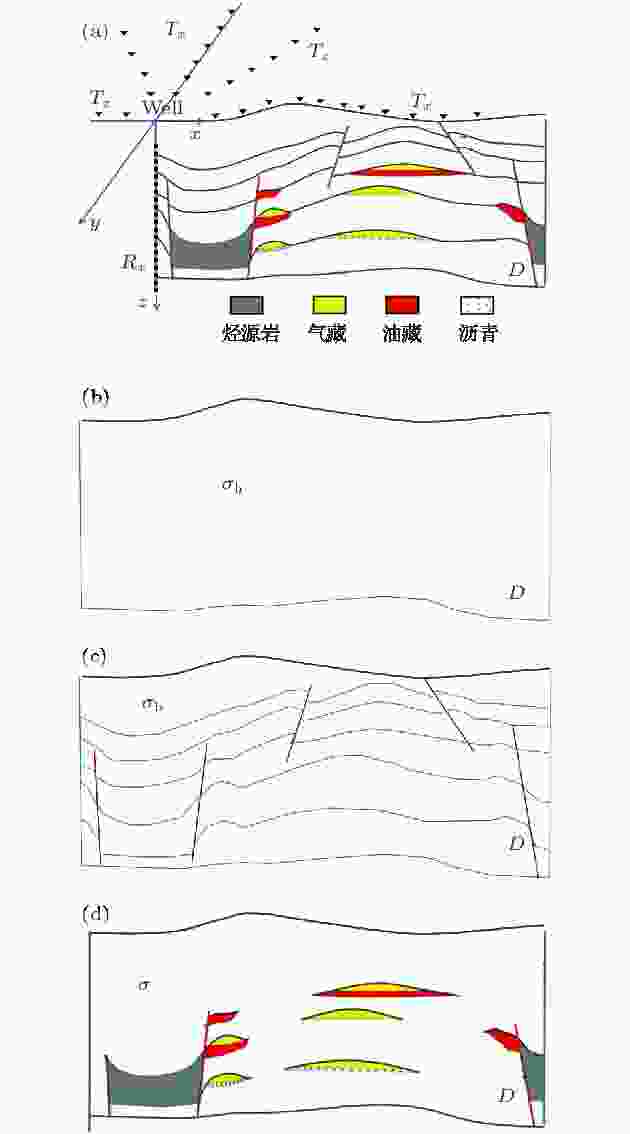图 3 观测系统及计算区域划分示意图　(a) 三维地井电磁; (b)参考空间介质; (c) 复杂地质构造背景介质; (d) 油气目标体
Figure3. Sketch of domain decomposition and observation system: (a) 3D SBEM; (b) reference model; (c) background model; (d) oil and gas model.

求解过程的对比度函数可表述为

$\chi (r) = \sigma /{\sigma _{\rm{h}}} - {\sigma _{\rm{b}}}/{\sigma _{\rm{h}}},$

其中$\sigma $及${\sigma _{\rm{b}}}$为油气目标及复杂地质构造的背景层介质的电导率; 当${\sigma _{\rm{b}}}$等于${\sigma _{\rm{h}}}$时, 表示不存在三维地形、不规则起伏层状背景介质, 为传统积分方程模拟; 当${\sigma _{\rm{b}}}$有别于${\sigma _{\rm{h}}}$时, 则表示考虑三维地形、不规则起伏的层状背景介质, 采用区域积分模拟.
对于如图3(b)所示的参考模型介质, 其电磁场响应作为求解图3(c)所示区域划分的异常电磁场响应的积分方程的入射场, 采用(1)式的三维积分方程求解过程耗费机时, 尤其是当解决多场源、多频率地井电磁场响应时, 其计算复杂度随场源数和频率数乘积倍增. Anderson算法采用滤波算子, 可提供多层层状介质在任意方向电偶极子和磁偶极子激励下的电磁响应^[21]. 此时, 定义入射场响应为${{E}}_{\rm{a}}^{\rm{i}}$, 因而三维地形与不规则起伏层状背景介质之间满足区域划分标准的小感应数范畴的三维电场${{{E}}_{\rm{b}}}({{r}})$的体积分方程为

$\begin{split} {{{E}}_{\rm{b}}}({{r}}) = & {{E}}_{\rm{a}}^i({{r}}) + {\rm{j}}\omega \dfrac{{k_{\rm{h}}^2}}{{k_{\rm{b}}^2}}\left(\bar {{I}} + \dfrac{{\nabla \nabla \cdot }}{{k_{\rm{b}}^2}}\right)(k_{\rm{b}}^2\bar {{I}} + \nabla \nabla \cdot )\\ & \times\int_D {{{{G}}_{\rm{A}}}({{r}},{{r}}') \cdot } \chi ({{r}}') \cdot {{{E}}_{\rm{b}}}({{r}}'){\rm{d}}{{r}}' .\end{split} $

式中$\chi (r) = {\sigma _{\rm{b}}}/{\sigma _{\rm{h}}} - 1$, ${{r}} \in {{D}}$且不等于${{r}}'$, $k_{\rm{h}}^2$和$k_{\rm{b}}^2$分别为参考模型子区域及小感应数子区域的波数, 利用稳定型双共轭梯度法求解, 可得到如图3(c)所示计算区域内任一点的电场.
假设如图3(d)所示子区域满足大感应数范畴, 则由 (9)式可获取三维地形与不规则起伏层状背景介质作为入射场的电场响应${{{E}}_{\rm{b}}}({{r}})$, 则三维地形、不规则起伏层状背景介质内油气目标体的电场响应的体积分方程表示为

$\begin{split}{{E}}({{r}}) = & {{E}}_{\rm{b}}({{r}}) + {\rm{j}}\omega \frac{{k_{\rm{b}}^2}}{{k^2}}\left(\bar {{I}} + \frac{{\nabla \nabla \cdot }}{{k^2}}\right)\left(k^2\bar {{I}} + \nabla \nabla \cdot\right)\\ & \times\int_D {{{{G}}_{\rm{A}}}({{r}},{{r}}') \cdot } \chi ({{r}}') \cdot {{E}}({{r}}'){\rm{d}}{{r}}',\end{split}$

式中${{r}} \notin {{D}}$且为井孔中接收点空间位置, $k^2$特指如图3(d)所示子区域满足大感应数范畴的波数. 再次利用稳定型双共轭梯度法求解, 即可获得由图3(c)所示计算区域引起、井孔内任一点接收的电场. 井孔内任一接收点的磁场响应则通过地井电磁满足的磁场积分方程, 根据上述电场积分方程的推导过程求解获取, 在此不再赘述.
至此, 三维地形条件下、不规则起伏层状背景介质内油气目标体勘探电磁场响应的模拟问题转化为区域划分的三个子区域的电磁场模拟问题, 其中, 参考模型子区域采用高斯滤波算子快速提供纯均匀空间或水平层状空间背景介质的入射场; 三维地形与不规则起伏层状背景介质的综合电磁响应、纯油气目标体的电磁响应则通过采用稳定型双共轭梯度法-快速傅里叶变换求解体积分方程快速获取, 由此实现区域积分方程的三维地井电磁响应模拟.

2

-->

3.1.算法验证

为了验证所采用的积分方程法(3D IE)三维数值模拟的有效性, 将本文模拟结果与阮百尧等^[22]使用边界积分方法(3D BIE)计算三维起伏地形频率域电磁响应的结果、Anderson滤波算法计算层状介质电磁响应的结果进行对比分析. 综合前人发表的研究成果, 采用均匀半空间介质地电结构模型, 导电率为0.01 S/m; 考虑放置于地面的垂直磁偶极源, 场源位于坐标系原点, 激发频率为1000 Hz, 单位电流强度供电; 若干接收点位于x轴方向主剖面(过场源点剖面)上, 点距为非均匀间距, 从靠近场源到远离场源采用的网格间距分别为1, 3, 7, 10, 30 m, 未考虑地形影响. 理论上, 场源及观测系统为三维, 电性结构是一维的, 水平磁场分量可通过三维边界积分方法、Anderson算法及三维积分方程方法模拟计算. 由磁偶极源在均匀空间介质引起的归一化水平磁场分量如图4所示. 模拟结果表明, 阮百尧等提出的边界积分方法、Anderson算法正演计算结果与此模型的三维积分方程模拟数值结果一致, 水平磁场分量随接收点离场源距离增大而逐渐衰减, 三种模拟数据间拟合误差小于1%, 从而达到检验本文三维数值模拟算法的可行性及有效性.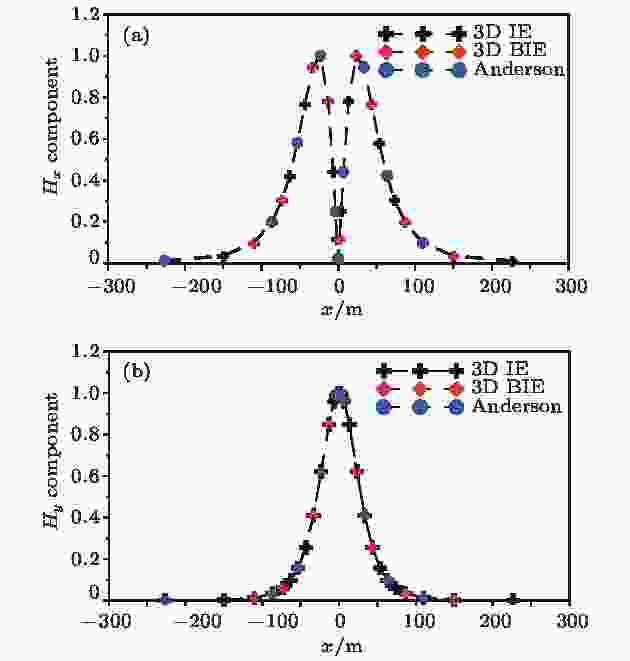
图 4 均匀半空间模型三维积分方程法(3D IE)、三维边界积分法(3D BIE)、Anderson算法模拟结果对比图
Figure4. Magnetic field of reference model calculated by 3D IE, 3D BIE and Anderson code.

计算效率方面, 针对上述验证模型, 在PC 12 G RAM和双 i5 CPU环境下, Anderson 算法采用半解析算法模拟计算, 具有高效的三维电磁场运算能力, 总耗时为0.1 s; 三维边界积分方程法模拟区域网格剖分数为30 × 30, 另需包含各边界20个网格作为截断边界, 因而总体网格数量需求较大, 计算耗时123 s; 本文引入快速算法及区域积分方程模拟算法, 区域剖分网格数量为20 × 20 × 20, 积分方程三维正演算法总耗时86 s, 传统积分方程法^[11] (矩量法)总耗时957 s (表1). 可见, 引入快速算法及区域划分策略后, 本文区域积分方程三维正演模拟针对包含空气在内的整体区域剖分的计算效率较矩量法提高显著, 与三维边界积分计算效率相比也有较好的效果, 但相比Anderson 算法在提供三维均匀介质或层状介质的一次场方面的高效特征而言, 后者更具高效性, 为后续将Anderson 算法融入区域积分方程法来模拟以提高计算效率奠定了基础.

模拟算法	截断边界	剖分方式	网格剖分	耗时/s
Anderson	不需要	无	不需要	0.1
三维边界积分	需要	全局剖分	50 × 50	123.0
区域积分	不需要	局部剖分	20 × 20 × 20	86.0
矩量法	不需要	局部剖分	20 × 20 × 20	957.0

表1均匀半空间介质地电结构模型的不同算法的电磁场模拟效率对比
Table1.Comparison of computational effectiveness of modeling electromagnetic field via different algorithms for a half homogeneous medium.

2 -->

3.2.三维地形响应模拟验证

由于三维起伏地形频率域的地井电磁场响应的模拟结果发表的较少, 本文将三维积分方程法的模拟算法用于三维起伏地形频率域地面电磁场响应的模拟计算, 并与三维边界积分的模拟结果对比. 如图5所示, 收发装置采用地面电磁观测系统, 垂直磁偶源位于山谷地形底部, 激发频率为1000 Hz; 接收点位于y = 0剖面, 点距为非均匀间距; 地下半空间介质导电率为0.01 S/m. 三维山谷地形为倒梯形体, 上顶面为200 m × 200 m, 下底面为40 m × 40 m, 纵向高差为50 m. 采用本文提出的区域划分方法, 将上述含山谷地形的模拟算例划分为层状介质参考模型(图3(b)), 即包含空气层和地下电导率为0.01 S/m的介质层; 将山谷地形作为区域划分异常目标体(图3(c)). 于是, 在参考模型中对比度函数为零, 而包含空气层的山谷地形目标区域的对比度为1, 需要求解的区域介质与参考模型介质在对比度函数上具有显著的差异, 保障了积分方程模拟的精度.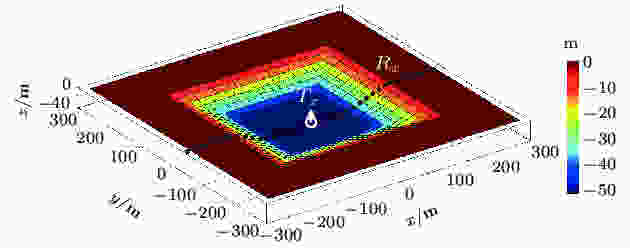
图 5 三维山谷地形及地面电磁观测系统示意图, T_x为场源位置, R_x为接收点位置
Figure5. Sketch of 3D valley terrain with surface electromagnetic. T_x denotes transmitter and R_x is receiver.

首先采用Anderson算法求解参考模型分布在y = 0剖面上各接收点的一次场响应, 将一次场响应作为(9)式右端项入射场, 采用稳定型双共轭梯度-快速傅里叶变换算法求解积分方程组, 即可获取三维地形电磁场响应. 三维边界积分方程模拟将地形问题转化为空气空间及介质空间的矢量面积分问题, 简化了三维边界积分求解过程; 针对地形区域采用加密三角单元积分(相应计算量增大), 并将地形影响视为常数项因(地形响应模拟精度有限). 图6所示为三维山谷地形的三维积分方程模拟、三维边界积分模拟地面水平磁场分量的归一化响应及二者模拟地形响应差值的对比情况. 如图6(a)和图6(b)所示, 两组磁场分量模拟结果的衰减变化趋势一致性较好, 地形起伏区域(x轴–100— –40 m, 40—100 m)在相应磁场响应曲线上均有所反映, 表明了本文区域积分方程模拟起伏地形的可行性. 基于上述两种算法模拟地形响应精度不同的问题, 绘制了三维区域积分方程算法相对三维边界积分方程模拟地形水平磁场响应的差值曲线(图6(c)和图6(d)). 差值曲线表明, 相对三维边界积分方程算法, 本文提出的区域积分方程算法模拟地形响应的幅值最小值达7% (H_y分量), 最大值达20% (H_x分量), 验证了本文正演模拟方法的有效性.
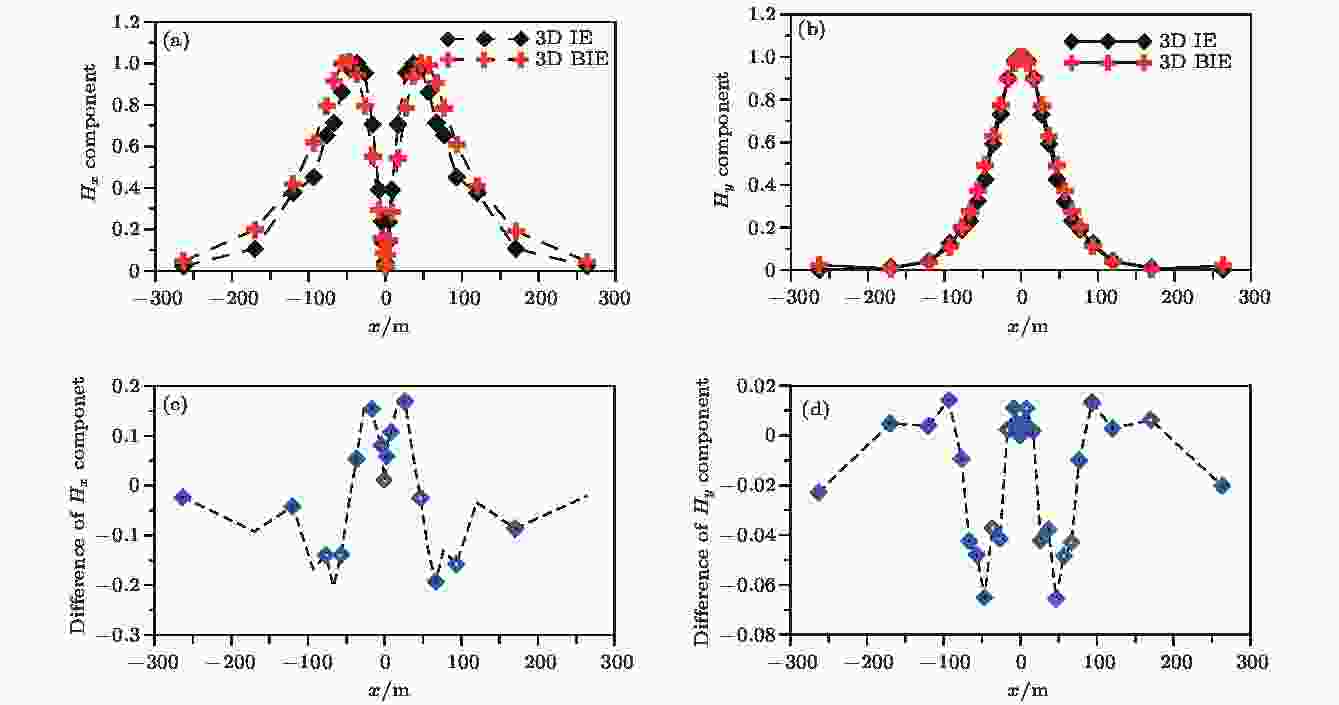图 6 三维山谷地形三维积分方程模拟、三维边界积分模拟地面磁场分量归一化响应及其差值对比图
Figure6. Magnetic field of 3D valley terrain calculated by 3D IE and 3D BIE: (a), (b) Total magnetic field; (c), (d) difference of magnetic field between IE and BIE.

2 -->

3.3.多方位地井电磁算例

为分析本文提出的区域积分方程方法在地井电磁观测系统上模拟的可行性, 设计均匀半空间层状介质模型, 导电率为0.01 S/m; 垂直电偶源位于地面, 其水平位置与接收井口距离为100 m, 激发频率为1000 Hz; 接收井深度方向0—100 m内布置若干纵向电场分量接收点, 间距为5 m. 图7所示三维区域积分方程方法(3D IE)与Anderson算法的模拟结果完全吻合, 数据间拟合误差小于1%, 验证了本文算法用于地井电磁场响应模拟计算的可行性, 为后续将Anderson算法嵌入三维地形地井电磁多方位观测的电磁场模拟降低计算代价奠定了基础.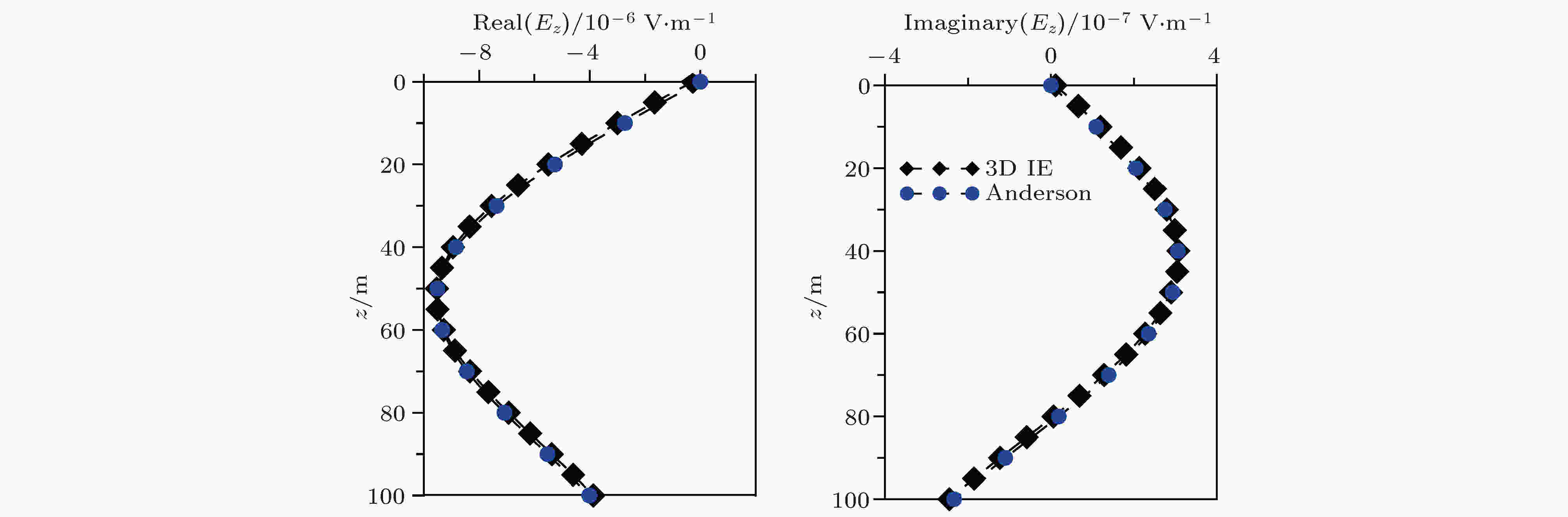
图 7 均匀半空间地井电磁观测三维积分方程法、Anderson算法模拟电场响应对比
Figure7. Electric field of reference model calculated by 3D IE and Anderson code for 3D SBEM.

进一步, 设计考虑三维地形条件下地井电磁多方位观测方式的算例分析, 探索地形对地井电磁场的影响规律. 如图8(a)所示, 假设三维山谷地形三方位地井电磁观测系统采用三方位水平径向电偶源, 分别为主剖面观测(T_x1位于地形上升中段)、旁侧观测(T_x2位于地形旁侧)及对侧观测(T_x3与地形在井孔的两侧); 为便于对比分析, 各场源与接收井水平距离均为300 m, 激发频率为25 Hz. 主剖面观测场源位于山谷地形内, 其余方位观测场源位于地面, 接收井0—100 m内布置若干纵向电场分量接收点, 间距为5 m, 如图8(b)—(d)所示.
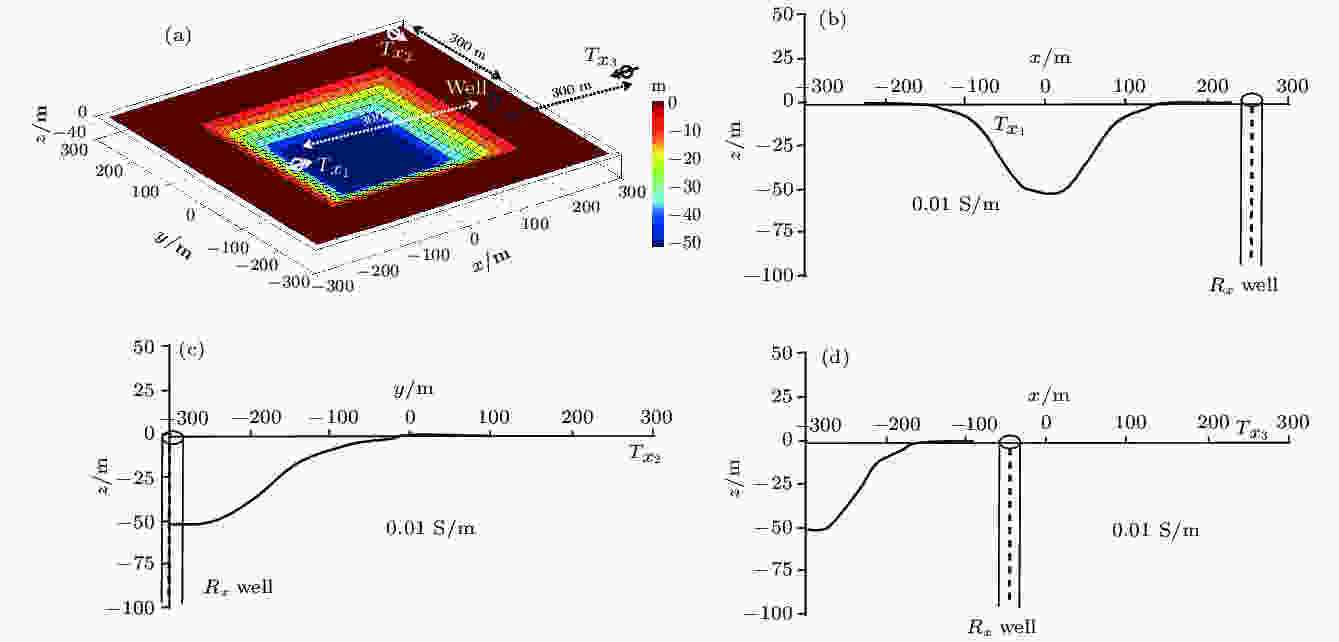图 8 三维山谷地形及多方位地井电磁观测示意图
Figure8. Sketch of 3D valley terrain with multi-azimuth SBEM.

本文采用Anderson算法计算区域划分参考模型的一次场响应, 利用区域积分方程方法模拟计算上述地井电磁多方位电磁场响应. 当场源与接收井孔之间存在地形空间时, 在地形空间深度范围内, 场源与接收点的传播空间受阻, 在观测总电场响应(黑色曲线)上体现为幅值低于散射场响应(红色曲线)的畸变现象(图9(a)). 在场源、地形底部与接收井孔测点为连线区域, 地形影响产生的上述畸变现象减弱, 但引起显著的高幅值异常, 揭示了地形存在. 当接收点深度大于地形深度范围, 地形影响基本无效, 总电场、散射场响应趋于正常分布, 并与Anderson算法提供的均匀空间电场响应曲线(蓝色曲线)分布吻合. 旁侧观测模拟结果如图9(b)所示, 由于地形与场源位置关于井孔位置为正交关系, 地形深度范围场源激发一次场占主导, 但与地形底部深部的相同位置接收点仍受到上述畸变现象影响; 大于地形深度接收点电场的响应则受频率域电磁法体积效应、旁侧影响干扰, 导致总场响应较Anderson算法提供的一次场响应的幅值增加. 由于井孔位于地形与场源中间, 对侧观测方式下地形引起的散射电场较微弱, 如图9(c)所示, 总场响应与Anderson算法提供的一次场的响应基本一致, 大于地形深度接收点电场的响应仍受体积效应、旁侧影响干扰.
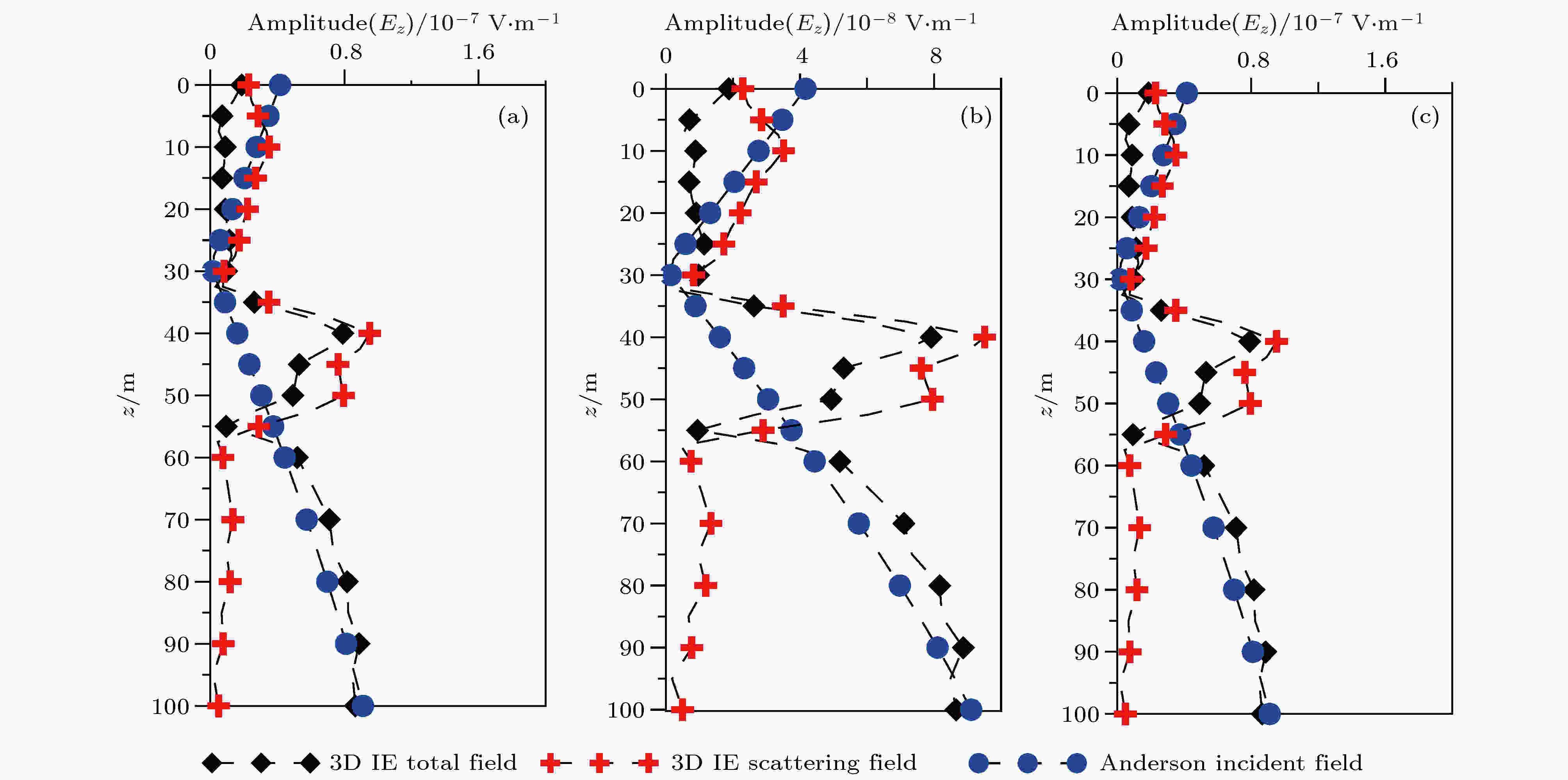图 9 三维山谷地形三方位地井电磁场响应　(a) T_x1场源; (b) T_x2场源; (c) T_x3场源
Figure9. Electric field of 3D valley terrain with multi-azimuth SBEM: (a) T_x1; (b) T_x1; (c) T_x1.

综上分析表明, 当场源布设于地形内或者距离地形比较近时, 地井电磁观测响应将会受到严重影响, 甚至出现电磁场幅值畸变现象, 严重干扰手续数据解译推断; 不同方位场源位置激发条件下, 地形对地井电磁响应的影响规律及幅值强度各异, 场值受到频域电磁勘探体积效应、旁侧影响的干扰亦有所不同, 该特征为有效识别三维地形影响及剔除相应地形影响提供了新的方法手段.

1) 针对三维地形频率域井筒电磁响应的高效模拟问题, 引入区域划分方法, 将三维起伏地形条件下复杂背景介质及目标体电磁场响应的模拟区域划分为参考模型、背景介质模型及目标体子区域, 结合Anderson算法、稳定型双共轭梯度-快速傅里叶变换算法, 对不同划分子区域采用不同算法进行高效模拟计算, 开展了三维区域积分方程模拟算法的研究, 解决了无需考虑增加地形剖分网格单元数量、截断误差累积及井筒特殊边界处理等问题, 而且通过积分方程模拟局部剖分特性、高效模拟特点, 构建了适用于三维井筒电磁勘探地形响应的模拟算法.
2) 基于Anderson算法及现有三维边界积分方程的模拟算法理论, 设计无地形均匀层状介质模型、含山谷地形均匀层状介质模型, 采用地面场源、接收点布设观测系统开展三维区域积分方程模拟算法的精确度及计算效率的分析. 研究表明: 三维区域积分方程模拟算法具有与解析解求解的Anderson算法相当的计算精度, 而Anderson算法在提供三维均匀层状介质一次场响应方面具有较高的计算效率, 因而可融入三维区域积分方程模拟算法以降低计算成本; 地形响应模拟方面, 三维区域积分方程模拟算法较三维边界积分方程具有更高的模拟精度及计算效率.
3) 考虑山谷地形的三维地井电磁多方位电磁勘探系统, 采用三维区域积分方程算法模拟场源位于主剖面、旁侧剖面及对侧剖面总电场及散射电场响应. 通过与Anderson算法提供无地形均匀层状介质的一次场响应对比分析表明: 三维地形场值响应对地井观测场值影响较大, 甚至出现误导后续数据推断解译的畸变现象; 地形、场源与井孔位置差异导致地形响应规律特征不同, 结合多方位地井电磁观测系统布设, 可有效甄别地形影响的存在性及干扰程度, 为高精度、高效剔除地形响应影响奠定了理论基础.