全文HTML
--> --> -->许多实际应用中都需要消除或抑制混沌行为, 即混沌控制. 1990年, Ott等[19]提出了OGY(Ott-Grebogi-Yorke)混沌控制方法, 此后, 各种混沌控制方法不断涌现. 常见的混沌控制方法有脉冲控制法[20,21]、外加周期微扰法[22]、延迟反馈法[23-25]、递归反步控制法[26-29]等. 脉冲控制法的控制信号是脉冲式的, 难以避免控制间隙外部噪声产生的严重干扰. 外加周期微扰法属于非反馈控制, 当系统的混沌行为消失后, 控制信号仍不为零, 通常适合在非自治系统的混沌控制中应用. 延迟反馈法在实现混沌控制时不需要确定目标轨道, 但其延迟周期难以确定. 带有递归反步控制器的非线性系统具有良好的全局稳定性、跟踪性和暂态性能. 本文基于李雅普诺夫稳定性理论和反步思想设计三个递归反步控制器, 将Chua多涡卷混沌系统中的混沌状态控制到不动点及期望值, 从而抑制其中的混沌行为.
由于混沌系统对初始条件的高度敏感性及对噪声的免疫性, 使得混沌理论在微弱信号检测领域具有广阔的应用前景. 1992年, Birx和Pipenberg[30]将混沌振子与复映射前馈神经网络结合检测淹没在高斯噪声中的微弱信号, 为微弱信号检测开辟了新思路. 之后, 大量****提出了各种基于Duffing混沌系统或改进型Duffing混沌系统的微弱信号检测方法. 但基于这类混沌系统的微弱信号检测方法有一定的局限性, 主要为系统由临界混沌状态转变为大尺度周期状态的现象不明显. 当待测信号的频率远大于系统本身的频率时, 系统就会回到混沌状态, 不能保持在临界混沌状态, 以至于达不到良好的检测效果. 因此, 研究基于非Duffing混沌系统的微弱信号检测方法是重要的. 2010年, 徐艳春和杨春玲[31]、Xu等[32]提出了基于Rossler混沌控制的强噪声背景下单频正弦信号检测方法. 2017年, Li和Zhang[33]采用两个混沌同步Chua系统来检测单频微弱正弦信号, 不需要跟踪相空间轨迹的改变, 只需要得到同步误差. 本文提出一种新多频微弱周期信号频率检测方法, 即利用Chua多涡卷混沌系统和递归反步控制器对信号的各频率进行检测. 首先, 判断Chua多涡卷混沌系统是否处于混沌域中的任一混沌状态(不需要处于临界混沌状态); 其次, 采用递归反步控制器将处于混沌状态的Chua多涡卷混沌系统控制到不动点; 最后, 通过频谱分析检测出信号的各频率.
2.1.新Chua双涡卷混沌系统
在经典Chua系统的基础上[1,34], 提出分段非线性对数函数



对数函数








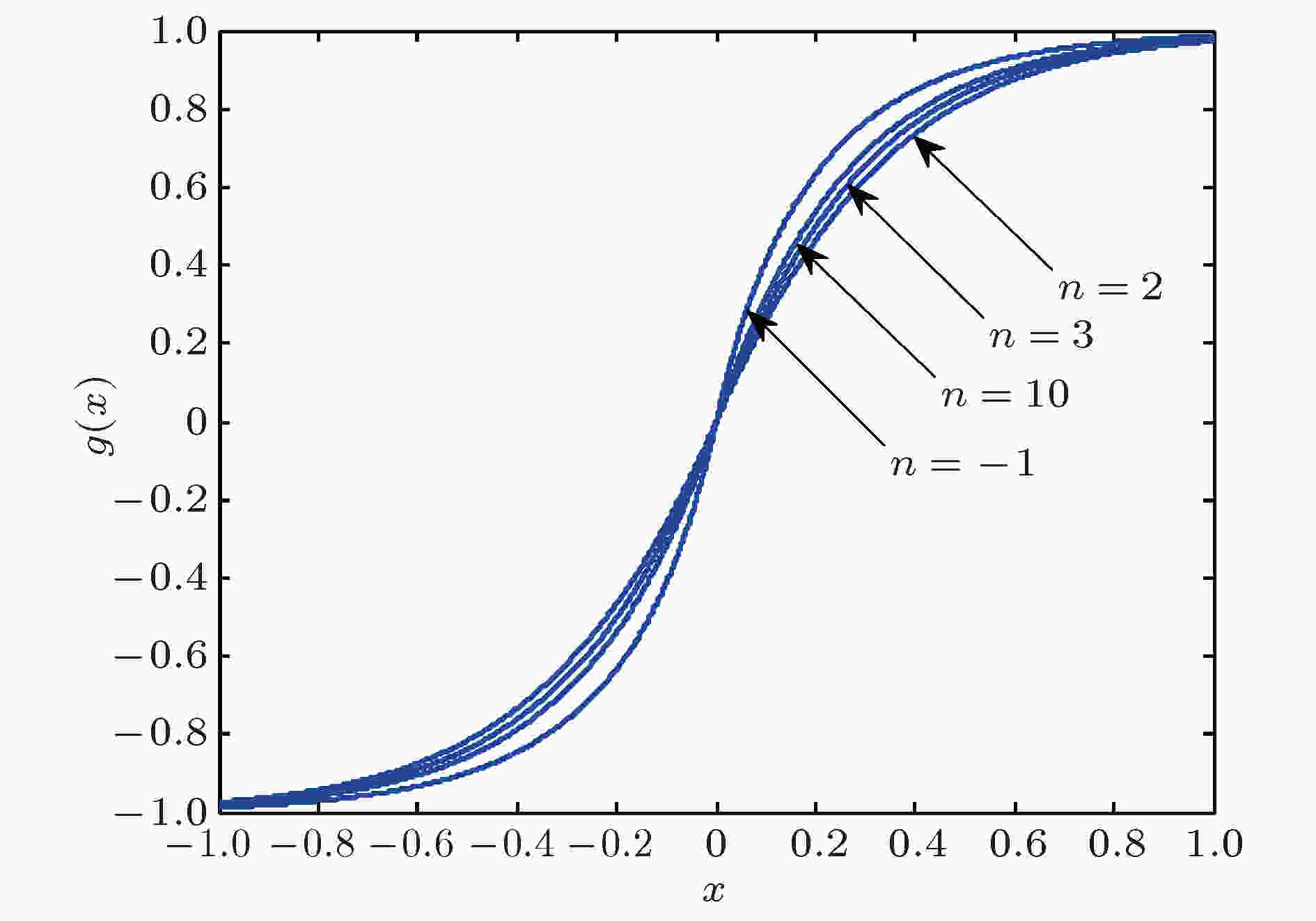 图 1 对数函数
图 1 对数函数Figure1. Logarithmic function.
以












 图 2 新Chua双涡卷混沌系统的电路图
图 2 新Chua双涡卷混沌系统的电路图Figure2. Circuit diagram of the novel Chua double-scroll chaotic system.

以下给出




















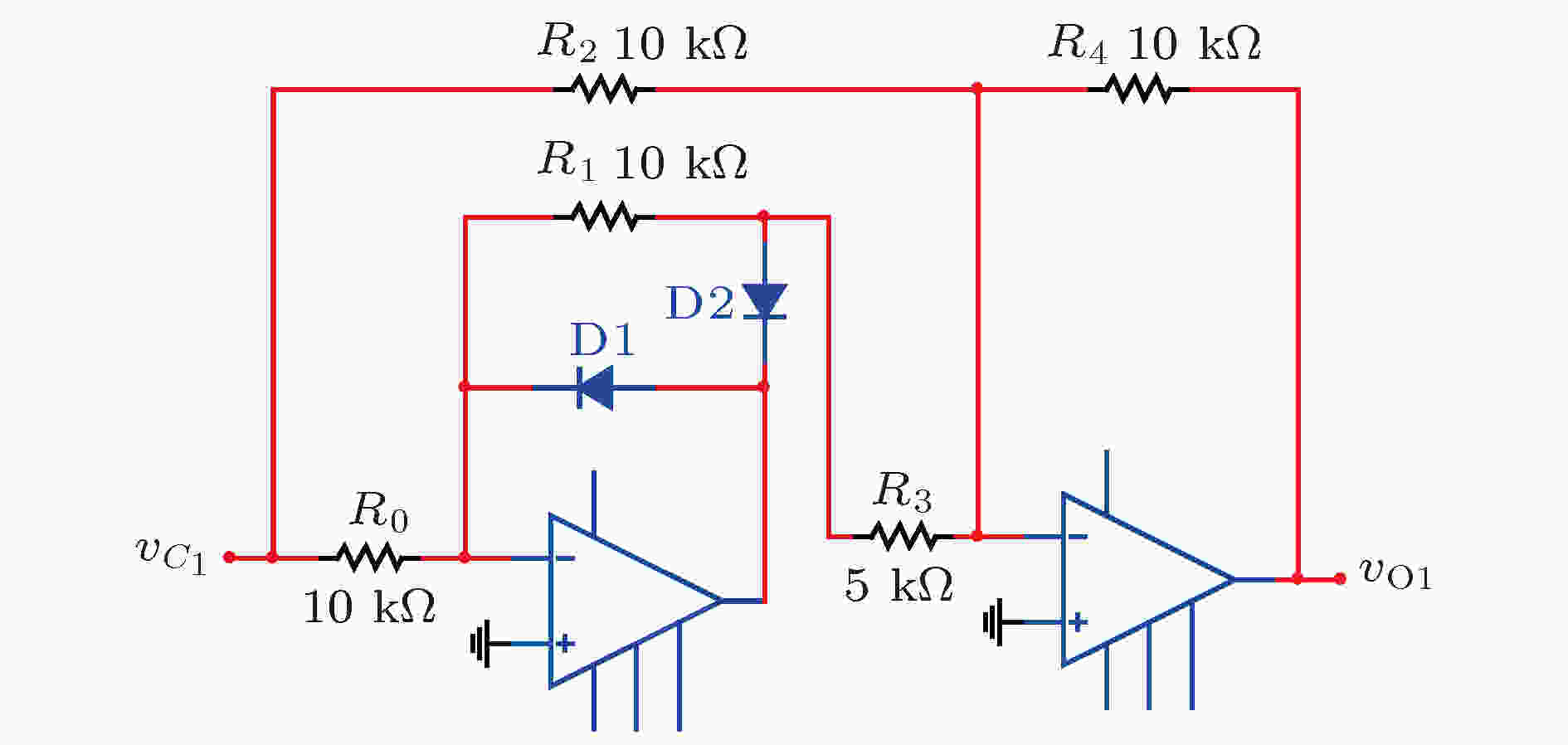 图 3
图 3 
Figure3. Circuit diagram of

 图 8
图 8 
Figure8. Circuit diagram of


由图3可得到(6)式.
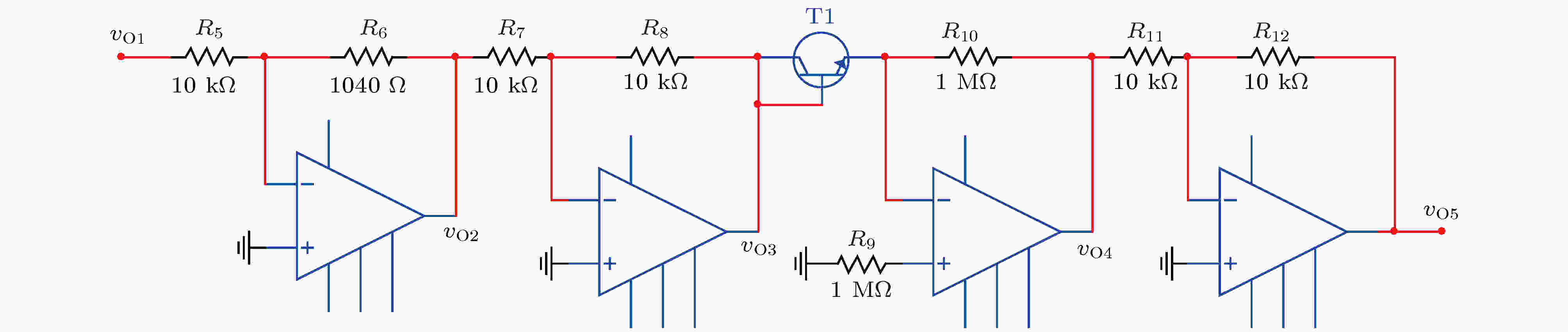 图 4
图 4 
Figure4. Circuit diagram of






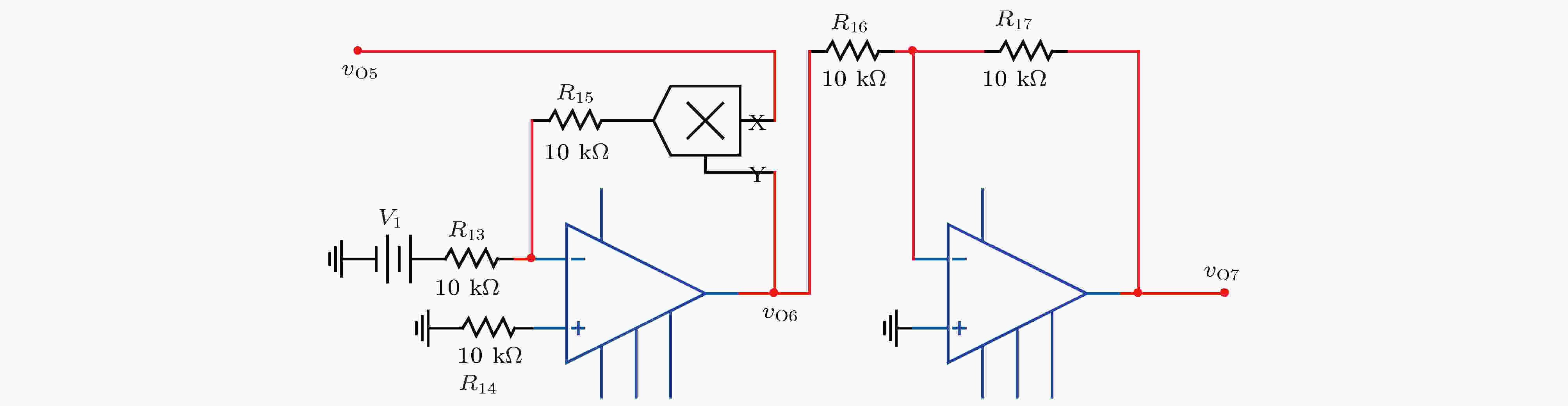 图 5
图 5 
Figure5. Circuit diagram of

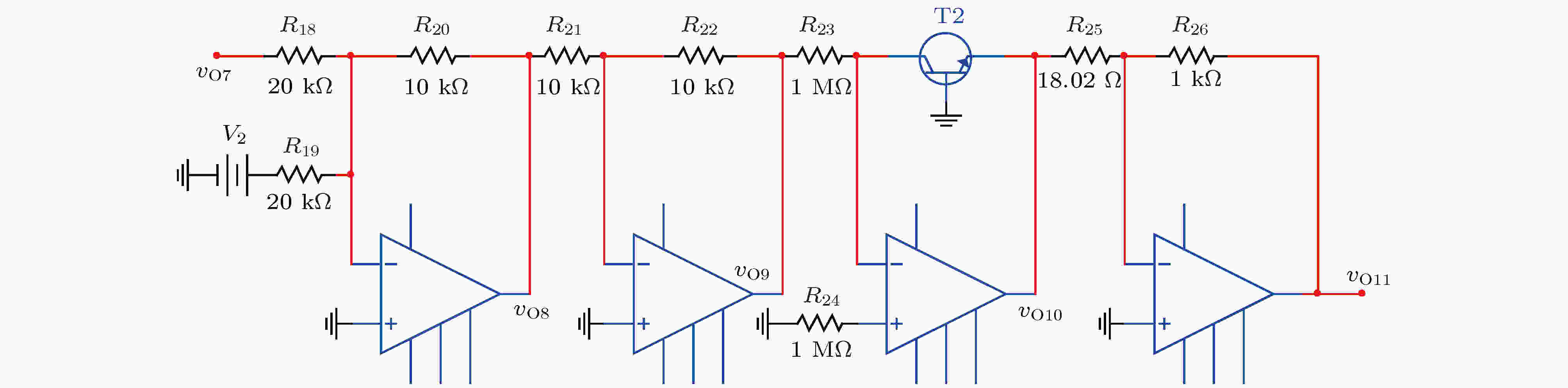 图 6
图 6 
Figure6. Circuit diagram of








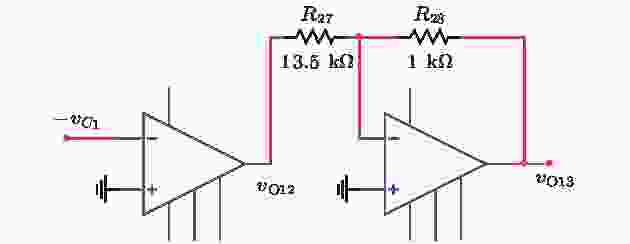 图 7
图 7 
Figure7. Circuit diagram of


综上所述, 图3—图8组成了对数函数

以























系统(20)式的三个李雅普诺夫指数(Lyapunov exponents, LE)






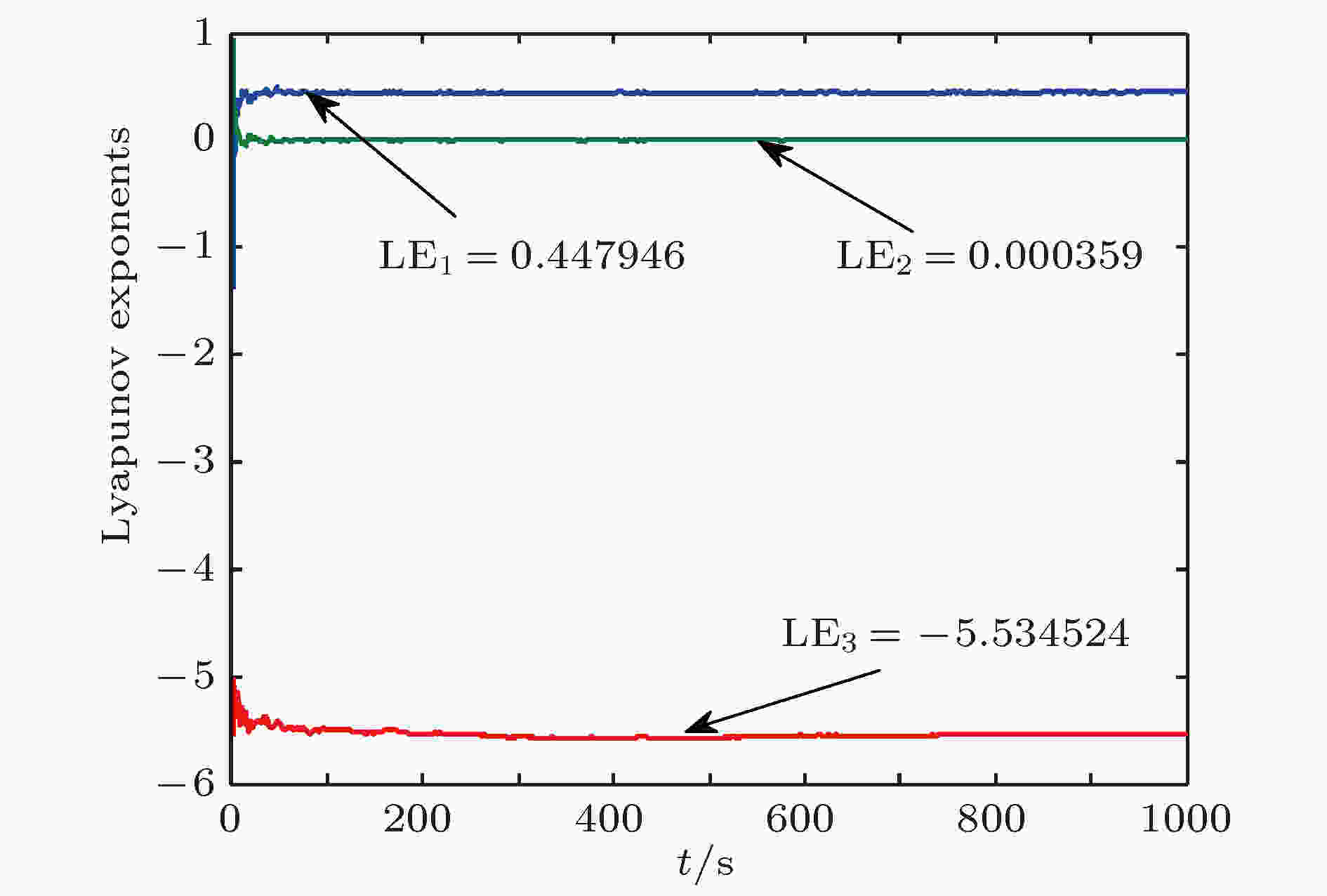 图 9 系统[(20)式]的李雅普诺夫指数
图 9 系统[(20)式]的李雅普诺夫指数Figure9. Lyapunov exponents of system (Equation(20)).
根据三个李雅普诺夫指数可得系统(20)式的分维数


新Chua双涡卷混沌系统[(20)式]的相图和时域图如图10所示. 图10(a)表示了新Chua双涡卷混沌系统x-y平面的相图, 图10(b)表示了新Chua双涡卷混沌系统x方向的时域图.
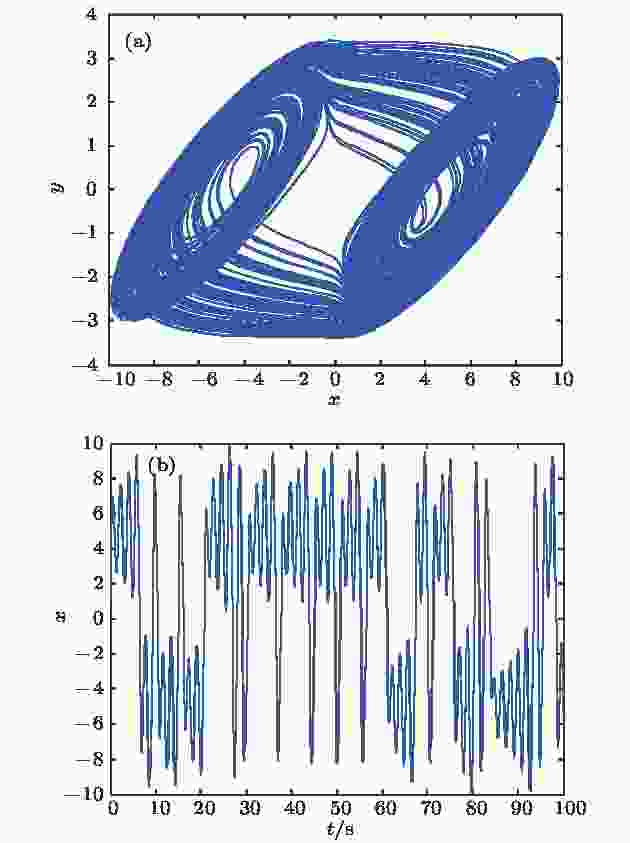 图 10 新Chua双涡卷混沌系统 (a)
图 10 新Chua双涡卷混沌系统 (a) 
Figure10. Novel Chua double-scroll chaotic system: (a) Phase diagram on the

2
2.2.Chua多涡卷混沌系统
对数函数序列的电路图与对数函数的电路图类似, 在对数函数电路图的基础上, 经过拓展平衡点即可得到对数函数序列的电路图, 这里不再详述.在新Chua双涡卷混沌系统的基础上, 引入对数函数序列






或

(24)式、(25)式中,



当




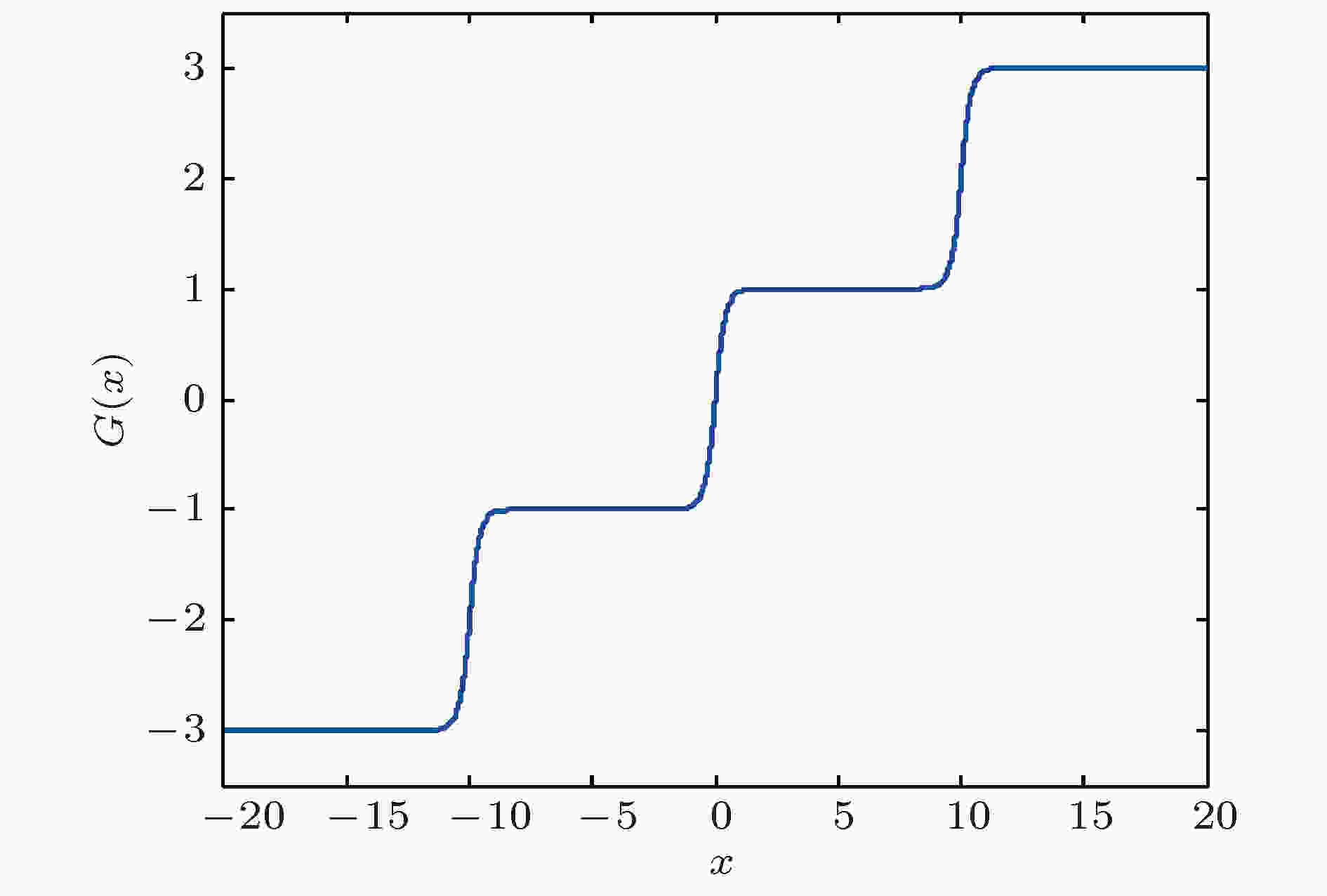 图 11 多分段对数函数序列[(24)式], 取M = 1
图 11 多分段对数函数序列[(24)式], 取M = 1Figure11. Multi-segment logarithmic function series(Equation(24)) with M = 1.
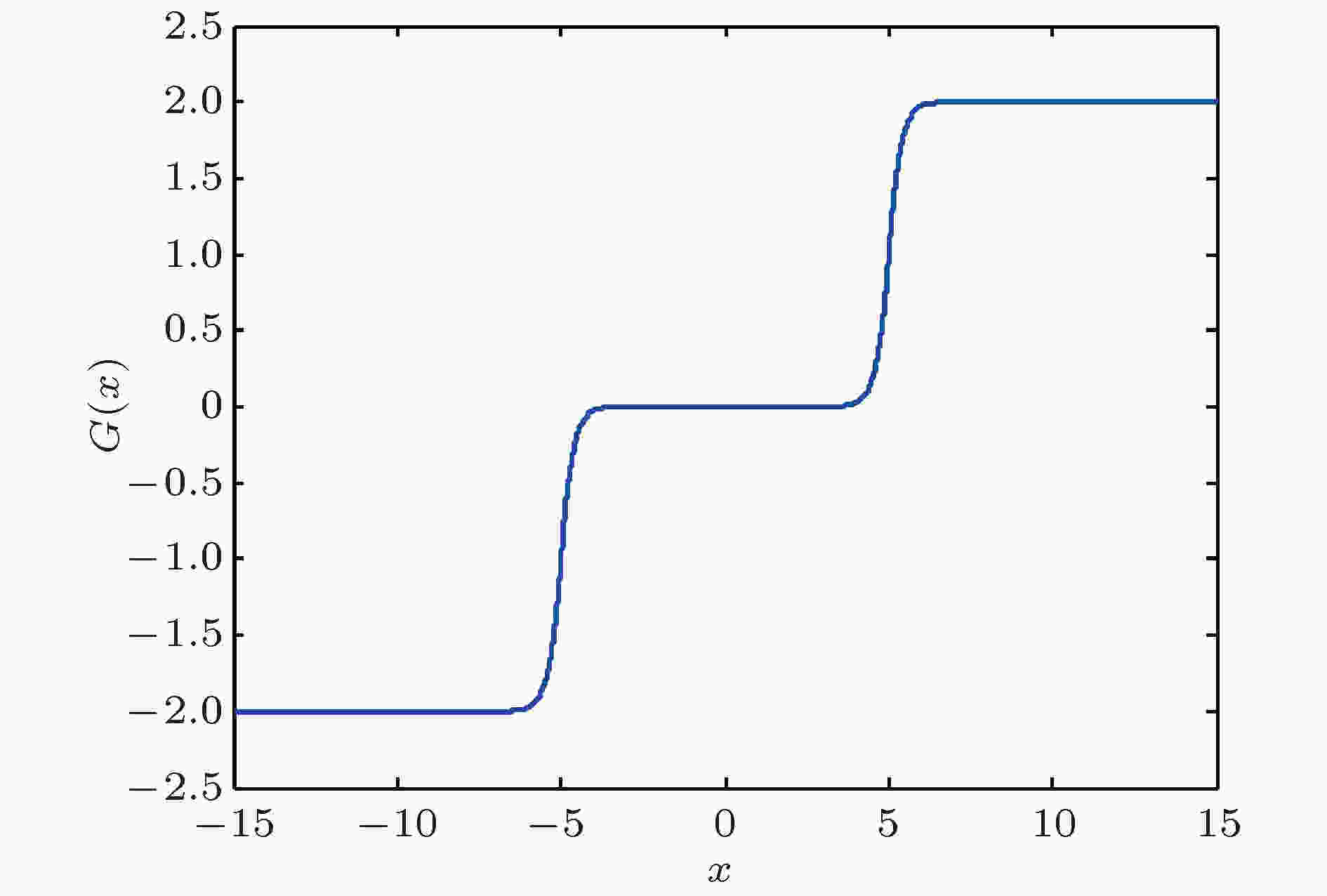 图 12 多分段对数函数序列[(25)式], 取N = 1
图 12 多分段对数函数序列[(25)式], 取N = 1Figure12. Multi-segment logarithmic function series(Equation(25)) with N = 1.
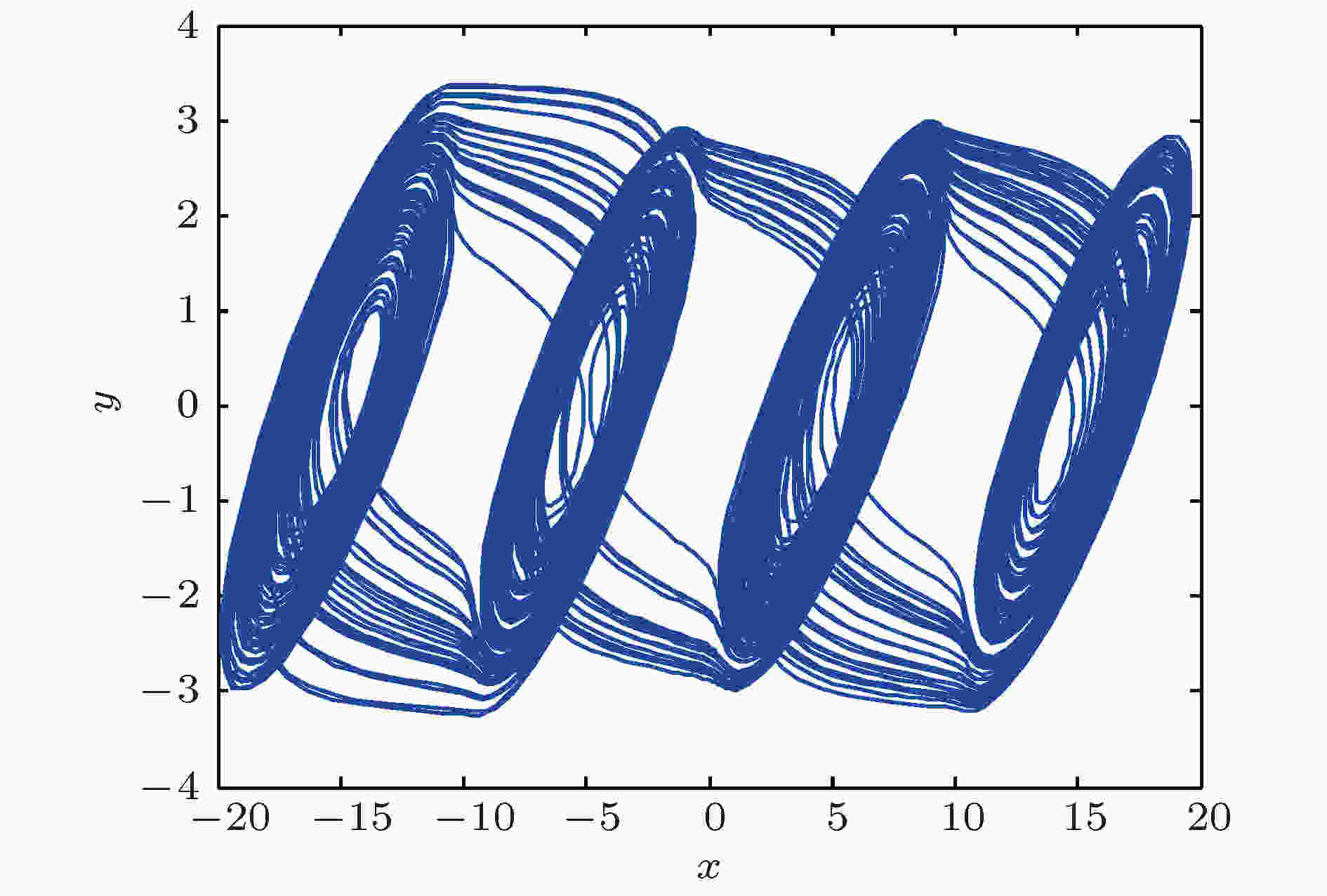 图 13 x-y平面4-涡卷混沌吸引子的相图
图 13 x-y平面4-涡卷混沌吸引子的相图Figure13. Phase diagram of the 4-scroll chaotic attractor on the x-y plane.
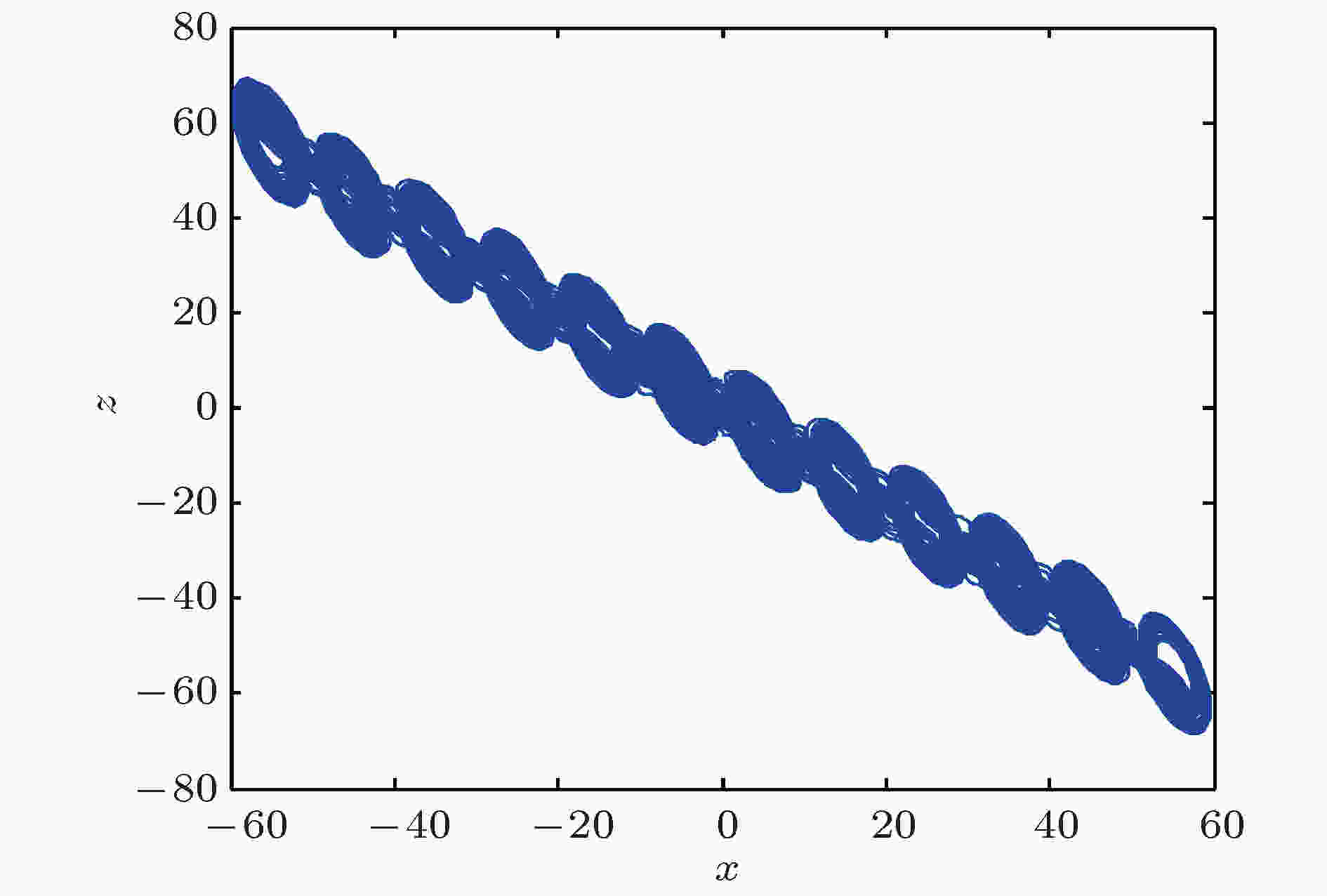 图 14 x-z平面12-涡卷混沌吸引子的相图
图 14 x-z平面12-涡卷混沌吸引子的相图Figure14. Phase diagram of the 12-scroll chaotic attractor on the x-z plane.
2
2.3.Chua多涡卷混沌系统的非线性动力学行为
32.3.1.对称性和不变性
在坐标变换
3
2.3.2.平衡点
令系统(23)式中的


对于


系统(23)式线性化的雅可比矩阵为





同理可得, 平衡点





综上所述, 系统(23)式可产生


以12-涡卷混沌吸引子为例, 分析其产生机制. 表1表示12-涡卷混沌吸引子的平衡点、特征值和平衡点的类型. 根据表1的特征值, 可知类型Ⅱ的平衡点












| 平衡点 | 特征值 | 平衡点的类型 |
| ${Q_0}\left( {0,0,0} \right)$ | $67.2809$,$ - 0.5730 \pm {\rm{i3}}{\rm{.9544}}$ | Ⅰ |
| ${Q_{1,2}}\left( { \pm 10,0,0} \right)$ | $67.2809$,$ - 0.5730 \pm {\rm{i3}}{\rm{.9544}}$ | Ⅰ |
| ${Q_{3,4}}\left( { \pm 20,0,0} \right)$ | $67.2809$,$ - 0.5730 \pm {\rm{i3}}{\rm{.9544}}$ | Ⅰ |
| ${Q_{5,6}}\left( { \pm 30,0,0} \right)$ | $67.2809$,$ - 0.5730 \pm {\rm{i3}}{\rm{.9544}}$ | Ⅰ |
| ${Q_{7,8}}\left( { \pm 40,0,0} \right)$ | $67.2809$,$ - 0.5730 \pm {\rm{i3}}{\rm{.9544}}$ | Ⅰ |
| ${Q_{9,10}}\left( { \pm 50,0,0} \right)$ | $67.2809$,$ - 0.5730 \pm {\rm{i3}}{\rm{.9544}}$ | Ⅰ |
| ${Q_{11,12}}\left( { \pm 5,0,0} \right)$ | $ - 6.2777$,$0.1389 \pm {\rm{i3}}{\rm{.5671}}$ | Ⅱ |
| ${Q_{13,14}}\left( { \pm 15,0,0} \right)$ | $ - 6.2777$,$0.1389 \pm {\rm{i3}}{\rm{.5671}}$ | Ⅱ |
| ${Q_{15,16}}\left( { \pm 25,0,0} \right)$ | $ - 6.2777$,$0.1389 \pm {\rm{i3}}{\rm{.5671}}$ | Ⅱ |
| ${Q_{17,18}}\left( { \pm 35,0,0} \right)$ | $ - 6.2777$,$0.1389 \pm {\rm{i3}}{\rm{.5671}}$ | Ⅱ |
| ${Q_{19,20}}\left( { \pm 45,0,0} \right)$ | $ - 6.2777$,$0.1389 \pm {\rm{i3}}{\rm{.5671}}$ | Ⅱ |
| ${Q_{2{\rm{1}},2{\rm{2}}}}\left( { \pm 55,0,0} \right)$ | $ - 6.2777$,$0.1389 \pm {\rm{i3}}{\rm{.5671}}$ | Ⅱ |
表112-涡卷混沌吸引子的平衡点、特征值和平衡点的类型
Table1.Equilibrium points, eigenvalues and types of equilibrium points for the 12-scroll chaotic attractor.
3
2.3.3.最大李雅普诺夫指数和庞加莱映射
当





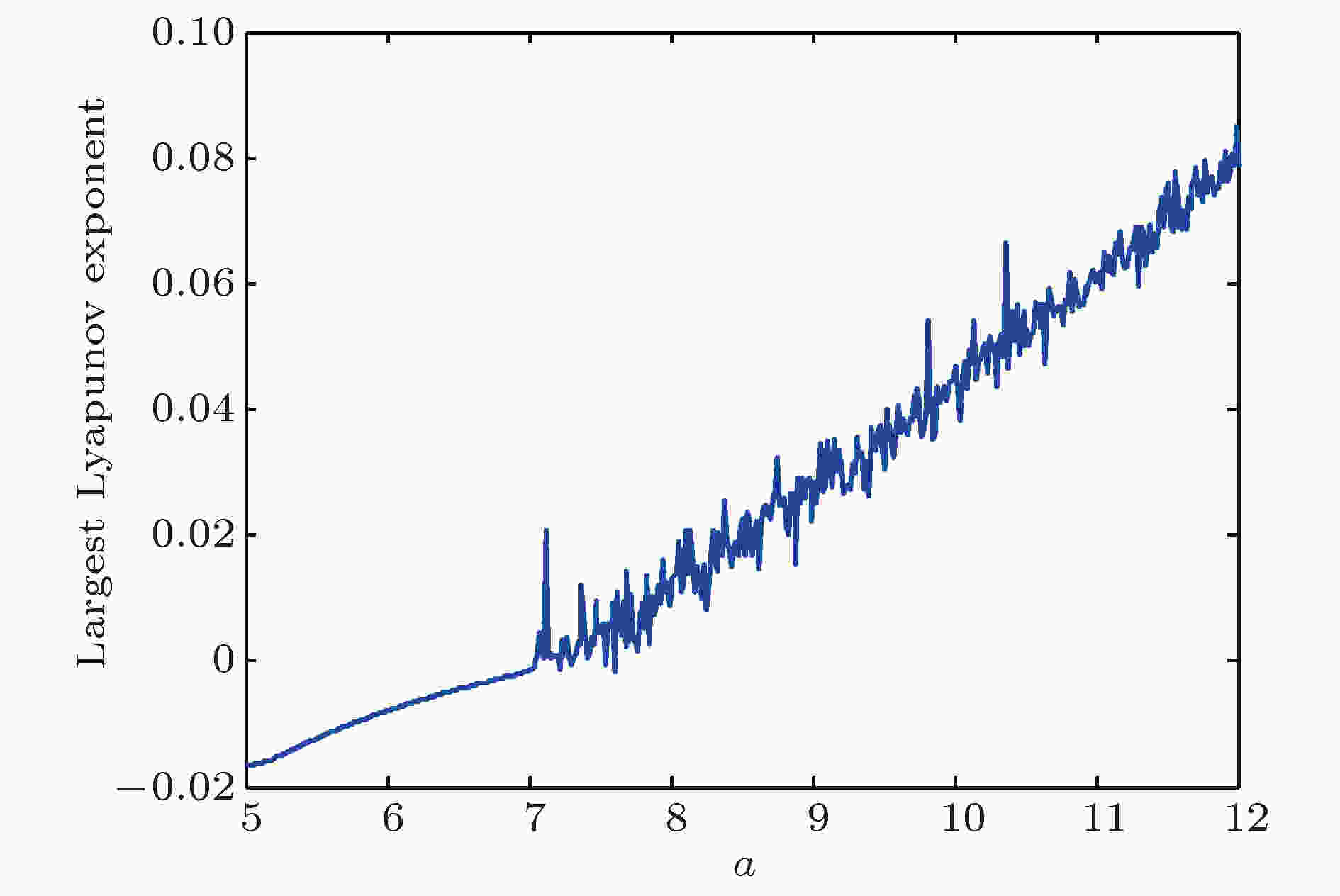 图 15 最大李雅普诺夫指数
图 15 最大李雅普诺夫指数Figure15. Largest Lyapunov exponent.
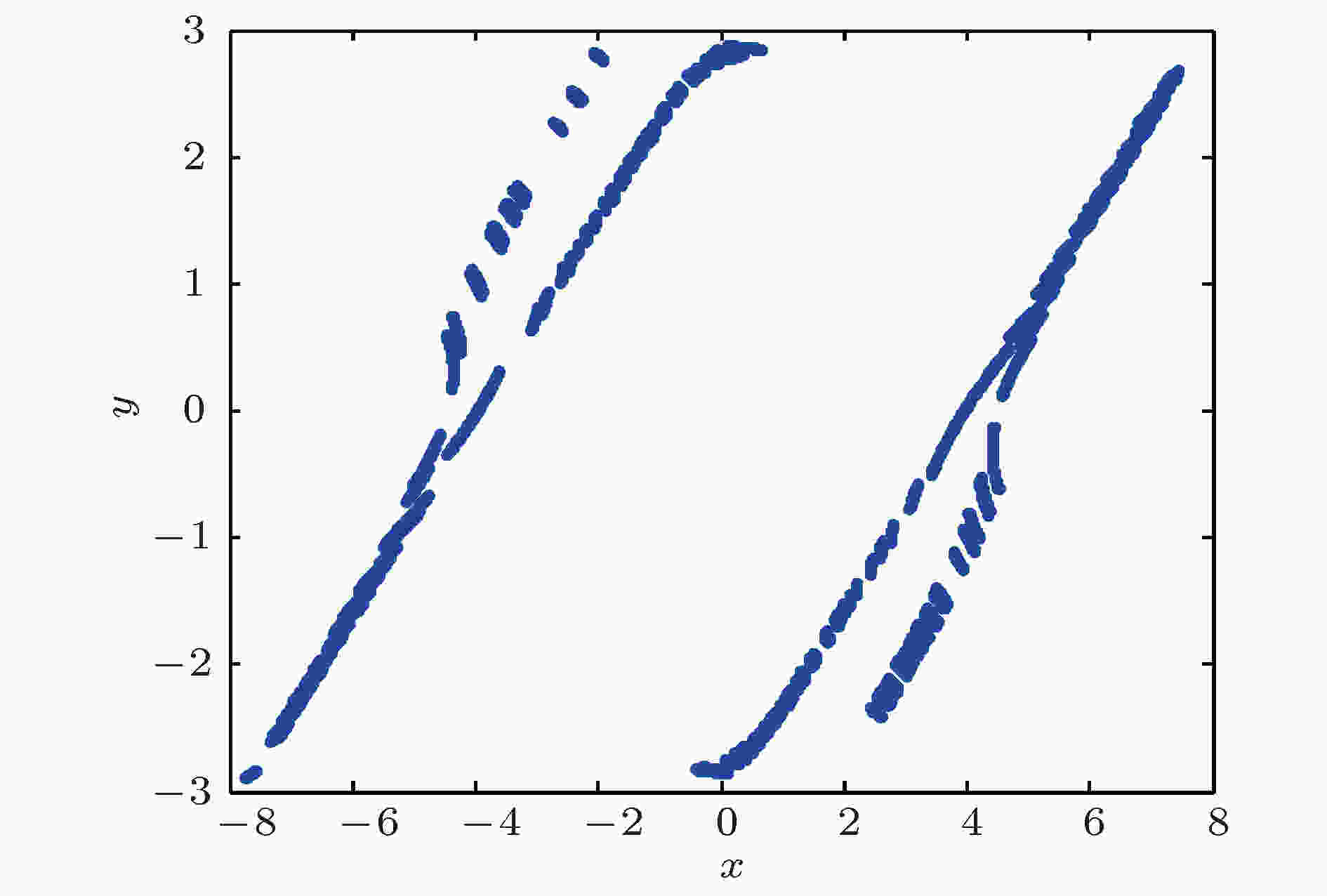 图 16 x-y平面的庞加莱映射
图 16 x-y平面的庞加莱映射Figure16. Poincaré mapping on the x-y plane.
3.1.递归反步控制器的设计
在Chua多涡卷混沌系统(23)式的基础上加入递归反步控制器, 可得受控Chua多涡卷混沌系统为
















2
3.2.仿真结果
以4-涡卷混沌系统为例验证递归反步控制器对混沌行为的控制效果. 假设初始条件为




递归反步控制器能够将4-涡卷混沌系统控制到正弦函数



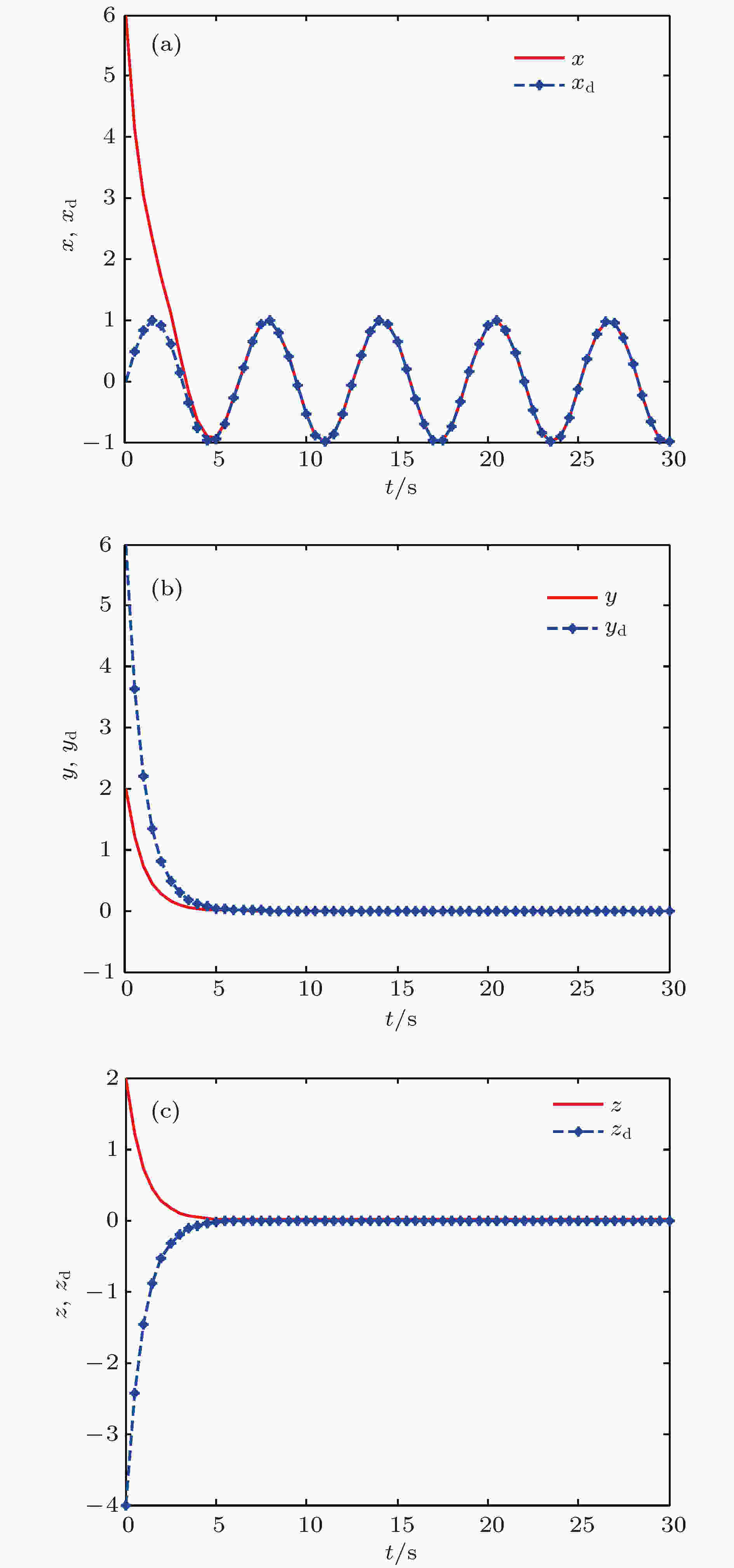 图 17 状态变量和期望值
图 17 状态变量和期望值
Figure17. Time domain diagram of state variables and desired values

 图 18 状态变量和期望值
图 18 状态变量和期望值
Figure18. Time domain diagram of state variables and desired values

4.1.检测原理和方法
本节采用Chua多涡卷混沌系统与递归反步控制器相结合的方法来进行微弱信号检测. 检测原理: 基于混沌控制理论与Chua多涡卷混沌系统对高斯噪声的免疫性, 利用递归反步控制器将含有高斯噪声和待测多频微弱周期信号的Chua多涡卷混沌系统控制到不动点, 然后进行频谱分析检测出信号的各频率, 检测原理图如图19所示. 图 19 检测原理图
图 19 检测原理图Figure19. Detection schematic diagram.
具体检测过程如下:
1)确定系统(23)式的参数, 使系统(23)式处于混沌状态.
2)将高斯噪声加入到系统状态方程(23)式的第二项, 如果系统(23)式仍处于混沌状态, 说明系统(23)式对高斯噪声免疫.
3)采用递归反步控制器(42)式, 将系统(23)式控制到不动点.
4)对检测系统(由系统(23)式、三个递归反步控制器(42)式、高斯噪声和待测多频微弱周期信号组成)的输出信号进行频谱分析, 检测出高斯噪声背景下待测多频微弱周期信号的各频率.
首先应用随机微分方程理论[38]分析Chua多涡卷混沌系统(23)式对高斯噪声的免疫性. 用














将(44)式表示为矢量微分方程的形式

将均值为0, 方差为0.001的高斯噪声

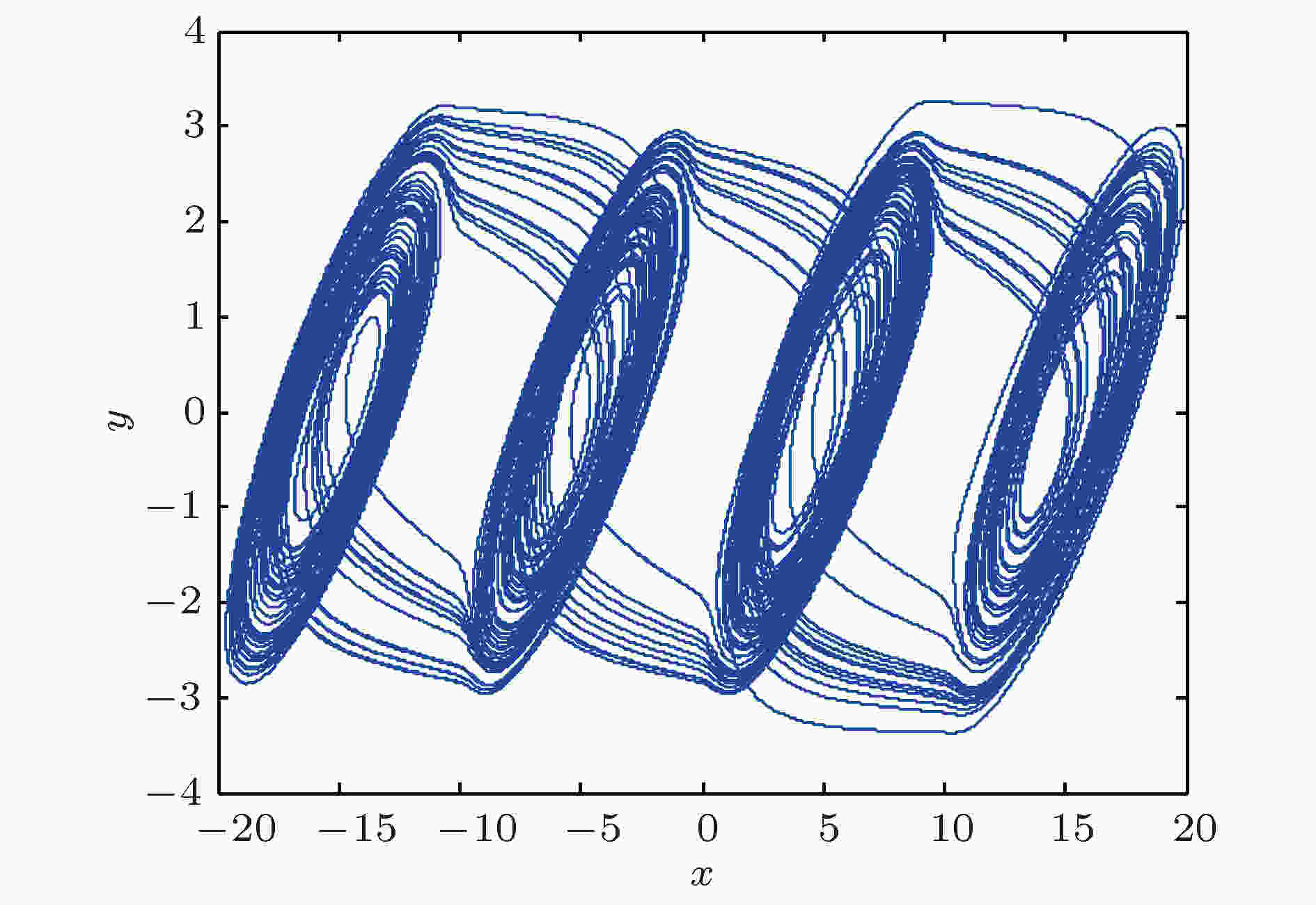 图 20 系统[(52)式]的相图
图 20 系统[(52)式]的相图Figure20. Phase diagram of system [Equation(52)].
2
4.2.检测结果
将输入信号






以4-涡卷混沌系统为例, 其中























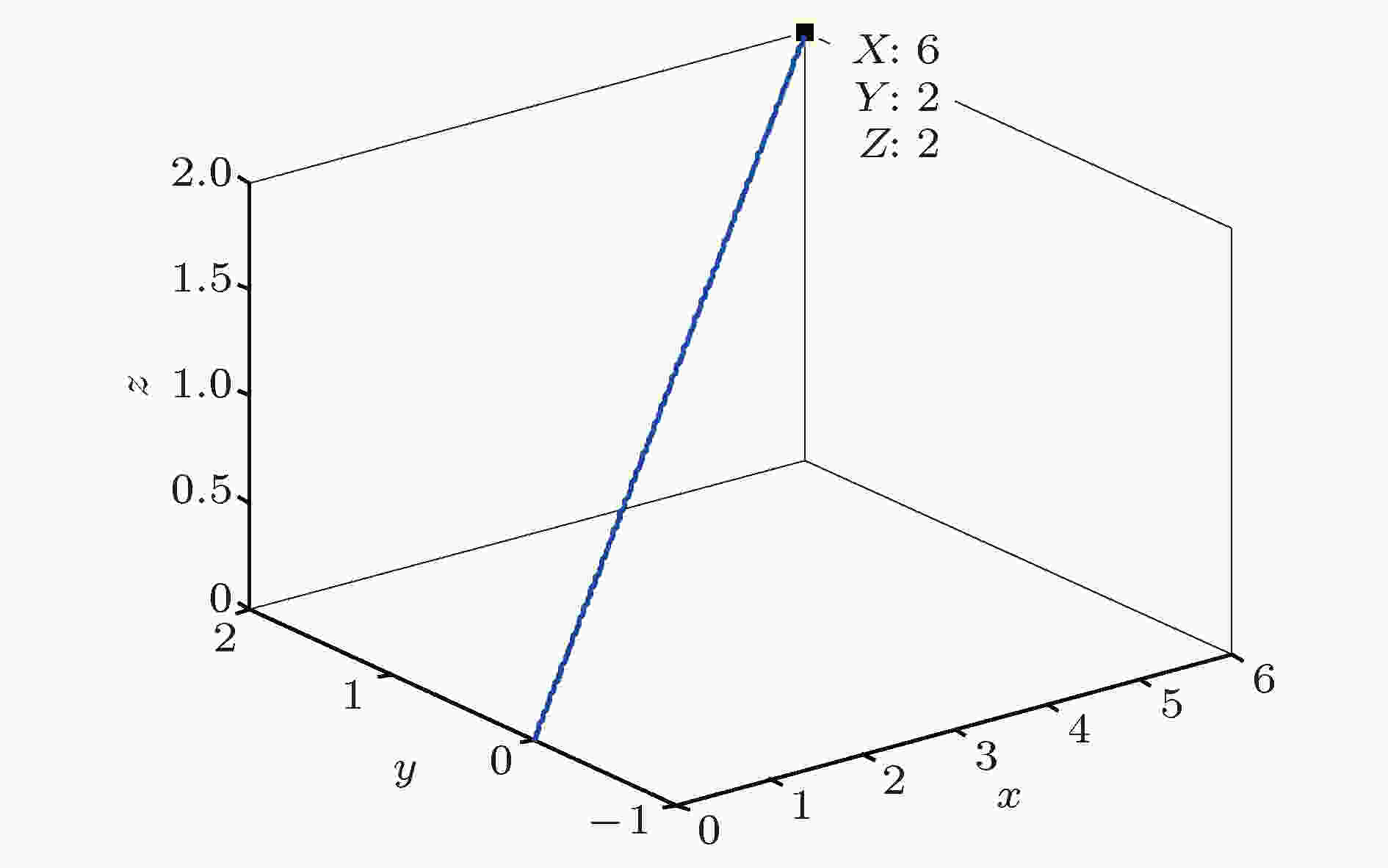 图 21 检测系统[(53)式]的相图
图 21 检测系统[(53)式]的相图Figure21. Phase diagram of the detection system [Equation(53)]
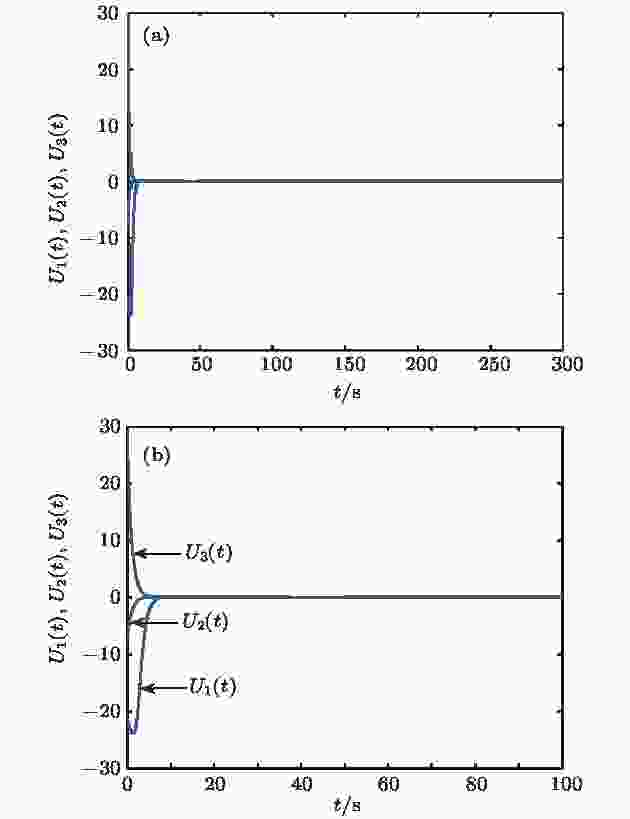 图 22 控制信号
图 22 控制信号



Figure22. Time domain diagram of control signals




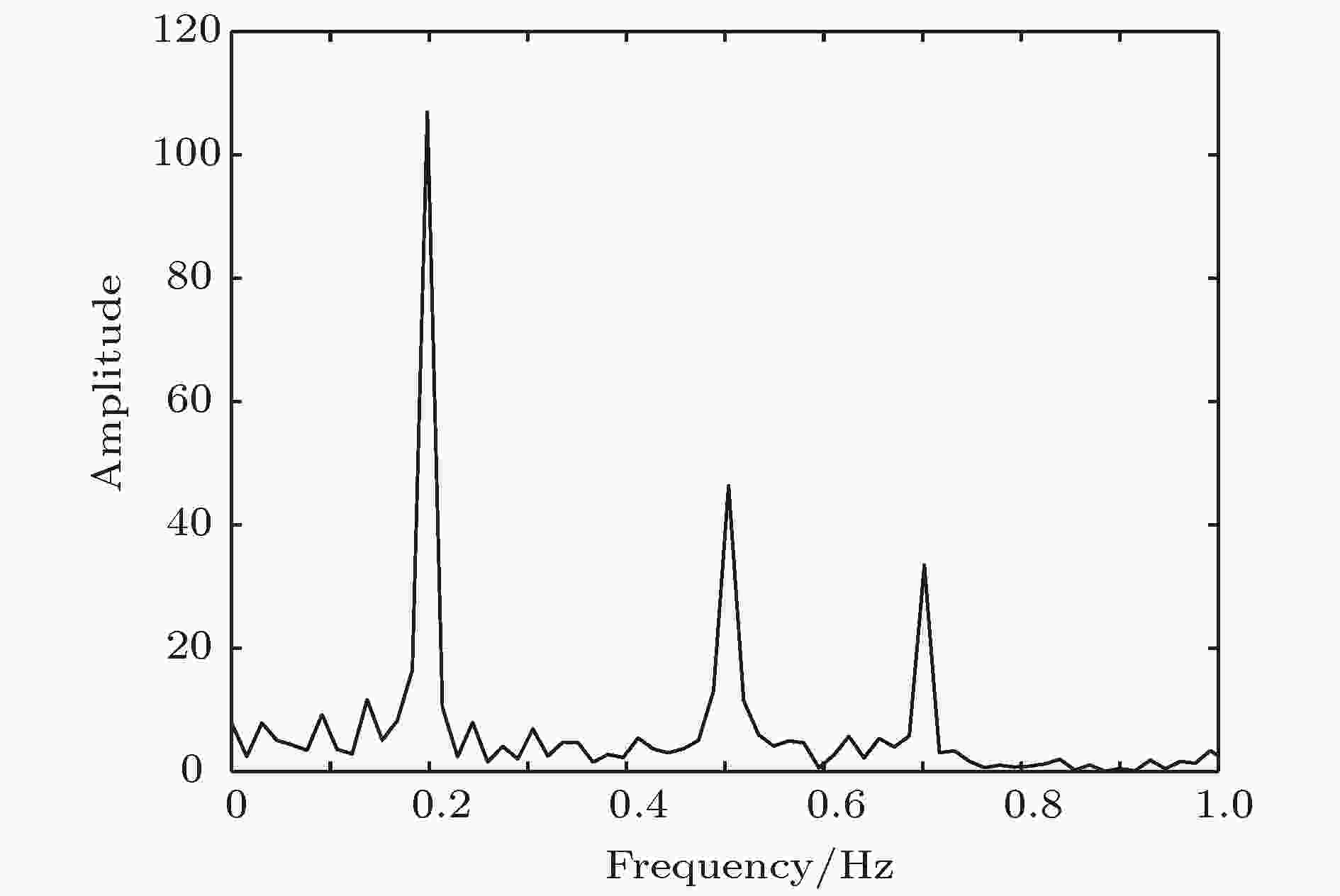 图 23 待测信号的频谱图
图 23 待测信号的频谱图Figure23. Frequency spectrum of the signal to be detected.
经过计算可得信噪比(signal-to-noise ratio, SNR)为
在微弱信号检测领域, 采用时域方法处理信号的最低SNR只有–10 dB左右[39], 而本文采用Chua多涡卷混沌系统和递归反步控制器相结合进行多频微弱周期信号检测得到的最低SNR为–19 dB, 提高了检测精度, 为基于非Duffing混沌系统的微弱信号检测提供了新思路.
