摘要:硅作为锂离子电池电极材料之一, 其应力效应尤为突出, 进而将影响电池性能. 本文建立了电化学反应-扩散-应力全耦合模型, 并研究了恒压充放电条件下扩散诱导应力、表面效应和颗粒间挤压作用对电压迟滞的影响. 结果发现, 应力及其导致的电压迟滞程度与颗粒尺寸相关. 在大颗粒(颗粒半径r > 100 nm)中, 扩散诱导应力是导致电势迟滞效应的主要因素, 这将导致电池能量耗散. 对于纳米级小颗粒(r < 100 nm)而言, 表面效应占据主导, 表面效应虽然能缓解电压迟滞, 同时却会使驱动电化学反应部分的过电势回线下移, 造成锂化容量衰减. 本文综合考虑了扩散诱导应力和表面效应, 得出: 半径为10 nm的颗粒将会使电极具备较好的综合性能. 此外, 对于硅电极而言, 颗粒间挤压作用会使应力回线向压应力状态演化, 进而导致锂化容量的衰减. 计算结果表明, 在电极设计中, 对孔隙率设定下限值有助于提升电极性能.
关键词: 锂离子电池/
表面效应/
颗粒间挤压作用/
电压迟滞

English Abstract

全文HTML

--> --> -->

电压迟滞效应是锂离子电池在使用过程中的常见现象^[1]. 在实际的充电-放电循环过程中, 电极电势随容量变化的演化曲线不重合, 由此形成电压迟滞回线. 电压迟滞效应将导致锂离子电池充放电过程中的能量耗散、降低充放电效率, 同时使电池状态不易于检测和控制. 因此, 控制电压迟滞效应对提升锂离子电池的性能具有重要意义.
近年来大量研究表明, 以硅材料作为电极材料可以提升电池容量^[2,3]. 然而由于硅在锂离子嵌入和嵌脱的过程中, 产生的应力比石墨等传统电极材料高得多, 因此, 与传统材料相比, 硅基电极表现出更强的应力-电压耦合效应. 对此, 大量****进行了相关研究, 有****发现压应力会抑制硅颗粒^[4]和纳米线^[5]中的锂化反应, 而拉应力则对锂化反应具有促进作用^[6]. Kim等^[7]利用应力和电压之间的耦合关系, 通过弯曲电极的方法制造出了能够收集电化学能的能量收集器. Piper等^[8]和Sethuraman等^[9]通过实验手段发现压应力对硅基电极的电压迟滞效应有显著影响. 因此, 研究硅等高容量电极材料中的应力-电压耦合效应具有重要的理论意义与应用价值.
现有文献中, 虽然有****从理论上揭示了应力-电压的耦合关系, 但这些研究通常基于简化后的电极结构, 如Bower等^[10]和Sethuraman等^[11]研究了应力效应对电池开路电势的影响, 并构建了薄膜电极中的应力-电势耦合模型. Lu等^[12]基于薄膜电极研究了应力和硅的塑性变形对电压迟滞的影响. 他们的研究讨论了应力对电压迟滞的影响, 并且针对表面自由的硅颗粒提出了影响的关键因素如材料特性和充电速率^[13].
尽管对简化电极结构的研究有助于从理论上揭示应力-电压耦合效应的内在机理, 然而实际电池中的电极是由活性颗粒、粘接剂、导电剂和孔隙构成的复合结构, 其复杂性远高于上述文献中的简化电极. 另一方面, 实际电极中活性颗粒间的挤压程度取决于电池的几何结构和材料特性, 其产生的力学效应对电极电压有着显著影响, 进而使上述文献中的结论无法直接应用于实际电池中. 此外, 由硅纳米颗粒构成的电极具备在高倍率充放电条件下不易开裂的优良机械性能^[14,15]. 然而, 当颗粒尺寸减小至纳米量级时, 表面效应将变得显著并影响电池的电压迟滞回线. 尽管Cheng等^[16]与Hao等^[17]已对电极颗粒的表面效应进行了探讨, 但是相比于扩散诱导应力, 循环充放电过程中表面效应对电压迟滞的影响仍有待于进一步的研究.
针对纳米级颗粒在实际电极中的应用, 本文构建了电化学反应-力学-扩散的多场耦合计算模型, 并通过该模型计算研究了纳米颗粒的表面效应和电极颗粒间挤压作用对锂离子电池电压迟滞效应的影响. 研究结果将对高容量电极的设计和提高电池的循环充放电性能提供优化方案.

本文研究的目标电极如图1所示. 可以看出, 实际的商业锂离子电池具有典型的多层结构, 每层由大量活性颗粒组成. 本文基于构建的电化学反应-力学-扩散的多场耦合计算模型, 先定量研究单个纳米级颗粒的表面效应对电压迟滞的影响, 然后引入电池结构的特性参数如孔隙率和等效杨氏模量, 研究电极颗粒间挤压对电压迟滞的影响.
图 1 锂离子电池中的多层电极结构
Figure1. Multi-scale hierarchical electrode structure in lithium ion battery.

2

-->

3.1.扩散方程

在电极颗粒内部, 锂离子沿着径向方向扩散, 可以使用球坐标系下的Fick定律来描述:

$\dfrac{{\partial {{c}}}}{{\partial t}} = D\dfrac{{{\partial ^2}c}}{{\partial {r^2}}} + 2\dfrac{D}{r}\dfrac{{\partial c}}{{\partial r}},$

其中, D为扩散系数, r为颗粒半径, c代表锂离子的浓度, t代表时间. 由于本文的研究重点在于应力对于电化学反应边界处的作用, 而非应力对于扩散行为的影响, 因此只在电化学反应边界处考虑应力影响, 而在扩散过程中的应力作用并不重要. 此外, 扩散的饱和效应^[18]也不是本文的研究重点.
2 -->

3.2.电化学反应边界条件

锂离子与活性材料之间的电化学反应可表示如下:

$H{\rm{ + }}x{\rm{L}}{{\rm{i}}^{\rm{ + }}}{\rm{ + }}x{{\rm{e}}^ - }\underset{{{\;\;k_a\;\;}}}{\overset{{{\;\;k_c\;\;}}}{\rightleftarrows}}{\rm{ L}}{{\rm{i}}_x}H,$

其中H代表活性材料.
根据修正的Butler-Volmer模型^[12,13], 电极表面的电化学反应速率同时受到电极电势和表面静水应力的影响, 如下:

$\begin{split}{i_{\rm{n}}} =\;& {i_0}\left\{ {\exp \left[ {\left( {1 - \alpha } \right)\dfrac{{F\left( {{E_{\rm{v}}} - {E_{{\rm{eq}}}}} \right) - {\sigma _{\rm{h}}}\varOmega }}{{{R_{\rm{g}}}T}}} \right]} \right.\\& \left. { - \exp \left[ { - \alpha \dfrac{{F\left( {{E_{\rm{v}}} - {E_{{\rm{eq}}}}} \right) - {\sigma _{\rm{h}}}\varOmega }}{{{R_{\rm{g}}}T}}} \right]} \right\},\end{split}$

其中, i_n, i₀, R_g, T, σ_h, Ω和α分别代表净电流密度、交换电流密度、理想气态常数、温度、电极表面的静水应力、偏摩尔体积和电荷传递系数; E_v代表施加给电极的电势, E_eq代表整个电极在平衡状态下的电势, E_v–E_eq为电极发生电化学反应时偏离平衡状态的程度, 即过电势, 过电势越大表示电极的电化学反应越偏离平衡态, 反之越接近于平衡态; σ_h和Ω反映了由机械应力导致的能量壁垒, 本质上揭示了锂离子在跨越固液相界面时发生的电化学反应要受到电极表面应力的阻碍作用. 交换电流密度i₀可表示为

${i_0} = F{k_0}c_{{\rm{L}}{{\rm{i}}^{\rm{ + }}}}^{1 - \alpha }{\left( {{c_{\max }} - {c_{{\rm{surf}}}}} \right)^{^{1 - \alpha }}}c_{{\rm{surf}}}^\alpha,$

式中, F, k₀, c_max, c_surf和${c_{{\rm{L}}{{\rm{i}}^{\rm{ + }}}}}$分别代表法拉第常数、平衡态的反应速率系数、锂离子在电极材料中的最大浓度、颗粒表面的锂离子浓度和溶液中的锂离子浓度.
电荷传递系数$\alpha $通常取0.5, 则电极电势可以由

${E_{\rm{v}}} = \dfrac{{2{R_{\rm{g}}}T}}{F}{\rm{arcsinh}}\left( {\dfrac{{{i_{\rm{n}}}}}{{2{i_0}}}} \right) + \dfrac{{{\sigma _{\rm{h}}}\varOmega }}{F} + {E_{{\rm{eq}}}}$

得到. (5)式表明, 电极电势同时取决于反应速率和应力状态. 甚至在开路状态下(i_n等于0), 电极中应力状态的变化也同样可以引起电极电势的变化.
依据定义, 平衡电势E_eq指的是电极在不考虑应力状态下的开路电势^[12], 而实际情况中, 一方面由于基底约束将不可避免地产生应力, 另一方面电极颗粒之间的挤压也会产生应力, 因此无应力状态的电极并不存在. 本文计算电极的平衡电势采用Sethuraman等^[19]的多项式拟合结果, 拟合结果同时考虑了锂化和去锂化的过程, 如(6)式和图2所示. 为尽可能地减小应力和其他副反应导致的误差, 实验中将电池进行了长时间的静置.
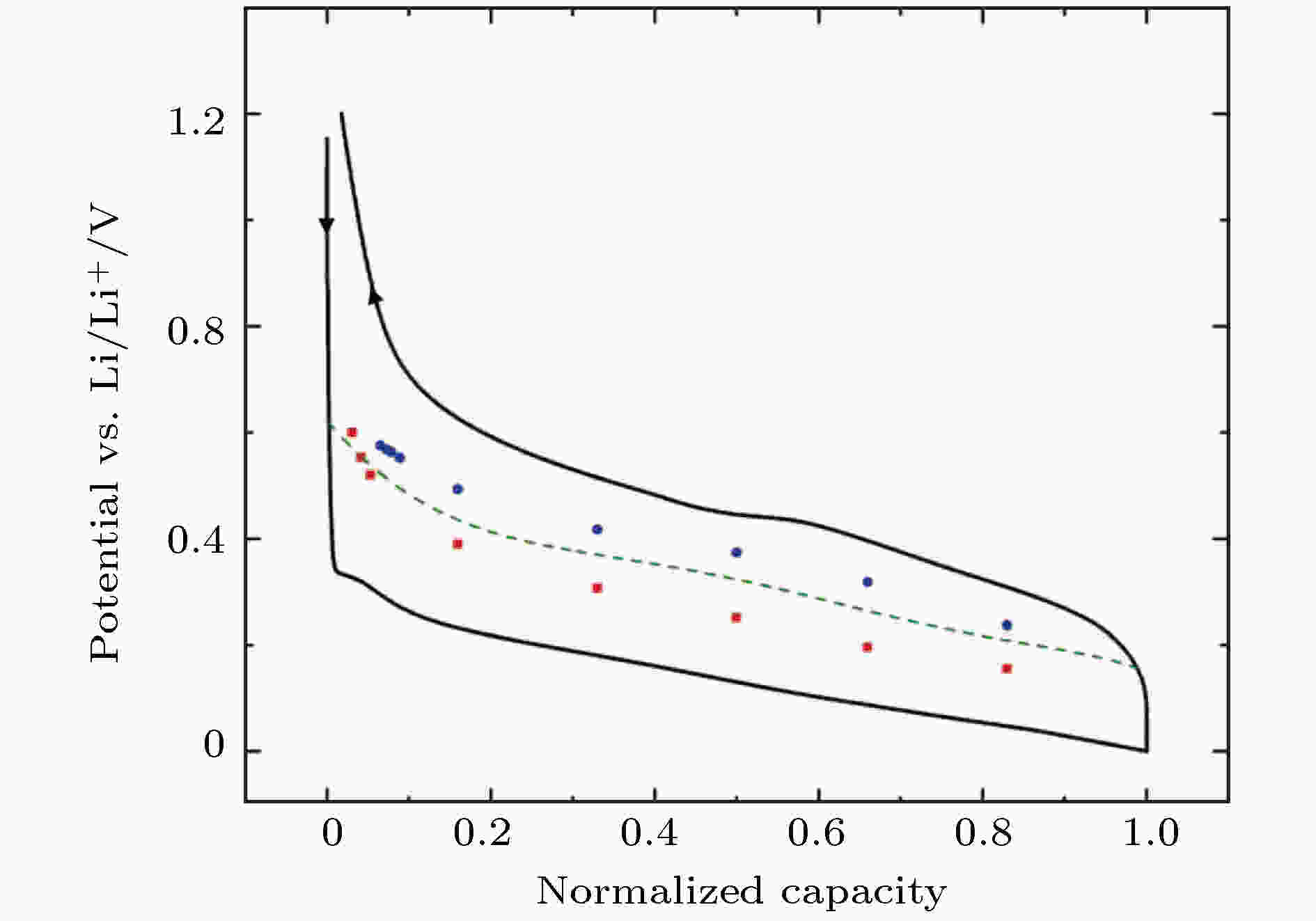图 2 Sethuraman等^[19]硅电极开路电势的拟合结果和实验结果, 其中红色的数据点是实验测得的锂化数据, 蓝色数据点是实验测得的去锂化数据, 实线是在C/8恒流充放电条件下的实验曲线, 虚线是依据实验数据拟合的结果
Figure2. Fitting results and experimental results of open-circuit potential of silicon electrode proposed by Sethuraman et al.^[19]. The red data point is the lithium data measured in the experiment, and the blue data point is the dilithiated data measured in the experiment. The solid line was obtained under a C/8 constant current charge-discharge operation, and the dashed line is the fitting function

$\begin{split}{E_{{\rm{eq}}}} = & - 4.76{z^6} + 9.34{z^5} - 1.8{z^4} - 7.13{z^3} \\ &+ 5.8{z^2}- 1.94z + 0.62,\;0 \leqslant z \leqslant 1,\end{split}$

其中z代表锂离子的归一化浓度.
硅电极存在两种基本的充放电规程, 即恒流充放电和恒压充放电. 本文基于恒压充放电规程进行计算, 即电极电势E_v控制为恒定值, 对电极为锂金属的半电池体系来说, 在忽略电解液中的电势差时, 由(3)式及流量与净电流密度的关系J = i_n/F可得锂化和去锂化的流量计算公式如下:

$J = {\rm{2}}\dfrac{{{i_{\rm{0}}}}}{F}\sinh \left( {\dfrac{{F\left( {{E_{\rm{v}}} - {E_{{\rm{eq}}}}} \right) - \varOmega {\sigma _{\rm{h}}}}}{{2{R_{\rm{g}}}T}}} \right).$

边界条件可表述为

$D\dfrac{{\partial {\rm{c}}}}{{\partial r}} = - 2\dfrac{{{i_{\rm{0}}}}}{F}{\rm{sinh}}\left( {\dfrac{{F\left( {{E_{\rm{v}}} - {E_{{\rm{eq}}}}} \right) - \varOmega {\sigma _{\rm{h}}}}}{{2{R_{\rm{g}}}T}}} \right),\;r = R,\tag{8a}$

$D\dfrac{{\partial {\rm{c}}}}{{\partial r}} = 0,\;\;\;\;r = 0\;,\tag{8b}$

式中i_n < 0代表锂化过程, 而i_n > 0代表去锂化过程.
2 -->

3.3.扩散诱导应力

关于球颗粒中扩散诱导应力, 本文采用Cheng和Verbrugge^[20]给出的解析解. 径向应力${\sigma _r}$和环向应力${\sigma _\theta }$可表述如下:

${\sigma _r}\left( r \right) = \dfrac{{2E\varOmega }}{{9(1 - v)}}\left[ {{c_{{\rm{av}}}}\left( R \right) - {c_{{\rm{av}}}}\left( r \right)} \right],\tag{9a}$

${\sigma _\theta }\left( r \right) = \dfrac{{E\varOmega }}{{9\left( {1 - v} \right)}}\left[ {2{c_{{\rm{av}}}}\left( R \right) + {c_{{\rm{av}}}}\left( r \right) - 3c\left( r \right)} \right],\tag{9b}$

其中, E代表杨氏模量, v代表泊松比, ${c_{{\rm{av}}}}\left( r \right) =$$ \left( {3/{r^3}} \right)\int_0^r {{r^2}c\left( r \right){\rm{d}}r} $用于计算半径为r的球颗粒的平均浓度, 球颗粒的静水应力通过${\sigma _{\rm{h}}}(r) =[{\sigma _r}\left( r \right) +$$ {\sigma _\theta }\left( r \right) + {\sigma _\phi }\left( r \right)]/3$计算. 考虑到颗粒表面的径向应力${\sigma _r}$为0, 环向应力${\sigma _\theta }(r) = {\sigma _\phi }(r)$, 综上, 粒表面的静水压力可表述为

${\sigma _{\rm h}} = \dfrac{{2E\varOmega }}{{9\left( {1 - v} \right)}}\left[ {{c_{{\rm{av}}}}\left( R \right) - c\left( R \right)} \right].$

但是, 当颗粒半径减小时, 表面效应会因为比表面积的增加而增强^[16,21]. 尤其是当颗粒尺寸达到纳米级尺度时, 表面能和表面应力会影响锂离子在电极中的扩散行为. 这就需要对表面应力的计算(10)式进行修正.
表面能和表面应力的概念最早来源于Gibbs^[22]的研究. 表面张力$\sigma _{\alpha \beta }^{{\rm{surf}}}$可用如下公式计算^[22-26]:

$\sigma _{\alpha \beta }^{{\rm{surf}}} = \gamma {\delta _{\alpha \beta }} + \dfrac{{\partial \gamma }}{{\partial {\varepsilon _{\alpha \beta }}}},$

式中, $\gamma $为单位面积的表面能, ${\varepsilon _{\alpha \beta }}$代表2 × 2表面应变张量, ${\delta _{\alpha \beta }}$是克罗内克函数. 对于固体而言, 由于固体表面的弹性变形有限, 表面应力和表面能并不相同.
在Gibbs的基础上, Gurtin等^[27-29]研究了更具普适性的表面弹性理论, 该理论广泛用于固体表面效应的研究. 对于本文各向同性的活性颗粒而言, 颗粒表面任意两个垂直方向的主应变是相等的, 即:

${\varepsilon _\theta } = {\varepsilon _{\theta \theta }} = {\varepsilon _{\phi \phi }}.$

因此, 表面应力本构关系为^[27]

$\sigma _\theta ^{{\rm{surf}}} = \sigma _{\theta \theta }^{{\rm{surf}}} = \sigma _{\varphi \varphi }^{{\rm{surf}}} = {\tau ^0} + {K^{\rm{s}}}{\varepsilon _\theta },$

式中,${\tau ^0}$是不依赖于变形的表面张力; ${K^{\rm{s}}}$代表表面模量^[30,31]. (13)式也可以理解为Miller和Shenoy线弹性表面本构关系模型在各向同性球颗粒情况下的应用.
Cheng和Verbrugge^[16]基于以上的理论, 推导出在线弹性框架下, 考虑表面效应的球颗粒应力计算公式, 如下:

$\begin{split}{\sigma _r}\left( r \right) =\; & \!\dfrac{{2E\varOmega }}{{9\left( {1 - \upsilon } \right)}}\left[\!{\left(\!\!{\dfrac{{1 - \dfrac{{{K^{\rm{s}}}}}{R}\dfrac{{\left( {1 - \upsilon } \right)}}{E}}}{{1 \!+\! \dfrac{{2{K^{\rm{s}}}}}{R}\dfrac{{\left( {1 - 2\upsilon } \right)}}{E}}}}\!\!\right)\!{c_{{\rm{av}}}}\left( R \right)} \right. \\& \left. {\begin{array}{*{20}{c}} {} \\ {-{c_{{\rm{av}}}}(r)} \\ {} \end{array}} \right] - \dfrac{{\dfrac{{2{\tau ^0}}}{R}}}{{1 + \dfrac{{2{K^{\rm{s}}}}}{R}\dfrac{{\left( {1 - 2v} \right)}}{E}}},\end{split} \tag{14a}$

$\begin{split} {\sigma _\theta }\left( r \right) = &\dfrac{{E\varOmega }}{{9\left( {1 - \upsilon } \right)}} \\ & \times \left[ {2\dfrac{{1 - \dfrac{{{K^{\rm{s}}}}}{R}\dfrac{{\left( {1 - \upsilon } \right)}}{E}}}{{1 \!+\! \dfrac{{2{K^{\rm{s}}}}}{R}\dfrac{{\left( {1 - 2\upsilon } \right)}}{E}}}{c_{{\rm{av}}}}(R) \!+\! {c_{{\rm{av}}}}(r) \!-\! 3c(r)} \right] \\ & - \dfrac{{\dfrac{{2{\tau ^0}}}{R}}}{{1 + \dfrac{{2{K^{\rm{s}}}}}{R}\dfrac{{\left( {1 - 2\upsilon } \right)}}{E}}}.\end{split} \tag{14b}$

当颗粒尺寸增大至可以忽略表面效应时, (14a)和(14b)式退化为(9a)和(9b)式. 从(14a)和(14b)式也同样可以看出, 当球颗粒尺寸非常小(纳米数量级)时, 表面效应的影响相当显著.
由(14a)和(14b)式可求得考虑表面效应时的静水应力为

$\begin{split} {\sigma _{\rm{h}}}\left( r \right) & = \dfrac{{{\sigma _r}\left( r \right) + 2{\sigma _\theta }\left( r \right)}}{3} \\ &= \dfrac{{2E\varOmega }}{{9\left( {1 - \upsilon } \right)}}\left[ {\dfrac{{1 - \dfrac{{{K^{\rm{s}}}}}{R}\dfrac{{\left( {1 + \upsilon } \right)}}{E}}}{{1 + \dfrac{{2{K^{\rm{s}}}}}{R}\dfrac{{\left( {1 - 2\upsilon } \right)}}{E}}}{c_{{\rm{av}}}}\left( R \right)} \right. \\ &\;\;\;\left. { - \begin{array}{*{20}{c}} {} \\ {c\left( r \right)} \\ {} \end{array}} \right] - \dfrac{{\dfrac{{2{\tau ^0}}}{R}}}{{1 + \dfrac{{2{K^{\rm{s}}}}}{R}\dfrac{{\left( {1 - 2\upsilon } \right)}}{E}}}.\end{split} $

(15)式中, 当r = R时, 可求得考虑表面效应时颗粒表面的静水应力, 即:

$\begin{split} {\sigma _{\rm{h}}}\left( R \right)\;& = \dfrac{{{\sigma _r}\left( r \right) + 2{\sigma _\theta }\left( r \right)}}{3} \\ &= \dfrac{{2E\varOmega }}{{9\left( {1 - \upsilon } \right)}}\left[ {\dfrac{{1 - \dfrac{{{K^{\rm{s}}}}}{R}\dfrac{{\left( {1 + \upsilon } \right)}}{E}}}{{1 + \dfrac{{2{K^{\rm{s}}}}}{R}\dfrac{{\left( {1 - 2\upsilon } \right)}}{E}}}} \right.{c_{{\rm{av}}}}\left( R \right) \\ & \;\;\;\left. {\begin{array}{*{20}{c}} {} \\ { - c\left( R \right)} \\ {} \end{array}} \right] - \dfrac{{\dfrac{{2{\tau ^0}}}{R}}}{{1 + \dfrac{{2{K^{\rm{s}}}}}{R}\dfrac{{\left( {1 - 2\upsilon } \right)}}{E}}}.\end{split}$

将(16)式与(10)式做差, 即可将如上的表面静水应力分离为两部分, 一部分为表面效应引起的应力$\sigma _{\rm{h}}^{\rm{s}}$, 另一部分为扩散诱导应力$\sigma _{\rm{h}}^{\rm{c}}$, 即:

$\begin{split}\sigma _{\rm{h}}^{\rm{s}} = & - \dfrac{{2E\varOmega }}{{9\left( {1 - \upsilon } \right)}}{c_{{\rm{av}}}}\left( R \right) \cdot \dfrac{{3{K^{\rm{s}}}\dfrac{{1 - \upsilon }}{{RE}}}}{{1 + \dfrac{{2{K^{\rm{s}}}}}{R}\dfrac{{1 - 2\upsilon }}{E}}}\\ & - \dfrac{{\dfrac{{2{\tau _0}}}{R}}}{{1 + \dfrac{{2{K^{\rm{s}}}}}{R}\dfrac{{1 - 2\upsilon }}{E}}},\end{split}\tag{17a}$

$\sigma _{\rm{h}}^{\rm{c}} = \dfrac{{2E\varOmega }}{{9(1 - v)}}\left[ {{c_{{\rm{av}}}}\left( R \right) - c\left( R \right)} \right].\tag{17b}$

由于表面效应通常取决于材料表面晶格结构的重配和材料的尺寸, 表面张力可能是压应力也可能是拉应力. 本文将硅材料不依赖于变形的表面张力${\tau _0}$和表面模量K^S分别取值为${\tau ^0} = 1\;{\rm{ J/}}{{\rm{m}}^2}$和K^S = 5 N/m^[31], 此时表面张力为压应力. 对于半径为1, 10和100 nm的颗粒而言, 由(16)式可以看出仅由$2{\tau ^0}/R$这项可产生2 GPa, 200 MPa和20 MPa的压应力, 可见随着颗粒尺寸的减小, 表面应力逐渐增大. 再由(17a)式可知, 随着颗粒尺寸的减小, 单纯由于表面效应引起的静水压力的变化量逐渐递增, 且在材料的整个充放电过程中体现为逐渐变大的压应力, 这将使材料表面有整体受压. 同时随着锂化容量的增加, 这种趋势愈发明显.
2 -->

3.4.颗粒间挤压效应

如图1所示, 在考虑颗粒间的挤压效应时, 由于实际电极内部的复杂结构, 实际电极中的应力分布是不均匀的. 本文采用参考文献[32]的公式计算颗粒间的挤压力:

${\sigma _{\rm{p}}} = \dfrac{{\beta ({c_{{\rm{av}}}}/{c_{\max }})}}{{\dfrac{{1 + {\mu _{\rm{m}}}}}{{2{E_{\rm{m}}}}} + \dfrac{{1 - 2{\mu _{\rm{p}}}}}{{{E_{\rm{p}}}}}}},$

其中, β是Vegard常数, 硅基电极中的β通常取0.24^[33]; E_p和$\mu_{\rm{p}}$分别是电极颗粒的杨氏模量和泊松比; 电极的等效杨氏模量E_m和泊松比$\mu_{\rm{m}}$可由电极孔隙率p计算而得,

${E_{\rm{m}}} = {E_{\rm{p}}}{\left( {1 - \dfrac{p}{{{\varepsilon _0}}}} \right)^n},\tag{19a} $

${\mu _{\rm{m}}} = {\mu _0} + {\left( {1 - \dfrac{p}{{{\varepsilon _1}}}} \right)^m}\left( {{\mu _{\rm{p}}} - {\mu _0}} \right),\tag{19b}$

式中, p为电极的孔隙率; ε₀, ε₁, ${\mu _0}$, m和n是拟合参数. 基于参考文献[34]中的有限元计算结果, 取ε₀ = 0.625, ε₁ = 0.5, ${\mu _0}$ = 0.14, m = 1.22, n = 2.23.
根据弹性力学理论, 对于表面受到均匀静水应力的弹性体而言, 其静水应力在弹性体内部的分布是均匀的. 因此, 电极颗粒中的静水应力是(16)式和(18)式之和.
上述公式描述了电化学反应、扩散和应力, 其中应力通过与应力耦合的电化学反应边界条件影响扩散过程, 而扩散过程又会进一步影响应力的分布. 因此, 可借助于MATLAB平台使用有限差分法进行数值求解. 在每一次迭代步中, 平衡电势E_eq和表面的静水应力σ_h可以通过锂离子浓度场c(r)求得, 然后将结果代入修正的Butler-Volmer公式中以得到电化学反应的边界条件, 最后根据扩散方程和得到的边界条件再次求解浓度场c(r). 最终可求得整个时间域内的浓度场和应力场.

大量文献表明, 当电极颗粒达到纳米级尺度时, 电极将表现出优良的性能, 由于纳米颗粒对溶液中锂离子具有很强的吸附力, 因此可提高电池的容量^[35]. 同时, 电池的高能量密度和锂离子的快速嵌入和脱嵌也在一定程度上取决于颗粒的尺寸^[36]. 这些都是纳米级颗粒对提高电池总体性能所带来的益处, 但是当随着颗粒尺寸的减小尤其是到达纳米级尺度时, 表面能和表面张力的影响逐渐变得显著^[16]. 这就不得不对活性颗粒的表面应力计算公式进行修正, 因此本节计算模拟纳米级颗粒的表面应力时使用考虑表面效应的球颗粒表面静水应力计算公式(16). 充放电规程为恒压充放电, 其中锂化时电极电势为0.24 V, 去锂化时电极电势为0.51 V. 锂化的终止条件为颗粒的最外层浓度达到饱和或反应电流${i_{\rm{n}}}$达到0, 去锂化的终止条件为颗粒的最外层浓度达到0或者反应电流${i_{\rm{n}}}$达到0.
2

-->

4.1.扩散诱导应力对电压迟滞的影响

依据(17b)式, 先讨论扩散诱导应力对电池电压迟滞的影响. 模拟过程使用的参数如表1所列.

E/GPa	ν	cmax/mol·m–3	Ω/m3·mol	D/m2·s–1
100[38]	0.27[37]	3.125 × 105[39]	4.25 × 10–6[13]	2 × 10–6[40]

表1活性材料的材料参数^[13,37-40]
Table1.The material parameters of active materials^[13,37-40]

图3(a)是700 nm的电极颗粒在恒压条件下的浓度演化图, x轴代表无量纲的半径$\overline r = r/R$, 变化范围由颗粒中心0至颗粒表面1; y轴是颗粒中的无量纲浓度$\overline c = c/{c_{\max}}$; 其中实线和虚线分别代表锂化和去锂化过程的浓度分布. 可以看出, 锂化阶段活性颗粒的浓度由外而内减少. 因此, 颗粒表层的膨胀量更大, 在颗粒内层的约束作用下外层受压. 同理, 在去锂化过程中, 浓度梯度为负, 导致颗粒表层受拉. 变化趋势上, 颗粒表层的浓度梯度先增大后减小, 因此应力的演化趋势也相应地先增加后减少. 从图3(b)可以看出, 不同尺寸的颗粒在锂化过程中扩散诱导应力为压应力, 而去锂化过程中其为拉应力, 从而形成了迟滞环.
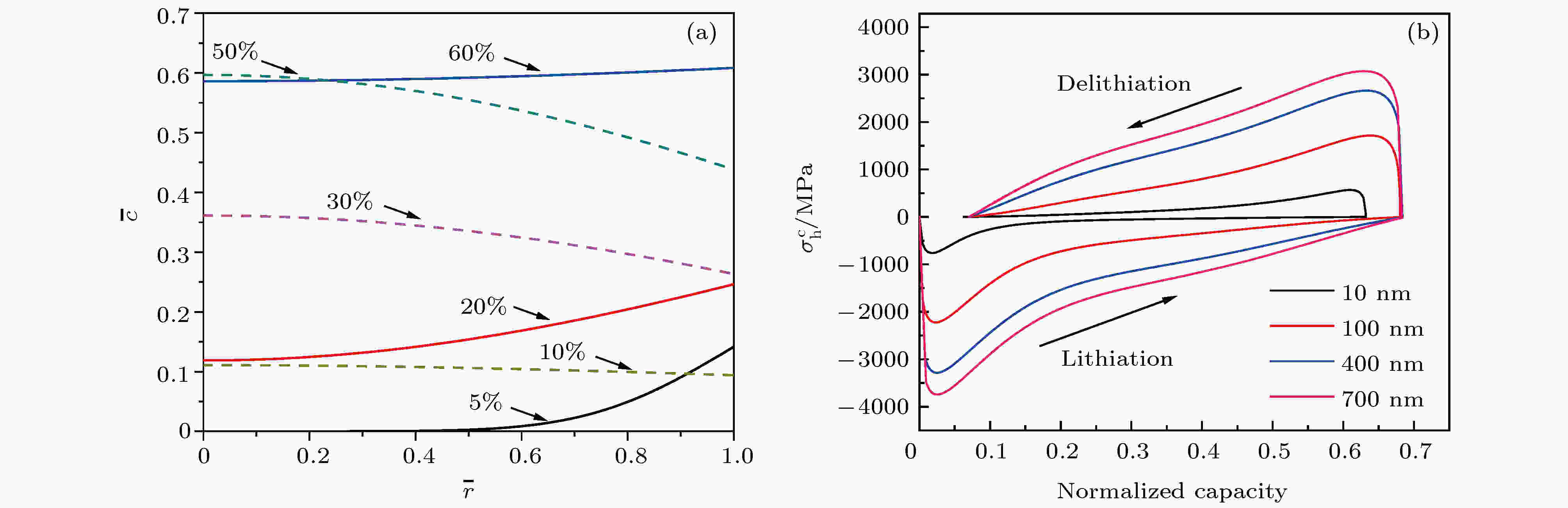图 3 扩散诱导应力对电压迟滞的影响　(a)电极颗粒在锂化和去锂化过程中锂离子的浓度分布; (b)一次充放电循环中, 不同尺寸的颗粒扩散诱导应力演化
Figure3. Effect of diffusion induced stress on voltage hysteresis: (a) Distribution of concentration of lithium ions in a electrode particle during lithiation and delithiation; (b) diffusion-induced stress evolution diagrams of particles with different sizes in primary charge-discharge cycle

由(3)式可知, 压应力阻碍锂化过程而拉应力阻碍去锂化过程. 扩散诱导应力分担的过电势为$\sigma _{\rm{h}}^{\rm{c}}\varOmega /F$, 因此图3(b)的应力迟滞环可转变为相应的过电势迟滞环. 此外, 同一充放电条件下更大的颗粒通常会产生更高的应力值. 此计算结果表现出尺寸效应, 即随着尺寸的缩小扩散诱导应力迟滞环在减小.
图4(a)—(d)分别是颗粒尺寸为10, 100, 400, 700 nm的各部分过电势演化曲线, 其中${E_{\rm{v}}} - {E_{{\rm{eq}}}}$是锂化和去锂化过程的总过电势, $\sigma _{\rm{h}}^{\rm{c}}\varOmega /F$为扩散诱导应力分担的部分过电势, $\dfrac{{2RT}}{F}{\rm{arcsinh}}\left( {\dfrac{{{i_{\rm{n}}}}}{{2{i_0}}}} \right)$代表驱动电化学反应部分的过电势. 与图3(b)结果一致, 大颗粒将产生更大的应力迟滞环, 应力分担的过电势迟滞环更大, 从而使更低的过电势用于驱动电化学反应. 因此, 大颗粒电极在一个充放电循环中由扩散诱导应力的作用会损失更多的能量.
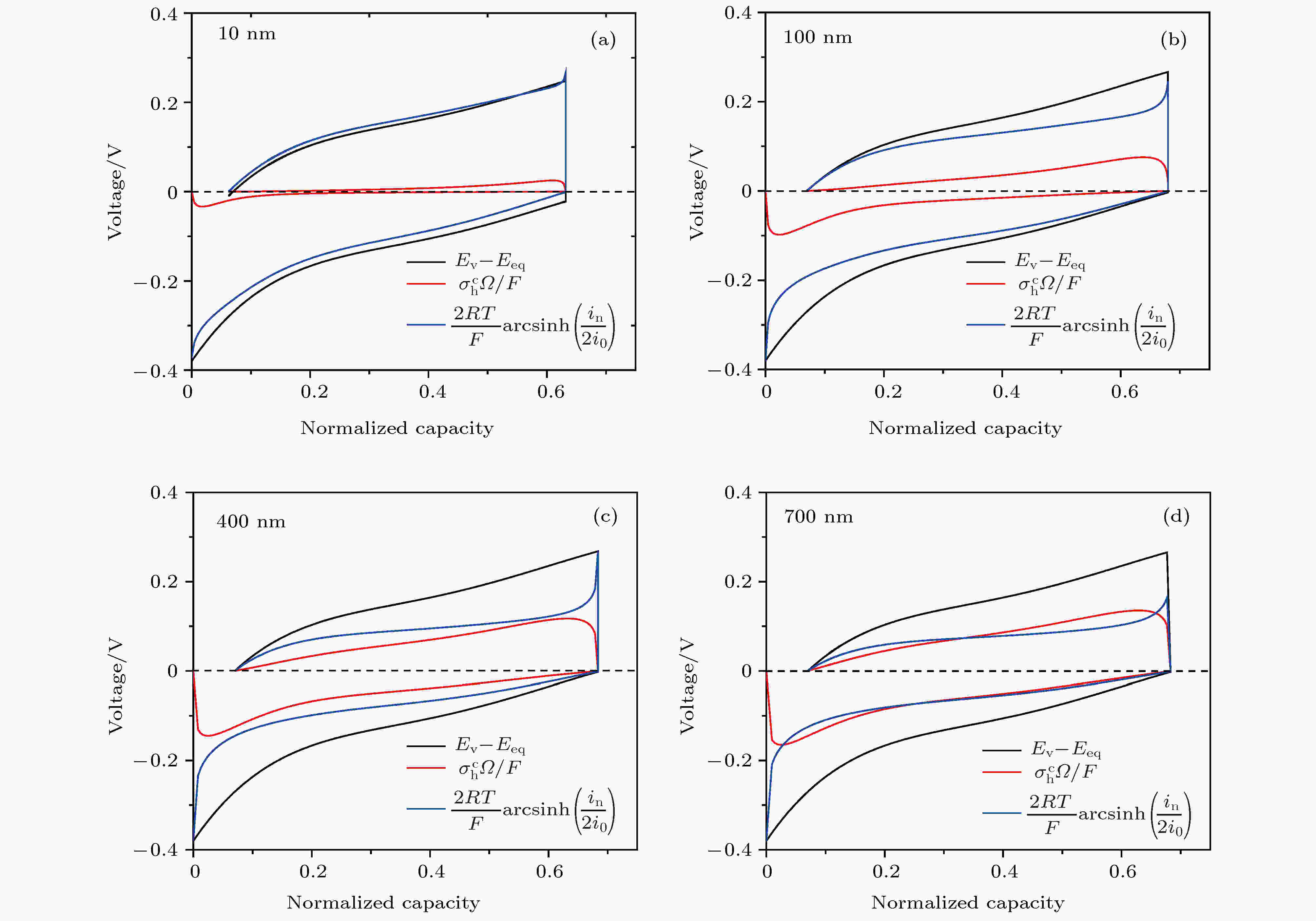图 4 (a)?(d)分别是颗粒尺寸为10, 100, 400, 700 nm的各部分过电势演化图
Figure4. (a)?(d) Overpotential evolution charts of each part with particle size of 10, 100, 400, 700 nm, respectively

为了进一步明确扩散诱导应力部分的过电势在总过电势中所占比重, 图5为锂化和去锂化过电势差值在不同颗粒尺寸下的变化关系. 此处的差值指的是在一次锂化和去锂化过程中最大值与最小值之差. 由于是恒压充放电, 所以总过电势的差值一直保持为750 mV. 随着颗粒尺寸从10 nm增加到700 nm, 扩散诱导应力部分的过电势差值由58.55 mV增加到300 mV, 所占百分比由7.8%增加到40%. 因此对于大颗粒来讲, 扩散诱导应力对电压迟滞的影响较为显著.
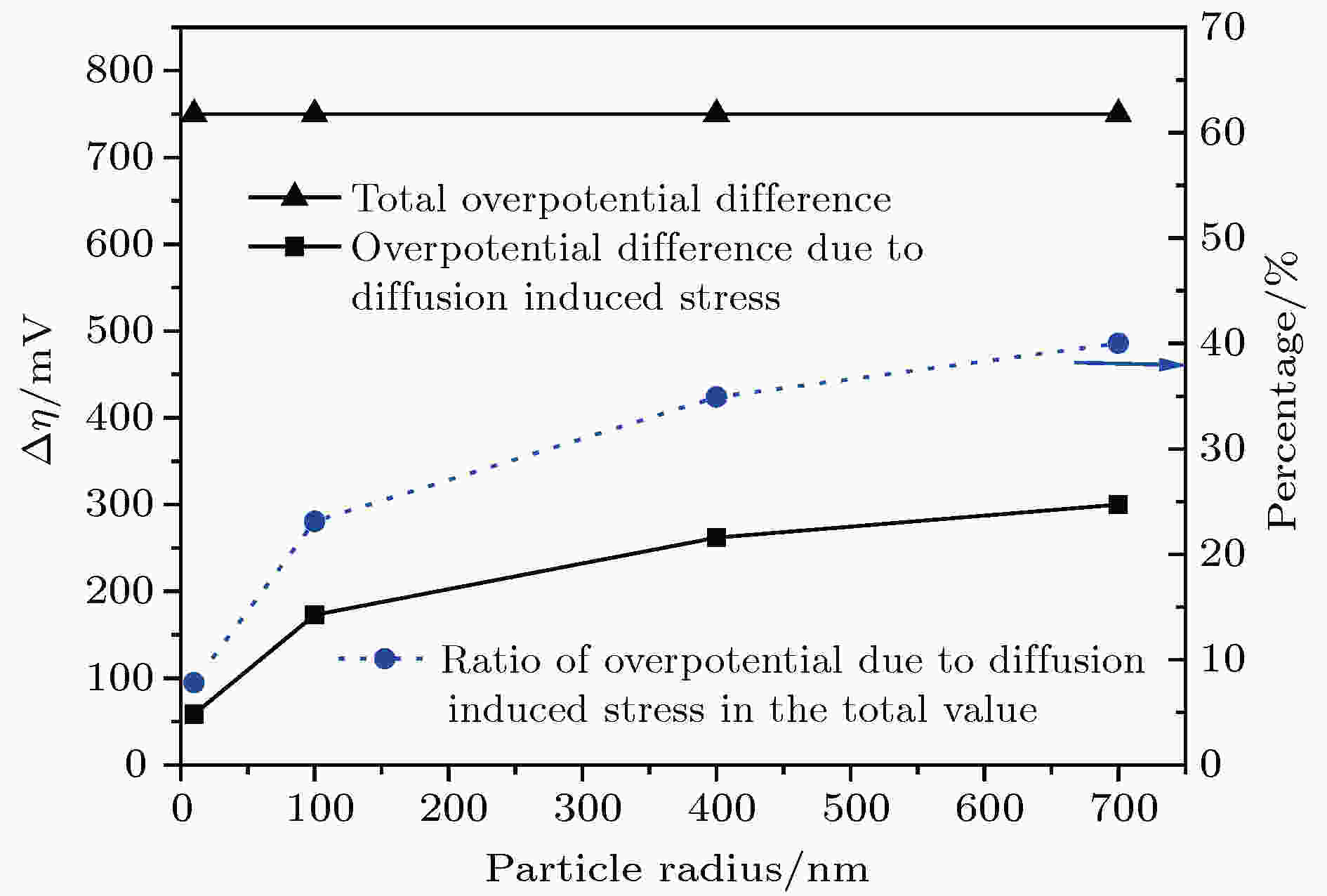图 5 应力分担过电势的差值、总过电势差值及其所占百分比在不同颗粒尺寸下的变化, 其中差值是指过电势回线中最大值与最小值之差
Figure5. Dependence of overpotential gap consumed by stress, total overpotential gap and the corresponding percentage on different particle sizes. The gap refers to the difference between the maximum value and the minimum value in the overpotential loop

2 -->

4.2.表面效应对电压迟滞的影响

由(17a)式可知表面效应引起的静水应力由两部分组成, 一部分取决于颗粒的平均锂离子浓度c_av(R), 表明扩散与表面效应是耦合的, 另一部分是不依赖于浓度的静水应力. 因此, 在充放电循环中由表面效应引起的表面张力与归一化浓度存在线性的变化关系且没有迟滞效应.
图6为不同尺寸的颗粒在一个充放电循环中由表面效应引起的静水应力演化图及相应的应力变化范围. 3张子图都表明表面应力随归一化浓度线性变化且无迟滞效应. 此外, 当颗粒尺寸小于100 nm时平均应力和应力的变化幅值增长很快. 从黑色曲线可以看出, 对于尺寸在100 nm以上的颗粒表面效应可以忽略.
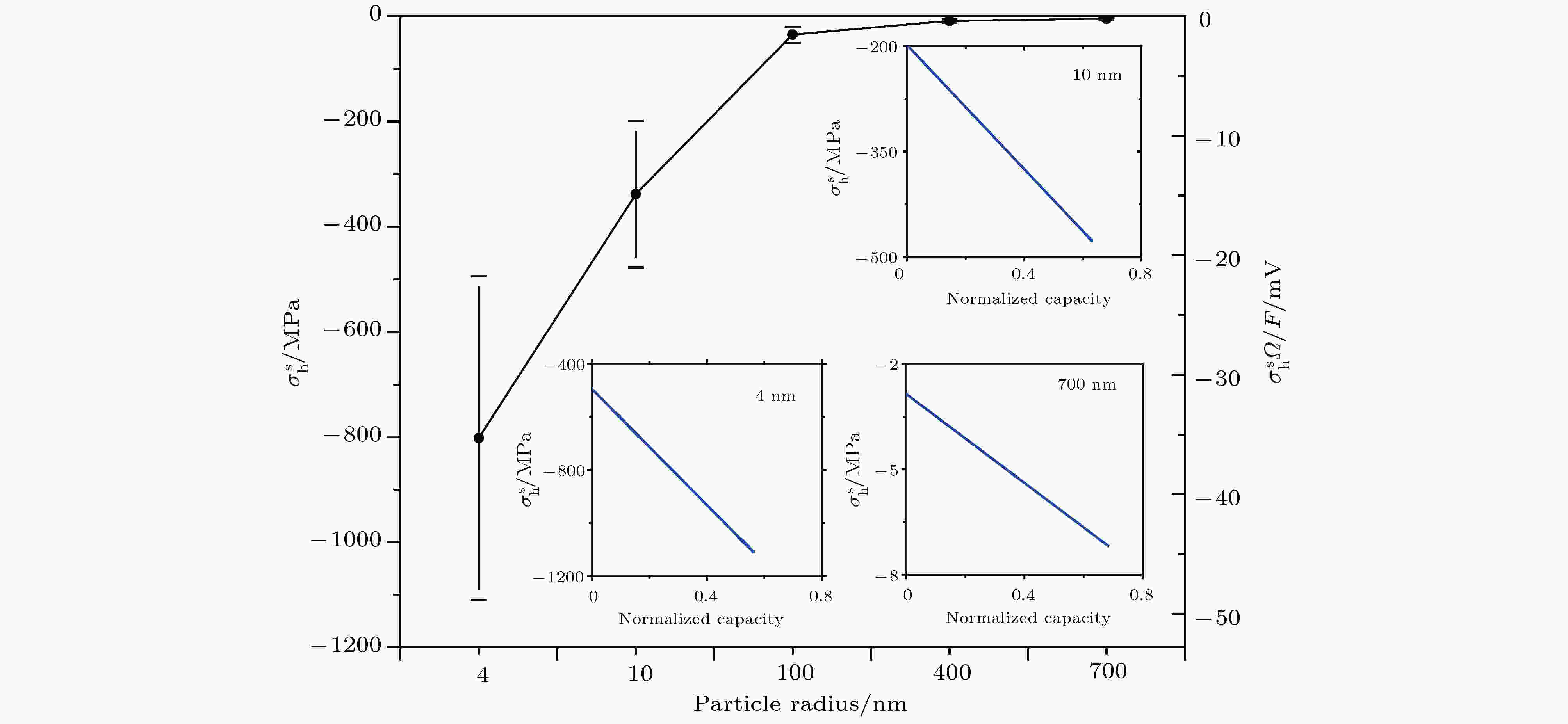图 6 由表面效应引起的表面张力及其分担过电势的演化曲线, 其中黑色曲线的应力值为一次充放电循环中的平均应力值, 竖直曲线为各自的变化范围; 3张子图为对应的表面张力演化曲线
Figure6. Evolution curve of surface tension due to surface effect and the corresponding overpotential. The dark line represents the mean stress in a cycle and the bar defines the range. The three subplots are evolutions of surface stress due to surface effects in a cycle

现在, 将扩散诱导应力和表面效应耦合在一起并讨论二者的相互竞争关系. 如图7(a)为不同颗粒尺寸下扩散诱导应力和表面效应耦合后的总应力演化曲线. 可以看出, 随着颗粒尺寸的减小, 应力迟滞效应在逐渐地减弱, 尤其在颗粒尺寸达到4 nm时, 应力迟滞环几乎消失. 另外, 随着颗粒尺寸的减小, 表面效应增强, 应力曲线整体上向压应力状态演化, 由对称状态向非对称状态演化. 这一现象预示着扩散诱导应力和表面效应之间的竞争机制. 依据图3(b)和图6, 当颗粒尺寸大于100 nm时, 扩散诱导应力占据主导而表面效应可以忽略, 进而导致明显的、对称的应力迟滞环. 然而, 当颗粒尺寸小于100 nm时, 表面效应变得显著而扩散诱导应力逐渐变得不明显, 原因为颗粒由外到内更短的扩散路径导致锂离子浓度趋于均匀.
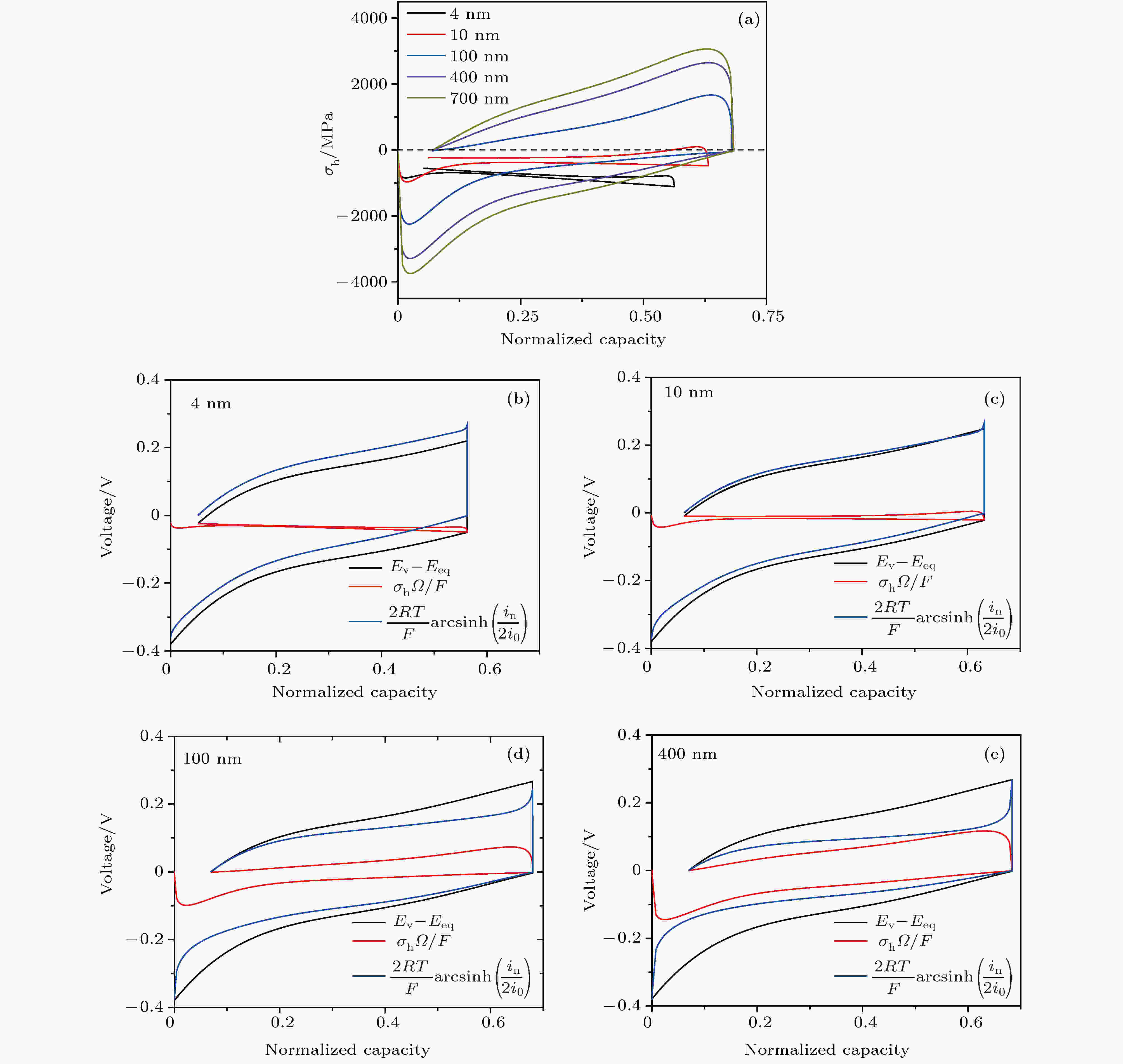图 7 (a)不同颗粒尺寸下, 表面张力和扩散诱导应力共同作用下的表面静水应力演化图; (b), (c), (d), (e)分别是颗粒尺寸为4, 10, 100和400 nm时的各部分过电势演化图
Figure7. (a) Evolution of surface hydrostatic stresses in consideration of both diffusion induced stress and surface effects under different particle sizes; (b), (c), (d), (e) evolutions of all parts of overpotential in the particles of 4, 10, 100 and 400 nm radius, respectively

图7(b)—(e)为不同颗粒尺寸下总过电势、总应力所占过电势和驱动电化学反应过电势的演化图. 可以看出, 随着颗粒尺寸的减少, 总应力所占过电势的回线在缩小, 使更高的过电势用于驱动实际的电化学反应. 同时由于颗粒表面效应的增强, 一方面使总应力所占过电势回线下移, 回线逐渐地失去对称性, 另一方面颗粒的锂化容量减少, 这是因为锂化过程表面效应产生的压应力阻碍了锂化过程.
综上所述, 在锂离子电极设计时, 需要考虑电极颗粒的最优尺寸, 如果颗粒尺寸过大, 扩散诱导应力所占过电势的回线将加大, 电压迟滞效应增强导致更多的能量损失. 如果颗粒尺寸太小, 表面效应将导致更高的表面张力, 阻碍锂化反应. 基于这两种因素, 需要将电极的颗粒尺寸控制在一个合理的范围内.
图8为基于上述计算结果, 不同颗粒尺寸下扩散诱导应力和由表面效应引起的静水应力对比图. 其中扩散诱导应力取为一次充放电循环中最大应力值与最小应力值之差的一半, 表面效应引起的静水应力取为一次充放电循环中应力的最大值的绝对值. 在以上参数选取下, 恒压充放电时, 表面效应和扩散诱导应力随颗粒尺寸的演化关系图如图8所示. 综合考虑表面效应和扩散诱导应力间的竞争机制, 应该选择表面效应和扩散诱导应力之和的最小值处对应的颗粒半径为最优尺寸. 两种效应之和的演化曲线如图9所示, 由图9可知, 半径为10 nm的颗粒对应的表面效应和扩散诱导应力之和最小, 即半径为10 nm的硅颗粒表现出较为均衡的综合性能. 因此, 从应力及其过电势回线的角度出发, 对于电极设计而言, 颗粒尺寸选取在10 nm左右是较为合理的选择.
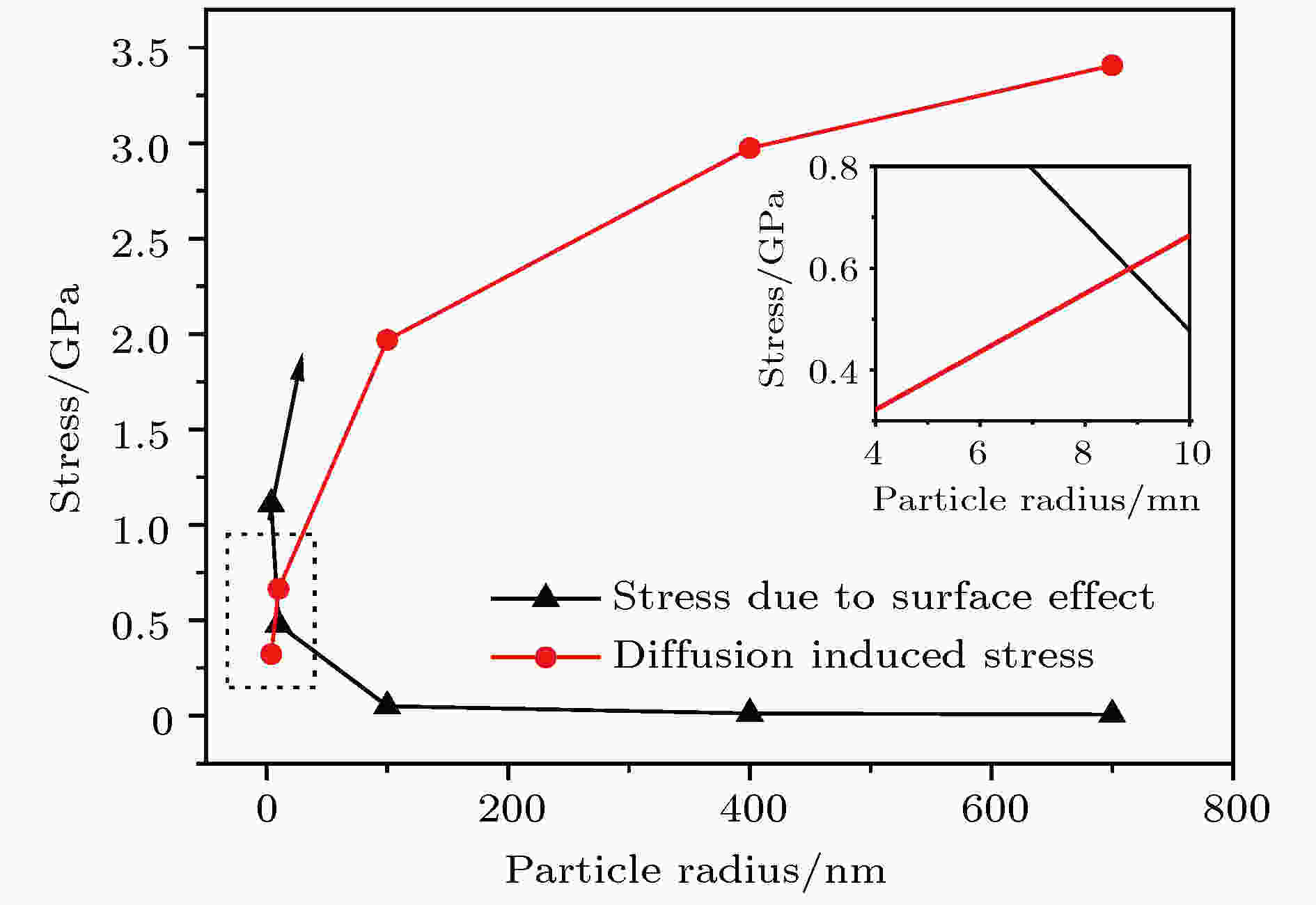图 8 不同颗粒尺寸下扩散诱导应力和表面效应引起的静水应力的绝对值对比
Figure8. Absolute values of the hydrostatic stress due to surface effects and the surface stress due to diffusion induced stress under different particle sizes.

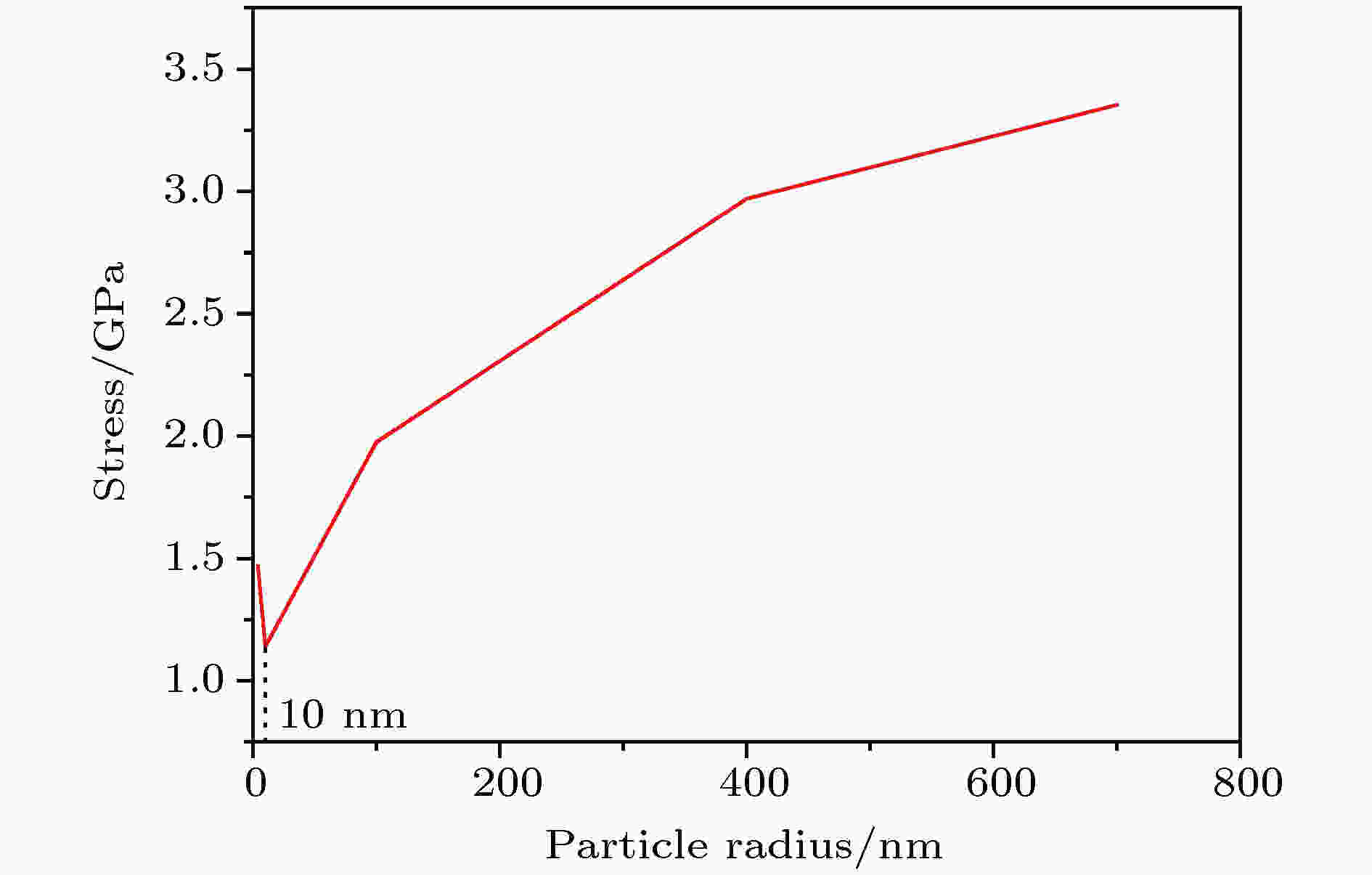图 9 不同颗粒尺寸下扩散诱导应力与表面效应之和的演化
Figure9. Evolution diagram of the sum of diffusion induced stress and surface effect under different particle sizes

2 -->

4.3.电极中颗粒间挤压对电压迟滞的影响

在充放电循环过程中锂离子电池的电极颗粒发生膨胀变形, 不可避免地要与周围的电极颗粒发生挤压, 从而产生颗粒间的压应力. 众所周知, 对于孔隙率较低的电极, 颗粒间的挤压力尤其显著. 因此, 本节讨论分析电极内颗粒间的挤压力对电压迟滞的影响. 考虑到通常情况下实际电极的颗粒尺寸为微米量级, 此部分颗粒尺寸取为1 μm, 充放电条件为恒压充放电, 锂化时电极电势保持为0.24 V, 去锂化时电极电势保持为0.51 V.
图10表明颗粒间的挤压作用显著影响了颗粒内的应力. 图10(a)为4种情况下即单独一个球颗粒和3种不同孔隙率电极内的球颗粒, 表面应力演化图. 可见由于颗粒间的挤压, 使应力迟滞回线逐渐失去对称性, 朝着压应力状态演化. 即使在较低的孔隙率条件下, 仍然十分明显.
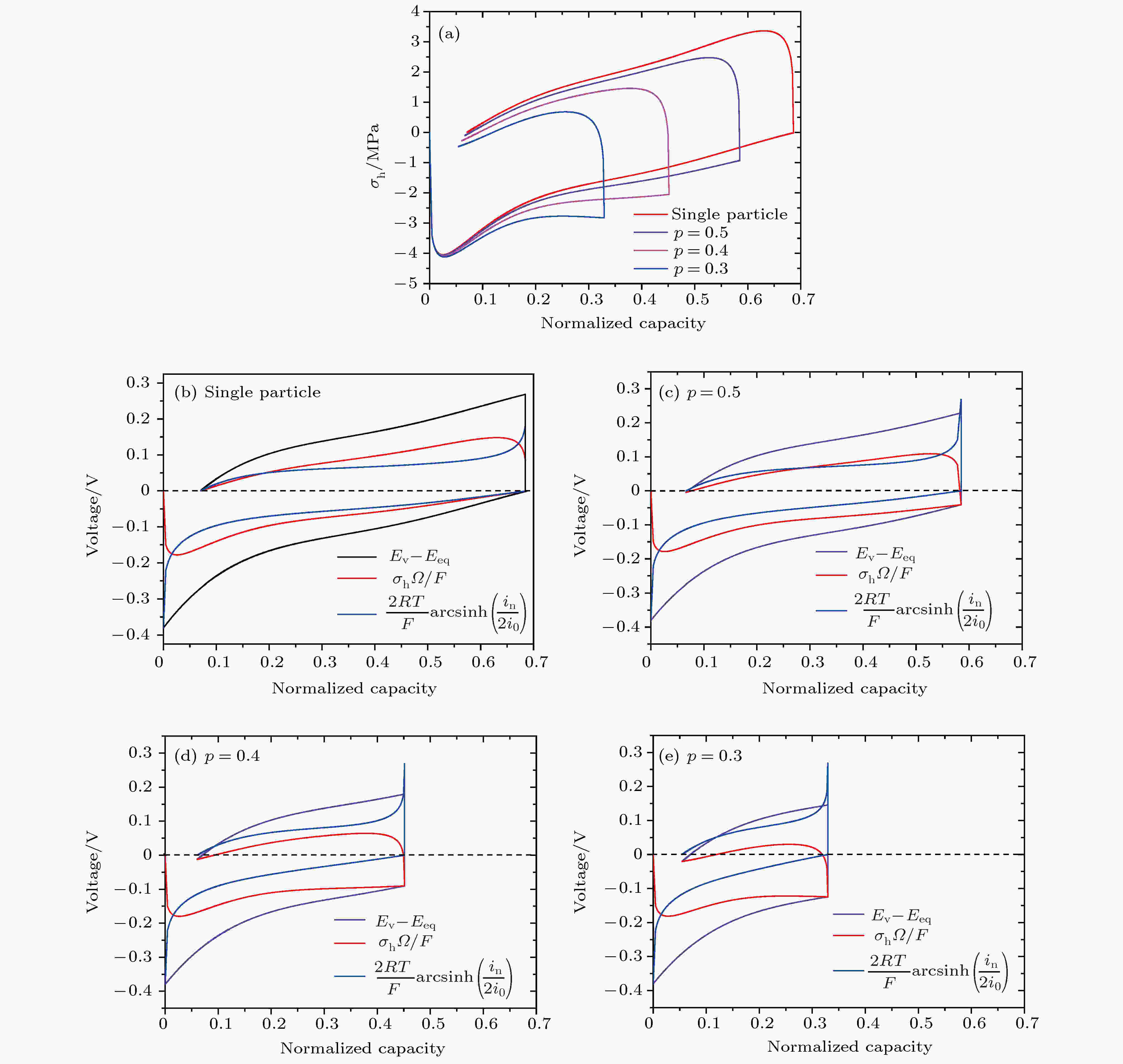图 10 颗粒间挤压对电压迟滞的影响　(a) 不同孔隙下电极的应力迟滞回线图; (b)?(e) 不同孔隙率下电极各部分过电势的回线图; 其中p为电池结构的孔隙率
Figure10. Impacts of interparticle compression on the voltage hysteresis: (a) Stress hysteresis for electrodes with different porosity ratios; (b)?(e) loop diagram of all parts of overpotential in the electrode with different porosity ratios. p is the porosity of the electrode structure.

图10(b)—(e)为上述4种情况下, 颗粒间挤压对各部分过电势的影响, 可见挤压力的存在使颗粒表面应力所占过电势的回线下移, 从而使实际驱动电化学反应部分的过电势回线上移, 并提前减小至0, 锂化反应终止. 这与前面的结论即压应力阻碍锂化过程的结论是一致的.
颗粒间的挤压预示着, 具备高容量、高能量密度的电极材料如硅材料, 由于其较高的颗粒间挤压力阻碍了锂化反应, 故需要对电极的孔隙率做一定程度的限制. 实际情况中, 一部分过电势用于克服压应力的阻碍作用, 因此使锂离子电池的容量在一定程度上衰减.

本文讨论了恒压充放电条件下颗粒表面效应和颗粒间挤压力对锂离子电池电压迟滞的影响. 计算结果表明扩散诱导应力和表面效应之间存在相互耦合和竞争的关系. 当颗粒尺寸大于100 nm时, 颗粒表面的扩散诱导应力占据主导, 较大的颗粒在锂化和去锂化过程中产生了较大的应力迟滞环, 进而应力分担的过电势迟滞环更大, 消耗了更高的总过电势, 引起能量耗散. 当颗粒尺寸小于10 nm时, 扩散诱导应力显著减小, 使应力迟滞效应几乎消失, 而较强的表面效应占据主导, 使锂化过程伴随着较大的压应力, 阻碍锂化反应. 根据文献[41]的理论, 这种扩散诱导应力与表面效应的竞争机制将影响最优颗粒尺寸的选择. 当同时考虑上述的扩散诱导应力和表面效应时, 由计算结果可知10 nm左右的硅颗粒具备良好的综合性能.
当考虑颗粒间挤压力时, 结果发现致密的电极结构能够加剧颗粒间的挤压, 消耗了更高的总过电势, 使应力回线下移同时驱动电化学反应部分的过电势回线上移, 锂化反应提前终止造成电池容量的衰减. 因此, 在实际的电极结构设计中, 应将电极孔隙率设定一个下限值, 因为过高的颗粒挤压作用将降低锂离子电池的容量.
此外我们认为在该研究领域还存在以下三方面值得进一步扩充和深入:
1)本文的应力计算模型局限于线弹性框架, 并未考虑实际电极材料的塑性, 因此一定程度上过高地评价了应力对电压迟滞问题的影响, 需要引入更为接近于实际情况的弹塑性模型来描述其力学行为, 进而更为合理精准地评价应力迟滞对于电池电压迟滞问题的贡献度;
2)本文在处理实际电极中颗粒的受力问题时忽略了粘接剂等其他材料的影响, 需要建立更为精准的计算模型来计算分析充放电过程中颗粒在实际电极中的应力演化过程;
3)本文颗粒的几何模型为球形, 但实际电极颗粒有可能是椭球型或是更加不规则的几何体, 因此对于椭球等其他几何形状的颗粒, 应力效应对电压迟滞问题的研究需进一步展开.