摘要: 由于纳米结构具有极高的表体比, 声子-表面散射机制对声子的热输运性质起到关键作用. 提出了表面低配位原子对声子的散射机制, 并且结合量子微扰理论与键序理论推导出该机制的散射率. 由于散射率正比于材料的表体比, 这种散射机制对声子输运的重要性随着纳米结构尺寸的减小而增大. 散射率正比于声子频率的4次方, 所以这种散射机制对高频声子的作用远远强于对低频声子的作用. 基于声子玻尔兹曼输运方程, 计算了硅纳米薄膜和硅纳米线的热导率, 发现本文模型比传统的声子-边界散射模型更接近实验值. 此发现不仅有助于理解声子-表面散射的物理机制, 也有助于应用声子表面工程调控纳米结构的热输运性质.
关键词: 声子-表面散射机制 /
低配位原子 /
纳米结构 /
热导率 English Abstract Mechanism of phonon scattering by under-coordinated atoms on surface Huo Long-Hua 1 ,Xie Guo-Feng 1,2 1.School of Physics and Optoelectronics, Xiangtan University, Xiangtan 411105, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11874145).Received Date: 12 February 2019Accepted Date: 06 March 2019Available Online: 01 April 2019Published Online: 20 April 2019Abstract: Because of high surface-to-volume ratio (SVR), the most prominent size effect limiting thermal transport originates from the phonon-surface scattering in nanostructures. Here in this work, we propose the mechanism of phonon scattering by the under-coordinated atoms on surface, and derive the phonon scattering rate of this mechanism by quantum perturbation theory combined with bond order theory. The scattering rate of this mechanism is proportional to SVR, therefore the effect of this mechanism on phonon transport increases with the feature-size of nanostructures decreasing. Due to the ω 4 dependence of scattering rate for this mechanism, the high-frequency phonons suffer a much stronger scattering than the low-frequency phonons from the under-coordinated atoms on surface. By incorporating this phonon-surface scattering mechanism into the phonon Boltzmann transport equation, we calculate the thermal conductivity of silicon thin films and silicon nanowires. It is found that the calculated results obtained with our model are closer to the experimental data than those with the classical phonon-boundary scattering model. Furthermore, we demonstrate that the influence of this phonon-surface scattering mechanism on thermal transport is not important at a very low temperature due to the Bose-Einstein distribution of phonons. However, with the increase of the temperature, more and more phonons occupy the high-frequency states, and the influence of this scattering mechanism on phonon transport increases. It is astonished that the phonon scattering induced by the under-coordinated atoms on surface is the dominant mechanism in governing phonon heat transport in silicon nanostructures at room temperature. Our findings are helpful not only in understanding the mechanism of phonon-surface scattering, but also in manipulating thermal transport in nanostructures for surface engineering.Keywords: phonon-surface scattering mechanism /under-coordinated atom /nanostructures /thermal conductivity 全文HTML --> --> --> 1.引 言 对纳米结构热输运的理解和调控对于热电器件的开发[1 -6 ] 以及纳米电子器件的热管理[7 -10 ] 起到非常重要的作用. 参与导热的声子主要集中在太赫兹频段, 由于纳米结构的特征尺寸可以小于太赫兹频段声子倒逆散射的自由程, 声子-表面散射机制占支配地位, 从而对纳米结构热输运产生极为重要的影响, 所以当材料尺寸进入纳米尺度, 热输运呈现出诸多不同于块体材料的新特征, 例如反常热导率、量子限制效应和傅里叶定律失效等[11 ] . 声子-表面散射机制影响和决定纳米结构热输运的诸多特征, 因此利用表面效应成为声子工程调控纳米结构热导率的有效手段. 然而目前人们对于声子-表面散射的物理机制不是十分清楚. 声子与表面作用有两种物理图像, 即基于粒子属性的非相干散射和基于波动属性的相干散射[12 ] . 传统的声子-表面非相干散射模型将声子被表面的散射视为粒子与容器边界的碰撞, 散射率公式为$ \tau _{\rm{B}}^{ - 1} = \dfrac{{1 - P}}{{1 + P}}\dfrac{v}{\varLambda }$ , $ v$ 为声子速度, $ \varLambda $ 为纳米结构的特征尺寸, P 为镜面因子. 早期的文献中将镜面因子作为一个常数来处理, 后来人们用Ziman公式加以完善[13 ] , Ziman公式表明镜面因子随声子波长$ \lambda $ 的减小或者表面粗糙度$ \delta $ 的增加而急剧降低. 虽然传统的声子-表面散射模型较好地解释了一些纳米结构热导率的实验现象和规律, 但是基于这种声子-表面散射模型的热导率计算结果往往比实验数据高, 而且纳米结构的尺寸越小, 计算值与实验值相对差别越大. 特别是当纳米结构的表面非常粗糙时, 例如电化学腐蚀方法制备的粗糙表面纳米线, 实验测量表明其热导率远远低于相同直径的平整表面纳米线[14 ] . 这种由于表面粗糙度增加而使纳米结构热导率远远低于Casimir极限(即$ P = 0$ )的现象, 无法用传统的声子-表面非相干散射模型来解释. 根据传统的声子-表面非相干散射模型, 纳米结构的热导率只能无限接近但不能低于Casimir极限. 声子不但具有粒子性, 还具有波动性, 声子被周期性分布的表面或界面反射可以产生干涉效应, 声子的相干性导致声子色散关系改变, 从而使声子群速度和态密度都发生变化, 并且相干效应还能产生声子带隙, 因此可以利用周期边界对声子的相干作用来调控纳米结构的热输运性质, 并取得经典调控方法无法达到的效果[15 , 16 ] . 对于多孔硅薄膜声子晶体, 在$ \lambda < p < {\varLambda _{\rm{U}}}$ 的尺寸范围(对于室温下工作的硅材料而言, 这正是目前纳米制备技术到达的尺寸范围, 其中$ p$ 为声子晶体的周期间距尺寸, $ \lambda $ 为占支配地位声子的波长, $ {\varLambda _{\rm{U}}}$ 为占支配地位声子的倒逆散射自由程), 近年来科学家们就声子相干输运是否占据支配地位这一问题展开了激烈的争论. Yu等[17 ] 和Hopkins等[18 ] 认为即使在室温下声子-表面相干散射也是导致多孔硅薄膜声子晶体热导率极度降低的原因, 但是基于完全相干模型得到的热导率计算值明显低于实验值[19 ] . 最近Lee等[20 ] 通过实验发现, 当温度超过14 K, 多孔硅薄膜中的孔是否周期分布对热导率没有影响, 因为非周期分布的孔破坏了声子的干涉效应, 所以他们认为多孔硅薄膜声子晶体中的声子-表面相干散射机制在温度14 K以上时是不重要的. Maire等[21 ] 和Wagner等[22 ] 给出了类似的结论, 即在$ \lambda < p < {\varLambda _{\rm{U}}}$ 的尺寸范围, 声子-表面非相干散射仍然占据主导地位. 然而在理论研究方面, 玻尔兹曼输运方程方法[23 ] 和蒙特卡罗模拟[24 ] 都表明应用传统的声子-表面非相干散射模型计算多孔硅薄膜声子晶体的热导率, 计算值明显高于实验值. 以上这些争议和矛盾都表明人们对于声子-表面散射的物理机制还不是很清楚, 需要对其做进一步研究.2.方法与模型 材料的表面并不等同于数学意义上的边界, 材料表面有非常丰富的物理和化学效应. 例如表面原子配位数降低导致表面原子键长收缩以及键能增强, 使得表面势阱变深, 从而导致电子在表面局域化, 表面散射降低了电导率[25 ] . 我们认为现有声子-表面散射机制研究的不足之处在于只考虑了表面的数学属性, 即表面的几何限制对粒子或者波的运动产生突变, 忽视了表面附近微观物理属性不同于内部, 以及由此产生对声子的作用. 表面原子键长收缩键能增强[26 ] , 对系统的哈密顿量产生微扰, 同理应该对声子输运性质产生重要影响, 因此我们提出表面低配位原子对声子的散射机制. 下面结合量子微扰理论与键序理论推导这种声子-表面散射机制的散射率.M 为原子质量; $ {\omega _k}$ 为简振模式$ k$ 的角频率; $ {{{a}}^ \dagger }$ , $ {{a}}$ 分别为声子产生和湮灭算符, 在量子力学的矩阵表达中非零元素如下:N 为矩阵的行号. 如果哈密顿量的微扰是$ {{{u}}_x}$ 或者$ {{\dot {{u}}}_x}$ 的二次函数($ {{{u}}_x}$ 指第x 个原子偏离平衡位置的位移, $ {{\dot {{u}}}_x}$ 则是相对应的速度), 那么哈密顿量的微扰算符可以表达为$ k'$ 的湮灭以及声子模式$ k$ 的产生, 即声子从$ k'$ 到$ k$ 的散射. Klemens根据量子力学微扰理论, 推导出声子散射率表达式为[27 ] $ V$ 为晶体体积, $ \omega $ 为角频率, $ \dfrac{{n'}}{n} $ 等于散射角余弦的平均值, 对于球对称散射其值为0. 只要找到相应的微扰源, 并且求出(4 )式中$ {c_{k,k'}}$ 的表达式, 就可以通过(5 )式求出该物理机制的声子散射率. 如果材料中有一个原子的力常数不同于其他原子, 根据Klemens理论[27 ] :$ G$ 为晶体中原子的总数. 因为$ v \propto \sqrt f $ ($ f$ 是原子间的力常数), 所以$ {\left( {\dfrac{{{\text{δ}}v}}{v}} \right)^2} = \dfrac{1}{4}{\left( {\dfrac{{{\text{δ}}f}}{f}} \right)^2}$ , $ {\text{δ}}f$ 是力常数的变化量. 结合(5 )式和(6 )式, 可以得到单个力常数缺陷对声子的散射率为$ \omega $ 的声子的总散射率正比于缺陷的数目, 如(8 )式所示:$ {N_{\rm{I}}}$ 为力常数缺陷的数目; $ x$ 为力常数缺陷的浓度.[28 ] 指出原子的配位数降低导致原子半径收缩, 低配位原子的化学键变短变强[29 ] , 即低配位原子之间的力常数增加. Sun[30 ] 提出了键弛豫理论, 给出了原子键收缩系数以及单键能计算式, 即$ z$ 为原子的配位数; $ d_z$ 是配位数为$ z$ 的原子键长; $ E_z$ 是配位数为$ z$ 的原子的单键能; $ C_z$ 为键收缩系数; $ {E_{\rm{b}}}$ 和$ {d_0}$ 分别为体内原子的单键能和键长; m 是一个与材料性质有关的因子, 对于硅, m = 4.88. 键弛豫理论将材料表面最外层的两层原子视为表面层, 表面层原子的配位数小于体内原子, 由量纲分析可得, 原子间力常数$ {f_z} = {\left. {{{\rm{d}}^2}u\left( r \right)/{\rm{d}}{r^2}} \right|_{r = {d_z}}}$ $ \propto {E_z}/d_z^2 $ , $ {u\left( r \right)}$ 为原子间作用势, $ r$ 为原子间距离. 根据(9 )式可知表面层低配位原子间力常数大于体内原子间力常数, 从而对晶格振动系统的哈密顿量产生微扰, 所以表面低配位原子对声子产生散射作用. 下面根据(8 )式和键弛豫理论来推导这种机制的声子散射率.$ x = 2{C_5}{d_0} \cdot $ SVR, SVR是材料的表体比, 即表面积除以体积. 根据(8 )式, 表面低配位原子对声子的散射率为$ {{f_{\rm{b}}}}$ 为体内原子间的力常数, $ {{f_5}}$ 为表层配位数为5的原子间力常数. 式中的因子1/2, 是因为表面层内的每个原子键连接着两个低配位原子, 所以只有一半的低配位原子对系统的哈密顿量产生微扰. 另一个因子$ {\left( {\dfrac{5}{6}} \right)^2}$ 则是因为Klemens在推导(7 )式过程中假设每个原子有6个最近邻原子, 而在本文模型中表层原子配位数为5, 即等效为每个原子有5个最近邻原子, 原子力常数改变引起的哈密顿微扰量矩阵元的平方应该乘以因子$ {\left( {\dfrac{5}{6}} \right)^2}$ . 由量纲分析可得, 原子间力常数${k_z} = $ $ {\left. {{{\rm{d}}^2}u\left( r \right)/{\rm{d}}{r^2}} \right|_{r = {d_z}}} \propto {E_z}/d_z^2$ , 基于(9 )式, (10 )式可写为11 )式给出了材料表面低配位原子对声子的散射率, 它表明该机制的声子散射率正比于材料的表体比. 对于宏观材料, 由于表体比极低, 这种声子散射机制的作用非常微小, 但是对于纳米材料, 表体比非常高, 而且随着尺寸的减小, 表体比越来越大, 该声子散射机制的作用越来越重要. 另外(11 )式还表明, 表面低配位原子对声子的散射率正比于声子频率的4次方, 是强烈频率相关的, 对高频声子的散射作用远远强于对低频声子的散射作用. 对于硅, $ m$ = 4.88, $ {d_0} = 0.263$ nm[31 ] , $ v = $ $ 6733$ m/s[32 ] , $ V/G = {a^3}/8$ , 晶格常数$ a = 0.543$ nm, 所以硅纳米结构表面低配位原子对声子的散射率为–1 .3.结果与分析 下面将这种表面低配位原子对声子的散射机制引入到声子玻尔兹曼输运方程, 来研究典型硅纳米结构, 如硅纳米薄膜平面内方向的热导率和硅纳米线的热导率. 图1 为薄膜和纳米线的示意图. 基于近弛豫时间近似以及德拜模型, 根据声子玻尔兹曼输运方程, 纳米结构在i 方向的热导率可以由积分公式(13 )式来计算[33 ] :图 1 薄膜和纳米线示意图Figure1. Schematic illustration of thin film and nanowire.$ {{\omega _{\rm{D}}}}$ 为德拜频率; $ {{k_{\rm{B}}}}$ 是玻尔兹曼常数; $ v_i$ 为群速度v i 方向的分量, 对于图1 所示薄膜平面内方向$ {v_i} = {v_X} = v{\rm{sin}}\theta {\rm{cos}}\psi $ , 而对于图1 所示纳米线$ {v_i} = {v_Z} = v{\rm{cos}}\theta $ , $ \theta $ 为声子波失与Z 轴的夹角, $ \psi $ 为声子波失在XY 平面的投影矢量与X 轴的夹角, $ \tau $ 为声子平均弛豫时间. 根据Matthiessen’s规则, $ {\tau ^{ - 1}} = \tau _{\rm{U}}^{ - 1} + \tau _{\rm{B}}^{ - 1} + \tau _{{\rm{Bond}}}^{ - 1}$ , $ \tau _{\rm{U}}^{ - 1}$ , $ \tau _{\rm{B}}^{ - 1}$ 和$ \tau _{{\rm{Bond}}}^{ - 1}$ 分别为声子-声子U过程散射率, 传统的声子-边界散射率, 以及(12 )式所示的表面低配位原子对声子的散射率.$ A\left( T \right)$ 是一个与温度有关的参数, 是由体材料硅的热导率来确定, 假设温度为T 时体硅的热导率为$ {\kappa _{{\rm{bulk}}}}$ , $ A\left( T \right)$ 的计算式为[34 ] [32 ] 的公式:$ L$ 为薄膜的厚度, $ D$ 为纳米线的直径. 传统的声子-边界散射率为[35 ] , 所以在我们的计算中镜面因子P = 0, 即完全漫散射.12 )式可知, 纳米结构表面低配位原子对声子的散射率正比于结构的表体比. 假设纳米线的长度远远大于直径, 薄膜的长和宽都远远大于厚度, 那么纳米线和薄膜的表体比分别为T = 300 K)硅纳米线和硅薄膜的热导率, 分别如图2(a) , (b) 所示. 图中黑色曲线是考虑表面低配位原子对声子散射的计算结果, 而红色曲线是不考虑这种表面散射机制的传统声子-边界模型的计算结果. 其中图2(a) 的实验数据来自文献[36 ], 图2(b) 的实验数据来自文献[37 —39 ]. 本文模型的计算结果与实验测量吻合较好, 而传统的传统声子-边界模型的计算结果则高估了纳米线和薄膜的热导率, 这种高估是由于传统模型没有考虑表面低配位原子对声子的散射机制. 而且从图2 可以看出, 当纳米线的直径(或者薄膜的厚度)越小, 传统声子-边界模型的计算结果与实验值的相对偏差越大, 这是因为纳米结构的特征尺寸越小, 其表体比越大, 表面低配位原子对声子的散射率越高, 如果在计算中不考虑这种散射机制, 必然导致计算值的偏差越大.图 2 硅纳米结构热导率计算值与实验值的比较 (a)纳米线; (b)薄膜Figure2. Comparison of thermal conductivities between models and experimental data for silicon nanostructures: (a) Nanowire; (b) thin film.图3 中给出了室温下直径为100 nm的硅纳米线中声子-声子U过程散射率$ \tau _{\rm{U}}^{ - 1}$ 、传统的声子-边界散射率$ \tau _{\rm{B}}^{ - 1}$ , 以及表面低配位原子对声子的散射率$ \tau _{{\rm{Bond}}}^{ - 1}$ 随声子角频率的关系. 将$ \tau _{\rm{B}}^{ - 1}$ 和$ \tau _{{\rm{Bond}}}^{ - 1}$ 两条曲线的交点横坐标定义为特征频率$ {\omega _{\rm{C}}}$ , 从图3 可知$ {\omega _{\rm{C}}}$ = 33.7 Trad/s, 对于角频率小于$ {\omega _{\rm{C}}}$ 的声子, 在上述三种散射机制中传统的声子-边界散射占据支配地位, 而对于角频率大于$ {\omega _{\rm{C}}}$ 的声子, 表面低配位原子对声子的散射机制最为重要. 根据德拜线性色散假设以及声子服从Bose-Einstein分布, 角频率大于$ {\omega _{\rm{C}}}$ 的声子占所有声子的比例为图 3 室温下声子各种散射率与角频率的关系Figure3. Various scattering rates of phonons as functions of phonon angular frequency at room temperature.$ {\omega _{\rm C}}$ = 33.7 Trad/s, T = 300 K, 从(19 )式可以得到R = 71.3%, 这表明在室温下对于硅纳米线中的大部分声子, 表面低配位原子对它们的散射率高于其他两种机制, 而传统的声子输运模型却忽视了这种极为重要的散射机制.12 )式和(17 )式可知, $ {\rm{\tau}} _{{\rm{Bond}}}^{ - 1}$ 和$ \tau _{\rm{B}}^{ - 1}$ 这两个散射率都与温度无关, 所以特征频率$ {\omega _{\rm{C}}}$ 也与温度无关, 只取决于纳米结构的几何形状. 在$ {\omega _{\rm{C}}}$ 给定的情况下, (19 )式所示的R 与温度有关. 图4 给出了横截面为圆形的硅纳米线R 与温度T 的关系. 由于声子服从Bose-Einstein分布, 在低温的情况下, 大部分的声子布居在低频态. 从图3 可知, 对于低频声子, 表面低配位原子对声子的散射率不但低于传统的声子-边界散射率, 也低于声子U散射率, 只有较少比例的高频声子, 表面低配位原子对其的散射率高于其他两种机制, 例如: 当T = 80 K时, R = 30.5%, 随着温度的进一步降低, R 还会快速下降. 随着温度的升高, 更多的声子布居在高频态, 表面低配位原子对声子的散射机制对于声子输运的影响增大, 当T = 120 K时, 已经有50%的声子, $ \tau _{{\rm{Bond}}}^{ - 1}$ 大于其他两种散射率.图 4 R 与温度的关系Figure4. R as a function of temperature.4.结 论 表面对声子的散射机制对于纳米结构中的声子输运行为起到关键作用. 纳米结构的表面有丰富而复杂的物理和化学效应, 对声子运动的影响不仅仅是简单的几何限制. 由于表面原子配位数降低, 原子键长收缩键能增强, 对晶格振动系统的哈密顿量产生微扰, 从而对声子产生散射. 基于键弛豫理论和量子微扰理论, 推导出了表面低配位原子对声子的散射率. 这种声子-表面散射机制的散射率正比于材料的表体比, 所以当纳米结构的特征尺寸越小表体比越大, 这种机制对声子输运的影响越强. 表面低配位原子对声子的散射率正比于声子频率的4次方, 所以这种散射机制对高频声子的作用特别强烈. 由于声子服从Bose-Einstein分布, 在极低的温度下, 高频声子所占的比例很小, 表面低配位原子散射机制对于声子输运的影响很小, 但是随着温度升高, 高频态声子的比例增加, 这种散射机制对声子输运的影响增强, 在室温下, 这种散射机制对硅纳米结构中的声子输运起到支配性作用. 应用声子玻尔兹曼输运方程, 计算了硅纳米薄膜和硅纳米线的热导率, 考虑了表面低配位原子对声子的散射机制, 热导率的计算值与实验值符合得很好. 纳米结构的热导率随着尺寸的减小而降低, 不仅是因为声子-边界散射更加频繁, 也因为表体比增加导致表面低配位原子对声子特别是对高频声子的散射更加强烈. 表面低配位原子对声子的散射不仅有助于理解声子-表面散射的物理机制, 也有助于应用声子表面工程调控纳米结构的热输运性质. 















































































 图 1 薄膜和纳米线示意图
图 1 薄膜和纳米线示意图


















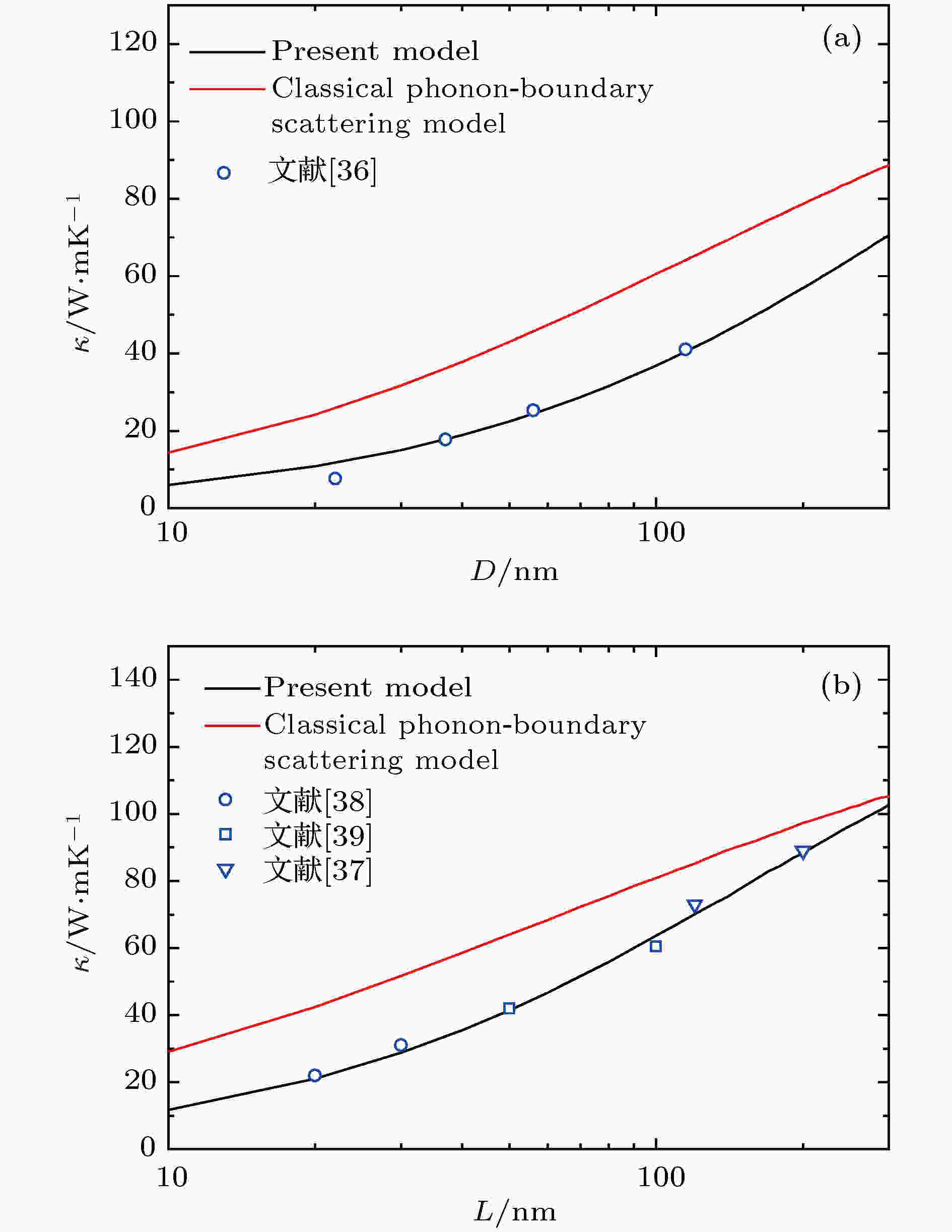 图 2 硅纳米结构热导率计算值与实验值的比较 (a)纳米线; (b)薄膜
图 2 硅纳米结构热导率计算值与实验值的比较 (a)纳米线; (b)薄膜

































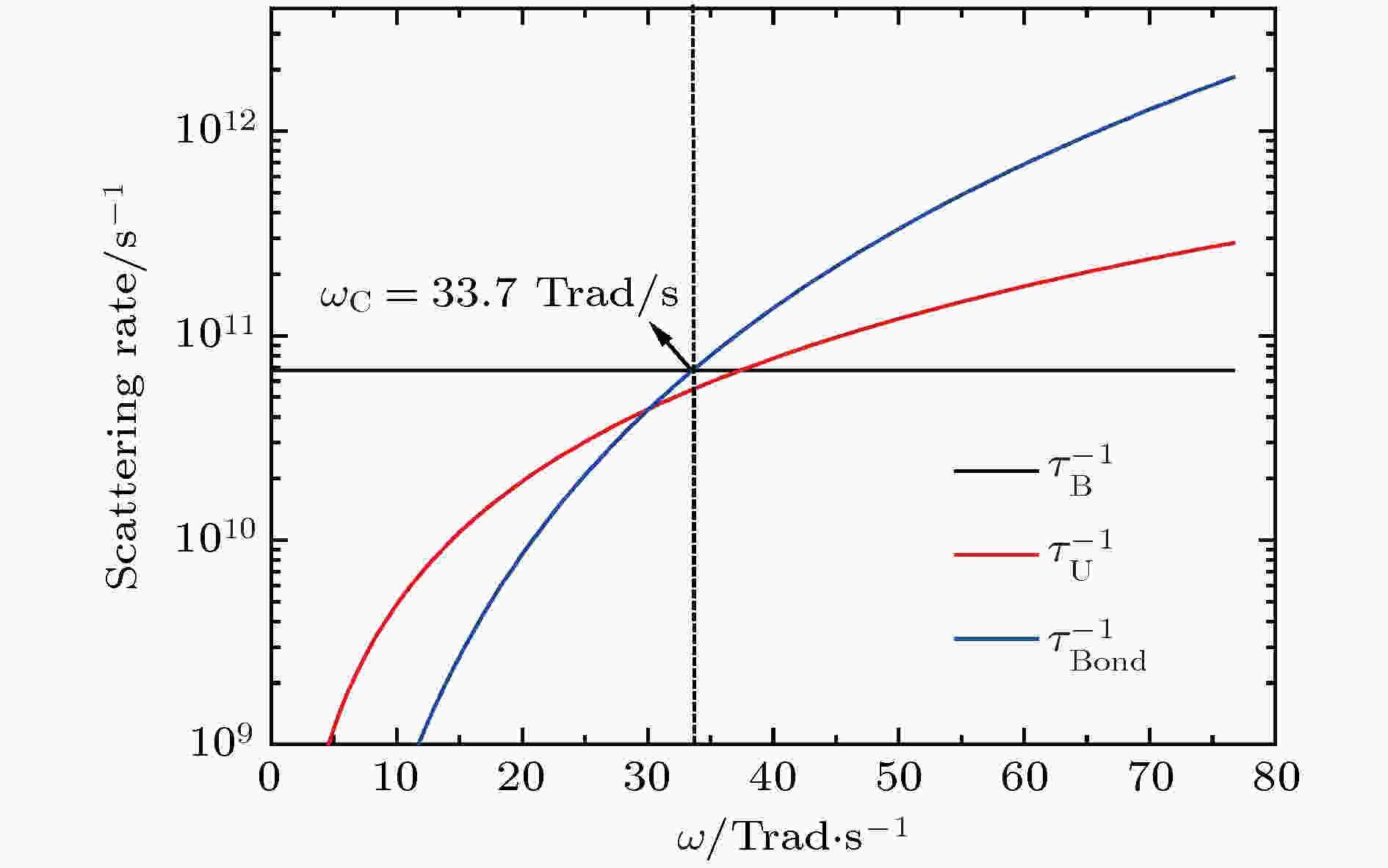 图 3 室温下声子各种散射率与角频率的关系
图 3 室温下声子各种散射率与角频率的关系







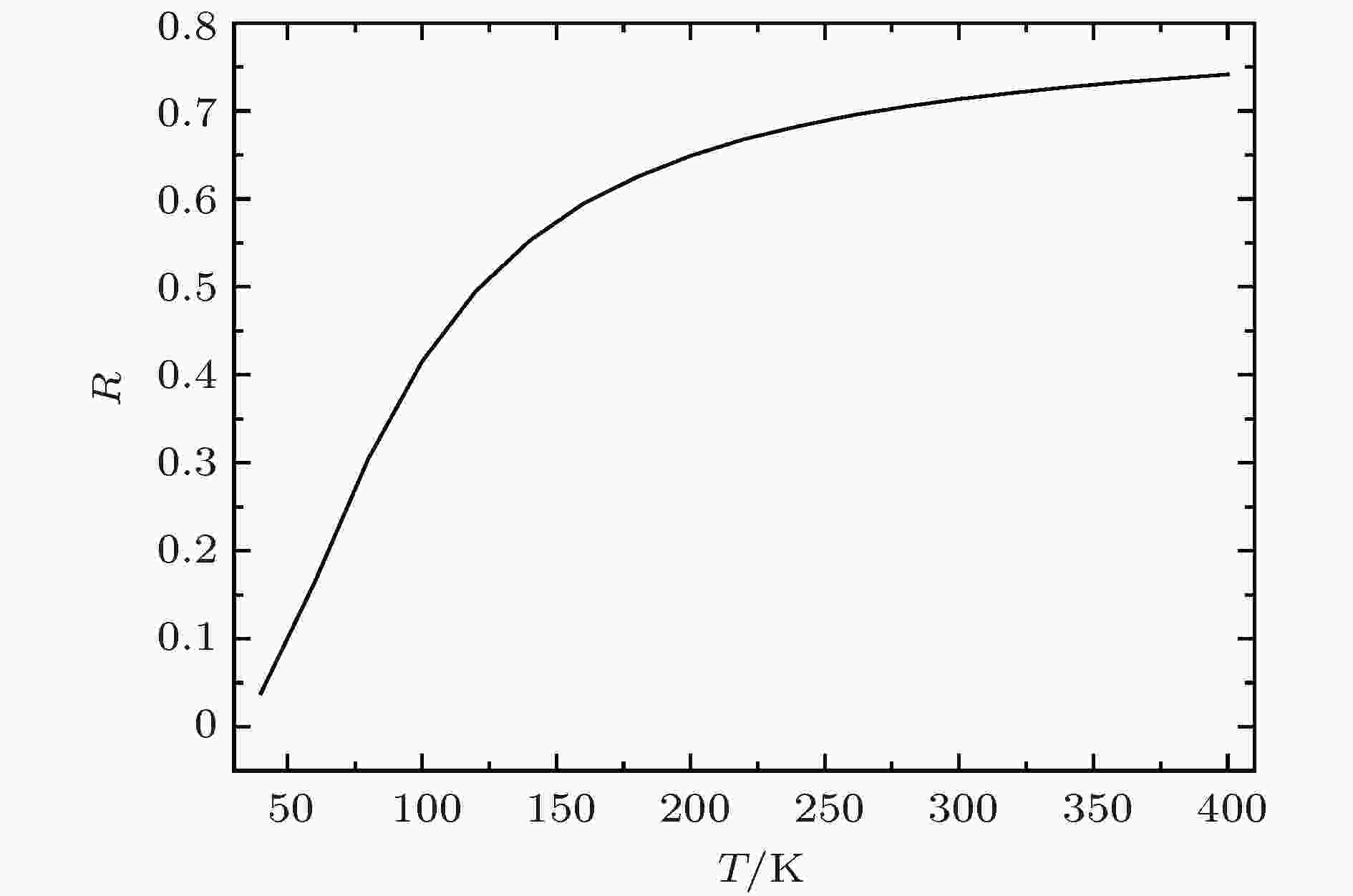 图 4 R与温度的关系
图 4 R与温度的关系