全文HTML
--> --> -->根据经典帕邢定律[1], 在无限大的两平行电极间, 临界击穿电压(能够引发击穿的电压下限, 下文均简称击穿电压)与电极间距d和间隙压强p的乘积有关, 其击穿电压曲线呈现为“U”型. 在此类工况中, 电极间的电场分布、压强分布都均匀, 间隙距离处处相等, 那么在击穿间隙的所有区域都会发生电子雪崩, 这种击穿过程可认为是一种全通道的放电过程. 然而, 在非匀强电场电极的工况中, 击穿放电并非全通道放电. Golden等[2,3]首先发现非匀强电场电极下的击穿电压与汤森放电模型的预估值不一致, 认为汤森电离系数在描述非匀强电场的电离次数时, 在不同间隙位置的描述方式会存在差异, 所以对汤森第一电离系数做出了修正, 得到了与试验较吻合的结果, 这是首次发现非匀强电场工况与全通道放电工况的机制不同. 接着, Osmokrovic等[4,5] 针对几种典型复杂电极进行了击穿电压的测量试验, 通过分析试验结果, 发现复杂电极间的击穿总会存在一个“临界区域”, 该区域会首先触发击穿, 接着击穿过程将快速蔓延至整个放电通道, 但在他的研究中仅说明这种“临界区域”会随着压强、电极结构的不同而改变, 没有揭示如何确定这种“临界区域”的具体位置, 并且相关的物理机制尚不清晰. 然而, 对于非匀强电场的电极来说, 获得“临界区域”的位置对于预估击穿电压以及研究电极点火的主要削蚀点均有着重要意义. 鉴于试验方法具有一定局限性, 因此, 本文将采用数值与试验结合的方法来对“临界区域”(本文称之为起始击穿路径)进行研究.
到目前为止, 关于低气压放电路径的数值研究鲜有报道, 所以本文将从高气压放电路径的研究来获得一些借鉴与启发. 由于高气压下的放电路径在大量统计数据中既具备一定的自相似性, 又会在流注传导时表现出一定的随机性. 于是, 根据这种客观物理规律, Niemeyer 等[6]建立了经典的流注分形模型, 主要实现流注顶端的电场强度能否维持放电持续的判断以及放电发展方向的随机判断. 接着, 如果考虑放电初始电场与放电中的电势降, 则需要修改电场强度的求解模型[7]. 在此基础上, Niemeyer[8]又提出先导的随机漫步模型, 通过在拉普拉斯背景电场中建立线性曲线坐标系来实现多条潜在先导路径的划分, 并计算了当地先导的扩散度, 进而求解了当地先导的扩散概率方程以实现放电路径的模拟, 所得计算结果的图像就像先导在无数阶梯中进行随机漫步一样. 但在实际情况中, 放电通道的电介质不都是均匀分布的, 因而还需要考虑将电导率、介电常数进行空间函数化处理, 以修正空间各位置的放电扩散概率[9]. 随后的研究, 主要表现为对扩散概率、分形维度等经验参数的修正[10-12].
实际上, 高气压的流注模型与低气压的电子雪崩模型有本质区别, 分形理论并不能适用于低气压的放电路径模拟. 但是, 通过对流注分形模型的认知, 可以确定低气压放电路径模拟需要2个关键条件: 第一, 模型应具备对放电维持的判断; 第二, 模型应具备对潜在放电路径的划分, 并且这种划分要符合客观规律(高气压的放电路径具有随机性, 故流注模型利用概率判断的扩散分形方法就非常符合客观规律). 因此, 本文在建立低气压放电的起始路径模型时将充分考虑这2个条件.
首先, 根据汤森放电理论, 电子雪崩放电过程的维持必须要有电离碰撞作为先决条件[13], 由此, 应引入模拟电离碰撞等相关的碰撞概率模型, 在以往的等离子体放电研究中, 蒙特卡罗模型是比较成熟的碰撞概率判断模型, 该模型曾应用于强电场间隙的逃逸电子流模拟[14,15]、小间隙的击穿放电模拟[16], 获得了计算结果与试验结果较高的吻合度. 其次, 低气压下的背景气体数密度较低, 这使得电子与背景气体发生弹性碰撞散射的概率较低. 同时, 电子运动受电场力约束较显著, 在击穿过程中即使发生散射也会再漂移到附近区域的电场线中, 从统计学角度来看, 这类似于一群电子沿着相邻几条电场线迁移. 因此, 本文采用“电子沿电场线”的运动假设, 认为潜在的击穿起始路径由若干条电场线组成, 且该假设在Macheret和Shneider[17]的“非散射传导”(forward-back)模型中也有体现. 结合上述2个条件, 我们建立一种基于电场线路径假设、蒙特卡罗碰撞模型的起始路径判断模型(determination of the critical path, DCP模型). 接着, 为验证DCP模型的计算精度, 开展2种电极结构的击穿放电试验, 以说明DCP模型的有效性. 在此基础上, 将DCP模型应用于其他4种有代表性结构的电极计算中, 获得稍不均匀电场下低气压击穿起始路径的位置规律和相关物理内涵.
DCP模型的整体计算流程如下:
Step.1 基于“电场线为电子运动轨迹”假设, 在电极间划分若干条候选击穿路径(可能成为起始击穿路径的路径);
Step.2 设定电极间的电压差(电极电压U0), 并将划分好的候选击穿路径以等电势线正交分割开来, 以路径线和等势线的交点为计算节点;
Step.3 在负电极表面的每一个计算节点设定相等数量(n0)的初始电子, 这些初始电子在电极电压的作用下会沿着各自的候选路径向正电极运动, 沿程计算电子动能变化、各类碰撞概率;
Step.4 统计每一条候选路径所发生的总电离次数以及所产生的正离子数量, 并计算这些正离子撞击负电极表面所产生的二次电子数量(nγ);
Step.5 筛选所有候选路径中nγ最多的一条记为起始击穿路径, 并判断这条起始路径的nγ, max与n0之间的关系. 若nγ, max明显低于n0, 则无法实现击穿, 适当升高电极电压(更新Step.2中的U0, 继续迭代计算); 若nγ, max明显高于n0, 则触发“过量击穿”, 适当降低电极电压(更新Step.2中的U0, 继续迭代计算); 若满足nγ, max接近n0, 则刚好实现临界击穿(计算收敛).
具体物理模型细节将于下文详细介绍.
2
2.1.计算节点划分
首先, 进行间隙中候选击穿路径的划分. 假定在负电极表面存在一些均匀分布的初始电子, 以这些电子来代表间隙中由宇宙射线等外界因素所触发的原始电子. 这些负电极表面的电子将会沿着各自的候选路径, 在电极电压(U0)的作用下运动到正电极表面. 这里, 由于低气压汤森放电中的空间电荷效应不显著, 忽略空间净电荷分布对电场的影响. 那么, 如果假设电子的运动路径为电场线, 则这些负电极表面均布的电子会通过均匀划分的候选路径向正电极运动(图1).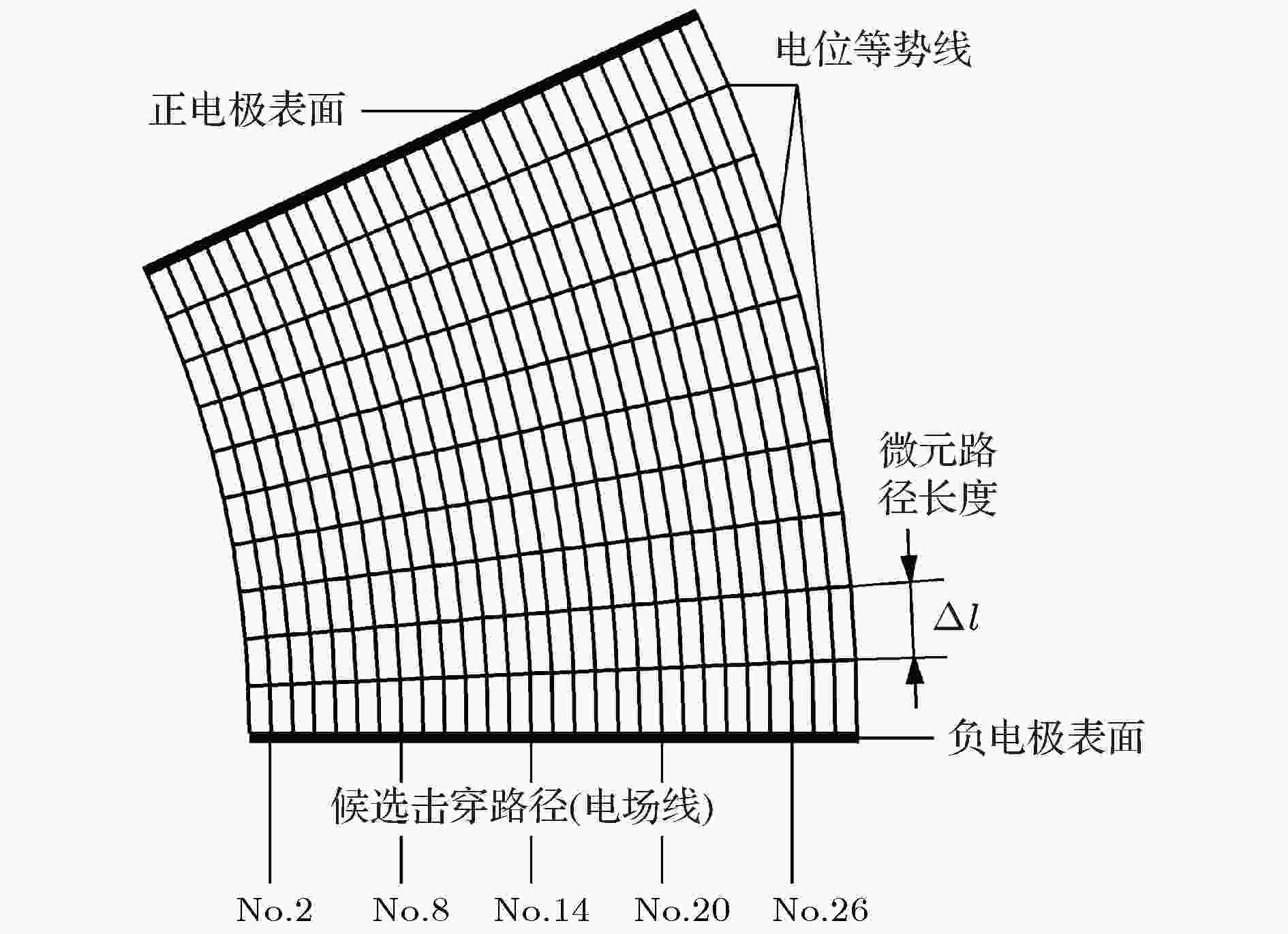 图 1 典型非平行电极间的计算节点划分示意图
图 1 典型非平行电极间的计算节点划分示意图Figure1. Schematic diagram of the mesh grid generation in nonparallel two-electrode gap
接着, 以若干电位等势线来分割候选路径, 使得所分割的微元路径上的电势降都相等. 于是, 整个间隙中由等势线和候选路径形成的交点, 就是计算节点.
2
2.2.电子动能及碰撞概率
假设每一条候选路径从负电极表面都会触发n0个初始电子向正电极运动. 这些电子会在电极电压(U0)的作用下增加动能, 并触发与背景中性气体的碰撞过程.根据2.1小节的阐述, 电子在任意候选路径上运动时, 每经过一个微元路径, 将会降低相同的电势能(





根据蒙特卡罗碰撞(Monte-Carlo collisions, MCC)模型, 一个电子在中性气体中, 在极短时间




第一种, 间隙压强均匀分布,





第二种, 如果间隙压强分布不均匀(通常由气体流动产生), 则需要通过求解数密度分布场来获得某一网格节点下的数密度分布数据, 但是, 求解数密度的网格节点与DCP模型的计算节点划分一般不同, 所以还需要利用插值(通常采用权重法)来获得DCP计算节点的




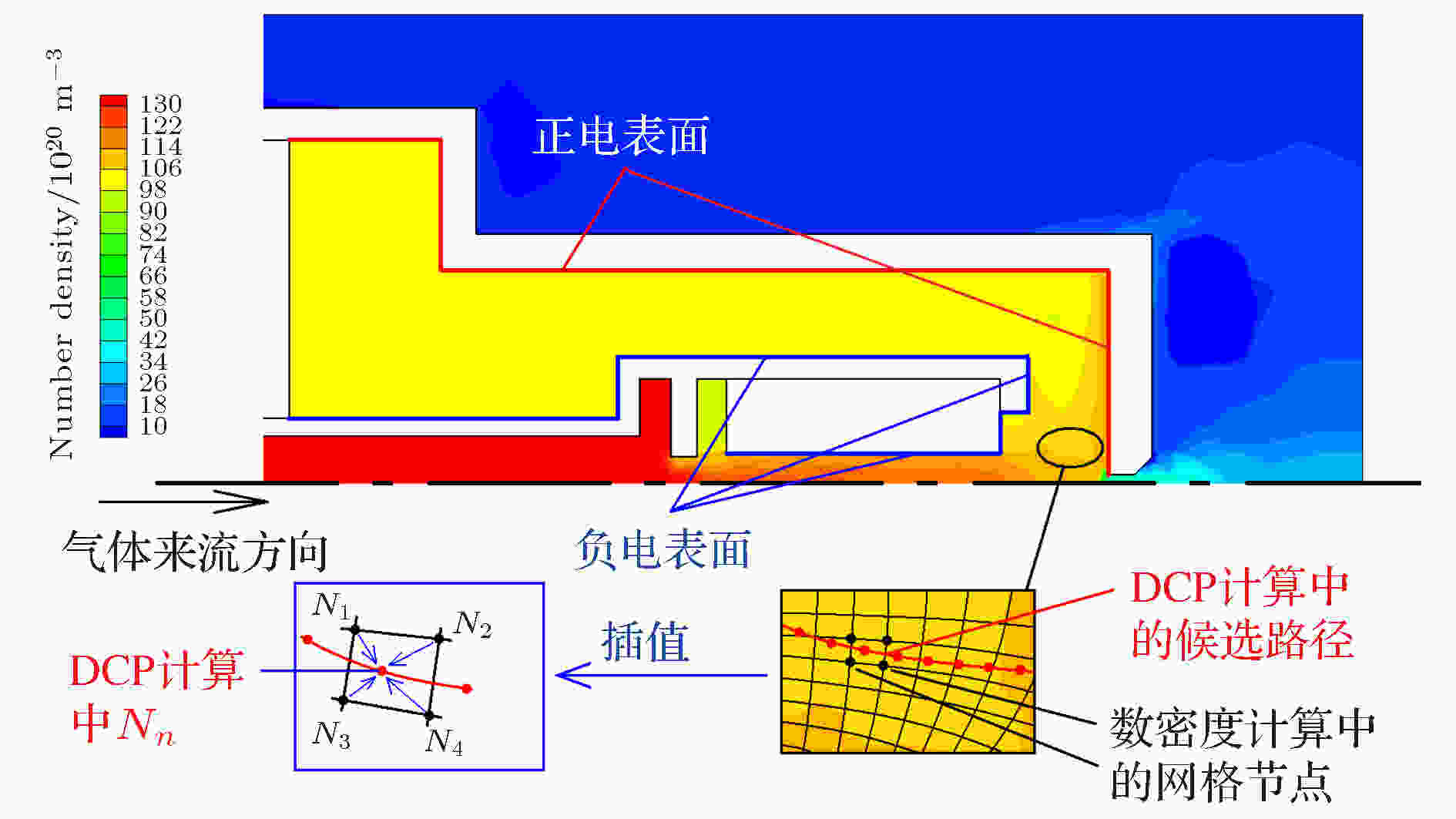 图 2 间隙压强不均布时的
图 2 间隙压强不均布时的
Figure2. Computational method of the

其次, (2)式中的







接着, (2)式中的

根据表1, 总碰撞截面

| 碰撞类型 | 碰撞截面公式/m2 | |
| 弹性碰撞 | $1.699 \times {10^{ - 19}}$ | ${E_{k,e}} \leqslant 0.159\; {\rm{ eV}}$ |
| $(0.076E_{k,e}^2 - 0.345E_{k,e}^{1.5} + 0.585{E_{k,e}} - 0.427E_{k,e}^{0.5} + 0.114)\times {10^{ - 17}}$ | $0.16\; {\rm{ eV}} < {E_{k,e}} \leqslant 2.8\; {\rm{ eV}}$ | |
| $( - 0.002E_{k,e}^2 + 0.03E_{k,e}^{1.5} - 0.166{E_{k,e}} + 0.402E_{k,e}^{0.5} - 0.317)\times {10^{ - 17}}$ | $2.8\; {\rm{ eV}} < {E_{k,e}} \leqslant 24.7\; {\rm{ eV}}$ | |
| $( - 0.0022E_{k,e}^{1.5} + 0.043{E_{k,e}} - 0.28567E_{k,e}^{0.5} + 0.6518)\times {10^{ - 17}}$ | $24.7\; {\rm{ eV}} < {E_{k,e}} \leqslant 50\; {\rm{ eV}}$ | |
| $0.00064 \times {10^{ - 17}}$ | ${E_{k,e}} > 50\; {\rm{ eV}}$ | |
| 激发碰撞 | $0.0$ | ${E_{k,e}} \leqslant 8.4\; {\rm{ eV}}$ |
| $(0.002E_{k,e}^2 - 0.023E_{k,e}^{1.5} + 0.098{E_{k,e}} - 0.188E_{k,e}^{0.5} + 0.135)\times {10^{ - 16}}$ | $8.4\; {\rm{ eV}} < {E_{k,e}} \leqslant 11\; {\rm{ eV}}$ | |
| $(0.0007E_{k,e}^2 - 0.012E_{k,e}^{1.5} + 0.08{E_{k,e}} - 0.23E_{k,e}^{0.5} + 0.23)\times {10^{ - 17}}$ | $11\; {\rm{ eV}} < {E_{k,e}} \leqslant 25\; {\rm{ eV}}$ | |
| $\begin{gathered}(0.1 \times {10^{ - 6}}E_{k,e}^2 + 0.8 \times {10^{ - 5}}E_{k,e}^{1.5} - 0.0002{E_{k,e}} + 0.002E_{k,e}^{0.5} + 0.001)\hfill \\ \times {10^{ - 17}} \hfill \\ \end{gathered} $ | $25\; {\rm{ eV}} < {E_{k,e}} \leqslant 500\; {\rm{ eV}}$ | |
| 电离碰撞 | $0.0$ | ${E_{k,e}} \leqslant 12.1\; {\rm{ eV}}$ |
| $(0.00136E_{k,e}^2 - 0.0226E_{k,e}^{1.5} + 0.14{E_{k,e}} - 0.38E_{k,e}^{0.5} + 0.387)\times {10^{ - 17}}$ | $12.1\; {\rm{ eV}} < {E_{k,e}} \leqslant 20\; {\rm{ eV}}$ | |
| $( - 0.0006E_{k,e}^2 + 0.014E_{k,e}^{1.5} - 0.133{E_{k,e}} + 0.574E_{k,e}^{0.5} - 0.93)\times {10^{ - 17}}$ | $20\; {\rm{ eV}} < {E_{k,e}} \leqslant 44\; {\rm{ eV}}$ | |
| $( - 1.6 \times {10^{ - 6}}E_{k,e}^2 + 0.1E_{k,e}^{1.5} - 0.024{E_{k,e}} + 0.022E_{k,e}^{0.5} - 0.02)\times {10^{ - 17}}$ | $44\; {\rm{ eV}} < {E_{k,e}} \leqslant 360\; {\rm{ eV}}$ | |
表1e-Xe的碰撞截面公式[18]
Table1.The e-Xe collision cross-section[18].



在电子与Xe原子发生电离或激发碰撞后, 动能会降低相对应的电离能级(12.1 eV)或激发能级(8.4 eV).
2
2.3.起始击穿路径判断
在每一条候选击穿路径中, 会由于高能电子触发的电离碰撞而产生大量的正离子, 这些正离子会在电极电压的作用下向负电极移动; 同样地, 由于离子-中性粒子的碰撞频率远小于电子-中性粒子(这里忽略离子的散射运动机制). 当离子到达负电极表面时, 会产生二次电子发射, 根据文献[19], 低能离子轰击不锈钢表面(后文所有工况均采用不锈钢为负电极)所产生的二次电子发射系数在0.021—0.023, 本文取0.022. 那么, 当某条候选路径在n0个初始电子的触发下产生nion个正离子时, 这些正离子轰击在负电极面所产生的二次电子可描述为第一, 如果

第二, 如果

第三, 如果

这里, c0为计算收敛的相对残差, 是一个趋近于0的正实数. 如果c0取0.001, 则表示由残差所约束的计算误差不会超过0.1%, 该数值越小, 计算精度越高; 但同样地, 迭代次数也会越多, 收敛速度越慢. 在本文的工况中, 综合考虑计算精度与速度, 取c0 = 1 × 10–4.
在第二或第三情况中, 本文给出调整电极电压U0的一个较为简单的迭代公式为


2
2.4.影响模型误差的参数
在DCP模型中, 除收敛参数c0外, 还有2个参数会影响模型的固有误差: 每条候选路径上的初始电子数量n0和微元路径上的电势降
n0主要影响碰撞概率判断所调用的样本空间大小, n0越大, 由MCC模型所计算的结果与实际结果偏差越小. 图3给出了重复多次计算后, case1(见第3节)中No.21候选路径的平均每个初始电子所产生的总电离次数的结果波动情况. 在一个比较极端的情况(n0 = 1)中, 结果波动非常明显, 这说明较少数量的初始电子会导致计算结果的随机性较高; 而当n0 = 200时, 计算结果的波动已经非常微弱, 即使在n0 = 500时, 这种波动的改善也不会太多. 这意味着, 这种波动误差无法根除, 但可以控制在某个范围内. 考虑n0对计算结果波动和计算时间的影响, 取n0 = 200比较合理, 可以将结果的波动控制在0.5%以内. 值得注意的是, 图3所展示的是MCC模型在计算中产生的不稳定性随n0的依变关系, 具有一定的普适性, n0 = 200对于其他工况而言也同样适用.
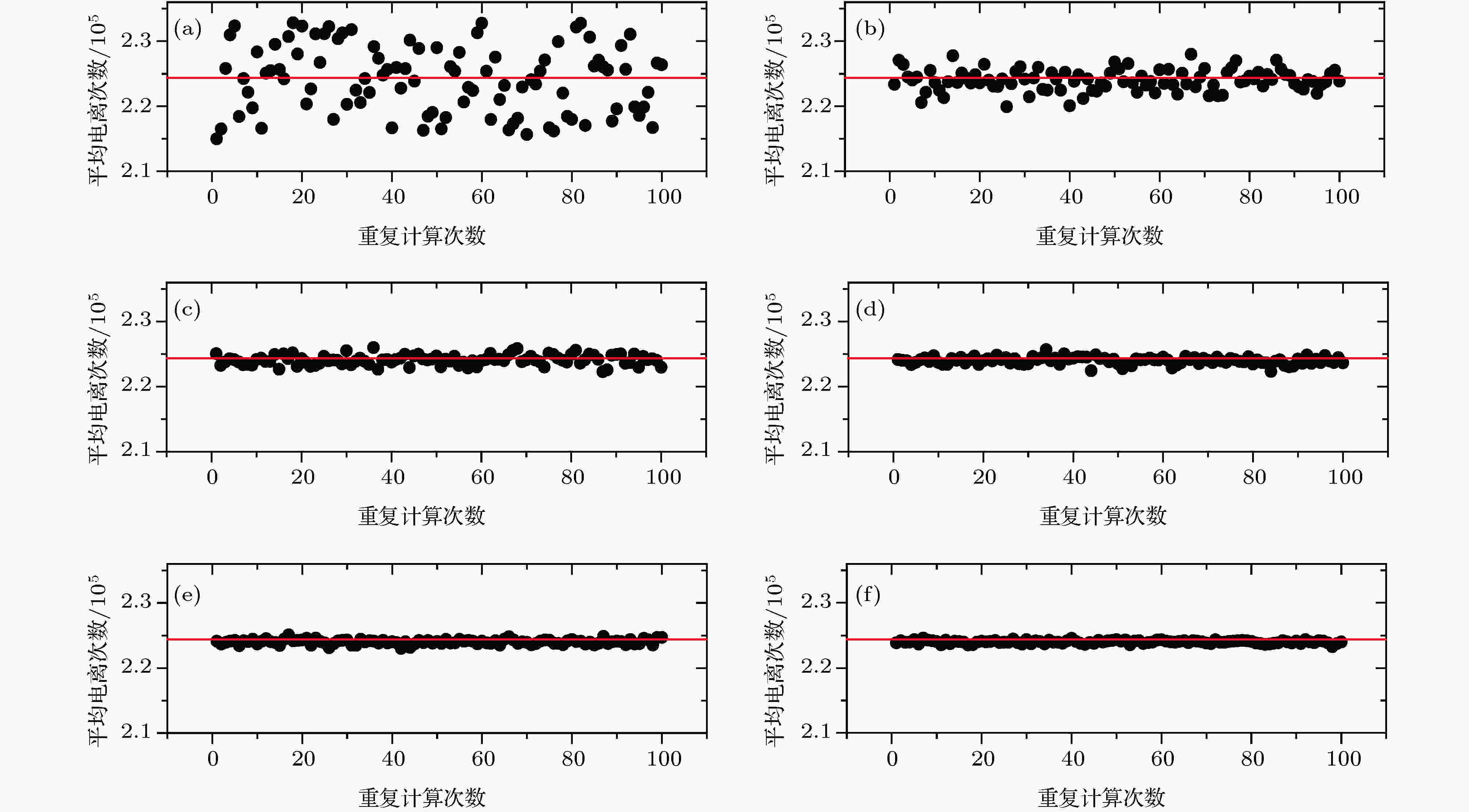 图 3 DCP计算结果稳定性随N0的依变关系(a) n0 = 1; (b) n0 = 10; (c) n0 = 50; (d) n0 = 100; (e) n0 = 200; (f) n0 = 500 (case 1, 间隙压强60 Pa, 临界击穿电压345 V)
图 3 DCP计算结果稳定性随N0的依变关系(a) n0 = 1; (b) n0 = 10; (c) n0 = 50; (d) n0 = 100; (e) n0 = 200; (f) n0 = 500 (case 1, 间隙压强60 Pa, 临界击穿电压345 V)Figure3. The computational stability of DCP model as a function of N0: (a) n0 = 1; (b) n0 = 10; (c) n0 = 50; (d) n0 = 100; (e) n0 = 200; (f) n0 = 500 (An example of case 1, gap pressure: 60 Pa, critical breakdown voltage: 345 V )



















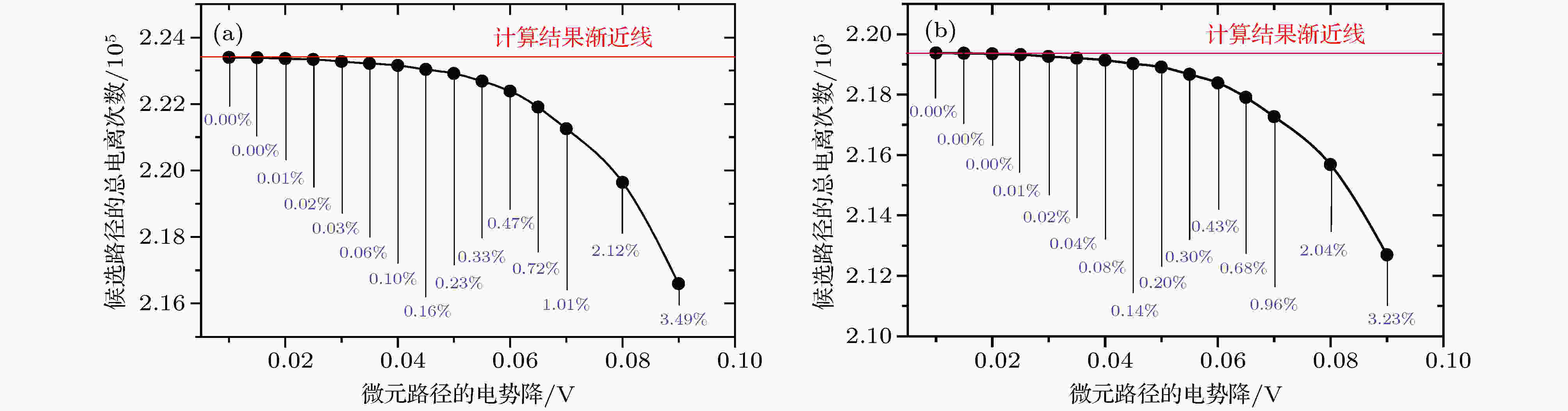 图 4 路径总电离次数的计算值随
图 4 路径总电离次数的计算值随
Figure4. The computational deviation of total ionization number in one path at different

本文限定的电场不均匀系数f也是有关模型误差的参数. 如果局部电场强度过高, 会导致电子运动到弱场强区域时, 脱离电场线轨迹. 因而, 关于f取值应该有上限值, 但本文所采用的验证试验工况只能覆盖f ≤ 3.97范围, 故将本文研究的电极范围限定在2.0—4.0. 此外, 背景压强对于“电子沿电场线运动”的假设有支撑作用, 当压强升高到一定程度时, 电子的流注特性会逐渐升高, DCP模型同样会失效, 根据验证试验结果, DCP模型在压强低于103 Pa量级时能够保证较高精度.
2
3.1.试验系统及测量方法
如图5所示, 整个试验在0.6 m(直径)× 2 m(长度)的真空舱内进行, 抽气系统由机械泵(负责粗抽)和分子泵(负责精抽)组成, 舱内压强范围可以控制在5 × 10–3 Pa到5000 Pa之间, 满足试验需要. 电极装置固定在图5中黑色虚线区域, 由于试验所用电极装置不止一个, 所以这里没有展示具体电极结构. 当击穿工况属于均匀压强分布时(如case 1), 采用流量通道2, 将气体工质快速分散到舱内, 并以玻璃罩来覆盖住电极装置区域, 以减少由于舱内气体流动导致的试验误差. 当击穿工况属于非均匀压强分布时(有气体来流的电极, 如case 2), 则采用流量通道1, 将气体工质通入电极内部, 并且不使用玻璃罩.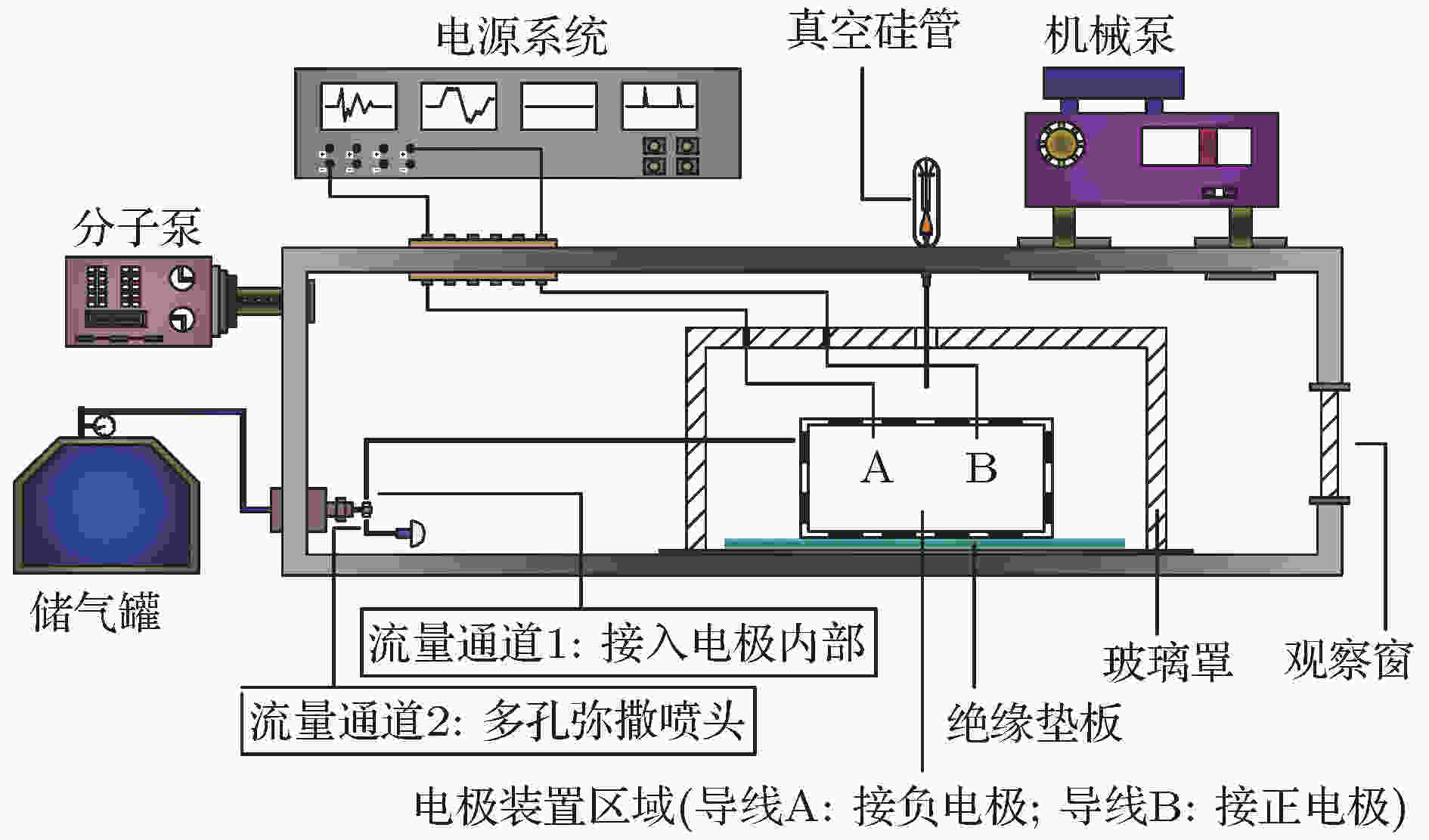 图 5 击穿试验系统布置
图 5 击穿试验系统布置Figure5. A diagram of the test layout
接着, 对起始击穿路径和击穿电压的测量方案进行讨论. 击穿电压的测量可以通过具有波形采集功能的电源系统来进行, 而起始击穿路径的测量就具有一定难度. 起初, 有2个方案进入考虑范围: (1)通过高速相机对电极间的放电闪光位置进行瞬间捕捉拍照; (2)通过多次循环试验考察负电极表面的离子轰击痕迹. 但是, 经过深入思考, 方案(1)存在一定的疑问: 放电闪光是由激发态原子退激所辐射的光子组成, 具有放电闪光的位置可以直接说明该位置最先产生激发碰撞, 但不能直接证明该路径就是电子雪崩过程最剧烈的路径, 即无法证明该路径就是起始击穿路径. 因此, 本文将采用方案(2)来测量起始击穿路径位置. 如果对整个放电过程进行合理的控制, 就可以在电极间制造只有起始路径发生击穿的放电过程. 那么, 在负电极表面所形成的正离子轰击痕迹, 就能够指向起始路径的位置. 由此, 方案(2)需要先认知放电过程的电压电流的时间特性曲线(VI-t曲线), 典型的VI-t曲线如图6所示.
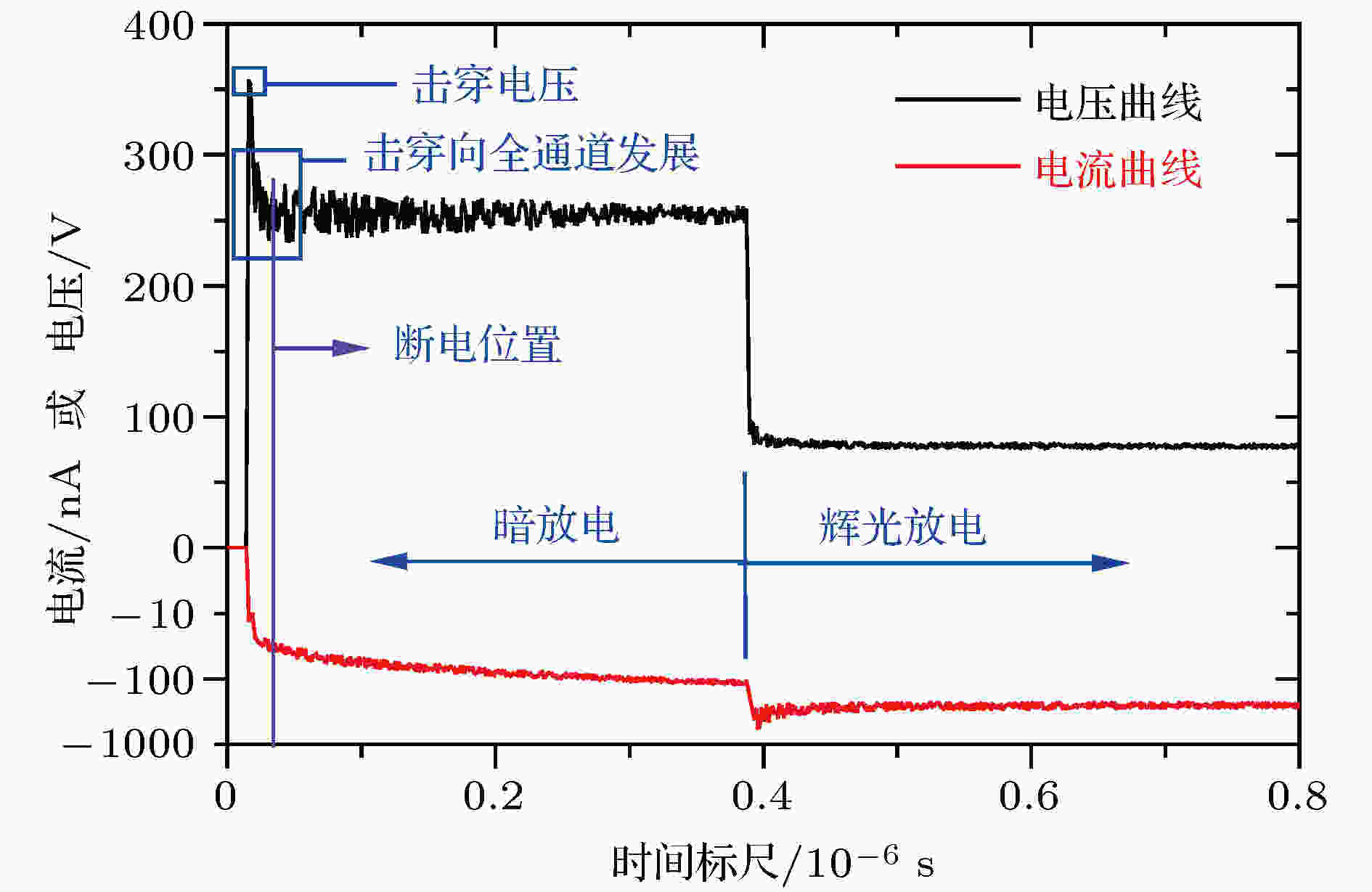 图 6 放电过程的VI-t曲线(数据来自case 1工况)
图 6 放电过程的VI-t曲线(数据来自case 1工况)Figure6. VI-t curve of the discharge process in case 1
图6中电压曲线的最高点就是起始击穿路径刚好发生击穿的时刻, 而采集到的电压数值就是击穿电压. 在起始路径的击穿刚触发后的0.05

2
3.2.仿真与试验结果对比
本文选取2种电极装置来验证DCP模型的计算精度: 圆片阶梯电极(case1)和磁等离子体动力学推力器(magneto-plasma dynamic thruster, MPDT, case2).3
3.2.1.Case 1
Case 1为圆片阶梯电极, 结构尺寸与候选路径划分见图7. 这里, 给出电场系数f, 以表征电极电场的不均匀程度(后文均有标注). 负电极表面的削蚀痕迹见图8(a), 击穿电压-间隙压强(V-p)曲线以及起始击穿路径的计算结果见图8(b).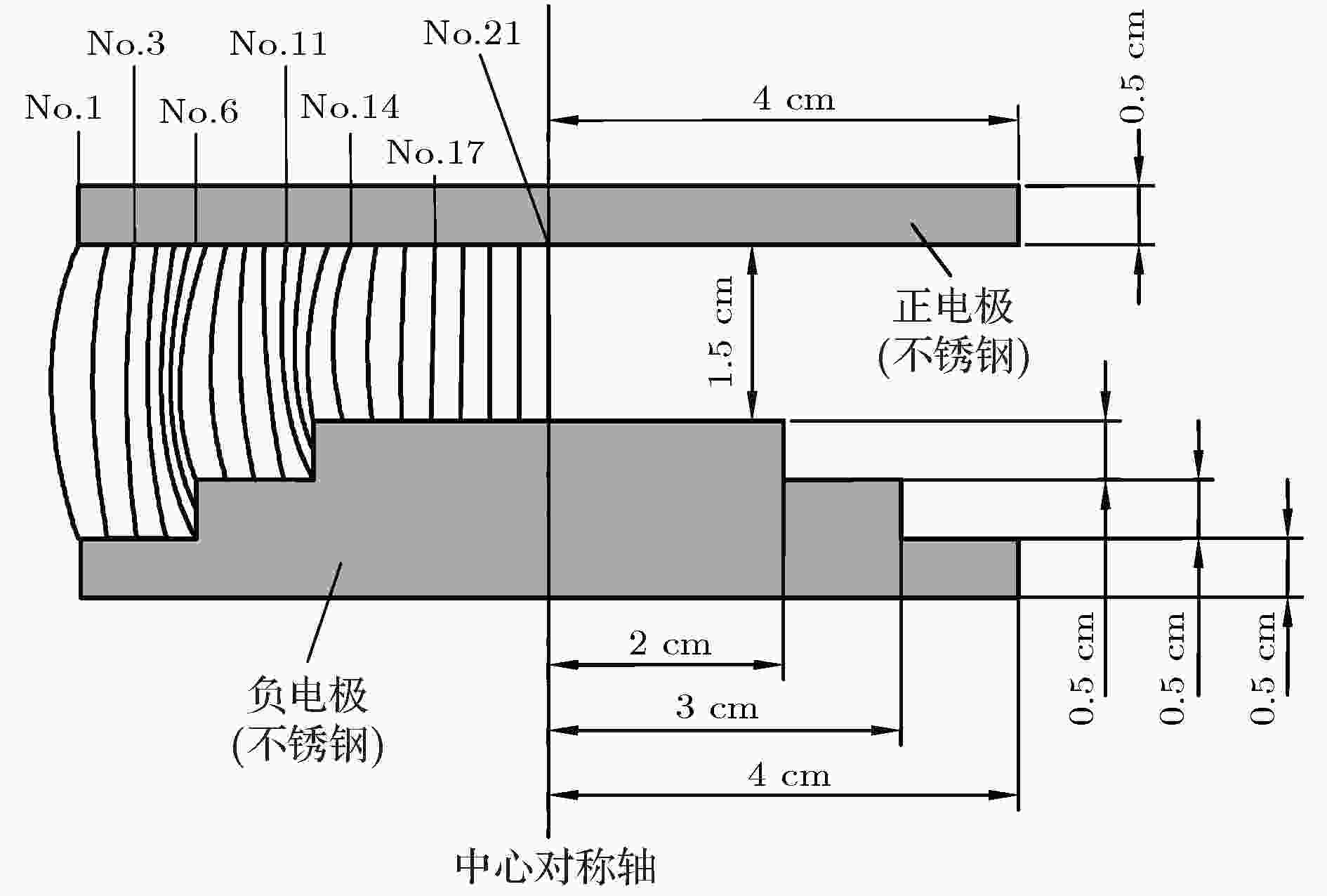 图 7 圆片阶梯电极的结构及候选路径划分(f = 3.97)
图 7 圆片阶梯电极的结构及候选路径划分(f = 3.97)Figure7. The geometry and potential path generation in the laddered plate electrode (f = 3.97)
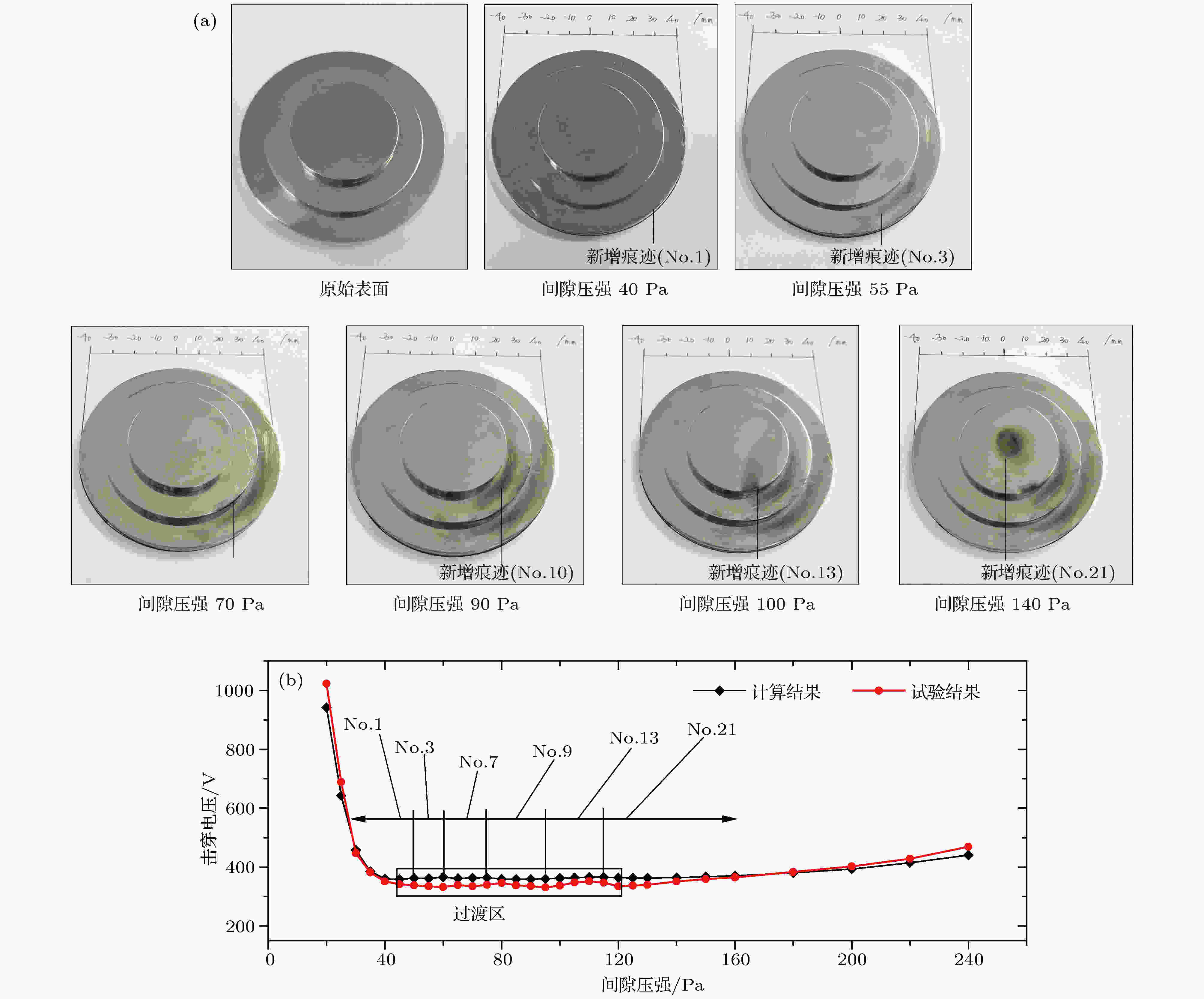 图 8 Case 1试验与计算结果对比(气体工质: Xe)
图 8 Case 1试验与计算结果对比(气体工质: Xe)Figure8. The comparison of the calculation and test results in case 1 (working medium: Xe)
根据图8(a), 这里进行2点关于试验现象的说明: 第一, 由于不锈钢电极含C元素, 在负电极表面削蚀过程中会产生一定的C原子沉积, 因此电极表面某些位置会有黑色痕迹(而case 2的负电极为W, 所以并没有这种黑色痕迹); 第二, 由于电极加工精度以及两电极安装的平行度难以达到绝对标准, 所以原本应在回转体电极一周都出现的削蚀痕迹, 只出现在某些局部位置, 但这些位置依然可以指向起始击穿路径. 根据试验结果, 我们发现负电极表面的新增痕迹趋势会随着间隙压强的变化而变化, 与Osmokrovic描述的临界区域变化的现象基本相符. 并且, 虽然电极表面痕迹所指向的起始路径与计算结果不完全一一对应, 但所呈现的路径转移趋势与计算结果可以保持定性一致. 在击穿电压的计算方面(图8(b)), DCP在case1的计算相对误差在0.56%—5.88%, 尤其在起始击穿路径转移的过渡区, 可基本捕捉击穿电压的变化趋势.
3
3.2.2.Case 2
Case 2为MPDT的击穿工况, MPDT属于电推进动力装置, 本文的MPDT采用20 kW级、推力为600 mN的原理样机, 该样机的应用平台为高轨XX卫星的轨道转移推进系统. MPDT的点火过程起始于阴极管与阳极环之间的击穿, 当放电足以令钨阴极管达到热发射温度时, MPDT则迅速进入稳定工作状态. 推力器的电极结构和候选路径划分见图9, 负电极(阴极管)表面的痕迹结果及击穿电压-气体流率(V-fr)曲线见图10. 其中, 气体工质为Ar, 关于Ar的碰撞截面公式见文献[20], Ar与其它材料负电极的二次电子发射系数见文献[21].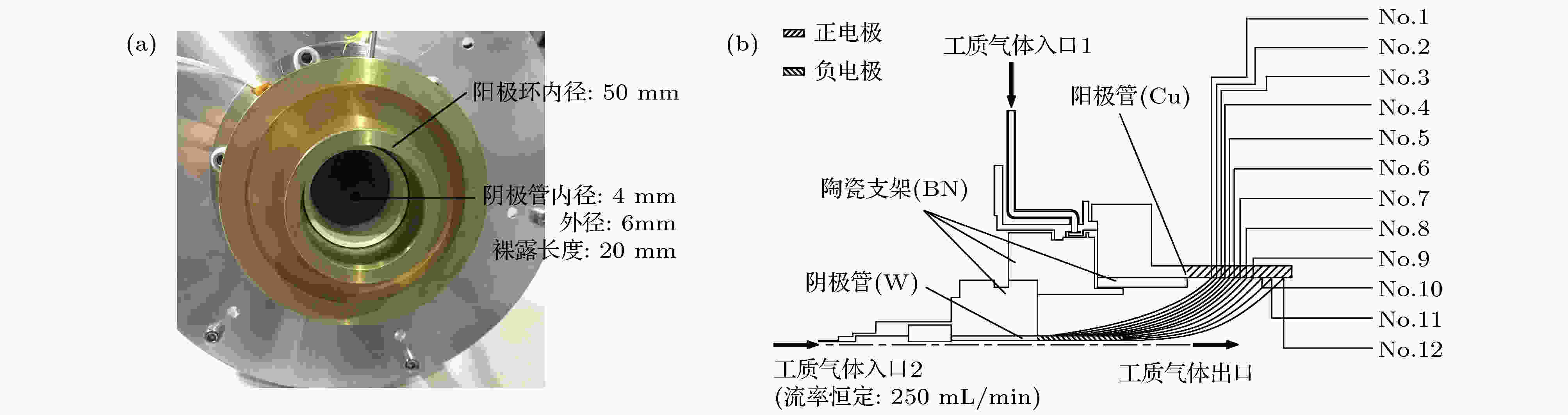 图 9 MPDT电极的相关信息 (a)实物照片; (b)电极结构及候选路径划分(f = 2.47)
图 9 MPDT电极的相关信息 (a)实物照片; (b)电极结构及候选路径划分(f = 2.47)Figure9. The relevant information of the MPDT: (a) Physical photograph; (b) the electrode geometry and potential path generation
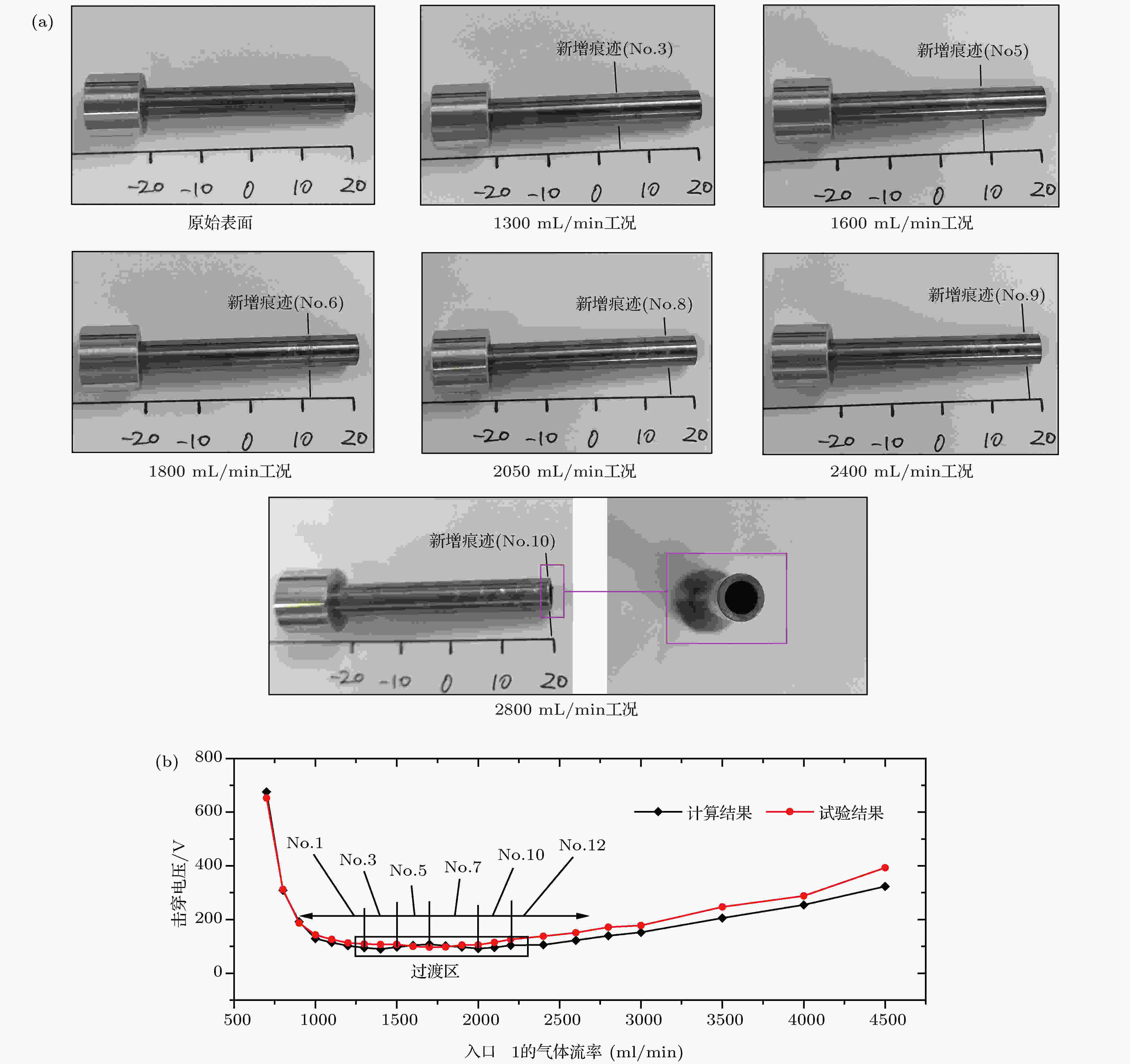 图 10 Case 2试验与计算结果对比(气体工质: Ar)
图 10 Case 2试验与计算结果对比(气体工质: Ar)Figure10. The comparison of the calculation and test results in case 2 (working medium: Ar)
据图10, 同样地, 负电极表面的新增痕迹趋势与起始路径计算结果的趋势在定性层面保持一致, 并且, 击穿电压的计算相对误差在0.42%—7.90%.
综上, 通过试验与计算结果的对比, 可以初步证实: 第一, 起始击穿路径确实会发生转移; 第二, DCP模型能够从定性角度捕捉起始击穿路径的转移方向.
2
4.1.case 3
Case 3为两非平行直板电极间的击穿工况, 如图11(a)所示, 电极在入纸面方面为无限长, 两电极结构完全相同, 计算结果见图11(b).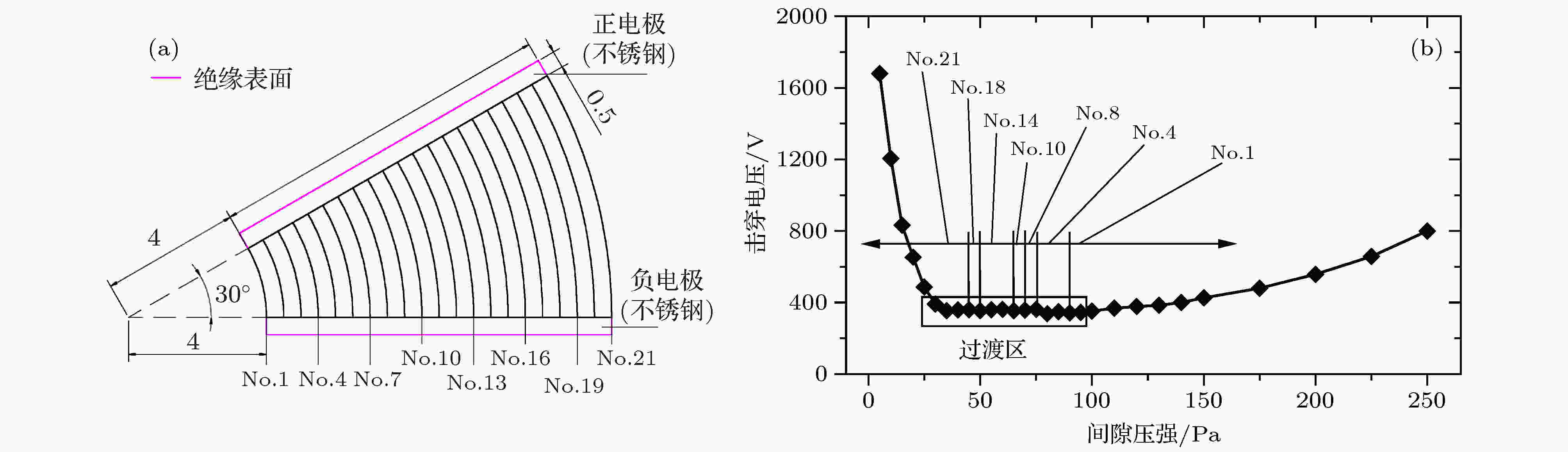 图 11 Case 3的计算输入条件及计算结果(气体工质: Xe) (a)电极结构及候选路径划分(f = 2.45); (b)V-p曲线的计算结果及起始路径分布
图 11 Case 3的计算输入条件及计算结果(气体工质: Xe) (a)电极结构及候选路径划分(f = 2.45); (b)V-p曲线的计算结果及起始路径分布Figure11. The input conditions and calculation results in case 3 (working medium: Xe): (a) The electrode geometry and potential path generation; (b) the calculation results of the V-p curve and the critical path distribution
2
4.2.Case 4
Case 4为无加热器空心阴极(heaterless hollow cathode, HHC)的工况. 在HHC点火过程中, 阴极管-触持极间会首先引发气体击穿, 通过离子轰击负电极表面而加热发射体, 使发射体达到工作温度(1300 K左右), 然后在阴极管-阳极板间进行稳定放电(阳极板在触持极右侧2—3 cm, 图12(a)未展示). 因此, HHC的点火性能主要依赖于气体击穿过程. HHC击穿所发生的正负电极结构见图12(a), 计算结果见图12(b).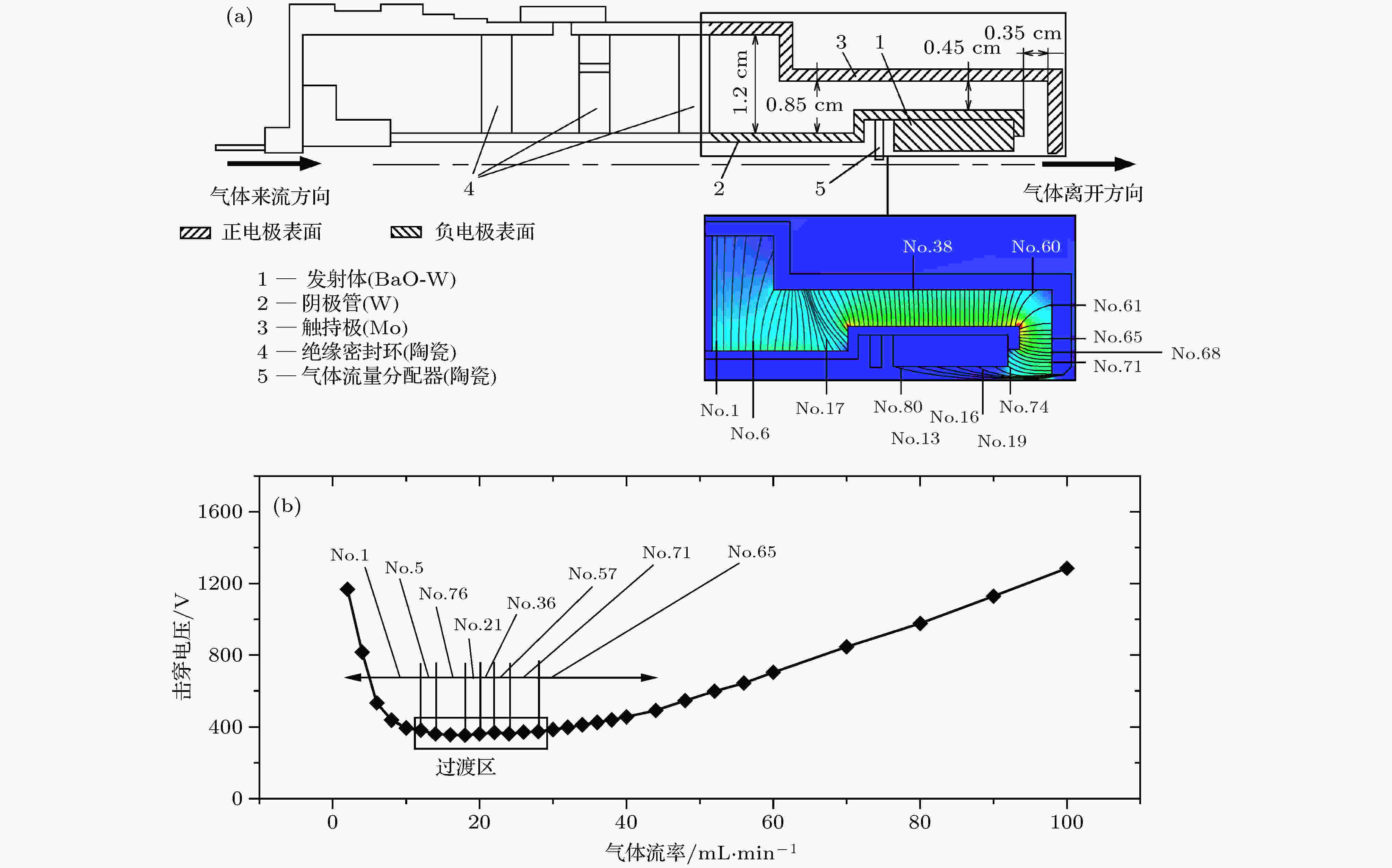 图 12 Case 4的计算输入条件及计算结果(气体工质: Xe) (a)电极结构及候选路径划分(f = 3.76); (b)V-fr曲线的计算结果及起始路径分布
图 12 Case 4的计算输入条件及计算结果(气体工质: Xe) (a)电极结构及候选路径划分(f = 3.76); (b)V-fr曲线的计算结果及起始路径分布Figure12. The input conditions and calculation results in case 4(working medium: Xe): (a) The electrode geometry and potential path generation; (b) the calculation results of the V-p curve and the critical path distribution
2
4.3.case 5
Case 5为两平行圆柱电极间的击穿工况, 电极在入纸面方面为无限长, 2个电极结构完全相同(图13(a)), 计算结果如图13(b). 气体工质为Ar.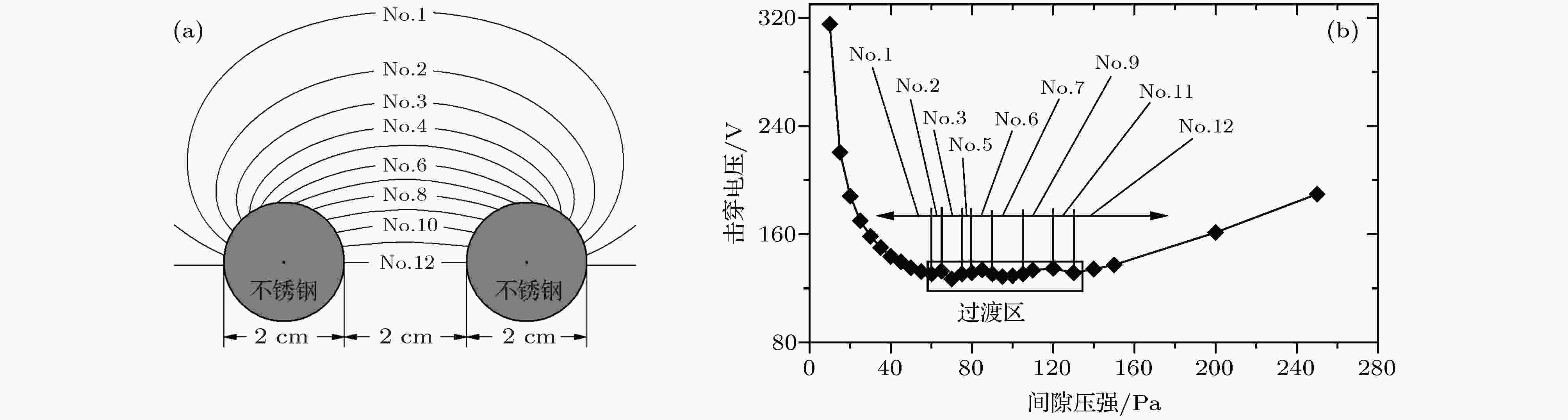 图 13 Case 5的计算输入条件及计算结果(气体工质: Ar): (a) 电极结构及候选路径划分(f = 3.43); (b) V-p曲线的计算结果及起始路径分布
图 13 Case 5的计算输入条件及计算结果(气体工质: Ar): (a) 电极结构及候选路径划分(f = 3.43); (b) V-p曲线的计算结果及起始路径分布Figure13. The input conditions and calculation results in case 5 (working medium: Ar): (a) The electrode geometry and potential path generation; (b) the calculation results of the V-p curve and the critical path distribution
2
4.4.case 6
Case 6为圆柱-直板电极间的击穿工况, 两电极在入纸面方向无限长, 并且, 两电极的中心轴线平行. 电极结构及候选路径划分见图14(a), 计算结果见图14(b). 气体工质为Xe.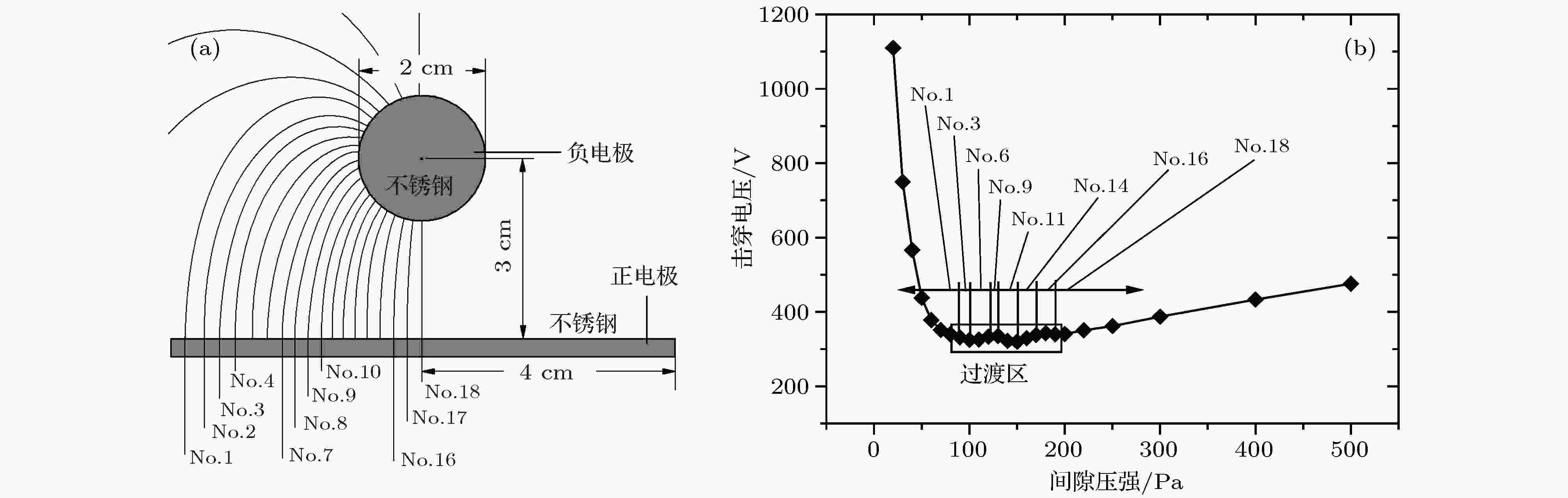 图 14 Case 6的计算输入条件及计算结果(气体工质: Xe) (a)电极结构及候选路径划分(f = 2.84); (b)V-p曲线的计算结果及起始路径分布
图 14 Case 6的计算输入条件及计算结果(气体工质: Xe) (a)电极结构及候选路径划分(f = 2.84); (b)V-p曲线的计算结果及起始路径分布Figure14. The input conditions and calculation results in case 6(working medium: Xe): (a) The electrode geometry and potential path generation; (b) the calculation results of the V-p curve and the critical path distribution
综上, 通过对case 1到case 6的对比分析, 发现这6个工况的计算或试验结果都存在一些共有的特性:
(1)在压强或气体流率上升过程中, 起始击穿路径并不是固定不变的, 会发生转移;
(2)在V-p曲线或V-fr曲线中, 曲线形貌与经典Paschen曲线不同, 在曲线的左支和右支中间总会存在一个过渡区, 其击穿电压会表现出“上下波动, 近似持平”的特性;
(3)起始击穿路径的转移方向总是表现为从较长路径向较短路径转移.
2
5.1.路径转移原因和过渡区特性
以case 3为例, 利用DCP模型将case 3所有候选击穿路径的V-p曲线都计算出来, 并与整个电极的V-p曲线放在一起做对比(图15).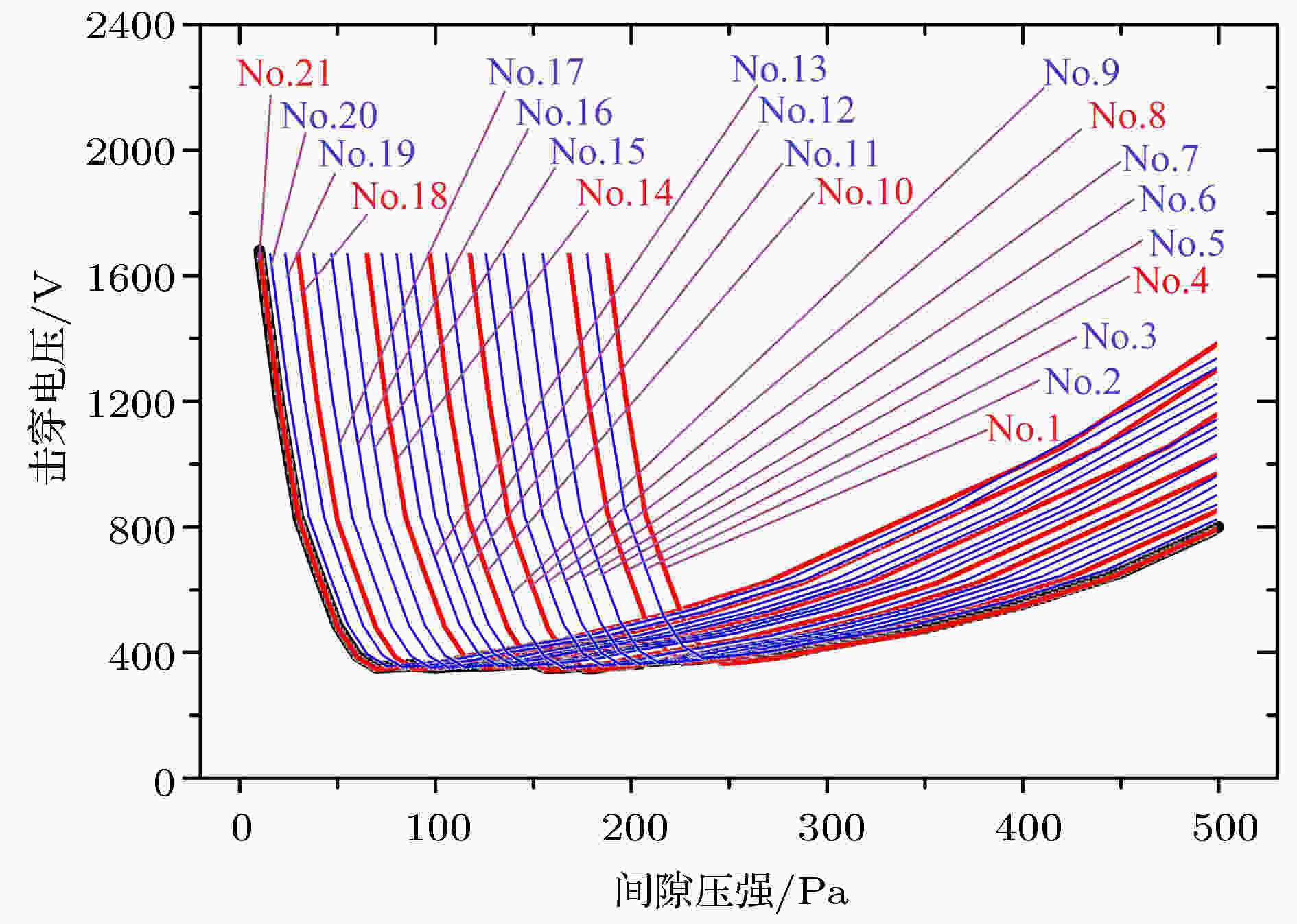 图 15 整个电极的V-p曲线形成原因(case 3)
图 15 整个电极的V-p曲线形成原因(case 3)Figure15. The formation reason of the entire V-p curve in the whole gap of case 3
图15所展示的蓝色细线为没有成为起始路径的候选路径的曲线, 而每一条红色细线为各起始击穿路径的曲线, 黑色粗线为整个电极的曲线(图11(b)的计算结果). 据图15, 并不是所有候选路径都有机会成为起始击穿路径, 只有那些可以达到全通道路径中最低V-p曲线的路径才能成为起始击穿路径, 并且, 每条起始路径都仅仅在某个压强范围内具备成为当前起始击穿路径的条件, 而在其他压强范围内则不具备条件, 所以, 当压强或气体流率变化时, 起始击穿路径就会轮流更替, 发生“频繁的路径转移”. 另一方面, 能够成为起始击穿路径的候选路径, 只能将自身V-p曲线的最优部分贡献给整个电极的V-p曲线. 例如, No.21将其左支贡献给黑色曲线, No.1将其右支贡献给黑色曲线, 而No.14, No.10, No.8, No.4和No.1会在60—190 Pa之间轮流将自身的最小电压区域(Paschen定律中称之为(pd)min区域)贡献给黑色曲线的过渡区. 因而, 过渡区每条起始路径的(pd)min区域在电压值上都是比较接近的, 取决于放电气体种类和电极材料. 因此, 过渡区的击穿电压会表现出“上下波动, 近似持平”的特性, 直到起始路径转移到最后一条路径时, 曲线才会继续上升.
2
5.2.路径转移方向
根据DCP数值模型, 判断起始路径的核心参数为每条候选路径的总的二次电子发射数量nγ, 而影响该参数的直接因素为每条候选路径的总电离次数. 因此, 为揭示路径转移规律, 这里先给出不同压强下, 各路径中所引发的电离碰撞次数分布. 依然以case 3为例, 选择No.18代表长路径, No.4代表段路径(参考图11(a)), 选择p = 40 Pa为低气压工况, p = 80 Pa为高气压工况. 利用DCP模型, 将每个计算节点的电离次数统计成云图(图16).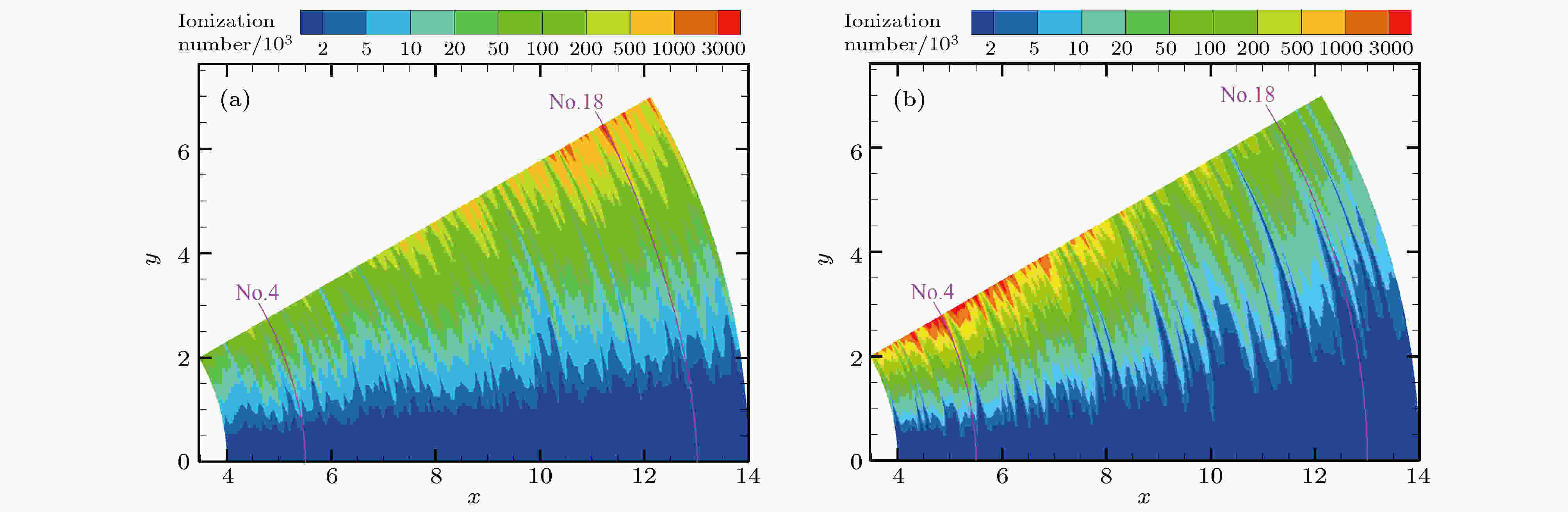 图 16 不同压强下电极间隙的电离碰撞次数分布(case 3) (a) p = 40 Pa; (b) p = 80 Pa
图 16 不同压强下电极间隙的电离碰撞次数分布(case 3) (a) p = 40 Pa; (b) p = 80 PaFigure16. The ionization collision number distribution at different gap pressures in case 3: (a) p = 40 Pa; (b) p = 80 Pa
根据图16, 发现在p = 40 Pa时, No.18的电离次数确实高于No.4, 在No.18附近有明显的电子雪崩形态; 而在p = 80 Pa时, 情况正好相反. 接着, 按照电离碰撞概率公式(第2节的8(b)式), 有4个参数会影响电离概率Pion:
































































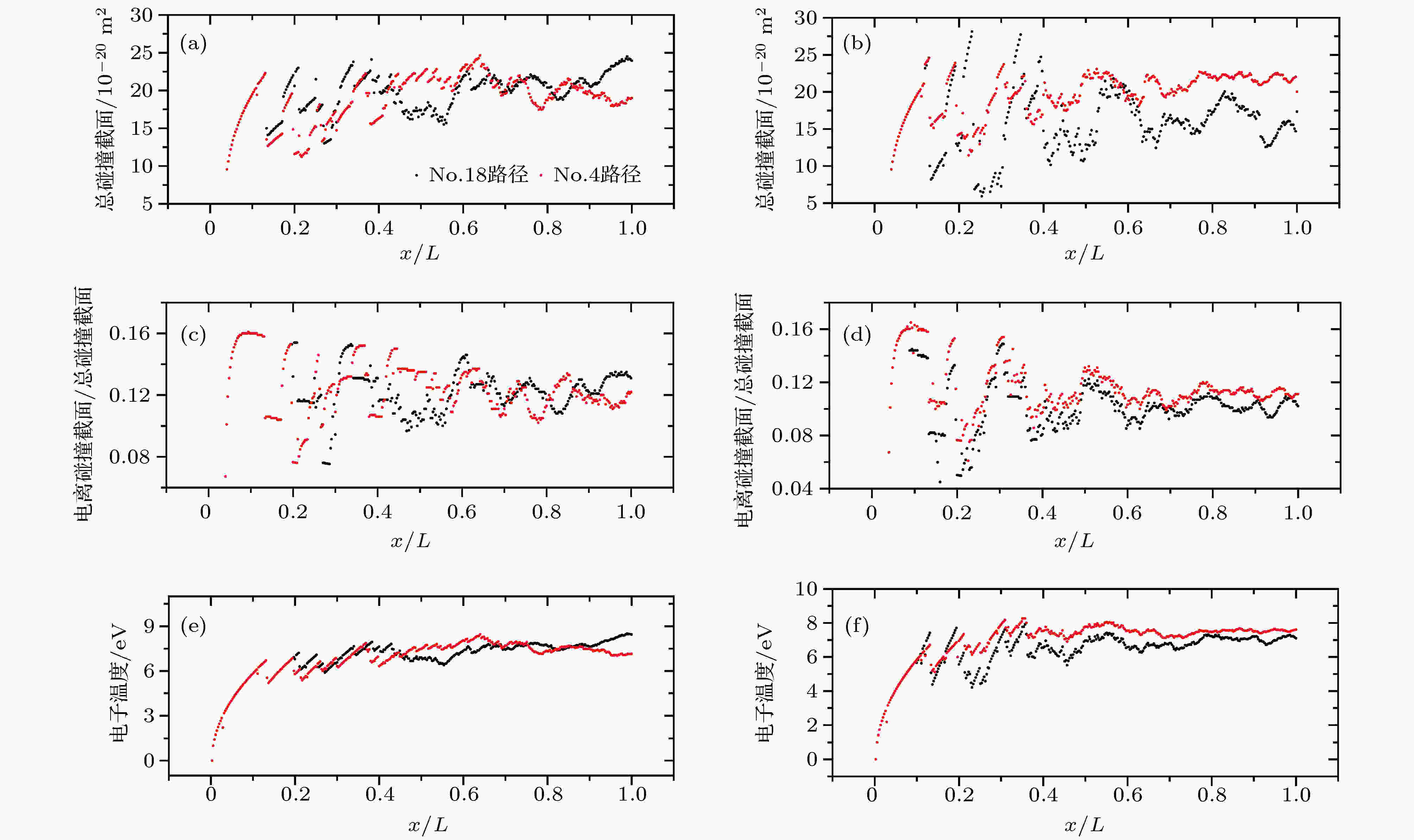 图 17
图 17 


























Figure17. The distribution of



























据图17(a)—(d), 在低气压下, No.4和No.18的







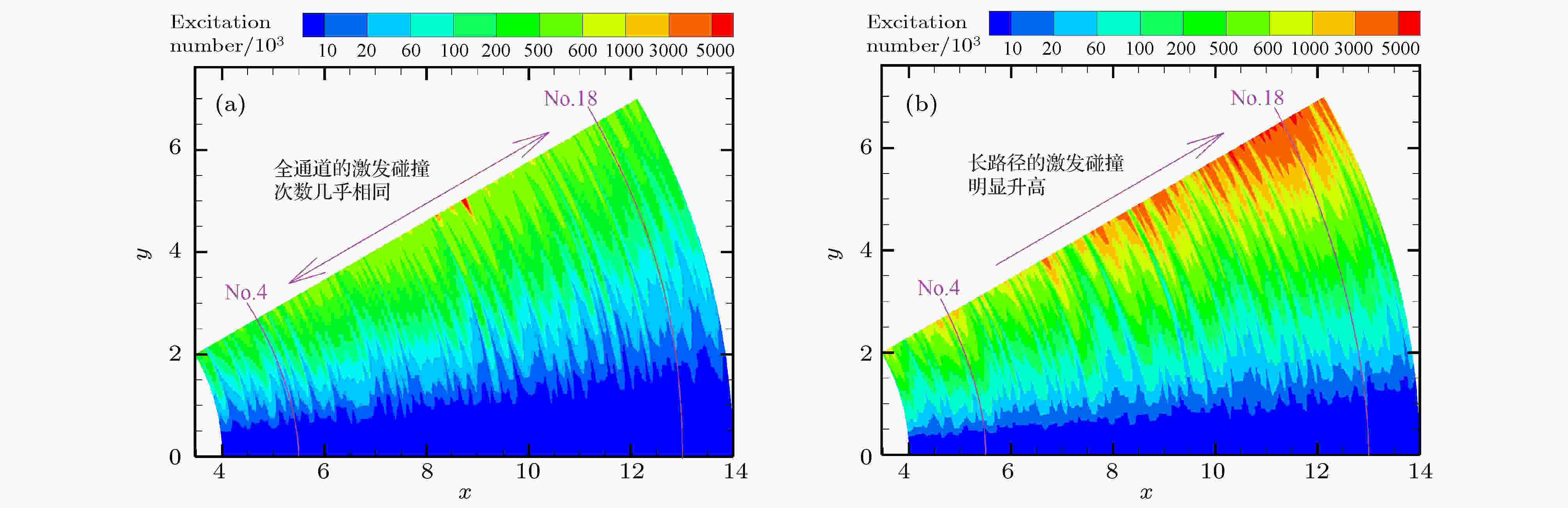 图 18 不同压强下电极间隙的激发碰撞次数分布(case 3) (a) p = 40 Pa; b) p = 80 Pa
图 18 不同压强下电极间隙的激发碰撞次数分布(case 3) (a) p = 40 Pa; b) p = 80 PaFigure18. The excitation collision number distribution at different gap pressures in case 3: (a) p = 40 Pa; (b) p = 80 Pa
图18显示: 在低气压工况中, 整个通道各候选路径的激发碰撞次数几乎相同, 并且碰撞次数较少, 这导致各个路径的电子动能损失都较少, 于是就形成了图17(e)的趋势(No.4和No.18的电子动能相当); 但在高气压工况中, 激发碰撞次数在长路径上明显增多, 这是由于长路径的

综上, 激发碰撞所导致的能损影响是起始路径转移的关键因素: 在低气压下, 激发碰撞在各路径的发生次数都较低, 其影响程度较小, 那么较长的路径更容易触发击穿; 但随着气压升高时, 激发碰撞在长路径中的发生次数明显升高, 其影响程度逐渐增加, 就导致起始路径逐渐从长路径向短路径转移.
1)在间隙压强或气体流率发生变化时, 起始击穿路径会发生转移, 这与Osmokrovic的试验结果吻合. 通过计算分析, 本文认为, 路径转移与每条候选路径各自的击穿电压曲线特性有关, 整个电极通道总会在不同工况下选择最可能发生击穿的那条路径来引发击穿, 因此, 起始击穿路径会在不同压强或流率工况下发生转移;
2)在V-p或V-fr曲线中, 曲线左支和右支之间总会存在一个过渡区, 过渡区的击穿电压会表现出上下波动、近似持平的变化趋势, 原因为过渡区的各起始击穿路径将其(pd)min部分贡献给整个通道的击穿曲线, 而这些(pd)min区域的击穿电压在数值上接近, 导致过渡区的曲线特性出现上下波动、近似持平, 只有转移到最后一条起始击穿路径后, 曲线才会上升;
3)当间隙压强或流率从低到高增加时, 起始路径的转移方向总会沿着较长路径向较短路径转移, 这是因为较低气压下各候选路径的激发碰撞次数均较少, 电子动能较高, 电离概率主要受路径长度影响, 击穿会选择较长路径, 而在较高气压下, 较短路径的激发碰撞次数明显低于较长路径, 其能损较低, 更易引发击穿.
