删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

Rh XIII—Cd XVI离子4s<sup>2</sup>4p<sup>3</sup>—4s4p<sup>4</sup>能级与

本站小编 Free考研考试/2021-12-29
摘要:用HFR (Hartree-Fock with relativistic corrections)方法对Rb V—Cd XVI离子4s24p3和4s4p4组态能级结构做了全面系统的理论计算研究. 通过分析能级结构参数的HFR理论计算值与基于实验能级拟合得到的计算值之比值随着原子序数Zc变化的规律, 运用广义拟合外推方法预言了这些离子能级结构参数. 由此进一步计算了Rh XIII, Pd XIV, Ag XV和Cd XVI离子4s24p3 (4S3/2, 2P1/2, 3/2, 2D3/2, 5/2)和4s4p4 (4P1/2, 3/2, 5/2, 2P1/2, 3/2, 2D3/2, 5/2, 2S1/2)组态能级以及电偶极跃迁波长与振子强度. 研究表明, 对于4s24p3组态, 单组态近似可以得到较满意的结果; 而对于4s4p4组态, 只有在考虑了4s24p24d的组态相互作用效应时, 计算结果的准确性才能明显得到提高. 同时, 本文还运用全相对论grasp2K-DEV程序包计算了Rh XIII—Cd XVI离子组态能级. 对于Rh XIII离子4s24p3 (2P1/2), Pd XIV离子4s24p3 (4S3/2, 2P1/2, 3/2, 2D3/2, 5/2)和4s4p4 (2P1/2, 3/2, 2D3/2, 5/2, 2S1/2), 能级均无实验值; 对于Ag XV和Cd XVI离子, 截至目前还没实验能级数据, 没有实验能级值的所有数据均仅来自本文的计算数值. 本文计算结果与已有实验值吻合得很好.
关键词: Rh XIII—Cd XVI离子/
能级/
跃迁波长/
振子强度

English Abstract


全文HTML

--> --> -->
1.引　言
Rh XIII, Pd XIV, Ag XV和Cd XVI离子属类砷等电子序列, 基组态为4s24p3, 较低激发组态为4s4p4, 4s24p24d及4s24p25s等. 对类砷低Z (原子序数)离子4s24p3—4s4p4, 4s24p3—4s24p25s跃迁排列的早期研究可以追溯到Moore[1]和Rao[2]的研究报道. Rahimullah等[3] 在1976年通过火花放电光谱实验技术首次得到了Y VII—Mo Ⅹ离子4s24p3—4s24p25s组态能级跃迁谱线和实验能级值. Reader和Acquista[4]在1981年对Y VII—Mo Ⅹ离子4s24p3—4s4p4, 4s24p3—4s24p25s组态能级跃迁做了较全面的实验研究, 同时根据获得的实验谱线波长, 在理论上确定了4s24p3, 4s4p4和4s24p25s组态能级数据. 从文献[4]可以看出, 在单组态近似条件下, 4s24p3和4s24p25s组态能级的理论计算值与实验值十分一致, 而4s4p4 组态能级理论值与实验值偏差明显较大. 1984年, Person和Pettersson[5]通过实验研究得到了Kr IV, Rb Ⅴ, Sr VI离子4s24p3—4s4p4跃迁排列中31条谱线, 理论计算确定的4s24p3组态能级数据与实验值的最大绝对偏差仅为2 cm–1, 而4s4p4组态能级绝对偏差的最大值却达到了469 cm–1. 这一研究结果进一步表明了对于4s4p4组态能级, 单组态近似条件下, 理论计算结果与实验值仍存在较大偏差. Biemont和Hansen[6]于1986年理论预言了Tc XI—Ag XV的4s24p3组态能级以及这些能级之间的磁偶极和电四极跃迁波长与跃迁速率. 1989年, Sullivan和Kane[7]通过激光等离子体光谱实验技术研究了Ru XII, Rh XIII离子的4s24p3—4s24p25s跃迁波长, 通过理论计算, 确定了这两个组态的精细结构能级. 1990年, Sullivan等[8]又采用同样的实验方法对Ru XII, Rh XIII, Pd XIV三个离子的4s24p3—4s4p4 组态跃迁能谱进行了较为详细的研究报道, 同时运用MCDF (multi-configuration Dirac-Fock)理论方法[9]中的扩展平均能级(extended average level, EAL)模型, 计算了4s24p3和4s4p4 组态能级, 分析了Rb V—Pd XIV离子MCDF理论值与实验能级值之差(EDF–EOBS)沿等电子序列随着Zc (Zc = Z – N + 1)变化的规律, 理论预言了Ru XII—Pd XIV离子4s24p3和4s4p4组态所有能级值, 但是, 对于Pd XIV离子4s24p3 组态没有能够建立总共5个能级的实验值, 而4s4p4组态只指认了该组态8个能级中的三个实验能级. 对上述文献综合分析发现, 对于As I序列离子低能激发组态而言, 在MCHF (multi-configuration Hartree-Fock)理论计算研究中, 单组态近似条件下4s24p3和4s24p25s组态能级的计算结果与实验值都十分接近. 关于这一问题, 文献[10]曾做过详细的研究报道, 本文不再赘述. 但从文献[3—5]报道可以看出, 在采用MCHF理论对4s4p4 组态能级计算研究中, 单组态近似计算的能级结果与实验值的偏差较大, 例如, 在文献[5]中, 单组态计算得到的As I—Mo X离子4s24p3组态能级的实验观测值与理论值的绝对偏差最大仅为13 cm–1, 而Kr IV—Mo X离子4s4p4组态能级的实验观测值与理论值的绝对偏差最大达到了469 cm–1, 而且大部分结果的绝对偏差超过了200 cm–1. 然而, 对于Rh XIII—Cd XVI离子4s4p4能级的计算研究, 除了文献[8]采用MCDF理论研究之外, 截至目前还没有采用MCHF理论研究的报道, 文献[8]采用MCDF理论计算的结果与实验值之间还有较大偏差. 对于Ag XV和Cd XVI离子, 目前还没有相关实验和理论研究的报道. 显然, 对于这些离子, 4s24p3—4s4p4组态能级与跃迁高精度理论计算研究有助于人们理解As I离子结构, 同时也可以为实验和其他理论研究提供数据参考. 为此, 本文在前人研究的基础上, 用HFR (Hartree-Fock with relativistic corrections)方法对Rb V—Cd XVI离子4s24p3 和4s4p4组态能级结构进行了全面系统的理论计算研究. 通过分析能级结构参数随着Zc变化的规律, 运用参数拟合外推方法计算了上述离子组态能级结构参数, 由此进一步计算了Rh XIII, Pd XIV, Ag XV和Cd XVI离子4s24p3—4s4p4组态能级以及电偶极跃迁谱线波长与振子强度. 为了便于理论和实验的进一步对比分析研究, 本文还运用全相对论grasp2K-DEV程序包计算了Rh XIII—Cd XVI离子组态能级.
2.理论计算方法
2
2.1.HFR方法概述
-->

2.1.HFR方法概述

本文计算采用Cowan程序包中的HFR理论方法[11]. 在HFR理论中, N电子原子体系的单电子径向波函数通过自洽场方法求解HFR方程获得. 体系波函数在所有可能的组态基矢空间展开, 表示为
$\psi = \sum\limits_{\beta J\gamma } {y_{\beta J}^\gamma \left| {\beta J\gamma } \right\rangle } , $
(1)式中, $\left| {\beta J\gamma } \right\rangle $是组态$\beta $中具有同一总角动量$J$的第$\gamma $个谱项基矢, $y_{\beta J}^\gamma $是其相应的基矢分量. 求和是对具有同一总角动量$J$的所有谱项基矢进行的.
原子体系的哈密顿算符(单位: Ry, 1 Ry = 13.606 eV)为
${\hat H_N} = - \sum\limits_{i = 1}^N \!{(\nabla _i^2 \!+\! \frac{2}{{{r_i}}})} +\! \sum\limits_{i = 1}^{N - 1}\! {\sum\limits_{j = i + 1}^N {\frac{2}{{{r_{ij}}}}} } +\! \sum\limits_{i = 1}^N {{\xi _i}({r_i})({l_i} \cdot {s_i})} , $
(2)式中, 第一项为单电子动能和在核场中的势能之和, 第二项为电子之间的库仑相互作用, 第三项为电子自旋-轨道相互作用. 哈密顿矩阵表示为
${h_{ij}} = \sum\limits_{ijk} {{C_{ijk}}{X^K}}, $
(3)式中, ${X^K}$表示Slater参数. 这些参数为库仑直接积分${F^K}$和交换积分${G^K}$, 自旋-轨道相互作用积分${\xi ^K}$, 组态相互作用积分${R^K}$等. ${C_{ijk}}$为相应角度系数. 电偶极跃迁的加权振子强度为
$gf = 3.0376 \times {10^{ - 4}}\sigma S, $
(4)式中, $\sigma $和$S$分别为电偶极跃迁的谱线波数(单位: cm–1)和线强度(单位: ${e^2}{a_0}^2$, e为电子电荷量, $a_0 $为玻尔半径).
下面描述具体的计算方法[12-14]. 首先在HFR理论计算时考虑了质量速度项和达尔文项修正, 同时还包括了近似Breit修正. 自洽场计算时, 所有离子径向积分参数统一标度为: 组态平均能为95%、自旋-轨道参数为100%、库仑相互作用(含组态相互作用)参数为85%. 计算过程中, 奇宇称和偶宇称组态能级值均以基态能级能量值作为参考点. 然后, 通过已有可靠实验能级值采用最小二乘拟合(least-square fitting, LSF)方法计算出离子的实验径向积分参数. 在此基础上, 再运用自行设计的FORTRAN程序, 分析径向参数的HFR和LSF值之比值随着Zc变化的规律, 采用广义最小二乘拟合(generalized least-square fitting, GLSF)外推(内插)计算方法, 得到径向积分参数的最佳优化计算结果. 最后, 利用这些积分参数计算出各能级值和有关的跃迁数据.
2
2.2.MCDHF方法概述
-->

2.2.MCDHF方法概述

本文MCDHF方法[15]计算采用的是全相对论grasp2K-DEV程序包[9,16?18]. 在MCDHF理论方法中, 对于N电子原子体系, 相对论单电子波函数采用狄拉克四分量旋量表示
${{ \varPhi} _{n\kappa m}}(r,\theta ,\phi ) = \frac{1}{r}\left\{ \begin{array}{l}{P_{n\kappa }}(r){\chi _{\kappa m}}(\theta ,\phi )\\{Q_{n\kappa }}(r){\chi _{ - \kappa m}}(\theta ,\phi )\end{array} \right\},$
(5)式中, $n$表示电子轨道主量子数, $\kappa $为包含了电子角动量$j$和宇称的相对论角量子数, $m$为磁量子数. 由(5)式定义的狄拉克旋量用于构建组态态函数(configuration state function, CSF), 表示为$\psi {\rm{(}}{\gamma _i}{J^{\pi} }{\rm{)}}$, CSF为Slater行列式的线性组合. 而原子态函数(atomic state function, ASF)则通过CSF的线性叠加得到, 表示为
$\Psi {\rm{(}}\varGamma {J^{\pi} }{\rm{)}} = \sum\limits_i^{} {{c_i}\psi {\rm{(}}{\gamma _i}{J^{\pi} }{\rm{)}}} , $
(6)式中, ${J^{\pi} }$为原子体系的总角动量和宇称, ${\gamma _i}$代表CSF的具体组态、耦合方式和高位数等区别于其他CSF的可能参数, ${c_i}$为展开系数. 相对论零阶有效哈密顿采用狄拉克-库仑(Dirac-Coulomb)算符(单位: a.u., 1 a.u.= 27.2114 eV), 表示为
$\hat H_N^{{\rm{DC}}} = \sum\limits_{i = 1}^N {\hat h_i^{\rm{D}}} + \sum\limits_{i = 1}^{N - 1} {\sum\limits_{j = i + 1}^N {\hat h_{ij}^{\rm{C}}} } , $
(7)式中, ${\hat h_i}^{\rm{D}} = c{{{\alpha }}_i} \cdot {{{p}}_i} + {c^2}{\rm{(}}{{\beta }_i} - 1{\rm{)}} + {V_i}{\rm{(}}r{\rm{)}}$为单电子狄拉克能量算符,$V{\rm{(}}r{\rm{)}}$为电子在原子核场中的势能, $\hat h_{ij}^{\rm{C}} = 1/{{r}_{{{ij}}}}$为电子之间的瞬时库仑排斥势. 组态相互作用计算时包括了完全横向虚拟光子相互作用效应, 量子电动力学效应(真空极化和自能修正)[19,20], 还包含了正常质量漂移和特殊质量漂移效应对能级的修正.
ASF展开中, 采用价电子与价电子之间的关联模型(VV)[21,22]. 对于类砷离子, 原子实记为C0≡1s22s22p63s23p63d10, 基组态为C04s24p3 (宇称量子数${\text{π}}$ = –1), 最低激发组态为C04s4p4 (宇称量子数${\text{π}}$ = +1), C0中的电子为非活动电子. 计算时, ASF构建均采用以多参考CSF作为零阶波函数展开方式进行. 对于奇宇称组态, 多参考CSF为4s24p3 (4S3/2, 2P1/2, 3/2, 2D3/2, 5/2) (${\text{π}}$ = –1), 对偶宇称, 多参考CSF为4s4p4 (4P1/2, 3/2, 5/2, 2P1/2, 3/2, 2D3/2, 5/2, 2S1/2) (${\text{π}}$ = +1). 允许电子激发为单激发和双激发. ASF展开为按照其轨道主量子数n逐层增加的展开方式进行, 表示为
C0 {4s24p3}(${\text{π}}$ = –1), C0{4s4p4}(${\text{π}}$ = +1)
→VV4 = C0{4s, 4p, 4d, 4f}　　→VV5 = VV4 + {5s, 5p, 5d, 5f, 5g}
→VV6 = VV5 + {6s, 6p, 6d, 6f, 6g, 6h}
→VV7 = VV6 + {7s, 7p, 7d, 7f, 7g, 7h, 7i}.
3.结果与讨论
为了得到Rh XIII—Cd XVI离子4s24p3—4s4p4能级与跃迁谱线波长, 本文首先对Rb V—Cd XVI离子4s24p3和4s4p4组态能级进行了全面系统的理论计算. 对于4s24p3组态, 根据文献[3—5]的研究结果, 单组态近似计算能够获得与实验值十分符合的计算结果. 在文献[10] 的MCHF单组态近似计算中, 通过引入4p壳层电子的等效静电相互作用算符参数$\alpha $(4p, 4p), 来考虑对包括弱组态累积效应在内的其他高阶能量修正, 同样获得了满意的结果. 因此, 本文在单组态近似条件下, 对4s24p3组态能级结构的Slater径向积分参数进行了全面系统的LSF理论优化计算. 这些参数是: 组态平均能Eav(4s24p3)、库仑相互作用直接积分F2(4p, 4p)、自旋与轨道相互作用积分${\zeta _{4{\rm{p}}}}$、等效静电相互作用算符参数$\alpha $(4p, 4p). 本文计算研究发现(参阅本文表3中本征矢纯度), 在偶宇称组态空间4s24p24d与4s4p4 组态能级本征矢之间有非常强的混合, 表明在MCHF计算时只有在考虑4s24p24d组态对4s4p4 组态能级的影响时, 才能得到更加准确的计算结果. 进一步计算研究表明, 虽然4s24p25s组态与4s4p4 组态能级本征矢之间也有混合情况, 但是其本征矢的占比很小, 例如, 对于Rb V和Cd XVI离子, 在4s4p4 组态能级的本征矢纯度占比中, 4s24p25s组态能级的本征矢纯度都不超过1%. 考虑到计算时的复杂性, 本文只考虑4s4p4和4s24p24d之间的组态相互作用效应. 这样在对4s4p4 组态能级做多组态计算时, 径向积分参数为: 组态平均能Eav(4s4p4)、库仑相互作用直接积分F2(4p, 4p)、自旋与轨道相互作用积分${\zeta _{4{\rm{p}}}}$、库仑相互作用交换积分G1(4p, 4p)、组态相互作用直接积分$R_{\rm{d}}^1$(4p4p, 4s4d), 同样通过引人4p壳层电子的等效静电相互作用算符参数$\alpha $(4p, 4p), 来考虑对包括弱组态累积效应在内的其他高阶能量修正. 表1列出了Rb V—Mo X离子4s4p4组态能级实验值与理论计算值之差(单位cm–1), 其中${\varDelta _{\rm{s}}}$表示Person和Pettersson[5]在单组态近似条件下, LSF计算得到的实验值与理论值之差; ${\varDelta _{\rm{m}}}$为本文在多组态(4s4p4 + 4s24p24d)近似条件下, LSF计算得到的实验值与理论计算值之差. 表1中只列出Rb V—Mo X离子数据, 这是因为只有这些离子有HF单组态近似结果可以比较. 从这些结果可以明显地看出, 本文计算的${\varDelta _{\rm{m}}}$值绝大多数不超过50 cm–1, ${\varDelta _{\rm{m}}}$的绝对值最大为140 cm–1, 最小仅为1 cm–1, 而Person和Pettersson[5]在单组态近似条件计算的${\varDelta _{\rm{s}}}$的绝对值绝大部分超过200 cm–1, 最大达到了382 cm–1, 最小为45 cm–1. 显然, 本文多组态计算结果要比Person和Pettersson[5]单组态近似条件下的计算值更加准确, 即本文多组态计算值更加接近实验结果.
离子能级Rb VSr VIY VIIZr VIIINb IXMo X
${\varDelta _{\rm{s}}}$${\varDelta _{\rm{m}}}$${\varDelta _{\rm{s}}}$${\varDelta _{\rm{m}}}$${\varDelta _{\rm{s}}}$${\varDelta _{\rm{m}}}$${\varDelta _{\rm{s}}}$${\varDelta _{\rm{m}}}$${\varDelta _{\rm{s}}}$${\varDelta _{\rm{m}}}$${\varDelta _{\rm{s}}}$${\varDelta _{\rm{m}}}$
2D5/2 218 7 260 –14 293 3 332 –5 373 –15 435 –29
4P5/2 –327 –8 –359 –50 –329 –33 –316 –7 –320 18 –334 36
2P3/2 –214 4 –25 –15 60 –7 100 –2 126 –1 151 –8
2D3/2 –212 12 –258 –71 –294 –47 –336 5 –382 66 –452 122
4P3/2 121 4 150 36 163 39 183 43 215 53 259 64
2S1/2 –259 8 –275 –25 –265 69 –271 1 –289 –75 –319 –140
2P1/2 468 17 300 102 210 –12 181 1 180 17 196 32
4P1/2 45 9 206 –4 162 –21 127 –36 97 –50 66 –59


表1Rb V—Mo X离子4s4p4组态能级实验值与理论计算值之差(单位cm–1)的比较
Table1.Comparasion of differences between observed and calculated levels values for the 4s4p4 configuration in Rb V?Mo X

离子能级Eexp/cm–1ELSF/cm–1EGLSF/cm–1EMCDHF/cm–1本征矢纯度
Rh XIII 4s24p3
4S3/2 0 0 0 0 71% + 21%2P3/2 + 9%2D3/2
2D3/2 35762 35820(58) 35863(101) 35992(230) 66% + 22%4S3/2 + 12%2P3/2
2D5/2 49151 49072(–79) 49110(–41) 49284(133) 100%
2P1/2 72267p 72237(–30)p 72279(12)p 72915(648) 100%
2P3/2 100673 100642(–31) 100722(49) 100668(–5) 68% + 25%2D3/2 + 7%4S3/2
4s4p4
4P5/2 284236 284230(–6) 284111(–125) 283365(–871) 87% + 6%2D5/2 + 5%4s24p24d 4P5/2
4P3/2 308739 308504(–235) 308770(31) 307548(–1191) 86% + 6%4s24p24d 4P3/2 + 5%2D3/2
4P1/2 313989 314205(36) 314507(518) 313218(–771) 82% + 11%2S1/2 + 6%4s24p24d 4P1/2
2D3/2 349977 350012(35) 349934(–43) 352413(2436) 69% + 14%4s24p24d 2D3/2 + 7%4P3/2
2D5/2 359733 359722(–11) 359614(–119) 361457(1724) 76% + 15%4s24p24d 2D5/2 + 7%4P5/2
2S1/2 395765 395592(–173) 395707(–58) 399771(4006) 47% + 26%2P1/2 + 9%4s24p24d 2S1/2
2P3/2 401975 401960(–15) 401883(–92) 408136(6161) 55% + 28%4s24p24d 2P3/2 + 8%2D3/2
2P1/2 439005 439001(–4) 439405(400) 444364(5359) 33% + 25%2S1/2 + 23%4s24p24d 2P1/2
Pd XIV 4s24p3
4S3/2 0 0 0 0 66% + 23%2P3/2 + 10%2D3/2
2D3/2 40021p 40092(71)p 40175(154)p 40147(126) 64% + 26%4S3/2 + 11%2P3/2
2D5/2 54958p 54852(–106)p 54935(–23)p 54996(38) 100%
2P1/2 79147p 79112(–35)p 79189(42)p 79766(619) 100%
2P3/2 113280p 113224(–56)p 113295(15)p 113113(–167) 66% + 26%2D3/2 + 8%4S3/2
4s4p4
4P5/2 305545 305506(–39) 305289(–256) 304542(–1003) 87% + 7%2D5/2 + 5%4s24p24d 4P5/2
4P3/2 333774 333809(35) 333389(–385) 332461(–1313) 86% + 6%2D3/2 + 6%4s24p24d 4P3/2
4P1/2 339032 339356(324) 339321(289) 338267(–765) 80% + 13%2S1/2 + 6%4s24p24d 4P1/2
2D3/2 376537p 377555(1019)p 376256(–281)p 378921(2384) 67% + 13%4s24p24d 2D3/2 + 9%4P3/2
2D5/2 388385p 387860(–525)p 387887(–498)p 389905(1520) 76% + 14%4s24p24d 2D5/2 + 8%4P5/2
2S1/2 425277p 424079(–1189)p 424752(–525)p 429012(3735) 45% + 28%2P1/2 + 9%4P1/2
2P3/2 432003p 431953(–50)p 431264(–739)p 438183(6180) 53% + 27%4s24p24d 2P3/2 + 10%2D3/2
2P1/2 468322p 468558(236)p 474603(6281)p 480060(11738) 30% + 25%2S1/2 + 21%4p24d 2P1/2
Ag XV 4s24p3
4S3/2 0 0 62% + 26%2P3/2 + 12%2D3/2
2D3/2 45260 45098 62% + 29%4S3/2 + 9%2P3/2
2D5/2 61485 61457 100%
2P1/2 86808 87360 100%
2P3/2 127267 127015 65% + 26%2D3/2 + 9%4S3/2
4s4p4
4P5/2 327358 326566 86% + 8%2D5/2 + 5%4s24p24d 4P5/2
4P3/2 358887 358483 81% + 8%4s24p24d 4P3/2 + 6%2D3/2
4P1/2 364986 364313 78% + 15%2S1/2 + 6%4s24p24d 4P1/2
2D3/2 403533 406661 64% + 12%4p24d 2D3/2 + 12%4P3/2
2D5/2 417320 419813 76% + 14%4s24p24d 2D5/2 + 9%4P5/2
2S1/2 454883 459653 43% + 29%2P1/2 + 10%4s24p24d 2S1/2
2P3/2 461039 469489 47% + 26%4s24p24d 2P3/2 + 12%2D3/2
2P1/2 510793 517520 26% + 24%2S1/2 + 20%4s24p24d 2P1/2
Cd XVI 4s24p3
4S3/2 0 0 58% + 28%2P3/2 + 14%2D3/2
2D3/2 51168 50914 59% + 33%4S3/2 + 8%2P3/2
2D5/2 68806 68729 100%
2P1/2 95174 95759 100%
2P3/2 142703 142486 64% + 27%2D3/2 + 9%4S3/2
4s4p4
4P5/2 350419 349499 85% + 7%2D5/2 + 5%4s24p24d 4P5/2
4P3/2 385245 385637 78% + 9%4s24p24d 4P3/2 + 5%2D3/2
4P1/2 391550 391382 76% + 17%2S1/2 + 5%4s24p24d 4P1/2
2D3/2 431691 435771 60% + 15%4s24p24d 2D3/2 + 10%4P3/2
2D5/2 447887 451301 76% + 13%4s24p24d 2D5/2 + 9%4P5/2
2S1/2 486090 491836 41% + 30%2P1/2 + 12%4s24p24d 2S1/2
2P3/2 489808 502144 33% + 23%4s24p24d 2P3/2 + 15%2D3/2
2P1/2 547585 556756 21% + 29%2S1/2 + 23%4s24p24d 2P1/2


表3Rh XIII—Cd XVI离子4s24p3, 4s4p4组态能级和本征矢纯度
Table3.Energy levels and percentage compositions of the 4s24p3 and 4s4p4 configurations for ions from Rh XIII to Cd XVI.

为了得到未知离子组态能级就需要运用GLSF外推(或内插)的方法. 首先计算这些离子的所有能级结构参数, 由这些参数, 进一步计算各离子4s24p3和4s4p4 组态能级值. 具体方法是: 对于已有4s24p3和4s4p4组态各能级实验值的离子, 本文以这些实验能级数据为基础, 用LSF方法获得所有这些离子组态能级结构参数. 对于目前还没有能级实验值的离子, 则通过分析这些参数随着Zc变化的特性, 运用GLSF外推(或内插)方法首先得到这些离子的所有能级结构参数.
图1给出了在GLSF外推计算过程中, 得到的各离子4s24p3, 4s4p4 和4s24p24d组态平均能量Eav随着Zc的变化情况. 根据本文计算, 对于Rb V离子4s4p4 和4s24p24d组态平均能分别为183473和238442 cm–1, 组态平均能之差为54969 cm–1. 而对于Cd XVI离子4s4p4 和4s24p24d组态平均能分别为457425 cm–1和631363 cm–1, 组态平均能之差为173938 cm–1 . 这一结果表明, 尽管这两个组态的平均能之差随着Zc 的增大在扩大, 但是这一差值远小于弱相互作用组态平均能差值的半经验判定标准106 cm–1 (详细分析说明请参阅文献[11]), 表明对于Rb V—Cd XVI离子, 4s24p24d与4s4p4 组态之间存在较强的相互作用. 从图1可以看到各离子组态平均能Eav随Zc变化十分光滑, 因此, 在本文的计算中各未知离子的Eav是通过比值外推计算得到的.
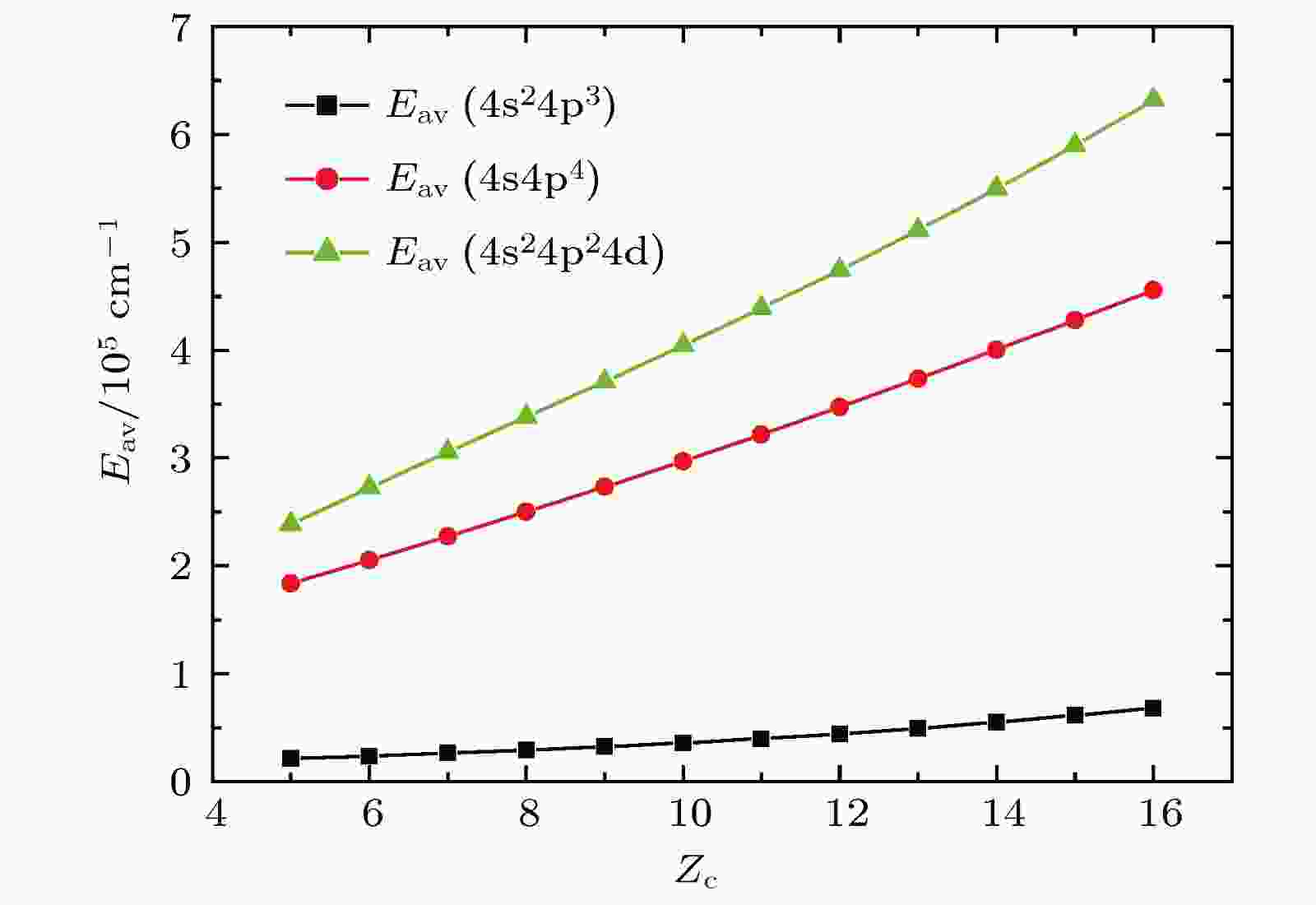图 1 4p3, 4s4p4和4p24d组态GLSF平均能Eav随Zc的变化
Figure1. Variations of GLSF average energy of 4p3, 4s4p4 and 4p24d configurations with Zc.

图2为4s24p3组态能级结构参数中, 库仑相互作用直接积分F2(4p, 4p), 自旋与轨道相互作用积分${\zeta _{4{\rm{p}}}}$, 4p壳层电子的等效静电相互作用算符参数$\alpha $(4p, 4p)的GLSF拟合计算值随着Zc变化情况. 从图2可以看出, F2(4p, 4p)值最大, 其次为${\zeta _{4{\rm{p}}}}$, $\alpha $(4p, 4p)最小. 尽管$\alpha $(4p, 4p)的值很小, 但反映了各种可能的能量高阶效应对离子能级的影响. 对于单组态近似, $\alpha $(4p, 4p)对于4s24p3组态能级的高精度计算具有重要意义. 从图2可以明显地看出F2(4p, 4p), ${\zeta _{4{\rm{p}}}}$ 的拟合计算值随Zc的增加其值逐渐增大, $\alpha $(4p, 4p)值缓慢减小, 但变化行为十分光滑.
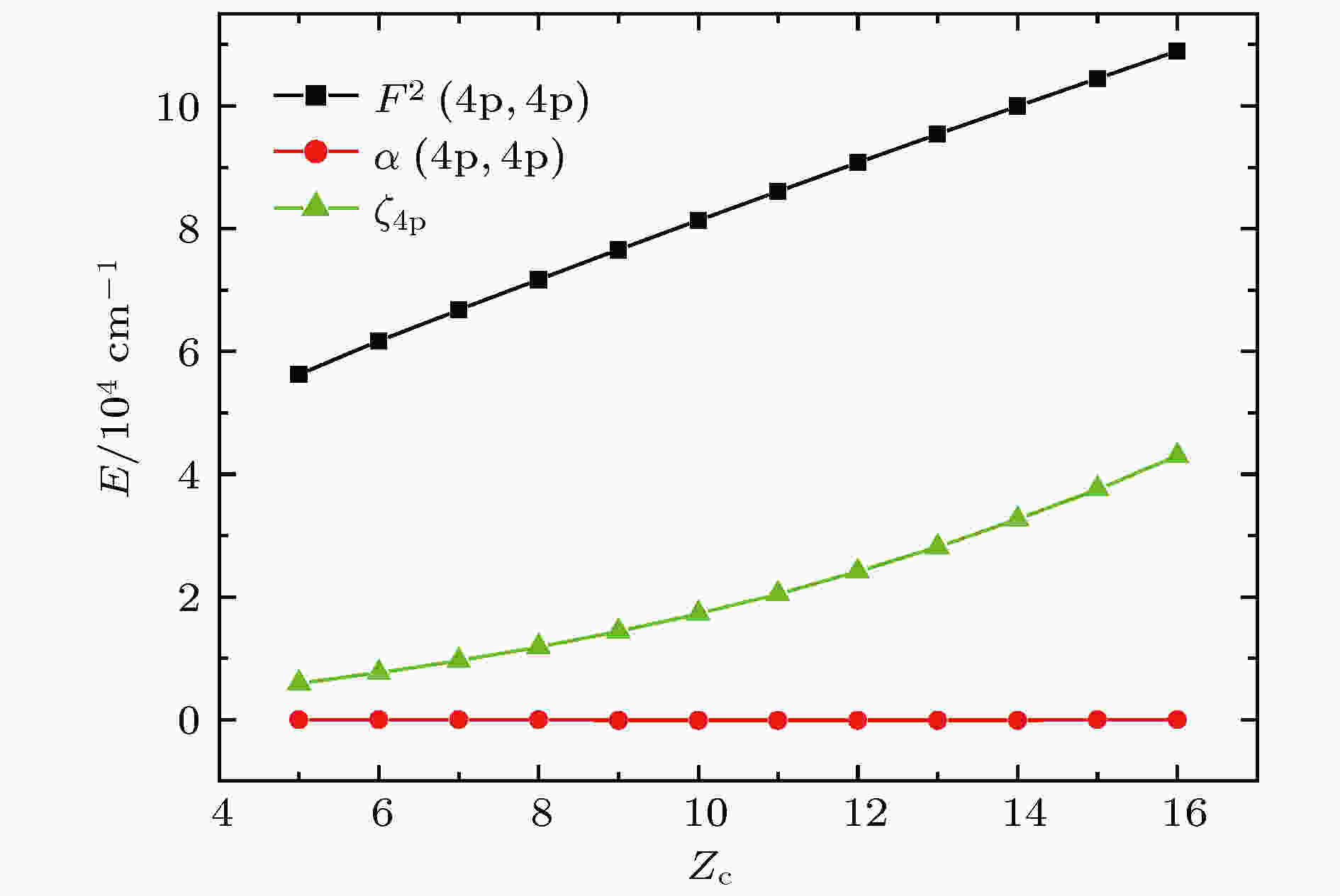图 2 4p3组态GLSF参数随Zc的变化
Figure2. Variations of 4p3 configuration GLSF parameters with Zc.

图3表示了在GLSF外推计算过程中各离子4s4p4组态能级结构参数中, 库仑相互作用直接积分F2(4p, 4p)、交换积分G1(4p, 5s)、自旋与轨道相互作用积分${\zeta _{4{\rm{p}}}}$、$\alpha $(4p, 4p)和组态相互作用积分G1(4p4p, 4s4p)随着Zc变化的情况. 从图3可以看出, 在4s4p4组态能级结构参数中, F2(4p, 4p)和G1(4p4p, 4s4p)的数值较为接近, 进一步表明了4s4p4 和4s24p24d组态之间存在较强相互作用效应. $\alpha $(4p, 4p)的值最小, 除$\alpha $(4p, 4p)外, 所有这些参数随Zc的增加其值逐渐增大. 从图3同样可以看到, 所有这些参数变化行为十分光滑.
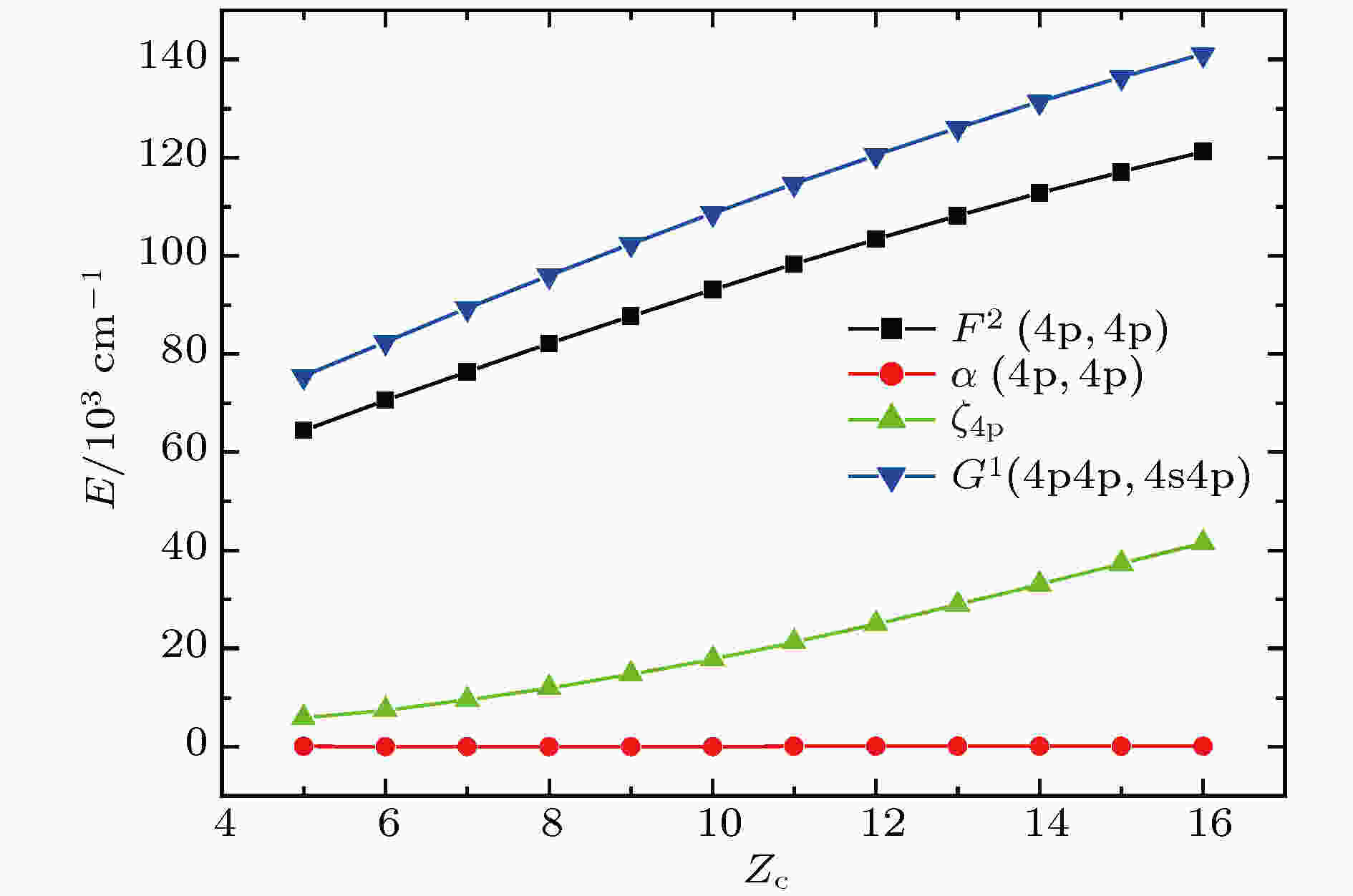图 3 4s4p4组态GLSF参数随Zc的变化
Figure3. Variations of 4s4p4 configuration parameters with Zc

表2列出了本文计算得到的Rh XIII, Pd XIV和Ag XV, Cd XVI离子4s24p3, 4s4p4和4s24p44d组态能级结构径向积分参数值(单位为1000 cm–1), 其中HFR, LSF和GLSF分别表示能级结构参数的HFR, LSF和GLSF计算值. 因为Ag XV和Cd XVI离子截至目前没有任何4s24p3和4s4p4组态能级实验值, 所以表2就没有列出LSF结果, 因而Ag XV和Cd XVI离子4s24p3和4s4p4组态能级结构参数值仅为本文GLSF外推计算结果, 所有离子能级与跃迁谱线波长均由这些参数计算得到. 这些参数可以为进一步研究这些离子结构提供重要的参考.
离子参数Rh XIIIPd XIVAg XVCd XVI
HFRLSFGLSFHFRLSFGLSFHFRGLSFHFRGLSF
Eav(4s24p3) 84293 49254 49278 93187 55055 54835 103082 61632 114034 67464
F2(4p, 4p) 135018 95436 95372 139395 99964 100188 143769 104494 148147 109733
$\alpha $(4p, 4p) 50 –65 –70 50 –67 –90 50 –61 50 –127
${\zeta _{4{\rm{p}}}}$ 52094 28120 28143 58686 32620 32403 65899 37541 73770 42137
Eav(4s4p4) 465733 373048 373412 494416 399046 401829 524621 428489 556932 460700
F2(4p, 4p) 134929 108077 108197 139305 112434 113134 143679 117141 148056 122299
$\alpha $(4p, 4p) 50 25 27 50 68 28 50 34 50 32
${\zeta _{4{\rm{p}}}}$ 52046 28688 28919 58636 43974 34588 65846 37300 73714 47415
G1(4s, 4p) 157248 125955 126094 162275 130973 131787 167303 136397 172339 142349
Eav(4s24p44d) 607730 512551 511233 639800 1064552 547714 673345 589678 708331 624580
F2(4p, 4p) 134980 113841 113545 139352 231866 119342 143723 125896 148098 130840
$\alpha $(4p, 4p) 50 –8170 –8516 50 –31872 –12109 50 –9682 50 –19122
${\zeta _{4{\rm{p}}}}$ 52183 26219 28282 58781 37685 32566 66000 44423 73875 44653
${\zeta _{4{\rm{d}}}}$ 6735 7573 6146 7648 361714 9397 8649 7711 9744 17964
F2(4p, 4d) 118694 100105 99845 122677 204120 105062 126654 110945 130628 115408
G1(4p, 4d) 146907 123899 123578 151575 252202 129812 156229 136856 160878 142141
G3(4p, 4d) 94580 79768 79561 97657 162489 83636 100724 88236 103787 91702
R(4p4p, 4s4d) 151283 121177 121309 156089 125980 126756 160886 131151 165684 136827


表2Rh XIII—Cd XVI离子4s24p3, 4s4p4和4s24p44d组态能级结构参数(单位: cm–1)
Table2.Energy parameters of configurations 4s24p3, 4s4p4 and 4s24p44d for ions from Rh XIII to Cd XVI.

表3 列出了Rh XIII, Pd XIV, Ag XV和Cd XVI离子4s24p3和4s4p4组态能级(单位为cm–1)和本征矢纯度(本征矢分量平方)的百分比构成情况, 本征矢纯度小于1%的分量没有列出. Eexp为文献[8]报道的实验值, 数据后面p表示该能级值为该文作者通过分析MCDF理论中的EAL模型计算的能级值与相应实验值之差(EDF – EOBS)随着Zc变化规律得到的预言值. ELSF, EGLSF和EMCDHF 分别为本文LSF, GLSF和MCDHF理论方法(VV7)的计算值, 圆括号“( )”内的数据为本文理论计算值与实验值之差, 圆括号后面有p表示该能级值为本文理论计算值与文献[8]的预言值之差. 对于Rh XIII和Pd XIV离子的4s24p3和4s4p4组态能级, 与已有实验值比较, 本文计算值与实验值之差一般不超过150 cm–1, 而Pd XIV离子4s24p3和4s4p4截止目前还没有足够的实验跃迁数据来建立完整的实验能级结构, 只有4s4p4(4P1/2, 3/2, 5/2)组态三个能级有实验数据, 本文LSF和GLSF计算的结果与这三个实验值十分一致. 基于MCDHF理论的全相对论grasp2K-DEV程序包是当前原子结构计算研究中重要的从头算程序之一, 为了给今后相关理论和实验研究提供更多一些的参考信息, 第六列为采用本文2.2节描述的MCDHF方法计算的结果, 圆括号里的数据为本文计算值与文献[8]的实验值或预言值之差, 显然, MCDHF计算结果(VV7)与实验值的绝对偏差普遍大于1000 cm–1. 例如, 对于Rh XIII离子4s4p4 2P3/2 能级, MCDHF理论值与实验值的绝对偏差最大为6161 cm–1, 最小的4s4p4 4P1/2能级绝对偏差也达到了771 cm–1. 从表3的本征矢纯度构成的百分比就可以看出, 偶宇称组态4s4p4和4s24p24d组态本征矢之间具有非常强的混合. 例如, 对Rh XIII, Pd XIV, Ag XV和Cd XVI离子, 在4s4p4 2P3/2能级本征纯度构成中, 4s24p24d 2P3/2能级本征纯度依次为28%, 27%, 26%和23%, 而在4s4p4 2P1/2的本征矢纯度构成中, 4s24p24d 2P1/2本征矢纯度均超过了20%. 这些情况表明, 在MCHF理论高精度的计算研究中, 对于类砷离子4s4p4组态而言, 4s24p24d对其组态能级结构的组态相互作用效应是不能被忽略的.
表4列出了本文GLSF能级结构参数计算得到的Rh XIII, Pd XIV, Ag XV和Cd XVI离子4s24p3—4s4p4组态能级电偶极跃迁谱线波长(单位: nm)和相应跃迁的加权振子强度(gf × 10，g为下能态的统计权重). 其中, $\lambda $和${\lambda _{\exp }}$分别表示本文计算值和文献[8]的实验结果, ${\varDelta _\lambda }$为实验值与理论值之差, 没有列出实验值的为截至目前还没有相关实验值的报道. Ag XV和Cd XVI离子4s24p3和4s4p4能级跃迁波长仅为本文预言值. 与已有实验值比较, 本文计算值与实验值的绝对偏差一般小于0.05 nm, 实验上发现的4s24p3 2D5/2—4s4p4 2P3/2跃迁的强线, 绝对偏差没有超过0.03 nm. 这些结果表明本文MCHF理论计算研究中, 对偶宇称组态考虑了4s24p24d对4s4p4组态能级的组态相互作用效应后的计算值是准确的. 与文献[8]的MCDHF理论计算研究得到的结果比较, 本文计算跃迁波长值更加准确. 例如, 对于Rh XIII和Pd XIV离子的4s24p3 4S3/2—4s24p4 4P5/2跃迁谱线, 文献[8]的MCDHF理论计算值分别为35.402 nm, 32.194 nm, 本文计算的相应值分别为35.197 nm, 32.749 nm, 可知前者与实验值的绝对偏差分别为0.216 nm和0.187 nm, 后者与实验值的绝对偏差分别为0.011 nm和0.017 nm; 对于Rh XIII和Pd XIV离子的4s24p3 2D5/2—4s24p4 2P3/2跃迁谱线, 文献[8]的计算值分别为27.841 nm, 26.062 nm, 本文计算的相应值分别为35.197 nm, 32.749 nm, 前者与实验值的绝对偏差分别为0.504 nm和0.464 nm, 而本文的绝对偏差分别为0.001 nm和0.026 nm. 此外, 从表4还可知, 对于Pd XIV离子4s24p3 4S3/2—4s24p4 4P1/2跃迁谱线, 文献[8]分析指出这是一条混合谱线(波长为24.499 nm), 本文计算结果为29.411 nm, ${\varDelta _\lambda }$为0.088 nm, 本文计算值与实验值的绝对偏差较大, 反映出本文计算结果与文献[8]的研究结果一致, 即4s24p4 4P1/2的实验能级还需要在实验上做进一步研究. 通过上面的分析可以看出, 与实验值比较本文计算值与实验值十分一致, 与文献[8]的MCDF理论结果比较, 本文计算结果更加准确.
离子跃迁$\lambda $/nm${\lambda _{\exp }}$/nm${\Delta _\lambda }$/nmgf × 10
Rh XIII
2P3/2—2D3/2 40.126 40.079b –0.047 0.01
4S3/2—4P5/2 35.197 35.186 –0.011 2.58
—4P3/2 32.386 32.394 0.008 2.42
2D5/2—2D5/2 32.205 32.197 –0.008 3.77
4S3/2—4P1/2 31.795 31.852 0.057 1.17
2D3/2—2D3/2 31.839 31.829 –0.01 3.74
2P1/2—2S1/2 30.918 1.87
2P3/2—2P1/2 29.526 29.56 0.034 3
4S3/2—2D3/2 28.576 0.27
2D5/2—2P3/2 28.346 28.345 –0.001 6.79
2D3/2—2S1/2 27.789 27.781 –0.008 2.08
—2P3/2 27.32 27.31 –0.01 0.59
—2P1/2 24.78 24.802 0.022 0.37
4S3/2—2P3/2 24.882 24.88 –0.002 0.34
—2P1/2 22.758 0.01
Pd XIV
2P3/2—2D3/2 38.008 0.01
4S3/2—4P5/2 32.749 32.732 –0.017 2.55
—4P3/2 29.92 29.964 0.044 2.59
2D5/2—2D5/2 29.993 29.974 –0.019 3.48
4S3/2—4P1/2 29.411 29.499b 0.088 1.2
2D3/2—2D3/2 29.766 3.6
2P1/2—2S1/2 28.908 1.84
2P3/2—2P1/2 27.534 2.54
4S3/2—2D3/2 26.603 0.23
2D5/2—2P3/2 26.499 26.525 0.026 6.36
2D3/2—2S1/2 25.973 2.02
—2P3/2 25.507 25.513 0.006 0.62
—2P1/2 17.106 0.82
4S3/2—2P3/2 23.148 0.37
—2P1/2 21.009 0.01
Ag XV
2P3/2—2D3/2 36.196 0.01
4S3/2—4P5/2 30.547 2.38
—4P3/2 27.863 2.73
2D5/2—2D5/2 28.102 3.96
4S3/2—4P1/2 27.398 1.27
2D3/2—2D3/2 27.911 3.94
2P1/2—2S1/2 27.168 1.94
2P3/2—2P1/2 26.739 0.01
4S3/2—2D3/2 24.781 0.36
2D5/2—2P3/2 25.027 6.14
2D3/2—2S1/2 24.412 2.27
—2P3/2 24.051 0.21
—2P1/2 21.93 0.07
4S3/2—2P3/2 21.69 0.19
—2P1/2 19.95 0.77
Cd XVI
2P3/2—2D3/2 34.603 0.01
4S3/2—4P5/2 28.537 2.26
—4P3/2 25.957 2.87
2D5/2—2D5/2 26.379 4.05
4S3/2—4P1/2 25.539 1.32
2D3/2—2D3/2 26.279 3.97
2P1/2—2S1/2 25.58 1.96
2P3/2—2P1/2 26.066 0.01
4S3/2—2D3/2 23.164 0.35
2D5/2—2P3/2 23.752 4.35
2D3/2—2S1/2 22.992 2.37
—2P3/2 22.797 0.01
—2P1/2 21.045 0.03
4S3/2—2P3/2 20.416 0.01
—2P1/2 18.999 1.54
注: ${\lambda _{\exp }}$表示实验值取自文献[8], b表示该谱线为混合谱线


表4Rh XIII—Cd XVI离子4s24p3—4s24p4跃迁波长和振子强度(gf × 10)
Table4.Wavelengths and oscillator strengths of transitions 4s24p3?4s24p4 for ions from Rh XIII to Cd XVI.

4.结　论
用HFR理论方法对Rb V—Cd XVI离子4s24p3和4s4p4组态能级做了全面系统的计算研究. 预言了Rh XIII, Pd XIV, Ag XV和Cd XVI离子4s24p3和4s4p4组态能级以及跃迁波长与振子强度. 本文的研究结果表明, 对于4s24p3组态, 在单组态近似条件下可以得到比较满意的能级结果, 而对于4s4p4组态, 在考虑了4s24p24d对其产生的组态相互作用效应才能获得更加准确的结果. 计算结果与已有实验值十分吻合, 表明本文预言结果是准确的. 与文献[8]的MCDF计算结果对比, 本文计算值更加准确. 本文还采用全相对论grasp2K-DEV程序包的VV模型计算了这四个离子的能级数据. 期望本文结果能对实验和理论进一步研究该序列离子结构提供必要的参考.
相关话题/计算 实验 结构 文献 电子
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 含磷酸胍基间作用的磷酸双乙酸胍晶体电子结构与光学性质研究
    摘要:基于磷酸胍基间作用在L-精氨酸磷酸盐晶体特异性与生物化学功能中的重要角色,已制备了含有磷酸胍基的新晶体磷酸双乙酸胍.本文采用第一性原理计算了磷酸双乙酸胍晶体的电子结构与三个晶向上的光学性质,探讨了其中基团间作用与光学性质的关联.结果表明,磷酸双乙酸胍晶体能隙为4.77eV,远小于磷酸二氢钾晶体 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 金属-光折变材料复合全息结构对表面等离激元的波前调控
    摘要:表面等离激元(surfaceplasmonpolaritons,SPPs)控制具有重要意义.表面电磁波全息法是在金属表面设计能有效控制SPP传输的凹槽阵列结构.本文提出一种新的SPP传输的控制方法,利用金属-光折变材料复合全息结构控制SPP传播.在金属表面覆盖一层光折变材料,两束SPP波在光折 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 同心椭圆柱-纳米管结构的双重Fano共振研究
    摘要:提出了一种同心椭圆柱-纳米管复合结构,该结构由金纳米管中内嵌椭圆形金柱构成,利用时域有限差分法分析了尺寸参数、周围环境及纳米管内核材料对该结构光学性质的影响.结果表明,调节椭圆柱芯的旋转角度可产生双重偶极-偶极Fano共振,其主要是由椭圆柱芯的纵向或横向偶极共振模式与纳米管的偶极成键和反成键模 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 激光刻蚀对镀金表面二次电子发射的有效抑制
    摘要:使用红外激光刻蚀技术在镀金铝合金表面制备了多种形貌的微孔及交错沟槽阵列.表征了两类激光刻蚀微阵列结构的三维形貌和二维精细形貌,分析了样品表面非理想二级粗糙结构的形成机制.研究了微阵列结构二次电子发射特性对表面形貌的依赖规律.实验结果表明:激光刻蚀得到的微阵列结构能够有效抑制镀金表面二次电子产额 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • B2-和B19'-NiTi表面原子弛豫、表面能、电子结构及性能的理论研究
    摘要:采用基于密度泛函理论的第一性原理系统研究了B2-和B19'-NiTi合金所有低指数表面的表面能、表面结构稳定性、表面电子结构等性质.计算结果表明两种NiTi合金所有低指数表面的原子弛豫主要集中在表面2—3个原子层,且以Ti原子为终止原子表面构型的原子振荡最为剧烈,Ni和Ti原子共同终止表面构型 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 三明治结构graphene-2Li-graphene的储氢性能
    摘要:本文使用密度泛函理论中的广义梯度近似对扩展三明治结构graphene-2Li-graphene的几何结构、电子性质和储氢性能进行计算研究.计算得知:位于单层石墨烯中六元环面心位上方的单个Li原子与基底之间的结合能最大(1.19eV),但小于固体Li的实验内聚能(1.63eV),然而,在双层石墨 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 光纤1/f 热噪声的实验研究
    摘要:光纤热噪声是限制光纤传感、测量系统性能的最终因素.但是低频区域呈1/f谱特性的光纤热噪声的形成机制迄今仍然存在争论.实验研究了光纤1/f热噪声水平与光纤内杂质离子浓度和光纤施加张力的关系,验证了这类热噪声来源于光纤内部的机械耗散引起的长度自发抖动,符合热机械噪声的理论假设.关键词:光纤光学/热 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 层状氧化钼的电子结构、磁和光学性质第一原理研究
    摘要:按照基于自旋密度泛函理论的赝势平面波第一原理计算方法,理论研究了两种层堆叠结构氧化钼(正交和单斜MoO3)的电子结构、磁性和光学特性,探讨其作为电致变色材料或电磁材料在光电子器件中的技术应用.采用先进的半局域GGA-PW91和非局域HSE06交换相关泛函精确计算晶体结构和带隙宽度.计算得出较低 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 空间电子辐照聚合物的充电特性和微观机理
    摘要:空间电子辐照聚合物的充电特性和微观机理是研究和防护航天器聚合物充放电特性的基础.采用蒙特卡罗方法模拟空间电子的散射过程,快二次电子模型模拟二次电子的产生,有限差分法求解电荷连续性方程、电流密度方程和泊松方程的电荷输运过程,俘获过程基于Poole-Frenkel效应来实现.基于电子散射/输运同步 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 实验优化设计Sr<sub>2</sub>MgSi<sub>2</sub>O<sub>7</sub>:Eu<sup>2
    摘要:为了得到最长有效余辉时间的Sr2MgSi2O7:Eu2+,Dy3+荧光粉,应用二次通用旋转组合设计对实验进行全程优化,建立了稀土离子掺杂浓度Eu2+,Dy3+和有效余辉时间的二元二次回归方程模型,应用遗传算法计算得到有效余辉时间的理论最大值.采用高温固相法合成了最优掺杂浓度Sr2MgSi2O7 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.