摘要:采用B3LYP/6-311++g(3df, 3pd)方法和基组对氟利昂物质CFC-11 (CFCl₃)分子进行了一系列的理论研究. 包括了该分子的基态结构、电偶极矩、总能量、最高占据分子轨道能级E_H和最低未占据分子轨道能级E_L、能隙、红外与拉曼光谱性质、C—F键解离, 并探讨电场对该分子的影响. 结果表明: 基态结构优化后的理论计算值和实验值的最大误差低于2%, C—F键受电场强度的增大而被拉长, 能隙E_g随E_H和E_L的变化出现先增大后减小; 电场影响着CFC-11分子的红外与拉曼光谱吸收强度, 红外与拉曼光谱随着电场变化出现红移或蓝移现象. 电场可作为一种辅助手段对其重叠或准重叠谱线进行分离. 势阱深度随反向电场逐渐增大而减小, 直至消失, 使得C—F键的束缚能力逐渐减弱. 本文有望为实现CFC-11分子最终发生解离而降解提供一种可行有效的调控手段.
关键词: 辐射场/
三氯一氟甲烷分子/
光谱性质/
降解

English Abstract

全文HTML

--> --> -->

三氯一氟甲烷(CFCl₃)是全氯氟烃(CFCs)中的一种, 俗称氟利昂-11 (CFC-11), 具有无腐蚀性、低沸点、高挥发性、比重大、热稳定性及化学稳定性强等特点. 作为生活中不可或缺的物质之一, CFC-11应用十分广泛, 如冰箱和空调制冷剂、泡沫塑料发泡剂、电子产品与精密零件仪器清洗剂、美容喷发剂、药剂等. CFC-11大部分(60%—70%)以气相形式存在于聚氨酯硬泡中, 其余的以液相形式溶入硬泡固相中^[1]. 据中国聚氨酯工业协会统计, 2011年我国聚氨酯行业产量增长约15%, 达到七百多万吨, 而聚氨酯硬泡约占聚氨酯泡沫体的一半.
值得注意的是, Molina和Rowland^[2]提出关于氟利昂破坏大气地球平流层内臭氧层的观点. CFC-11会破坏大气地球平流层内臭氧层, 是全球气候变暖的罪魁祸首之一. 地球上大气臭氧层能够吸收大多数来自太阳的有害辐射, 能有效保护地球生物, 对人类生存及家园至关重要. 自1985年正式发现臭氧破洞后^[3], 根据《蒙特利尔议定书修正案》规定, 在2000年前停止生产和使用氟利昂. 但有关CFC-11物质的控制和降解仍然是人们关注的焦点, 如Vollmer等^[4]报道了至今近80年来大气对流层中CFC-11分子的排放情况, Schuck等^[5]提出在Taunus天文台建立监测氯氟烃的长期方法, LeedhamElvidge等^[6]分析了包含CFC-11在内的氟利昂物质的测量, 并估算氯氟烃在大气中的生命周期. 对CFC-11的研究主要集中于大气环境污染监测^[4-8]、高温降解^[9-11]、激光解离动力学^[12]、介质阻挡放电^[13]等方面.
辐射场本质上是一种电磁波, 90%以上是电场对该分子的作用, 电场作用下会产生分子的高能激发态及次级电子、改变分子的电子结构、发生键的碎裂及新自由基生成等一系列的化学变化, 且关于分子外电场效应的研究得到了许多研究者的密切关注^[14-19]. 谢安东等^[14]计算了UO₃分子在自辐射场下的光谱性质, 结果显示分子能级对自辐射场有强依赖性, 尹文怡等^[15]对GaN在辐射场中的物理特性和光谱进行了计算研究, 结果表明电场可对其光谱进行调控. 李亚莎等^[16]研究绝缘材料盐交联聚乙烯分子(XLPE)在外电场下的特性, 得到临界击穿场强为11.16 GV/m, 电场可导致XLPE中C—C键断裂、载流子浓度升高、导电性能提升等现象, 从而降低了XLPE的绝缘性能. 基于此, 有必要对CFC-11分子在辐射场中的光谱与解离特性进行理论计算. 目前尚未见关于CFC-11分子在辐射场中的研究报道.
本文选用B3LYP/6-311++g(3df, 3pd)方法及基组, 对CFC-11分子进行优化来获取该分子的基态稳定构型, 再探索外加电场对CFC-11分子的轨道能级、能隙、偶极矩、红外与拉曼光谱的影响, 最后探究外电场中CFC-11的解离特性. 通过本研究可进一步认识在辐射场作用下CFC-11分子的光谱特征和解离特性, 为降解该污染物提供理论依据.

辐射场可分为电场和磁场, 起主要作用的电场占其94%. 在近似处理下, 辐射场中分子体系的总Hamilton量表示为^[14-19]

$H = {H_0} + {H_{{\mathop{\rm int}} }}, $

式中H₀为无场时的Hamilton量, H_int为电场与分子相互作用产生的附加Hamilton量. 在偶极近似下有

${H_{{\mathop{\rm int}} }} = - \mu \cdot F, $

其中$\mu $为分子电偶极矩, F为偶极电场.
本文选B3LYP/6-311++g(3df, 3pd)方法沿z轴方向加不同强度的静态偶极电场(其强度为–0.04, –0.03, –0.02, –0.01, 0.01, 0.02, 0.03, 0.04 a.u., 相当于–2.057—2.057 V/?)来考察该分子的红外与拉曼光谱特性, 在不同场强度下优化得到的CFC-11基态分子结构基础上, 计算场对C—F键解离的影响.

2

-->

3.1.CFC-11分子的基态结构

采用B3LYP/6-311++g(3df, 3pd)方法和基组对CFC-11分子结构进行优化计算, 分子结构如图1所示. 所有频率均为正值, 表明该分子结构是稳定的. 该分子属于C_3V点群, R(C—F)和R(C—Cl)键长分别为0.1338, 0.1775 nm, ∠ClCCl键角为110.57°, 文献[20]R(C—F)和R(C—Cl)键长分别为0.1362, 0.1754 nm, 相差0.0024, 0.0021 nm, 误差分别为1.7%, 1.19%; 键角∠ClCCl为111°, 相差0.43°, 误差仅为0.38%. 表明本文的计算与实验值吻合, 方法选取合理.
图 1 CFC-11分子的几何结构
Figure1. Equilibrium structure of CFC-11 molecule.

2 -->

3.2.辐射场中CFC-11分子的基本性质

沿主轴z方向(即C—F连线)外加电偶极化电场, 选用B3LYP/6-311++g(3df, 3pd)方法和基组探究电场对CFC-11分子结构及特性的影响, 计算结果列入表1中. 从表1和图2可知, 沿着z的正向加大电场时, Cl原子受电场作用向C原子方向移动, F原子则向C原子方向远离, C—F键长的变化比C—Cl键的变化更明显. 从图1可知, 外加电场正是C—F连线的z方向, C—F键受到电场作用力强于C—Cl键, 变化程度大于C—Cl键. 此外, C—F键随电场的增加逐渐增大, 表示化学键因电场强度的增加而变得脆弱. 如此, 电场增大可使化学键越容易发生解离.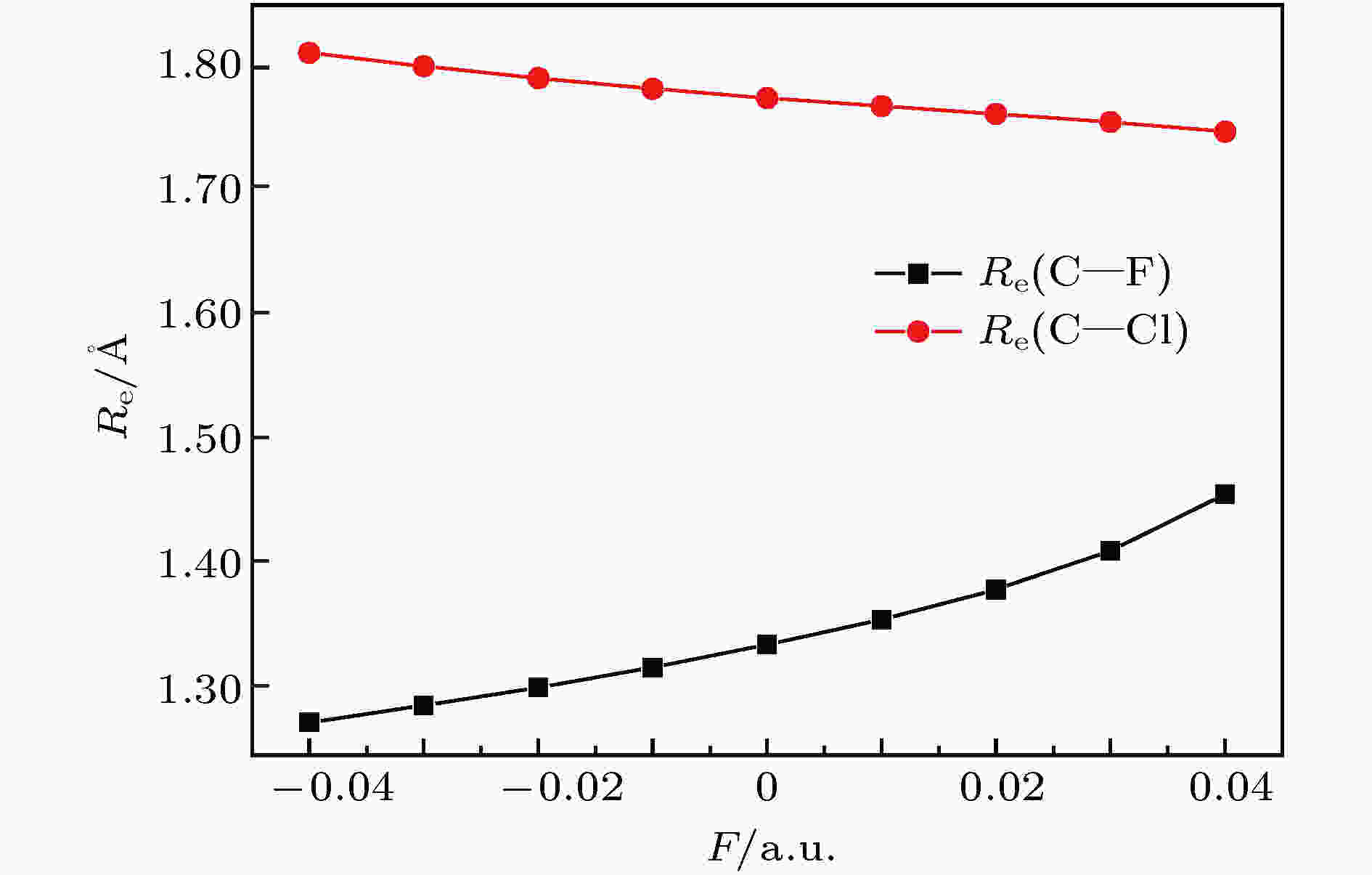
图 2 键长随电场的变化
Figure2. Bond length variation with external electric field.

F/a.u.	Re(C—F)/?	Re(C—Cl)/nm	E/hartree	$\mu$/Debye
–0.04	1.2764	1.8118	–1518.7025	5.0491
–0.03	1.2898	1.8010	–1518.6855	3.6168
–0.02	1.3043	1.7916	–1518.6740	2.2462
–0.01	1.3199	1.7830	–1518.6678	0.9145
0.00	1.3385	1.7757	–1518.6668	0.4044
0.01	1.3582	1.7692	–1518.6710	1.7191
0.02	1.3825	1.7628	–1518.6803	3.0657
0.03	1.4135	1.7563	–1518.6952	4.4805
0.04	1.4587	1.7486	–1518.7158	6.0486

表1不同电场下计算得到的CFC-11分子参数(1 hartree = 110.5 × 10^–21 J)
Table1.Calculated parameters of CFC-11 molecule under different external electric field.

表1还列出了不同电场强度下优化得到的CFC-11分子的电偶极矩$\mu$、总能量E. 如图3所示: 无电场时的分子偶极矩最小, $\mu= 0.4044$ Debye; 有电场时, 分子偶极矩随着强度的增加而增加. 这是因为受外界电场的影响, 分子内电场与外电场相互作用, 分子中所有电子排布发生定向偏移, 电负性相反的电荷分别沿着电场的正反方向移动, 分子被拉伸, 即分子在电场作用下产生极化, 极性增大. 根据偶极矩的定义, $\mu = R \cdot q$, R表示等效正负电荷之间的距离, q为等效正负电荷量. 随着电场强度增加, 等效R, q增加导致偶极矩$\mu$增加, 分子极性增加. 由图4可知, 分子的总能量随外电场的增加先增大后减小. 体系的势能在数值上正比于电荷电量的平方, 反比于等效键长, 即$U = - (k{q^2})/r$. 如外电场从0 a.u.增加到0.04 a.u.时, 电子的定向移动随强度的增大越明显, 导致其分子内库仑力的吸引力增大, 此外分子偶极矩也增大, 因此根据势能公式可知哈密顿量H中的势能绝对值增加, 分子体系的总能量随之逐渐减小. 反之, 电场强度、偶极矩在数值上均增大, 势能在数值上增大, 致使分子体系总能量随之降低.
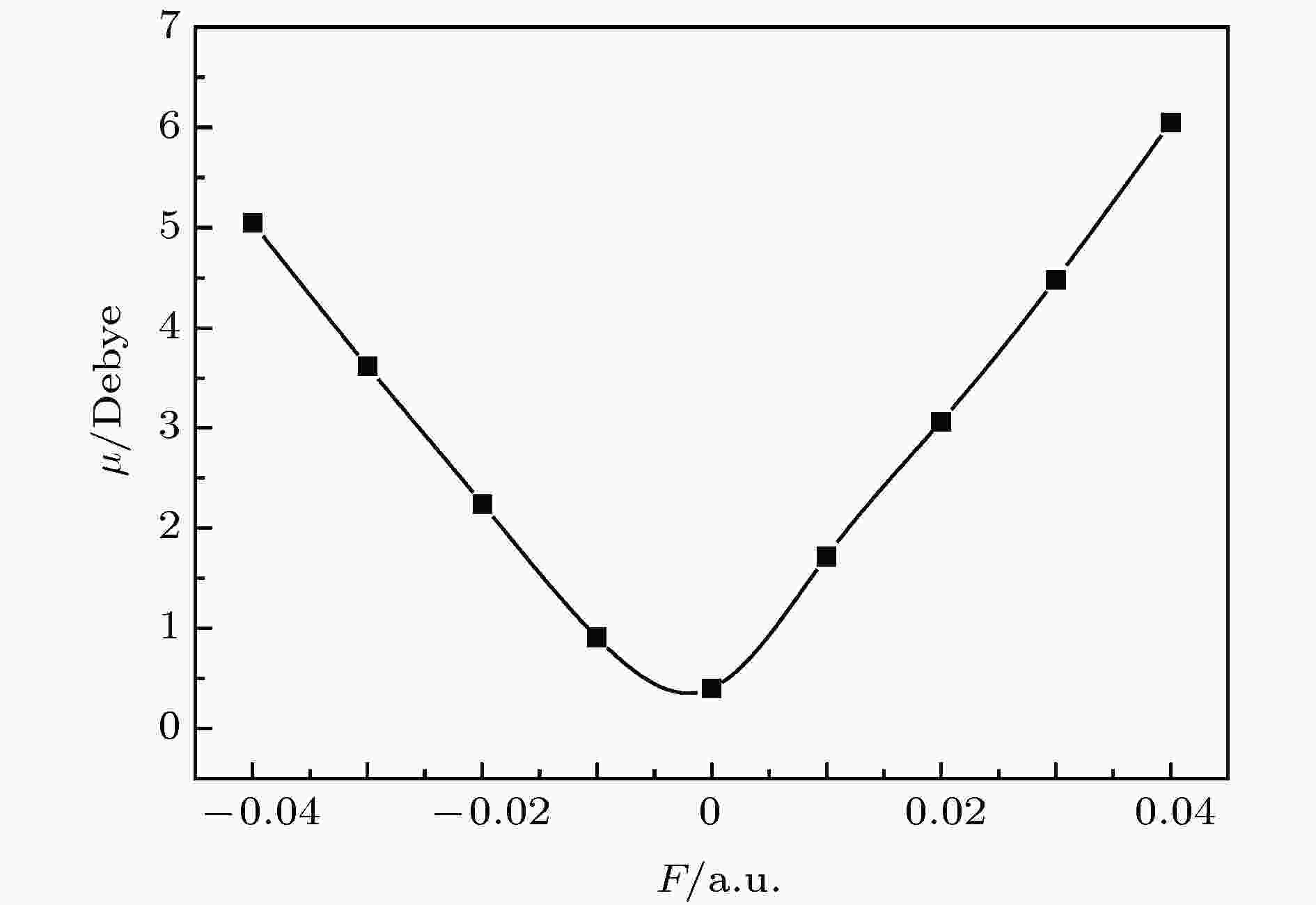图 3 偶极矩随电场的变化
Figure3. Dipole moment variation with external electric field.

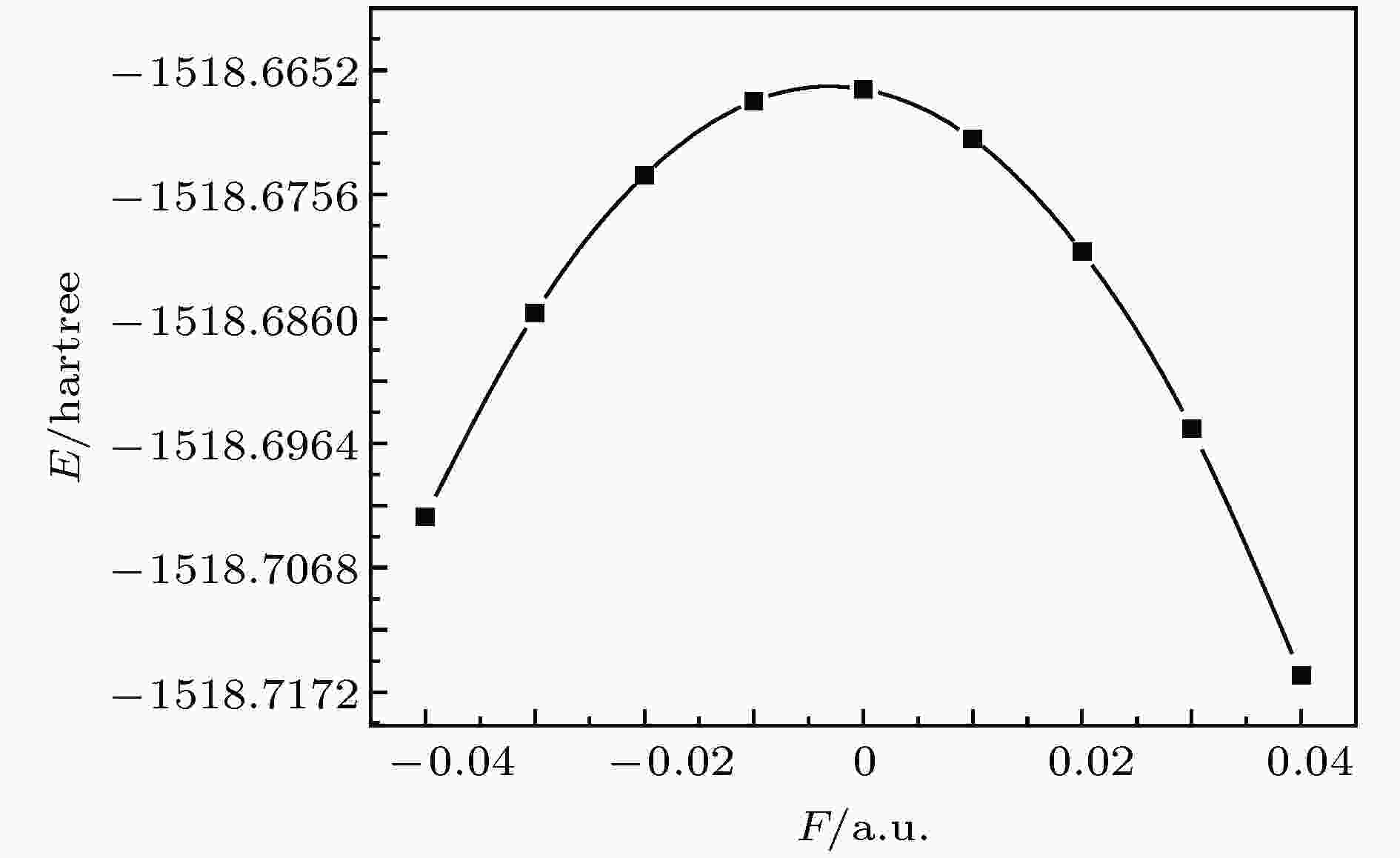图 4 总能量随电场变化
Figure4. Total energy variation with external electric field.

2 -->

3.3.辐射场中CFC-11分子的轨道能级分布特征

前线轨道理论认为^[17,18]分子参与化学反应, 优先起作用的是最低未占据分子轨道(LUMO)和最高占据分子轨道(HOMO), 其中LUMO能级E_L在数值上相当于分子的电子亲和势, 能级越低意味着分子接受电子的能力越强. HOMO能级E_H反映了分子失去电子能力的强弱, HOMO能级越高意味着分子就越容易失去电子. 能隙E_g代表电子从占据轨道向未占据轨道发生跃迁的能力, E_g = E_L – E_H, 在一定程度上代表分子参与化学反应的能力^[17,18], 化学活性随能隙减小而增大, 化学活性越大, 则分子越不稳定.
本文选用上述同样的方法和基组, 计算了电场中CFC-11分子轨道能级, 如图5所示, 分子的最高占据轨道能级升高, 最低未占据轨道能级则是先增大, 到F = 0.02 a.u.后开始降低. 图6显示, 随着电场的变化, 能隙随E_H和E_L的变化出现先增大后减小. 当电场强度大于0.02 a.u.时, 其能隙急剧下降, 电场处于0 a.u.至–0.04 a.u.时, 能隙随电场数值的增大而减小, 占据轨道上的电子越容易被激发. 正向与反向电场强度增加, 对能隙的影响略有差异. 总之, 电场的增强加剧了分子不稳定性, 如C—F键发生断裂等现象. 此外, E_g的大小与紫外光谱有直接关联, E_g的减小可观察到紫外光谱的吸收向长波方向移动, 即产生红移.
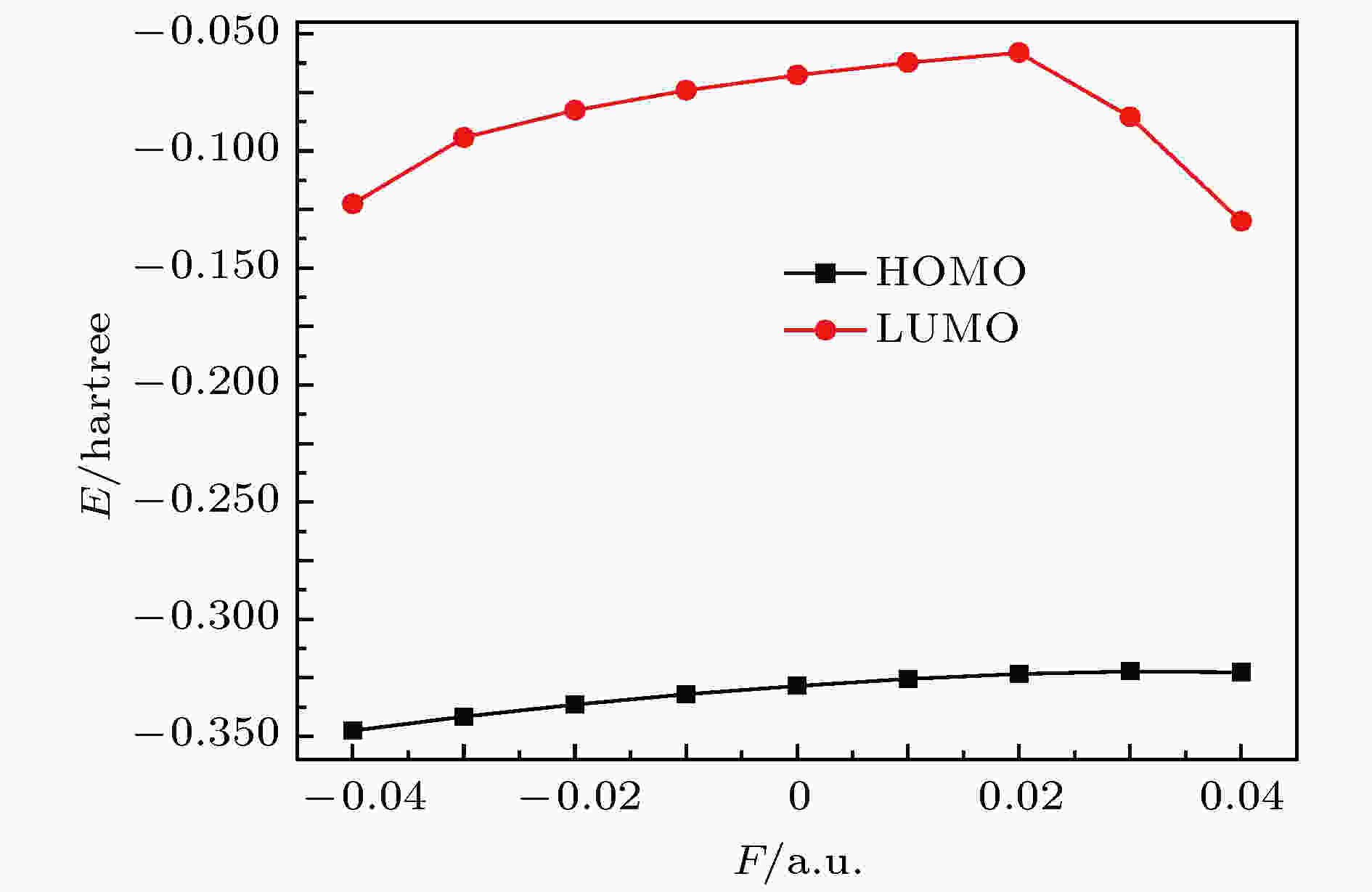图 5 HOMO和LUMO能级随电场变化
Figure5. The HOMO and LUMO energy level variation with external electric field.

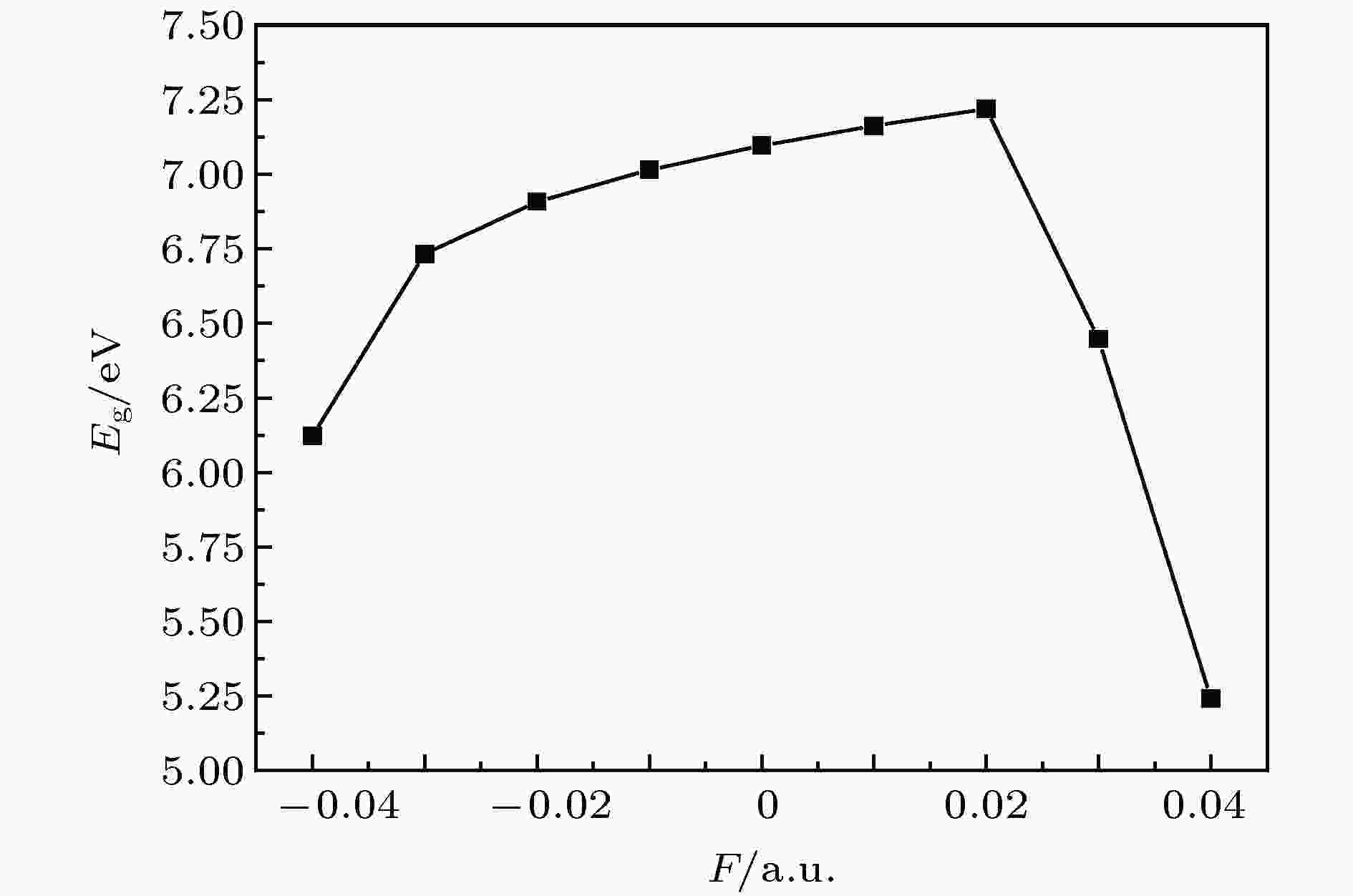图 6 能隙随电场变化
Figure6. Energy gap variation with external electric field.

2 -->

3.4.辐射场中CFC-11分子的红外与拉曼光谱特性

采取B3LYP/6-311++ g(3df, 3pd)方法和基组对CFC-11分子红外与拉曼光谱进行了计算. 无电场时(表2), 该分子的红外谱共有六种简正模. 如最强峰847 cm^–1 C—Cl₃的d-deform振动, 本文得到的二度简并值为802.3721, 802.4017 cm^–1. 在次强峰位置于1085 cm^–1 C—F的stretch振动, 本文计算值为1071.2887 cm^–1等. 与实验对比可见, 计算得到的红外光谱值与实验值相吻合, 也进一步展示了所选方法的合理性.

Frequency	本文	实验值[21]	实验值[22]	实验值[23]
f1/cm–1	1071.2887	1085	1085	1085
f2/cm–1	526.5703	535	—	535
f3/cm–1	347.5578	350	—	351
f4/cm–1	802.3721, 802.4017	847	846	847
f5/cm–1	394.9112, 394.9163	394	—	395
f6/cm–1	242.9898, 242.9928	241	—	243

表2无电场时CFC-11分子的红外谱实验值与计算值
Table2.Experiment data and calculated data of infrared spectrum for CFC-11 molecule without external electric field.

红外光谱随电场的变化如图7所示. 电场对红外谱的影响较为明显, 如: 当电场从0 a.u.增大到0.04 a.u., 最强峰C—Cl₃振动光谱随着电场增大向长波方向移动, 出现红移; 电场从0 a.u.减小到–0.04 a.u., 红外光谱则向短波方向移动, 出现蓝移. 而次强峰位置于C—F的振动则与之相反.
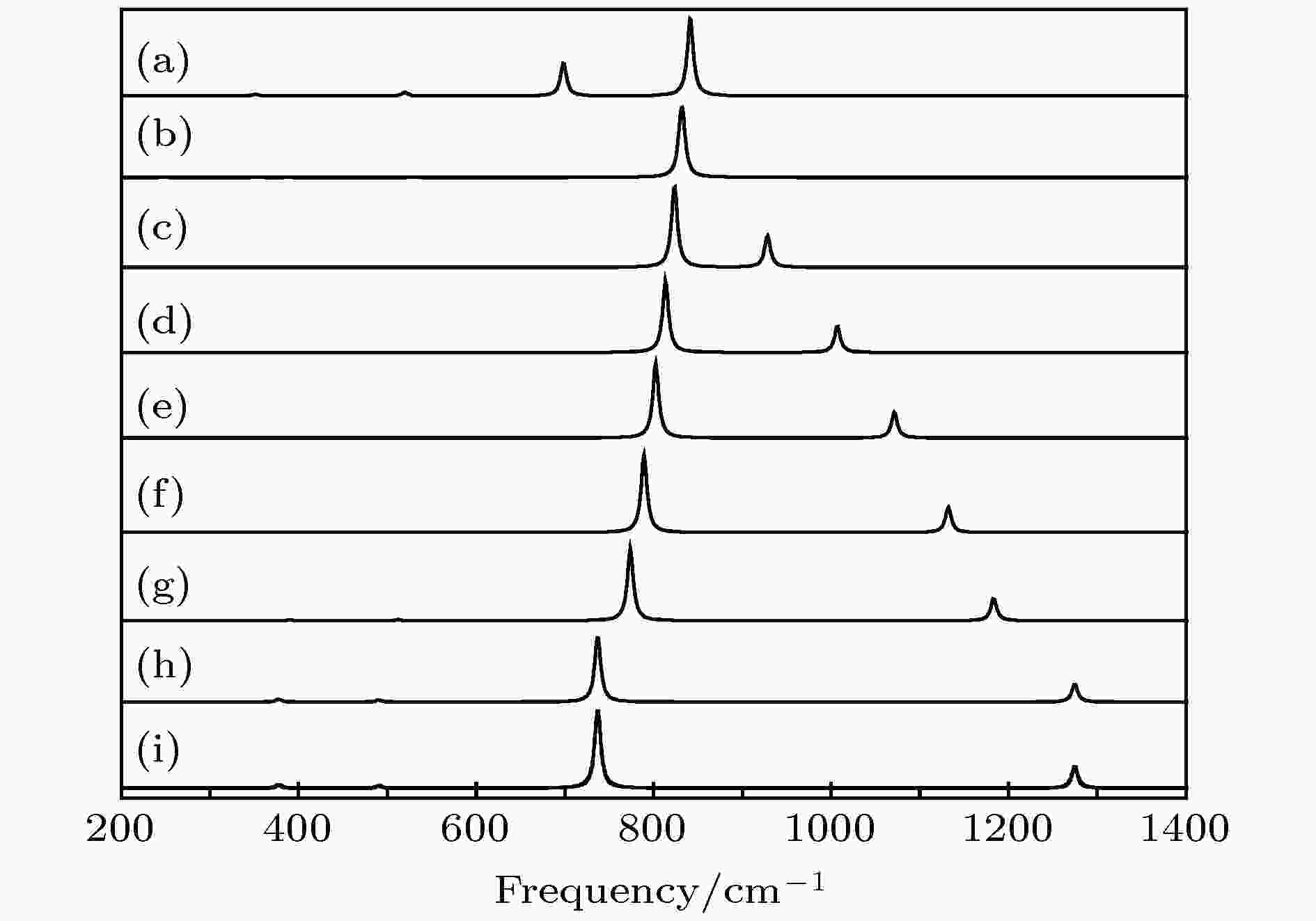图 7 红外光谱随电场强度的变化　(a) –0.04 a.u.; (b) –0.03 a.u.; (c) –0.02 a.u.; (d) –0.01 a.u.; (e) a.u.; (f) 0.01 a.u.; (g) 0.02 a.u.; (h) 0.03 a.u.; (i) 0.04 a.u.
Figure7. Variation of the infrared intensities with external electric field: (a) –0.04 a.u.; (b) –0.03 a.u.; (c) –0.02 a.u.; (d) –0.01 a.u.; (e) 0 a.u.; (f) 0.01 a.u.; (h) 0.02 a.u.; (g) 0.03 a.u.; (i) 0.04 a.u..

为了更清楚地看到电场对红外谱的影响, 图8是从图7中选取一条谱线的放大图, 其谱线位于242.99 cm^–1 (见表2), 图8(a)是电场强度分别为0, –0.01, –0.02, –0.03, –0.04 a.u.的谱线特征, 图8(b)是电场强度分别为0, 0.01, 0.02, 0.03, 0.04 a.u.的谱线特征. 电场对红外光谱强度吸收是复杂的. 从图8(a)可知, 首先是CFC-11分子的红外谱强度发生改变, 无电场时的吸收强度不为零, 电场强度为–0.01和–0.02 a.u.的红外谱几乎消失, –0.03 a.u.的谱强度与0 a.u.时相近, 在0.04 a.u.强度增加非常明显. 其次, 谱线的位置受电场的影响, 谱线蓝移非常微弱. 由图8(b)可知, 电场对谱线吸收强度逐渐递增, 谱线的位置随电场强度增加出现红移. 图9同样也选取了图7中另一条位于802.4 cm^–1的谱线, 图9(a)是电场强度分别为0, –0.01, –0.02, –0.03, –0.04 a.u.的谱线特征, 图9(b)是电场强度分别为0, 0.01, 0.02, 0.03, 0.04 a.u.的谱线特征. 对比图9(a)和图9(b)可知, 电场只是对谱线的位置进行了改变, 对其红外谱吸收强度的影响微弱. 综合图8(a)、图8(b)、图9(a)、图9(b)可得, 电场对不同谱线吸收谱强度的影响不同, 但对谱线位置出现红移或者蓝移的方向却是一致的.
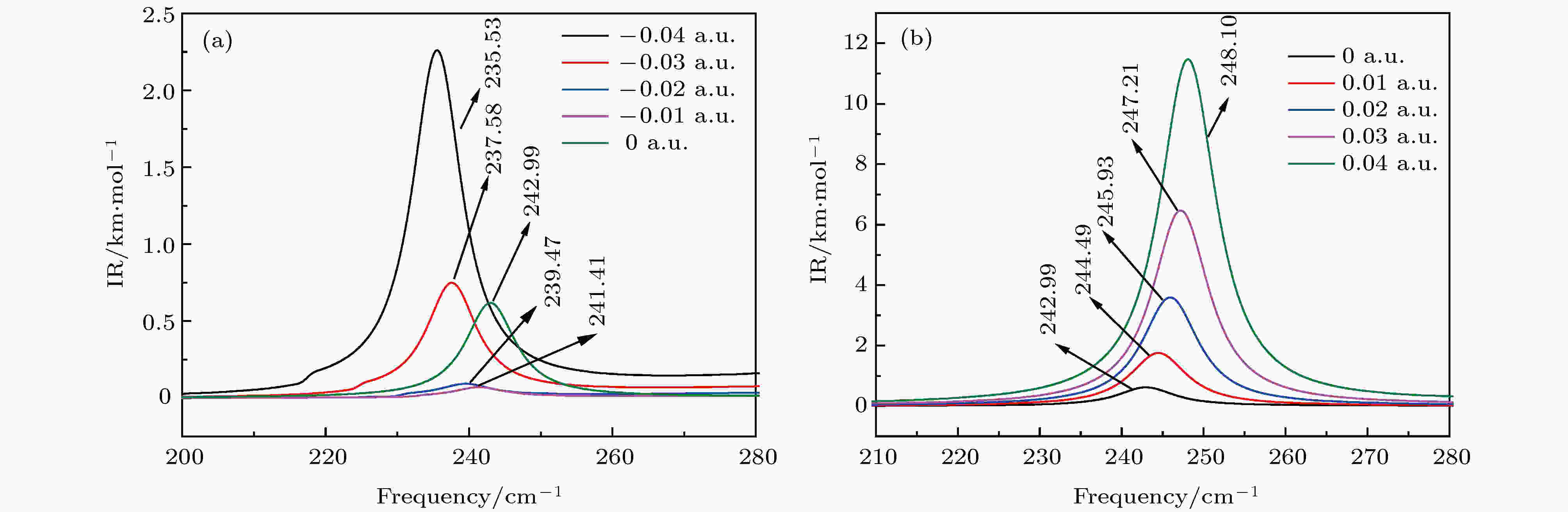图 8 红外谱线242.99 cm^–1随电场的变化　(a)反向电场; (b)正向电场
Figure8. Variation of infrared spectrum of 242.99 cm^–1 with external electric field: (a) Negative electric field; (b) positive electric field.

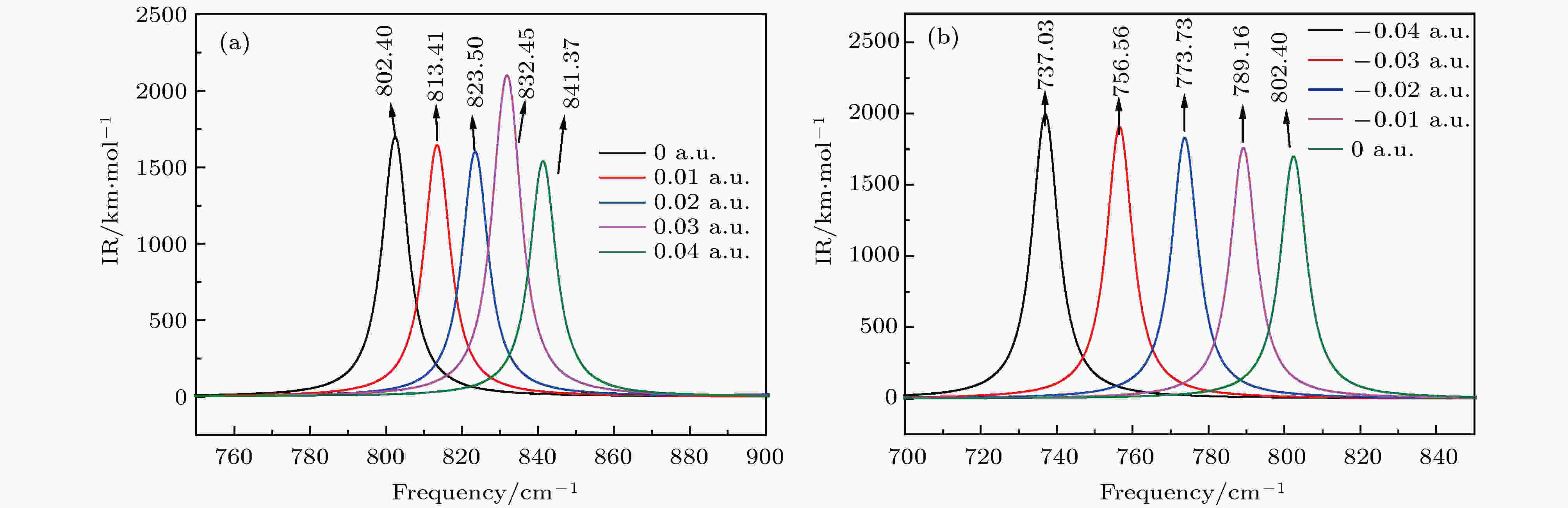图 9 红外谱线802.40 cm^–1随电场的变化　(a)反向电场; (b)正向电场
Figure9. Variation of infrared spectrum of 802.40 cm^–1 with external electric field: (a) Negative electric field; (b) positive electric field.

此外, 鉴于电场作用下谱线的移动以及对红外谱强度的影响, 在多种分子或多种基团混合中, 当谱线重叠或紧挨着而很难区分各基团或各分子谱带来的信息时, 电场可作为一种辅助手段对其谱线分离, 从而实现获取各种分子信息.
不同电场强度下的拉曼光谱绘制于图10中, 共6条拉曼光谱谱线, 可见电场可以改变拉曼光谱谱峰的位置和强度. 同上述红外光谱一样, 分别选取图10中的局部谱线, 即394.42和802.40 cm^–1拉曼光谱谱线, 并且绘制于图11(a)、图11(b), 及图12(a)、图12(b)中, 其中图11(a)和图12(a)是拉曼光谱随反向电场的变化, 图11(b)和图12(b)则是随正向电场的变化.
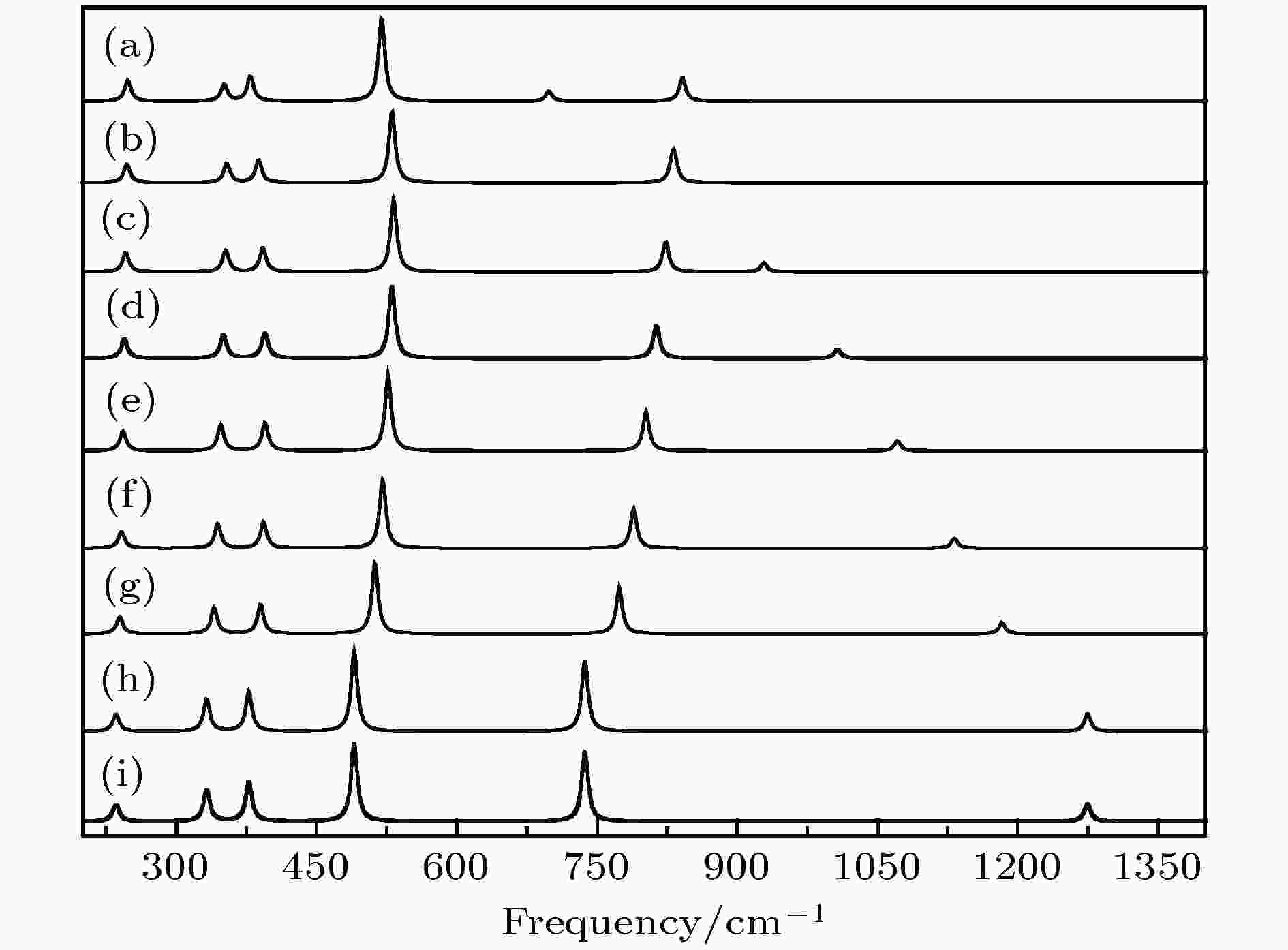图 10 拉曼光谱随电场强度的变化　(a) –0.04 a.u.; (b) –0.03 a.u.; (c) –0.02 a.u.; (d) –0.01 a.u.; (e) 0 a.u.; (f) 0.01 a.u.; (g) 0.02 a.u.; (h) 0.03 a.u.; (i) 0.04 a.u.
Figure10. Variation of Raman spectrum with external electric field: (a) –0.04 a.u.; (b) –0.03 a.u.; (c) –0.02 a.u.; (d) –0.01 a.u.; (e) 0 a.u.; (f) 0.01 a.u.; (h) 0.02 a.u.; (g) 0.03 a.u.; (i) 0.04 a.u..

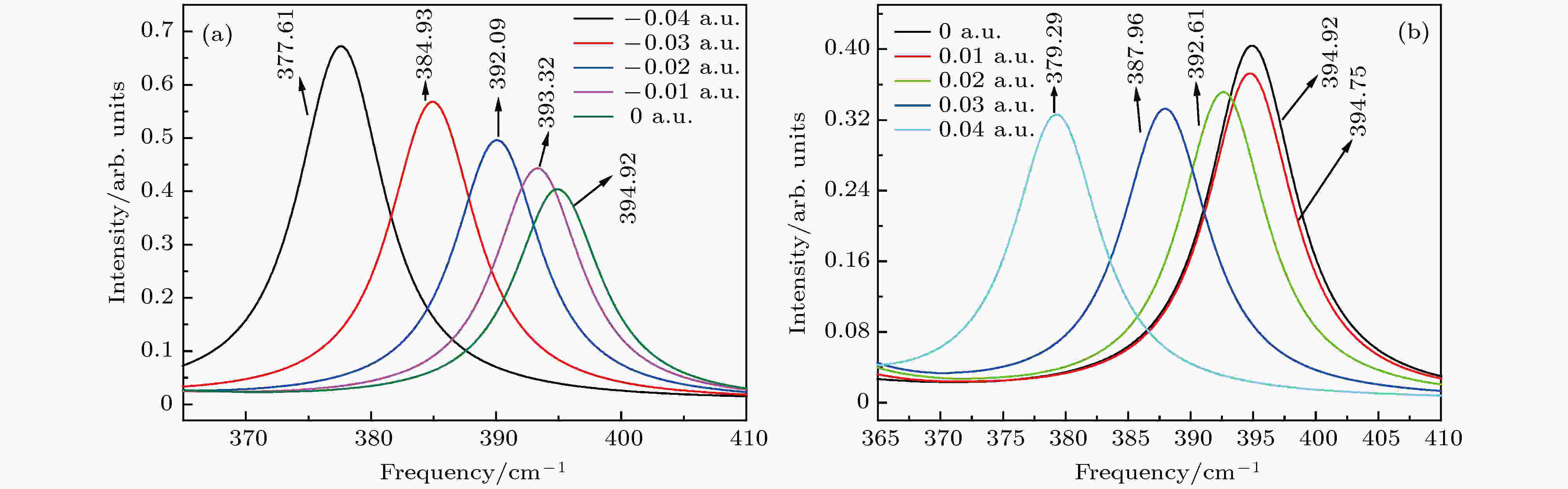图 11 拉曼谱394.42 cm^–1随电场的变化　(a)反向电场; (b)正向电场
Figure11. Variation of Raman spectrum of 394.42 cm^–1 with external electric field: (a) Negative electric field; (b) positive electric field.

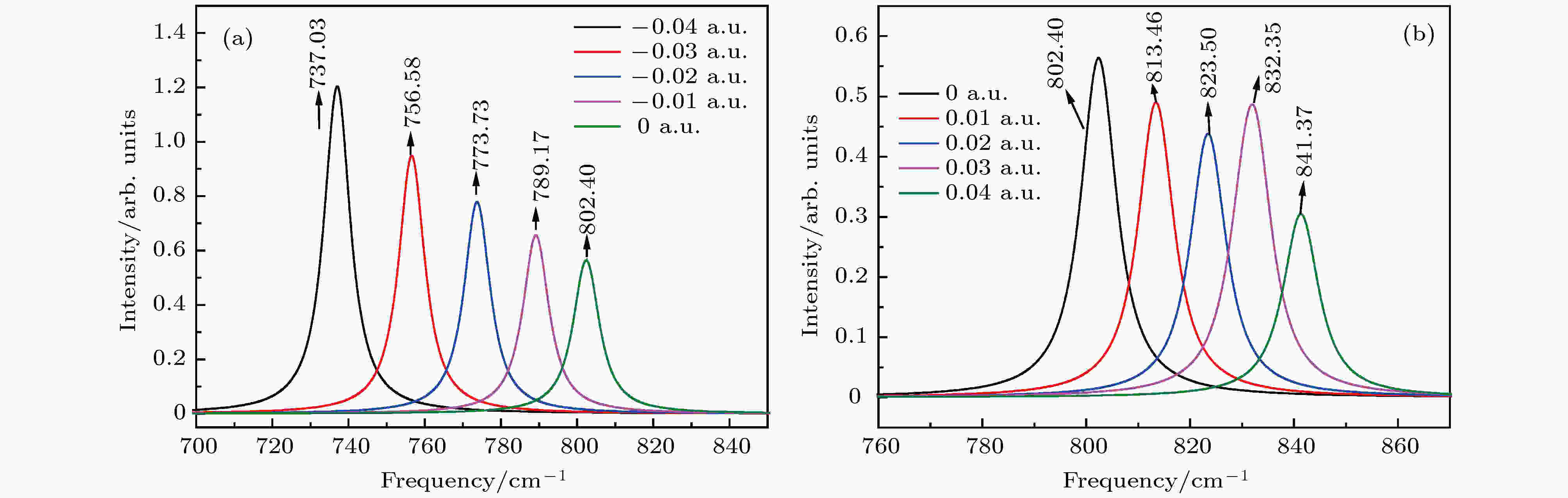图 12 拉曼谱802.40 cm^–1随电场的变化　(a)反向电场; (b)正向电场
Figure12. Variation of Raman spectrum of 802.40 cm^–1 with external electric field: (a) Negative electric field; (b) positive electric field.

综合图11(a)、图11(b)、图12(a)和图12(b)可看出, 正向电场作用下的拉曼光谱向长波方向移动, 反向电场作用下拉曼光谱则向短波方向移动, 这与红外光谱随电场的变化一致. 拉曼光谱线394.42 cm^–1强度在反向电场区随着电场的增大而增大, 在正向电场区随电场强度的增大而减小; 在802.40 cm^–1拉曼光谱谱线中, 随着反向电场强度的增加拉曼光谱强度增加, 随着正向电场的增加, 拉曼光谱强度则有高有低.
综上, 外加电场可以对分子或基团红外谱和拉曼谱进行调控, 也可用于分子或基团谱线分离, 实现对分子或基团谱线信息的捕捉.
2 -->

3.5.辐射场中分子C—F的解离特性

本文还计算了不同电场强度下CFC-11分子中的C—F键势能曲线. 依然选用B3LYP/6-311++ g(3df, 3pd)方法, 如图1, 沿着z方向分别加正向电场至0.04 a.u., 反向电场至–0.04 a.u., C—F键扫描范围从0.8 ?到5.8 ?, 步长设置为0.05 ?, 共101个数据点. 将扫描的势能点分别绘制于图13和图14中. 由图13(a)和图14可知, 处于势阱最低位置时, 无电场时的势阱值要高于有电场时的值. 这与图4结果一致. 从图13可以看出C—F键值大于1.7 ?时, 有电场时的势能曲线高于无电场时的曲线, 且势垒一直存在, 从图13(b)可看到电场为0.04 a.u. 的势能曲线与无电场时出现二次相交, 势能曲线整体上将出现一个稳定点的极小值和非稳定点极大值, 类似于“火山态”^[19], 这表明在极小值与极大值之间的能垒随电场增大逐渐减小, 继续增大电场强度, 解离会逐渐变得容易. 图14中C—F键的势能曲线随电场强度增大, 能垒逐渐减小, C—F键的束缚能力逐渐减弱, 当电场增加到一定程度时, 能垒消失, 分子发生解离.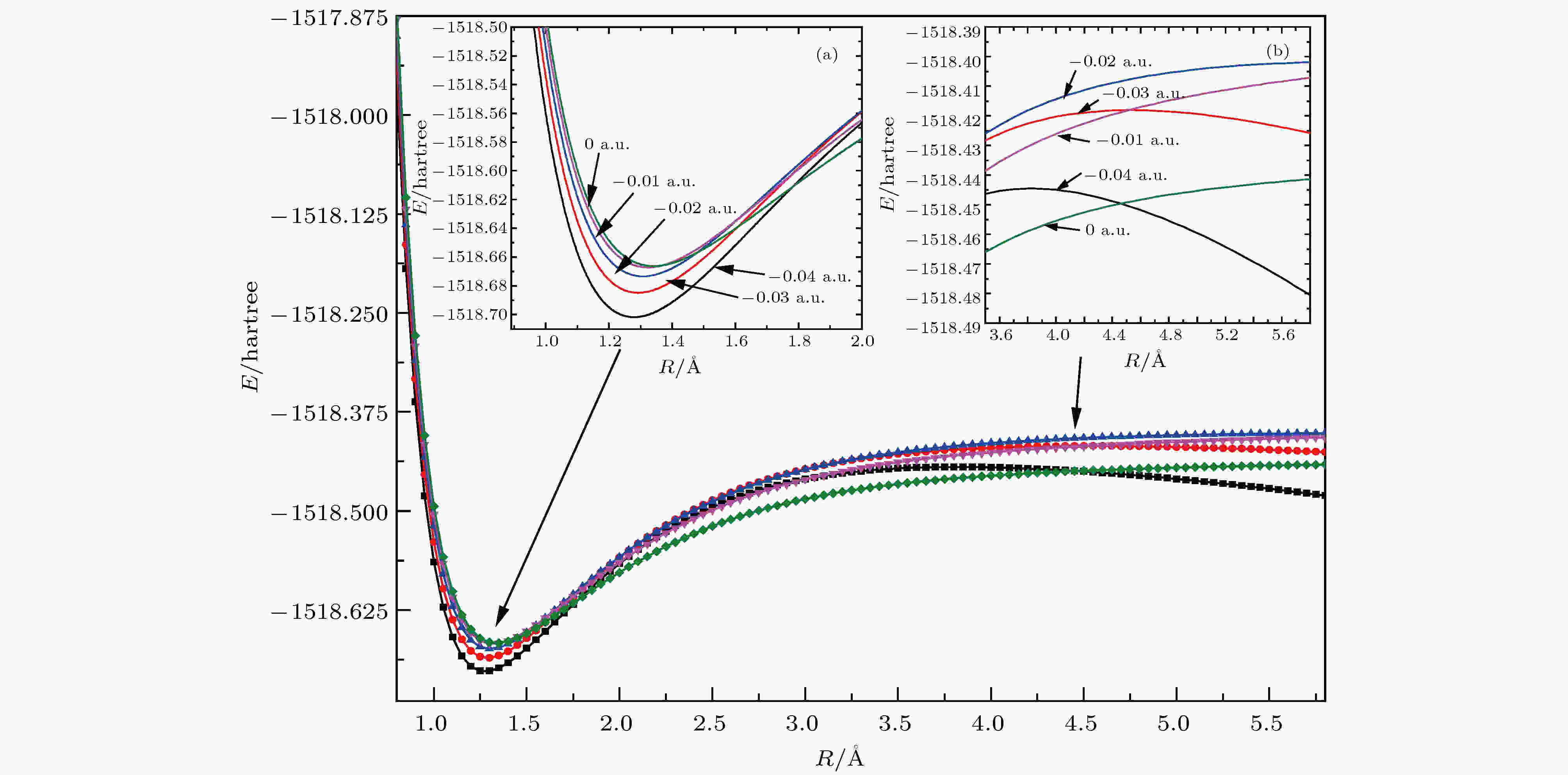
图 13 反向电场下C—F键势能曲线
Figure13. Potential energy curve variation with negative electric field.

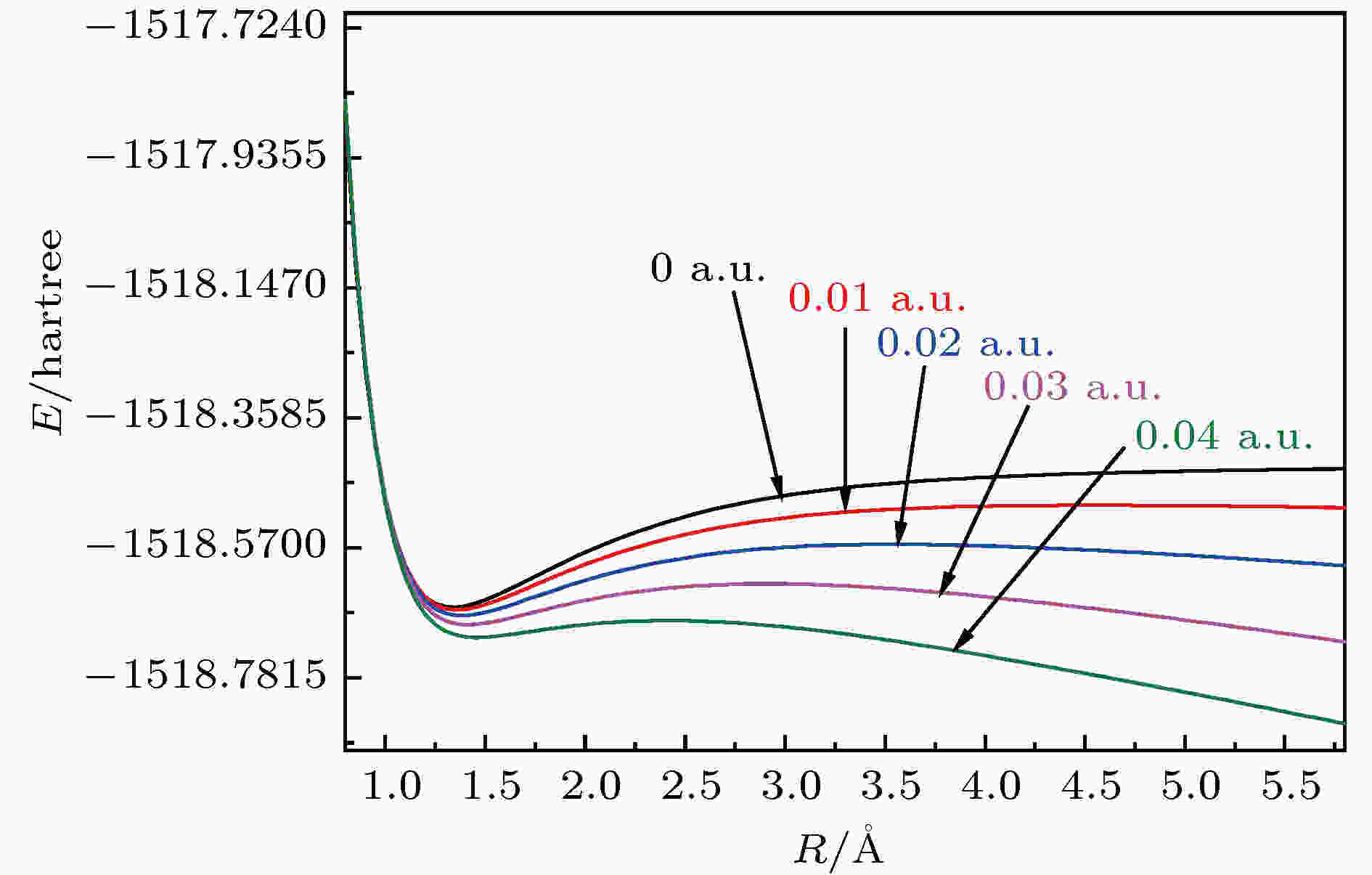图 14 正向电场下C—F键势能曲线
Figure14. Potential energy curve variation with positive electric field.

图13和图14中C—F键在电场中的势能曲线差异明显, 这是因为电场中C—F键长的变化比C—Cl键的变化要明显. 正向电场下, F原子远离C原子, F原子周围的电子云与其他原子干涉越来越小, 能垒逐渐减弱, 解离越来越容易. 在反向电场中, F原子向C原子靠拢, 加大了C原子与其他原子的电子相互作用, 但由于电场的存在, 导致C—F键暂时更加“紧密”, 能垒增强, 即出现高于无电场时的能垒. 当C—F键逐渐增大, 这种“紧密”被打破, 势能曲线二次相交现象即出现.
综上, CFC-11分子中的C—F键在电场作用下将会发生断裂, 从而使得该分子发生降解, 该结果为降解该污染物提供了一种理论依据.

本文采用B3LYP/6-311++ g(3df, 3pd)方法计算了电场对CFC-11分子的基态结构、红外与拉曼光谱、C—F键解离的特征. 结果表明: 无电场时优化的结构与实验值一致, 计算频率与实验值吻合, 选择方法合理; C—F受电场强度的增大越容易发生解离; 能隙E_g随E_H和E_L的变化出现先增大后减小.
本文无电场时计算的红外谱与实验值相吻合. 电场对红外谱产生分子振动斯塔克效应, 红外与拉曼光谱随着电场变化出现红移或蓝移现象, 同时影响红外与拉曼光谱吸收强度. 电场可作为一种辅助手段对其谱线分离而获取各种分子信息.
不同强度下对CFC-11分子中的C—F键进行势能面扫描, 能垒逐渐反向电场增大而减小, C—F键的束缚能力逐渐减弱, 当电场增加到一定程度时, 能垒消失, 分子发生解离. 本文有望为实现CFC-11分子最终发生解离而降解提供一种可行有效的调控手段.