摘要: BeC是一个具有丰富低激发电子态的分子, 本文基于动态权重完全活性空间自冾场方法获得的参考波函数, 采用多参考组态相互作用方法对BeC分子进行高精度的从头计算, 获得了BeC分子
$ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ ,
${\rm{A}}^3 {\text{Π}}$ ,
$ {{\rm{b}}^1} {{\text{Δ}} } $ ,
${{\rm{c}}^1} {\text{Π}}$ 和
$ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ 共5个电子态的势能曲线. 为了获得精确的光谱结果, 在计算中考虑了标量相对论效应修正, 并把相互作用能外推至完全基组极限. 在此基础上获得了这些态的光谱常数和偶极距, 以及一些允许跃迁的跃迁偶极距、弗兰克-康登因子和辐射寿命. 最后, 通过扩展的Rydberg函数拟合获得了基态势能曲线精确的解析表达式.
关键词: 动态权重 /
光谱常数 /
跃迁特性 /
BeC English Abstract Spectroscopic properties and analytical potential energy function of ground and low-lying excited states of BeC moleule Zhang Ji-Cai Sun Jin-Feng Shi De-Heng Zhu Zun-Lue College of Physics and Materials Science, Henan Normal University, Xinxiang 453007, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 61275132, 11274097).Received Date: 11 September 2018Accepted Date: 19 December 2018Available Online: 01 March 2019Published Online: 05 March 2019Abstract: Diatomic molecule BeC has a complex electronic structure with a large number of low-lying excited states that are all strongly bound electronic states. Thus, the BeC molecule has the abundant spectral information. In this work, the potential energy curves and wavefunctions of $ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ , ${\rm{A}}^3 {\text{Π}}$ , $ {{\rm{b}}^1} {{\text{Δ}} } $ , ${{\rm{c}}^1} {\text{Π}}$ and $ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ states of the BeC molecule are calculated by using the internally contracted multi-reference configuration interaction (MRCI) approach, which is based on the use of a dynamically weighted complete active space self-consistent field (DW-CASSCF) procedure. To improve the reliability and accuracy of calculation, the scalar relativistic corrections and the extrapolation of potential energy to the complete basis set limit are taken into account. On the basis of the calculated potential energy curves and wavefunctions, the spectroscopic constants (T e , R e , ${\omega _{\rm{e}}}$ , ${\omega _{\rm{e}}}{x_{\rm{e}}}$ , ${\omega _{\rm{e}}}{y_{\rm{e}}}$ , B e , ${\alpha _{\rm{e}}}$ , and D e ) and permanent dipole moments of those states are determined, the results of which are in good agreement with the existing available experimental and theoretical values. The obtained permanent dipole moments indicate that the electrons transfer from Be to C and the polarity for molecule is $ {\rm{B}}{{\rm{e}}^{{\text{δ}} + }}{{\rm{C}}^{{\text{δ}} - }}$ . The transition properties of the spin-allowed ${\rm{A}}^3 {\text{Π}}$ ?$ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ , ${{\rm{c}}^1} {\text{Π}}$ ?$ {{\rm{b}}^1} {{\text{Δ}} } $ , ${{\rm{c}}^1} {\text{Π}}$ ?$ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ transitions are predicted, including the transition dipole moments, Franck-Condon factors, and radiative lifetimes. The radiative lifetimes for the ${\rm{A}}^3 {\text{Π}}$ ?$ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ transitions are predicated to be at a $ {{\text{μ}}\rm{ s}}$ level, and the good agreement with previous theoretical values is found. Radiative lifetimes for ${{\rm{c}}^1} {\text{Π}}$ ?$ {{\rm{b}}^1} {{\text{Δ}} } $ and ${{\rm{c}}^1} {\text{Π}}$ ?$ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ transitions are also evaluated at the levels of $ {{\text{μ}}\rm{ s}}$ and ms, respectively. The PEC for the ground state is fitted into accurate analytical potential energy functions by using the extended-Rydberg potential function.Keywords: dynamically weighted /spectroscopic constants /transition properties /BeC 全文HTML --> --> --> 1.引 言 作为在银河系中质量丰度位列第四的元素, 碳在地壳中的含量仅为0.2%, 质量丰度排名为第十五, 而铍是最轻的碱土金属元素, 被广泛应用于制造轻便硬质合金. 铍以及含铍合金具有独特的物理化学特性, 在电子、原子能和航空航天等不同的工业领域中得到广泛应用. 碳化铍在等离子体物理[1 ,2 ] 、宇宙化学[3 -5 ] 以及新材料的开发等领域有着非常大的潜在应用. 但是到目前为止, 仅有少数几个实验和理论工作来研究铍-碳二元团簇[6 -15 ] , 因对Be与C相互作用的研究能够为碳化铍二元团簇的研究提供可靠的理论依据, 所以, 对双原子分子BeC的理论研究引起了广泛关注[6 -19 ] .[7 ] 通过研究发现BeC分子具有强束缚双激发态的特性, 并给出了这些低激发电子态的势能曲线和光谱常数; 同年, Borin和Omellas[8 ] 使用多参考单双激发组态相互作用方法研究了BeC分子的电子结构和光谱性质, 计算了13个低激发电子态的势能曲线, 给出了这些态的光谱常数、激发能、振动能级以及偶极距等数据. 在2004年, Pelegrini等[10 ] 利用 6-311+G 基组并使用多参考组态相互作用 (multi-reference configuration interaction, MRCI) 方法研究了BeC分子第一离解极限下的基态$ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ 和激发态${\rm{A}}^3 {\text{Π}}$ 两个电子态, 获得了平衡位置、谐振频率以及离解能等相关光谱常数. Teberekidis等[19 ] 使用单双激发的多参考布里渊-维格纳耦合簇 (multireference Brillouin-Wigner coupled cluster method restricted to single and double excitations, MRBW-CCSD) 方法, 通过外推至完全基组极限, 获得了基态的平衡位置、离解能等光谱常数. BeC分子有非常低的电子激发态, 该激发态大约高于基态2300 cm–1 , 因此, 利用单参考方法研究该体系将是一个挑战. 实验上已经获得BeC分子的基态转动常数B 0 = 1.162 cm–1 , 但由于势的复杂形状和实验数据的稀缺, 没有获得平衡位置等其他光谱常数的信息[6 ] .[20 ] 和Dawes等[21 ] 提出了一种动态权重方法, 即在完全活性空间自洽场 (complete active space self-consistent feld, CASSCF) 计算中通过自动改变态的平均权重来获得光滑的势能曲线. 本文采用动态权重态平均完全活性空间自洽场 (dynamically weighted state averaged complete active space self-consistent feld, DW-SA-CASSCF) 方法得到的函数作为利用内收缩多参考组态相互作用 (internally contracted multi-reference configuration interaction, icMRCI)[22 ,23 ] 方法进行计算的参考波函数, 研究了BeC分子第一和第二离解极限下5个电子态 ($ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ , ${\rm{A}}^3 {\text{Π}}$ , $ {{\rm{b}}^1} {{\text{Δ}} } $ , ${{\rm{c}}^1} {\text{Π}}$ 和$ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ ) 的光谱和跃迁性质, 并对基态$ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ 的解析势能函数进行了有益探索.2.计算方法 由Deskevich等[20 ] 和Dawes等[21 ] 所提出的DW-SA-CASSCF能量表达式为E CAS, i i 个态的CAS能量, ${\omega _i}$ 是这个态的权重, 该参数是所有CAS态能量的显函数, 求和遍布所有态平均中的N 个态. 能量相关权重函数定义为[20 ,21 ] :$ {\text{Δ}} E$ 是第i 个分子态与分子基态能量的差值. 根据这个定义可以看出, 渐进简并态在计算时具有相同的权重, 能量越高的激发态其权重越小.[20 ] 和Dawes等[21 ] 推荐使用的双曲正割函数$f(\Delta E) \propto {\operatorname{sech} ^2}[-\beta (E-$ ${E_0}) ]$ 则很好地满足了要求. 函数中衰减系数$ \beta $ 依靠经验进行优化, 通常取值为3 eV. 程序开始运行时, 所有的态具有相同的权重, 然后进行第二次迭代计算, 此时各个态的权重由(2 )式来确定, 反过来也会稍微改变各个态的能量值, 直到SA-CASSCF能量达到自洽时迭代停止 (一般进行3—6次迭代). 当误差改变小于指定的值 (大多数情况下, 10–6 a.u.是一个合理的选择, 此时随后的MRCI计算收敛将好于10–7 a.u., 1 a.u. = 2625.4984 kJ/mol) 时, 从DW-MCSCF计算中获得的轨道被当作随后icMRCI计算的参考轨道. 目前, 尽管动态权重程序已经内置于Molpro中, 但在输入文件中写入一个简单的循环结构将更便于应用.[24 ] 开发的量子化学从头计算Molpro2010程序包计算BeC分子的电子结构时, 本文采用动态权重方法来获得MRCI的参考态. 为了更精确地预测分子结构(0.001 ?)或能量 (小于1 kcal/mol, 1 kcal/mol = 4.184 kJ/mol), 对于第一、第二主族的原子, 必须以适当的方式考虑内层的非价电子对体系的影响[25 ] . 所以本文直接使用考虑了核价相关效应的aug-cc-pCVQZ和aug-cc-pCV5Z基组[26 ,27 ] , 并在此基础上将能量外推至完全基组极限. 计算时取核间距从1.18—11.8 ?之间的60个点做单点能计算.[28 ] [29 ] 获得的两点外推公式$E_{{\rm{CAS}}}^\infty $ 和$E_{{\rm{corr}}}^\infty $ 分别是外推至完全基组极限的参考能和相关能, L 是基组所含基函数所具有的最高角量子数. 考虑Davidson修正后, 获得的总能记为 icMRCI+Q/Q5.[30 -32 ] 使用三阶DKH3 获得了与实验更接近的结果, 因此考虑BeC分子的相对论效应修正时, 本文使用三阶DKH3 哈密顿近似进行相对论修正(记为+DK).3.结果和讨论 23.1.势能曲线和光谱参数 3.1.势能曲线和光谱参数 Be原子的基态和第一激发态光谱项为1 Sg 和3 Pu . 如表1 所列, BeC分子前三个离解通道是由基态Be原子和C原子的三个最低价态3 Pg , 1 Dg 和1 Sg 构成. Barker等[6 ] 通过第一原理计算获得Be原子第一激发态与基态的能级差是21846 cm–1 (加Davidson修正) 或22033 cm–1 (不加Davidson修正), 发现不加修正的能量更接近于实验值21978.3 cm–1 [33 ] , 更高离解通道Be(3 Pu )+C(1 Dg ) 的计算也表明未加修正的能量更接近实验值. 本文通过进一步计算发现 (见表1 ), 第三离解极限Be(1 Sg )+C(1 Sg ) 也存在同样的情况, 但对于第二离解极限Be(1 Sg )+C(1 Dg ) 包含Davidson修正的能量(10169.70 cm–1 )比不包含Davidson修正的能量(10124.12 cm–1 )更接近于实验值(10192.66 cm–1 )[34 ] . 所以, 在本文中仅研究了前两个离解通道对应的5个电子态. 原子态 $ {\text{Λ}}{\text{-}}{\rm S}$态 相对能量/cm–1 本文 (无Q) 本文 (+Q) 实验值[34 ] Be(1 Sg )+C(3 Pg ) $ {{\rm{X}}^3} {{\text{Σ}} ^ - } $, ${\rm{A}}^3 {\text{Π}}$ 0 0 Be(1 Sg )+C(1 Dg ) $ {{\rm{b}}^1} {{\text{Δ}} } $, ${{\rm{c}}^1} {\text{Π}}$, $ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ 10124.12 10169.70 10192.66 Be(1 Sg )+C(1 Sg ) ${2^1}{{\text{Σ}} ^ + } $ 21679.58 21581.62 21648.03
表1 BeC分子6个态的离解极限关系Table1. Dissociation relationship of six electronic states of BeC molecule.图1 是利用 icMRCI+Q/Q5+DK 方法计算获得的BeC分子5个态的势能曲线. 由于${\rm{A}}^3 {\text{Π}}$ 态与更高的$ ^3{\text{Π}} $ 态(也即$ 2^3{\text{Π}} $ 态)存在避免交叉, 使${\rm{A}}^3 {\text{Π}}$ 态具有了双势阱结构的势能曲线, 同时也表明这2个对称性相同的电子态之间存在较强的相互作用, 为了得到准确的结果, 在计算中必须同时对这两个电子态进行优化. 从图1 可以看出, 这5个电子态均为束缚态, 都具有非常深的势阱. 使用LEVEL8.0[35 ] 程序对这些势进行拟合可以获得相应的光谱常数, 具体数值见表2 . 为了便于对比, 已有的实验和理论计算结果也列在表2 中. 对于BeC分子的基态$ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ , 其特征组态为${\rm{1}}{{\text{σ}}^{{\text{αβ}}}}{\rm{2}}{{\text{σ}}^{{\text{αβ}}}}{\rm{3}}{{\text{σ}}^{{\text{αβ}}}}$ $ {\rm{4}}{{\text{σ}}^{{\text{αβ}}}}{\rm{1}}{{\text{π}}^{{\rm{αα}}}}{\rm{5}}{{\text{σ}}^0}{\rm{2}}{{\text{π}}^0}{\rm{6}}{{\text{σ}}^0}{\rm{7}}{{\text{σ}}^0}$ 和 $ {\rm{1}}{{\text{σ}}^{{\text{αβ}}}}{\rm{2}}{{\text{σ}}^{{\text{αβ}}}}{\rm{3}}{{\text{σ}}^{{\text{αβ}}}}{\rm{4}}{{\text{σ}}^{\rm{α}}}{\rm{1}}{{\text{π}}^{{\rm{αα}}}}{\rm{5}}{{\text{σ}}^{\text{β}}}{\rm{6}}{{\text{σ}}^0}$ ${\rm{7}}{{\text{σ}}^0}$ . 我们预测的势阱深度为2.1873 eV, 势阱能够支持34个振动束缚态. 实验报道了基态振动谱项${\text{Δ}} {G_{1/2}}$ = 902 cm–1 , 我们计算的结果为911 cm–1 , 与实验符合得很好. 计算的B 0 = 1.165 cm–1 也与相应的实验值1.162 cm–1 非常接近, 同时我们的光谱结果也与其他理论结果相符合.图 1 BeC分子5个电子态的势能曲线(1 Hartree = 2625.4984 kJ/mol)Figure1. Potential energy curves of five states of BeC molecule (1 Hartree = 2625.4984 kJ/mol). T e /cm–1 R e /nm${\omega _{\rm{e}}}$/cm–1 $ {\omega _{\rm{e}}}{x_{\rm{e}}} $/cm–1 102 ${\omega _{\rm{e}}}$у e /cm–1 B e /cm–1 $ {10^3}{\alpha _{\rm{e}}}$/cm–1 D e /eV ${{{\rm{X}}^3}{\text{Σ}}^- } $ 0 0.1673 918.08 7.350 17.87 1.1783 15.644 2.1873 Cal. [6 ] 0 0.1661 937.9 9.6 — 1.19 — — Cal. [7 ] 0 0.1693 905 — — — — 2.04 Cal. [8 ] 0 0.1667 951 8.42 — 1.183 — 2.39 Cal. [10 ] 0 0.1683 925 11.25 — — — 2.14 Cal. [19 ] 0 0.1680 — — — — — 2.04 ${{\rm{A}}^3}{\text{Π}}$ 8916.35 0.1771 772.74 8.692 199.89 1.0518 28.367 1.0777 Cal. [7 ] 9033.41 0.1799 — — — — — 0.92 Cal. [8 ] 9466 0.1756 764 14.69 — 1.0752 — 1.16 Cal. [10 ] 8961 0.1791 874 26.26 — — — 1.03 $ {{\rm{b}}^1}{\text{Δ}} $ 7823.39 0.1675 933.50 8.301 7.56 1.1714 16.700 2.4408 Cal. [7 ] 8872.10 0.1693 904 — — — — 2.27 Cal. [8 ] 8732 0.1668 956 7.6 — 1.1757 — 2.63 $ {{\rm{c}}^1}{\text{Π}} $ 10909.21 0.1760 834.80 7.138 9.20 1.0551 14.365 2.0933 Cal. [7 ] 11291.76 0.1778 818 — — — — 1.97 Cal. [8 ] 11618 0.1758 847 6.94 — 1.0612 — 2.24 $ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ 12139.14 0.16698 936.21 17.553 126.98 1.1764 16.000 1.9060 Cal. [7 ] 12582.24 0.1693 905 — — — — 1.81 Cal. [8 ] 13579 0.167 955 7.3 — 1.1732 — 2.02 注: Cal. 为理论计算值.
表2 BeC分子$ {{\rm{X}}^3}{\text{Σ}} $ , ${{\rm{A}}^3}{\text{Π}}$ , $ {{\rm{b}}^1} {{\text{Δ}} } $ , ${{\rm{c}}^1} {\text{Π}}$ 和$ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ 等5个态的光谱参数Table2. Spectroscopic constants of the five states of BeC molecule.图 1 所示, ${\rm{A}}^3 {\text{Π}}$ 态与基态$ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ 对应同一个解离通道 Be(1 Sg )+C(3 Pg ). 计算表明${{\rm{A}}^3}{\text{Π}}$ 态的第一个势阱难以支持稳定的束缚振动态, 所以后面的讨论主要针对第二个势阱. ${{\rm{A}}^3}{\text{Π}}$ 态在平衡位置附近具有单参考特征, 其波函数主要是由电子组态$ {\rm{1}}{{\text{σ}}^{{\text{αβ}}}}{\rm{2}}{{\text{σ}}^{{\text{αβ}}}}{\rm{3}}{{\text{σ}}^{{\text{αβ}}}}{\rm{4}}{{\text{σ}}^{\rm{α}}}{\rm{1}}{{\text{π}}^{{\rm{αα}}}}{\rm{5}}{{\text{σ}}^{\rm{α}}}{\rm{6}}{{\text{σ}}^0}{\rm{7}}{{\text{σ}}^0}$ 构成. 通过组态分析可以确定基态通过单电子$1{\text{π}} \to 5{\text{σ}} $ 激发可以获得${{\rm{A}}^3}{\text{Π}}$ 态. 文献[7 ,10 ,17 ]中采用 MRCISD+Q 方法结合较小的基组获得了激发态的光谱常数, 其中文献[10 ]计算的激发能与本文结果最为接近, 其他光谱常数如平衡位置、离解能等均有不同. ${{\rm{A}}^3}{\text{Π}}$ 态的势阱深度大约为1.0777 eV, 能够支持8个振动态.1 Sg )+C(1 Dg ) 对应三个电子态: $ {{\rm{b}}^1} {{\text{Δ}} } $ , ${{\rm{c}}^1} {\text{Π}}$ , $ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ . 从图 1 可以看出, 这三个态也都有很深的势阱. 这三个电子态的势阱能够容纳的振动态数目分别为37, 34 和28. 通过对它们的波函数分析发现${{\rm{c}}^1} {\text{Π}}$ 在平衡位置附近与${{\rm{A}}^3}{\text{Π}}$ 态相似, 也具有单组态特征, 而$ {{\rm{b}}^1} {{\text{Δ}} } $ 和$ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ 两个电子态则具有显著的多组态特征.3.2.跃迁特性 -->3.2.跃迁特性 采用icMRCI方法, 在cc-pCVQZ基组的基础上计算了BeC分子5个电子态在核间距R = 0.1—0.8 nm的永久偶极距, 结果如图2 所示. 从图2 中可以看出, 当核间距离较小时, 5个态的电偶极距均为负值, 表明分子极性为$ {\rm{B}}{{\rm{e}}^{{\text{δ}} + }}{{\rm{C}}^{{\text{δ}} - }}$ , 即Be失去电子, 而C得到电子. 这从图3 基态的Mulliken电荷布局可以更加明显的展示出来: 当核间距较小时, Be带正电, C带负电, 而当核间距比较大时, Be和C两个原子将均不带净电荷, 电偶极距趋于零值, 同时, Be和C原子的Mulliken电荷也分别为零.图 2 BeC分子5个电子态的偶极矩(1 Debye = 3.336 × 10–30 C·m)Figure2. Dipole moments of five electronic states of BeC(1 Debye = 3.336 × 10–30 C·m).图 3 BeC分子基态的Mulliken电荷分布Figure3. Mulliken population for the ground state BeC molecule.${{\rm{A}}^3}{\text{Π}}$ —$ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ , ${{\rm{c}}^1} {\text{Π}}$ —$ {{\rm{b}}^1} {{\text{Δ}} } $ 以及${{\rm{c}}^1} {\text{Π}}$ —$ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ 等三个允许跃迁的跃迁偶极矩, 计算结果如图4 所示. ${{\rm{A}}^3}{\text{Π}}$ —$ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ 有一个突变源自${{\rm{A}}^3}{\text{Π}}$ 与一个更高的$ ^3{\text{Π}} $ 激发态之间的避免交叉引起的. Wright和Kolbuszewski[7 ] 以及Borin和Ornellas[8 ] 在1993年通过计算均发现了这个现象. BeC分子的低激发态都有较深的势阱, 使得该分子具有非常丰富的光谱信息. ${{\rm{c}}^1}{\text{Π}}$ —$ {{\rm{b}}^1} {{\text{Δ}} } $ 以及${{\rm{c}}^1}{\text{Π}}$ —$ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ 之间的跃迁偶极矩随着核间距的变化发生跃变, 这是由于和更高的激发态的避免交叉导致波函数产生组态交换引起的.图 4 跃迁偶极距曲线Figure4. Transition dipole moment curves.$ {{\rm{A}}^3}{\text{Π}} -{{\rm{X}}^3} {{\text{Σ}} ^ - } $ , ${{\rm{c}}^1}{\text{Π}}$ —$ {{\rm{b}}^1} {{\text{Δ}} } $ 以及${{\rm{c}}^1}{\text{Π}}$ —$ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ 之间的电偶极跃迁是允许跃迁. 根据前面Molpro计算得到的分子势能数据以及跃迁偶极距, 应用LEVEL 8.0[35 ] 程序, 计算获得了这三个允许跃迁的弗兰克-康登因子, 结果如表3 所列. 表3 列出了所有$\nu'$ —$\nu'' $ 之间数值大于0.1跃迁的弗兰克-康登因子. 根据弗兰克-康登原理, 当两个电子态的平衡位置接近时, 对角的Franck-Condon因子越大, 表明上下态中的振动量子数相同的振动态的波函数重叠最大, 相应的垂直跃迁几率就越大, 这从表3 计算结果可以看出. 因为${{\rm{A}}^3}{\text{Π}}$ 和$ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ , ${{\rm{c}}^1}{\text{Π}}$ 和$ {{\rm{b}}^1} {{\text{Δ}} } $ 以及${{\rm{c}}^1}{\text{Π}}$ 和$ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ 这些态之间的平衡位置相差很小, ${{\rm{A}}^3}{\text{Π}}$ —$ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ , ${{\rm{c}}^1}{\text{Π}}$ —$ {{\rm{b}}^1} {{\text{Δ}} } $ , ${{\rm{c}}^1}{\text{Π}}$ —$ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ 态之间0—0跃迁的弗兰克-康登因子都大于其他振动态之间的因子.$\nu '$—$ \nu ''$ FC $\nu '$—$ \nu ''$ FC $\nu '$—$ \nu ''$ FC $\nu '$—$ \nu ''$ FC $\nu '$—$ \nu ''$ FC $\nu '$— $ \nu ''$ FC ${\rm{A}}^3 {\text{Π}}$—${\rm{X}}^3 {\text{Σ}}^-$ 0—0 0.5439 0—1 0.3653 1—0 0.3049 1—2 0.4143 1—3 0.1670 2—0 0.1080 2—1 0.2660 2—3 0.3601 2—4 0.2276 3—2 0.1654 3—4 0.2908 3—5 0.2691 4—2 0.1763 4—5 0.2255 4—6 0.2993 5—3 0.1561 5—6 0.1639 5—7 0.3216 6—3 0.1070 6—4 0.1273 6—6 0.1339 6—7 0.1052 6—8 0.3348 6—9 0.1183 7—4 0.1095 7—5 0.1000 7—7 0.1618 7—9 0.3342 7—10 0.1531 ${{\rm{c}}^1}{\text{Π}}$ —${{\rm{b}}^1}{\text{Δ}}$ 0—0 0.6237 0—1 0.3153 1—0 0.2701 1—1 0.1740 1—2 0.3999 1—3 0.1368 2—1 0.2689 2—3 0.3470 2—4 0.2322 3—1 0.1518 3—2 0.1803 3—4 0.2122 3—5 0.2964 4—2 0.1894 4—4 0.1027 4—5 0.1045 4—6 0.3042 4—7 0.1238 5—3 0.1634 5—5 0.1435 5—7 0.3138 6—3 0.1236 6—4 0.1268 6—6 0.1567 6—8 0.2968 7—4 0.1289 7—7 0.1495 7—9 0.2690 8—5 0.1219 8—8 0.1212 8—10 0.2380 9—11 0.2025 10—12 0.1699 ${{\rm{d}}^1}{\text{Σ}}$—${{\rm{c}}^1}{\text{Π}}$ 0—0 0.6164 0—1 0.2717 1—0 0.3232 1—1 0.1693 1—2 0.2617 2—1 0.4016 2—3 0.1699 2—4 0.1850 3—1 0.3901 3—2 0.3513 3—5 0.1510 4—2 0.2362 4—3 0.2156 4—4 0.1073 4—6 0.1068 5—3 0.3014 5—4 0.1011 5—5 0.1501 6—4 0.3109 6—6 0.1613 7—4 0.1292 7—5 0.3175 7—7 0.1442 8—5 0.1801 8—6 0.2945 8—8 0.1054 9—6 0.2192 9—7 0.2612 10—7 0.2563 10—8 0.2265
表3 ${{\rm{A}}^3}{\text{Π}}$ —$ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ , ${{\rm{c}}^1}{\text{Π}}$ —$ {{\rm{b}}^1} {{\text{Δ}} } $ , $ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ —${{\rm{c}}^1}{\text{Π}}$ 跃迁的弗兰克-康登因子Table3. Franck-condon factor for ${{\rm{A}}^3}{\text{Π}}$ ?$ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ , ${{\rm{c}}^1}{\text{Π}}$ ?$ {{\rm{b}}^1}{{\text{Δ}} } $ , $ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ ?${{\rm{c}}^1}{\text{Π}}$ transitions.5 )式可以计算这些振动态的自发辐射寿命$ {\tau _{\nu '}}$ ${A_{\nu ', \nu ''}}$ 是自发辐射爱因斯坦跃迁几率系数, 可由(6 )式计算[36 ] $\bar \nu $ 是跃迁频率,${\Psi _{\nu'}}$ 和${\Psi _{\nu''}}$ 是振动波函数,$D$ 为跃迁偶极距,${{\left({2 - {\delta _{0, \varLambda ' + \varLambda ''}}} \right)}/{\left({2 - {\delta _{0, \varLambda '}}} \right)}}$ 是考虑跃迁态的简并因子. 表4 列出了${\rm{A}}^3 {\text{Π}}$ , $ {{\rm{b}}^1}{{\text{Δ}} } $ , ${{\rm{c}}^1}{\text{Π}}$ 和$ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ 态振动量子数$\nu '$ = 0—7 等8个振动能级的辐射寿命. Pelegrini等[10 ] 通过使用 6-311+G(3d1f) 基组和MRSDCI方法, 计算了$ {\rm{A}}^3 {\text{Π}} -{{\rm{X}}^3} {{\text{Σ}} ^ - } $ 跃迁时$\nu'$ = 0—2等3个振动能级的辐射寿命, 结果也列在表 4 中. 从表 4 可以看出, Pelegrini等[10 ] 计算的结果与本文的结果较为接近, 而其他振动态的自发辐射寿命目前还没有相关的理论和实验数据. 跃迁 辐射寿命$/{{\text{μ}}{\rm{ s}}}$ $\nu '$ = 0 $\nu '$ = 1 $\nu '$ = 2 $\nu '$ = 3 $\nu '$ = 4 $\nu '$ = 5 $\nu '$ = 6 $\nu '$ = 7 ${\rm{A}}^3 {\text{Π}}$—${{\rm{X}}^3}{{\text{Σ}} ^ - }$ 14.66 14.64 14.46 13.82 12.99 12.16 11.65 11.31 Cal.[10 ] 14.0 14.5 15.6 ${{\rm{c}}^1} {\text{Π}}$—$ {{\rm{b}}^1} {{\text{Δ}} } $ 191.10 166.59 161.38 159.48 151.88 176.09 197.32 239.85 ${{\rm{c}}^1} {\text{Π}}$—$ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ 2730.00 1010.00 630.00 460.00 380.00 330 280.00 230.00
表4 ${\rm{A}}^3 {\text{Π}}$ , $ {{\rm{b}}^1} {{\text{Δ}} } $ , ${{\rm{c}}^1}{\text{Π}}$ 和$ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ 态几个振动能级的辐射寿命Table4. Radiative lifetime of the vibrational energy levels for ${\rm{A}}^3 {\text{Π}}$ , $ {{\rm{b}}^1} {{\text{Δ}} } $ , ${{\rm{c}}^1} {\text{Π}}$ and $ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ states.3.3.解析势能函数 -->3.3.解析势能函数 目前, 获得分子势能数据主要是通过第一原理计算、Rydbery-Klein-Rees(RKR)反演法和逆向微扰法等三种途径, 但得到的都是离散的数据点. 本文通过研究已有的各种形式的解析势能函数, 其中下面这种扩展的Rydberg函数[37 ] 在相同参数的情况下给出了最优的拟合结果D e 是离解能, R e 为分子的平衡位置, C k E e (R i R i V (R i R i N 是需要拟合的从头计算势能数据点的数目. 进行拟合前, D e 和R e 取自于从本文的理论计算值.[38 ] 独特的稳健全局优化算法对BeC分子基态$ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ 的势能数据点进行了曲线拟合. 当取10个可调参数时, 如表5 所列, 得到的均方根偏差已小于5.03 × 10–5 a.u., 表明该解析势能函数可以精确描述基态势能曲线.参数 C1 C2 C3 C4 C5 参数值 4.584720688 6.825173375 4.979780662 2.012372055 1.900852427 参数 C6 C7 C8 C9 C10 参数值 –5.415648763 –6.033517345 12.82526525 –6.086434893 0.939009741
表5 BeC分子基态解析势能函数参数值Table5. The values for the analytic parameters for the ground state of BeC molecule.4.结 论 利用高精度的从头计算MRCI+Q方法, 本文研究了BeC分子第一和第二离解极限对应的基态$ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ 和4个低激发态 (${\rm{A}}^3 {\text{Π}}$ , $ {{\rm{b}}^1}{{\text{Δ}} } $ , ${{\rm{c}}^1} {\text{Π}}$ 和$ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ ) 的光谱性质, 计算得到这五个态的势能曲线, 并使用LEVEL程序拟合得到了相应的光谱常数. 计算的结果与最新报道的实验值符合得很好. 当前的计算还给出了5个电子态的永久偶极矩, 结果表明在这几个激发态的R e 处BeC的极性均为$ {\rm{B}}{{\rm{e}}^{{\text{δ}} + }}{{\rm{C}}^{{\text{δ}} - }}$ . 本文还讨论了偶极允许跃迁${\rm{A}}^3 {\text{Π}}$ —$ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ , ${{\rm{c}}^1} {\text{Π}}$ —$ {{\rm{b}}^1} {{\text{Δ}} } $ , ${{\rm{c}}^1} {\text{Π}}$ —$ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ 的跃迁特性, 其中包括相应的跃迁偶极矩、Franck-Condon因子以及辐射寿命. 结果显示: ${\rm{A}}^3 {\text{Π}}$ —$ {{\rm{X}}^3} {{\text{Σ}} ^ - } $ 和${{\rm{c}}^1} {\text{Π}}$ —$ {{\rm{b}}^1} {{\text{Δ}}} $ 自发跃迁的辐射寿命处在 ${\rm{{\text{μ}} s}} $ 量级, ${{\rm{c}}^1} {\text{Π}}$ —$ {{\rm{d}}^1}{{\text{Σ}} ^ + } $ 自发跃迁的辐射寿命则为 ms量级. 最后, 我们还通过扩展的Rydberg函数拟合获得了基态势能曲线精确的解析表达式. 




























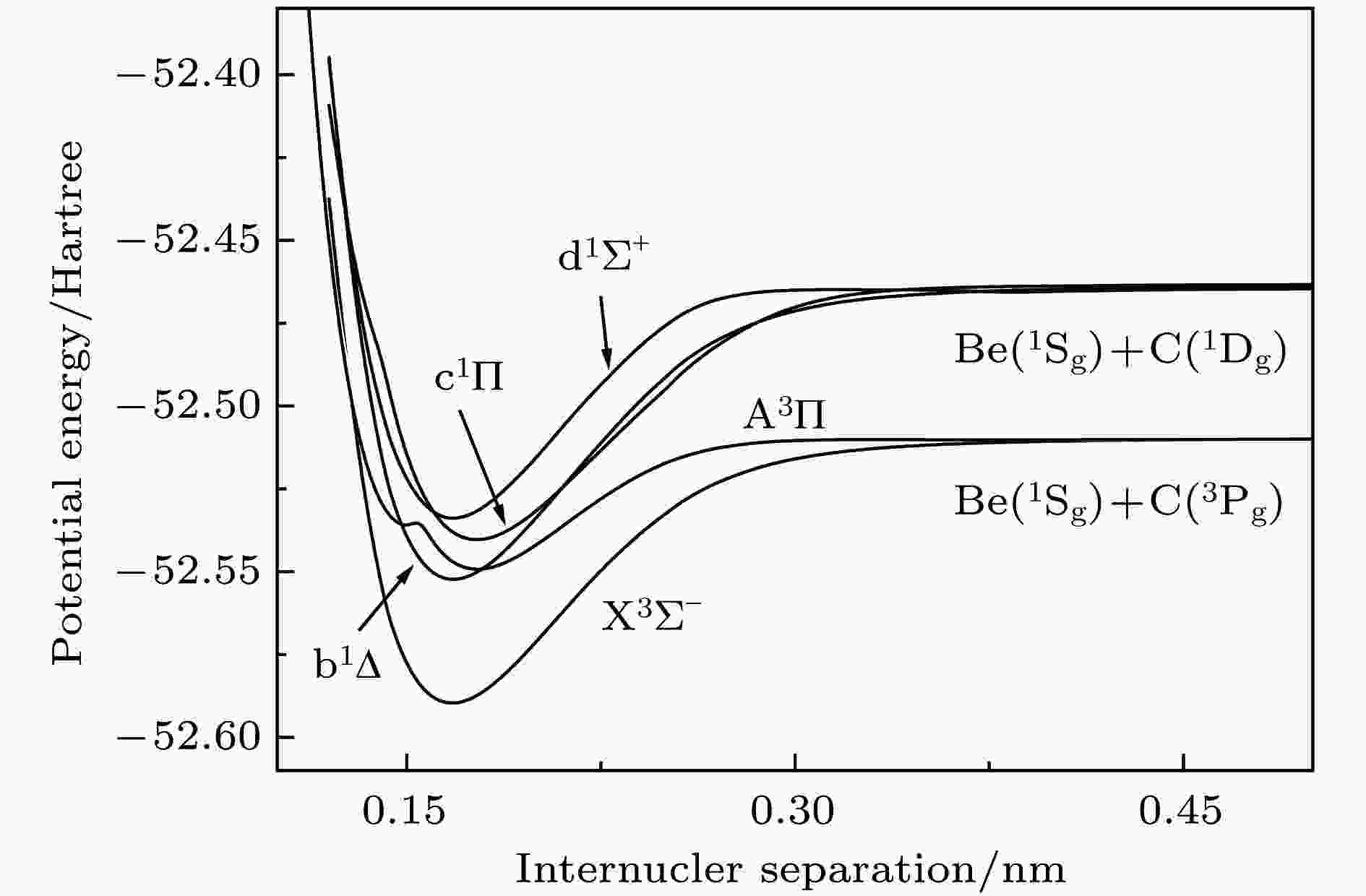 图 1 BeC分子5个电子态的势能曲线(1 Hartree = 2625.4984 kJ/mol)
图 1 BeC分子5个电子态的势能曲线(1 Hartree = 2625.4984 kJ/mol)






































 图 2 BeC分子5个电子态的偶极矩(1 Debye = 3.336 × 10–30 C·m)
图 2 BeC分子5个电子态的偶极矩(1 Debye = 3.336 × 10–30 C·m)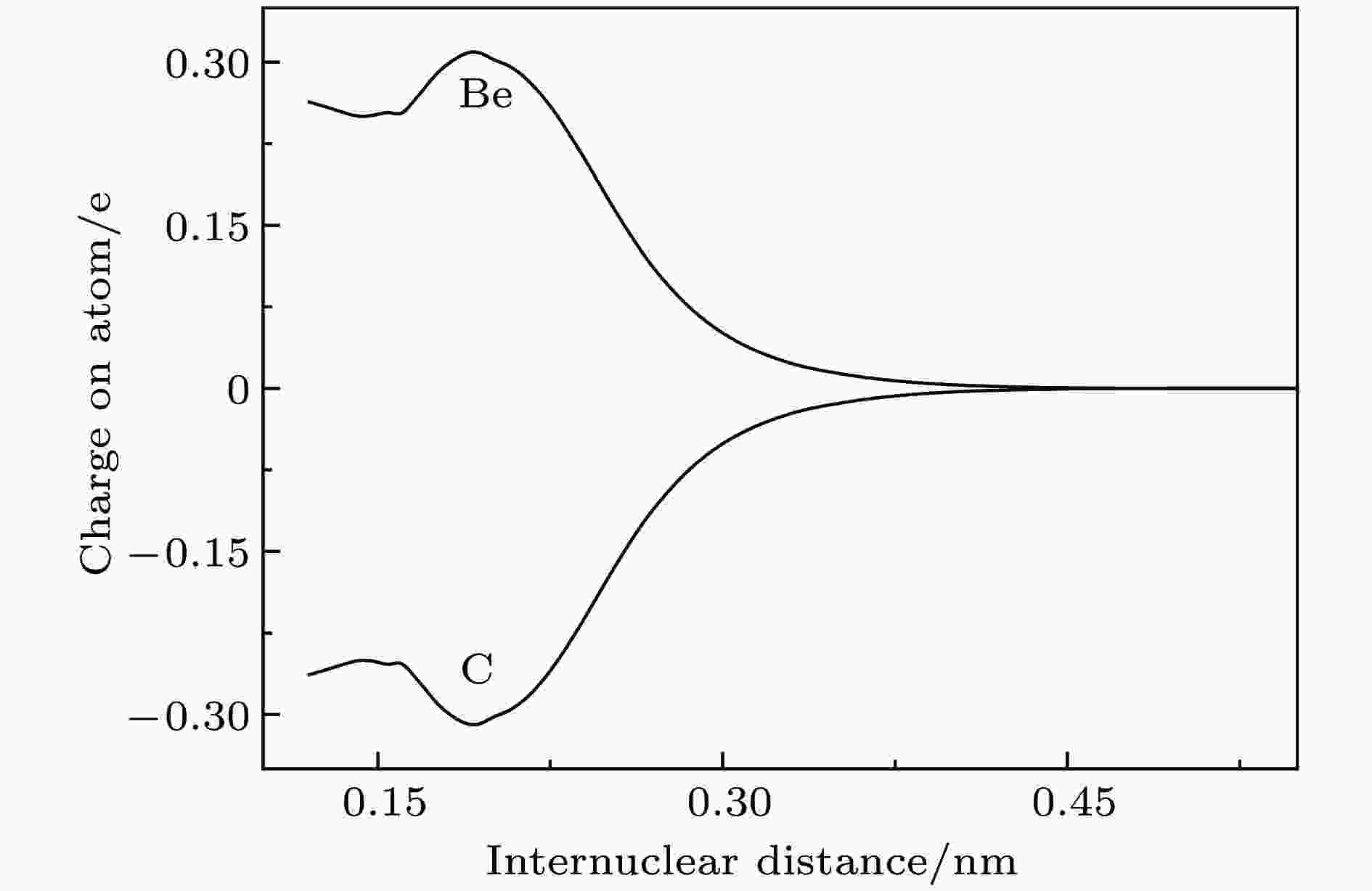 图 3 BeC分子基态的Mulliken电荷分布
图 3 BeC分子基态的Mulliken电荷分布



























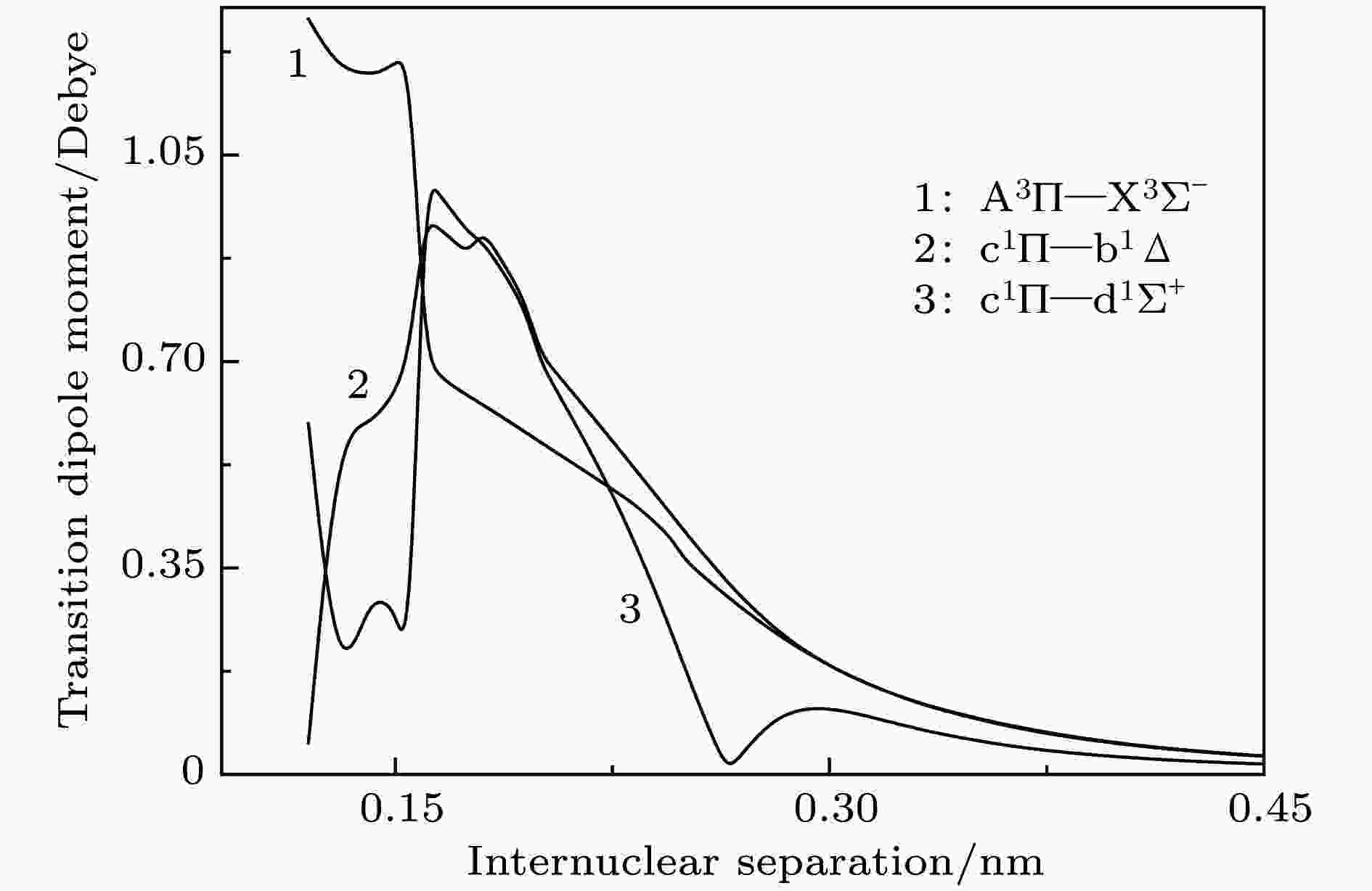 图 4 跃迁偶极距曲线
图 4 跃迁偶极距曲线

















































































































































































