删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于绝对节点坐标法的平面梁有限变形下变形重构

本站小编 Free考研考试/2022-01-01


引言


随着智能材料和传感器技术的发展, 对各类柔性结构的健康监测和主动控制得到了越来越多的应用. 在航天领域, 对于大型柔性空间结构, 尤其是大型天线及反射器, 其结构变形的掌握程度直接关乎其性能和精度[1], 在结构完整性监测和故障诊断上也很重要; 在医疗器械领域, 先进柔性穿刺针和其他微创手术工具对于精确地识别其在人体内的载荷状况和变形具有很高的要求[2]; 在机器人领域, 可靠高效的变形感知技术是相对传统刚性机器人具有结构简单、成本低廉、强适应力等许多优势的连续介质机器人实用化必须的技术[3]. 对于以上问题, 利用分布式光纤网络[4]进行结构健康监测[5]和主动控制[6]方面的信息获取是一个非常具有前景的解决方案. 其中, 如何利用离散的应变信息进行变形重构是相关问题的核心, 但已有的利用应变信息对柔体结构进行姿态监测的研究较少, 且往往是利用单纯基于曲率的几何关系而非将力学中更完备的应变?位移关系也纳入考虑来进行曲面或曲线的变形重构, 这限制了相关方法在获取更完整精确的变形信息方面的能力, 也不利于后续将变形重构得出的信息直接应用于载荷识别和健康监测等方面.

早期, Davis等[7]进行了利用光纤光栅传感器进行形态感知的初步尝试, 利用梁在特定载荷下的变形模式对测量的应变进行拟合, 进而实现对变形的预测; Foss和Haugse[8]利用位移振型和应变振型的对应关系, 通过模态转换给出了位移?应变转换矩阵, 将拟合用的变形模式范围由特定载荷情况扩展到了动力学的模态范畴; Tessler等[9-10]和Gherlone等[11]基于有限元方法中应变—位移的变分关系, 用最小二乘列式的形式进行求解, 发展出了一种逆有限元方法, 进一步拓宽了相关问题的求解空间, 相较之前的方法在准确性和理论完备性上得到了显著的提升. Tessler及其团队在后续对iFEM方法在单元类型[12-13]和应用方面[14-15]进行了大量的延伸, 逆有限元方法因其不受材料性质及载荷特征影响的特性和其与有限元方法高度相关带来的可扩展性引起了许多其他研究者关注[16-17].

以上提到的方法均可以视作变形重构问题在线性的试探函数法框架下求解方法的演进, 也意味着它们均只适用于应变与位移映射关系可线性近似的小变形情况, 对于在航空航天、精密医疗器械等领域得到越来越广泛运用的柔性结构无法取得足够好的效果, 而后者相较于前者对于变形感知也具有更高的需求. 为了应对这些需求, Ko等[18]基于经典梁理论, 对梁进行简单的分段和线性近似, 并采用类似于浮动坐标系的方法连接各段, 从而在低成本线性计算的基础上完成非线性的近似, 对于作为其研究对象的机翼的较大变形取得了不错的效果, 但这种较为粗糙的近似无法满足较高的精度要求, 且实际未考虑轴向变形的影响, 而对于那些更大变形的情况, 此方法则变得不再适用; Yi等[19]将应变向曲率转化, 再将曲率在被测梁长度方向上进行连续化处理来获取梁上各点的空间坐标, 这对于大变形情况具有极佳的适应性, 但在曲率的连续性方面处理有一定困难, 文中采取的数值积分方法在计算效率方面也有局限性. 基于曲率的方法在变形重构问题及相关应用的研究中实际上得到了大量的应用, 如Roesthuis等[20]将FBG传感器阵列采集的应变信息利用基于曲率的重构方法转化为形态信息, 以实现柔性针头刺入软组织后的精确控制; Xu等[21]使用正交网状的FBG传感器阵列结构建立了一种柔性板三维形状测量系统, 同样也是通过应变信息到曲率信息再到形态信息的方式实现的.

需要注意的是, 以上的非线性变形重构都是单纯基于几何关系的变形重构, 且都是以曲率?转角的微分关系为基础建立相关算法. 此类方法并非基于系统完整的应变?位移场力学关系, 实际上忽视了被测体长度方向上变化的影响, 也不能方便地与力学相关方面的理论与应用相结合, 这都限制了上述方法的适用范围.

绝对节点坐标法(absolute nodal coordinate formulation, ANCF)是Shabana等[22-24]为了处理强非线性耦合问题而发展出的一种方法, 通过取各单元节点在整体坐标系下完整的位置和角度作为广义坐标实现了较为精确的非线性建模. 绝对节点坐标法建立的质量阵为常数阵, 广义力表达简洁, 无科氏力和离心力项, 在大变形下的动力学问题中得到了广泛地应用. 对于本文涉及的有限变形下平面梁变形重构问题而言, 绝对节点坐标法提供的应变?位移关系模型简洁, 能够精确地将应变与节点位移间的关系以标准的二次型形式表达, 进而帮助建立起可靠易行的求解算法.

本文部分继承了变形重构逆有限元方法的思想, 将梁的应变?位移重构问题视为一种最优化问题, 旨在对被测对象进行有限元离散后, 通过引入ANCF形函数对大变形下的非线性应变?节点位移关系进行描述, 构建目标函数并以位移作为决策变量. 继而采用最优化方法进行位移的求解, 建立一种能够具有可扩展性和较高精确性的有限变形下应变?位移重构方法. 相对于已有的曲率连续化方法而言, 利用有限元方法, 将应变?位移场进行较为系统的重构, 不仅在轴向大变形条件下具有较好的适应性, 对在此方面具有需求的相关工作, 例如文献[25]中涉及的振动控制和文献[26]中涉及的载荷识别也具有相当的意义.


1.
有限变形下的平面梁变形重构问题


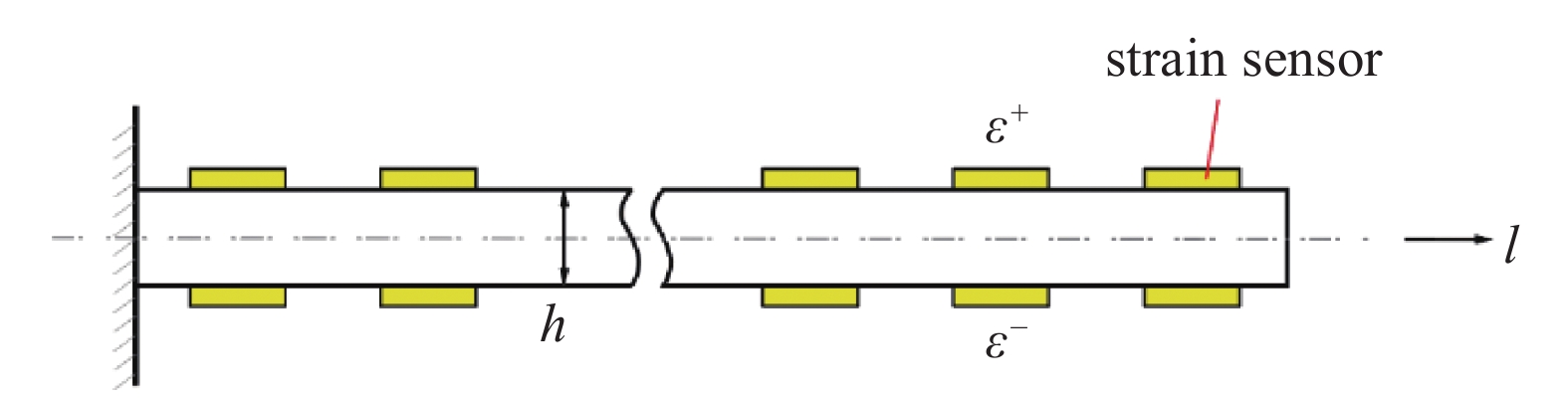
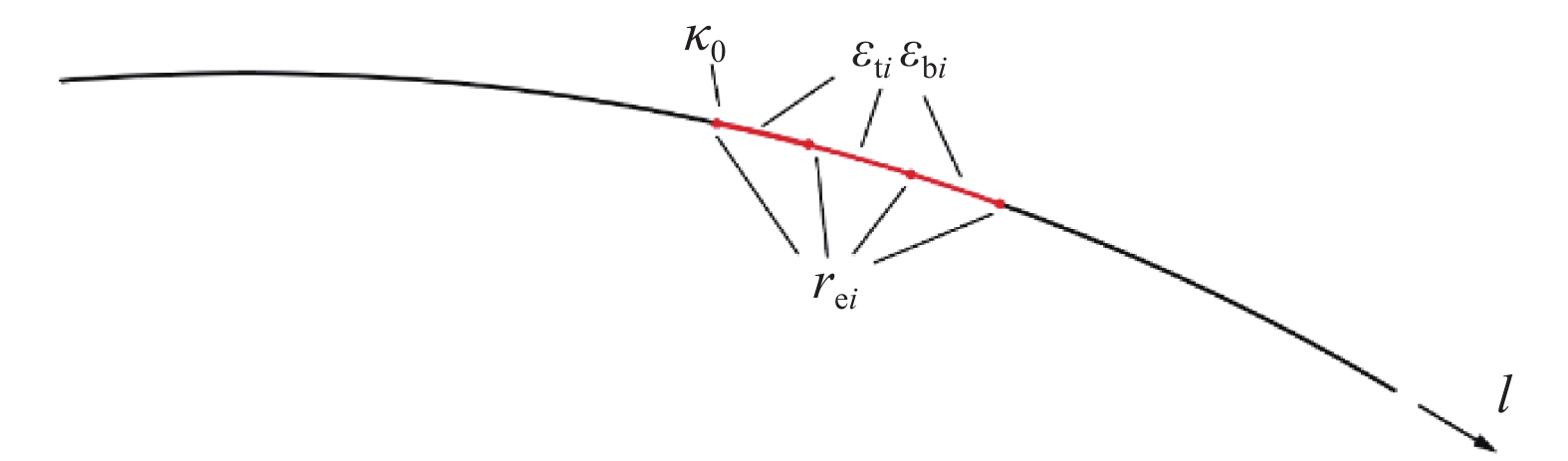
如图1所示, 一个典型的基于应变的平面梁变形重构模型由对称布置在被测梁上下表面各点的应变传感器组成. 当平面梁受载荷影响发生变形时, 应变传感器获取变形导致的应变, 利用相关应变信息理论上可以准确地重构出被测梁的变形状态.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-338-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
基于应变信息的平面梁变形重构模型



Figure
1.
Shape reconstruction model of plane beam based on strain information



下载:
全尺寸图片
幻灯片


各种变形重构方法中对分布式的应变测量数据进行处理的方式各不相同, 如上文提到的基于曲率连续性的方法中将应变转化为曲率, 或是模态叠加法中将应变转化为模态坐标. 但这些方法无疑都是利用连续化的应变?位移关系描述来处理离散的应变测量值与位移之间的关系. 而基于此, 考虑到用一种普适性的方式对平面梁重构问题进行描述有助于更完整地展现问题并在同一种背景下对各种算法的核心部分进行比较, 可以将梁的应变?位移重构问题采用连续形式以下式进行表达







$$ left. begin{array}{l} mathop {arg min }limits_{{boldsymbol{r}}left( l
ight)} errleft[ {{boldsymbol{r}}left( l
ight)}
ight] = displaystyleint_0^L {{{boldsymbol{R}}^{{
m{lT}}}}{{boldsymbol{R}}^{
m{l}}}} {
m{d}}l {{boldsymbol{R}}^{
m{l}}} = {boldsymbol{varepsilon}} left( {{boldsymbol{r}},l}
ight) - {{boldsymbol{varepsilon}} _0}left( l
ight) end{array}
ight} $$
(1)

其中, $l$为梁上某点的坐标, ${{boldsymbol{varepsilon}} _0}left( l
ight)$代表连续化的测量应变, ${boldsymbol{varepsilon}} left( {{boldsymbol{r}},l}
ight)$是通过某种应变?位移关系建立的、与位移相关的向量形式的应变函数. $ errleft[ {{boldsymbol{r}}left( l
ight)}
ight] $是以位移函数为宗量的泛函形式的变形重构误差函数. 对于不同变形重构方法, 式(1)中的${boldsymbol{varepsilon}} left( {{boldsymbol{r}},l}
ight)$可替换为各方法中所采用的连续化的应变?位移关系函数. 可以看出, 问题的核心是${boldsymbol{varepsilon}} left( {{boldsymbol{r}},l}
ight)$所体现的应变?位移关系.

在现有的平面梁变形重构研究中, 被最广泛采用的思路是利用线性化的平面梁应变、转角与挠度的微分关系进行逐点的递推计算, 即依赖于Euler-Bernoulli梁方程进行讨论, 如Ko法等等.

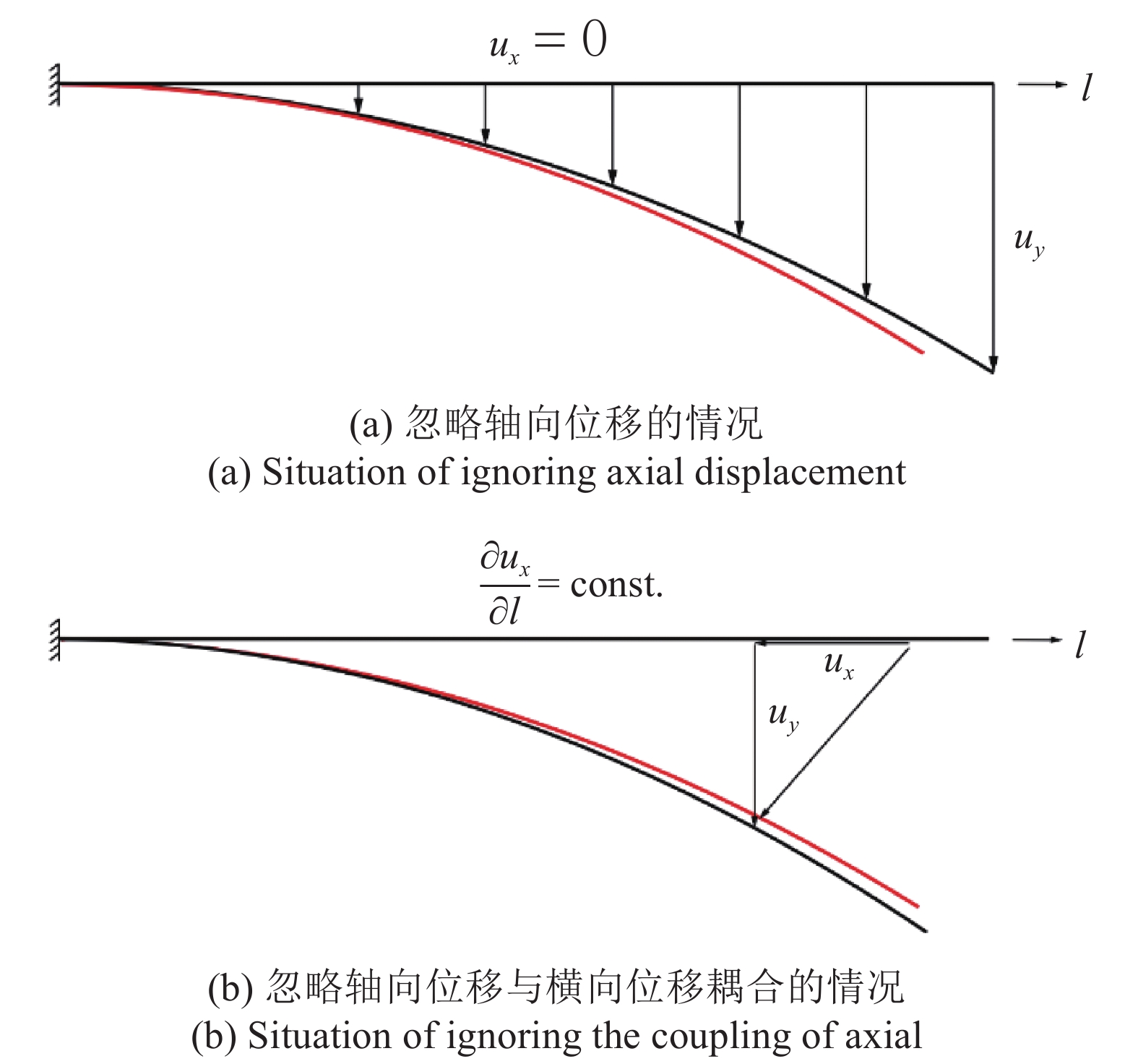
此类方法, 包括那些基于相似的线性微分关系, 通过待定参数法[27]或逆有限元方法[28]等构建变形重构算法的方法, 其共有的局限性在于由于忽略了梁上各点轴向的位移[28-29], 或将轴向位移进行简单的线性化[27], 进而忽视了轴向位移对曲率的影响, 或者说轴向位移与横向位移的耦合效应. 图2展示了这两种情况, 其中红色代表实际的被测对象变形, 黑色代表在对应的处理方式下重构出的变形状态. 由于这两种处理方式中对变形模式的简化, 导致了变形重构的误差. 这在小变形条件下误差可以忽略, 且计算简便, 但随变形增大误差也显著扩大, 显然不能适用于柔性梁结构的变形重构. 针对柔性结构的变形重构经典方法是借助单纯基于曲率的几何关系, 通过Frenet标架将由应变结算的曲率、挠率和曲线切向、法向和副法向向量纳入到统一的微分方程中, 再由数值积分方式进行重构[30]. 朱晓锦等[31]采用同样是基于曲率的方法, 不同之处在于是借助运动坐标系和密切平面将曲率与形状联系起来. 这类算法在轴向变形较大的情况下会引起严重误差, 在应用于空间结构时, 由于其对梁变形模式的过度简化, 局部扭转和横向剪切也都会导致此类方法失去适用性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-338-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
基于线性应变?位移关系的变形重构



Figure
2.
Deformation reconstruction based on linear strain displacement relationship



下载:
全尺寸图片
幻灯片


因此, 在有限变形的条件下, 一种能够更加精确、更加完整系统地描述测试对象变形状态的应变?位移关系需要被引入变形重构方法之中.


2.
变形重构问题的ANCF描述


在前述的平面梁变形重构问题的形式下, 通过有限元方法对被测物进行离散可以将相关问题改造成与分布式的应变测量条件相适应的离散形式. 而由于已有的相关研究因其使用的线性的应变?位移关系在大变形方面存在局限性, 本文通过引入ANCF单元, 获得梁在有限变形条件下系统性的应变?位移关系, 继而构建出基于ANCF的变形重构求解问题来对已有方法做出改进. 相较于已有的方法, 使用ANCF可以实现对有限变形条件下被测体应变?位移关系的精确描述.


2.1
变形重构问题的有限元离散化


为了适应分布式的应变测量条件, 引入有限元法中的形函数概念, 对被测梁进行分段离散并使用节点位移进行表示, 其中${boldsymbol{q}}$为整体的节点位移, ${{boldsymbol{q}}_{
m{e}}}$表示单个单元的节点位移







$$ left. begin{array}{l} mathop {arg min }limits_{boldsymbol{q}} errleft( {boldsymbol{q}}
ight) = displaystylesumlimits_{i = 0}^n {int_0^1 {{boldsymbol{R}}{{_i^xi }^{
m{T}}}{boldsymbol{R}}_i^xi } {
m{d}}xi } {boldsymbol{R}}_i^xi = {{boldsymbol{varepsilon}} _{
m{e}}}left( {xi ,{{boldsymbol{q}}_{{
m{e}}i}}}
ight) - {{boldsymbol{varepsilon}} _{0i}}left( xi
ight) end{array}
ight} $$
(2)

考虑到应变测量值实际上不是连续的, 实际上的各应变传感器测量的空间范围通常也无法简化为点, 且单个单元内应变变化应较小. 因此参考A. Tessler发展的逆有限元法[32]中的处理方式, 将测量值视为对应单元内的平均应变, 并设置${{boldsymbol{varepsilon}} _{
m{e}}}left( {xi ,{{boldsymbol{q}}_{{
m{e}}i}}}
ight)$由轴向应变与弯曲应变组成, 则平面梁的应变?位移重构问题可改写为下式







$$ left. begin{array}{l} mathop {arg min }limits_{{{boldsymbol{q}}_{
m{e}}}} errleft( {{{boldsymbol{q}}_{
m{e}}}}
ight) = displaystylesumlimits_{i = 1}^n {{{tilde{boldsymbol{R}}}_i}^{text{T}}} {{tilde{boldsymbol{R}}}_i} {tilde{boldsymbol{R}}} = displaystyleint_0^1 {{{boldsymbol{varepsilon}} _{
m{e}}}left( {xi ,{{boldsymbol{q}}_{{
m{e}}i}}}
ight){
m{d}}xi } - {{hat {boldsymbol{varepsilon}} }_i} end{array}
ight} $$
(3)







$$ {hat {boldsymbol{varepsilon}} _i} = left[ {begin{array}{*{20}{c}} {{{hat varepsilon }_{{
m{t}}i}}} {{{hat varepsilon }_{{
m{b}}i}}} end{array}}
ight] = left[ {begin{array}{*{20}{c}} {dfrac{{hat varepsilon _i^ + + hat varepsilon _i^ - }}{2}} {hat varepsilon _i^ + - hat varepsilon _i^ - } end{array}}
ight] $$
(4)

$ hat {boldsymbol{varepsilon}} $代表单元内由应变测量信息借助平截面梁假设获得的、与$ {{boldsymbol{varepsilon}} _{
m{e}}}left( {xi ,{{boldsymbol{q}}_{
m{e}}}}
ight) $格式相适应的测量轴向应变$ {hat varepsilon _{
m{t}}} $及测量弯曲应变$ {hat varepsilon _{
m{b}}} $, 且视作是单元内对应应变值的平均. 式(3)与式(4)建立起了一个对基于有限元方法利用分布式应变测量信息的平面梁变形重构问题的完整描述.


2.2
逆梯度缩减ANCF平面索梁单元


接下来需要找到一种合适的形函数及应变表达, 即确定$ {{boldsymbol{varepsilon}} _{
m{e}}}left( {xi ,{{boldsymbol{q}}_{
m{e}}}}
ight) $的具体函数表达. 为了适应有限变形条件下的实际需要, 再考虑到计算复杂度和泛用性方面的因素, 本文采用欧拉梁假设, 使用缩减ANCF平面索梁单元中应用的形函数形式来进行推导.

在缩减ANCF平面梁单元中, 单元节点坐标可表示为







$$ left. begin{array}{l} {{boldsymbol{q}}_{
m{e}}}{text{ = }}{left[ {begin{array}{*{20}{c}} {{boldsymbol{r}}_{
m{e}}^{
m{T}}left| {_{xi = 0}}
ight.}&{dot {boldsymbol{r}}_{
m{e}}^{
m{T}}left| {_{xi = 0}}
ight.}&{{boldsymbol{r}}_{
m{e}}^{
m{T}}left| {_{xi = 1}}
ight.}&{dot {boldsymbol{r}}_{
m{e}}^{
m{T}}left| {_{xi = 1}}
ight.} end{array}}
ight]^{
m{T}}} {{boldsymbol{r}}_{
m{e}}} = {left[ {begin{array}{*{20}{c}} {{{{r}}_x}}&{{{{r}}_y}} end{array}}
ight]^{
m{T}}} end{array}
ight} $$
(5)

单元内部的坐标插值关系可表示为







$$begin{array}{l} {boldsymbol{S}}( xi ) = [ {begin{array}{*{20}{c}} {{S_1}( xi ){{boldsymbol{I}}_2}}&{{S_2}( xi ){{boldsymbol{I}}_2}}&{{S_3}( xi ){{boldsymbol{I}}_2}}&{{S_4}( xi ){{boldsymbol{I}}_2}} end{array}} ] end{array} $$
(6)







$$ {{boldsymbol{r}}_{
m{e}}}left( {xi ,{{boldsymbol{q}}_{
m{e}}}}
ight) = {boldsymbol{S}}left( xi
ight){{boldsymbol{q}}_{
m{e}}} = left[ {begin{array}{*{20}{c}} {{{{r}}_{{
m{e}}x}}left( xi
ight)} {{{{r}}_{{
m{e}}y}}left( xi
ight)} end{array}}
ight] ;;;;qquadqquadqquad$$
(7)

式中${S_1}( xi ) = 1 - 3{xi ^2} + 2{xi ^3} ,;{S_2}( xi ) = L( {xi - 2{xi ^2} + {xi ^3}} ) ,;{S_3}( xi ) =$$3{xi ^2} - 2{xi ^3} ,; {S_4}( xi ) = L( { - {xi ^2} + {xi ^3}} )$.

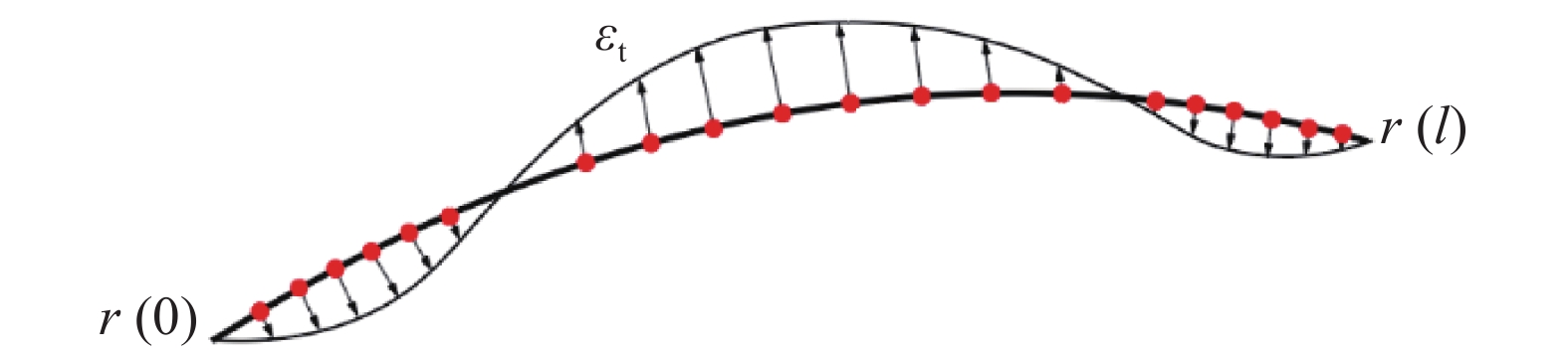
需要注意的是, 如图3所示, 梯度缩减ANCF索梁单元因轴向应变及弯曲应变耦合会导致在此描述中单元内的物质点(图3中用红点表示)在变形时向两端密集, 导致此单元中部在此描述下相对实际情况有轴向伸长的趋势, 而两端有轴向压缩的趋势, 即引起虚假轴向应变. 而对应变进行单元内的平均可以在很大程度上避免此类耦合效应引起的单元内部畸变问题[33]. 这也是采用平均应变而非由特定点利用对应的形函数值进行拟合的另一个原因.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-338-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
梯度缩减ANCF梁单元内部的虚假轴向应变



Figure
3.
False axial strain in gradient reduction ANCF beam element



下载:
全尺寸图片
幻灯片


使用Green-Lagrangian应变张量作为应变测度, 并根据相关推导[34], 得到如下形式的轴向变形导致的线应变和弯曲变形导致的线应变







$$ begin{array}{l} {{boldsymbol{varepsilon}} _{
m{e}}}left( {{{boldsymbol{r}}_{
m{e}}},xi }
ight) = left[ {begin{array}{*{20}{c}} {{{{varepsilon}} _{
m{t}}}left( xi
ight)} {{{{varepsilon}} _{
m{b}}}left( xi
ight)} end{array}}
ight] = left[ {begin{array}{*{20}{c}} {dfrac{1}{2}{boldsymbol{q}}_{
m{e}}^{
m{T}}{boldsymbol{S}}'{{left( xi
ight)}^{
m{T}}}{boldsymbol{S}}'left( xi
ight){{boldsymbol{q}}_{
m{e}}} - dfrac{1}{2}} {dfrac{{hleft( xi
ight)}}{{{f^3}left( xi
ight)}}{boldsymbol{S}}'left( xi
ight){{boldsymbol{q}}_{
m{e}}} times {boldsymbol{S}}''left( xi
ight){{boldsymbol{q}}_{
m{e}}}} end{array}}
ight] end{array} $$
(8)

其中$ fleft( xi
ight) $表示伸长率. 进一步进行单元内的平均







$$ int_0^1 {{{boldsymbol{varepsilon}} _{
m{e}}}left( {{{boldsymbol{r}}_{
m{e}}},xi }
ight){
m{d}}xi } = left[ {begin{array}{*{20}{c}} {dfrac{1}{2}{boldsymbol{q}}_{
m{e}}^{
m{T}}{{boldsymbol{S}}_{
m{t}}}{{boldsymbol{q}}_{
m{e}}} - dfrac{1}{2}} {dfrac{{bar h}}{{{{bar f}^3}}}{boldsymbol{q}}_{
m{e}}^{
m{T}}{{boldsymbol{S}}_{
m{b}}}{{boldsymbol{q}}_{
m{e}}}} end{array}}
ight] $$
(9)







$$ {{boldsymbol{S}}_{
m{t}}} = int_0^1 {{{{boldsymbol{S}}'}^{
m{T}}}{boldsymbol{S}}'{
m{d}}xi } $$
(10)







$$ {{boldsymbol{S}}_{
m{b}}} = int_0^1 {left( {{{boldsymbol{S}}'_1}^{
m{T}}{{{boldsymbol{S}}''_2}} - {{boldsymbol{S}}'_2}^{
m{T}}{{{boldsymbol{S}}''_1}}}
ight){
m{d}}xi } $$
(11)

式中的$ {{boldsymbol{S}}_1} $和$ {{boldsymbol{S}}_2} $分别为形函数$ {boldsymbol{S}} $的第一行和第二行, 全式是运用矩阵运算的相关定义推导整理而来. 式(9)中的$bar f$为伸长率的单元内均值. 如果伸长率$f$采用精确值, 对于结果精确度的贡献较小, 但对计算的复杂度影响很大, 且易受之前提到的轴向伪应变效应的影响. 为简化求解过程, 参照ANCF在处理动力学问题时已有的简化方法[35]将单元内$f$简化为一由测量值直接确定的常数值$bar f$







$$ bar f = sqrt {2{{hat varepsilon }_{
m{t}}} + 1} $$
(12)

$bar h$同样是为了计算效率而作的简化. 另外为了适应轴向大变形下可能出现的梁高度方向的变化, 在变形前后体积不变、同一垂直法线的截面内部受轴向变形的影响面积发生成比例放大或缩小的近似假设下, 使用均匀化处理的伸长率$bar f$对梁的初始高度$hleft( xi
ight)$进行近似校正







$$ bar h = dfrac{1}{{sqrt {bar f} }}int_0^1 {hleft( xi
ight){
m{d}}xi } $$
(13)

$ {{boldsymbol{S}}_{
m{t}}} $及$ {{boldsymbol{S}}_{
m{b}}} $分别称为轴向应变矩阵和弯曲应变矩阵, 在此种简化下, 可以避免在求解过程中为了获得$ {{boldsymbol{S}}_{
m{t}}} $及$ {{boldsymbol{S}}_{
m{b}}} $进行复杂的数值积分运算, 二者可预先计算并存储, 极大地简化了相关求解过程, 同时使应变对节点位移的函数为标准二次型格式, 利于后续优化求解过程中Jacobian矩阵与Hesse矩阵的求取. 而$bar f$与$bar h$通过测量的应变直接得出, 同样能使后续计算尽量简化.

将式(9)代入式(3)进行整理, 可将平面梁的变形重构问题写为以下非线性最小二乘形式







$$ begin{array}{l} mathop {arg min }limits_{{{boldsymbol{q}}_{
m{e}}}} {F_0}left( {{{boldsymbol{q}}_{
m{e}}}}
ight) = {R_{
m{t}}} + {R_{
m{b}}} end{array} $$
(14)

式中






$${R_{
m{t}}} = dfrac{1}{2}{left( {dfrac{1}{2}{boldsymbol{q}}_{
m{e}}^{
m{T}}{{boldsymbol{S}}_{
m{t}}}{{boldsymbol{q}}_{
m{e}}} - dfrac{1}{2} - dfrac{{{{hat varepsilon }^ + } + {{hat varepsilon }^ - }}}{2}}
ight)^2};;;$$






$${R_{
m{b}}} =dfrac{1}{2}left[ {dfrac{{bar h}}{{{{bar f}^3}left( xi
ight)}}q_{
m{e}}^{
m{T}}{S_{
m{b}}}{q_{
m{e}}} - } left( {{{hat varepsilon }^ + } - {{hat varepsilon }^ - }}
ight)
ight]^2$$

通过式(14)可以构建出单个缩减ANCF平面索梁单元内从应变到位移的推导关系, 本文将由此种关系建立起的单元格式称之为逆缩减ANCF平面索梁单元.


3.
基于逆ANCF单元的变形重构方法


显然, 通过逆缩减ANCF平面索梁单元对变形重构问题进行求解是一个非线性优化问题的求解过程, 需要借助相关数值优化方法建立一个可靠的求解算法. 由于式(14)所提的变形重构问题的非线性特征与其已知量和决策变量间数目间的不匹配特性, 本问题符合文献[36]中的不适定性数值最优化问题的定义, 此类问题的根源是解的确定性不足, 问题的提法不够完备. 问题的不适定性在求解时表现为无法正确收敛和收敛过程的不稳定, 例如出现目标函数Hesse矩阵不正定的情况. 对于一般的不适定性最优化问题可以通过增加适当的限制使之改造为适定性问题, 而对于本问题, 可以通过引入缩减ANCF单元外的、由实际情况带来的限制以使本问题实现稳定的求解. 所引入的关系分别为节点自由度间自相关性条件、节点处的${C^2}$连续性条件以及边界条件, 这些条件的引入同时也能使本方法在单元密度较低时取得较好的效果. 而在求解过程中, 由于不同工况对求解算法提出了不同的要求, 通过建立逐单元和多单元两种求解格式, 并通过递推的方法组装单元, 提升了本方法对不同应用工况的泛用性.


3.1
对逆ANCF单元的修正


之前提到了将单元内应变平均化会导致一些问题, 最主要的就是因待求解单元自由度与测量信息数目上不匹配导致的不适定性问题. 针对此问题, 并结合变形重构问题的特点, 下文进行了讨论并给出了修正方法.


3.1.1
简化节点自由度

首先需要注意的是, 节点的4个坐标分量中, 平动坐标对自然坐标的偏导数项不是独立的. 如果直接使用节点四自由度的形式作为数值最优化求解的决策变量会导致考虑其自相关约束的求解列式较为复杂, 也影响计算效率. 此外, 偏导数项的物理意义不够明确, 这对边界条件的参数化和后续在载荷感知等领域的扩展也不利. 因此本文使用以下缩减的节点位置向量进行替代







$$ begin{split} {bar {boldsymbol{q}}_{
m{e}}} = {left[ {begin{array}{*{20}{c}} {{{{r}}_x}left| {_{xi = 0}}
ight.}&{{{{r}}_y}left| {_{xi = 0}}
ight.}&{theta left| {_{xi = 0}}
ight.}&{{{{r}}_x}left| {_{xi = 1}}
ight.}&{{{{r}}_y}left| {_{xi = 1}}
ight.}&{theta left| {_{xi = 1}}
ight.} end{array}}
ight]^{{{
m{T}}}}}end{split} $$
(15)

原始节点位置向量与缩减的节点位置向量二者间的联系可以用下式表示







$$ begin{split} &frac{{partial {{boldsymbol{q}}_{
m{e}}}}}{{partial bar {boldsymbol{q}}_{
m{e}}^{
m{T}}}} = {{boldsymbol{T}}_{
m{e}}} =&left[ {begin{array}{*{20}{c}} 1&0&0&0&0&0 0&1&0&0&0&0 0&0&{ - fleft( 0
ight)sin left( {theta left| {_{xi = 0}}
ight.}
ight)}&0&0&0 0&0&{fleft( 0
ight)cos left( {theta left| {_{xi = 0}}
ight.}
ight)}&0&0&0 0&0&0&1&0&0 0&0&0&0&1&0 0&0&0&0&0&{ - fleft( 1
ight)sin left( {theta left| {_{xi = 1}}
ight.}
ight)} 0&0&0&0&0&{fleft( 1
ight)cos left( {theta left| {_{xi = 1}}
ight.}
ight)} end{array}}
ight]end{split} $$
(16)

式中$ fleft( 0
ight) $及$ fleft( 1
ight) $两项分别代表着两个节点处的伸长率, 在实际求解时均使用简化的、由应变测量值可以直接给出的$bar f$替代. 在进行后续的优化求解时, 由于目标函数与决策变量间的微分关系是迭代过程中的主要依据, 上式表示的二者联系可以使缩减的节点位移向量在进行迭代完全替代原来的节点位移向量.


3.1.2
边界约束及曲率连续性约束

为了唯一地确定在某一边界条件下的被测对象的变形, 需要同时引入边界条件和曲率连续性条件. 利用外点罚函数方法可以方便地实现这一点. 一个典型的受边界约束和曲率连续性约束的逆ANCF单元如图4所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-338-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
边界约束及曲率连续性约束示意图



Figure
4.
Schematic diagram of boundary constraints and curvature continuity constraints



下载:
全尺寸图片
幻灯片


记边界条件为







$$ {{q}}_j^i = {{q}}_{{
m{const}}j}^i,;;{{q}}_j^i in q_{
m{BC}}^i $$
(17)

其中$q_{
m{BC}}^i $是单元受边界条件限制的位移分量的集合. 需要注意的是, 本方法所指的边界条件不完全是力学意义上的边界条件, 而是指可以直接获得的某点处的坐标信息, 例如陀螺仪和编码器一类传感器得到的坐标信息同样当作边界条件处理. 根据上述记法, 可以在最小二乘列式中引入罚函数项来表示边界条件







$$ P_{{
m{eBC}}}^i = frac{1}{2}sum {{{left( {{{q}}_j^i - {{q}}_{{
m{const}}j}^i}
ight)}^2}} ,;{{q}}_{
m{j}}^i in q_{
m{BC}}^i $$
(18)

在分段求解时, 可以如图4通过已经求解并确定位移的节点对未经求解的相应单元施加边界条件.

ANCF单元在节点处只具有${C^1}$连续性, 这对利用基于ANCF的逆有限元方法重构被测对象完整连续的应变场是不利的. 如图4所示, 可以利用施加额外约束条件的方法迫使本方法中ANCF单元节点处具有${C^2}$连续性, 即保证除平动坐标和转角外, 曲率和弯曲引起的应变在相邻单元间也是连续的, 以消除ANCF单元的这种局限性. 将前一个单元的末端曲率作为下一个单元起始点曲率的目标值, 同样通过外点罚函数形式进行约束条件的施加. 记前一个单元的末端曲率为$ {kappa ^{i - 1}}left| {_{xi = 1}}
ight. $, 则相关限制条件可以表示为







$$ begin{split} P_{{
m{eAD}}}^i = &frac{1}{2}{left( {{kappa ^i}left| {_{xi = 0}}
ight. - {kappa ^{i - 1}}left| {_{xi = 1}}
ight.}
ight)^2} = &frac{1}{2}{left[ {frac{{{boldsymbol{S}}'left( 0
ight){{boldsymbol{q}}_{
m{e}}} times {boldsymbol{S}}''left( 0
ight){{boldsymbol{q}}_{
m{e}}}}}{{{{bar f}^3}}} - {kappa ^{i - 1}}left| {_{xi = 1}}
ight.}
ight]^2} end{split} $$
(19)

加入曲率连续性限制条件的算法不仅解决了适定性问题, 同时相较于经典的ANCF单元, 在节点处${C^2}$连续的本方法显然更加精确且接近实际. 这带来了能够以较少的测点与单元进行精确的变形重构的优势.

这里需要说明的是, 部分求解分段可能没有已求解共节点分段的节点曲率信息, 例如最初求解的分段. 这时它们的曲率约束条件可以根据实际条件给出, 例如简支端和无弯矩作用的自由端曲率可设为0. 对于通常没有作用于内部的大载荷因而曲率分布较为均匀的固支端单元, 可将由其测量应变直接转化为的曲率作为端部曲率, 这样既保证了计算的稳定性也不会引起大的误差. 在此基础上, 还可以使固支端单元短一些, 亦即使对应的测点靠近端部, 能够进一步保证这种近似的合理性从而避免误差.


3.2
逐单元求解过程与多单元整体求解过程


综上, 利用经过上述修正的逆ANCF单元, 可以构建出平面梁变形重构的方法. 鉴于整体求解时决策变量维度过大, 准确收敛难度较大, 考虑将被测体进行分段求解, 并利用ANCF单元的特性构造递推组装算法. 基于此, 建立了逐单元求解和多单元整体求解两种求解算法. 其中逐单元求解算法由于每次求解的决策变量维度小且每一迭代步的时间复杂度约为$Oleft( {{n^3}}
ight)$, 计算效率通常高于多单元求解算法; 而多单元整体求解方法可以利用已知的边界条件对求解进行校正, 以防止误差在长度范围上的积累. 二者实际可以在同一测量工作中混合使用, 以克服二者各自的局限性.


3.2.1
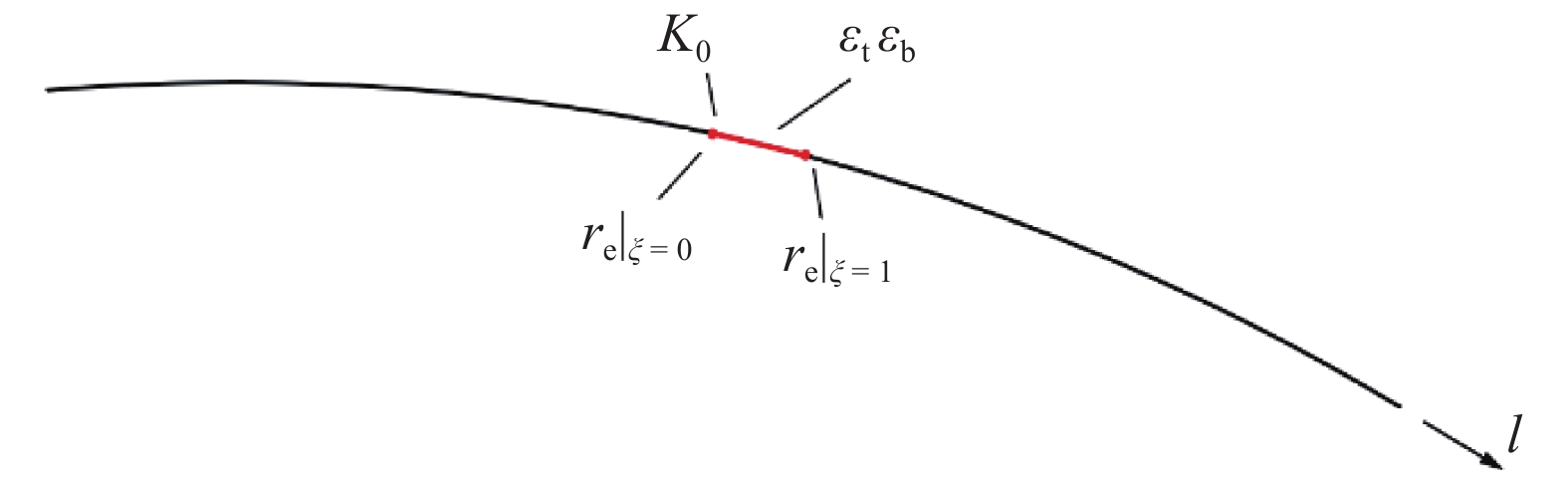
逐单元迭代求解过程

对于单个单元, 将测量的应变信息${varepsilon _{
m{t}}}$, ${varepsilon _{
m{b}}}$代入式(14)中, 并将已求解共节点分段的共用节点处曲率${kappa _0}$和位置信息${left. {{{boldsymbol{r}}_{
m{e}}}}
ight|_{xi = 0}}$通过式(18)和式(19)引入, 可以得到基于单个单元的变形重构最小二乘列式







$$ begin{split}& mathop {arg min }limits_{{{boldsymbol{q}}_{
m{e}}}} {F_{
m{e}}}left( {{{boldsymbol{q}}_{
m{e}}}}
ight) =& qquad {F_{{
m{e}}0}}left( {{{boldsymbol{q}}_{
m{e}}}}
ight) + {sigma _{
m{BC}}}{P_{{
m{eBC}}}}left( {{{boldsymbol{q}}_{
m{e}}}}
ight) + {sigma _{{
m{AD}}}}{P_{{
m{eAD}}}}left( {{{boldsymbol{q}}_{
m{e}}}}
ight) end{split} $$
(20)

从而求出此单元未求解节点处的位移${left. {{{boldsymbol{r}}_{
m{e}}}}
ight|_{xi = 1}}$, 如图5所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-338-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
逐单元变形重构



Figure
5.
Shape reconstruction in a single element



下载:
全尺寸图片
幻灯片


式中${sigma _{{{
m{BC}}}}}$及${sigma _{{
m{AD}}}}$分别为边界约束条件和曲率连续性条件对应的罚因子, 理论上会影响方法的收敛速度和收敛性. 但在数值仿真中证明, 本文涉及的算例中二者取值在${10^{ - 1}}$~${10^2}$间均能取得较好的效果, 在保证精度的情况下二者的取值范围相当大, 即本方法的变形重构效果对罚因子的取值不敏感. 本文之后的数值仿真中罚因子项均取为1.

在单个单元条件下进行如上式描述的最小二乘列式迭代求解复杂度有限, 最小二乘列式的梯度向量和Hesse矩阵形式较为简单, 因此可以使用基本的Newton法进行稳定便捷的求解.

Newton法需要目标函数的梯度向量和Hesse矩阵. 用$nabla {F_{{
m{e}}0}}left( {{{bar{boldsymbol{q}}}_{
m{e}}}}
ight)$, ${nabla ^2}{F_{{
m{e}}0}}left( {{{bar{boldsymbol{q}}}_{
m{e}}}}
ight)$, $nabla {P_{{
m{eBC}}}}left( {{{bar{boldsymbol{q}}}_{
m{e}}}}
ight)$, ${nabla ^2}{P_{
m{eBC}}}left( {{{bar{boldsymbol{q}}}_{
m{e}}}}
ight)$, $nabla {P_{{
m{eAD}}}}left( {{{bar{boldsymbol{q}}}_{
m{e}}}}
ight)$和${nabla ^2}{P_{{
m{eAD}}}}left( {{{bar{boldsymbol{q}}}_{
m{e}}}}
ight)$分别表示式中各项梯度向量和Hesse矩阵. 需要注意的是, 在迭代过程中使用的此处各项均改为使用缩并的节点自由度. 以$ {F_{{
m{e}}0}}left( {{{bar{boldsymbol{q}}}_{
m{e}}}}
ight) $项为例, 为了方便求解列式, 将相关项转为矩阵形式表达, 记$ {F_{{
m{e}}0}}left( {{{bar{boldsymbol{q}}}_{
m{e}}}}
ight) $项残差为







$$ {{boldsymbol{r}}^{
m{err}}} = left[ {begin{array}{*{20}{c}} {{{r}}_{
m{t}}^{
m{err}}} {{{r}}_{
m{b}}^{
m{err}}} end{array}}
ight] = left[ {begin{array}{*{20}{c}} {{varepsilon _{
m{t}}} - {{hat varepsilon }_{
m{t}}}} {{varepsilon _{
m{b}}} - {{hat varepsilon }_{
m{b}}}} end{array}}
ight] $$
(21)

则残差的Jacobian矩阵为







$$ {{boldsymbol{J}}_{
m{re}}} = left[ {begin{array}{*{20}{c}} {{{left( {dfrac{{partial r_{{
m{t}}}^{
m{err}}}}{{partial {{boldsymbol{q}}_{
m{e}}}}}}
ight)}^{
m{T}}}dfrac{{partial {{boldsymbol{q}}_{
m{e}}}}}{{partial bar {boldsymbol{q}}_{
m{e}}^{
m{T}}}}} {{{left( {dfrac{{partial r_{
m{b}}^{
m{err}}}}{{partial {{boldsymbol{q}}_{
m{e}}}}}}
ight)}^{
m{T}}}dfrac{{partial {{boldsymbol{q}}_{
m{e}}}}}{{partial bar {boldsymbol{q}}_{
m{e}}^{
m{T}}}}} end{array}}
ight] = left[ {begin{array}{*{20}{c}} {{boldsymbol{q}}_{
m{e}}^{
m{T}}{{boldsymbol{S}}_{
m{t}}}{{boldsymbol{T}}_{
m{e}}}} {dfrac{{2bar h}}{{{{bar f}^3}}}{boldsymbol{q}}_{
m{e}}^{
m{T}}{{boldsymbol{S}}_{
m{b}}}{{boldsymbol{T}}_{
m{e}}}} end{array}}
ight] $$
(22)

进而有







$$ nabla {F_{{
m{e}}0}}left( {{{bar {boldsymbol{q}}}_{
m{e}}}}
ight) = {boldsymbol{J}}_{{text{re}}}^{
m{T}}{{boldsymbol{r}}^{
m{err}}} $$
(23)

将残差中某项的Hesse阵记为$ {nabla ^2}{{r}}_i^{
m{err}} $, 则有







$$ {nabla ^2}{F_{{
m{e}}0}}left( {{{bar {boldsymbol{q}}}_{
m{e}}}}
ight) = {boldsymbol{J}}_{
m{re}}^{
m{T}}{{boldsymbol{J}}_{
m{re}}} + sumlimits_{i = 1}^n {{{r}}_i^{
m{err}}} {nabla ^2}{{r}}_i^{
m{err}} $$
(24)

最小二乘列式中其他两项罚函数的计算过程均类似, 结合式(18)及式(19), 分别通过边界条件或一端的曲率求出各项的残差并结合各项Jacobian矩阵进行计算, 此处不赘述.

因此总体最小二乘列式的相关参数可表示为







$$begin{split} nabla {F_{
m{e}}}left( {{{bar{boldsymbol{q}}}_{
m{e}}}}
ight) = &nabla {F_{{
m{e}}0}}left( {{{bar{boldsymbol{q}}}_{
m{e}}}}
ight) + {sigma _{
m{BC}}}nabla {P_{{
m{eBC}}}}left( {{{bar{boldsymbol{q}}}_{
m{e}}}}
ight) + & {sigma _{{
m{AD}}}}nabla {P_{{
m{eAD}}}}left( {{{bar{boldsymbol{q}}}_{
m{e}}}}
ight) end{split}qquad$$
(25)







$$ begin{split} {nabla ^2}{F_{
m{e}}}left( {{{bar{boldsymbol{q}}}_{
m{e}}}}
ight) =& {nabla ^2}{F_{{
m{e}}0}}left( {{{bar{boldsymbol{q}}}_{
m{e}}}}
ight) + {sigma _{
m{BC}}}{nabla ^2}{P_{{
m{eBC}}}}left( {{{bar{boldsymbol{q}}}_{
m{e}}}}
ight) + &{sigma _{{
m{AD}}}}{nabla ^2}{P_{{
m{eAD}}}}left( {{{bar{boldsymbol{q}}}_{
m{e}}}}
ight)qquadqquad end{split} $$
(26)

则Newton法列式可记为







$$ {d_k} = {left[ {{nabla ^2}{F_{
m{e}}}left( {{{bar{boldsymbol{q}}}_{{
m{e}}k}}}
ight)}
ight]^{ - 1}}nabla {F_{
m{e}}}left( {{{bar{boldsymbol{q}}}_{{
m{e}}k}}}
ight) $$
(27)

其中$k$表示第$k$次迭代, ${d_k}$表示第$k$迭代步. 在实际数值仿真中, 逐单元的变形重构过程中Newton法在各类工况下都相当稳定, 不会出现${nabla ^2}Fleft( {{{bar{boldsymbol{q}}}_{{
m{e}}k}}}
ight)$奇异等情况.

对于单个单元, 通常在求解时已知的曲率和其他边界条件能够让对单个单元进行的变形重构问题变为适定的.


3.2.2
多单元整体迭代求解过程

多单元求解算法的优势在于能够适应分散的边界条件, 在处理此类问题时能结合边界条件进行求解. 另外对于迭代求解过程中剩余量较小的情况, 这种算法在某种程度上能够减少迭代的次数, 这预示着此种求解算法在对被测物变形情况进行动态跟踪时具有一定优势.

对于多个单元同时求解的情况, 借鉴有限元方法中刚度矩阵的组集方式, 引入布尔映射矩阵${{boldsymbol{B}}_i}$建立整体坐标至局部坐标的映射. 将各单元测量的应变信息${varepsilon _{{
m{t}}i}}$, ${varepsilon _{{
m{b}}i}}$代入式(14)中同时将各单元由此得到的罚函数项求和, 并将求解共节点分段的共用节点处曲率${kappa _0}$和位置信息${{boldsymbol{r}}_{{
m{e}}1}}$由式(18)和式(19)引入, 即可得到多单元整体求解列式







$$ begin{split} mathop {arg min }limits_{boldsymbol{q}} {F_{
m{m}}}left( {boldsymbol{q}}
ight) = &{F_{{
m{m}}0}}left( {boldsymbol{q}}
ight) + {sigma _{{
m{mBC}}}}{P_{{
m{mBC}}}}left( {boldsymbol{q}}
ight) + &{sigma _{{
m{mAD}}}}{P_{{
m{mAD}}}}left( {boldsymbol{q}}
ight) end{split} $$
(28)

从而求出此分段中各未求解节点的坐标${{boldsymbol{r}}_{{
m{e}}i}}$, 如图6所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-338-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
多单元变形重构



Figure
6.
Shape reconstruction in multi element



下载:
全尺寸图片
幻灯片


在式(28)中, 整体坐标的形式为







$$ {boldsymbol{q}} = {left[ {begin{array}{*{20}{c}} {{boldsymbol{r}}_{{
m{e}}1}^{
m{T}}}&{dot {boldsymbol{r}}_{{
m{e}}1}^{
m{T}}}& cdots &{dot {boldsymbol{r}}_{{
m{e}}n}^{
m{T}}} end{array}}
ight]^{
m{T}}} $$
(29)

边界条件罚函数项$ {P_{{
m{mBC}}}} $及曲率连续性条件罚函数项$ {P_{{
m{mAD}}}} $为







$$ {P_{{
m{mBC}}}} = frac{1}{2}sum {{{left( {{{{q}}_i} - {{{q}}_{{
m{const}}i}}}
ight)}^2}} ,;{{{q}}_i} in {q_{{
m{mBC}}}};;;;;qquadqquad$$
(30)







$$ left. {begin{array}{*{20}{l}} {P_{{
m{mAD}}}} = dfrac{1}{2}displaystylesumlimits_{i = 2}^n {{{left( {{kappa ^i}left| {_{xi = 0}}
ight. - {kappa ^{i - 1}}left| {_{xi = 1}}
ight.}
ight)}^2}}= qquad dfrac{1}{2}displaystylesumlimits_{i = 2}^n left[ dfrac{{{{{boldsymbol{S}}'_i}}left( 0
ight){boldsymbol{q}}_{
m{e}}^i times {{{boldsymbol{S}}''_i}}left( 0
ight){boldsymbol{q}}_{
m{e}}^i}}{{{{bar f}_i}^3}} -
ight. qquad qquad left. dfrac{{{{{boldsymbol{S}}'_{i - 1}}}left( 1
ight){boldsymbol{q}}_{
m{e}}^{i - 1} times {{{boldsymbol{S}}''_{i - 1}}}left( 1
ight){boldsymbol{q}}_{
m{e}}^{i - 1}}}{{bar f_{i - 1}^3}}
ight]^2 = qquad dfrac{1}{2}displaystylesumlimits_{i = 2}^n {{{left( {{{boldsymbol{q}}^{
m{T}}}{boldsymbol{R}}_{{
m{mAD}}}^i{boldsymbol{q}}}
ight)}^2}} {boldsymbol{R}}_{{
m{mAD}}}^i = dfrac{{{boldsymbol{B}}_i^{
m{T}}left[ {{boldsymbol{S}}_{i1}^{'{
m{T}}}left( 0
ight){{{boldsymbol{S}}''_{i2}}}left( 0
ight) - {boldsymbol{S}}_{left( {i - 1}
ight)2}^{'{
m{T}}}left( 0
ight){{{boldsymbol{S}}''_{left( {i - 1}
ight)1}}}left( 0
ight)}
ight]{{boldsymbol{B}}_i}}}{{{{bar f}_i}^3}} -qquad dfrac{{{boldsymbol{B}}_{i - 1}^{
m{T}}left[ {{boldsymbol{S}}_{i1}^{'{
m{T}}}left( 1
ight){{{boldsymbol{S}}''_{i2}}}left( 1
ight) - {boldsymbol{S}}_{left( {i - 1}
ight)2}^{'{
m{T}}}left( 1
ight){{{boldsymbol{S}}''_{left( {i - 1}
ight)1}}}left( 1
ight)}
ight]{{boldsymbol{B}}_{i - 1}}}}{{bar f_{i - 1}^3}}end{array}}
ight} $$
(31)

式中$ {q_{{
m{mBC}}}} $是全部受边界条件约束的节点坐标分量集合. 注意到$ {boldsymbol{R}}_{{
m{mAD}}}^i $是常量矩阵, 因此易于计算$ {P_{{
m{mAD}}}} $的梯度.

式(28)中的基本最小二乘列式$ {F_{{
m{m}}0}}left( {boldsymbol{q}}
ight) $为







$$ begin{array}{l} min {F_{{
m{m}}0}}left( {boldsymbol{q}}
ight) = displaystylesumlimits_{i = 1}^n {left( {{{{R}}_{{
m{mt}}i}} + {{{R}}_{{
m{mb}}i}}}
ight)} end{array} $$
(32)

式中






$${R_{{
m{mt}}i}} = dfrac{1}{2}{left( {dfrac{1}{2}{{boldsymbol{q}}^{
m{T}}}{boldsymbol{B}}_i^{
m{T}}{{boldsymbol{S}}_{{
m{t}}i}}{{boldsymbol{B}}_i}{boldsymbol{q}} - dfrac{1}{2} - {{hat varepsilon }_{{
m{t}}i}}}
ight)^2}$$






$${R_{{
m{mb}}i}} = dfrac{1}{2}left( {dfrac{{{{bar h}_i}}}{{f_i^3}}{{boldsymbol{q}}^{
m{T}}}{boldsymbol{B}}_i^{
m{T}}{{boldsymbol{S}}_{{
m{b}}i}}{{boldsymbol{B}}_i}{boldsymbol{q}} - } {{{hat varepsilon }_{{
m{b}}i}}}
ight)^2$$

将式(32)写成矩阵形式, 即可将残差记为







$$ begin{split} {boldsymbol{r}}_{
m{m}}^{
m{err}} =& {left[ {begin{array}{*{20}{c}} {{{r}}_{{
m{mt}}1}^{
m{err}}}&{{{r}}_{
m{mb1}}^{
m{err}}}& cdots &{{{r}}_{{
m{mt}}n}^{
m{err}}} end{array}}
ight]^{
m{T}}}= & {left[ {begin{array}{*{20}{c}} {{varepsilon _{
m{mt1}}} - {{hat varepsilon }_{
m{mt1}}}}&{{varepsilon _{
m{mb1}}} - {{hat varepsilon }_{
m{mb1}}}}& cdots &{{varepsilon _{{
m{mb}}n}} - {{hat varepsilon }_{{
m{mb}}n}}} end{array}}
ight]^{
m{T}}} end{split} $$
(33)

残差的Jacobian矩阵为







$$ {{boldsymbol{J}}_{
m{rm}}} = left[ {begin{array}{*{20}{c}} {{{left( {dfrac{{partial r_{
m{mt1}}^{
m{err}}}}{{partial {boldsymbol{q}}}}}
ight)}^{
m{T}}}dfrac{{partial {boldsymbol{q}}}}{{partial {{bar{boldsymbol{q}}}^{
m{T}}}}}} {{{left( {dfrac{{partial r_{
m{mb1}}^{
m{err}}}}{{partial {boldsymbol{q}}}}}
ight)}^{
m{T}}}dfrac{{partial {boldsymbol{q}}}}{{partial {{bar{boldsymbol{q}}}^{
m{T}}}}}} vdots {{{left( {dfrac{{partial r_{{
m{mb}}n}^{
m{err}}}}{{partial {boldsymbol{q}}}}}
ight)}^{
m{T}}}dfrac{{partial {boldsymbol{q}}}}{{partial {{bar{boldsymbol{q}}}^{
m{T}}}}}} end{array}}
ight] = left[ {begin{array}{*{20}{c}} {{{boldsymbol{q}}^{
m{T}}}{boldsymbol{B}}_1^{
m{T}}{{boldsymbol{S}}_{{
m{t}}i}}{{boldsymbol{B}}_1}{{boldsymbol{T}}_{{
m{m}}}}} {dfrac{{2{{bar h}_2}}}{{{{bar f}^3}}}{{boldsymbol{q}}^{
m{T}}}{boldsymbol{B}}_{2}^{
m{T}}{{boldsymbol{S}}_{{
m{b}}i}}{{boldsymbol{B}}_2}{{boldsymbol{T}}_{{
m{m}}}}} vdots {dfrac{{2{{bar h}_n}}}{{{{bar f}^3}}}{{boldsymbol{q}}^{
m{T}}}{boldsymbol{B}}_n^{
m{T}}{{boldsymbol{S}}_{{
m{b}}i}}{{boldsymbol{B}}_n}{{boldsymbol{T}}_{{
m{m}}}}} end{array}}
ight] $$
(34)

进而$ {F_{{
m{m}}0}}left( {boldsymbol{q}}
ight) $对应的使用缩并节点自由度的梯度向量$ nabla {F_{{
m{m}}0}}left( {bar{boldsymbol{q}}}
ight) $及Hesse阵$ {nabla ^2}{F_{{
m{m}}0}}left( {bar{boldsymbol{q}}}
ight) $可表示为







$$ nabla {F_{
m{m0}}}left( {bar{boldsymbol{q}}}
ight) = {boldsymbol{J}}_{
m{rm}}^{
m{T}}{boldsymbol{r}}_{{
m{m}}}^{
m{err}} $$
(35)







$$ {nabla ^2}{F_{
m{m0}}}left( {bar{boldsymbol{q}}}
ight) = {boldsymbol{J}}_{
m{rm}}^{
m{T}}{{boldsymbol{J}}_{
m{rm}}} + sumlimits_{i = 1}^n {{{r}}_{{{
m{m}}}i}^{
m{err}}} {nabla ^2}{{r}}_{{{
m{m}}}i}^{
m{err}} $$
(36)

边界条件罚函数项$ {P_{{
m{mBC}}}} $及曲率连续性条件罚函数项$ {P_{{
m{mAD}}}} $的梯度向量及Hesse阵以相同形式写出, 此处不赘述.

由于整体求解算法下决策变量维度不可避免的增大, 在大剩余量条件下收敛稳定性往往较差, 很多时候需要采用更加复杂、鲁棒性更高的最优化求解方法才能进行顺利求解, 此处不作深入讨论, 后文中整体求解方法的实现使用由Dogleg方法求解子问题的信赖域方法.


3.3
单元递推组装


进行分段求解之后, 还需要一种方法将被测对象的各自独立的分段连接起来. 已经知道每个节点的3个坐标分量(${{{r}}_1}$, ${{{r}}_2}$, $theta $)都是线性独立的, 同一节点的3个坐标分量互不影响, 且具有线性可加性, 各段内部的变形实际上决定了从一个节点指向另一个节点的位移向量. 如图7, 经过方向余弦矩阵进行坐标转换处理以后, 得到的位移向量从一个节点坐标指向另一个节点坐标. 因此, 可以在对各段分别进行求解之后再进行连接, 由于之前提到的各坐标分量间的独立可加性, 这种连接不会破坏一维二节点ANCF单元在节点处的连续.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-338-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
单元递推组装



Figure
7.
Unit recursively assemble



下载:
全尺寸图片
幻灯片


具体算法是将每段均视为受一端固支的边界条件限制, 根据测量应变和已进行求解的共节点相邻段的末端曲率, 进行自由端位移的求解. 当然, 这还依赖于事先规定的递推求解顺序.

通过这种形式的求解, 能够得到从固支端指向自由端的位置向量, 记为







$$ {bar {boldsymbol{r}}_{{
m{e}}i}} = {left[ {begin{array}{*{20}{c}} {{bar r_{i1}}}&{{bar r_{i2}}}&{{{ bar theta }_i}} end{array}}
ight]^{
m{T}}} $$
(37)

进行逐段拼接, 即依次确定各节点的位置向量, 记为







$$ {{boldsymbol{r}}_{{
m{e}}i}} = {left[ {begin{array}{*{20}{c}} {{r_{i1}}}&{{r_{i2}}}&{{theta _i}} end{array}}
ight]^{
m{T}}} $$
(38)

拼接时, 其中的平动坐标分量需要经过方向余弦矩阵进行旋转处理, 角度可以直接相加, 计算如下







$$ begin{split} {{boldsymbol{r}}_{{
m{e}}i}}& = {{boldsymbol{r}}_{{
m{e}}left( {i{{ - }}1}
ight)}} + left[ {begin{array}{*{20}{c}} {cos {theta _{i - 1}}}&{ - sin {theta _{i - 1}}}&0 {sin {theta _{i - 1}}}&{cos {theta _{i - 1}}}&0 0&0&1 end{array}}
ight]left[ {begin{array}{*{20}{c}} {{bar r_{i1}}} {{bar r_{i2}}} {{bar theta_i}} end{array}}
ight] & = {{boldsymbol{r}}_{{
m{e}}left( {i{{ - }}1}
ight)}} + {{boldsymbol{A}}_i}{{ {bar{boldsymbol{r}}}}_{{
m{e}}i}} end{split} $$
(39)

由此, 就获得了逐节点的求解结果. 如果需要整体连续的变形状态, 可以将形函数代入, 即可得到连续的位移函数. 需要注意的是, 此处得到的是基于初始构型和自然坐标的位移描述.

由于实际应用中具体情况的不同, 以上单元组装方法可以根据需要而预先设计规划并灵活使用.


3.4
算法流程


综合以上, 将整体的算法流程进行总结:

(1)将被测对象进行单元划分. 在这一过程中, 要考虑工作中载荷位置及大小对应变分布的影响及应变测量设备的实际限制. 单元及测点密度选取的标准是使在预计的变形范围内单元内的应变都可以通过本文使用的ANCF方法较好地描述, 这也意味着在应变变化较为剧烈的部分应增大测点密度才能使变形重构效果理想;

(2)根据之前对逐单元求解方式和多单元求解方式的各自特点及适应范围的讨论, 进行各独立求解分段的划分;

(3)由式(10)及式(11)计算各单元的轴向应变矩阵$ {boldsymbol{S}}_{
m{t}}^i $和弯曲应变矩阵$ {boldsymbol{S}}_{
m{b}}^i $;

(4)根据测量的应变信息, 各求解分段按顺序应用其对应的求解迭代算法和事先设定的收敛终止规则, 在依次传递节点曲率信息的基础上进行独立的求解. 其中单单元分段由式(20)所示的最小二乘列式进行求解; 多单元分段由式(28)所示的最小二乘列式进行求解;

(5)借由式(39)进行整体坐标的组装.


4.
数值仿真


本节进行本方法的仿真验证. 下述全部算例所需的原始数据, 包括应变及位移均由ABAQUS计算给出. 即对图8 ~ 图12所示的仿真工况, 即均使用ABAQUS进行仿真分析, 从而得到各个工况下的应变及对应的位移数据, 将由应变重构出的位移数据与仿真得到的位移数据相比较. 下列算例的ABAQUS分析均使用B22单元, 进行几何非线性条件下的静态通用分析步. 此算例运行于MATLAB R2020a软件环境下, 处理器型号为i7-10700.



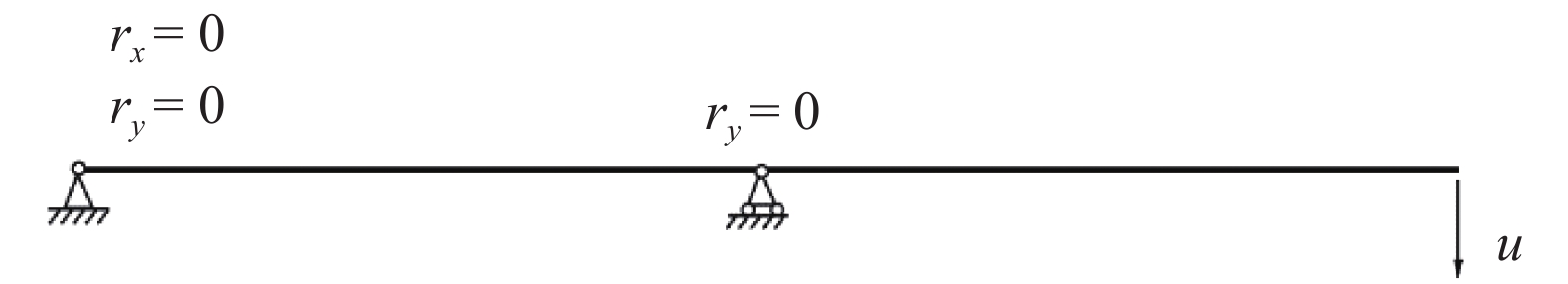onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-338-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
位移载荷下的外伸梁示意图



Figure
8.
Schematic of overhanging beam under displacement load



下载:
全尺寸图片
幻灯片


本节使用3个算例来展示并验证本算法在有限变形条件下的变形重构效果. 首先是在一个给定边界条件下, 将逐单元求解过程和多单元求解过程混合使用, 进行不同单元密度下的效果验证, 以初步展示本方法的重构效果; 第2个算例是在一端固支、自由端受横向载荷的简单载荷下, 将不同的经典平面梁变形重构方法进行对比, 验证本方法在大变形条件下的优越性; 最后一个算例将本方法与基于曲率连续化的方法进行对比, 以验证本方法在轴向大变形条件下具有更佳的适应性.


4.1
大变形工况下的重构效果验证


为了验证本方法中边界条件相关部分的有效性, 设计了一种分散边界条件下的变形工况, 如图8所示, 以一根40 cm的细长梁为对象, 在自由端施加竖直方向的位移载荷$u$. 此被测对象一端简支, 在其中部20 cm处进行竖直方向的铰接约束.

为验证本方法在不同测量条件下的性能, 模拟使用不同的测点个数及对应的单元密度进行建模和求解, 在各种单元密度下, 都采用均匀划分单元的方式. 此处对左侧两处铰接中的部分进行整体求解, 并将边界条件使用式(18)的形式代入求解过程中, 右侧自由部分则进行逐单元求解. 逐单元求解部分的各单元间及其与整体求解部分的连接处使用单元组装方法进行连接, 为了直观地看出重构效果, 为重构得到的节点坐标定义如下的相对误差表征







$$ {d_{{{e}}rr}} = frac{1}{n}frac{1}{{bar d}}sqrt {sumlimits_{i = 1}^n {{{left( {{d_i} - {{hat d}_i}}
ight)}^2}} } $$
(40)

其中$n$为节点数, ${d_i}$为重构得到的各节点坐标分量, ${hat d_i}$为仿真得到的对应位移分量, $bar d$为在整个被测对象上对应项的模的均值.

本算例与后续算例以两次迭代残差间的差值小于设定值为迭代终止条件.

图9中依次给出了20测点、10测点、4测点数下施加不同位移载荷时本方法重构出的变形状态(图9中以散点表示的节点坐标)与仿真得到的变形状态(图9中以实线表示)的对比. 为模拟平面梁的大变形情况, 将位移载荷分别设置为50 mm, 100 mm, 200 mm, 其中200 mm的位移载荷已达到被测梁长度的一半, 是相当极端的变形情况. 从图9(a)中可以看出, 在20测点时, 各种载荷条件下本方法由应变重构出的变形状态均与仿真得到的变形状态均基本重合, 这说明本方法能够较为精确地实现有限变形条件下的变形重构; 在10测点(图9(b))下, 重构效果依然良好; 而在最为极端的4测点(图9(c))下, 位移载荷在50 mm和100 mm情况下的重构效果仍然很好, 只有位移载荷200 mm时存在较明显误差. 正如前面分析, 误差产生的原因是4个测点已经不足以精确反映被测对象内部的应变分布. 上述结果表明, 本文方法对不同程度的大变形重构都具有较高的精度和收敛性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-338-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
大变形条件下不同测点数的重构效果



Figure
9.
Reconstruction performance of different number of measuring points under large deformation



下载:
全尺寸图片
幻灯片


进一步在表1 ~ 表3给出各仿真工况下重构的相对误差及计算用时. 从表1可以看出, 在各位移载荷下, 总体的重构相对误差接近, 200 mm位移载荷工况比另两种位移载荷工况相对误差略微增大; 在计算时间方面, 各位移载荷工况计算用时也都相近. 这证明了本方法在不同变形条件下的精度和收敛性. 表2除同样体现上述规律外, 可以看出10测点数与20测点数条件下重构的相对误差及计算用时仍然差距不大, 这说明在合适的测点数范围内, 测点数对重构效果影响有限. 表3中展示了在较为极端的4测点条件下的仿真情况, 此测点数下重构相对误差较之前有较大增加, 特别是200 mm位移载荷条件下出现较明显的误差, 而计算用时方面则变化很小. 如之前分析, 这说明4测点已经不足以精确反映被测对象内部应变分布, 而200 mm位移载荷工况下相对误差显著高于此测点数下另两种位移载荷工况, 则证明此种原因导致的误差对于变形程度大的情况更加显著. 在计算用时方面, 不同测点数及位移载荷工况下用时均较为接近, 这说明本方法在各工况下均具有较好的收敛性.




表
1
20个测点下的相对误差及计算用时



Table
1.
Reconstruction error and calculation time under 20 measuring points condition



table_type1 ">
$u$/mm${x_ {
m{err} } }$		$ {y_{{
m{err}}}} $		$ {theta _{{
m{err}}}} $		t/s
506.28×10?43.68×10?47.42×10?80.137
1006.20×10?43.82×10?42.88×10?70.138
2007.96×10?46.86×10?41.10×10?50.145





下载:
导出CSV
|显示表格






表
2
10个测点下的相对误差及计算用时



Table
2.
Reconstruction error and calculation time under 10 measuring points condition



table_type1 ">
$u$/mm${x_ {
m{err} } }$		${y_ {
m{err} } }$		${theta _ {
m{err} } }$		t/s
508.67×10?43.75×10?49.12×10?70.118
1008.31×10?43.69×10?44.12×10?60.123
2009.18×10?46.04×10?42.56×10?40.124





下载:
导出CSV
|显示表格






表
3
4个测点下的相对误差及计算用时



Table
3.
Reconstruction error and calculation time under 4 measuring points condition



table_type1 ">
$u$/mm${x_ {
m{err} } }$		${y_ {
m{err} } }$		${theta _ {
m{err} } }$		t/s
502.38×10?31.53×10?35.34×10?50.113
1002.68×10?31.64×10?32.60×10?40.113
2005.29×10?22.49×10?21.88×10?20.118





下载:
导出CSV
|显示表格



单纯从单次重构所需的时间可以看出, 本方法计算需时实际较短. 考虑到以相近的变形状态作为初值能够进一步缩减迭代步数, 以及储存的轴向应变矩阵及弯曲应变矩阵在同一被测对象的不同变形状态下无需重复计算, 本方法在变形状态动态追踪方面应该也具有潜力.


4.2
与已有方法的对比


之前提到了线性逆有限元法、Ko法以及基于曲率连续化的方法的特点及其局限性, 在此处以较为简单的悬臂梁受自由端较大数值方向位移载荷时的工况, 给出以上方法与逆ANCF单元方法的实际效果的比较. 使用图10所示的仿真设置进行不同变形重构方法的对比.

本算例下各种仿真条件下的不同方法均采用20测点, 单元以均匀方式布置. 具体效果如图11.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-338-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
位移载荷下的悬臂梁示意图



Figure
10.
Schematic of cantilever beam under displacement load



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-338-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
不同方法的悬臂梁变形重构仿真结果



Figure
11.
Reconstruction performance of cantilever beam in different methods



下载:
全尺寸图片
幻灯片


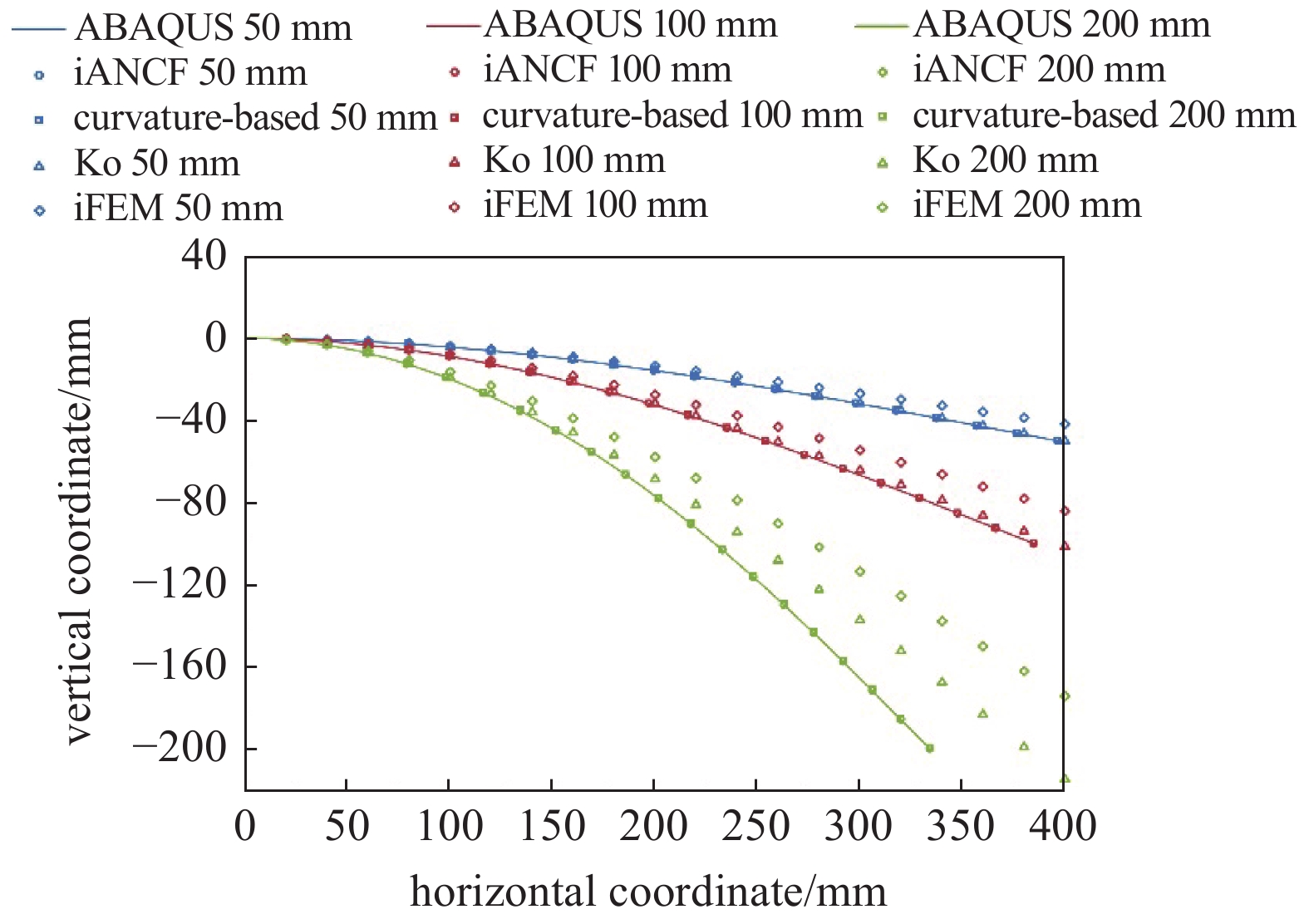
图11中给出了施加不同位移载荷时本方法、曲率连续化方法、Ko方法和逆有限元重构效果的对比. 从图中可以看出, Ko法与逆有限元法由于其线性化特性及忽略了轴向位移影响, 随变形程度增大显著提升. 逆有限元方法相较于用分段去对横向位移进行近似非线性计算的Ko法而言误差更大. 这充分说明了在有限变形条件下基于线性假设的变形重构方法的局限性. 曲率连续化方法和本方法在此仿真算例的各种位移载荷设置下重构得到的变形状态均能与仿真给出的变形状态高度重合.

在此种轴向变形不显著的情况下, 单纯基于曲率的方法与逆ANCF单元法均可以准确地重构出被测体的变形, 效果差异差距不显著. 因此设计如图12的仿真验证轴向大变形情况下ANCF方法的表现.

此算例依旧使用20测点, 其中轴向和横向的位移载荷设为相等, 均为$u$. 结果见图13, 随横向和轴向位移载荷的增大, 被测对象的轴向变形愈加显著, 此时, 曲率连续化方法的重构误差明显增加, 而本方法仍然能保证较高的精度. 可以看出, 本方法对轴向大变形情况的适应性明显高于单纯基于曲率的方法.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-338-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
轴向大变形条件下的简支梁示意图



Figure
12.
Schematic of simply supported beam under large axial deformation



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-338-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
轴向大变形条件下曲率连续化方法和iANCF方法的对比



Figure
13.
Comparison of curvature-based method and iANCF under large axial deformation



下载:
全尺寸图片
幻灯片



5.
结论


本文继承了逆有限元法的思想, 利用非线性的缩减ANCF平面梁单元对梁的应变?位移映射关系进行描述, 进而采用数值优化方法的思想进行位移的求解. 将求解格式分为逐单元与整体两种, 前者求解稳定且计算量小, 后者能够实现对边界条件的灵活适应. 而通过单元的连接算法, 二者实际上可以在实际应用中相互融合.

通过多个数值算例证明了本算法的有效性, 在大变形条件下能够用较少的测点实现精确的变形重构. 此外, 相较于已有的柔性结构变形重构算法而言, 本方法引入梯度缩减ANCF单元来刻画被测对象的应变场和位移场间的关系, 进而成功地将能够实现精确变形重构的变形模式范围扩展到了能用ANCF方法描述的任意变形模式. 结合已有的不同类型ANCF单元, 本文提出的利用ANCF单元构造优化问题进而建立变形重构算法的思想能够推广到不同类型的被测对象及场景. 而由于本方法与有限元方法的高度融合, 也能够自然地将应用范围扩展到与有限元相关的动静载荷识别、振动控制及健康监测方面.

相关话题/计算 测量 信息 图片 过程
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 考虑混凝土塑性耗散的CDM-XFEM裂缝计算方法
    引言混凝土结构是建筑、交通、水利等领域的重要基础材料,其可塑性高、耐久性好是受广泛应用的主要原因.但混凝土抗拉强度远低于抗压强度[1],结构在服役期间受外界载荷的影响容易产生裂缝[2],裂缝的出现不仅会降低结构刚度,还为外部侵蚀介质的侵入提供了快捷通道,从而加速内部钢筋锈蚀[3-4]、降低结构承载力 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 颗粒材料计算力学专题序
    颗粒材料广泛地存在于自然环境、工业生产和日常生活等诸多领域,其受加载速率、约束条件等因素的影响具有复杂的力学行为.颗粒材料常与流体介质、工程结构物耦合作用并共同组成复杂的颗粒系统,并呈现出非连续性、非均质性的复杂力学特性.目前,离散元方法已成为解决不同工程领域颗粒材料问题的有力工具,然而其在真实颗粒 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 椭球颗粒体系剪切过程中自由体积的分布与演化
    引言颗粒物质是由大量离散固体相互作用而形成的复杂体系,在自然界和工业界广泛存在.以水利和岩土工程中的堆石体为例,由于取材方便,且对地形、地质条件有较强的适应性,在堆石坝、路堤、机场高填方地基等工程建设中得到广泛应用.这些工程一旦出现问题和隐患,将会严重威胁人民生命财产安全,因此迫切需要深入研究颗粒材 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 一种新的玻尔兹曼方程可计算模型构造与分析
    引言近年来,随着对临近空间战略意义认识的加深,各航空航天大国发展了众多临近空间飞行器.为满足长航时、大载荷、高超声速巡航等需求,这类临近空间飞行器通常整体尺寸较大,各部件间差异显著,飞行过程会出现多物理多场耦合、多流区共存的多尺度复杂流动现象,传统的数值模拟方法如基于宏观连续介质假设的纳维?斯托克斯 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 页岩凝析气藏相平衡的快速准确计算方法
    引言随着以煤炭、石油和木柴为代表的传统能源消耗带来的巨量的空气污染日益引起全社会的关注,天然气作为一种相对较为清洁的能源得到了广泛的重视[1].近年来在非常规油气藏勘探和开发技术上的迅猛发展,使得具有巨大潜在储量但一直得不到有效开发的以页岩气为代表的非常规油气资源成为了投资热点和研究焦点[2].中国 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于Darcy-Stokes耦合模型的多孔介质颗粒悬浮液等效黏性系数计算
    引言颗粒悬浮液广泛存在于自然界及工程应用领域,其黏性特征对悬浮液的流动行为有着重要的影响[1-4].早在1905年,Einstein[5]就研究了低浓度条件下球形固体颗粒对流体黏性的影响,给出了悬浮液等效黏度系数计算的一个强有力的理论框架,并得到了低浓度球形颗粒悬浮液的著名的Einstein黏性公式 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于主应变场的混凝土全表面开裂特征实时测量与分析
    引言混凝土结构服役过程中产生裂纹是不可避免的,而裂纹的扩展是混凝土结构承载能力、耐久性及防水性降低的主要原因.在实验室测试新型混凝土结构或混凝土材料时,测量裂纹发展过程对于揭示混凝土结构的破坏机理、评价混凝土结构的力学性能十分重要[1].目前在实验室检测混凝土表观裂纹仍以传统的人工方法为主,用马克笔 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • DVC中内部散斑质量评价及计算体素点的优化选择
    引言数字体图像相关方法(digitalvolumecorrelation,DVC)是二维数字图像相关方法(two-dimensionaldigitalimagecorrelation,2DDIC)在三维体图像上的拓展.通过比较体成像设备获取的被测试样变形前后数字体图像,该方法可测量物体内部三维全场变 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于人工弹簧模型的周期结构带隙计算方法研究1)
    冯青松*,杨舟*,郭文杰,*,2),陆建飞&,梁玉雄**华东交通大学铁路环境振动与噪声教育部工程研究中心,南昌330013&江苏大学土木工程与力学学院,江苏镇江212013RESEARCHONBANDGAPCALCULATIONMETHODOFPERIODICSTRU ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 自由场空泡溃灭过程能量转化机制研究1)
    韩磊,张敏弟,2),黄国豪,黄彪,3)北京理工大学,北京100081ENERGYTRANSFORMATIONMECHANISMOFAGASBUBBLECOLLAPSEINTHEFREE-FIELD1)HanLei,ZhangMindi,2),HuangGuohao,HuangBiao,3)Beiji ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.