删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

剪切流场中含内流立管横向涡激振动特性

本站小编 Free考研考试/2022-01-01


引 言


海洋立管作为深海资源开发中输送海底油气或其他矿产混合物的重要部件, 一旦在海洋波浪和洋流的作用下发生涡激振动, 则极易引起立管的疲劳破坏. 因此海洋立管的涡激振动响应得到国内外****的持续关注, 对海洋立管在外部环境荷载作用下产生的涡激振动的机理和响应已有大量的研究, 特别是针对大长细比的柔性立管[1-3]. 这些研究主要运用实验和数值模拟方法, 针对均匀流和剪切流中的柔性立管, 分析了涡激振动的模态、频率以及驻波和行波响应等, 为深入理解涡激振动机理和响应规律奠定了基础[1-3]. 在这些研究中, 一些****关注了外部条件对立管涡激振动响应的影响规律, 如来流角度和边界条件等, 其中, Chaplin等[4]研究了不同来流流向对悬链线立管水动力系数以及振动响应的影响机理; Xu等[5]、高云等[6]和徐万海等[7]则通过实验和数值的方法研究分析了不同来流角度和不同剪切流中柔性圆柱体流体力特性及其系数的变化规律, 并且对结构的能量输入区域和输出区域进行了划分; Chen等[8]关注了三角形刚性柱体在不同来流流场中的振动响应和流场特性, 分析了不同来流角度下柱体在不同约化速度下的振动响应, 并且着重关注了随着约化速度增加产生的驰振现象; 李非凡等[9]和及春宁等[10-11]采用浸入边界法对细长柔性圆柱在均匀流、剪切流以及倾斜流条件下的涡激振动进行三维数值模拟, 主要研究了涡激振动的频率、阻力系数、能量传递以及主播和行波响应等; 同时, Seyed-Aghazadeh等[12]研究分析了不同边界条件对涡激振动响应的影响机理和规律. 除此之外, Song等[13]通过实验发现立管顺流向和横向的多模态响应并且立管振动频率与涡泻脱落频率一致, Hu等[14]进一步研究了不同质量比和阻尼比下的串列立管涡激振动响应, 并且发现质量比小的情况下立管涡激振动迟滞现象明显. 在柔性立管涡激振动数值模拟研究中, Bao等[15]运用厚切片理论预报了涡激振动的结构响应、水动力系数以及涡泻脱落形态等; Qu等[16-17]则改进了尾流振子模型, 数值预报了柔性圆柱体的锁频现象和相位角变化; Yuan等[18]和Zhang等[19]基于半经验时域模型研究了立管在稳定流和振荡流中的涡激振动响应, 主要分析其振动、频率和模态随不同参数的变化规律, Lin等[20]运用SDVM-FEM耦合方法研究了柔性立管产生的驻波和行波响应, 并且分析了其相应的流场特性, 这些研究为海洋工程界深入理解和认识立管涡激振动机理和响应规律奠定了坚实的基础. 然而, 这些研究主要考虑外流的作用, 海洋立管输送海底油气或其他矿产资源时, 内流对立管水动力响应的影响不可忽视, 因此, 研究含内流立管的涡激振动具有重要意义.

当介质在立管内部流动时, 立管受到流动介质产生的内部作用力, 可导致海洋立管复杂的涡激振动响应. 近几年, 越来越多的****开始对考虑内外流共同影响下海洋立管的涡激振动进行探究. 研究证明, 在一定的内流速度下, 管道结构发生失稳现象[21]. 同时, 一些****通过实验和数值模拟方法研究了含内流海洋立管涡激振动响应, Guo等[22]、李朋[23]和吴天昊[24]通过模型试验, 研究了含内流顶张立管和悬臂立管的动力响应, 主要关注立管振动频率和位移变化规律. Jiang等[25]、Duan等[26-27]、Thorsen等[28]、Wang等[29]和李艳等[30]则运用数值手段研究了含稳定内流海洋立管的涡激振动响应, 分析了内流速度和密度对立管涡激振动模态、频率和位移的影响机理. 然而在实际海洋工程中, 海洋立管输送的物质存在多相流动, 因此, Zhu等[31]、Meng等[32]和Li等[33]关注了含气液两相内流立管振动响应, 主要研究了不同的气液两相内流作用下立管对外流的动力响应. 这些研究证明, 在内流的影响下, 海洋立管涡激振动特性更加复杂, 涡激振动的频率和主导模态等都会发生变化.

虽然含内流海洋立管涡激振动特性研究已经引起国内外****的广泛关注, 但是目前对含内流海洋立管涡激振动响应的研究刚刚起步, 相关的文献报道并不多见, 特别是剪切流作用的情况更是鲜有报道. 鉴于此, 本文旨在研究含内流海洋立管在剪切外流作用下的横向涡激振动响应, 分析内流对立管在剪切流中涡激振动响应机理和特性的影响.


1.
立管涡激振动数学模型


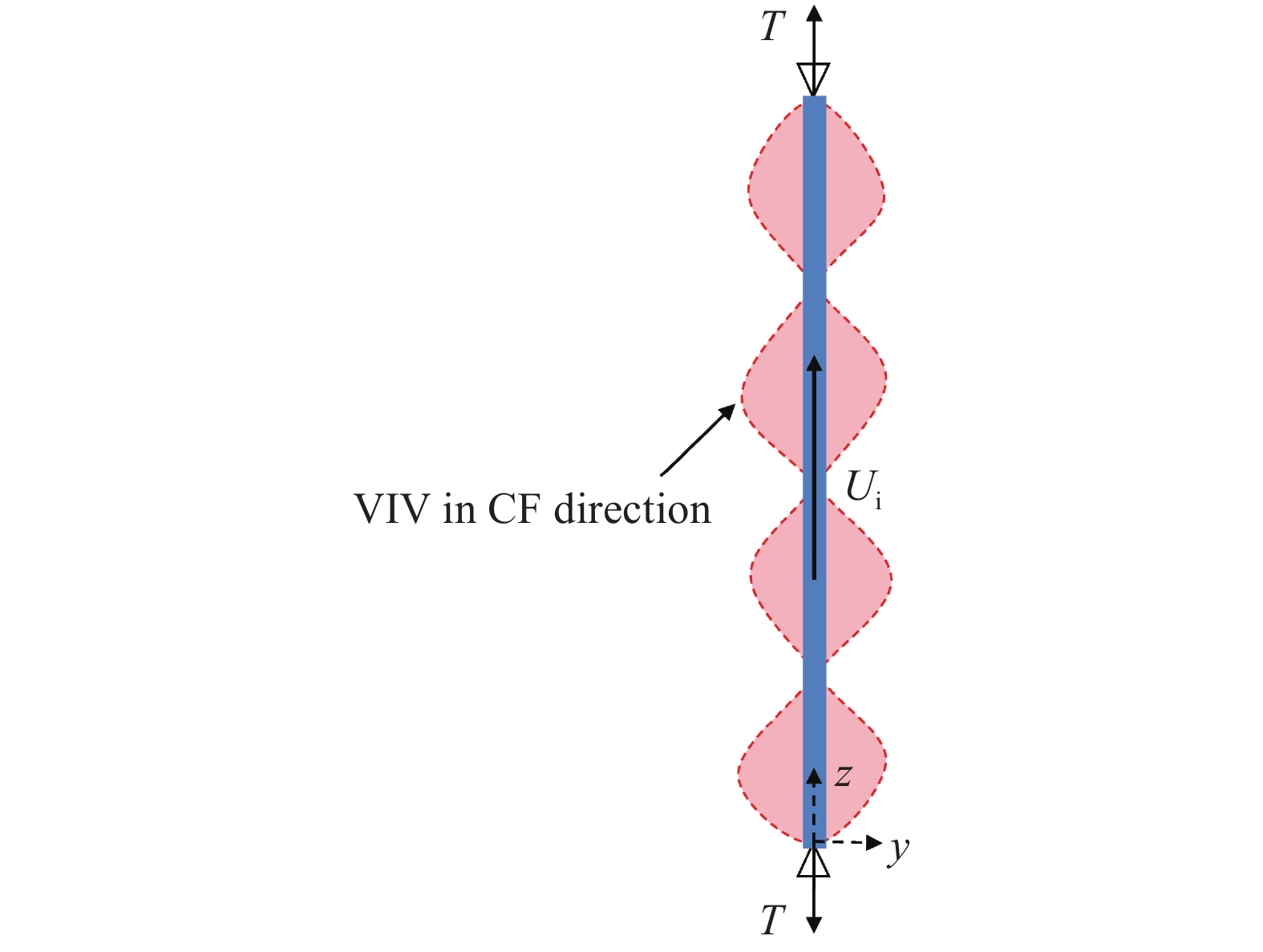
本研究主要针对两端简支立管(如图1所示), 研究其横向涡激振动响应, 立管被施以预张力$T$, 并且含有速度为${U_{
m{i}}}$的内流. 含内流立管横向涡激振动控制方程可表示为[21]







$$begin{split}& left( {{m_{
m{r}}} + {m_{
m{f}}}}
ight)frac{{{partial ^2}y({textit{z}},t)}}{{partial {t^2}}} + cfrac{{partial y({textit{z}},t)}}{{partial t}} + 2{m_{
m{f}}}{U_{
m{i}}}frac{{{partial ^2}y({textit{z}},t)}}{{partial {textit{z}}partial t}} + & qquad left( {{m_{
m{f}}}U_{
m{i}}^2 - T}
ight)frac{{{partial ^2}y({textit{z}},t)}}{{partial {{textit{z}}^2}}} + EIfrac{{{partial ^4}y({textit{z}},t)}}{{partial {{textit{z}}^4}}} = {F_{{
m{CF}}}}({textit{z}},t) [-8pt] end{split} $$
(1)



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-171-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
含内流立管横向涡激振动示意图



Figure
1.
Schematic of vortex-induced?vibration?(VIV) for a riser considering internal flow. CF stands for cross-flow



下载:
全尺寸图片
幻灯片


其中, ${m_{
m{r}}}$和${m_{
m{f}}}$为单位长度立管和内流的质量, $c$为立管的阻尼系数, ${U_{
m{i}}}$为内流速度, $EI$为弯曲刚度, ${F_{{
m{CF}}}}$为外部流体力. 方程中第3项和第4项表示立管内流对立管涡激振动响应的影响, 其中第3项为内流对立管所施加的科氏力, 而第4项则表示内流流动所产生的离心力对立管涡激振动的影响. ${F_{{
m{CF}}}}$包含附加质量力和涡激力







$${F_{{
m{CF}}}} = - {m_{{
m{a}}}}ddot y + {F_{{
m{ex,CF}}}}$$
(2)

其中, 附加质量${m_{{
m{a}}}} = {C_{{
m{a}}}}{m_{
m{e}}}$, 附加质量系数${m_{{
m{a}}}}$取为1.0, ${m_{
m{e}}}$为立管排开水单位长度质量.

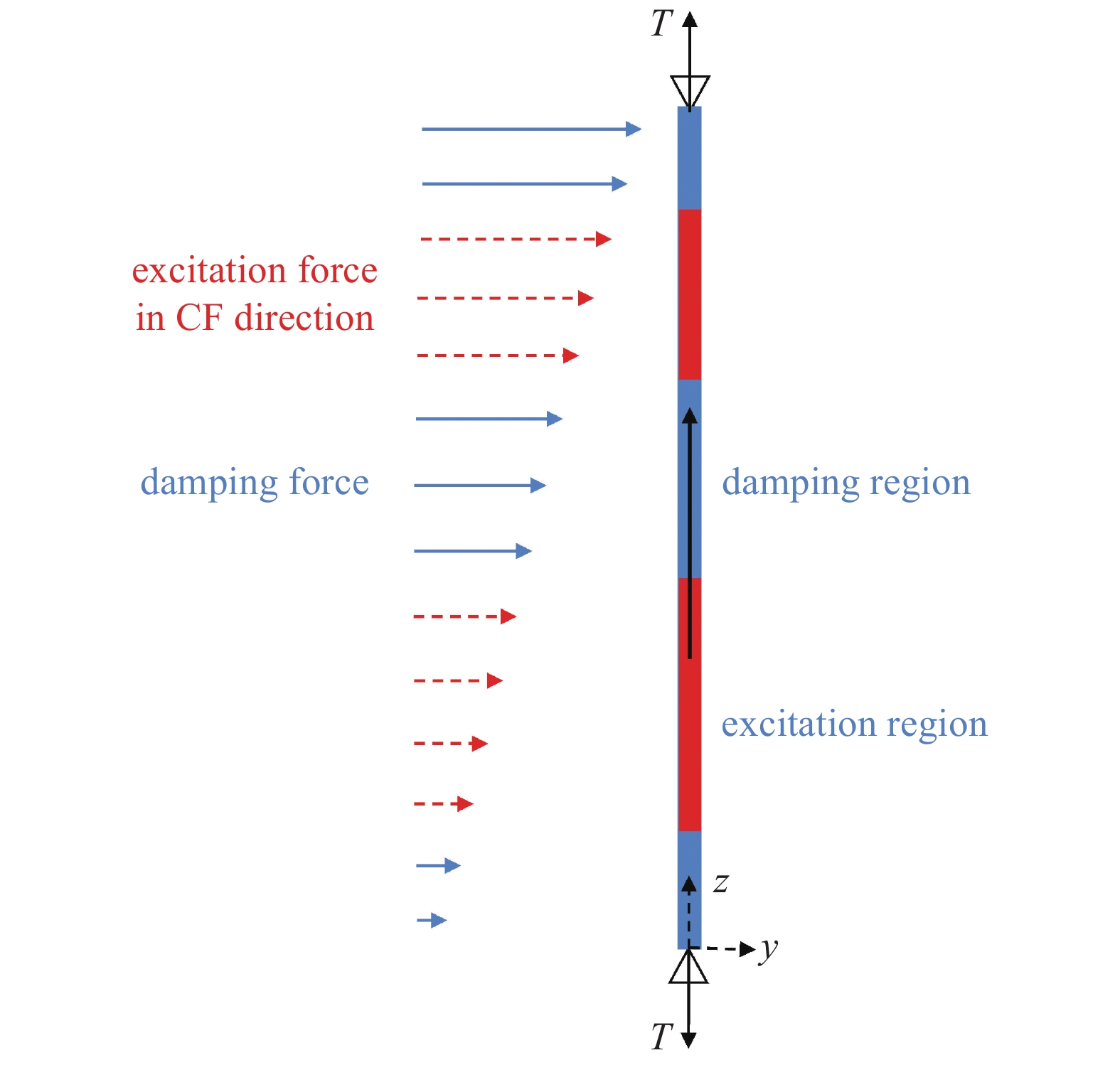
为了确定外部涡激力, 需要首先对立管在横向上的激励区和阻尼区进行判定, 可通过确定立管上无因次激励频率来判断激励区和阻尼区(如图2).



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-171-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
含内流立管横向激励区和阻尼区示意图



Figure
2.
Identification of excitation and damping regions of a fluid-conveying riser



下载:
全尺寸图片
幻灯片


由模态分析可得到立管的各阶固有频率, 再结合流场并基于方程(2)获得立管各节点在每阶固有频率下的无因次频率







$$f_{{
m{CF}},i}^*({textit{z}}) = frac{{{omega _{{
m{CF}},i}}}}{{2{text{π}} }}frac{{{D_{{
m{e}}}}}}{{{U_{{
m{e}}}}({textit{z}})}}$$
(3)

其中, $f_{{
m{CF}},i}^*({textit{z}})$表示第$ i $阶固有频率下节点${textit{z}}$的无因次频率, ${D_{{
m{e}}}}$为立管的直径, ${U_{{
m{e}}}}({textit{z}})$为外部剪切流在节点${textit{z}}$处流速, ${omega _{{
m{CF}},i}}$表示第$i$阶固有圆频率. 由于模型中的斯托哈尔数并不是恒定的, 根据实际雷诺数对节点${textit{z}}$的斯托哈尔数进行修正[34].

剪切流中, 沿立管轴向都存在激励区和阻尼区. 基于涡激振动的半经验频域预报模型VIVANA, 可根据以下标准来判定立管的激励区和阻尼区







$$0.125 leqslant f_{{
m{CF}},i}^*({textit{z}}) leqslant 0.2$$
(4)

当立管在节点${textit{z}}$处第$i$阶无因次激励频率在0.125 ~ 0.2区间内时, 则该节点处于第$ i $阶激励频率下的激励区内, 相反该节点则位于该阶激励频率的阻尼区内. 然而, 在多频响应下, 直接通过该标准得到的各激励频率的激励区可能发生重叠. 针对发生重叠的激励区, 本文采用等长度退让的方法处理多频响应下激励区发生重叠的问题[34].

确定立管横向上的激励区后, 激励区内节点${textit{z}}$处的第$i$阶激励力可以表示为







$$begin{split}& {F_{{
m{{
m{ex,CF}}}}}}({textit{z}}) = & qquad frac{1}{2}{
ho _{
m{e}}}{D_{{
m{e}}}}U({textit{z}})_{
m{e}}^2{C_{{
m{L}},{
m{CF}},i}}({textit{z}})cos ({omega _{{
m{CF}},i}} cdot t + {varphi _{{
m{CF}},i}}) [-6pt] end{split} $$
(5)

其中, ${
ho _{
m{e}}}$为外部流体密度, ${C_{{
m{L}},{
m{CF}},i}}({textit{z}})$为节点${textit{z}}$处激励力系数, ${varphi _{{
m{CF}},i}}$为相位角. 基于Gopalkrishnan[35]刚性圆柱体强迫振荡试验结果(图3), 根据同一无因次频率下的激励力系数${C_{
m{L}}}$与无因次幅值之间的关系曲线(图4)可确定${C_{{
m{L}},{
m{CF}},i}}({textit{z}})$.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-171-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
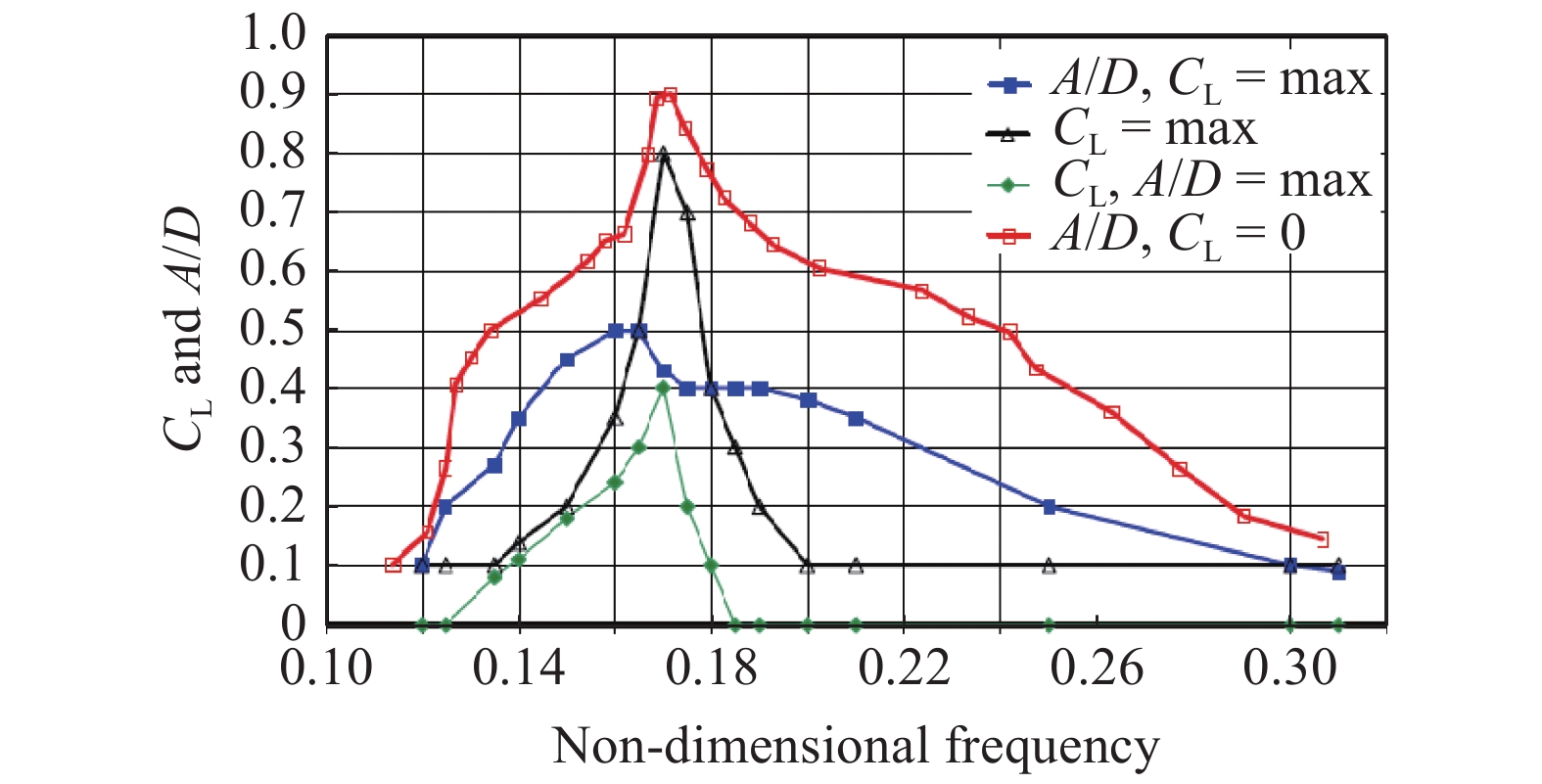
横向激励力系数模型参数[34]



Figure
3.
Excitation coefficient for CF VIV[34]



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-171-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
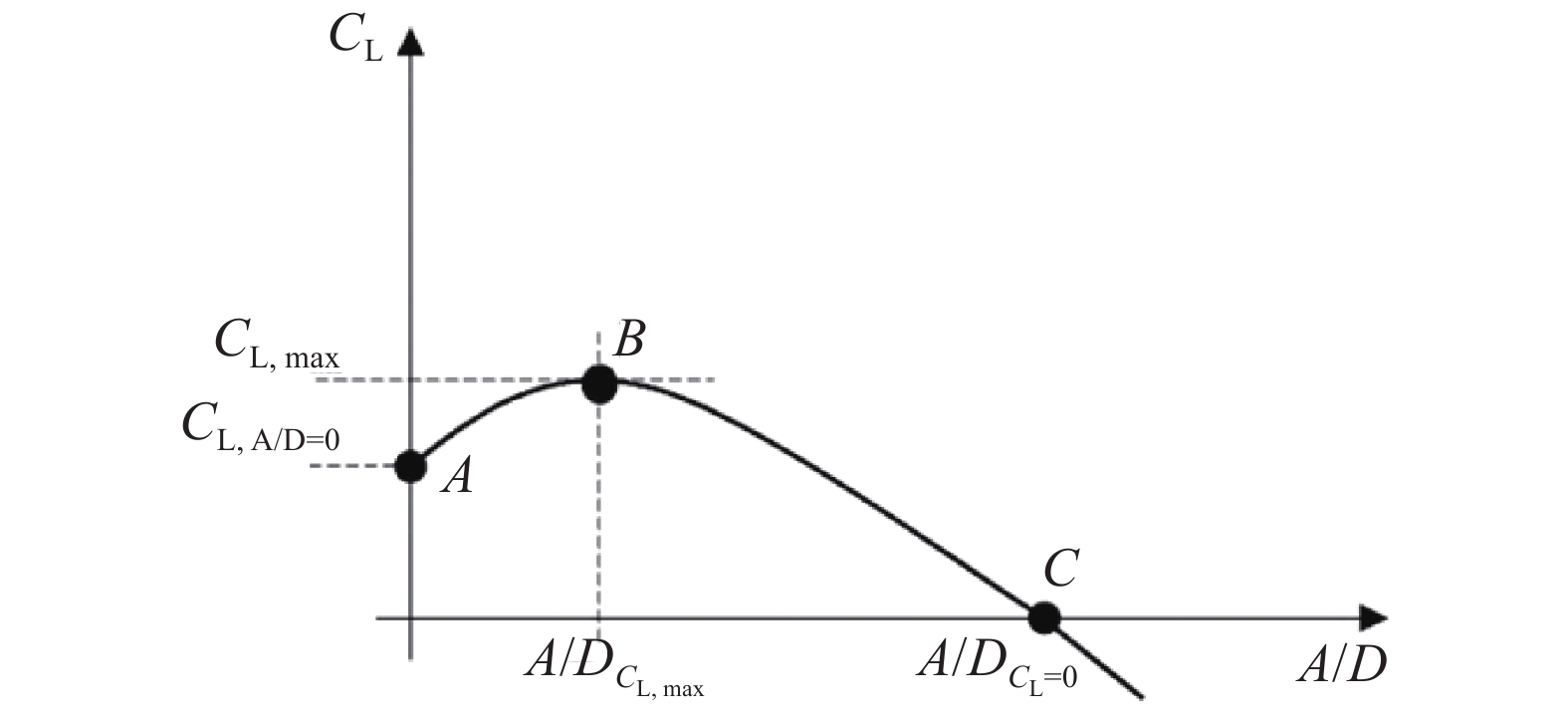
激励力系数与无因次幅值的函数曲线[34]



Figure
4.
Function of excitation coefficient and non-dimensional amplitude[34]



下载:
全尺寸图片
幻灯片


相位角${varphi _{{
m{CF}},i}}$则是根据Zhang等[19]提出的方法确定, 依不同的振型, 可以分别设为0和${text{π}} $.

在阻尼区节点${textit{z}}$处的阻尼力则采用VIVANA中水动力阻力模型[35]







$${F_{{
m{damp}} ,{
m{CF}}}}({textit{z}}) = - {C_{{
m{damp}} }}({textit{z}})frac{{partial y({textit{z}},t)}}{{partial t}}$$
(6)

其中, ${F_{{
m{damp}} ,{
m{CF}}}}({textit{z}})$为节点${textit{z}}$处第$i$阶激励频率的水动力阻力, ${C_{{
m{damp}}}}({textit{z}})$为阻尼区内阻尼系数.

采用有限单元法对立管横向振动控制方程进行离散, 运用Newmark-β逐步积分方法求解方程, 进而研究含内流海洋立管横向涡激振动特性.


2.
模型验证


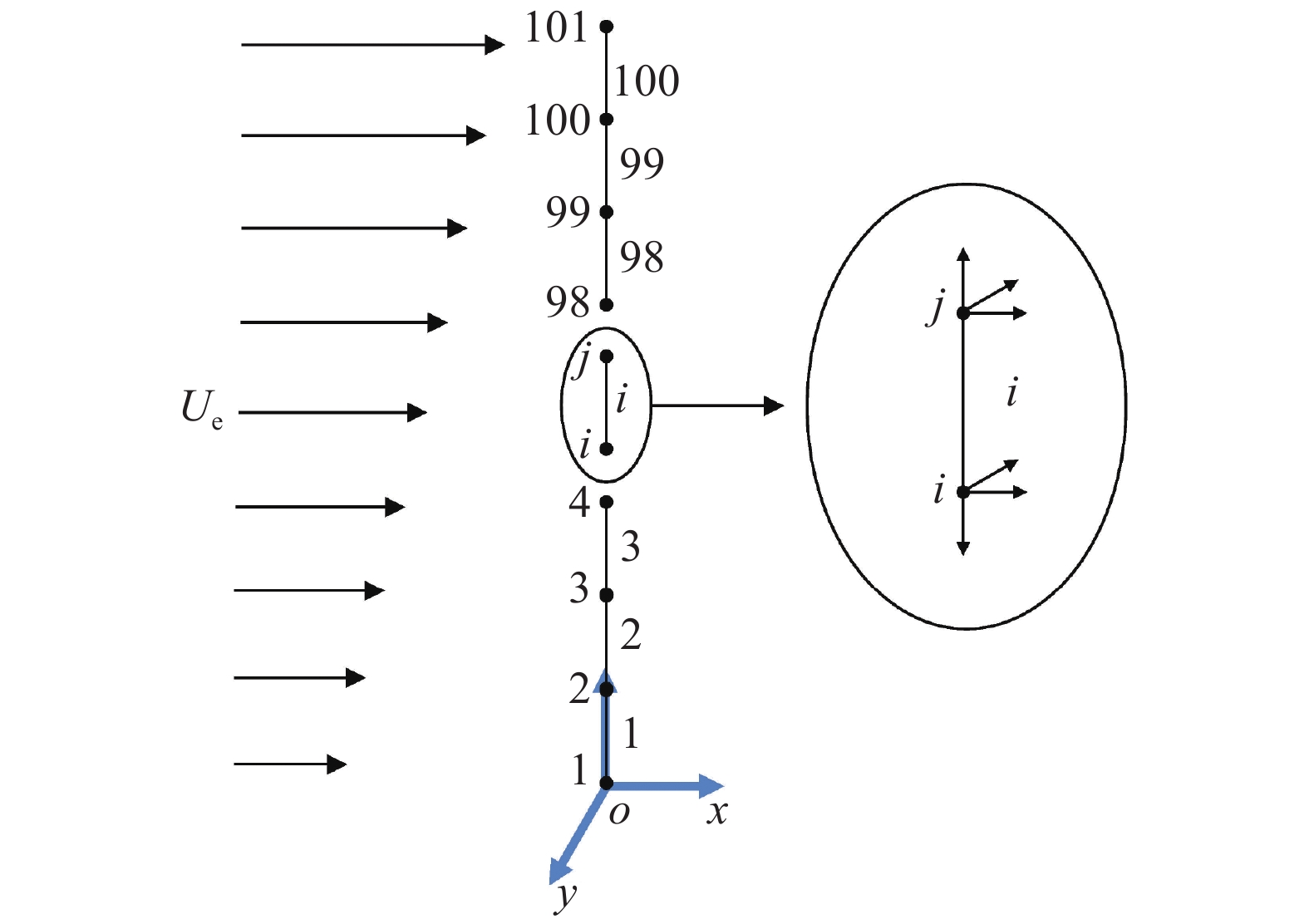
运用有限元方法将模型进行离散, 将模型离散为100个单元, 如图5所示, 之后运用Newmark-β法求解离散方程.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-171-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
立管离散单元示意图



Figure
5.
Schematic of discretized elements of the fluid-conveying riser



下载:
全尺寸图片
幻灯片


首先, 通过将数值计算结果与实验结果进行对比, 验证模型的准确性, 本文中选用的对比数据为宋磊建的模型实验数据[36], 该模型实验的具体参数如表1.




表
1
模型实验立管参数[36]



Table
1.
Parameters of the experimental riser model[36]



table_type1 ">
ParameterValue
length L/m6.75
outer diameter De/m0.031
inner diameter di/m0.027
bending stiffness EI/N·m21476.76
pretension T/N3000
mass per unit mr/kg1.768
damping ratio c/%0.3





下载:
导出CSV
|显示表格



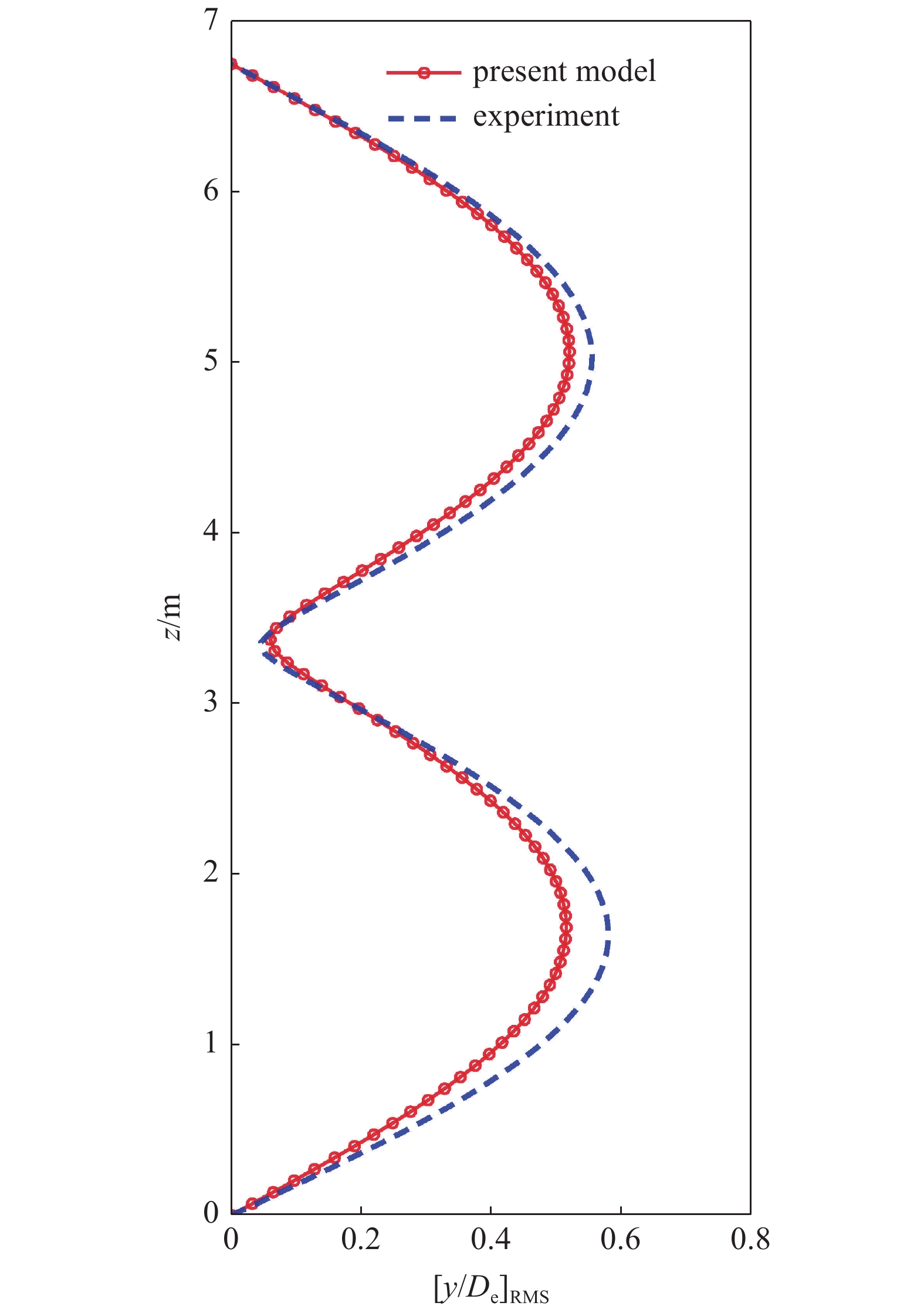
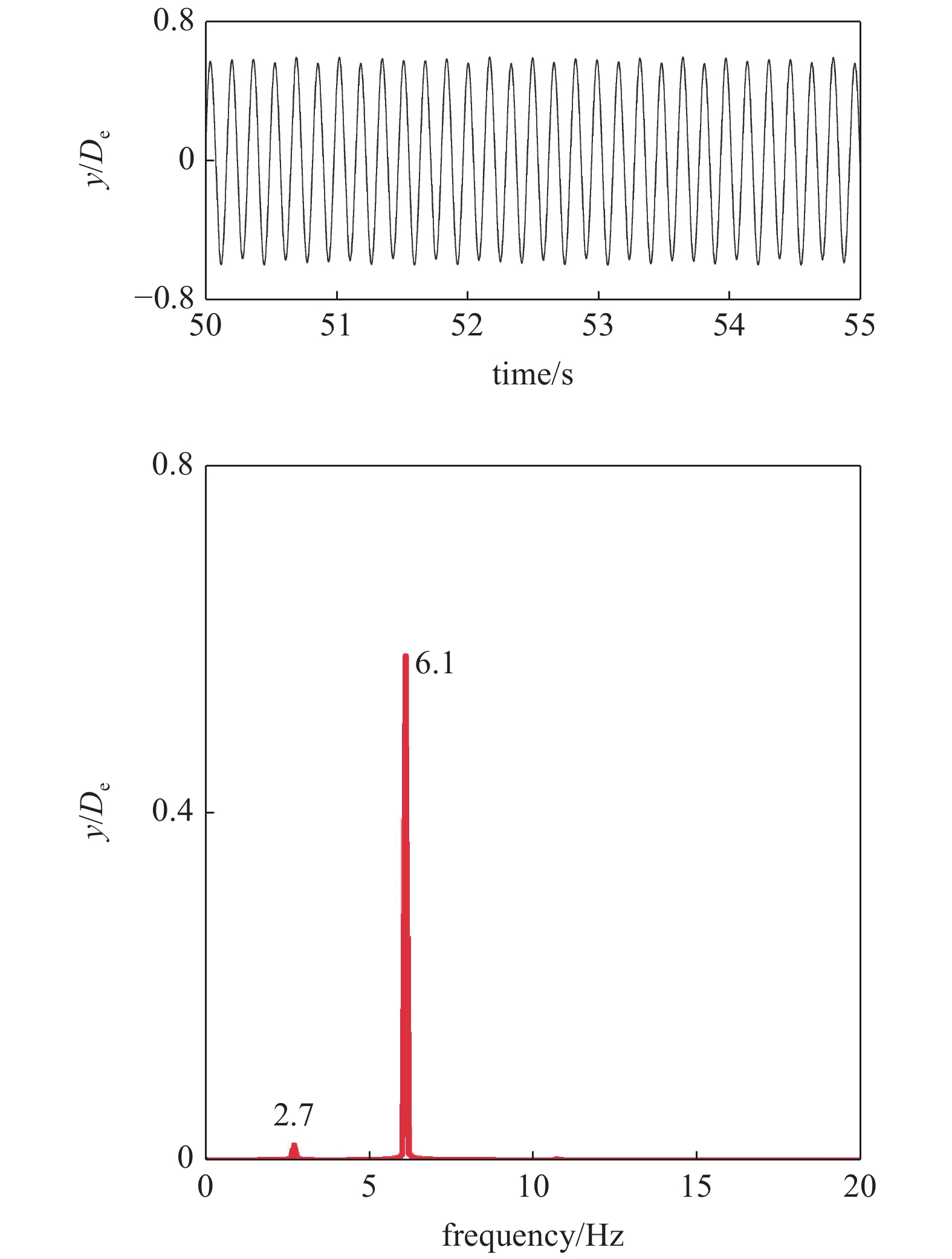
如图6所示, 在外部剪切流流速为1.5 m/s (线性剪切流中最大流速为1.5 m/s, 最小流速为0)情况下, 不含内流的立管在横向上的位移均方根与实验结果吻合较好, 数值模拟和实验中立管涡激振动的主导振动模态都为二阶模态. 同时, 数值模拟中立管节点25在横向上的主导振动频率为6.1 Hz (图7), 而实验中立管在横向上的主导振动频率为5.4 Hz. 值得注意的是立管在剪切流作用下会产生多频率涡激振动, 从图7中可以看出, 立管在横向上存在另一个振动频率2.7 Hz, 这是由于外部剪切流流速沿立管轴向变化, 导致立管不同位置产生不同的模态响应, 从而引起立管整体发生多模态多频率涡激振动响应. 然而, 由于数值模拟中所选取的附加质量系数和激励系数等原因, 数值模拟结果与实验结果存在一定的误差, 但是误差都较小.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-171-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
横向均方根位移对比



Figure
6.
Comparison of CF RMS between numerical and experiment results



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-171-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
横向振动时历曲线和振动频率



Figure
7.
Time history of vibration and vibrating frequency in CF direction



下载:
全尺寸图片
幻灯片



3.
含内流海洋立管横向涡激振动特性



3.1
内流对立管固有频率的影响


立管结构的固有频率可以依据下式求得[37]







$$left| {{boldsymbol{K}} - {omega ^2}{boldsymbol{M}}}
ight| = 0$$
(7)

式中, $omega $表示立管各阶圆频率, ${boldsymbol{K}}$和${boldsymbol{M}}$分别为立管的刚度矩阵和质量矩阵, 其中立管的刚度矩阵受内流速度和质量的影响. 含内流立管的固有频率随着内流速度和密度变化规律如图8和图9所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-171-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
立管固有频率随着内流速度变化规律



Figure
8.
Variation of natural frequency with the increase of the internal flow velocity



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-171-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
立管固有频率随着内流密度变化规律



Figure
9.
Variation of natural frequency with the increase of the internal fluid density



下载:
全尺寸图片
幻灯片


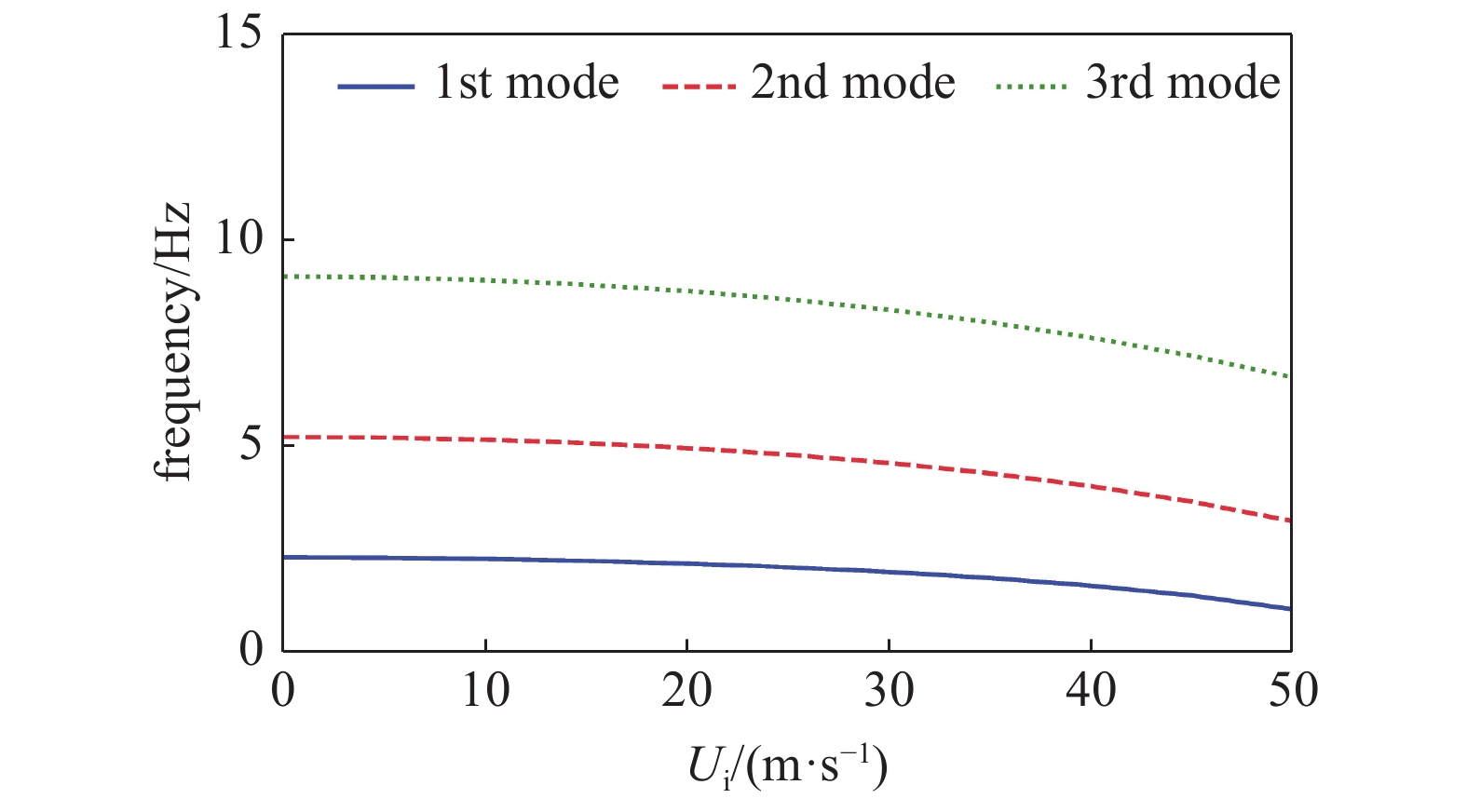
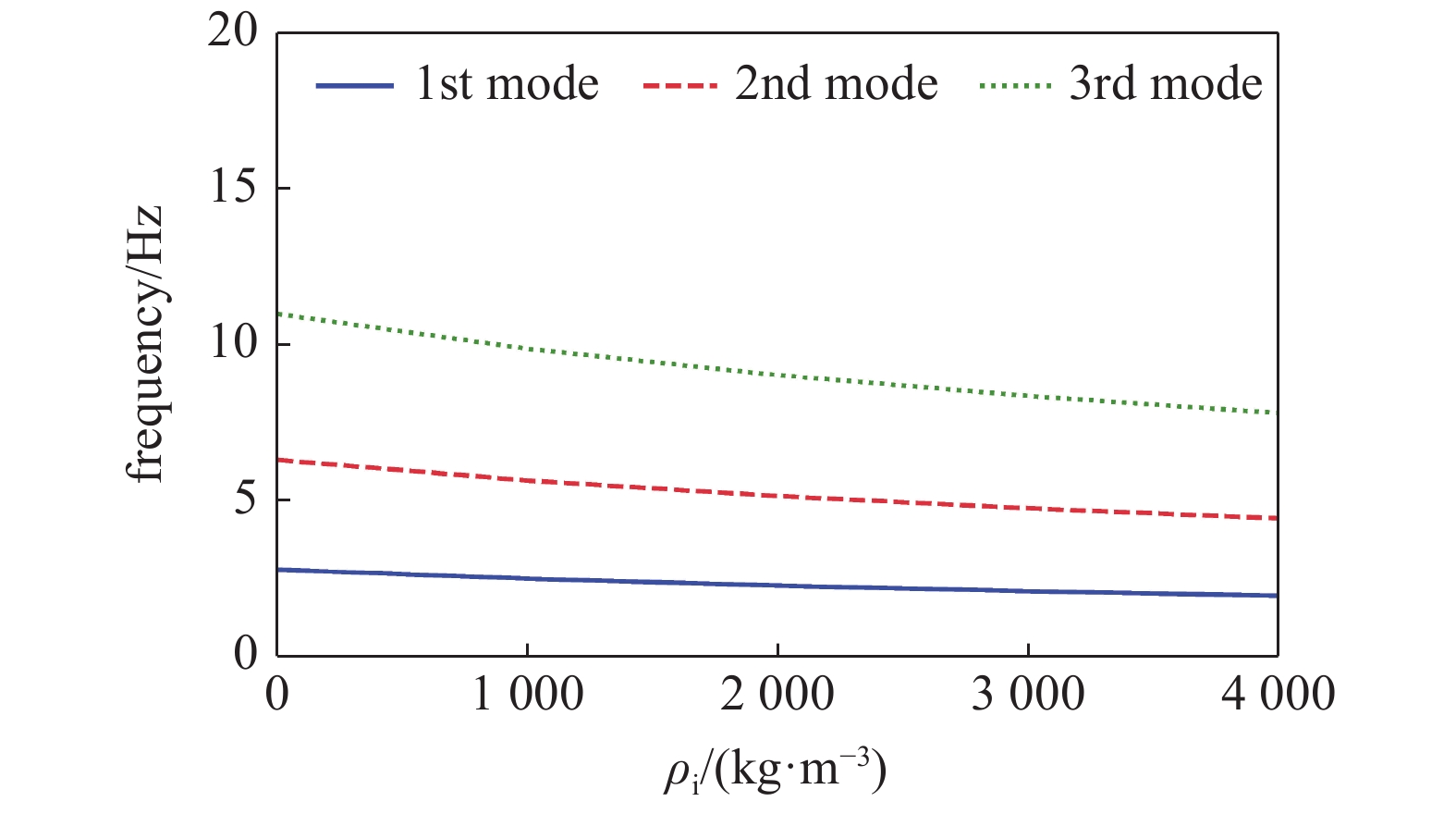
从图中可以看出内流的速度和密度影响立管固有频率, 随着内流密度和速度增大, 立管的前3阶固有频率降低. 若内流密度设为2000 kg/m3, 当内流速度从0 m/s增大到50 m/s时, 立管的前3阶固有频率分别从2.33 Hz, 5.23 Hz和9.12 Hz减小到1.06 Hz, 3.2 Hz和6.68 Hz; 若内流速度设为10 m/s, 当内流密度从1000 kg/m3增大到4000 kg/m3, 立管的前3阶固有频率分别从2.51 Hz, 5.66 Hz和9.88 Hz减小到1.96 Hz, 4.45 Hz和7.81 Hz. 从式(7)看出, 立管内流的速度和密度增大可导致立管刚度减小, 从而减小立管固有频率.


3.2
横向振动频率



3.2.1
内流速度的影响

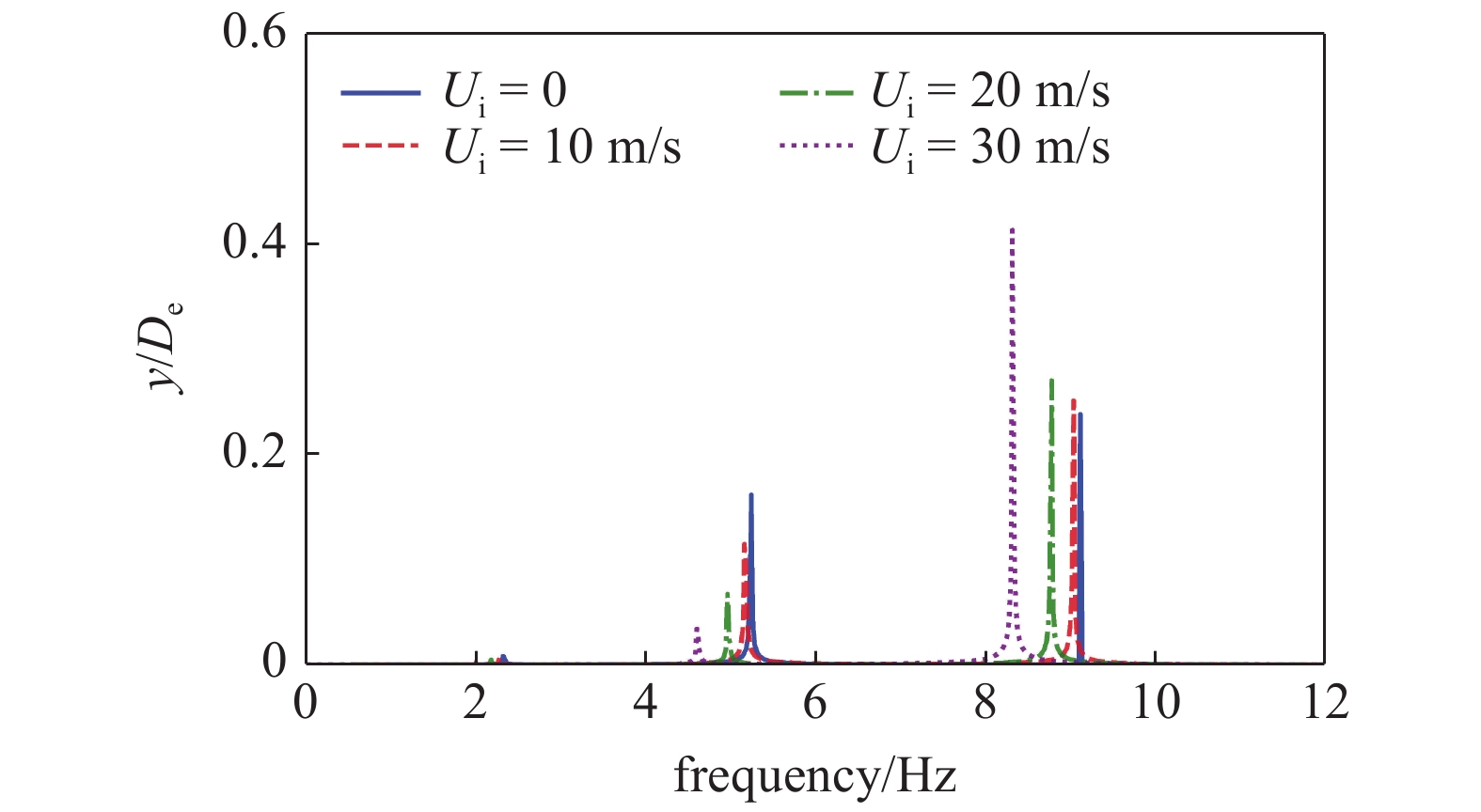
将立管内流密度设为2000 kg/m3, 立管外部剪切流速度为1.5 m/s, 图10展示了随着内流速度的增大, 立管节点50处横向振动频率的变化规律. 由于剪切流的作用, 立管在横向上出现多频率多模态涡激振动现象.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-171-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
横向振动频率随着内流速度的变化趋势



Figure
10.
Variation of CF vibrating frequency with the increase of the internal flow velocity



下载:
全尺寸图片
幻灯片


从图10可以看出, 立管横向振动的主导频率随着内流速度的增大而减小. 当立管内流速度从0增大到10 m/s时, 横向主导振动频率减小的幅度较小, 大约从9.15 Hz减小到9.08 Hz; 而当内流速度增大到20 m/s和30 m/s时, 横向主导振动频率随着内流速度的增大明显降低, 大约分别降低到8.8 Hz和8.2 Hz. 出现这种现象的原因是, 当存在内流时, 立管的固有频率随着内流速度的增大而降低, 立管涡泻频率在特定的内流速度下锁定到新的较低的固有频率, 从而引起在此频率下的涡激振动响应.


3.2.2
内流密度的影响

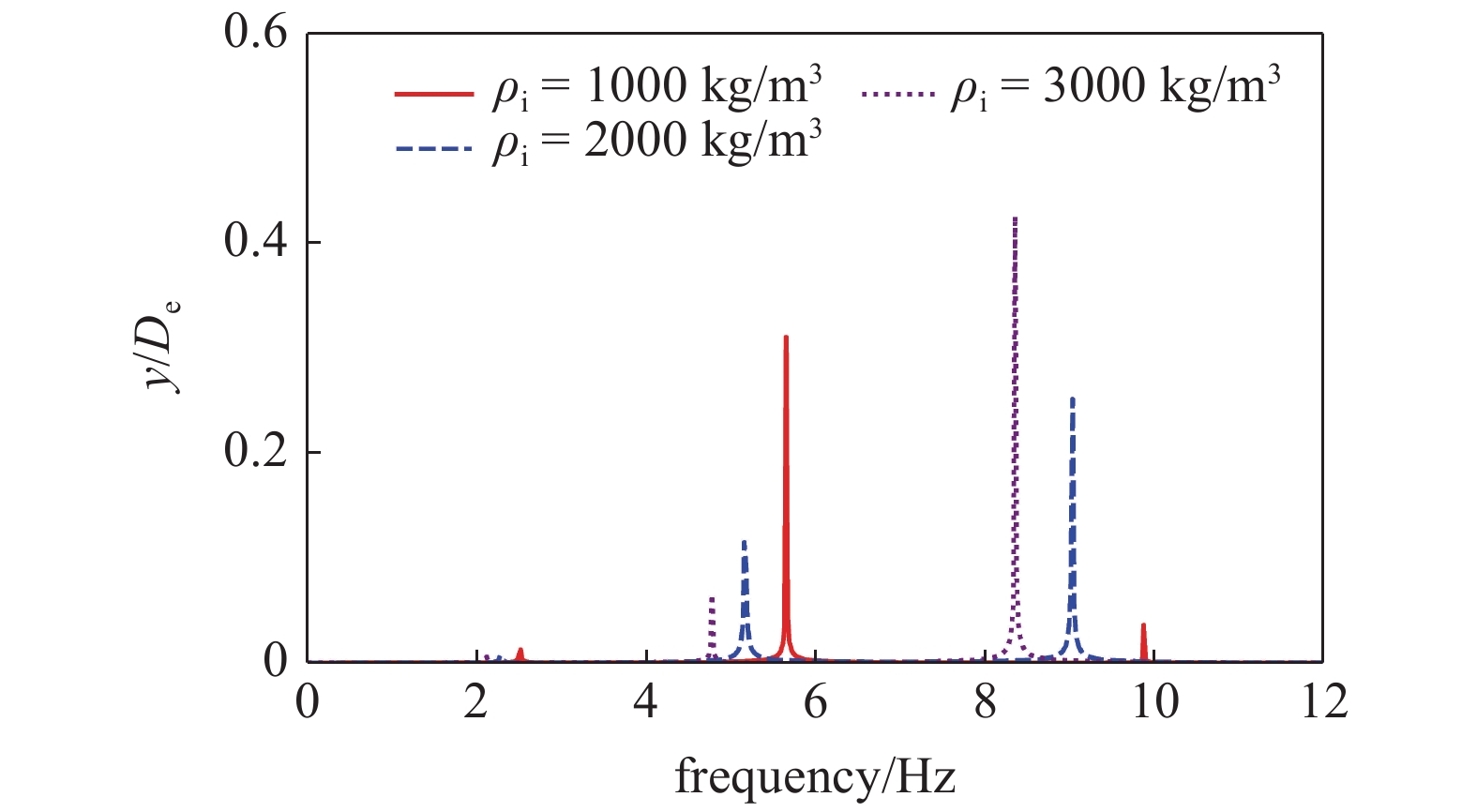
由于立管系统在深海资源开发中输送油气混合物以及固液矿产混合物, 所以需要研究不同内流密度对立管涡激振动的影响规律. 同样在立管外部剪切流速度为1.5 m/s, 将立管内流速度设为10 m/s, 分别研究内流密度1000 kg/m3, 2000 kg/m3和3000 kg/m3对立管横着涡激振动参数的影响规律, 其中密度1000 kg/m3接近油气混合物密度, 而密度2000 kg/m3和3000 kg/m3则接近固液矿产混合物密度. 内流密度的变化对立管横向涡激振动频率影响规律如图11所示. 从图11可以看出, 当立管内流密度为1000 kg/m3时, 立管横向振动的主导频率约为5.6 Hz, 当内流密度增大到2000 kg/m3时, 其主导频率转换到9.08 Hz. 出现这种现象的原因与新的主导模态响应激发以及固有频率的降低有关, 当内流速度从1000 kg/m3增大到2000 kg/m3时, 立管横向涡激振动的主导模态从二阶响应变换到3阶模态响应, 从而导致立管在横向上的主导振动频率从5.6 Hz跳跃到9.08 Hz; 而随着内流密度的继续增大, 立管固有频率降低并且没有发生模态响应转换, 从而导致立管横向涡激振动响应与新的固有频率锁定, 因此当内流密度增大到3000 kg/m3时, 立管横向上的主导振动频率降为8.4 Hz. 值得注意的是, 立管涡激振动的频率转换与模态转换同时发生.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-171-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
横向振动频率随着内流密度的变化趋势



Figure
11.
Variation of CF vibrating frequency with the increase of the internal fluid density



下载:
全尺寸图片
幻灯片



3.3
横向均方根位移



3.3.1
内流速度的影响

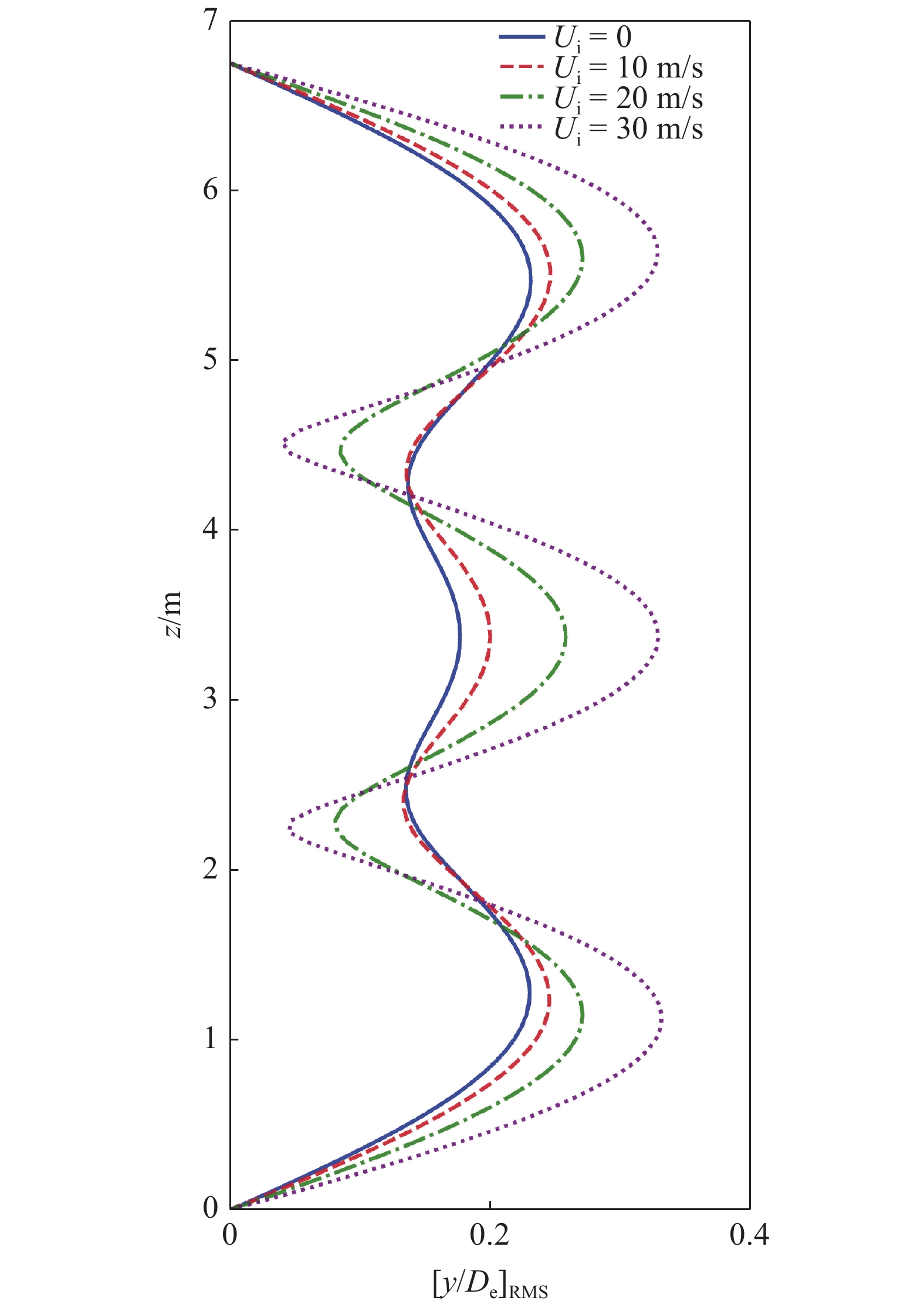
立管横向均方根位移随着内流速度的变化规律如图12所示. 从图12中可以看出, 随着内流速度的增大, 立管在横向上的最大均方根位移是不断增大的, 值得注意的是, 均方根位移的增大在内流速度较大的时候比较明显, 而内流速度较小时, 增大较慢. 当内流速度从0增大到10 m/s的时候, 立管横向的最大均方根位移几乎不变, 大约为0.24; 而当内流速度增大到20 m/s和30 m/s时, 立管横向的最大均方根位移显著增大, 大约为0.27和0.33. 立管横向最大均方根位移的增大是由于内流对立管涡激振动产生影响.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-171-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
横向均方根位移随着内流速度变化趋势



Figure
12.
Variation of CF RMS with the increase of the internal flow velocity



下载:
全尺寸图片
幻灯片


约化速度是研究立管涡激振动特性的一个重要参数, 有如下表达形式







$${U_{
m{r}}} = frac{{{U_{
m{e}}}}}{{{f_n}{D_{
m{e}}}}}$$
(8)

其中, ${f_n}$是立管的第n阶固有频率. 立管横向涡激振动振幅随着约化速度${U_{
m{r}}}$先增大后减小, 并且一般在约化速度为6时达到最大值[38]. 当立管内流速度从0增大到10 m/s, 约化速度大约从4.3增大到4.45, 进而导致立管横着涡激振动振幅增大, 随着内流速度继续增大到20 m/s和30 m/s, 约化速度大约增大到4.6和4.8, 相应地, 立管在横向上的涡激振动振幅增大. 由此可见, 内流流速通过影响约化速度, 进而改变立管横向涡激振动振幅. 值得注意的是, 剪切流引起的立管横向涡激振动响应沿轴向一般应该是不对称的, 但本研究中立管的长度较短, 这种不对称特征未能充分体现.


3.3.2
内流密度的影响

而立管横向均方根位移随内流密度的变化如图13所示. 从图13中可以看出, 当不发生模态转换时, 立管在横向上的最大均方根位移随内流密度的增大而增大, 当内流密度为2000 kg/m3时, 立管在横向上的最大均方根位移大约为0.24, 当内流密度增大到3000 kg/m3时, 其值约为0.35. 值得注意的是, 当立管在横向上发现模态转换时, 横向最大均方根位移值发生跳跃现象, 如当立管由二阶模态响应变为3阶模态响应, 其横向均方根位移最大值约从0.3 (1000 kg/m3)跳跃到0.24 (2000 kg/m3). 横向最大均方根位移随内流密度的增大而增大同样是由于密度变化引起约化速度变化, 从而导致立管横向涡激振动振幅改变. 当内流密度从1000 kg/m3增大到2000 kg/m3时, 其约化速度大约从4.8减小到4.45, 进而导致立管在横向上的涡激振动振幅减小, 而当内流密度继续增大到3000 kg/m3, 约化速度跳跃到接近5, 立管振动振幅相应增大.



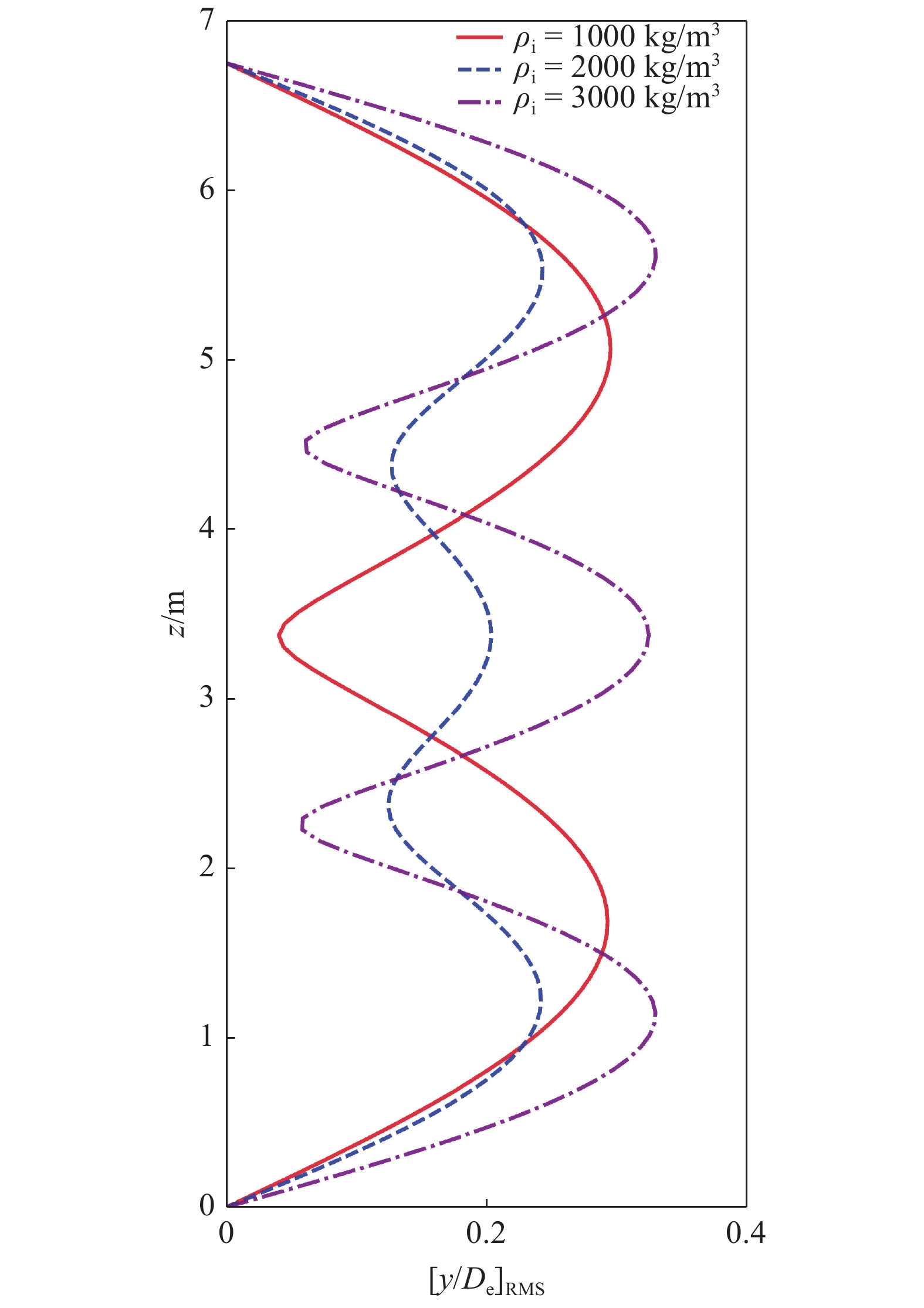onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-171-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
横向均方根位移随着内流密度变化趋势



Figure
13.
Variation of CF RMS with the increase of the internal fluid density



下载:
全尺寸图片
幻灯片


值得注意的是, 本研究中, 立管的主导振动模态在内流速度的影响下并没有改变, Duan等[26-27]证明了随着内流速度的增大, 立管在横向上的主导模态是增大的, 但是这种模态转换只是在内流速度较大时才发生. 显然, 本研究中内流速度还没有引起立管在横向上振动的模态转换. 而内流密度的增大对立管横向振动的主导模态影响明显, 如图13所示. 当内流密度为1000 kg/m3时, 立管横向振动的主导模态为二阶振动响应; 当内流密度增大到2000 kg/m3和3000 kg/m3时, 立管横向振动发生模态转化, 变为3阶模态主导响应. 发生模态转换的原因同样是由于内流密度增大降低立管固有频率, 从而激发新的涡激振动模态响应, 进而发生模态转换.


4.
结论


本文基于欧拉?伯努利梁理论和半经验时域水动力模型, 研究了内外流耦合作用下海洋立管在剪切流场中的横向涡激振动响应, 分析和讨论了立管在横向上的均方根位移、主导振动模态和频率等随内流速度和密度的变化规律.

海洋立管在剪切流作用下发生多模态多频率涡激振动响应, 深水立管在剪切流作用下的横向涡激振动响应沿立管轴向一般是不对称的, 立管较短时, 这种不对称特征不明显. 内流速度和密度的增大, 导致立管固有频率降低, 因此涡激力频率锁定在新的较低固有频率上, 激发新的横向涡激振动模态响应, 进而改变立管横向涡激振动振动频率, 导致立管在横向上的主导振动频率随内流速度和密度的增大而减小. 并且, 内流密度的增大可引起立管发生模态转换和频率转换. 同时, 立管固有频率的变化影响约化速度, 进而改变立管横向涡激振动均方根位移, 因此, 立管横向最大均方根位移随内流速度和密度的增大而增大, 特别是当内流速度和密度较大时, 横向最大均方根位移增大明显.

相关话题/海洋 图片 实验 质量 动力

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.