黏弹性液滴热毛细迁移的对流不稳定1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

章绍能, 胡开鑫^,²⁾宁波大学机械工程与力学学院力学系, 浙江宁波 315211

CONVECTIVE INSTABILITY IN THERMOCAPILLARY MIGRATION OF A VISCOELASTIC DROPLET¹⁾

Zhang Shaoneng, Hu Kaixin^,²⁾School of Mechanical Engineering and Mechanics, Ningbo University, Ningbo 315211, Zhejiang, China

通讯作者: 2)胡开鑫, 副教授, 主要研究方向: 非牛顿流体, 微重力流体. E-mail:hukaixin@nbu.edu.cn

收稿日期:2020-12-22接受日期:2021-03-8网络出版日期:2021-05-19

基金资助:

1)国家自然科学基金.11872032
国家自然科学基金.U1738119
国家自然科学基金.11532015
浙江省自然科学基金.LY21A020006

Received:2020-12-22Accepted:2021-03-8Online:2021-05-19
作者简介 About authors

摘要
液滴在温度分布不均的固壁面上产生的热毛细迁移广泛存在于微流控、喷墨印刷等应用中, 对其流动进行稳定性分析对液滴迁移的精准控制具有重要意义. 本文采用线性稳定性理论研究了附壁黏弹性液滴在热毛细迁移中的对流不稳定性, 得到了不同Prandtl数($Pr$)下的临界Marangoni数($Ma_{\rm c})$与弹性数的函数关系, 并分析了临界模态的流场和能量机制. 研究发现: 流体弹性激发了更多不稳定模态, 小$Pr$的临界模态为斜波和流向波, 而中高$Pr$的临界模态为斜波和展向稳态模态. 强弹性使得$Ma_{\rm c}$显著下降, 而弱弹性略微增强了流动稳定性. 在中$Pr$下, $Ma_{\rm c}$随$Pr$的增大而增大. 对于斜波模态, 扰动温度的振幅可存在于流场中间区域, 而其他两种模态的温度振幅只存在于自由表面上, 并且在高$Pr$下的流线分布几乎是对称的. 能量分析表明: 随着弹性数增大, 基本流做功由正变负; 在小$Pr$中, 扰动应力做功既可能耗散能量又可能提供能量; 在高$Pr$中, 基本流做功可忽略不计. 对于同向流向波, 扰动速度和扰动应力做功在垂直方向上均存在多次振荡. 将液滴迁移与热毛细液层进行对比发现, 由于基本流和边界条件的不同, 两者在临界模态和扰动流场中均存在较大差异.
关键词： 热毛细迁移;黏弹性液滴;稳定性分析

Abstract
Thermocapillary migration of a droplet placed on a non-uniformly heated solid surface appears in a variety of practical applications, such as microfluidics, inkjet printing, et al. The flow stability analysis is crucial for the precise control of droplet migration. In the present work, the convective instability in thermocapillary migration of a wall-attached viscoelastic droplet is examined by linear stability analysis. The relation between the critical Marangoni number ($Ma_{\rm c}$) and the elastic number is obtained at different Prandtl numbers ($Pr$). The flow fields and energy mechanisms of preferred modes are analyzed. The results show that more kinds of preferred modes are excited by the elasticity. The preferred modes at small $Pr$ are the oblique and streamwise waves, while those at moderate and high $Pr$ are oblique waves and spanwise stationary modes. The strong elasticity significantly reduces the $Ma_{\rm c}$, while the weak elasticity slightly enhances the flow stability. $Ma_{\rm c}$ increases with $Pr$ at moderate $Pr$. For the oblique wave, the amplitude of perturbation temperature may appear in the middle region of flow field, while the amplitudes of other two modes only exist on the free surface. The distribution of streamlines is almost symmetric at high $Pr$. The energy analysis shows that the work done by the basic flow changes from positive to negative when the elastic number increases. The work done by the perturbation stress may either dissipate or provide energy at small $Pr$, while the work done by the basic flow is negligible at high $Pr$. For the downstream streamwise wave, the perturbation velocity and the work done by perturbation stress fluctuate several times in the vertical direction. Comparing the droplet migration with thermocapillary liquid layers, it can be found that due to the differences of basic flow and boundary conditions, there are quite different between their preferred modes and perturbation flow fields.
Keywords：thermocapillary migration;viscoelastic droplet;stability analysis

PDF (2551KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
章绍能, 胡开鑫. 黏弹性液滴热毛细迁移的对流不稳定¹⁾. 力学学报, 2021, 53(5): 1313-1323 DOI:10.6052/0459-1879-20-443
Zhang Shaoneng, Hu Kaixin. CONVECTIVE INSTABILITY IN THERMOCAPILLARY MIGRATION OF A VISCOELASTIC DROPLET¹⁾. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(5): 1313-1323 DOI:10.6052/0459-1879-20-443

引言

当液滴置于温度分布不均的固体壁面上, 其表面张力梯度会驱动液滴产生热毛细迁移. 这种现象广泛存在于微流控装置^[1]、喷墨印刷^[2]和材料加工^[3]等多种工业应用中. 为了对液滴在固壁面上的迁移过程进行精准控制, 近几十年来****们从理论分析^[4]、数值模拟^[5-7]和实验^[8-10]等方面对液滴的热毛细迁移进行了广泛的研究. 此外关于液滴的研究还包括液滴撞击固体表面^[11]、通过液桥形成液滴^[12]和液滴喷射^[13]等.

为了得到液滴发生迁移所需要的条件, Ford和Nadim^[14]从多个方面对液滴在固体表面上的热毛细迁移速度进行了理论分析, 并得出了液滴迁移速度方程. Smith^[15]研究了二维液滴在施加温度梯度的固壁面上的迁移, 并利用润滑理论推导了液滴形状方程. Chen等^[16]通过理论与实验两方面对基底上液滴的控制进行研究, 得出了液滴迁移速度的影响因素, 其结果与Ford和Nadim^[14]的研究理论一致. Brzoska等^[17]通过实验研究了液滴在不可润湿固体表面对水平温度梯度的反应, 发现只有液滴半径大于临界半径时液滴才会移动. Haj-Hariri等^[18]模拟了恒定温度梯度下可变形液滴的三维热毛细迁移, 发现迁移速度与液滴形状有关. Pratap等^[19]通过理论和实验研究了癸烷液滴在PDMS镀层表面上的热毛细迁移, 实验得出了液滴迁移速度随液滴大小和温度梯度的变化关系, 与理论预测结果一致. Dai等^[20-23]建立了石蜡油滴在单向和全向热梯度作用下迁移的理论模型并进行实验, 还通过实验研究了球板之间液桥的热毛细迁移, 并且从基本原理、评估方法和设计操作策略对界面液体流动进行综述.

在液滴热毛细迁移过程中, 若雷诺数过大可能会发生流动失稳, 使得内部形成湍流. 如果液滴足够薄时还会发生破裂^[24], 甚至产生指纹式不稳定^[25]. 此时的液滴迁移是不可控的, 所以对液滴迁移进行流动稳定性分析是必要的. 热毛细对流不稳定性的研究已具有多年的历史, Davis^[26]以及Schatz和Neitzel^[27]已对此进行了综述. Smith和Davis^[28]采用线性稳定性理论研究了热毛细液层的对流不稳定, 发现存在两种不稳定性, 分别为静止的纵向转动和不稳定的水热波. 他们的结论得到了实验^[29]和数值模拟^[30]的验证. Burelbach等^[31]对液膜因热毛细不稳定而发生破裂进行了详细讨论. Hu等^[32]对附壁液滴热毛细迁移的流动失稳进行了理论分析, 结果表明: 临界Marangoni数总是随着液滴迁移速度的增大而减小.

目前对液滴热毛细迁移的研究主要集中在牛顿流体. 然而许多工业应用中的液滴是聚合物流体, 既有黏性又有弹性. 黏弹性热毛细液层的研究结果表明: 流体中的弹性决定了流动失稳的临界数、模态和机制^[33]. 然而目前尚无研究关注弹性对液滴热毛细迁移的影响. 本文采用线性稳定性理论研究了附壁黏弹性液滴在热毛细迁移中的对流不稳定性, 得到了临界参数, 画出了扰动流场图, 并进行了能量分析.

1 控制方程

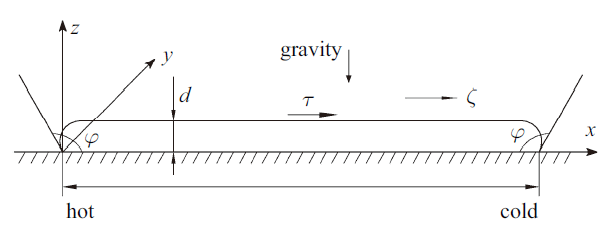
考虑一扁平液滴放置于固壁平面上, 如图1所示. 平面水平方向上的温度梯度会导致液滴的表面张力梯度, 进而驱动液滴热毛细迁移. 其中$x$, $y$和$z$分别代表流向、展向和法向, 坐标原点为液滴最左侧接触固壁面的位置. $\varphi $为接触角, $\zeta $为迁移速度, 令液滴厚度$d$为特征长度. 重力作用下液滴毛细长度为$\kappa^{-1}=\sqrt {{{{\sigma }'_{0} }/{\left( {\rho g} \right)}}} $, ${\sigma }'_{0} ,\rho ,g$分别为表面张力、流体密度和重力加速度, 液滴厚度和毛细长度的关系为$d=2\kappa^{-1}\sin \left( {{\varphi /2}} \right)$^[34]. 假设液滴厚度$d$远小于宽度$L$, 则液滴宽度远大于毛细长度, 此时液滴可看成薄膜. 所以假设液滴扁平是合理的, 除边缘外液滴内的流动可近似看作为平行剪切流.

图1

新窗口打开|下载原图ZIP|生成PPT
图1在刚性平面上的扁平液滴的热毛细迁移

Fig.1Thermocapillary migration of a flat droplet on the rigid plane

流动的无量纲控制方程组由下式给出, 分别为连续性方程, 动量方程和能量方程

(1)$\nabla \cdot { u}=0$

(2)$Re\left( {\frac{\partial { u}}{\partial t}+{ u}\cdot \nabla { u}} \right)=-\nabla p+\nabla \cdot { \tau }-G\nabla z$

(3)$\frac{\partial T}{\partial t}+{ u}\cdot \nabla T=\frac{1}{Ma}\nabla^{2}T$

其中${u},p,T$分别为速度、压强和温度, ${ \tau }$为应力张量. 重力因数$G$, Reynolds数$Re$, Marangoni数$Ma$和Prandtl数$Pr$分别定义为

(4)$\begin{eqnarray} G=\frac{\rho gd^{2}}{\mu U},\ \ Re=\frac{\rho Ud}{\mu },\ \ Pr=\frac{\mu }{\rho \chi },\ \ Ma=Re\cdot Pr \end{eqnarray}$

其中$U={{b\gamma d}/\mu }$为特征速度, $\mu $为动力黏度, $\chi $为热扩散系数, $b$为温度梯度, $\gamma =-\mbox{d}{\sigma }'_{0} /\mbox{d}T $为表面张力的温度变化率.

采用Oldroyd-B流体模型来反映聚合物高分子稀溶液的本构关系. 其本构方程为^[35]

(5)$\begin{eqnarray} \left( {1+\lambda \frac{\delta }{\delta t}} \right){ \tau }=\left( {1+\eta \frac{\delta }{\delta t}} \right){S} \end{eqnarray}$

其中${S}=\nabla {u}+\left( {\nabla {u}}\right)^{\rm T}$为应变率张量, $\lambda =({\mu }/{\hat{{G}}})({U}/{d})$为Weissenberg数, $\hat{{G}}$为弹性模量. ${\eta /\lambda }$为溶剂黏度与总黏度的比, 当$\lambda = \eta $时, 流体退化为牛顿流体. ${\delta }/{\delta t}$为上随体导数

(6)$\begin{eqnarray} \frac{\delta { \tau }}{\delta t}=\frac{\partial { \tau }}{\partial t}+{ u}\cdot \nabla { \tau }-\left( {{ u}\nabla } \right)\cdot { \tau }-{ \tau }\cdot \left( {\nabla { u}} \right) \end{eqnarray}$

定义$z =$ 0为固壁面, $z =$ 1为自由面. 设固壁面流向温度线性分布, 液滴整体以速度$\zeta $向右迁移, 并以液滴整体为参考系, 则固壁面边界条件为

(7)$\begin{eqnarray} u\vert_{z=0} =-\zeta ,\ \ \left. T \right|_{z=0} =-x \end{eqnarray}$

自由面边界条件为

(8)$\begin{eqnarray} \left. {\tau_{13} } \right|_{z=1} =\left. {-\frac{\partial T}{\partial x}} \right|_{z=1} ,\ \left. {\tau_{23} } \right|_{z=1} =\left. {-\frac{\partial T}{\partial y}} \right|_{z=1} ,\ \left. {\frac{\partial T}{\partial z}} \right|_{z=1} =0\quad \end{eqnarray}$

分别表示热毛细效应和热流量. 假设液滴基本流是平行的, 温度在$x$方向的分布是线性的, 则有

(9)$\begin{eqnarray} {u}=\left( {u_{0} \left( z \right),0,0} \right),\ \ T_{0} \left( {x,z} \right)=-x+T_{\rm b} \left( z \right) \end{eqnarray}$

其中带有下标0的变量表示基本流, $T_{\rm b}$为垂直方向上的温度分布. 在液滴整体参考系中, 任意垂直截面上的质量流量为0, 可推出基本流

(10)$u_{0}(z)=-\zeta\left(1-3 z+\frac{3}{2} z^{2}\right)+\left(-\frac{1}{2} z+\frac{3}{4} z^{2}\right)$

(11)$T_{\mathrm{b}}(z)=z^{2} M a\left[\frac{\zeta}{8}(-2+z)^{2}+\frac{z}{4}\left(\frac{1}{3}-\frac{z}{4}\right)\right]$

根据液滴迁移中驱动力与黏滞力的平衡关系, 可推导迁移速度的表达式$\zeta =({2\cos \varphi +1})/{6}$^[32]. 可知迁移速度只与液滴的接触角有关, 因为一般固液接触角$\varphi \in \left[ {0^{\circ},180^{\circ}} \right]$, 所以$\zeta \in \left[ {-{1}/{6},{1}/{2}} \right]$.

分析流动稳定性. 液滴自由面的变形量级由毛细数$Ca={Ma}/({Pr\cdot S})$反映^[28], $S=\rho d{\sigma }'_{0} /\mu^{2}$为表面张力数. 对于硅油$Ca$通常为0.001^[29]. 因此可以假设自由面不变形, 而只考虑液滴内部的对流不稳定. 采用模态分析方法, 在基本流场中叠加正则小扰动

(12)$(u, T, P, \tau)=\left(u_{0}, T_{0}, P_{0}, \tau_{0}\right)+\delta$

(13)$\delta=(\widehat{u}, \hat{v}, \hat{w}, \widehat{T}, \widehat{P}, \widehat{\tau}) \exp [\sigma t+\mathrm{i}(\alpha x+\beta y)]$

(14)${\tau }_{0} ={u}'_{0} \left( z \right)\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {2\left( {\lambda -\eta } \right){u}'_{0} \left( z \right)} & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \\ \end{array} }} \right]$

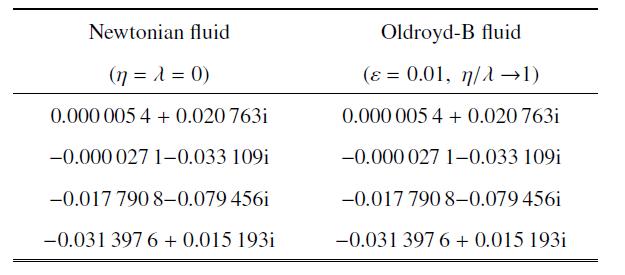
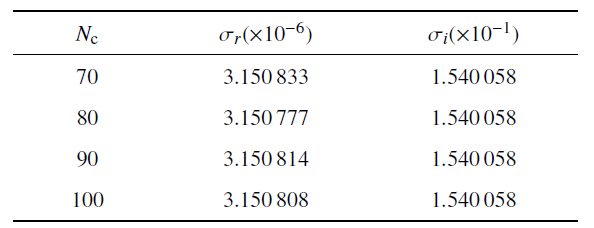
因为黏弹性流体的弹性作用, 在${\tau }_{0} $中存在一正应力. 式中无下标0的变量表示扰动, $\sigma =\sigma_{\rm r} +{\rm i}\sigma_{\rm i} $, $\sigma _{\rm r} $和$\sigma_{\rm i} $分别为增长率和频率, $\alpha ,\beta $分别表示在$x,y$轴上的波数. 总波数、波传播角和波速分别用$k=\sqrt {\alpha ^{2}+\beta^{2}} $, $\theta =\tan^{-1}(\beta /\alpha )$和$c=-\sigma_{\rm i} /k$表示. 扰动方程和边界条件在附录A中给出. $\sigma $可以通过Chebyshev配点法求解, 配置点数$N_{\rm c}$通常设置为70$\sim$100. 表1中对牛顿流体^[32]与$\eta /\lambda \to 1$时的Oldroyd-B流体特征值进行比较, 两者结果完全一致. 表2中给出了临界模态不同配置点下特征值的趋势情况. 从表中可以看出, 本文数值结果是足够准确的.

Table 1
表1
表1$Pr = 0.01$, $\zeta = 0.2$, $Ma = 15.5$, $k = 1.49$, $\theta =83.4^{\circ}$时牛顿流体与Oldroyd-B流体最不稳定特征值的比较
Table 1A comparison of most unstable eigenvalues for Newtonian fluid and Oldroyd-B fluid at $Pr = 0.01$,$\zeta = 0.2$, $Ma= 15.5$, $k = 1.49$, $\theta =83.4^{\circ}$

新窗口打开|下载CSV

Table 2
表2
表2$Pr=1$, $\zeta = 0.1$, $\eta /\lambda =0.1$, $\varepsilon = 0.01$, $Ma = 123.61$, $k = 2.582$, $\theta =46.5^{\circ}$时不同配置点数下的中性模态特征值
Table 2Eigenvalues of neutral modes computed by different numbers of collocation points at $Pr=1$, $\zeta = 0.1$, $\eta /\lambda = 0.1$, $\varepsilon = 0.01$, $Ma=123.61$, $k = 2.582$, $\theta =46.5^{\circ}$

新窗口打开|下载CSV

2 数值结果

定义临界Marangoni数$Ma_{\rm c}$为所有波数下中性Marangoni数$Ma_{\rm N}(\sigma_{\rm r} =0)$的最小值

(15)$\begin{eqnarray} Ma_{\rm c} =\mathop{\min }\limits_{\alpha ,\beta } Ma_{\rm N} \left( {Pr,\varepsilon } \right) \end{eqnarray}$

为简便起见, 只考虑$\zeta = 0.1$, ${\eta /\lambda }=0.1$的情况, 即迁移速度中等且溶剂黏度占主导. 在计算中, 分析$Ma_{\rm c}$与弹性数$\varepsilon ={\lambda }/{Re}={\mu ^{2}}/({\hat{{G}}\rho d^{2}})$之间的关系. 因为后者只与流体的性质和流动几何特性有关, 而与特征速度$U$无关.

2.1 临界曲线

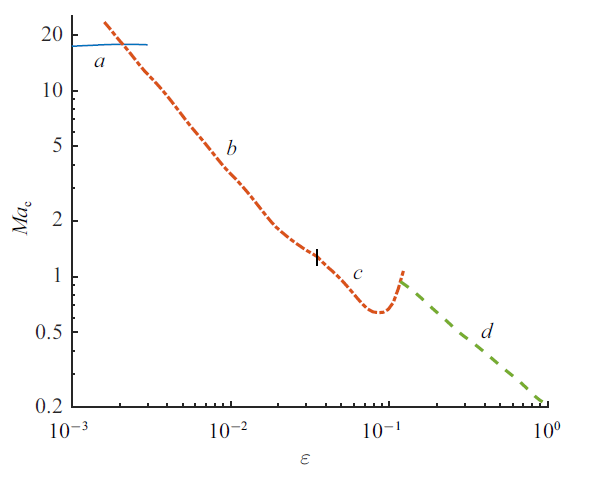
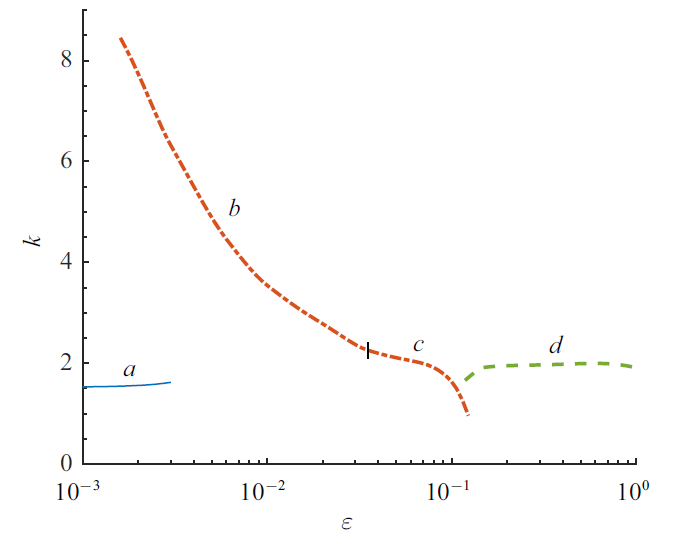
根据Prandtl数的定义可知, Prandtl数反映流体内热对流和热传导的相对重要性. Prandtl数较小时失稳由惯性机制引起, Prandtl数较大时失稳机制由热毛细机制引起. 当Prandtl数在1附近时, 热传导与热对流的重要性相当, 此时流体失稳机制会变得更加复杂, 所以本文选择了Prandtl数为0.3, 1和3进行计算.

图2$\sim\!$图5为$Pr= 0.01$时$Ma_{\rm c}$、波数、波传播角和波速随$\varepsilon $ 的变化曲线. 可以发现曲线存在3种临界模态, 当$\varepsilon <0.002$和$\varepsilon > 0.12$时(图2$\sim\!$ 图5中的曲线$a$和$d$), 临界模态为逆向斜波($\theta >90^{\circ})$; $0.002<\varepsilon < 0.035$时(图2$\sim\!$图5中的曲线$b$), 临界模态为同向流向波($\theta =0^{\circ})$; $0.035<\varepsilon<0.12$时(图2$\sim\!$图5中的曲线$c$), 波的传播方向发生变化, 此时的临界模态为逆向流向波($\theta =180^{\circ})$. 综合起来可以看出, 曲线$a$的各临界值均随$\varepsilon $的增大而略微增大; 曲线$b$和$c$对应的流向波的$Ma_{\rm c}$先随$\varepsilon $ 的增大而减小, 随后有短暂的上升, 波数一直随$\varepsilon $ 的增大而减小, 波速先随$\varepsilon $ 的增大而减小直到0, 此时模态从同向流向波转为逆向, 之后随$\varepsilon $ 的增大而增大; 曲线$d$的$Ma_{\rm c}$随$\varepsilon $的增大而减小, 波传播角随$\varepsilon $的增大而迅速减小, 而波数的变化是微小的, 波速随$\varepsilon $的变化并不是单调的.

图2

新窗口打开|下载原图ZIP|生成PPT
图2$Pr=0.01$时$Ma_{\rm c}$ 随$\varepsilon $ 的变化曲线, 其中$a$, $d$为逆向斜波, $b$为同向流向波, $c$为逆向流向波

Fig.2Variation of $Ma_{\rm c}$ with $\varepsilon $ at $Pr=0.01$, where $a$ and $d$ show upstream oblique waves, $b$ shows downstream streamwise wave, $c$ shows upstream streamwise wave

图3

新窗口打开|下载原图ZIP|生成PPT
图3$Pr=0.01$时波数随$\varepsilon $ 的变化曲线, 其中$a$, $d$为逆向斜波, $b$为同向流向波, $c$为逆向流向波

Fig.3Variation of wave number with $\varepsilon $ at $Pr=0.01$, where $a$ and $d$ show upstream oblique waves, $b$ shows downstream streamwise wave, $c$ shows upstream streamwise wave

图4

新窗口打开|下载原图ZIP|生成PPT
图4$Pr=0.01$时波传播角随$\varepsilon $ 的变化曲线, 其中$a$, $d$为逆向斜波

Fig.4Variation of wave propagation angle with $\varepsilon $ at $Pr=0.01$,where $a$ and $d$ show upstream oblique waves

图5

新窗口打开|下载原图ZIP|生成PPT
图5$Pr=0.01$时波速随$\varepsilon $ 的变化曲线, 其中$a$, $d$为逆向斜波, $b$为同向流向波, $c$为逆向流向波

Fig.5Variation of wave speed with $\varepsilon $ at $Pr=0.01$, where $a$ and $d$ show upstream oblique waves, $b$ shows downstream streamwise wave, $c$ shows upstream streamwise wave

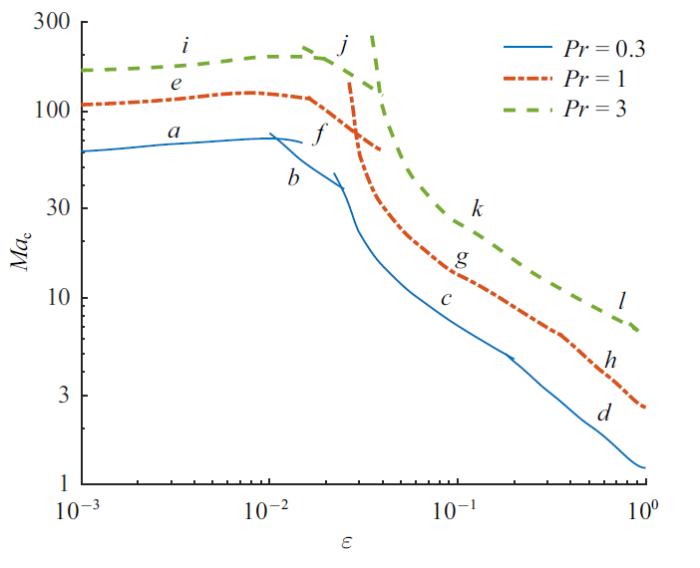
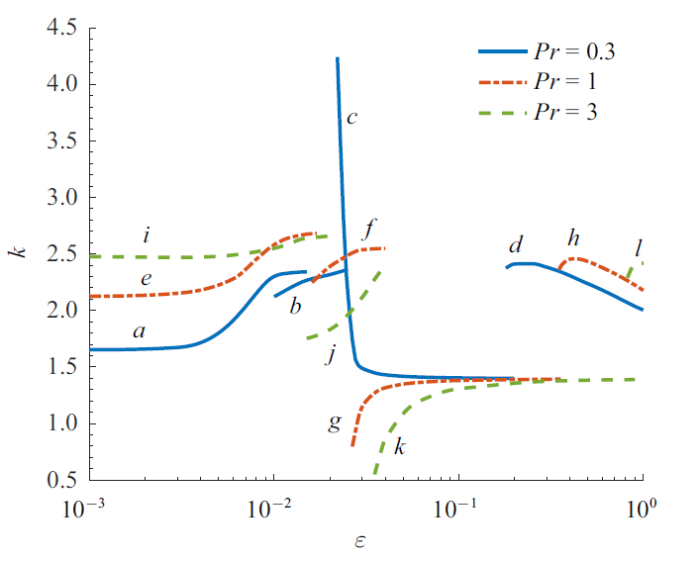
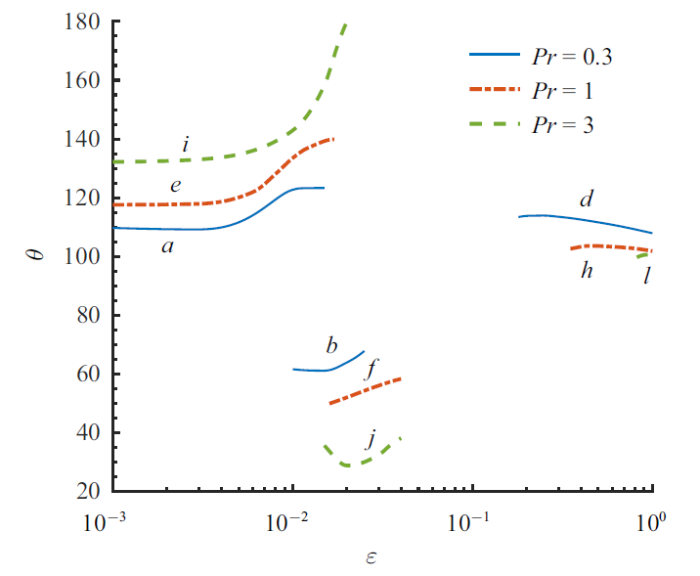
图6$\sim\!$图9为$Pr=0.3$, 1和3时$Ma_{\rm c}$、波数、波传播角和波速随$\varepsilon $ 的变化曲线. 可以发现每个Prandtl数均存在3种相同的临界模态, 且$Ma_{\rm c}$随$Pr$的增大而增大. 对于$Pr=1$, 当$\varepsilon <0.017$, $\varepsilon > 0.35$时(图6$\sim\!$图9中的曲线$e$和$h$), 临界模态为逆向斜波($\theta >90^{\circ})$; $0.017 <\varepsilon <0.028$时(图6$\sim\!$图9中的曲线$f$), 临界模态为同向斜波($\theta <90^{\circ})$; $0.028 <\varepsilon <0.35$时(图6$\sim\!$图9中的曲线$g$), 临界模态为展向稳态模态($\theta =90^{\circ}$, $c=0)$. 综合起来可以看出, 对于$Ma_{\rm c}$, 曲线$e$随$\varepsilon $的增大略有上升, 而其余曲线均随$\varepsilon $的增大而减小; 对于波数, 曲线$h$开始随$\varepsilon $的增大有短暂的上升随后减小, 而其余曲线均随$\varepsilon $的增大而增大, 其中曲线$g$的波数开始有明显变化, 随后只有微小变化; 对于传播角, 曲线$e$和$f$均随$\varepsilon $的增大而增大, 曲线$h$则无明显变化; 对于波速, 曲线$e$的后半段存在轻微变化, 曲线$f$ 随$\varepsilon $的增大而减小, 曲线$h$随$\varepsilon $的增大有明显增大. 其余Prandtl数的曲线特征是类似的.

图6

新窗口打开|下载原图ZIP|生成PPT
图6$Pr=0.3$, 1和3时$Ma_{\rm c}$ 随$\varepsilon $ 的变化曲线, 其中$a$, $d$, $e$, $h$, $i$,$l$曲线对应逆向斜波; $b$, $f$, $j$曲线对应同向斜波; $c$, $g$, $k$曲线对应展向稳态模态

Fig.6Variation of $Ma_{\rm c}$ with $\varepsilon $ at $Pr=0.3$, 1 and 3, where $a$, $d$, $e$, $h$, $i$, $l $ curves correspond to upstream oblique wave; $b$, $f$, $j$ curves correspond to downstream oblique wave; $c$, $g$, $k $ curves correspond to spanwise stationary mode

图7

新窗口打开|下载原图ZIP|生成PPT
图7$Pr=0.3$, 1和3时波数随$\varepsilon $ 的变化曲线, 其中$a$, $d$, $e$, $h$, $i$, $l$曲线对应逆向斜波; $b$, $f$, $j$曲线对应同向斜波; $c$, $g$, $k$曲线对应展向稳态模态

Fig.7Variation of wave number with $\varepsilon $ at $Pr=0.3$, 1 and 3, where $a$, $d$, $e$, $h$, $i$, $l $ curves correspond to upstream oblique wave; $b$, $f$, $j$ curves correspond to downstream oblique wave; $c$, $g$, $k $ curves correspond to spanwise stationary mode

图8

新窗口打开|下载原图ZIP|生成PPT
图8$Pr=0.3$, 1和3时波传播角随$\varepsilon $ 的变化曲线, 其中$a$, $d$, $e$, $h$, $i$, $l$曲线对应逆向斜波; $b$, $f$, $j$曲线对应同向斜波

Fig.8Variation of wave propagation angle with $\varepsilon $ at $Pr=0.3$, 1 and 3, where $a$, $d$, $e$, $h$, $i$, $l $ curves correspond to upstream oblique wave; $b$, $f$, $j$ curves correspond to downstream oblique wave

图9

新窗口打开|下载原图ZIP|生成PPT
图9$Pr=0.3$, 1和3时(I)波速随$\varepsilon $ 的变化曲线, 其中$a$, $d$, $e$, $h$, $i$,$l$曲线对应逆向斜波; $b$, $f$, $j$曲线对应同向斜波

Fig.9Variation of wave speed with $\varepsilon $ at $Pr=0.3$, 1 and 3, where $a$, $d$, $e$, $h$, $i$, $l$ curves correspond to upstream oblique wave; $b$, $f$, $j$ curves correspond to downstream oblique wave

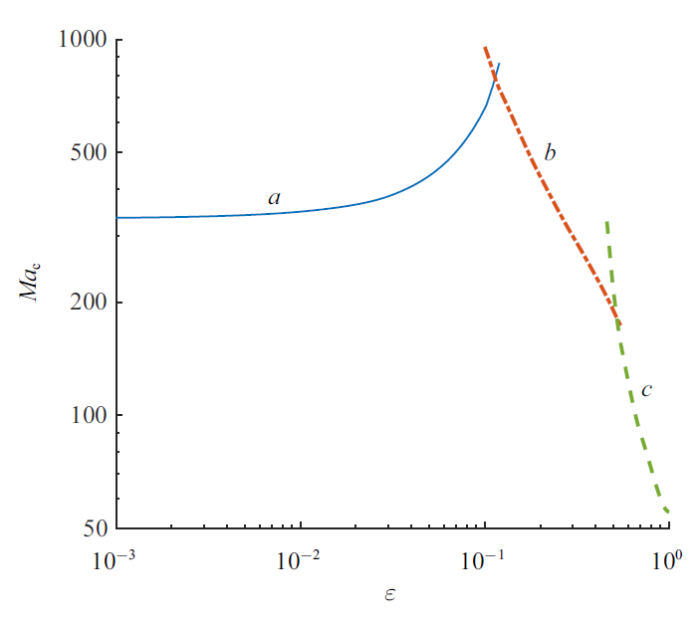
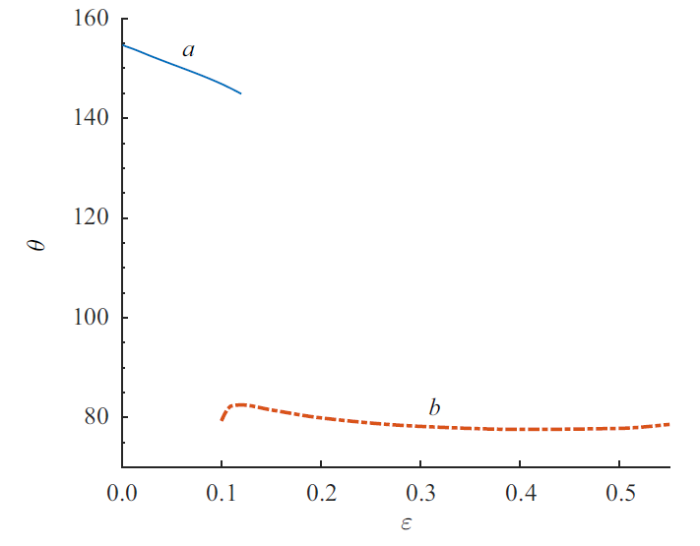
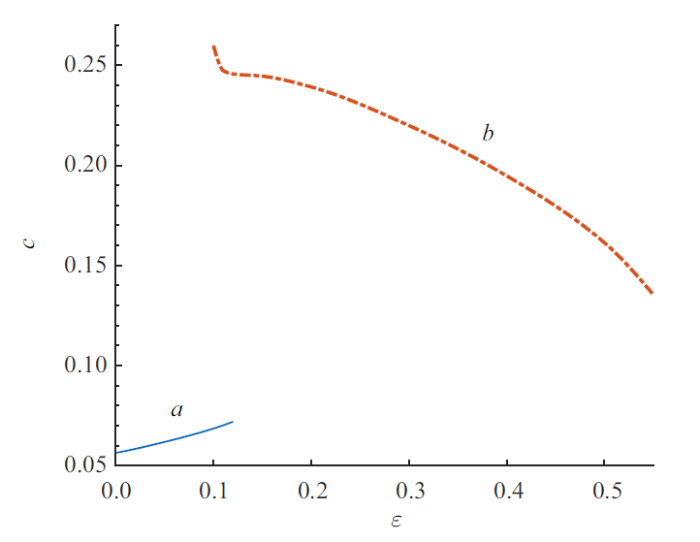
图10$\sim\!$图13为$Pr=100$时$Ma_{\rm c}$、波数、波传播角和波速随$\varepsilon$的变化曲线. 可以发现曲线也存在3种与$Pr = 1$类似的临界模态, 当$\varepsilon <0.12$时(图2$\sim\!$图5中的曲线$a$), 临界模态为逆向斜波$(\theta >90^{\circ})$; $0.12< \varepsilon <0.55$时(图2$\sim\!$图5中的曲线$b$), 临界模态为同向斜波$(\theta <90^{\circ})$; $\varepsilon>0.55$时(图2$\sim\!$图5中的曲线$c$), 临界模态为展向稳态模态$(\theta =90^{\circ}$, $c=0)$. 第一种模态的$Ma_{\rm c}$随$\varepsilon$的增大而增大, 而后两种模态的$Ma_{\rm c}$随$\varepsilon$的增大而减小. 综合各曲线可以看出, 曲线$a$的波数和传播角均随$\varepsilon$的增大而减小, 而波速随$\varepsilon$的增大而增大; 曲线$b$的波数和波速均随$\varepsilon$的增大而减小, 而传播角无明显的变化; 曲线$c$的波数随$\varepsilon$ 的增大而增大.

图10

新窗口打开|下载原图ZIP|生成PPT
图10$Pr=100$时$Ma_{\rm c}$ 随$\varepsilon $ 的变化曲线, 其中$a$对应逆向斜波, $b$对应同向斜波, $c$对应展向稳态模态

Fig.10Variation of $Ma_{\rm c}$ with $\varepsilon $ at $Pr=100$, where $a$ shows upstream oblique waves, $b$ shows downstream oblique wave, $c$ shows upstream streamwise wave

图11

新窗口打开|下载原图ZIP|生成PPT
图11$Pr=100$时波数随$\varepsilon $ 的变化曲线, 其中$a$对应逆向斜波, $b$对应同向斜波, $c$对应展向稳态模态

Fig.11Variation of wave number with $\varepsilon $ at $Pr=100$, where $a$ shows upstream oblique waves, $b$ shows downstream oblique wave, $c$ shows upstream streamwise wave

图12

新窗口打开|下载原图ZIP|生成PPT
图12$Pr=100$时波传播角随$\varepsilon $ 的变化曲线, 其中$a$对应逆向斜波, $b$对应同向斜波

Fig.12Variation of wave propagation angle with $\varepsilon $ at $Pr=100$, where $a$ shows upstream oblique waves, $b$ shows downstream oblique wave

图13

新窗口打开|下载原图ZIP|生成PPT
图13$Pr=100$时波速随$\varepsilon $ 的变化曲线, 其中$a$对应逆向斜波, $b$对应同向斜波

Fig.13Variation of wave speed with $\varepsilon $ at $Pr=100$, where $a$ shows upstream oblique waves, $b$ shows downstream oblique wave

2.2 扰动流场

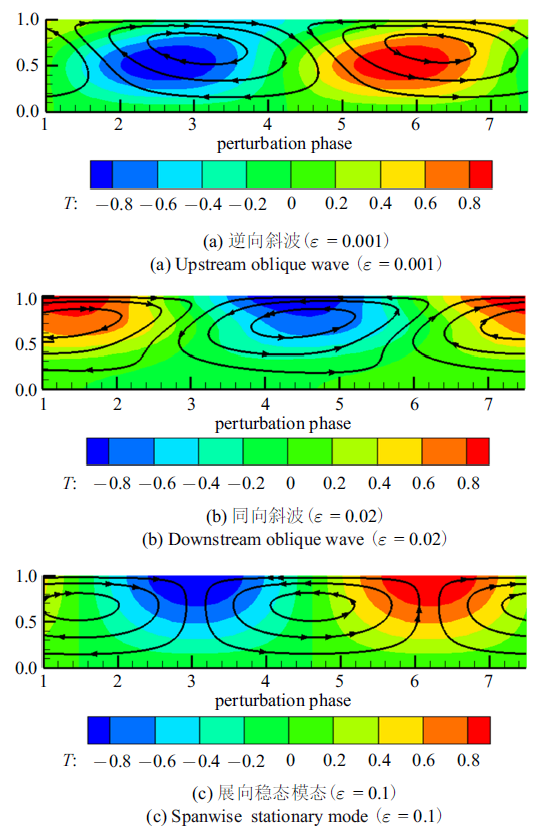
为了能更加清晰地了解流动失稳的机制, 绘制了不同临界模态下的等温线图和流线图, 并将最大扰动温度进行归一化. 为了比较不同参数下的流场, 将扰动的波长固定为2$\pi $, 此时原点表示扰动初始位置, 横轴数值表示扰动的相位, 横轴方向为波的传播方向.

图14$\sim\!$图16分别显示了$Pr$为0.01, 1和100时, 不同临界模态所对应的扰动流场. 从图中可以看出, 当$Pr = 0.01$时, 各模态温度场的热点均分布在自由表面. 在图14(b)流场中, 一个大涡内还存在两个小涡, 扰动速度在垂直方向上存在多次振荡, 并且扰动基本分布在表面. 当$Pr=1$时, 图15(c)与图16(c)几乎一致, 而且除了逆向斜波的温度场热点分布在流场中间区域外, 其余模态的热点均分布在自由表面. 当$Pr=100$时, 斜波对应的温度场的热点均存在于中间区域, 且各模态的流线分布几乎呈对称状态.

图14

新窗口打开|下载原图ZIP|生成PPT
图14$Pr = 0.01$时不同临界模态所对应的扰动流场

Fig.14Perturbation flow field of the different preferred modes at $Pr = 0.01$

图15

新窗口打开|下载原图ZIP|生成PPT
图15$Pr=1$时不同临界模态所对应的扰动流场

Fig.15Perturbation flow field of the different preferred modes at $Pr=1$

图16

新窗口打开|下载原图ZIP|生成PPT
图16$Pr=100$时不同临界模态所对应的扰动流场

Fig.16Perturbation flow field of the different preferred modes at $Pr=100$

2.3 能量分析

扰动能量的变化率可以写成以下形式^[15]

(16)$\begin{eqnarray}\frac{\partial E_{\rm kin} }{\partial t}=-\frac{1}{2Re}\int {({ \tau }:{S}){\rm d}^{3}r} +\frac{1}{Re}\int {{ u}\cdot { \tau }\cdot { n}{\rm d}^{2}r}-\int {{ u}} \cdot [({ u}\cdot \nabla ){u}_{0} ]{\rm d}^{3}r=-N+M+I \end{eqnarray}$

式中$N$为扰动应力做的功, $M$为Marangoni力在表面做的功, $I$为扰动流与基本流之间的相互作用. 这里将扰动动能进行归一化处理, 即$\int {\left| {{ u}} \right|^{2}d^{3}r=1} $. 表3中给出了不同$Pr$数下各扰动能量变化项的值. 可以发现, 随着弹性数增大, $I$由正变负. $Pr=100$时, $I$几乎可以忽略, $N > 0$代表耗散, 说明扰动能量的来源是Marangoni力在表面做的功. $Pr=1$时, $M$和$N$均大于0, 而$I$既可能耗散能量又可能提供能量. $Pr = 0.01$时, 各项值均可变化符号, 并且$N$和$I$是主要的耗散或能量来源. 由式(5)可知在牛顿流体^[32]中, ${ \tau }={S}$, $N$始终大于0, 对应黏性耗散. 而对于黏弹性流体, 弹性引起了${ \tau }$与${S}$之间的相位差, 在一些情况下可能对扰动做正功.

Table 3
表3
表3不同$Pr$数下各扰动能量变化项的值
Table 3Values of perturbation energy variation terms at different $Pr$

新窗口打开|下载CSV

图17分别为$Pr =0.01$时各临界模态扰动应力做功和扰动流与基本流之间的相互作用在垂直方向上的分布. 各模态对应的弹性数$\varepsilon $分别为0.001, 0.01和0.1. 其中

(17)$-N=\int {P_{N} } {\rm d}z,\ \ P_{N} =-\frac{1}{2Re}\int {\left( {{\tau }:{S}} \right)} {\rm d}^{2}r$

(18)$I=\int {P_{I} } {\rm d}z,\ \ P_{I} =-\int {u\cdot \left( {w\cdot {u}'_{0} } \right)} {\rm d}^{2}r$

图17

新窗口打开|下载原图ZIP|生成PPT
图17$Pr = 0.01$时各临界模态扰动应力做功(a)和扰动流与基本流之间的相互作用(b)在垂直方向上的分布. 其中, UOW代表逆向斜波, DSW代表同向流向波, USW代表逆向流向波

Fig.17Distribution of (a) the work done by perturbation stress and (b) the interaction between the perturbation flow and the basic flow in vertical direction of the different preferred modes at $Pr = 0.01$. Here, UOW stands for upstream oblique wave, DSW stands for downstream streamwise wave, USW stands for upstream streamwise wave

从图17中可以看出, 在液滴下半区域($z < 0.5$)各临界模态的$P_{N}$和$P_{I}$变化均较为平缓. 而在液滴上半区域($z > 0.5$)中, 同向流向波的$P_{N}$和$P_{I}$存在多次的振荡. 对于逆向流向波, $P_{N}$和$P_{I}$的最值均在$z =0.8$附近.

2.4与热毛细液层对比

将液滴热毛细迁移与黏弹性热毛细液层^[33]进行对比可以发现: 在小Prandtl数下, 液层中存在展向稳态模态, 而液滴中只有斜波和流向波; 当弹性数足够大时, 液层的临界模态均为展向稳态模态, 而液滴在小和中Prandtl数下的临界模态为斜波; 对于展向稳态模态, 液层的等温线几乎是垂直的, 而在液滴中扰动温度在自由表面处存在振幅.

3 结论

本文采用线性稳定性理论研究了附壁黏弹性液滴在热毛细迁移中的对流不稳定性, 分析了不同Prandtl数下弹性数对流动稳定性的影响, 并结合流场图和能量分析发现以下结论:

(1)由于流体弹性的影响, 激发了更多不稳定模态. 小Prandtl数的临界模态为斜波和流向波, 而中高Prandtl数的临界模态为斜波和展向稳态模态.

(2)弹性数对流动稳定性的影响并不是单调的. 弱弹性略微增强了流动稳定性, 而强弹性使得临界Marangoni数显著下降.

(3)对于斜波模态, 扰动温度的振幅可以存在于流场中间区域, 而其他两种模态的温度振幅只存在于自由表面上, 并且在高Prandtl数下的流线分布几乎是对称的.

(4)随着弹性数增大, 基本流做功由正变负; 在小Prandtl数中, 扰动应力做功既可能耗散能量又可能提供能量; 中高Prandtl数下, 扰动应力做功对能量进行耗散, Marangoni力在表面做功为流动主要能量来源.

(5)通过液滴迁移与热毛细液层对比发现, 由于基本流和边界条件的不同, 使得两者稳定性结果存在较大的差异.

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

Karbalaei

, Kumar

, Cho

. Thermocapillarity in microfluidics-a review
Micromachines, 2016,7(2):13

DOI URL [本文引用: 1]

[2]

Basaran

, Gao

, Bhat

. Nonstandard inkjets
Annual Review of Fluid Mechanics, 2013,45(1):85-113

DOI URL [本文引用: 1]

[3]

Shankar Subramanian

RBR

. The Motion of Bubbles and Drops in Reduced Gravity. Cambridge University Press, 2005: 3411-3416

[本文引用: 1]

[4]

Liu

, Zhang

. Modelling thermocapillary migration of a microfluidic droplet on a solid surface
Journal of Computational Physics, 2015,280:37-53

DOI URL [本文引用: 1]

[5]

. Steady thermocapillary migration of a droplet in a uniform temperature gradient combined with a radiation energy source at large Marangoni numbers
Physical Review E, 2018,98(1):013110

DOI URL [本文引用: 1]

[6]

叶学民, 张湘珊, 李明兰等. 自润湿流体液滴的热毛细迁移特性
物理学报, 2018,67(18):223-234

(Ye

Xueming

, Zhang

Xiangshan

, Li

Minglan

, et al. Thermocapillary migration characteristics of self-rewetting drop
Acta Physica Sinica, 2018,67(18):223-234 (in Chinese))

[7]

张波. 热辐射下液滴/气泡自发迁移的数值研究. [硕士论文]
北京: 华北电力大学, 2018

[本文引用: 1]

(Zhang

. Numerical investigation on spontaneous droplet/bubble migration under thermal radiation. [Master Thesis]
Beiijing: North China Electric Power University, 2018 (in Chinese))

[本文引用: 1]

[8]

钟源, 杜海存, 张莹等. 单向温度梯度下异质液滴的热毛细迁移
过程工程学报, 2018,18(4):697-703

[本文引用: 1]

(Zhong

Yuan

, Du

Haicun

, Zhang

Ying

, et al. Thermocapillary migration of heterogeneous droplets with unidirectional temperature gradient
The Chinese Journal of Process Engineering, 2018,18(4):697-703 (in Chinese))

[本文引用: 1]

[9]

孙涛, 姜存华, 沈达鹏等. 水平固体表面温度梯度下硅油液滴运动
微纳电子技术, 2017(7):52-58

( Sun

Tao

, Jiang

Cunhua

, Shen

Dapeng

, et al. A silicone oil droplet motion under temperature gradient on horizontal solid surface
Micronanoelectronic Technology, 2017(7):52-58 (in Chinese))

[10]

钟源. 液滴撞击不同固体表面动力学特性及热毛细迁移研究. [硕士论文]
南昌: 南昌大学, 2019

[本文引用: 1]

( Zhong

Yuan

. Research on dynamic characteristics of droplets impacting different solid surfaces and thermocapillary migration. [Master Thesis]
Nanchang: Nanchang University, 2019(in Chinese))

[本文引用: 1]

[11]

尚超, 阳倦成, 张杰等. 镓铟锡液滴撞击泡沫金属表面的运动学特性研究
力学学报, 2019,51(2):380-391

[本文引用: 1]

(Shang

Chao

, Yang

Juancheng

, Zhang

Jie

, et al. Experimental study on the dynamic characteristics of galinstan droplet impacting on the metal foam surface
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(2):380-391 (in Chinese))

[本文引用: 1]

[12]

霍元平, 王军锋, 左子文等. 滴状模式下液桥形成及断裂的电流体动力学特性研究
力学学报, 2019,51(2):425-431

[本文引用: 1]

(Huo

Yuanping

, Wang

Junfeng

, Zuo

Ziwen

, et al. Electrohydrodynamic characteristics of liquid bridge formation at the dripping mode of electrosprays
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(2):425-431 (in Chinese))

[本文引用: 1]

[13]

刘赵淼, 徐元迪, 逄燕等. 压电式微滴按需喷射的过程控制和规律
力学学报, 2019,51(4):1031-1042

[本文引用: 1]

(Liu

Zhaomiao

, Xu

Yuandi

, Pang

Yan

, et al. Study of process control on piezoelectric drop-on-demand ejection
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(4):1031-1042 (in Chinese))

[本文引用: 1]

[14]

Ford

, Nadim

. Thermocapillary migration of an attached drop on a solid surface
Physics of Fluids, 1994,6(9):3183-3185

DOI URL [本文引用: 2]

[15]

Smith

. Thermocapillary migration of a 2-dimensional liquid droplet on a solid-surface
Journal of Fluid Mechanics, 1995,294(1):209-230

DOI URL [本文引用: 2]

[16]

Chen

, Troian

, Darhuber

, et al. Effect of contact angle hysteresis on thermocapillary droplet actuation
Journal of Applied Physics, 2005,97(1):014906

DOI URL [本文引用: 1]

[17]

Brzoska

, Brochard-Wyart

, Rondelez

. Motions of droplets on hydrophobic model surfaces induced by thermal gradients
Langmuir, 1993,9(8):2220-2224

DOI URL [本文引用: 1]

[18]

Haj-hariri

, Shi

, Borhan

. Thermocapillary motion of deformable drops at finite Reynolds and Marangoni numbers
Physics of Fluids, 1997,9(4):845-855

DOI URL [本文引用: 1]

[19]

Pratap

, Moumen

, Subramanian

. Thermocapillary motion of a liquid drop on a horizontal solid surface
Langmuir, 2008,24(9):5185-5193

DOI URL [本文引用: 1]

[20]

Dai

, Khonsari

, Shen

, et al. Thermocapillary migration of liquid droplets induced by a unidirectional thermal gradient
Langmuir, 2016,32(30):7485-7492

DOI URL [本文引用: 1]

[21]

Dai

, Huang

, Wang

, et al. Ringlike migration of a droplet propelled by an omnidirectional thermal gradient
Langmuir, 2018: acs.langmuir.7b04259

[22]

Dai

, Chong

, Huang

, et al. Migration of liquid bridges at the interface of spheres and plates with an imposed thermal gradient
Langmuir, 2020,36:6268-6276

DOI URL

[23]

Dai

, Huang

, Wang

, et al. Directional interfacial motion of liquids: Fundamentals, evaluations, and manipulation strategies
Tribology International, 2021,154:106749

DOI URL [本文引用: 1]

[24]

Bowen

, Tilley

. Thermally induced van der Waals rupture of thin viscous fluid sheets
Physics of Fluids, 2012,24(3):931-1198

[本文引用: 1]

[25]

Cazabat

, Heslot

, Troian

, et al. Fingering instability of thin spreading films driven by temperature gradients
Nature, 1990,346(6287):824-826

DOI URL [本文引用: 1]

[26]

Davis

. Thermocapillary instabilities
Annual Review of Fluid Mechanics, 1987,19(1):403-435

DOI URL [本文引用: 1]

[27]

Schatz

, Neitzel

. Experiments on thermocapillary instabilities
Annual Review of Fluid Mechanics, 2001,33(1):93-127

DOI URL [本文引用: 1]

[28]

Smith

, Davis

. Instabilities of dynamic thermocapillary liquid layers. Part 1. Convective instabilities
Journal of Fluid Mechanics, 1983,132(1):119-144

DOI URL [本文引用: 2]

[29]

Riley

, Neitzel

. Instability of thermocapillary-buoyancy convection in shallow layers. Part 1. Characterization of steady and oscillatory instabilities
Journal of Fluid Mechanics, 1998,359:143-164

DOI URL [本文引用: 2]

[30]

, Imaishi

, Azami

, et al. Three-dimensional oscillatory flow in a thin annular pool of silicon melt
Journal of Crystal Growth, 2004,260(1-2):28-42

DOI URL [本文引用: 1]

[31]

Burelbach

, Bankoff

, Davis

. Nonlinear stability of evaporating/condensing liquid films
Journal of Fluid Mechanics, 1988,195(1):463-494

DOI URL [本文引用: 1]

[32]

, Yan

, Chen

. Instability of thermocapillary-buoyancy convection in droplet migration
Physics of Fluids, 2019,31(12):122101

DOI URL [本文引用: 4]

[33]

, He

, Chen

. Instability of thermocapillary liquid layers for Oldroyd-B fluid
Physics of Fluids, 2016,28(3):93-127

[本文引用: 2]

[34]

Brochard

. Motions of droplets on solid surfaces induced by chemical or thermal gradients
Langmuir, 1995,5(2):193-213

[本文引用: 1]

[35]

Bird

, Curtiss

, Armstrong

, et al. Dynamics of Polymeric Liquids, Volume 2: Kinetic Theory
John Wiley & Sons, Inc, 1987

[本文引用: 1]