非连续数字图像相关方法在裂纹重构中的应用 1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

汤文治^,²⁾, 肖汉斌, 邹晟武汉理工大学物流工程学院,武汉 430063

APPLICATION OF DISCONTINUOUS DIGITAL IMAGE CORRELATION IN CRACK RECONSTRUCTION ¹⁾

Tang Wenzhi^,²⁾, Xiao Hanbin, Zou ShengSchool of Logistics Engineering, Wuhan University of Technology, Wuhan 430063, China

通讯作者: 2) 汤文治,在读博士研究生,主要研究方向：裂纹识别与诊断、数字图像相关方法的力学应用.E-mail:future_tang@126.com

收稿日期:2019-04-17接受日期:2019-06-19网络出版日期:2019-07-18

基金资助:

1) 中央高校基本科研业务费专项资金.2015-JL-015
国家科技支撑计划.2015BAF06B016

Received:2019-04-17Accepted:2019-06-19Online:2019-07-18
作者简介 About authors

摘要
数字图像相关方法作为一种新的非接触式位移测量方法,在力学工程中有广泛的应用前景,然而受限于标准方法对图像变形的连续性要求,这种高效的测量方法在断裂力学领域的推广受到了限制. 为解决这一问题,提出采用引入子区分离数学模型,代替标准方法的连续模型,来对非连续区域进行精确识别和匹配的非连续数字图像相关方法. 研究子区被裂纹等非连续分割后原始像素点的位移情况,并引入裂纹张开向量用以表征被分割子区的主区和副区的位移关系;从而建立子区分离模型的数学表达式,并且为所提出的模型设计相应的图像相关算法;然后将所提出的非连续数字图像相关方法应用于重构平板拉伸试验开裂过程中图像的位移. 研究结果表明,相比于标准的数字图像相关方法,所提出的非连续数字图像相关方法解决了图像相关法在非连续区域失效的问题,提高了数字图像相关方法对位移测量的正确率,特别是能够准确重构裂纹面及附近的位移场,其测量精度能够达到亚像素级别.
关键词： 位移场测量;非连续数字图像相关;子区分离模型;裂纹重构;裂纹张开向

Abstract
The digital image correlation (DIC) method is a new non-destructive, contactless displacement measurement approach and it can be broadly applied in mechanical engineering with wide application prospect. However, this efficient and convenient displacement measurement method is difficult to apply in fracture mechanics due to the limitation that continuous deformation is required when processing the deformed images with standard digital image correlation methods. Aiming at solving this problem, this paper proposes a novel discontinuous digital image correlation (DDIC) method by introducing the splitted subset model to take the place of continuous model and use it to analyze the discontinuous areas where standard digital image correlation method is not valid in. The displacement of the original pixel points is studied when discontinuities such as cracks occurs, and the crack opening vector is introduced to represent the displacement relationship between the master zone and the slave zone after subset splitting into two parts. Thus the mathematical model of the splitted subset can be established by using the crack opening vector to correlate the master zone and the slave zone, and the corresponding image correlation algorithm can be designed based on this model. Afterwards, the proposed discontinuous digital image correlation method is used to measure the displacements of the deformed images obtained from the cracking process when a tensile test is applied to the notched plate. The research results show that the proposed DDIC method works well in both continuous and discontinuous areas, and when compared with the standard DIC method, the DDIC method is capable to solve the validation problem of image correlation method in discontinuous region, and improves the accuracy for displacement measurement, moreover, the proposed method is able to reconstruct the crack faces and the displacement fields in the vicinity region crack, and the accuracy of displacement measurement can be controlled within the range of subpixel level.
Keywords：displacement field measurement;discontinuous DIC;splitted subset model;crack reconstruction;crack opening vector

PDF (9704KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
汤文治, 肖汉斌, 邹晟. 非连续数字图像相关方法在裂纹重构中的应用 ¹⁾. 力学学报[J], 2019, 51(4): 1101-1109 DOI:10.6052/0459-1879-19-098
Tang Wenzhi, Xiao Hanbin, Zou Sheng. APPLICATION OF DISCONTINUOUS DIGITAL IMAGE CORRELATION IN CRACK RECONSTRUCTION ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2019, 51(4): 1101-1109 DOI:10.6052/0459-1879-19-098

引言

由于裂纹常用于结构的生命周期中,对裂纹及其扩展情况的监测和控制始终是一个重要的研究课题. 目前对这一问题的研究主要集中在裂纹检测和识别,如超声波探伤^[1]、红外热波法^[2]、电磁探测^[3]和裂纹图像识别^[4-6]等. 这些方法只能检测裂纹是否发生,但不能通过采集详细的裂纹位移及应变场来进行有价值的断裂力学分析,从而预测裂纹的扩展以及评估裂纹结构的安全性. 因此,一种有效的裂纹场识别和重建方法对于结构安全工程具有重要意义.

得益于计算机技术的发展,目前国内外一些****提出将数字图像相关(digital image correlation,DIC)方法运用到对裂纹结构的位移场重构中. DIC方法是由Peters和Ranson于1982年提出^[7],随后由Chu等将其应用于试验力学领域^[8-9],并逐渐发展为一种成熟的非接触式位移场测量手段. 但是该技术在断裂力学领域中的应用受到了很大的限制,其核心问题在于DIC提出之初建立的基本数学模型假设了图像变形必须连续均匀^[7-9]. 研究人员为了克服裂纹这种典型的非连续图像对DIC方法应用的限制,从不同的角度对标准DIC方法进行了大量改进, 以期能够准确地得到裂纹附近的位移场.

蒋玮等^[10]、王阳等^[11]、邹宇明等^[12]采用了DIC方法测量不同材料裂纹的J积分,得到了较好的计算结果, 但是采用的方法还是McNeill等^[13],Sutton等^[14]早期提出的裂纹面远端围线积分法,此方法回避了直接计算裂纹面近场的位移以及对裂纹形态的重构,没有解决根本问题. Réthoré等^[15-16]则采用了"扩展数字图像相关法"来处理裂纹面,他们将图像网格化,采用有限元类似的思想计算形状函数,从而获得节点位移,这种方法在本质上已经不属于数字图像相关法, 同时该方法计算量也极大. Jin和Bruck^[17]采用遗传算法来解决DIC对位移连续性的限制问题,提出将图像上每一个像素点的垂直和水平位移都作为参数来进行图像相关算法,需要耗费极大的计算资源,同时,这种算法的通用性也较低,对于理想的连续变形,算法的计算精度相较于经典DIC算法反而有所下降. Helm等^[18]提出用特殊的拟正则光斑对样品表面进行处理,根据他们的观测结果,拟正则光斑能够很好地帮助识别样品表面的非连续性, 然而此方法仅局限于实验室阶段. Blader等^[19]则扩展了潘兵^[20]的RG-DIC方法,使分析结果尽可能接近非连续,然而还是无法得到准确的非连续结果. Hassan等^[21-22]则参考Poissant等^[23]的分割子区思想,将被裂纹割裂的子区看成独立的子区,该方法在识别裂纹上达到了一定效果. 更多的计算方法如网格自适应^[24]、组合条纹投影^[25]、裂尖显微网格^[26-27]等都在解决测量裂纹面近场位移的问题上提供了较多参考方案.

本文针对标准数字图像相关方法对测量裂纹等非连续附近位移场的局限性,提出子区分离数学模型,允许被分割的子区组合还原并参与子区相关计算,通过特殊设计的非连续数字图像相关方法,能够实现裂纹面附近位移场的精确重构. 该方法易于实现并且能得到亚像素级别的位移结果, 可作为一种可靠的高精度裂纹位移形态测量手段,应用于裂纹扩展分析和裂纹监测系统等领域.

1 非连续数字图像相关

1.1 数字图像相关基本原理

数字图像相关方法是基于关联变形前后两张图像的像素区或者子区像素值的一个统计过程,通常采用灰度图像进行分析^[28-29]. 假设图像上的点在变形后只发生了位移的改变,而该点的像素取值不变,并且,对于包含足够多像素的区域,变形前后该区域具有唯一性^[30]. 因此,可以通过对比变形前后两幅图像上像素区之间的统计学关系,来确定各像素(区)的位移结果.

在参考图像$R$中选取某一像素点为中心点$P$并选取其周围$(2M+1)\times (2M+1)$像素区域为其子区$A$,同样,在变形图像$C$中也选取某一像素并以其为中心点$P^\ast$, 选取其周围相同尺寸的像素区为其子区$A^\ast$,对变形前后的像素区灰度值进行统计相关分析, 即可确定中心点在变形前后两幅图像中的位移情况. 目前常用的相关函数主要有互相关函数(CC)和最小平方距离函数(SSD),并且潘兵等^[31]在数学上证明了它们的等效性,有式 \begin{equation} \label{eq1} C_{{SSD}} = 2-2C_{{CC}}(1) \end{equation}

它们的零均值归一化(ZN)函数^[32-33]可分别写为

$$\begin{align*} &C_{{ZNCC}} = \sum\limits_{{i} =-M}^M {\sum\limits_{i =-M}^M {\left[ {\dfrac{\left( {f\left( {x_i ,y_i } \right)-\overline f } \right)\left( {f^\ast \left( {x_i^\ast ,y_i^\ast } \right)-\overline {f^\ast } } \right)}{\Delta f\Delta f^\ast }} \right]} }\quad (2a)\\ &C_{{ZNSSD}} = \sum\limits_{{i} =-M}^M {\sum\limits_{i =-M}^M {\left[ {\dfrac{f\left( {x_i ,y_i } \right)-\overline f }{\Delta f}-\dfrac{f^\ast \left( {x_i^\ast ,y_i^\ast } \right)-\overline {f^\ast } }{\Delta f^\ast }} \right]} } ^2 \quad (2b) \end{align*} $$

式中,$f(x_{i},y_{i})$和$f^\ast(x_{i}^\ast,y_{i}^\ast$)分别为参考图像$R$和变形图像$C$中第$i$个像素点在坐标($x_{i},y_{i})$ 和坐标($x_{i}^\ast,y_{i}^\ast$)处的灰度值;其他参数表达式如下

(3) $$ \left. \begin{array}{l} \overline {f} = \dfrac{1}{\left ( {2M + 1} \right)} \sum\limits_{i =-M}^M { \sum\limits_{i =-M}^M {f\left( {x_i ,y_i } \right)} } \\ \overline {f^\ast } = \dfrac{1}{\left( {2M + 1} \right)}\sum\limits_{i =-M}^M {\sum\limits_{i =-M}^M {f^\ast \left( {x_i^\ast ,y_i^\ast } \right)} } \\ \Delta f = \sqrt {\sum\limits_{i =-M}^M {\sum\limits_{i =-M}^M {\left[ {f\left( {x_i ,y_i } \right)-\overline {f} } \right]} ^2} } \\ \Delta f^\ast = \sqrt {\sum\limits_{i =-M}^M {\sum\limits_{i =-M}^M {\left[ {f^\ast \left( {x_i^\ast ,y_i^\ast } \right)-\overline {f^\ast } } \right]} ^2} } \end{array} \right\}$$

式(2)中,零均值归一化互相关函数$C_{ZNCC} \le $1,零均值归一化最小平方距离函数$C_{ZNSSD} \ge $0,并且它们越接近其对应的极值,表示两被计算的两子区一致性越高. 在变形图像$C$中找出与参考图像$R$中子区$A$一致性最高的子区$A^\ast$, 即可确定参考图像中的像素点$P$在变形图像中的对应像素点$P^\ast$. 由式(1)可知式(2a)和式(2b)具有等效性,后文采用$C_{ ZNSSD}$作为相关函数进行讨论.

1.2 子区分离模型

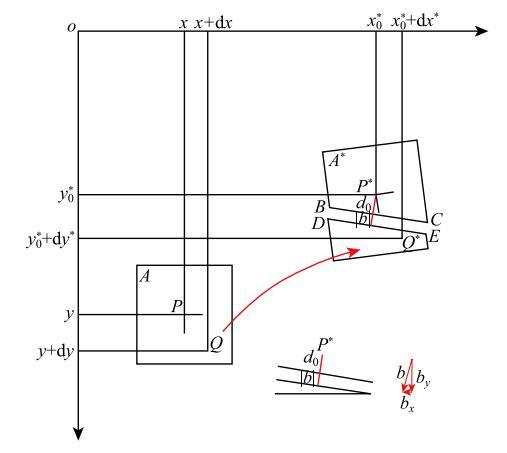
考虑物体的真实表面而非数字图像,其中灰度值在任何地方都是连续的. 对于参考图像$R$中的子区$A$,其中心点$P$在图像$R$中的坐标为($x,y)$, $Q$点是$P$点附近的一点,坐标为($x_{q}$,$y_{q})$. 它们在图像变形后分别移动到子区$A^\ast$中的点$P^\ast(x_{0}^\ast$,$y_{0}^\ast$) 和点 $Q^\ast(x_{q}^\ast$,$y_{q}^\ast$). 由固体力学可知,点$Q$的位移($u_{q}$,$v_{q})$可以从点$P$的位移($u$,$v)$推导出 \begin{equation} \label{eq5} \left. {{\begin{array}{*{20}c} {u_{q} = u + \dfrac{\partial u}{\partial x}{d}x + \dfrac{\partial u}{\partial y}{d}y} \\ {v_{q} = v + \dfrac{\partial v}{\partial x}{d}x + \dfrac{\partial v}{\partial y}{d}y} \\ \end{array} }} \right\}(4) \end{equation}

由于子区$A$和$A^\ast$相对于它们所处的图像尺寸很小, 并且除了裂纹附近区域外,图像的整体形变也都非常微小, 可以假设分开$A^\ast$的裂纹两裂纹面投影在图像上的边界线在子区内近似为两条直线$BC$和$DE$, 并且它们近似平行,$BC$为靠近中心点$P^\ast$侧的裂纹边界,如图1所示.

图1

新窗口打开|下载原图ZIP|生成PPT
图1变形前后的子区分离模型

Fig. 1Splitted subset before and after deformation

注意到有几何关系 \begin{equation} \label{eq6} \left. {{\begin{array}{*{20}c} {{d}x^\ast-{d}x = u_{q}-u + {{b}}_x H(\alpha )}\\ {{d}y^\ast-{d}y = v_{q}-u + {{b}}_y H(\alpha )}\\ \end{array} }} \right\}(5) \end{equation} 其中,$b=(b_{x},b_{y})$为裂纹张开向量,它表示变形图像中子区被裂纹分割后的位移情况,对于常见的Ⅰ型裂纹(撕开型)主导开裂情况^{[34 - 35]},在小尺寸上,可以认为它垂直于裂纹面,指向另一裂纹面,可表征裂纹的开裂方向和大小.

$H(\alpha $)为Heavide函数,用于判断任意点$Q^\ast$与中心点$P^\ast$是否分布在裂纹的同侧,可用数学式表达 \begin{equation} \label{eq7} {H}(\alpha ) = \left\{ {{\begin{array}{*{20}l} 0, & {\alpha > 0}\\ 1, & {\alpha \le 0} \end{array} }} \right.(6) \end{equation} 其中,{$\alpha $}为判断函数,通过计算点$Q^\ast$和点$P^\ast$分别与裂纹线$BC$方程$g_{{BC}} = 0$的关系进行同侧判断 \begin{equation} \label{eq8} \alpha = g_{BC} (x_0^\ast ,y_0^\ast )g_{BC} (x_{q}^\ast ,y_{q}^\ast )(7) \end{equation}

为获取裂纹线$BC$的表达式, 考虑引入最少变量原则,定义$P^\ast$到裂纹线$BC$的距离为$d_{0}$,故裂纹线$BC$的表达式可写作

$$ \begin{align*} &g_{ BC}(x,y) = y-y_0^\ast-d_0 \dfrac{b_y }{\sqrt {b_x^2 + b_y^2 } }+ \\ &\qquad \dfrac{b_x }{b_y }\left( {x-x_0^\ast-d_0 \dfrac{b_y }{\sqrt {b_x^2 + b_y^2 } }} \right) = 0(8) \end{align*} $$

将式(7)代入式(8)即可确定每次计算的Heavide函数$H$({$\alpha $})值. 而由式(4)和式(5)可以求得点$Q^\ast$的灰度为 \begin{equation} \label{eq10} f^\ast (Q^\ast ) = f^\ast \left( {{\begin{array}{*{20}c} {x_{q} + u + \dfrac{\partial u}{\partial \mbox{x}}{d}x + \dfrac{\partial u}{\partial \mbox{y}}{d}y + b_x H(\alpha )} \\ {y_{q} + v + \dfrac{\partial v}{\partial \mbox{x}}{d}x + \dfrac{\partial v}{\partial \mbox{y}}{d}y + b_y H(\alpha )} \end{array} }} \right)(9) \end{equation}

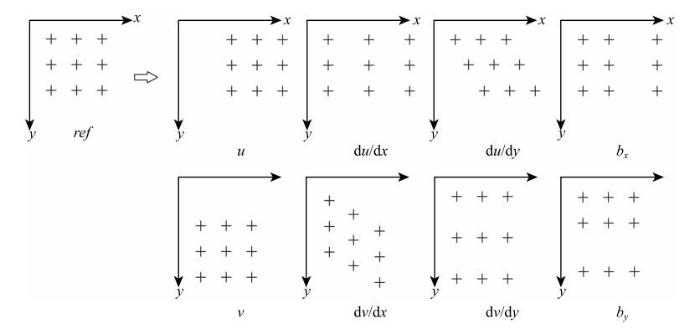
由式(9)可知,如果知道裂纹的张开向量${{b}}=(b_{x},b_{y})$和中心点$P$距离裂纹面的距离$d_{0}$, 并且能够得到$P$点的位移和各向一阶偏导,那么就能得到子区中任意$Q$点在变形图像中的位置$Q^\ast$; 同理,如果通过图像相关算法确定了所有$Q$在变形图像中的位置$Q^\ast$, 那么就能够计算出$P$点的变形和裂纹信息$\left(u,v,\dfrac{\partial u}{\partial x},\dfrac{\partial u}{\partial y},\dfrac{\partial v}{\partial x},\dfrac{\partial v}{\partial y},b_x ,b_y ,d_0 \right)$,图2为前8个变量分别代表的子区变形的几何含义,子区图像的任意变形都可由这8种变化线性组合得到.

图2

新窗口打开|下载原图ZIP|生成PPT
图2各变量的几何含义

Fig. 2The deformation of each variable

1.3 算法的实现

将式(9)中的变量按照功能分为两组向量,分别为：表示$P$点位移和旋转的向量${{\rho }}$以及表示裂纹位置和张开方向的向量$\beta $,即 \begin{equation} \label{eq11} \left. {\begin{array}{ll} {{\rho }} = \left[ {u,v,\dfrac{\partial u}{\partial x},\dfrac{\partial u}{\partial y},\dfrac{\partial v}{\partial x},\dfrac{\partial v}{\partial y}} \right] \\ {{\beta }} = \left[ {b_x ,b_y ,d_0 } \right] \\ \end{array}} \right\}(10) \end{equation}

采用式(2b)作为相关准则,可以知道,当式(9)代入其中时,能够使该式取得最小值的变量组合$({{\rho }},{{\beta }})$即为DIC的解.

注意到向量$\beta $中元素的值要远大于向量${{\rho }}$中的值,可以采用可变大小的子区分次求解, 考虑先用小尺寸的子区进行预处理,以获得像素级别的向量$\beta $值.

之后,为了获得亚像素级别的计算精度,可选用稍大尺寸子区,并且对原始图像像素点之间进行必要的插值算法,目前采用较多的是三次B样条曲线插值^[36-38]. 之后采用典型的亚像素NR算法^[21-22]作为收敛准则 \begin{equation} \label{eq12} {{Q}}_{i + 1} = {{Q}}_i- {{ H}} ^{-1}\nabla {{Q}}_i(11) \end{equation} 式中,$i$为计算的迭代次数,$H$为由$\textbf{Q}$$_{i}$的二阶偏导组成的Hessian矩阵,$\textbf{Q}$$_{i}$和 $\textbf{Q}$$_{i}$分别为 \begin{equation} \label{eq13} \left. {\begin{array}{l} {{Q}}_i = \left[ {{{\rho }},{{\beta }}} \right]^{ T} \nabla {{Q}}_i = \left[ {\dfrac{\partial C_{znssd} }{\partial {{\rho }}}\dfrac{\partial C_{znssd} }{\partial {{\beta }}}} \right]^{T} \\ \end{array}} \right\}(12) \end{equation}

运用以上NR算法计算子区分离模型即可得到亚像素级别的位移解.

2 裂纹重构有效性验证

2.1 试验设计

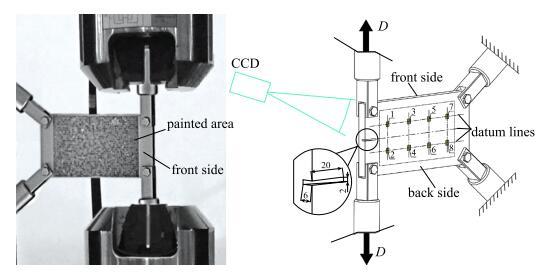
为了测试所提出算法的工程应用前景,采用 200 mm$\times $100 mm$\times $12 mm的常见低碳钢板Q235 ($E$=210 GPa,$\nu $=0.3)作为样本母材. 板材正面通过随机喷涂,在居中处形成大小为160 mm$\times $94 mm的类高斯斑点区域. 背面用铣刀沿宽度中心线从边缘向内切割出20 mm $\times $2 mm的倾斜细槽,细槽最深处6 mm在样本边缘,用以控制裂纹的初始生成位置和方向, 背面喷涂区域投影范围内还均匀分布有8个垂直方向的应变传感器G1-G8, 传感器的敏感栅长度为4 mm,其中G1,G3,G5,G7位于上列, 其余位于下列,他们的中心基线垂直方向间隔50 mm,水平方向间隔40 mm. 板材4角开有圆孔,用于安装夹具,裂纹端夹具垂直,以施加拉伸载荷,另端固定.

在实验室条件下,采用拉伸试验机匀速的施加垂直方向的拉伸位移载荷$D=40\mu m/(st)$, 由正前方的CCD相机每间隔2 s进行一次拍摄,以采集试件加载前以及加载开裂过程中,试件表面的散斑位移图像并保存于电脑端,试验设置如图3所示. 试验总计运行时长为100 s,共采集样品表面散斑图像51张,图像分辨率为5568$\times $2944像素.

图3

新窗口打开|下载原图ZIP|生成PPT
图3试验设置

Fig. 3Setup of experiment

2.2 裂纹重构结果与讨论

选取第0 s图像作为原始参考图像,并选取第86 s图像作为典型的变形图像进行数字图像相关分析. 采用绘图软件切除图像边缘的无效区域以及图像中不关注的区域,仅保留下大小为1500$\times $900像素大小的感兴趣区域(region of interest,ROI). 图4为所选取图像的ROI区域,可以看到变形图像的ROI区域包含了清晰的裂纹.

图4

新窗口打开|下载原图ZIP|生成PPT
图4变形前后的ROI区域

Fig. 4ROI in original and deformed images

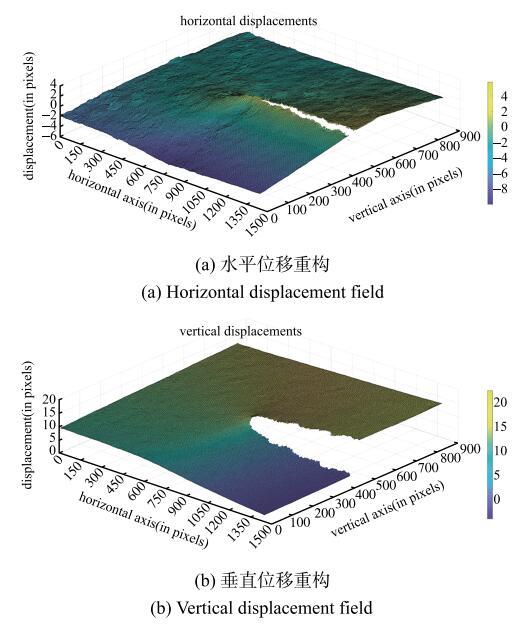
所提出的非连续数字图像相关算法采用Matlab(The MathWorks, Natick, MA, USA)进行编程实现,首先采用了23$\times $23的子区尺寸进行裂纹面测量,之后将子区尺寸设置为53$\times $53像素. 最终计算得到的ROI区域位移结果如图5所示. 可以看到对连续区域的位移场重构除了水平位移结果上部分点的轻微曲翘,整体结果基本平滑,效果良好. 而对非连续区域(裂纹)附近的重构也能很好的建立裂纹面,并且所重构的裂纹形状符合图4中所观测的裂纹路径.

图5

新窗口打开|下载原图ZIP|生成PPT
图5对ROI区域的位移场重构结果

Fig. 5Reconstructed displacement fields of ROI

图6

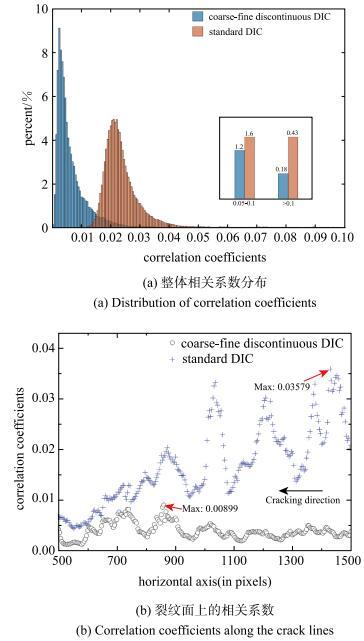
新窗口打开|下载原图ZIP|生成PPT
图6不同方法计算的相关系数对比

Fig. 6Correlation coefficients obtained by discontinuous DIC and Standard DIC

进一步将所提出的非连续图像相关方法与标准图像相关方法进行对比研究,对所选取的两幅图像进行相关分析后分别得到各自的相关系数. 对两组相关系数进行整理后,结果如图6所示. 相关系数越小,表明进行匹配的子区越相似,其出现匹配错误的概率也越低,而对于整个ROI区域,由于存在大量的计算点,样本范围大,根据统计原理,可以认为对应的位移计算准确率越高. 图6(a)显示所提出的非连续相关方法能够有效的降低整体的错误率,图6(b)显示在对裂纹面位移进行重构时,所提出方法仍能保持较低的错误率.

将由非连续图像相关方法得到的位移结果与传感器收集的结果进行对比,研究所提出方法的实际结果偏差,此时认为传感器结果为标准参考量. 应变传感器采集的应变数据$\varepsilon $可转化为像素位移量 \begin{equation} \label{eq14} D_{r} = \kappa \varepsilon l(13) \end{equation} 其中,$l$ 为敏感栅长度,$l=4 mm;\kappa $为单位转换系数,可计算得$\kappa $=15.7894像素/mm. 绝对位移偏差$E_{d}$即可由下式计算得到 \begin{equation} \label{eq15} E_{d} = (D_{u}-D_{d} )-\kappa \varepsilon l(14) \end{equation} 式中,$D_{u}$ 和 $D_{ d}$分别为从非连续图像相关方法重构的位移结果中,采集的传感器上下基准点的位移. 计算结果如表1所示. 可以看到重构的位移精度能达到0.01像素级别,与标准参考量的偏差也不超过0.06像素, 充分说明所提出方法的计算优越性,能够应用于高精度的非连续位移场重构中.

Table 1
表1
表1传感器处重构结果垂直位移以及与传感器数据的偏差
Table 1Vertical direction displacements and errors at positions of 8 gages

新窗口打开|下载CSV

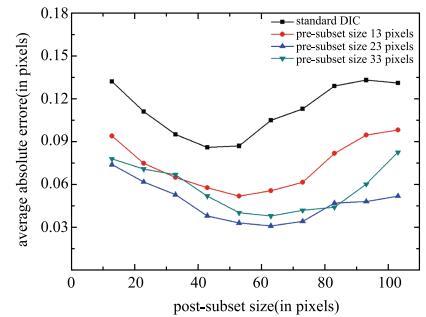
采用不同大小的子区尺寸来进行位移场重构,以此研究非连续数字图像相关法对子区尺寸选取的敏感性,寻找最佳的子区尺寸以得到最优结果. 图7为选用不同子区尺寸时,计算结果的平均绝对位移偏差,图中用不同的线条表示采用不同的子区进行过预处理. 从图7中能够观测到,所提出的非连续数字图像相关方法相较于标准DIC方法,有着明显更优的计算准确度,位移偏差减小了1/2. 同时对子区尺寸的选取有更好的相容性.

图7

新窗口打开|下载原图ZIP|生成PPT
图7不同尺寸子区的平均绝对位移偏差

Fig. 7Summary of average absolute errors in laboratory experiment

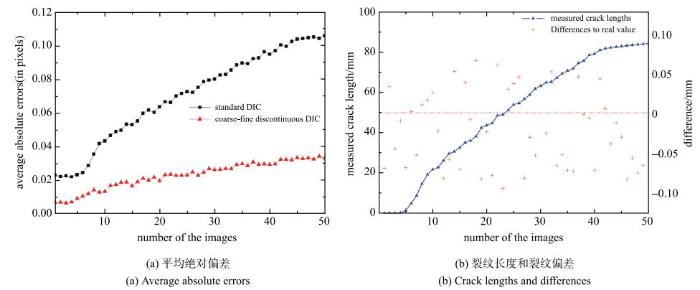
对采集到的全体图像进行裂纹位移场以及裂纹面重构,采用前文使用的子区尺寸设置, 以观测试验过程中裂纹的扩展情况. 图8为50张变形图位移重构的结果汇总,其中图8(a)为各次位移重构结果的平均绝对位移偏差统计, 图8(b)为由采集到的各次测量裂纹长度,结果单位转换为了工程常用的毫米制, 其中通过右侧$Y$轴一并展示了重构的裂纹长度与实际观测裂纹长度的偏差.

对比图8(a)中标准方法和非连续数字图像相关方法得到的各次位移重构结果的平均绝对位移偏差,所提出方法在样板表面开裂前,即图像还是连续时,能够将平均绝对偏差控制在0.01像素以下,远低于标准方法;而在图像出现裂纹后,此项数值有所增长,但在可接受范围内,而标准方法已经难以得到有效的裂纹附近位移. 图8(b)则显示裂纹在大约第8 s开始出现,并且快速失稳扩展至20 mm以上,之后稳定扩展至80 mm,整体结果基本符合理论趋势;由偏差统计可以看到, 所提出方法对较难区分的裂尖特征,其重构精度依旧能控制在0.05 mm左右.

由以上研究可以看出,所提出的非连续数字图像相关方法对标准DIC方法在各方面均有较大提升,克服了标准方法不能应用于重构裂纹等非连续表面的问题, 能够成功地对裂纹结构位移场以及裂纹面形状进行精确重构,计算结果能够达到亚像素级别. 并且本文所采用的试验过程,可以作为一个标准的非接触式裂纹监测系统案例,应用于工程实际中.

图8

新窗口打开|下载原图ZIP|生成PPT
图8试验过程中各图像的平均绝对偏差和裂纹长度

Fig. 8Average absolute errors and crack length of each image during the test

3 结论

本文提出了一种基于子区分离模型的非连续数字图像相关方法,用于解决标准数字图像相关方法在非连续表面失效的问题,并将其应用于对裂纹结构位移场的重构中.研究结果表明：

(1)所提出的子区分离模型能够有效的解决标准数字图像相关法在非连续表面失效的问题,重构的裂纹面符合观测结果,重构的位移场在连续和非连续区域均有良好表现.

(2)非连续图像相关方法能够有效降低测量位移场时的图像相关系数,尤其是在非连续区域,从而提高位移场重构的精度,减少错误率. 采用合理的子区尺寸,位移场重构结果的平均绝对偏差在0.05像素左右,远低于标准方法. 整体测量精度能达到亚像素级别.

(3)对试验得到的所有图像进行分析,得到了裂纹从起裂到失稳,再到稳定扩展的全裂纹扩展过程数据. 测量得到的数据符合理论结果,能够作为一种可靠的非接触式位移精确测量方法,快速重构裂纹结果的位移场,应用于研究裂纹开裂过程、监测裂纹的扩展.

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

姚旭龙, 张艳博, 孙林等. 基于区域相关性的岩石损伤声发射探测与成像方法研究
岩石力学与工程学报, 2017,36(9):2113-2123

[本文引用: 1]

( Yao

Xulong

, Zhang

Yanbo

, Sun

Lin

, et al. Research on acoustic emission inspecting and imaging method for rock damage based on regional correlation
Chinese Journal of Rock Mechanics and Engineering, 2017,36(9):2113-2123(in Chinese))

[本文引用: 1]

[2]

顾桂梅, 贾文晶 . 钢轨轨底裂纹红外热波无损检测数值模拟分析
红外技术, 2018,40(3):294-299

URL [本文引用: 1]

针对传统超声波检测方法的不足, 本文提出红外热波无损检测技术检测钢轨轨脚两侧的裂纹, 在 ANSYS有限元分析软件中对钢轨轨脚裂纹红外热波无损检测实验进行了数值模拟分析, 并搭建了钢轨裂纹红外热波检测实验的实验平台, 对仿真结果进行了验证。钢轨轨底裂纹红外热波无损检测实验仿真主要包括 3部分: 建立钢轨实体模型并对其进行网格划分, 热流密度模拟热波载荷施加在钢轨轨脚表面进行求解分析, 对求解结果生成钢轨轨脚表面的温度分布云图和温度随时间变化曲线图。仿真与实验结果表明: 红外热波无损检测方法可以弥补传统超生波检测方法的不足, 可以检测得到钢轨轨底两侧的裂纹。

( Gu

Guimei

, Jia

Wenjing

. Numerical simulation analysis of infrared thermal wave nondestructive testing of rail bottom crack
Infrared Technology, 2018,40(3):294-299(in Chinese))

URL [本文引用: 1]

Isla

, Cegla

. EMAT phased array: A feasibility study of surface crack detection
Ultrasonics, 2017,78:1-9

DOI URL [本文引用: 1]

[4]

王博, 王霞, 陈飞等. 航拍图像的路面裂缝识别
光学学报, 2017,37(8):119-125

[本文引用: 1]

( Wang

, Wang

Xia

, Chen

Fei

, et al. Pavement crack recognition based on aerial image
Acta Optica Sinica, 2017,37(8):119-125(in Chinese))

[本文引用: 1]

[5]

Hyun-Woo

, Hyuk-Jin

, Jae-Chan

. Analysis of crack image recognition characteristics in concrete structures depending on the illumination and image acquisition distance through outdoor experiments
Sensors, 2016,16(10):1646-1658

DOI URL

[6]

Zhao

, Wang

, Ye

. Surface shape recognition method for crack detection
Journal of Electronic Imaging, 2014,23(3):033013

DOI URL [本文引用: 1]

[7]

Peters

, Ranson

. Digital imaging technique in experimental stress analysis
Optical Engineering, 1982,21(3):427-431

[本文引用: 2]

[8]

Che

, Ranson

, Sutton

. Applications of digital-image-correlation techniques to experimental mechanics
Experiment Mechanics, 1985,25(3):232-244

DOI URL [本文引用: 1]

[9]

Bruck

, Mcneill

, Sutton

, et al. Digital image correlation using Newton-Raphson method of partial differential correction
Experiment Mechanics, 1985,29(3):261-267

[本文引用: 2]

[10]

蒋玮, 蒋险峰, 黄裕龙 . 基于数字图像相关的J积分测量方法
机械强度, 2018,40(3):687-694

[本文引用: 1]

( Jiang

Wei

, Jiang

XianFeng

, Huang

YuLong

. A J-integral measurement method based on digital image correlation
Journal of Mechanical Strength, 2018,40(3):687-694(in Chinese))

[本文引用: 1]

[11]

王阳, 李高春, 伍鹏等. 基于数字图像相关方法的端羟基聚丁二烯推进剂复合型裂纹J积分测量
兵工学报, 2019,40(2):284-291

[本文引用: 1]

( Wang

Yang

, Li

Gaochun

, Wu

Peng

, et al. J-integral measurement of mixed mode cracks of htpb propellant based on digital image correlation method
Acta Armamentarii, 2019,40(2):284-291(in Chinese))

[本文引用: 1]

[12]

邹宇明, 高怡斐 . 数字图像相关方法在A508-3钢J积分测试中的应用
材料与冶金学报, 2018,17(4):269-275

[本文引用: 1]

( Zou

Yuming

, Gao

Yifei

. Application of digital image correlation method in J-integral test of A508-3 Steel
Journal of Materials and Metallurgy, 2018,17(4):269-275(in Chinese))

[本文引用: 1]

[13]

Mcneill

, Peters

, Sutton

. Estimation of stress intensity factor by digital image correlation
Engineering Fracture Mechanics, 1987,28(1):101-112

DOI URL [本文引用: 1]

[14]

Sutton

, Turner

, Chao

, et al. Experimental investigations of three-dimensional effects near a crack tip using computer vision
International Journal of Fracture, 1992,53(3):201-228.

[本文引用: 1]

[15]

Réthoré

, Hild

, Roux

. Extended digital image correlation with crack shape optimization
International Journal for Numerical Methods in Engineering, 2008,73(2):248-272

DOI URL [本文引用: 1]

[16]

Réthoré

, Hild

, Roux

. Shear-band capturing using a multiscale extended digital image correlation technique
Computer Methods in Applied Mechanics and Engineering, 2007,196(49-52):5016-5030

DOI URL [本文引用: 1]

[17]

Jin

, Bruck

. Pointwise digital image correlation using genetic algorithms
Experimental Techniques, 2010,29(1):36-39

[本文引用: 1]

[18]

Helm

. Digital image correlation for specimens with multiple growing cracks
Experiment Mechanics, 2008,48(6):753-762

DOI URL [本文引用: 1]

[19]

Blaber

, Adair

, Antoniou

. Ncorr: Open-source 2D digital image correlation matlab software
Experimental Mechanics, 2015,55(6):1105-1122

DOI URL [本文引用: 1]

[20]

Pan

. Reliability-guided digital image correlation for image deformation measurement
Applied Optics, 2009,48(8):1535-1542

DOI URL [本文引用: 1]

[21]

Hassan

, Dyskin

, MacNish

, et al. Discontinuous digital image correlation to reconstruct displacement and strain fields with discontinuities: Dislocation approach
Engineering Fracture Mechanics, 2018,189:273-292

DOI URL [本文引用: 2]

[22]

Hassan

. Digital image correlation for discontinuous displacement measurement using subset segmentation
Optics and Lasers in Engineering, 2019,115:208-216

DOI URL [本文引用: 2]

[23]

Poissant

, Barthelat

. A novel "subset splitting" procedure for digital image correlation on discontinuous displacement fields
Experiment Mechanics, 2010,50(3):353-364

DOI URL [本文引用: 1]

[24]

Fagerholt

, B?rvik

, Hopperstad

. Measuring discontinuous displacement fields in cracked specimens using digital image correlation with mesh adaptation and crack-path optimization
Optics and Lasers in Engineering, 2013,51(3):299-310

DOI URL [本文引用: 1]

[25]

Nguyen

, Huntley

, Burguete

, et al. Shape and displacement measurement of discontinuous surfaces by combining fringe projection and digital image correlation
Optical Engineering, 2011,50(10):101505-101505

DOI URL [本文引用: 1]

[26]

罗豪鑫, 陈传勇, 张丽娜等. 基于显微网格法/数字图像相关技术的疲劳裂纹尖端变形场
材料科学与工程学报, 2018,36(5):75-79

[本文引用: 1]

( Luo

Haoxin

, Chen

Chuanyong

, Zhang

Lina

, et al. Micro grid method/digital image correlation technique-based study of deformation fields around fatigue crack tip
Journal of Materials Science and Engineering, 2018,36(5):75-79(in Chinese))

[本文引用: 1]

[27]

施祎, 杨晓光, 苗国磊等. 基于数字图像相关方法微裂纹萌生试验研究
推进技术, 2019

[本文引用: 1]

( Shi

, Yang

Xiaoguang

, Miao

Guolei

, et al. Study on an experiment investigation method of micro crack initiation based on digital image correlation method
Journal of Propulsion Technology, 2019(in Chinese))

[本文引用: 1]

[28]

潘兵, 谢惠民, 戴福隆 . 数字图像相关中亚像素位移测量算法的研究
力学学报, 2007,39(2):245-252

[本文引用: 1]

( Pan

Bing

, Xie

Huimin

, Dai

Fulong

. An investigation of sub-pixel displacements registration algorithms in digital image correlation
Chinese Journal of Theoretical and Applied Mechanics, 2007,39(2):245-252(in Chinese))

[本文引用: 1]

[29]

俞鑫炉, 付应乾, 董新龙等. 混凝土一维应力层裂实验的全场DIC分析
力学学报, 2019,51(4):

[本文引用: 1]

( Yu

Xinlu

, Fu

Yingqian

, Dong

Xinlong

, et al. Full field DIC analysis of one-dimensional spall strength for concrete
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(4): (in Chinese))

[本文引用: 1]

[30]

Mccormick

, Lord

. Digital image correlation
Material Today, 2010 13(12):52-54

[本文引用: 1]

[31]

Pan

, Xie

, Guo

, et al. Full-field strain measurement using a two-dimensional Savitzky-Golay digital differentiator in digital image correlation
Optical Engineering, 2007,46(3):033601

DOI URL [本文引用: 1]

[32]

Giachetti

. Matching techniques to compute image motion. Image Vis Comput
Image and Vision Computing, 2000,18(3):247-260

DOI URL [本文引用: 1]

[33]

Tong

. An evaluation of digital image correlation criteria for strain mapping applications
Strain, 2010,41(4):167-175

[本文引用: 1]

[34]

贺屹, 蔡力勋, 陈辉 , 等. 求解Ⅰ型裂纹构元J积分的半解析方法
力学学报, 2018,50(3):579-588

[本文引用: 1]

( He

, Cai

Lixun

, Chen

Hui

, et al. A semi analytical method to solve j-integral for mode-Ⅰcrack components
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(3):579-588(in Chinese))

[本文引用: 1]

[35]

于思淼, 蔡力勋, 姚迪等. 准静态条件下金属材料的临界断裂准则研究
力学学报, 2018,50(5):1063-1080

[本文引用: 1]

( Yu

Simiao

, Cai

Lixun

, Yao

, et al. The critical strength criterion of metal materials under quasi-static loading
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(5):1063-1080(in Chinese))

[本文引用: 1]

[36]

Pan

, Wei

, Jiang

, et al. Performance of global look-up table strategy in digital image correlation with cubic B-spline interpolation and bicubic interpolation
Theoretical and Applied Mechanics Letters, 2016,6(3):126-130

DOI URL [本文引用: 1]

[37]

Jiwari

. Lagrange interpolation and modified cubic B-spline differential quadrature methods for solving hyperbolic partial differential equations with Dirichlet and Neumann boundary conditions
Computer Physics Communications, 2015,193:55-65

DOI URL

[38]

苏勇, 张青川, 徐小海等. 数字图像相关技术中插值偏差的理论估计
力学学报, 2016,48(2):495-510

DOI Magsci [本文引用: 1]

<p>数字图像相关测量的普及提出了建立散斑质量评价体系要求,即发展针对不同的数字散斑图能够评估测量精度的标准方法.其中,数字图像相关计算中插值误差引起亚像素位移系统偏差(插值偏差)的估计是评价散斑质量的重要参数,然而至今插值偏差与散斑图结构及其插值方法之间的深层机制仍然不明,而且缺乏快速有效的手段估计插值偏差的量级.基于傅里叶方法获得了插值偏差的解析表达式.在满足采样定理的情况下,对其简化得到了插值偏差的带限近似形式和正弦近似形式.插值偏差的正弦近似形式解释了插值偏差随亚像素平移呈正弦形式变化的现象.基于插值偏差的正弦近似公式,提出了决定插值算法用于相关匹配优劣的插值偏差核概念,它表征了插值算法对散斑图特定频率的偏差响应,插值偏差是由插值偏差核与图像功率谱乘积的积分决定的.基于理论分析,提出了一种通过散斑频谱和插值偏差核估计插值偏差的简便有效算法,较之于传统的散斑图平移方法有明显的速度优势.分析了模板大小对估计精度的影响,并通过模拟进行了验证.解释了插值偏差产生的深层机理,解决了长久以来插值偏差难以快速估计的问题.不仅可以用于插值偏差估计,也可以用于插值算法优化,滤波模板选取等问题.对建立散斑质量评价体系,从而制作方便用户的水转印标准散斑也有推动作用.</p>

( Su

Yong

, Zhang

Qingchuan

, Xu

Xiaohai

, et al. Theoretical estimation of interpolation bias error in digital image correlation
Chinese Journal of Theoretical and Applied Mechanics, 2016,48(2):495-510(in Chinese)

DOI Magsci [本文引用: 1]