AN INTERFACE TRACKING METHOD OF COUPLED YOUNGS-VOF AND LEVEL SET BASED ON GEOMETRIC RECONSTRUCTION1)
ZhangManman中图分类号:O359.1
文献标识码:A
通讯作者:
收稿日期:2018-12-19
网络出版日期:2019-05-18
版权声明:2019力学学报期刊社 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (18627KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
运动界面问题[1-2]兴起于20世纪80年代末,从著名的格子类方法(单元粒子法(particlein cell, PIC)、单元流体法(fluid in cell, FLIC)和标记粒子法(markerand cell, MAC))迅速发展到现在常用的波前追踪方法(front trackingmethod)[3-7]、流体体积分数方法(volume of fluid,VOF)[8-11]、水平集方法(level set method)[12-13].界面追踪方法可分为三类：(1)界面捕获法(front capturingmethod)：VOF方法、水平集方法、相域法(phase-field method)[14]; (2) 边界拟合方法(boundary-fitting approach)[15]; (3)波前追踪方法.第一种方法的优点是使用与主场流动同一套网格,通过定义的体积函数捕捉流动界面,因此该方法相对容易实施.但是缺点是其准确性受到对流方程解的数值耗散的限制,为了避免这种情况发生,重构/重新初始化体积函数以提高界面捕捉的精确性.第二种方法是边界拟合法,是通过追踪背景网格点确定界面的位置,该方法可以准确追踪界面位置,但仅适用于小变形、几何形状简单的界面捕捉,且应用于三维捕捉存在困难,直到2001年困难被Hu等[16]解决,并对移动球形颗粒进行了3D数值模拟,取得到了非常好的结果.第三种方法是波前追踪方法,该方法解决了固定网格上的流场,并以拉格朗日方式通过一组界面标记点跟踪界面位置.优势是可以准确地捕捉到相界面,但在气泡运动中因不能捕捉到气泡的大变形、破碎,以致不能广泛应用.1992年,Tryggvason等[17]将界面捕获(frontcapturing)和追踪技术(trackingtechnique)耦合得到一种新的波前追踪方法,该方法原理：一套网格用于求解流体流动;一组自适应元元素用来标记运动界面;并用一套运动方程处理两相流,即把两相看作是物性参数可变的单相流体.利用该方法对不可压缩流动的相界面进行追踪,为防止在相界面处出现数值耗散,在相界面处,人工设置了一定的厚度,优点是在相界面附近产生过渡区,使流体特性从界面一侧的值到另一侧的值平滑连续地变化.相界面的人造厚度取决于网格的大小,且在计算过程中保持不变.广泛应用的VOF方法和水平集方法在进一步发展,获得界面精度更高的追踪方法.2012年,Wang等[18]提出了一种二阶VOF方法,使用二阶龙格库塔(Runge-Kutta)方法来平滑界面,继承了CLSVOF[19-24]质量守恒和精确计算界面曲率的基础上,通过直接在重构界面上寻找最近点而忽略每个计算单元中的界面配置,显著简化了复杂的几何过程.Haghshenas等[19]将VOF与水平集代数耦合得到A-CLSVOF方法,主要用于模拟界面毛细管流动,该方法的特点是VOF与水平集单向耦合,提高了表面张力计算的准确性及减少了虚假流动.Sussman等[20]提出一种用于计算3D轴对称不可压缩两相流的CLSVOF方法,该方法可以很好地处理界面的合并和破碎,因与水平集方法的耦合,计算具有表面张力的问题时,精度比VOF准确.基于CLSVOF良好的守恒性及可以准确计算曲率,Chakraborty等[21]使用CLSVOF方法对静止牛顿液体中单气泡上升及双气泡上升过程中气泡的合并进行了研究.Zhao等[24]研究了一种新的CLSVOF方法,该方法的新颖处在于它是在一种可以嵌套的网格系统下对流场进行数值计算,其中包括对结构化网格的嵌入、重叠以及移动,并且有较高的质量守恒性及良好的界面捕获能力.2016年,Ansari等[25]将传统的CLSVOF方法进行改进得到VOSET方法,不再使用CLSVOF方法中求解水平集方法下的对流方程和距离函数方程的方法,而使用高阶WENO或无振荡格式(ENO)方案计算更复杂的一阶对流导数方程,并用该方法模拟单个气泡的上升,结果与实验有良好的一致性.李康等[26]基于代数重构思想,采用双正弦构造了双正弦界面重构方法.在界面附近,采用DSINC获得体积分数的重构,使双正弦界面重构方法具备了多维数值计算的能力.在处理大变形的问题上,贾祖朋等[27]基于水平集函数提出了耦合欧拉--拉格朗日(Eulerian-Lagrangian)方法,其中拉格朗日方法采用相容显示有限元拉式方法,欧拉方法采用基于近似黎曼(Riemann)解的有限体积欧拉方法,界面处采用新的水平集和Ghost方法进行计算.在可压缩多相流领域,Ha等[28]提出一种压缩高分辨率界面捕捉的方法,优点是简单便于实现、并可处理高密度比和强冲击的可压缩多相流.
VOF模型是应用于固定欧拉网格的界面追踪技术.在VOF模型中,流体共享一组动力学方程,并在整个计算域中跟踪每个计算单元中每种流体的体积分数.VOF在数值模拟中保证质量守恒,但是不能准确计算界面曲率,而水平集方法可准确计算界面曲率但质量不守恒.引起质量不守恒的原因是水平集函数在迭代一段时间后将不再是距离函数.由于水平集函数是平滑且连续的,因此可精确计算空间梯度,所以能对由曲率引起的界面变化和表面张力精确计算.另一方面,VOF方法质量守恒的原因是在迭代过程中,计算和追踪计算域中每个网格中特定相的体积分数而不是界面本身.由于VOF函数(特定相的体积分数)在界面上是不连续的,因此VOF方法的弱点是空间导数的计算.所以将VOF和水平集方法耦合在一起可以弥补两者的不足.在研究中发现单纯的VOF方法,能够"捕捉"到界面,但是由于迭代过程中,数学方法的各种内在机理,譬如数值耗散、数值色散性以及非线性效应等,捕捉的界面不够准确.所以就需要对界面进行加工,就是所谓的界面重构(reconstruction).本文采用"米"状相邻网格Youngs[29]方法,并将VOF和水平集方法进行耦合,发展了一种Youngs-VOF与水平集耦合的界面追踪方法.采用Youngs-VOF耦合水平集方法模拟气泡上升并与实验[30]对比,对溃坝--自由表面流动的数值计算与实验进行对比,验证Youngs-VOF耦合水平集方法是一种可以精确模拟二维、三维,大气泡、自由表面等流动的数值计算方法.
1 算法
1.1 Youngs-VOF
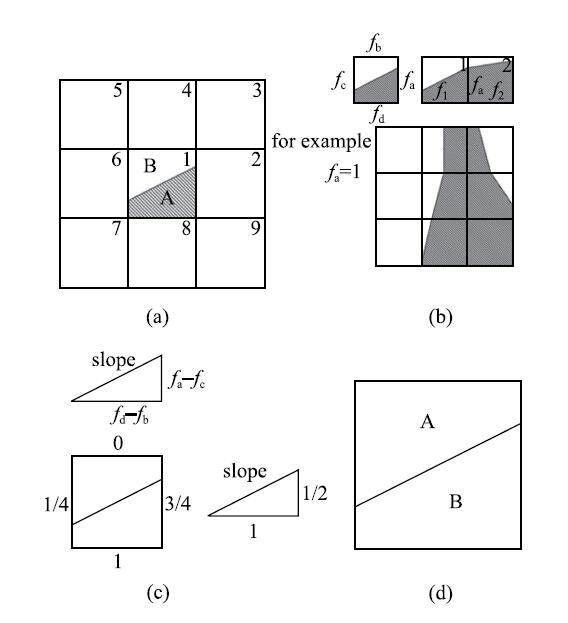
在VOF模型中,使用由Hirt和Nichols[31]发展的施主--受主(donor-acceptor)型的"零阶"方法形成的Youngs-VOF一阶重构方法.施主{--}受主方法和Youngs-VOF方法都是采用网格内具有法向量的直线近似,但Youngs-VOF方法使用一阶函数计算斜率,提高了界面的准确性.两种方法重构界面与实际界面对比可知Youngs-VOF方法得到的界面更准确,如图1所示.经典的Youngs方法计算单元格界面斜率原理如图2,过程为(假设已经通过VOF方法得到中心单元的体积分数)：第一步,计算中心单元流体界面相邻4个单元的体积分数($f_{a}$, $f_{\rm b}$, $f_{\rm c}$, $f_{d})$;第二步,计算斜率;第三步,根据斜率和中心单元的体积分数可得到中心单元界面的具体位置.该方法仅采用了与中心单元格相邻的${x,y}$方向上的4个单元格2,4,6,8进行计算,忽略了与中心单元格对角相连的4个单元格1,3,5,7,从而产生一定的误差.本文将经典的Youngs重构法概括为"十"状相邻单元的Youngs方法.Rudman等[32]将经典的Youngs重构法进行改进,充分利用相邻单元的信息,通过采用式(1)$\sim$式(3)计算法线得到界面斜率(式(1)和式(2)分别为法向分量沿${x,y}$方向分解得到的$n_{i,j}^x,n_{i,j}^y ,F$变量分布如图3所示),使计算更准确.本文将这种方法概括为"米"状相邻单元Youngs方法.三维原理与二维原理相似,主要概括为两点：首先将法向量分解为$x, y,z$三个方向的法向分量,将相应方向两侧的网格以加权平均的思想进行运算得到法向分量,加权系数以网格位置不同而定,同类位置的网格具有相同的系数(二维网格有两种,三维网格有三种),具体过程见文献[33].将"米"状相邻单元的Youngs方法与VOF方法耦合,采用几何方法对面通量进行近似,假定两个流体之间的界面在每个单元内具有线性斜率,并使用该线性形状计算流体通过单元面的流量.Youngs-VOF方法避免了数值耗散,不需设置人工厚度进行两相之间的过渡.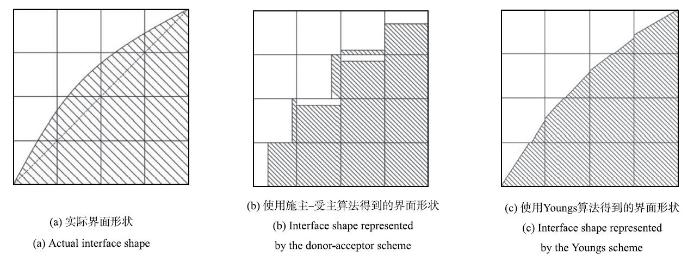
显示原图|下载原图ZIP|生成PPT图 1Youngs-VOF和donor-acceptor重构界面与实际界面的对比
-->Fig. 1Reconstructed interfaces applied with the Youngs-VOF and donor-acceptor methods versus the actual interface
-->
显示原图|下载原图ZIP|生成PPT图 2使用Youngs方法重构界面过程示意图
-->Fig. 2Diagram with Youngs method to reconstruct the interface
-->
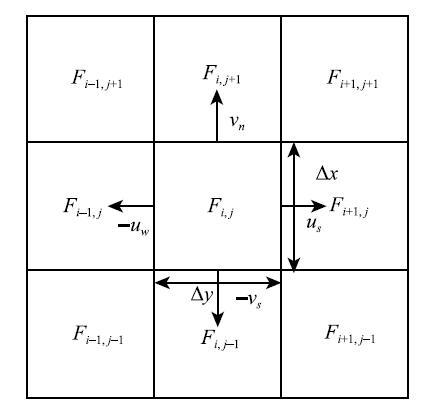
显示原图|下载原图ZIP|生成PPT图 3中心单元网格速度分布示意图
-->Fig. 3Diagram of center cell grid velocity distribution
-->
$$n_{i,j}^x = - \frac{1}{\Delta x}\left( \begin{array}{ccc} 1 & 2 & 1 \\ \end{array}\right)\left(\begin{array}{cccccc} F_{i{ + }1{ + }1}{-}F_{i{ - }1{ + }1} \\ F_{i{ + }1}{ - }F_{i{ - }1} \\ F_{i{ + }1{ - }1}{-}F_{i{ - }1{ - }1}\\ \end{array}\right) (1)$$
$$n_{i,j}^y = - \frac{1}{\Delta y}\left( {{\begin{array}{*{20}c} 1 & 2 & 1 \\ \end{array} }} \right)\left( {{\begin{array}{cccc} F_{i{ + }1{ - }1}{ - }F_{i{ + }1{ + }1} \\ F_{i{ - }1}{ - }F_{i{ + }1} \\ F_{i{ - }1{ - }1} { - }F_{i{ - }1{ + }1} \\ \end{array} }} \right) (2)$$
$$k{ = }n_{i,j}^x / n_{i,j}^y~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ {(3)}$$
1.2 水平集方法
水平集函数$\varphi $被定义为到相界面的符号距离函数$$\varphi \left( {x,t} \right) = \left\{\begin{array}{llll} + \left| d \right|, &{\rm if}~~{x \in \varOmega _1 } \\ 0,&{\rm if}~~{x \in \varGamma } \\ - \left| d \right|, &{\rm if}~~{x \in \varOmega _2 } \\ \end{array}\right. (4)$$
式中,$d$为到相界面的距离, $\varOmega _1 ,\varOmega _2$分别表示的是主相和副相. 相界面是零等值面,$\varphi \left( {x,t}\right)$在两相流系统中可以表示为$\varGamma = \left\{ {x\left|{\varphi \left( {x,t} \right) = 0} \right.} \right\}$,水平集函数用与VOF模型类似的方式给出,其中${u}$为流场速度
$$\frac{\partial \varphi }{\partial t} + \nabla \cdot \left( {{ u}\varphi } \right) = 0 (5)$$
1.3 Youngs-VOF耦合水平集算法计算过程
本节耦合算法计算过程如下：(1) 水平集函数的初始化
对距离函数进行初始定义,根据体积分数值,计算域可分为两部分：$\varphi > 0,\varphi < 0.$
(2) 界面相邻区域的标记
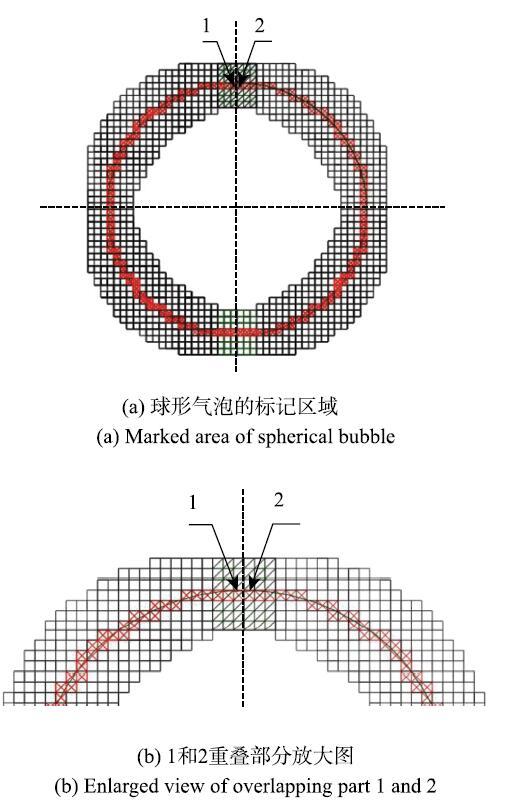
对界面相邻区域进行标记,计算标记区域与界面的中心距离.大量的标记区域,使得表面张力的计算更加准确,但计算量特别大.因此在保证准确度的情况下,需确定标记区域的范围.本文标记区域选取范围为中心单元相邻的7$\times $7单元网格区域.对一个球形气泡进行7$\times $7区域标记如图4(a).由图可知,标记过程中两相邻的包含界面的单元标记区域会产生重复,见图4(b),重复区域为两相邻单元共用区域,图中单斜线标记区域为1和2中心单元共用区域.
显示原图|下载原图ZIP|生成PPT图 4标记区域示意图
-->Fig. 4Marked area schematic
-->
(3) 标记区域距离函数的计算
通过界面单元的体积分数值和界面法线计算界面线坐标.通过该坐标,可以在几何上计算标记单元中心与界面线之间的距离.选择其中的最小距离作为标记单元与界面的最小距离.
最小距离$d$的选择基于Youngs-VOF方法见图5,以$A$为界面中心点,当画出的距离三角形状为钝角三角形$\Delta{ABC}$,则距离选择$AB$和$AC$中的最小距离,即$d = \min \left\{{{AB}, {AC}} \right\}$;当三角形是锐角三角形$\Delta{ABE}$,则作三角形的高$AD$为最短距离,即$d ={AD}$,总之在单元内部寻找最短距离.确定最小距离后,距离函数的正负可以根据式(4)确定.
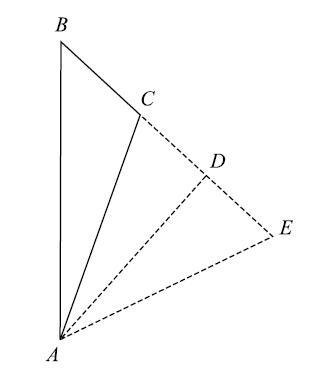显示原图|下载原图ZIP|生成PPT图 5确定最小距离示意图
-->Fig. 5Determine the minimum distance
-->
(4) 重构界面
采用水平集函数与VOF几何上的耦合实现界面重构,耦合过程流程图如图6.Youngs-VOF耦合水平集方法原理是首先根据VOF函数得到的体积分数值以及辅助计算初始距离函数,然后对界面附近的区域进行标记.为标记区域的界面单元计算最小距离. 利用距离函数$\varphi $更精确地计算界面法向量.最后,利用"米"状相邻单元的Youngs方法重构界面,迭代数次达到良好准确的界面.
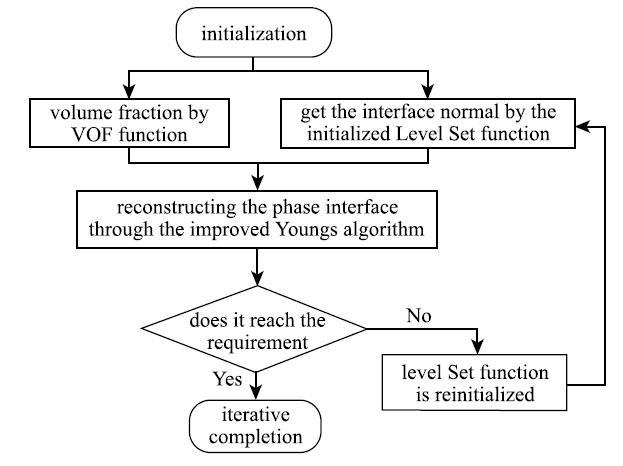显示原图|下载原图ZIP|生成PPT图 6Youngs-VOF耦合水平集方法流程图
-->Fig. 6Youngs-VOF coupled Level Set method flow chart
-->
水平集函数是距离函数,多次迭代求解过程中,距离函数不能一直维持其约束,原因是界面变形、不平整轮廓以及界面厚度的变化.这些误差在迭代过程中积累导致质量和动量求解过程中产生大量误差.因此每个时间步下都需要对水平集函数进行重新初始化,以便保持为距离函数.Youngs-VOF耦合水平集方法比单纯的VOF复杂,首先VOF函数对水平集函数的初始化提供一个依据,水平集耦合的主要作用是对VOF 求得的法向量进行校正来精确计算界面曲率;每次迭代对水平集函数的初始化过程为：水平集函数的初始化、水平集函数本身的运算、水平集函数对界面法向量的校正.
2 数值验证
2.1 气泡在水中自由上升
2.1.1 物理模型及流体的基本假设图7为气泡的计算时的初始位置图,矩形区域及气泡位置根据文献[34]可得,当计算区域的径向尺寸大约是气泡直径的4倍时,边界效应可以忽略不计;计算区域的轴向尺寸约为气泡直径的12倍.理想的球形气泡最初位于底部以上两个气泡直径的对称轴上.假定液体和气泡在初始状态下都是静止的. 气相为空气,液相为水,则可认为：(1) 流体是牛顿流体,不可压缩和等温的; (2)忽略气泡内部的流动,且内部压力和气泡体积恒定; (3)等温系统忽略由液体压力引起的气体密度变化,气相视为不可压缩流体.
显示原图|下载原图ZIP|生成PPT图 7气泡初始位置图
-->Fig. 7Bubble initial position
-->
压力--速度耦合算法使用的是PISO算法,动量方程使用二阶迎风格式离散化,水平集方程使用一阶迎风格式离散化.流场求解的具体步骤如图8所示.
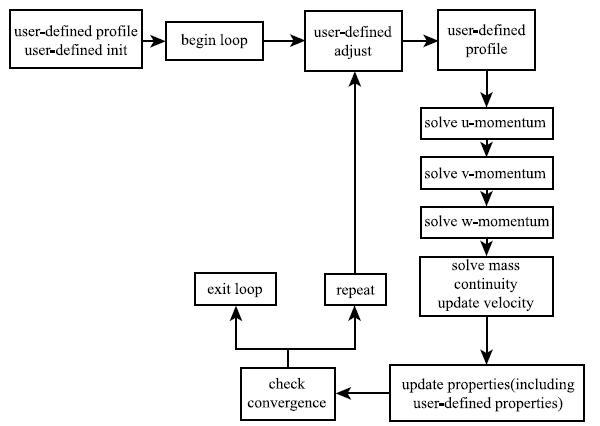显示原图|下载原图ZIP|生成PPT图 8流场求解流程图
-->Fig. 8Flow field solution flow chart
-->
2.1.2 表面张力
动量方程如下
$$\frac{\partial \left( {\rho { u}} \right)}{\partial t} + \nabla \cdot \left( {\rho { {uu}}} \right) = - \nabla p + \nabla \cdot \mu \left[ {\nabla { u} + \left( {\nabla { u}} \right)^{\rm T}} \right] - { F}_{sf} + \rho { g} (6)$$
数值模拟中动量方程产生的源项是气泡的表面张力引起的,原因是气液两相流中,非球形气泡区域,表面张力通过减小界面面积,使自由能最小化.表面张力模型使用的是,,Brackbill,,等[35],提出的连续表面张力模型(CSF), $F_{\rm CSF} = \sigma k\nabla \alpha $,式中,$\alpha $为体积分数. 公式(6)中表面张力${ F}_{\rm sf} $为
$${ F}_{\rm sf} = \sigma \kappa \delta \left( \varphi \right){n}{(7)}$$
式中,$\sigma$ 为表面张力系数,$\kappa$为局部平均界面曲率,可估算为
$$\kappa = \nabla \cdot \left. {\frac{\nabla \varphi }{\left| {\nabla \varphi } \right|}} \right|_{\varphi = 0} {(8)}$$
${n}$为界面局部法向量,可估算为
$${ n} = \left. {\frac{\nabla \varphi }{\left| {\nabla \varphi } \right|}} \right|_{\varphi = 0} (9)$$
式(7)中的$\delta \left( \varphi \right)$为
$$\delta \left( \varphi \right) = \left\{\begin{array}{llll} 0,&\left| \varphi \right| \ge \lambda \\ \dfrac{1 + \cos \left( {\pi \varphi / \lambda } \right)}{2\lambda }, & \left| \varphi \right| < \lambda \\ \end{array}\right. (10)$$
式中,$\lambda $为界面厚度.式(7)在迭代过程中会产生虚假流动,可采用两种方式进行改善,一种是密度校正方法,另一种使用Heaviside函数进行缩放.本文使用密度校正方法,通过引入密度比${\rho }/{(\rho _1 + \rho _2)}$进行修改得
$${ F}_{\rm sf} = \frac{\rho\sigma \kappa \delta \left( \varphi \right){ n} }{0.5\left( {\rho _1 + \rho _2 } \right)} (11)$$
式中,$\rho $为基于体积的平均密度.
实际数值计算程序中,表面张力不是直接添加到动量方程的源项,而是通过散度定理表示为体积力的方式将体积力添加到动量方程的源项中,如公式
$$F_{\rm vol} = \sum\limits_{{\rm pairsi} j,i < j} {\sigma _{ij} \frac{\alpha _i \rho _i \kappa _j \nabla \alpha _j + \alpha _j \rho _j \kappa _i \nabla \alpha _i }{\left( {\rho _i + \rho _j } \right)/2}} (12)$$
根据数值计算条件,对模型进行简化,即当界面所在网格单元只存在两相(即两相流动)时可得：$\kappa _i = - \kappa _j $,$\nabla \alpha _i = - \nabla \alpha _j $.式(12)简化为
$$F_{\rm vol} = \sigma _{ij} \frac{\rho \kappa _i \nabla \alpha _i }{\left( {\rho _i + \rho _j } \right)/2} (13)$$
2.1.3 体积分数方程离散化
每个时间步下对体积分数方程(14)进行求解
$$\frac{\partial F}{\partial t} + \nabla \cdot \left( {{ V}F} \right) = 0 (14)$$
式中,${ V} = u{ i} + v{ j}$, $u$和$v$为$x$和$y$方向的速度分量. 对对流项进行一阶近似和时间项进行二阶欧拉离散化得到如下的显式离散方程
$$F_{i,j}^{n + 1} = F_{i,j}^n - \frac{1}{\Delta V}\left[ {\left( {G_{x,e}^n - G_{x,w}^n } \right) + \left( {G_{y,n}^n - G_{y,s}^n } \right)} \right] (15)$$
式中,$G_x = uF\Delta t\Delta y$和$G_y = vF\Delta t\Delta x$分别为水平和竖直方向上的体积分数通量. 网格为结构化网格,可用算术平均方法计算4个不同方向上的面速度,速度分布如图3,即
$$\left. {{\begin{array}{*{20}c} {u_{\rm e} = 0.5\left( {u_{i + 1,j} + u_{i,j} } \right)} \\ {v_{\rm s} = 0.5\left( {v_{i,j - 1} + v_{i,j} } \right)} \\ {u_{\rm w} = 0.5\left( {u_{i - 1,j} + u_{i,j} } \right)} \\ {v_{\rm n} = 0.5\left( {v_{i,j + 1} + v_{i,j} } \right)} \\ \end{array} }} \right\} (16)$$
根据节点值进行一阶迎风离散化得出面通量的值
$$\begin{array}{lll} F_{x,{\rm e}} = \left\{ \begin{array}{lll} u_{\rm e} F_{i,j} \Delta t\Delta y,&{\rm if} ~~ u_{\rm e} > 0 \\ u_{\rm e} F_{i + 1,j} \Delta t\Delta y,& {\rm else} \\ \end{array} \right. \\ F_{x,n} = \left\{\begin{array}{lll} v_{\rm n} F_{i,j} \Delta t\Delta x, &{\rm if}~~{v_{\rm n} > 0} \\ v_{\rm n} F_{i,j + 1} \Delta t\Delta x,& {\rm else} \\ \end{array}\right. \end{array} (17) $$
2.1.4 梯度空间离散化
梯度值作用是构造单元面上的标量值,以及计算二次扩散项和速度导数.梯度值计算使用的是基于单元的最小二乘法,最小二乘法基础假设是：两个点间的梯度变化是线性的.最小二乘法的优点是能达到基于节点的格林--高斯(Green-Gauss)方法的精确度,但比基于节点的格林--高斯方法节约储存空间.利用最小二乘法单元之间的变化量与中心单元值在两单元之间的单位变化量的关系可表示为
$$\left. {{\begin{array}{lll} {\left( {\nabla \phi } \right)_{c0} \cdot \Delta r_i = \left( {\phi _{ci} - \phi _{c0} } \right)} \\ {\left( {\nabla \phi } \right)_{c0} \cdot \Delta r_j = \left( {\phi _{cj} - \phi _{c0} } \right)} \\ {\left( {\nabla \phi } \right)_{c0} \cdot \Delta r_k = \left( {\phi _{ck} - \phi _{c0} } \right)} \\ {\left( {\nabla \phi } \right)_{c0} \cdot \Delta r_n = \left( {\phi _{cn} - \phi _{c0} } \right)} \\ \end{array} }} \right\} (18) $$
式中,$\phi $为任一变量值.
基于单元最小二乘法的中心单元梯度示意图见图9所示.
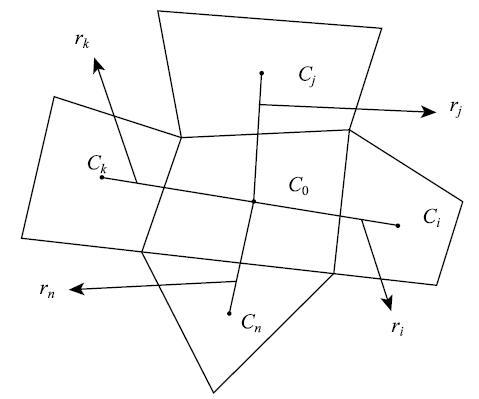显示原图|下载原图ZIP|生成PPT图 9基于单元最小二乘法的中心单元梯度示意图
-->Fig. 9Diagram of central cell gradient of least squares cell based
-->
2.1.5 结果分析
为了验证Youngs-VOF耦合水平集方法的正确性,首先进行了数值计算并与文献[30]进行对比,结果如图10,图10(a)$\sim $图10(c)表明,本文方法与实验结果有良好的一致性,图10(d)显示本文方法与实验结果有微小的差别,理论分析数值计算条件简化的过程中对气泡的运动产生了一定的影响,但最终的结果基本一致.Youngs-VOF耦合水平集方法与VOF方法数值计算结果的对比如图10,Youngs-VOF耦合水平集方法与VOF方法计算获得的气泡图形基本一致,见图10(a)和图10(b),但Youngs-VOF耦合水平集方法获得的气泡边界更加清晰;图10(c)表明随着气泡上升,当气泡出现锐利的边界时,VOF方法捕捉的界面出现了模糊边缘,且图中捕捉到的界面出现了部分失真,气泡下方出现了许多小气泡,且随着气泡的不断上升,气泡下方的小气泡越来越多.综上所述,Youngs-VOF耦合水平集方法与文献结果基本吻合.并且与VOF方法模拟出的结果对比,Youngs-VOF耦合水平集方法计算出的界面比VOF方法计算出的界面要更加的清晰、锐利.
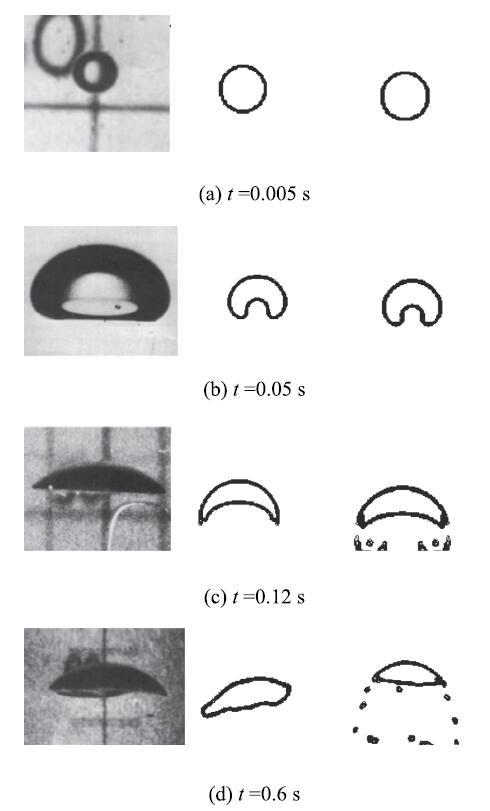显示原图|下载原图ZIP|生成PPT图 10不同时刻实验照片与模拟对比图(左边为实验,中间为Youngs-VOF耦合水平集方法,右边为VOF方法)
-->Fig. 10Comparision of bubble shapes observed in experiments and predicted in simulation under different moments(The left is the experiment,the middle is the Youngs-VOF coupled with Level Set method,the right is the VOF method)
-->
2.2 剪切运动
剪切运动广泛存在于各种复杂流动中,使用Youngs-VOF耦合水平集方法对剪切流场进行数值计算与文献[32]纯VOF结果进行对照.图11为预设剪切流场. 图12(a)计算区域为4000 mm$\times $4000mm,网格数量为200$\times $200,圆心坐标为$\left( {500~{\pi},250~{\pi }} \right)$,半径$R = 1000~{\pi } / 5$mm,圆形区域内为水,其他区域为空气,流场在$t$=7.5${\pi}$~s时,流动方向由顺时针变为逆时针.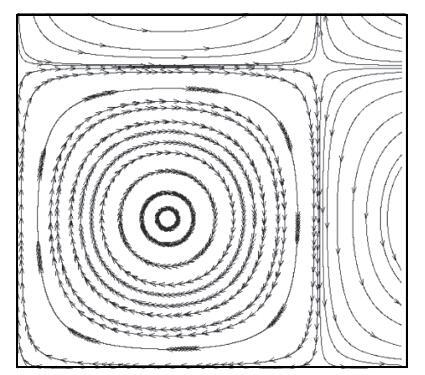
显示原图|下载原图ZIP|生成PPT图11剪切流场示意图
-->Fig. 11Shear flow field diagram
-->
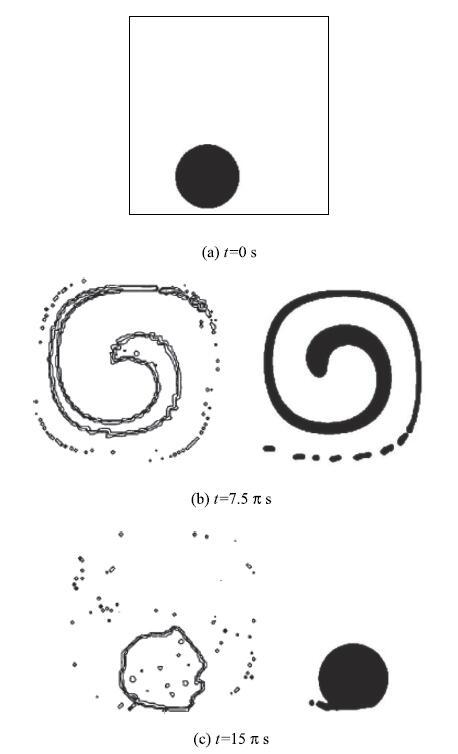显示原图|下载原图ZIP|生成PPT图12剪切流场结果
-->Fig. 12Results for shearing field
-->
由图12(b)所示,当$t$=7.5${\pi}$ s,圆形水滴在剪切流场作用下,呈现与流场相似的形状,左边为纯VOF的结果,右边为Youngs-VOF耦合水平集方法的结果.由图可知,VOF方法得到的结果界面呈波浪锯齿状,表现出了VOF方法不能准确计算界面曲率以及表面张力的缺点,右图显示的界面光滑,且完整显示了整个界面.由图12(c)所示,当流场逆时针剪切7.5 ${\pi}$~s后,右图基本回到初始形状,左图与初始形状差别较大,主要表现为界面光滑性差、界面成波浪锯齿状.
2.3 溃坝模拟
2.3.1 物理模型及数值算法为验证Youngs-VOF耦合水平集方法在自由表面流动中可以准确的捕捉界面.本文依照文献[36]进行数值计算. 实验中流体参数为$\rho $=997 ${kg} /{\rm m}^{{3}}$, $\nu $=8.9$\times $10$^{ - 7}~{\rm m}^{2}/{\rm s}$, 表面张力为0.072 ${\rm N}/{\rm m}$.实验与数值计算的不同点在于：第一,实验中定义零时刻是闸门开始往上移动的时刻,与释放水流有一段时间,而数值计算是瞬间全部释放;第二是实验中为增加拍摄照片的对比度而增加荧光粒子,而数值计算则没有增加更多的干扰.这两种因素对最终的现象并没有造成实质性的干扰,所以可以忽略,但这也说明了数值计算的优点,可以避免很多不必要的干扰.
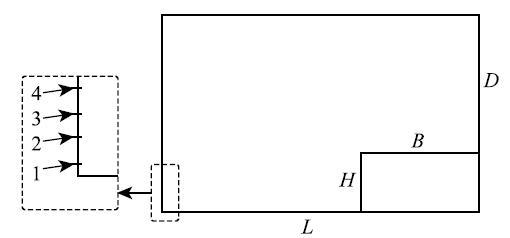
数值计算流体参数以及表面张力采用与实验相同的数值,便于验证.图13为二维溃坝初始模型示意图(与实验模型参数一致),图中,$L$=1610mm, $D$=1000 mm,$H$=300 mm, $B$=600 mm,1,2,3,4位置距离底部的距离分别为3,15,30,80 mm.三维数值计算模型仅在二维模型的基础上增大了150 mm的厚度. 分别对135$\times $ 90,270 $\times $ 180,540 $\times $ 360,\linebreak1080 $\times $720网格数进行数值计算,通过对4种网格下1$\sim$4处压力变化过程进行对比;1080$\times $720对数值计算变化影响较小,但计算速度非常慢,最终确定将540 $\times$ 360网格下的数值计算结果与文献实验现象进行对比.为验证Youngs-VOF耦合水平集方法模拟三维模型的准确性,对270 $\times$ 180 $\times $20的网格进行了数值计算并与二维模型以及实验进行对比.表面张力模型、体积分数方程离散化方法和梯度空间离散化方法与2.1节中气泡水中自由上升中的方法相同.
显示原图|下载原图ZIP|生成PPT图13溃坝初始模型图
-->Fig. 13Broken dam initial model diagram
-->
2.3.2 结果分析
数值计算结果如图14所示.图14中,左、中、右分别表示的为实验结果、三维270$\times $180$\times$20网格下的计算结果与二维540$\times $360网格下的计算结果.由图14可知,实验与计算的结果有一致的流动现象.并且三维计算结果与二维计算结果和实验结果都达到了很好的一致性.说明Youngs-VOF耦合水平集方法可以准确捕捉自由表面流动并且对三维模型具有很好的适用性.
显示原图|下载原图ZIP|生成PPT图14溃坝--自由表面变化图
-->Fig. 14Dam break--free surface change diagram
-->
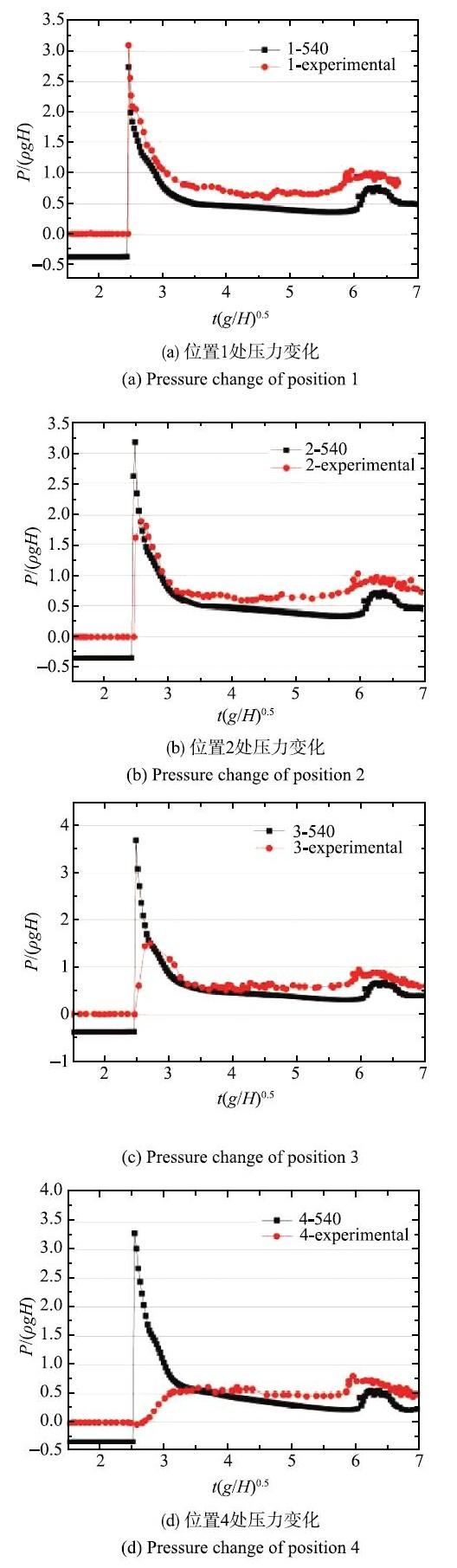
图15为540$\times$360网格下的数值计算结果与文献实验结果的压力对比图,横纵坐标分别为无量纲化量即$t^{* }=t(g/H)^{0.5}$和$P^{*}=P/(\rho gH)$. 以下数值结果是经过4种网格对比后的结果.由图15(a)$\sim$图15(d)可知,数值结果与实验结果基本一致,但因壁面存在一定阻力,压力普遍比实验数值低.图15(a)$\sim$图15(c)数值结果基本与实验吻合,但图15(d)中$t^{*}$=3前两者相差较多,其原因为：数值计算显示水流第一次到达左壁面用时$t=$0.43s左右,但是实验是通过撤走挡板让水自由流动,假设瞬间撤走挡板,撤走挡板的时间不会低于0.1s,所以撤走挡板对流动产生一定的影响,具体为：挡板会对上方的流体进行约束,使下方流体速度变大,上方流体速度变小;数值计算则不会产生这种影响,这就造成位置偏高的位置4处的压力主要由爬流造成,因为撤走挡板时由于挡板的约束使得流体层较薄,不足以对位置4产生瞬间的冲击压力,但是对于位置较低的1$\sim$3不会产生影响.总体对比可知,实验结果与计算结果基本一致.
显示原图|下载原图ZIP|生成PPT图15压力对比图
-->Fig. 15Pressure comparison chart
-->
从流动现象分析,由于流体流动到左壁面处,水流冲击压力会使位置1$\sim$4处的压力陡然增加,所以就会产生图15中压力几乎垂直增加的情况.当水流爬升到一定的高度开始脱落壁面,这时压力逐渐变小,造成图15中显示的曲线平缓下降.
3 结论
(1) 对单个气泡在水中自由上升进行数值计算并与与参考文献进行对比,验证了Youngs-VOF耦合水平集方法的有效性.通过对Youngs-VOF耦合水平集方法与VOF方法的模拟结果对比,Youngs-VOF耦合水平集方法计算结果更清晰、锐利.(2) 通过对溃坝--自由表面流动进行数值计算并与实验对比,验证了Youngs-VOF耦合水平集方法的精确性与稳定性.对三维溃坝的数值计算也表明本文的算法可以准确的计算三维数值模型.
(3) Youngs-VOF耦合水平集方法为几何重构方法,避免利用高阶导数本身的稳定性去求解水平集对流方程和距离函数方程的代数计算方法.Youngs-VOF耦合水平集方法为纯欧拉法,与拉格朗日法相比,效率提高(比如粒子法单个网格下对界面追踪需要填充许多粒子,存储参数变多,运算效率变差)并且可以准确的捕捉界面.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . 锛歍he study of interfacial motion of gas-liquid phase is very important in science and engineering. Considering the non-equilibrium flow calculation, a unified gas-kinetic scheme for gas-liquid two phase interface capturing is presented in this paper. Since the free transport and particle collision are coupled to update the macroscopic variables and microscopic distribution functions, the unified gas-kinetic scheme can solve the non-equilibrium flow. The van der Waals (vdW) equation of state (EOS) is included to describe the coexistence of gas and liquid and the phase transition between them. Because of the characteristics of vdW EOS, the interface between gas and liquid can be captured naturally through condensation and evaporation processes. As a result, the new scheme can solve the gas-liquid two phase problems. Finally, the proposed method is used to obtain the numerical solution of Maxwell construction, which agrees well with the corresponding theoretical solution. Then, the Laplace鈥檚 theorem is verified by numerical calculation of the surface tension of the droplet corresponding to the van der Waals state equation. In addition, the collision of the two droplets is simulated, which proves the validity of the scheme further. However, due to the characteristics of the van der Waals equation of state, the constructed scheme is only applicable to the case where the liquid/gas two-phase density ratio is less than 5. . 锛歍he study of interfacial motion of gas-liquid phase is very important in science and engineering. Considering the non-equilibrium flow calculation, a unified gas-kinetic scheme for gas-liquid two phase interface capturing is presented in this paper. Since the free transport and particle collision are coupled to update the macroscopic variables and microscopic distribution functions, the unified gas-kinetic scheme can solve the non-equilibrium flow. The van der Waals (vdW) equation of state (EOS) is included to describe the coexistence of gas and liquid and the phase transition between them. Because of the characteristics of vdW EOS, the interface between gas and liquid can be captured naturally through condensation and evaporation processes. As a result, the new scheme can solve the gas-liquid two phase problems. Finally, the proposed method is used to obtain the numerical solution of Maxwell construction, which agrees well with the corresponding theoretical solution. Then, the Laplace鈥檚 theorem is verified by numerical calculation of the surface tension of the droplet corresponding to the van der Waals state equation. In addition, the collision of the two droplets is simulated, which proves the validity of the scheme further. However, due to the characteristics of the van der Waals equation of state, the constructed scheme is only applicable to the case where the liquid/gas two-phase density ratio is less than 5. |
| [2] | . 针对低渗透煤层渗流问题，考虑启动压力梯度及其引起的动边界和动边界内吸附气解吸作用的渗流模型研究目前仅限于单相流，而更符合实际的气--水两相渗流动边界模型未见报道.本文综合考虑了煤层吸附气的解吸作用、气--水两相渗流、非达西渗流、地层应力敏感等影响因素，进行了低渗透煤层的气--水两相渗流模型研究.采用了试井技术中的“分相处理”方法，修正了两相渗流的综合压缩系数和流度，并基于含气饱和度呈线性递减分布的假设，建立了煤层气藏的气--水两相渗流耦合模型.该数学模型不仅可以描述由于低渗透煤层中渗流存在启动压力梯度而产生的可表征煤层有效动用范围随时间变化的移动边界，还可以描述煤层有效动用范围内吸附气的解吸现象以及吸附气解吸作用所引起的煤层含气饱和度的上升；为了提高模型精度，控制方程还保留了二次压力梯度项.采用了稳定的全隐式有限差分方法进行了模型的数值求解，并验证了数值计算方法的正确性，获得了模型关于瞬时井底压力与压力导数响应的双对数特征曲线，由此分析了各渗流参数的敏感性影响.本文研究结果可为低渗透煤层气藏开发的气--水两相流试井技术提供渗流力学的理论基础. . 针对低渗透煤层渗流问题，考虑启动压力梯度及其引起的动边界和动边界内吸附气解吸作用的渗流模型研究目前仅限于单相流，而更符合实际的气--水两相渗流动边界模型未见报道.本文综合考虑了煤层吸附气的解吸作用、气--水两相渗流、非达西渗流、地层应力敏感等影响因素，进行了低渗透煤层的气--水两相渗流模型研究.采用了试井技术中的“分相处理”方法，修正了两相渗流的综合压缩系数和流度，并基于含气饱和度呈线性递减分布的假设，建立了煤层气藏的气--水两相渗流耦合模型.该数学模型不仅可以描述由于低渗透煤层中渗流存在启动压力梯度而产生的可表征煤层有效动用范围随时间变化的移动边界，还可以描述煤层有效动用范围内吸附气的解吸现象以及吸附气解吸作用所引起的煤层含气饱和度的上升；为了提高模型精度，控制方程还保留了二次压力梯度项.采用了稳定的全隐式有限差分方法进行了模型的数值求解，并验证了数值计算方法的正确性，获得了模型关于瞬时井底压力与压力导数响应的双对数特征曲线，由此分析了各渗流参数的敏感性影响.本文研究结果可为低渗透煤层气藏开发的气--水两相流试井技术提供渗流力学的理论基础. |
| [3] | . The rise of bubbles in viscous liquids is not only a very common process in many industrial applications, but also an important fundamental problem in fluid physics. An improved numerical algorithm based on the front tracking method, originally proposed by Tryggvason and his co-workers, has been validated against experiments over a wide range of intermediate Reynolds and Bond numbers using an axisymmetric model [J. Hua, J. Lou, Numerical simulation of bubble rising in viscous liquid, J. Comput. Phys. 22 (2007) 769鈥795]. In the current paper, this numerical algorithm is further extended to simulate 3D bubbles rising in viscous liquids with high Reynolds and Bond numbers and with large density and viscosity ratios representative of the common air鈥搘ater two-phase flow system. To facilitate the 3D front tracking simulation, mesh adaptation is implemented for both the front mesh on the bubble surface and the background mesh. On the latter mesh, the governing Navier鈥揝tokes equations for incompressible, Newtonian flow are solved in a moving reference frame attached to the rising bubble. Specifically, the equations are solved using a finite volume scheme based on the Semi-Implicit Method for Pressure-Linked Equations (SIMPLE) algorithm, and it appears to be robust even for high Reynolds numbers and high density and viscosity ratios. The 3D bubble surface is tracked explicitly using an adaptive, unstructured triangular mesh. The numerical model is integrated with the software package PARAMESH, a block-based adaptive mesh refinement (AMR) tool developed for parallel computing. PARAMESH allows background mesh adaptation as well as the solution of the governing equations in parallel on a supercomputer. Further, Peskin distribution function is applied to interpolate the variable values between the front and the background meshes. Detailed sensitivity analysis about the numerical modeling algorithm has been performed. The current model has also been applied to simulate a number of cases of 3D gas bubbles rising in viscous liquids, e.g. air bubbles rising in water. Simulation results are compared with experimental observations both in aspect of terminal bubble shapes and terminal bubble velocities. In addition, we applied this model to simulate the interaction between two bubbles rising in a liquid, which illustrated the model鈥檚 capability in predicting the interaction dynamics of rising bubbles. |
| [4] | . A front tracking method combined with the real ghost fluid method (RGFM) is proposed for simulations of fluid interfaces in two-dimensional compressible flows. In this paper the Riemann problem is constructed along the normal direction of interface and the corresponding Riemann solutions are used to track fluid interfaces. The interface boundary conditions are defined by the RGFM, and the fluid interfaces are explicitly tracked by several connected marker points. The Riemann solutions are also used directly to update the flow states on both sides of the interface in the RGFM. In order to validate the accuracy and capacity of the new method, extensive numerical tests including the bubble advection, the Sod tube, the shock-bubble interaction, the Richtmyer-Meshkov instability and the gas-water interface, are simulated by using the Euler equations. The computational results are also compared with earlier computational studies and it shows good agreements including the compressible gas-water system with large density differences. |
| [5] | . 本文发展了基于Front Tracking的直接数值模拟方法研究气液两相界面的迁移特性,该方法对气液两相采用半隐式的分步法直接求解N-S方程,耦合Front Tracking Method获得两相界面的三维变形。针对无边界以及垂直壁面附近静止水中的单个气泡上升过程进行模拟,研究气泡运动的机理以及气泡与壁面的相互作用。数值模拟准确再现了气泡的上升过程和变形,不同Re数下气泡的上升速度计算结果同经验关联式非常吻合,验证了该方法的有效性。随后分析了气泡周围流场的结构,发现壁面对气泡周围流场的抑制是壁面对气泡作用力的主要原因,将导致气泡逐渐偏离垂直壁面。 . 本文发展了基于Front Tracking的直接数值模拟方法研究气液两相界面的迁移特性,该方法对气液两相采用半隐式的分步法直接求解N-S方程,耦合Front Tracking Method获得两相界面的三维变形。针对无边界以及垂直壁面附近静止水中的单个气泡上升过程进行模拟,研究气泡运动的机理以及气泡与壁面的相互作用。数值模拟准确再现了气泡的上升过程和变形,不同Re数下气泡的上升速度计算结果同经验关联式非常吻合,验证了该方法的有效性。随后分析了气泡周围流场的结构,发现壁面对气泡周围流场的抑制是壁面对气泡作用力的主要原因,将导致气泡逐渐偏离垂直壁面。 |
| [6] | . 本文利用基于Front Tracking的3D直接数值模拟方法对高粘度流体中倾斜壁面附近上升的气泡进行了直接数值模拟,以研究气泡与壁面相互作用以及壁面附近气泡运动的机理。在不同的壁面倾斜角(10°,30°和50°)下针对Eo数分别等于0.7和10的两种典型工况计算了气泡的变形、运动轨迹和上升速度并与实验进行了对比.发现倾斜壁面使得气泡被压扁,在较大的倾斜角下气泡不对称变形程度更大、由此导致的流场不对称性也更大,表明壁面垂直方向的速度受到抑制是壁面引发升力的原因.对于不同的倾角,气泡最终都会沿着倾斜表面滑动,而且倾角越大,气泡中心越接近壁面。气泡的上升速度则随着倾角的增大而单调减小,同实验结果的对比吻合良好。 . 本文利用基于Front Tracking的3D直接数值模拟方法对高粘度流体中倾斜壁面附近上升的气泡进行了直接数值模拟,以研究气泡与壁面相互作用以及壁面附近气泡运动的机理。在不同的壁面倾斜角(10°,30°和50°)下针对Eo数分别等于0.7和10的两种典型工况计算了气泡的变形、运动轨迹和上升速度并与实验进行了对比.发现倾斜壁面使得气泡被压扁,在较大的倾斜角下气泡不对称变形程度更大、由此导致的流场不对称性也更大,表明壁面垂直方向的速度受到抑制是壁面引发升力的原因.对于不同的倾角,气泡最终都会沿着倾斜表面滑动,而且倾角越大,气泡中心越接近壁面。气泡的上升速度则随着倾角的增大而单调减小,同实验结果的对比吻合良好。 |
| [7] | . 基于流体体积法(volume of fluid,VOF)，数值模拟了装满黏性液体的圆柱形汽缸中的裙带气泡的浮升运动，研究了侧壁面约束对裙带气泡浮升动力学的影响.用雷诺数(Re)、韦伯数(We)、长宽比()、裙带厚度(T=d)和裙带长度(L=d)等参数来表征不同约束比条件下(1:16Cr610)裙带气泡的运动和变形特性，分别在全局参考系和局部参考系下分析了壁面对气泡内外流场的影响.模拟结果显示，当Cr>8时，裙带气泡的行为特性与在无界流域条件下的情况相当，可视作壁面无关的.当Cr<8时，壁面对裙带气泡的浮升速度和形状演化有显著影响.随着壁面的靠近，裙带气泡受到的阻力增大，造成浮升速度下降.约束比降低使裙带厚度增厚而长度变短直至裙带消失，裙带气泡受挤压而被拉长并逐渐变为椭圆球帽形最后到子弹形.相反，约束比增大时，裙带气泡尾流效应增强，气泡边缘处流场产生明显的循环流动(涡环)，促使裙带的形成.研究表明壁面会加剧裙带气泡产生破碎，印证了前人的推断.模拟结果与已有的经验公式吻合良好，分析了前人公式的适用性. . 基于流体体积法(volume of fluid,VOF)，数值模拟了装满黏性液体的圆柱形汽缸中的裙带气泡的浮升运动，研究了侧壁面约束对裙带气泡浮升动力学的影响.用雷诺数(Re)、韦伯数(We)、长宽比()、裙带厚度(T=d)和裙带长度(L=d)等参数来表征不同约束比条件下(1:16Cr610)裙带气泡的运动和变形特性，分别在全局参考系和局部参考系下分析了壁面对气泡内外流场的影响.模拟结果显示，当Cr>8时，裙带气泡的行为特性与在无界流域条件下的情况相当，可视作壁面无关的.当Cr<8时，壁面对裙带气泡的浮升速度和形状演化有显著影响.随着壁面的靠近，裙带气泡受到的阻力增大，造成浮升速度下降.约束比降低使裙带厚度增厚而长度变短直至裙带消失，裙带气泡受挤压而被拉长并逐渐变为椭圆球帽形最后到子弹形.相反，约束比增大时，裙带气泡尾流效应增强，气泡边缘处流场产生明显的循环流动(涡环)，促使裙带的形成.研究表明壁面会加剧裙带气泡产生破碎，印证了前人的推断.模拟结果与已有的经验公式吻合良好，分析了前人公式的适用性. |
| [8] | . In this paper, we improve the multi-dimensional THINC (tangent of hyperbola for interface capturing) scheme [F. Xiao, Y. Honma, T. Kono, A simple algebraic interface capturing scheme using hyperbolic tangent function, Int. J. Numer. Meth. Fluid. 48 (2005) 1023]. The THINC scheme is a VOF (volume of fluid) type method. In the original THINC scheme, one-dimensional THINC scheme was straightforwardly used for multi-dimensional cases. In this paper, we propose the WLIC (weighed line interface calculation) method to extend the THINC scheme to multi-dimension. In the WLIC method, the interface is reconstructed by taking an average of line interfaces along x, y and z coordinates with the weights calculated from surface normal. The WLIC method can extend the THINC scheme to multi-dimension while maintaining simplicity of implementation and achieve a higher accuracy than the original THINC scheme. The WLIC method can readily extend the THINC scheme to three-dimension. |
| [9] | . A three-dimensional volume-of-fluid (VOF) interface-sharpening method is developed on the general curvilinear grid for two-phase incompressible flows. In this method, a VOF discretization scheme is formulated for the advection of a two-fluid interface. To maintain interface sharpness, a treatment is applied by solving an interface-sharpening equation after each advection time step, thereby reducing the numerical diffusion error in the solution of the discretization scheme. To demonstrate the accuracy and capability of the advection scheme, several numerical experiments involving three benchmark tests of pure advection were conducted. The results show that the method can realize a sharp interface reliably and efficiently, and reasonable mass conservation is obtained. For the flow field of viscous incompressible flows, the Navier鈥揝tokes equations are solved by adopting the dual-time preconditioning method. A fully implicit method with a highly efficient lower-upper symmetrical Gauss鈥揝eidel (LU-SGS) algorithm based on a dual-time stepping technique as a sub-iteration scheme is employed to advance the solution in time. To validate the proposed method for computing incompressible free surface flows, a dam-break flow over a dry horizontal bed and the water entry of a hemisphere with one degree of freedom are simulated. Comparisons of the predicted results with the available experimental data are presented herein. |
| [10] | . In direct numerical simulations of multiphase flows, based on the Volume of Fluid (VOF) approach, the advection of the volume fraction field is a crucial point. The choice of the discretisation scheme for the transport of the volume fraction is decisive for an accurate description of surface dynamics. In this paper we assess two numerical methods: a high order discretisation scheme, namely the surface compression scheme, and an interface reconstruction scheme based on a piecewise linear interface calculation (PLIC). We compare accuracy, convergence rate and computational cost of these methods with results from literature. The comparative study includes reference 2D and 3D advection test cases. Moreover, the advection algorithm is tested coupled to an incompressible Navier鈥揝tokes solver and used to simulate a rising bubble in a liquid for different E枚tv枚s and Reynolds numbers. We establish via the advection tests and through the study of rising bubbles that the PLIC method converges to second order while the compression method fails to converge systematically. The computational overhead of both methods is negligible compared to an incompressible flow solver to which it might be coupled. |
| [11] | . 对于部分充液箱体中液体小幅晃动问题，自由液面处的黏性耗散是总阻尼的重要组成部分.影响液体晃动阻尼的因素很多，导致阻尼计算的精度有限，为了提高阻尼的计算精度，提出了一种基于流体体积组分方法的阻尼计算方法. 采用该方法求解阻尼时，可以满足所有壁面的黏性无滑移条件，计算出具体的阻力值而不是一个范围.运用该方法的阻尼计算结果与已发表的试验结果更加吻合，特别是在液高比h/R<1时. . 对于部分充液箱体中液体小幅晃动问题，自由液面处的黏性耗散是总阻尼的重要组成部分.影响液体晃动阻尼的因素很多，导致阻尼计算的精度有限，为了提高阻尼的计算精度，提出了一种基于流体体积组分方法的阻尼计算方法. 采用该方法求解阻尼时，可以满足所有壁面的黏性无滑移条件，计算出具体的阻力值而不是一个范围.运用该方法的阻尼计算结果与已发表的试验结果更加吻合，特别是在液高比h/R<1时. |
| [12] | . Aiming for the simulation of colloidal droplets in microfluidic devices, we present here a numerical method for two-fluid systems subject to surface tension and depletion forces among the suspended droplets. The algorithm is based on an efficient solver for the incompressible two-phase Navier-Stokes equations, and uses a mass-conserving level set method to capture the fluid interface. The four novel ingredients proposed here are, firstly, an interface-correction level set (ICLS) method; global mass conservation is achieved by performing an additional advection near the interface, with a correction velocity obtained by locally solving an algebraic equation, which is easy to implement in both 2D and 3D. Secondly, we report a second-order accurate geometric estimation of the curvature at the interface and, thirdly, the combination of the ghost fluid method with the fast pressure-correction approach enabling an accurate and fast computation even for large density contrasts. Finally, we derive a hydrodynamic model for the interaction forces induced by depletion of surfactant micelles and combine it with a multiple level set approach to study short-range interactions among droplets in the presence of attracting forces. |
| [13] | . . |
| [14] | . A general interface tracking method based on the phase-field equation is presented. The zero phase-field contour is used to implicitly track the sharp interface on a fixed grid. The phase-field propagation equation is derived from an interface advection equation by expressing the interface normal and curvature in terms of a hyperbolic tangent phase-field profile across the interface. In addition to normal interface motion driven by a given interface speed or by interface curvature, interface advection by an arbitrary external velocity field is also considered. In the absence of curvature-driven interface motion, a previously developed counter term is used in the phase-field equation to cancel out such motion. Various modifications of the phase-field equation, including nonlinear preconditioning, are also investigated. The accuracy of the present method is demonstrated in several numerical examples for a variety of interface motions and shapes that include singularities, such as sharp corners and topology changes. Good convergence with respect to the grid spacing is obtained. Mass conservation is achieved without the use of separate re-initialization schemes or Lagrangian marker particles. Similarities with and differences to other interface tracking approaches are emphasized. |
| [15] | . <div class="abstract" data-abstract-type="normal">In this paper numerical results are presented for the buoyancy-driven rise of a deformable bubble through an unbounded quiescent fluid. Complete solutions, including the bubble shape, are obtained for Reynolds numbers in the range 1 ≤ <span class='italic'>R ≤ 200 and for Weber numbers up to 20. For Reynolds numbers <span class='italic'>R ≤ 20 the shape of the bubble changes from nearly spherical to oblate-ellipsoidal to spherical-cap depending on Weber number; at higher Reynolds numbers ‘disk-like’ and ‘saucer-like’ shapes appear at <span class='italic'>W = <span class='italic'>O(10). The present results show clearly that flow separation may occur at a <span class='italic'>smooth free surface at intermediate Reynolds numbers; this fact suggests a qualitative explanation of the often-observed irregular (zigzag or helical) paths of rising bubbles. |
| [16] | . Since the initial publication of Hu et al. (1992, Theor. Comput. Fluid Dyn.3, 285), the numerical method developed for direct simulations of fluid–solid systems using the arbitrary Lagrangian–Eulerian (ALE) technique has undergone continuous modifications. Some of the modifications were described in H. H. Hu (1996, Int. J. Multiphase Flow22, 335). In this paper, we will present the most up-to-date implementation of the method and the results of several benchmark test problems. |
| [17] | . Attention is given to a method to simulate unsteady multifluid flows in which a sharp interface or a front separate incompressible fluids of different density and viscosity. The flow field is discretized by a conservative finite difference approximation on a stationary grid, and the interface is explicitly represented by a separate, unstructured grid that moves through the stationary grid. Since the interface deforms continuously, it is necessary to restructure its grid as the calculations proceed. In addition to keeping the density and viscosity stratification sharp, the tracked interface provides a natural way to include surface tension effects. Both 2D and 3D full numerical simulations of bubble motion are presented. |
| [18] | . A second-order volume-of-fluid method (VOF) is presented for interface tracking and sharp interface treatment on general structured grids. Central to the new method is a second-order distance function construction scheme on a general structured grid based on the reconstructed interface. A novel technique is developed for evaluating the interface normal vector using the distance function. With the normal vector, the interface is reconstructed from the volume fraction function via a piecewise linear interface calculation (PLIC) scheme on the computational domain. Several numerical tests are conducted to demonstrate the accuracy and efficiency of the present method. In general, the new VOF method is more efficient than both the high-order level set and the coupled level set and volume-of-fluid (CLSVOF) methods. The results from the new method are better than those from the benchmark VOF method, particularly in the under-resolved regions, and are comparable to those from the CLSVOF method. Breaking waves over a submerged bump and around a wedge-shaped bow are simulated to demonstrate the application of the new method and sharp interface treatment in a two-phase flow solver on curvilinear grids. The computational results are in good agreement with the available experimental measurements. |
| [19] | . In this study, an Algebraic Coupled Level Set-Volume of Fluid (A-CLSVOF) method is proposed for the simulation of interfacial capillary flows. The Volume of Fluid (VOF) method is utilized to incorporate one-way coupling with the Level Set (LS) function in order to improve the accuracy of the surface tension force calculation and to reduce the presence of parasitic currents. In this method, both VOF and LS functions are transported where the new volume fraction determines the interface seed position utilized by the reinitialization procedure for the LS field. Computational efficiency is enhanced through the use of the advected LS field, serving as an initial condition for the reinitialization procedure. The Hamilton–Godunov function is used with a second order (in space and time) discretization scheme to produce a signed distance function. In order to evaluate the performance of the methodology implemented here for capillary dominant flows, four different cases were considered: 1. static droplet; 2. capillary wave relaxation; 3. Rayleigh–Taylor instability and 4. droplet impact on a liquid pool. The simulations demonstrated reduction in spurious currents, accurately predicted capillary pressure and demonstrated overall improvements in efficiency and error reduction owing to the addition of LS advection. The present methodology is tested against previously published experimental results for a droplet impact on a deep liquid pool. Simulation results demonstrate excellent agreement with measured interface height up to and beyond the formation of a Rayleigh–Jet and break-up formation of a secondary daughter drop. |
| [20] | . |
| [21] | . This paper investigates some fundamental aspects of rising gas bubbles in stagnant Newtonian liquids using a coupled level-set and volume-of-fluid (CLSVOF) method. The coupled method not only calculates the geometric properties (normal and curvature) of the bubble surface accurately but also satisfies compliance of mass conservation very well. The method solves a single set of governing equations for both phases using variable transportive properties on a fixed Eulerian two-dimensional mesh in axisymmetric coordinates. We computed the terminal shapes and Reynolds numbers (Re) of isolated gas bubbles rising in stagnant liquids for low to high E02tv02s number (Eo<340) and Morton number (M<44). In addition, the drag co-efficients for a single bubble rising in liquid with M8210614 are computed. The rise and shape of two co-axial gas bubbles with same size in stagnant liquid and the evolution history of the bubble coalescence process are examined. Furthermore, the mechanisms of bubble-bursting at a free surface and formation of liquid jets are also studied qualitatively. The computational results are compared with the experimental results available in literature. It is observed that the predicted results are in good agreement with experimental counterpart. Finally, the formation of gas bubbles from a submerged orifice in quiescent and co-flowing liquids for low Reynolds number flows is discussed where the viscosity ratio of liquid to gas is about 16, 474. |
| [22] | . 运用CLSVOF方法数值模拟了三维单气泡在液体中的上升和变形过程,分别考察了液体的表面张力和浮力对上升气泡变形的影响.计算结果表明:CLSVOF方法能比较精确地跟踪三维单气泡在液体中的上升过程;在相同密度比和粘度比情况下,随着液体表面张力的减小和液体浮力的增大,气泡底部形成的射流使得气泡下缘凹陷变得明显,变形幅度加大,射流穿透气泡的时间提前. . 运用CLSVOF方法数值模拟了三维单气泡在液体中的上升和变形过程,分别考察了液体的表面张力和浮力对上升气泡变形的影响.计算结果表明:CLSVOF方法能比较精确地跟踪三维单气泡在液体中的上升过程;在相同密度比和粘度比情况下,随着液体表面张力的减小和液体浮力的增大,气泡底部形成的射流使得气泡下缘凹陷变得明显,变形幅度加大,射流穿透气泡的时间提前. |
| [23] | . Reconstructing the interface within a cell, based on volume fraction and normal direction, is a key part of multiphase flow solvers which make use of piecewise linear interface calculation (PLIC) such as the Coupled Level Set Volume of Fluid (CLSVOF) method. In this paper, we present an iterative method for interface reconstruction (IR) in general convex cells based on tetrahedral decomposition. By splitting the cell into tetrahedra prior to IR the volume of the truncated polyhedron can be calculated much more rapidly than using existing clipping and capping methods. In addition the root finding algorithm is designed to take advantage of the nature of the relationship between volume fraction and interface position by using a combination of Newton's and Muller's methods. In stand-alone tests of the IR algorithm on single cells with up to 20 vertices the proposed method was found to be 2 times faster than an implementation of an existing analytical method, while being easy to implement. It was also found to be 3.4鈥11.8 times faster than existing iterative methods using clipping and capping and combined with Brent's root finding method. Tests were then carried out of the IR method as part of a CLSVOF solver. For a sphere deformed by a prescribed velocity field the proposed method was found to be up to 33% faster than existing iterative methods. For simulations including the solution of the velocity field the maximum speed up was found to be approximately 52% for a case where 12% of cells lie on the interface. Analysis of the full simulation CPU time budget also indicates that while the proposed method has produced a considerable speed-up, further gains due to increasing the efficiency of the IR method are likely to be small as the IR step now represents only a small proportion of the run time. |
| [24] | . We present a new coupled level set and volume-of-fluid (CLSVOF) method for free surface flow simulations on an overset grid system. The coupled method takes advantages of the strengths of the level set (LS) method and the volume-of-fluid (VOF) method, and is superior to either single method. The novelty of the present method lies in that we develop the methodology for an overset grid system of embedding, overlapping and moving structured grids. The new methodology accurately captures interface and greatly preserves mass on an overset grid system by demonstrating the 3D sphere advection test. The method is coupled to a well validated Reynolds-Averaged Navier鈥揝tokes incompressible flow solver. The method is validated with the dam-breaking flow interacting with a 3D obstacle (square structure/circular cylinder) by comparing the numerical results with available experimental and numerical studies. The water impact of a sphere case is further performed to demonstrate the capabilities of the new method on a complicated moving overset grid system. |
| [25] | . 61A code has been developed to study the interface changes of gas–liquid two-phase flows.61A scheme called VOSET is introduced in the present research.61The method computes the surface tension with a good accuracy.61The effect of bubble initial topology on its terminal shape is investigated by VOSET. |
| [26] | . 基于代数重构思想,发展了一种新的双界面函数重构方法,并采用双正弦函数构造了双正弦界面重构方法(double sine interface capturing,DSINC).为验证不同界面函数对界面捕捉效果的影响,用数值方法求解了可压缩五方程模型,其中对流项的离散采用五阶WENO(weighted essentially non-oscillatory method)格式,时间积分采用三阶Runge--Kutta方法,通量计算分别考虑了HLL和HLLC方法,而状态方程采用Mie-Gr¨uneisen状态方程.在数值计算中,在界面附近,采用DSINC来获得体积分数的重构,而在远离界面的区域采用WENO格式来获得高阶插值状态.相比采用单界面函数的方法,如双曲正切界面重构方法(tangent of hyperbola for interface capturing,THINC),DSINC方法同样具有界面重构算法简单,在程序中添加方便等特点,两者区别在于,DSINC方法在重构过程中未知函数更易于求解,而无需求解复杂的非线性超越方程,这就使其具有易于向多维扩展的能力.一些典型的两相流动问题,如圆形水柱对流问题,两相三波点问题和激波-界面不稳定性问题等被用作不同界面函数对界面捕捉效果的影响对比.对比分析发现,DSINC与THINC在界面捕捉效果上大致保持一致,并在计算中表现出了较好的稳定性.双界面函数重构思想可以为多相流动界面的代数重构提供了一种新的思路. . 基于代数重构思想,发展了一种新的双界面函数重构方法,并采用双正弦函数构造了双正弦界面重构方法(double sine interface capturing,DSINC).为验证不同界面函数对界面捕捉效果的影响,用数值方法求解了可压缩五方程模型,其中对流项的离散采用五阶WENO(weighted essentially non-oscillatory method)格式,时间积分采用三阶Runge--Kutta方法,通量计算分别考虑了HLL和HLLC方法,而状态方程采用Mie-Gr¨uneisen状态方程.在数值计算中,在界面附近,采用DSINC来获得体积分数的重构,而在远离界面的区域采用WENO格式来获得高阶插值状态.相比采用单界面函数的方法,如双曲正切界面重构方法(tangent of hyperbola for interface capturing,THINC),DSINC方法同样具有界面重构算法简单,在程序中添加方便等特点,两者区别在于,DSINC方法在重构过程中未知函数更易于求解,而无需求解复杂的非线性超越方程,这就使其具有易于向多维扩展的能力.一些典型的两相流动问题,如圆形水柱对流问题,两相三波点问题和激波-界面不稳定性问题等被用作不同界面函数对界面捕捉效果的影响对比.对比分析发现,DSINC与THINC在界面捕捉效果上大致保持一致,并在计算中表现出了较好的稳定性.双界面函数重构思想可以为多相流动界面的代数重构提供了一种新的思路. |
| [27] | . 提出了一种基于水平集的Eulerian-Lagrangian耦合方法，其中Lagrangian方法采用相容显式有限元拉氏方法，Eulerian方法采用基于近似Riemann解的有限体积Eulerian方法，多介质界面处理采用新的水平集和Ghost方法计算. 给出了若干数值算例，包括激波管问题以及金属和气体的运动界面及其大变形问题，并分别与精确解和相容显式有限元拉氏方法的计算结果进行了对比. 数值结果表明，该方法计算结果正确，精度较高，能够准确捕捉物质界面，适用于处理大变形问题. . 提出了一种基于水平集的Eulerian-Lagrangian耦合方法，其中Lagrangian方法采用相容显式有限元拉氏方法，Eulerian方法采用基于近似Riemann解的有限体积Eulerian方法，多介质界面处理采用新的水平集和Ghost方法计算. 给出了若干数值算例，包括激波管问题以及金属和气体的运动界面及其大变形问题，并分别与精确解和相容显式有限元拉氏方法的计算结果进行了对比. 数值结果表明，该方法计算结果正确，精度较高，能够准确捕捉物质界面，适用于处理大变形问题. |
| [28] | . In this paper, a compressive high-resolution interface-capturing scheme is presented for the computation of compressible multi-fluid flows with high-density ratios and strong shocks. The proposed scheme is coupled with a preconditioned dual-time compressible mixture solver for robust and accurate computations over a wide range of Mach numbers. The scheme is simple and relatively easy to implement. It does not require any calculations for the interface curvature and the normal vector. The numerical approximations were implemented on general, structured grids using an implicit MUSCL upwind approach. Validation tests were conducted for a single reversible vortex, advection of an air-water interface, dam-break flow, and air shock-helium bubble interaction. Finally, a three-dimensional gas-lift flow is presented to demonstrate the capability of the present scheme for handling an interface with large jumps in pressure, temperature, and density. |
| [29] | |
| [30] | . |
| [31] | . Several methods have been previously used to approximate free boundaries in finite-difference numerical simulations. A simple, but powerful, method is described that is based on the concept of a fractional volume of fluid (VOF). This method is shown to be more flexible and efficient than other methods for treating complicated free boundary configurations. To illustrate the method, a description is given for an incompressible hydrodynamics code, SOLA-VOF, that uses the VOF technique to track free fluid surfaces. |
| [32] | |
| [33] | . The algorithm proposed in this paper can be used to deal with interface of mixed cell (including free surface cell) in remapping step of twostep 2-d and 3-d multi-component Eulerian hydrodynamics numerical methods. In a mixed cell the interface is regarded as a straight line in 2-d problems or plane in 3-d problems. The whole method is composed of three steps: (1) Using area fractions of eight cells in 2-d problems or volume fractions of twenty six cells in 3-d problems surrounding the mixed cell to determine the normal orientation of the interface. (2) Determining the equation (position) of the interface with the area fraction (2-d) or volume fraction (3-d) of the mixed cell. (3) Calculating the flux passing across the boundary of cell, and area fraction (2-d) or volume fraction (3-d) of cell at next time. In the last part of this paper, some 2-d and 3-d results of calculation in comparison with results of MEPH (simplified SLIC) are presented. |
| [34] | . An improved numerical algorithm for front tracking method is developed to simulate the rising of a bubble in quiescent viscous liquid due to buoyancy. In the new numerical algorithm, volume correction is introduced to conserve the bubble volume while tracking the bubble’s rising and deforming, and volume flux conservation based SIMPLE algorithm is adopted to solve the Navier–Stokes equation for fluid flow using finite volume method. The new front tracking algorithm is validated systematically by simulating single bubble rising and deforming in quiescent viscous liquid under different flow regimes. The simulation results are compared with the experimental measurement in terms of terminal bubble shape and velocity. The simulation results demonstrate that the new algorithm is robust in the flow regimes with larger ranges of Reynolds number ( Re < 200), Bond number ( Bo < 200), density ratio ( ρ l/ ρ b < 1000) and viscosity ratio ( μ l/ μ b < 500). The new front tracking algorithm is also applied to investigate bubble rising and deforming behaviour in the various flow regimes of “air bubble/water solution” system under effects of Reynolds number, Bond number, density ratio, viscosity ratio as well as the bubble initial shape, which have been explored previously by experiments. The predicted bubble shape and terminal velocity agree well with the experimental results. Hence, the new modelling algorithm expands the conventional front tracking method to more realistic and wider applications. |
| [35] | . A new method for modeling surface tension effects on fluid motion has been developed. Interfaces between fluids of different properties, or “colors,” are represented as transition regions of finite thickness, across which the color variable varies continuously. At each point in the transition region, a force density is defined which is proportional to the curvature of the surface of constant color at that point. It is normalized so that the conventional description of surface tension on an interface is recovered when the ratio of local transition region thickness to local radius of curvature approaches zero. The continuum method eliminates the need for interface reconstruction, simplifies the calculation of surface tension, enables accurate modeling of two- and three-dimensional fluid flows driven by surface forces, and does not impose any modeling restrictions on the number, complexity, or dynamic evolution of fluid interfaces having surface tension. Computational results for two-dimensional flows are given to illustrate the properties of the method. |
| [36] | . 61Dam break on dry bed experiment series for 2 filling heights is discussed in detail.61Flow kinematics is analyzed and compared with the literature.61Statistical analysis of pressure loads, rise–decay times and impulses is provided.61Pressure vs. dam-break filling height does not follow a linear trend.61Measurements conducted with off-centered pressure sensor to assess 3D dynamics. |
