STUDY ON LOW-SPEED WATER ENTRY OF SUPER-HYDROPHOBIC SMALL SPHERES1)
HuangChao, WenXi, LiuMoubin中图分类号:TB126,U661.1
文献标识码:A
版权声明:2019力学学报期刊社力学学报期刊社 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (14485KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
物体跨越气-液界面进入液体中的现象广泛存在于工程领域和自然界中.在工程领域,军事应用的需求推动着物体入水研究的发展,例如对空投鱼雷入水[1]、弹丸入水[2]、航行体水下发射[3]、船舶入水砰击、跨介质飞行器入水[4]等的研究.而在自然界中,鲣鸟高速冲入水中捕鱼、水黾的水上跳\跃[5]、蛇怪蜥蜴在水上奔跑[6]等奇特现象的研究则大大推进了仿生学的发展.可见入水问题的研究与应用领域十分广阔.
物体在跨越自由液面入水的过程中,除了与流体发生相互作用之外,还存在与空气的耦合作用.在一定的条件下,物体入水时会向水中卷入空气形成空泡,空泡的运动还可能形成指向物体的射流,这些都会对物体的受力及其运动过程产生影响[7- 12].Worthington和Cole[13-14]首次采用闪光照相法获得了小球入水的空腔形态,并发现了物体的表面性质(粗糙度)和入水速度会对是否形成空泡产生影响.此后****们不断对此问题进行了更多探究,Bell[15]进一步确认了物体表面性质对入水空泡的影响,并发现液体的表面张力越强,空泡现象越显著.二战前后,受军事应用需求的驱动,May[16-17]研究了小球表面不同的涂层(油脂、树脂、硅胶等)对空泡形成的影响,发现表面有涂层的小球相比表面光滑没有涂层的小球,可以更低的入水速度形成空泡,并且空泡的动力学行为满足弗劳德数Fr}相似,即空泡的运动主要是由惯性力和重力主导.Birkhoff和Zarantonello[18]发现在不同的弗劳德数Fr}范围内,空腔表现出不同的闭合行为,在$20<Fr<70$范围内,空腔闭合的位置在其长度的中部,称之为深闭合空泡,而当$Fr>150$时,空腔的闭合的位置发生在自由面附近,称之为表面闭合空泡.Lee等[19]和Yan等[20]则分别研究了高弗劳德数Fr}和低弗劳德数Fr}下的小球入水空泡的动力学行为.
在工程应用驱动的背景下,上述研究中采用的小球的特征尺寸和特征速度较大,相应的雷诺数Re}和韦伯数We}均较高,因此在分析中往往是惯性力主导流动,黏性力和表面张力的影响通常忽略不计.
进入二十一世纪以来,得益于表面科学和高速摄影技术的迅速发展,入水问题受到了人们的广泛关注.Duez等[21]发现通过给球体表面镀上一层纳米涂层,改变其浸润特性使其表面具有疏水性后(疏水性可以用固体表面的浸润性能来表征,与表面的化学成分和微观结构有关,主要特征量为接触角),球体在入水过程中变得更容易产生空泡,并给出了空泡产生极限速度与毛细数Ca}的关系.该项研究具有非常重要的意义,即物体的入水行为会受到微尺度结构与宏观尺度流动耦合作用的影响,这是一个多尺度流固耦合问题,引起了人们极大地兴趣.在此基础上,人们对小球入水空泡问题开展了更为细致的研究,如液膜的运动行为[22- 23]、空泡对小球阻力的影响[24 -25]、接触线钉扎的性质[26]、液滴的铺展振\荡[27]等.
在空泡研究方面,Duclaux等[28]研究了疏水小球入水空泡的坍塌行为,并建立了描述空泡运动的理论模型.Aristoff等[29 -31]扩展了Duclaux等的空泡模型,主要考虑了表面张力的影响,并结合实验给出了疏水小球在小邦德数Bo}下4种闭合类型的空泡.叶阳辉等[32]模拟了小韦伯数We}下疏水小球入水空腔的准静态和深闭合现象.孙钊等[33]数值模拟了不同表面接触角小球的入水,获得了无空泡、深闭空泡合、表面闭合空泡和类表面闭合空泡,并给出了空泡形态临界速度与球体表面接触角的关系.此外,Lee和Kim[34]通过实验观测到在小韦伯数We}和小邦德数Bo}条件下,轻质小球撞击自由液面后存在下沉、反弹和漂浮振荡等不同的运动行为.
上述研究表明,对于韦伯数We}和邦德数Bo}较小的入水问题,表面张力的影响变得越发显著,入水空泡的类型和小球的运动形式将变得多样化和复杂化.
本文在Aristoff等[29]工作的基础上,采用高速摄影方法在实验室水箱中开展超疏水小球低速入水实验,通过进一步拓展实验参数空间,研究了$10^{-3}<Bo<10^{2}$范围内小球的低速入水空泡行为,并结合理论分析总结了不同类型空泡的特性,以期为微小颗粒物沉降、工业涂装等相关问题的研究提供参考.
1 实验研究
1.1 实验方法
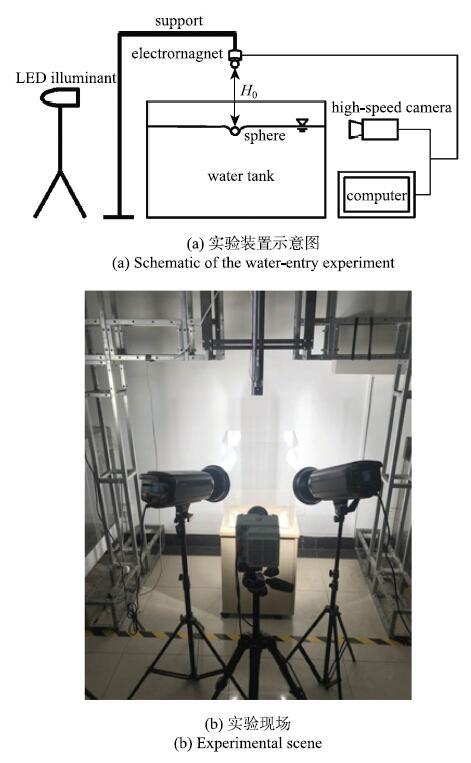
小球入水实验在实验室水箱中进行,实验装置如图1所示,包括：水箱、支架、电磁铁、光源、高速相机和计算机等.水箱采用有机玻璃加工而成,深0.5 m,长0.4 m,宽0.3 m.小球通过控制固定在支架上的直流电磁铁断电后释放,自由落入水箱中,通过释放高度$H_{0}$可以粗略估算小球的初始入水速度$U_{0}\approx $ (2gH}$_{0})^{1 /2}$,$g$为重力加速度,实验中小球的初始入水速度$U_{0}$为0.2$\sim$10 m/s. 采用Phantom VEO 41高速摄像机拍摄小球的入水过程,并校验入水速度,综合考虑小球的运动速度和范围,将拍摄参数设定为：图像分辨率800px $\times $ 1280 px,拍摄速率3000 fps.实验采用两组LED光源提供照明,通过调整角度使高速相机视场内的亮度均匀一致.实验流体采用过滤后的自来水,水温12${^\circ}$C,室温24${^\circ}$C$\sim$26${^\circ}$C,空气湿度40%.
超疏水小球采用涂层工艺制作,小球基材为低碳钢,涂层材料采用溶胶凝胶法制备的纳米二氧化硅涂层,每个小球均匀涂装3层超疏水涂层,小球的半径$R_{0}$为0.175$\sim $10 mm.采用静滴法[35]测量得到小球的前进接触角$\theta$}$_{a}$为150$^\circ$$\pm $5$^\circ$.
显示原图|下载原图ZIP|生成PPT图1实验装置...
-->Fig. 1Experimental facility
-->
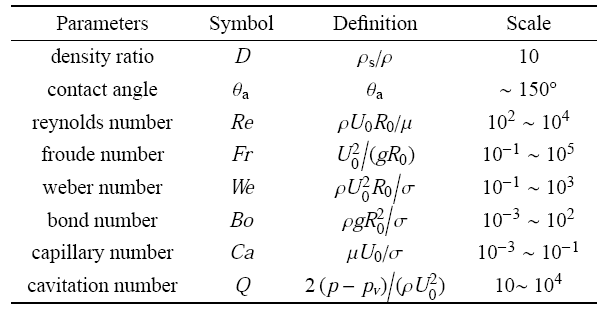
对于小球低速垂直入水问题,存在一些影响入水物理过程的关键参数.与小球相关的参数有小球的半径$R_{0}$、密度$\rho $}$_{s}$、接触角$\theta $}$_{a}$;与撞水过程有关的参数为入水初速度$U_{0}$;与流体相关的参数有水的密度$\rho$}、动力黏性系数$\mu $}、表面张力系数$\sigma $}.将这些参数转化为无量纲形式,选取实验的参数区间如表1所示.另外,对于高速入水冲击问题,当空化数$Q<1$时,可能形成空化现象,而对于本文研究的低速入水问题,空化数$Q\gg 1$,因此不需要考虑空化效应.
Table 1
表1
表1实验参数区间
Table 1Experimental parameters and scope
 |
新窗口打开
1.2 实验结果
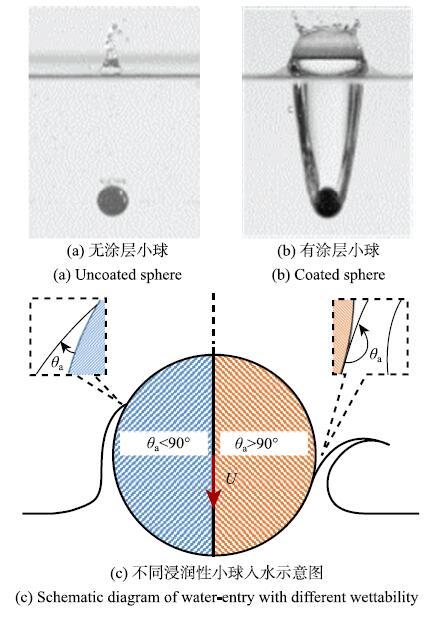
首先针对有涂层超疏水小球和无涂层光滑小球的入水现象进行对比实验,验证疏水性对小球入水空泡行为的影响.图2(a)和图2(b)给出了材质、尺寸、入水初速度均相同的无涂层小球和有涂层小球,撞击水面后6.67ms时刻的图像($R_{0}$ = 3 mm,$U_{0}$ = 4.48 m/s,We} =824.8,Bo} = 1.21).可以看到,无涂层光滑小球入水后没有明显的空泡现象,而有涂层小球入水后在其后方形成了一个形状规则的轴对称空腔.超疏水涂层主要影响的是小球表面液体的接触角和接触线的移动行为,在小球撞击水面的过程中,气液两相界面与固体表面接触后形成接触线,由于小球与其周围液体之间的速度差,接触线相对小球以较高的速度运动,其运动将直接影响小球入水后的流动现象.如图2(c)所示,对于无涂层光滑小球,其表面具有亲水性质($\theta$}$_{a}<90^\circ$),液膜跟随着接触线,沿小球的表面一直向上运动,直到在小球的顶点汇合,然后脱离小球,使其完全浸没;而对于有涂层小球,其表面具有疏水性质($\theta$}$_{a}>90^\circ$),液膜一开始也会沿着小球的表面向上运动,但很快接触线减速并钉扎在小球表面,使液膜与小球形成流动分离,导致小球尾部形成空腔.Duez等[21]认为这种润湿效应与接触线的稳定性有关,当接触线的运动超过极限速度后会失去稳定,并发生流动分离,形成飞溅现象.Ding等[26]进一步通过数值模拟结果解释了接触线弯月面附近的旋涡是导致接触线钉扎和流动分离的原因.在上述实验的基础上,针对有涂层超疏水小球在10$^{ -1}<We<10^{3}$,10$^{-3}<Bo<10^{2}$参数范围内开展入水实验.通过实验我们观察到了5种小球入水及空泡动力学行为,分别是：小球漂浮振荡、准静态空泡、浅闭合空泡、深闭合空泡和表面闭合空泡.其中,第1种运动状态下未形成空泡,小球停留在自由面上做阻尼振荡,而后4种运动状态下小球均完全沉入水中,形成与Aristoff等[29]对疏水小球垂直入水研究相似的4种空泡闭合类型,下面逐一进行介绍.
显示原图|下载原图ZIP|生成PPT图2疏水涂层对入水空泡的影响...
-->Fig.2The influence of surface coating on a water-entry cavity
-->
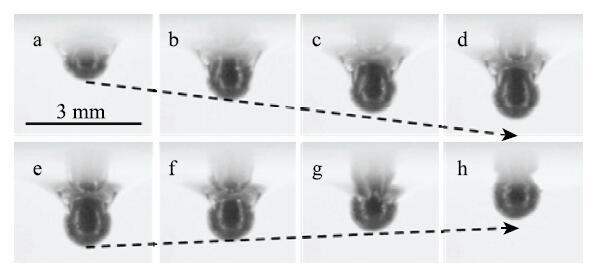
图3给出了典型的超疏水小球漂浮振荡运动状态,各幅图像的时间间隔$\Deltat$ = 2.67 ms,整个过程大约经历0.02 s.从图中可以看到,小球撞击水面后被自由面捕获,并形成弯月面,小球先做减速下沉运动,速度减小到零后反向加速上浮,如此反复做振荡运动,并且振荡的幅度很快衰减,最终小球会停留在自由面的弯月面上.在整个运动过程中,接触线在小球的经向反复上下移动,但接触角基本保持不变,小球上方的空腔不会闭合,因此也就不会形成空泡.这是由于小球受到表面张力的作用较大,惯性力和重力不足以使小球完全沉入水中.因此,这种空泡行为只在韦伯数We}较小($<1$)和邦德数Bo}很小($\ll1$)的时候才会出现,这时表面张力占主导地位,在这种情况下才会出现小球撞击水面后被自由面捕获的现象,我们将这种入水行为称为漂浮振荡(floatingoscillation).
显示原图|下载原图ZIP|生成PPT图3小球漂浮振荡($\Delta t$ = 2.67ms,$R_{0}$ = 0.6 mm,$U_{0}$ =0.28 m/s,\ We} = 0.64,Bo} = 0.05)...
-->Fig.3Floating oscillation of sphere ($\Delta t$ = 2.67ms,$R_{0}$ = 0.6 mm,\ $U_{0}$ = 0.28m/s,We} = 0.64,Bo} = 0.05)
-->
图4(a)给出了韦伯数We}增大到$O(1)$时,超疏水小球的入水运动过程,各幅图像的时间间隔$\Deltat$为2 ms,小球大约经历0.01s后完全沉入水中,在下沉过程中小球几乎保持匀速,这主要是由于小球撞击水面的惯性力与弯月面产生的表面张力相当,小球处于接近平衡的运动状态.从图中可以看到,小球撞击水面后的初始运动与漂浮振荡状态的运动相似,但接触线会一直沿着小球的经线方向向上移动,直到在小球的顶端附近融合,使小球完全沉入水中,小球边缘均匀的一圈光晕表明,小球表面存在一层薄薄的气膜(airfilm),因此可以认为水对小球的浸润为Cassie-Baxter状态.对于空腔的这种闭合行为,由于惯性力与表面张力相当,因此,将其称为准静态(quasi-static)[29]空泡.
由于邦德数Bo}仍然很小,准静态空泡闭合的深度与毛细长度$l_{c}$ = ($\sigma $}/$\rho $g})$^{1 / 2} \approx $2.7 mm相当,即重力的影响可以忽略.实验中观察到空泡闭合后,在有些情况下小球是完全浸没于水中,如图4(a)中的$f$,而在有些情况下小球顶端则会夹带一个很小的气泡,如图4(b)中的$c$,这主要取决于接触线的运动特性.如果接触线在空腔闭合时恰好运动到小球的顶端,弯月面在此融合,则小球会完全浸没于水中,不夹带入气泡;如果接触线在空泡闭合之前形成钉扎,弯月面的融合发生在接触线的上方,则会在小球顶端形成一个很小的气泡,在这种情况下小球表面的Cassie-Baxter状态不太明显,水对小球的浸润可能形成的是部分浸润的亚稳态[36].从韦伯数We}的大小来看,韦伯数We}较小(We}$\sim$1)时,小球的入水速度较低,接触线基本不会在空泡闭合之前形成钉扎,形成的是完全浸没状态;而韦伯数We}较大(We}$>$1)时,小球的入水速度相对较高,接触线的相对移动速度也较高,较易在空泡闭合之前形成钉扎,从而在小球顶端形成一个小气泡.
显示原图|下载原图ZIP|生成PPT图4准静态空泡...
-->Fig.4Quasi-static impact cavity
-->
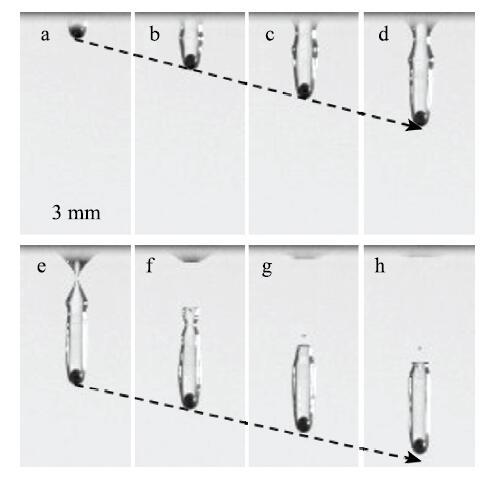
图5给出了韦伯数We}继续增大到$O(10)$以后,超疏水小球的入水运动过程,各幅图像的时间间隔$\Deltat$为2.33 ms.从图中可以看到,小球入水后其后部形成了细长的圆柱形空气腔,接触线钉扎在小球的赤道线附近,形成陡峭的空泡壁面.小球入水约11.5ms后,空腔在较浅的位置发生闭合形成空泡,闭合位置的深度与毛细长度$l_{c}$相当,空泡形成后,小球则带着细长形状的空泡继续向下运动.在空腔闭合之前,小球的运动速度减小较少,而在空腔闭合之后,小球速度的减小变得明显.由于空腔闭合发生在距离自由面较浅的位置,因此将这种行为称为浅闭合(shallowseal)空泡.这种运动状态还有一个特点就是在细长圆柱状的空泡壁面上能够观察到向下传播的毛细波,毛细波是小球撞击初始静止的自由面产生的,其运动速度略低于小球的速度,取决于韦伯数We}[29].
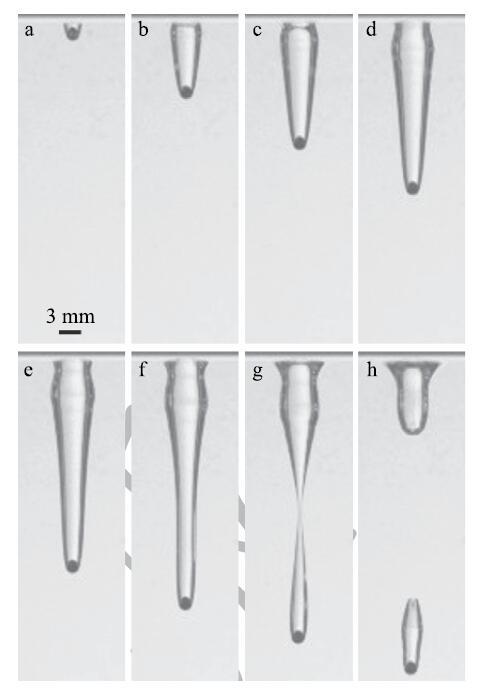
进一步增大韦伯数We},小球入水的空泡闭合行为将会有一些变化,如图6所示,各幅图像的时间间隔$\Deltat$为2.67 ms.从图中可以看到,由于入水初速度的增加,小球入水后空气腔被拉得更长,空腔的壁面更加光滑,空腔在约小球入水深度的1/2处发生闭合,形成空泡,空腔闭合后会形成方向相反的射流(worthington jet).由于空腔闭合发生的位置较\深,因此将这种闭合行为称为深闭合(deep seal)空泡[18,29,32-33].
显示原图|下载原图ZIP|生成PPT图5浅闭合空泡($\Delta t$ = 2.33ms,$R_{0}$ = 0.9 mm,$U_{0}$ = 1.58m/s,\ We} = 31,Bo} = 0.11)...
-->Fig.5Shallow seal impact cavity ($\Delta t$ = 2.33ms,$R_{0}$ = 0.9mm,\ $U_{0}$ = 1.58 m/s,We} = 31,Bo} = 0.11)
-->
显示原图|下载原图ZIP|生成PPT图6深闭合空泡($\Delta t$ = 2.67ms,$R_{0}$ = 0.9 mm,$U_{0}$ = 3.17m/s,\ We} = 124,Bo} = 0.11)...
-->Fig.6Deep seal impact cavity ($\Delta t$ = 2.67 ms,$R_{0}$= 0.9mm,\ $U_{0}$ = 3.17 m/s,We} = 124,Bo} = 0.11)
-->
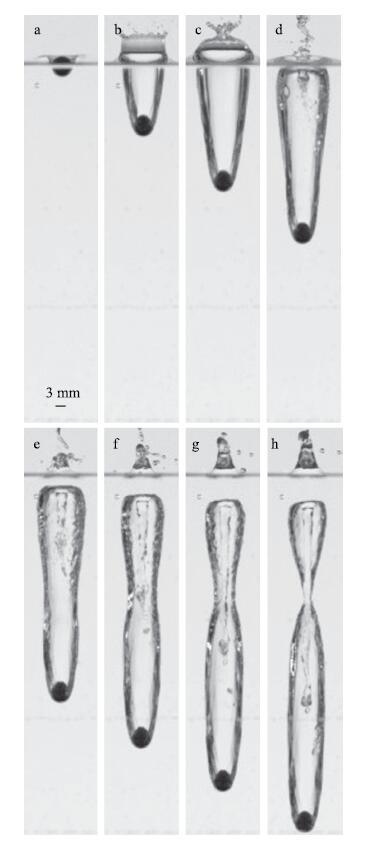
当韦伯数We}增大到$O(10^{3})$时,小球入水的空腔闭合发生在水面之上,形成表面闭合(surfaceseal)空泡[18,29,33],如图7所示,图中各幅图像的时间间隔$\Deltat$为4.0 ms.这种闭合行为主要是由小球撞击引起自由面飞溅的水幕在气动压力和表面张力的作用下向内收拢融合导致,由于水幕的融合发生在自由面,因此称为表面闭合.当水幕融合之后,由于小球\继续向下运动,空泡的体积增大,空泡内气体的压力相应减小,使得空泡的上端被水面向下推开,并形成指向小球运动的射流.
显示原图|下载原图ZIP|生成PPT图7表面闭合空泡($\Delta t$ = 4.0ms,$R_{0}$ = 3 mm,$U_{0}$ = 4.48m/s,\ We} = 825,Bo} = 1.21)...
-->Fig.7Surface seal impact cavity($\Delta t$ = 4.0 ms,$R_{0}$= 3mm,\ $U_{0}$ = 4.48 m/s,We} = 825,Bo} = 1.21)
-->
2 理论分析
通过改变小球入水的实验参数,我们得到了超疏水小球入水及空泡的动力学行为与韦伯数We}和邦德数Bo}的关系谱图,如图8所示.可以看到,小球入水及空泡主要存在5种现象,随着韦伯数We}的增加,沿纵轴从下至上依次为：漂浮振荡($\square$符号)、准静态闭合($\blacktriangle$符号)、浅闭合({\psfig{figure=1-1.eps}}符号)、深闭合($\bullet$符号)和表面闭合($\blacklozenge$符号).图8中的黑色实线为准静态与浅闭合的分界线,黑色点划线为浅闭合与深闭合的分界线,黑色虚线为深闭合与表面闭合的分界线.这三条分界线是根据文献[29]中的空泡理论模型计算得到,可以看到理论预测的结果与实验结果符合较好.其中,浅闭合空泡与深闭合空泡的分界线在$Bo\simO(1)$附近有一定差异,这主要与理论模型的简化假设以及两种空泡闭合行为的区分准则有\关[29].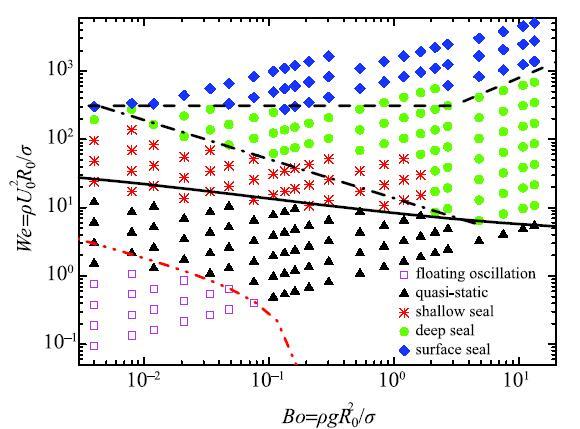
显示原图|下载原图ZIP|生成PPT图8超疏水小球入水冲击与空泡行为与韦伯数We}和邦德数Bo}的关系图解($\theta$}$_{a}$ = 150$^\circ$)...
-->Fig.8Relation schema of super-hydrophobic spheres waterentry impact and cavity behaviors between We} number andBo}\ number ($\theta $}$_{a}$ = 150$^\circ$)
-->
在实验的参数区间中,当韦伯数We}和邦德数$Bo$均很小(We}$<O(1)$,Bo} $<O(10^{ -1}))$时,由于惯性力、重力均小于表面张力,小球撞击水面受阻,停留在弯月面附近漂浮振荡,不会形成空腔,也没有空泡产生;当韦伯数We}增大($O(1)<We<O(10)$),小球撞击水面的惯性力与弯月面产生的表面张力同量级,小球处于接近平衡的运动状态,形成类似"准静态"的匀速向下运动;当韦伯数We}进一步增大后(We}$>O(10)$),惯性力占主导地位,小球以较高的速度入水后,接触线钉扎在小球赤道线附近,从而在小球后方形成一个轴对称空腔,空腔在不同的条件下可能形成浅闭合、深闭合和表面闭合现象.针对这3种现象,可以从动力学的角度进行区分,若只考虑径向运动,空腔形成后的运动可简化为的Rayleigh-Basant问题.对于浅闭合现象,发生在韦伯数We}较小的区间,对应的小球入水速度低,空腔较浅,因此空腔周围流场中压力的影响都很小,主要考虑空腔的径向膨胀和收缩,从时间关系上看,空腔的闭合应该发生在其最初形成的位置(即水面),但实际上由于弯月面的影响,最终闭合发生在毛细长度$I_{c}$深度附近;对于深闭合现象,发生在韦伯数We}较高的区间,这是由于小球入水速度增大,空腔较深,静水压力的影响使得深闭合先于浅闭合发生,根据Duclaux等[28]的理论分析,深闭合大约发生在小球入水深度的1/2处,深闭合的位置与小球的入水速度呈线性关系,实验结果与之基本一致;对于表面闭合现象,发生在韦伯数We}更高的区间,由于小球入水速度较高,小球撞击引起自由面形成明显的飞溅水幕,因此需要考虑水面之上发生的运动,飞溅的水幕在气动压力和表面张力的作用下向内收拢融合,从而在水面最先形成表面闭合.
从邦德数Bo}的影响来看,在邦德数Bo} $<O(10^{ -1})$范围内,小球入水及空泡的动力学行为随着韦伯数We}的增加,依次经历漂浮振荡、准静态闭合、浅闭合、深闭合和表面闭合5种状态;在邦德数$O(10^{-1})<Bo<O(1)$范围内,漂浮振荡状态不再发生,这主要是由于小球受到重力的影响增大,表面张力不足以将小球支撑在水面上;而当邦德数$Bo>O(1)$后,浅闭合状态也不再发生,此时毛细波的速度相对较慢,对空泡的闭合影响很小.
图8中双点划线为小球漂浮振荡与准静态空泡的分界线,下面针对这条分界线进行理论分析.根据实验结果,在邦德数Bo} $<O(10^{ -1})$和韦伯数We} $<$\$O(1)$范围内,小球入水后将被自由面捕获,进入漂浮振荡状态,而超出这个范围小球将下沉,形成准静态空泡状态.要确定漂浮振荡与准静态下沉之间的分界线,就需要对小球入水运动的受力进行分析.
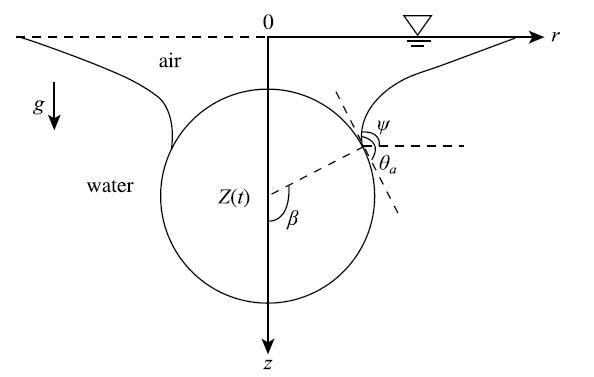
考虑小球入水后以速度$Z'$向下运动,$Z$为小球中心距离初始自由面的位置,如图9所示.小球入水的过程中,受到惯性、重力、流体阻力、表面张力等的作用,运动方程可以写为
\begin{equation}\label{eq1} \left( {m + m_{a} } \right){Z}" = mg-F_{d}- F_{b}-F_{s} \tag{1}\end{equation}
式中,$m$和$m_{a}$分别为小球的质量和附加质量,$g$为重力加速度,$F_{d}$为小球受到的阻力,包括黏性阻力$F_{vd}$和形状阻力$F_{fd}$,$F_{b}$为小球受到的浮力,$F_{s}$为小球受到的表面张力.
显示原图|下载原图ZIP|生成PPT图9超疏水小球跨越气-液界面示意图($We<O(1)$)...
-->Fig.9Schematic diagram of super-hydrophobic spherestraddling thegas-liquid interface (We} $<O(1)$)
-->
在Bo} $<O(10^{-1})$,Re} $ \ggO(1)$的条件下,小球受到的附加惯性力、黏性阻力和形状阻力均是小量,可以忽略,而在$Z\simR_{0}$范围内,小球受到的浮力$F_{b}$同样也远小于表面张力$F_{s}$,这样式(1)可简化为
\begin{equation}\label{eq2} \frac{4}{3}\pi R_0^3 \rho_ {s} {Z}" =\frac{4}{3}\pi R_0^3 \rho _{s} {g}-2\pi R_0 \sigma\sin \beta \sin \psi \tag{2}\end{equation}
式中,$\rho $}$_{s}$为小球的密度;$R_{0}$为小球的半径;$\sigma$}为流体表面张力系数;$\beta$}为接触线位置与$z$轴之间的夹角;$\psi $} =$\theta $}$_{a}$ + $\beta -\pi $}.
式(2)表明,在邦德数Bo} $<O(10^{-1})$和韦伯数 We$<O(1)$范围内,表面张力主导着超疏水小球的入水运动行为,小球在入水过程中的减速主要是由表面张力引起.方程(2)的求解需要通过实验得到$\beta$}随时间变化的函数$\beta =\beta$($t)^{[37],对于尺寸很小的小球,要想精确的测量这个数据存在很大难度,因此,这里通过相似律[34]和力的平衡分析来确定小球撞击自由面后是漂浮振荡状态,还是准静态下沉状态的物理准则.
考虑小球的惯性力($\sim$$ \rho $$_{s}R^{3}Z")$与表面张力($\sim $$\sigma $R})、重力($\sim$$\rho $}$_{s}R^{3}g)$的平衡,可以得到小球入水过程中加速度的量级$Z"\sim\sigma $/$\rho $}$_{s}R^{2}g$.这里考虑重力的原因是小球的密度比$D$ = $\rho $}$_{s}$/$\rho$}较大,在邦德数Bo}相对不太小的时候,重力仍会对小球的运动产生影响.小球运动的特征时间可以通过毛细长度和小球的运动速度得到,$t_{c}$ = ($\sigma $}/$\rho $gU}$_{0}^{2})^{1 /2}$,即毛细波通过毛细长度的时间$t_{c}\sim $We}$^{-1/ 2}$. 由前面的实验分析可知小球准静态下沉的特征速度$U_{s}$与小球入水初始速度满足线性关系,即$U_{s}\simU_{0}$,而小球漂浮振荡的特征速度$U_{f}$与减加速度$Z"$有关,即$U_{f}\sim Z"t_{c}$.考虑小球入水后准静态下沉和漂浮振荡的极限状态,速度减小到零时,二者应满足平衡关系,可以得到如下表达式
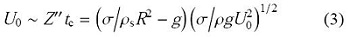
将上式化简,并引入表1中定义的无量纲参数后得到
\begin{equation}\label{eq4} We\sim D^{-1}Bo^{-\frac{1}{2}}-Bo^{\frac{1}{2}}\tag{4}\end{equation}
上式给出了小球撞击自由面后漂浮振荡/下沉形成空泡的临界关系,但其分界线的初值还未知,这可以通过实验来确定.通过实验观察,我们发现小球入水后进入漂浮振荡状态的最小邦德数$Bo\approx0.162$,同时,考虑小球运动方程(2)式中惯性力、表面张力和重力项的系数关系,最终确定漂浮振荡与准静态之间的临界关系为
\begin{equation}\label{eq5} We = \frac{3}{2}D^{-1}Bo^{-\frac{1}{2}} -Bo^{\frac{1}{2}} \tag{5}\end{equation}
方程(5)即为图8中的双点划线,可以看到小球入水漂浮振荡状态与准静态的分界线与相似律符合较好,在曲线的下方,小球入水后被自由面捕获,进入漂浮振荡状态,而在曲线上方,小球入水后将下沉,形成准静态空泡、浅闭合空泡、深闭合空泡和表面闭合空泡等状态.
3 结论
本文采用实验方法研究了超疏水小球(半径0.175$\sim $10mm)的低速入水及空泡动力学行为,获得了小球及空泡的5种运动状态,重点分析了这些运动行为与韦伯数We}和邦德数Bo}之间的关系,并通过理论分析推导了小球漂浮振荡与下沉的无量纲关系,得到以下结论.(1)超疏水小球入水后会出现：小球漂浮振荡、准静态空泡、浅闭合空泡、深闭合空泡和表面闭合空泡5种类型的动力学行为.
(2)超疏水小球的入水及空泡动力学行为主要与韦伯数We}有关.在邦德数Bo} $<O(10^{ -1})$范围内,随着韦伯数We}的增加,小球入水及空泡的动力学行为依次经历漂浮振荡、准静态闭合、浅闭合、深闭合和表面闭合.在邦德数$O$(10$^{-1})$ $<$ Bo}$<O(1)$范围内,漂浮振荡现象不再发生.当邦德数$Bo>O(1)$后,浅闭合现象也不再发生.
(3)小球漂浮振荡与下沉现象的临界关系可以用相似律关系描述.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . . |
| [2] | . . |
| [3] | . . |
| [4] | . . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | |
| [11] | . |
| [12] | . . |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . . |
| [24] | . |
| [25] | . |
| [26] | . |
| [27] | . . |
| [28] | . |
| [29] | . |
| [30] | |
| [31] | . |
| [32] | . |
| [33] | . . |
| [34] | . |
| [35] | . |
| [36] | . . |
| [37] | . |
