TRAJECTORY SIMULATION OF SELF-PROPELLED ELASTIC RODS IN FLUID1)
WangJun中图分类号:O351.2
文献标识码:A
版权声明:2019力学学报期刊社力学学报期刊社 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (28513KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
利用生物运动的力学、变形学等机理研究游动或飞行生物与环境流体的耦合运动,对于仿生共融机器人的发展有着重大意义. 在设计仿生机器人之前,将生物体简化为力学模型,并选取快速准确的数值算法进行运动模拟,根据虚拟的可视化模拟结果,可以为机器人各类参数的选取及优化提供参考,降低真实实 验失败的可能性,也降低实验成本,为真实的模拟提供可行的方向. 本文的仿真分析系统针对有自主驱动的弹性绳在流体中运动轨迹进行数值模拟,可以为水中细长形软体机器人的研发提供理论基础. 这类机器人具有体积小,活动灵活,可以通过狭长地段的特点,对于海洋探索与搜救意义重大.
水下软体机器人游动模式大多基于鱼类游动的理论模型,鱼类游动的激励模式主要分为躯干激励(带鱼、鳝鱼)、翼鳍激励、喷射激励(章鱼)[1 - 2],其中躯干激励又分为摆动激励与波动激励,现在大多水下细长的软体机器人都以波动形式驱动. 针对细长游动体,Lighthill [3]最早提出了大摆幅细长条理论,推导出鱼类游动中推力和游动效率的计算公式,该理论广泛应用于鳗鲡科鱼类推进模式,并进行响应游动分析. 基于这个理论, Weihs [4]建立了鳗状游动细长体力学模型,进一步,Wu等[5 - 6] 依次提出了二维波动板理论与三维波动板理论. 后续建立的模型也都是对基于细长条理论进行改进和优化. 然而,由于大变形体流固耦合问题理论分析工具有限,对模型的分析常常采用数值方法,通过所得到的数值计算结果,对设计的构型进行虚拟仿真. 于是,采用何种数值计算方法就变得十分重要了.
针对鳗鲡形游动,传统数值计算方法共有两种：(1)给定固体部分的波动形态与游动速度,模拟固体周围流场变化[7];(2)给定游动生物的波动形态,同时求解固体的前进速度与流场变化[8]. 后者是固体和流体双向耦合计算方法,对真实情况的模拟更加精细,特别是对实验样机的设计更具指导价值. 因此,建立完整高效并具有数值稳定性的细长体游动的计算模型,核心问题是提出与实际生命体接近的柔性体的波动形态以及相应的流固耦合算法.
对于鱼体的波动形态,最早是Lighthill [3]通过实验观察与研究获得的,通过后人完善与补充,形成了一套拟合这些躯干激励型鱼类游动曲线的函数模型[9]. 大多的仿鱼机器人模拟都采用此模型. 基于常曲率假设条件下,文献${[10]将细长柔性体离散为有限段刚体,刚体间由扭转弹簧连接,因此细长体可以弯曲不可伸缩. 这种力学模型简单,易于理解,计算速度快,但是也有两种缺陷. 第一,直接以理想波动函数作为固体的运动模型,忽视了在与流体耦合计算过程中肌肉收缩,也就是弹性力的作用. 第二,肌肉收缩除了使鱼体产生弯曲效果外,还有伸缩效果,这种忽略有可能降低对生物游动模拟的相似度. 尝试通过改进这种模型来解决上述的两个缺陷是本文研究的主要动机. 本文的研究目标也是模拟可以自主波动的细长柔性体游动,提出用可离散的弹性绳模型代替离散刚体模型,这是因为弹性绳在水中既可以由于生物主动力进行波动运动,也可由于弹性内力与外力发生伸缩与弯曲运动.
弹性绳与流体相互作用涉及到流固耦合的计算问题,其算法繁杂,根据具体问题进行假设与简化,也发展出了许多新的算法,但总的来说有三类. 第一类是所谓的边界配合法,边界网格会随固体运动更新改变,因此需要对界面进行特殊处理,并通过有效的算法完成流固耦合界面流体与固体上力学量的传递,典型的方法是任意拉格朗日方法[11], 这类方法的主要优点是处理流固耦合界面附近计算时,计算精度高,但是需要不断对网格进行更新,耗费大量空间,计算效率较低. 第二类是非边界配合法,这类方法不必时时更新网格的形状,在处理界面有大变形或者扭曲问题方面,具有很大的优越性,然而, 流固边界上的值则需要通过流体网格与固体网格差值得到,界面处计算精度不如边界配合法. 典型的非边界配合法有浸入边界法 [12]. 第三类为粒子方法,其中主要有SPH法[13]. 由于我们研究的问题是柔性体的大变形问题,具体来说,弹性绳在封闭正方形流场中的自主泳动运动,故采用浸入边界法,将流场数据储存在欧拉网格上,弹性绳数据储存在在拉格朗日网格上,如图1所示. 同时基于动量守恒方程,提出通过修正流体速度场的方法简化耦合作用的计算方法(immersed-boundary method for momentum equations),尝试通过这种简洁的方法实现对弹性绳体自主泳动的实时快速轨迹计算和模拟.
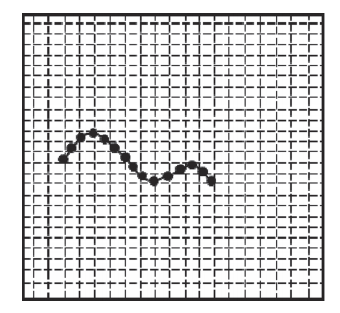显示原图|下载原图ZIP|生成PPT图1流场与弹性绳的离散形式...
-->Fig. 1Discretization scheme of fluid and rods
-->
由于数值计算的最终目的是为实验提供理论依据,因此已有的关于柔性细长体的泳动实验结果也可以为数值算法的可信度提供参考依据. Jia等[14]将有主动驱动的细绳放置于肥皂液中,观察不同细绳长度与密度以及不同驱动频率与幅度对细绳的动力学响应的影响. 接着,Jia等[15-16]又从理论上与实验上研究了两根有主动驱动的细绳同时浸入肥皂液中运动时,考虑两根细绳的耦合作用,各个物理参数对于动力学响应的影响. 卢振利等[17]进行了多关节机器蛇在水中蜿蜒运动的实验,测试了各个控制参数对运动速率和方向的影响. 中国科技大学与南洋理工大学针对摆动激励共同研发了由形状记忆合金(shape memory alloys, SMA)驱动躯干波动形水下软体机器人原型机[18],英国帝国理工大学研究人员又将SMA材料替换为离子交换树脂金属复合材料(ionic polymer--metal composites, IPMC) [19],使机器人运动更为灵活,可以穿越细小狭窄的地带.
本文提出同时考虑拉压与弯曲的弹性绳的力学模型,模拟水中无鳍无腿生命体的泳动,建立该力学模型在水中自主游动与流体相互耦合轨迹的快速计算方法和仿真模拟. 算法考虑生物内力(弹性力)、生物体与外界流体相互耦合作用,通过弹性绳主动变形、流场动力响应、弹性绳运动结果3个步骤,实现了对模拟以正弦波动形式运动的弹性绳在水中的运动轨迹计算和模拟,目的是通过实时快速的数值计算和仿真模拟意在模拟,认识有关的物理参数对于弹性绳泳动轨迹以及稳定性控制的影响规律,为开发应用技术提供理论支撑和参考依据.
1 弹性绳的二维建模
1.1 基于弹性能的模型建立
随着生物仿生研究的兴起,越来越多的水下机器蛇游动模型被提出,有"C"型游动"S"型游动,最广泛采用的是鳗鱼型游动方式,机器蛇通过波浪形的运动与水相互作用,向前运动.这些理论都是基于不可压缩的细长体模型,将固体离散为无数段刚体,刚体间由弹簧或铰链连接,也就是刚体-弹簧结构[20],因此固体可以弯曲不可伸缩.本文考虑肌肉的拉伸效应,以无腿无鳍的一类可伸缩环节水生体的运动为原型,提出同时考虑拉压与弯曲效应的弹性绳模型[21],弹性绳的弯曲与拉伸压缩代表生物体肌肉收缩,储存了生物主动运动产生的生物势能与肌肉被动改变产生的弹性势能,简化模型如图2所示.图2(a)为一段弯曲的弹性绳,弹性绳中储存了拉伸弹性势能与扭转弹性势能,通过选取合适的材料参数,可以将这段弹性绳简化为图2(b)所示模型,模型由$n$段具有集中质量的弹性杆以及$n-1$个连接杆件的扭转弹簧构成,弹性杆与扭转弹簧分别储存弹性绳弯曲状态下的拉压弹性势能与扭转弹性势能,可以作为无腿无鳍的水中生物运动的简化力学模型.为更加简洁地建立图2(b)中所示简化弹性绳模型的动力学方程,我们将力学模型简化表示为图3(a).假定弹性杆质量集中分布于杆件两端,即图中${m}_0 ,{m}_1 ,\cdots,{m}_{n} $,每个集中质量上施加的力包括内力${f}_{{inter}}$与外力${f}_{{exter}}$,外力由流体与弹性绳耦合作用产生,内力由弹性杆拉伸与扭转弹簧的扭转产生,模拟肌肉运动时被动产生的弹性内力.图(b)为变形后模型的几何示意图,$n+1$个集中质量坐标依次为$X_1 ,X_2,\cdots ,X_{n+1} $. 拉压内力正比于弹性杆长度的改变量,${l}_{i}^0$为每一段弹性杆初始长度,${l}_{i} $为每一段弹性杆变形后的长度.扭转内力正比于弹性杆之间转角的改变量,${\varphi }_{i}^0$描述每两段弹性杆间的初始转角,${\varphi }_{i}$为变形后每两段弹性杆之间的转角. 相应的,假设${\alpha}^{i}$是每段弹性杆拉伸弹性系数,${\beta}^{i}$为扭转弹簧的扭转弹性系数.
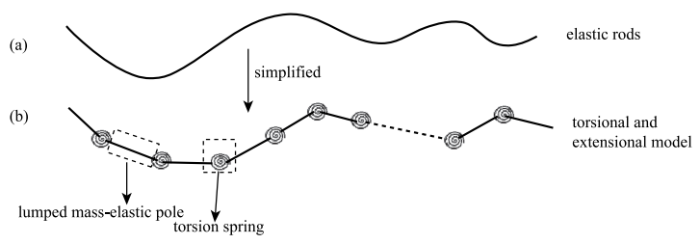显示原图|下载原图ZIP|生成PPT图2(a)弹性绳示意图 和 (b)考虑拉压与扭转的简化模型...
-->Fig.2(a) Elastic rods and (b) extensional and torsional model
-->
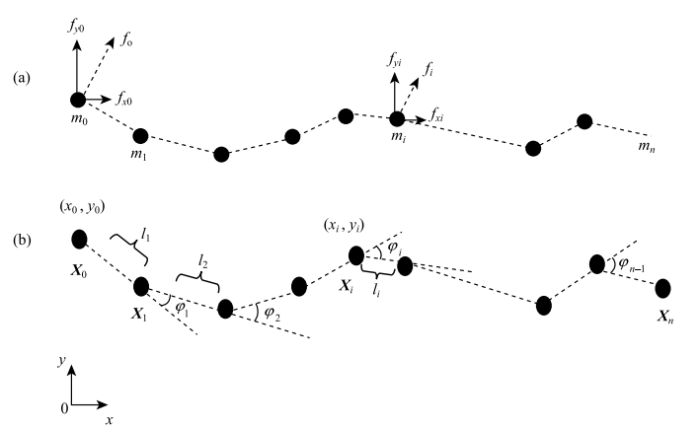显示原图|下载原图ZIP|生成PPT图3(a)简化弹性绳模型受力分析图 和 (b)简化弹性绳模型坐标示意图...
-->Fig.3(a) Force analysis of simplified model and (b) geometry of simplified model
-->
1.2 动力学方程与求解
首先,我们从能量角度计算内力,弹性绳弯曲后图3(a)中储存的弹性能为\begin{equation}\label{eq1} {E}_{p} = \frac{1}{2}\left[\mathop \sum\limits_{{i} = 1}^{n} {\alpha }^{i}({l}_{i}-{l}_{i}^0 )^2 +\mathop \sum \limits_{{i} = 1}^{{n}-1} {\beta }^{i}\left({{\varphi }_{i}-{\varphi }_{i}^0 }\right)^2 \right]\tag{1}\end{equation}
其中, ${E}_{p} $为弹性能,${\alpha}^{i}$为弹性杆等效弹性系数,${\beta}^{i}$为扭转弹簧弹性系数,弹性能对坐标求梯度可以求得弹性内力${ f_{inter}}$为
\begin{equation}\label{eq2} f_{inter}=\nabla E_{p}\tag{2}\end{equation}
且弹性绳的运动符合牛顿第二定律 $${{m a}} = {{m}} {{{X}} }= {{{ f}}_{{{inter}}}} + {{{f}}_{{{exter}}}}\tag3$$其中,${m}$为离散质量, $X({\ddot x_0,{\ddot x_1, \ldots,{\ddot x_n,{\ddot y_0,{\ddot y_1, \cdots ,{\ddot y_n})$为每段离散体加速度, ${f_{{{exter}}}}({f_{x0, \cdots,{f_{xn},{f_{y0, \cdots ,{f_{yn}})$为每段离散体受到的平均外力,最后,采用Leap-Frog法,对弹性绳变形的动力学方程进行求解.
当图2和图3所示的弹性绳体自主变形的内力${f}_{{inter}}$所受到的外力${f}_{{inter}}$已知,则可以通过图4所示的计算求解流程,得到弹性绳自主变形随时间的演化.在本文中,假设弹性绳自主变形运动的波型为
\begin{equation}\label{eq4} {y}_{i} = {A}_{{rod}}\cdot \mbox{sin}\left({{k}_{{rod}} \cdot{x}_{i} + {\omega }_{{rod}}\cdot{t} +{\varphi }_{{rod}} } \right)\tag{4}\end{equation}
其中,$i=0,1,\cdots ,n, {A}_{{rod}}$为波动激励的幅度,${k}_{{rod}} $为波动激励的频率,${\omega}_{{rod}} $为波动激励的角速度,${\varphi }_{{rod}}$为波动激励的相位角. 弹性绳运动模拟的具体流程如图4所示.
显示原图|下载原图ZIP|生成PPT图4弹性绳运动轨迹求解流程...
-->Fig.4Flow chart of solving rods
-->
弹性绳的运动学形态由主动波动模型,弹性力以及外力(流场作用力)共同决定.弹性绳所受到的外力${f}_{{inter}}$来自弹性绳在水中自主泳动时与流体耦合作用的作用力.
2 流固耦合作用算法
2.1 基于动量的浸入边界法
流固耦合问题的本质是在一个给定的区域内,流体与固体之间能量的不断交换.从物理角度来说,是流体与固体在耦合界面上不断发生能量交换,这个界面也就是图5中的${\varGamma}$.从数值模拟的角度来说,这个界面则是固体求解器与流体求解器之间数据交换,这个数据交换的传递程序,就是耦合程序.耦合算法的第一步是区域离散化,根据离散方式的不同有网格法与粒子法,前者发展较为成熟,如有限元法[22],有限差分法,后者近年来也快速发展,光滑粒子动力学.我们利用非边界配合法的基本思想,将流体数据储存在欧拉网格上,而固体数据储存在拉格朗日网格上.常用的浸入边界法[23]是将耦合作用力通过一系列计算简化为网格力,通过更新网格力更新流体与固体.基于该想法,提出了一种简单的速度修正算法,即直接修正网格的速度,使得修正网格速度后,绳的每个节点所在的流体网格区域内流体与该节点隔离体总动量守恒,也就是该区域流体增多(减少)的动量等于该节点隔离体减少(增加)的动量.将满足上述物理关系的网格速度修正,视为近似耦合作用力真实改变的流场速度.然后根据修正的流体速度场,更新流体速度,同时使得流固耦合界面满足特定边界条件,达到更新固体的形状与位置的目的.取出弹性绳上的一个集中质量及其所在的流体网格,分析他们的相互作用以及数据更新方式,如图5中虚线部分所示.
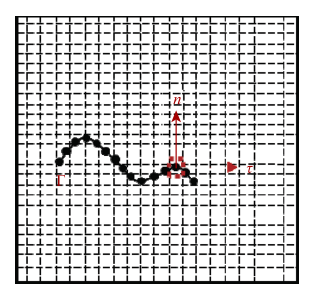显示原图|下载原图ZIP|生成PPT图5流场与弹性绳的耦合界面${\varGamma }$...
-->Fig.5Coupling interface of fluid-rods interaction
-->
===图6中左图为图5中取出的隔离体在耦合作用前速度示意图.假设取出集中质量为第${i}$个,所在流场网格坐标为$\left( {{k,{l}}\right)$.左图中,${{U}}_{ir}$是更新前绳质点速度,可由上一节中弹性绳坐标求得
\begin{equation}\label{eq5} U_{ir}=X_i\tag{5}\end{equation}
流场网格采用MAC格式,将横向速度$ {u}_{{k,{l}}$与纵向速度${v}_{{k,{l}}$分别储存在面心上,因此${{U}}_{if}(u_{if, v_{if})$需插值得到
\begin{equation}\label{eq6} {u}_{{if}} = \mbox{inter}\left( {{u}_{{k,{l}}},{u}_{{k} + 1,{l}}} ,{u}_{{k,{l} + 1} ,{u}_{{k} + 1,{l} + 1} }\right)\tag{6}\end{equation}
\begin{equation}\label{eq7} {v}_{{if}} = \mbox{inter}\left( {{v}_{{k,{l}}},{v}_{{k} + 1,{l}}} ,{v}_{{k,{l} + 1} ,{v}_{{k} + 1,{l} + 1} }\right)\tag{7}\end{equation}
===图6右图为耦合作用后,对流场与绳进行速度修正的方式,${\delta u,\delta v$为流场速度的修正量,${\delta {U}_{ir}}$为弹性绳速度修正量,${{U}_{ir}^*}U_{if}^*$为更新后的绳质点速度与该点流体速度,${\delta }U_{if}^\ast $根据网格速度插值得到.
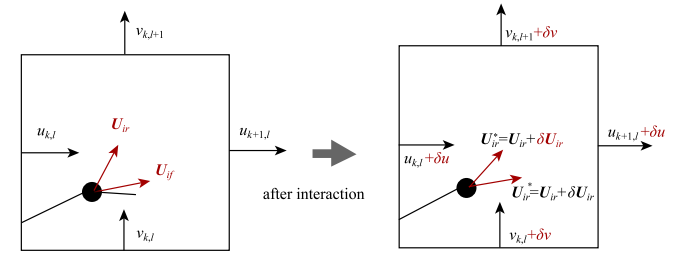显示原图|下载原图ZIP|生成PPT图6速度修正耦合算法示意图...
-->Fig.6Coupling algorithm of velocity correction
-->
更新后的速度场满足绳的每个节点所在的流体网格区域内流体与该节点隔离体总动量守恒的关系,即
\begin{equation}\label{eq8} {\rho }_{f} \int {\delta {U}_{if}{d}S}+\rho\int\deltaU_{ir}{d}I=0\tag{8}\end{equation}
(8)化简后可得
\begin{equation}\label{eq9} \left( {{\delta u,{\delta v}} \right) + {k}_{{inter}} \left( {{n}_1 {\delta u}_{{ir}} ,{n}_2 {\delta v}_{{ir}} }\right) = (0,0)\tag{9}\end{equation}
其中,${k}_{{inter}} $为耦合影响因子, ${\rho }_{f}$为流体密度,${\rho }_{r} $为弹性绳子密度
\begin{equation}\label{eq10} {k}_{{inter}} = {\rho }_{r} {dl} / {\rho}_{f} {h}^2\tag{10}\end{equation}
同时,考虑边界条件,忽略水的黏性,假定弹性绳充分光滑,忽略摩擦带来的损耗,忽略边界层效应,认为耦合边界上切线方向上流体与固体可以发生滑移,而由于固体不可穿透,流体不会穿过固体,也不会与固体分离,因此法线方向上,弹性绳质点速度与该点所在的流体速度一致,边界条件为
\begin{equation}\label{eq11} U^*_{if}\cdot n=U_{ir}\cdot n\tag{11}\end{equation}\begin{equation}\label{eq12}U^*_{ir}\cdot \tau=U_{ir}\cdot\tau\tag{12}\end{equation}
联立式(9), 式(11), 式(12)可以求出${\delta u,\delta v$以及${\delta{U}_{ir}}$,同时,也可以求得等效耦合力,也就是式(3)中的${{f}_{exter}}$为
\begin{equation}\label{eq13}f_{exter}\cdot {d}t=\rho_{r}\int\delta U_{ir}{d}l\tag{13}\end{equation}
根据速度修正的方法,依据动量守恒定律,并满足可滑移边界条件,求得了通过耦合作用后弹性绳与流体的速度场.但是,更新后流体速度场此时不满足不可压缩条件,因此接下来我们还需要根据流体满足的控制方程重新修正流体速度场.
2.2 二维流场求解
假设上节得到的流场速度为${{U}_{f}^*}(t, X),X$为流场网格点坐标,需要根据流体控制方程更新$\Deltat$时间后的流场速度,将修正后的速度场表示为${{U}_{f}^*}(t+\Delta t,X)$.对于二维不可压缩牛顿流体,流场的压强与速度由Navier-Stokes方程控制,本文不考虑流体黏性影响,因此控制方程表示为$$\frac{{\partial {{{U}}_{{f}}}}}{{\partial {{t}}}} +{{{U}}_{{f}}}\cdot \nabla {{{U}}_{{f}}} = -\frac{1}{{{\rho}}}\nabla {{P}} + {{g}}\tag{14}$$
$$\nabla \cdot{{{U}}_{{f}}} = 0\tag{15} $$
其中,$U_{f} $为流场速度,$P$为压强,${\rho }$为流场密度.流场采用网格法(欧拉网格),并使用MAC网格[27]储存流体数据,将流速度储存在网格线中点,将压强储存在网格中心处,如图7所示,该方法可以提高数值计算的精度.采用分裂法求解流体方程,分为3个步骤:施加合外力、输运(即为随体导数的改变)和确保速度场散度为零.
显示原图|下载原图ZIP|生成PPT图7流场速度与压强示意图...
-->Fig.7Velocity and pressure of fluid
-->
假设${w}_0 \left( {X} \right)$是$t$时刻的流场网格$X$点的速度(如图7中的${u}_{{k,{l}} )$
\begin{equation}\label{eq16} {w}_0 \left( {X} \right) = {U}_{f}^{\ast } \left( {{t,{X}}} \right)\tag{16}\end{equation}
${w}_1 \left( {X} \right)$是施加外力后的流场$X$点速度,根据向前欧拉公式
\begin{equation}\label{eq17} {w}_1 \left( {X} \right) = {w}_0 \left({X} \right) + \Delta {t}\cdot {f}\left( {{X,{t}}}\right)\tag{17}\end{equation}
其中${f}\left( {{X,{t}} \right)$是$t$时刻$X$处离散体受到的外力,$\Delta{t}$是时间间隔,${w}_2 \left({X} \right)$是经过输运后的流体速度
\begin{equation}\label{eq18} {w}_2 \left( {X} \right) = {w}_1 \left({{p}\left( {{X,-\Delta{t}}} \right)} \right)\tag{18}\end{equation}
其中${p}\left( {{X,-\Delta{t}} \right)$是采用Stam [28]提出的半拉格朗日法得到,就是为了得到$q$在一个网格点处的新值,沿着该点合速度场逆向运动,找到下一时刻运动到该点的流体粒子,该点流场速度就是原网格点下一时刻的新速度值.
${w}_3 \left({X} \right)$是经过第3个步骤投影后$t+{d}t$时刻的流体网格速度
\begin{equation}\label{eq19} {w}_3 \left( {X} \right) = {w}_2 \left({X} \right)-\frac{1}{{\rho }}\nabla {p}\tag{19}\end{equation}
对式(19)两边求梯度,由于最终求得流场不可压缩,${w}_3 \left({X} \right)$梯度为零,式(19)可化简为
\begin{equation}\label{eq20} \nabla \cdot{w}_2 \left( {X} \right) =\frac{1}{{\rho }}\nabla ^2{p}\tag{20}\end{equation}
因此流场的求解最终即为泊松方程的求解,采用五点差分法进行数值求解.将求得的压强代回式(19),可以得到${w}_3 \left( {X}\right)$,即为更新的网格速度
\begin{equation}\label{eq21} {w}_3 \left( {X} \right) = {U}_{f}^{\ast }\left( {{t} + \Delta{t,{X}} }\right)\tag{21}\end{equation}
2.3 充分耦合法
在之前的计算步骤中,一个物理时间步内,首先根据绳的主动运动,在固体网格上求解固体运动,通过动量方法进行耦合面上固体与流体的数据交换,最后求解不可压缩流场[24].但是如果每个时间步内,3个步骤依次计算,在耦合求解部分施加边界条件,而在流体求解器中确保不可压缩破坏了边界条件,会导致数值不稳定,因此,每个时间步内需要增加子迭代算法,如图8所示.具体来说,每个时间步内,更新弹性绳后,循环进行施加耦合边界条件,更新流体与绳速度,对流体施加外力,输运与确保不可压缩这几个步骤,直到收敛,保证流体速度场既满足不可压缩条件,又满足耦合边界条件后,再进入下一个时间步.
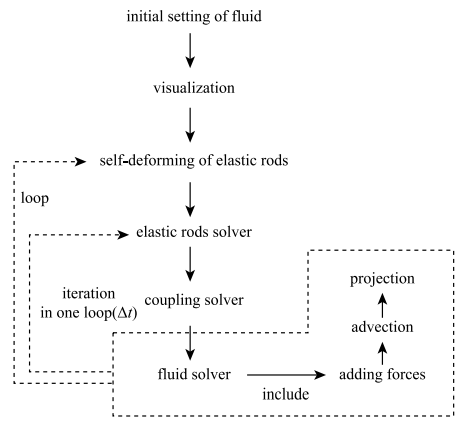显示原图|下载原图ZIP|生成PPT图8弹性绳运动轨迹模拟程序流程图...
-->Fig.8The process of simulating swimming elastic rods
-->
4 自主泳动弹性绳运动轨迹模拟结果
基于开源软件平台OpenFrameworks,使用C++对前文的所有算法进行编程与整合,就完成了一套可伸缩弹性绳水下运动轨迹模拟程序.弹性绳涉及的控制参数有:拉伸与扭转弹性系数${\alpha }_{i} $与${\beta}_{i}$,以及弹性绳运动趋势的参考函数的相关参数,本文控制弹性绳以正弦形式波动,${A}_{{rod}} $为控制弹性绳的摆动幅度,${\omega }_{{rod}}$为控制泳动频率,${k}_{{rod}} $为摆动形态, ${\varphi }_{{rod}} $为摆动的初始相位.其中,弹性绳的运动形态与数值稳定性对弹簧的拉伸与扭转弹性系数非常敏感,拉伸弹性系数过大导致弹性绳运动幅度非常小,而系数过小则任何外力可能导致弹性绳变形过大而数值逸散,同样的对于扭转弹性系数,数值太大导致弹性绳刚性过大无法游动,太小又使得弹性绳容易受到外界干扰数值逸散.在数值稳定的范围内,我们选取弹性参数${\alpha }_{i} =0.05\mbox{~N}/\mbox{mm}^2$,${\beta }_{i} =500\mbox{~N}/\mbox{mm}^2. $
除了弹性绳相关系数,耦合影响因子与迭代次数也影响着模拟结果的稳定性与快速性,耦合因子${k}_{{inter}}$由弹性绳与流体密度以及网格划分尺寸决定,本文实验中确定${k}_{{inter}} = 2$.迭代次数增加提高计算的精度,但同时会大大降低模拟的速度,当迭代次数大于一定大小时,模拟结果差异不大,如图9所示,其中,图中初始流场静止,红线代表弹性绳的运动,黑色箭头代表受到影响的流场区域以及流速方向大小.因 此我们选取迭代次数为10进行快速模拟.
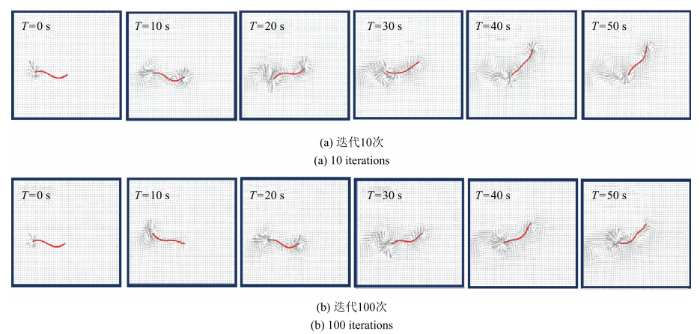显示原图|下载原图ZIP|生成PPT图9每个时间步内不同迭代次数的轨迹模拟...
-->Fig.9Simulating results of different iterations in one time step
-->
为了将模拟结果与文献${[14]中的实验进行比较,取可比较的参数为${A}_{{rod}} = 0.03$,${k}_{{rod}} = 6{\pi }$,${k}_{{inter}}= 2$,迭代次数为10,结果如图10 (a)所示.当细绳以摆动形式前进时,分析发现绳的主动游动与被动泳动中的变形相位基本一致,也就是说,绳的主动驱动频率与被动运动的频率基本一致,这一模拟结果与文献${[14]中第14页的结论相吻合.
值得注意的是,比较图10(a)与图10(b)可得,当增大主动驱动泳动频率时,随着驱动频率的增大,绳的游动速率也随之增大.该结果与文献${[17]蛇形机器人水中蜿蜒游动实验的结果(见文献${[17]中图17)相吻合,同时图10所示的模拟结果中绳的前进方向和泳动姿态与文献${[17]中图18的实验结果一致.真实多模块的蛇形机器人泳动过程中蜿蜒前进的效果并不好(见文献${[34]中图7),这是由于刚性所致.如果使用IPMC驱动,则机器人增加了柔性,在水中\蜿蜒前进的步态与前进方向实验结果(见文献${[19]中图11)则与本文模拟结果(图11,参数选取与文献${[19]中图11相同)相吻合,这说明本文仿真计算使用的弹性绳模型与耦合方法对细长形软体机器人的设计具有参考价值.
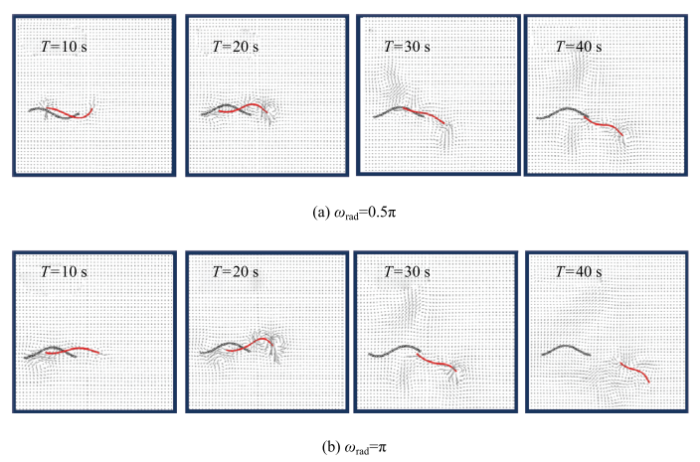显示原图|下载原图ZIP|生成PPT图10(a) ${\omega }_{{rod}} =0.5{\pi }$ (b) ${\omega }_{{rod}} = {\pi,$其中,黑线为主动控制模型,红线泳动路线...
-->Fig.10(a) ${\omega }_{{rod}} = 0.5{\pi }$ (b) ${\omega}_{{rod}} = {\pi }$, black lines represent self-controlmodel, red lines represent simulationswimming path
-->
接着测试初相位对于泳动结果的影响,当改变弹性绳参考运动函数的初相位时,弹性绳的运动方向会发生改变.其他参数设定为${\alpha }_{i} = 0.05$,${\beta }_{i} =500$,${A}_{{rod}} = 0.03$,${\omega }_{{rod}} =10$,${k}_{{rod}} = 6{\pi }$,${k}_{{inter}} =2$,迭代次数=10. 从图12模拟结果来看,当${\varphi }_{{rod}}$在0到0.12${\pi}$范围内时,运动一段时间后将向左游动,当${\varphi }_{{rod}}$在0.12${\pi }$到0.5${\pi}$范围内时,运动一段时间后将向右游动. 当${\varphi }_{{rod}}$约为0.12${\pi }$时,可以基本实现向前的自主游动.
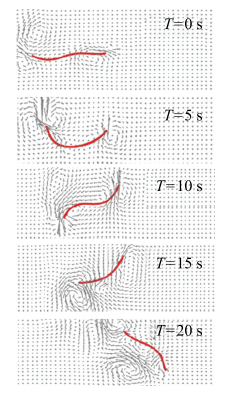显示原图|下载原图ZIP|生成PPT图11${A}_{{rod}} = 2.5 ,{\omega}_{{rod}} = {\pi } , {\varphi }_{{rod}} =0.5{\pi }$时的仿真结果...
-->Fig.11Simulation results of ${A}_{{rod}} = 2.5, {\omega}_{{rod}} = {\pi ,{\varphi }_{{rod}} =0.5{\pi }$
-->
显示原图|下载原图ZIP|生成PPT图12改变${\varphi }_{{rod}} $后弹性绳的运动轨迹...
-->Fig.12Simulating results of different initial phase
-->
从图12可以看出,在弹性绳泳动过程中,由头部附近流体产生的涡沿着绳表面向后运动并在尾部达到最大并脱离,流场中的反卡门涡街随着尾部的往复摆动产生,而当尾部的涡增大时,绳的前进速度明显降低,由此可见,真实设计机器鱼时,需要改变摆动形式或鱼尾的形状以有效减弱这种脱落涡,这一结论也与真实鱼类的尾鳍形状可以利用这些涡中的能量来推进游动相符合.当然,尾迹的模拟并不趋于真实,这是由于流体求解中大量的数值耗散以及对粘性项的忽略导致.
在图10(a)和图10(b),尾端向上运动而尾部向下弯曲,上部压力大于上部压力,压力差使得绳向前运动的同时向左游动,而在图10(d)和图10(e)中看到了相反的结构,尾端向下运动而尾部向上弯曲,绳向右前方运动,数值结果也验证了改变初相位可以改变绳的运动方向.
5 结论
本文针对固体被流场包围,耦合作用发生在两相交界面上且固体结构会发生明显变形的一类流固耦合问题,具体来说,是具有主动力的自由弹性绳在二维不可压缩牛顿流体中的运动问题.以充分耦合法为基本思想,将核心算法主要分为三个部分,包括弹性绳的主动运动与被动形变,流场的求解,以及耦合作用的求解.弹性绳模型既考虑柔性体生物自主运动的作用,提出动态参考模型,人为改变动态参考模型的函数来视为柔性体的内在驱动力,又考虑弹性体内力、与外界流体相互耦合作用力对弹性绳的动态影响.同时,弹性绳模型同时考虑了拉伸弹性力与扭转弹性力对于模拟肌肉运动的作用.流场的单独求解基于网格法,采用了Stam 在stable fluid中提出的半拉格朗日法求解N-S方程中输运项的方法.耦合作用的求解是本文核心内容,提出的算法基于非边界配合法的基本思想.通过接修正网格的速度,使得修正网格速度后,绳的每个节点所在的流体网格区域内流体与该节点隔离体总动量守恒,我们依据这个物理关系进行网格速度的修正,视为近似耦合作用力真实改变的流场速度.然后根据这个修正的流体速度场,更新流体速度,同时使得流固耦合界面满足特定边界条件,达到更新固体的形状与位置的目的.结合流体与固体单独的求解器与我们耦合部分算法进行编程,我们完成了一套弹性绳在流场中的快速动态模拟程序,并对每一个参数进行了数值实验.弹性绳形态对弹性系数的改变敏感,合适的弹性系数可以通过数值实验得到,弹性绳参考模型的振幅,频率与相位控制着弹性绳的运动方式,在流场中表现为运动速度与方向不同,同时,参数过大将导致数值不稳定;通过改变初相位可以改变弹性绳的运动方向,实现自主蜿蜒游动前行.这一些数值实验结果鱼仿真平台可以为真实软体机器鱼的研究提供部分理论参考依据.我们也将继续改进算法的精度,并将算法应用于三维仿真平台的开发中,同时,进一步设计实验验证仿真结果的准确性,期望能将仿真数据用于真实的仿生鱼的研发当中.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | . . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . |
| [12] | . |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . . |
| [18] | . |
| [19] | . |
| [20] | . . |
| [21] | . |
| [22] | . . |
| [23] | . . |
| [24] | . . |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | . |
| [29] | |
| [30] | |
| [31] | . . |
| [32] | . . |
| [33] | . . |
| [34] | . . |
