 , 周伟, 阎昱, 李强, 何东
, 周伟, 阎昱, 李强, 何东北方工业大学机械与材料工程学院, 北京 100144
PARAMETER DETERMINATION METHOD OF GOTOH YIELD CRITERION BASED ON NON-ASSOCIATED FLOW RULE1)
WangHaibo , ZhouWei, YanYu, LiQiang, HeDong
, ZhouWei, YanYu, LiQiang, HeDong中图分类号:TG301
文献标识码:A
通讯作者:
收稿日期:2018-06-8
网络出版日期:2018-09-18
版权声明:2018力学学报期刊社力学学报期刊社 所有
基金资助:
展开
摘要
关键词:
Abstract
Keywords:
-->0
PDF (7122KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引言
板料塑性成形是工业制造领域的重要生产方式, 关于成形过程的描述始终是先进成形技术的核心目标. 为了确保对其成形过程有比较精确的描述, 针对不同板料已经建立了较为系统性用于描述塑性行为的屈服准则. 且大部分研究内容中, 普遍地认可通过正交性法则定义塑性应变增量的塑性势函数和定义屈服面的屈服函数相同, 并将其归纳为关联流动法则(associated flow rule, AFR)[1]. AFR不仅求解方便; 同时在精度允许的范围内也具备工程应用价值.随着新技术的产生, 各种板料的性能得到日益更新, 屈服准则也相应地演化出了众多系列[2], 早先Mises屈服准则因其形式简单、推导方便的特点得到了极大的使用, 但只局限于板料各向同性的前提. 实践表明, 板料的各向异性问题不容忽视[3]. 近半个世纪以来, 屈服准则相继朝着各向异性的角度发展, 较早的有Hill48[4]屈服准则, 因形式简单、普遍适用性好而得到了众多****的认可, 但针对$r<1$的材料有着明显的局限性, 为此, Hill[5-7]针对不同问题完善了一系列屈服准则; Barlat等[8-10]提出了另外一个系列的屈服准则, 主要侧重于分析铝合金的各向异性行为, 形式复杂, 大多数是建立在某类材料或某些应力状态的基础上而提出的; 另外, Gotoh[11], Montheillet等[12], Banabic 等[13] 也相继提出了高次屈服准则. Gotoh 屈服准则是基于四次屈服函数的塑性各向异性理论提出的, 与二次屈服函数相比, 四次屈服函数具有更大的柔性, 可以达到更高的各向异性描述精度[11]. 且与其他高次多参数准则相比, Gotoh屈服准则的参数可以对材料性能显式表达, 使用方便[14]. 胡卫龙等[15] 改进了Gotoh屈服准则, 使其不再局限于应力主轴与试验主轴一致的情形, 且更适用于描述双向等拉和单向拉伸试验.
为了描述各向异性, Hill[16], Barlat等[17-18], Kim 等[19]基于AFR先后展开了一系列研究, 但并不能全面地表征各向异性更显著的板料. 鉴于此, 非关联流动法则 (non-associated flow rule, NAFR)受到重视, 其与AFR的区别是: 屈服函数和塑性势函数表征各向异性的参数分别由应力和变形力学性能表达. 自21世纪起, 许多研究者先后提出将NAFR用于描述金属板的变形行为[20-25], 使得即使是$r$ 值较低的板料在双拉路径下也能得到精确的表征[21]. Park等[26]根据NAFR推导了对称的切线模量, 并评估了AA2090-T3 和AA5042 板料的凸耳成形数及精度, 获得了与试验点高度一致的结果. Cvitanic 等[27]为消除变形对屈服准则的影响, 将等效塑性应变扩展为多项式函数, 并应用NAFR改善了屈服函数在表征各向异性中的准确性和灵活性. Zhang 等[28] 结合流动规律在各向异性与应变的演化关系中表明: 基于NAFR 的屈服理论与试验点拟合精度最优. 失效预测方面有广泛的研究[29-30], 关于AZ31B 镁合金, Ahn 等[31]将其结合NAFR展开研究发现, 很好地拟合了失效的各向异性行为. Lian 等[32]根据非关联Hill48塑性模型验证了其在成形极限预测中的影响, 与经典模型相比, 非关联模型对成形极限图的左右两边具有明显适用性. 关于Gotoh准则, Soare等[33]系统地考虑了其高次形式, 并在判断屈服面外凸的先决条件下提出了改进的解析公式, 但计算方法是以AFR为出发点. 目前涉及NAFR对各向异性行为的研究主要集中于Hill, Barlat系列, 以Gotoh准则为基础的文献几乎没有.
本文基于NAFR推导了Gotoh四次屈服函数的参数解析解表达式, 并结合Yld2000-2d准则共同对板料成形各向异性行为进行对比研究, 分析了流动理论对屈服准则误差精度的影响, 研究结果将为屈服准则合理求解参数提供建议, 并为成形问题的进一步深入奠定基础.
1 非关联流动法则
1.1 弹-塑性切线模量
屈服准则作为所有状态变量的函数, 可以用一般形式表达成\begin{equation*}F( \sigma, \alpha,\bar{\sigma}_y)=f_y( \sigma- \alpha)-\bar{\sigma}_y(\bar{\varepsilon}^\text p)=0\tag*{(1)}\end{equation*}
式中, $f_y(\sigma- \alpha)$为连续可微的屈服函数, $\sigma$为应力张量, $ \alpha$为背应力张量, 本文不考虑复杂加载过程中的包辛格效应等变形行为, 不单独进行强化方式的讨论, 故令$ \alpha= 0$, $\bar{\sigma}_y$为等效应力, $\bar{\varepsilon}^\text p$ 为对应的等效塑性应变.
对于各向异性塑性应变增量, 可用流动正交性法则加以概括, 即塑性变形时屈服曲面上某点的塑性应变增量的合成张量沿着屈服表面的法向, 具体形式如下
\begin{equation*}\text d \varepsilon^\text p=\text d\bar{\varepsilon}_\text p\dfrac{\partial f_\text p( \sigma)}{\partial \sigma}\tag*{(2)}\end{equation*}
式中, $f_\text p( \sigma)$为连续可微的塑性势函数, $\text d\bar{\varepsilon}_\text p$ 为非负的比例系数. 结合单位体积塑性功相等原理有
\begin{equation*}\text dw=\bar{\sigma}_y\text d\bar{\varepsilon}^\text p=\bar{\sigma}_\text p\text d\bar{\varepsilon}_\text p\tag*{(3)}\end{equation*}
其中, $\bar{\sigma}_\text p$为塑性势函数对应的等效塑性应力, 与屈服函数中等效应力的定义相同, 因此有
\begin{equation*}f_\text p( \sigma)-\bar{\sigma}_\text p(\bar{\varepsilon}_\text p)=0\tag*{(4)}\end{equation*}
由式(1)、式(3)和式(4)可得
\begin{equation*}\text d\bar{\varepsilon}^\text p/\text d\bar{\varepsilon}_\text p=\bar{\sigma}_\text p/\bar{\sigma}_y=f_\text p/f_y\tag*{(5)}\end{equation*}
显然, 若函数$f_\text p$与$f_\text y$完全一致, 则采用的研究方法为关联流动法则; 反之为非关联流动法则.
根据胡克定律, $ \sigma$增量可以线性表示为[34]
\begin{equation*}\text d\sigma= C^\text e\cdot\text d \varepsilon^\text e= C^\text e\cdot(\text d\varepsilon-\text d\varepsilon^\text p)\tag*{(6)}\end{equation*}
$ C^\text e$为弹性切线模量, $\text d\varepsilon^\text e$和$\text d\varepsilon^\text p$分别代表弹性、塑性应变增量. 联立式(2)、式(6) 得到
\begin{equation*}\text d\sigma= C^\text e\cdot\Bigg(\text d\varepsilon-\dfrac{\partial f_\text p}{\partial\sigma}\text d\bar{\varepsilon}_\text p\Bigg)= C^\text e\cdot\Bigg(\text d\varepsilon-\dfrac{\partial f_\text p}{\partial\sigma}\dfrac{f_y}{f_\text p}\text d\bar{\varepsilon}^\text p\Bigg)\tag*{(7)}\end{equation*}
在变形过程中, 根据一致性原理可得式(4)有
\begin{equation*}\begin{split}&\dfrac{\partial f_\text p}{\partial\sigma}:\text d\sigma-\dfrac{\text d\bar{\sigma}_\text p}{\text d\bar{\varepsilon}_\text p}\text d\bar{\varepsilon}_\text p=\\&\quad\quad\dfrac{\partial f_\text p}{\partial\sigma}:\Bigg\lbrack C^{\text e}\cdot\Bigg\lgroup \text d\varepsilon-\text d\bar{\varepsilon}_\text p\dfrac{\partial f_\text p}{\partial\sigma}\Bigg\rgroup\Bigg\rbrack-\dfrac{\text d\bar{\sigma}_\text p}{\text d\bar{\varepsilon}_\text p}\text d\bar{\varepsilon}_\text p=0\end{split}\tag*{(8)}\end{equation*}
再对式(8)进行变换, 得到等效塑性应变增量
\begin{equation*}\text d\bar{\varepsilon}_\text p=\dfrac{\dfrac{\partial f_\text p}{\partial\sigma}: C^\text e\cdot\text d \varepsilon}{\dfrac{\partial f_\text p}{\partial\sigma}: C^\text e\cdot\dfrac{\partial f_\text p}{\partial\sigma}+\dfrac{\text d\bar{\sigma}_\text p}{\text d\bar{\varepsilon}_\text p}}\tag*{(9)}\end{equation*}
再由式(5)有
\begin{equation*}\text d\bar{\varepsilon}^\text p=\dfrac{\dfrac{\partial f_\text p}{\partial\sigma}: C^\text e\cdot\text d\varepsilon}{\dfrac{f_y}{f_\text p}\dfrac{\partial f_\text p}{\partial\sigma}: C^\text e\cdot\dfrac{\partial f_\text p}{\partial\sigma}+\dfrac{\text d\bar{\sigma}_\text p}{\text d\bar{\varepsilon}^\text p}}\tag*{(10)}\end{equation*}
将式(9)、式(10)代入式(7)中, 得到
\begin{equation*}\dfrac{\text d\sigma}{\text d\varepsilon}= C^{\text{ep}}= C^\text e-\dfrac{ C^\text e:\dfrac{\partial f_\text p}{\partial\sigma}\otimes\dfrac{\partial f_\text p}{\partial\sigma}: C^\text e}{\dfrac{\partial f_\text p}{\partial\sigma}: C^\text e\cdot\dfrac{\partial f_\text p}{\partial\sigma}+\dfrac{\text d\bar{\sigma}_\text p}{\text d\bar{\varepsilon}_\text p}}\tag*{(11)}\end{equation*}和
\begin{equation*}\dfrac{\text d\sigma}{\text d\varepsilon}= C^{\text{ep}}= C^\text e-\dfrac{\dfrac{f_y}{f_\text p} C^\text e:\dfrac{\partial f_\text p}{\partial\sigma}\otimes\dfrac{\partial f_\text p}{\partial\sigma}: C^\text e}{\dfrac{f_y}{f_\text p}\dfrac{\partial f_\text p}{\partial\sigma}: C^\text e\cdot\dfrac{\partial f_\text p}{\partial\sigma}+\dfrac{\text d\bar{\sigma}_\text p}{\text d\bar{\varepsilon}^\text p}}\tag*{(12)}\end{equation*}
关于式(11)和式(12), $ C^\text {ep}$为弹\mbox{?}塑性切线模量, 此处所得到的结果均是对称的. 在非关联流动理论中, 与非对称弹-塑性切线模量相比, 对称的弹-塑性切线模量能够更有效地进行有限元分析.
1.2 屈服准则参数表达式的求法
Gotoh屈服准则的具体形式如下\begin{equation*}\begin{split}&f=A_1\sigma^4_x+A_2\sigma^3_x\sigma_y+A_3\sigma^2_x\sigma^2_y+A_4\sigma_x\sigma^3_y+A_5\sigma^4_y+\\&\quad\quad\Big(A_6\sigma^2_x+A_7\sigma_x\sigma_y+A_8\sigma^2_y\Big)\sigma^2_{xy}+A_9\sigma^4_{xy}=\bar{\sigma}^4\end{split}\tag*{(13)}\end{equation*}
式中, $x,y$为正交各向异性主轴, $A_1\sim A_9$为相互独立的各向异性特征参数, 可由材料的具体试验确定, $\bar\sigma$为等效应力. 在平面应力状态下, 设应力比为$\sigma_x:\sigma_y:\sigma_{xy}=1:k_1:k_2$, 即应力分量与等效应力$\bar\sigma$的关系, 有
\begin{equation*}\left.\begin{split}&\sigma_x=\bar{\sigma}/\sqrt[4]{K}\\&\sigma_y=k_1\bar{\sigma}/\sqrt[4]{K}\\&\sigma_{xy}=k_2\bar{\sigma}/\sqrt[4]{K}\\\end{split}\right\}\tag*{(14)}\end{equation*}
其中
\begin{equation*}\begin{split}&K=A_1+A_2k_1+A_3k^2_1+A_4k^3_1+A_5k^4_1+\\&\quad\quad\Big(A_6+A_7k_1+A_8k^2_1\Big)k^2_2+A_9k^4_2\end{split}\tag*{(15)}\end{equation*}
根据单位体积塑性功相等原理, 有
\begin{equation*}\sigma_x\text d\varepsilon^\text P_x+\sigma_y\text d\varepsilon^\text P_y+\sigma_{xy}\text d\varepsilon^\text P_{xy}=\bar{\sigma}\text d\bar{\varepsilon}^\text p\tag*{(16)}\end{equation*}
其中, $\text d\varepsilon^\text p_x,\text d\varepsilon^\text p_y,\text d\varepsilon^\text p_{xy}$分别为塑性应变增量的分量, $\text d\bar\varepsilon^\text p$ 为等效塑性应变增量. 由式(16) 积分得到
\begin{equation*}\varepsilon^\text p_x+k_1\varepsilon^\text p_y+k_2\varepsilon^\text p_{xy}=\bar{\sigma}/\sigma_x\cdot\bar{\varepsilon}^\text p\tag*{(17)}\end{equation*}
根据Drucker公设及应力比可得
\begin{equation*}\begin{split}&\text d\varepsilon^\text p_x:\text d\varepsilon^\text p_y:\text d\varepsilon^\text p_{xy}=\\&\quad\quad\Big(4A_1+3A_2k_1+2A_3k^2_1+A_4k^3_1+2A_6k^2_2+\\&\quad\quad A_7k_1k^2_2\Big):\Big(A_2+2A_3k_1+3A_4k^2_1+4A_5k^3_1+\\&\quad\quad 2A_8k_1k^2_2+A_7k^2_2\Big):2\Big(A_6k_2+A_7k_1k_2+\\&\quad\quad A_8k^2_1k_2+2A_9k^3_2\Big)=\varepsilon^\text p_x:\varepsilon^\text p_y:\varepsilon^\text p_{xy}\end{split}\tag*{(18)}\end{equation*}
由式(14)可知, 在同一加载比例中($k_1$和$k_2$为常数), $\bar\sigma/\sigma_x=\sqrt[4]{K}$. 联立式(17)和式(18) 可推出塑性应变分量与等效塑性应变的对应关系
\begin{equation*}\begin{split}&\varepsilon^\text p_x=\Big(4A_1+3A_2k_1+2A_3k^2_1+A_4k^3_1+2A_6k^2_2+A_7k_1k^2_2\Big)\cdot\\&\quad\quad\bar{\varepsilon}^\text p\Big/\Big(4\sqrt[4]{K^3}\Big) &\varepsilon^\text p_y=\Big(A_2+2A_3k_1+3A_4k^2_1+4A_5k^3_1+2A_8k_1k^2_2+A_7k^2_2\Big)\cdot\\&\quad\quad\bar{\varepsilon}^\text p\Big/\Big(44\sqrt[4]{K^3}\Big) &\varepsilon^\text p_{xy}=2\Big(A_6k_2+A_7k_1k_2+A_8k^2_1k_2+2A_9k^3_2\Big)\cdot\\&\quad\quad\bar\varepsilon^\text p\Big/\Big(4\sqrt[4>]{K^3}\Big)\end{split}\tag*{(19)}\end{equation*}
板料成形时其屈服曲面是处处外凸的, 因此对参数的取值有着严格的约束关系. 其中$A_1$, $A_5$, $A_9$恒大于零; 在屈服曲面中, 存在$\sigma_x=0$和$\sigma_y=0$两种情况, 为保证外凸性, 根据Hessian Matrix[35]可知, 要同时满足下列不等式
$$0\leqslant A_6\leqslant6\sqrt{A_1A_9}, 0\leqslant A_8\leqslant6\sqrt{A_5A_9}(20)$$
$$\left.\begin{matrix}&A_3>0\\&|A_2|<\sqrt{(8/3)A_1A_3}\\&|A_4|<\sqrt{(8/3)A_5A_3}\\\end{matrix}\right\}(21)$$
考虑到参数最终所得值与求解方法有着极为显著的关系, 在众多的研究文献中, 针对多参数的屈服准则有许多处理办法, 如权重法, 并通过调整权重的大小获得合适的参数值. 因此, 为妥善处理Gotoh屈服准则这类问题, 并在保证外凸性的前提条件下, 此处规定
\begin{equation*}A_7=-\sum\omega_{\theta}\cdot r_{\theta}+\xi(\theta=0,22.5,45,67.5,90)\tag*{(22)}\end{equation*}
式中, $\omega_\theta$为与轧制方向所成角度$\theta$下的权重值, $r_\theta$为对应的各向异性指数, $\xi$为调节参数, 通过调整$\omega_\theta$和$\xi$的取值, 始终能求出最合适的参数$A_7$, 使得$A_6$、$A_8$满足式(20)从而获得与试验点更好的拟合、屈服面外凸的效果.
(1)屈服函数
将轧制方向定义为参考方向, 则该方向上的屈服应力为参考应力, 即有$\sigma_0=\bar\sigma=\sigma_x$. 在研究板料的平面应力状态时, 假定与轧制方向所成角度为$\theta$的单向拉伸应力为$\sigma_\theta$, 则根据应力转换公式, $xOy$ 平面内的应力分量为
\begin{equation*}\sigma_x=\sigma_{\theta}\text{cos}^2\theta,\sigma_y=\sigma_{\theta}\text{sin}^2\theta,\sigma_{xy}=\sigma_{\theta}\text{sin}\theta \text{cos}\theta\tag*{(23)}\end{equation*}
将其代入屈服准则表达式中得到单拉下屈服应力为
\begin{equation*}\begin{split}&\sigma_{\theta}=\sigma_0/\Big\lbrack A_1\text{cos}^8\theta+(A_2+A_6)\text{cos}^6\theta\text{sin}^2\theta)+\\&\quad\quad(A_3+A_7+A_9)\text{cos}^4\theta\text{sin}^4\theta+\\&\quad\quad(A_4+A_8)\text{cos}^2\theta\text{sin}^6\theta+A_5\text{sin}^8\theta)^{0.25}\Big\rbrack\end{split}\tag*{(24)}\end{equation*}
在实验时将分别进行$0^\circ$, $45^\circ$, $90^\circ$, $22.5^\circ$和$67.5^\circ$的单向拉伸以及$\sigma_x:\sigma_y=1:1$, $\sigma_x:\sigma_y=p(\sigma_x>\sigma_y)$, $\sigma_x:\sigma_y=q(\sigma_x<\sigma_y)$ 的双向拉伸试验. 即对应的$\sigma_\theta$为已知值, 设$\sigma_b$为双向等拉时的应力值、$\sigma_p,\sigma_q$分别对应另外两种双拉下的$\sigma_x$值. 则轧制方向单向拉伸有
\begin{equation*}A_1=\sigma^4_0/\sigma^4_0=1\tag*{(25)}\end{equation*}
垂直轧制方向单向拉伸可得
\begin{equation*}A_5=\sigma^4_0/\sigma^4_{90}\tag*{(26)}\end{equation*}
其他角度单拉可同理分别导出如下
\begin{align*}&A_1+A_2+A_3+A_4+A_5+A_6+A_7+A_8+A_9=\\&\quad\quad 16\sigma^4_0/\sigma^4_{45}\tag*{(27)}\end{align*}
\begin{align*}&\dfrac{17+12\sqrt{2}}{64}A_1+\dfrac{3+2\sqrt{2}}{64}A_2+\dfrac{A_3}{64}+\dfrac{3-2\sqrt{2}}{64}A_4+\\&\quad\quad\dfrac{17-12\sqrt{2}}{64}A_5+\dfrac{3+2\sqrt{2}}{64}A_6+\dfrac{A_7}{64}+\\&\quad\quad\dfrac{3-2\sqrt{2}}{64}A_8+\dfrac{A_9}{64}=\dfrac{\sigma^4_0}{\sigma^4_{22.5}}\tag*{(28)}\end{align*}
\begin{equation*}\begin{split}&\dfrac{17-12\sqrt{2}}{64}A_1+\dfrac{3-2\sqrt{2}}{64}A_2+\dfrac{A_3}{64}+\dfrac{3+2\sqrt{2}}{64}A_4+\\&\quad\quad\dfrac{17+12\sqrt{2}}{64}A_5+\dfrac{3-2\sqrt{2}}{64}A_6+\dfrac{A_7}{64}+\\&\quad\quad\dfrac{3+2\sqrt{2}}{64}A_8+\dfrac{A_9}{64}=\dfrac{\sigma^4_0}{\sigma^4_{67.5}}\end{split}\tag*{(29)}\end{equation*}
双向拉伸$\sigma_x:\sigma_y=1:1$, 得出$\sigma_{xy}=0$, 有
\begin{equation*}A_1+A_2+A_3+A_4+A_5=\sigma^4_0/\sigma^4_b\tag*{(30)}\end{equation*}
其他两种双向拉伸情形亦可得到
\begin{equation*}A_1p^4+A_2p^3+A_3p^2+A_4p+A_5=(p\sigma_0/\sigma_p)^4\tag*{(31)}\end{equation*}
\begin{equation*}A_1q^4+A_2q^3+A_3q^2+A_4q+A_5=(q\sigma_0/\sigma_q)^4\tag*{(32)}\end{equation*}
综合式(25) $\sim$式(32), 假定$A_7$取1, $p=2$, $q=0.5$求解得到式(A1).
(2) 塑性势函数
根据Drucker公设, 得到Gotoh屈服准则的塑性应变增量$\text d\varepsilon^\text p_x,\text d\varepsilon^\text p_y,\text d\varepsilon^\text p_{xy}$分别为
\begin{equation*}\left.\begin{split}&\text d\varepsilon^\text p_x=\text d\lambda(4A_1\sigma^3_x+3A_2\sigma^2_x\sigma_y+2A_3\sigma_x\sigma^2_y+\\&\quad\quad A_4\sigma^3_y+2A_6\sigma_x\sigma^2_{xy}+A_7\sigma_y\sigma^2_{xy}) &\text d\varepsilon^\text p_y=\text d\lambda(A_2\sigma^3_x+2A_3\sigma^2_x\sigma_y+3A_4\sigma_x\sigma^2_y+\\&\quad\quad 4A_5\sigma^3_y+2A_8\sigma_y\sigma^2_{xy}+A_7\sigma_x\sigma^2_{xy}) &\text d\varepsilon^\text p_{xy}=2\text d\lambda(A_6\sigma^2_x\sigma_{xy}+A_7\sigma_x\sigma_y\sigma_{xy}+A_8\sigma^2_y\sigma_{xy}+\\&\quad\quad2A_9\sigma^3_{xy})\end{split}\right\}\tag*{(33)}\end{equation*}
将式(23)代入式(33)得到
\begin{equation*}\left.\begin{split}&\text d\varepsilon^\text p_x=\Big\lbrack 4A_1\text{cos}^6\theta+(3A_2+2A_6)\text{cos}^4\theta\text{sin}^2\theta+\\&\quad\quad(2A_3+A_7)\text{cos}^2\theta\text{sin}^4\theta+A_4\text{sin}^6\theta\Big\rbrack\sigma^3_{\theta}\text d\lambda\\&\text d\varepsilon^\text p_y=\Big\lbrack A_2\text{cos}^6\theta+(2A_3+A_7)\text{cos}^4\theta\text{sin}^2\theta+\\&\quad\quad(3A_4+2A_8)\text{cos}^2\theta\text{sin}^4\theta+4A_5\text{sin}^6\theta\Big\rbrack\sigma^3_{\theta}\text d\lambda\\&\text d\varepsilon^\text p_{xy}=2\Big\lbrack A_6\text{cos}^5\theta\text{sin}\theta+(A_7+2A_9)\text{cos}^3\theta\text{sin}^3\theta+\\&\quad\quad A_8\text{cos}\theta\text{sin}^5\theta\Big\rbrack\sigma^3_{\theta}\text d\lambda\end{split}\right\}\tag*{(34)}\end{equation*}
则加载方向的塑性应变增量$\text d\varepsilon^\text p_\theta$和宽度方向的塑性应变增量$\text d\varepsilon^\text p_{\theta+90}$为
\begin{equation*}\left.\begin{split}&\text{d}\varepsilon^{\text{p}}_{\theta}=\text{d}\varepsilon^{\text{p}}_{x}\text{cos}^{2}\theta+\text{d}\varepsilon^{\text{p}}_{y}\text{sin}^2\theta+\text d\varepsilon^\text p_{xy}\text{sin}\theta\text{cos}\theta\\&\text d\varepsilon^\text p_{\theta+90}=\text d\varepsilon^\text p_x\text{sin}^2\theta+\text d\varepsilon^\text p_y\text{cos}^2\theta-\text d\varepsilon^\text p_{xy}\text{sin}\theta\text{cos}\theta\end{split}\right\}\tag*{(35)}\end{equation*}
按照塑性变形体积不变, 即$\text d\varepsilon^\text p_x+\text d\varepsilon^\text p_y+\text d\varepsilon^\text p_z=0$ 的假设, 推理出厚度方向的塑性应变增量为
\begin{align*}\text{d}\varepsilon^{\text{p}}_{z}=&-\Big(\text{d}\varepsilon^{\text{p}}_{x}+\text{d}\varepsilon^{\text{p}}_{y}\Big)=-\Big\lbrack(4A_{1}+A_{2})\text{cos}^{6}\theta+\\&(3A_{2}+2A_{6}+2A_{3}+A_{7})\text{cos}^{4}\theta\text{sin}^{2}\theta+\\&(2A_{3}+A_{7}+3A_{4}+2A_{8})\text{cos}^{2}\theta\text{sin}^{4}\theta+\\&(A_{4}+4A_{5}\text{sin}^{6}\theta)\Big\rbrack\sigma^{3}_{\theta}\text{d}\lambda\tag*{(36)}\end{align*}
则$\theta$角度下的各向异性指数为
\begin{equation*}\begin{split}&r_\theta=\dfrac{\text d\varepsilon^\text p_{\theta+90}}{\text d\varepsilon^\text p_z}=\Big[A_2\text{cos}^8\theta+(4A_1+2A_3-2A_6+\\&\quad A_7)\text{cos}^6\theta\text{sin}^2\theta+(3A_2+3A_4+2A_6-2A_7+\\&\quad 2A_8-4A_9)\text{cos}^4\theta\text{sin}^4\theta+(2A_3+4A_5+A_7-2A_8) &\quad\text{cos}^2\theta\text{sin}^6\theta+A_4\text{sin}^8\theta\Big]\Big/\Big[-[(4A_1+A_2)\text{cos}^6\theta+\\&\quad(3A_2+2A_6+2A_3+A_7)\text{cos}^4\theta\text{sin}^2\theta+(2A_3+\\&\quad A_7+3A_4+2A_8)\text{cos}^2\theta\text{sin}^4\theta+(A_4+4A_5)\text{sin}^6\theta\Big]\end{split}\tag*{(37)}\end{equation*}
即
\begin{align*}&r_{0}=\dfrac{-A_{2}}{4A_{1}+A_{2}}\tag*{(38)}\\&r_{90}=\dfrac{-A_{4}}{4A_{5}+A_{4}}\tag*{(39)}\\&r_{45}=\dfrac{A_{9}-A_{1}-A_{2}-A_{3}-A_{4}-A_{5}}{2(A_{1}+A_{2}+A_{3}+A_{4}+A_{5})+A_{6}+A_{7}+A_{8}}\tag*{(40)}\\&r_{22.5}=\Big\lbrack-\Big(3+2\sqrt{2}\Big)A_{1}-\Big(5+3\sqrt{2}\Big)A_{2}-3A_{3}+\\&\quad\quad\Big(3\sqrt{2}-5\Big)A_{4}+\Big(2\sqrt{2}-3\Big)A_{5}+\Big(1+\sqrt{2}\Big)A_{6}-\\&\quad\quad A_{7}+\Big(1-\sqrt{2}\Big)A_{8}+A_{9}\Big\rbrack/\Big\lbrack\Big(20+14\sqrt{2}\Big)A_{1}+\\&\quad\quad\Big(8+5\sqrt{2}\Big)A_{2}+4A_{3}+\Big(8-5\sqrt{2}\Big)A_{4}+\Big(20-\\&\quad14\sqrt{2}\Big)A_{5}+\Big(2+\sqrt{2}\Big)A_{6}+2A_{7}+\Big(2-\sqrt{2}\Big)A_{8}\Big\rbrack\tag*{(41)}\\&r_{67.5}=\Big\lbrack\Big(2\sqrt{2}-3\Big)A_{1}+\Big(3\sqrt{2}-5\Big)A_{2}-3A_{3}-\\&\quad\quad\Big(3\sqrt{2}+5\Big)A_{4}-\Big(2\sqrt{2}+3\Big)A_{5}+\Big(1-\sqrt{2}\Big)\cdot\\&\quad\quad A_{6}-A_{7}+\Big(1+\sqrt{2}\Big)A_{8}+A_{9}\Big\rbrack~\Big/~\Big\lbrack\Big(20-\\&\quad\quad 14\sqrt{2}\Big)A_{1}+\Big(8-5\sqrt{2}\Big)A_{2}+4A_{3}+\Big(8+5\sqrt{2}\Big)\cdot\\&\quad\quad A_{4}+\Big(20+14\sqrt{2}\Big)A_{5}+\Big(2-\sqrt{2}\Big)A_{6}+2A_{7}+\\&\quad\quad\Big(2+\sqrt{2}\Big)A_{8}\Big\rbrack\tag*{(42)}\end{align*}
考虑$\sigma_x:\sigma_y=p~(\sigma_x>\sigma_y)$双向拉伸, 结合应变比$\rho=\text d\varepsilon_2/\text d\varepsilon_1=\varepsilon_2/\varepsilon_1=\text{tan}\beta$ ($\beta$代表平面应力状态下塑性应变比方向角)和Drucker 公设所得式(33), 化简得到$\rho_p$为
\begin{align*}\rho_{p}=\dfrac{p^{3}A_{2}+2p^{2}A_{3}+3pA_{4}+4A_{5}}{A_{4}+2pA_{3}+3p^{2}A_{2}+4p^{3}A_{1}}\tag*{(43)}\end{align*}
同理, 在$\sigma_x:\sigma_y=q(\sigma_x<\sigma_y)$双向拉伸状态时
\begin{align*}\rho_{q}=\dfrac{q^{3}A_{2}+2q^{2}A_{3}+3qA_{4}+4A_{5}}{A_{4}+2qA_{3}+3q^{2}A_{2}+4q^{3}A_{1}}\tag*{(44)}\end{align*}
同样取$p=2$, $q=0.5$(平面应变状态)联立式(25)、式(38) $\sim$式(44), 得到式(A2).
上述推导中所涉及的应变增量均为塑性应变量, 相应的弹性应变增量由应力分量并根据广义胡克定律求出, 在此不再详述.
NAFR的本质是屈服函数与塑性势函数都采用同一函数形式, 但其参数分别由不同的材料性能确定, 屈服函数由应力力学性能求解参数得到, 主要用于应力各向异性问题表征、应力计算等, 塑性势函数是由各向异性指数$r$值求解参数构成, 旨在描述变形问题、各向异性指数$r$值的分布规律以及塑性流动方向. 关联流动法则中, 只能有一组根据不同力学性能综合确定的参数用于各向异性问题描述, 即屈服函数与塑性势函数完全相同.
1.3 屈服准则局限性讨论
上述基于NAFR, 给出了Gotoh屈服准则两组参数求解方法. 由于AFR通常是选择其中一组求解方法, 即假设选择应力力学性能得出的参数作为最终的解, 然而实际应用中既有应力各向异性又有变形各向异性的问题待描述, 故存在片面性. 此处根据式(A1)、式(A2)对轧制方向单拉过程中变形各向异性进行讨论.\begin{align*}r_{0}=&\dfrac{-A_{2}}{4A_{1}+A_{2}}=\Big(-21\sigma^{4}_{90}\sigma^{4}_{b}\sigma^{4}_{p}\sigma^{4}_{q}+32\sigma^{4}_{90}\sigma^{4}_{b}\sigma^{4}_{0}\cdot\\&\sigma^{4}_{q}+\sigma^{4}_{90}\sigma^{4}_{b}\sigma^{4}_{p}\sigma^{4}_{0}-12\sigma^{4}_{90}\sigma^{4}_{0}\sigma^{4}_{p}\sigma^{4}_{q}+24\sigma^{4}_{0}\cdot\\&\sigma^{4}_{b}\sigma^{4}_{p}\sigma^{4}_{q}\Big)\Big/\Big(3\sigma^{4}_{90}\sigma^{4}_{b}\sigma^{4}_{p}\sigma^{4}_{q}+32\sigma^{4}_{90}\sigma^{4}_{b}\sigma^{4}_{0}\cdot\\&\sigma^{4}_{q}+\sigma^{4}_{90}\sigma^{4}_{b}\sigma^{4}_{p}\sigma^{4}_{0}-12\sigma^{4}_{90}\sigma^{4}_{0}\sigma^{4}_{p}\sigma^{4}_{q}+24\sigma^{4}_{0}\cdot\\&\sigma^{4}_{b}\sigma^{4}_{p}\sigma^{4}_{q}\Big)\tag*{(45)}\end{align*}
根据式(45)可以看出, 板料的$r$值与屈服应力之间存在确定的隐式关系, 若考虑$90^\circ$ 单向拉伸或其他加载路径变形状态, 同样存在与屈服应力相关的隐式, 然而, 板料在不同加载路径下的各向异性指数$r$值是板料本身固有的属性, 与屈服应力无关, 即采用该方法求解参数时隐含了上述局限性.
假设选择变形各向异性法得出的参数作为最终的解. 分析垂直轧制方向的单拉状态, 从式(26) 可得
\begin{equation*}\sigma_{90}=\sigma_0/\sqrt[4]{A_5}\tag*{(46)}\end{equation*}
同理, 双向等拉下的屈服应力有
\begin{equation*}\sigma_b=\sigma_0/\sqrt[4]{A_1+A_2+A_3+A_4+A_5}\tag*{(47)}\end{equation*}
由式(A2)可得
\begin{align*}&\sigma_{90}=\sqrt[4]{\dfrac{(r_0+3r_{90}+3r_0r_{90}+1)}{(3r_0+r_{90}+3r_0r_{90}+1)}}\cdot\sigma_0\tag*{(48)}\\&\sigma_{b}=\sqrt[4]{\dfrac{(2r_0+6r_{90}+6r_0r_{90}+2)}{(5r_0+5r_{90}+3r_0r_{90}+3)}}\cdot\sigma_0\tag*{(49)}\end{align*}
由式(48)、式(49)可知, 变形各向异性法同样导致类似状况, 使得屈服应力与各向异性指数$r$ 存在隐含关系, 但板料在不同加载路径下的屈服应力是其本身固有的力学性能, 与$r$值不存在直接关系, 即利用变形各向异性法计算参数时存在以上缺陷. 考虑其他加载路径同样可以得出类似的局限性, 相应的表达式不再列出. 因此, 实际应用中应根据具体的研究内容选择合适的参数求解法.
2 金属板料试验屈服行为的表征
钢板和铝合金板均属各向异性板料, 但它们在性能上具有明显的差异, 如钢板$r$值通常大于1, 而铝合金板一般小于1, 为了分析不同性能板料各向异性和屈服行为的特点, 本文分别对5754O 铝合金板料$(t=1)$、DP980先进高强钢$(t=1.2)$和SAPH440结构钢$(t=2.4)$进行与轧制方向成不同角度单拉以及不同比例双拉的复杂加载试验, 得到复杂加载路径下的屈服应力$\sigma$ 和各向异性指数$r$值等力学性能, 结合Yld2000-2d屈服准则将其用于各向异性的预测, 并详细对比分析平面应力状态下对屈服行为的描述精度. Yld2000-2d屈服准则参数由$r_0,~r_{45},~r_{90},~r_b$ 和$\sigma_0/\sigma_0,~\sigma_{45}/\sigma_0,~ \sigma_{90}/\sigma_0,~\sigma_b/\sigma_0$ 确定, 得到的函数记为Yld2000-2d(AFR); 基于AFR 的Gotoh 屈服准则参数由$r_0,~r_{45},~r_{90}$ 和$\sigma_0,~\sigma_{22.5},~\sigma_{45},~\sigma_{67.5},~\sigma_{90},~\sigma_b$ 确定,记为Gotoh(AFR), 则Gotoh(NAFR)表示基于NAFR下的理论函数.2.1 5754O铝合金板料的分析
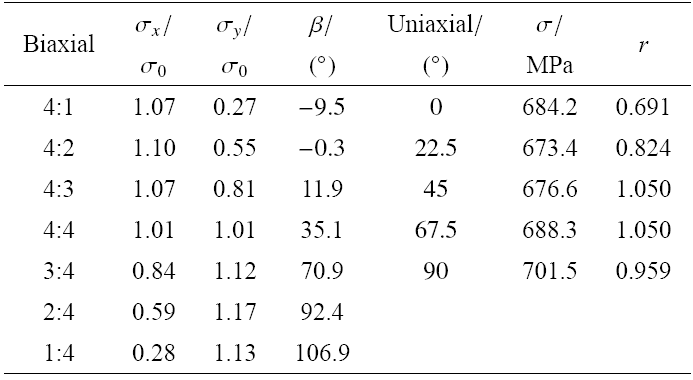
为了进行5754O铝合金[36]板料的各向异性分析, 首先给出板料的力学性能数据$(\varepsilon^\text p_0=0.002)$, 见表1所示, 具体包括了与轧制方向成$\theta$角度的单拉试验点(应力、$r$ 值)和双拉试验点, 其中$\beta$为平面应力状况下的塑性应变比方向角. 将力学性能代入上述的参数求解表达式中, 所得结果列于表2, 取$A_7=-4.688$.Table 1
表1
表15754O铝合金的力学性能
Table 1Mechanical properties of 5754O aluminum alloy
 |
新窗口打开
Table 2
表2
表2根据5754O铝合金求解的各向异性参数值
Table 2The values of anisotropy parameter solved according to5754O aluminum alloy
 |
新窗口打开
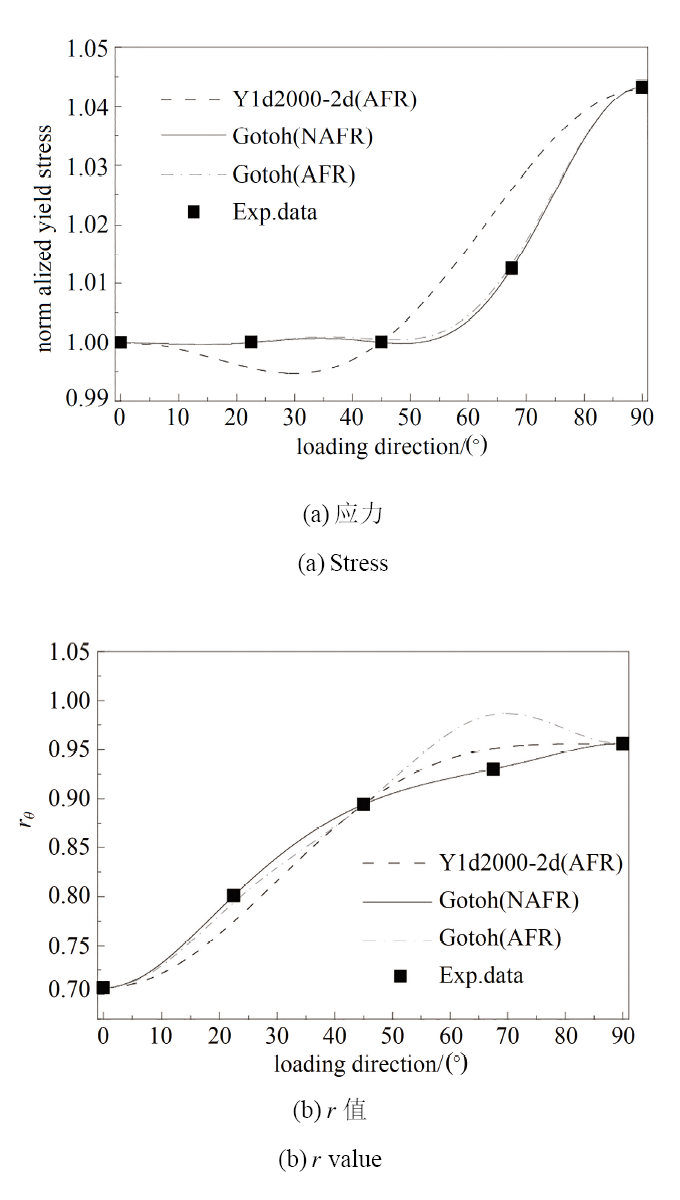
针对5754O铝合金, 将以上结果代入式(24)和式(37)分别用于应力、$r$值的计算, 并结合Yld2000-2d屈服准则绘制曲线图与试验点进行对比. 关于金属板料的各向异性分布状况如图1 所示; 平面应力状态下理论屈服轨迹与实验点的对比结果如图2所示; 考虑到剪应力的存在, 在分析含剪应力作用下的屈服曲面见图3.
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图15754O铝合金各向异性
-->Fig.1Anisotropy of 5754O aluminum alloy
-->
 显示原图|下载原图ZIP|生成PPT
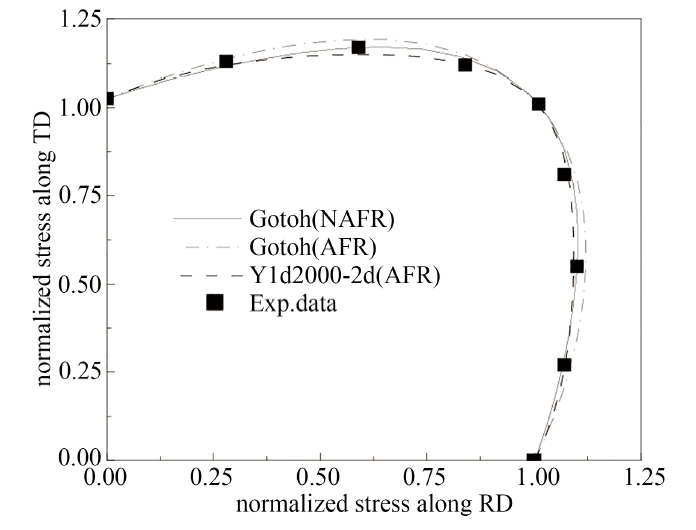
显示原图|下载原图ZIP|生成PPT图25754O铝合金板料屈服轨迹
-->Fig.2Yield locus of 5754O aluminum alloy sheet
-->
 显示原图|下载原图ZIP|生成PPT
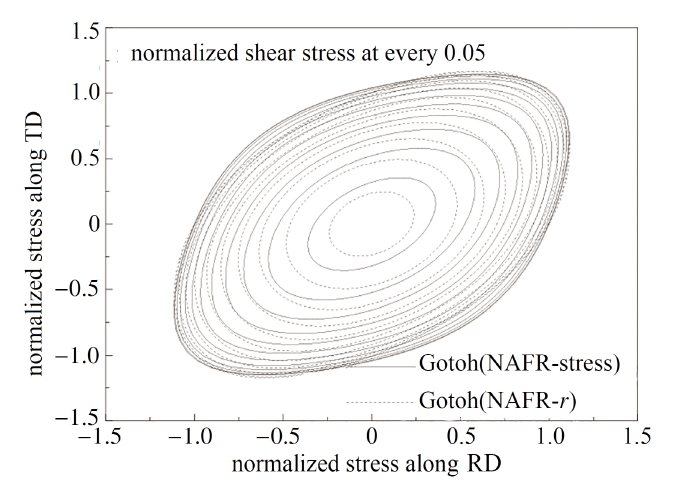
显示原图|下载原图ZIP|生成PPT图35754O铝合金含剪应力屈服轨迹
-->Fig.3Shear stress yield locus of 5754O aluminum alloy
-->
图1中, 关于$r$值和正则化屈服应力的分布证实, 基于NAFR的Gotoh函数与试验结果吻合很好, 而建立在AFR下的Gotoh及Yld2000-2d函数与试验点存在些许差异.
由图2总结出, 应用NAFR的Gotoh函数能够更精确地预测平面应力状态下的屈服轨迹, Yld2000-2d屈服准则不仅参数求解难度高, 且预测精度略微不足; 图3指出, 尽管考虑到剪应力的影响, 但基于NAFR的 Gotoh函数仍可对屈服行为进行精确表征.
2.2 DP980先进高强钢的分析
下面对DP980先进高强钢的各向异性和屈服行为进行分析, 给出了DP980先进高强钢[37-38]的力学性能数据$(\varepsilon^\text p_0=0.002)$, 如表3所示, 为了较准确的评价理论屈服轨迹与试验点的误差, 取$A_7=-5.974$. 其中Gotoh, Yld2000-2d 屈服准则的各向异性参数计算结果, 如表4所示.Table 3
表3
表3DP980先进高强钢的力学性能
Table 3Mechanical properties of DP980 advanced high strength steel
 |
新窗口打开
Table 4
表4
表4由DP980先进高强钢求解的各向异性参数
Table 4The values of anisotropy parameter solved by DP980 advanced high-strength steel
 |
新窗口打开
结合本文所考虑的参数求解方法, 将$A_1\sim A_9$、$\beta_1\sim \beta_8$分别用于描述该金属板料在单向拉伸状态下的力学性能分布预测、绘制平面应力状态下的屈服行为和涉及剪应力的屈服面, 具体内容分别见图4、图5和图6所示.
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图4DP980先进高强钢各向异性
-->Fig.4Anisotropy of DP980 advanced high strength steel
-->
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图5DP980先进高强钢板料屈服轨迹
-->Fig.5Yield locus of DP980 advanced high strength steel
-->
 显示原图|下载原图ZIP|生成PPT
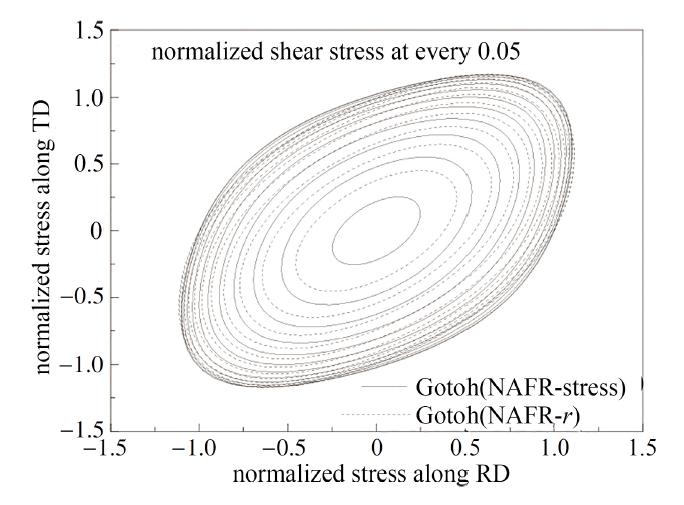
显示原图|下载原图ZIP|生成PPT图6DP980先进高强钢含剪应力屈服轨迹
-->Fig.6Shear stress yield locus of DP980 advanced high strength steel
-->
图4可以看出, 基于AFR的Yld2000-2d准则对应力各向异性预测最次; 基于AFR的Gotoh准则对$r$ 值的预测也存在较大偏差.
由图5可见, Gotoh根据NAFR推导的理论函数其对应的屈服轨迹与试验点最接近, 其他理论屈服轨迹与试验点结果皆存在稍大差异; 图6表明, 随着剪应力值的增大, Gotoh准则导出的两表面之间差异更加显著, 这是因为剪切各向异性系数取决于它是用$r$值还是用屈服应力来定义.
2.3 SAPH440结构钢的分析
近年来, 由于汽车的迅速发展, 汽车构架、车轮等结构件有着极大的需求, 具有钢质纯净、组织均匀、冲压性能良好等特点的SAPH440结构钢得到了广泛的应用. 为了探索SAPH440结构钢的复杂变形行为, 其力学性能数据[39] $(\varepsilon^\text p_0=0.002)$ 如表5 所示, 取$A_7=-5.477$. 计算所得参数值如表6所示.Table 5
表5
表5SAPH440结构钢的力学性能
Table 5Mechanical properties of SAPH440 structural steel
 |
新窗口打开
Table 6
表6
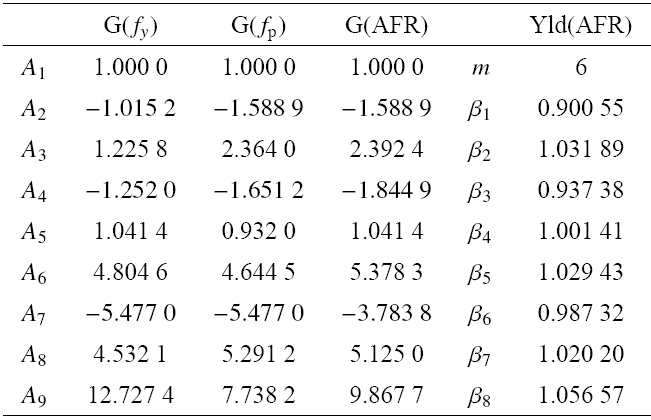
表6根据SAPH440结构钢求解的各向异性参数
Table 6The values of anisotropy parameter solved by SAPH440 structural steel
 |
新窗口打开
应力和$r$值的各向异性分布曲线对比图如图7所示, 由图可见, 不同屈服准则针对同种板料在描述各向异性时有显著影响; 基于不同流动规律的同一屈服准则, 其各向异性表征能力也明显不同, 与5754O、DP980板料的预测规律相似.
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图7SAPH440结构钢各向异性
-->Fig.7Anisotropy of SAPH440 structural steel
-->
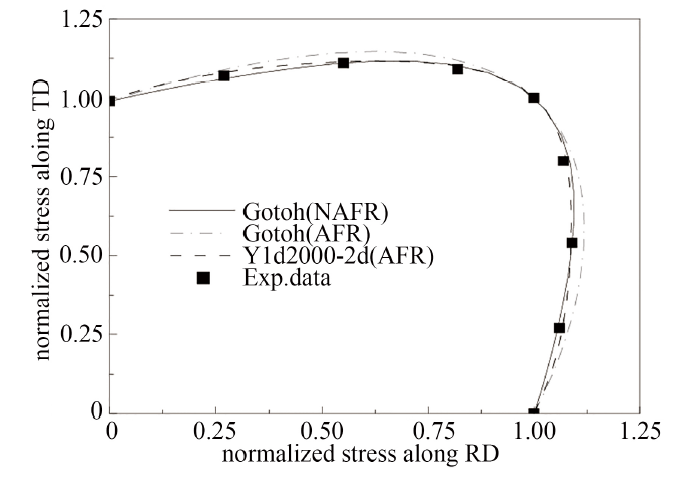
图8旨在针对平面应力状态, 表征理论与试验屈服轨迹随应力比的变化趋势, 若以等双拉为界, 理论屈服轨迹均呈明显的不对称现象, Gotoh(NAFR)以及Yld2000-2d(AFR)对应的屈服轨迹与试验点都较为接近, 其余曲线偏差较大; 图9为考虑到剪应力的复杂加载路径下, 其屈服面的对比, 由图9可以看出, 屈服面始终呈外凸状.
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图8SAPH440结构钢板料屈服轨迹
-->Fig.8Yield locus of SAPH440 structural steel
-->
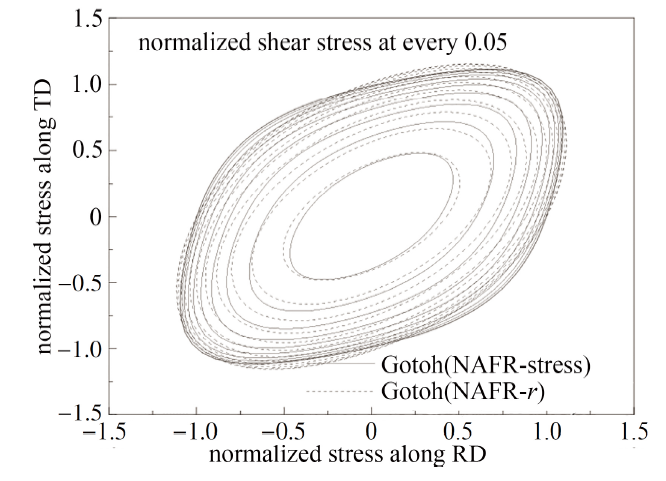
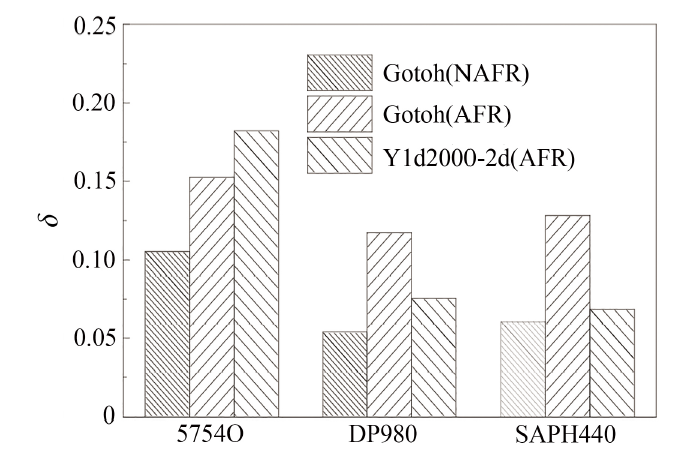
通过上述分析表明: 基于NAFR的Gotoh屈服函数对各向异性屈服行为有着更准确的表征能力, 无论是应力、$r$值和平面应力状态下的屈服轨迹, 其与试验点最为接近. 为了更可靠的评价理论屈服轨迹与试验点的吻合程度, 其精度误差见如图10所示, 结果显示: 基于NAFR得到的Gotoh函数拟合误差最低, 效果最好. 图3、图6和图9在考虑到剪应力的状态下, 进一步验证了板料其屈服面外凸的情形, 表明板料屈服面在复杂加载路径下始终呈外凸状.
关于误差计算公式如下
\begin{equation*}\delta=\sum\limits^n_{i=1}\dfrac{d_i}{\sqrt{(x^2_i+y^2_i)}}\tag*{(50)}\end{equation*}
其中$(x_i,~y_i)$为试验点坐标, $d_i$为试验点与曲线的法向距离, $n$为试验点个数.
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图9SAPH440结构钢含剪应力屈服轨迹
-->Fig.9Shear stress yield locus of SAPH440 structural steel
-->
 显示原图|下载原图ZIP|生成PPT
显示原图|下载原图ZIP|生成PPT图10误差对比图
-->Fig.10Chart of deviation
-->
3 结 论
以Gotoh四次多项式屈服准则为主, 具体分析了基于NAFR求解其参数表达式的过程, 并将其分别用于研究3种板材在小变形范围内复杂加载路径下的屈服行为, 得出以下结论:(1)对于各向异性板料来说, 两种参数求解方法所求的参数明显不同, 得到的屈服应力比曲线和$r$值曲线随加载角度的变化关系也不同. 当参数是根据应力力学性能求解得到时, 屈服准则更适用于表征涉及应力方面的函数关系; 当参数是根据$r$值计算得到时, 屈服准则更适用于揭示与塑性变形相关的关系. 由于屈服准则本身的局限性, 若交换描述对象, 则均不能对各向异性行为作出精确表征.
(2)板料的屈服轨迹受面内各向异性的影响较为明显, 以等双拉为界的上下两部分屈服轨迹呈不对称形状. 在理论屈服轨迹对比中, 基于NAFR得到的理论屈服轨迹与试验点吻合的很好, 误差小, 与两种关联流动曲线相比, 具有更显著的准确性.
(3)在含剪应力屈服轨迹中, 外凸的曲面形状能够得到合理的反映, 即复杂加载路径下板料的屈服轨迹始终保证外凸. 考虑到上述方面的比较, 实际应用中, 相比于常规解法, 基于NAFR的屈服准则具备明显适用性.
附录 参数求解表达式
\begin{equation*}\left.\begin{split}&A_1=1, A_5=\sigma^4_0/\sigma^4_{90}, A_7=1\\&A_2=\dfrac{-2\sigma^4_0}{\sigma^4_b}+\dfrac{16\sigma^4_0}{3\sigma^4_p}+\dfrac{\sigma^4_0}{6\sigma^4_q}-\dfrac{\sigma^4_0}{\sigma^4_{90}}-\dfrac{7}{2}\\&A_3=\dfrac{7\sigma^4_0}{2\sigma^4_{90}}+\dfrac{5\sigma^4_0}{\sigma^4_b}-\dfrac{8\sigma^4_0}{\sigma^4_p}-\dfrac{\sigma^4_0}{2\sigma^4_q}+\dfrac{7}{2}\\\end{split}\right\}\tag*{(A1)}\end{equation*}\begin{equation*}\left.\begin{split}&A_4=\dfrac{8\sigma^4_0}{3\sigma^4_p}+\dfrac{\sigma^4_0}{3\sigma^4_q}-\dfrac{2\sigma^4_0}{\sigma^4_b}-\dfrac{7\sigma^4_0}{2\sigma^4_{90}}-1\\&A_6=\dfrac{(8+4\sqrt{2})\sigma^4_0}{\sigma^4_{22.5}}+\dfrac{(8-4\sqrt{2})\sigma^4_0}{\sigma^4_{67.5}}-\dfrac{4\sigma^4_0}{\sigma^4_{45}}+\\&\quad\quad\dfrac{2\sigma^4_0}{\sigma^4_b}-\dfrac{16\sigma^4_0}{3\sigma^4_p}-\dfrac{\sigma^4_0}{6\sigma^4_q}-\dfrac{7}{2}\\&A_8=\dfrac{(8-4\sqrt{2})\sigma^4_0}{\sigma^4_{22.5}}+\dfrac{(8+4\sqrt{2})\sigma^4_0}{\sigma^4_{67.5}}-\dfrac{4\sigma^4_0}{\sigma^4_{45}}+\\&\quad\quad\dfrac{7\sigma^4_0}{2\sigma^4_{90}}+\dfrac{2\sigma^4_0}{\sigma^4_b}+\dfrac{8\sigma^4_0}{3\sigma^4_p}-\dfrac{\sigma^4_0}{3\sigma^4_q}\\&A_9=\dfrac{24\sigma^4_0}{\sigma^4_{45}}+\dfrac{7\sigma^4_0}{2\sigma^4_{90}}-\dfrac{5\sigma^4_0}{\sigma^4_b}+\dfrac{8\sigma^4_0}{\sigma^4_p}+\dfrac{\sigma^4_0}{2\sigma^4_q}-\\&\quad\quad\dfrac{16\sigma^4_0}{\sigma^4_{22.5}}-\dfrac{16\sigma^4_0}{\sigma^4_{67.5}}+\dfrac{5}{2}\end{split}\right\}\tag*{(A1)}\end{equation*}\begin{equation*}\left.\begin{split}&A_1=1,A_7=1\\&A_2=\dfrac{-4r_0}{r_0+1}\\&A_3=\dfrac{5r_0+5r_{90}+39r_0r_{90}-1}{2r_0+6r_{90}+6r_0r_{90}+2}\\&A_4=\dfrac{-4r_{90}(3r_0+1)}{r_0+3r_{90}+3r_0r_{90}+1}\\&A_5=\dfrac{3r_0+r_{90}+3r_0r_{90}+1}{r_0+3r_{90}+3r_0r_{90}+1}\end{split}\right\}\hskip 18mm\tag*{(A2)}\end{equation*}
其中$A_6$, $A_8$, $A_9$由$22.5^\circ$, $45^\circ$, $67.5^\circ$方向上的单拉$r$值确定.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | |
| [2] | . . |
| [3] | . . |
| [4] | |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . |
| [12] | . |
| [13] | . |
| [14] | . [博士论文]. . [PhD Thesis]. |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . |
| [24] | . |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | . |
| [29] | . |
| [30] | . |
| [31] | . |
| [32] | , |
| [33] | . |
| [34] | |
| [35] | . . |
| [36] | . . |
| [37] | |
| [38] | . |
| [39] |
