, 胡平STRESS-CONSTRAINED TOPOLOGY OPTIMIZATION BASED ON IMPROVED BI-DIRECTIONAL EVOLUTIONARY OPTIMIZATION METHOD
WangXuan, HuPing中图分类号:O342,O346
通讯作者:
收稿日期:2017-08-22
接受日期:2018-03-1
网络出版日期:2018-02-10
版权声明:2018《力学学报》编辑部《力学学报》编辑部 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (5742KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
近20年来连续体结构拓扑优化获得了快速发展,成为工程创新设计的强有力工具. 各种拓扑优化方法,例如基于材料分布的均匀化方法[1]、密度法/各向同性实体材料惩罚法(solid isotropic material with penalization, SIMP)[2]、渐进结构优化法(evolutionary structural optimization, ESO)[3]、独立连续映射法(independent continuous mapping method, ICM)[4],基于几何边界描述的水平集方法(level set method, LSM) [5],以及最近发展的移动可变形组件法(moving morphable components, MMC) [6],都被用来解决各种结构拓扑优化设计问题[7,8,9,10,11,12,13,14].由应力集中、或高应力值所引起的结构断裂、疲劳破坏严重影响其使用寿命,因此研究应力约束拓扑优化问题具有重要意义. 与体积约束下的刚度最大化模型相比,考虑应力约束的拓扑优化有其自身的难点. 第一个难点是所谓的“奇异解现象” [15,16]. 奇异解现象起源于桁架优化问题,Cheng和Jiang对拓扑优化问题中的奇异解给出了数学解释[15],即它主要是由应力约束的不连续导致的. Duysinx和Bendsoe[17]指出在应力约束的连续体拓扑优化中也存在奇异解现象. 目前常用的处理奇异解现象的方法包括
应力约束拓扑优化设计的第二个难点在于应力作为一个局部的物理量所引起的大量局部性约束. 一般情况下,为了较为准确 地计算结构的应力场,需要加密有限元网格,导致局部应力约束的数目增加,从而显著增加了局部应力约束的敏度分析的计算 代价[20,21]. 为了处理这个问题,通常采用逼近最大局部函数值的凝聚函数将局部应力约束转化为一个全局的应力约束[18,20-26]或者“分块”的应力约 束[21,23,27]. 目前较为常用的凝聚函数有P 范数[20,21,22,23]和Kieisselmeier-Steinhauser (K-S)函数[18,20,24-28],其中Yang和Chen[24]早在1996年采用K-S函数将诸多应力约束化为一个应力约束. 另外一种有效方式是隋允康等利用von Mises强度理论,借助应变能将应力约束全局化,从而显著减少了应力约束个数[4].
应力约束拓扑优化问题的第三个难点在于应力的高度非线性行为. 临近区域密度值的改变对结构某些关键区域的应力水平和非线性行为产生严重影响,特别是具有较大的空间应力梯度区域,如有凹陷角、拐角处[18,23,29]. 这就要求结构拓扑优化列式具备有效降低或者消去应力集中现象的能力,而且需要求解算法与优化列式保持数值一致性以确保优化问题的稳定收敛[23,29].
大部分考虑应力相关的拓扑优化问题都是基于SIMP法[17-27,30]和水平集方法[29,31-33]. 此外,Cai等[28,34]将水平集函数与有限胞元法结合,提出了一种求解应力约束拓扑优化问题的新框架. 隋允康 等[4,35-37]基于ICM法提出了一系列有效求解应力约束拓扑优化问题的策略,更多关于应力约束和其他力学性能约束的处 理方法可以参照文献[38]. 荣见华等[39]将ICM法与ESO方法结合,通过每步迭代不断更新位移和应力约束,提出了一种新的应力优化思路.
调查发现,常规的ESO/BESO法[8,40]研究应力约束的拓扑优化问题鲜有报道,这是因为对于考虑应力约束的优化问题而 言,结构的应力值对设计变量的变化特别敏感,从而常规的仅包含0
1 应力约束拓扑优化列式
1.1 拓扑优化模型
结构拓扑优化的目的是寻找一个满足某些约束条件的最优的材料分布,以使结构获得某种最优的结构行为,如结构的重量最轻或刚度最大化. 本文与文献[19,28,33]一样,考虑应力和体积约束下的柔顺性最小化问题,其对应的数学列式可表示如下Find: x
Min: $C = {\pmb F}^{\rm T}{\pmb U}$
$S.t.: \left\{ \begin{array}{l} {\pmb K}{\pmb U} ={\pmb F} \\ \sum_{e = 1}^{N_e } V_e x_e = V_0 f_{\rm v} \\ \sigma_{\max}^{\rm vM} = {\max } \left( \sigma _e^{\rm vM}\right) \leqslant \sigma ^\ast , \ \ e = 1,2, \cdots, N_e \end{array} \right. \ \ (1)$其中, ${\pmb x} = \left[ {x_1 ,x_2 , \cdots ,x_{N_e } } \right]$为单元设计变量的集合,$N_e$为总的设计变量的数目;$C$表示结构的柔顺性目标函数; ${\pmb K}$为结构的整体刚度阵,由单元刚度阵${\pmb K}_e$组装形成;${\pmb U},{\pmb F}$分别为结构的位移向量和载荷列阵;$V_e ,V_0$分别为第$e$个单元的体积和整个设计域的体积,$f_v $为准许的材料体积分数;$\sigma _e^{\rm vM} $为每个单元的vonMises应力,$\sigma _{\max}^{\rm vM} ,\sigma^\ast $为结构的最大von Mises应力及其约束限值.
1.2 插值格式
如上文所述,与柔顺性最小化问题不同的是,应力约束拓扑优化问题存在其自身的难点,如奇异最优解现象、大量局部应力约束导致的巨大计算量及应力约束的高度非线性问题等.为了克服应力约束的奇异性问题,获得清晰的拓扑构型,这里采用文献[23]的方法,对结构刚度和应力采用不同的幂指数进行惩罚.弹性模量、应力与单元密度之间的关系可定义为$ E_e^\ast = x_e^{p_1 } E_0\,, \ \ {\pmb\sigma}_e = x_e^{p_2 } {\pmb\sigma}_e^0 (2) $
式中, ${\pmb\sigma}_e^0 ={\pmb D}_0{\pmb B \pmb u}_e = [\sigma _{e,x} ,\sigma _{e,y} ,\tau _{e,xy} ]^{ T}$是在 第$e$个单元中心点处计算得到的包含3个应力分量的应力列阵;$p_1 ,p_2$分别为弹性模量和应力的惩罚参数,本文取$p_1 =3$, $p_2= 0.5$;$E_0 , {\pmb D}_0$分别为实体材料的弹性模量、弹性矩阵,${\pmb B}$为应变位移矩阵. 式(1)中每个单元的von Mises应力可以通过下式计算
$ \sigma _e^{\rm vM} = \left( {\sigma _{e,x}^2 + \sigma _{e,y}^2 - \sigma _{e,x} \sigma _{e,y} + 3\tau _{e,xy}^2 } \right)^{1 / 2} (3) $
1.3 全局应力度量
为了减少局部应力约束导致的计算代价,通常采用凝聚函数来形成一个全局的应力约束. 较为常用的凝聚函数有P 范数和K-S函数. 不失一般性,本文使用K-S函数作为凝聚函数$ \sigma^{\rm KS}=\dfrac 1{\mu} \ln \Big [ \sum^{N_e}_{e=1} \exp \Big ( \mu \dfrac{\sigma^{\rm vM}_e}{\sigma^*}\Big ) \Big ] (4) $
理论上当参数$\mu $的值趋向于无穷大时,上式中的全局函数$\sigma^{\rm KS}$趋向于${\sigma _{\max}^{\rm vM} }/{\sigma ^{\ast }}$,因此,式(1)中的全局应力约束变为
$ \sigma ^{\rm KS} \leqslant 1 (5) $
需要注意的是,由于式(4)中参数$\mu $不可能取无穷大,这样会导致全局函数$\sigma^{\rm KS}$不能很好地逼近${\sigma _{\max}^{\rm vM} } / {\sigma ^{\ast }}$,为此, 利用式(6)来修正式(5)中的约束
$ \bar {\sigma }^{\rm KS} = c\sigma ^{\rm KS} \leqslant 1 (6) $
其中,修正参数 $c = {\sigma _{\max}^{\rm vM} }/ {\left( {\sigma ^{\ast } \cdot \sigma ^{\rm KS}} \right)}$.
2 灵敏度分析
2.1 目标函数和应力约束的敏度
利用伴随法可推导优化列式目标函数的敏度为$ \dfrac{\partial C}{\partial x_e } = - {\pmb u}_e^{\rm T} \dfrac{\partial {\pmb K}_e }{\partial x_e }{\pmb u}_e (7) $
根据链式法则很容易得到式(4)中$\sigma ^{\rm KS}$关于设计变量的敏度为
$ \dfrac{\partial \sigma^{\rm KS} }{\partial x_e } = \dfrac{\partial \sigma^{\rm KS} }{\partial \sigma _e^{\rm vM} }\left( {\dfrac{\partial \sigma _e^{\rm vM} }{\partial {\pmb\sigma}_e }} \right)^{\rm T}\dfrac{\partial {\pmb\sigma}_e }{\partial x_e } (8) $
从上式可以看出,要计算全局应力约束函数的敏度必须先确定K-S函数对von Mises应力的导数、von Mises应力对应力分量的导数、应力分量对设计变量的导数,下面分别计算这三项.
2.2 K-S函数对von Mises应力的导数
对式(4)中的K-S函数关于每个单元的von Mises应力求导可得$ \dfrac{\partial \sigma^{\rm KS} }{\partial \sigma _e^{\rm vM} } = \dfrac{\exp\left({\mu \dfrac{\sigma _e^{\rm vM} }{\sigma^\ast }} \right)}{\sigma^\ast \left( {\sum_{e = 1}^{N_e } {\exp\left({\mu \dfrac{\sigma _e^{\rm vM} }{\sigma^\ast }} \right)} } \right)} (9) $
2.3 von Mises应力对应力分量的导数
式(3)中von Mises应力关于3个应力分量的导数可表示为$ \left.\begin{array}{l} \dfrac{\partial \sigma _e^{\rm vM} }{\partial \sigma _{e,x} } = \dfrac{1}{2\sigma _e^{\rm vM} }\left( {2\sigma _{e,x} - \sigma _{e,y} } \right) \\ \dfrac{\partial \sigma _e^{\rm vM} }{\partial \sigma _{e,y} } = \dfrac{1}{2\sigma _e^{\rm vM} }\left( {2\sigma _{e,y} - \sigma _{e,x} } \right) \\ \dfrac{\partial \sigma _e^{\rm vM} }{\partial \tau _{e,xy} } = \dfrac{3\tau _{e,xy} }{\sigma _e^{\rm vM} } \end{array} \right\} (10) $
2.4 应力分量对设计变量的导数
根据式(2)可推导应力分量关于设计变量的导数$ \dfrac{\partial {\pmb \sigma}_e }{\partial x_e } = p_2 x_e^{\left( {p_2 - 1} \right)} {\pmb D}_0 {\pmb B}{\pmb u}_e + x_e^{p_2 } {\pmb D}_0 {\pmb B}\dfrac{\partial {\pmb u}_e }{\partial x_e } (11) $
将式(9)~式(11)代入式(8),再结合式(6),可得
$ \dfrac{\partial \bar {\sigma }^{\rm KS} }{\partial x_e } = C \dfrac{\partial \sigma^{\rm KS} }{\partial \sigma _e^{\rm vM} }\left( {\dfrac{\partial {\pmb\sigma}_e^{\rm vM} }{\partial {\pmb\sigma}_e }} \right)^{\rm T} \cdot \Big( p_2 x_e^{\left( {p_2 - 1} \right)} {\pmb D}_0 {\pmb B}{\pmb u}_e + x_e^{p_2 } {\pmb D}_0 {\pmb B}\dfrac{\partial{\pmb u}_e }{\partial x_e } \Big) (12) $
3 拉格朗日乘子法及优化算法
3.1 拉格朗日乘子的确定
在渐进结构优化方法中,由于结构体积作为进化参数所以体积约束很容易满足. 其他的约束均通过拉格朗日乘子法将约束函数引入到目标函数中,因此,修改的目标函数可表示为$ f = {\pmb U}^{\rm T}{\pmb K}{\pmb U }+ \lambda \left( {\bar {\sigma }^{\rm KS} - 1} \right) (13) $
其中$\lambda $为拉格朗日乘子. 可以看出：如果$\bar {\sigma }^{\rm KS} =1 $,则修改的目标函数等于原来的目标函数;否则,如果$\bar {\sigma }^{\rm KS}\leqslant 1$,取$\lambda = 0$,此时说明应力约束已经满足了;如果$\bar {\sigma }^{\rm KS} > 1$,$\lambda $趋向于无穷大,这说明需要在随后的迭代中减小结构的应力来满足应力约束.
为了计算式(13)中修改的目标函数关于设计变量的灵敏度,需要先确定拉格朗日乘子的值. 为了在程序中方便地实施计算,可将拉格朗日乘子重新定义为
$ \lambda = \dfrac{1}{\omega } - 1 (14) $
其中参数$\omega $的取值范围为[10-10,1]. 确定合适的参数$\omega$将使得应力约束条件满足. 因此,根据当前的应力值和敏度值估算下一次迭代的应力值
$ \bar {\sigma }_{k + 1}^{\rm KS} \approx \bar {\sigma }_k^{\rm KS} + \sum_{e = 1}^{N_e } {\dfrac{\partial \bar {\sigma }_k^{\rm KS} }{\partial x_e }} \Delta x_e (15)$
其中$k$为当前的迭代数. 根据下一次迭代的应力值及应力约束的限值采用二分法确定参数$\omega $,具体实施过程详见文献[41]. 一旦获得参数$\omega$的值,即可通过式(14)确定拉格朗日乘子的值,进而确定修改的目标函数关于设计变量的敏度
$ \dfrac{\partial f}{\partial x_e } = - {\pmb u}_e^{\rm T} \dfrac{\partial {\pmb K}_e }{\partial x_e }{\pmb u}_e + \lambda \dfrac{\partial \bar {\sigma }^{\rm KS} }{\partial x_e } (16) $
在渐进结构优化法中,设计变量的变化是根据敏度数的相对排序确定的[41,42,43],第$e$个单元所对应的敏度数可定义为
$ \alpha _e = - \dfrac{\partial f}{\partial x_e } (17) $
3.2 数值处理
为避免棋盘格和网格依赖性等数值不稳定问题,采用式(18)对式(17)中定义的单元敏度数过滤$ \tilde {\alpha }_e^ = \Bigg (\sum_{i = 1}^{Nr} {w_{e,i} \alpha _i } \Bigg)\Bigg / \,\Bigg(\sum_{i = 1}^{Nr} {w_{e,i} } \Bigg) (18)$
其中权重$w_{e,i} $定义为
(19)
式中$r_{e,i} $为单元$e$和单元$i$之间的距离,$N_r$是以单元$e$为中心、半径为$r_{\min} $的圆形邻域内的单元个数.
另外,数值研究表明,考虑敏度数的历史信息可以有效地改善优化过程的稳定性,即采用前后两轮迭代的敏度数的均值作为当前敏度数的修正值来参与迭代,其表达式为
$ \hat {\alpha }_e^k = \dfrac{1}{2}(\tilde {\alpha }_e^k + \tilde {\alpha }_e^{k - 1} ) (20)$
BESO方法从完整的设计域开始,在优化过程中结构的体积不断地减小直到获得目标体积. 在每一步迭代中均以$\Delta x_e $的步长来更新设计变量,实现设计变量的增加或减少. 在常规的BESO方法[41,42]中,$\Delta x_e =1$意味着设计变量只能取0或1两个值,在文献[43]中,取$\Delta x_e = 0.02$,这意味着设计变量除了取0$\sim$1值之外,还可以取其他一些中间值. 本文考虑应力约束的结构拓扑优化问题,在研究中发现最大应力值$\bar {\sigma }^{\rm KS} $对设计变量的变化特别敏感,因此通过使设计变量变化量$\Delta x_e $随着迭代步数的增加而逐渐减小的策略来稳定优化过程.
3.3 优化算法
改进的渐进结构优化方法求解应力约束拓扑优化问题的算法流程可归纳如下.(1) 定义构型参数：定义容许体积分数$f_{\rm v}$、体积进化率$ER$及应力约束限值$\sigma^\ast $等构型参数.
(2) 有限元分析：求解位移场和应力场,进而根据式(4)计算$\sigma ^{\rm KS}$的值.
(3) 材料体积更新：通过$V_{k + 1} = V_k (1 -ER)$决定下一个迭代步的材料体积,其中为材料体积进化率. 一旦到达目标体积分数$f_{\rm v} $,后续迭代中保持目标体积分数不变 .
(4) 灵敏度分析：根据式(7)和式(12)分别计算目标函数和应力约束函数的敏度,在此基础上根据3.1节的算法确定拉格朗日乘子的值.
(5) 敏度过滤及稳定性处理：根据式(17)定义单元敏度数,然后对敏度数进行过滤,再根据式(21)修正单元敏度数.
(6) 设计变量更新：通过下式来更新设计变量
$ x_e^{k + 1} = \left\{ \!\!\begin{array}{ll} {\min\left( {x_e^k + \Delta x_e \,, \ 1} \right)} \,, & \hat {\alpha }_e^k \geqslant \alpha _{\rm th} \max\left( {x_e^k - \Delta x_e\,, \ x_{\min} } \right) \,, & \hat {\alpha }_e^k < \alpha _{\rm th} \right.(21) $
其中$\Delta x_e = \max\left( {\zeta \Delta x_e ,10^{ - 3}} \right)$,$\zeta$是小于1的正常数,其目的是使设计变量变化量$\Delta x_e$随着迭代步数的增加而逐渐减小. $\Delta x_e$初值的选取不宜太大或太小,初值太大会导致目标函数和应力约束函数震荡,太小则不利于收敛. $x_{\min} $取很小的正数,作为设计变量下限以防止刚度矩阵奇异,这里取$x_{\min}= 10^{ - 4}$. $\alpha _{\rm th} $为敏度数阈值,可通过下一次迭代的目标体积及单元敏度数的排序确定,具体过程见文献[42].
(7) 收敛性判断：重复式(2) ~式(6),直到满足下列收敛条件之一,优化过程停止迭代
$ {\Big | \sum_{i = 1}^5 {(C_{k - i + 1} } - C_{k - 5 - i + 1} )\Big|}\Bigg / {\sum_{i = 1}^5 {C_{k - i + 1} } } \leqslant \mu _1 (22)$
$ {\Big | \sum_{i = 1}^5 (\sigma _{\max, k - i + 1}^{\rm vM} - \sigma _{\max, k - 5 - i + 1}^{\rm vM} )\Big | } \Bigg / \sum_{i = 1}^5 \sigma _{\max, k - i + 1}^{\rm vM} \leqslant \mu _2 (23)$
式中,$k$为当前的迭代步数,$\mu _1 ,\mu _2 $分别为柔顺性和最大von Mises应力的容许收敛误差,本文取$\mu _1 = \mu _2= 1\times 10^{ - 6}$.
4 数值算例与讨论
本节通过3个平面应力问题拓扑优化算例来展示本文改进的BESO方法处理应力约束拓扑优化问题的有效性.除非特殊声明,所有算例中变量和几何参数均使用无量纲参数,完全实体材料的杨氏模量$E_0$和泊松比分别设置为1.0和0.3,平面应力单元的厚度设为1.所有设计变量的初始值取$x_e = 1$,取参数$\mu = 10$,$\zeta = 0.99$,体积进化率$ER =0.01$,设计变量改变量$\Delta x_e = 0.04$.4.1 算例1
考虑经典的L形梁优化问题[20,23-26,28-31],几何区域和边界条件如图1所示,结构左边顶部固支,右上角A点受载荷$F = 10$作用,为了避免载荷作用点处的应力集中,将集中载荷平均分配到如图 1所示的邻近的5个节点上. 初始结构在载荷$F$作用下的最大的von Mises应力为7.770 6. 在本算例中,设置材料体积分数和应力约束限值分别为$f_v=0.4$, $\sigma^{\ast } = 6.0$. 结构由6400个四节点四边形单元来离散,过滤半径取$r_{\min} = 4$.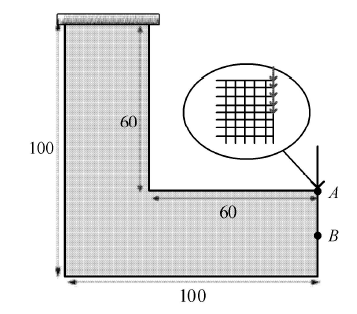
显示原图|下载原图ZIP|生成PPT图1L形梁设计域和边界条件
-->Fig. 1Design domain and boundary condition for L-shaped beam
-->
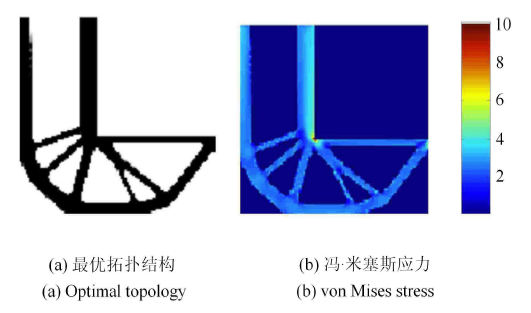
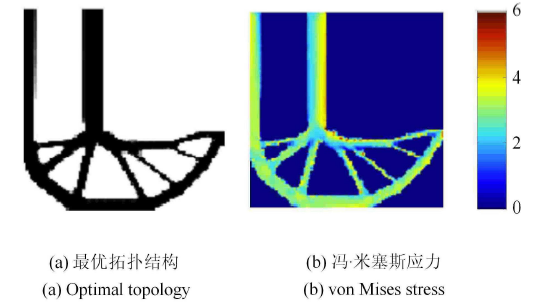
图2和图3展示了本文方法获得的优化结果,其中图2 是仅考虑体积约束的刚度最大化优化结果,图3是同时考虑了体积和应力约束的优化结果.
从图2可以看出,不考虑应力约束的L形梁在拐角处出现了明显的应力集中现象,而在考虑应力约束的情况下,L形梁的拐角处 出现了带有弧度的圆角(图3),这说明本文方法是非常有效的,可以获得边界灰度单元很少的清晰的拓扑构型,产生有效降 低应力集中效应的设计.
显示原图|下载原图ZIP|生成PPT图2不考虑应力约束L形梁的拓扑优化设计
-->Fig. 2Optimal topology designs for L-shaped beam without stress constraint
-->
显示原图|下载原图ZIP|生成PPT图3应力和体积约束下L形梁的拓扑优化设计
-->Fig. 3Optimal topology designs for L-shaped beam with stress and volume constraints
-->
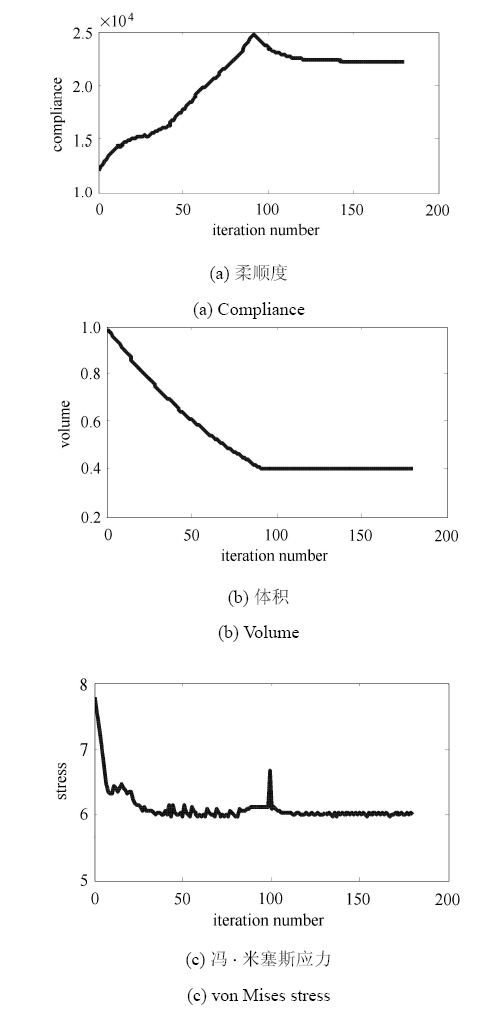
图4给出了体积和应力约束下L形梁优化问题目标函数和约束函数的迭代历史. 最终的柔顺度、体积分数及最大的von Mises应力值(无量纲)列于表1中. 从图4可以看出,本文方法迭代过程稳健,最终设计很好地满足了体积约束和应力约束. 从表1可以看出,基于体积约束下的最小柔顺性优化模型获得的最终结构的最大应力值(9.649 3)大于初始结构的最大应力值(7.770 6),优化后结构虽然减重了,但是L形梁拐角处的应力集中效应会使结构容易发生断裂等破坏行 为;而基于式(1)描述的优化模型获得的结构的最大应力值(6.004 6)比初始结构的最大应力值(7.770 6)要小, 这样在对结构进行减重的同时还增加了结构的强度.
显示原图|下载原图ZIP|生成PPT图4体积和应力约束下L形梁目标函数和约束函数的迭代历史
-->Fig. 4Iterative histories of objective and constraint functions of L-shaped beam with volume and stress constraints
-->
Table 1
表1
表1算例1 L形梁优化结果
Table 1Optimal results for L-shaped beam in Ex.1
| Case | Compliance | Volume | Max stress |
|---|---|---|---|
| Case 1 | 20 255 | 0.4 | 9.649 3 |
| Case 2 | 22 219 | 0.4 | 6.004 6 |
新窗口打开
4.2 算例2
第2个算例考虑L形梁右边中点B处(图1)受集中载荷作用的优化问题. 在本算例中,设置材料体积分数和应力约束限值分别为$f_v=0.4, \sigma ^{*}= 6.0$. 载荷的大小和方向以及结构的离散网格与算例1相同.为了避免应力集中效应,与算例1类似,将集中载荷均匀分布到相邻的5个网格节点上.初始结构在载荷$F$作用下的最大的von Mises应力为7.772 5,过滤半径取$r_{min} = 3.5$.图5展示了本文方法获得的优化结果,其中图5(a)是体积约束下的刚度最大化优化结果,图5(b)是体积约束下的应力最小化优化结果,图5(c)是体积和应力约束下的刚度最大化优化结果. 为了便于辨识,其优化结果分别标记为Case 1 、Case 2和Case 3. 此处Case 3的应力约束限值是根据Case 2的优化结果选取的. 最终的柔顺度、体积分数及最大的von Mises应力值列于表2中.
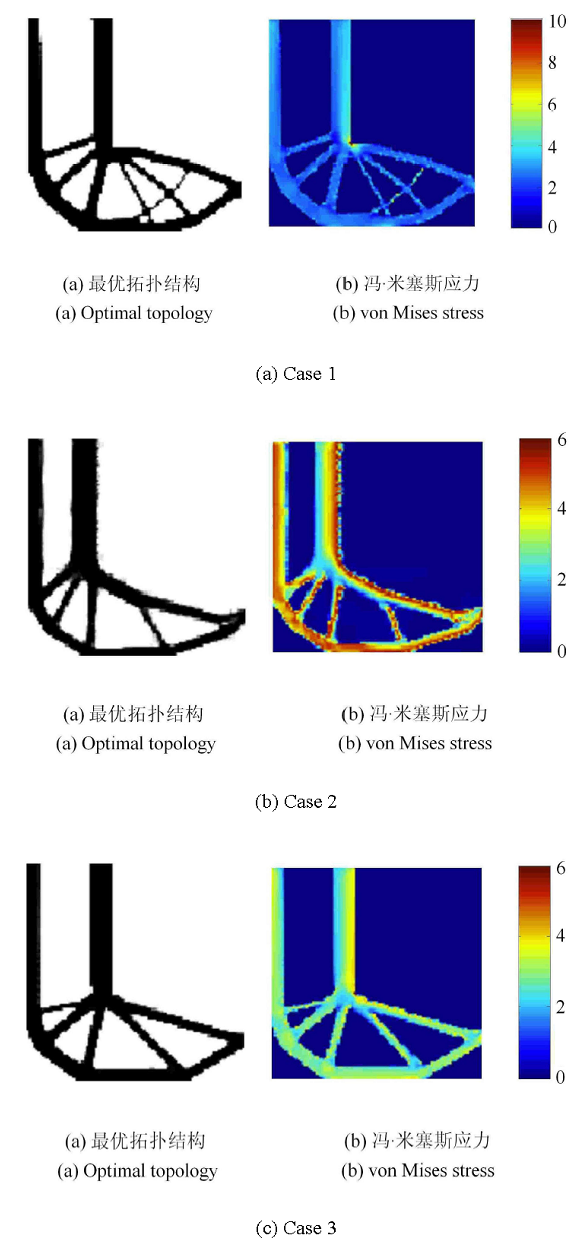显示原图|下载原图ZIP|生成PPT图5L形梁的拓扑优化设计
-->Fig. 5Optimal topology designs for L-shaped beam
-->
Table 2
表2
表2算例2 L形梁优化结果
Table 2Optimal results for L-shaped beam in Ex.2
| Case | Compliance | Volume | Max stress |
|---|---|---|---|
| Case 1 | 20 008 | 0.4 | 10.173 9 |
| Case 2 | 38 640 | 0.4 | 5.778 5 |
| Case 3 | 21 099 | 0.4 | 5.999 7 |
新窗口打开
从图5和表2可知,无论是否考虑应力约束或最小化,本文改进的BESO方法均可以获得清晰的拓扑构型. 考虑应力的拓扑构型与不 考虑应力的拓扑构型不同,体积约束下刚度最大化的L形梁(Case 1的结果)在拐角处存在明显的应力集中效应,优化后结构的最大应力(10.173 9)要比初始结构的最大应力(7.772 5)要大,而考虑 应力的优化设计(Case 2和Case 3的结果)能够有效降低应力集中效应. 工程中的应力集中效应可能导致结构破坏事故,因此,对于设计者而言,从构型概念设计时就限制最大应力是非常有必要的.
4.3 算例3
第3个算例考虑T形梁优化问题,几何区域和边界条件如图6所示,结构左边和右边完全固支,顶部左边点受集中载荷$F =10$作用,为了避免载荷作用点处的应力集中,将载荷平均分配到如图6所示的邻近的5个节点上.初始结构在载荷$F$作用下的最大的von Mises应力为4.563 3. 在本算例中,设置材料体积分数和应力约束限值分别为$f_v=0.4$, $\sigma ^{\ast }= 3.8$,过滤半径取$r_{\min}= 3.5$. 结构由 8 800 个四节点四边形单元来离散.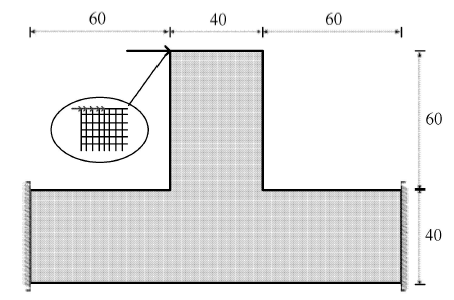
显示原图|下载原图ZIP|生成PPT图6T形梁设计域和边界条件
-->Fig. 6Design domain and boundary condition for T-shaped beam
-->
图7展示了本文方法获得的优化结果,其中图7(a)是体积约束下的刚度最大化优化结果,图7(b)是体积约束下的应力最小化优化结果,图7(c)是体积和应力约束下的刚度最大化优化结果. 为了便于辨识,其优化结果分别标记为Case1 , Case 2和Case 3. 此处Case 3的应力约束限值也是根据Case 2的优化结果选取的. 最终的柔顺度、体积分数及最大的von Mises应力值列于表3中.
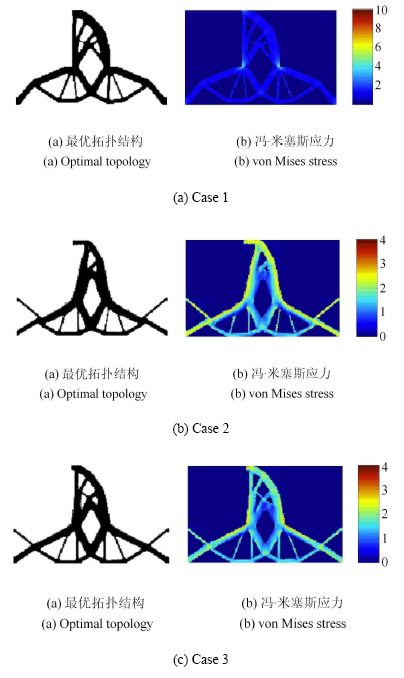显示原图|下载原图ZIP|生成PPT图7T形梁的拓扑优化设计
-->Fig. 7Optimal topology designs for T-shaped beam
-->
Table 3
表3
表3T形梁优化结果
Table 3Optimal results for T-shaped beam
| Case | Compliance | Volume | Max stress |
|---|---|---|---|
| Case 1 | 7 107.1 | 0.4 | 6.432 3 |
| Case 2 | 10 385 | 0.4 | 3.226 9 |
| Case 3 | 8 496.2 | 0.4 | 3.801 5 |
新窗口打开
从优化结果可以看出基于刚度优化的设计(图7(a))与应力相关设计(图7(b)、图7(c))的拓扑构型明显不同,体积约束下基于刚度优化的T形梁在两个拐角处出现了明显的应力集中现象,其最大应力(6.432 3)比初始结构的最大应力(4.563 3)要大,而考虑应力的设计能够有效降低应力集中效应. 这说明本文改进的BESO方法可以有效地获得降低应力集中效应的拓扑构型设计.
5 结 论
本文建立改进的BESO方法求解了应力约束的拓扑优化问题,采用K-S函数来凝聚局部应力约束以减少与局部应力约束相关的计算代价,利用拉格朗日乘子法施加应力约束,由二分法确定拉格朗日乘子的值. 然后,详细推导了基于BESO方法的应力约束拓扑优化模型及其灵敏度列式,三个算例表明本文方法可有效地处理应力相关的拓扑优化问题. 比较发现,考虑应力约束和不考虑应力约束的拓扑构型不同;考虑应力约束的设计能够有效降低结构关键区域的应力集中效应.The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | . |
| [4] | . . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . . |
| [9] | . . |
| [10] | . . |
| [11] | . . |
| [12] | . . |
| [13] | . . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . |
| [24] | . |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | . |
| [29] | . |
| [30] | . |
| [31] | . |
| [32] | . |
| [33] | . |
| [34] | . |
| [35] | . . |
| [36] | . . |
| [37] | . . |
| [38] | |
| [39] | . . |
| [40] | . |
| [41] | . |
| [42] | . |
| [43] | . |
