, 胡杰NONLINEAR MECHANICS MODEL FOR JOINT INTERFACE OF ASSEMBLED STRUCTURE
WangDong中图分类号:O342
文献标识码:A
收稿日期:2017-04-14
接受日期:2017-11-7
网络出版日期:2018-02-20
版权声明:2018《力学学报》编辑部《力学学报》编辑部 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (1206KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引言
大型武器装配结构中存在着多种形式的连接结构,如螺栓、楔环、铆接、过盈配合等。这些结构部组件之间主要是通过各种各样的连接界面传递载荷。连接界面上复杂的接触机理是造成结构出现复杂非线性动力学行为的主要原因[1,2]。连接结构动力学问题就成为制约复杂结构动力学分析、高保真预测仿真、设计、优化和控制等问题的关键和瓶颈所在,而其核心问题是建立考虑连接界面非线性行为的力学模型[3,4]。连接界面力学建模研究的主要挑战来源于由界面的非线性、时变性、不确定性等引起的跨尺度、多物理场等复杂力学行为,以及对连接界面直接试验观测的困难性[5]。振动环境下,连接界面在法向发生接触、分离和碰撞;在切向发生黏着、摩擦和滑动,这些力学行为都具有明显的非线性和跨尺度等特点。如,界面法向碰撞行为既可能发生在微观尺度上,也可能发生在宏观尺度上;切向滑动行为既包括微观尺度的滑移,也包括宏观尺度的滑动,结合面微观滑移发生在微纳米尺度上,而宏观滑动则可能发生在毫米尺度以上。****们通过试验和理论研究发现连接界面上的黏滑行为,表现为恢复力-位移的非线性软化以及迟滞非线性等特征[1,2,6,7]。这些行为直接造成了刚度、阻尼的非线性。一方面,刚度随着变形增加而减小,体现为恢复力与位移的刚度非线性软化,且发生宏观滑移之后仍然存在滑移刚度;另一方面,阻尼随着载荷是变化的,表现为恢复力与能量耗散的幂级数特性[7]。连接界面非线性力学行为的实验研究主要有两大类,一类是静态实验方法,利用准静态试验机进行静力试验,并结合数字图像处理技术方法开展研究工作[8]。另一类是动态实验方法,采用共振实验原理研究典型连接界面的非线性力学行为[9,10,11,12,13]。静力试验的主要缺点是分辨率低,实验结果很容易被夹具的弹性变形所掩盖;而动态实验法的优点是分辨率高,但控制难度较大。 Gaul等人对螺栓连接结构施加周期性激励作用,验证了激励力-位移的非线性软化刚度特征,并发现了随着切向载荷的增大,界面逐步从微观黏滑状态演化到宏观滑移状态[12]。Sandia针对螺栓连接结构展开了深入的研究,发现了连接界面的非线性刚度软化、迟滞非线性等特征[13]。此外,****们也有通过有限元方法得出位移和恢复力的非线性软化刚度特性,揭示连接界面上由微观滑移引起的刚度软化、迟滞非线性等行为[14,15]。
结构动力学问题中,传统上对于连接界面一般采用忽略非线性或采用等效线性化方法进行处理[1,5]。等效线性化处理方法就是用线性的等效刚度和等效阻尼元件模拟连接界面,模型参数利用模态试验结果进行标定。等效线性化处理方法忽略了界面非线性的本质,常常出现在某种试验条件下标定的模型无法预测其他试验条件下结构动力学行为的问题。因此,这些处理方法无法满足连接结构非线性动力学研究的需要。随着接触力学、摩擦学和塑性力学等学科的发展,人们开始从不同的角度来考虑连接问题,建立了多种描述连接界面非线性行为的模型。
第一类方法是基于唯象的数学模型,采用数据拟合的方法描述结合面上的黏滑摩擦行为[16,17]。经典的模型主要有考虑黏滑特性的Iwan弹簧滑块模型[18,19]、Lugre毛刷模型[20]、 Valanis模型等[20],如图1所示。以上模型都是根据连接界面上黏滑行为抽象出来的唯象数学模型,多数参数缺少真实的物理意义,难以描述表面粗糙度特征和接触机理对非线性行为的影响。
相比于Lugre毛刷模型和Valanis模型,Iwan模型能够更好的描述连接界面的微观黏滑演化过程,而且模型的部分参数具有一定的物理意义。Iwan模型是由弹簧和滑块组成的Jenkins单元串联或并联组成的弹簧滑块系统,通过引入概率密度函数描述Jenkins单元临界滑移力的分布特性,根据受力平衡状态方程建立恢复力-位移关系的唯象模型。Segalman采用幂函数描述Iwan模型滑块临界滑移力分布,提出了一种描述连接界面刚度非线性的四参数模型[21],但模型不能描述宏观滑移后的剩余刚度。李一堃等人提出可以同时描述微观滑移阶段能量耗散幂次关系和宏观滑移阶段残余刚度现象的六参数Iwan模型[7,22]。Song等人对Iwan模型并联一弹簧,描述连接界面发生滑移之后的刚度,提出一种修正的Iwan连接梁单元,这种单元可以直接应用到连接梁结构的有限元仿真程序中[23,24]。
显示原图|下载原图ZIP|生成PPT图 1连接结构典型的“唯象”模型[
-->Fig. 1Typical constitutive model for joints[
-->
第二类方法是考虑结合面上微观接触机理和粗糙度特征等进行建模。从实际接触表面是绝对粗糙的假设入手,首先分析界面微凸体的弹塑性接触变形和黏滑摩擦行为,再结合粗糙面形貌参数和数理统计分析方法推导出接触界面的非线性力学模型[25,26]。相比于第一类方法,后者能够比较真实地反映结合面上的接触机理,也能够较好地表征粗糙度参数对黏滑行为的影响,而且模型的参数大多都具有明确的物理意义。
由于对摩擦机理的认识还很不充分,结合面切向建模的研究成果还不多,研究者大都采用弹性接触理论和库仑摩擦关系进行研究[27,28]。Mindlin等人基于经典的Hertz理论与局部库仑摩擦定律给出了弹性变形下切向力和相对位移的关系,将微凸体的滑移行为分为黏着和滑移[29]。Phan-Thien将GW模型和经典库仑摩擦定律相结合,导出了粗糙表面切向接触力学模型,该模型假设结合面切向临界滑移力为常数,并假设微凸体处于非黏即滑的状态,忽略界面滑动前的微观滑移现象,因而导出的切向力和相对位移为简单双线性关系[30]。
Jones以GW模型为基础,给出了一种考虑微凸体微观滑移行为的结合面摩擦模型,该模型认为切向相对位移和法向变形与切向的恢复力都有关,并且当法向变形不变时切向恢复力和相对位移表现为线性关系[31]。Farhang等人假设粗糙表面微凸体高度分布为正态函数,结合Mindlin解将切向恢复力转化为法向接触载荷进行计算,导出了界面切向位移和切向恢复力、界面能量耗散之间的关系,并采用级数展开的方法近似地研究了切向恢复力、相对位移、能量耗散之间的非线性关系[32]。王东等人考虑单个微凸体黏滑行为和粗糙度为指数函数分布建立了一种考虑粗糙结合面黏滑摩擦行为的参数化力学模型[33]。Paggi等人考虑单个微凸体弹性接触影响的局部滑移行为,基于幂函数的粗糙度分布函数研究了黏着区域对粗糙面滑移力和滑移刚度的影响[34]。牛成超等人建立了基于微凸体弹性接触的粗糙表面摩擦模型,并利用该模型模拟心盘的摩擦行为[35]。李玲等人考虑微凸体弹性接触,利用平均法建立了栓接结合部等效线性化刚度和阻尼模型[36]。以上的模型都只考虑微凸体的弹性接触行为。
随着接触载荷的增加,界面上将可能出现塑性变形的微凸体[37]。Fujimoto等人根据试验研究和理论分析给出了完全塑性变形情况下切向恢复力与相对位移的双线性关系,这为考虑接合面塑性变形影响的黏滑摩擦建模奠定了基础[38]。Eriten等人考虑不同法向载荷下微凸体弹塑性变形对摩擦系数的影响,利用数理统计分析方法建立了粗糙界面跨尺度力学模型[39,40]。王东等人建立了一种同时考虑微凸体弹、塑性变形影响的黏滑摩擦模型[41,42],但只考虑了完全弹性和完全塑性两种情况,忽略了弹塑性变形的影响。
本文从连接结合面上单个微凸体的接触行为着手,建立考虑微凸体恢复力、变形或位移、能量耗散的非线性关系,然后采用数理统计分析的方法建立跨尺度力学模型,或采用赋予唯象模型参数物理意义的途径建立结合面降阶力学模型。针对整体装配结构中连接界面这种局部非线性特点,建立等效的降阶非线性力学模型。
1 基于统计分析的跨尺度力学建模
研究表明[26,31],两个粗糙表面间的接触可以等效为一个粗糙面与一个光滑面之间的接触问题,因此本文只考虑一粗糙表面与一理想刚性平面的接触问题。与GW模型基本假设类似,不考虑刚性平面的粗糙度,认为粗糙表面覆盖着高度随机分布的顶端为球截状的微凸体,微凸体的曲率半径相同,高度服从高斯分布,并假设微凸体之间变形互不耦合。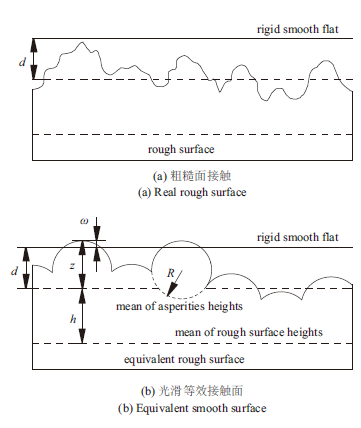
显示原图|下载原图ZIP|生成PPT图 2粗糙结合面接触示意图
-->Fig. 2Contact schematic of rough surface with multi-summits
-->
如图2所示, R为微凸体曲率半径,z为微凸体的高度,d为刚性平面与微凸体平均高度平面间的距离,h为微凸体平均高度与粗糙面平均高度平面间的距离。刚性平面受到法向载荷与粗糙表面接触,微凸体将发生变形,其法向接触接近量为
$W=z-d$ (1)
1.1 微凸体接触建模
如图3所示,在法向载荷N的作用下,两球被压紧,形成接触半径为a的圆形区域,在接触区域内结合面的摩擦系数为f。受到切向载荷T的作用后,产生切向相对位移为δ。由于接触压力沿接触表面分布的不均匀性,在接触区边缘发生滑移,并且随着切向载荷的增大,滑动区域不断向接触中心演化,在接触区域形成滑动区和黏着区两部分。图3中,中心黏着区的半径为c,滑动区为宽度为a-c,p表示法向接触压力分布,q表示由于黏滑作用产生的切向力分布。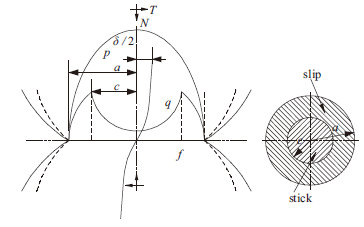
显示原图|下载原图ZIP|生成PPT图 3单个微凸体黏滑状态示意图
-->Fig. 3Schematic of stick-slip zone for asperity contact
-->
经典Mindlin理论给出了弹性接触界面上接触压力和切向剪力的分布规律,以及切向载荷与相对变形之间的关系为
$T\left( \delta ,m \right)=\left\{ \begin{matrix} fN\left[ 1-{{\left( 1-\frac{\delta }{{{\delta }_{\text{0}}}} \right)}^{3/2}} \right] & \delta \le {{\delta }_{\text{0}}} \\ fN & \delta >{{\delta }_{\text{0}}} \\ \end{matrix} \right.$ (2)
式中, m表示与材料、接触特性等效相关参数集合,δ0为弹性微凸体发生宏观滑动时的切向相对变形。
${{\delta }_{0}}\text{=}\frac{3fN}{16Ga}$ (3)
式中,G为等效剪切模量,G=G1/(2-v1),G1为微凸体材料剪切模量,v1为微凸体材料泊松比。
Hertz弹性接触理论给出了法向接触变形与法向接触载荷、实际接触半径之间的关系为
$\left. \begin{aligned} N=\frac{4}{3}E{{R}^{1/2}}{{\omega }^{3/2}} \\ a={{\left( R\omega \right)}^{1/2}} \\ \end{aligned} \right\}$ (4)
式中,E 为等效弹性模量,$E={{E}_{1}}/\left( 1-\nu _{1}^{2} \right)$,E1为微凸体杨氏模量。
将式(4)带入式(3),可得弹性微凸体发生宏观滑动时刻的切向相对变形为
${{\delta }_{0}}=\frac{fE\omega }{4G}$ (5)
将式(4)和式(5)代入式(2),可以得到显含法向接近量的切向载荷和相对变形的关系式
$T\left( \delta ,m \right)=\left\{ \begin{matrix}\frac{4}{3}fE{{R}^{1/2}}{{\omega }^{3/2}}\left[ 1-{{\left( 1-\frac{4G\delta }{fE\omega } \right)}^{3/2}} \right] & \omega \ge \frac{4G\delta }{fE} \\\frac{4}{3}fE{{R}^{1/2}}{{\omega }^{3/2}} & \omega <\frac{4G\delta }{fE} \\\end{matrix} \right.$ (6)
式(6)描述了在单向拉伸切向载荷作用下,切向恢复力与相对变形的关系。式中第一部分为黏着微凸体贡献的恢复力,而第二部分为滑移微凸体的贡献。在给定法向接触变形的情况下,随着切向变形的增加,切向恢复力也逐渐增加,直至滑移情况,描述了微凸体逐渐从黏着接触状态演化到完全滑动状态的演化过程。
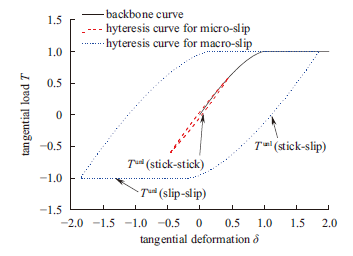
在周期性激励作用下,恢复力-相对变形的关系分为黏-黏(stick-stick),黏-滑(slip-stick),滑-滑(slip-slip)三种状态,如图4所示。
显示原图|下载原图ZIP|生成PPT图 4黏-滑摩擦行为影响的迟滞曲线
-->Fig. 4Hysteresis curve affected by stick-slip frictional
-->
在周期性载荷作用下,微凸体在卸载过程中的恢复力可以表示为
$T_{\text{e}}^{unl}\left( \delta ,{{\delta }_{\max }},m \right)=f{{N}_{\text{e}}}\left\{ \begin{matrix}-1 & \omega <{{\omega }_{1}} \\2{{\left[ 1-\frac{2G\left( {{\delta }_{\max }}-\delta \right)}{fE\omega } \right]}^{3/2}}-1 & {{\omega }_{1}}<\omega <{{\omega }_{2}} \\2{{\left[ 1-\frac{2G\left( {{\delta }_{\max }}-\delta \right)}{fE\omega } \right]}^{3/2}}-{{\left( 1-\frac{4G{{\delta }_{\max }}}{fE\omega } \right)}^{3/2}}-1 & {{\omega }_{2}}<\omega \\\end{matrix} \right.$ (7)
式中,临界切向滑移变形对应的法向接触变形为
$\begin{matrix} {{\omega }_{1}}=\frac{2G\left( {{\delta }_{\max }}-\delta \right)}{fE} & {{\omega }_{2}}=\frac{4G{{\delta }_{\max }}}{fE} \\ \end{matrix}$ (8)
由式(7)可知,微凸体恢复力满足Masing映射准则[1,13]：
$T_{\text{e}}^{unl}\left( \delta ,{{\delta }_{\max }},m \right)={{T}_{\text{e}}}\left( {{\delta }_{\max }},m \right)-2{{T}_{\text{e}}}\left( \frac{{{\delta }_{\max }}-\delta }{2},m \right)$ (9)
单个微凸体接触的能量耗散满足
${{D}_{\text{e}}}\left( \delta ,m \right)=\int_{-{{\delta }_{\max }}}^{{{\delta }_{\max }}}{\left( {{T}^{rel}}-{{T}^{unl}} \right)d}\delta ==4fN\frac{fE\omega }{4G}\left\{ \begin{matrix} \frac{{{\omega }_{s}}}{\omega }\left[ 1+{{\left( 1-\frac{{{\omega }_{s}}}{\omega } \right)}^{3/2}} \right]-\frac{4}{5}\left[ 1-{{\left( 1-\frac{{{\omega }_{s}}}{\omega } \right)}^{5/2}} \right] & {{\omega }_{s}}\le \omega \\ \frac{{{\omega }_{s}}}{\omega }-\frac{\text{4}}{5} & {{\omega }_{s}}>\omega \\ \end{matrix} \right.$ (10)
式中,
${{\omega }_{\text{s}}}=\frac{4G\delta }{fE}$
1.2 粗糙面接触行为
在粗糙表面法向接触问题中,GW模型假设微凸高度服从高斯随机分布,采用概率统计分析的方法建立了整个粗糙表面法向载荷与法向接触变形之间的关系。假设微凸体高度随机分布规律为高斯分布,其函数式为$\varphi (z)=\frac{1}{\sqrt{2\pi }\sigma }{{e}^{-\frac{{{z}^{2}}}{2{{\sigma }^{2}}}}}$ (11)
式中,σ为高斯分布方差。
整个粗糙面上的切向接触载荷为：
(12)将式(4)带入到式(12),可得
${{T}_{rough}}\left( \delta ,m \right)=\frac{4}{3\sqrt{2\pi }\sigma }\eta {{A}_{\text{n}}}fE{{R}^{1/2}}\left\{ \int_{0}^{\infty }{{{\omega }^{3/2}}{{e}^{-\frac{{{\left( \omega +d \right)}^{2}}}{2{{\sigma }^{2}}}}}d\omega }-\int_{0}^{\infty }{{{\omega }^{3/2}}{{e}^{-\frac{{{\left( \omega +d+{{\omega }_{\text{s}}} \right)}^{2}}}{2{{\sigma }^{2}}}}}d\omega } \right\}$ (13)
正则化之后的切向接触载荷定义为
${{\bar{T}}_{rough}}=\frac{{{T}_{rough}}}{fN}=1-\frac{\int_{0}^{\infty }{{{\omega }^{3/2}}\exp \left[ -\frac{{{\left( \omega +d+{{\omega }_{\text{s}}} \right)}^{2}}}{2{{\sigma }^{2}}} \right]d\omega }}{\int_{0}^{\infty }{{{\omega }^{3/2}}\exp \left[ -\frac{{{\left( \omega +d \right)}^{2}}}{2{{\sigma }^{2}}} \right]d\omega }}$ (14)
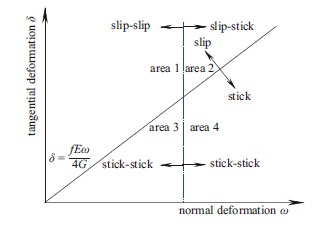
粗糙面同时受到切向和法向载荷作用,界面上微凸体的黏滑状态与切向变形和法向变形都有关,如图5所示。图5中,曲线上微凸体处于临界滑移状态;曲线之上方的微凸体发生滑移,但是,法向接触变形增加将导致部分微凸体从滑移状态转化为黏着状态;曲线之下方的微凸体都处于黏着状态。
基于数理统计分析的方法,由式(7)计算整个粗糙面上卸载过程对应的切向恢复力为
$T_{rough}^{unl}\left( \delta ,{{\delta }_{\max }},m \right)=\eta {{A}_{\text{n}}}\left\{ \begin{align} \int_{0}^{{{\omega }_{1}}}{-f{{N}_{\text{e}}}\varphi \left( \omega +d \right)d\omega } \\ +\int_{{{\omega }_{1}}}^{{{\omega }_{2}}}{f{{N}_{\text{e}}}\left\{ 2{{\left[ 1-\frac{2G\left( {{\delta }_{\max }}-\delta \right)}{fE\omega } \right]}^{3/2}}-1 \right\}\varphi \left( \omega +d \right)d\omega } \\ +\int_{{{\omega }_{2}}}^{\infty }{f{{N}_{\text{e}}}\left\{ 2{{\left[ 1-\frac{2G\left( {{\delta }_{\max }}-\delta \right)}{fE\omega } \right]}^{3/2}}-{{\left( 1-\frac{4G{{\delta }_{\max }}}{fE\omega } \right)}^{3/2}}-1 \right\}\varphi \left( \omega +d \right)d\omega } \\ \end{align} \right\}$ (15)
将式(12)带入到式(15),可得
$T_{rough}^{unl}\left( \delta ,{{\delta }_{\max }},m \right)={{T}_{rough}}\left( {{\delta }_{\max }},m \right)-2{{T}_{rough}}\left( \frac{{{\delta }_{\max }}-\delta }{2},m \right)$ (16)
显示原图|下载原图ZIP|生成PPT图 5粗糙面上黏着和滑移微凸体分布
-->Fig. 5Distribution for stick and slip asperities of rough surface
-->
同时,得到粗糙面在加载过程中的恢复力为
$T_{rough}^{rel}\left( \delta ,{{\delta }_{\max }},m \right)=-T_{rough}^{unl}\left( -\delta ,{{\delta }_{\max }},m \right)$ (17)
由式(17)可知,粗糙界面恢复力也满足Masing映射准则。
在一个循环加载过程中,单位周期的能量耗散可以表示为
$\begin{align} {{D}_{rough}}\left( {{\delta }_{\max }},m \right)=\int_{-{{\delta }_{\max }}}^{{{\delta }_{\max }}}{\left( T_{rough}^{rel}-T_{rough}^{unl} \right)d}\delta \\ =8\int_{0}^{{{\delta }_{\max }}}{{{T}_{rough}}\left( \delta ,m \right)d}\delta \\ \begin{matrix} {} & {} \\ \end{matrix}-4{{T}_{rough}}\left( {{\delta }_{\max }},m \right)\bullet {{\delta }_{\max }} \end{align}$ (18)
1.3 参数验证
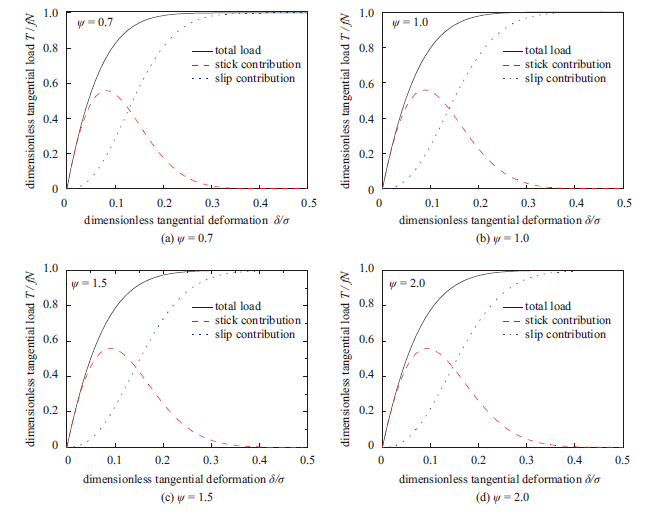
根据以上的推导过程,采用文献[42]中不同粗糙面参数预测切向恢复力,粗糙面参数与塑性指数关系如表1所示,预测的切向恢复力如图6所示。Table. 1
表 1
表 1粗糙面特征参数和塑性指数关系
Table. 1Surface properties and plasticity index
| Material properties | E=207E3, v1=v2=0.29, H=1.96E3 | |||
|---|---|---|---|---|
| Roughness properties | σ/R | β | ψ | σ |
| 1 | 0.000160 | 0.0339 | 0.7 | 0.8225 |
| 2 | 0.000302 | 0.0414 | 1.0 | 0.8849 |
| 3 | 0.000658 | 0.0476 | 1.5 | 0.9143 |
| 4 | 0.001144 | 0.0541 | 2.0 | 0.9343 |
新窗口打开
显示原图|下载原图ZIP|生成PPT图 6塑性指数影响的切向恢复力与相对变形
-->Fig. 6Tangential deformation versus total tangential load of rough surface with different plasticity index
-->
由图 6可知,在微观黏滑阶段,随着切向变形增加,切向载荷曲线的斜率逐渐下降,表现为连接结构刚度的软化。由黏着作用产生的切向力先增加后减少,而由滑移产生的切向力逐渐增加,直到最后完全由滑移作用产生切向恢复力,表现为宏观滑移,那么连接结构产生切向力逐渐由黏着作用演化为滑移作用,能够较好的反映连接结构的黏滑演化过程。随着塑性指数的增加,最大静摩擦力逐渐减小,量纲一化的滑动摩擦力接近于1,而连接界面上的摩擦系数满足
$u=\underset{\delta \to \infty }{\mathop{\lim }}\,\frac{T}{N}=f$ (19)
由上式可知,微凸体局部库伦摩擦定律的摩擦系数等于粗糙面平均摩擦系数,那么对于微观尺度的摩擦定律在宏观尺度照样适用。
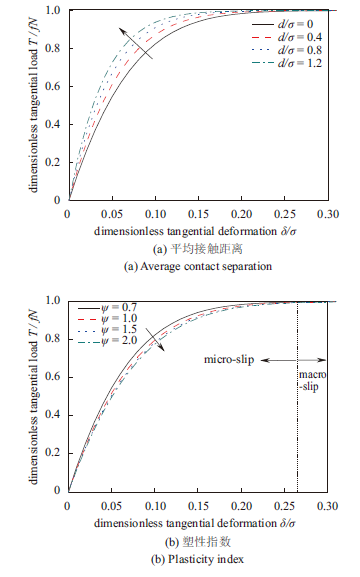
显示原图|下载原图ZIP|生成PPT图 7粗糙面不同接触特征影响的切向恢复力与相对变形
-->Fig. 7Tangential deformation versus total tangential load of rough surface affected by roughness parameters
-->
由图7可知,切向接触载荷随着接触变形的增加而增加,但是曲线的斜率逐渐较小为0,表明界面刚度的非线性软化特征。随着平均接触距离的增加,相同的切向接触载荷将产生较小的接触变形。由式(13)可知,切向接触载荷由平均接触距离和切向变形共同决定的（d+ωs）,当式(13)给定切向接触载荷时,较大的平均接触距离将对应较小的切向变形。因此,在图中平均接触距离较大的曲线在接触距离较小之上,表现为更大的连接刚度,也更加容易进入宏观滑移阶段。
由表1可知,塑性指数越大,σ越大,切向接触载荷由（ω+d+ωs）/σ 决定,当式(13)给定切向接触载荷时,较大的粗糙面参数使得（ω+d）/σ 较小,将对应较大的切向变形。因此,在图中粗糙面参数较大的曲线在粗糙面参数较小之下。
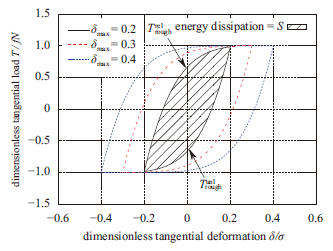
在周期循环加载过程中,恢复力与相对变形曲线围成区域的面积为单位周期的能量好散,如图8所示。由式(13)、(16~18)计算相对变形与能量耗散的关系,如图9所示。
显示原图|下载原图ZIP|生成PPT图8迟滞曲线与能量耗散关系
-->Fig. 8Relationship between hysteresis curve and energy dissipation
-->
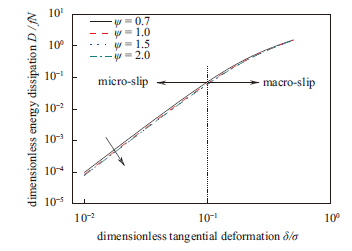
显示原图|下载原图ZIP|生成PPT图 9塑性指数对能量耗散的影响
-->Fig. 9Energy dissipation versus total tangential deformation with different plasticity index
-->
由图9中能量耗散与切向变形幅值幂级数关系可知,随着塑性指数的增加,能量耗散的值偏低,这是由界面粗糙度增加造成的。界面粗糙度增加,塑性指数增加,临界接触接触变形减小,那么发生黏着的微凸体贡献将增加,造成能量耗散偏低,但是能量耗散与变形幅值的幂级数并不会降低,反而增加,因为黏着微凸体的幂级数是大于2的,而滑移微凸体的能量耗散那幂级数是等于2的。
1.4 试验验证
为了验证本文粗糙界面跨尺度建模方法正确性,将本文提出的模型与公开文献[40]中试验数据进行对比,文献中试验装置如图10所示,对比结果如图11所示。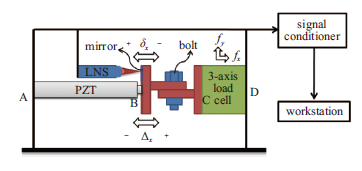
显示原图|下载原图ZIP|生成PPT图 10试验装置示意图[
-->Fig. 10Profile of experimental equipment
-->
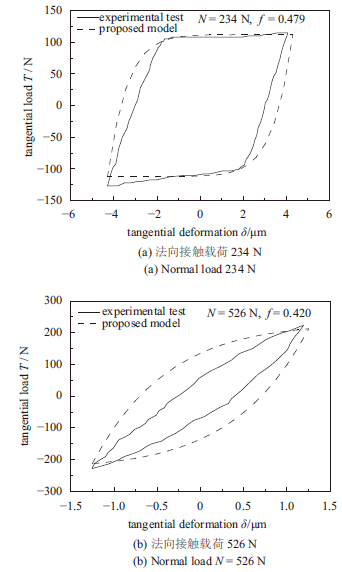显示原图|下载原图ZIP|生成PPT图 11与试验结果的对比
-->Fig. 11Comparison of proposed model and experimental test under different normal contact load
-->
由图11可知,在法向界面接触载荷较小时,模型预测切向载荷与试验吻合较好,但是在接触载荷较大时,差异较大,最大的误差达到100%,这种偏差是模型忽略了界面上塑性变形微凸体对切向载荷的贡献。在载荷较小时,界面上微凸体发生塑性变形较少,而在较大的界面接触载荷作用时,界面上的接触行为主要受到塑性变形的微凸体的影响。
2 基于唯象模型的降阶力学建模
2.1 改进Iwan模型
为了获得栓接结合部刚度软化的非线性特征[6,7,24],设计如图12a)所示的搭接连接系统模型,模型中下连接件固定,上连接件考虑为一维运动的刚体。x、q分别为结合面的相对位移、对应的临界滑移力,连接界面的柔性采用Iwan模型进行描述。
显示原图|下载原图ZIP|生成PPT图 12搭接结构和Iwan模型
-->Fig. 12Schematic of joint interface and Iwan model
-->
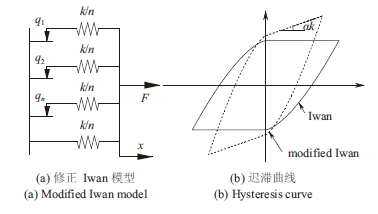显示原图|下载原图ZIP|生成PPT图 13修正Iwan模型与迟滞曲线
-->Fig. 13Schematic of modified Iwan model and hysteresis curve
-->
如图12 b)所示,Iwan模型采用n→∞个Jenkins单元并联组成的子系统描述结合面多尺度黏滑摩擦行为。考虑螺栓结构在发生宏观滑移后仍具有一定的刚度,所以再并联一个刚度kα=αk的线性弹簧单元描述发生宏观滑动后的剩余刚度,如图13 a)所示。子系统中每个线性弹簧的刚度都为ki=k/n,但每个滑块的临界滑移力qi并不相同。当系统切向受载时,临界滑移力小的滑块先发生滑动,随着相对位移增大,越来越多的滑块发生滑移,直至全部滑块都发生滑移,即结合界面出现了宏观滑动。因此,该模型能够复现连接界面上跨尺度黏滑摩擦过程。
一种改进的Iwan模型被用来为了描述连接界面刚度非线性软化和能量耗散幂级数特性两个特征。与Song等人[23,24]提出的改进Iwan相同,但是滑块临界滑移力的分布不是均匀的,采用一种指数形式的概率分布。
$\phi (q)=\left\{ \begin{matrix} c{{q}^{\chi }} & 0\le q\le {{f}_{q}} \\ 0 & else \\ \end{matrix} \right.$ (20)
式中,fq为系统发生宏观滑动时对应的临界宏观滑移力,χ 为幂指数, χ<0.
滑块临界滑移的分布规律满足归“1”,即所有滑块的概率分布之和为1,概率分布函数的系数满足：
$c=1/\int_{0}^{\infty }{\phi (q)dq}$ (21)
对处于初始平衡位置的Iwan模型受到单调载荷的情况,其恢复力的一般表达式为
$F(x)=\int\limits_{0}^{kx}{q}\phi (q)dq+kx\int\limits_{kx}^{\infty }{\phi (q})dq+\alpha kx$ (22)
将式(20)代入式(22)中,可得
$F(x)=\left\{ \begin{matrix} (1+\alpha )kx-\frac{{{\left( kx \right)}^{\chi +2}}}{\left( \chi +2 \right)f_{q}^{\chi +1}} & 0\le x\le {{f}_{q}}/k \\ \frac{\chi +1}{\chi +2}{{f}_{q}}+\ \ \alpha kx & x\ge {{f}_{q}}/k \\ \end{matrix} \right.$ (23)
上式中,第一部分为Jenkins单元贡献的连接恢复力,而第二部分为并联弹簧的贡献,αkx。对于式(23),如果参数χ=0,模型将退化为Song的修正Iwan模型,当参数χ=-1或fq=0,模型都将退化为一线性模型,而此时的连接恢复力为
$F(x)=\alpha kx\ $ (24)
为了使模型更加具有普适性,将式(23)改写为无量纲形式。
$f(r)=\frac{F\left( x \right)}{{{F}_{s}}}=\left\{ \begin{matrix} r\frac{\left( 1+\alpha \right)\left( \chi +2 \right)-{{r}^{\chi +1}}}{\alpha \left( \chi +2 \right)+\chi +1} & 0\le r\le 1 \\ 1+\frac{\alpha \left( r-1 \right)\left( \chi +2 \right)}{\chi +1+\alpha \left( \chi +2 \right)} & r\ge 1 \\ \end{matrix} \right.$ (25)
式中,r 为无量纲相对变形,r=x/xs。 xs 宏观滑移变形,Fs 宏观滑移力,表示为
${{x}_{s}}={{f}_{q}}/k$ (26)
${{F}_{s}}=\int_{0}^{{{f}_{q}}}{\phi (q)dq}=\left( \frac{\chi +1}{\chi +2}+\alpha \right){{f}_{q}}$ (27)
对于式(25),微观黏滑段(r <1)表达式与Segalman四参数模型相同,当参数α=0时,模型将退化为Segalman的四参数Iwan模型。本文模型在宏观滑移段(r >1)描述的恢复力-变形存在非零的滑移刚度,而且本文提出的模型描述的恢复力-变形在黏滑过渡点(r =1)是光滑连续的,这也与Segalman四参数Iwan模型有所不同。根据式(25)可知,宏观滑移阶段的滑移刚度可以表示为
${{k}_{s}}=\alpha k=\frac{\alpha {{F}_{s}}\left( \chi +2 \right)}{\chi +1+\alpha \left( \chi +2 \right)}$ (28)
在文献[1,13]中,并联Jenkins单元的Iwan模型是满足Masing映射准则的。在周期载荷作用下,将循环加载过程分为加载和卸载,根据加载激励的幅值,将两个过程恢复力定义为
$\begin{matrix} {{F}_{rel}}(x)=-{{F}_{0}}+2F\left( \frac{{{x}_{0}}+x}{2} \right) & \dot{x}\ge 0 & reloading \\ \end{matrix}$ (29)
$\begin{matrix} {{F}_{unl}}(x)={{F}_{0}}-2F\left( \frac{{{x}_{0}}-x}{2} \right) & \dot{x}\le 0 & unloading \\ \end{matrix}$ (30)
式中, x0为加载激励幅值对应的变形值,定义为：
${{F}_{0}}=F({{x}_{0}})$ (31)
将式(22)带入到式(29)、(30),可得：
${{F}_{unl}}(x)=-\int_{0}^{k\left( {{x}_{0}}-x \right)/2}{q\phi (q)dq}+\int_{k\left( {{x}_{0}}-x \right)/2}^{k{{x}_{0}}}{\left( q+kx-k{{x}_{0}} \right)\phi (q)dq}+kx\int_{k{{x}_{0}}}^{\infty }{\phi (q)dq}+\alpha kx$ (32)
${{F}_{rel}}(x)=\int_{0}^{k\left( {{x}_{0}}+x \right)/2}{q\phi (q)dq}+\int_{k\left( {{x}_{0}}+x \right)/2}^{k{{x}_{0}}}{\left( k{{x}_{0}}+kx-q \right)\phi (q)dq}+kx\int_{k{{x}_{0}}}^{\infty }{\phi (q)dq}+\alpha kx$ (33)
再将式(20)、(21)分别带入到(32)、(33),可得
${{F}_{unl}}(x)=\left\{ \begin{matrix} \left\{ \begin{matrix} \alpha kx+\frac{\chi +1}{\chi +2}{{f}_{q}}-k\left( {{x}_{0}}-x \right)+2\frac{{{\left( k\frac{{{x}_{0}}\text{-}x}{2} \right)}^{\chi +2}}}{\left( \chi +2 \right)f_{q}^{\chi +1}} & \frac{{{x}_{0}}\text{-}x}{2}\le {{x}_{s}} \\ \alpha kx\text{-}\frac{\chi +1}{\chi +2}{{f}_{q}} & else \\ \end{matrix}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \right. & {{x}_{0}}>{{x}_{s}} \\ (1+\alpha )kx-\frac{{{\left( k{{x}_{0}} \right)}^{\chi +2}}}{\left( \chi +2 \right)f_{q}^{\chi +1}}+2\frac{{{\left( k\frac{{{x}_{0}}-x}{2} \right)}^{\chi +2}}}{\left( \chi +2 \right)f_{q}^{\chi +1}} & {{x}_{0}}\le {{x}_{s}} \\ \end{matrix} \right.$ (34)
${{F}_{rel}}(x)=\left\{ \begin{matrix} \left\{ \begin{matrix} \alpha kx-\frac{\chi +1}{\chi +2}{{f}_{q}}+k\left( {{x}_{0}}+x \right)-2\frac{{{\left( k\frac{{{x}_{0}}+x}{2} \right)}^{\chi +2}}}{\left( \chi +2 \right)f_{q}^{\chi +1}} & \frac{{{x}_{0}}+x}{2}\le {{x}_{s}} \\ \alpha kx+\frac{\chi +1}{\chi +2}{{f}_{q}} & else \\ \end{matrix}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \right. & {{x}_{0}}>{{x}_{s}} \\ (1+\alpha )kx+\frac{{{\left( k{{x}_{0}} \right)}^{\chi +2}}}{\left( \chi +2 \right)f_{q}^{\chi +1}}-2\frac{{{\left( k\frac{{{x}_{0}}+x}{2} \right)}^{\chi +2}}}{\left( \chi +2 \right)f_{q}^{\chi +1}} & {{x}_{0}}\le {{x}_{s}} \\ \end{matrix} \right.$ (35)
与式(17)和式(18)计算方法相同,恢复力-相对位移曲线的面积为单位周期的能量耗散。将式(34)和(35)带入到式(36)中,同时将式(36)中的能量耗散转化为无量纲形式。
$\begin{align} d\left( r \right)=\frac{D}{{{F}_{s}}{{x}_{s}}}=4\frac{\chi +1}{\alpha +\frac{\chi +1}{\chi +2}} \\ \begin{matrix} {} & {} \\ \end{matrix}\times \left\{ \begin{matrix} \frac{{{r}^{\chi +3}}}{\left( \chi +3 \right)\left( \chi +2 \right)} & r<1 \\ \frac{1}{\left( \chi +3 \right)\left( \chi +2 \right)}+\frac{r-1}{\chi +2} & r\ge 1 \\ \end{matrix} \right. \end{align}$ (36)
本文模型能量耗散的幂级数为(χ+3),这与Song模型是不同的,Song模型的幂级数值为3。
因此,由式(25)和(36)可知,本文提出修正Iwan模型是Segalman和Song模型的推广,即参数取特定值时,本文提出的模型将退化为Segalman或Song的Iwan模型。由这两式可知,恢复力和相对变形的关系可以由四参数{α, χ, xs, Fs }进行表示,本文提出的四参数可以描述连接界面刚度软化和能量耗散幂级数特征,这与文献中[7, 22]六参数有所不同。
参数xs为宏观滑移相对变形,由结合面材料属性、法向作用力、摩擦系数等决定。
参数Fs为宏观滑移恢复力,由结合面法向作用力和摩擦系数决定。
参数χ决定能量耗散与切向相对位移的幂级数值,参数反映在周期激励作用下能量耗散和周期振荡作用力幅值(相对位移最大值)的幂级数特性,由结合面材料属性和接触条件决定。
参数α为剩余刚度系数,决定发生宏观滑移的状态,参数反映切向宏观滑移力,由结合面法向作用力和摩擦系数决定。
参数Fs和xs一起决定微观滑移向宏观滑移过渡的状态,以及振荡载荷作用下能量耗散的幅值特性,是反映切向黏滑过程的主要特征量一起决定微观滑移向宏观滑移过渡的状态,以及振荡载荷作用下能量耗散的幅值特性,是反映切向黏滑过程的主要特征量。
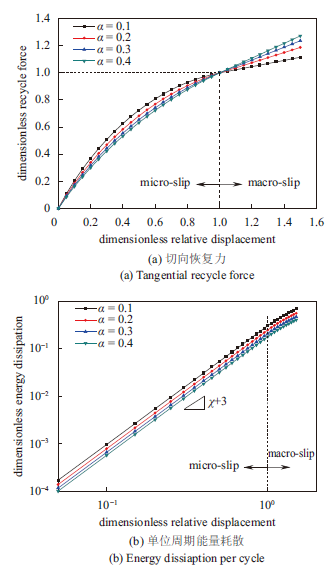
由式(25)和(36)可知,无量纲化恢复力和能量耗散只与参数α和χ有关。利用本文模型预测连接结构刚度软化和能量耗散幂级数特征,如图14所示,其中参数选取为：χ=-0.5,α=0.1, 0.2, 0.3, 0.4。
显示原图|下载原图ZIP|生成PPT图 14改进Iwan模型参数验证结果
-->Fig. 14Parameters investigation for proposed Iwan model
-->
由图14可知,剩余刚度系数越大预测宏观滑移阶段的滑移刚度越大,但是在微观黏着阶段的刚度却更小。黏着阶段能量耗散与相对变形幅值的幂级数值为(χ+3),在宏观滑移阶段斜率值有所下降。
2.2 参数辨识方法
由式(25)、(29)、(30),可知,在周期载荷作用下,连接界面恢复力与相对变形的关系可由图15表示。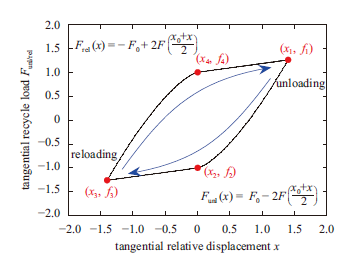
显示原图|下载原图ZIP|生成PPT图 15连接界面恢复力与相对变形
-->Fig. 15Recycle force of joint interface for unloading and reloading process
-->
由图15可知,在单个循环周期内,恢复力和相对变形存在四个转折点,包括最大值、最小值点(x1,f1)/(x3,f3)和加载、卸载黏滑分界点(x2, f2)/(x4, f4)。加载和卸载阶段均可以分为黏着阶段和滑移阶段。根据加载和卸载阶段的对称性,从转折点(x1, f1) 到转折点(x2, f2)的黏着阶段(或转折点(x3, f3) 到转折点(x4, f4)的黏着阶段)可以被用来辨识宏观滑移力Fs宏观相对变形xs。
${{f}_{1}}-{{f}_{2}}={{f}_{3}}-{{f}_{4}}=2{{F}_{s}}$ (37)
${{x}_{1}}-{{x}_{2}}={{x}_{4}}-{{x}_{3}}=2{{x}_{s}}$ (38)
同时,从转折点(x2, f2) 到转折点(x3, f3)的滑移阶段(转折点(x4, f4) 到转折点(x1, f1)的滑移阶段)可以被用来辨识剩余刚度。
${{k}_{s}}=\frac{{{f}_{1}}-{{f}_{4}}}{{{x}_{1}}-{{x}_{4}}}=\frac{{{f}_{2}}-{{f}_{3}}}{{{x}_{2}}-{{x}_{3}}}$ (39)
由式(37~39)可知,利用周期载荷下恢复力-相对变形的参数{f1, f2, f3, f4} 和{x1, x2, x3, x4}辨识宏观滑移力Fs和滑移相对变形xs,以及剩余刚度,而与剩余刚度相关的参数χ和 α需要通过参数拟合方法得到。
2.3 有限元模型验证
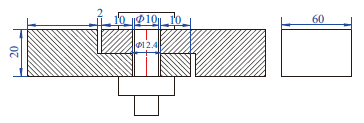
(1) 螺栓搭接结构以典型螺栓连接结构为研究对象,结构的尺寸和有限元模型如图16、17所示。
显示原图|下载原图ZIP|生成PPT图 16螺栓连接结构有限元模型几何尺寸
-->Fig. 16Geometry schematic of shear lab joint
-->
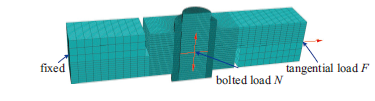显示原图|下载原图ZIP|生成PPT图 17螺栓连接结构有限元网格模型
-->Fig. 17Finite element meshing of shear lab joint
-->
(2) 有限元计算结果
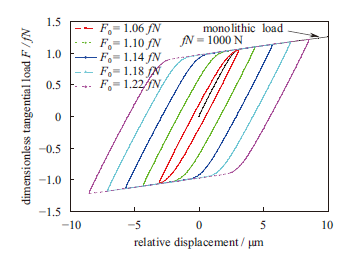
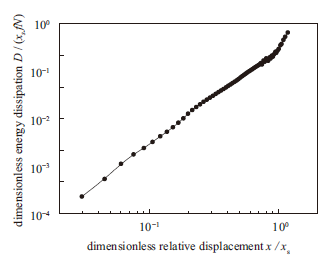
连接界面存在会引起刚度软化和能量耗散幂级数特性,以及迟滞非线性行为,如图18、19、20所示。由图18可知,恢复力随着相对变形的增加而增加,而恢复力-相对变形斜率却随着变形增加而减小。由图19可知,在周期激励载荷作用下,恢复力和相对变形也表现出迟滞的非线性特征。由图20可知,在微观黏着阶段,单位周期能量耗散与相对变形幅值在双对数坐标系下为线性关系,表现为幂级数特征,因此,采用有限元方法可以捕捉到连接界面上典型非线性特征。
显示原图|下载原图ZIP|生成PPT图 18螺栓连接界面切向恢复力与相对变形
-->Fig. 18Relationship between recycle force and relative deformation under different normal loads
-->
显示原图|下载原图ZIP|生成PPT图 19螺栓连接界面切向恢复力迟滞特性
-->Fig. 19Hysteresis curve of force-deformation with different tangential load amplitude
-->
显示原图|下载原图ZIP|生成PPT图 20单位周期能量耗散与相对变形
-->Fig. 20Energy dissipation per cycle versus relative deformation
-->
(3) 参数辨识结果
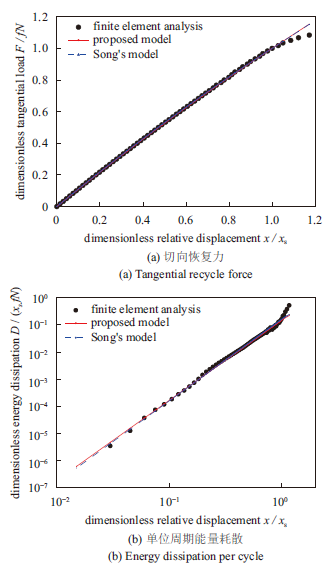
利用图19中恢复力和相对变形迟滞关系和式(37)、(38)可以辨识连接界面上宏观滑移力和相对变形。利用辨识获得宏观滑移力Fs和xs将有限元结果进行无量纲化处理,再利用参数拟合的方法辨识出参数χ、α。利用辨识获得四参数Iwan模型,并预测连接界面上的刚度软化和能量耗散幂级数特征,将结果与Song模型预测的结果以及有限元结果进行对比,结果如图21所示。
显示原图|下载原图ZIP|生成PPT图 21有限元分析的参数辨识结果
-->Fig. 21Fitting to the results of finite element analysis
-->
根据有限元计算结果辨识出Iwan模型参数为α=3.99,χ=-0.05,Fs =1060 N,xs = 1.39 um。由图21可知,本文提出的改进Iwan四参数模型和Song模型都能较好的预测恢复力-相对变形的刚度软化以及单位周期能量耗散的幂级数特征,两种模型预测的结果相差较小。这是由于本文模型拟合参数χ为-0.05,而对于Song模型,参数χ=0,导致两模型预测的恢复力和能量耗散相差不大。
3 结论
本文首先基于微观接触力学理论和概率统计分析的方法建立一种粗糙界面黏滑摩擦模型。研究了粗糙面塑性指数和平均接触距离对切向非线性特征的影响,并且与公开文献中的试验结果进行对比。结果表明,随着塑性指数的增加,刚度有所降低,但是随着平均接触距离的增加,刚度有所增加。与公开文献中试验结果相比,界面预紧力载荷较小时,模型预测切向载荷与试验吻合较好,但是在接触载荷较大时,差异较大,这是由于忽略了微凸体混合弹塑性接触变形影响造成的。其次,本文提出一种改进的Iwan四参数模型描述连接界面宏观滑移后的剩余刚度特征以及能量耗散与相对变形幅值的幂级数特性,且本文模型是Sandia四参数模型和Song改进Iwan模型的推广形式。采用精细有限元获得的非线性特征,结合系统辨识方法获得模型参数,并利用有限元结果进行验证。结果表明本文的四参数模型能够较好地描述连接界面的黏滑摩擦行为。
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | |
| [2] | |
| [3] | . |
| [4] | . . |
| [5] | . . |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . |
| [12] | . |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . . |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . . |
| [23] | [D]. |
| [24] | . |
| [25] | . |
| [26] | . |
| [27] | . . |
| [28] | . , |
| [29] | . |
| [30] | . |
| [31] | . |
| [32] | [C]. 2007. |
| [33] | . . |
| [34] | . |
| [35] | . . |
| [36] | . . |
| [37] | . . |
| [38] | . |
| [39] | . |
| [40] | . |
| [41] | . . |
| [42] | . |
