中国科学院力学研究所流固耦合系统力学重点实验室,北京 100190
STABILITY OF PLASTIC FLOW OF METALLIC CHIPS
MaWei中图分类号:TG506
文献标识码:A
通讯作者:
收稿日期:2017-08-04
接受日期:2017-09-8
网络出版日期:2017-09-10
版权声明:2018《力学学报》编辑部《力学学报》编辑部 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (11464KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引言
关于材料切削过程的研究已经持续了数百年[1-2]. 金属切削作为一个广泛应用的工程技术涉及到诸多基础科学 问题[3-4]. 基于工程应用观点,工程师主要关注如何提高材料的机加工能力、质量和效率, 如何提高刀具材料的硬度和延长其使用寿命, 如何更好地对钛、镍等难加工材料以及具有复杂构型的零部件进行高精度、高效率的加工. 易见,这些应用背景较强的工程技术问题直接与机加工工艺的优化程度和加工设备的先进程度相关. 另一方面,从基础研究的观点看,科学家关注的是金属切削过程中的基本物理现象. 例如,如何更好地认识材料的可加工性?切削能量的耗散机制是什么?切削过程中材料去除和切屑形成的机理是什么?对这些基 础科学问题的正确认识将有助于指导机加工工艺和技术的改进. 实际上,金属切削过程与切屑材料的塑性流动行为及其稳定性等力学行为密切相关. 因此,基于技术科学的思想[5-6] 并应用连续介质力学理论,可以合理地解决金属切削过程涉及的基础科学问题,为生产实践服务.迄今,关于材料切削机理的研究已取得丰硕成果. 但是,随着工程实践中新技术应用的快速增长、新型材料的广泛应用, 机加工工艺和技术长期以来面临着新的挑战,也给材料切削过程的基础研究不断提出新的科学问题. 关于材料切削机理研究的发展历程和现状, 读者可以参阅文献[7,8,9,10,11,12,13,14,15,16].
本文研究金属正交切削过程中切屑材料的塑性流动行为及其稳定性. 材料正交切削过程的主要特点是工件移动方向与切刀前缘 垂直[8],如图1 所示. 其典型实例如刨削和车削加工. 该过程中切削能耗散机制、材料去除过程中切屑形成机制以及工件加工表面完整性等主要物理现象与一般车、铣和钻等工艺过程相同, 主要差别仅限于几何方面, 即前者工件材料的变形处于平面应变状态,后者工件变形发生在三维空间内. 因此,通过对材料正交切削过程的研究,可以很好地认识材料机加工过程的物理本质,正交切削问题的数学分析过程比较简单. 这是人们长期关注和研究材料正交切削过程的原因.
显示原图|下载原图ZIP|生成PPT图1金属正交切削过程
-->Fig. 1The orthogonal cutting process of metals
-->
本文以实验观察为基础,应用连续介质力学基本理论, 建立描述材料正交切削过程的物理模型,并给出相应的数 学表述. 为研究切屑材料塑性流动稳定性建立平面应变状态下判断材料塑性失稳行为普遍判据. 在复杂应力加载情形和简单应力加载情形下,该判据可对材料的局部和非局部塑性流动失稳行为进行评价. 通过对材料切削过程中切屑材料塑性流动行为和稳定性的研究,揭示材料去除和切屑形成的基本机理.
1 切削实验结果
材料正交切削过程的模拟实验在自行研制的模拟切削实验平台上完成. 高速冲击加载系统可以是霍普金森压杆装置,也可以是一级 轻气炮装置. 这样可在较大范围的切削速度条件下进行材料正交切削的模拟实验[17]. 实验材料为4 种金属合金,即Ti6Al4V 合金, Al 7075 合金, AISI 4340 钢和AISI 1045 钢. 假设这些试验材料服从Johnson-Cook 本构模型[18]. 相关的材料性能和J-C 本构模型参数在表1 中给出. 切削条件为：切削速度小于200 m/s、切削厚度100 m 和零切刀倾角. 通过对收集的切屑样品进行扫描电镜微观分析,观察到金属材料切削过程的一个共性是随切削速度的增大连续切屑转变成锯齿切屑(图2). 其中连续切屑材料经历了高强度均匀剪切流动过程,锯齿切屑的主剪切区中材料经历了剪切局部变形过程[19]. 4 种金属材料的切屑形貌转变发生的临界切削速度不等,说明临界速度与切削条件和工件材料性能相关. 仅依据实验结果不易精确确定临界速度的具体量值. 但可以估计各试验材料近似临界速度的值为：Ti6Al4V 为0.5 m/s, Al 7075 为6 m/s, AISI 4340 为6.7 m/s, AISI 1045 为39 m/s. 这些临界速度将用在后文切屑材料塑性流动稳定性的理论分析中. 关于实验过程的更多细节读者可参阅文献[12,14],此处不再繁述.Table 1
表 1
表 14 种金属的材料性能和J-C 本构模型参数
Table 1The material properties and the J-C constitutive model parameters of the four testing metals
| Ti6Al4V[28] | AISI 4340[29] | AISI 1045[14] | Al 7075[30] | |
|---|---|---|---|---|
| Density | 4 420 | 7 830 | 7 850 | 2 770 |
| Elastic modulus | 114 | 200 | 210 | 71 |
| Poisson’s ratio | 0.342 | 0.29 | 0.3 | 0.3 |
| Specific heat | 560 | 477 | 452 | 885 |
| Thermal conductivity | 7.2 | 38 | 50 | 130 |
| Expansion coefficient | 9.2#x00D7;10 - 6 | 3.2#x00D7;10 - 5 | 1.5#x00D7;10 - 5 | 2.32#x00D7;10 - 5 |
| Melting temperature | 1 930 | 1 793 | 1 765 | 893 |
| Taylor-Quinney coefficient | 0.9 | 0.93 | 0.93 | 0.9 |
| J-C constitutive model parameters | Ti6Al4V[28] | AISI 4340[29] | AISI 1045[14] | Al 7075[30] |
| 782 | 792 | 496 | 546 | |
| 498 | 510 | 434 | 678 | |
| 0.28 | 0.26 | 0.307 | 0.71 | |
| 0.028 | 0.014 | 0.047 | 0.024 | |
| 1 | 1.03 | 0.804 | 1.56 | |
| 1 | 1 | 1 | 1 |
新窗口打开
显示原图|下载原图ZIP|生成PPT图24 种金属切屑材料样品的扫描电镜断面微观观察
-->Fig. 2The SEM observation of the cross-section of chip samples of the four testing metals
-->
2 材料正交切削模型及数学表述
图3 所示为材料正交切削过程的二维分析模型. 假设工件材料变形满足J-C 本构方程和J$_2$ 流动定律.切刀和切屑间接触满足干摩擦条 件，摩擦系数 $\mu ={\rm tan} \alpha _{\rm f}$ 为常数，$\alpha_{\rm f}$ 为摩擦角. 切削条件由切削速度$V_{0}$、切削厚度$h_{0}$、切刀倾角$\alpha_{\rm T}$ 或剪切角$\varphi $ 给定. 为研究切削过程中切屑材料塑性流动的稳定性，该模型考虑切屑材料沿切刀与切屑接触面的物质流动现象. 认为切屑形成区为包括主剪切区(PSZ) 和次剪切区(SSZ) 的平行四边形区域$OABC$. 引起切屑材料塑性变形的载荷有沿剪切面作用的剪应力$\sigma_{12}$ 和沿切刀与切屑接触面分布的压力$p_{N}$. 这里提出的材料二维正交切削模型不同于通常一维正交切削模型[8-9, 20-23]. 前者着重描述平面应变状态下切屑材料塑性流动行为及其形成机制[24-25]；后者仅考虑剪切平面内剪应力的作用，关注锯齿切屑的形成机制及其主剪切区的材料剪切带失稳行为.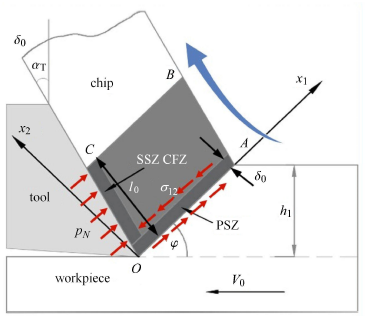
显示原图|下载原图ZIP|生成PPT图3材料二维正交切削模型
-->Fig. 3The two-dimensional orthogonal cutting model of materials
-->
以切削速度$V_{0}$、切削厚度$h_{0}$ 和材料熔化的温差$T_{\rm m}-T_{0}$ 为基本单位，定义无量纲的时间、空间坐标、速度、应力和温度为
$\left.\begin{aligned} \hat {t}=\dfrac{V_0 t}{h_0 }, \hat {x}_1 = \dfrac{x_1 }{h_0 }, \hat {x}_2 = Re\dfrac{x_2 }{h_0 }\\ \hat {v}_1 = \dfrac{v_1 }{V_0 } , \hat {v}_2 = Re\dfrac{v_2 }{V_0 }\\ \hat {\sigma }_{ij} = \dfrac{\sigma _{ij} }{A_0 }, \hat {\dot {\varepsilon }}_{ij} = \dfrac{\dot {\varepsilon }_{ij} }{\dot {\varepsilon }_0 }, \hat {T} = \dfrac{T}{T_{\rm m} - T_0 } \end{aligned} \right\} $ (1)
这里顶标"$\wedge $"表示相关量是无量纲的. 为方便计,下面讨论无量纲关系时所有无量纲量的顶标"$\wedge $"将略去. 对连续介质力学基本方程进行无量纲化,得到描述切屑材料二维塑性流动过程的无量纲形式的基本控制方程如下：
能量平衡方程
$\dot {T} + v_1 T_{,1} + v_2 T_{,2} - R_{\rm h} \left( {T_{,11} + Re^2T_{,22} }\right) =\\R_{\rm c} \left( {\sigma _{11} \dot {\varepsilon }_{11} + \sigma _{22} \dot{\varepsilon }_{22} + 2\sigma _{12} \dot {\varepsilon }_{12} } \right)$ (2)
动量平衡方程
$\left. \begin{aligned} \dot {v}_1 + v_1 v_{1,1} + v_2 v_{1,2} = Re^{ - 1}\sigma _{11,1} + \sigma_{12,2} \\ \dot {v}_2 + v_1 v_{2,1} + v_2 v_{2,2} = \sigma _{12,1} + Re\sigma _{22,2} \end{aligned} \right \}$ (3)
连续性条件
$v_{1,1} + v_{2,2} = 0$ (4)
变形协调条件
$\varepsilon _{11,22} + \varepsilon _{22,11} = 2\varepsilon _{12,12}$ (5)
无量纲形式的J-C 本构方程为
$\sigma _{\rm eq} = \left( {1 + B_0 \varepsilon _{\rm eq}^n } \right)\left( {1 + C_0 \ln \dot {\varepsilon }_{\rm eq} } \right)\left[ {1 - \left( {T - T_0 } \right)^m} \right]$ (6)
无量纲形式的应变和应变率分量为
$\left. \begin{aligned} \varepsilon _{11} = u_{1,1} ,\ \ \varepsilon _{22} = u_{2,2} ,\ \ 2\varepsilon_{12} = Reu_{1,2} + Re^{ - 1}u_{2,1} \\ \dot {\varepsilon }_{11} = v_{1,1} , \ \ \dot {\varepsilon }_{22} = v_{2,2}, \ \ 2\dot {\varepsilon }_{12} = Rev_{1,2} + Re^{ - 1}v_{2,1} \end{aligned} \right\} $ (7)
在无量纲化方程(2)$\sim$(7)(7) 时,引入三个无量纲参量
$Re = \dfrac{\rho V_0^2 }{A_0 }, \ \ R_{\rm h} = \dfrac{\lambda }{\rho ch_1 V_0 }, \ \ R_{\rm c} = \dfrac{\beta A_0 }{\rho c\left( {T_{\rm m} - T_0 } \right)}$ (8)
这里, $\rho $, $c$, $\lambda $, $T_{0}$ 和$T_{\rm m}$ 分别为工件材料的质量密度、比热、热导率、室温和熔点温度，是具有量纲的量. $\beta $ 为热功转换系数. 式(8) 中3 个无量纲参数分别是：雷诺数$Re$ 表示材料惯性与变形阻尼之比；热雷诺数$R_{\rm h}$ 表示材料塑性变形过程中传导热与对流热之比；参数$R_{\rm c}$表示材料塑性变形过程中的热功转换效应.
无量纲形式的二维控制方程 (2)~(6) 描述了工件移动产生的切屑材料沿切刀与切屑接触面的物质运动,也描述了切屑形成区$OABC$内材料平面应变状态下的塑性流动过程,以及锯齿切屑中主剪切区的材料剪切带失稳行为. 但是,直接应用该二维方程系进行剪切带失稳行为的分析是不方便的. 因为后者往往可以简化成一维塑性流动过程. 值得注意的是当雷诺数$Re \gg 1$ ($Re \approx 10$)时,二维方程(2) 和(3) 转化成前人提出的一维普朗特边界层方程系. 该一维方程可以方便地描述锯齿切屑材料的剪切带失稳行为[26]. 那么,这两组方程是否能同时用来描述金属切削过程中切屑材料平面应变状态下的塑性流动行为和剪切带失稳行为,将取决于 雷诺数$Re$的值. 从图2 中的切削实验结果可见,金属切削过程中切屑从连续状转变成锯齿状的临界速度一般在1~10 m/s 量级. 在此速度量级雷诺数$Re$通常为一小量. 也就是说条件$Re \gg 1$ (如$Re \approx 10$) 对应的切削速度远大于切屑形貌转变发生的实际临界速度. 因此，有必要对雷诺数$Re$ 进行修正. 以便使$Re=10\gg1$ 对应的切削速度等于切屑形貌转变的临界速度. 这样，两组方程描述了切屑材料在平面应变状态下的塑性流动行为，也描述了锯齿切屑中材料的一维剪切带失稳行为，并且也表征了连续切屑与锯齿切屑间的转换过程
为此,在控制方程 (2)~(6) 中用修正后的雷诺数$Re=\rho V_{0}^{2}/A_{0}$. 其中修正函数$\chi $ ($V_{0})$ 与切削条件和工件材料性能相关，定义为
$\chi( {V_0 }) =\begin{equation} \left \{ \begin{array} \ \left( {{\tau _{\rm s} } /{\rho V_{\rm 0i}^2 }} \right) \left( {Re_{\rm c} + Re_0 {\left( {V_{\rm 0i}^2 - V_0^2 } \right)}/{V_0^2 }} \right) \\\left( {Re_0 ≤ Re < Re_c } \right) \\ \left( {{Re_{\rm c} \tau _{\rm s} } /{\rho V_0^2 }} \right) - \left( {1 - {V_{\rm 0i} } / {V_0 }} \right)\left( {1 - {V_{\rm 0T} }/ {V_0 }} \right) \\ \left( {Re \geqslant Re_{\rm c} } \right) \end{array} \right. \end{equation}$ (9)
这里参数$Re _{0} =1$对应于初始切削速度$V_{0} =0$. 临界参数$Re_{\rm c}=10$, 对应于切削过程中连续切屑转变成锯齿切屑的临界速度$V_{\rm 0i}$, 其近似值可由图2 中的实验结果得到;$V_{\rm 0T}$表示高速切削过程中锯齿切屑转变成连续切屑的临界速度,其值由数值模拟结果确定[15-16].
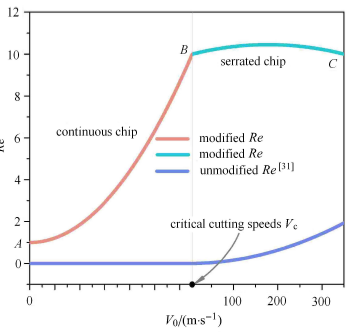
图4给出修正前后雷诺数$Re$随切削速度的变化曲线. 可见,在切削过程中,尽管切削速度超过300 m/s,未经修正的雷诺数$Re$(该图中蓝线表示) 始终为一小数($\ll 10$);修正后的雷诺数$Re$不再为小数. 对于考虑的四种金属材料,总能找到一个连续切屑向锯齿切屑转变的临界切削速度对应于$Re=10$. 二维方程 (2)~(6) 相应地转变成一维普朗特边界层方程系. 可见,如果在方程 (2)~(6) 中采用修正后的雷诺数$Re$, 这些方程不仅描述了材料正交切削过程中切屑材料平面应变塑性流动行为, 而且, 当切屑形貌由连续状转变成锯齿状后,由其得到的一维普朗特边界层方程 相应地也描述了锯齿切屑中材料的剪切带失稳行为.
显示原图|下载原图ZIP|生成PPT图4修正前后的雷诺数$Re$与切削速度的关系曲线
-->Fig. 4The relationship curves of the corrected and uncorrected Reynolds number $Re$ with the cutting speeds
-->
为研究材料正交切削过程中切屑材料塑性流动稳定性,对方程 (2)~(6) 进行线性稳定性分析,得到复杂应力加载条件下评价材料塑性流动失稳性的普遍判据如下
$F_{\rm inst}=\dfrac{(F_1+F_2R_0+F_3R_{\rm c}Q_0)R_{\rm h}P_0 }{F_4Q_0} > 1$ (10)
这里各系数函数$F_{i}$ ($i =1,2,3,4$)具有形式
$\left. \begin{aligned}F_1=2 \eta _{12} \varPi^1\Big[ n_1 n_2 \left( \eta _{11}\sigma _{11\left( 0\right)} + \eta _{22} \sigma _{22(0)} \right) + Re\left( n_2^2 \eta _{11} + n_1^2 \eta _{22} \right)\sigma _{12(0) } \Big] \\F_2 = 2\eta _{12} \varPi^1\Big[ n_1 n_2 \left( {\eta _{11} \varTheta _{11}^2 + \eta _{22} \varTheta _{22}^2 }\right) + Re\left( n_2^2 \eta _{11} + n_1^2 \eta_{22} \right)\varTheta _{12}^2 \Big] -\\ 2\eta _{12} \varPi^2\Big [ n_1 n_2 \left( {\eta _{11} \varTheta _{11}^1 + \eta _{22} \varTheta _{22}^1 } \right) +Re\left( n_2^2 \eta _{11} + n_1^2 \eta _{22} \right)\varTheta _{12}^1 \Big] \\ F_3 = 2\eta _{12} \varPi ^1\Big[ n_1 n_2 \left( {\eta _{11} \varXi _{11}^2 + \eta_{22} \varXi _{22}^2 } \right) + Re\left( {n_2^2 \eta _{11} + n_1^2 \eta _{22} } \right)\varXi _{12}^2 \Big] -\\ 2\eta _{12} \varPi ^2\Big[ n_1 n_2 \left( {\eta _{11} \varXi _{11}^1 + \eta _{22} \varXi _{22}^1 }\right) + Re\left( {n_2^2 \eta _{11} + n_1^2 \eta _{22} } \right)\varXi _{12}^1 \Big] \\ F_4 = 2\eta _{12} \Big [ n_1n_2 (\eta_{11} \varXi_{11}^1 + \eta _{22} \varXi _{22}^1 )+ Re ( n_2^2 \eta _{11} + n_1^2 \eta _{22} )\varXi _{12}^1 \Big ] \end{aligned} \right\} $ (11)
其中
$\left. \begin{aligned}\varPi^1= n_1 n_2 \left( p_{11} + p_{22} \right) + \left( \dfrac{n_1^2 }{Re^2} + n_2^2 \right)p_{12} \\ \varPi^2 = \dot {\varepsilon }_{11(0)} p_{11} + \dot{\varepsilon }_{22(0)} p_{22} +\dfrac{1}{2}\left(Re\dfrac{\partial v_{1(0)} }{\partial x_2 } +\dfrac{1}{Re}\dfrac{\partial v_{2(0)} }{\partial x_1 } \right)p_{12 } \\ \varXi_{ij}^1 = n_1 n_2 \left( q_{11ij} + q_{22ij} \right) + \left(\dfrac{n_1^2 }{Re^2} + n_2^2 \right)q_{12ij }\end{aligned} \right\} $ (12a)
$\left. \begin{aligned} \varXi _{ij}^2 = \dot {\varepsilon }_{11(0)} q_{11ij} + \dot{\varepsilon }_{22(0)} q_{22ij }+\dfrac{1}{2}\left( Re\dfrac{\partial v_{1(0)} }{\partial x_2 } +\dfrac{1}{Re}\dfrac{\partial v_{2(0) }}{\partial x_1 } \right)q_{12ij} \\ \varTheta _{ij}^1 = n_1 n_2 \left( r_{11ij} + r_{22ij} \right) + \left(\dfrac{n_1^2 }{Re^2} + n_2^2 \right)r_{12ij } \\\varTheta _{ij}^2 = \dot {\varepsilon }_{11(0)}r_{11ij} + \dot {\varepsilon }_{22(0)} r_{22ij} + \dfrac{1}{2}\Big ( Re\dfrac{\partial v_{1(0)}}{\partial x_2 } + \dfrac{1}{Re}\dfrac{\partial v_{2(0)} }{\partial x_1 } \Big )r_{12ij} \\n_i=\dfrac{k_i}{k_0}, \ \ k^2_0=k^2_1+k^2_2 \\ \eta _{11} = \dfrac{\delta \varepsilon _{11}}{\delta e_N }, \ \ \eta _{22} = \dfrac{\delta \varepsilon _{22} }{\delta e_N }, \ \ \eta _{12} =\dfrac{\delta \varepsilon _{12} }{\delta e_S } \\ \delta e_N=\delta v_{11}+\delta v_{22}, \ \ \deltae_S=\delta v_{12} \ p_{ij}= \dfrac{P_{ij}}{P_0 }, \ \ q_{ijkl} = \dfrac{Q_{ijkl} }{Q_0 }, \ \r_{ijkl} = \dfrac{R_{ijkl }}{R_0 } \\ P_0 = P_{11} + P_{22} + P_{12} \\ Q_0 = Q_{1111} + Q_{1122} + Q_{1112} + Q_{2211} + Q_{2222} + Q_{2212} + Q_{1211} + Q_{1222} + Q_{1212} \\ R_0 = R_{1111} + R_{1122} + R_{1112} + R_{2211} + R_{2222} + R_{2212} + R_{1211} + R_{1222} + R_{1212} \\ P_{ij} = \dfrac{\partial \sigma _{ij }}{\partial T} = - \sigma _{\rm eq }m\dfrac{\left( T - T_0 \right)^{m -1}}{1 - \left( T - T_0 \right)^m} \\ Q_{ijkl} = \dfrac{\partial \sigma _{ij }}{\partial e_{kl}} = \dfrac{\left( 1 +\delta _{ij}\right)2e_{kl} \sigma _{\rm eq}^2 }{9s_{ij} \varepsilon _{\rm eq} }\dfrac{C_0 n\left( \varepsilon_{\rm eq} \right)^{n - 1}}{1 + B_0 \left( \hat {\varepsilon }_{\rm eq} \right)^n} \\ R_{ijkl} = \dfrac{\partial \sigma _{ij} }{\partial \dot {e}_{ij }} = \dfrac{2C_0\left( 1 + \delta _{kl} \right)\sigma _{\rm eq}^2 \dot {e}_{ij}}{9s_{kl} \dot {\varepsilon }_{\rm eq}^2\left( 1 + C_0 \ln \dot {\varepsilon }_{\rm eq} \right)}\end{aligned} \right\} $ (12b)
式(10)~式(12) 的具体推导过程及各相关参数的意义参见文献[12, 27].
判据(10) 的分子和分母分别表示切屑形成过程中材料塑性变形的热软化效应$p_0$和应变硬化效应$Q_0$. 分子括号中的第1项$F_1$表示外加应力载荷产生的材料软化效应;第2项$F_{2}R_{0}$为复杂应力加载条件下不同应变率分量产生的材料硬化与材料软化之间的耦合效应. 在高速切削过程中该项的影响较明显,当切削速度充分低时可以忽略; 第3项$F_{3}R_{\rm c}Q_{0}$为热传导机制相关的不同应变分量产生的材料硬化与材料软化之间的耦合效应. 在低速切削过程中该项的影响较明显,在高速切削过程中可以忽略. 物理意义上,如果失稳函数$F_{\rm Inst} \le1$,表示 材料应变硬化效应强于材料热软化效应,切屑材料的塑性流动是稳定的;如果$F_{\rm Inst}>1$,表示材料热软化效应 强于应变硬化效应,切屑材料的塑性流动可能是不稳定的. 这时判据(10) 给出切屑材料塑性失稳的必要条件. 判据(10) 是在平面应变状态加载条件下得到的. 从系数函数$F_{i}(i=1,2,3,4)$的表达式易见,如果在这些函数中加上其他3 个应力、应变和应变率分量,可以方便地将该判据推广到一般三维加 载情形[17]. 还可以看出在简单加载条件下函数$F_{2}$ 和$F_{3}$均等于零. 表明这两项在简单加载条件下自然消失. 这时,由该判据可以得到单轴拉伸加载条件下判断材料颈缩失稳的相应判据[12],以及在简单剪切加载条件下得到判断材 料剪切带失稳的相应判据[12,27]. 可见判据(10) 具有一定的普遍性.
为了考察$OABC$内材料塑性流动行为,需要对该区域中的应力和速度场进行求解. 为此,首先建立相关的速 度、速度梯度和应力边界条件[27] 如下
$\left. \begin{aligned} {\rm OA:} \ v_1 |_{\rm OA} = \dfrac{\cos \alpha _{\rm T} }{\cos \left( \varphi -\alpha _T\right)}, \ v_2 |_{\rm OA} = \sin \varphi \\ v_{2,1} |_{\rm OA} = \dfrac{Re}{\delta _0 } v_1|_{\rm OA} , \ \ v_{1,2} |_{\rm OA} = \dfrac{1}{Re\delta _0 } v_1 |_{\rm OA} \\ {\rm OC:} \left \{ \begin{array} \ \{v_1 |_{\rm OC} = \sin \varphi \tan \left( {\varphi - \alpha _{\rm T} } \right), \ \ v_2|_{\rm OC} = \sin \varphi \\ V_{1,1} |_{\rm OC} =- v_{2,2} |_{\rm OC}= \cos \varphi - v_1 |_{\rm OA}\\\sigma _{\rm N} |_{\rm OC} = - \dfrac{Re c_1 }{2}\dfrac{\cos \alpha _f }{\cos \left( \varphi - \alpha _{\rm T} \right)}\\\sigma _{\rm T} |_{\rm OC} = - \dfrac{Re c_1 }{2}\dfrac{\sin \alpha _{\rm f} }{\cos \left( \varphi -\alpha _{\rm T} \right)} \ \end{array} \right. \\ {\rm AB, BC}: \ \sigma_{\rm N} |_{\rm AB}=\sigma_{\rm T} |_{\rm AB}= \sigma_{\rm N}|_{\rm BC}=\sigma_{\rm T}|_{\rm BC}=0 \ \end{aligned} \right\}$ (13)
其中$c_{1}$为工件材料的无量纲波速. 控制方程(2)~(6) 和边界条件(13) 构成确定切屑形成区OABC中材料塑性流 动行为定解问题的数学表述. 应用小参数摄动方法可以得到该问题速度场和应力场精确解的线性主部为
$\left. \begin{aligned} v_1 = v_{1,1} |_{\rm OC} \left( {x_1 - \dfrac{1}{2}} \right) +\left. {v_{1,2} } \right|_{\rm OA} \left( {x_2 + \delta _0 Re} \right) \\ v_2 = \left. {v_{2,1} } \right|_{\rm OA} \left( {x_1 - l_0 \dfrac{\tan \left({\phi - \alpha _T } \right)}{2Re}} \right) +\left. {v_{2,2} } \right|_{\rm OC} \left( {x_2 -\dfrac{l_0 }{2}} \right) + \dfrac{\sin \phi }{l_0 } \end{aligned} \right\}$ (14)
和
$\left \{ \begin{array} \\sigma_{12}= \dfrac{S_0 }{I_0 }\left[ I_1 \left( 1 - x_1 \right) + I_2 \left( l_0 - x_2 \right) \right] \\ \sigma _{11} = S_0 f_{11} \left( 1 - x_1 + x_2 \dfrac{\tan \left( \varphi -\alpha _T \right)}{Re} \right) + \sigma _{12} \tan \left( \varphi - \alpha _{\rm T} \right)\\ \sigma _{22} = S_0 f_{12} \left( 1 - x_1 + x_2 \dfrac{\tan \left( \varphi -\alpha _{\rm T} \right)}{Re} \right) + \sigma _{12} \tan \left( \varphi - \alpha_{\rm T}\right) \end{array} \right.$ (15)
其中$\delta_{0}=0.17$和$l_{0} =\sin(\varphi +\alpha _{\rm T}-\alpha _{\rm f})/\cos\alpha _{\rm f}$分别是 经切削厚度法化的主剪切区宽度及切刀/切屑接触区长度[27](图3). 式(15) 中各系数$I_{0}$, $ I_{1}$, $I_{2}$,$f_{11}$, $f_{12}$ 和$S_{0}$ 具有形式
$\left. \begin{aligned} I_0=2 \cos \left( \varphi - \alpha _{\rm T} \right)\cos \left( \alpha _{\rm f} - \alpha_{\rm T} \right)\cdot \left[ 1 - \tan ^2\left(\varphi - \alpha _{\rm T}\right) \right] \\ I_1 = Re\tan \left( \varphi - \alpha _{\rm T} \right)\left( \cos \varphi - \sin \varphi\right) \\ I_2 = \cos \varphi-\sin \varphi \tan ^2\left( \varphi - \alpha _{\rm T} \right) \\ f_{11} = \sigma _N |_{OC} \dfrac{\cos \left( \varphi + \alpha _{\rm f} -\alpha _{\rm T} \right)}{\cos \left( \varphi - \alpha _{\rm T} \right)\cos \alpha _{\rm f} } \\ f_{12} = - \sigma _{\rm T} |_{OC} \dfrac{\sin \left( \varphi + \alpha _{\rm f}- \alpha _{\rm T} \right)}{\cos \left( \varphi - \alpha _{\rm T} \right)\sin \alpha _{\rm f} } \\ S_0 = \dfrac{\left( Re - Re_0 \right)^2}{Re}\dfrac{I_0 }{I_1 + I_2 l_0}\left( 1 + B_0 \gamma _{\rm c} \right) \end{aligned} \right\}$ (16)
其中$\gamma_{\rm c} =0.6$[32].
3 结果与讨论
对于所考虑的4 种金属材料,图5 中给出判据(10) 中失稳函数$F_{\rm Inst}$ 随雷诺数$Re$的变化曲线. 结果表明在低速切 削过程中,由热传导机制产生的应变硬化效应$F_{3}R_{\rm c}Q_{0}$将对材料热软化效应产生明显影响. 而与应变率敏感性相关的应变硬化效应$F_{2}R_{0}$对材料热软化效应的影响是可以忽略的. Ti6Al4V 合金材料具有低的热导性. 与其相关的材料应变硬化效应对材料热软化效应的影响较弱,使失稳函数随雷诺数$Re$变化过程中没有出现负值. 其他3 种材料具有较好的热导性. 在低速切削过程中与其相关的材料应变硬化效应强于外加应力产生的材料软化效应,使失稳函数取得负值. 所以,失稳函数的负值表示材料良好的热导性相关的应变硬化效应强于应力载荷产生的热软化效应,使切屑材料的塑性流动处于稳态.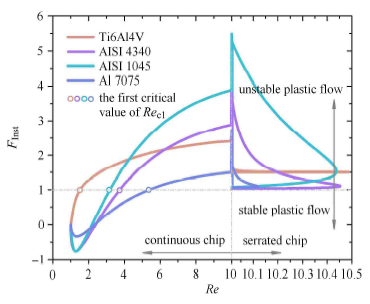
显示原图|下载原图ZIP|生成PPT图54 种金属材料的失稳函数随雷诺数$Re$的变化规律
-->Fig. 5The regulation of the instability function $F_{\rm Inst}$ of four kinds of metals varying with the Reynolds number $Re$
-->
根据失稳判据(10) 可对切屑塑性流动稳定性做出判断. 分3种情形：(1) 当切削速度较低时,4 种材料均存在一个关于雷诺数$Re$的取值区间$[1, Re_{\rm c1} ]$,当$Re \in [1,Re_{\rm c1}]$ 时，$F_{\rm Inst} ≤ 1$. 表明连续切屑材料的塑性流动是稳定的. 这里的$Re_{\rm c1}$确定了连续切屑材料稳态塑性流动的上限,称为第一临界参数, 相应的切削速度称为第一临界速度,用$V_{\rm 0c1}$表示,其值见表2. (2) 当切削速度较高时,即$Re \geqslant Re_{\rm c}=10$ 时，$F_{\rm Inst} >1$, 意味着锯齿切屑形成. 此时切屑材料非稳态的塑性流动由剪切带失稳引起[33]. 临界参数 $Re_{c}=10$对应于连续切屑向锯齿切屑转变的临界状态. (3) 当切削速度适中, $Re \in (Re_{\rm c1}$, $Re_{\rm c})$ 时，$F_{\rm Inst} >1$. 意味着连续切屑的塑性流动可能丧失稳定性, 这时需要进一步考察切屑形成过程中应力 随应变的变化规律,以便确定切屑材料塑性流动的稳定性.
Table 2
表2
表2临界参数$Re_{\rm c1}$ 和$Re_{\rm c2}$ 的值及对应的临界速度$V_{\rm 0c1}$ 和$V_{\rm 0c2}$ 的值
Table 2The values of the critical parameters $Re_{\rm c1}$ and $Re_{\rm c2}$ and the corresponding values of the critical cutting speeds $V_{\rm 0c1}$ and $V_{\rm 0c2}$
| Ti6Al4V | AISI 4340 | AISI 1045 | Al 7075 | |
|---|---|---|---|---|
| $Re_{\rm c1}$ | 1.52 | 3.75 | 3.19 | 5.41 |
| $V_{\rm 0c1}$/(m$\cdot$s-1) | 0.12 | 3.6 | 19.24 | 4.2 |
| $Re_{\rm c2}$ | 2.04 | 2.04 | 2.04 | 2.04 |
| $V_{\rm 0c2}$/(m$\cdot$s-1) | 0.17 | 2.21 | 13.26 | 2.04 |
新窗口打开
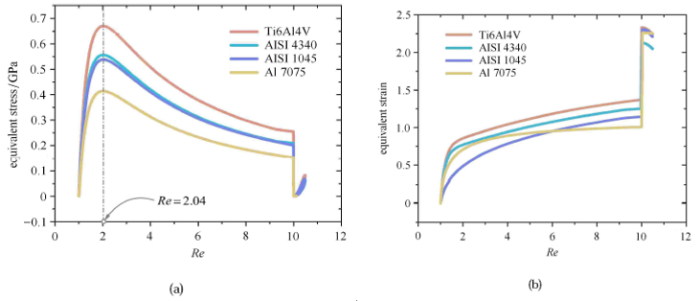
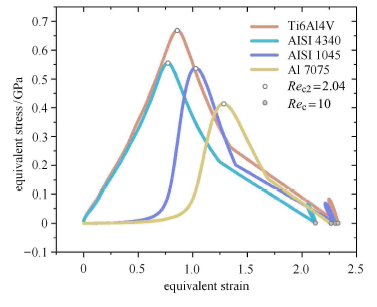
图6(a) 中给出切屑形成区的材料等效应力随雷诺数$Re$的变化曲线. 可见4 种材料在切削过程中随$Re=Re_{\rm c2}=2.04$的变化规律是相同. 即当$Re=Re_{\rmc}=10$时4 种金属切屑中的等效应力同时达到最大值. 当$Re$时,由于剪切带失稳导致等效应力同时取最小值. 值得注意的是对于4 种材料,峰值应力对应于雷诺数$Re_{\rm c2}=2.04$的同一个值$V_{\rm 0c2}$, 称为第二临界参数. 对应的切削速度称为第二临界速度,用$Re$表示. 图6(b) 中给出材料等效应变随雷诺数$Re$的变化曲线. 同样随$Re=Re_{\rmc}=10$增加,4 种材料均表现出相同的单调增加的变化规律. 当$Re < Re_{\rm c2}$时,剪切带失稳使等效应变同时达到最大值. 根据这些等效应力和等效应变与雷诺数Re 的关系曲线可以建立两者间的联系,如图7 所示. 这些曲线也具有相同的变化规律. 当$Re \in (Re_{\rmc2} < Re_{\rm c})$时,切屑材料的塑性变形处于应变硬化阶段,连续切屑的塑性流动是稳态的;当$Re_{\rmc}=10$时,切屑材料的塑性变形进入热软化阶段,连续切屑的塑性流动可以是非稳态的; $Re$对应于剪切带失稳已发生的大应变零应力状态. 当$Re$时,主剪切区中材料经历的剪切带失稳导致锯齿切屑形成.
显示原图|下载原图ZIP|生成PPT图6种金属材料的等效应力和应变随参数$Re$ 的变化规律
-->Fig. 6The regulation of the equivalent stresses and equivalent strains of four kinds of metals varying with the Reynolds number $Re$
-->
显示原图|下载原图ZIP|生成PPT图74种材料的等效应力与应变关系曲线
-->Fig. 7The equivalent stress-strain relationship curves of fourkinds of metals
-->
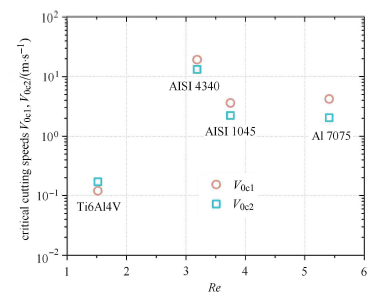
这里，所考虑的四种金属材料服从J-C 本构定律[18, 28]，其塑性流动的稳定性取决于材料热软化和应变硬化两种机制的竞争. 判据(10) 只给出判断材料塑性流动失稳的必要条件. 即满足条件$F_{\rm Inst} >1$ 表示塑性流动可能会丧失稳定性. 该条件与材料应力- 应变变化规律结合将给出判断材料塑性流动稳定性的充要条件. 图8 中给出满足条件$F_{\rm Inst} >1$ 确定的切屑材料塑性失稳可能发生的第一临界切削速度$V_{\rm 0c1}$ 随雷诺数$Re$ 的变化. 为了便于比较，图中也标出根据峰值应力或条件$Re=Re_{\rm c2}$ 确定的第二临界切削速度$V_{\rm 0c2}$. 为清晰起见，表2 中给出了这些临界速度的具体数据. 按照切屑材料塑性失稳的充要条件，两个临界速度中较大者应是连续切屑材料塑性流动失稳发生的真实临界速度, 因此，Ti6Al4V 合金的临界速度由条件$Re=Re_{\rm c2}$ 确定为0.17m/s；对其他3 种材料的临界速度由条件$F_{\rm Inst} >1$ 分别确定, Al 7075 为3.6m/s，AISI 4340 为19.24m/s, AISI 1045 为4.2m/s. 不论何种情形，在金属切削过程中总存在一个临界速度，当切削速度大于该临界速度时，连续切屑的塑性流动将由稳态的转变为非稳态的.
最后给出几点说明：(1) 连续切屑形成过程中材料的塑性失稳是在平面应变状态下发生的. 其塑性变形特点是非局部均匀压剪复合变形; 而锯齿切屑中剪切带失稳过程主要由剪应力载荷引起，具有变形局部化的特点. (2) 理论上，由条件$F_{\rm Inst} > 1$ 和$Re=Re_{\rm c2}$ 确定的连续切屑材料塑性失稳的临界速度应该是严格相等的. 图8 中的结果表明两者间存在一定误差. 一个原因是前节求得的切屑形成区$OABC$ 内材料塑性变形的速度和应力结果是问题的近似解. 显然，在切屑形成区$OABC$ 内的速度和应力应该是空间分布的非线性函数. 近似解(12) 和(13) 只取了非线性精确解的线性主部. 另外，为简单起见，判据(10) 中忽略了温度梯度、应变率梯度以及物质对流现象的影响. 这是产生误差的另一原因. (3) 在对雷诺数$Re$ 修正过程中，通过函数 $\chi (V_{0})$ 预先设定了$Re=Re_{\rm c}$ 对应于连续切屑转变为锯齿切屑的临界状态. 即给出锯齿切屑主剪切区中材料剪切带失稳的临界条件. 考虑到上述产生误差的原因，在图8 中两组临界速度结果中如果忽略其差别，则4种材料的两组临界速度应该相等. 即对应于雷诺数$Re$ 的同一个值$Re_{\rm c1}=Re_{\rm c2}$. 表明修正后的雷诺数$Re$也能描述材料切削过程中连续切屑的非局部塑性失稳行为. 可见，在材料正交切削过程中，雷诺数$Re$ 扮演了主控参数的角色.
显示原图|下载原图ZIP|生成PPT图8两种临界速度的分布及其比较
-->Fig. 8The distribution of two kinds of critical cutting speeds and their comparison
-->
4 结论
通过金属正交切削过程的研究得到以下结论：(1) 通过切削实验测定4 种金属材料切屑由连续状转变成锯齿状的临界速度, 该临界速度与材料性能和切削条件相关;
(2) 在连续介质力学框架内,建立了描述金属正交切削的物理模型, 给出含3 个无量纲参量的描述金属正交切削过程和切屑材料塑性流动行为基本理论框架;
(3) 建立的判断材料塑性流动稳定性的判据具有一定的普遍性,给出判断切屑材料塑性失稳的必要条件;
(4) 金属切屑的塑性流动有两种失稳模式：锯齿切屑形成过程中主剪切区内材料经历的剪切局部失稳和连续切屑形成过程中材料经历的平面应变加载条件下的塑性失稳. 前者表现出材料剪切变形的局部化,后者表现为材料非局部均匀的塑性流动;
(5) 修正后的雷诺数{Invalid MML} 可以作为主控参数描述金属正交切削过程中连续切屑材料塑性流动的非局部失稳行为和锯齿切屑的剪切局部失稳行为.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | . |
| [4] | |
| [5] | . . |
| [6] | |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . |
| [12] | . |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | |
| [18] | . |
| [19] | . . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . |
| [24] | . |
| [25] | . . |
| [26] | . . |
| [27] | . |
| [28] | . |
| [29] | . |
| [30] | . |
| [31] | . |
| [32] | . |
| [33] | . |
