刘君^*,, 张雨勤
大连理工大学 海岸与近海工程国家重点实验室,大连 116024

CFD SIMULATION ON THE PENETRATION OF FFP INTO UNIFORM CLAY

LiuJun^*, ZhangYuqin
^* State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology Dalian, 116024, China
中图分类号:TU470.3
文献标识码:A

通讯作者:*^*通讯作者：刘君,教授,主要研究方向：海洋岩土工程,计算土力学. E-mail: junliu@dlut.edu.cn*^*通讯作者：刘君,教授,主要研究方向：海洋岩土工程,计算土力学. E-mail: junliu@dlut.edu.cn
收稿日期:2017-08-21
接受日期:2017-10-30
网络出版日期:2018-02-20
版权声明:2018《力学学报》编辑部《力学学报》编辑部 所有
基金资助:国家自然科学基金项目（No.51479027, 51539008）资助.

展开

摘要
圆锥静力触探法(Cone penetration test, CPT)广泛应用于土的抗剪强度测试中。在此基础上发展的自由落体式贯入仪(Free fall penetrometer, FFP),依靠自由下落获得的动能和自身重力势能贯入土中,不需要借助外部加载装置,提高其使用的便捷性。但在动力贯入过程中FFP与土的相互作用更为复杂,涉及到土体的率效应和拖曳阻力等的影响。因此,对FFP各项受力和相关参数的准确分析有助于提高其实用性以及测量的准确性。作者采用基于计算流体动力学(computational fluid dynamics, CFD)的分析软件ANSYS CFX 17.0模拟FFP在均质黏土中的贯入过程,借助动网格的大变形分析方法来模拟FFP贯入过程中的运动边界问题。提出了薄层单元法模拟FFP与土体的界面摩擦接触行为。在CFD模拟中,土体材料采用非牛顿流体来模拟,其剪切强度受土体切应变率的影响(即土体的率效应)。通过模拟贯入仪在黏土中以不同的速度贯入的过程,研究FFP的端部阻力和侧壁阻力与贯入速率、土体强度和密度、界面摩擦系数以及率效应参数之间的关系,建立了端部承载力系数、端部和侧壁率效应参数及拖曳系数的表达式,并提出了土体不排水抗剪强度的预测方法,为FFP测试数据的解析提供依据。

关键词：自由落体式贯入仪;土体率效应;拖曳阻力;承载力系数;土性测试;计算流体动力学
Abstract
The cone penetration test (CPT) has been widely used to measure the soil undrained shear strength. On the basis of CPT, the free fall penetrometer (FFP) is developed to improve the test efficiency, which penetrates into soil by its kinetic energy gained from free fall in the water/air column and potential energy. However, the soil-FFP interaction is rather complex, which refers to the shear strain rate effect and drag force. Therefore, it is necessary to analyze the forces acting on the FFP accurately to improve its practicability and the accuracy of soil strength measurement. The FFP penetration procedure in uniform soils was simulated in the present study by using the commercial software ANSYS CFX 17.0, which is based on the computational fluid dynamics (CFD) approach. The dynamic mesh approach was applied to simulate the moving boundary. The thin layer element method was proposed to simulate the FFP-soil interaction. In the CFD simulation, the soil was modeled as non-Newtonian fluid and the shear strain rate effect was considered. Different FFP velocities, soil strengths and densities, interface frictional coefficients and shear strain rate parameters were considered to investigate their effects on the bearing and sleeve resistances of FFP. The fitted formulas of the cone bearing capacity factor, the strain rate parameters and drag coefficients for the cone and sleeve were established based on the present numerical results. In addition, the process to estimate the undrained shear strength of clayed soils was put forward, which may be beneficial for analyzing the recorded data from FFP.

Keywords：FFP;rate effect;drag force;bearing capacity;soil testing;CFD

-->0
PDF (2121KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
刘君, 张雨勤. FFP在黏土中贯入过程的CFD模拟[J]. 力学学报, 2018, 50(1): 167-176 https://doi.org/10.6052/0459-1879-17-284
Liu Jun, Zhang Yuqin. CFD SIMULATION ON THE PENETRATION OF FFP INTO UNIFORM CLAY[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(1): 167-176 https://doi.org/10.6052/0459-1879-17-284

引言

随着近海能源的消耗殆尽以及对能源需求的不断扩大,海上油气资源开采已经从近海逐渐向能源储量丰富的深海发展。深海的特殊环境对深海的地质勘测以及基础安装等方面有更高的要求。自由落体式贯入仪(Free fall penetrometer, FFP)能够依靠在水中自由下落获得的动能和自身重力势能贯入海床土中,目前在深海开发作业中得到较为广泛的应用,如深海核废料的处理^[1],土质勘测(图1a)^[2,3]以及深海锚固系统(如鱼雷锚(图1b),OMNI-Max锚)^[4,5,6]等。尤其在土质勘测方面,相比传统的静力触探实验(如圆锥静力触探法(Cone penetration test, CPT),T形(T-bar)和球形(ball)贯入仪等),FFP不需要大型的加载仪器,能够实现较大区域内的快速测量作业^[7]。图1a所示为在100 g离心机试验^[8]以及北冰洋海域测试^[9]中所使用的FFP。室内试验所用FFP的直径为D=10 mm,长度L=120 mm,锥尖角度为β=60°(如图1c所示)。但是FFP在动力贯入过程中的受力要比静力压入方式的受力更加复杂,因此对勘测数据的分析存在一定的难度^[7],也使得深海锚固系统的设计更加困难。
FFP在高速贯入海床土中时,主要受到端部阻力(F_t)和侧壁阻力(F_f)的作用(如图1c所示,其中W_s为FFP浮重力)。由于FFP周围土体经受高剪应变率并发生大变形,因此需要考虑土体的率效应对FFP贯入过程和测量结果的影响^{[11, 12]}。土体的率效应指土的不排水抗剪强度随切应变率提高而增加的现象。以鱼雷锚为例,实际工程中锚的贯入速度可达到30 m/s^[13],土体的切应变率比标准贯入速度时的高了2~3个量级^[12]。Einav和Randolph^[14]对比分析了表征土体率效应的三种模型,式(1)所示为其中的半对数模型
${{s}_{\text{u}}}=\left[ 1+\lambda \log (\frac{{\dot{\gamma }}}{{{{\dot{\gamma }}}_{\text{ref}}}}) \right]{{s}_{\text{u0}}}$ (1)
其中,$\dot{\gamma }$为土体的切应变率,λ为土的率效应参数,表示土体的切应变率每提高一个量级,对应的土体不排水抗剪强增加的程度（如λ=0.1,表示土体的切应变率每提高一个数量级,土体不排水抗剪强度提高10%）,其取值范围为0.08~0.38^[12],s_u0为参考切应变率${{\dot{\gamma }}_{\text{ref}}}$下的不排水抗剪强度。在经验计算中,常取$\dot{\gamma }$ = v/D,其中D为贯入物体的直径。其他描述土体切应变率效应的模型可以参考文[12, 14]。
深海海床土体一般为低强度软黏土^[15],在经受高剪应变率时会呈现粘滞性流体的性质。所以,FFP贯入过程中受到的端部和侧壁阻力中也会包含拖曳阻力。而关于FFP在土中的拖曳阻力问题的研究成果比较少,主要原因在于实验中难以通过测量的手段来确定各部分的拖曳阻力。而在动力锚沉贯过程的理论计算中^[4,16,17],拖曳阻力系数(C_d)通常取动力锚在水中的拖曳阻力系数^[18]。因此,对FFP在土中贯入过程所受到拖曳阻力的研究很有必要。
在考虑土体的率效应以及拖曳阻力的情况下,F_t和F_f可以用式(2)表示。
${{F}_{\text{t}}}={{R}_{\text{f}1}}\cdot {{N}_{\text{c}}}{{s}_{\text{u}}}{{A}_{\text{t}}}+{{F}_{\text{d},\text{t}}}$ (2a)
${{F}_{\text{f}}}={{R}_{\text{f}2}}\cdot \alpha {{s}_{\text{u}}}{{A}_{\text{f}}}+{{F}_{\text{d},\text{f}}}$ (2b)
其中R_f1和R_f2分别为端部和侧壁的率效应系数,表征土体率效应分别对端部以及侧壁阻力的增强效应;N_c为端部承载力系数;α为FFP与土体之间的摩擦系数,其取值范围为0~1 (0表示完全光滑,1表示完全粗糙),常取为1/S_t (S_t为土的灵敏度,其取值范围一般为2~9^[19,20]);A_t和A_f分别为FFP端部投影面积和侧壁面积;F_d,t和F_d,f分别为端部和侧壁的拖曳阻力。
显示原图|下载原图ZIP|生成PPT
图1FFP实例以及FFP模型示意图
-->Fig.1Applications of FFP and schematic of FFP model
-->

****通过大量试验探究发现FFP在土中贯入时R_f1小于R_f2 ^[3,21,22]。另外,Einav等^[14]用基于塑性力学的理论分析研究也表明侧壁的率效应系数较高。在数值模拟方面,一些****用基于耦合欧拉-拉格朗日大变形有限元方法(Coupled Eulerian-Lagrangian, CEL)研究了率效应对动力锚沉贯深度的影响^[16,17,23],但上述研究没有具体分析端部和侧壁的率效应系数以及影响因素。
因此,为解决上述所存在的问题,本文用基于流体动力学(computational fluid dynamics, CFD)的商业软件ANSYS CFX17.0模拟FFP在均质黏土中的贯入过程。之前有****用CFX研究了海底管线与海床土体^{[24, 25]}、海底滑坡引起的泥石流^{[26, 27]}的相互作用以及锚的动力贯入过程^[28]等问题,表明用非牛顿流体来模拟海洋土能够很好地模拟海洋土与结构之间的高速大应变的相互作用。本文将采用相同的海洋土模拟方法,分别计算分析无率效应土体和有率效应土体情况下FFP的受力。研究FFP的运动速度(v)、土体密度(ρ)、土体强度(s_u0)、界面摩擦系数(α)以及土体率效应参数(λ)等因素对端部阻力、侧壁阻力以及对应的率效应系数的影响。首先根据无率效应土中的计算结果,分析FFP的端部承载力系数(N_c)、端部拖曳阻力系数(C_d,t)、侧壁拖曳阻力系数(C_d,f)以及侧壁摩擦力特性;结合所得的相关系数,以及FFP在有率效应均质土中计算所得的端部阻力以及侧壁阻力,分析其端部的率效应系数(R_f1)以及侧壁的率效应系数(R_f2)。根据数值计算的结果可以分别给出N_c、C_d,t、C_d,f以及R_f1、R_f2的计算表达式,从而总结出采用FFP测量均质黏土不排水抗剪强度的方法。

1 CFX数值模型

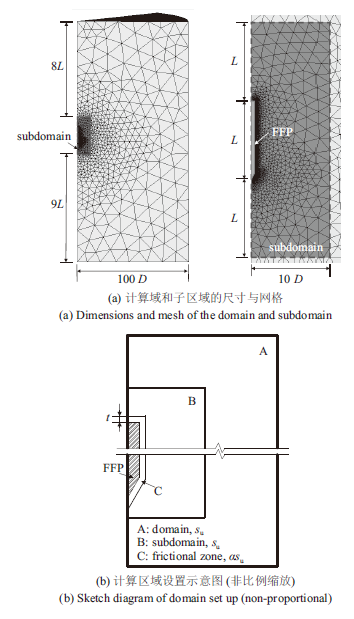
根据计算模型的轴对称性质,取1/8模型进行建模(图2a)以提高计算效率。所选用的FFP长度为L = 13.04 m,直径D = 1.2 m,锥尖角度β=60°(如图1c所示)。FFP在初始时刻预埋入土中,这样在贯入过程中FFP与土体的接触面积不会发生变化,以简化计算与受力分析过程。
本文用动网格的方法来模拟FFP贯入过程中的运动边界问题,并利用CFX中的子区域(subdomain)方法^[24,25,28]来提高计算效率和计算精度。Hawlader等^[24,25]用该方法模拟了海底管线与海床土体之间的相互作用,并分析得出该方法能够在保证计算精度的基础上有效提高计算效率。在FFP贯入的过程中,子区域(图2b中的B区域)内的网格以相同的速度与FFP一起运动,因此该区域内的网格不会发生变形,而在子区域以外的网格则会有一定的变形(详见2.1内容)。由于这些地方的网格相对大,但应变很小,不至于导致网格畸变,影响计算结果的精度^[24]。利用子区域的方法能够有效的解决运动边界问题,且不需要对子区域外部的网格进行更新,只需将其变形量控制在合理的范围内,这样能够有效的提高计算效率。所有区域内的网格均为非结构的四面体欧拉网格,并且在FFP的外侧设置了5层总厚度为5 mm的边界层^[27]。模型计算区域以及子区域的尺寸如图2a所示,计算域半径R = 100D,以消除边界效应对计算结果的影响;子区域距离计算域上端和底部分别为8L和9L,以使FFP的运动范围在计算域中部,防止子区域以外的网格发生影响计算结果的变形。
本文用薄层单元的方法来模拟FFP与土体的界面摩擦。即定义与FFP相接触的一定厚度区域(即图2b中的C区域为摩擦区域)内的土体强度为αs_u,而保持其他区域单元内的土体强度为s_u。计算模型的各个区域设置示意图以及对应的土强度如图2b所示。通过对摩擦区域厚度(t)的收敛性计算(如表1所示),可以得到t=0.025D时已满足计算精度要求,并且具有较高的计算效率。由于子区域内的网格在计算过程中不变形,所以在FFP与土体之间设置薄层单元来模拟界面效应是合适的,尽管界面内存在非常大的切应变。
Table 1
表1
表1摩擦区域厚度(t)收敛性分析
Table 1Convergence analysis of the frictional domain thickness

t	Mesh quantity /million	Ff/N	Deviation	Iteration time /s
0.05D	0.18	3945.1	11.7%	3.1
0.025D	0.42	3661.7	3.6%	7.9
0.0125D	1.70	3532.6	——	26

Note: v=0.12 m/s,s_u0=2 kPa,ρ=1.6 g/mm³,α=0.3Computer configuration: Core i7,4.00 GHz,16 GB(RAM)
新窗口打开
计算域的上端为开口边界条件(opening),侧壁为自由滑移壁面(free slip wall),而底面为无滑移壁面(no slip wall)。对称面均设置为对称边界(symmetry)。FFP与土之间的接触面为无滑移壁面,即与FFP接触的土体相对于FFP的速度为0。子区域B与外部区域A之间的面设置为交界面(interface),允许流体自由的流入流出。FFP的运动通过CFX表达式来控制。本文中FFP均以恒定的速度向下运动,运动距离均为L。
本文采用非牛顿流体来模拟土体。在流体力学中,切应力τ一般表示为
$\tau =\mu \cdot \dot{\gamma }$ (3)
因此可以通过定义动力粘滞系数(μ)来表征土体的不排水抗剪强度s_u。根据式(1)和(3),动力粘滞系数为
$\mu =\frac{\tau }{{\dot{\gamma }}}=\frac{{{s}_{\text{u}}}}{{\dot{\gamma }}}=\left[ 1+\lambda \log (\frac{{\dot{\gamma }}}{{{{\dot{\gamma }}}_{\text{ref}}}}) \right]\frac{{{s}_{\text{u0}}}}{{\dot{\gamma }}}$ (4)
其中流体的切应变率$\dot{\gamma }$可以在每个计算步中得到。对于无率效应的均质土,s_u = s_u0 为一个常数。而在考虑率效应的情况下,s_u与土体的切应变率相关,如式(1)和(4)所示,其中参考切应变率${{\dot{\gamma }}_{\text{ref}}}$取为0.024 s^-1。本文中的各个参数取值范围如表2所示。
显示原图|下载原图ZIP|生成PPT
图2CFX网格设置与模型尺寸
-->Fig.2CFX mesh and model dimensions
-->

Table 2
表2
表2参数及取值范围
Table 2Range of selected parameters

Parameter	Value
Penetration velocity, v, m/s	3, 6, 12, 24, 30
Soil undrained shear strength, su0, kPa	1, 2, 4, 10, 15, 20
Soil density, ρ, g/mm3	1.4, 1.6, 1.8
Frictional coefficient, α	0.05,0.3, 0.6, 1.0
Coefficient of shear strain rate effect, λ	0, 0.1, 0.2, 0.3

新窗口打开

2 结果与分析

2.1 网格变形分析

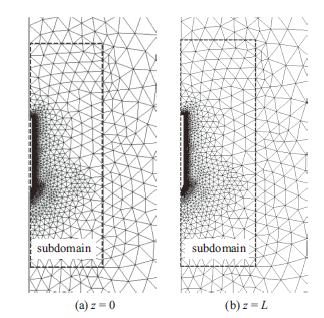
图3a和3b分别为初始位置(z = 0)和FFP运动了z = L (z为FFP相对初始位置运动的距离)深度后的网格情况。可以看到上部A1区域内的网格会随着FFP向下运动而有一定的拉伸,而位于底部的A2区域内的网格则会被压缩。当FFP和子区域的运动距离相对计算域尺寸较小时,可以将子区域以外的网格变形控制在合理的范围内,如本文模型所示。图4所示为两个位置时(z = 0和z = L)对应的子区域附近的网格变形情况。根据子区域的性质,其内部的网格不会发生变形,而且该区域以外一定范围内的网格变形量也很小。在子区域取合理的尺寸的情况下,网格的变形不会对计算精度产生较大的影响^[24]。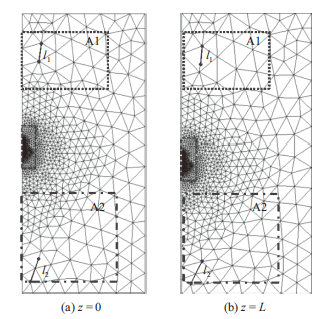
显示原图|下载原图ZIP|生成PPT
图3计算域内网格变形
-->Fig 3.Mesh deformation in the domain
-->

显示原图|下载原图ZIP|生成PPT
图4子区域内以及周边网格变形
-->Fig 4.Mesh deformation in and around the subdomain
-->

2.2 无率效应的结果分析

本文首先模拟了不考虑土体率效应(λ=0)情况下FFP的受力情况。分别计算了摩擦系数α = 0.05,0.3,0.6和1.0时,FFP以不同的贯入速度,在不同强度和密度的土体中匀速运动时的端部阻力F_t以及侧壁阻力F_f,以分析FFP的受力特性并推导相关系数。
Zakeri等^[24]用CFX模拟了海底滑坡中泥石流对海底管线的冲击作用,在流体力学框架内得出阻力系数C_D与非牛顿流体雷诺数R_en之间的关系。Randolph和White^[29]在Zakeri等^[26]的基础上,以土力学的视角重新审视泥石流对管线的作用,认为泥石流对管线的冲击作用可表述为由于土的剪切强度引起的端承阻力以及由于土的惯性作用而引起的拖曳阻力两部分,并对Zakeri等^[26]的计算数据进行重新分析,给出海底管线的端部承载能力系数以及拖曳阻力系数。Liu等^[27]也用该方法研究分析了泥石流以不同角度冲击海底管线时的受力特性。本文采用类似的方法,对FFP在运动过程中的受力进行分析。
非牛顿流体的雷诺数可以表示为^[24]
${{R}_{\text{e}}}_{\text{n}}=\frac{\rho {{U}_{\infty }}^{2}}{\tau }$ (5)
其中${{U}_{\infty }}$为上游自由流体的流速,在FFP的分析中即为其运动速度v。而在土力学中,FFP的端部阻力可表示为端承阻力和拖曳阻力两部分,在不考虑率效应的情况下,式(2a)可以重新改写为
${{F}_{\text{t}}}={{N}_{\text{c}}}{{s}_{\text{u}0}}{{A}_{\text{t}}}+\frac{1}{2}{{C}_{\text{d,t}}}\rho {{v}^{2}}{{A}_{\text{t}}}$ (6)
其中C_d,t为端部拖曳阻力系数。根据式(5)和(6)可得
${{N}_{\text{t}}}=\frac{{{F}_{\text{t}}}}{{{s}_{\text{u}0}}{{A}_{\text{t}}}}={{N}_{\text{c}}}+{{C}_{\text{d,t}}}\frac{{{R}_{\text{en}}}}{2}$ (7)
则不同工况下计算所得的N_t与R_en/2可以进行线性拟合,所得的截距即为FFP的端部承载力系数N_c,其斜率即为C_d,t。
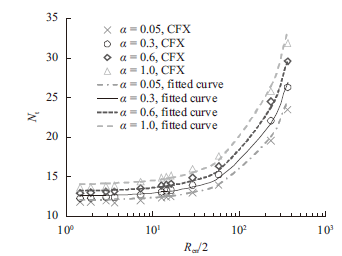
各工况计算所得的端部阻力F_t如表3所示。由表中数据对比可以发现,随着v的增大,F_t也会有明显增长,主要是因为拖曳阻力的作用。随着摩擦系数α的增大,F_t也有稍微增大的趋势。图5所示为N_t与R_en/2之间的关系以及线性拟合结果。根据式(7),不同摩擦系数下的N_c与C_d,t值如表4所示。随着α的增大,N_c和C_d,t均有增大的趋势。Ma等^[30]用大变形有限元方法计算了CPT在均质黏土中的N_c值,结果表明N_c与土体刚度系数(I_r)和摩擦系数α相关,在I_r取50~500,α分别为0.05,0.3,0.6和1.0时的N_c值如表4所示,本文的计算结果均在其范围之内。根据本文的计算结果可以得出N_c、C_d,t与α之间的关系分别如下
${{N}_{\text{c}}}\text{=}11.875+2.07\alpha $ (8)
${{C}_{\text{d,t}}}\text{=}0.034+0.02\alpha $ (9)
显示原图|下载原图ZIP|生成PPT
图5N_t与R_en/2之间的关系
-->Fig.5Bearing coefficient N_t vs. R_en/2
-->

分析FFP的侧壁受力可以发现,在s_u0以及α相同的情况下,随着FFP运动速度的增大,侧壁阻力有增大的趋势(见表3),这表明FFP侧壁上除了有摩擦力作用外,也有拖曳阻力的作用,约占侧壁阻力的10%~15%。因此式(2b)所示的侧壁阻力F_f在不考虑率效应的情况下可以表示为式(10)
${{F}_{\text{f}}}\text{=}\alpha {{s}_{\text{u0}}}{{A}_{\text{f}}}+\frac{1}{2}{{C}_{\text{d,f}}}\rho {{v}^{2}}{{A}_{\text{f}}}$ (10)
其中C_d,f为侧壁的拖曳阻力系数,其取值与R_en相关。不同摩擦系数情况下,C_d,f与R_en之间的关系如图6所示。α增大时,C_d,f有增大的趋势;但是C_d,f会随着R_en的增大而减小。C_d,f与α、R_en之间的关系如式(11)所示
${{C}_{\text{d,f}}}\text{=}\frac{0.2\alpha }{{{R}_{\text{en}}}^{0.9}}$ (11)
显示原图|下载原图ZIP|生成PPT
图6侧壁拖曳阻力系数C_d,f与R_en之间的关系
-->Fig. 6Sleeve drag coefficient C_d,f vs. R_en
-->

Table 4
表4
表4不同摩擦系数下FFP的C_d,t与N_c值
Table 4Values of C_d,t and N_c of FFP for different frictional coefficients

α	Cd	Nc(this study)	Nc(Ma et al.[30])
0.05	0.035	11.98	9.64~13.38
0.3	0.04	12.5	9.96~13.56
0.6	0.047	13.12	10.35~13.94
1.0	0.054	13.95	10.87~14.46

新窗口打开
Table 3
表3
表3无率效应均质土中F_t与F_f计算结果
Table 3Simulation results of F_t and F_f in uniform soils without shear strain rate effect

Case	v /(m·s-1)	ρ /(g·mm-3)	su0 /kPa	Ren	α=0.05		α=0.3		α=0.6		α=1.0
					Ft/kN	Ff/kN	Ft/kN	Ff/kN	Ft/kN	Ff/kN	Ft/kN	Ff/kN
1	3	1.6	2	7.2	3.29	0.65	3.50	3.92	3.70	7.69	3.91	12.66
2	6	1.6	2	28.8	3.49	0.65	3.72	3.96	3.95	7.83	4.23	12.93
3	12	1.6	2	115.2	3.93	0.66	4.31	3.93	4.61	7.85	4.96	13.05
4	24	1.6	2	460.8	5.51	0.69	6.23	3.99	6.91	7.75	7.29	12.95
5	30	1.6	2	720	6.62	0.71	7.43	4.06	8.35	7.91	9.01	12.89
6	6	1.4	2	25.2	3.46	0.64	3.68	3.96	3.92	7.82	4.19	12.91
7	6	1.8	2	32.4	3.51	0.66	3.74	3.96	3.98	7.84	4.27	12.95
8	6	1.6	1	57.6	1.83	0.33	1.96	1.94	2.91	3.93	2.25	6.51
9	6	1.6	4	14.4	6.75	1.30	7.16	7.89	7.62	15.57	8.10	25.63
10	6	1.6	10	5.76	16.81	3.31	17.46	19.55	18.47	38.35	19.49	63.08
11	6	1.6	15	3.84	24.99	4.95	26.01	29.17	27.47	57.13	28.94	93.86
12	6	1.6	20	2.88	33.27	6.53	34.56	38.73	36.47	75.78	38.39	124.43

新窗口打开

2.3 考虑土体率效应的结果分析

土体的率效应如式(1)所示,在考虑土体率效应的情况下,FFP的端部阻力与侧壁阻力计算式(2)可以改写为式(12)和(13)
${{F}_{\text{t}}}={{R}_{\text{f}1}}\cdot {{N}_{\text{c}}}{{s}_{\text{u}}}{{A}_{\text{t}}}+\frac{1}{2}{{C}_{\text{d},\text{t}}}\rho {{v}^{2}}{{A}_{\text{t}}}$ (12)
${{F}_{\text{f}}}={{R}_{\text{f}2}}\cdot \alpha {{s}_{\text{u}}}{{A}_{\text{f}}}+\frac{1}{2}{{C}_{\text{d},\text{f}}}\rho {{v}^{2}}{{A}_{\text{f}}}$ (13)
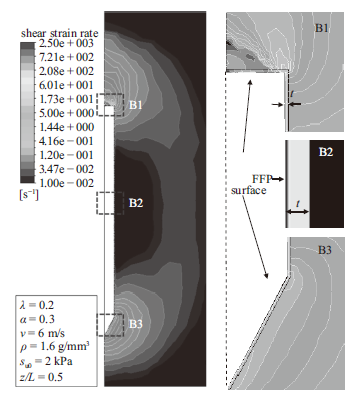
本文计算了率效应参数λ分别取0.1,0.2和0.3时的各工况,研究FFP的运动速度、土体密度、土体强度以及摩擦系数对R_f1和R_f2的影响,各参数的取值如表2所示。表5为λ = 0.2,α = 0.3时的一组工况计算结果,由该表可知R_f2 > R_f1;且随着v的增大,R_f1和R_f2均有明显增大的趋势。但是随着s_u0的提高,率效应系数反而会减小。土体密度对R_f1和R_f2的影响都很小。图7所示为表5中工况2计算所得的FFP周边土体切应变率分布情况,可以看到FFP的前端(B3)和尾部(B1)对土体的扰动范围比较大。虽然FFP侧壁的切应变率较高,但是剪切带范围很小(图7中B2区域所示),集中在距离FFP较小厚度范围之内。Chow等^[31]通过室内模型试验研究了FFP贯入过程中不同的贯入速度以及土强度对率效应的影响,试验结果表明FFP端部的率效应系数也会随着贯入速度的增大而增大,随着土强度的提高而减小,并给出土体不排水抗剪强度与率效应系数之间的关系如下
${{R}_{\text{fl(mean)}}}\text{=}2.945-0.029{{s}_{\text{u}(\text{CRP})}}$ (14)
其中R_fl(mean)为同一土样中不同贯入速度测得的率效应系数平均值,s_u(CRP)为通过静压实验测得的土体不排水抗剪强度。由于实验方法的限制,所测得的阻力中包含了土体的浮力以及拖曳阻力等的作用,因此用该实验测量结果计算所得的率效应系数相比本文数值模拟的结果要偏大,且土强度的影响也比较显著。
表5中R_f为用式(15)所得的平均率效应系数。由表中结果可以得到R_f1<R_f,而R_f2>R_f(对于其他的λ和α情况下结果相同),即如果按照平均率效应计算,会高估端部的率效应而低估侧壁的率效应。
${{R}_{\text{f}}}\text{=}1+\lambda \cdot \log \frac{v/D}{{{{\dot{\gamma }}}_{\text{ref}}}}$ (15)
显示原图|下载原图ZIP|生成PPT
图7表4工况2土体切应变率分布(为显示清楚,B2区域与B1和B3区域的放大系数不同)
-->Fig. 7Shear strain rate of soil for case 2 in Table 4
-->

Table 5
表5
表5λ = 0.2,α = 0.3情况下FFP的计算结果
Table 5Simulation results of FFP for λ = 0.2, α = 0.3

Case	va /(m·s-1)	ρ /(g·mm-3)	su0 /kPa	Ren	λ=0.2,α=0.3
					Ft/kN	Ff/kN	Rf1	Rf2	Rf1/Rf	Rf2/Rf
1	3	1.6	2	7.2	4.217	6.963	1.182	1.930	0.842	1.375
2	6	1.6	2	28.8	4.602	7.363	1.256	2.030	0.859	1.387
3	12	1.6	2	115.2	5.440	7.637	1.355	2.090	0.890	1.372
4	24	1.6	2	460.8	7.740	7.792	1.454	2.112	0.918	1.333
5	30	1.6	2	720	9.255	7.955	1.467	2.151	0.915	1.342
6	6	1.4	2	25.2	4.589	7.353	1.258	2.029	0.860	1.386
7	6	1.8	2	32.4	4.653	7.374	1.265	2.031	0.865	1.388
8	6	1.6	1	57.6	2.430	3.701	1.283	2.031	0.877	1.387
9	6	1.6	4	14.4	8.954	14.581	1.244	2.018	0.850	1.379
10	6	1.6	10	5.76	21.827	35.762	1.226	1.988	0.838	1.359
11	6	1.6	15	3.84	32.543	53.070	1.222	1.971	0.835	1.346
12	6	1.6	20	2.88	43.257	70.163	1.219	1.956	0.833	1.337

新窗口打开
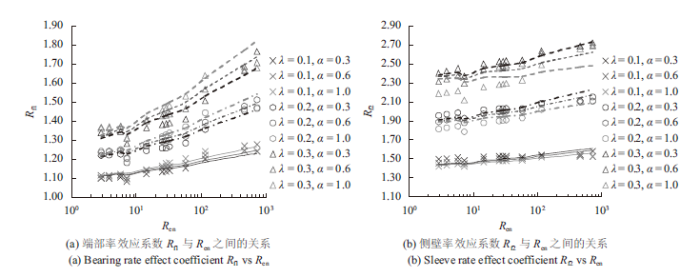
图8所示为不同摩擦系数α和率效应参数λ下R_f1和R_f2与R_en之间的关系,可见R_f1和R_f2都会随着率效应参数λ的增大而明显增大,说明率效应参数的选取将会对端承项以及摩擦项的率效应产生很大的影响。随着摩擦系数的增大,R_f1会有增大的趋
势,而R_f2则会减小,但是摩擦系数对R_f1和R_f2的影响都比较小。根据计算结果可以得到R_f1和R_f2与R_en和λ之间满足以下关系
${{R}_{\text{f}1}}\text{=(1+}\lambda \text{log}\frac{v/D}{{{{\dot{\gamma }}}_{ref}}}{{)}^{1/3}}\cdot (1+0.18\lambda ){{R}_{\text{en}}}^{\lambda (0.151-0.14\lambda +0.06\alpha )}$ (16)
${{R}_{\text{f2}}}\text{=(1+}\lambda \text{log}\frac{v/D}{{{{\dot{\gamma }}}_{ref}}}{{)}^{1/3}}\cdot (1+3.2\lambda ){{R}_{\text{en}}}^{\lambda (0.246-0.55\lambda -0.07\alpha )}$ (17)
上式结果与计算结果的对比如图8所示。式(17)的计算结果与CFX计算结果在λ = 0.3,α = 1.0时候会有较大偏差,最大偏差在10%左右。α = 1.0是数值模拟中摩擦系数的极限值,在实际应用中,物体与土体之间的摩擦系数一般都小于1。工程中常用1/S_t (S_t为土的灵敏度系数)作为土体的界面摩擦系数,对于墨西哥湾和几内亚湾等区域的海洋土,S_t一般在2~6的范围内^[18],中国南海海洋土的灵敏度则达到5~9^[19]。因此,在工程应用的参数范围内,式(16)和(17)能够很好地描述率效应系数的变化规律。
显示原图|下载原图ZIP|生成PPT
图8不同λ和α下FFP率效应系数与雷诺数R_en之间的关系
-->Fig. 8Shear strain rate coefficients of FFP vs. R_en for different parameters of λ and α
-->

Tab. 6
表6
表6土体不排水抗剪强度以及参数反演结果
Tab. 6Back analysis of soil undrained shear strength and coefficients

Case	va /(m·s-1)	Fta /kN	Ffa /kN	vb /(m·s-1)	Ftb /kN	Ffb /kN	CFX parameters			Back calculation
							α	λ	su0 /kPa	αest	λest	su0,est /kPa
1	2	20.27	46.49	5	21.42	51.07	0.5	0.15	10	0.479	0.166	9.941
2	2	20.27	46.49	10	23.01	54.25	0.5	0.15	10	0.467	0.182	9.865
3	5	19.23	10.87	10	20.59	11.32	0.1	0.15	10	0.103	0.189	9.317
4	5	20.33	12.14	10	21.78	12.73	0.1	0.2	10	0.103	0.230	9.503

新窗口打开

2.4 土体不排水抗剪强度的计算

根据2.2和2.3的内容,可以总结出FFP在贯入过程中的受力特性以及相关系数的变化规律与计算方法。如果通过测量得到FFP的端部阻力以及侧壁阻力,用上述方法可以反演出所测土体的不排水抗剪强度、率效应参数以及界面摩擦特性。如在两个试探速度v_a和v_b下,分别测得FFP端部阻力F_t,a和F_t,b以及侧壁阻力F_f,a和F_f,b,根据式(12)和(13)以及相关系数的表达式,可以反演出相应的摩擦系数α_est、率效应系数λ_est以及土体强度s_u0,est。具体过程为在各参数的取值范围内,采用最小二乘法或枚举法进行试算,寻找综合偏差(式(18))最小的最优解。
$\delta ={{\left( \frac{{{F}_{\text{t},\text{a}}}-{{{{F}'}}_{\text{t},\text{a}}}}{{{F}_{\text{t},\text{a}}}} \right)}^{2}}+{{\left( \frac{{{F}_{\text{t},\text{b}}}-{{{{F}'}}_{\text{t},\text{b}}}}{{{F}_{\text{t},\text{b}}}} \right)}^{2}}+{{\left( \frac{{{F}_{\text{f},\text{a}}}-{{{{F}'}}_{\text{f},\text{a}}}}{{{F}_{\text{f},\text{a}}}} \right)}^{2}}+{{\left( \frac{{{F}_{\text{f},\text{b}}}-{{{{F}'}}_{\text{f},\text{b}}}}{{{F}_{\text{f},\text{b}}}} \right)}^{2}}$ (18)
其中,F'_ta,F'_tb,F'_fa和F'_fb分别为由试算参数根据式(12)和(13)计算得到的阻力值。本文以CFX计算结果作为测量值,共计算了4组工况,如表6所示。各工况的反演结果也列于表6中。反演结果与原参数吻合很好,表明本文的方法可以用来测量土的强度特性、率效应特性以及界面摩擦特性。

3 结论

本文采用CFX方法研究了FFP在均质土中运动时的受力特性,用动网格结合子区域的方法模拟运动边界问题,并提出薄层单元方法来模拟FFP与土体之间的界面摩擦。通过分析FFP在无率效应均质土和有率效应的均质土中的受力特性,得出以下结论：
(1)在运动过程中,FFP的端部受到端承阻力和拖曳阻力的作用,端承阻力系数N_c和端部拖曳阻力系数C_d,t随着摩擦系数α的增大而增大,给出了N_c和C_d,t的表达式;
(2)FFP的侧壁除了摩擦作用外也会受到拖曳阻力的作用,约占侧壁阻力的10%~15%,且侧壁拖曳阻力系数C_d,f与α和非牛顿流体雷诺数R_en相关,给出了C_d,f与α和R_en之间的表达式;
(3)FFP的R_f1和R_f2随着贯入速度v的增大而增大,随着土强度s_u0的提高而减小,而土体密度和摩擦系数对R_f1和R_f2的影响都比较小;侧壁率效应系数R_f2大于平均率效应系数,而端部率效应系数R_f1要小于平均率效应系数,文中给出了R_f1和R_f2的表达式;
(4)通过测量得到不同速度下FFP的端部阻力以及侧壁阻力,依据本文方法可以反演出所测土体的不排水抗剪强度、土的率效应参数以及界面摩擦特性。因此,本文研究结果为FFP测量土的工程特性提供了依据。虽然本文的研究采用FFP匀速运动的方式,但实际的FFP是自由落体运动,一次沉贯过程包含很多的速度及其对应的阻力,因此,利用一次试验中的不同数据点就可以反演土性参数。本文研究结果也为鱼雷锚以及其他类似于FFP形状的锚体在土中运动过程所受阻力的计算提供参考。
The authors have declared that no competing interests exist.

---

参考文献文献选项 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]	1 Freeman TJ, Murray CN, Francis TJG, et al. Modelling radioactive waste disposal by penetrator experiments in the abyssal Atlantic Ocean [J]. Nature, 1984, 310(5973): 130-133 [本文引用: 1]
[2]	Dayal U, Allen JH.Instrumented impact cone penetrometer .Canadian Geotechnical Journal, 1973, 10(3): 397-409 [本文引用: 1]
[3]	Chow SH, O'Loughlin CD, White DJ, et al. An extended interpretation of the free-fall piezocone test in clay . Geotechnique, 2017(ahead of print )URL [本文引用: 2]
[4]	O’Loughlin CD, Richardson MD, Randolph MF. Penetration of dynamically installed anchors in clay .Geotechnique, 2013, 63(11):909-919 [本文引用: 2]
[5]	Shelton JT.OMNI-Maxtrade anchor development and technology. Oceans IEEE, 2007: 1-10 [本文引用: 1]
[6]	Wang D, Bienen B, Nazem M, et al.Large deformation finite element analysis in geotechnical engineering . Computers and Geotechnics, 2015, 65(1): 104-114 [本文引用: 1]
[7]	Chow SH, Airey DW.Free-falling penetrometers: a laboratory investigation in clay .Journal of Geotechnical and Geoenvironmental Engineering, 2013, 140(1): 201-214 [本文引用: 2]
[8]	Chow SH, O′Loughlin CD. Randolph MF. Soil strength estimation and pore pressure dissipation for free-fall piezocone in soft clay .Geotechnique, 2014, 64(10):817-827 [本文引用: 1]
[9]	Stark N, Radosavljevic B, Quinn B, et al.Application of portable free-fall penetrometer for geotechnical investigation of Arctic nearshore zone .Canadian Geotechnical Journal, 2017, 54(1): 31-46 [本文引用: 1]
[10]	Araujo JBD, Machado RD, Junior CJDM.High Holding Power Torpedo Pile: Results for the First Long Term Application// International Conference on Offshore Mechanics and Arctic Engineering. 2004:417-421
[11]	韩聪聪,刘君. 板翼动力锚沉贯深度模型试验研究 . 海洋工程,2016, 34(5):92-100 [本文引用: 1] (Han Congcong, Liu Jun.Model tests on the penetration depth of gravity installed plate anchors .The Ocean Engineering, 2016, 34(5): 92-100 (in Chinese)) [本文引用: 1]
[12]	刘君,李明治,韩聪聪. 土体率效应对动力锚沉贯深度影响 . 大连理工大学学报, 2017, 57(1): 68-77 [本文引用: 3] (Liu Jun, Li Mingzhi, Han Congcong.Influence of soil strain-rate effect on embedment depth of dynamically installed anchors .Journal of Dalian University of Technology, 2017, 57(1): 68-77 (in Chinese)) [本文引用: 3]
[13]	O’Loughlin CD, Richardson MD, Randolph MF. Centrifuge tests on dynamically installed anchors// International Conference on Ocean, Offshore and Arctic Engineering, Honolulu, 2009 (80238) [本文引用: 1]
[14]	Einav I, Randolph M.Effect of strain rate on mobilised strength and thickness of curved shear bands . Geotechnique, 2006, 56(7): 501-504 [本文引用: 2]
[15]	Zhou M, Hossain MS, Hu Y, et al.Behaviour of ball penetrometer in uniform single-and double-layer clays .Geotechnique, 2013, 63(8): 682-694 [本文引用: 1]
[16]	Kim YH, Hossain MS, Wang D.Effect of strain rate and strain softening on embedment depth of a torpedo anchor in clay .Ocean Engineering, 2015, 108: 704-715 [本文引用: 2]
[17]	Liu H, Xu K, Zhao Y.Numerical investigation on the penetration of gravity installed anchors by a coupled Eulerian-Lagrangian approach .Applied Ocean Research, 2016, 60: 94-108 [本文引用: 2]
[18]	Øye I.Simulation of trajectories for a deep penetrating anchor .CFD Norway Report, 2000 [本文引用: 2]
[19]	Low HE, Lunne T, Andersen KH, et al.Estimation of intact and remoulded undrained shear strengths from penetration tests in soft clays .Geotechnique, 2010, 60(11): 843-859 [本文引用: 2]
[20]	Palix E, Wu H, Chan N, et al.Liwan 3-1: how deepwater sediments from South China Sea compare with Gulf of Guinea sediments . Offshore Technology Conference. 2013, OTC24010 [本文引用: 1]
[21]	Dayal U, Allen JH.The effect of penetration rate on the strength of remolded clay and sand samples .Canadian Geotechnical Journal, 1975, 12(3): 336-348 [本文引用: 1]
[22]	Steiner A, Kopf AJ, L’Heureux JS, et al. In situ dynamic piezocone penetrometer tests in natural clayey soils—a reappraisal of strain-rate corrections .Canadian Geotechnical Journal, 2013, 51(3): 272-288 [本文引用: 1]
[23]	Kim YH, Hossain MS.Dynamic installation of OMNI-Max anchors in clay: numerical analysis .Geotechnique, 2015, 65(12): 1029-1037 [本文引用: 1]
[24]	Hawlader B, Dutta S, Fouzder A, et al. Penetration of steel catenary riser in soft clay seabed: finite-element and finite-volume methods . International Journal of Geomechanics, 2015, 15(6): 04015008-1-04015008-12 [本文引用: 7]
[25]	Hawlader B, Fouzder A, Dutta S. Numerical modeling of suction and trench formation at the touchdown zone of steel catenary riser . International Journal of Geomechanics, 2016, 16(1): 04015033-1-04015033-14 [本文引用: 3]
[26]	Zakeri A.Submarine debris flow impact on suspended (free-span) pipelines: Normal and longitudinal drag forces . Ocean Engineering, 2009, 36(6-7):489-499 [本文引用: 3]
[27]	Liu J, Tian J, Yi P.Impact forces of submarine landslides on offshore pipelines .Ocean Engineering, 2015, 95(95):116-127 [本文引用: 3]
[28]	Liu J, Zhang Y. Numerical simulation on the dynamic installation of the gravity installed plate anchor in clay: a fluid dynamic approach// ASME , Proceedings of the 36th International Conference on Ocean, Offshore and Arctic Engineering, 2017: OMAE2017-61570 [本文引用: 2]
[29]	Randolph MF, White DJ.Interaction forces between pipelines and submarine slides — A geotechnical viewpoint .Ocean Engineering, 2012, 48(7):32-37 [本文引用: 1]
[30]	Ma H, Zhou M, Hu Y, et al. Interpretation of layer boundaries and shear strengths for soft-stiff-soft clays using CPT data: LDFE analyses . Journal of Geotechnical & Geoenvironmental Engineering, 2016, 142(1):04015055-1-04015055-12 [本文引用: 2]
[31]	Chow SH, Airey D.Free-falling penetrometers: a laboratory investigation in clay .Journal of Geotechnical & Geoenvironmental Engineering, 2014, 140(1):201-214 [本文引用: 1]