, Peijun GuoImplicit numerical integration of an elasto-plastic constitutive model for structured clays
DajiangGeng中图分类号:TU432
文献标识码:A
收稿日期:2017-11-21
接受日期:2017-12-1
网络出版日期:2018-02-20
版权声明:2018《力学学报》编辑部《力学学报》编辑部 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (833KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
天然结构性软土和重塑土的力学性质是不同的,主要表现在各向异性、应变软化性和土体强度随着结构性散失而逐渐降低[1,2]。因此,在对处于天然原状土中的工程结构物进行有限元模拟时采用重塑软土的弹塑性本构模型是不尽合理的[3,4],需采用可以考虑软土的结构性的模型。近十年来,国内外研究人员提出了各种能够描述结构性土性质的弹塑性模型[5,6,7,8,9,10]。为更好的反映原状软土变形特性,这些模型一般都有高度的非线性性。本构模型构建后,将高度非线性的本构模型进行数值算法实现,并且将其应用到有限元软件中,使其发挥工程计算的实用价值,这是岩土工程数值计算的关键。为此,本文以考虑土体结构性的SANICLAY模型[6]为例,对高度非线性的弹塑性本构模型的隐式算法实现进行探讨。弹塑性本构模型的数值实现方法主要可以分为显式算法与隐式算法两大类。与隐式算法相比,一般显式算法[11]计算精度低,因此实际应用较少。与显式算法相比较,由于隐式算法的计算精度高,能够实现自校正,不发生误差传递,因此在弹塑性本构模型的数值实现过程中一般采用隐式的弹性预测—塑性修正算法。在塑性修正步一般会用Newton- CPPM法求解回退映射非线性方程组,而Newton算法需确保Jacobian矩阵是可逆矩阵,否则无法进行求解。同时,Newton法是一种局部收敛性算法,选取迭代初值的合理性会直接影响算法收敛性。因此Jacobian矩阵奇异与不收敛是用Newton法求解高度非线性方程组所遇到的主要问题。
对此国内外****提出了一些解决办法。对于具有局部收敛性的Newton迭代算法,只要所选取的初值与真实解十分接近,采用该算法得到的解总可以收敛到问题的真解。基于此原理,Bicanic[12]、Stupkiewicz[13]等用辅助投影面法对迭代初始值进行了改进,然而如何有效地建立辅助投影面这个问题未能得到很好的解答;Jia、Majid、Penasa等[14,15,16,17,18,19]应用多步法改进迭代初始值,多步法的本质是将一个增量步分为多个增量步然后进行求解,这无疑会造成计算量的大幅增加,降低计算效率;Hernandez等[20]用显示方法改进一部分状态变量的迭代初始值,然而对哪些状态变量的迭代初始值进行改进才能有效改进收敛性,该问题没得到有效解决。为了避免求解Jacobian矩阵以减少每个迭代步计算量,提高计算效率,Wang[19]、Brannon[21]、Homel[22,23]等用分阶段迭代算法求高度非线性回退映射方程组的解,该算法的核心思想是首先采用一定的方法求出一致性参数,然后视一致性参数为已知量,求其余状态变量的值。然而,当单独应用分阶段迭代算法时仍存在不收敛问题,尤其对于高度非线性本构模型更是如此。除此之外,Bilotta[24]、Contrafatto[25]、Perez[26]等用优化方法或搜索技术求非线性回退映射方程组的解,该类方法的计算过程一般较为复杂,相应的计算量较大,所以该方法在弹塑性本构模型数值实现中应用十分有限。
在高度非线性弹塑性本构模型的隐式算法实现中,为避免出现Jacobian矩阵奇异和不收敛问题,本文提出了两种改进的隐式算法。
1 SANICLAY模型简介
Taiebat等[6]在原始的SANICLAY模型[27]基础上,通过考虑原状软土的结构性破坏的过程,构建了可考虑原状软土结构性的SANICLAY弹塑性模型。模型采用的是非关联流动法则,通过引入旋转硬化考虑各向异性,增加表征土体强度的内变量来表示土体结构性随变形的发展逐渐降低,此外,该模型能表征应变软化效果。1.1 弹性关系
模型采用的弹性关系是非线性的$\dot{\sigma }=C:{{\dot{\varepsilon }}^{e}}$ (1)
其中, $\dot{\sigma}$为应力增量, ${{\dot{\varepsilon }}^{e}}$为应变增量对应的弹性部分,c为弹性刚度
$C={\lambda }'\delta \delta +2GI$ (2)
其中,
${\lambda }'=K-\frac{2}{3}G,\begin{matrix} {} \\ \end{matrix}K=\frac{1+e}{k}p,\begin{matrix} {} \\ \end{matrix}G=\frac{3(1-2\mu )}{2(1+\mu )}\frac{1+e}{k}p$
$\delta $与I分别为二阶和四阶等同张量, ${\lambda}'$、$K$、G和$\mu$分别为Lame常数、体积变形模量、剪切变形模量与泊松比,e表示的是孔隙比,k表示在$e-\ln p$空间内回弹线斜率。对应力б实施加法分解б=pδ+s即可得球应力p与偏应力s。
1.2 塑性势函数及流动法则
模型塑性势函数$\begin{align} \psi \left( \sigma ,{{S}_{f}},\alpha \right)=\frac{3}{2}\left( s-p\alpha \right):\left( s-p\alpha \right) \\ -\left( {{M}^{*2}}-\frac{3}{2}\alpha :\alpha \right)p({{p}_{\alpha }}-p) \\ \end{align}$ (3)
式中,a为表示塑性势函数旋转的二阶张量;${{p}_{\alpha }}$是保证塑性势函数通过当前的应力状态的一标量;${{M}^{*}}={{S}_{f}}M$,Sf是表示摩擦结构性的另一标量,$M$通过应力Lode角${{\theta }_{\alpha }}$在拉和压临界状态线的斜率${{M}_{e}}$与${{M}_{c}}$间插值得到
$M=\Theta \left( {{\theta }_{\alpha }} \right){{M}_{c}}=\frac{2m}{\left( 1+m \right)-\left( 1-m \right)\cos \left( 3{{\theta }_{\alpha }} \right)}{{M}_{c}}$
式中,
$\begin{align} m=\frac{{{M}_{e}}}{{{M}_{c}}},\begin{matrix} {} \\ \end{matrix}\cos \left( 3{{\theta }_{\alpha }} \right)=\sqrt{6}tr\left( n_{\alpha }^{3} \right) \\ {{n}_{\alpha }}=\frac{\gamma /{{\chi }_{\alpha }}-\alpha }{\sqrt{\left( \gamma /{{\chi }_{\alpha }}-\alpha \right):\left( \gamma /{{\chi }_{\alpha }}-\alpha \right)}},\begin{matrix} {} \\ \end{matrix}\gamma =\frac{s}{p} \\ \end{align}$
${{\chi }_{\alpha }}$是一模型参数。以应力$\sigma $为变量,对塑性势函数ψ求导,$r\text{=}{\partial \psi}/{\partial \sigma}$即为塑性流动方向。
1.3 屈服函数
模型屈服函数$\begin{align} \Phi \left( \sigma ,{{S}_{i}},{{S}_{f}},{{p}_{0}},\beta \right)=\frac{3}{2}\left( s-p\beta \right):\left( s-p\beta \right) -\left( {{N}^{*2}}-\frac{3}{2}\beta :\beta \right)p({{p}_{0}}^{*}-p) \\ \end{align}$ (4)
式中,$\beta$是表示屈服函数旋转的二阶张量;${{p}_{0}}^{*}={{S}_{i}}{{p}_{0}}$,${{N}^{*}}={{S}_{f}}N$,${{S}_{i}}$和${{p}_{0}}$分别为表示各向同性结构性和各向同性硬化的标量;${{S}_{i}}$与${{S}_{f}}$均为表征结构性的大于等于1的内变量,随着土体变形发展,软土结构性逐渐散失,其对应的值趋近于1;和M类似,N通过应力Lode角${{\theta }_{\beta }}$在${{N}_{e}}$与${{N}_{c}}$间插值得到
$N=\Theta \left( {{\theta }_{\beta }} \right){{N}_{c}}=\frac{2{n}'}{\left( 1+{n}' \right)-\left( 1-{n}' \right)\cos \left( 3{{\theta }_{\beta }} \right)}{{N}_{c}}$
式中,
$\begin{align} {n}'=\frac{{{N}_{e}}}{{{N}_{c}}},\begin{matrix} {} \\ \end{matrix}\cos \left( 3{{\theta }_{\beta }} \right)=\sqrt{6}tr\left( n_{\beta }^{3} \right) \\ {{n}_{\beta }}=\frac{\gamma /{{\chi }_{\beta }}-\beta }{\sqrt{\left( \gamma /{{\chi }_{\beta }}-\beta \right):\left( \gamma /{{\chi }_{\beta }}-\beta \right)}} \\ \end{align}$
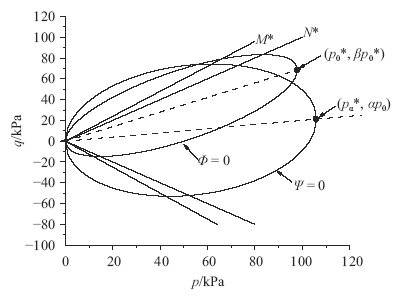
${{\chi }_{\beta }}$也是一模型参数。如图1所示,在$q-p$平面内（其中广义剪应力$q=\sqrt{\tfrac{3}{2}s:s}$）,塑性势函数和屈服函数均为倾斜椭圆。以应力$\sigma $为自变量对屈服函数$\Phi $求导,$ n\text{=}{\partial \Phi }/{\partial \sigma }\;$即为屈服方向。
显示原图|下载原图ZIP|生成PPT图1屈服函数和塑性势函数
-->Fig.1Yield function and plastic potential function
-->
1.4 硬化规则
塑性势函数和屈服函数中共有${{S}_{i}}$、${{S}_{f}}$、${{p}_{0}}$、$\alpha $、$\beta $ 5个内变量,相应的演化规则为：${{\dot{S}}_{i}}=-{{k}_{i}}\left( \frac{1+e}{\lambda -k} \right)\left( {{S}_{i}}-1 \right)\dot{\varepsilon }_{d}^{p}=\dot{\Lambda }{{\bar{S}}_{i}}$ （5）
${{\dot{S}}_{f}}=-{{k}_{f}}\left( \frac{1+e}{\lambda -k} \right)\left( {{S}_{f}}-1 \right)\dot{\varepsilon }_{d}^{p}=\dot{\Lambda }{{\bar{S}}_{f}}$ （6）
${{\dot{p}}_{0}}=\left( \frac{1+e}{\lambda -k} \right){{p}_{0}}\dot{\varepsilon }_{v}^{p}=\dot{\Lambda }{{\bar{p}}_{0}}$ （7）
$\dot{\alpha }=\dot{\Lambda }\bar{\alpha }$ （8）
$\dot{\beta }=\dot{\Lambda }\bar{\beta }$ （9）
塑性体变增量$\dot{\varepsilon }_{v}^{p}$与塑性偏应变增量${{\dot{e}}^{p}}$是由塑性应变增量${{\dot{\varepsilon }}^{p}}$加法分解${{\dot{\varepsilon }}^{p}}=\tfrac{1}{3}\dot{\varepsilon }_{v}^{p}\delta +{{\dot{e}}^{p}}$得到的,$\dot{\varepsilon }_{d}^{p}=\sqrt{\left( 1-A \right){{\left( \dot{\varepsilon }_{v}^{p} \right)}^{2}}+A{{\left( \dot{\varepsilon }_{q}^{p} \right)}^{2}}}$,$\dot{\varepsilon }_{q}^{p}=\sqrt{\tfrac{2}{3}{{{\dot{e}}}^{p}}:{{{\dot{e}}}^{p}}}$;$\lambda $为$e-\ln p$空间内压缩线斜率;$A$、${{k}_{i}}$与${{k}_{f}}$表示模型参数; \dot{\Lambda }为一致性参数; ${\bar{S}}_{i}$, ${\bar{S}}_{f}$, $\bar{p}_{0}$, $\bar{\alpha}$和$\bar{\beta}$可以参考相关文献[6]中的模型理论推导得出。
2 数值实现
考虑原状软土结构性的SANICLAY模型所考虑的因素较为全面,这使模型较为复杂,导致模型有高度非线性,模型数值实现难度较大。综合本文中第一部分内容可看出,当采用隐式弹性预测—塑性修正算法对该模型数值实现过程中有可能造成不收敛的因素包括：模型采用的弹性关系依赖于孔隙比和球应力;塑性势函数与屈服函数的曲率均较大;该模型引入了旋转硬化考虑各向异性;模型中内变量比较多,并且相应的演化规则非线性程度较高。总之,能导致模型非线性程度增强的因素都可能造成数值实现过程中的不收敛。此外,当采用隐式算法对模型进行数值实现的过程中,应变硬化向应变软化的过渡段,可能会出现Jacobian矩阵奇异的情况。为解决不收敛问题和避免Jacobian矩阵奇异问题,本文引入同伦算法对Newton迭代法的迭代初值进行改进,形成了同伦-Newton-CPPM算法。为避免求Jacobian矩阵以减小单个迭代步的计算量,本文还提出了一种两阶段迭代算法。2.1 同伦-Newton-CPPM算法
弹塑性本构模型的数值实现主要包括状态变量的更新与一致切线刚度的计算两部分内容。（1）状态变量的更新
对考虑土体结构性的SANICLAY模型采用隐式算法进行状态变量的更新主要包括弹性预测、塑性检验与塑性修正三步。第$n+1$个增量步对应的基本方程为
$\left( \begin{matrix} {{\sigma }_{n+1}}-{{\sigma }_{n}}-{{C}_{n+1}}:\Delta {{\varepsilon }_{n+1}}\text{+}\Delta \Lambda {{C}_{n+1}}:{{r}_{n+1}} \\ {{\xi }_{n+1}}-{{\xi }_{n}}-\Delta \Lambda {{{\bar{\xi }}}_{n\text{+}1}} \\ {{\Phi }_{n+1}} \\ \end{matrix} \right)\text{=}\left( \begin{matrix} 0 \\ 0 \\ 0 \\ \end{matrix} \right)$ (10)
式中,$\xi \text{=}{{\left( \begin{matrix} {{S}_{i}} & {{S}_{f}} & {{p}_{0}} & \alpha & \beta \\ \end{matrix} \right)}^{T}}$和$\bar{\xi }\text{=}{{\left( \begin{matrix} {{{\bar{S}}}_{i}} & {{{\bar{S}}}_{f}} & {{{\bar{p}}}_{0}} & {\bar{\alpha }} & {\bar{\beta }} \\ \end{matrix} \right)}^{T}}$分别为内变量及对应的演化方向。
1）弹性预测：
$\sigma _{n+1}^{trial}-{{\sigma }_{n}}-C_{n+1}^{trial}:\Delta {{\varepsilon }_{n+1}}=0$ (11)
式中,带有上标trial的量表示的是经弹性预测步后得出的状态变量。由于$C_{n+1}^{trial}$依赖于 $\sigma _{n+1}^{trial}$,式（11）为以$\sigma _{n+1}^{trial}$为未知量的非线性方程组,可采用Newton迭代法求解。相应的迭代初值可取为$\sigma _{n+1}^{trial\text{(0)}}={{\sigma }_{n}}+{{C}_{n}}:\Delta {{\varepsilon }_{n+1}}$,迭代收敛标准
${{e}_{\sigma }}\text{=}\frac{\left| \sigma _{n+1}^{trial\left( i \right)}-{{\sigma }_{n}}-C_{n+1}^{\left( i \right)}:\Delta {{\varepsilon }_{n+1}} \right|}{\left| \sigma _{n+1}^{trial\left( i \right)} \right|}\le \text{TO}{{\text{L}}_{\sigma }}$
其中,上标$(i)$表示第$i$次迭代,${{e}_{\sigma }}$和$\text{TO}{{\text{L}}_{\sigma }}$分别表示$\sigma $的相对误差和相应的误差限。
2）塑性检验：如果$\Phi _{n+1}^{trial}\le 0$,这说明软土处于弹性状态,否则应该进行塑性修正。
3）塑性修正：一般需要采用Newton迭代法求解${{\sigma }_{n+1}}$、${{\xi }_{n+1}}$和$\Delta \Lambda $为未知量的非线性方程组式（10）,简记为$F(x)=0$,其中,$x\text{=}{{\left( \begin{matrix} {{\sigma }_{n+1}} & {{\xi }_{n+1}} & \Delta \Lambda \\ \end{matrix} \right)}^{T}}$。为使迭代初值更接近于问题的真解,以增强收敛性,减少迭代次数,本文结合切平面算法[28,29]取迭代初值
$\begin{align} \Delta {{\Lambda }^{\text{(0)}}}=\frac{\Phi _{n+1}^{trial}}{n_{n+1}^{trial}:C_{n+1}^{trial}:r_{n+1}^{trial}\text{+}{{K}_{p}}_{n+1}^{trial}} \\ \sigma _{n+1}^{\text{(0)}}={{\sigma }_{n}}+C_{n+1}^{trial}:\Delta {{\varepsilon }_{n+1}}-\Delta {{\Lambda }^{\text{(0)}}}C_{n+1}^{trial}:r_{n+1}^{trial} \\ \xi _{n+1}^{\text{(0)}}={{\xi }_{n}}+\Delta {{\Lambda }^{\text{(0)}}}\bar{\xi }_{n+1}^{trial} \\ \end{align}$ (12)
其中,${{K}_{p}}$表示塑性模量。迭代收敛的标准取为
$\begin{align} {{e}_{\sigma }}\text{=}\frac{\left| \sigma _{n+1}^{\left( i \right)}-{{\sigma }_{n}}-C_{n+1}^{\left( i \right)}:\Delta {{\varepsilon }_{n+1}}\text{+}\Delta {{\Lambda }^{(i)}}C_{n+1}^{\left( i \right)}:r_{n+1}^{\left( i \right)} \right|}{\left| \sigma _{n+1}^{\left( i \right)} \right|}\le \text{TO}{{\text{L}}_{\sigma }} \\ {{e}_{\xi }}\text{=}\frac{\left| \xi _{n+1}^{\left( i \right)}-{{\xi }_{n}}-\Delta {{\Lambda }^{(i)}}\bar{\xi }_{n+1}^{\left( i \right)} \right|}{\left| \xi _{n+1}^{\left( i \right)} \right|}\le \text{TO}{{\text{L}}_{\xi }} \\ {{e}_{\Phi }}=\left| \Phi _{n+1}^{\left( i \right)} \right|\le \text{TO}{{\text{L}}_{\Phi }} \\ \end{align}$
式中,${{e}_{\sigma }}$与${{e}_{\xi }}$分别为$\sigma $和$\xi $的相对误差,${{e}_{\Phi }}$为屈服函数ф的绝对误差,$\text{TO}{{\text{L}}_{\sigma }}$、$\text{TO}{{\text{L}}_{\xi }}$和$\text{TO}{{\text{L}}_{\Phi }}$表示相应误差限。
回退映射非线性方程组式（10）一共包含7个非线性方程（组）,其中,第1个方程组的非线性程度主要决定于塑性势函数和弹性关系,第2~6个方程（组）的非线性程度主要决定于硬化规则,第7个方程的非线性程度主要决定于屈服函数。考虑软土结构性的SANICLAY模型较复杂导致非线性方程组式（10）的非线性程度大大增加,求解难度随之加大。
Newton法是一种局部收敛性迭代算法,当所采用的迭代初始值位于收敛域内时,该方法求非线性方程组才能收敛于真解。然而,由式（12）得出的与切平面法相应的迭代初始值并不能确保必定处于收敛域内,对于某些增量步有可能出现不处于收敛域内的情况,这会导致迭代求解过程不收敛。因此,本文引入大范围收敛算法—同伦算法[30,31,32,33],形成了同伦-Newton-CPPM隐式算法。所采用的同伦方程为
$H(x,t)=\left( 1-t \right)u\left( x-{{x}^{\left( 0 \right)}} \right)+tF(x)=0,\begin{matrix} {} \\ \end{matrix}t\in \left[ 0,1 \right]$ (13)
显然,同伦方程满足$H({{x}^{\left( 0 \right)}},0)=0$和$H(x,1)=F(x)$,只要求出同伦方程$H(x,t)=0$的解曲线$x=x(t)$,就可以得出回退映射方程组$F(x)=0$的解$x=x(1)$。
同伦方程的求解方法主要包括数值延拓法、参数微分法和弧长微分法3种。为不使得求解更为复杂,本文采用最简单的数值延拓法：将$t\in \left[ 0,1 \right]$等分$0={{t}_{0}}<{{t}_{1}}<......<{{t}_{N}}=1$,此时可以选用Newton迭代法求出同伦方程$H(x,t)$的解$x=x(t)$在点${{t}_{k}}$处的数值解。在采用Newton迭代法求解$H(x,{{t}_{k}})=0$时,所对应的Jacobian矩阵为${\partial H}/{\partial x}\;=\left( 1-{{t}_{k}} \right)uD+{{t}_{k}}{\partial F}/{\partial x}$,其中$D$表示单位阵。显然,当回退映射方程组所对应的Jacobian矩阵${\partial F}/{\partial x}$不可逆时,只要参数u的取值合理,总可以使${\partial H}/{\partial x}$可逆。通过求解同伦方程得到${{x}_{N}}$后,以${{x}_{N}}$为迭代初值,采用Newton迭代法即可以对回退映射方程组进行求解。
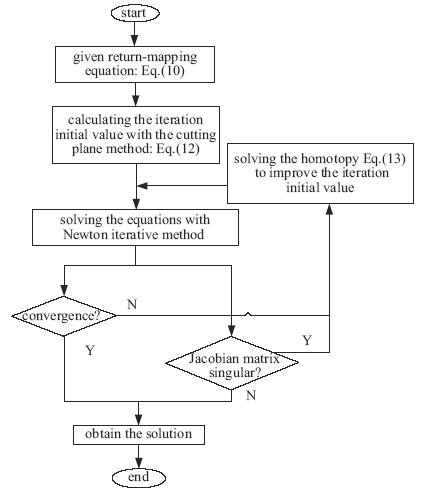
采用同伦-Newton-CPPM隐式算法求解回退映射方程组的过程如图2所示。在本文求解过程中,对于给定的回退映射方程组,先按式（12）取迭代初值采用Newton-CPPM隐式算法进行求解,如果出现不收敛或Jacobian矩阵奇异的情况,引进同伦方程（13）,并采用数值延拓法求解同伦方程得到修正后的迭代初值,然后再次采用Newton-CPPM隐式算法进行求解。理论上说,同伦-Newton-CPPM隐式算法可以同时解决不收敛或Jacobian矩阵奇异问题,在后文中对其具体应用也说明了这一点。
显示原图|下载原图ZIP|生成PPT图2同伦-Newton-CPPM隐式算法
-->Fig.2Homotopy-Newton-CPPM implicit algorithm
-->
（1）一致切线刚度的计算
当状态变量在弹性或弹塑性状态时,相应的一致切线刚度$D$显然是不同的。1）弹性状态时,${{\sigma }_{n+1}}$和${{\varepsilon }_{n+1}}$满足${{\sigma }_{n+1}}-{{\sigma }_{n}}-{{C}_{n+1}}:\Delta {{\varepsilon }_{n+1}}=0$,将${{\sigma }_{n+1}}$和$\Delta {{\varepsilon }_{n+1}}$同时视作变量,对该式微分,即可确定一致切线刚度${{D}_{n+1}}={d{{\sigma }_{n+1}}}/{d\Delta {{\varepsilon }_{n+1}}}\;$。
2）弹塑性状态时,${{\sigma }_{n+1}}$和${{\varepsilon }_{n+1}}$满足回退映射方程组式（10）,将${{\sigma }_{n+1}}$、${{\xi }_{n+1}}$、$\Delta \Lambda $、$\Delta {{\varepsilon }_{n+1}}$视作变量,对该方程组微分,得到微分方程组,然后消去$d{{\xi }_{n+1}}$与$d\Delta \Lambda $即可得到$d{{\sigma }_{n+1}}$和$d\Delta {{\varepsilon }_{n+1}}$间的关系,从而确定一致切线刚度${{D}_{n+1}}={d{{\sigma }_{n+1}}}/{d\Delta {{\varepsilon }_{n+1}}}\;$。
2.2两阶段迭代算法
当采用隐式的弹性预测—塑性修正算法时,在塑性修正步,不论采用已有的Newton-CPPM算法,还是采用本文提出的同伦-Newton-CPPM算法进行状态变量的更新,都要采用Newton迭代法求解回退映射非线性方程组。在求解过程中,对于每个迭代步都要求一次Jacobian矩阵,并且对Jacobian矩阵求逆,这会大大增加单个迭代步的计算量。而Jacobian矩阵的确定先要求出众多的偏导,而对较复杂的弹塑性本构模型,这些偏导是不容易求出的,即使求出其形式也比较复杂。对于考虑土体结构性的SANICLAY模型,其偏导的形式就比较复杂,这会大大增加单次迭代的计算量。为减小单次迭代的计算量,同时避免矩阵求逆运算,本文借鉴显式算法提出了一种两阶段迭代算法。对回退映射非线性方程组式（10）的求解,在每个迭代步中先求出$\Delta {{\Lambda }^{(i+1)}}$,然后再回代得出状态变量$\sigma _{n+1}^{(i+1)}$和$\xi _{n+1}^{(i+1)}$,具体过程为：
第一阶段：求$\Delta {{\Lambda }^{(i+1)}}$,其迭代格式为
$\Delta {{\Lambda }^{(i+1)}}=\Delta {{\Lambda }^{(i)}}-\left( {{\left. {{\left( \frac{d\Phi }{d\Delta \Lambda } \right)}^{-1}} \right|}_{\Delta \Lambda =\Delta {{\Lambda }^{(i)}}}} \right)\Phi \left( \Delta {{\Lambda }^{(i)}} \right)$ （14）
其中,
$\begin{align} \frac{d\Phi }{d\Delta \Lambda }=\frac{\partial \Phi }{\partial \sigma }:\frac{\partial \sigma }{\partial \Delta \Lambda }+\sum{\frac{\partial \Phi }{\partial \xi }*\frac{\partial \xi }{\partial \Delta \Lambda }} \\ \text{ =}-\left( \frac{\partial \Phi }{\partial \sigma } \right)_{n+1}^{\left( i \right)}:C_{n+1}^{\left( i \right)}:r_{n+1}^{\left( i \right)}+\sum{\left( \frac{\partial \Phi }{\partial \xi } \right)_{n+1}^{\left( i \right)}*\bar{\xi }_{n+1}^{\left( i \right)}} \\ \end{align}$
式中,当硬化内变量$\xi $为二阶张量时,*表示并联式双点积,当硬化内变量$\xi $为标量时,$*$表示数乘。
第二阶段：求状态变量$\sigma _{n+1}^{(i+1)}$和$\xi _{n+1}^{(i+1)}$,其回代格式为
$\begin{align} \sigma _{n+1}^{(i+1)}={{\sigma }_{n}}+C_{n+1}^{(i)}:\left( \Delta {{\varepsilon }_{n+1}}-\Delta {{\Lambda }^{(i\text{+}1)}}r_{n+1}^{(i)} \right) \\ \xi _{n+1}^{(i+1)}={{\xi }_{n}}+\Delta {{\Lambda }^{(i\text{+}1)}}\xi _{n+1}^{(i)} \\ \end{align}$ （15）
所采用的迭代初值为式（12）。
显然,两阶段迭代算法是不同于Newton迭代法的局部收敛性方法,按式（12）所给出的迭代初值并不一定在该算法的收敛域内。当迭代初值不在收敛域内时,会导致回退映射非线性方程组式（10）求解过程不收敛,此时,需要采取一定的手段对迭代初值进行改进。本文采用显式算法重新确定迭代初值,然后再次采用两阶段迭代算法进行迭代求解。后文中的实践表明,该方法是行之有效的。
3 不同算法对比
为明确本文所提出的两种隐式算法的计算精度、收敛性和计算效率,将4种数值实现算法：显式算法;传统隐式算法;同伦-Newton-CPPM算法;两阶段迭代算法进行了对比,同时也为后续研究工作中采用何种算法提出建议。以原状软土的不排水三轴压缩试验为原型,进行单单元计算分析。具体的,在计算中采用3维8节点实体单元,SANICLAY模型参数的取值见文献[6],初始应力为轴向${{\sigma }_{a}}=74.667kPa$,周向${{\sigma }_{r}}=37.667kPa$。采用的是单调增加的应变控制式比例加载${{{\varepsilon }_{a}}}/{{{\varepsilon }_{r}}}\;={2}/{\left( -1 \right)}\;$,加载终止条件为轴向应变达到${{\varepsilon }_{a}}=0.150$。具体计算中,对每种算法均考虑了增量步的步长${{I}_{n}}$为10-1、10-2、10-3和10-4四种情况。计算结果及对比如表1所示,表1中的收敛性Cov可直接反映出相应算法的收敛性,计算时间${t}'$可间接地反映计算效率高低,应力应变曲线（$q-{{\varepsilon }_{q}}$曲线）的对比、$q$峰值${{q}_{f}}$的对比、$q$终值${{q}_{t}}$的对比可反映相应算法的计算精度。
Table 1
表1
表1计算结果对比表
Table 1Comparison of calculation results
| Algorithm | ${{I}_{n}}$ | ${{C}_{ov}}$ | ${t}'$/s | ${{q}_{f}}$/kPa | ${{q}_{t}}$/kPa. |
|---|---|---|---|---|---|
explicit | 10-1 | × | × | × | × |
| 10-2 | √ | 2.70 | 68.11 | 69.78 | |
| 10-3 | √ | 31.60 | 61.53 | 42.02 | |
| 10-4 | √ | 397.30 | 60.93 | 41.15 | |
traditional implicit | 10-1 | × | \ | \ | \ |
| 10-2 | × | \ | \ | \ | |
| 10-3 | × | \ | \ | \ | |
| 10-4 | √ | 504.30 | 62.38 | 33.21 | |
| homotopy-Newton-CPPM | 10-1 | √ | 233.70 | 61.20 | 34.46 |
| 10-2 | √ | 35.70 | 62.25 | 33.37 | |
| 10-3 | √ | 50.70 | 62.37 | 33.22 | |
| 10-4 | √ | 512.40 | 62.38 | 33.21 | |
two-stage iterative | 10-1 | × | \ | \ | \ |
| 10-2 | × | \ | \ | \ | |
| 10-3 | √ | 20.60 | 62.37 | 33.22 | |
| 10-4 | √ | 269.90 | 62.38 | 33.21 |
新窗口打开
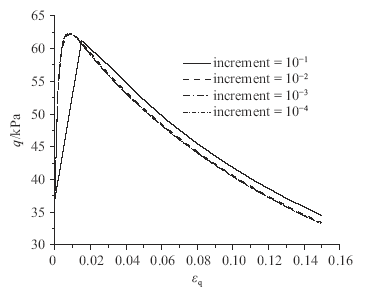
无论采用传统隐式算法,还是同伦-Newton-CPPM算法,还是两阶段迭代算法,只要是隐式算法,在增量步步长相同的情况,得出的$q-{{\varepsilon }_{q}}$曲线都是相同的,如图3所示。
结合图3和表1可以看出,对传统隐式算法,只有在增量步长取得很小（如10-4）的情况下才能得出收敛的结果,该算法收敛性很差。对同伦-Newton-CPPM算法,当增量步步长特别大（如10-1）时即可收敛,随着增量步步长的减小,计算时间大幅增加,计算精度基本不变。为了节约计算时间,建议采用该算法将步长适当取得大一些。对两阶段迭代算法,只有在增量步步长较小（如10-3）时才收敛,该算法的收敛性介于传统隐式算法和同伦-Newton-CPPM算法之间。三种隐式算法的收敛性由好到差依次为同伦-Newton-CPPM、两阶段迭代算法、传统隐式算法。
当取相同的增量步长10-4时,传统隐式算法、同伦-Newton-CPPM和两阶段迭代算法所对应的计算时间分别为504.30s、512.40s和269.90s。对应的计算效率由高到低依次为两阶段迭代算法、传统隐式算法、同伦-Newton-CPPM算法。与传统隐式算法和同伦-Newton-CPPM算法相比,两阶段迭代算法不需要计算复杂的Jacobian矩阵,不需要对Jacobian矩阵进行求逆运算,所以其计算效率最高。传统隐式算法直接采用弹性预测所得的结果作为迭代初值,同伦-Newton-CPPM算法的迭代初值是由切平面算法和同伦算法得出的,所以传统隐式算法比同伦-Newton-CPPM算法的计算效率要稍高。
对三种隐式算法,当增量步长分别取10-4、10-2和10-3时,可以得到收敛且准确的结果,对应的计算时间分别为504.30s、35.70s和20.60s。显然,整体上看,计算效率由高到低依次为两阶段迭代算法、同伦-Newton-CPPM算法、传统隐式算法。
显示原图|下载原图ZIP|生成PPT图3隐式算法$q-{{\varepsilon }_{q}}$曲线
-->Fig.3$q-{{\varepsilon }_{q}}$curve obtained by implicit algorithm
-->
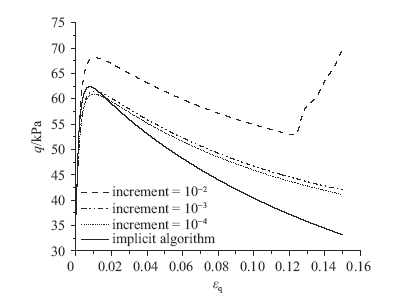
显式算法与隐式算法计算结果对比如图4所示,结合图4和表1可以看出,对于显式算法,随增量步步长减小,计算所耗时间大幅度增加,计算效率大幅降低,计算精度得到逐渐提高,然而,当增量步步长取值很小（如10-4）时,计算精度仍然较差。与隐式算法相比较,显式算法存在误差积累和精度低的缺点。
显示原图|下载原图ZIP|生成PPT图4显式算法$q-{{\varepsilon }_{q}}$曲线
-->Fig.4$q-{{\varepsilon }_{q}}$curve obtained by explicit algorithm
-->
综合以上分析可看出,对高度非线性的弹塑性本构模型,当采用显式算法进行数值实现时,增量步长取得很小,计算量很大时,所得结果仍然误差很大,建议尽量不使用。当采用隐式算法,如同伦-Newton-CPPM算法和两阶段迭代算法,进行数值实现时,随增量步长的减小,计算趋于收敛,收敛时所得结果误差极小,如果继续盲目减小增量步长,计算量会大幅增加,计算效率大幅降低,计算精度却基本没有提高。在具体的数值计算中,合理增量步长的选择是较为重要的,步长太大有可能会造成计算精度低或不收敛,太小会造成计算量大幅增加,计算效率降低,计算精度却没有提高,建议用变步长方法。
总体来看,本文提出的两种隐式算法都可以有效地解决Jacobian矩阵奇异和不收敛问题,均能对高度非线性弹塑性本构模型进行有效的数值实现。
在实际工程计算中,最常见的是不收敛问题。为在保证计算精度的前提下改善收敛性,建议采用同伦-Newton-CPPM算法进行高度非线性弹塑性本构模型的数值实现。当Jacobian矩阵比较难求出时也可用本文所提出的两阶段迭代算法。
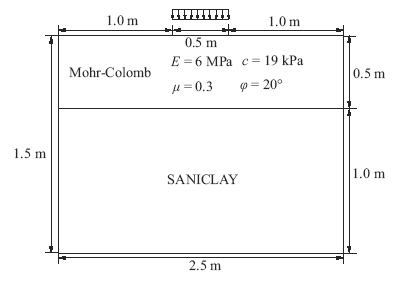
4 多单元分析
本文的算法比较是在简单的应变路径作用下的比较,然而在工程实际中往往需要进行多单元计算分析,材料点的应力路径和应变路径往往是比较复杂的,因此有必要对同伦-Newton-CPPM算法和传统隐式算法在多单元分析中的适用性进行对比分析。以典型的地基承载力试验为原型建立如图5所示的几何模型,土体分为两层,上层采用Mohr-Colomb模型,参数取值如图5所示,下层采用考虑土体结构性的SANICLAY模型,除各向同性硬化内变量
显示原图|下载原图ZIP|生成PPT图5几何模型
-->Fig.5Geometric model
-->
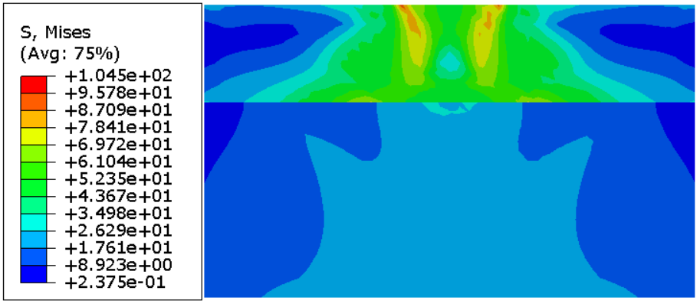显示原图|下载原图ZIP|生成PPT图6同伦-Newton-CPPM算法得出的Mises应力云图
-->Fig.6Contour of Mises stress obtained by Homotopy-Newton-CPPM implicit algorithm
-->
显示原图|下载原图ZIP|生成PPT图7传统隐式算法得出的Mises应力云图
-->Fig.7Contour of Mises stress obtained by the traditional implicit algorithm
-->
对于同伦-Newton-CPPM算法,当加载位移达到0.06m时仍能得到如图6所示的结果,而对传统隐式算法,当位移加载超过0.0112m时即出现了不收敛,计算无法继续进行,只得出了如图7所示的结果。对传统隐式算法计算过程中材料点的状态变量的值进行监控发现,当位移超过0.0112m时,传统隐式算法对部分材料点的状态变量无法进行准确有效的更新,导致整体出现了不收敛。这表明,相对传统隐式算法而言,同伦-Newton- CPPM算法不仅可以用于简单的应变路径分析,用于多单元岩土工程数值计算分析也是可行的。
5 结论
本文主要进行高度非线性弹塑性本构模型的隐式算法实现。以考虑土体结构性的SANICLAY模型为例,结合模型理论对可能导致模型数值实现过程中不收敛和Jacobian矩阵奇异的原因进行总结与分析。为解决不收敛和Jacobian矩阵奇异问题,本文提出了同伦-Newton-CPPM隐式算法和两阶段迭代算法,将新提出的两种隐式算法与传统隐式算法、显式算法在收敛性、计算效率、计算精度三方面进行了对比。主要得出如下结论：1 与隐式算法相比,显式算法虽然比较简单,但存在误差的传递和积累,计算精度很差,不建议使用。对高度非线性弹塑性本构模型,传统的隐式算法收敛性差,计算效率低。
2 新提出的同伦-Newton-CPPM隐式算法和两阶段迭代算法均可以有效解决传统隐式算法所存在的不收敛和Jacobian矩阵奇异问题,均可以有效地对高度非线性弹塑性本构模型进行数值实现。而且同伦-Newton-CPPM隐式算法的收敛性比两阶段迭代算法要好很多。
3 在实际工程计算中,建议优先采用同伦-Newton -CPPM算法进行高度非线性弹塑性本构模型的数值实现。当Jacobian矩阵较难求出时也可以采用本文提出的两阶段迭代算法。
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . . |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . . |
| [11] | . |
| [12] | |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . |
| [24] | . |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | . |
| [29] | . |
| [30] | . |
| [31] | . |
| [32] | . . |
| [33] | . |
