, 嵇正波, 马晨波南京林业大学机械电子工程学院,南京 210037
REANALYSIS OF THE CONTACT MECHANICS FOR ROUGH SURFACES
SunJianjun, JiZhengbo, MaChenbo中图分类号:TH113
文献标识码:10.6052/0459-1879-17-272
通讯作者:
收稿日期:2017-08-6
接受日期:2017-12-18
网络出版日期:2017-12-20
版权声明:2018《力学学报》编辑部《力学学报》编辑部 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (448KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引言
粗糙表面接触力学问题是粗糙表面接触理论研究的主要问题 [1],涉及真实接触面积、接触压力及其两者之间的关系等. 一百多年来,工程问题的不断出现和相继解决,推动着粗糙表面接触理论的持续发展,如 Hertz 理论 [2]、G-W 模型 [3]、 W-A模型 [4] 和 M-B 模型 [5]. 利用这些理论,人们通过正确设计密封接触面的微凸峰形状及尺寸,实现了宇宙飞船的舱门密封 [1]. 尽管如此,研究人员至今仍在孜孜不倦地探索着这一课题 [6-13]. 这是因为：一方面,新的粗糙表面接触问题不断出现;另一方面,人们认识粗糙表面接触规律的过程是曲折的,有时存在一定的不足甚至错误.本文拟通过对现有粗糙表面接触力学模型的发展回顾和分析,指出其存在的问题;提出初始分形表面轮廓不因接触面积$\alpha$变化而变 化的思想和接触界面孔隙率概念,研究建立接触界面孔隙率、真实接触面积和接触压力分形模型,探讨受载过程中粗糙表面的接触力学特性,比较模型计算结果与文献实验数据,考察模型的正确性,以期为新建模型的应用提供理论基础.
1 现有模型的发展回顾、存在的问题
1.1 现有模型的发展回顾
(1) 基于统计学特征的粗糙表面接触力学研究. Greenwood 等 [3] 将粗糙微凸体简化为曲率相同的球截体,第一个提出基于表面 微凸体纯弹性变形的粗糙表面弹性接触模型 (简称 G-W 模型);随后,Greenwood 和 Tripp[14]、Bush 等 [15] 相继进行了更为 深入具体的研究,Pullen 等 [16] 则建立了基于表面微凸体完全塑性变形的粗糙表面塑性接触模型. 为了弥补上述接触模型忽略微凸体弹、塑性变形区间,以及只考虑单一形变的缺陷,Chang 等 [17] 基于微凸体变形体积守恒原 理建立了具有弹性和塑性变形的粗糙表面弹 -- 塑性接触模型 (简称 CEB 模型),但该模型在临界屈服点上的接触载荷值存在跳跃式变化, 两者过渡区间的弹塑性变形未予考虑. Zhao 等 [18] 通过研究,提出了包含弹性、弹塑性和塑性三种变形状态的表面接触模型,并在后续工作中解决了微凸体接触压力 变化和承载面积变化在变形转化临界点处连续光滑问题 [19].(2) 基于分形理论的粗糙表面接触力学研究.
Majumdar和Bhushan 利用分形函数$z(x)$ 表征等效粗糙表面特性,首次提出基于分形理论的粗糙表面弹性和塑性接触模型[5 (简称M-B模型). Chung[20通过研究也获得了相似的弹-塑性接触模型,与M-B 模型一样,也没有考虑介于弹性与塑性之间的弹塑性接触问题.
1994年Wang和Komvopoulos[21] 考虑了微接触点大小分布域扩展因子的作用,对 M-B 模型进行了相应的改进修正. 文献 [22-24] 依据修正 M-B 模型推导出了单个微凸体的接触面积与微凸体法向变形量成反比的关系. 与 M-B 模型的变形机制一致,Liu 等 [25] 也认为单个微凸体的接触面积随微凸体法向变形量增大而增大,当接触面积 小于临界接触面积时变形为塑性变形,反之为弹性变形. 文献 [26-28] 提出了用基底开口尺寸表达轮廓曲线的思路,通过定义不同层次微凸体的指数$n$, 来描述微凸体变形,并指出在一定接触载荷下高层次微凸体是向低层次转变的;丁雪兴等 [29] 基于基底长度,建立了粗糙表面分形接触模型,力图采用一有效长度来消除接触长度尺度内微凸体中空隙区对其法向变形量和接触面积等理论预测值带来的误差,但之后又 认为基底长度随接触面积变化而变化,结果得到了与 M-B 模型相同的微凸体变形机制.
1.2 存在的问题
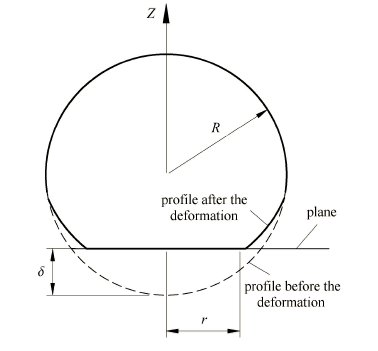
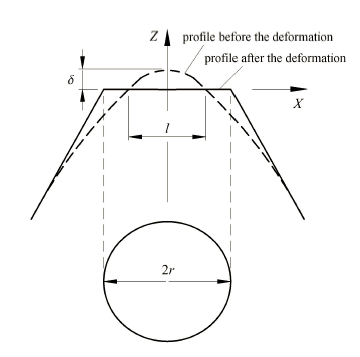
基于统计学特征的粗糙表面接触力学研究,以球截体为模型,假设接触面积小于球截体轮廓开口截面积 (如图 1 所示), 认为 “微凸体先 发生弹性变形,再发生弹塑性变形或是完全塑性变形”;由于分析过程中采用的表征粗糙表面的统计参数随采样长度和仪 器分辨率的变 化而变化,致使微凸体的各变形临界值存在不确定性.基于分形理论的粗糙表面接触力学研究,采用分形参数描述粗糙表面克服了采样长度和仪器分辨率的影响,但大多数研究采用对应于接 触面积$a$的尺寸$l = \sqrt a $描述单个微凸体初始表面轮廓[5],导致初始表面轮廓曲线随接触面积$a$变化而变化,如图 2 所示,以及由此得出 “微凸体先发 生完全塑性变形,再发生弹塑性变形、弹性变形” 违背实际的结论;Morag 等[26]和Liou等[27] 注意到这一问题, 并采用微凸体基底开口尺寸描述微凸体轮廓,纠正了 M-B 模型中微凸体变形是从塑性变形起向 弹性变形模式转变的错误,而其将取样长度$L =1/\gamma^{n}$作为最大微凸体基底尺寸,由此得到临界压缩量与取样长度相关的结论有待商榷;文献[28]虽然指出微凸体的变形性质决定于粗糙表面初始形貌的微凸体等级,也给出了弹性临界等级、第一弹塑性临界等级和第二弹塑性临界等 级计算式,但没有给出粗糙表面初始形貌的微凸体等级的计算方法.
显示原图|下载原图ZIP|生成PPT图 1单个微凸体 G-W 弹性接触模型
-->Fig. 1A single asperity contact profile in G-W model
-->
显示原图|下载原图ZIP|生成PPT图 2单个微凸体 M-B 接触模型
-->Fig. 2A single asperity contact profile in M-B model
-->
2 粗糙表面接触力学分形模型的建立
2.1 基本假设
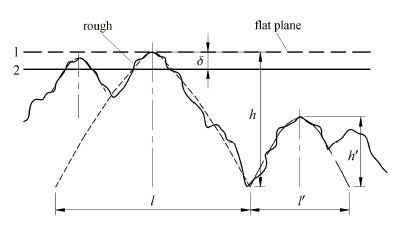
(1) 两粗糙表面间的接触可以等效为一个粗糙表面与一个刚性光滑平面的接触,如图 3 所示. 等效粗糙表面满足各向同性的分形特性, 粗糙表面二维轮廓曲线可以采用 Weierstrass-Mandelbrot 函数 (W-M 函数) 表征 [5,30]$Z\left( X \right) = G^{D - 1}\sum\limits_{n = n_{\min } }^\infty {\dfrac{\cos \left( {2 \pi \gamma ^nX} \right)}{\gamma ^{\left( {2 - D} \right)n}}} $ (1)
式中,$Z(X)$ 为粗糙表面轮廓曲线的高度,$X$ 为轮廓的位移坐标,$D$ 为表面轮廓分形维数,$1< D< 2$,$G$ 为轮廓特征尺度系数;$\gamma^{n}$ 表示轮廓曲线的空间频率,$n_{\min}$ 为组成粗糙表面轮廓曲线的微凸体最低层次指数;对于服从正态分布的表面,取$\gamma = 1.5$. $D$ 和$G$ 可由二维W-M 函数的功率谱获得,最低截止频率$\gamma^{n_{\min}}$ 与微凸体最大高度有关.
显示原图|下载原图ZIP|生成PPT图3一等效粗糙表面与一个刚性光滑平面的接触
-->Fig. 3Contact between a rough surface and a rigid flat plane
-->
(2) 假设表面受压时只有微凸体发生变形而没有宏观基体变形,发生变形前后微凸体的体积不变.
(3) 微凸体变形前后在垂直于粗糙度深度方向的任一截面均为圆截面.
(4) 忽略接触过程中微凸体之间的相互作用和接触过程中的材料硬化.
(5) 分形粗糙表面与刚性光滑平面接触时,微凸体的接触面积大小分布密度函数[21] 可以表征为
$n\left( a \right) = \dfrac{D}{2}\psi ^{\tfrac{2 - D}{2}}a_{\rm L}^{\tfrac{D}{2}} a^{- \tfrac{D}{2} - 1}$
式中,$a$为微接触点的面积,$\psi $ 为真实接触面积与最大微接触点面积之比$A_{r}/a_{\rm L}$ 的修正系数,$a_{L}$ 为微接触点 的最大面积.
2.2 单个微凸体接触变形
对于式 (1) 描述的由一系列不同尺寸的余弦波状微凸体叠加而成的粗糙表面,依据上述假设,则轮廓上任何一个微凸体,变形前 的轮廓曲线均可描述为$z\left( x \right) = G^{D - 1}l^{2 - D}\cos \left( {\dfrac{ \pi x}{l}}\right)\,, \ \ - \dfrac{l}{2} < x < \dfrac{l}{2}$ (2)
式中,$l$ 为微凸体轮廓基底直径, $l=1/\gamma^{n}$. 当~$n=n_{\min}$,最大波的基底$l=1/\gamma^{n_{\min}}$; $n=n_{\min}+1$,对应波的基底$l'=1/\gamma^{{n_{\min}}^{ + 1}}$; 以此类推,可获得各应波的基底尺寸。
考虑到微凸体原始轮廓的表征参数不因承载而变化,这里定义的l与 Majumder-Bhushan[5] 描述的与载荷作用后形成的 微凸体接触面对应的轮廓开口尺寸不同,而是一个只与接触面形貌参数及微凸体高度相关的参数.
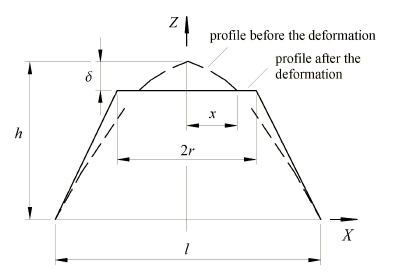
图4为单个接触微凸体接触变形示意图. 其中l为微凸体基底的尺寸,h为微凸体的高度幅值,$\delta $为实际压缩量, 取值范围为$0 \leqslant \delta <h$,具体大小与所受载荷有关, $2x$ 为用一刚性平面截取微凸体轮廓所得的截断长度, $2r$为按承载前后骨架体积不变原则求得的微凸体压缩量为$\delta $时的实际接触长度.
显示原图|下载原图ZIP|生成PPT图 4单个微凸体的接触变形
-->Fig. 4Contact deformation of a single asperity
-->
对于满足式 (2) 的微凸体,其高度和轮廓线上顶点的曲率半径分别为
$h = G^{D - 1}l^{2 - D}$ (3)
$R = \left. {\left| { {\left[ {1 + \left( {\frac{d z}{d x}}\right)^2} \right]^{\tfrac{3}{2}}}\Bigg / {\frac{d ^2z}{d x^2}}} \right.}\right|_{x = 0} = \dfrac{1}{G^{D - 1}l^{-D} \pi^2}$ (4)
对于确定的粗糙表面,最大微凸体的高度$h$ 与粗糙表面的平均粗糙度$Ra$ 之间的关系可以表达成$h=Ra/k$,$k$ 为粗糙表面的完整系数;当粗糙表面配对平面时,$k=1$ [14]。
粗糙面在接触压力作用下从位置1形变至位置2时,某一与刚性光滑平面接触的微凸体的接触面积将由变形前的轮廓横截面积$ x^{2}$墩粗为变形后的实际接触面积$a$. 变形前微凸体体积$V_0 = \dint_0^h {\pi }x^2 \dz$,假设变形后微凸体具有圆台特征,则变形后体积~$V_{1}$ 为
$V_1 = \dfrac{ \pi G^{D-1}l^{2-D}}{3}\cos \dfrac{{\pi }x}{l}\left( {r^2 + \dfrac{lr}{2} + \dfrac{l^2}{4}} \right)$. 通过简化
$\left( a \right)^{1/2} = \left( { {\pi }r^2} \right)^{1/2} = 2x$ (5)
考虑到变形前后微凸体体积相等,并比较简化成圆台后的微凸体体积与变形前的体积,求取$V_{1}-V_{0}$ 极值,可获得简化 式(5) 给变形带来的误差为${\left({V_1 - V_0 } \right)}/ {V_0 } = 3.24\%$.
利用图 4 所示的几何关系,实际压缩量$\delta $可表示为
$\delta = G^{D - 1}l^{2 - D}\left( {1 - \cos \dfrac{ \pi x}{l}} \right) $ (6)
实际压缩量$\delta $是由变形情况,即接触点产生弹性变形、弹塑性变形或塑性变形情况决定的。
(1) 弹性变形状态存在条件
按照 Hertz 接触理论,微凸体的接触面半径$r$可表示为 [2]
$r = \dfrac{ \pi p_0 R}{2E}$ (7)
式中,$p_{0}$ 为接触点上最大接触应力, $E$ 为当量弹性模量,$E = \left( {\dfrac{1 - \nu _1^2 }{E_1 } + \dfrac{1- \nu _2^2 }{E_2 }} \right)^{ - 1}$,$\nu_{1}$ 和 $\nu _{2}$ 为硬质环、软质环 材料泊松比, $E_{1}$ 和~$E_{2}$ 为硬质环、软质环材料弹性模量.将式 (4) 代入式 (7),并简化得
$\left( { {\pi }a} \right)^{1/2} = \dfrac{p_{0} }{2EG^{D - 1}l^{-D}})$ (7a)
接触面上的平均接触压力$p_m$为弹性接触压力$p_e$
$p_{\rm e} = p_{\rm m} = \dfrac{2}{3}p_0 = \dfrac{4}{3}EG^{D - 1}l^{- D} \left( { {\pi }a} \right)^{1/2}$ (8)
当$p_m$小于屈服极限$\sigma_y$时,微凸体处于弹性状态;当$p_m$等于$\sigma_y$时微凸体出现初始屈服. 临界弹性变形面积$a_{ec}$可以表示为
$a_{\rm ec} = \dfrac{1}{{\pi}}\left( {\dfrac{3\sigma _{\rm y}}{4EG^{D - 1}l^{ - D }}} \right)^2 $ (9)
当$a \leqslant a_{\rm ec}$,则微凸体发生弹性变形;否则,发生弹塑性或完全塑性变形.
(2) 完全塑性变形存在条件
当平均接触压力$p_{\rm m}$ 等于$3 \sigma_{\rm y}$时,微凸体完全屈服 [31],即塑性接触压力$p_{p}=3\sigma_y$, 此时
$\dfrac{p_{\rm m} }{\sigma _{\rm y} } = \dfrac{2}{3}\left[ {1 + \ln \left( {\dfrac{1}{3} \dfrac{E}{\sigma_{\rm y} } \dfrac{r}{R} } \right)} \right] $ (10)
将式 (4) 代入式 (10) 可得
$a_{\rm pc} = \dfrac{9{\rm e}^7}{{\pi }^3}\left( {\dfrac{\sigma _{\rm y} }{EG^{D - 1}l^{ - D}}} \right)^2)$ (10a)
(3) 弹塑性变形状态存在条件
当$a_{\rm ec} \leqslant a \leqslant a_{pc}$ 时,微凸体发生弹塑性变形,这一阶段微凸体接触面积和接触压力的关系极为复杂。
考虑到在初始屈服临界点和完全塑性变形临界点,接触面积和接触压力的变化是连续和光滑的,参照文献[19] 构造一个样板函数
$f\left( a \right) = - 2\left( {\dfrac{a - a_{\rm ec} }{a_{\rm pc} - a_{\rm ec} }}\right)^3 + 3\left( {\dfrac{a - a_{\rm ec} }{a_{\rm pc} - a_{\rm ec} }} \right)^2$ (11)
则可导出
$p_{\rm ep} = p_{\rm e} + \left( {p_{\rm p} - p_{\rm e} } \right) f\left( a \right) = \dfrac{4}{3}EG^{D - 1}l^{ - D }\left( { {\pi }a} \right)^{1 /2} +\\ \left[ {3\sigma _{\rm y} - \dfrac{4}{3}EG^{D - 1}l^{ - D }\left( { {\pi }a} \right)^{1/ 2}} \right]\cdot \left[ { - 2\left( {\dfrac{a - a_{\rm ec} }{a_{\rm pc} - a_{\rm ec} }} \right)^3 +3\left( {\dfrac{a - a_{\rm ec} }{a_{\rm pc} - a_{\rm ec} }} \right)^2} \right] $ (12)
2.3 粗糙表面的真实接触面积和接触载荷
两粗糙表面接触时的真实接触面积~$A_{\rm r}$ 和总的接触载荷~$F_{\rm c}$ 与最大微凸体的变形状态相关。对于$a_{\rm L} < a_{\rm ec}$,接触表面上的所有接触点都处于弹性变形状态,真实接触面积$A_{\rm r}$ 为弹性接触面积$A_{\rm re}$,所承受的载荷$F_{\rm c}$ 为弹性接触载荷$F_{\rm e}$
$A_{\rm r} = A_{\rm re} = \dint_0^{a_{\rm L} } n\left( a \right)a\d a =\dfrac{D}{2 - D}\psi ^{{\left( {2 - D} \right)} / 2}a_{\rm L}$ (13)
$ F_{\rm c} = F_{\rm e} = \dint_{0}^{a_{\rm L} } {p_{\rm e} } an\left( a \right)\d a =$
$\qquad \dint_0^{a_{\rm L} } \dfrac{4 {\pi }^{1/2}}{3}EG^{D - 1}l^{-D}a^{3/2}n\left( a\right)\da $ (14)
对于$a_{\rm ec}<a_{\rm L}<a_{\rm pc}$,接触表面上的接触点处于弹塑性变形状态,真实接触面积$A_{\rm r}$ 由弹性接触面积$A_{\rm re}$ 和弹塑性接触面积$A_{\rm rep}$ 组成,所承受的载荷$F_{\rm c}$ 为弹性接触载荷与弹塑性载荷之和,即
$ A_{\rm r} = A_{\rm re} + A_{\rm rep} = \int_0^{a_{\rm ec} } {n\left( a \right)ad a} +\int_{a_{\rm ec} }^{a_{\rm L}} {n\left( a \right)ad a} =\dfrac{D}{2 - D}\psi ^{{\left( {2 - D} \right)} /2}a_{\rm L} $ (15)
$ F_{\rm c} = \int_{0}^{a_{\rm ec} } {p_{\rm e} } n\left( a \right)ad a + \int_{a_{\rm ec} }^{a_{\rm L} } {p_{\rm ep} \left( a \right)} n\left( a \right)ad a =\int_0^{a_{\rm ec} } {\frac{4{\pi }^{1 /2 }}{3}EG^{D - 1}l^{- D}a^{3/2}n\left( a \right)d a + } \\ \int_{a_{\rm ec}}^{a_{\rm L} } \Bigg \{ \dfrac{4{\pi }^{1 /2 }}{3}EG^{D - 1}l^{- D}a^{1/2} +\left( {3\sigma _{\rm y} - \dfrac{4{\pi }^{1 /2 }}{3}EG^{D - 1}l^{- D}a^{1/2}} \right)\cdot $
$ \qquad \left[ { - 2\left( {\dfrac{a - a_{\rm ec} }{a_{\rm pc} - a_{\rm ec} }} \right)^3 +3\left( {\dfrac{a - a_{\rm ec} }{a_{\rm pc} - a_{\rm ec} }} \right)^2} \right] \Bigg \} n\left( a \right)a d a $ (16)
对于$a_{\rm L}>a_{\rm pc}$,接触表面上的接触点处于塑性变形状态,真实接触面积$A_{\rm r}$ 由弹性接触面积$A_{\rm re}$、弹塑性接触面积$A_{\rm rep}$ 和塑性接触面积$A_{\rm rp}$ 组成,所承受的载荷$F_{\rm c}$ 为弹性载荷、弹塑性载荷与塑性接触载荷三者之和,即
$ A_{\rm r} = A_{\rm re} + A_{\rm rep} + A_{\rm rp} =$
$\int_0^{a_{\rm ec} } {n\left( a \right)ad a} +\int_{a_{\rm ec} }^{a_{\rm pc} } {n\left( a \right)ad a} + \int_{a_{\rm pc} }^{a_{\rm L} } {n\left( a \right)ad a} =\dfrac{D}{2 - D}\psi ^{{\left( {2 - D} \right)}/ 2}a_{\rm L} $(17)
$ F_{\rm c} = \int_{0}^{a_{\rm ec} } {p_{\rm e} } n\left( a \right)ad a + \int_{a_{\rm ec} }^{a_{\rm pc} } {p_{\rm ep} \left( a \right)} n\left( a \right)ad a + \int_{a_{\rm pc} }^{a_{\rm L} } {p_{\rm p} \left( a \right)} n\left( a \right)ad a =\\ \int_0^{a_{\rm e c} } {\dfrac{4 {\pi }^{ 1/2}}{3}EG^{D - 1}l^{ - D}a^{3/2}n\left( a \right)d a + } \int_{a_{\rm e c} }^{a_{\rm pc} } \Bigg\{ \dfrac{4 {\pi }^{ 1/2 }}{3}EG^{D - 1}l^{ - D }a^{1/ 2} +\left( {3\sigma _{\rm y} - \dfrac{4 {\pi }^{ 1/2 }}{3}EG^{D - 1}l^{ - D }a^{1 / 2}} \right)\cdot \\ \left[ { - 2\left( {\dfrac{a - a_{\rm ec} }{a_{\rm pc} - a_{\rm ec} }} \right)^3 + 3\left( {\dfrac{a - a_{\rm ec} }{a_{\rm pc} - a_{\rm ec} }} \right)^2} \right] \Bigg\} n\left( a \right)ad a +\int_{a_{\rm pc} }^{a_{\rm L} } {3\sigma _{\rm y} } n\left( a \right)ad a $ (18)
尽管 式(13), 式(15) 和式(17) 在形式上完全一致,但由于最大微凸体的变形性质不同,各式中$a_{\rm L}$ 不同,实际的接触面积是不一样的. 因此,计算真实接触面积时,必须先行判断最大微凸体的变形性质.
这里需要说明的是,基本假设(5) 是Wang 和Komvopoulos 针对文献[5]关于``微凸体的接触面积大小分布密度函数'' 的一些不足作出相应改进;推导微凸体发生完全塑性变形条件时引用的文献[31],其所做的``表面受压时只有微凸体发生变形而没有宏观基体变形、发生变形前后微凸体的体积不变、微凸体变形前后在垂直于粗糙度深度方向的任一截面均为圆截面以及忽略接触过程中微凸体之间的相互作用和接触过程中的材料硬化'' 等假设符合本文模型的应用条件;参照文献[19]构造的样板函数只是用来分配弹塑性区间中弹性面积和塑性面积的权重,没有涉及到其他模型的推导条件和过程,不影响所建模型兼容性.
3 与实验数据的比较
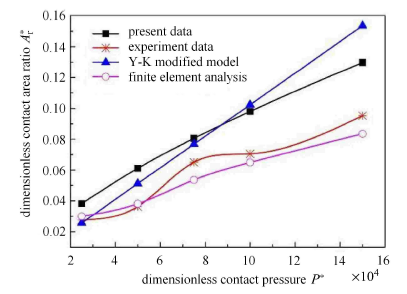
为了验证本模型,现将本模型与Kucharski 实验模型32,Y-K 修正模型33以及Sahoo 有限元分析模型34进行对比。实验材料为钢,弹性模量$E =200$ GPa,泊松比 $\nu =0.3$,屈服强度400 MPa,硬度(HV) 为1.12 GPa,粗糙表面分形特征参数$D =1.3$ ($D_{\rm s} =2.3$),$G =1.36 \times 10^{ - 11}$ m. 比较结果如图5 所示. 与实验数据在整体变化规律上是一致的,本文模型的计算值略大于实验值,主要原因是所建模型中未能考虑接触变形过程中相邻接触微凸体之间的相互作用,以及材料的强化作用,致使计算值大。
显示原图|下载原图ZIP|生成PPT图 5本文模型和 Kucharski 实验数据的对比
-->Fig. 5Comparison with the Kucharski test data
-->
4 粗糙表面的接触力学特性分析
4.1 孔隙率的变化
将描述表面形貌的参数$D$ 和$G$、粗糙峰高度$h$ 代入式(3) 可得微凸体基底实际尺寸. 则初始孔隙率 $\phi_{0}$ 可求$ \phi _0 = 1 - \dfrac{\int_0^h {n\left( a \right)a \cdot ad z\left(x \right)} }{A_{\rm n} h} = 1 - \dfrac{2 - D}{2}a_{\rm L}^{\tfrac{D}{2} - 1} \int_{0}^{a_{\rm L}} {a^{1 - \,\tfrac{D}{2}}} \sin \dfrac{\sqrt { {\pi }a} }{l}d \dfrac{\sqrt { {\pi }a} }{l} $ (19)
在接触压力$p_{\rm c}$ 作用下,接触表面产生压缩量 $\delta $,即接触端面的高度由$h$ 减小至$h- \delta $。
此时,接触端面上计算 单元体的体积由$V_{0}=L\cdot L\cdot h$ 变为$V'_{0} $,则变形后接触端面的孔隙率为
$ \phi = \dfrac{{V}'_0 - \left( {1 - \phi _0 } \right)V_0 }{{V}'_0 } = \dfrac{h\phi _0-\delta }{h-\delta }$ (20)
式中, $\phi_{0}$ 为接触界面的初始孔隙率.
采用Maple 语言编程,计算分析受载过程中,粗糙轮廓表面参数$D$ 和$G$、接触压力$p_{\rm c}$ 对接触端面孔隙率的影响。
粗糙表面的 硬质环和软质环的粗糙度高度分别取$h_{1}=0.2 \upmu $m 和$h_{2}=0.4 \upmu $m,则根据等效粗糙度高度$h= \sqrt {h_1^2 + h_2 ^2} $ 可得等效粗糙峰高度$h=0.447\upmu $m,$E=20$GPa,$\sigma _{y}=100$ MPa.
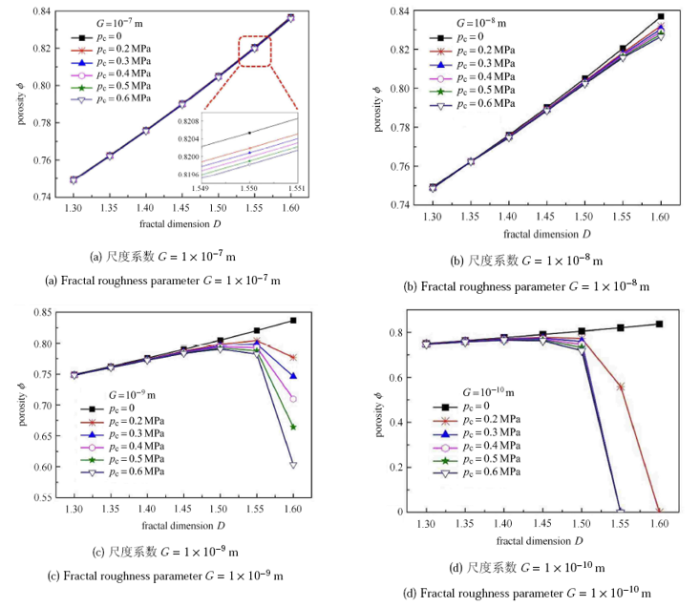
接触界面孔隙率随各参数的变化情况如图6 所示. $p_{\rm c}=0$ 即没有施加接触压力时,接触界面的初始孔隙率$\phi _{0}$ 随着分形维数$D$ 的增大而增大,这是因为$D$ 越大,一方面,粗糙表面越复杂,接触界面间很多细小孔隙被表现出来;另一方面,接触界面总的孔隙量变小,但微凸体细化使得接触界面的微凸体总体积变小,导致孔隙率增大. 随着接触压力$p_{\rm c}$ 的增大,微凸体被挤压变形填充接触界面间的孔隙,总体积变小,导致孔隙率增大. 随着接触压力$p_{\rm c}$ 的增大,微凸体被挤压变形填充接触界面间的孔隙,孔隙率$\phi $减小;尺度系数$G$ 越小,意味着微凸体越细化,越易被压缩变形,填充孔隙,直至填实,此时的孔隙率$\phi $ 变为零。
对于$G=1\times10^{ - 9}$m 的表面,当$p_{\rm c}<0.3$ MPa 时,最大孔隙率的表面分形维数$D=1.55$,当$p_{\rm c}>0.4$ MPa 时,最大孔隙率的表面分形维数降低至1.50;对于$G=1\times10^{ - 10}$m 的表面,当$p_{\rm c}<0.3$MPa 时,最大孔隙率的表面分形维数$D=1.45$,当$p_{\rm c}>0.4$\,MPa 时,最大孔隙率的表面分形维数降低至1.40。
显示原图|下载原图ZIP|生成PPT图 6接触压力对接触界面孔隙率的影响
-->Fig. 6Influence of contact pressure on the porosity
-->
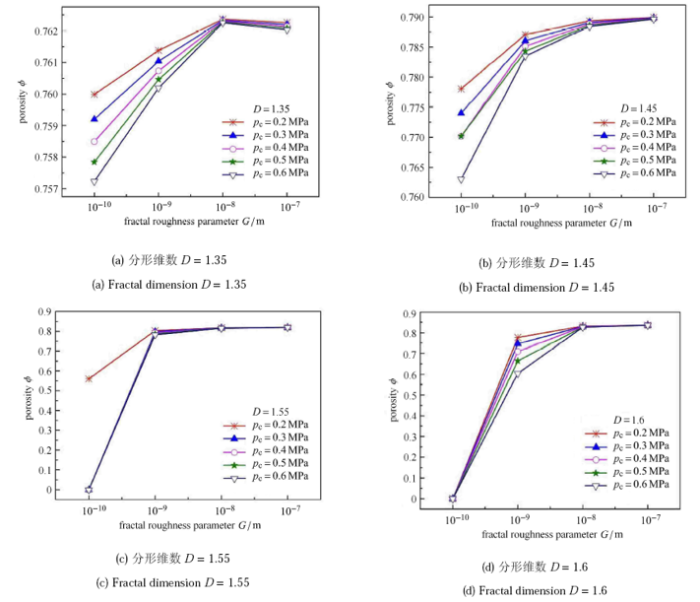
图7描述了一定接触压力下,一定分形维数表面,孔隙率随尺度系数变化的规律. 分形维数小于 1.35 的表面,孔隙率随尺度系数的减小先 增大后减小;分形维数大于 1.45 的表面,孔隙率随尺度系数减小持续减小,其减小速度随尺度系数变小而加快.
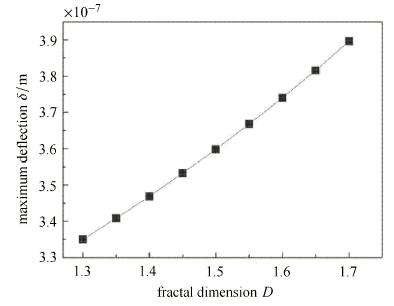
图8表达了在一定载荷下,微凸体受压变形填满接触界面孔隙时的最大法向变形量$\delta $与端面形貌参数之间的关系. 分形维 数越大,孔隙率大,需要更多的微凸体变形量来填充,因而,压实所需要的最大变形量$\delta $也就越大.
显示原图|下载原图ZIP|生成PPT图 7尺度系数对接触端面孔隙率的影响
-->Fig. 7Influence of contact pressure on the porosity
-->
显示原图|下载原图ZIP|生成PPT图 8分形维数与最大变形量 (孔隙率为 0 时) 的关系
-->Fig. 8Influence of fractal dimension on maximum deflection
-->
4.2 接触面积变化规律
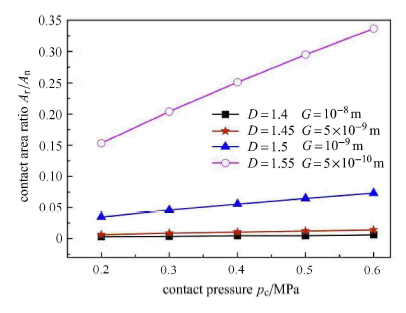
(1) 接触压力$p_{\rm c}$ 对$A_{r}/A_{n}$ 的影响图9示出了不同$D, G$ 组合下的粗糙表面的真实接触面积$A_{\rm r}/A_{\rm n}$ 随接触压力$p_{\rm c}$ 的变化关系. 接触压力$p_{\rm c}$ 增大,微凸体被压产生的法向变形量增大,致使接触端面间的真实接触面积增大.
显示原图|下载原图ZIP|生成PPT图 9载荷对真实接触面积的影响
-->Fig. 9Influence of contact pressure on the real contact area
-->
(2) 端面形貌参数$D, G$ 对$ A_{\rm r}/A_{\rm n}$ 的影响
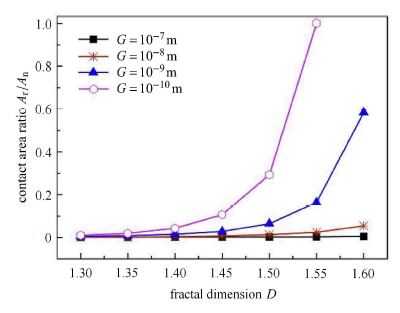
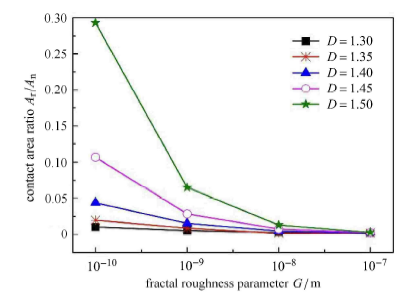
图10和图11 为接触压力$p=0.5$\,MPa、不同$G$ 值下真实接触面积$ A_{\rm r}/A_{\rm n}$ 分别与分形维数$D$、尺度系数$G$ 的关系曲线. $D$ 增大,微凸体细化,微凸体曲率半径$R$ 变小,对于一定的载荷,真实接触面积比$ A_{\rm r}/A_{\rm n}$ 增大。
$D$ 较小时,微凸体较大,微凸体曲率半径$R$ 较大,$G$ 对微凸体的贡献小;$G$ 的减小致使较大的微凸体曲率半径$R$ 变小,法向压缩量增大,真实接触面积增大;$D$ 较大时,微凸体较小,随着$D$ 的增大,$G$ 对微凸体的贡献也变大,$G$ 的减小致使微凸体曲率半径$R$ 变小越为明显,法向压缩量增大,真实接触面积急剧增大。
显示原图|下载原图ZIP|生成PPT图 10分形维数对真实接触面积的影响
-->Fig. 10Influence of fractal parameter on the real contact area
-->
显示原图|下载原图ZIP|生成PPT图 11尺度系数对真实接触面积的影响
-->Fig. 11Influence of the fractal roughness parameter on the real contact area
-->
5 结论
(1)基于承载前后骨架体积不变原则、微凸体轮廓基底尺寸$l$、 分形维数$D$ 和尺度系数$G$,建立了新的粗糙表面接触模型. 微凸体变形机制研究表明,粗糙表面微凸体承载变形依次为弹性变形、弹塑性变形和塑性变形。
(2)接触界面的孔隙率随端面形貌、接触压力等参数的变化而变化. 接触界面的初始孔隙率$\phi _{0}$ 随着分形维数$D$ 的增大而增大;接触压力$p_{\rm c}$ 增大,孔隙率$\phi $ 减小,并随着分形维数$D$ 的增大和尺度系数$G$ 减小,孔隙率快速减小,直至填实,变为零。
(3) 接触界端面间的真实接触面积随接触压力$p_{\rm c}$ 和分形维数$D$ 的增大而增大. $D$ 较小时,$G$ 的增大对真实接触面积的增大影响较小;$D$ 较大时,$G$ 的增大对真实接触面积的增大作用明显。The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . . |
| [2] | . |
| [3] | . |
| [4] | |
| [5] | . |
| [6] | . . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . . |
| [12] | . . |
| [13] | . . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . . |
| [23] | . . |
| [24] | . . |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | . . |
| [29] | . . |
| [30] | . |
| [31] | |
| [32] | . |
| [33] | . |
| [34] | . |
