, 谭辉, 宝鑫, 王东洋, 李述涛清华大学土木工程系,北京 100094
The seismic wave input method for soil-structure dynamic interaction analysis based on the substructure of artificial boundaries
LiuJingbo中图分类号:TU311.3
文献标识码:A
通讯作者:
收稿日期:2017-10-11
接受日期:2017-10-26
网络出版日期:2018-02-20
版权声明:2018《力学学报》编辑部《力学学报》编辑部 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (1571KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引言
近年来,随着大型建/构筑物的兴建和地下空间的开发利用,大型结构-地基动力相互作用、地下结构地震反应等土-结构动力相互作用问题成为研究的热点。对于此类问题,由于地基为半无限空间,其动力反应特性与地上结构有很大区别[1]。研究土-结构动力相互作用问题,主要的分析方法包括原型观测、模型试验和数值模拟,其中随着计算机技术的发展和有限元、有限差分等数值分析方法的日益完善,数值模拟成为研究此类问题的主要手段。对于土-结构动力相互作用模型地震反应的数值模拟,合理地处理半无限地基和实现地震动输入是数值计算需要解决的关键问题。最早解决半无限地基问题的方法是将截断边界取到足够远,使得在计算时间内由截断边界反射回来的波无法到达感兴趣的区域[2],但是这一处理方法导致计算量过大,计算过程耗时过多。也有一些****推荐采用有限元与动力无限元的耦合模型[3,4],解决对散射波的吸收问题。目前最常用的方法是在截断边界处设置人工边界条件,允许计算区域内部的外行波到达边界时不发生反射,以此模拟真实半无限地基的辐射阻尼。人工边界条件根据表达形式的不同可分为位移型人工边界,如透射边界[5],和应力型人工边界,如粘性边界[6]和粘弹性边界[7],其中应力型人工边界因其具有足够的精度和易于在通用有限元软件中设置的优点,近年来得到广泛应用和发展[8,9,10,11,12,13]。
无限元和人工边界都可以较好地处理内源问题,但对于地震反应分析这类外源问题,还需要解决地震动的输入问题。Joyner和Chen[14]根据粘性边界,推导了一维模型人工边界上的等效荷载,以此完成地震动输入。赵崇斌等[15]针对有限元与无限元耦合模型,通过固定近域边界,求解远域入射简谐波在固定边界产生的荷载,再将该荷载施加在近域边界上以完成地震动输入。Wolf[16]提出了自由场边界法,在计算区域外侧设置吸收边界和独立的自由场区域,根据波场分解原理,由自由场确定自由波场运动,吸收边界确定散射波场运动,叠加得到计算区域的总波场,该方法需对三个计算区域联立分步求解计算,计算量较大。Nielsen[17]基于自由场边界法,将粘性边界和自由场单元集成为一种边界单元,并在有限元软件ABAQUS中实现了剪切波的竖直入射。目前对于工程问题,有时采用地上结构地震反应计算的思路,在地下结构地震反应分析中提出一些近似的处理方法,例如将计算模型底部取到基岩,假设基岩为刚性,将地震动由基岩处以位移或加速度的形式输入[18,19,20],对侧面边界不做处理或只设置人工边界,由于这一方法不能模拟地震波在人工边界上的输入和传播过程,将导致进一步的误差。刘晶波等[21]建议在模型的所有截断边界都设置人工边界条件,并以粘弹性边界为例,将输入地震动转化为人工边界上的等效输入荷载,推导了一种适用于粘弹性人工边界的地震动输入方法,也被称为波动法。研究表明[22,23,24,25],将地震动输入转化为人工边界上的等效输入荷载的波动法具有较高的精度。
波动法概念清晰,理论完备,但是等效输入地震荷载计算较为复杂,除了需要确定自由场对应人工边界位置处的应力,还要确定引入人工边界条件带来的附加力,除此之外,在确定等效输入地震荷载时,还需要确定不同人工边界面上荷载的作用方向和人工边界节点代表的单元面积。因此,在研究土-结构动力相互作用模型的地震反应时,相比其他地震动输入方法,波动法虽然计算结果更准确,但是处理技术复杂,计算工作量大,导致实际应用中存在一定的不便。本文基于波动法的基本理论,提出一种新的地震波动输入方法,该方法同样是先求解等效输入地震荷载,然后在人工边界面上施加该荷载实现地震波动输入,但是新方法的等效输入地震荷载求解过程简单,且处理更为便捷,并适用于各类应力型人工边界。通过弹性半空间和成层半空间在竖直入射和斜入射地震波动作用下的算例与解析解对比验证了该方法的正确性和有效性。
1 基于自由场有限元模型的地震波动输入方法
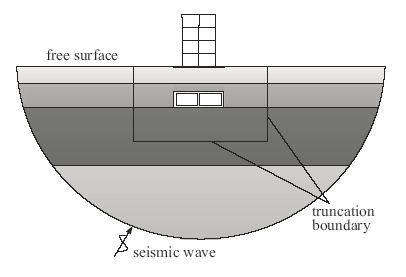
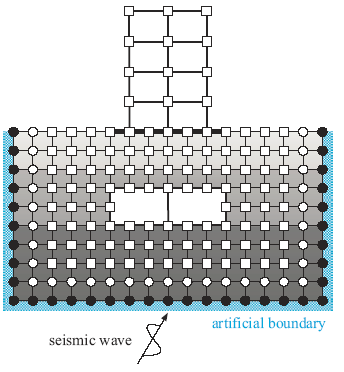
为了研究图1所示的土-结构动力相互作用系统在地震作用下的动力反应,数值计算时首先需要从成层地基中截取包括结构在内的有限的区域进行建模,有限元模型如图2所示,在截断边界处需要设置人工边界来吸收内部的散射波。根据处理地震波动输入的波动法[21]的原理,可将地震波动输入转化为在人工边界上施加等效荷载,该荷载称为等效输入地震荷载。土-结构动力相互作用系统在等效输入地震荷载作用下的运动方程为：$[M]\{\ddot{u}\}+[C]\{\dot{u}\}+[K]\{u\}=\{F\}$ (1)
其中,$\{u\}$、$\{\dot{u}\}$和$\{\ddot{u}\}$分别为有限元模型节点的位移、速度和加速度向量;$\{F\}$为施加于人工边界处的等效输入地震荷载向量;$[M]$、$[C]$和$[K]$分别为土-结构系统有限元模型的质量、阻尼和刚度矩阵,对于应力型人工边界,通常由弹簧、阻尼和质量系统组成,因此在$[M]$、$[C]$和$[K]$中已集成了人工边界条件。如果已知等效输入地震荷载$\{F\}$,即可以采用时域或频域分析方法,由式(1)得到地震作用下土-结构系统的动力反应。
显示原图|下载原图ZIP|生成PPT图1土-结构动力相互作用问题示意图
-->Fig.1A model of soil-structure dynamic interaction
-->
显示原图|下载原图ZIP|生成PPT图2土-结构动力相互作用系统有限元模型
-->Fig.2Finite element model of soil-structure dynamic interaction
-->
输入地震波可以是土层场地中的自由波场,也可以是土层场地下卧半空间中的入射波场,若为后者,则当地震波竖直入射时,可以采用一维计算程序SHAKE91、EERA等获得自由场地震反应[26, 27];当地震波斜入射时,可采用一维化时域算法首先获得自由场有限元模型中竖向一列节点的运动,再根据地震行波的传播规律,经几何扩展得到成层半空间中的自由波场[28, 29]。因此土-结构系统地震反应分析中输入地震波的自由波场可作为已知条件存在。
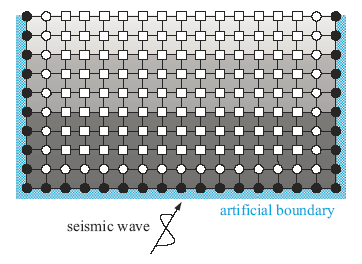
地震波的输入与自由场有关,与内部结构无关,确定的等效输入地震荷载应保证人工边界的位移场与自由波场相一致,因此等效输入地震荷载的确定仅与自由场有关。为获得等效输入地震荷载,建立与土-结构动力相互作用系统对应的自由场有限元模型,如图3所示。在自由场有限元模型的人工边界节点施加等效输入地震荷载$\{F\}$,有限元模型的运动方程如下：
$[{{M}^{0}}]\{\ddot{u}\}+[{{C}^{0}}]\{\dot{u}\}+[{{K}^{0}}]\{u\}=\{F\}$ (2)
其中,$[{{M}^{0}}]$、$[{{C}^{0}}]$和$[{{K}^{0}}]$分别为自由场有限元模型的质量、阻尼和刚度矩阵,其中也集成了人工边界条件;$\{u\}$、$\{\dot{u}\}$和$\{\ddot{u}\}$分别为有限元模型节点的位移、速度和加速度向量。
显示原图|下载原图ZIP|生成PPT图3自由场有限元模型
-->Fig.3Finite element model of free field
-->
在等效输入地震荷载作用下,自由波场运动满足式(2),因此
$[{{M}^{0}}]\{{{\ddot{u}}^{0}}\}+[{{C}^{0}}]\{{{\dot{u}}^{0}}\}+[{{K}^{0}}]\{{{u}^{0}}\}=\{F\}$ (3)
其中,$\{{{u}^{0}}\}$、$\{{{\dot{u}}^{0}}\}$和$\{{{\ddot{u}}^{0}}\}$分别为自由场有限元模型节点对应的自由波场的位移、速度和加速度向量。
式(3)给出了根据已知自由场运动,计算等效输入地震荷载的公式,当自由场模型的运动与已知的输入地震波场一致时,由式(3)可以获得等效输入地震荷载：
$\{F\}=[{{M}^{0}}]\{{{\ddot{u}}^{0}}\}+[{{C}^{0}}]\{{{\dot{u}}^{0}}\}+[{{K}^{0}}]\{{{u}^{0}}\}$ (4)
$\{F\}$即为实现地震波动输入而需要施加的等效荷载。因此,可以建立自由场有限元模型,在截断边界上设置人工边界,然后对模型所有节点施加自由场运动,由此得到的人工边界节点的约束反力即为土-结构动力相互作用问题分析中为实现地震波动输入而需要的等效输入地震荷载。
以上推导提供了一种可以直接基于自由场有限元模型确定等效输入地震荷载的方法,但是需要建立额外的自由场有限元模型,并对整体模型进行动力分析,计算工作量较大,因此需要采取进一步的处理方法。
2 基于人工边界子结构的地震波动输入方法
上一节给出了基于自由场有限元模型的地震波动输入方法,可以根据含有人工边界条件的自由场有限元模型和已知的自由波场确定等效输入地震荷载。这一方法虽然可以实现地震波动输入,但由于需要采用整体自由场有限元模型进行计算方可获得等效输入地震荷载,因而这一方法的实用性受到影响。下面利用有限元方法的特点,开展进一步的分析和处理。对于图2和图3所示的土-结构动力相互作用系统和自由场有限元模型,将单元节点按区域分为三类：人工边界节点(用实心圆符号●表示)、与人工边界相邻的内部节点(用空心圆符号○表示)和其余节点(用空心方形符号□表示)。根据以上节点的划分,可以定义人工边界区和人工边界子结构,人工边界区：由含有人工边界节点的单元组成的区域;人工边界子结构：由人工边界区单元构成的有限元子结构模型。
按照以上节点划分,土-结构动力相互作用系统有限元模型和自由场有限元模型的运动方程(1)和(2)可以分别写成以下分块矩阵的形式：
$\begin{align} \left[ \begin{matrix} {{M}_{\text{II}}} {{M}_{\text{IC}}} 0 \\ {{M}_{\text{CI}}} {{M}_{\text{CC}}} {{M}_{\text{CB}}} \\ 0 {{M}_{\text{BC}}} {{M}_{\text{BB}}} \\ \end{matrix} \right]\left\{ \begin{matrix} {{{\ddot{u}}}_{\text{I}}} \\{{{\ddot{u}}}_{\text{C}}} \\{{{\ddot{u}}}_{\text{B}}} \\\end{matrix} \right\}+\left[ \begin{matrix}{{C}_{\text{II}}} {{C}_{\text{IC}}} 0 \\{{C}_{\text{CI}}} {{C}_{\text{CC}}} {{C}_{\text{CB}}} \\ 0 {{C}_{\text{BC}}} {{C}_{\text{BB}}} \\ \end{matrix} \right]\left\{ \begin{matrix}{{{\dot{u}}}_{\text{I}}} \\{{{\dot{u}}}_{\text{C}}} \\{{{\dot{u}}}_{\text{B}}} \\\end{matrix} \right\} \\ +\left[ \begin{matrix}{{K}_{\text{II}}} {{K}_{\text{IC}}} 0 \\{{K}_{\text{CI}}} {{K}_{\text{CC}}} {{K}_{\text{CB}}} \\ 0 {{K}_{\text{BC}}} {{K}_{\text{BB}}} \\ \end{matrix} \right]\left\{ \begin{matrix}{{u}_{\text{I}}} \\{{u}_{\text{C}}} \\{{u}_{\text{B}}} \\\end{matrix} \right\}=\left\{ \begin{matrix} 0 \\ 0 \\ {{F}_{\text{B}}} \\\end{matrix} \right\} \\\end{align}$ (5)
$\begin{align} \left[ \begin{matrix}M_{\text{II}}^{\text{0}} M_{\text{IC}}^{\text{0}} 0 \\M_{\text{CI}}^{\text{0}} M_{\text{CC}}^{\text{0}} M_{\text{CB}}^{\text{0}} \\ 0 M_{\text{BC}}^{\text{0}} M_{\text{BB}}^{\text{0}} \\ \end{matrix} \right]\left\{ \begin{matrix}{{{\ddot{u}}}_{\text{I}}} \\{{{\ddot{u}}}_{\text{C}}} \\{{{\ddot{u}}}_{\text{B}}} \\\end{matrix} \right\}+\left[ \begin{matrix}C_{\text{II}}^{\text{0}} C_{\text{IC}}^{\text{0}} 0 \\C_{\text{CI}}^{\text{0}} C_{\text{CC}}^{\text{0}} C_{\text{CB}}^{\text{0}} \\ 0 C_{\text{BC}}^{\text{0}} C_{\text{BB}}^{\text{0}} \\ \end{matrix} \right]\left\{ \begin{matrix}{{{\dot{u}}}_{\text{I}}} \\{{{\dot{u}}}_{\text{C}}} \\{{{\dot{u}}}_{\text{B}}} \\\end{matrix} \right\} \\ +\left[ \begin{matrix}K_{\text{II}}^{\text{0}} K_{\text{IC}}^{\text{0}} 0 \\K_{\text{CI}}^{\text{0}} K_{\text{CC}}^{\text{0}} K_{\text{CB}}^{\text{0}} \\ 0 K_{\text{BC}}^{\text{0}} K_{\text{BB}}^{\text{0}} \\ \end{matrix} \right]\left\{ \begin{matrix}{{u}_{\text{I}}} \\{{u}_{\text{C}}} \\{{u}_{\text{B}}} \\\end{matrix} \right\}=\left\{ \begin{matrix} 0 \\ 0 \\ {{F}_{\text{B}}} \\\end{matrix} \right\} \\\end{align}$ (6)
其中下标B、C、I分别表示对应于人工边界节点、与人工边界相邻的内部节点和其余内部节点;上标0表示自由场;$\{{{F}_{\text{B}}}\}$为作用于人工边界节点的等效输入地震荷载。
考虑有限元离散化模型的特点,对比图2和图3,及式(5)和式(6)可以发现,如果自由场有限元模型人工边界区单元的网格划分与土-结构动力相互作用系统的相同,则有
$\left\{ \begin{align} [M_{\text{CB}}^{\text{0}}]=[{{M}_{\text{CB}}}] \\ [M_{\text{BC}}^{\text{0}}]=[{{M}_{\text{BC}}}] \\ [M_{\text{BB}}^{\text{0}}]=[{{M}_{\text{BB}}}] \\\end{align} \right.$, $\left\{ \begin{align} [C_{\text{CB}}^{\text{0}}]=[{{C}_{\text{CB}}}] \\ [C_{\text{BC}}^{\text{0}}]=[{{C}_{\text{BC}}}] \\ [C_{\text{BB}}^{\text{0}}]=[{{C}_{\text{BB}}}] \\\end{align} \right.$, $\left\{ \begin{align} [K_{\text{CB}}^{\text{0}}]=[{{K}_{\text{CB}}}] \\ [K_{\text{BC}}^{\text{0}}]=[{{K}_{\text{BC}}}] \\ [K_{\text{BB}}^{\text{0}}]=[{{K}_{\text{BB}}}] \\\end{align} \right.$ (7)
将计算等效输入地震荷载的式(4)写成分块矩阵的形式,并将式(7)代入,得：
$\begin{align} \left\{ \begin{matrix} 0 \\ 0 \\ {{F}_{\text{B}}} \\\end{matrix} \right\}=\left[ \begin{matrix}M_{\text{II}}^{\text{0}} M_{\text{IC}}^{\text{0}} 0 \\M_{\text{CI}}^{\text{0}} M_{\text{CC}}^{\text{0}} {{M}_{\text{CB}}} \\ 0 {{M}_{\text{BC}}} {{M}_{\text{BB}}} \\ \end{matrix} \right]\left\{ \begin{matrix}\ddot{u}_{\text{I}}^{\text{0}} \\\ddot{u}_{\text{C}}^{\text{0}} \\\ddot{u}_{\text{B}}^{\text{0}} \\\end{matrix} \right\}+\left[ \begin{matrix}C_{\text{II}}^{\text{0}} C_{\text{IC}}^{\text{0}} 0 \\C_{\text{CI}}^{\text{0}} C_{\text{CC}}^{\text{0}} {{C}_{\text{CB}}} \\ 0 {{C}_{\text{BC}}} {{C}_{\text{BB}}} \\ \end{matrix} \right]\left\{ \begin{matrix}\dot{u}_{\text{I}}^{\text{0}} \\\dot{u}_{\text{C}}^{\text{0}} \\\dot{u}_{\text{B}}^{\text{0}} \\\end{matrix} \right\} \\ \text{ }+\left[ \begin{matrix}K_{\text{II}}^{\text{0}} K_{\text{IC}}^{\text{0}} 0 \\K_{\text{CI}}^{\text{0}} K_{\text{CC}}^{\text{0}} {{K}_{\text{CB}}} \\ 0 {{K}_{\text{BC}}} {{K}_{\text{BB}}} \\ \end{matrix} \right]\left\{ \begin{matrix}u_{\text{I}}^{\text{0}} \\u_{\text{C}}^{\text{0}} \\u_{\text{B}}^{\text{0}} \\\end{matrix} \right\} \\\end{align}$(8)
由式(8)可以得到作用于人工边界的等效输入地震荷载为：
$\begin{align} \{{{F}_{\text{B}}}\}=[{{M}_{\text{BC}}}]\{\ddot{u}_{\text{C}}^{\text{0}}\}+[{{M}_{\text{BB}}}]\{\ddot{u}_{\text{B}}^{\text{0}}\}+[{{C}_{\text{BC}}}]\{\dot{u}_{\text{C}}^{\text{0}}\}+[{{C}_{\text{BB}}}]\{\dot{u}_{\text{B}}^{\text{0}}\} \\ \text{ }+[{{K}_{\text{BC}}}]\{u_{\text{C}}^{\text{0}}\}+[{{K}_{\text{BB}}}]\{u_{\text{B}}^{\text{0}}\} \\ \end{align}$ (9)
式(9)表明,只要人工边界节点及相邻内部节点的运动与自由场保持一致,人工边界上的外荷载即为实现地震波动有效输入的等效荷载;等效输入地震荷载的确定仅与人工边界子结构(与人工边界相连单元组成的子结构系统)有关,与内部其余节点无关;人工边界子结构可由土-结构动力相互作用系统有限元模型直接得到,而不用额外建立自由场有限元模型。
以上理论推导证明,在人工边界上实现地震波动有效输入的等效输入地震荷载可以由对人工边界子结构的动力分析获得,由此,本文提出一种新的地震波动输入方法,称为基于人工边界子结构的地震波动输入方法。新方法与原波动法的波动输入方式一致,即通过在人工边界节点上施加等效输入地震荷载来实现地震波动输入,但等效输入地震荷载的求解不再需要对自由波场进行应力分析和对人工边界产生的附加荷载进行单独求解,而是通过人工边界子结构模型的动力分析直接获得实现地震动输入的等效输入地震荷载。
下面以图1所示成层半空间中土-结构动力相互作用模型的地震反应问题为例,介绍本文提出的基于人工边界子结构的地震波动输入方法的具体实施步骤：
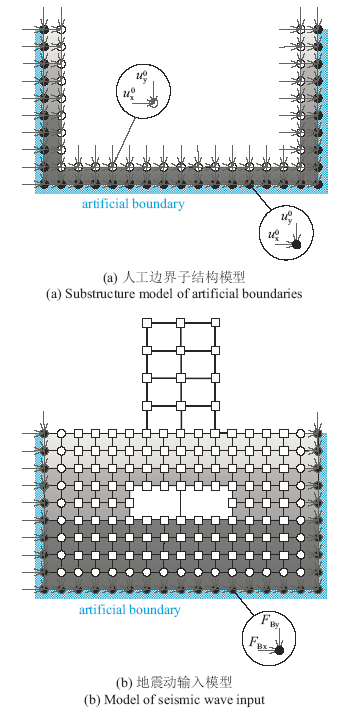
(1)建立图2所示的土-结构动力相互作用系统的有限元模型,并在截断边界处设置相应的人工边界条件,删去除包含人工边界节点的单元以外的所有单元,即只保留人工边界节点和与人工边界相邻的内部节点所包围的单元,得到对应的人工边界子结构模型,如图4(a)所示。
(2)根据入射地震波采用一维或一维化方法进行自由场分析,获得自由波场。确定子结构模型中所有节点对应的自由场位移时程$\{{{u}^{0}}\}$,该位移时程由入射波场位移和反射波场位移叠加而成。对人工边界子结构模型所有节点施加对应的自由波场位移时程$\{{{u}^{0}}\}$,如图4(a)所示,对子结构模型进行动力分析,求得人工边界节点的反力$\{{{F}_{\text{B}}}\}$,$\{{{F}_{\text{B}}}\}$即为实现地震波动有效输入的等效输入地震荷载。
(3)对如图4(b)所示的土-结构系统有限元模型的人工边界节点施加由步骤(2)获得的等效输入地震荷载
显示原图|下载原图ZIP|生成PPT图4基于人工边界子结构的地震波动输入方法计算步骤
-->Fig.4The calculation procedure of the seismic wave input method based on the substructure of artificial boundaries
-->
以上为本文提出的基于人工边界子结构的地震波动输入方法的具体步骤,需要说明的是,利用人工边界子结构模型计算等效输入地震荷载时,按照公式(9)需要给定子结构模型节点的位移、速度和加速度,但实际应用时只要给定节点的位移,有限元软件可以自动求解速度和加速度,而无需人为地再给定速度和加速度。同理,也可以只给定子结构节点的速度或者加速度,即采用子结构模型求解等效输入地震荷载,给定子结构节点的运动时只需要给定位移、速度和加速度三者之中的任意一个。
基于人工边界子结构的地震波动输入方法,给出了求解人工边界上等效输入地震荷载的另一种途径,这一方法对人工边界条件没有限制,因此可以用于粘性人工边界、粘弹性人工边界,也可以用于其他形式更为复杂的应力型人工边界。
在采用新方法计算时,为了优化求解等效输入地震荷载的效率,可以采用以下三种处理方法：
方法一,对图2所示的土-结构动力相互作用系统有限元模型,固定除人工边界节点和与其相邻内部节点外的其余节点,对人工边界节点和相邻节点施加自由波场位移时程{u0},完成动力计算。
方法二,采用生死单元法,杀死除包含人工边界节点的单元以外的其他单元,对子结构施加自由波场位移时程进行动力计算。
方法三,删除人工边界子结构以外的其他单元,采用包含人工边界节点的单元组成的子结构模型进行动力计算。
通过计算比较发现,在常用的有限元软件中,方法一最耗时,方法二次之,方法三计算效率最高。其原因是,方法一虽然固定了其余节点的运动,但是软件计算过程中仍然需要对内部单元进行求解;方法二动力分析过程耗时与方法三接近,但由于内部单元的存在,单元数量大,导致处理过程更加耗时。综合考虑,方法三的处理方式计算效率最高,因此本文推荐采用方法三求解等效输入地震荷载。
3 均匀弹性半空间地震波动竖直入射算例
3.1脉冲波入射算例
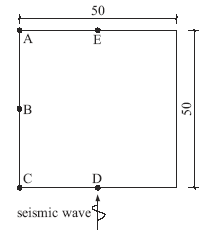
为了验证本文提出的新方法,首先研究均匀弹性半空间自由场的地震波动输入问题,介质的材料参数如下,质量密度$\rho =2000\text{kg/}{{\text{m}}^{3}}$,剪切波速${{c}_{\text{s}}}=200\text{m/s}$,泊松比$\nu =0.25$。计算区域如图5所示,模型尺寸为$\text{50m}\times \text{50m}$,有限元单元尺寸为$\text{1m}\times \text{1m}$,采用四节点平面应变单元,侧面和底面人工边界采用粘弹性人工边界,模型底部竖直入射剪切波采用式(10)所示的δ函数的有限差分近似[7]：$\left. \begin{align} u(\tau )=16\left[ {{G}_{4}}(\tau )-4{{G}_{4}}(\tau -\frac{1}{4})+6{{G}_{4}}(\tau -\frac{1}{2})-4{{G}_{4}}(\tau -\frac{3}{4})+{{G}_{4}}(\tau -1) \right] \\ {{G}_{4}}(\tau )={{\tau }^{3}}H(\tau ),\text{ }\tau =\frac{t}{T} \\ \end{align} \right\}$(10)
其中T是脉冲持时,$H(\tau )$是Heaviside函数。
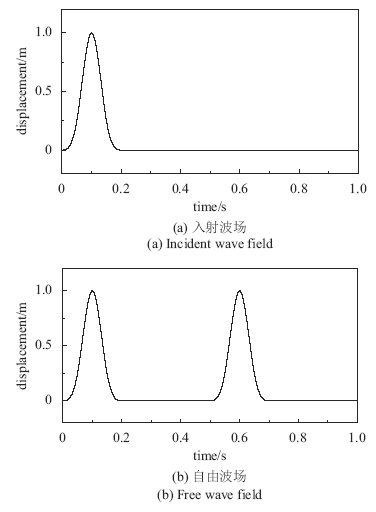
入射脉冲波位移时程如图6(a)所示,脉冲持时0.2s,计算时长1s,时间步长为0.002s,模型底部人工边界处自由波场水平位移时程如图6(b)所示。
显示原图|下载原图ZIP|生成PPT图5均匀半空间有限域模型
-->Fig.5Homogeneous half-space finite domain model
-->
显示原图|下载原图ZIP|生成PPT图6均匀半空间有限域模型底部边界处的位移时程
-->Fig.6The displacement of the bottom boundary of the homogeneous half-space finite domain model
-->
原波动法[21]基于粘弹性人工边界,从理论上给出了地震波动输入的等效输入荷载形式,并已得到广泛应用。根据原波动法,粘弹性人工边界节点处的等效输入荷载为：
$\begin{align} {{F}_{\text{N}}}\left( t \right)={{\sigma }^{0}}\left( t \right)A+{{C}_{\text{N}}}\dot{u}_{\text{N}}^{0}\left( t \right)+{{K}_{\text{N}}}u_{\text{N}}^{0}\left( t \right) \\ {{F}_{\text{T}}}\left( t \right)={{\tau }^{0}}\left( t \right)A+{{C}_{\text{T}}}\dot{u}_{\text{T}}^{0}\left( t \right)+{{K}_{\text{T}}}u_{\text{T}}^{\text{0}}\left( t \right) \\\end{align}$ (11)
其中${{F}_{\text{N}}}(t)$、${{F}_{\text{T}}}(t)$分别为人工边界节点处的法向和切向等效输入地震荷载,${{\sigma }^{0}}\left( t \right)$、${{\tau }^{0}}\left( t \right)$分别为人工边界对应自由场的正应力和剪应力,${{C}_{\text{N}}}$、${{C}_{\text{T}}}$分别为粘弹性人工边界法向和切向阻尼器的阻尼系数,${{K}_{\text{N}}}$、${{K}_{\text{T}}}$分别为粘弹性人工边界法向和切向弹簧的刚度系数,$u_{\text{N}}^{0}\left( t \right)$、$\dot{u}_{\text{N}}^{0}\left( t \right)$分别为人工边界节点法向对应自由场的位移和速度,$u_{\text{T}}^{\text{0}}\left( t \right)$、$\dot{u}_{\text{T}}^{\text{0}}\left( t \right)$分别为人工边界节点切向对应自由场的位移和速度,A为人工边界节点代表的单元面积。
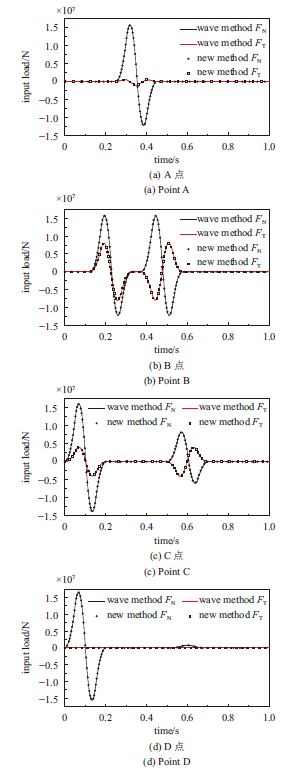
利用原波动法求得图5中A、B、C、D四个人工边界节点处的等效输入地震荷载和采用本文提出的新方法求得的等效输入地震荷载对比如图7所示,结果表明,本文提出的新方法求得的等效输入地震荷载与原波动法完全一致,从而直接验证了新方法的正确性。
显示原图|下载原图ZIP|生成PPT图7新方法与原波动法求得的等效输入地震荷载
-->Fig.7The equivalent input seismic loads calculated by the new method and the original wave method
-->
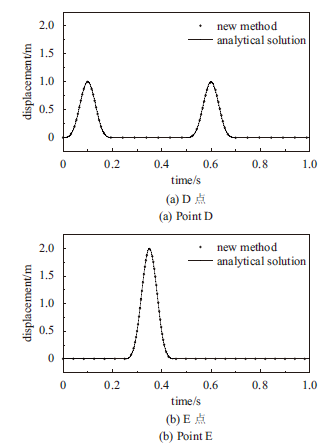
利用新方法求得的等效输入地震荷载进行地震动输入,得到均匀半空间有限域模型底部观测点D和自由表面观测点E的位移时程与解析解的对比如图8所示。计算结果表明,本文提出的新方法求得的有限域在剪切波竖直入射下的水平位移反应与解析解完全相同,表明该方法可以实现地震波动的有效输入。
显示原图|下载原图ZIP|生成PPT图8脉冲波作用下均匀半空间有限域观测点位移
-->Fig.8The displacements of observation points on the homogeneous half-space finite domain under pulse wave
-->
3.2 实际地震波入射算例
下面进行实际地震波动输入的算例分析,弹性半空间的材料参数、计算模型同3.1节,输入的地震波选取图9所示的峰值加速度为0.2g的Kobe波,计算时长40s,时间步长为0.01s,采用新方法完成地震波动输入求得的有限域模型底部边界观测点D和自由表面观测点E的水平位移时程与解析解对比如图10所示。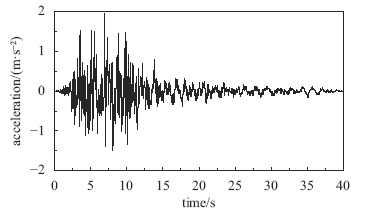
显示原图|下载原图ZIP|生成PPT图9Kobe波加速度时程
-->Fig.9Acceleration time history of Kobe wave
-->
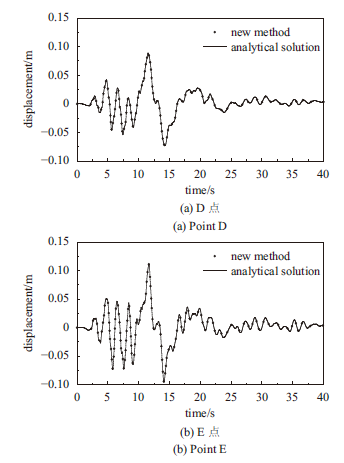
显示原图|下载原图ZIP|生成PPT图10Kobe波作用下均匀半空间有限域观测点的水平位移
-->Fig.10The horizontal displacements of observation points on the homogeneous half-space finite domain under Kobe wave
-->
由图10可以看到有限元解与解析解完全一致,表明对于均匀弹性半空间竖直入射地震波动输入问题,基于人工边界子结构的地震波动输入方法可以准确地实现地震波动输入。
4 成层弹性半空间地震波动竖直入射算例
4.1脉冲波入射算例
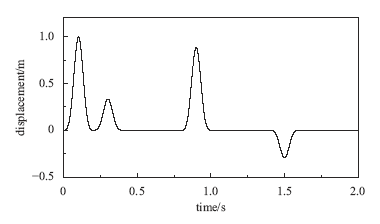
为了进一步验证本文提出方法的有效性,选取成层弹性半空间算例进行计算分析,半无限空间表面有一覆盖层,有限域模型竖向尺寸为50m,如图11所示,覆盖层厚30m,弹性半空间取20m深,介质材料参数为：质量密度${{\rho }_{1}}={{\rho }_{2}}=2000\text{kg/}{{\text{m}}^{3}}$,剪切波速${{c}_{\text{s1}}}=100\text{m/s}$,${{c}_{\text{s2}}}=200\text{m/s}$,泊松比${{\nu }_{1}}={{\nu }_{2}}=0.25$。有限元单元尺寸为$\text{1m}\times \text{1m}$,采用四节点平面应变单元。底部边界处入射脉冲波位移时程如图6(a)所示,脉冲持时为0.2s,计算时长为2s,时间步长为0.002s,底部边界处自由波场水平位移时程解析解如图12所示。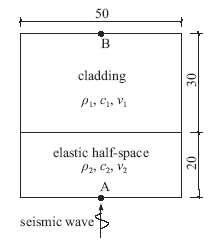
显示原图|下载原图ZIP|生成PPT图11成层半空间有限域计算模型
-->Fig.11Layered half-space finite domain model
-->
显示原图|下载原图ZIP|生成PPT图12成层半空间有限域模型底部边界处自由波场位移时程
-->Fig.12Free field displacement time history of the bottom boundary of the layered half-space finite domain model
-->
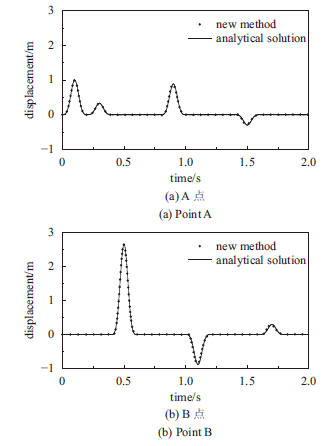
采用本文提出的新方法,进行成层半空间地震波输入和地震反应计算,得到成层半空间有限域计算模型底部观测点A和自由表面观测点B的水平位移时程与解析解对比如图13所示。
显示原图|下载原图ZIP|生成PPT图13脉冲波作用下成层半空间有限域模型观测点水平位移
-->Fig.13The horizontal displacements of observation points on the layered half-space finite domain under pulse wave
-->
4.2 实际地震波入射算例
对于成层弹性半空间,同样选用图9的Kobe波进行实际地震波输入,计算时长40s,时间步长为0.01s,采用新方法求得有限域模型底部观测点A和自由表面观测点B的水平位移时程与解析解对比如图14所示。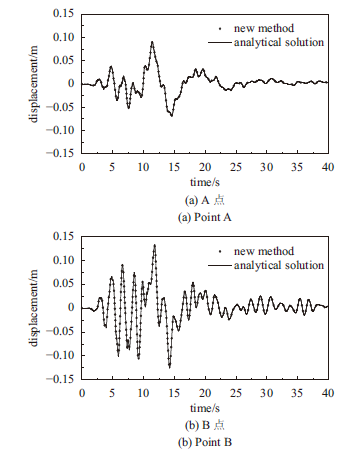
显示原图|下载原图ZIP|生成PPT图14Kobe波作用下成层半空间有限域模型观测点水平位移
-->Fig.14The horizontal displacements of observation points on the layered half-space finite domain under pulse wave
-->
脉冲波和实际地震波竖直入射的算例结果表明,采用本文提出的基于人工边界子结构的地震波动输入方法进行地震动输入,得到有限域地震反应与解析解一致,因此新方法适用于成层半空间的竖直入射地震波的输入问题。
5 地震波斜入射算例
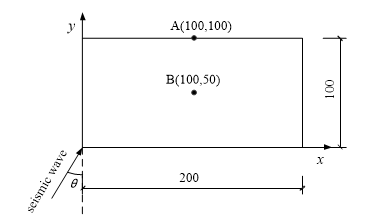
相比地震波竖直入射问题,地震波斜入射问题的计算量更大、计算难度更高,本节分别以SV波和P波斜入射算例验证本文提出的地震波动输入方法应用于地震波斜入射问题的可行性。取二维计算有限域如图15所示,模型尺寸为$\text{200m}\times \text{100m}$,有限元单元尺寸为$\text{1m}\times \text{1m}$,材料参数同4.1小节,地震波入射角为θ,A和B为有限域内的两个观测点。有限元模型人工边界仍采用粘弹性人工边界,边界上的等效输入地震荷载采用本文提出的新方法求解,对于均匀介质地震波斜入射问题,自由场位移根据入射波场位移和经自由表面反射的反射波场位移叠加得到,对于SV波入射和P波入射问题,由于波型转换,同时存在反射的SV波和P波。
显示原图|下载原图ZIP|生成PPT图15地震波斜入射有限域计算模型
-->Fig.15Finite domain model for oblique incidence of seismic wave
-->
5.1 SV波斜入射算例
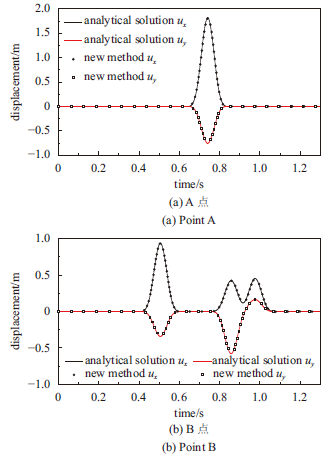
SV波斜入射的入射角为θ=20°,入射波位移时程如图6(a)所示,时间步长取0.002s,计算持时为1.3s。采用本文提出的波动输入方法对有限域进行地震波动输入求得有限域的动力反应,图16是有限域在0.4s、0.7s、0.8s和1.0s时刻的波场快照,从图中可以看到入射的SV波和反射的SV波和P波的波阵面。图17中给出了观测点A和B的位移时程曲线,从图中可以看到数值计算得到的位移与解析解一致,验证了新方法实现斜入射SV波输入的正确性。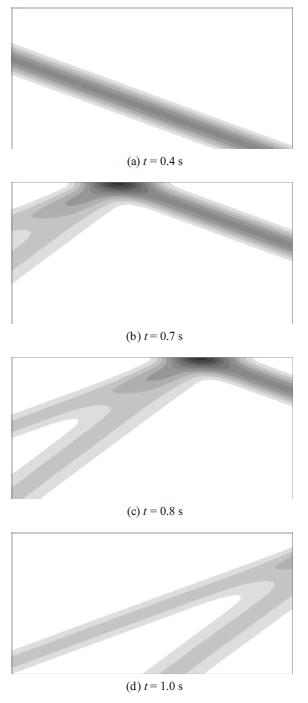
显示原图|下载原图ZIP|生成PPT图16SV波斜入射时有限域波场快照
-->Fig.16Snapshots of finite domain under oblique incident SV wave
-->
显示原图|下载原图ZIP|生成PPT图17SV波斜入射时观测点的位移时程
-->Fig.17Displacements of observation points under oblique incident SV wave
-->
5.2 P波斜入射
P波斜入射的入射角为θ=30°,入射波位移时程如图6(a)所示,时间步长取0.002s,计算持时为1.3s。同样采用本文提出的波动输入方法对有限域进行地震波动输入求得有限域的动力反应,图18是有限域在0.3s、0.5s、0.6s和0.8s时刻的波场快照,从图中可以看到入射的P波和反射的P波和SV波的波阵面。图19中给出了观测点A和B的位移时程曲线,从图中可以看到数值计算得到的位移同样与解析解一致,验证了新方法实现斜入射P波输入的正确性。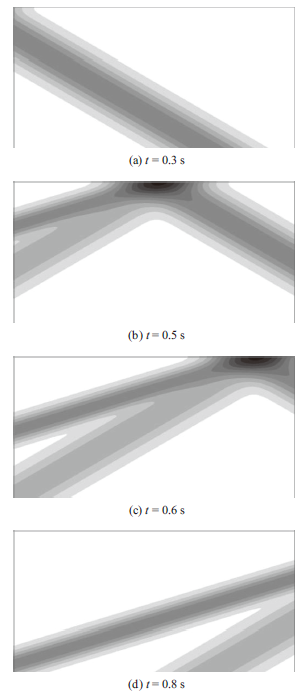
显示原图|下载原图ZIP|生成PPT图18P波斜入射时有限域波场快照
-->Fig.18Snapshots of finite domain under oblique incident P wave
-->
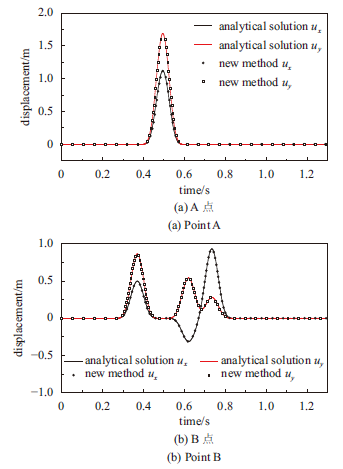显示原图|下载原图ZIP|生成PPT图19P波斜入射时的观测点位移时程
-->Fig.19Displacements of observation points under oblique incident P wave
-->
6 结论
波动法是现有土-结构动力相互作用问题分析中地震动输入方法中精度较高的方法,但其实施较为复杂,工作量较大。本文基于波动法和有限元模型的特点,提出了一种新的波动输入方法基于人工边界子结构的地震波动输入方法,通过对包含人工边界节点的单元组成的子结构模型进行动力分析,直接求得等效输入地震荷载并以此完成地震波动的有效输入,通过地震波竖直入射和斜入射的算例验证,可以得到以下结论：(1)新方法以原波动法为基础,通过求得人工边界上的等效输入地震荷载来进行地震波动输入,新方法利用了有限元模型离散化的特点,通过对人工边界子结构的节点施加自由场位移并进行动力分析,求解得到人工边界节点上的反力,即等效输入地震荷载,避免了原波动法确定等效输入地震荷载时的复杂求解过程,同时保证新方法求得的等效输入地震荷载与原波动法一致。
(2)新方法用于处理竖直入射地震波动输入时,无论是均匀弹性半空间还是成层弹性半空间,有限域地震反应计算结果都与解析解一致,表明该方法可以准确地实现竖直入射地震波输入。同时,均匀半空间的SV波和P波斜入射的算例证明了新方法同样适用于斜入射地震波动的输入问题。
(3)新方法对于采用的人工边界形式和单元划分均没有限制,并且只需要确定人工边界子结构模型节点对应的自由场运动(位移、速度或加速度三者只需其一),等效输入地震荷载就可以由子结构模型动力分析直接获得,同时由于子结构模型人工边界节点与土-结构动力相互作用模型的人工边界节点一一对应,因此等效输入地震荷载的提取和施加过程便于实现,可以大大提高计算效率。
(4)新方法不需要根据人工边界节点的运动和人工边界条件单独求解引入人工边界条件带来的附加力,因此对选用的人工边界条件并无限制,可以用于不同类型的应力型人工边界。
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | . |
| [4] | . |
| [5] | . . |
| [6] | [J]. |
| [7] | . . |
| [8] | [博士论文]. [PhD Thesis]. |
| [9] | . . |
| [10] | . |
| [11] | . . |
| [12] | . . |
| [13] | //陆新征编. 第14届全国结构工程学术会议. 烟台市, //Lu Xinzheng eds. Proceedings of the 14th National Conference on Structural Engineering, Yantai, 2005. |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | |
| [20] | . |
| [21] | . . |
| [22] | . |
| [23] | . |
| [24] | . . |
| [25] | . . |
| [26] | . |
| [27] | . |
| [28] | . . |
| [29] | . . |
