, 王梁FLUID-STRUCTURE INTERACTION ANALYSIS OF LOCAL STRESSES IN ATHEROSCLEROTIC PLAUQE AND THE INTERVENTION OF ENHANCED EXTERNAL COUNTERPULSATION TREATMENT
DuJianhang, WangLiang中图分类号:O38
文献标识码:A
通讯作者:
收稿日期:2017-05-2
接受日期:2017-12-29
网络出版日期:2017-12-29
版权声明:2018《力学学报》编辑部《力学学报》编辑部 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (9102KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引言
颈动脉粥样硬化斑块破裂是造成缺血性卒中的主因[1-2]. 目前临床中以动脉管腔的狭窄度作为斑块分级的唯一特异性标记[3],当狭窄度超过 70% 时则建议通过内膜切除术摘除斑块.然而这种风险评估和管理方法被广泛认为是不足够的[4-6],NASCET 及 ECST 等大型多中心临床试验结果显示轻微 (\le50%) 及中度 (50%~69%) 水平颈动脉狭窄的患者才是遭受卒中威胁的主要群体[2-3,5,7].因此寻求更好的晚期斑块失稳、破裂的预测性指标,降低急性缺血性事件的发生风险,成为了当前斑块研究最迫切的课题[3-7]。晚期斑块进程及破裂涉及应力条件、斑块形态、血液条件、细胞活性及基因组活性等多方面因素,其机理目前尚未得到透彻解析[4, 8-9]. 斑块局部的应力与应变环境被普遍认为起着至关重要的作用[5, 7],基于生物机械力的风险指示因子被认为对于评估 斑块的稳定性具有潜在的可能性[7]. 然而这些因子在实际应用中是否能更好地预测与斑块破裂相关的严重心血管事件目前尚未得到充分的论证[8]。
低水平及振荡的动脉壁面切应力 (wall shear stress, WSS) 被广泛认为与动脉粥样硬化的发病及早期发展存在正相关性[3]. 然而对于晚期的斑块, 研究[11-12]显示高水平 WSS 的分布区域与更大的斑块坏死核心和更薄的纤维帽相关,因而与斑块破裂更为相关[13]. 另一方面,由于考虑到斑块结构应力 (plaque structural stress, PSS) 在量级上远远大于 WSS(约 103~105倍[6, 15]),因此很多研究者认为 PSS 在晚期斑块进程及最终破裂中 起着更重要的作用[4,6,14-17]. Richardson 等[16]认为过高的 PSS 水平是斑块破裂的主因. Tang 等[4]和 Teng 等[14]提出了用临界斑块壁面应力 (3D critical plaque wall stress, 3D CPWS) 作为代表斑块结构应力的风险因子,认为颈动脉和冠脉的斑块破裂位置均与局部的高 3D CPWS 分布相关;William 等[18]认为当斑块中存在过薄的纤维帽 (小于 60 m) 时将导致过大的斑块结构应力,并建议将此应力的阀值定为 300 kPa。
然而,上述大部分工作本质上研究的其实是血管和斑块本身的变化对生物机械力的影响,而并非是后者的变化所诱导的斑块生物力学 响应. Ohayon 等[19]的研究也显示了斑块和血管的结构及组成的变化将显著改变 PSS 的水平. 因此在此基础上探讨生物机械力因子作为斑块破裂的风险预测因子,可能是有局限性的。
本文旨在研究血流动力学以及斑块结构与组成材料属性等因素对斑块局部应力的影响,引入国内外临床中广泛应用的增强型体外反搏 (enhanced external counterpulsation, EECP) 技术,显著干预心动周期里动脉的血流灌注及动脉内压,进而采用流 固耦合 (fluid-structure interaction, FSI) 数值仿真的方法评价斑块局部的动力响应。
EECP 是欧美和中国心脑血管专业学会临床指南推荐的安全有效的无创性辅助循环疗法[20-22],推荐级别为：IIa(脑卒中)/IIb(冠心病). 近年来大量基础研究[23-25]表明 EECP 疗法通过改善动脉的血流动力学环境及提高 WSS 水平,有利于改善内皮功能及抑制动脉粥样硬化病变的发生;对于晚期斑块,我们的前期研究[26-27]显示 EECP 作用明显改变了斑块部位的局部应力分布水平及分布特性,然而这些改变是否会显著干预晚期斑块进程、增加与高血压相关的不良事件发生风险目前尚不清晰[28],成为其临床应用中备受关注的课题. 本文在探索动脉粥样硬化晚期斑块进程力学机制的基础上,同时希望从力学的角度进一步探索 EECP 作用对斑块的影响。
1 动物实验与在体血流动力学测量
本文以一头雄性猪为实验体,采用高脂高胆固醇饲料喂饲方法建立实验致动脉粥样硬化的动物模型[23],进而进行在体基础血流动力学测量,所得的数据用于后续的 FSI 数值仿真. 实验体原始体重为 6.3 kg,经过 90 d 高脂喂饲,最终体重为 45.5 kg。测量内容包括正常生理状态和 EECP 状态 (反搏压为 0.035 MPa) 下的左侧颈总动脉血流率、左心室血压以及心电图. 其中血流率的测量采用超声多普勒系统 (ATL-HDI-5000, Philip Com America) 配 5~10 MHz 多频高分辨率线阵探头;血压的测量采用尖端压力传感器 (TP-400T,NihonKohden,日本). 并采用医用增强型体外反搏系统 (Shuangshan EECP-MCI, 中国广州). 图 1 为连续 3 个心动周期的在体测量结果,从图中可见,EECP 作用明显地改变了心动周期里的血流和血压脉动模式,明显提高了心动周期里的血流灌注水平和血压水平。
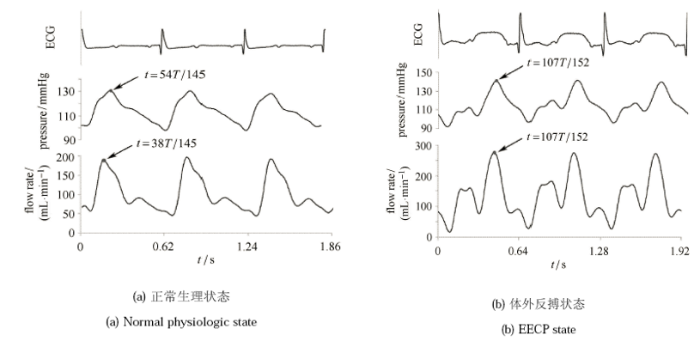显示原图|下载原图ZIP|生成PPT图1在体血流动力学测量数据 (1 mmHg=133.3 Pa)
-->Fig. 1In vivo hemodynamic measurement (1 mmHg=133.3 Pa)
-->
2 数值仿真模型
2.1 三维理想化的具有晚期斑块结构的动脉几何模型
建立如图 2 所示的具有晚期斑块结构的三维动脉模型. 动脉正常段的管腔直径为 0.4 cm,壁厚 0.05 cm;斑块区域的长度 为 0.8 cm (2 倍管腔直径),斑块部位的狭窄度为 50%. 为消除入口效应,入口面设置在离狭窄区喉部 4 cm 的地方 (10 倍管腔直 径);出口面至狭窄喉部的距离取 4 cm;纤维帽 (fibrous cap, FC) 的厚度取 3 种情况：600 m, 200 m 和 65 m,其中 200 m 和 65 m 被认为是颈动脉和冠状动脉斑块高风险失稳的临界情况,厚度在 600 m 到 1 000 m 被认为是低风险情况[13]。图2为$FC=600m$ 情况的具有晚期斑块结构的动脉模型,切片 S1~S8 的纵向位置分别为 (以入口处为$Z=0$)：0.04,0.041,0.042,0.043,0.044,0.045,0.046,0.047 m。
2.2 斑块组织的材料特性
动脉粥样硬化斑块组织的材料特性被认为对斑块的结构应力有显著影响29-30. 假设血管壁和斑块均为超弹性、 各向同性、不可压缩和均质的,则组织的材料特性可以用改进的非线性 Mooney-Rivlin 模型来描述,其应变能方程如下4-5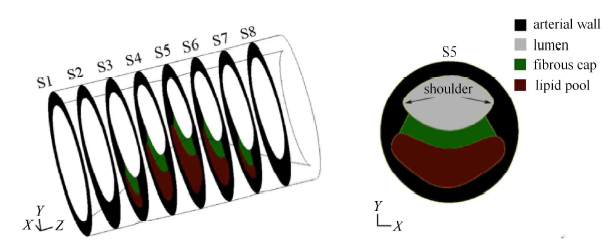
显示原图|下载原图ZIP|生成PPT图 2三维理想化的具有晚期斑块结构的动脉模型
-->Fig. 23D ideal model of artery with advanced AS plaque
-->
$\left. \begin{array}\\ W = c_1 (I_1 - 3) + c_2 (I_2 - 3) + D_1 [\exp (D_2 (I_1 - 3)) - 1] \\ I_1 = \sum {C_{ii} , \ \ I_2 } = \dfrac{1}{2}[I_1^2 - C_{ij} C_{ij} ] \end{array} \right\} $ (1)
式中,$I_{1}$ 和 $I_{2 }$ 是第1 和第2 应变常量;${\pmb C} = [C_{ij} ] ={\pmb X}^{\rm T}{\pmb X}$ 是右柯西-格林变形张量;($x_{i})$ 是当前位置,($a_{i})$ 为原始位置;$c_{i}$ 和 $D_{i}$ 是材料参数。
考虑到血管壁和纤维帽组织的材料属性在斑块进程中相对较稳定,而脂质池组织由于受炎症、内出血及微钙化等因素影响, 其材料属性变化较大,因此本文只考虑脂质池组织材料属性的变化影响,并分为以下 3 种情况：正常 (Case 1)、较硬 (Case 2) 和较软 (Case 3). 其中 材料参数按文献[4,5]取。
Case 1: $c_1=2$kPa, $c_2=0$, $D_1=2$Pa;Case 2: $c_1=3$kPa, $c_2=0$, $D_1=3$kPa,$D_2=1.5$; Case3: $c_1=1$kPa, $c_2=0$, $D_1=1$kPa,$D_2=1.5$. 图~3 所示为~3 种情况下的材料应力-拉伸曲线。
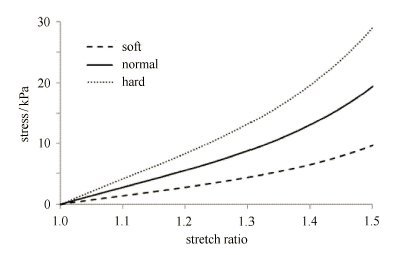显示原图|下载原图ZIP|生成PPT图 3斑块脂质池组织材料的应力 -- 拉伸曲线
-->Fig. 3Stress-stretch curves of lipid pool component
-->
2.3 控制方程与边界条件
动脉粥样硬化斑块的生物力学研究涉及管腔内的血流动力学及血管和斑块本身的结构动力学,是典型的流固耦合问题. 假设血管壁和 脂质池是超弹性、各向同性、不可压缩及均质的,则在动脉内压的作用下,其动力过程满足以下控制方程$\sigma _{ij,j}^{\rm S} = 0$ (2)
$\left. { d}^{\rm S}_j \right|_{\rm innerwall} = \left. { d}^{\rm f}_j \right|_{\rm innerwall} $ (3)
$\left. {\sigma _{ij,j}^{\rm S} \cdot n_j } \right|_{\rm innerwall} = \left. {\sigma _{ij,j}^{\rm f} \cdot n_j } \right|_{\rm innerwall} $ (4)
其中,${d}^{\rm S}_j$, ${d}^{\rm f}_j$, $\sigma _{ij,j}^{\rm S} $ 和 $\sigma _{ij,j}^{\rm f} $ 分别是固体和流体的位移和应力张量。
同时提出以下约束条件：对于血管的入口截面,给定径向、轴向和周向的线位移约束条件;对于出口截面,给定轴向位移的约束条件; 对于血管的外边界,由于受到外部组织的作用,因此实际上处于受约束和自由状态之间,其数学表达分别如式 (5) 和式 (6) 所示[26]. 本文考虑到血管本身具有较大的径向形变,因此按自由边界处理
$\left. { {d}^{\rm S}_j \cdot n_j } \right|_{\rm outerwall,fixed} = 0$ (5)
$\left. {\sigma _{ij,j}^{\rm S} \cdot n_j } \right|_{\rm outerwall,free} = 0 $ (6)
假设血液是不可压缩的黏性牛顿流体,在动脉管腔内作层流运动,则其控制方程为以下的任意拉格朗日 -- 欧拉描述的 Navier-Stokes 方程
$ \rho [\partial {\pmb u } / \partial t + (({\pmb u } - {\pmb u }_g ) \cdot \nabla ) {\pmb u} ] = - \nabla p + \mu \nabla ^2{\pmb u} $ (7)
$ \nabla \cdot {\pmb u} = 0$ (8)
$\left. {\pmb u} \right|_\varGamma = (0,0,0) $ (9)
式中,${\pmb u}$ 为流体速度, ${\pmb u}_{\rm g}$ 为网格速度, $p$ 是压力, $\rho $ 是流体密度,$\mu $ 是动力学黏度,$\varGamma$ 表示腔体内边界。
边界条件及求解方法如下[26-27]：利用测量的血液流量波按刚性直管脉动流的 Womersley 算法计算轴向速度分布作为入口速度边界条件进行 FSI 计算,获得速度场、血流剪切力 (flow shear stress, FSS ) 和压力差;利用测量的压力曲线作为入口压力边界和求得的压力差计算出口压力边界,再次进行 FSI 计算,求解 PSS。
对在体测量的流量波进行傅里叶变换
$Q(t) \approx \sum_{n = 0}^N B_n {\rm e}^{{\rm j}n\omega t}$ (10)
则根据 Womersley 算法,心动周期里的轴向速度分布$w(r,t)$为
$ w(r,t) = \dfrac{2B_0 }{\pi R_0^2 }\Big[1 - \Big(\dfrac{r}{R_0 }\Big)^2 \Big] + \dsum_{n = 1}^N \dfrac{B_n }{\pi R_0^2 }\Bigg[\Bigg(1 - \dfrac{{\rm J}_0 \Big (\alpha _n \dfrac{r}{R_0 }{\rm j}^{3 / 2}\Big )}{ {\rm J}_0 (\alpha _n {\rm j}^{3 / 2})}\Bigg) \Bigg / $
$ \qquad\Bigg (1 - \dfrac{2{\rm J}_1 (\alpha _n {\rm j}^{3 / 2})}{\alpha _n {\rm j}^{3 /2}{\rm J}_0 (\alpha _n {\rm j}^{3 / 2})} \Bigg) \Bigg] {\rm e}^{{\rm j}n\omega t} $ (11)
式中,$Q(t)$ 是流率;$N$ 是傅里叶变换的阶数,本文取~20; ${\rm j} = \sqrt { - 1} $;$\omega =2\pi / T$ 是角频率;$T$ 心动周期;$B_{n}$ 傅里叶系数;$R_{0}$ 动脉内半径;$\alpha _n $ 为~Womersley 数,且$\alpha_n = R_0 \sqrt {n\omega / \nu } $;$\nu $ 是血液的运动学黏度;${\rm J}_{0 }$ 和$ {\rm J}_{1}$分别是~0 阶和~1 阶的虚宗~Bessel 函数。
图 4为正常生理状态和 EECP 状态下心动周期里不同时刻点的入口速度剖面,用于进行后续的流场及 FSS 求解。
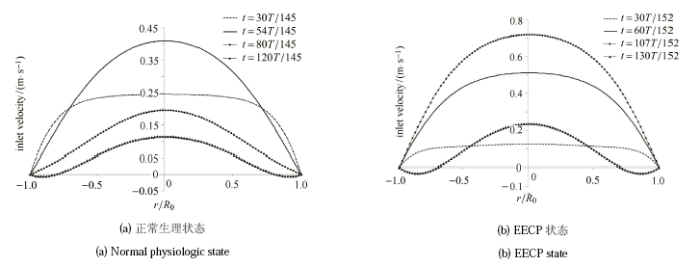显示原图|下载原图ZIP|生成PPT图 4心动周期不同时刻点的入口速度边界条件
-->Fig. 4Inlet velocity boundary conditions at different time points of cardiac cycle
-->
2.4 数值求解策略
本文分别建立血流流动模型和血管壁及斑块的结构动力模型,通过交界处定义流固耦合边界条件,建立 FSI 模型,进而采用有限 元软件 Adina 进行 FSI 模型的弱耦合求解. Adina 采用非结构化有限元方法求解流体和固体模型,采用非线性增量迭代方法处理 FSI 问题,结构和流体模型控制方程的有限 元求解均采用 Newton-Raphson 迭代法,达到二阶精度. 本文的求解网格按照 Huang 等 [5]的方案设置, 较好地兼顾独立性及计算量. 其中,流体模型为 18 800 单元;结构模型为 28 416 单元,具体如图 5 所示。
显示原图|下载原图ZIP|生成PPT图5计算网格图
-->Fig. 5Numerical mesh strategy
-->
3 计算结果
3.1 速度分布
图6为计算所得的管腔内血流速度分布 ($FC=600\mu m$,材料属性为 Case 2). 其中正常生理状态取$t=38 T /145$时刻 (收缩期 流量峰值点),EECP 状态取$t =107 T /152 $时刻 (舒张期流量峰值点)。 结果显示,由于受到局部斑块的影响, 动脉中最大的血流速度出现在狭窄的颈部,狭窄下游出现血液回流区. 正常生理状态和 EECP 状态下,血流速度的峰值分别为 57.71 cm/s 和 105.4 cm/s. 此外,EECP 作用明显提高了回流区的血流速度,上述 2 种情况下回流区的最大流速分别为 5.44 cm/s 和 18.95 cm/s。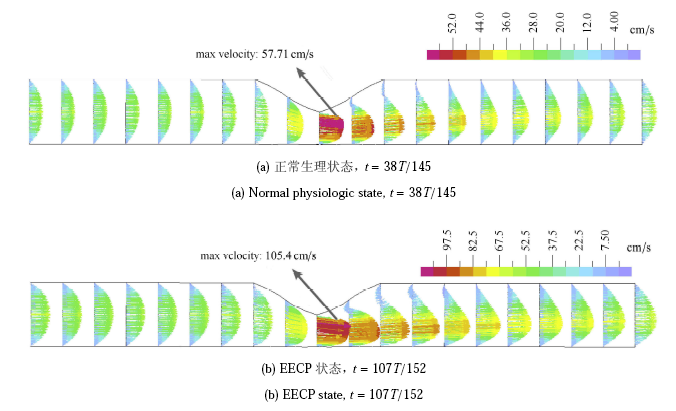
显示原图|下载原图ZIP|生成PPT图6血流速度分布($FC=600\mu $m,Case 2)
-->Fig. 6Blood velocity distributions. ($FC=600\mu $m,Case 2)
-->
3.2 FSS/WSS 分布
图7为 $FC=200 \mu m$,脂质池材料为 Case 1 时,正常生理状态 ($t=38T/145$) 和 EECP 状态 ($t=107T/152$) 下的 FSS/WSS 分布对比. 本文沿用文献[4,5] 的方法,采用最大流动剪切力表示 FSS,血管管腔表面处的 FSS 则为壁面切应力 WSS. 计算结果显示斑块位置的管腔狭窄部位是心动周期里 WSS 的高水平分布区域. 从图 7 可见,对于狭窄部位,纤维帽与管腔接触处的 WSS 水平明显高于管腔肩部及非斑块位置的 WSS 水平;WSS 的峰值 (max WSS, MWSS) 发生在局部狭窄区喉部横截面 (S5 截面) 上的狭窄顶点与管腔肩部之间的中部位置上,呈左右对称分布;在正常生理状态和 EECP 状态下,MWSS 计算值分别为 15.73 Pa 和 34.24 Pa。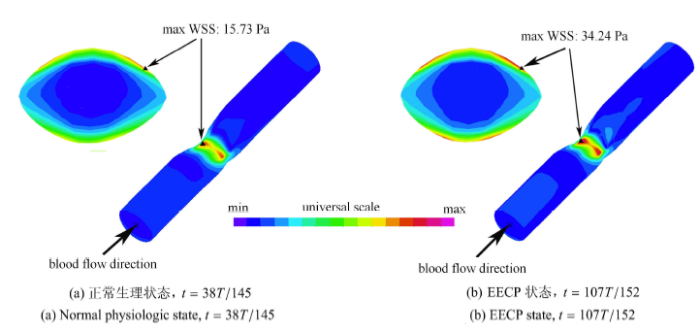
显示原图|下载原图ZIP|生成PPT图7局部狭窄段的 FSS/WSS 分布. $FC=200\mu $m,Case 1
-->Fig. 7FSS/WSS distributions at locally stenotic zone. $FC=200\mu $m,Case 1
-->
3.3 PWS 分布
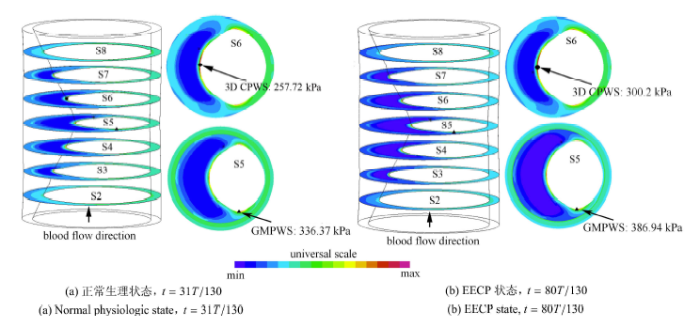
本文采用文献 [4,5] 的方法,以斑块壁面应力 (plaque wall stress, PWS) 代表 PSS,以斑块最大主应力 (stress-P1) 作为 PWS 计算值;将模型内最大的 PWS 定义为全局最大斑块壁面应力 (global max plaque stress, GMPWS);将斑块易损部位 (纤维帽) 处的最大 PWS 定义为临界斑块壁面应力 (3D CPWS)。图8为 $FC=65 \mu m$,脂质池材料为 Case 3 时正常生理状态($t=54T/145$) 和 EECP 状态 ($t=107T/152$) 下的动脉狭窄处的 PWS 分布图. 如图所示,在斑块区域,斑块的纤维帽处是心动周期里 PWS 分布水平较高的区域;而斑块的脂质池位置是 PWS 分布水平较低的区域。
GMPWS 发生在狭窄区喉部处横截面 (S5) 的肩部位置上. 在上述的 FC 厚度及斑块脂质池材料属性情况下,GMPWS 的计算值分别为 336.37 kPa(正常生理状态) 和 386.94 kPa (EECP 状态);3D CPWS 则发生在狭窄区喉部下游的 S6 截面处的纤维帽对称轴上 (如图 8 所示),其计算值分别为 257.72 kPa(正常生理状态) 和 300.2 kPa(EECP 状态). 表 1 为不同生理状态,不同斑块结构和斑块组成材料属性下的壁面切应力及斑块结构应力统计表. 其中,正常生理状态采用时间点为：$t=38T/145$(WSS) 和$t=54T/145$(PWS);EECP 状态采用时间点为 $t=107T/152$(WSS 和 PWS)。
显示原图|下载原图ZIP|生成PPT图 8局部狭窄部位的 PWS 分布图 ($FC=65 \mu m$,Case 3)
-->Fig. 8PWS distributions at locally stenotic zone ($FC=65 \mu m$,Case 3)
-->
Table 1
表1
表1流动切应力和斑块结构应力计算结果统计
Table 1Summary of flow shear stress and plaque wall stress
| Normal physiologic state | EECP state | |||||||
|---|---|---|---|---|---|---|---|---|
| Case 1 | Case 2 | Case 3 | Case 1 | Case 2 | Case 3 | |||
| FC=65$\mu$ m | MWSS/Pa GMPWS/kPa 3D CPWS/kPa | 15.73 336.71 206.92 | 15.72 337.12 170.43 | 15.76 336.37 257.72 | 34.28 386.43 241.21 | 34.19 386.15 193.65 | 34.56 386.94 300.20 | |
| FC=200$\mu$ m FC=600$\mu$m | MWSS/Pa GMPWS/kPa 3D CPWS/kPa MWSS/Pa GMPWS/kPa 3DCPWS/kPa | 15.73 354.18 100.29 15.72 364.48 95.99 | 15.72 353.00 99.80 15.71 363.30 95.95 | 15.75 355.55 100.86 15.73 365.69 96.04 | 34.24 404.51 113.77 34.15 412.91 108.92 | 34.16 402.81 113.20 34.10 411.57 108.86 | 34.48 406.42 114.41 34.30 414.26 108.99 | |
新窗口打开
统计结果显示,当局部狭窄的狭窄度一定时,动脉血流切应力 (FSS/WSS) 水平主要受心动周期里的血流灌注水平影响,当心动周期 里的最大血流率从正常生理状态的 174.9 mL/min 上升到 EECP 状态的 278.6 mL/min (提升 59.3%),MWSS 从 (15.74 $\pm$0.02) Pa 上升到 (34.34$\pm$0.19) Pa(提升达 118.1%$\pm$1.1%). FC 厚度和脂质池材料属性的变化对 WSS 水平的影响极为微小,各种情况下均不超过 1%。
动脉内压、FC 厚度和脂质池材料属性三者对斑块的结构应力的分布水平均有一定影响,其中尤以前两者为甚. 综合考虑各种 FC 厚 度和脂质池材料属性情况,当动脉内压峰值从正常生理下状态的 130.59 mmHg (1 mmHg=133.2 Pa) (收缩压) 提升到 EECP 状态下的 140.86 mmHg(舒张压),心动周期里的 GMPWS 和 3D CPWS 分布从 (351.82$\pm$12.19) kPa 和 (136.0$\pm$60.88) kPa 上升到 (401.33$\pm$11.75) kPa 和 (155.85$\pm$72.03) kPa。
晚期斑块的 FC 厚度是影响动脉 PWS 分布水平的另一个主要因素,但其对 GMPWS 和 3D CPWS 两者的影响特性是不同的,而且对后者的影响要明显大于前者. GMPWS 水平随着 FC 厚度的减少而呈下降趋势;与此相反的是 3D CPWS 随着 FC 厚度的减少而呈上升趋势. 当 FC 厚度从 600 m 减少到 200 m 和 65 m 时,GMPWS 分别下降：2.81%$\pm$0.04% 和 7.62%$\pm$0.4%(正常生理状况) 以及 2.05%$\pm$0.07% 和 6.4%$\pm$0.2%(EECP 状态);而 3D CPWS 则分别上升：4.50%$\pm$0.51% 和 120.51%$\pm$45.57%(正常生理状况) 以及 4.48%$\pm$0.5% 和 124.93%$\pm$48.86%(EECP 状态). 此外需要注意的是,当 FC 最薄 (65 m) 而同时脂质池材料最软 (Case 3) 时,斑块的 3D CPWS 达到极值：257.72 kPa(正常生理状态) 及 300.20 kPa(EECP 状态), 这与文献 [18,29] 的研究结论是吻合的。
仅当斑块的 FC 厚度为 65$\mu$ m 时,脂质池材料属性对 3D CPWS 水平有较为显著的影响,其他情况下这种影响极为微小. 当$FC=65 \mu m$,脂质池材料从较硬情况变成正常和较软情况时,斑块的 3D CPWS 水平分别提升 21.41% 和 51.22%(正常生理状态),以及 24.56% 和 55.02%(EECP 状态)。
4 结论与展望
本文计算的 MWSS, GMPWS 和 3D CPWS 位置分别是纤维帽边缘、管腔肩部和纤维帽中部,与 Verslius 等 [31]总结的斑块破裂发生的 3 种可能位置相吻合,因此我们推测这 3 种应力因子可能与晚期斑块进程及最终破裂均有一定的关联性. 同时本文的计算显示这 3 个重要的应力因子中只有 3D CPWS 显著受纤维帽厚度的影响,且与后者成负相关性关系;当纤维帽较薄 (FC=65 \mu m$) 时也只有 3D CPWS 显著受脂质池材料属性的影响. 由于纤维帽厚度及斑块组成的材料属性被普遍认为在晚期斑块进程及最终破裂中起着重要的作用[4,18,29-30],因此我们推测 3D CPWS 可能在晚期斑块进程及破裂中起着比其他两个因子更关键的作用.在 EECP 长达 30 年的临床应用中,尚未有其可能会增加粥样硬化斑块破裂等不良心血脑管急性事件发生风险的报道. 我们早前及本文的研究均显示 EECP 大幅提升了斑块局部的应力水平及应力在心动周期内的分布特性26-27,这是否会对斑块进程及重构产生慢性的影响,有何种影响,以及是否需要引起临床的重视,则需要作结合影像学观察的进一步深入研究。
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . |
| [12] | . |
| [13] | . . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . |
| [24] | . |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | . |
| [29] | . |
| [30] | . |
| [31] | . |
