中物院高性能数值模拟软件中心, 北京 100088; 北京应用物理与计算数学研究所, 北京 100088
ACCURATE COMPUTATION ON DYNAMIC SIFS USING IMPROVED XFEM
WenLongfei, WangLixiang, TianRong中图分类号:TB115,O346.1
文献标识码:A
通讯作者:
收稿日期:2018-01-30
接受日期:2018-04-12
网络出版日期:2018-06-10
版权声明:2018《力学学报》编辑部《力学学报》编辑部 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (16609KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引言
重大装备关键零部件冲击断[1]裂、强冲击下建筑物毁伤评估、作战设备冲击防护、高速冲击下材料层/断裂[2]、以及武器跌落与炸药低冲击起爆等应用问题中均涉及动力学裂纹扩展问题. 准确描述裂纹尖端附近应力奇异场, 对于裂纹起始时间与扩展速度评估尤为重要[3]. 其中, 动态应力强度因子(dynamic stress intensity factor, DSIF)作为线弹性断裂力学中裂纹尖端应力场与位移场的主要描述参数, 研究其计算方法, 分析其影响参数, 提高其计算精度有着重要的科学意义与工程价值.目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4]、多尺度有限元法[5]、边界元法(BEM) [6]、无网格法(MLM) [7]、扩展有限元法(XFEM) [8,9,10,11]、数值流形法(NMM) [12,13]、比例边界有限元法(SBFEM) [14]、相场模型(phase-field model) [15]、混合方法[16] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等.
传统FEM[4]模拟裂纹扩展时, 裂纹必须与网格对齐, 裂纹扩展步长依赖于网格尺寸, 为捕捉裂尖应力奇异性需要布置稠密网格, 裂纹扩展过程中需要不断重新划分网格等. 频繁的网格重分重映不仅使得计算实施繁琐, 同时引入大量映射误差, 导致算法在计算动力学问题时能量守恒性差. 因此, 裂纹扩展模拟成为传统有限元经典难题之一.
XFEM[8-11]因克服上述传统FEM困难而获得极大成功,目前已成为裂纹扩展模拟的主要方法之一. 然而, 在实际工程应用中, 该方法一直存在两大困扰: 一是源于单位分解插值的线性相关性[11-18], 当在局部或全求解域上进行插值强化时, 总体刚度矩阵高度病态[19-22]; 二是裂尖强化插值无法直接推广应用于动力学计算[23-26]. 其中第2个问题具体又体现在: (1) 裂尖额外自由度引起"零时间步长"问题——当裂纹位置逐渐靠近强化节点时, 单元的临界时间步长会趋于零[23-24]; (2) 裂尖额外自由度引起能量正确传递问题. "零时间步长"问题直到2009 年Elguedj等[24]提出裂尖质量集中技术才得以解决. 能量正确传递问题在于: 额外自由度对应的质量、速度和加速度项均与裂尖位置历史相关; 当裂尖离开单元时, 如果简单地舍弃原有裂尖强化自由度, 两个时间步之间的能量无法正确传递, 会破坏能量守恒原则[23,25-26]. 这一问题长期困扰XFEM在动力学问题中的应用[23].
为克服XFEM上述两大困难, 笔者提出一种无裂尖额外自由度、条件性态良好的改进型扩展有限元法[27,28,29,30,31,32], 并将其用于静、动力学裂纹扩展分析. 该方法消除了裂尖额外自由度, 解决了现有XFEM线性依赖性和总体方程病态问题, 总体刚度矩阵条件数恢复了h-2 (XFEM为h-6) 变化的性质. 同时, 由于没有裂尖额外自由度, 裂尖单元的质量集中、零时间步长及能量正确传递问题均得到解决.
目前国内关于动力学裂纹扩展的研究尚少. 江守燕等[11]使用XFEM对稳定裂纹的DSIF进行分析; 杨永涛等[12] 基于NMM分析了稳定裂纹的DSIF; 刘鹏等[33]研究压电材料中裂纹的DSIF计算方法; 刘学聪等[34]给出一种新型裂尖加强函数用于显式动态裂纹分析, 将节点的奇异附加自由度由8 个减少为2个. 更多内容, 可参考庄茁等[35] 与余天堂[36]的XFEM专著. 目前中文文献中对DSIF 的分析还多集中于稳定裂纹, 很少见之于扩展裂纹. 即便考虑裂纹扩展, 也未考虑裂纹扩展速度的影响.
有鉴于此, 本文基于改进型XFEM, 采用Newmark隐式算法进行时间积分, 重点研究动力学扩展裂纹应力强度因子的求解方法, 特别地, 考虑裂纹扩展速度项与惯性项的影响. 通过数值算例研究网格单元尺寸、质量矩阵、时间步长、裂尖加强区域、惯性项、速度项及相互作用积分区域J-domain的网格与单元尺寸对DSIF求解精度的影响, 验证改进型XFEM计算动态裂纹的应力强度因子的精度问题, 并与常规XFEM计算结果进行对比.
1 动力学问题的改进型扩展有限元方法
1.1 动力学控制方程
对于计算域内每一点, 应满足应力平衡方程$\begin{equation}\nabla\cdot{\sigma}+{b}= \rho\dfrac{\partial^2{u}}{\partial t^2}, {in} \varOmega \end{equation}$ (1)
式中, ${\sigma}$为柯西应力张量, ${b}$为单位体积的体力, $\rho$为密度, ${u}$ 为位移, $t$ 为时间.
对于线弹性体, 应力?应变关系为
$\begin{equation} {\sigma}={D}:{\varepsilon} \end{equation}$ (2)
式中,D为弹性矩阵.
几何关系为
$\begin{equation} {\varepsilon}=\nabla_s{u} \end{equation}$ (3)
边界条件为
$\begin{equation}\left. \begin{split} {u}=\bar{{u}}({x},t), {on} {\Gamma}_{{u}} \\ {\sigma}\cdot{n}=\bar{ t}({x},t), {on} {\Gamma}_{{t}} \\ {\sigma}\cdot{n}= 0, {on} {\Gamma}_{{c}} \end{split}\right\} \end{equation}$ (4)
式中, ${n}$为单位外法向量, ${\bar{u}}$和${{\bar t}}$分别表示位移边界$ {\Gamma}_{u}$上的约束和应力边界$ {\Gamma}_{t}$ 上的约束, $ {\Gamma}_{c}$ 为裂纹面.
初始条件为
$\begin{equation}\left. \begin{split} {u}({x},t=0)=\bar{{u}}(0) \\ {\dot u}({x},t=0)={\dot{\bar{u}}}(0) \end{split}\right\} \end{equation}$ (5)
式中, ${\bar{u}}$(0) 和${\dot{\bar{u}}}$(0) 分别表示初始位移和速度.
1.2 改进型扩展有限元法
1.2.1 常规扩展有限元法常规XFEM的位移逼近为
$\begin{equation} \begin{split} u^h({x})=\sum_{i\in N}N_iu_i+\sum_{i\in K}N_i(H({x})-H({x}_i))d_i+ \\ \sum_{i\in T}N_i\sum_k\big(\varphi_k({x})-\varphi_k({x}_i)\big)\alpha_{ki} \end{split} \end{equation}$ (6)
其中, $N$为所有节点集, $K$为阶跃函数加强节点集, $T$为裂尖加强节点集, 节点加强方式如图1所示. ${d_i}$ 为阶跃加强自由度, ${a_{ki}}$为裂尖加强自由度, $H({{x}})$为Heaviside 函数, $\varphi ({{x}})$为裂尖奇异性加强函数, 其表达式为
$\begin{equation}H({x})=\begin{cases} 1, & f({x},t)\geqslant0 \\ -1, & f({x},t)<0 \end{cases}\end{equation}$ (7)
$\varphi({x})=\phi(r,\theta)=\Big\{\sqrt r {sin}(\theta/2),\sqrt r {cos}(\theta/2),\\ \sqrt r {sin}(\theta/2){sin}(\theta),\sqrt r {cos}(\theta/2){sin}(\theta) \Big\}$ (8)
$f({x},t)$为t时刻的裂纹面水平集.
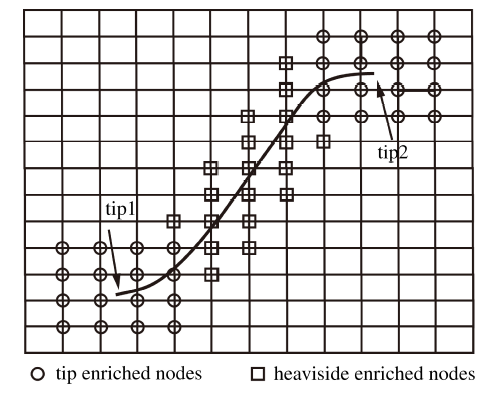显示原图|下载原图ZIP|生成PPT图1任意裂纹问题
-->Fig.1Arbitrary crack problem
-->
1.2.2 改进型扩展有限元法
改进型XFEM基于无额外自由度单位分解法[27], 消除了裂尖额外自由度, 可以达到最优收敛且整体方程条件属性良好[28,29,30,31,32], 其位移逼近可表示为如下形式
$\begin{equation} \begin{split} u^h( x)=\sum_{i\in I}N_iu_i+\sum_{i\in K}N_i\big(H( x)-H( x_i)\big)d_i+ \\ \sum_{i\in T}\left[N_i( x)\left \lgroup\sum_{k\in I_{i}}\phi^i_k( x)u_k\right\rgroup\right] \end{split} \end{equation}$ (9)
其中, $I$为非裂尖加强节点集, 即标准有限元节点和阶跃加强节点的合集; $T$为裂尖加强节点合集; ${u_i}$与${u_k}$为常规有限元自由度, ${d_i}$为阶跃加强自由度; $\phi_k^i({{x}})$为定义在节点$i$的``节点局部影响域''$P_{i}$上的局部逼近函数, $P_{i}$为距离节点$i$ 一定范围内所有单元组成的单元集, 如图2所示. ${I_i} = \{ k \in I:{x_k}\in {P}_i^{}\}$为节点$i$ 的节点局部影响域$P_{i}$ 上节点编号集合,${J_i} = \{ k \in I:{x_i} \in {P}_k^{}\} $为包含节点$i$ 的节点局部影响域编号集合. 显然, ${I_i}$ 和${J_i}$ 两个集合完全相同,分开定义是只是为了明确逻辑关系.
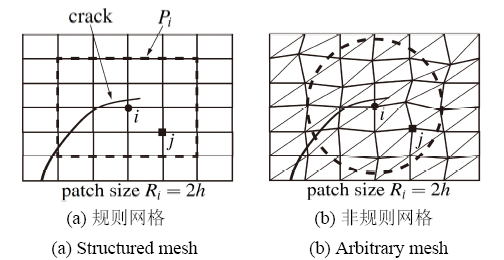显示原图|下载原图ZIP|生成PPT图2单元片的定义
-->Fig.2Definition of nodal patch
-->
在
$\phi^i_k( x)= p^{T}( x)\Bigg[ A^{-1} p_k-\dfrac{( A^{-1} p_i)( p^{T}_i A^{-1})}{ p^{T}_i A^{-1} p_{i}} p_k+ \dfrac{ A^{-1}{ p}_{i}}{ p^{T}_i{ A}^{-1} p_i}\delta_{ik}\Bigg]$ (10)
${A}=\sum _{k\in I_i} {{p}}_k{{p}}_k^{T}$ (11)
${p}({x})=\left[1,\dfrac {x-x_i}{R_i},\dfrac {y-y_i}{R_i},\dfrac{\varphi({x})-\varphi({x}_i)}{\sqrt{R_i}}\right]^{T}$ (12)
其中, $\delta $为Kronecker delta函数, ${{p}_{k}} ={p}({x}_{k})$ , $R_{i}$代表节点局部影响域$P_{i}$ 的尺寸, $\varphi({{x}})$为裂尖奇异性加强函数, 见式(8). 由于, ${{p}_{i}} = \left[ {1,{\rm{ }}0,{\rm{}}0,{\rm{ }}\cdots,{\rm{ }}0} \right]$, 故式(10)可写为如下形式
$\begin{equation} \phi^i_k({x})={p}^{T}({x})\left\lgroup {A}^{-1}{p}_k-\dfrac{1}{{A}^{-1}_{11}}{A}^{-1}_{(1)}{A}^{-T}_{(1)}{p}_k+\dfrac{1}{{A}^{-1}_{11}}{A}^{-1}_{(1)}\delta_{ik}\right\rgroup \end{equation}$ (13)
其中, ${{A}}_{(1)}^{ - 1}$为${{A}}_{}^{ - 1}$的第1列, ${{A}}_{11}^{-1}$ 为${{A}}_{(1)}^{-1}$的第1个元素.
通过与常规扩展有限元法(式(6))对比可知, 改进型XFEM在裂尖加强区域通过周围有限元节点构造奇异性高阶逼近(对应式(9)中最后一项),消除了常规XFEM的裂尖额外自由度${a_{ki}}$.
由于无裂尖加强自由度, 改进型XFEM在动力学计算中, 裂尖加强单元可以直接采用标准有限元的集中质量矩阵; 同样, 由于无裂尖相关额外自由度,故无需常规XFEM为保证裂尖额外自由度上能量正确传递的特殊处理(动态裂纹扩展中)[29,30,31].
1.3 基于改进型XFEM的控制方程离散
由含裂纹结构体动力学控制方程及改进型扩展有限元位移逼近, 运用虚功原理, 可得如下控制方程离散形式$\begin{equation} \begin{bmatrix} {M}^{uu} {M}^{ud}\\{M}^{du} {M}^{dd} \end{bmatrix} \begin{pmatrix} {\ddot{u}}\\ {\ddot{d}} \end{pmatrix}+ \begin{bmatrix} {K}^{uu} {K}^{ud}\\{K}^{du} {K}^{dd} \end{bmatrix} \begin{pmatrix} {u}\\ {d} \end{pmatrix}= \begin{pmatrix} {F}^u\\ {F}^d \end{pmatrix} \end{equation}$ (14)
其中
${K}^{rs}_{ij}=\int_ {\Omega}\left({B}^r_i\right)^{T}{D}({B}^s_j)d {\Omega}$ (15)
${M}^{rs}_{ij}=\int_ {\Omega}\rho({N}^r_i)^{T}{N}^s_jd {\Omega}$ (16)
${F}^u_i=\int_{ {\Gamma}^t_0}{\tilde{N}}_i^{T}{\bar{t}}_{i0}{d} {\Gamma}+\int_ {\Omega}{\tilde{N}}^{T}_i{b}_i{d} {\Omega}$ (17)
${F}^d_i=\int_{ {\Gamma}^t_0}\tilde{H}{\tilde{N}}^{T}_i{\bar{t}}_{i0}{d} {\Gamma}+\int_ {\Omega}\tilde{H}{\tilde{N}}^{T}_i{b}_i{d} {\Omega}, i\in K$ (18)
其中, ${B}$为应变矩阵, 对于常规自由度为${B_{i}^{u}}$, 对于阶跃加强自由度为${B_{i}^{d}}$, 具体形式如下所示
${B}^u_i=\begin{bmatrix}{\Phi}_{i,x} & 0\\0 & {\Phi}_{i,y}\\ {\Phi}_{i,y} & {\Phi}_{i,x} \end{bmatrix}, {\Phi}= \begin{cases} \tilde{N}, i\in I \\ \sum_{k\in J_i}~\tilde{N}_k\phi^k_i, i\in T \end{cases}$ (19)
${B}^d_i= \begin{bmatrix} \left(\tilde{N}_i\tilde{H}\right)_{i,x} & 0\\ 0 & \left(\tilde{N}_i\tilde{H}\right)_{i,y}\\ \left(\tilde{N}_i\tilde{H}\right)_{i,y} & \left(\tilde{N}_i\tilde{H}\right)_{i,x} \end{bmatrix}$ (20)
其中, ${{D}}$为弹性矩阵, $\tilde H = H({{x}}) - H({{{x}}_i})$ , ${\tilde N_i}$为经过混合单元修正后的有限元形函数, 限于篇幅, 详细内容可参见文献[31].
1.4 Newmark时间积分
选取Newmark法作为改进型XFEM的隐式时间积分算法. 在第n+1时间步, 空间和时间离散方程如下${\dot{U}}_{n+1}={\dot{U}}_n+\Delta t(1-\beta){\ddot{U}}_n+\Delta t\beta{\ddot{U}}_{n+1}$ (21)
${U}_{n+1}={U}_n+\Delta t{\dot{U}}_n+\Delta t^2\left(\dfrac{1}{2}-\alpha\right){\ddot{U}}_n+\Delta t^2\alpha{\ddot{U}}_{n+1}$ (22)
${\tilde{K}U}_{n+1}=\Delta{\tilde{P}}$ (23)
${\tilde{K}}={K}+\dfrac{1}{\alpha\Delta t^2}{M}$ (24)
$\Delta{\tilde{P}}=\Delta {P}+\bigg[\bigg\lgroup\dfrac{1}{2\alpha}-1\bigg\rgroup{\ddot{U}}_n+\dfrac{1}{\alpha\Delta t}{\dot{U}}_n\bigg]{M}$ (25)
其中, ${U}$, ${{\dot U}}$, 和${{\ddot U}}$分别表示节点位移、速度和加速度, $\Delta t$ 为当前时刻的时间步长. $\alpha$ 和 $\beta$为Newmark参数, 当 $\alpha\geqslant 0.5$, $\beta \geqslant 0.25{\left( {\alpha+0.5}\right)^2}$ 时, Newmark法计算是稳定的. 本文取$\alpha=1/4$, $\beta=1/2$.
2 动态扩展裂纹的应力强度因子计算
动态应力强度因子作为表征动载作用下裂纹尖端应力?应变场奇异程度的重要参量, 是裂纹扩展趋势或裂纹扩展驱动力的度量, 是判断裂纹起始与裂纹扩展速度的重要依据.2.1 动力学问题相互作用积分
相互作用积分方法具有精度高、适应范围广(弹性、塑性、温度、接触等问题)的特点, 在应力强度因子求解中被广泛使用. 目前国内文献对相互作用积分的应用还多集中于静力学裂纹和动态稳定裂纹, 关于动态扩展裂纹的相互作用积分与其辅助场函数构造的文献较少.对于线弹性各向同性材料, 动态相互作用积分可表述为[25]
$\begin{equation}\begin{split}I^{{int}}=\int_A\begin{bmatrix}\begin{pmatrix}\sigma ^{{aux}}_{ij}u^{{real}}_{i,k}+\sigma^{{real}}_{ij}u^{{aux}}_{i,k} \end{pmatrix}-W^{({real,aux})}\delta_{kj}\end{bmatrix}q_{k,j}{d}S+ \\ \int_A\rho\ddot{u}^{{real}}_iu^{{aux}}_{i,k}q_{k}{d}S+\int_A\rho\dot{u}^{{real}}_l\dot{u}^{{aux}}_l\delta_{kj}q_{k,j}{d}S+ \\ \int_A\begin{bmatrix}\sigma^{{aux}}_{ij,j}u_{i,k}+\rho\begin{pmatrix}\dot{u}^{{aux}}_i\dot{u}^{{real}}_{i,k}+\dot{u}^{{real}}_i\dot{u}^{aux}_{i,k}\end{pmatrix}\end{bmatrix}q_k{d}S\end{split}\end{equation}$ (26)
其中, $\left( {\sigma _{ij}^{{\rm{real}}},\varepsilon _{ij}^{{\rm{real}}},u_i^{{\rm{real}}}} \right)$为真实场, $\left( {\sigma _{ij}^{{\rm{aux}}},\varepsilon _{ij}^{{\rm{aux}}},u_i^{{\rm{aux}}}} \right)$为动力学裂纹辅助场; $W_{}^{({\rm{real, aux}})} = \sigma _{ij}^{{\rm{real}}}\varepsilon _{ij}^{{\rm{aux}}} = \sigma _{ij}^{{\rm{aux}}}\varepsilon _{ij}^{{\rm{real}}}$为相互作用积分应变能密度; $A$是相互作用积分区域, 为了精确计算应力强度因子, 相互作用积分区域采用图3所示的环绕裂纹尖端的$4\times4$个额外单元, 又称为[25-26, 38-42]. 这些单元仅用于计算动态相互作用积分, 独立于原计算网格, 且跟随裂纹尖端移动; $q$ 为虚拟裂纹扩展场, 其方向平行于裂纹表面
$\begin{equation}q=\begin{cases}0,&{outside A}\\ 1,&{at crack tip}\\ {linear,}&{inside A} \end{cases} \end{equation}$ (27)
(27) 式(26)中第1项为静力学裂纹的相互作用积分公式, 第2项为动力学稳定裂纹分析所考虑的惯性项贡献[11-12,33], 后两项这里称为扩展速度贡献项.
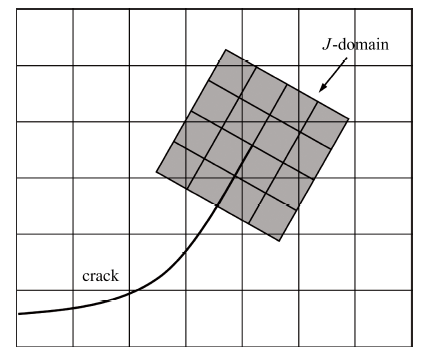显示原图|下载原图ZIP|生成PPT图3相互作用积分
-->Fig.3Interaction integral
-->
对于二维平面应变问题, 该能量释放率与动态应力强度因子关系为
$\begin{equation} I^{{int}}=\dfrac{2(1-v^2)}{E}(f_1(\dot{a})K^{{dyn}}_{I}K^{{aux}}_{I}+f_2(\dot{a})K^{{dyn}}_{{II}}K^{{aux}}_{{II}}) \end{equation}$ (28)
其中,
$\begin{equation}\left.\begin{split} &f_i(\dot{a})=\dfrac{4\alpha_i(1-\alpha^2_j)}{(\kappa+1)D} \\ &\alpha_{d}=\sqrt{1-\bigg(\dfrac{\dot{a}}{c_{d}}\bigg)^2},~ \alpha_{s}=\sqrt{1-\bigg(\dfrac{\dot{a}}{c_{s}}\bigg)^2} \\ &D=4\alpha_{d}\alpha_{s}-(1+\alpha^2_{s})^2 \end{split}\right\} \end{equation}$ (29)
其中,
$\begin{equation} c_{d}=\sqrt{\dfrac{\lambda+2\mu}{\rho}},~c_{s}=\sqrt{\dfrac{\mu}{\rho}} \end{equation}$ (30)
$D$ 是关于裂纹扩展速度$\dot{a}$ 的函数, $\lambda$和$\mu$为拉梅常数. 当裂纹扩展速度等于瑞雷波速${c_{r}}$ 时, $D(\dot{a})=0$.
通过选择合适的裂纹辅助场, 可以得到不同的应力强度因子. 当$K_{\rm{I}}^{{\rm{aux}}} = 1$, $K_{{\rm{II}}}^{{\rm{aux}}} =0$ , 可以直接求得真实裂纹尖端场的I型分量 $K_{\rm{I}}^{{\rm{dyn}}}$. 同理, 当$K_{\rm{I}}^{{\rm{aux}}} =0$, $K_{{\rm{II}}}^{{\rm{aux}}} = 1$, 可以直接求得$K_{{\rm{II}}}^{{\rm{dyn}}}$ .
2.2 动力学问题裂纹辅助场
本节将给出计算动态应力强度因子用到的所有辅助场信息, 对Freund[37]和Réthoré等[25]的相关工作进行推导和总结. 限于篇幅, 本文仅以I型裂纹为例.以裂纹尖端为原点建立坐标系, 裂纹扩展方向为$x$轴正向, 假设扩展速度为 $\dot a$, 则坐标系内任一点 $P(x,y)$的坐标可表示为
$\begin{equation} \bar{x}=x-\dot{a}t, \bar{y}=y \end{equation}$ (31)
定义
$\begin{equation} \left. \begin{split} r_{d}=\sqrt{\bar{x}^2+\alpha^2_{d}\bar{y}^2}, \theta_{d}={tan}^{-1}\left(\alpha_{d}\bar{y}/\bar{x}\right) \\ r_{s}=\sqrt{\bar{x}^2+\alpha^2_{s}\bar{y}^2}, \theta_{s}={tan}^{-1}\left(\alpha_{s}\bar{y}/\bar{x}\right) \end{split} \right\} \end{equation}$ (32)
则可以得到裂纹尖端位移场与应力场为
$\begin{equation}\left. \begin{split} u_1=&2C_{I}\left[\left(\alpha^2_{s}+1\right)\sqrt{r_{d}}~{cos}\left(\theta_{d}/2\right)-\right.\\ &\left.2\alpha_{d}\alpha_{s}\sqrt{r_{s}}~{cos}\left(\theta_{s}/2\right)\right] \\ u_2=&2C_{I}\left[-\alpha_{d}\left(\alpha^2_{s}+1\right)\sqrt{r_{d}}~{sin}\left(\theta_{d}/2\right)+\right.\\ &\left.2\alpha_{d}\sqrt{r_{s}}~{sin}\left(\theta_{s}/2\right)\right] \\ C_{I}=&K^{dyn}_{I}\bigg/\left(\mu D\sqrt{2\pi}\right) \end{split} \right\} \end{equation}$ (33)
$\begin{equation} \left. \begin{split} \sigma_{11}=&\mu C_{I}\left[\left(\alpha^2_{s}+1\right)\right.\left(2\alpha^2_{d}-\alpha^2_{s}+1\right)~{cos}\left(\theta_{d}/2\right)\big/\sqrt{r_{d}}- \\ &\left.4\alpha_{d}\alpha_{s}~{cos}\left(\theta_{s}/2\right)\big/\sqrt{r_{s}}\right] \\ \sigma_{22}=&\mu C_{I}\left[-\left(\alpha^2_{s}+1\right)^2~{cos}\left(\theta_{d}/2\right)\big/\sqrt{r_{d}}+\right. \\ &\left.4\alpha_{d}\alpha_{s}~{cos}\left(\theta_{s}/2\right)\big/\sqrt{r_{s}}\right] \\ \sigma_{12}=&\mu C_{I}\left[2\alpha_{d}\left(\alpha^2_{s}+1\right){sin}\left(\theta_{d}/2\right)\big/\sqrt{r_{d}}-\right. \\ &\left.2\alpha_{d}\left(\alpha ^2_{s}+1 \right){sin}\left(\theta_{s}/2\right)\big/\sqrt{r_{s}}\right] \end{split} \right\} \end{equation}$ (34)
由式(31)和式(32)可得
$\begin{equation} \left. \begin{split} &\partial r_i/\partial x={cos}\theta_i, \partial\theta_i/\partial x=-{sin}\theta_i/r_i \\ &\partial r_i/\partial y=\alpha_i~{cos}\theta_i, \partial\theta_i/\partial y=\alpha_i~{cos}\theta_i/r_i \\ &\partial x/\partial t=-\dot{a}, \partial y/\partial t=0, \end{split} \right\} \end{equation}$ (35)
则裂纹尖端速度场
$\begin{equation} \left. \begin{split} \dot{u}_1=&-\dot{a}C_{I}\left[\left(\alpha^2_{s}+1\right){cos}\left(\theta_{d}/2\right)\big/\sqrt{r_{d}}-\right. \\ &\left.2\alpha_{d}\alpha_{s}{cos}\left(\theta_{s}/2\right)\big/\sqrt{r_{s}}\right] \\ \dot{u}_2=&-\dot{a}C_{I}\left[\alpha_{d}\left(\alpha^2_{s}+1\right){sin}\left(\theta_{d}/2\right)\big/\sqrt{r_{d}}-\right. \\ &\left.2\alpha_{d}~{sin}\left(\theta_{s}/2\right)\big/\sqrt{r_{s}}\right] \end{split} \right\} \end{equation}$ (36)
同理, 由式(33)~式(35)可得位移和应力偏导场$u_{i,k}$ 与 $\sigma _{ij,k}$.
2.3 动力学问题裂纹扩展准则
在动力学分析中等效动态应力强度因子可表述为[34,35,36,37,38]$\begin{equation} K_{\theta\theta}={cos}^3\left\lgroup\dfrac{\theta_{c}}{2}\right\rgroup K^{\rm{dyn}}_{I}-\dfrac{3}{2}{cos}\left\lgroup\dfrac{\theta_{c}}{2}\right\rgroup{sin}(\theta_{c})K^{\rm{dyn}}_{{II}} \end{equation}$ (37)
Freund[37,45]给出了如下等效动态应力强度因子与裂纹扩展速度的关系式
$\begin{equation} \dot{a}= \begin{cases} 0, & K_{\theta\theta}<K_{\rm{IC}} \\ c_{r}\left\lgroup1-\left\lgroup\dfrac{K_{\rm{IC}}}{K_{\theta\theta}} \right\rgroup^2\right\rgroup, & {otherwise} \end{cases} \end{equation}$ (38)
其中, $c_{r}$为瑞雷波速, ${K_{IC}}$ 为材料断裂韧度. Freund与合作者 [45,46,47]通过实验验证了该公式的正确性. 假设每个时间步中裂纹扩展速度不变, 则裂纹扩展步长可近似表述为$\Delta a = \dot a\Delta t$ , 其中$\Delta t$ 是每一步的时间步长. 裂纹的扩展方向可以根据最大周向应力准则得到
$\begin{equation} \theta_{c}=2~{arctan}\left\{\dfrac{1}{4}\left[\dfrac{K^{\rm{dyn}}_{I}}{K^{\rm{dyn}}_{{II}}}-{sign}\left(K^{\rm{dyn}}_{{II}}\right)\sqrt{8+\left\lgroup\dfrac{K^{\rm{dyn}}_{I}}{K^{\rm{dyn}}_{{II}}}\right\rgroup^2 } \right]\right\} \end{equation}$ (39)
3 算例
3.1 受拉半无限大板
含I型裂纹的受拉的半无限大板问题是动态强度因子精度分析的经典算例 [11-12, 23-25, 29, 38-43]. 问题模型如图4 所示, 板长$L=10 {m}$, 高H = 2 m, 裂纹长度$a=5 {m}$, 材料密度$\rho = 8000 {kg/m}^{3}$, E = 210 GPa, v = 0.3. 平面应变假设. 在t = 0 时刻, 板上缘受到突然施加大小为$\sigma_{0} = 500 {kPa}$ 均布拉应力作用. 该问题的动态应力强度因子解析解为[37]$\begin{equation} K^{\rm{dyn}}_{I}(t)= \begin{cases} 0, & t<t_{c} \\ \dfrac{1-\dot{a}/c_{r}}{1-\dot{a}/2c_{r}}\dfrac{2\sigma_0}{1-\mu}\sqrt{\dfrac{c_{d}(t-t_{c})(1-2\mu)}{{\pi}}}, & t\geqslant t_{c} \end{cases} \end{equation}$ (40)
其中, $\dot a$ 是裂纹的瞬时扩展速度, ${t_{c}} = H/{c_{d}}$ 为应力波从梁上缘到达裂尖的时间. 若无特别说明在本论文中裂尖强化区域半径 ${R^{tip}} = 1.0h$, J-domain 区域网格为4×4, J-domain单元尺寸$h_J=1.0h$, h为网格单元尺寸, 总模拟时间t = 1.0 ms.
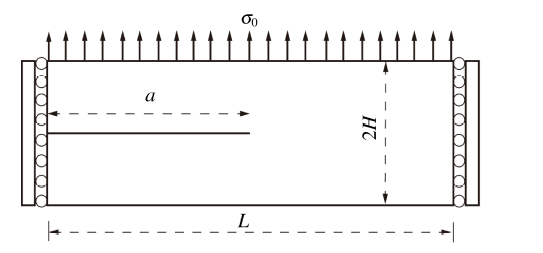显示原图|下载原图ZIP|生成PPT图4含I型裂纹的受拉半无限大板
-->Fig.4Geometry and loading for mode I semi-infinite crack problem
-->
3.1.1 裂纹保持稳定
(1) 网格尺寸对DSIF的影响
采用如下3种的网格, 分别为19×39, 29×59和39×79, 计算时间步长取为$\Delta t$ = 10µs, 一致质量矩阵. 图5 给出了3种网格下应力强度因子随时间变化曲线. 由图可知: (1) 在网格较稀疏的情况下, 改进型XFEM可以获得较高的计算精度; (2) 随着网格的加密, 动态应力强度因子值越来越逼近解析解, 有着良好的收敛性.
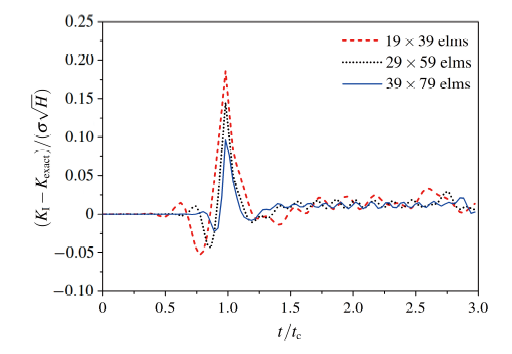显示原图|下载原图ZIP|生成PPT图5稳定裂纹动态应力强度因子随单元尺寸变化
-->Fig.5DSIF vs. element size
-->
(2) 裂尖强化区域对DSIF的影响
如图6所示, 考虑5种不同的裂尖强化区域半径, $R^{tip}$取值范围为1.0h~3.0h(小于1.0h 不能满足最小二乘插值节点个数, 大于3.0h结果偏差较大), 离散网格取$29\times 59$, 计算时间步长取$\Delta t=10 {µ}s$ , 一致质量矩阵. 图6 给出了不同裂尖加强区域下动态应力强度因子的变化情况. 由图6可知: (1) 当裂尖强化区域半径小于2.0h 时, DSIF 对解析解逼近得越好; 当$R^{tip}<1.7h$ 时, 随强化区域增大, 精度提高; (2) 当强化区域半径大于$2.0h$ 时, 裂尖强化区域增大, DSIF 精度变差. 这是因为裂尖强化区域面积太大, 而真实裂尖场影响域相对裂纹长度是很小的. 根据笔者分析, $R^{tip}$ 的取值为$1.0h \sim 2.0h$ 时可以获得较好的结果.
(3) 时间步长对DSIF的影响
离散网格取为19×39, 时间步长分别取为1 µs, 2µs, 5µs, 10µs, 20µs, 50µs, 一致质量矩阵. 不同时间步长对应DSIF 的误差变化曲线见图7. 从图7可以看出, 随着时间步长的减小, 数值解越来越逼近解析解. 但是当时间步长小于一定数值时(在网格19×39 下约为10µs, 时间步长的变化对精度影响很小. 同时较小的时间步长会导致更长的计算时间. 因此在实际应用中要同时兼顾计算效率与计算精度.
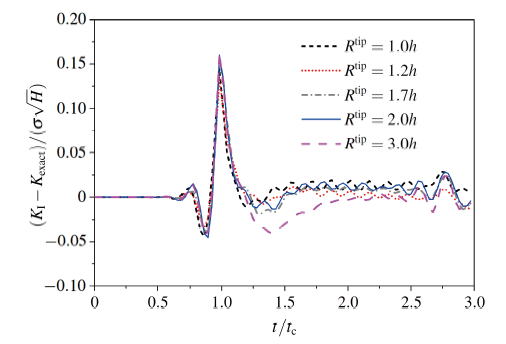显示原图|下载原图ZIP|生成PPT图6稳定裂纹动态应力强度因子随裂尖加强区域变化
-->Fig.6DSIF vs. tip enriched area
-->
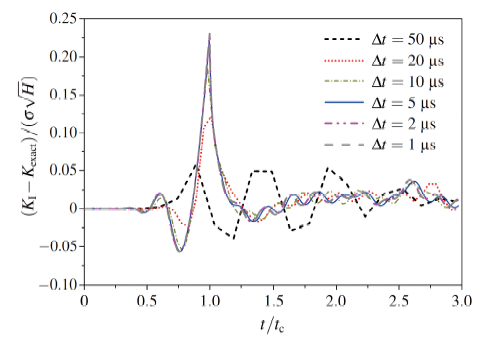显示原图|下载原图ZIP|生成PPT图7稳定裂纹动态应力强度因子随时间步长变化
-->Fig.7DSIF vs. critical time step size
-->
(4) 集中质量与一致质量对DSIF的影响
离散网格取为29×59, 时间步长取为$\Delta t$=10 µs, 考虑一致质量矩阵与集中质量矩阵对DSIF的影响, 结果如图8 所示. 集中质量矩阵的计算效率要高于一致质量矩阵, 两者的DSIF平均误差相差不大, 当选用集中质量矩阵时, 在t=tc时刻作用, 误差小于一致质量矩阵, 之后随时间延长, 数值震荡要稍大于一致质量结果.
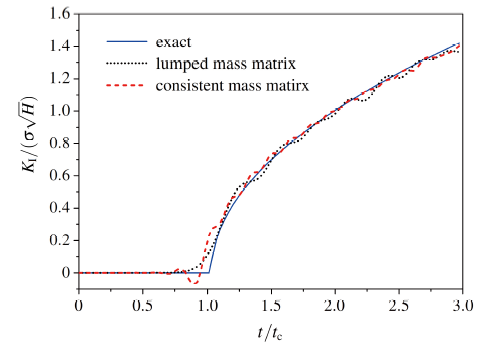显示原图|下载原图ZIP|生成PPT图8质量矩阵对DSIF的影响
-->Fig.8The effect of mass matrix on the DSIF
-->
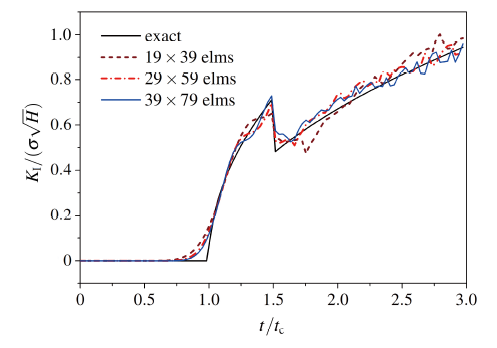
3.1.2 裂纹先稳定后扩展
对于图4所示问题, 裂纹在t=1.5tc 之前保持稳定, 之后以1500 m/s的速度匀速扩展.
(1) 网格尺寸对DSIF的影响
采用3种不同密度的网格, 分别为19×39, 29×59和39×79, 计算时间步长取为
显示原图|下载原图ZIP|生成PPT图9先稳定后扩展裂纹动态应力强度因子随单元尺寸变化
-->Fig.9DSIF vs. element size
-->
(2) 惯性项与扩展速度项对DSIF的影响
惯性项与扩展速度项是动力学裂纹应力强度因子求解与静力学的主要区别. 图10给出了对应不考虑和考虑惯性项、扩展速度项时DSIF 的误差随时间的变化曲线, 其中Case A为不考虑惯性项与扩展速度项, 对应式(18) 第1 项; Case B 为仅考虑惯性项影响, 对应式(18) 中第1和第2项; Case C为仅考虑惯性项影响, 即式(18)中第1和第2项, 同时动态相互作用积分与动态应力强度因子的关系式(式(28))改为采用如下稳定裂纹关系式
$\begin{equation}I^{\rm{int}}=\dfrac{2(1-v^2)}{E}\left(K^{\rm{dyn}}_{I}K^{\rm{aux}}_{I}+K^{\rm{dyn}}_{\rm{II}}K^{\rm{aux}}_{\rm{II}}\right)\end{equation}$ (41)
CaseD为考虑惯性项与扩展速度项, 对应式(18)所有项.
离散网格取为39×79, 时间步长取为
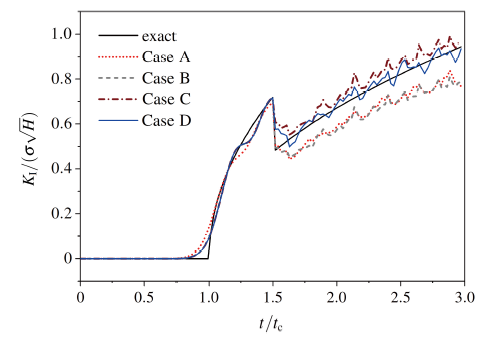显示原图|下载原图ZIP|生成PPT图10惯性项与扩展速度项对动态应力强度因子变化
-->Fig.10The effect of inertia term and crack velocity term on the DSIF
-->
(3) J-domain单元网格对DSIF的影响
理论上相互作用积分应该是与路径无关的, 但是由于数值积分的误差造成了路径相关性, 因此, 相互作用积分区域J-domain 大小选择是否合理将直接影响DSIF的求解精度. 而J-domain的大小由其网格单元数目与单元尺寸决定.
首先考虑J-domain单元网格对DSIF的影响, 考虑如下4种J-domain网格, 分别为2×2, 4×4, 6×6 和8×8, J-domain 单元尺寸hJ=1.0h . 计算网格取为39×79, 时间步长
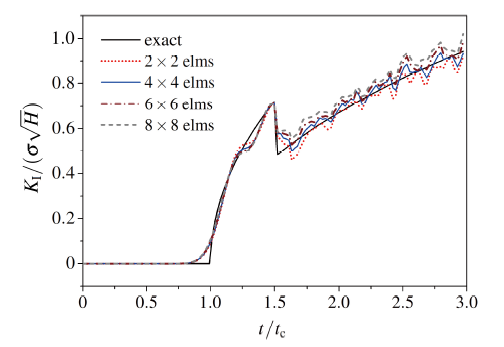显示原图|下载原图ZIP|生成PPT图11J-domain单元网格对动态应力强度因子变化
-->Fig.11The effect of J-domain mesh on the DSIF
-->
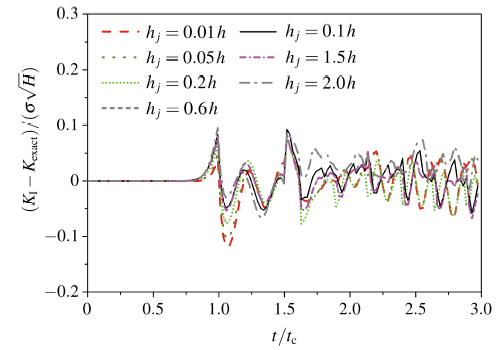
(4) J-domain单元尺寸对DSIF的影响
计算网格与时间步长如上. J-domain单元网格为4×4, J-domain单元尺寸在0.01h 到2.0h 之间取值.
图12给出了不同J-domain单元尺寸对DSIF的影响结果. 由图可知, 结果精度对J-domain区域单元尺寸变化不敏感, 震荡幅度变化不大, 甚至当 J-domain 单元尺寸取为计算网格单元尺寸的0.01倍时, 仍可以具有较高的计算精度. 考虑到计算效率与计算稳定性, 推荐的J-domain单元尺寸取值范围为0.5h~1.5h.
显示原图|下载原图ZIP|生成PPT图12J-domain单元尺寸动态应力强度因子变化
-->Fig.12The effect of element size of J-domain on the DSIF
-->
(5) 与文献结果对比
这是一个富有挑战性的算例, XFEM的很多文献对这个问题进行了模拟分析[23-24,38-43], 但是得到的动态应力强度因子结果总是存在工程不可接受的数值震荡[39].
对于震荡的原因, 目前还没有统一的认识, 主要包含如下几个方面: 裂纹跨越单元时,单元逼近函数的跳变[29,40]; 裂纹扩展过程中能量一致性问题[24-25,41]; 时间离散精度不够[48]; 低阶有限元引起的应力波频散[42]等. 图13 将本文计算结果与其中经典文献[24,39-41]对于该问题的的计算结果进行了比较. 比较表明, 改进型XFEM给出该问题目前为止震荡最小、精度最好的数值解答.
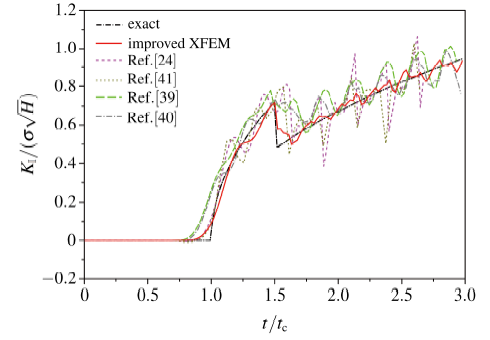显示原图|下载原图ZIP|生成PPT图13改进型XFEM与XFEM动态应力强度因子对比
-->Fig.13The comparison of improved XFEM and XFEMs on accuracy assessment of dynamic SIF for moving crack
-->
3.2 Kalthoff实验?动态裂纹扩展测试
Kalthoff实验常常作为检验动态裂纹扩展模拟准确性的标准算例[24,38-42]. 在实验中, 一个初速度V0 的弹体去冲击一含两个对称边裂纹的平板, 如图14所示, 两裂纹间距与弹体直径相对应. 其中L=100mm, H=200mm, a=50mm, 材料密度$\rho = 8000 {kg/m}^{3}$, $E=190 {GPa}$, $v=0.3$. 断裂韧度$K_{IC}=68~{MPa}\cdot \sqrt{m}$. 弹体冲击速度为: $V_{0}=20 {m/s}$. 考虑4 种计算网格, 分别为19×19, 39×39, 79×79 和199×199, 时间步长分别取为2 μs, 1 μs, 1 μs和0.5 μs, 集中质量矩阵, 模拟时间为$1.0\times10^{-4}~{s}$. 在低速冲击下, 该实验裂纹最终扩展路径与水平方向夹角在70° 左右. 裂纹扩展速度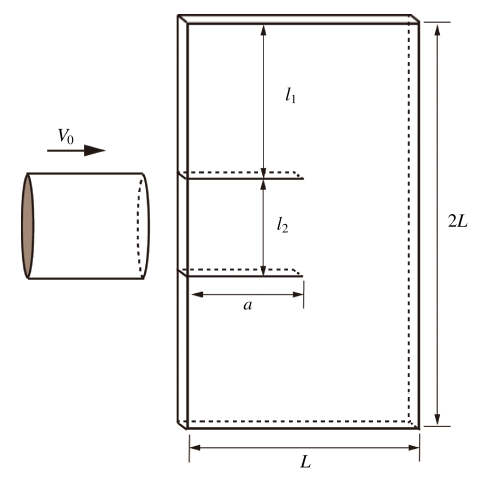
显示原图|下载原图ZIP|生成PPT图14Kalthoff实验
-->Fig.14Geometry of Kalthoff’s experiment
-->
图15给出了不同网格裂纹扩展路径与裂纹长度随时间变化曲线的结果对比. 显然, 裂纹最终路径和裂纹扩展速度随着网格加密最终收敛. 裂纹扩展方向与水平方向夹角在67°左右. 初始扩展方向约70°, 最终沿大约67°方向贯穿整个靶板. 结果与文献[38-42, 44] 结果一致.
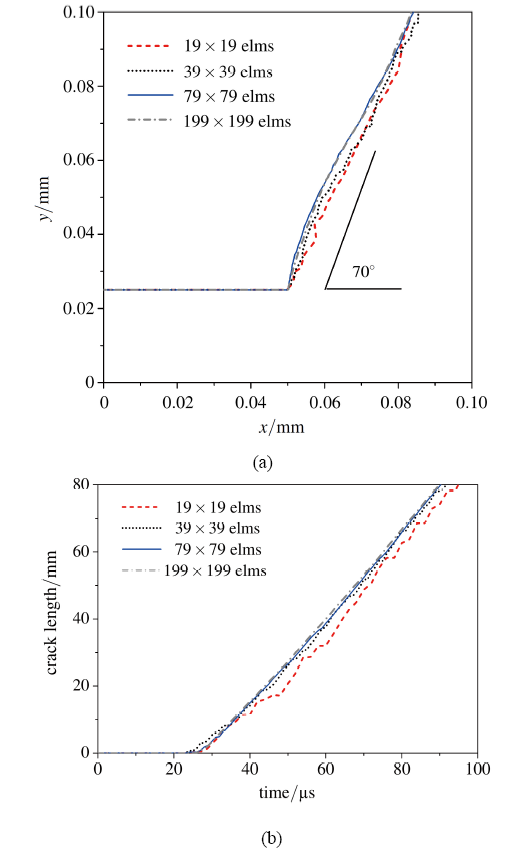显示原图|下载原图ZIP|生成PPT图15模拟结果 (a) 裂纹路径; (b) 裂纹长度随时间变化
-->Fig.15Comparison of the results obtained by implicit and explicit time integrators. (a) final crack path; (b) crack length vs time
-->
4 结论
改进型XFEM具有裂尖强化不引入额外自由度、条件性态良好、全局插值、和动力学计算实施容易等特点. 本文考虑了该方法在动力学裂纹扩展问题中的应用, 通过典型算例分析了动力学裂纹应力强度因子求解中网格、时间步长、加强区域、质量矩阵及J-domian等因素的影响, 结论如下:(1) 改进型XFEM有着良好的收敛性. 在网格较稀疏的情况下, 可获得较高的计算精度; 随着网格加密, 数值解逼近解析解.
(2) 裂尖加强区域取值为1.0h ~ 2.0h时, 计算结果最理想.
(3) 对于给定网格, 随着时间步长减小, 数值解越来越逼近解析解.
(4) 在动态裂纹扩展中, 惯性项与速度贡献项的影响不可忽略.
(5) 对于问题3.1, 相互作用积分区域J-domian的网格取4×4或6×6时结果最理想, 此外J-domian 网格单元尺寸的选取对DSIF影响不大, 但考虑网格质量与计算误差等因素的影响, 推荐采用0.5h~1.5h.
(6) 对于问题3.1, 改进型XFEM给出该问题目前为止震荡最小、精度最好的数值解答.
未来工作围绕复杂裂纹扩展和裂纹群相互作用展开.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . . |
| [2] | . . |
| [3] | . |
| [4] | . . |
| [5] | . . |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . . |
| [10] | . . |
| [11] | . . |
| [12] | . . |
| [13] | . |
| [14] | . . |
| [15] | . |
| [16] | . . |
| [17] | . |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . |
| [24] | . |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | . |
| [29] | . |
| [30] | . . |
| [31] | . . |
| [32] | . . |
| [33] | . . |
| [34] | . . |
| [35] | |
| [36] | |
| [37] | |
| [38] | . |
| [39] | . |
| [40] | . |
| [41] | . |
| [42] | . |
| [43] | . |
| [44] | . |
| [45] | . |
| [46] | . |
| [47] | . |
| [48] | . |
