, 甄文强A ZERO-ENERGY MODE CONTROL METHOD OF NON-ORDINARY STATE-BASED PERIDYNAMICS
LiPan中图分类号:O34
文献标识码:A
通讯作者:
收稿日期:2017-11-20
接受日期:2018-01-19
网络出版日期:2018-02-10
版权声明:2018《力学学报》编辑部《力学学报》编辑部 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (10325KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引言
近场动力学(peridynamics, PD)是一种新的无网格方法,采用积分方程代替传统连续介质力学中的微分方程,不再基于连续性假设建模.它兼有分子动力学方法和无网格方法的优点,避免了有限元、有限差分等传统方法在面临不连续问题时的奇异性,又突破了分子动力学方法在计算尺度上的缺陷,在研究损伤、断裂、失稳等不连续问题时具有明显优势[1,2,3,4,5].最初的PD键理论不涉及应力、应变等概念,影响数值分析结果与传统实验和数值结果的对比[6,7].由于只考虑两物质点之间中心相互作用力,其模型的泊松比为固定值(三维问题和平面应变问题为1/4,平面应力问题为1/3),且无法正确反映材料的塑性、黏性等特征[8,9,10]. PD非普通状态理论克服了PD键理论的不足,能够引入传统本构关系和破坏准则,受到了越来越广泛的关注. 谷新保等[11]采用PD非普通状态理论模拟了含圆孔平板的裂纹扩展和连接过程. 刘肃肃等[12]引入传统单参量非线性本构模型,实现了复合材料非线性行为的模拟.Foster等[13]在PD非普通状态理论中引入率相关塑性本构模型,Tupek等[14]引入传统损伤模型.采用节点积分计算效率高,但会引起零能模式,单元可以在微小的扰动下无限地变形下去,而不消耗任何能量. 与光滑粒子流体动力学(smoothed particle hydrodynamics,SPH)[15]以及无网格伽辽金方法[16,17,18,19]类似,PD非普通状态理论在采用节点积分时,也会产生零能模式,引起位移场和应力、应变场的数值振荡,影响计算精度甚至得到完全错误的结果. 目前,****们提出了多种零能模式控制方法,Breitenfeld等[20,21]提出在力状态的基础上增加沙漏力,通过调节沙漏力控制零能模式,若沙漏力太小,零能模式无法得到有效控制,若沙漏力太大,运动方程的解被沙漏力主导,易造成结果不收敛,因此沙漏力的取值至关重要. Wu[22]将物质点处的位移用其近场范围内的平均值代替,得到稳定的位移场. Becker[23]利用速度与其近场范围内速度平均值的加权替换物质点处的原始速度,得到稳定的速度场. Wu和Becker的方法本质上是一种数据平滑技术,不仅针对零能模式,它还可以处理其他因素引起的数值振荡问题. 他们的方法虽然避免了增加沙漏力控制,但应力、应变场数值不稳定问题仍没有得到解决. PD非普通状态理论中的零能模式主要由计算近似变形梯度过程中的误差引起,因此,提高近似变形梯度的计算精度同样可以减小数值振荡,抑制零能模式. Yaghoobi等[24]通过固定近场范围内各个物质点的影响函数,将近似变形梯度的计算精度从一阶提高到二阶、四阶,甚至六阶,减小了计算的数值不稳定性. 但影响函数不再为正值,易造成数值奇异. Silling[25]通过最小位能原理推导出稳定的关联材料模型,从材料不稳定而不是传统数值不稳定的角度控制零能模式. 方法思路好,但它仍需要通过大量数值实验确定合适的常数取值,耗费计算时间,且文献算例得到的带孔平板的破坏模式并不太理想.
上述方法大多需要通过大量数值实验确定零能模式控制参数,耗费计算时间. 而避免了增加沙漏力的平滑技术处理没有解决应力、应变场的不稳定问题. 因此有必要提出一种新的零能模式控制方法.
本文基于线性化PD键理论,推导非均匀变形状态对应弹性系数张量的具体形式,建立基于线性键理论的稳定关联材料模型,并应用于含圆孔平板、三点弯试件的线弹性分析以及损伤破坏分析. 结果表明,该模型物理意义明确,可以有效抑制零能模式引起的数值不稳定性,避免复杂的参数调节过程,提高了计算效率.
1 近场动力学非普通状态基本理论
1.1 运动方程
PD非普通状态理论的运动方程为[26]$ \rho \ddot {\pmb u}({\pmb x},t) = \int_H \Big \{ \underline{\pmb T} [{\pmb x},t]\left\langle {{\pmb x}' - {\pmb x}} \right\rangle - \underline{\pmb T} [{\pmb x}',t]\left\langle {{\pmb x} - {\pmb x}'} \right\rangle \Big\} d V' + {\pmb b} ({\pmb x},t) (1) $
其中,$\rho $为材料密度,$\ddot{\pmb u}$为物质点的加速度,$d V'$是初始结构中物质点${\pmb x}'$所占的体积,${\pmb b}$代表单位体积物质所受的外载荷, $\underline{\pmb T} [{\pmb x},t]\left\langle {{\pmb x}' - {\pmb x}} \right\rangle $为物质点${\pmb x}'$对${\pmb x}$的力状态,$H = \{{\pmb x}' \in R:\left\| {{\pmb x}' - {\pmb x}} \right\| \leqslant \delta \}$为空间域内物质点${\pmb x}$的近场范围,$\delta $为近场半径,如图1所示.
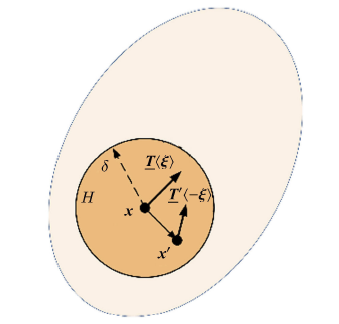显示原图|下载原图ZIP|生成PPT图1物质点与其近场范围内其他物质点的相互作用
-->Fig.1Pairwise interaction of a material point with its neighboring points
-->
在${\pmb x}$的近场范围内,物质点${\pmb x}$与${\pmb x}'$的相对位置以及两者之间键的变形状态分别为
$ \left.\!\!\bal {\pmb\xi }= {\pmb x}' - {\pmb x} \underline{\pmb Y} \left\langle {{\pmb x}' - {\pmb x}} \right\rangle = {\pmb \xi} + {\pmb \eta }= {\pmb u}' + {\pmb x}' - ({\pmb u} + {\pmb x}) \end{array}\!\!\right\} (2) $
计算物质点处的离散化变形梯度[27]
$ \left.\!\!\bal {\pmb F} =\Big [\int_H { \omega }\left\langle {\pmb \xi }\right\rangle \langle \underline{\pmb Y} ({\pmb \xi} )\rangle \otimes {\pmb \xi })\d V_\xi \Big ] \cdot{\pmb K}^{ - 1} {\pmb K} = \int_H \omega \left\langle {\pmb \xi} \right\rangle ({\pmb \xi} \otimes {\pmb \xi} ) \d V_\xi \end{array}\!\!\right\} (3) $
其中,${\pmb K}$称为形变张量,$\omega \left\langle {\pmb \xi} \right\rangle $为作用键的影响函数,它是两点相对位置$\left| {\pmb \xi} \right|$的函数.
根据连续介质力学,物质点的应变张量可以表示为
$ {\pmb E} = \dfrac{1}{2}({\pmb F}^T{\pmb F} - {\pmb I}) (4) $
令连续介质力学应变能和PD应变能相等,可得PD力状态的表达式$^{[28]}$
$ \left.\bal \underline{\pmb T} \left\langle {\pmb \xi} \right\rangle = \omega \left\langle {\pmb \xi} \right\rangle {\pmb P}{\pmb K}^{- 1}{\pmb \xi} {\pmb P} ={\pmb F}{\pmb S} \end{array}\!\!\right\} (5)$
其中,${\pmb P}$为第一类Piola-Kirchhoff应力,${\pmb S}$为第二类Piola-Kirchhoff应力.
将式(5)代入式(1)可得PD非普通状态理论的运动方程
$ \rho \ddot {\pmb u}({\pmb x},t) = \int_H \Big\{ \omega \;\left\langle {\pmb x}' - {\pmb x} \right\rangle {\pmb F}_x {\pmb S}_x {\pmb K}_x ^{ - 1}({\pmb x}' - {\pmb x}) - \omega \left\langle {{\pmb x} - {\pmb x}'} \right\rangle {\pmb F}_{x'} {\pmb S}_{x'} {\pmb K}_{x'} ^{ - 1}({\pmb x} - {\pmb x}') \Big \} \d V' + {\pmb b}({\pmb x},t) (6)$
1.2 损伤定义
在PD理论中一般采用键的临界伸长率破坏准则,认为键的伸长率达到临界伸长率时,两点之间的作用键发生断裂. 键的伸长率$s$的表达式为[2,29-31]$ s = \dfrac{\left| {{\pmb \xi} + {\pmb \eta} } \right| - \left| {\pmb \xi} \right|}{\left| {\pmb \xi} \right|} (7)$
二维情况下各向同性线弹性材料的键临界伸长率$s_{\rm c}$的表达式为
$ s_{\rm c}= \sqrt {\dfrac{G_{\rm c} }{[6\mu / \pi + 16(K - 2\mu ) / (9\pi ^2)]\delta }} (8) $
其中,$K$为材料的体积模量,$\mu $为剪切模量,$G_{\rm c} $为断裂能.
此外,也可以基于应力状态定义损伤$^{[32]}$. 首先定义物质点${\pmb x}$和${\pmb x}'$之间的平均第一主应力
$ \sigma _1 ({\pmb x},{\pmb x}') = (\sigma _1 ({\pmb x}) + \sigma _1 ({\pmb x}') ) / 2 (9)$
定义各物质点的局部损伤值
$ \varphi ({\pmb x},t) = 1 - \dfrac{\int_H \mu ({\pmb x}, {\pmb x}',t)\d V' }{\int_H \d V' } (10) $
其中,$\mu ({\pmb x}, {\pmb x}',t)$为表征物质点对是否断裂的函数,其表达式为
$\mu ({\pmb x}, {\pmb x}',t) = \left\{ \begin{array}{ll} 1,& s < s_{\rm c} \ {\rm or} \ \sigma _1 ({\pmb x}, {\pmb x}') < f_{\rm t} 0, & s \geqslant s_{\rm c} \ {\rm or} \ \sigma _1 ({\pmb x}, {\pmb x}') \geqslant f_{\rm t} \end{array} \right. (11) $
其中,$f_{\rm t} $为材料的拉伸强度;$\varphi ({\pmb x},t)$取值范围在[0,1]之间,0表示该物质点邻域内无作用键断裂,1表示邻域内的键全部断裂.
通过影响函数引入损伤
$ \omega \left\langle {\pmb\xi} \right\rangle = \left\{\!\!\begin{array}{ll} 0 , & s \geqslant s_{\rm c} \ {\rm or} \ \sigma _1 ({\pmb x}, {\pmb x}') \geqslant f_{\rm t} 1 , & {\rm else} \end{array}\!\! \right. (12)$
将损伤因子$d$定义为断裂键个数与作用键总数的比值
$d = \dfrac{n_{\rm fail} }{n_{\rm total} } (13)$
1.3 运动方程求解
尽管PD运动方程是动态形式的,但采用动态松弛法进行求解时仍可用于解决准静态问题. 根据动态松弛方法,引入虚拟惯性项和虚拟阻尼项之后运动方程式(6)可以改写成[2,33]$ {\pmb\varLambda} \ddot {\pmb U}({\pmb x},t) + c^n{\pmb\varLambda} \dot {\pmb U}({\pmb x},t) ={\pmb f}({\pmb x},t) {\pmb f}({\pmb x},t) = \int_H \Big [ \omega \;\left\langle {{\pmb x}' - {\pmb x}} \right\rangle {\pmb F}_x {\pmb S}_x {\pmb K}_x ^{ - 1}({\pmb x}' - {\pmb x}) - \omega \;\left\langle {{\pmb x} - {\pmb x}'} \right\rangle {\pmb F}_{x'} {\pmb S}_{x'} {\pmb K}_{x'} ^{ - 1}({\pmb x} - {\pmb x}') \Big] \d V' + {\pmb b}({\pmb x},t) (14) $
其中,${\pmb f}({\pmb x},t)$为物质点${\pmb x}$所受的单位体积合力;${\pmb \varLambda }$为质量密度对角阵,对角元素 $\lambda_{ii} \geq \dfrac 14 \Delta t^2 \dsum_j | K_{ij} |$, $\dsum_j| K_{ij} |=\dsum^N_{j=1} \dfrac{|{\pmb \xi}_{(i)(j)}\cdot{\pmb e}|}{| {\pmb\xi}_{(i)(j)} |} \dfrac c{| {\pmb\xi}_{(i)(j)}|}$.
在自适应动态松弛法中,为了使运动方程的解尽快收敛到稳定解,每一个载荷步阻尼系数$c^n$都需要重新计算,计算公式为
$ \left.\bal c^n = 2\sqrt {(({\pmb U}^n)^{\rm T}{}'{\pmb K}^n{\pmb U}^n) / (({\pmb U}^n)^ {\rm T}{\pmb U}^n)} {}'K_{ii}^n = - (f_i^n / \lambda _{ii} - f_i^{n - 1} / \lambda _{ii} ) / (\Delta t\dot {u}_i^{n - 1 / 2} ) \right\} (15) $
2 基于线性化键理论的稳定关联材料模型
Silling[25]将零能模式看作材料不稳定性,通过最小位能原理推导出一种稳定的关联材料模型,其力状态表达式为$ \underline{\hat {\pmb T}}\left\langle {\pmb \xi} \right\rangle = \omega \left\langle {\pmb \xi } \right\rangle (\hat {\pmb \sigma }({\pmb F}) {\pmb K}^{ - 1}{\pmb \xi } + \dfrac{GC}{\omega _0 }\underline{\pmb z}\left\langle {\pmb \xi} \right\rangle ) (16) $
其中,$\hat {\pmb\sigma }({\pmb F})$为第一类Piola-Kirchhoff应力,${\pmb F}$为变形梯度,$G$为正常数,$C = 18K / \pi \delta ^5$,$\omega _0 = \int_{H_{x} } \omega \left\langle {\pmb \xi } \right\rangle \d V_\xi $,$\underline{\pmb z}\left\langle {\pmb \xi} \right\rangle =\underline{\pmb Y}\left\langle {\pmb \xi} \right\rangle - {\pmb F}{\pmb \xi} $,表示变形状态的非均匀部分.
Silling在推导稳定关联材料模型的过程中,将非均匀变形状态$\underline{\pmb z}\left\langle {\pmb \xi} \right\rangle $对应弹性系数张量$\underline{\beta }\left\langle {\pmb \xi }\right\rangle $的具体形式直接取为键理论微模量的常数倍,没有考虑微模量随不同作用键的变化. 公式中包含常数$G$,需要通过大量数值实验确定合适的取值. 常数$G$不是无量纲的量,其取值与物质点体积相关. 因此,对于不同的离散模型,数值相差较大,增大了零能模式控制难度.
为了克服以上困难,本文基于线性化PD键理论,推导出弹性系数张量$\underline{\beta }\left\langle {\pmb \xi} \right\rangle $以及非均匀变形对应力状态$\underline{\pmb T}^{\rm s}\left\langle {\pmb \xi} \right\rangle $的具体形式.
对于微弹性材料,线性化之后键理论本构力函数和力状态的表达式分别为[1,34]
$ \left.\bal {\pmb f}^{\rm b}({\pmb \eta} , {\pmb \xi} ) = \omega \left\langle {\pmb \xi} \right\rangle C\left\langle {\pmb \xi} \right\rangle \cdot {\pmb \eta } \underline{\pmb T}^{\rm b}\left\langle {\pmb \xi} \right\rangle = \dfrac{1}{2}{\pmb f}^{\rm b}({\pmb \eta}, {\pmb \xi} )= \dfrac{1}{2}\omega \left\langle {\pmb \xi} \right\rangle C\left\langle {\pmb \xi } \right\rangle \cdot {\pmb \eta } \end{array}\!\!\right\} (17) $
物质点${\pmb x}$处的弹性能密度$^{[1]}$
$ W_u ({\pmb x}) = \dfrac{1}{2}\int_H w({\pmb \eta} , {\pmb \xi} ) \d V_\xi = \dfrac{1}{2}\int_H \dfrac{1}{2}{\pmb \eta} \cdot \omega \left\langle {\pmb \xi } \right\rangle C\left\langle {\pmb \xi }\right\rangle \cdot {\pmb \eta} \d V_\xi (18) $
其中,$\omega \left\langle {\pmb \xi}\right\rangle $为影响函数;$C\left\langle {\pmb \xi} \right\rangle = c{\pmb \xi} \otimes {\pmb \xi}/ \left| {\pmb \xi}\right|^3$为弹性系数张量,$c = 18K / \pi \delta ^4$为键理论中的材料微模量$^{[35]}$;${\pmb \eta} = {\pmb u}' -{\pmb u}$为物质点之间的相对位移.
采用线性化键理论,根据非均匀变形状态$\underline{\pmb z}\left\langle {\pmb \xi} \right\rangle $以及其对应的弹性系数张量$\underline{\beta }\left\langle {\pmb \xi} \right\rangle $,可得到物质点$x$处的弹性能密度
$ \hat{ W}^{\rm s} = \dfrac{1}{2}\int_H \underline{\pmb z}\left\langle {\pmb \xi }\right\rangle \cdot \underline{\beta }\left\langle {\pmb \xi} \right\rangle \cdot \underline{\pmb z}\left\langle {\pmb \xi} \right\rangle \d V_\xi = \dfrac{1}{2}(\underline{\beta }\underline{\pmb z})\cdot \underline{\pmb z} (19) $
对比式(18)和式(19) 后发现,弹性系数张量$\underline{\beta }\left\langle {\pmb \xi} \right\rangle $可以表示为
$ \underline{\beta }\left\langle {\pmb \xi}\right\rangle = \dfrac{1}{2}\omega \left\langle {\pmb \xi} \right\rangle C\left\langle {\pmb \xi} \right\rangle (20) $
因此,式(19)可以改写为
$ \hat {W}^{\rm s} = \dfrac{1}{2}\Big(\dfrac{1}{2}\omega C\underline{\pmb z}\Big)\cdot \underline{\pmb z}(21)$
弹性能密度增量为
$ \d\hat {W}^s = \Big(\dfrac{1}{2}\omega C\underline{\pmb z}\Big)\cdot \d\underline{\pmb z} = \underline{\pmb T}^{\rm s'}\left\langle {\pmb \xi} \right\rangle \cdot \d\underline{\pmb z}\left\langle {\pmb \xi} \right\rangle = \dfrac{1}{2}\int_H \Big[\omega \left\langle {\pmb \xi} \right\rangle C\left\langle {\pmb \xi} \right\rangle \cdot z_i \left\langle{\pmb \xi}\right\rangle - \Big (\int_H \omega \left\langle {\pmb \eta} \right\rangle C\left\langle {\pmb \eta}\right\rangle z_i \left\langle {\pmb \eta} \right\rangle \eta_j \d V_\eta \Big) \omega \left\langle {\pmb \xi} \right\rangle {\pmb \xi} _p K_{pj}^{ - 1} \Big] \d Y_i \left\langle {\pmb \xi} \right\rangle \d V_\xi = \underline{\pmb T}^{\rm s}\left\langle{\pmb \xi} \right\rangle \cdot \d\underline{\pmb Y}\left\langle {\pmb \xi} \right\rangle (22) $
其中,$\underline{\pmb T}^{\rm s}\left\langle {\pmb \xi} \right\rangle $为非均匀变形状态引起的力状态
$ \underline{\pmb T}^{\rm s}\left\langle {\pmb \xi} \right\rangle = \dfrac{1}{2}\Big [\omega \left\langle {\pmb \xi} \right\rangle C\left\langle {\pmb \xi} \right\rangle \underline{\pmb z}\left\langle {\pmb \xi} \right\rangle - \omega \left\langle {\pmb \xi} \right\rangle \Big(\int_H \omega \left\langle {\pmb \eta} \right\rangle C\left\langle {\pmb \eta} \right\rangle \underline{\pmb z}\left\langle {\pmb \eta} \right\rangle \otimes {\pmb\eta} \d V_\eta ){\pmb K}^{ - 1}{\pmb \xi} \Big] \end{array} (23) $
结合式(5)和式(23),得到稳定关联材料模型的力状态
$ \underline{\hat{\pmb T}}\left\langle {\pmb \xi} \right\rangle = \omega \left\langle {\pmb \xi} \right\rangle ({\pmb P }- {\pmb \sigma}^s) {\pmb K}^{ - 1}{\pmb \xi }+ \dfrac{1}{2}\omega \left\langle {\pmb \xi} \right\rangle C\left\langle {\pmb \xi} \right\rangle \underline{\pmb z}\left\langle {\pmb \xi} \right\rangle (24) $
其中,${\pmb \sigma}^{\rm s}$定义为
$ {\pmb \sigma}^{\rm s}= \dfrac{1}{2}\int_H {\omega \left\langle {\pmb \eta} \right\rangle C\left\langle {\pmb \eta} \right\rangle \underline{\pmb z}\left\langle {\pmb \eta} \right\rangle } \otimes {\pmb \eta} \d V_\eta (25) $
若令弹性系数$C\left\langle {\pmb \xi} \right\rangle $为常数,则
$ {\pmb \sigma}^s{\pmb K}^{ - 1} = \dfrac{1}{2}C \Big(\int_H {\omega \left\langle {\pmb \eta} \right\rangle \underline{\pmb z}\left\langle {\pmb \eta} \right\rangle } \otimes {\pmb \eta} \d V_\eta \Big) {\pmb K}^{ - 1} = \dfrac{1}{2}C \Big[\int_H \omega \left\langle {\pmb \eta} \right\rangle (\underline{\pmb Y}\left\langle {\pmb \eta} \right\rangle - {\pmb F}{\pmb \eta} ) \otimes {\pmb \eta} \d V_\eta \Big] {\pmb K}^{ - 1} = \dfrac{1}{2}C \Big[\Big(\int_H \omega \left\langle {\pmb \eta} \right\rangle \underline{\pmb Y}\left\langle {\pmb \eta}\right\rangle \otimes {\pmb \eta} \d V_\eta \Big){\pmb K}^{ - 1} - {\pmb F} \Big(\int_H {\omega \left\langle {\pmb \eta} \right\rangle {\pmb \eta} } \otimes {\pmb \eta} \d V_\eta \Big ) {\pmb K}^{ - 1} \Big ] = \dfrac{1}{2}C({\pmb F} - {\pmb F}{\pmb K}{\pmb K}^{ - 1}) ={\bf 0} (26) $
此时,式(24)简化为式(16). 因此,Silling提出的稳定关联材料模型是式(24)的一种特殊情况.
可见,基于线性化PD键理论建立的稳定关联材料模型,推导过程和公式具有明确的物理含义. 推导出的力状态公式中不涉及
常数$G$,避免了计算中调节参数的复杂过程.
3 算例
3.1 含圆孔平板的拉伸模拟
中心含圆孔平板长150 mm,宽50 mm,厚1 mm,孔直径为20 mm,受拉伸载荷作用. 板的弹性模量为210 GPa,泊松比为0.3[25],将其简化为平面应力问题进行模拟. 平板均匀离散为7 184个粒子,相邻粒子间的间距$\Delta x=1.0$ mm,近场半径$\delta = 3\Delta x$,离散模型如图2所示.采用位移逐步加载,共4 000个加载步,每步施加位移为5.0$\times $10$^{-5}$ mm,时间步长为1.0 s.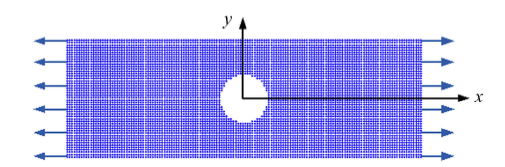
显示原图|下载原图ZIP|生成PPT图2含圆孔平板离散模型
-->Fig.2Discrete model of plate with a circular hole
-->
3.1.1 线弹性分析
图3和图4分别给出无零能模式控制和采用基于线性化键理论的稳定关联材料模型(linearized bond-based peridynamics based stabilized correspondence material model,LBSCMM)时$x$方向位移云图和平板$x$方向位移沿$x$轴的分布曲线,可以看出PD非普通状态理论产生明显的数值不稳定性,且在靠近圆孔的位置最为明显,体现了零能模式控制的必要性.基于线性化键理论的稳定关联材料模型有效地抑制了零能模式引起的数值振荡,得到了稳定的位移场.
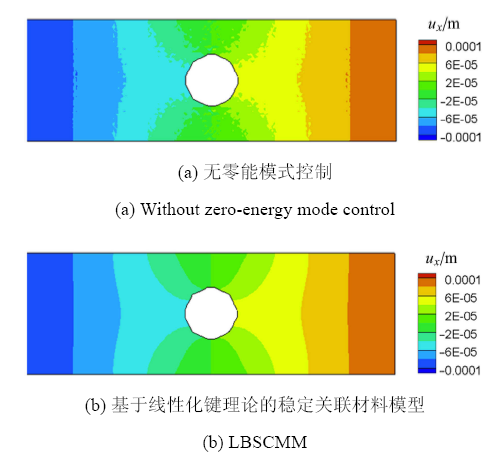显示原图|下载原图ZIP|生成PPT图3平板$x$方向位移云图
-->Fig.3$x$-directional displacement contours of plate
-->
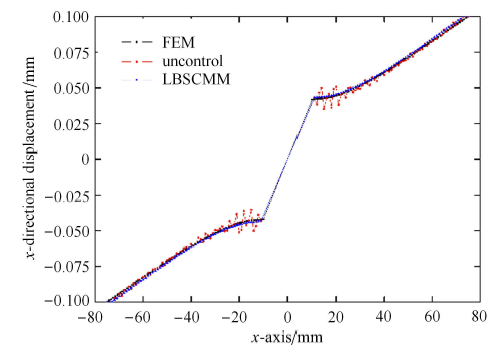显示原图|下载原图ZIP|生成PPT图4平板$x$方向位移沿$x$轴的分布曲线
-->Fig.4$x$-directional displacement of plate along $x$-axis
-->
3.1.2 损伤分析
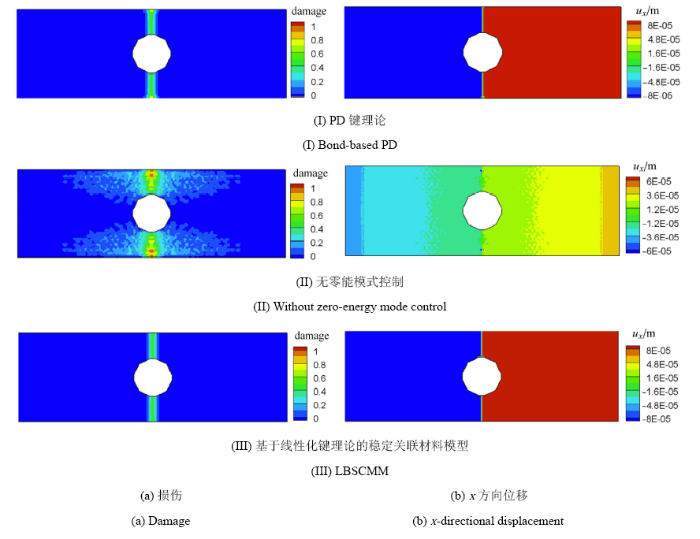
在上述线弹性模型的基础上考虑材料损伤,研究零能模式对材料损伤破坏过程的影响. 采用临界伸长率破坏准则,键临界伸长率$s_{\rm c}= 0.002$.图5和图6分别给出无零能模式控制和采用基于线性化键理论的稳定关联材料模型时带孔平板的破坏模式、损伤演化过程.由于PD键理论没有零能模式控制问题,图中也同时给出了键理论的模拟结果进行对比.可见PD非普通状态理论中的零能模式使得平板试件过早地产生损伤,裂纹贯穿之后损伤仍在加剧,且损伤区域较大,严重 偏离实际情况.本文模型模拟得到的平板试件破坏模式以及损伤演化过程与PD键理论模拟结果吻合很好,表明本文模型在零能模式控制方面的正确性和有效性.
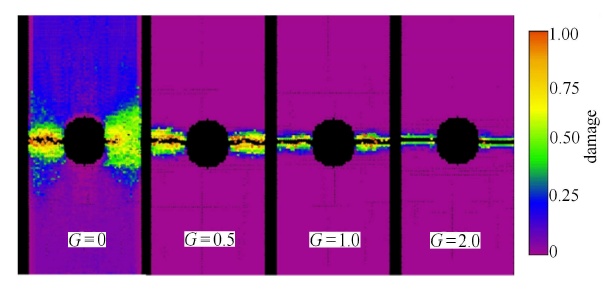
文献[25]通过调节常数$G$的取值控制零能模式,只给出平板的最终破坏模式,没有涉及损伤演化过程,如图7所示.然而$G$的取 值会影响损伤演化过程,从而得到不同的载荷-位移曲线.因此,常数$G$的取值与试件的损伤演化过程、最终破坏模式、载荷-位移曲线均相关,调节过程具有一定难度.本文模型则避免了常数调节过程,提高了计算效率,且试件破坏模式与文献[25]的结果相比更好.
显示原图|下载原图ZIP|生成PPT图5平板零能模式对材料损伤和变形的影响
-->Fig.5Influence of zero-energy mode on material damage and deformation of plate
-->
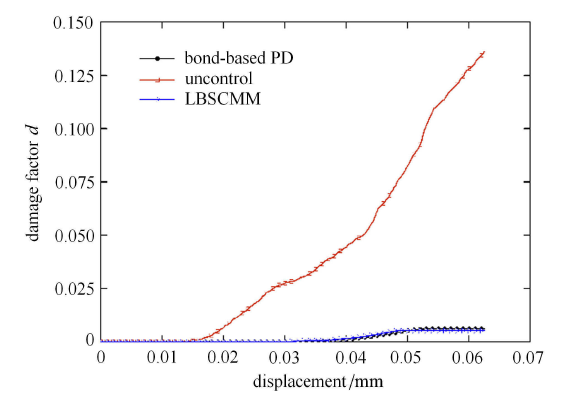
显示原图|下载原图ZIP|生成PPT图6平板损伤因子随加载位移的变化
-->Fig.6Change of damage factor with increasing displacement of plate
-->
显示原图|下载原图ZIP|生成PPT图7Silling模拟得到的平板损伤云图[
-->Fig.7Damage contours of plate obtained by Silling[
-->
3.2 三点弯模拟
三点弯试件尺寸参数如下：$L =136$ mm,$H =34$ mm,厚度$B =17$ mm,初始裂缝长度$a =17$ mm,将其简化为平面应力问题进行模拟. 试件被均匀离散为5 127个粒子,相邻粒子间的间距$\Delta x =1.0$ mm,近场半径$\delta = 3\Deltax$,几何模型和离散模型如图8所示. 试件上表面中心施加压缩位移载荷,下表面在距离中心$L$/2处对$y$方向位移进行约束. 加载过程包括4 000个加载步,每步加载位移为6.25$\times $10$^{ - 5}$ mm,时间步长为1 s. 试件采用PBX9501的同密度代用材料Mock 900-21制成,Mock 900-21的材料参数如表1所示.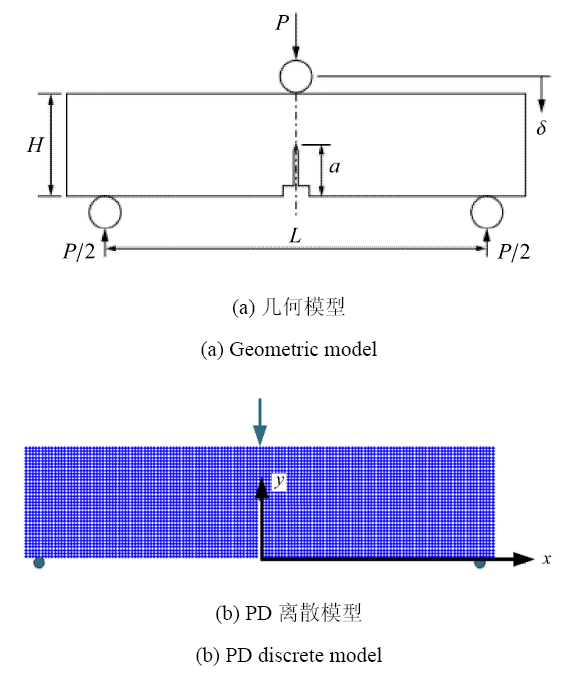
显示原图|下载原图ZIP|生成PPT图8三点弯试件示意图
-->Fig.8Three-point bend specimen with a single edge notch
-->
Table 1
表 1
表 1Mock 900-21材料常数[
Table 1Material parameters of Mock 900-21[
 |
新窗口打开
3.2.1 线弹性分析
图9和图10分别给出无零能模式控制和采用基于线性化键理论的稳定关联材料模型时$x$方向位移云图和三点弯试件位移沿$x$轴的分布曲线,可以看出PD非普通状态理论产生明显的数值不稳定性,且在靠近缺口和受约束位置最为明显. 基于线性化键理论的稳定关联材料模型有效地抑制了零能模式引起的数值振荡,得到了稳定的位移场.
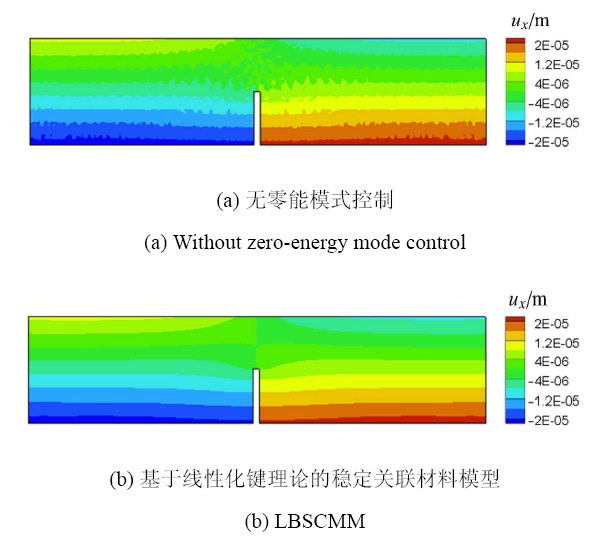显示原图|下载原图ZIP|生成PPT图9三点弯试件$x$方向位移云图
-->Fig.9$x$-directional displacement contours of three-point bend specimen
-->
显示原图|下载原图ZIP|生成PPT图10三点弯试件$x$方向位移和$y$方向位移沿$x$轴的分布曲线
-->Fig.10$x$-directional displacement and $y$-directional displacement of three point bend specimen along $x$-axis
-->
3.2.2 损伤分析
在上述线弹性模型的基础上考虑材料损伤,研究零能模式对材料损伤破坏过程的影响,采用最大主应力破坏准则.图11和图12分别给出无零能模式控制和采用基于线性化键理论的稳定关联材料模型时三点弯试件的破坏模式、损伤演化过程,以及同等条件下PD键理论的模拟结果.可见PD非普通状态理论中的零能模式使得三点弯试件损伤集中在缺口附近,并迅速向周边扩展,严重偏离实际情况.本文模型模拟得到的三点弯试件破坏模式以及损伤演化过程与PD键理论模拟结果吻合很好,表明本文模型有效抑制了零能模式引起的数值不稳定性.另外,结合图10和图11可以发现,零能模式对线弹性阶段影响较小,但却严重影响结构的损伤演化过程和破坏模式.
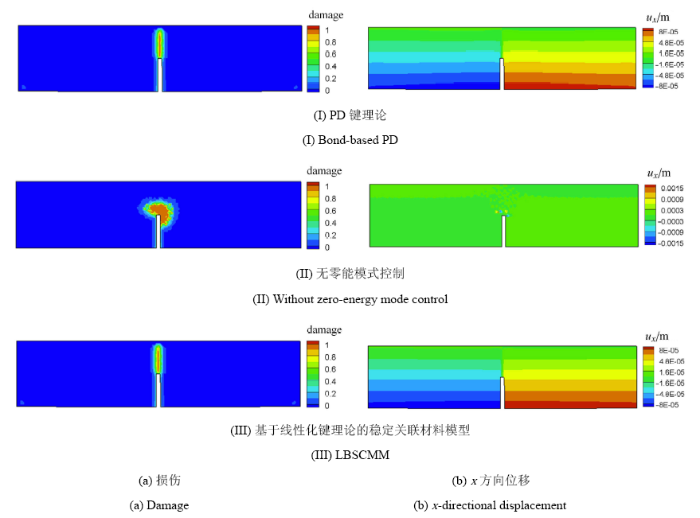显示原图|下载原图ZIP|生成PPT图11三点弯试件零能模式对材料损伤和变形的影响
-->Fig.11Influence of zero-energy mode on material damage and deformation of three-point bend specimen
-->
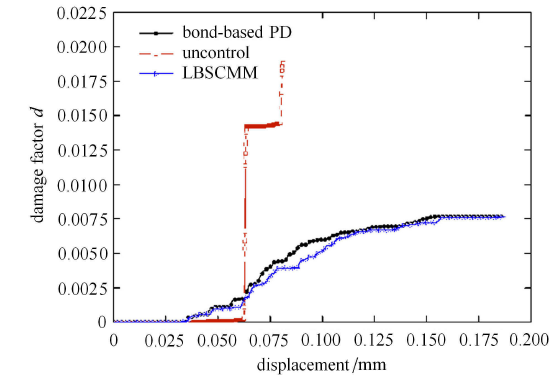显示原图|下载原图ZIP|生成PPT图12三点弯试件损伤因子随位移的变化
-->Fig.12Change of damage factor with increasing displacement of three-point bend specimen
-->
4 结论
近场动力学非普通状态理论克服了近场动力学键理论的缺陷,能够将传统本构关系和破坏准则引入PD框架.与其他无网格法类似,采用节点积分的近场动力学非普通状态理论会产生零能模式,引起数值振荡.本文基于线性化PD键理论,推导出非均匀变形状态对应弹性系数张量的具体形式,建立基于线性化PD键理论的稳定关联材料模型,研究了含圆孔平板、三点弯试件的线弹性行为以及损伤破坏行为,得出以下结论：
(1)PD非普通状态理论无零能模式控制的情况下,数值振荡引起结构提早产生损伤并断裂,导致失效载荷偏小,或损伤在缺口附近集中,并迅速向周边扩展,使得破坏模式与实际不相符.
(2)本文提出的基于线性化PD键理论的稳定关联材料模型有效地抑制了零能模式引起的数值振荡,使得线弹性分析与有限元结果一致,破坏模式以及损伤演化过程与PD键理论结果吻合很好,验证了本文提出模型的正确性和有效性.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . . |
| [2] | . |
| [3] | . . |
| [4] | . . |
| [5] | . . |
| [6] | . |
| [7] | |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . . |
| [12] | . . |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . . |
| [19] | . . |
| [20] | . |
| [21] | |
| [22] | . |
| [23] | . |
| [24] | . |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | . |
| [29] | . |
| [30] | . |
| [31] | . |
| [32] | . |
| [33] | . |
| [34] | . |
| [35] | . |
| [36] | . |
