高晨彤¹, 黎亮¹, 章定国^1,*,, 钱震杰²
1 南京理工大学理学院,南京 210094
2 农业部南京农业机械化研究所,南京 210014

DYNAMIC MODELING AND SIMULATION OF ROTATING FGM TAPERED BEAMS WITH SHEAR EFFECT

GaoChentong¹, LiLiang¹, ZhangDingguo^1,*,, QianZhenjie²
1 School of Science, Nanjing University of Science and Technology, Nanjing 210094,China
2 Nanjing Research Institute for Agricultural Mechanization Ministry of Agriculture, Nanjing 210014, China
中图分类号:O313
文献标识码:A

通讯作者:通讯作者:章定国,教授,主要研究方向：多体系统动力学. E-mail：zhangdg419@mail.njust.edu.cn
收稿日期:2018-01-4
接受日期:2018-03-27
网络出版日期:2018-06-10
版权声明:2018《力学学报》编辑部《力学学报》编辑部 所有
基金资助:国家自然科学基金(11772158, 11502113, 11602120)和中央高校基本科研业务费专项资金(30917011103)资助项目.

展开

摘要
本文对一类中心刚体-柔性梁系统在大范围转动下的刚柔耦合动力学问题进行了研究. 柔性梁为功能梯度材料(functionally graded materials, FGM)楔形变截面梁,材料体积分数在梁轴向呈幂律分布变化. 以弧长坐标来描述柔性FGM梁的几何位移关系,分别使用倾角和拉伸应变变量描述柔性梁的横向弯曲和纵向拉伸变形,并计及剪切效应. 采用假设模态法离散变形场,运用第二类拉格朗日方程进行方程推导,得到系统考虑剪切效应的刚柔耦合动力学模型. 基于全新的刚柔耦合动力学建模理论,研究不同轴向材料梯度分布的FGM楔形梁,通过数值仿真计算,分析讨论不同的转速、梯度分布规律以及变截面参数对系统动力学特性的影响. 结果表明,剪切效应对大高跨比的FGM楔形梁的变形影响较为明显,不容忽略;材料梯度分布规律和截面参数的选取均会对旋转FGM楔形梁的动力学响应和频率产生较大影响. 本文提出的考虑剪切效应的倾角刚柔耦合动力学模型是对以往非剪切模型的进一步完善,可应用于工程中的 Timoshenko梁结构的动力学问题求解.

关键词：功能梯度材料梁;倾角;剪切角;刚柔耦合;动力学仿真
Abstract
In this paper, the rigid-flexible coupling dynamics of the rigid-flexible beam system under large overall rotating motion is studied. The flexible beam is a functionally graded material (FGM) tapered beam, and its material properties are assumed to vary along the beam axis with a power law relation. The geometrical displacement relationship of the flexible FGM beam is described by the arc coordinate. The transverse bending and longitudinal stretching of the flexible beam are considered by the variables of the slope angle and the stretching strain, respectively, and the shear effect is taken into account. The assumed modes method is used to describe the deformation field, and Lagrange’s equations of the second kind are used to derive the equations to obtain the rigid-flexible coupling dynamic model considering the shear effect. Based on the new rigid-flexible coupling dynamics modeling theory, dynamics of the FGM tapered beams with different axial gradients are studied. The influences of different rotating speeds, gradient distributions and variable cross-section parameters on the dynamic characteristics of the system are analyzed by numerical simulations. The results show that the effect of shear on the deformation of FGM tapered beam with depth-span ratio is obvious. The distribution of the material gradient and the selection of the cross-section parameters will have a great influence on the dynamic responses and frequencies of the rotating FGM tapered beam. The rigid-flexible coupling dynamic model considering the shear effect is a further improvement of the previous non-shear model, which can be applied to solve the dynamic problems of the Timoshenko beam structures.

Keywords：FGM beam;slope angle;shear angle;rigid-flexible coupling;dynamic simulation

-->0
PDF (3600KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
高晨彤, 黎亮, 章定国, 钱震杰. 考虑剪切效应的旋转FGM楔形梁刚柔耦合动力学建模与仿真[J]. 力学学报, 2018, 50(3): 654-666 https://doi.org/10.6052/0459-1879-18-011
Gao Chentong, Li Liang, Zhang Dingguo, Qian Zhenjie. DYNAMIC MODELING AND SIMULATION OF ROTATING FGM TAPERED BEAMS WITH SHEAR EFFECT[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(3): 654-666 https://doi.org/10.6052/0459-1879-18-011

引言

叶片是航空发动机系统中十分重要的组成部分,其工作性能对飞行安全有着重大的影响,这类结构通常可以简化为大范围旋转运动 的中心刚 体-柔性梁系统对其动力学行为进行建模分析. 在航空发动机叶片高速旋转时,会受到气动力、热应力等因素的影响,这就要求发动机叶片具有较高的可靠性以及承受高温高压的 能力,因此对满足多方面性能要求的新型复合材料结构的动力学特性的研究变得十分必要. 功能梯度材料(functionally graded material, FGM)就是在这种工程需求中出现的一种新型材料^[1],它通常可以集中几种不同材料的优良性能,在航空航天领域的应用前景 十分广泛.
对于柔性梁的研究是柔性多体系统动力学中较为常见的一个课题,近年来,许多****对做大范围运动的中心刚体-柔性梁系统进行了深入的研究并取得了重大的成果^{[2,3,4,5,6,7,8,9,10,11,12,13]},这些研究大多体现在系统大位移运动与其自身非线性变形的耦合上. 1987年,Kane等^[3]提出了“动力刚化”效应,引起学术界对这一问题的深入研究. 经过数十年的研究,国内外****已经建立了各种不同形式的刚柔耦合动力学模型,捕捉到了被以往零次近似耦合模型所忽略的动力刚化项. Yoo等^[4,5]在对柔性梁变形精确描述的基础上对柔性梁的动力学模型以及其振动特性进行了深入研究,并进行了动力学仿真. Yan等^[6]基于Hamilton原理运用假设模态法建立了旋转柔性梁系统的动力学方程,并对其频率特性做出了研究. Yang 等^[7]将纵横振动的二次耦合变形量计入柔性梁 变形位移中,建立了一次近似刚柔耦合动力学方程. 和兴锁等^[8]认为在一次近似模型中仅将二次变形量考虑在纵向变形量中是不够的,在梁的纵向和横向变形中都应该将耦合项考虑在内. 刘锦阳等^[9]采用假设模态法离散柔性梁系统,通过虚功原理推导出动力学方程,对柔性梁的动力学特性进行了研究. 章定国等^[10]对三维大位移运动下的柔性梁的“动力刚化”及“动力柔化”效应进行了讨论,对传统柔性梁动力学模型进行了改进. Cai等^[11]通过Hamilton原理,运用假设模态法建立了柔性梁系统的一次近似耦合模型,并进行了仿真对比. 王新栋等^[12]以非线性梁理论为基础,运用假设模态法对空间变量进行了离散,对旋转叶片的刚柔耦合问题做出了研究. Li 等^[13]建立了倾角模型,以旋转Euler-Bernoulli梁为对象,运用假设模态法建立了系统的刚柔耦合动力学方程,并进行仿真分析,验证了模型的准确性.
随着柔性梁建模理论的发展与日益成熟,****们将更多的工程应用需求考虑到柔性梁系统动力学中去. 考虑到在实际工程应用中, 剪切效应有着不可忽略的作用,变截面梁也更为常见. 韩广才等^[14]运用Hamilton原理以及有限元法建立了考虑剪切效应的柔性叶片系统连续动力学方程,研究了叶片预扭角及截面 变化对叶片末端响应的影响. 陈思佳等^[15]建立了中心刚体-柔性梁系统的高次耦合动力学方程,并研究了变截面柔性梁的截面参数的改变对末端响应的影响. 在复杂的工况下,材料组成对梁性能的影响尤为重要,在柔性梁模型的基础上,对旋转功能梯度材料梁的研究也日益丰富. 黎亮 等^[16]研究了功能梯度参数沿厚度方向分布的FGM柔性梁在大范围运动下的动力学特性,讨论了功能梯度分布规律及材料梯 度指数对柔性梁动力学特性的影响. Oh等^[17]研究了功能梯度薄壁梁在温度场中的动力学特性,并考虑了柔性梁初始扭转的影响. Yuan等^[18]在Timoshenko梁模型假设的基础上,研究了复合材料梁的运动,推导得出了该模型的非耦合二阶微分方程,并对该 方程的简化做出了讨论. Zarrinzadeh等^[19]采用有限元法研究了具有6种不同边界条件的旋转轴向功能梯度楔形梁的自由振动特性. Rajasekaran^[20]使用微分变换法(differential transformation method, DTM)和DQEL (differential quadrature element method of lowest order)法研究了旋转轴向FGM锥形梁的自由弯曲振动特性,对柔性梁的锥度比、剪切变形参数及转速等对柔性梁固有频率的影响进行了讨论分析. Li等^[21]在倾角模型的基础上,对材料沿轴向梯度分布的FGM楔形梁进行了研究. Das^[22]基于Timoshenko梁假设,采用Hamilton原理,对做旋转运动的FGM梁系统自由振动频率进行了研究. 梁波等^[23]以旋转Euler-Bernoulli梁为对象,考虑了几何非线性和纵向振动的影响,研究了纵向和横向振动的FGM梁的非线性动力学问题. Li等^[24]基于高阶近似刚柔耦合理论和热力学理论,研究了变温场环境下旋转中心刚体-FGM梁系统的动力学问题. Frikha等^[25]采用有限元法,提出了一种基于高阶剪切变形理论的双节点四自由度节点梁单元,对FGM梁进行了研究. Paul等^[26]采用 Hamilton原理,对预应力FGM梁的自由振动特性进行了研究. Wattanasakulpong等^[27]以切比雪夫配置法和三阶剪切变形理论,对不同边界条件的FGM梁自由振动耦合运动进行了研究. Hadji等^[28]针对FGM梁的动力学特性,提出了一种新的一阶剪切变形理论, 对FGM板动力学特性进行了推广. 李容容等^[29]针对旋转FGM圆环形截面柔性悬臂梁的横向振动问题,基于Euler-Bernoulli梁理论和Hamilton原理,建立 了自由振动时的运动微分方程. 章孝顺等^[30]考虑到纵向变形对曲率的影响,建立了考虑大变形效应的系统刚柔耦合动力学模型,并进行了动力学仿真. 方建士等^[31]建立了叶片建立了系统的高次刚柔耦合动力学模型,对柔性叶片的频率转向问题进行了研究. 范纪华等^[32]基于Bezier 插值方法和B样条法对柔性杆变形场进行了描述,并阐述了这两种方法的优点.
本文对旋转运动的中心刚体-功能梯度梁系统的动力学特性进行研究. 为了贴近实际应用,除了考虑到柔性梁的横向弯曲变形和纵向拉伸变形,还将剪切角加入已有的倾角刚柔耦合动力学 模型^[13],运用第二类Lagrange方程建立旋转中心刚体-柔性梁系统的刚柔耦合动力学方程. 通过仿真对比得出剪切角对柔性梁末端响应的影响. 假设功能梯度梁材料特性沿梁轴向按幂律规律分布,对几种不同参数的FGM梁的动力学响应和频率进行对比分析,并对不同截面 函数下梁末端变形及固有频率的变化规律进行描述.

1 动力学方程

1.1 系统物理模型

如图1所示的刚柔耦合系统,一FGM梁以悬臂方式连接在中心刚体上,中心刚体绕定轴转动,以转动轴为原点,建立平面惯性坐标 系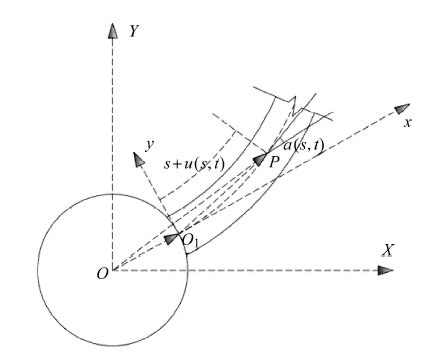 O- XY,以柔性梁与中心刚体的连接点为原点,建立固结于柔性梁上的浮动坐标系 O1- xy,其中, x轴与未变形时柔 性梁轴线重合,与 X轴夹角为 θ0,梁上任意截面的位置可由柔性梁中轴线上弧长 s来描述($0 \leqslant s \leqslant l$). 坐标中心刚体半径为 r0,转动惯量为 Joh,柔性梁长度为 l,密度为 ρ(s),横截面积为 A(s),惯性矩为 I(s),倾角 α(s,t)为弧长坐标 s处中轴线切线与 x轴夹角.
显示原图|下载原图ZIP|生成PPT
图1柔性梁变形示意图
-->Fig. 1Flexible beam deformation
-->

1.2 变形场描述

图1中, OP为点 P在 O- XY坐标系中的矢径, 坐标为 [x0(s,t),y0(s,t)]T,表示为
$\left.\begin{array}{l} x_0 (s,t) = r_0 \cos \theta _0 (t) + \\ \int _0^s {\cos [\theta _0 (t) + \alpha (\tau ,t)][1 + \varepsilon (\tau ,t)] d\tau } \\ y_0 (s,t) = r_0 \sin \theta _0 (t) + \\ \int _0^s {\sin [\theta _0 (t) + \alpha (\tau ,t)][1 + \varepsilon (\tau ,t)] d\tau } \end{array}\!\! \right \} $ (1)
点 P的变形矢量坐标可以表示为
$\left.\begin{array}{l} u(s,t) = \int _0^s {\cos \alpha (\tau ,t) [1 + \varepsilon (\tau ,t)] d\tau } - s \\ v(s,t) = \int _0^s {\sin \alpha (\tau ,t) [1 + \varepsilon (\tau ,t)] d\tau } \end{array}\!\! \right \} $(2)
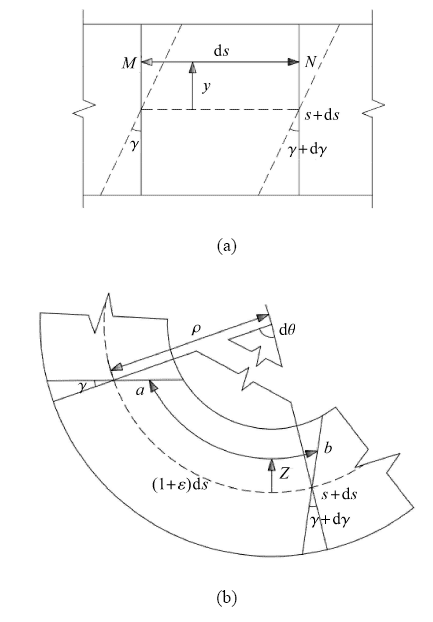
图2是对梁单元的变形描述. 梁上任意一点 M, N位于弧长坐标 s, s+ds处,变形前 M, N连线与梁中轴线平行, 且距离为 y. 微元 MN变形前长度为 ds,变形后沿中轴线拉伸量为 ε,转过角度为 dθ, MN长度变为 (1+ε)ds, M点处剪切角大小为 γ, N点处剪切角大小为 γ+dγ, ρ为曲率半径.
显示原图|下载原图ZIP|生成PPT
图2梁单元变形描述
-->Fig.2Beam element deformation description
-->

系统动能由中心刚体的转动和柔性梁的运动两部分组成,可以写为
$K = \dfrac{1}{2}J_{\rm oh} \dot {\theta }_0 + \dfrac{1}{2} \int _0^l \rho (s)A(s)\cos \gamma (s,t)(\dot {x}_0^2 + \dot {y}_0^2 ) s $(3)
由图2(b)中几何关系得
$\delta d\theta=(1+\varepsilon)ds $(4)
变形后 MN的变形应变为
$\varepsilon _y = \dfrac{(1 + \varepsilon )ds - yd\theta - ds}{ds} =\varepsilon - y\dfrac{ d\theta }{ds} $(5)
梁的轴向变形由轴向拉伸、弯曲变形、剪切变形三部分引起,梁的总变形能可以写为
$ P=\dfrac 12 \int^l_0 \Bigg[ E(s)A(s)\varepsilon^2 (s,t)+ \\ E(s)I(s) \Big ( \dfrac{d\alpha (s,t)}{ds} -\dfrac{d\gamma (s,t)}{ds} \Big )^2 +\dfrac{G(s)A(s)}{k} \gamma^2(s,t) \Bigg ] ds$ (6)
等式右端三项分别为轴向拉伸、弯曲变形、剪切变形所引起的变形能,其中G为剪切模量,k为剪切修正系数.

1.3 动力学方程

为表达方便,以下推导将变量 E(s), ρ(s), A(s), I(s)分别记为 E, ρ, A, I,将 θ0(t), ε(s,t), γ(s,t)分别记为 θ0, ε, γ. 采用假设模态法对柔性梁的变形进行描述,将倾角、拉伸应变、剪切角进行离散处理
$ \left.\begin{array} \alpha (s,t) = {\pmb\phi}_{1} (s){\pmb A}(t) \\ \varepsilon (s,t) = {\pmb\phi} _{2} (s){\pmb B}(t) \\ \gamma (s,t) = {\pmb\phi}_{3} (s){\pmb C}(t) \end{array} \!\! \right\}$ (7)
其中, A(t), B(t)和 C(t)分别为梁倾角变量、拉伸变量及剪切角关于时间变化量的广义坐标列矢量. ?i(s)为一端固支另一端自由的梁模态试函数行向量,各元素为
$\phi _{ i} (s) = \sin [(i - 0.5) \pi s / l] / \sqrt 2 , \ \ i = 1,2, \cdots, N$ (8)
将梁的动能与势能代入第二类拉格朗日方程
$ \dfrac{d}{dt}\left( {\dfrac{\partial K}{\partial \dot {q}}} \right) - \dfrac{\partial K}{\partial q} + \dfrac{\partial V}{\partial q} = F_q $(9)
得到系统的动力学方程
${\pmb M}\ddot {\pmb q} = {\pmb Q} $(10)
式中, M为广义质量阵, q为广义坐标列阵, Q为广义力阵. 分别可以表示为
$\left.\begin{array}{l1} { M} = \left[\!\!\begin{array}{cccc} {{\pmb M}_{11} } & {{\pmb M}_{12} } & {\pmb M}_{13} & {\pmb M}_{14} \\{{\pmb M}_{21} } & {{\pmb M}_{22} } & {\pmb M}_{23} & {\pmb M}_{24} \\ {{\pmb M}_{31} } & {{\pmb M}_{32} } & {\pmb M}_{33} & {\pmb M}_{34} \\ {\pmb M}_{41} & {\pmb M}_{42} & {\pmb M}_{43} & {\pmb M}_{44} \end{array} \!\! \right] \\ \ddot {\pmb q} = \left[ \begin{array}{l} {\ddot {\theta }_0 } \\ \ddot{\pmb A} \\ \ddot{\pmb B} \\ \ddot{\pmb C} \end{array} \!\!\right] , \ \ {\pmb Q} = \left[\!\! \begin{array}{c} { Q}_{\theta _0 } \\ {\pmb Q}_{\pmb A} \\ {\pmb Q}_{\pmb B} \\ {\pmb Q}_{\pmb C} \end{array} \!\! \right] \end{array}\!\!\right\} $(11)
式中各项分别为
$ M_{11} = J_{\rm oh} + \int _0^l \rho A\cos {\pmb\phi}_3 {\pmb C} \\ \Bigg\{ r_0^2 + 2r_0 \int _0^s (1 + {\pmb\phi}_{2} {\pmb B} )\cos {\pmb\phi}_{1} {\pmb A} \tau + \\ \Bigg[\int _0^s (1 + {\pmb\phi}_{ 2} {\pmb B})\cos {\pmb\phi}_{ 1} {\pmb A} \tau \Bigg]^2 + \\ \Bigg[ \int _0^s (1 + {\pmb\phi} _{ 2} {\pmb B})\sin {\pmb\phi}_{ 1} {\pmb A} \tau \Bigg]^2\Bigg\} s $(12)
$ {\pmb M}_{12} = {\pmb M}_{21} ^{\rm T} = \int _0^l {\rho A} \cos {\pmb\phi}_3 {\pmb C}\Bigg[ r_0 \int _0^s {\pmb\phi}_{ 1} (1 +{\pmb\phi} _{ 2} {\pmb B})\cos {\pmb\phi}_{ 1} {\pmb A} \tau + \\ \int _0^s (1 + {\pmb\phi} _{ 2} {\pmb B})\cos {\pmb\phi}_{ 1} {\pmb A} \tau \cdot \int _0^s {\pmb\phi}_{ 1} (1 + {\pmb\phi}_{ 2} {\pmb B})\cos {\pmb\phi}_{ 1} {\pmb A} \tau + \\ \int _0^s (1 + {\pmb\phi}_{ 2} {\pmb B})\sin {\pmb\phi}_{ 1} {\pmb A} \tau \cdot \int _0^s {\pmb\phi}_{ 1} (1 + {\pmb\phi} _{ 2} {\pmb B})\sin {\pmb\phi}_{ 1} {\pmb A} \tau \Bigg ] s $ (13)
$ {\pmb M}_{13} = \int _0^l \rho A\cos {\pmb\phi}_3 {\pmb C} \Bigg[ r_0 \int _0^s {\pmb\phi}_{2} \sin {\pmb\phi}_{1} {\pmb A} \tau + \\ \int _0^s (1 + {\pmb\phi} _{2} {\pmb B})\cos {\pmb\phi}_{1} {\pmb A} \tau \cdot \int _0^s {\pmb\phi}_{2} \sin{\pmb\phi}_{1} {\pmb A} \tau - \\ \int _0^s (1 + {\pmb\phi}_{2} {\pmb B})\sin {\pmb\phi}_{1} {\pmb A} \tau \cdot \int _0^s {\pmb\phi}_{2} \cos {\pmb\phi} _{1} {\pmb A} \tau \Bigg ] s $(14)
$ {\pmb M}_{22} = \int _0^l \rho A\cos {\pmb\phi}_{ 3} {\pmb C }\Bigg[ \int _0^s {\pmb\phi}_{ 1}^{\rm T} (1 + {\pmb\phi}_{ 2} {\pmb B })\cos {\pmb\phi}_{ 1} {\pmb A} \tau \cdot \\ \int _0^s {\pmb\phi}_{ 1} (1 + {\pmb\phi}_{ 2} {\pmb B})\cos {\pmb\phi}_{ 1} {\pmb A} \tau + \\ \int _0^s {\pmb\phi}_{ 1}^{\rm T} (1 + {\pmb\phi}_{ 2} {\pmb B})\sin {\pmb\phi}_{ 1} {\pmb A} \tau \cdot \int_0^s {\pmb\phi}_{ 1} (1 + {\pmb\phi}_{ 2} {\pmb B} )\sin {\pmb\phi}_{ 1} {\pmb A} \tau \Bigg ] s $(15)
$ {\pmb M}_{23} = {\pmb M}_{32} ^{\rm T} = \int _0^l \rho A\cos {\pmb\phi} _{ 3} {\pmb C} \Bigg[ \int _0^s {\pmb\phi}_{ 1}^{\rm T} (1 + {\pmb\phi}_{ 2} {\pmb B})\cos {\pmb\phi}_{ 1} {\pmb A} \tau \cdot \\ \int _0^s {\pmb\phi}_{ 2} \sin {\pmb\phi}_{1} {\pmb A} \tau - \int _0^s {\pmb\phi}_{ 1}^{\rm T} (1 + {\pmb\phi}_{ 2} {\pmb B} )\sin {\pmb\phi}_{ 1} {\pmb A} \tau \cdot \int _0^s {\pmb\phi} _{ 2} \cos {\pmb\phi} _{ 1} {\pmb A} \tau \Bigg] s $(16)
$ {\pmb M}_{33} = \int _0^l \rho A\cos {\pmb\phi}_{ 3} {\pmb C} \Bigg[ \int _0^s {\pmb\phi}_{ 2}^{\rm T} \sin {\pmb\phi}_{ 1} {\pmb A } \tau \cdot \int _0^s {\pmb\phi}_{ 2} \sin {\pmb\phi}_{ 1} {\pmb A} \tau + \\ \int _0^s {\pmb\phi}_{ 2}^{\rm T} \cos {\pmb\phi}_{ 1} {\pmb A} \tau \cdot \int _0^s {\pmb\phi}_{ 2} \cos {\pmb\phi}_{ 1} {\pmb A} \tau \Bigg] s $(17)
$ Q_{\theta _0 } = F_\tau - \int _0^l \rho A \dot {\pmb C} ( - {\pmb\phi} _3 \sin {\pmb\phi}_3 {\pmb C}) \dot {\theta }_0 \\ \Bigg[ r_0^2 + 2r_0 \int _0^s (1 + {\pmb\phi}_{ 2} {\pmb B})\cos {\pmb\phi}_{ 1} {\pmb A } \tau + \Big( \int _0^s (1 + {\pmb\phi}_{ 2} {\pmb B})\cos {\pmb\phi}_{ 1} {\pmb A} \tau ^2 \Big) + \\ \Big( \int _0^s (1 + {\pmb\phi}_{ 2} {\pmb B})\sin {\pmb\phi}_{ 1} {\pmb A} \tau ^2 \Big) \Bigg] \\ +r_0 \int _0^s [{\pmb\phi}_{ 1} \dot {\pmb A} (1 + {\pmb\phi}_{ 2} {\pmb B})\cos {\pmb\phi}_{ 1} {\pmb A} + {\pmb\phi}_{ 2} \dot {\pmb B}\sin {\pmb\phi}_{ 1} {\pmb A}] \tau + \\ \int _0^s (1 + {\pmb\phi}_{ 2} {\pmb B})\cos {\pmb\phi}_{ 1} {\pmb A} \tau \cdot \int _0^s [{\pmb\phi}_{ 1} \dot {\pmb A} (1 + {\pmb\phi}_{ 2} {\pmb B})\cos{\pmb\phi}_{ 1} {\pmb A} + {\pmb\phi}_{ 2} \dot {\pmb B}\sin {\pmb\phi}_{ 1} {\pmb A}] \tau - \int _0^s (1 + {\pmb\phi}_{ 2} {\pmb B})\sin {\pmb\phi}_{ 1} {\pmb A} \tau \cdot \\ \int _0^s \Big[ - {\pmb\phi}_{ 1} \dot{\pmb A} (1 + {\pmb\phi} _{ 2} {\pmb B})\sin {\pmb\phi}_{1} {\pmb A} + {\pmb\phi}_{2} \dot {\pmb B}\cos {\pmb\phi}_{ 1} {\pmb A} \Big] \tau s - \int _0^l {\rho A} \cos {\pmb\phi} _3 {\pmb C}\Bigg\{ 2\dot {\theta }_0 \\ \Big[ r_0 ( \int _0^s {\pmb\phi}_{ 2} \dot {\pmb B}\cos {\pmb\phi} _{ 1} {\pmb A} \tau - \\ \int _0^s {\pmb\phi} _{ 1} \dot {\pmb A}(1 +{\pmb\phi}_{ 2} {\pmb B})\sin{\pmb\phi} _{ 1} {\pmb A} \tau ) + \int _0^s (1 + {\pmb\phi}_{ 2} {\pmb B})\cos {\pmb\phi}_{ 1} {\pmb A} \tau \Big] \cdot \\ \int _0^s \Big [{\pmb\phi}_{ 2} \dot {\pmb B}\cos{\pmb\phi}_{ 1} {\pmb A} - {\pmb\phi}_{ 1} \dot {\pmb A}(1 + {\pmb\phi}_{ 2} {\pmb B})\sin {\pmb\phi}_{ 1} {\pmb A} \Big] \tau + \\ \int _0^s (1 + {\pmb\phi}_{ 2} {\pmb B})\sin {\pmb\phi}_{ 1} {\pmb A} \tau \cdot \int _0^s \Big [{\pmb\phi}_{ 2} \dot {\pmb B}\sin {\pmb\phi}_{ 1} {\pmb A} + {\pmb\phi}_{ 1} \dot {\pmb A}(1 + {\pmb\phi}_{ 2} {\pmb B})\cos {\pmb\phi}_{ 1} {\pmb A} \Big] \tau + \\ \Bigg[ r_0 + \int _0^s (1 + {\pmb\phi}_{ 2} {\pmb B})\cos {\pmb\phi} _{ 1} {\pmb A} \tau \Bigg ] \cdot \\ \Bigg[ 2 \int _0^s {\pmb\phi}_{ 1} \dot {\pmb A} \cdot {\pmb\phi}_{ 2} \dot {\pmb B}\cos {\pmb\phi}_{ 1} {\pmb A} \tau - \int _0^s {\pmb\phi}_{ 1} \dot {\pmb A} \cdot {\pmb\phi} _{ 1} \dot{\pmb A} (1 + {\pmb\phi} _{ 2} {\pmb B})\sin {\pmb\phi} _{ 1} {\pmb A} \tau \Bigg] + \\ \int _0^s (1 + {\pmb\phi}_{ 2} {\pmb B})\sin {\pmb\phi}_{ 1} {\pmb A} \tau \cdot \Bigg[ 2 \int _0^s {\pmb\phi}_{ 1} \dot{\pmb A} \cdot {\pmb\phi}_ {2} \dot{\pmb B} \sin{\pmb\phi}_{ 1} {\pmb A} \tau + \int _0^s {\pmb\phi} _{ 1} \dot{\pmb A} \cdot {\pmb\phi}_{ 1} \dot{\pmb A} (1 + {\pmb\phi}_{ 2} {\pmb B})\cos {\pmb\phi}_{ 1} {\pmb A} \tau \Bigg ] \Bigg \} s $(18)
$ {\pmb Q}_{ A} = \int_0^l \rho A\rho A\cos {\pmb\phi} _{ 3} {\pmb C}\Bigg\{ \dot {\theta }_0^2 \Bigg[ - r_0 \int_0^s (1 + {\pmb\phi} _{ 2} {\pmb B}){\pmb\phi} _{ 1}^{\rm T} \sin {\pmb\phi}_{ 1} {\pmb A}\tau - \int_0^s (1 + {\pmb\phi} _{ 2} {\pmb B})\cos {\pmb\phi} _{ 1} {\pmb A} \tau \cdot \int_0^s (1 + {\pmb\phi} _{ 2} {\pmb B}){\pmb\phi} _{ 1}^{\rm T} \sin {\pmb\phi} _{ 1} {\pmb A}\tau + \\ \int_0^s (1 + {\pmb\phi} _{ 2} {\pmb B})\sin {\pmb\phi} _{ 1} {\pmb A }\tau \cdot \int_0^s (1 + {\pmb\phi} _{ 2} {\pmb B}){\pmb\phi} _{ 1}^{\rm T} \cos {\pmb\phi} _{ 1} {\pmb A}d \tau \Bigg] + \dot {\theta }_0 \Big[ - 2\int_0^s (1 + {\pmb\phi} _{ 2} {\pmb B} ){\pmb\phi} _{ 1}^{\rm T} \sin {\pmb\phi} _{ 1} {\pmb A}\tau \cdot \\ \int_0^s \Big[{\pmb\phi} _{ 1} \dot{\pmb A} (1 + {\pmb\phi} _{ 2} {\pmb B} )\cos {\pmb\phi} _{ 1} {\pmb A}+{\pmb\phi} _{ 2} \dot{\pmb B} \sin {\pmb\phi} _{ 1} {\pmb A} \Big]\tau - 2\int_0^s (1 + {\pmb\phi} _{ 2} {\pmb B}){\pmb\phi} _{ 1}^{\rm T} \cos {\pmb\phi} _{ 1} {\pmb A}\tau \cdot \\ \int_0^s \Big[ - {\pmb\phi} _{ 1} \dot{\pmb A} (1 + {\pmb\phi} _{ 2} {\pmb B})\sin {\pmb\phi} _{ 1} {\pmb A} + {\pmb\phi} _{ 2} \dot {\pmb B}\cos {\pmb\phi} _{ 1} {\pmb A}\Big ]\tau -2\int_0^s {\pmb\phi} _{ 1} \dot{\pmb A} \cdot {\pmb\phi} _{ 2} \dot {\pmb B}\cos {\pmb\phi} _{ 1} {\pmb A}\tau \cdot \int_0^s {\pmb\phi} _{ 1}^{\rm T} (1 + {\pmb\phi} _{ 2} {\pmb B})\cos {\pmb\phi} _{ 1} {\pmb A }\tau + \\ \int_0^s {\pmb\phi} _{ 1} \dot{\pmb A} \cdot {\pmb\phi} _{ 1} \dot {\pmb A}(1 + {\pmb\phi} _{ 2} {\pmb B})\sin {\pmb\phi} _{ 1} {\pmb A} \tau \cdot \int_0^s {\pmb\phi} _{ 1}^{\rm T} (1 + {\pmb\phi} _{ 2} {\pmb B})\cos {\pmb\phi} _{ 1} {\pmb A}\tau -2\int_0^s {\pmb\phi} _{ 1} \dot{\pmb A} \cdot {\pmb\phi} _{ 2} \dot {\pmb B}\sin {\pmb\phi} _{ 1} {\pmb A}\tau \cdot \\ \int_0^s {\pmb\phi} _{ 1}^{\rm T} (1 + {\pmb\phi} _{ 2} {\pmb B})\sin {\pmb\phi} _{ 1} {\pmb A} \tau - \int_0^s {\pmb\phi} _{ 1} \dot{\pmb A} \cdot {\pmb\phi} _{ 1} \dot {\pmb A}(1 + {\pmb\phi} _{ 2} {\pmb B})\cos {\pmb\phi} _{ 1} {\pmb A} \tau \cdot \int_0^s {\pmb\phi} _{ 1}^{\rm T} (1 + {\pmb\phi} _{ 2} {\pmb B})\sin {\pmb\phi} _{ 1} {\pmb A}\tau \Bigg \} s - \\ \int_0^l \rho A\dot{\pmb C} - {\pmb\phi} _3 \sin {\pmb\phi} _3 {\pmb C} \Bigg\{ \dot {\theta }_0 \Big[ r_0 \int_0^s {\pmb\phi} _{ 1}^{\rm T} (1 + {\pmb\phi} _{ 2} {\pmb B})\cos {\pmb\phi} _{ 1} {\pmb A}\tau + \int_0^s (1 + {\pmb\phi} _{ 2} {\pmb B})\cos {\pmb\phi} _{ 1} {\pmb A} \tau \cdot \int_0^s {\pmb\phi} _{ 1}^{\rm T} (1 + {\pmb\phi} _{ 2} {\pmb B})\cos {\pmb\phi} _{ 1} {\pmb A}\tau + \\ \int_0^s (1 + {\pmb\phi} _{ 2} {\pmb B})\sin {\pmb\phi} _{ 1} {\pmb A} \tau \cdot \int_0^s {\pmb\phi} _{ 1}^{\rm T} (1 + {\pmb\phi} _{ 2} {\pmb B})\sin {\pmb\phi} _{ 1} {\pmb A}d \tau \Big] + \int_0^s [{\pmb\phi} _{ 1} \dot{\pmb A} (1 + {\pmb\phi} _{ 2} {\pmb B} )\cos {\pmb\phi} _{ 1} {\pmb A} + {\pmb\phi} _{ 2} \dot{\pmb B} \sin {\pmb\phi} _{ 1} {\pmb A}] \tau \cdot \\ \int_0^s {\pmb\phi} _{ 1}^{\rm T} (1 + {\pmb\phi} _{ 2} {\pmb B})\cos {\pmb\phi} _{ 1} {\pmb A}\tau + \int_0^s [ - {\pmb\phi} _{ 1} \dot{\pmb A} (1 + {\pmb\phi} _{ 2} {\pmb B})\sin {\pmb\phi} _{ 1} {\pmb A} + {\pmb\phi} _{ 2} \dot {\pmb B}\cos {\pmb\phi} _{ 1} {\pmb A}]\tau \cdot \\ \int_0^s [ - {\pmb\phi} _{ 1}^{\rm T} (1 + {\pmb\phi} _{ 2} {\pmb B} )\sin {\pmb\phi} _{ 1} {\pmb A}]\tau \Bigg \} s - \int_0^l EI {\pmb\phi}'^{\rm T}_{ 1} {\pmb\phi}'_{ 1} s{\pmb A} - \int_0^l EI {\pmb\phi}'^{\rm T}_{ 3} {\pmb\phi}'_{ 1} s {\pmb C} $(19)
$ {\pmb Q}_{ B} = \int_0^s \rho A\cos {\pmb\phi} _{ 3} {\pmb C} \Bigg\{ \dot {\theta }_0^2 \Bigg[ r_0 \int_0^s {\pmb\phi} _{ 2}^{\rm T} \cos {\pmb\phi} _{ 1} {\pmb A}\tau + \int_0^s (1 + {\pmb\phi} _{ 2} {\pmb B})\cos {\pmb\phi} _{ 1} {\pmb A}\tau \cdot \int_0^s {\pmb\phi} _{ 2}^{\rm T} \cos {\pmb\phi} _{ 1} {\pmb A}\tau + \\ \int_0^s (1 + {\pmb\phi} _{ 2} {\pmb B})\sin {\pmb\phi} _{ 1} {\pmb A }\tau \cdot \int_0^s {\pmb\phi} _{ 2}^{\rm T} \sin {\pmb\phi} _{ 1} {\pmb A}\tau \Bigg ] + 2\dot {\theta }_0 \Bigg[ \int_0^s {\pmb\phi} _{ 2}^{\rm T} \cos {\pmb\phi} _{ 1} {\pmb A}\tau \cdot \int_0^s {\pmb\phi} _{ 1} \dot {\pmb A}(1 + {\pmb\phi} _{ 2} {\pmb B}) \cos {\pmb\phi} _{ 1} {\pmb A} + \\ {\pmb\phi} _{ 2} \dot{\pmb B} \sin {\pmb\phi} _{ 1} {\pmb A} \Bigg ]\tau - \int_0^s {\pmb\phi} _{ 2}^{\rm T} \sin {\pmb\phi} _{ 1} {\pmb A}\tau \cdot \int_0^s \Big[ - {\pmb\phi} _{ 1} \dot{\pmb A}(1 + {\pmb\phi} _{ 2} {\pmb B}) \sin {\pmb\phi} _{ 1} {\pmb A} + {\pmb\phi} _{ 2} \dot {\pmb B}\cos {\pmb\phi} _{ 1} {\pmb A}\Big]\tau \Big ]- \\ \int_0^s [2{\pmb\phi} _{ 1} \dot{\pmb A} \cdot {\pmb\phi} _{ 2} \dot {\pmb B} \cos {\pmb\phi} _{ 1} {\pmb A} - {\pmb\phi} _{ 1} \dot {\pmb A}(1 + {\pmb\phi} _{ 2} {\pmb B}){\pmb\phi} _{ 1} \dot{\pmb A}\sin {\pmb\phi} _{ 1} {\pmb A}]\tau \cdot \int_0^s {\pmb\phi} _{ 2}^{\rm T} \sin {\pmb\phi} _{ 1} {\pmb A}\tau + \int_0^s [2{\pmb\phi} _{ 1} \dot{\pmb A} \cdot {\pmb\phi} _{ 2} \dot{\pmb B} \sin {\pmb\phi} _{ 1} {\pmb A} + \\ {\pmb\phi} _{ 1} \dot{\pmb A} (1 + {\pmb\phi} _{ 2} {\pmb B}){\pmb\phi} _{ 1} \dot{\pmb A}\cos {\pmb\phi} _{ 1} {\pmb A}]\tau \cdot \int_0^s {\pmb\phi} _{ 2}^{\rm T} \cos {\pmb\phi} _{ 1} {\pmb A}\tau \Bigg\} s - \int_0^l \rho A\dot{\pmb C}X- {\pmb\phi} _3 \sin {\pmb\phi} _3 {\pmb C} \dot {\theta }_0 \Bigg[ r_0 \int_0^s {\pmb\phi} _{ 2}^{\rm T} \sin {\pmb\phi} _{ 1} {\pmb A}d \tau + \\ \int_0^s (1 + {\pmb\phi} _{ 2} {\pmb B})\cos {\pmb\phi} _{ 1} {\pmb A} \tau \cdot \int_0^s {\pmb\phi} _{ 2}^{\rm T} \sin {\pmb\phi} _{ 1} {\pmb A}\tau - \int_0^s (1 + {\pmb\phi} _{ 2} {\pmb B})\sin {\pmb\phi} _{ 1} {\pmb A}\tau \cdot \int_0^s {\pmb\phi} _{ 2}^{\rm T} \cos {\pmb\phi} _{ 1} {\pmb A}\tau + \\ \int_0^s [{\pmb\phi} _{ 1} \dot{\pmb A}(1 + {\pmb\phi} _{ 2} {\pmb B})\cos {\pmb\phi} _{ 1} {\pmb A} + {\pmb\phi} _{ 2} \dot {\pmb B}\sin {\pmb\phi} _{ 1} {\pmb A}]\tau \cdot \int_0^s {\pmb\phi} _{ 2}^{\rm T} \sin {\pmb\phi} _{ 1} {\pmb A}\tau \Bigg] + \int_0^s \Big[ - {\pmb\phi} _{ 1} \dot {\pmb A}(1 + {\pmb\phi} _{ 2} {\pmb B})\sin {\pmb\phi} _{ 1} {\pmb A} + \\ {\pmb\phi} _{ 2} \dot{\pmb B}\cos {\pmb\phi} _{ 1} {\pmb A} \Big]\tau \cdot \int_0^s {\pmb\phi} _{ 2}^{\rm T} \cos {\pmb\phi} _{ 1} {\pmb A}\tau \Big\} s - \int_0^l {EA} {\pmb\phi} _{ 2}^{\rm T} {\pmb\phi} _{ 2} s{\pmb B} $(20)
由于式(1)不含 γ项,因此式(11)广义坐标列阵中不含 C?项
$\left.\begin{array}{ll} {\pmb M}_{14} = {\pmb M}_{41} ^{\rm T} = {\bf 0} , \ \ {\pmb M}_{24} = {\pmb M}_{42} ^{\rm T} = {\bf 0} \\ {\pmb M}_{34} = {\pmb M}_{43} ^{\rm T} = {\bf 0} , \ \ {\pmb M}_{44} = {\bf 0} \end{array}\right\} (21)$
$ {\pmb Q }_{ C} = \dfrac{1}{2} \int _0^l \rho A \dot{\pmb C} (- {\pmb\phi}_3 \sin {\pmb\phi}_3 {\pmb C}) \cdot \Big \{ - \sin \theta _0 \cdot \\ \Big[ \dot {\theta }_0 \Big(r_0 + \int _0^s \Big(1 +{\pmb\phi}_{ 2} {\pmb B} \Big)\cos {\pmb\phi}_{ 1} {\pmb A}\tau + \\ \int _0^s {\pmb\phi}_{ 1} \dot{\pmb A} (1 +{\pmb\phi}_{ 2} {\pmb B})\cos {\pmb\phi}_{ 1} {\pmb A} + {\pmb\phi}_{ 2} \dot {\pmb B}\sin {\pmb\phi}_{ 1} {\pmb A})\Big ) \Big ] \Big\} \tau + \\ \cos \theta _0 \cdot \Bigg\{ \int _0^s \Big[ - {\pmb\phi}_{ 1} \dot {\pmb A}(1 + {\pmb\phi}_{ 2} {\pmb B})\sin {\pmb\phi}_{ 1} {\pmb A} + \\ {\pmb\phi}_{ 2} \dot{\pmb B} \cos{\pmb\phi}_{ 1} {\pmb A} \Big ] \tau -\dot {\theta }_0 \int _0^s (1 + {\pmb\phi}_{ 2} {\pmb B} )\sin {\pmb\phi}_{ 1} {\pmb A} \tau \Bigg\} ^2 + \\ \sin \theta _0 \cdot \Bigg\{ \int _0^s \Big[ - {\pmb\phi}_{ 1} \dot{\pmb A} (1 + {\pmb\phi}_{ 2} {\pmb B})\sin {\pmb\phi}_{ 1} {\pmb A} + \\ {\pmb\phi}_{ 2} \dot{\pmb B} \cos {\pmb\phi}_{ 1} {\pmb A} \Big] \tau - \dot {\theta }_0 \int _0^s (1 + {\pmb\phi}_{ 2} {\pmb B} )\sin {\pmb\phi}_{ 1} {\pmb A} \tau \Bigg\} + \\ \cos \theta _0 \cdot \Big\{ \dot {\theta }_0 \Big[ r_0 + \int _0^s (1 + {\pmb\phi}_{ 2} {\pmb B} )\cos {\pmb\phi}_{ 1} {\pmb A} \tau \Big] + \\ \int _0^s \Big [{\pmb\phi}_{ 1} \dot{\pmb A} (1 + {\pmb\phi} _{ 2} {\pmb B})\cos {\pmb\phi}_{ 1} {\pmb A} + {\pmb\phi} _{ 2} \dot {\pmb B}\sin {\pmb\phi}_{ 1} {\pmb A}\Big] \tau )^2 \Big\} - \\ \int _0^l {EI} {\pmb\phi}'^{\rm T}_{ 1}{\pmb\phi}'_{ 3} s {\pmb A} - \int _0^l {EI} {\pmb\phi}'^{\rm T}_{ 3}{\pmb\phi}'_{ 3} s {\pmb C} + \\ \int _0^l \dfrac{GA}{k} {\pmb\phi}'^{\rm T}_{ 3} {\pmb\phi}'_{ 3} s{\pmb C} $(22)
式(10)~式(22)即为考虑剪切的中心刚体-柔性梁系统的刚柔耦合动力学模型,该模型考虑了做大位移运动的柔性梁系统的横向弯曲、纵向拉伸及剪切角的耦合,是基于Timoshenko梁模型假设下获得的完整倾角动力学模型(slope angle model of Timoshenko beam,SAMTB). 将方程中与C和 ?3有关的项舍去,方程即退化为不考虑剪切效应的Euler-Bernoulli梁倾角刚柔耦合动力学模型.

2 动力学仿真

2.1 对剪切倾角模型的验证

上文已经建立了系统的刚柔耦合动力学模型,为了验证其正确性,本节首先与以往文献所建立的模型进行对比,编写程序对上节所建立的刚柔耦合动力学方程进行求解,计算时取前三阶模态. 设系统由静止开始加速转动,已知柔性梁大范围运动规律与文献^[9]给出的规律相同
$\dot {\theta }_0 = \left\{ \begin{array}{ll} \dfrac{\omega _0 }{T}t - \dfrac{\omega _0 }{2 \pi }\left( {\sin \dfrac{2 \pi }{T}t} \right) , & 0 \leqslant t \leqslant T \\ \omega _0 , & t > T \end{array}\right. $(23)
其中, $T =15$ s, 柔性梁物理参数为：长$l =8$ m, 梁横截面积$A =7.297 \times 10^{ - 5 }$ m$^{2}$, 惯性 矩$I=8.219 \times 10^{ - 9 }$ m$^{4}$, 梁密度 $\rho =2.767 \times 10 ^{3 }$ kg/m$^{3}$, 弹性模量$E =6.895\times 10^{10 }$ N/m$^{2}$, 梁宽比$R_{\rm b} =1$, 梁高比$R_{\rm h} =1$.
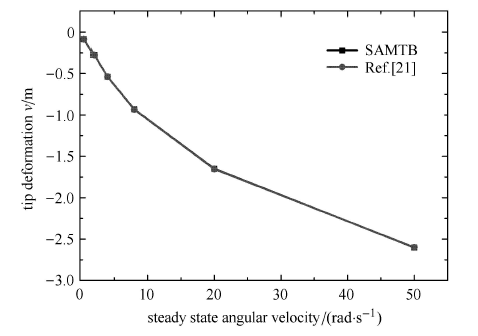
对不同转速下柔性梁末端横向变形进行对比,分别取转速 ω0=0.6,2,4,8,20和50 rad/s,对梁末端横向变形进行计 算. 由图3对比可以看出,在不同转速下,本文建立的考虑剪切角的柔性梁倾角模型与文献[9]细长梁模型计算出的末端最大横向变形一 致,本文模型虽然考虑了剪切效应,但在对细长梁计算时,剪切效应的影响十分微小,由此说明本文所提出的动力学模型 是正确的.
显示原图|下载原图ZIP|生成PPT
图3不同转速下柔性梁末端变形对比
-->Fig. 3Comparison of tip deformation of flexible beam at different speed
-->

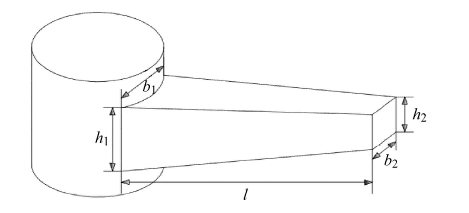
为研究剪切效应对FGM梁末端变形的影响, 对不同尺寸FGM楔形梁进行分析, 如图4所示, 柔性梁为楔形梁, 由铝和陶瓷两种材料构成, 相关参数为： $\rho_{a}=2 027$ kg/m$^{3}$, $E_{a}=70$ GPa, $\rho_{z}=5 700$ kg/m$^{3}$, $E_{z} =200$ GPa. 梁的物理参数沿轴向呈幂律分布
$ {\lambda }(s) = ( {\lambda }_a - {\lambda }_z )\xi ^N + {\lambda }_z $(24)
其中 $\xi = s/l$, $N$为功能梯度指数, 表示材料的均匀程度. 系统的其他物理参数为：长$l =4$ m, 梁宽比$R_{\rm b}=b_{2} : b_{1} =0.2$, 梁高比$R_{\rm h}=h_{2}: h_{1} =0.4$.
显示原图|下载原图ZIP|生成PPT
图4楔形梁系统几何示意图
-->Fig. 4Wedge beam system
-->

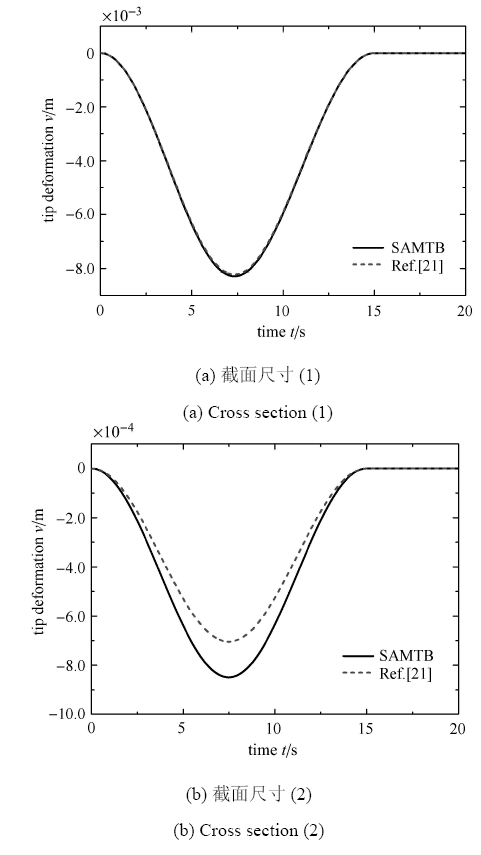
图5给出了固定端横截面积和惯性矩分别取为(1) A0=4.601×10-4m², I0=2.031×10-7m⁴; (2) A0=3.255×10-3m², I0=2.768×10-5m⁴时末端横向变形与 文献^[21]所得结果对比曲线,其中文献^[21]计算结果以通过数值计算与以往文献对比验证其正确. 由图中可以看出,当截面积较小时,剪切倾角模型与文献^[21]计算出的结果基本一致,截面积数量级增大后,梁末端横向变形差异明显. 说明当梁的横截面积与长度的比值较大时,剪切效应的影响十分明显.
显示原图|下载原图ZIP|生成PPT
图5不同截面尺寸功能梯度柔性梁末端变形对比
-->Fig. 5Comparison of tip deformation of flexible beam with different cross sections
-->

2.2 考虑剪切角的动力学模型的仿真

为了研究不同截面参数对FGM楔形梁动力学响应的影响,本节进行大范围运动已知情形下系统动力学仿真,各种物理参数同上节,大范围运动规律如下
$ \dot {\theta }_0 = \left\{\begin{array}{ll} \dfrac{6}{15}t - \dfrac{6}{2 \pi }\sin ( {\dfrac{2\pi }{15}t} )rad/s, & 0 \leqslant t \leqslant T \\ 6rad/s, & t > T \end{array}\right. $(25)
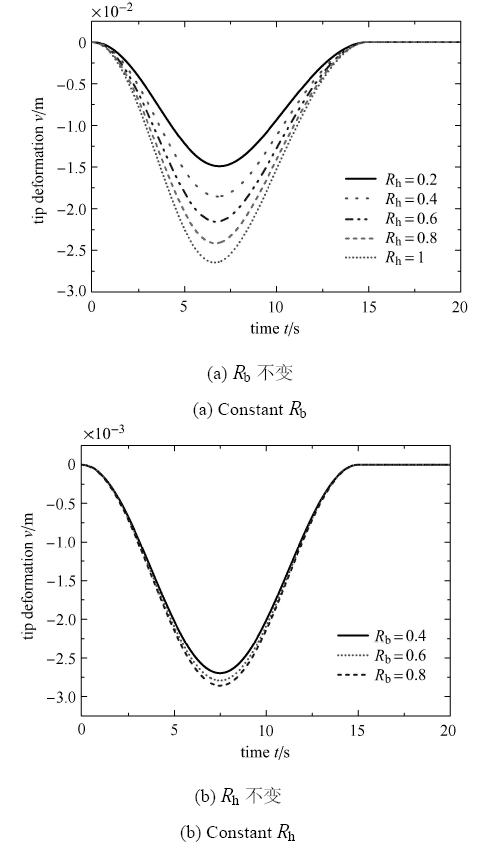
考虑两种变截面FGM楔形梁：(a)控制宽度比不变,改变高度比;(b)控制高度比不变,改变宽度比. 两种情形下FGM楔形梁 的末端变形分别如图6(a)和图6(b)所示. 从图6可以看出,当 Rb不变时,梁末端变形随着 Rh的增大而呈现有规律 的减小;当 Rh不变时,梁末端变形虽然也会随着 Rb的增大而有所减小,但变化十分微小. 由此可以看出,梁高 比 Rh对梁末端变形的影响较大,在设计中,通过对参数 Rh的改变来对FGM楔形梁进行结构设计会更为有效.
显示原图|下载原图ZIP|生成PPT
图6不同R_{\mathrm{b}}和R_{\mathrm{h}}时柔性梁末端变形对比
-->Fig. 6Contrast of tip deformation of flexible beam with different R_{\mathrm{b}} and R_{\mathrm{h}}
-->

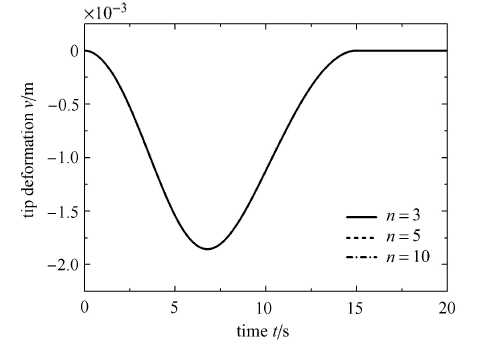
为了研究不同阶数模态对计算结果的影响,以下分别取模态阶数为3,5和10进行计算,大范围转动规律如式(25),取楔 形梁长 l=4m,梁宽比 Rb=0.2,梁高比 Rh=0.4,固定端横截面积 A0=4.601×10-4m²,惯性矩 I0=2.031×10-7m⁴ 计算结果如图7所示,从图7可以看出, 对于3种模态阶数的取值,计算结果基本一致,但阶数取10时,计算效率较低,所以,在满足计算精度要求的情况下, 可取前3阶模态函数进行计算.
以下选取两种情况对FGM楔形梁进行计算, 分 别改变FGM梁的尺寸,对其末端变形进行分析对比.
显示原图|下载原图ZIP|生成PPT
图7不同模态阶数取值时柔性梁末端变形对比
-->Fig. 7Contrast of tip deformation of flexible beam with different modal order
-->

第1种情况：悬臂端截面材料为铝,自由端截面材料为陶瓷;
第2种情况：悬臂端截面材料为陶瓷,自由端截面材料为铝.
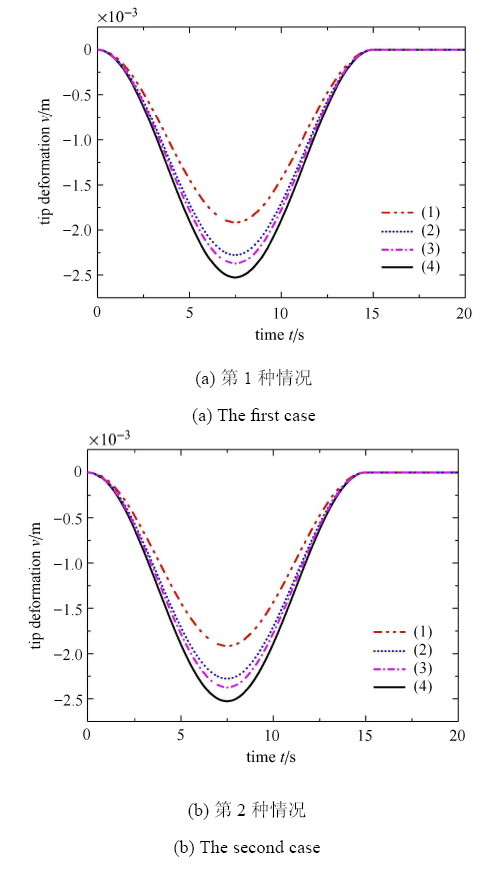
对于以上两种情况,分别选取(1) A0=4.601×10-4m², I0=2.031×10-7m⁴; (2) A0=3.225×10-4m², I0=1.873×10-7m⁴; (3) A0=2.103×10-4m², I0=1.030×10-7m⁴; (4) A0=1.313×10-4m², I0=8.376×10-8m⁴计算柔性梁末端变形,结 果如图8所示. 从计算结果可以看出,改变柔性梁的截面尺寸,在数量级不改变的情况下,对于以上两种情况,均有相似的影响, 即柔性梁末端变形随着梁尺寸的改变呈大致均匀的变化. 在相同的几何尺寸下,第2种情况柔性梁末端变形峰值较大.
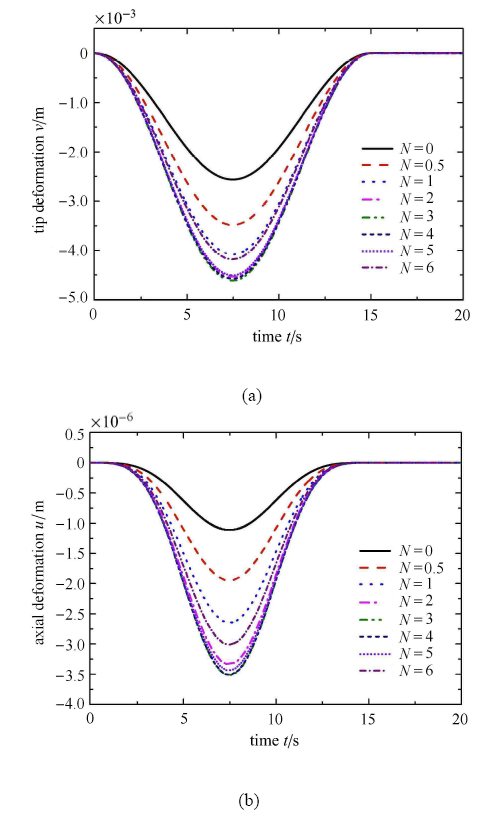
在第1种情况下,分别选取几种不同的功能梯度指数来研究其对FGM楔形梁末端变形的影响,图9给出了功能梯度 指数分别取0,0.5,1,2,3,4,5,6时梁末端变形规律,从图9可以看出,柔性梁末端横向变形及轴向变形随功能梯度指 数呈先增后减的趋势,而且FGM梁的末端响应与纯材料梁( N=0)的末端响应有着明显的不同,所以,材料的选取及功能梯度参数的取值对FGM梁动力学特性有着重大的影响.
显示原图|下载原图ZIP|生成PPT
图8不同截面尺寸柔性梁末端变形对比
-->Fig. 8Comparison of deformation of flexible beam ends with different cross sections
-->

显示原图|下载原图ZIP|生成PPT
图9不同功能梯度参数FGM梁末端变形对比
-->Fig. 9Comparison of the deformation of the ends of FGM beam with different functional gradient parameters
-->

3 振动分析

3.1 模型比较及验证

本节中将推导得出旋转轴向FGM梁的横向弯曲无量纲固有频率特征方程,通过与其他文献所得结果对比,验证其正确性. 此外,对不同比例的楔形梁的固有频率进行研究分析,通过调整梁的宽度比、高度比研究其对FGM梁频率的影响.
定义无量纲变量
$\sigma = \dfrac{R}{l} , \ \ \lambda = \sqrt {\dfrac{\rho _0 A_0 l^4\Omega ^2}{EI}} , \ \ \xi=\dfrac{s}{l} $(26)
将楔形梁的密度和弹性模量用无量纲变量表示
$\left.\begin{array}{ll} \rho (\xi ) = \sum_{i = 0}^p {a_i \xi ^i} \\ E(\xi ) = \sum_{i = 0}^q {b_i \xi ^i} \end{array}\right\} $(27)
式中, p和 q分别为求和式中多项式的次数, ai和 bi为各项中的常系数.
将式(11)矩阵中第二行用泰勒公式展开,并省去二次以上项,可以得到梁的横向弯曲自由振动方程
$ \tilde{\pmb M }_{22}^{\rm T} \ddot{\pmb A} + \tilde {\pmb K }_{22}^{\rm T} {\pmb A} = {\bf 0} $(28)
其中
$\tilde {\pmb M}_{22}^{\rm T} = \int _0^l \rho (s){\pmb A}(s) {\pmb\psi}_2^{\rm T}{\pmb\psi}_2 s (29)$
$ \tilde {\pmb K}_{22}^{\rm T} = \varOmega ^2 \int _0^l \rho (s){\pmb A}(s)[(R + s){\pmb\psi}_3 - {\pmb\psi}_1^{\rm T} {\pmb\psi}_1 ] s + \\ \int _0^l E(s) I(s){\pmb\phi}'^{\rm T}_A (s){\pmb\phi}'_A (s) s - \\ \Big[ \int _0^l {E(s)} I(s){\pmb\phi}'^{\rm T}_A (s){\pmb\phi}'_A (s) s \Big ]^2 \Big / \\ \Big[\int _0^l {E(s)} I(s){\pmb\phi}'^{\rm T}_A (s){\pmb\phi}'_A (s) s - \\ \int _0^l \dfrac{G(s){\pmb A}(s)}{k}{\pmb\phi}'^{\rm T}_A(s){\pmb\phi}' _A (s) s\Big] $(30)
对方程(28)进行无量纲处理,可以得到系统的无量纲横向弯曲自由振动方程
${\mathop{\pmb M}\limits^{\frown}}_{22}^{\rm T} \ddot{\pmb A} +{\mathop{\pmb K}\limits^{\frown}}_{22}^{\rm T} {\pmb A} = {\bf 0} $(31)
其中
${\mathop{\pmb M}\limits^{\frown}}_{22}^{\rm T} = \int _0^{1} \Bigg [ \sum_{i =0}^p a_i \xi ^i(1 - \xi + \xi R_{\rm b} )(1 - \xi + \xi R_h ) {\pmb\psi}_1^{\rm T} (\xi ){\pmb\psi}_1 (\xi) \Bigg] \xi $ (32)
${\mathop{\pmb K}\limits^{\frown}}_{22}^{\rm T} = \lambda ^2 \int _0^1 \Bigg \{ \sum_{i = 0}^p a_i \xi ^i(1 - \xi + \xi R_{\rm b} )(1 - \xi + \xi R_{\rm h} ) \cdot \\ [(\sigma + \xi ){\pmb\psi}_3 ( \xi ) - {\pmb\psi} _1^{\rm T} (\xi ){\pmb\psi}_1 ( \xi ) ] \Bigg \} \xi + \\ \int _0^1 \Bigg [ \sum_{i = 0}^q b_i \xi ^i(1 - \xi + \xi R_{\rm b} )^3(1 - \xi + \xi R_{\rm h} ) {\pmb\phi}'^{\rm T}(s){\pmb\phi}' (s) \Bigg] \xi + \\ \int _0^1 \Bigg[ \sum_{i = 0}^q b_i \xi ^i(1 - \xi + \xi R_{\rm b} )^3(1 - \xi + \xi R_{\rm h} ) \Bigg]^2{\pmb\phi}'^{\rm T}(s){\pmb\phi}' (s)\Big / \\ \Bigg[\sum_{i = 0}^q b_i \xi ^i(1 - \xi + \xi R_{\rm b} )^3(1 - \xi + \xi R_{\rm h} ) - \\ \dfrac{1}{k(1 + \mu )}\sum_{i = 0}^p a_i \xi ^i(1 - \xi + \xi R_{\rm b} )(1 - \xi + \xi R_{\rm h} ) \xi \Bigg] (33)$
求解方程(31),可以得到特征方程
$\omega ^2{\mathop{\pmb M}\limits^{\frown}}_{22}^{\rm T} {\pmb \varPsi } = {\mathop{\pmb K}\limits^{\frown}}_{22}^{\rm T} {\pmb \varPsi } $ (34)
其中, ω是无量纲固有频率, Ψ是特征向量矩阵,求解这一方程,得出的结果即为旋转轴向FGM梁系统 的横向弯曲无量纲固有频率.
分别给出3组不同系数 ai, bi取值情况下等截面FGM梁的横向弯曲无量纲第一固有频率,所得结果与文献^[21]、文献^[19]进行对比. 由表1可以得出, 本文所建立的SAMTB模型计算出的FGM梁系统的横向弯曲无量纲第一固有频率与其他文献中的结果基本一致.
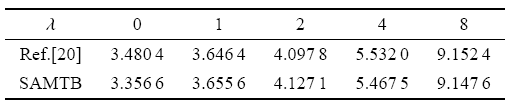
表2给出了本文剪切倾角模型与文献^[20]计算得出的均质Timoshenko梁固有频率对比数据,取 Rh=Rb=0.8, E=3.059G, σ=0. 从表2可以看出,在不同 λ取值情况下,本节公式计算得出的固有频率值与文献[20]的计算结果基本吻合.
Table 1
表 1
表 1等截面FGM梁系统的横向弯曲无量纲第一固有频率
Table 1Cross-sectional FGM beam system transverse bending dimensionless first natural frequency


新窗口打开
Table 2
表 2
表 2楔形均质Timoshenko梁的横向弯曲无量纲第一固有频率
Table 2Transverse bending of wedge-shaped timoshenko beams Dimensionless first natural frequency


新窗口打开

3.2 不同比例楔形梁固有频率对比

以下研究不同的宽度比和高度比对FGM楔形梁横向弯曲无量纲固有频率的影响,密度函数和弹性模量函数分别取 为 a0=1和 b0=26, b1=16, b2=6, b3=-4, b4=1. 分别取 Rh=1, Rb=1; Rh=0.8, Rb=0.6; Rh=0.5, Rb=0.5; Rh=0.4, Rb=0.2. 在不同 σ, λ的情况下,计算得出第一阶无量纲固有频率. 表3为采用剪切倾角模型计算出的4种不同宽度比及高度比下第一阶无量纲固有频率.
Table 3
表 3
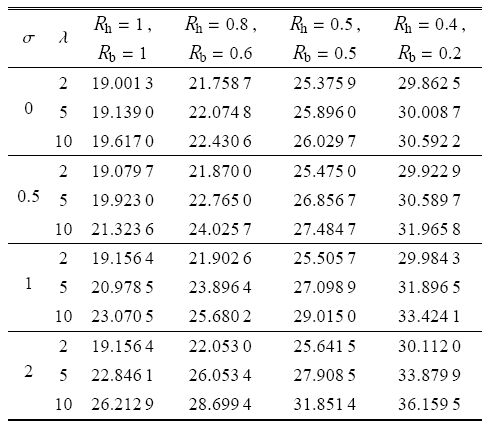
表 34种不同截面梁的横向弯曲第一阶无量纲固有频率比较
Table 3Comparison of the first order non-dimensional natural frequencies of four different cross-section beams


新窗口打开
从表3可以看出,对于FGM楔形梁,在控制其他参数不变的情况下,其横向弯曲无量纲第一阶固有频率随着 Rh, Rb的减 小而增大,变化程度在不同 σ, λ取值时基本一致;在控制 σ, Rh, Rb不变时,固有频率随 λ增大而增大,且 σ取值越大时,变化越明显.

4 结 论

提出了SAMTB动力学建模方法,该方法通过梁轴线上点的弧长坐标描述变形,利用梁倾角、纵向拉伸量、剪切角等变量写出系统的动能和势能表达式,运用第二类拉格朗日方程建立了考虑剪切效应的旋转梁系统的倾角刚柔耦合动力学模型. 通过对工程中出现的旋转FGM楔形梁的动力学响应及频率的仿真计算,验证了基于Timoshenko梁理论的旋转梁刚柔耦合动力学模型的正确性. 该模型可推广应用于计算FGM楔形梁类变材料、变截面结构的动力学问题. 研究表明,FGM楔形梁的梁高比对梁末端变形的影响较梁宽比的影响更为显著;材料组分及梯度分布规律和截面参数的选取均会对旋转FGM楔形梁的频率产生较大影响.
本文的创新之处在于：以倾角模型为基础,考虑了剪切效应的影响,建立了全新的中心刚体-柔性梁系统刚柔耦合动力学模型;计算了FGM梁系统动力学响应,而对于这类功能梯度材料,一般商业软件并没有相应的计算模块对其进行分析;研究了材料的选取及分布均匀程度对系统动力学特性的影响;推导出了考虑剪切效应的中心刚体-FGM梁系统横向弯曲振动方程,并对这类系统的振动特性进行了分析.
The authors have declared that no competing interests exist.

---

参考文献文献选项 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]	Koizumi M. FGM activities in Japan .Composites Part B,1997,28B:1-4 [本文引用: 1]
[2]	吴胜宝, 章定国, 康新等. 刚体-微梁系统的动力学特性 . 机械工程学报, 2010, 46(3): 76-82 [本文引用: 1] (Wu Shengbao, Zhang Dingguo, Kang Xin. Dynamic properties of hub-microbeam system .Journal of Mechanical Engineering, 2010, 46(3): 76-82 (in Chinese)) [本文引用: 1]
[3]	Kane TR,Ryan R,Banerjee AK. Dynamics of a cantilever beam attached to a moving base .Journal of Guidance,Control and Dynamics,1987,10(2):139-151 [本文引用: 2]
[4]	Yoo HH, Ryan RR, Scott RA. Dynamics of flexible beams undergoing overall motions .Journal of Sound & Vibration, 1995, 181(2): 261-278 [本文引用: 2]
[5]	Yoo HH, Chung J. Vibration analysis of rotating cantilever beams .Journal of Sound and Vibration, 1998, 212(5): 807-828 [本文引用: 2]
[6]	Yan A. Frequency analysis of a rotating cantilever beam using assumed mode method with coupling effect .Mechanics Based Design of Structures & Machines, 2006, 34(1): 25-47 [本文引用: 2]
[7]	Yang H, Hong JZ, Yu Z. Dynamics modelling of a flexible hub-beam system with a tip mass .Journal of Sound & Vibration, 2003, 266(4): 759-774 [本文引用: 2]
[8]	和兴锁, 邓峰岩, 王睿. 具有大范围运动和非线性变形的空间柔性梁的精确动力学建模 . 物理学报, 2010, 59(3): 1428-1436 [本文引用: 2] (He Xingsuo, Deng Fengyan, Wang Rui. Exact dynamic modeling of a spatial flexible beam with large overall motion and nonlinear deformation .Acta Physica Sinica, 2010, 59(3): 1428-1436 (in Chinese)) [本文引用: 2]
[9]	刘锦阳, 洪嘉振. 柔性体的刚-柔耦合动力学分析 . 固体力学学报, 2002, 23(2): 159-166 [本文引用: 4] (Liu Jinyang, Hong Jiazhen. Rigid-flexible coupling dynamics analysis of flexible body .Journal of Solid Mechanics, 2002, 23(2): 159-166(in Chinese)) [本文引用: 4]
[10]	章定国,余纪邦. 做大范围运动的柔性梁的动力学分析 . 振动工程学报,2006,19(4):475-480 [本文引用: 2] (Zhang Dingguo, Yu Jibang. Dynamical analysis of a flexible cantilever beam with large overall motions .Journal of Vibration Engineering, 2003, 81(32): 2829-2841 (in Chinese)) [本文引用: 2]
[11]	Cai GP, Hong JZ, Yang SX. Dynamic analysis of a flexible hub-beam system with tip mass .Mechanics Research Communications, 2005, 32(2): 173-190 [本文引用: 2]
[12]	王新栋, 邓子辰, 王艳等. 基于时间有限元方法的旋转柔性叶片动力学响应分析 . 应用数学和力学, 2014, 35(4): 353-363 [本文引用: 2] (Wang Xindong, Deng Zichen, Wang Yan, et al. Dynamic behavior analysis of rotational flexible blades based on time-domain finite element method .Applied Mathematics and Mechanics, 2014, 35(4): 353-363 (in Chinese)) [本文引用: 2]
[13]	Li L, Zhu WD, Zhang DG, et al. A new dynamic model of a planar rotating hub-beam system based on a description using the slope angle and stretch strain of the beam .Journal of Sound & Vibration, 2015, 345: 214-232 [本文引用: 3]
[14]	韩广才, 吴艳红, 王寅超等. 旋转叶片刚柔耦合系统动力学分析 . 哈尔滨工程大学学报, 2011, 32(6): 736-741 [本文引用: 1] (Han Guangcai, Wu Yanhong, Wang Yinchao, et al. Dynamic analysis of a rotating blade with a rigid-flexible coupling pre-twisted angle and variable cross-section .Journal of Harbin Engineering University, 2011, 32(6): 736-741 (in Chinese)) [本文引用: 1]
[15]	陈思佳, 章定国. 中心刚体-变截面梁系统的动力学特性研究 . 力学学报, 2011, 43(4): 790-794 [本文引用: 1] (Chen Sijia, Zhang Dingguo. Dynamics of hub-variable section beam systems .Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(4): 790-794 (in Chinese)) [本文引用: 1]
[16]	黎亮, 章定国, 洪嘉振. 中心刚体-功能梯度材料梁系统的动力学特性 . 机械工程学报, 2013, 49(13): 77-84 [本文引用: 1] (Li Liang, Zhang Dingguo, Hong Jiazhen. Dynamics of hub-functionally graded material beam systems .Journal of Mechanical Engineering, 2013, 49(13): 77-84 (in Chinese)) [本文引用: 1]
[17]	Oh SY, Librescu L, Song O. Vibration of turbomachinery rotating blades made-up of functionally graded materials and operating in a high temperature field .Acta Mechanica, 2003, 166(1-4): 69-87 [本文引用: 1]
[18]	Yuan J, Pao YH, Chen W. Exact solutions for free vibrations of axially inhomogeneous Timoshenko beams with variable cross section .Acta Mechanica, 2016, 227(9): 1-19 [本文引用: 1]
[19]	Zarrinzadeh H, Attarnejad R, Shahba A. Free vibration of rotating axially functionally graded tapered beams .Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering, 2012, 226(4): 363-379 [本文引用: 2]
[20]	Rajasekaran S. Free vibration of centrifugally stiffened axially functionally graded tapered Timoshenko beams using differential transformation and quadrature methods .Applied Mathematical Modelling, 2013, 37(6): 4440-4463 [本文引用: 3]
[21]	Li L, Zhang D. Dynamic analysis of rotating axially FG tapered beams based on a new rigid-flexible coupled dynamic model using the B-spline method .Composite Structures, 2015, 124: 357-367 [本文引用: 5]
[22]	Das D. Free vibration and buckling analyses of geometrically non-linear and shear-deformable FGM beam fixed to the inside of a rotating rim .Composite Structures, 2017, 179(1): 628-645 [本文引用: 1]
[23]	梁波,赵永刚,姚世平.FGM梁考虑纵向振动的动力学分析 .甘肃科学学报,2017, 29(5): 1-5 [本文引用: 1] (Liang Bo, Zhao Yonggang, Yao Shiping. Dynamic analysis of FGM beam considering longitudinal vibration . Journal of Gansu Sciences, 2017, 29(5): 1-5 (in Chinese)) [本文引用: 1]
[24]	Li LI, Zhang DG, Guo YB, et al. Dynamics of rigid-flexible coupling FGM beam systems in variable temperature fields .Journal of Vibration Engineering, 2017, 30(1): 9-19 [本文引用: 1]
[25]	Frikha A, Hajlaoui A, Wali M, et al. A new higher order C 0, mixed beam element for FGM beams analysis .Composites Part B Engineering, 2016, 106: 181-189 [本文引用: 1]
[26]	Paul A, Das D. Free vibration analysis of pre-stressed FGM Timoshenko beams under large transverse deflection by a variational method .Engineering Science & Technology An International Journal, 2016, 19(2): 1003-1017 [本文引用: 1]
[27]	Wattanasakulpong N, Bui TQ. Vibration analysis of third-order shear deformable FGM beams with elastic support by chebyshev collocation method .International Journal of Structural Stability & Dynamics, 2017, 18: 1850071 [本文引用: 1]
[28]	Hadji L, Daouadji TH, Bedia EA. Dynamic behavior of FGM beam using a new first shear deformation theory .Earthquakes & Structures, 2016, 10(2): 451-461 [本文引用: 1]
[29]	李容容, 王忠民, 姚晓莎. 旋转FGM圆环形截面柔性梁的振动特性 . 应用力学学报, 2017, 34(3): 417-423 [本文引用: 1] (Li Rongrong, Wang Zhongmin, Yao Xiaosha. Vibration characteristics of rotating flexible ring beam made of functionally graded material .Journal of Applied Mechanics, 2017, 34(3): 417-423 (in Chinese)) [本文引用: 1]
[30]	章孝顺, 章定国, 洪嘉振. 考虑曲率纵向变形效应的大变形柔性梁刚柔耦合动力学建模与仿真 . 力学学报, 2016, 48(3): 692-701 [本文引用: 1] (Zhang Xiaoshun, Zhang Dingguo, Hong Jiazhen. Rigid-flexible coupling dynamic modeling and simulation with the longitudinal deformation induced curvature effect for a rotating flexible beam under large deformation .Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(3): 692-701 (in Chinese)) [本文引用: 1]
[31]	方建士, 章定国. 旋转薄板的一种高次动力学模型与频率转向 . 力学学报, 2016, 48(1): 173-180 [本文引用: 1] (Fang Jianshi, Zhang Dingguo. A high-order rigid-flexible coupling model and frequency veering of a rotating cantilever thin plate .Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(1): 173-180 (in Chinese)) [本文引用: 1]
[32]	范纪华, 章定国. 基于变形场不同离散方法的柔性机器人动力学建模与仿真 . 力学学报, 2016, 48(4): 843-856 [本文引用: 1] (Fan Jihua, Zhang Dingguo. Dynamic modeling and simulation of flexible robots based on different discretization methods .Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(4): 843-856 (in Chinese)) [本文引用: 1]