, 宋琛琛ONE KIND OF TRANSVERSE ISOTROPIC STRENGTH CRITERION AND THE TRANSFORMATION STRESS SPACE1)
WanZheng, SongChenchen中图分类号:TU43
文献标识码:A
通讯作者:
收稿日期:2018-04-20
网络出版日期:2018-09-18
版权声明:2018力学学报期刊社力学学报期刊社 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (3848KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
自然界中的很多天然材料具备强烈的各向异性,比如岩石、木材、土壤等材料在宏观尺度上各方向上表现出较大的差异性. 显然,从变形以及破坏机理角度解释,则是由于材料组成材料在细观层次上具有显著的差异性所导致的. Oda等[1]的试验结果证实：对于岩土材料而言,则是由于微观颗粒在自然沉积作用过程中颗粒的空间排列定向性以及土壤团粒胶结过程中的复杂作用而形成的结果. 一般而言,对于层状水平分布的岩土材料,由于在水平方向内颗粒间的随机分布状态,颗粒长轴一般平行于水平沉积面,因而形成了正交各向异性,也可称之为横观各向同性性质.Abelev等[2]针对大主应力与沉积面呈不同夹角下的试样开展了真三轴排水加载测试,结果表明：大主应力方向与沉积面法向一致的试样表现出了更高的应力比强度,而当大主应力方向与沉积面法向相互垂直时,则表现出了较低的应力比强度.Kirkgard等[3]针对旧金山湾区黏土的试验结果也得到了相同的结论.Duncan等[4]首先发现饱和自然沉积黏土在不排水剪切加载测试中随着大主应力与沉积面夹角的变化会产生差异显著的应力应变关系结果.Yong等[5]针对灵敏性黏土开展的无侧限压缩强度测试表明,最小强度值仅为最高强度值的60%.Nishimura 等[6]发现自然沉积黏土的强度具有很强的沉积方向依赖性.同样,Yamada等[7]、Ochiai等[8]、Miura 等[9]、Hight等[10]、Tatsuoka等[11]以及Pradhan等[12]针对砂土所开展的一系列三轴压缩、真三轴加载以及空心圆柱扭剪等复杂加载测试结果表明：自然沉积砂土强度以及应力应变关系特性同样具有强烈的沉积方向依赖性.为描述横观各向同性性质,从细观机理上揭示与描述上述各向异性强弱程度,Oda等[13]建议采用组构张量来描述微观颗粒形状信息的长细比以及长轴在空间中分布方向等宏观统计信息.为了研究各向异性对砂土应力应变关系以及强度特性的影响,Li等[14]和Dafalias等[15]建议将一般应力$\sigma _{ij}$ 与组构张量$F_{ij}$进行并乘以得到一组反映各向异性性质的联合应力不变量,使用上述组合应力来构建弹塑性本构模型. Pietruszczak 等[16]和Mroz等[17]建议了一个随组构量变化的黏聚力和内摩擦角的强度指标,以此反映各向异性对于临界状态的影响.Hashiguchi等[18]为了能够反映原生各向异性,将组构张量中的3个主分量直接引入到本构模型中屈服面的转轴分量中,通过屈服面在应力空间中初始位置的不同来反映各向异性程度.
国内****对 各向异性的研究一直处于热点状态.张连卫等[19]基于SMP准则,将构成SMP面的3个平面的摩擦角表达为该平面随沉积面夹角变化的变量,构造了反映沉积面信息的ASMP准则.曹威 等[20]在SMP准则基础上,将组构张量参量引入 摩擦法则表达式中,以反映横观各向同性砂土的各向异性.姚仰平等[21]采用SMP空间滑移面与沉积面之间的夹角作为基本变量,构造了反映横观各向同性材料强度的应力比公式.Kong等[22]采用考虑了岩土组构张量修正的加载应力量,并与各向同性SMP准则相结合,得到了考虑微观结构影响的横观各向同性强度准则.路德春等[23]采用微观结构张量在滑动面法线方向上的投影,定义了一个反映三维横观各向同性的强度参数,并利用此参数来修正SMP准则,据此建立了一个反映横观各向同性土体的强度准则. 刘洋等[24-26]也采用反映微观信息的组构张量与应力相结合的方法对各向异性 进行 研究.此外,黄茂松等[27]从微观机理出发,也对各向异性性质进行了探讨.王国盛等[28]针对混凝土的加载速率效应提出了S强度准则.高江平等[29]考虑菱形十二面单元体主剪面上3个主剪应力与3个正应力都会对材料破坏产生影响,建议了三剪应力统一强度准则.
上述已提出的各类各向异性准则,按照构建的思路来分类,可大致分为如下几类：(1)将大主应力与沉积面夹角作为反映各向异性程度的变量来对已有的各向同性强度准则进行修正;(2)根据组构张量来构造各向异性状态变量,用来修正既有各向同性准则;(3)利用组构张量与应力量进行并乘得到联合应力不变量来修正各向同性准则;(4)基于SMP准则或者某一强度准则,用物理破坏面与沉积面夹角作为状态变量来修正各向同性准则;(5)扩展经典各向同性准则为考虑各向异性强度准则.
上述 方法各有利弊,采用大主应力与沉积面夹角来作为判断各向异性程度发挥的变量,显然比较直观,然而在某些情况下,比如平面应变条件下,各向异性强度值与上述夹角并不呈现单调关系,而是形成"V''字形曲线,显然若采用上述加载角与沉积面夹角作为各向异性状态变量存在弊端. 利用组构张量表达的各向异性程度状态变量来直接修正既有的强度准则,可能具有一定的实用性,但仍然不具有普适性. 利用组构张量与普通应力量按照某种规则相结合为联合应力不变量的方法能够在一定程度上考虑了各向异性对于应力量的修正作用,但联合应力不变量的构造方法目前只是猜想阶段,缺乏严谨的理论证明. 采用基于某种准则的破坏面与沉积面的夹角作为状态变量,由于破坏面与沉积面都具有明确的物理概念,且夹角与各向异性强度呈现单调关系,表明具有较好的归一性. 但在某些路径下,如三轴压缩或三轴伸长加载情况下,会出现较多的破坏面,需要进行筛选,选择其中最小强度值,这可能会违背物质客观性原理. 利用经典准则扩展为各向异性准则,只是对原有准则在一定程度上的修补,缺乏物理机理以及普适性.
基于已提出的适用于具有凝聚力以及摩擦性材料的a强度准则[30],在有效滑移面的物理概念上,考虑沉积面的位置关系,利用有效滑移面与材料沉积面之间夹角作为反映各向异性程度的状态变量.由于a准则在偏平面上是能够反映包括金属材料的Von-Mises准则到岩土材料的SMP准则,在子午面上是幂函数表达式,因而其适用范围大,且具有明确的物理涵义.按照上述各向异性状态变量所构建的各向异性强度准则,能够反映诸多材料的各向异性性质,如金属、岩石、混凝土、黏土、砂土等.通过上述各向异性强度准则公式,在主应力空间中按照将各向异性a准则变换为Von-Mises准则的变换思路[31],推导了变换应力公式,该变换应力公式实质上是从各向异性应力空间到各向同性应力空间的转换方程.
1 强度准则
根据已提出的a强度准则,如图1所示,立方体表示材料单元,当材料发生破坏时,按照应力比的思想,则假设存在空间有效滑移面$ABC$,在$ABC$面上等效主剪应力$\tau _{\rm en}$与主法向力$\sigma _{\rm en}$之比成为一个材料常数.其中$\varphi _{\rm e12}$表示由第一、第二主应力所构成的有效摩擦角,而$\varphi_{e23}$表示由第二、第三主应力所构成的有效摩擦角.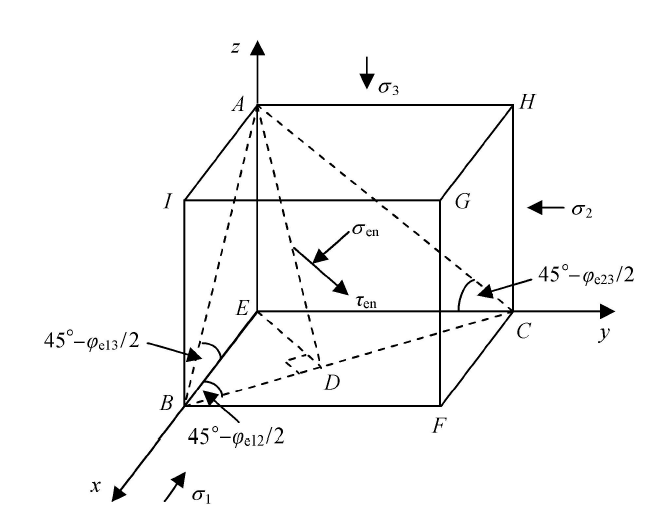
显示原图|下载原图ZIP|生成PPT图1空间坐标系中的滑移面
-->Fig. 1The slip plane in three dimensional space coordinate
-->
在直角三角形$AEB$中, 可知 $\tan \,( 45^\circ - \varphi _{\rm e13}/2 )= \dfrac{EA}{EB}$,令$EA=1$,根据三角函数关系求解上式可得到
如下公式
$$ EB = {\rm tan} \varphi_{\rm e13} + {\rm sec} \varphi_{\rm e13} (1)$$
同理亦可得到
$ EC = \tan \varphi _{\rm e23} + {\rm sec} \varphi _{\rm e23} (2)$
$\tan \varphi _{\rm e13} = \dfrac{\left( {\sigma _1 - \sigma _3 } \right)\sqrt {\sigma _1\sigma _3 + b_{13}^2 } - b_{13} \left( {\sigma _1 + \sigma _3 } \right)}{2\sigma _1 \sigma _3 } (3)$
$\tan \varphi _{\rm e23} = \dfrac{\left( {\sigma _2 - \sigma _3 } \right)\sqrt {\sigma _2\sigma _3 + b_{23}^2 } - b_{23} \left( {\sigma _2 + \sigma _3 } \right)}{2\sigma _2 \sigma _3 } (4)$
引入参数$a_{13}$, $a_{23}$来表示$b_{13}$, $b_{23}$,由于参数$b$是关于$a$的一次函数,因此可知当 由
$\sigma_{1}$, $\sigma_{3}$以及$\sigma_{2}$,
$\sigma_{3}$所构成的两个空间滑移面与水平面所成的夹角可分别表示为$45^\circ-\varphi_{e13}/2$以及$45^\circ-\varphi _{\rm e23}/2$,两者所对应的有效摩擦角可分别由$\tau -\sigma$空间内的摩尔圆外切直线的反正切值来表示,相应的直线截距则可分别表示为
$b_{13} = a_{13} R = {a_{13} \left( {\sigma _1 - \sigma _3 } \right)}/ 2 (5)$
$b_{23} = a_{23} R = {a_{23} \left( {\sigma _2 - \sigma _3 } \right)}/ 2 (6)$
$ EB = \dfrac{\left( {\sigma _1 - \sigma _3 } \right)\sqrt {\sigma _1\sigma _3 + 0.25a_{13}^2 \left( {\sigma _1 - \sigma _3 } \right)^2} - 0.5a_{13} \left( {\sigma _1^2 - \sigma_3^2 } \right)}{2\sigma _1 \sigma _3 } \,+$
$\qquad \sqrt {1+\left[ {\dfrac{\left( {\sigma _1 - \sigma _3 }\right)\sqrt {\sigma _1 \sigma _3 + 0.25a_{13}^2 \left( {\sigma _1 - \sigma _3 } \right)^2} - 0.5a_{13}\left( {\sigma _1^2 - \sigma _3^2 } \right)}{2\sigma _1 \sigma _3 }} \right]^2} (7)$
$ EC = \dfrac{\left( {\sigma _2 - \sigma _3 } \right)\sqrt {\sigma _2\sigma _3 + 0.25a_{23}^2 \left( {\sigma _2 - \sigma _3 } \right)^2} - 0.5a_{23} \left( {\sigma _2^2 - \sigma_3^2 } \right)}{2\sigma _2 \sigma _3 } \,+$
$\qquad \sqrt {1 + \left[ {\dfrac{\left( {\sigma _2 - \sigma _3 }\right)\sqrt {\sigma _2 \sigma _3 + 0.25a_{23}^2 \left( {\sigma _2 - \sigma _3 } \right)^2} - 0.5a_{23}\left( {\sigma _2^2 - \sigma _3^2 } \right)}{2\sigma _2 \sigma _3 }} \right]^2} (8)$
由图可见,由于确定了夹角$ABE$与夹角$ACE$,则相应的空间滑移面为平面的假设前提下则已完全确定下来,另外的 $\sigma_{1}$, $\sigma_{2}$之间构成的夹角则由三角函数的正切值定义可求出
$$\tan \left( {45^ \circ - {\varphi _{\rm e12} }/ 2} \right) = \dfrac{EC}{EB} (9)$$
可解出
$$\varphi _{\rm e12} = 2\arctan \left( {\dfrac{EB - EC}{EB + EC}} \right) (10) $$
根据式(1)与式(2)的关系,将其代入可得
$ \varphi _{\rm e12} = 2\arctan \left( {\dfrac{\tan \varphi _{\rm e13} - \tan \varphi _{\rm e23} + {\rm sec} \varphi _{\rm e13} - {\rm sec} \varphi _{\rm e23} }{\tan \varphi _{\rm e13} + \tan \varphi_{\rm e23} +{\rm sec} \varphi _{\rm e13} + {\rm sec} \varphi _{\rm e23} }} \right) $ (11)
式(11)即为空间有效滑移面中用以确定有效滑移面($ES\!MP$)空间位置的3个角的关系式.
如图2所示,若需确定有效滑移面$ES\!MP$,则需要先确定该面的法线方向,法线方向可由余弦来表示.
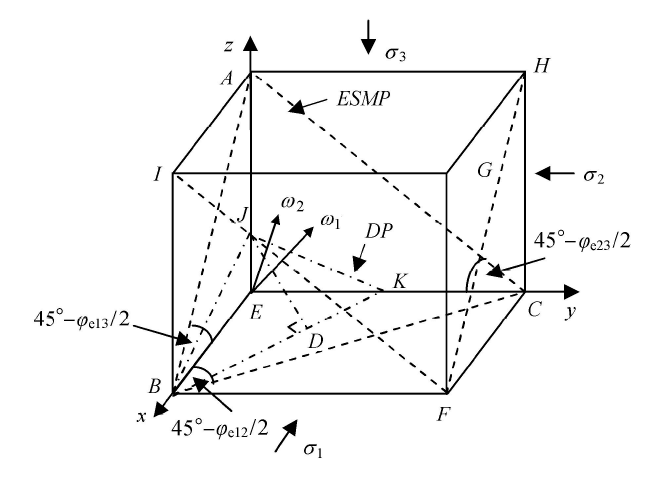显示原图|下载原图ZIP|生成PPT图2空间坐标系中的滑移面与沉积面
-->Fig. 2The slip plane and depositional plane in three dimensional space coordinate
-->
空间滑移面的方向余弦可表示为： $\omega_{1}(l_{1}$, $m_{1}$, $n_{1})$,而岩土材料在空间坐标系中存在一个空间沉积面($DP$),此空间沉积面可以用该面的方向向量表示,则可令空间沉积面的方向余弦表示为： $\omega_{2}(l_{2}$,$m_{2}$, $n_{2})$,则两空间平面的夹角可由两方向向量点积反余弦值表示
$$\alpha = \arccos \left( {\dfrac{l_1 l_2 + m_1 m_2 + n_1 n_2 }{\sqrt {l_1^2 + m_1^2 + n_1^2 } \sqrt {l_2^2 +m_2^2 + n_2^2 } }} \right) (12)$$
强度可由应力比表示,由于强度值随上述夹角$\alpha $变化,显然,当$\alpha =\alpha_{\min}=0^\circ$时,则空间滑移面与空间 沉积面相重合,此时由于沉积面之间联结最为薄弱,因而强度最低,当$\alpha=\alpha_{\max}$时,则空间滑移面与空间沉积面呈现最大夹角状态,此时最难破坏,因而强度最高,而当$0^\circ <\alpha <\alpha_{\max}$时,则应力比介于上述两者之间,由此可见,可利用上述两者极端应力比强度值,选用合理的插值函数进行表达,根据上述思路,可利用比较简单的内插函数来表示各向异性强度表达式
$$M_\alpha = f\left( {M_{\min } ,M_{\max } ,\alpha } \right) (13)$$
空间沉积面法向单位向量为$\omega_{2}$,法向量在3个空间坐标方向的投影分别如图3所示,$\omega_{2}$与$xy$平面夹角为$\alpha _{1}$,其在$xy$平面的投影向量与$x$轴夹角为$\alpha_{2}$. 则显然,空间沉积面法向方向可表示为
$$\omega_{2}(l_{2}, m_{2}, n_{2})= \omega_{2}(\cos \alpha _{1} \cos \alpha_{2}, \cos \alpha_{1} \sin\alpha_{2}, \sin \alpha_{1}) (14)$$
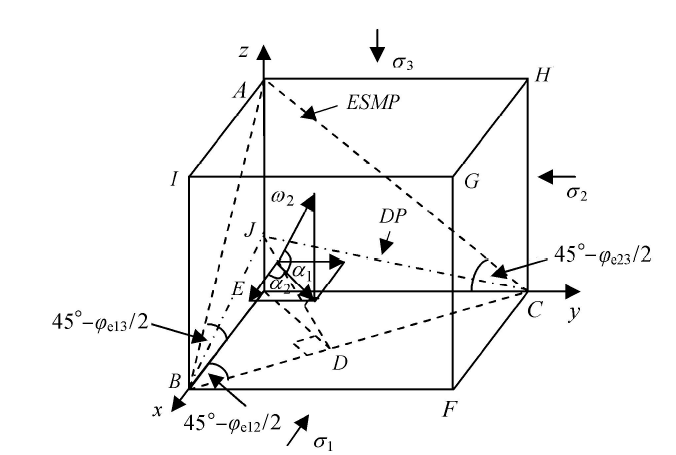显示原图|下载原图ZIP|生成PPT图3空间坐标系中沉积面方向投影
-->Fig. 3The project vector of depositional plane in three dimensional space coordinate
-->
首先 求出有效空间滑移面与沉积面夹角为90$^\circ$时的强度值.
令
$$r = \sqrt {EB^2 + EC^2 + EB^2EC^2} (15)$$
则有效空间滑移面法向向量分量可表示为
$l_1 = \dfrac{EC}{r} (16)$
$m_1 = \dfrac{EB}{r} (17)$
$ n_1 = \dfrac{EB\cdot EC}{r} (18)$
$s_{\Delta AEB} = \dfrac{EB}{2} (19)$
$s_{\Delta AEC} = \dfrac{EC}{2} (20)$
$s_{\Delta EBC} = \dfrac{EB\cdot EC}{2} (21)$
$\sin \angle BAC = \dfrac{r}{\sqrt {1 + r^2} } (22)$
根据三角函数关系,可知
$$\tan \angle BAC = r (23)$$
根据对正四面体$AEBC$的力平衡关系,并利用上述公式,可得到等效正应力公式. 则等效正应力可表示为
$\sigma _{\rm en} = \dfrac{l\sigma _1 s_{\Delta AEC} + m\sigma _2 s_{\Delta AEB} +n\sigma _3 s_{\Delta EBC} }{s_{\Delta BAC} } (24)$
$\sigma _{\rm en} = \dfrac{\sigma _1 EC^2 + \sigma _2 EB^2 + \sigma _3EB^2EC^2}{r^2} (25)$
$\tau _{\rm en} = \sqrt {\left( {\dfrac{\sigma _1 EC}{r}} \right)^2 + \left( {\dfrac{\sigma _2 EB}{r}}\right)^2 + \left( {\dfrac{\sigma _3 EBEC}{r}} \right)^2 - \sigma _{\rm en}^2 } (26)$
经推导可得到如下公式
$ \dfrac{\tau _{\rm en} }{\sigma _{\rm en} } = \Big [ EB \cdot EC \cdot $
$ \sqrt {\left( {\sigma _1 - \sigma _2 } \right)^2 + EB^2\left({\sigma _2 - \sigma _3 } \right)^2 + EC^2\left( {\sigma _3 - \sigma _1 } \right)^2} \Big ] \Big / $
$ \Big ( \sigma _1 EC^2 + \sigma _2 EB^2 + \sigma _3 EB^2EC^2 \Big) = \tan \varphi _{\rm mo} (27)$
其中, $\varphi_{\rm mo}$表示空间有效滑移面的内摩擦角.
当处于三轴压缩时,则式(27)可表达为
$$\dfrac{\tau _{\rm en} }{\sigma _{\rm en} } = c_1 (28)$$
此时,大小主应力分别可表示为
$$\left.\begin{array}{l} {\sigma _1 = p + \dfrac{2}{3}q_{\rm c} } {\sigma _2 = \sigma _3 = p - \dfrac{1}{3}q_{\rm c} } \end{array} \right \} (29)$$
将式(29)代入 式(27)中,可得到 关于$p$, $q_{\rm c}$的函数
$ f\left( {p,q_c } \right) = \Big( q_{\rm c} EB_{\rm c} EC_{\rm c} \sqrt {1 + EC_{\rm c}^2 }\Big ) \Big / $
$\qquad \Big[ \left( {p + {2q_{\rm c}} / 3} \right)EC_{\rm c}^2 + \left( {p - {q_{\rm c}} /3}\right)EB_{\rm c}^2 \left( {1 + EC_{\rm c}^2 } \right) \Big] (30)$
$r_{\rm c} = \sqrt {EB_{\rm c}^2 + EC_{\rm c}^2 + EB_{\rm c}^2 EC_{\rm c}^2 } (31)$
采用破坏时应力比的表示方法,$M=q_{\rm c}/p$,则可表示为
$A_1 = M\sqrt {\left( {1 + \dfrac{M}{3} - \dfrac{2M^2}{9}} \right) + \dfrac{a_{13}^2 M^2}{4}} -a_{13} \left( {M + \dfrac{M^2}{6}} \right)$ (32)
$EB_{\rm c} = \dfrac{A_1 + \sqrt {4\left( {1 + M /3 - {2M^2}/9} \right)^2 + A_1^2 } }{2\left({1 + M /3 - {2M^2}/ 9} \right)} (33)$
其中,$M$表示三轴压缩时所对应的破坏应力比. 若三轴伸长下的破坏应力比为$M_{\rm e}$,且设三轴伸长破坏应力比与三轴压缩破坏应力比之比值为$\lambda $,则$M_{\rm e}=\lambda M$.
$ EC_{\rm c} = 1 (34)$
$ r_{\rm c}^2 = 2EB_{\rm c}^2 + 1 (35)$
由于在三轴压缩路径下,方程式(27)与式(30)完全相等,因此得到
${3\sqrt 2 q_{\rm c} EB_{\rm c} }\big / \big[\left( {3p + 2q_{\rm c} } \right) + 2\left( {3p -q_{\rm c} } \right)EB_{\rm c}^2 \big ] = $
$ \Big [ \sqrt {\left( {\sigma _1 - \sigma _2 } \right)^2 + EB^2\left( {\sigma _2 - \sigma_3 } \right)^2 + EC^2\left( {\sigma _3 - \sigma _1 } \right)^2} \Big ] \Big /$
$ \big ( \sigma _1 {EC} / {EB} + \sigma _2 {EB} / {EC} + \sigma _3 EBEC \big ) (36)$
式(36)即为偏平面上广义偏应力强度公式.
子午面上可采用考虑静水压力效应的关于平均应力的双曲线函数来作为强度表达式
$$q_{\rm c} = M_{\rm f} p_{\rm r} \left( {\dfrac{p + \sigma _{0} }{p_{\rm r} }} \right)^n (37)$$
2 横观各向同性${ a}$强度准则
对于各向异性的考虑,需要将式(37)中应力比强度$M_{\rm f}$表示为有效滑移面与沉积面夹角的函数即可.则显然需要构造一个表示夹角的关系式. 首先需满足以下两个条件：(1) 首先满足夹角越大,则强度值越大的单调规律;
(2) 需要构造一个各向同性函数,以此满足物质客观性原理.
其中,右端的$\varphi_{\rm mo}$表示有效滑移面的内摩擦角,在各向异性情形下,通常$\tan \varphi_{\rm mo}$并非恒定值,可由函数$\tan \varphi_{\rm mo}=F ( \alpha ,M)$来表示. $\alpha$表示滑移面与沉积面的夹角,各向异性程度的度量参数,因此上述函数包含了描述各向异性方向以及各向异性程度双重信息.
同理由有效滑移面与有效沉积面夹角公式由余弦表示,可表示为
$\beta={\rm arccos} \big[ (EC \cos \alpha_1 \cos \alpha_2+ EB\cos\alpha_1\sin\alpha_2+$
$ECEB\sin \alpha_1) \big/ r \big ] (38) $
由于在三轴压缩条件下,可得到式(38)的简化表达式为
$\beta={\rm arccos} \big [ (\cos\alpha_1\cos\alpha_2+ EB_{\rm c}\cos\alpha_1\sin\alpha_2+$
$EB_{\rm c}\sin\alpha_1 ) /r_{\rm c} \big] (39)$
采用组构张量与应力不变量按照某种运算规则构造的联合应力不变量,从某种程度上考虑了微观信息对于强度的贡献,但在某些情况下,仅仅考虑了主应力方向与沉积面之间夹角 $\delta $对于各向异性强度的影响,且一般建立两者的单调关系函数,然而,由Matsuoka等[32]关于砂土在平面应变的强度测试结果表明,平面应变强度与 $\delta $ 是非单调关系,两者关系出现先减小后增大的规律特点. 若采用空间滑动面与沉积面夹角$\zeta $ 与强度值建立关系,会发现两者具有单调关系.
在上述试验规律的启示下,可以假设在三维应力情况下,强度值与空间滑移面和沉积面夹角的关系仍然是单调递增关系.基于上述 推理,采取一种最简单的非线性插值公式,可得到计算任意有效滑移面与沉积面夹角的各向异性强度应力比公式
$$M_\beta=M_{\rm n}+(M_{\rm x}-M_{\rm n}) \Big(\dfrac{\beta}{\beta_{\rm x}}\Big)^2 (40)$$
其中,x表示max的简称,表示最大值,而n为min的缩写,表示最小值. 分析式(40)可知,强度应力比随夹角$\beta$呈现二次函数 的单调递增关系,完全符合试验点的单调递增规律特点.
显然,由试验及直观分析可知,当大主应力加载方向与沉积面法向一致时,此时存在最大的角度$\beta _{\rm x}$.而当$ES\!MP$面与沉 积面相重合时,则显然存在最小的夹角$\beta _{\rm n}=0$. 对于$M_{\rm x}$的确定,可由图4所示加载工况,根据沉积面与大主应力轴相垂直条件下的三轴压缩试验来确定最终的内摩擦角,由摩擦角可通过式(41)计算得到. 而$M_{\rm n}$则针对的是当 $\beta=0$时的强度应力比,显然直接确定较为困难,可间接通过由顺沉积面的三轴压缩试验得到的强度值$M_{0}$来求出,由图5可见,采用的是大主应力方向与沉积面法向相互垂直时候的加载工况,$M_{0}$为此种加载条件下的强度应力比. 其中表达式 为
$$ M_{\rm x} = \dfrac{6\sin \varphi _v }{3-\sin \varphi _v } (41) $$
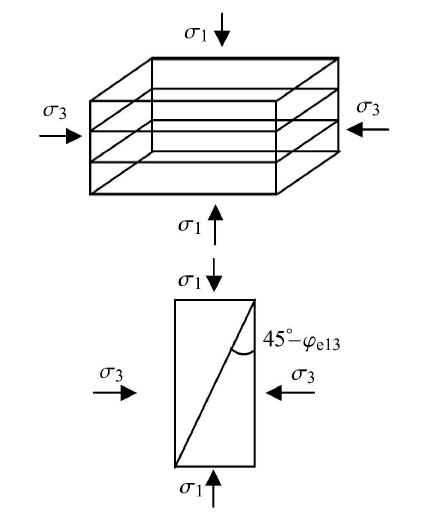显示原图|下载原图ZIP|生成PPT图4大主应力与沉积面垂直时的三轴压缩示意图
-->Fig. 4Triaxial compression condition with major principal stress vertical to the depositional plane
-->
显示原图|下载原图ZIP|生成PPT图5大主应力与沉积面平行时的三轴压缩示意图
-->Fig. 5Triaxial compression condition with major principal stress parallel to the depositional plane
-->
强度应力比最小值$M_{\rm n}$可通过 式(40)变形导出,由通过常规试验测试得到的强度值$M_{0}$以及最大值$M_{\rm x}$表示
$$M_{\rm n} = \dfrac{M_0 - M_{\rm x} \left[ {\dfrac{\arccos ({EB_0 }/{r_0})}{\beta _{\rm x} }} \right]^2}{1 - \left[ {\dfrac{\arccos ({EB_0 }/ {r_0 })}{\beta _{\rm x} }} \right]^2} (42)$$
其中
$ EB_0 = \dfrac{A_0 + \sqrt {4\left( {1 + {M_0 }/ 3 - {2M_0^2 } / 9} \right)^2 + A_0^2 } }{2\left( {1 + {M_0 }/ 3 - {2M_0^2 }/9} \right)} (43)$
$A_0 = M_0 \sqrt {\left( {1 + \dfrac{M_0 }{3} - \dfrac{2M_0^2 }{9}} \right) + \dfrac{a_{13}^2M_0^2 }{4}} - a_{13} \left( {M_0 + \dfrac{M_0^2 }{6}} \right)$ (44)
$r_0 = \sqrt {1 + 2EB_0^2 } (45)$
$\beta _{\rm x} = \arccos \left( {\dfrac{1}{r_{\rm x} }} \right) (46)$
$r_{\rm x} = \sqrt {1 + 2EB_{\rm x}^2 } (47)$
$EB_{\rm x} = \dfrac{A_{\rm x} + \sqrt {4\left( {1 + {M_{\rm x} }/ 3 - {2M_{\rm x}^2 }/9} \right)^2 + A_{\rm x}^2 } }{2\left( {1 + {M_{\rm x} }/3 - {2M_{\rm x}^2 } /9} \right)} (48)$
$A_{\rm x} = M_{\rm x} \sqrt {\left( {1 + \dfrac{M_{\rm x} }{3} - \dfrac{2M_{\rm x}^2 }{9}}\right) + \dfrac{a_{13}^2 M_{\rm x}^2 }{4}} - a_{13} \left( {M_{\rm x} + \dfrac{M_{\rm x}^2 }{6}} \right)$ (49)
考察各向异性 对 三轴压缩强度的影响规律,由于微观颗粒在重力场及外部自然作用下会形成一定的排序分布,在空间中微观颗粒会产生定向性,若用空间椭球体作为对长方体颗粒的近似,则长轴会平行于沉积方向,而垂直于沉积面的法向方向是沉积面的空间对称轴.由于长轴方向平行于沉积面的分布形态是形成岩土体的一种稳态结构,因而,在这种作用下形成的岩土体在自然界非常普遍. 下面关于空间沉积面在空间中的排布方式,按照研究方便考虑3种特殊情况,分别对应空间有效滑移面与沉积面的3个特殊位置.
(1) 考察式(38),若当沉积面法向方向与$z$轴相一致时,则可知 $\alpha_{1}=90^\circ $, $\alpha_{2}=\alpha_{3}=90^\circ$, 则滑移面与沉积面夹角表示为
$$\beta = \arccos \dfrac{EC\cdot EB}{r} (50)$$
(2) 当沉积面法向方向与$x$轴相一致时,则可知 $\alpha_{3}=90^\circ $, $\alpha _{1}=\alpha _{2}=0^\circ$, 则滑移面与沉积面夹角表示为
$$\beta = \arccos \dfrac{EC }{r} (51)$$
(3) 当沉积面法向方向与$y$轴相一致时,则可知 $\alpha_{2}=90^\circ $, $\alpha _{1}=\alpha _{3}=0^\circ $,
则滑移面与沉积面夹角表示为
$$\beta = \arccos \dfrac{EB }{r} (52)$$
综合考虑偏平面与子午面上强度表达式,联立式(27)、式(36)、式(37)、式(40),可得到最终关于各向异性的岩土非线性强度准则
$$ \dfrac{3\sqrt 2 EB_{\rm x} - 3p\left( {1 + 2EB_{\rm x}^2 } \right)\tan \varphi _{\rm mo} }{2\tan\varphi _{\rm mo} \left( {1 - EB_{\rm x}^2 } \right)} \,- \qquad M_\beta p_{\rm r} \left( {\dfrac{p +\sigma _{0} }{p_{\rm r} }} \right)^n = 0 (53)$$
式(53)即为表示各向异性强度准则表达式.
下面具体讨论当参量取值不同时强度准则的表现形式.
(1)对于各向异性强度准则偏平面表示式,当式(53)中$M_{\beta }$与$M_{\rm x}$,$M_{0}$各不相等时,则表示的是一般的横观各向异性强度应力比,此时,$M_{\beta }$为一随 $\beta $ 变化 的强度值,此时强度准则为横观各向异性$a$准则.
(2)对于各向异性强度准则偏平面表示式, 当式(53)中$M_{\beta }=M_{\rm x}=M_{0}$时,则由于其两相互垂直方向的应力比强度相同,则介于两者之间的任意应力比强度值都相同,则此时,$M_{\beta }$为一恒定值. 当$a_{13}=a_{23}$时,则此时强度准则退化为a准则.
(3) 当$a_{13}=a_{23} =0$时,则强度准则退化为偏平面上为SMP准则的非线性强度准则.
(4)当$M_{\rm x}$与$M_{0}$都不为零,而$a_{13}=a_{23} =0$时,则强度准则退化为偏平面上为各向异性SMP准则的非线性强度准则.
3 主要参数意义及确定方法
3.1 参数${\pmb a}$对于偏平面上强度准则曲线的影响
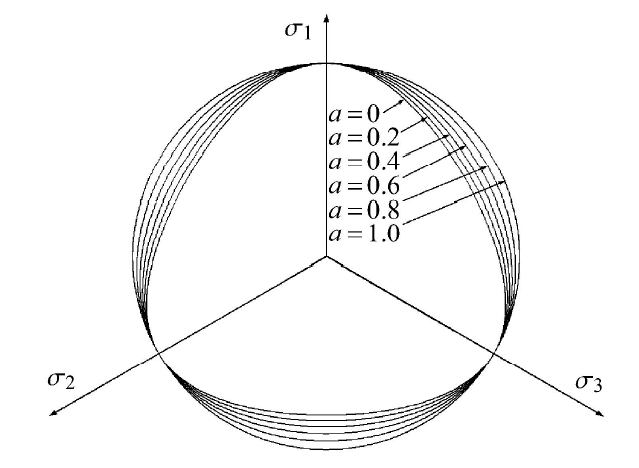
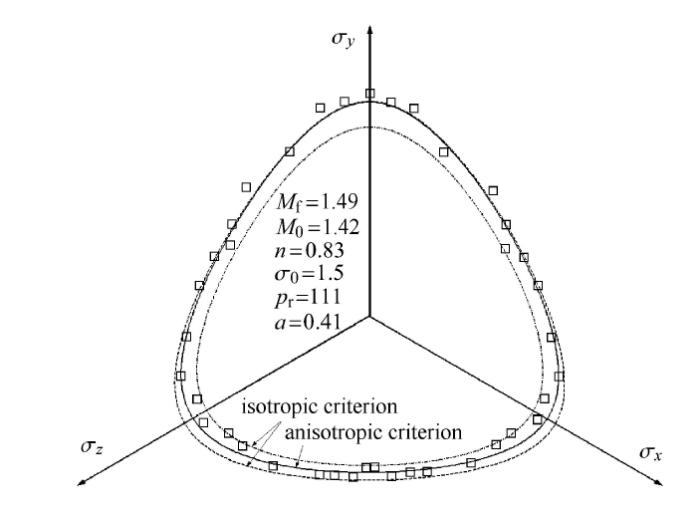
通常为了简化考虑,将参数$a_{13}=a_{23}= a$来作为参数使用.为了确定参数$a$,可通过沉积面相对于空间坐标系为固定情形来 考察$a$对 强度曲线性状的影响.如图6所示,为简化问题,可取沉积面平行于$xy$平面作为固定试样.分别考虑三轴压缩与三轴伸长两种应力路径下的强度值. 由三轴伸长与三轴压缩的强度值之比$\lambda$来确定参数$a$的取值.如图7所示,$a$参数是影响偏平面上曲边三角形"胖瘦''程度的参数,而其"胖瘦''程度与常规三轴伸长与三轴压缩强度比值量$\lambda $ 唯一相关,基于上述特点,可利用参数$\lambda $以及$M_{\rm x}$来表达参数$a$.因在三维加载路径下的强度特性,其反映各向异性程度信息由式(40)来表达,而参数$a$仅仅是考虑中主应力对于偏平面上强度曲线性状的影响,因而参数$a$并无考虑原生各向异性信息.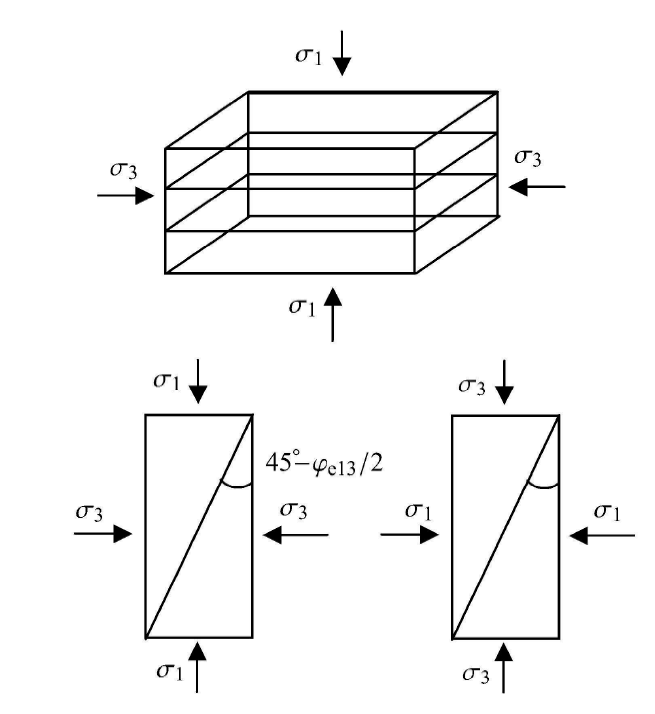
显示原图|下载原图ZIP|生成PPT图6大主应力与沉积面垂直时的三轴压缩及三轴伸长示意图
-->Fig. 6Triaxial compression and triaxial extension conditions with major principal stress vertical to the depositional plane
-->
显示原图|下载原图ZIP|生成PPT图7各向同性不同$a$值下偏平面上的破坏曲面
-->Fig. 7Failure surfaces with different $a$ value at deviatoric plane in isotropic stress space
-->
通过近似,可取如下公式作为确定参数$a$的确定表达式.
$$a = \sqrt {\left( {1 + \dfrac{3}{M_{\rm x} }} \right)\left( {\lambda - \dfrac{3}{3 + M_{\rm x} }} \right)} (54)$$
对于各向同性a准则,当参数$a$变化时,由图7可见,随着$a$值由0$\sim$1逐渐增大,偏平面上强度曲线由表示SMP准则的曲边三角形逐步过渡到表示Von-Mises准则的圆形曲线. 由此可见,参数$a$关于中主应力对于强度应力比的影响非常明确直接,可以直接决定中主应力对于强度的贡献程度.
3.2 参数${\pmb n}$意义及确定
图8和图9所示分别为不同幂参数$n$值下的破坏曲线和主应力空间中破坏面形态.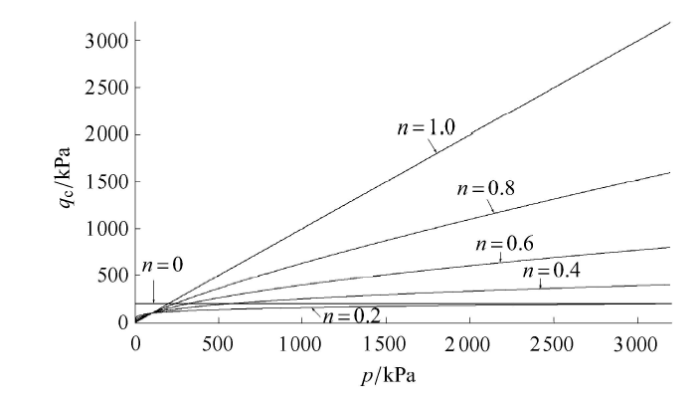
显示原图|下载原图ZIP|生成PPT图8不同幂参数$n$值下破坏曲线形态
-->Fig. 8Failure curves with different $n $ value
-->
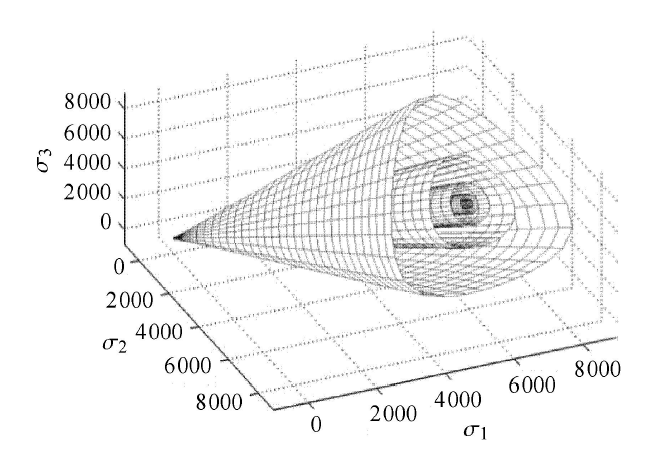显示原图|下载原图ZIP|生成PPT图9不同幂参数$n$值下主应力空间中破坏面形态
-->Fig. 9Failure surfaces with different $n$ value in isotropic stress space
-->
从图8可看出,在子午面上,由下到上分别对应不同$n$值下的破坏曲线,分别对应$n =0.2$, 0.4, 0.6, 0.8,1.0时的破坏曲线. 由图9可见,与之相对应的在主应力空间中,由内到外可见依次的破坏面.由此可看出,参数$n$对于破坏形态的影响主要体现在两个方面.第一,在子午面上,随着$n$值增大,则子午面上破坏线逐渐趋近于一条斜直线,随着$n$值减小逐渐趋近于零,则破坏线逐渐趋近于平行于球应力轴的水平直线,当为水平直线时,则破坏时对应的广义偏应力恒定不变,即不受静水压力影响,起决定作用的是广义偏应力.而当$n$值介于0与1之间时,则子午面上对应的是一条幂函数曲线,随着球应力的增大,则广义偏应力也逐渐增大,但增加率逐渐减小,体现了非线性特点,表明静水压力对于三轴压缩下的剪切强度有直接影响.第二,在偏平面上,随着$n$值的增大,则三轴压缩对应的广义偏应力强度相应增大,在相同的球应力下,随着三轴压缩剪切强度的增大,则不同罗德角作用下的强度值差异逐渐显著,也就是应力诱导各向异性程度逐渐加深,而随着$n$值趋近于零,则屈服面开口减小,且三轴压缩与三轴伸长强度逐渐相等,偏平面上由曲边三角形渐渐趋向于圆形,反映材料的各向同性性质增强.
通过式(37)变形可得到如下的关系式
$$\ln \dfrac{q_{\rm c} }{p_{\rm r} } = n\ln \dfrac{p + \sigma _0 }{p_{\rm r }} + \ln M_{\rm f} (55)$$
以等式左右两端的对数分别为变量,则上述公式显然是关于参数$n$的一次函数,利用三轴压缩试验结果,可将对应不同静水压力下的剪切强度整理在对数坐标系内,拟合出的直线型曲线,斜率为$n$,而截距值为ln $M_{\rm f}$.
3.3 参数$\sigma_{0}$涵义及确定
$\sigma _{0}$为强度曲线与静水压力轴的左交点值,其物理意义表示材料在拉伸条件下的强度值,可以反映出材料的凝聚力特性. 在实际状态中三向拉伸作用下的强度值,一般很难实现,对于无黏性土,则取为0. 对于具有拉伸强度的材料,如混凝土等,根据过镇海的建议,可将其取为单轴拉伸强度值的0.9倍.3.4 参数${p}_{\rm r}$涵义及确定
参数$p_{\rm r}$反映在一定静水压力下,将剪切强度$q$归一化的特征压力. 另外,也起到将静水压力无量纲化的作用,通常在砂土等散粒体条件下,可取为一个大气压力值. 参数$p_{\rm r}$的确定可根据式(37),由对试验结果整理在对数坐标系内,根据拟合出来的直线来确定参数$p_{\rm r}$的值.3.5 参数${M}_{\rm x}$与${M}_{0}$涵义及确定
作为反映各向异性的参数,通常只需确定沉积面与空间有效滑移面的呈现最大夹角和最小夹角状态下的三轴压缩强度值,即可得到相应的$M_{\rm x}$与$M_{\rm n}$值. $M_{\rm x}$根据大主应力方向垂直于沉积面加载条件下的三轴压缩强度值来测试得到,而$M_{\rm n}$可间接通过$M_{0}$用 式(42)求取得到,而$M_{0}$则是利用大主应力与沉积面顺层方向的三轴压缩强度测试得到.4 各向异性对强度曲线影响
由图3可知,当空间沉积面的法线不与三维空间坐标轴的任一轴重合时,即空间沉积面处于三维空间的一般位置时,则沉积面与有效滑移面的夹角可由 式(38)来表述,通过 式(40)可知,应力比强度值是夹角 $\beta $ 的单增函数. 当沉积面空间位置一旦确定后则是固定不变的,而随着主应力大小以及方向的调整,显然有效滑移面始终是动态变化的,在非三轴压缩条件下,则其强度值始终是小于$M_{\rm x}$,随着夹角 $\beta $ 在零度附近变化,则强度值也会相应的升高或降低,若按照大主应力与沉积面法向夹角为加载角的定义,则强度值会随着加载角产生先减小后增大的规律.如图10所示,为便于描述,按照主应力的变化在偏平面上将全部区域分为3个象限I、II、III.
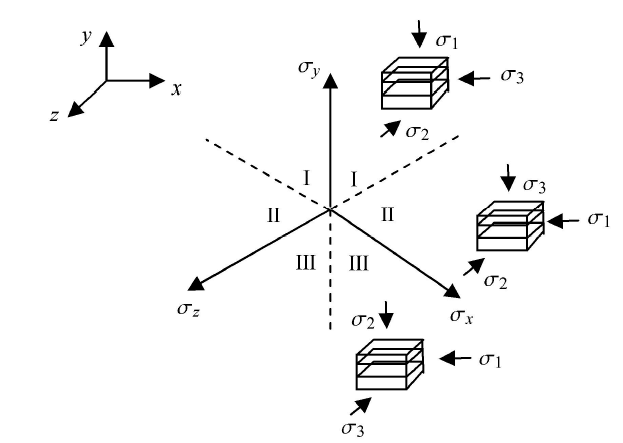显示原图|下载原图ZIP|生成PPT图10描述各向异性状态的偏平面空间区划图
-->Fig.10Zones describing anisotropic state in deviatoric plane
-->
(1)当沉积面法线方向与$x$轴,即$\sigma_{1}$方向相一致时,则显然,由图11可见,当为各向同性强度准则时,如图11中的虚 线与点划线,即当$M_{\rm f}$为恒定值时,则破坏曲线在偏平面上为一个几何对称图形,对于实线,及$M_{\rm f}$为一个变量时,则此时的破坏曲线仅仅关于材 料主轴对称.
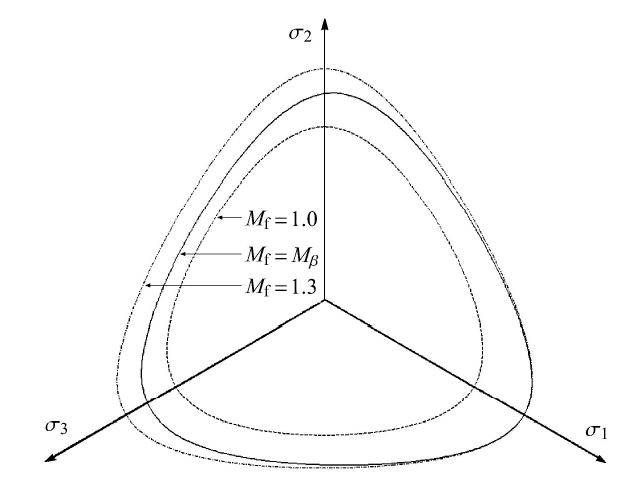显示原图|下载原图ZIP|生成PPT图11各向异性强度准则(沉积面垂直于$x$轴)
-->Fig.11Failure surface of anisotropic criterion (depositional plane vertical to the $x$ axis)
-->
由图12可见,当沉积面垂直于$y$轴时,则此时最大应力比为位于与$\sigma _2$轴相重合的纵轴上,而两侧的几何破坏线关于该轴几何对称分布.
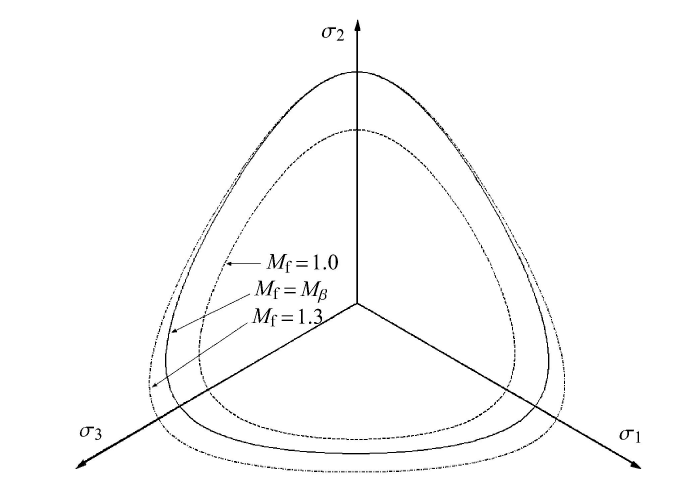显示原图|下载原图ZIP|生成PPT图12各向异性强度准则(沉积面垂直于$y$轴)
-->Fig.12Failure surface of anisotropic criterion (depositional plane vertical to the $y$ axis)
-->
由图13可见,当沉积面垂直于$z$轴时,则此时最大应力比为位于与 $\sigma_{3}$轴相重合的轴线上,而两侧的几何破坏线关于该轴几何对称分布.
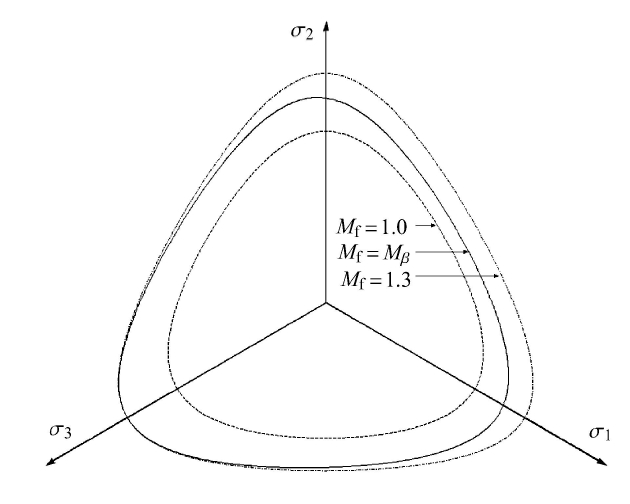显示原图|下载原图ZIP|生成PPT图13各向异性强度准则(沉积面垂直于$z$轴)
-->Fig.13Failure surface of anisotropic criterion (depositional plane vertical to the $z$ axis)
-->
综合图11 $\sim$图13可见,采用考虑有效滑移面与沉积面的夹角作为反映各向异性程度的状态量,能够有效地反映出材料本身沉积面对于强度应力比的影响规律.
5 基于横观各向同性${\rm a}$准则的变换应力公式
为了可简单合理的将已有的基于$p-q$空间的二维弹塑性模型推广到能应用于描述原生各向异性特性对本构关系的影响规律,基于所提的横观各向同性a准则,将其应用于构造变换应力方程[33-35],由此可将横观各向同性应力空间转变为各向同性应力空间.其基本思路是,先将一般的考虑各向异性的广义偏应力$q$进行归一化处理,即将对于某一特定加载条件下的$q$转换为$q_{\rm f}$,即第一步实现了将各向异性转换为各向同性,$q_{\rm f}$即为对应大主应力方向与沉积面法向方向一致的三轴压缩的广义偏应力强度值.然后再通过将各个偏应力分量放大到对应Von-Mises圆的对应点上,第二步是将各向同性应力空间中中主应力对应力比强度的影响归一化处理. 通过上述两步骤,即可实现由各向异性应力空间与各向同性应力空间的转换.由Satake等针对纯摩擦特性所提出的基于SMP准则的形状函数,基于摩擦角的概念而提出,因而本文中的有效摩擦角可将其替换以得到基于有效摩擦角的形状函数.
$q = \dfrac{3\sqrt 3 p\sin \varphi _{\rm mo} }{2\sqrt {2 + \sin ^2\varphi _{\rm mo} }\cos \psi } (56)$
$\varphi _{\rm mo} = \tan ^{ - 1}\cdot$
$\left[ {\dfrac{\sqrt {\left( {\sigma _1 - \sigma _2 } \right)^2 + EB^2\left( {\sigma _2- \sigma _3 } \right)^2 + EC^2\left( {\sigma _3 - \sigma _1 } \right)^2} }{\sigma _1 {EC} / {EB} + \sigma _2{EB} / {EC} + \sigma _3 EB\cdot EC}} \right] $(57)
${EB}, {EC}$是$\sigma_{1}$, $\sigma_{2}$, $\sigma_{3}$的函数,具体见式(8)、式(9)、式(27)
$$\psi = \dfrac{1}{3}\cos ^{ - 1}\left[ { - \left( {\dfrac{3}{2 + \sin ^2\varphi_{\rm mo} }} \right)^{3 /2}\sin \varphi _{\rm mo} \cos 3\theta } \right] (58)$$
其中, $\theta $ 为应力罗德角,可表示为
$$ \theta=\tan^{-1} \dfrac{\sqrt 3 ( \sigma_2-\sigma_3)}{2\sigma_1-\sigma_2-\sigma_3} (59)$$
对应a准则的偏平面上的形状函数可表示为
$${g}\left( \theta \right) = \dfrac{\sqrt 3 \left( {\sqrt {8 + \sin ^2\varphi_{\rm mo} } - \sin \varphi _{\rm mo} } \right)}{4\sqrt {2 + \sin ^2\varphi _{\rm mo} } \cos\psi } (60)$$
由于已知有基于a准则的形状函数,因此,可得到在对应任意一个球应力$p$下的三轴压缩路径下的广义偏应力$q_{\rm c}$,表示为
$$q_c = \dfrac{q}{ {g}\left( \theta \right)} = \dfrac{6p\sin \varphi_{\rm mo} }{\left( {\sqrt {8 + \sin ^2\varphi _{\rm mo} } - \sin \varphi _{\rm mo} } \right)} (61)$$
考虑到偏平面上各向异性的修正,最终得到偏平面上考虑各向异性的a准则
$$q_{\rm ac} = \dfrac{M_{\rm f} }{M_\beta }q_{\rm c} = \dfrac{6M_{\rm f} p\sin \varphi _{\rm mo} }{M_\beta\left( {\sqrt {8 + \sin ^2\varphi _{\rm mo} } - \sin \varphi _{\rm mo} } \right)} (62)$$
基于各向异性强度准则的转换应力公式可表达为
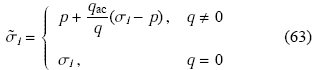
将其推广为一般应力表示的转换应力公式
$\tilde {\sigma }_{ij} = \left\{ \begin{array}{ll} p\delta _{ij} + \dfrac{q_{\rm ac} }{q}(\sigma _{ij} - p\delta _{ij}) \,, & q \ne 0 \sigma _{ij} \,, & q = 0 \end{array} \right. (64)$
$\dfrac{\partial \tilde {\sigma }_j }{\partial \sigma _i } = \dfrac{1}{3} +\dfrac{s_j }{q}\dfrac{\partial q_{\rm ac } }{\partial \sigma _i } +\dfrac{q_{\rm ac } }{q}\left( {\delta _{ij} - \dfrac{1}{3} -\dfrac{3}{2q^2}s_i s_j } \right) (65) $
式(62)中$\dfrac{\partial q_{\rm ac} }{\partial \sigma _i }$可表示为
$\dfrac{\partial q_{\rm ac } }{\partial \sigma _i } = \dfrac{M_{\rm f}}{M_\beta }\left[{\dfrac{1}{3}\dfrac{\partial q_{\rm c} }{\partial p} + A_5 \dfrac{\partial q_{\rm c} }{\partial \sin \varphi_{\rm mo} }\left( {1 + \tan ^2\varphi _{\rm mo} } \right)^{ - \tfrac{3}{2}}} \right] (66)$
$A_5 = B_i + \left( {\dfrac{\partial \tan \varphi _{\rm mo} }{\partial EB}\dfrac{\partial EB}{\partial \sigma _i } + \dfrac{\partial \tan \varphi _{\rm mo}}{\partial EC}\dfrac{\partial EC}{\partial \sigma _i }} \right) (67)$
$\dfrac{\partial q_{\rm c} }{\partial \sin \varphi _{\rm mo} } = {24p}\Big/ \Big[\left( {4 +\sin ^2\varphi _{\rm mo} } \right)\sqrt {8 + \sin ^2\varphi _{\rm mo} } -$
$\qquad \sin \varphi _{\rm mo} \left( {8 + \sin ^2\varphi _{\rm mo} } \right) \Big] (68)$
令
$\sigma _{\rm A} = \sigma _1 EC^2 + \sigma _2 EB^2 + \sigma _3 EB^2EC^2 (69)$
$\sigma _{\rm B} = \sigma _1^2 EC^2 + \sigma _2^2 EB^2 + \sigma _3^2 EB^2EC^2 (70)$
$\sigma _{\rm C} = \sigma _{1}^{2} + \sigma_{2}^{2} + \sigma _{1}^{2} EC^2 + \sigma _3^{2}EC^2 (71)$
$\sigma _{\rm D} = \sigma _{2}^{2} + \sigma _2^{2} EC^2 + \sigma _3^{2} EC^2 + \sigma _3^{2}EC^4 (72)$
$\sigma _{\rm E} = \sigma _{1}^{2} + \sigma _{2}^{2} + \sigma _2^{2} EB^2 + \sigma _3^{2} EB^2 (73)$
$\sigma _{\rm F} = \sigma _1^{2} + \sigma _1^{2} EB^2 + \sigma _3^{2} EB^2 + \sigma _3^{2}EB^4 (74)$
$\sigma _{\rm G} = \sqrt {\sigma _{1} \sigma _{3} + 0.25a^2\left( {\sigma _{1} - \sigma _{3} }\right)^2} (75)$
$\sigma _{\rm H} = \sqrt {\sigma _2 \sigma _{3} + 0.25a^2\left( {\sigma _2 - \sigma _{3} }\right)^2} (76)$
$\sigma _{\rm L} = \Big \{\left( {\sigma _{1} - \sigma _{3} } \right)\Big[\left( {\sigma _{1} +\sigma _{3} } \right) - \sigma _i + \left( { - 1} \right)^{\delta _{i1} + 1}\cdot $
$\qquad 0.5a^2\left( {\sigma _{1} - \sigma _{3} } \right)\Big]\,\Big\} \Big/ (2\sigma _{\rm G}) (77)$
$\sigma _{\rm M} = \sqrt {{4}\sigma _{1}^{2} \sigma _{3}^{2} + \left[ {\left( {\sigma _{1} -\sigma _{3} } \right)\sigma _G - 0.5a\left( {\sigma _{1}^{2} - \sigma _{3}^{2} } \right)} \right]^2} $(78)
$\sigma _{\rm N} = \left( {\sigma _{1} - \sigma _{3} } \right)\sigma _{\rm G} - 0.5a\left({\sigma _{1}^{2} - \sigma _{3}^{2} } \right) (79)$
$\sigma _{\rm O} = $
$\dfrac{4\sigma _i \sigma _j^{2} \left( {1 - \delta _{ij} } \right) + \sigma _{\rm N} \left[{\left( { - 1} \right)^{\delta _{i1} + 1}\sigma _{\rm G} + \sigma _{\rm L} + \left( { - 1} \right)^{\delta_{i1} }a\sigma _i } \right]}{\sigma _{\rm M} }$ (80)
$\sigma _{\rm P} = $
$\dfrac{\left( {\sigma _2 - \sigma _{3} } \right)\left[ {\left( {\sigma _2 + \sigma _{3} }\right) - \sigma _i + \left( { - 1} \right)^{\delta _{i2} + 1}0.5a^2\left( {\sigma _2 - \sigma _{3} }\right)} \right]}{2\sigma _{\rm H} } $ (81)
$\sigma _{\rm Q} = \sqrt {{4}\sigma _2^{2} \sigma _{3}^{2} + \left[ {\left( {\sigma _2 - \sigma_{3} } \right)\sigma _{\rm H} - 0.5a\left( {\sigma _2^{2} - \sigma _{3}^{2} } \right)} \right]^2} (82)$
$\sigma _{\rm R} = \left( {\sigma _2 - \sigma _{3} } \right)\sigma _{\rm H} - 0.5a\left({\sigma _2^{2} - \sigma _{3}^{2} } \right) (83)$
$\sigma _{\rm S} = $
$\dfrac{4\sigma _i \sigma _j^{2} \left( {1 - \delta _{ij} } \right) + \sigma _{\rm R} \left[{\left( { - 1} \right)^{\delta _{i2} + 1}\sigma _{\rm H} + \left. {\sigma _{\rm P} - \left( { - 1}\right)^{\delta _{i2} + 1}a\sigma _i } \right]} \right.}{\sigma _{\rm Q }} $ (84)
$\delta _{\rm A} = \left( {EC^2\delta _{i1} + EB^2\delta _{i2} + EB^2EC^2\delta _{i3} } \right) (85)$
$R_1 = \sigma _1 - \sigma _2 - EC^2\left( {\sigma _3 - \sigma _1 } \right) (86)$
$R_2 = EB^2\left( {\sigma _2 - \sigma _3 } \right) - \sigma _1 + \sigma _2 (87)$
$R_3 = EC^2\left( {\sigma _3 - \sigma _1 } \right) - EB^2\left( {\sigma _2 - \sigma _3 }\right) (88)$
$R = \sqrt {\left( {\sigma _1 - \sigma _2 } \right)^2 + EB^2\left( {\sigma _2 - \sigma _3 }\right)^2 + EC^2\left( {\sigma _3 - \sigma _1 } \right)^2} $(89)
$B_i = \dfrac{EB\cdot EC}{\sigma _{\rm A} }\left( {\dfrac{R_1 \delta _{i1} + R_2 \delta _{i2} +R_3 \delta _{i3} }{R} - \dfrac{R\delta _{\rm A} }{\sigma _{\rm A} }} \right) (90)$
$\dfrac{\partial \tan \varphi _{\rm mo} }{\partial EB} = \dfrac{{1}}{\sigma _{\rm A}^2 }\Bigg\{ \left[ {R\cdot EC + \dfrac{EB^2EC\left( {\sigma _2 - \sigma _3 } \right)^2}{R}} \right]\sigma _A - $
$\qquad 2R\cdot EB^2EC\left( {\sigma _2 + \sigma _3 EC^2} \right)\Bigg \} (91)$
$\dfrac{\partial \tan \varphi _{\rm mo} }{\partial EC} = \dfrac{{1}}{\sigma _{\rm A}^2 }\Bigg\{\left[ {R\cdot EB + \dfrac{EB\cdot EC^2\left( {\sigma _3 - \sigma _1 } \right)^2}{R}} \right]\sigma _A - $
$\qquad 2R\cdot EB\cdot EC^2\left( {\sigma _1 + \sigma _3 EB^2} \right) \Bigg\} (92)$
$\dfrac{\partial EB}{\partial \sigma _i } = \left\{ \!\!\begin{array}{l} \dfrac{\left( { - 1}\right)^{\delta _{i1} + 1}\left( {\sigma _{\rm G} - a\sigma _i } \right) + \sigma _{\rm L} + \sigma _O}{{2}\sigma _{1} \sigma _{3} } - \qquad \dfrac{\left( {\sigma _{1} - \sigma _{3} } \right)\sigma _G+ \sigma _{\rm M} - 0.5a\left( {\sigma _{1}^{2} - \sigma _{3}^{2} } \right)}{{2}\sigma _i^2 \sigma _j \left({1 - \delta _{ij} } \right)} \,, \hskip 3.5cm i \ne 2,j \ne 2 0 \,, \hskip 3cm \, i = 2\end{array} \!\! \right.$ (93)
$\dfrac{\partial EC}{\partial \sigma _i } = \left\{ \!\! \begin{array}{l} 0 \,, \hskip 3cm \, {i = 1} \dfrac{\left( { - 1} \right)^{\delta _{i2} + 1}\left( {\sigma _{\rm H} - a\sigma_i } \right) + \sigma _{\rm P} + \sigma _{\rm S} }{{2}\sigma _2 \sigma _{3} } - \qquad\dfrac{\left( {\sigma _2 - \sigma _{3} } \right)\sigma _{\rm H} + \sigma _{\rm Q} - 0.5a\left( {\sigma _2^{2}- \sigma _{3}^{2} } \right)}{{2}\sigma _i^2 \sigma _j \left( {1 - \delta _{ij} } \right)} \,, \hskip 3.5cm i \ne 1,j \ne 1\end{array} \!\!\right.$ (94)
式(56) $\sim $式(64)为将普通应力转换为变换应力空间的变换应力公式,而式(65) $\sim$式(94)为将变换应力空间中变换应力应用到具体本构模型中时微分的导函数公式.
6 准则及变换应力法的试验验证
为了便于对所提横观各向同性a准则及其变换应力公式进行验证,分别采用如下的岩土材料,在真三轴加载条件下的破坏以及应力应变关系试验结果进行对比分析. 表1为4种岩土材料的参数.Table 1
表1
表1岩土材料参数
Table 1Geomaterial parameters
| Materials | a criterion | |||||
|---|---|---|---|---|---|---|
| a | ρ0/MPa pr/MPa | M0 | n | Mx | ||
| San Francisco bay mud | 0.41 | 0.001 5 | 0.111 | 1.42 | 0.83 | 1.49 |
| Cambria sand | 0.41 | 0.001 5 | 0.111 | 1.55 | 1.0 | 1.61 |
| Santa Monica Beach sand | 0.23 | 0.001 5 | 0.111 | 1.71 | 1.0 | 1.83 |
| Touremire shale | 0.3 | 6.5 | 40.0 | 1.35 | 0.6 | 1.62 |
| Kaolin clay | 0.3 | 0.002 | 0.15 | 0.86 | 1.0 | 0.91 |
新窗口打开
6.1 强度准则预测
图14和图15中圆圈表示Kirkgard等[36]关于旧金山湾黏土的常规三轴压缩试验结果,对该试验结果用图14所示的双对数坐标系下进行整理,可拟合出一条直线作为标定子午面上强度参数$n$, $p_{\rm r}$, $\sigma_{0}$的依据曲线.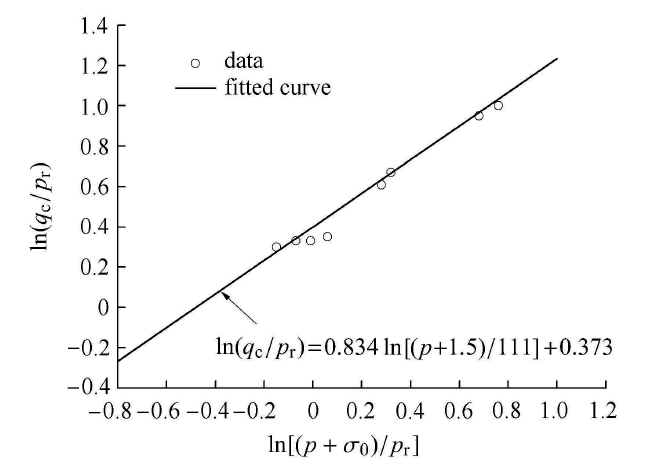
显示原图|下载原图ZIP|生成PPT图14旧金山湾黏土试验数据直线拟合曲线
-->Fig.14Fitted line with test data for San Francisco bay clay
-->
显示原图|下载原图ZIP|生成PPT图15旧金山湾黏土试验数据幂函数拟合曲线
-->Fig.15Fitted curve using power function with test data for San Francisco bay clay
-->
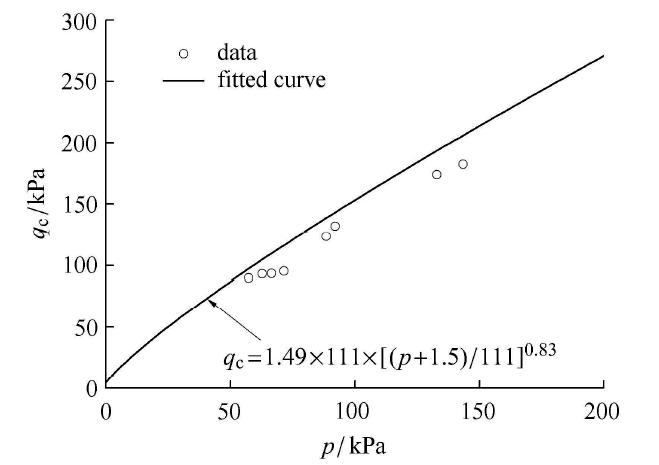
图15是该试验点在$p-q$坐标系下的整理结果,由图可见,采用幂函数曲线作为拟合该试验点具有 较好的规律性.由此幂函数 曲线,可以标定出参数$M_{\rm f}$.
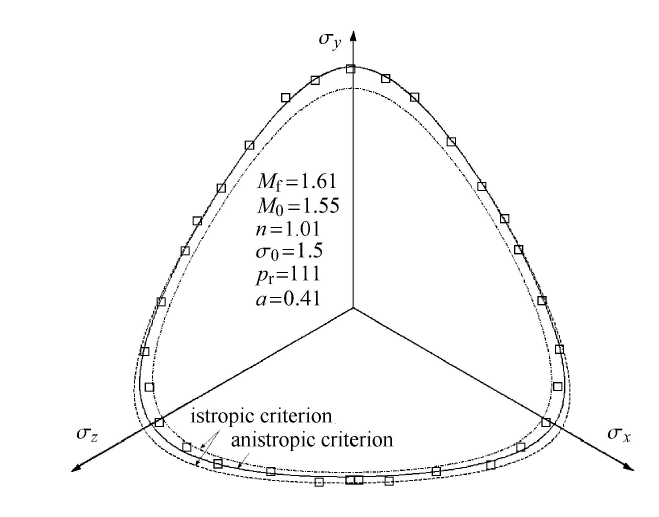
图16为偏平面上对旧金山湾黏土的破坏数据进行预测对比结果. 图中的破坏点表示在真三轴压缩条件下的破坏点测试数据. 图中虚线以及点划线分别表示当采用$M_{\rm f} =1.49$以及1.32时用各向同性a准则预测的破坏曲线,而实线则表示采用所建议的横观各向同性a准则预测的破坏曲线. 由图可见,破坏点的分布规律在$y$轴两侧呈现左右对称分布,且随着应力罗德角 $\theta $ 的增大,呈现不规律分布, $\theta =60^\circ$区域所对应的应力比强度要大于 $\theta =180^\circ$所对应的区域. 采用各向同性a准则过高地估计了 $\theta =180^\circ$所对应的区域的应力比强度值,而采用横观各向同性a准则则较好地预测了该区域的强度变化特点.
显示原图|下载原图ZIP|生成PPT图16旧金山湾黏土偏平面上试验数据与预测对比结果
-->Fig.16Comparison result with prediction and test data for San Francisco bay clay in deviatoric plane
-->
图17所示离散点数据为对应真三轴条件下不同$b$值条件下的土体内摩擦角分布规律.其中,圆圈、方形格与五角星分别对 应I、II、III区的试验结果.图中实线、虚线、点划线分别表示采用横观各向同性a准则所预测的结果,采用各向同性a准则由于未能考虑土体各向异性的影响,因而无法反映不同象限内各向异性对于内摩擦角的影响规律.图中点线表示由采用各向同性a准则所预测的结果,显然当处于I象限内,两者差别不大,但根据试验结果可知,随着进入II、III象限,内摩擦角整体出现了下降趋势,而采用所建议准则反映出了这一规律.同时,由于a准则对于$b$值或者中主应力对于内摩擦角的影响规律可明显反映出来,随着$b$值的增大,内摩擦角先增大后减小.
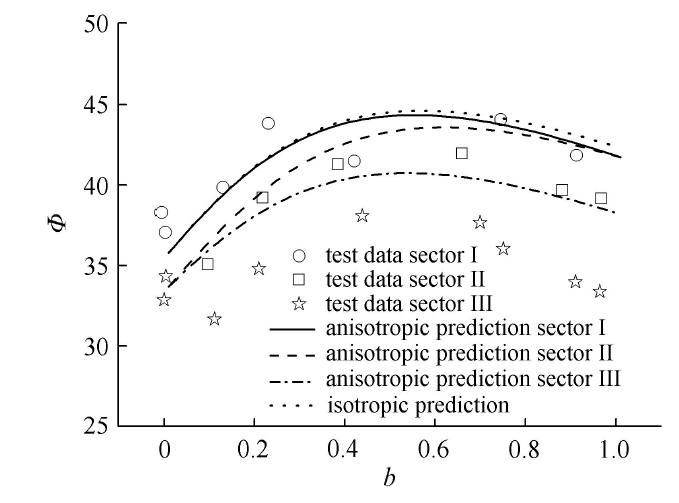显示原图|下载原图ZIP|生成PPT图17旧金山湾黏土不同$b$值条件下对应的内摩擦角预测对比结果
-->Fig.17Comparison result with prediction and test data of friction angle for San Francisco bay clay with different $b$ value
-->
图18中离散点为Ochiai等[37]关于Cambria砂土在偏平面上的真三轴试验结果,由图可见,采用各向同性a准则无法合理考虑当 $\theta $ =120$^\circ$区域以及180$^\circ$区域的应力比强度较低的现象,而采用横观各向同性a准则则可合理的考虑上述区域应力比强度降低的现象.
显示原图|下载原图ZIP|生成PPT图18Cambria砂土偏平面上试验数据与预测对比结果
-->Fig.18Comparison result with prediction and test data for Cambria sand in deviatoric plane
-->
图19所示离散点数据为对应真三轴条件下不同$b$值条件下的土体内摩擦角分布规律. 由对比可见,所建议的a准则可合理地考虑中主应力系数$b$值对于内摩擦角的影响规律特点,即随着$b$值增大,先增大后减小. 所建议的考虑各向异性的a准则还可将3个区域内的随象限增大内摩擦角整体减小现象反映出来.
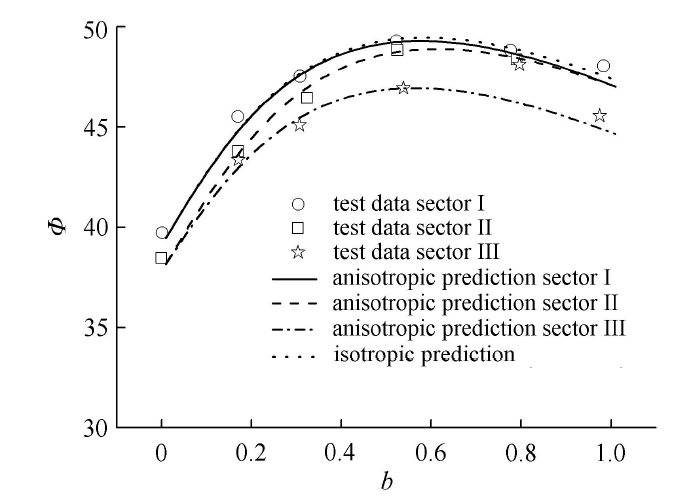显示原图|下载原图ZIP|生成PPT图19Cambria砂土不同$b$值条件下对应的内摩擦角预测对比结果
-->Fig.19Comparison result with prediction and test data of friction angle for Cambria sand with different $b$ value
-->
图20中离散点为Abelev等[38]关于Santa Monica海滩砂土所做的真三轴试验结果. 由图可见,砂土由于自身的离散性,收到中主应力影响更为明显. 整体在偏平面上的投影更趋近于较为尖锐的三角形. 由于原生各向异性的影响,在 $\theta =180^\circ$区域出现了较 $\theta =60^\circ$区域应力比强度更低的现象. 采用各向同性a准则过高的估计了该区域强度,而采用所建议的a准则可较好地考虑该区域应力比强度降低现象.
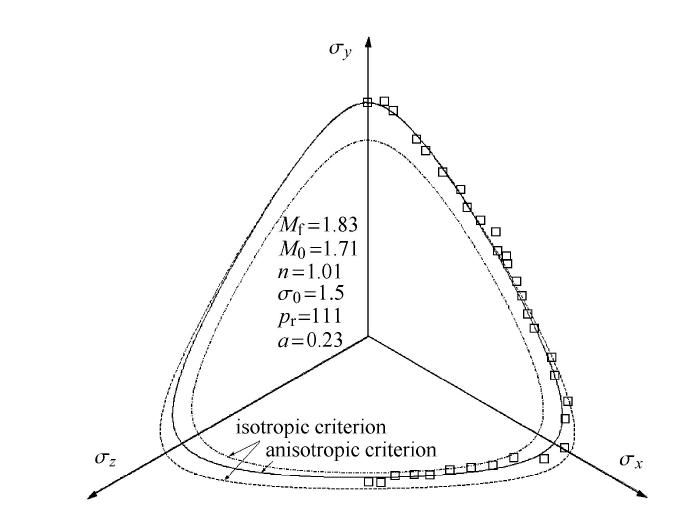显示原图|下载原图ZIP|生成PPT图20Santa Monica 海滩砂土偏平面上试验数据与预测对比结果
-->Fig.20Comparison result with prediction and test data for Santa Monica beach sand in deviatoric plane
-->
图21中离散点为对应的随$b$值影响的内摩擦角分布曲线.由对比可见,采用横观各向同性a准则可明显区分出3个象限内的内摩擦角整体 降低现象.对于图中圆圈当$b$值较大时出现的突变点以及五角星出现的增大现象,由于对应的是接近常规三轴伸长区域,对应此区域时,颗粒受到的应力诱导各向异性对最终结果产生了影响,但整体规律仍然是随$b$值先增大后减小的特点.
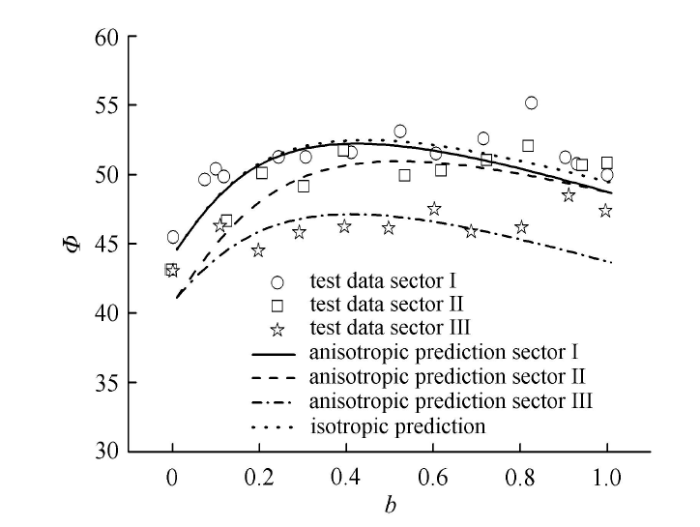显示原图|下载原图ZIP|生成PPT图21Santa Monica 海滩砂土不同$b$值条件下对应的内摩擦角预测对比结果
-->Fig.21Comparison result with prediction and test data of friction angle for Santa Monica beach sand with different $b$ value
-->
图22中离散点为Niandou等[39]关于Touremire页岩在不同加载角下的常规三轴压缩试验结果,加载角是按照大主应力与沉积面法向夹角来定义的. 由对比可见,随着加载角逐步增大,相对应的广义偏应力强度值逐渐减小.另一方面,随着平均应力$p$的增大,广义偏应力强度值也随之增大,且呈现明显的非线性增大规律.
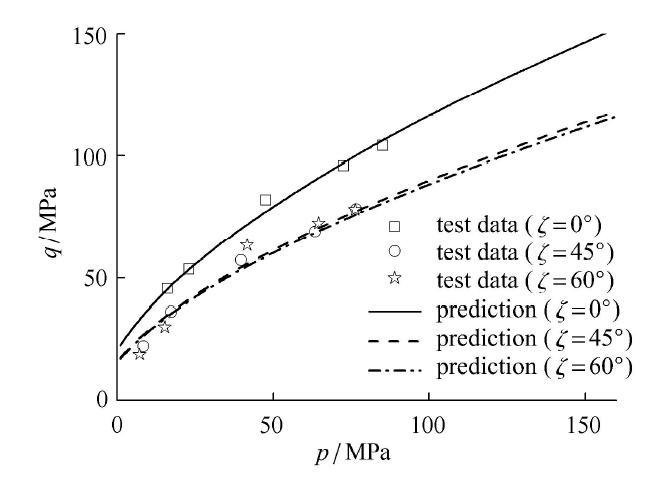显示原图|下载原图ZIP|生成PPT图22Touremire页岩不同加载角下常规三轴压缩试验结果与预测对比
-->Fig.22Comparison result with prediction and test data of strength for Touremire shale with different loading directions under conventional triaxial compression condition
-->
图23为相对应的Touremire页岩在不同围压条件下广义偏应力强度值随加载角的变化规律. 由图可见,随着加载角从0$^\circ$到90$^\circ$变化,强度值呈现先减小后增大的规律特点,所建议的横观各向同性a准则可以准确地描述上述规律.且由试验点可观测到,趋近于90$^\circ$附近的强度值要稍微低于0$^\circ$的强度值,所建议准则也能描述上述特点,预测值在90$^\circ$附近略低于试验值,一方面未能合理考虑材料微观组构对于宏观强度特性的影响,另一方面可看到对于围压为1\,MPa时,预测值偏高,说明静水压力对于各向异性材料强度也会发生作用.若想得到更好的预测结果,可以考虑将材料组构以及静水压力效应更合理的扩展到所建议的强度准则中.
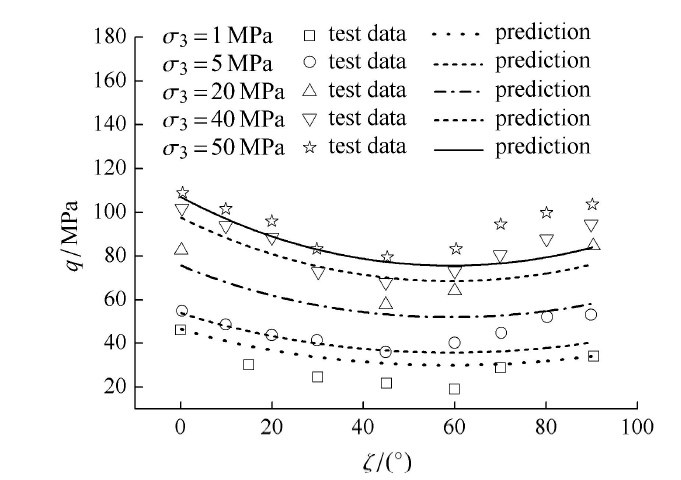显示原图|下载原图ZIP|生成PPT图23Touremire页岩不同围压下常规三轴压缩试验结果与预测对比
-->Fig.23Comparison result with prediction and test data of strength for Touremire shale with different confining pressures under conventional triaxial compression condition
-->
6.2 变换应力法应用预测
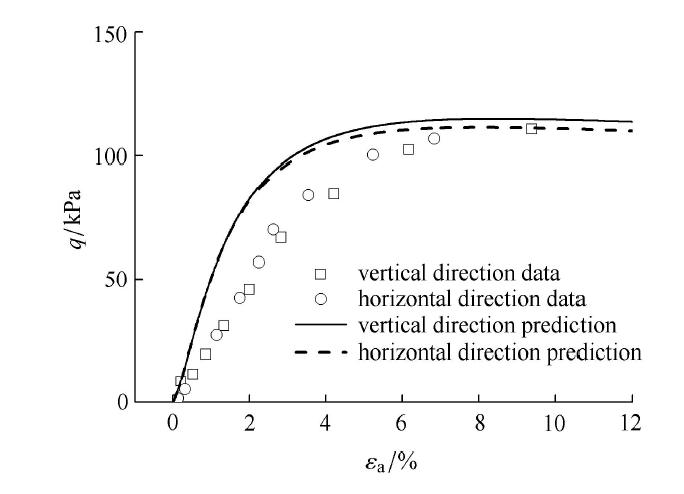
图24$\sim$图26中离散点为Banerjee 等[40]关于高岭土所做的常规三轴加载试验结果,约束条件为不排水条件.其中,方框点表示大主应力方向与试样沉积面法向方向一致的测试结果,而圆形点则表示大主应力与试样沉积面法向方向相垂直方向的测试结果.采用所提出的考虑各向异性的变换应力公式对动力UH模型[41]进行一般化处理,用三维化后的动力UH模型进行预测,图24$\sim$图26中两条曲线即为预测曲线.其中实线表示大主应力方向垂直于沉积面的预测结果,而虚线则表示大主应力平行于沉积面的预测结果.图24中广义偏应力与轴应变的关系对比结果,由图可见,当大主应力方向与沉积面相垂直时,测试结果表明了试样更高的模量以及抗剪强度,当两者方向相一致时,测试结果表现出试样较低的模量以及较低的抗剪强度.采用所提的各向异性变换应力方法对动力UH模型三维化后的模拟表明,上述模量以及强度的提高都与试验结果所揭示的规律完全一致.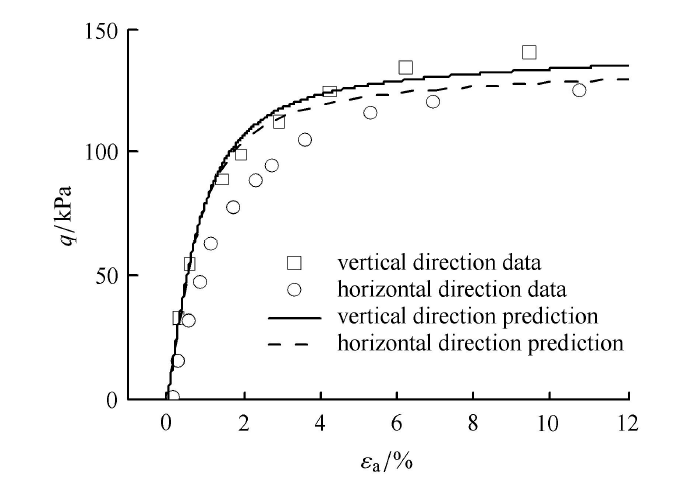
显示原图|下载原图ZIP|生成PPT图24Kaolin 黏土不同加载方向下广义偏应力与轴应变预测对比结果
-->Fig.24Comparison result with prediction and test data of relationship between deviatoric stress and axial strain for Kaolin clay with different loading directions
-->
显示原图|下载原图ZIP|生成PPT图25Kaolin 黏土不同加载方向下孔隙水压力与轴应变预测对比结果
-->Fig.25Comparison result with prediction and test data of relationship between pore pressure and axial strain for Kaolin clay with different loading directions
-->
显示原图|下载原图ZIP|生成PPT图26Kaolin 黏土不同加载方向下有效应力路径预测对比结果
-->Fig.26Comparison result with prediction and test data of effective stress path for Kaolin clay with different loading directions
-->
图25为对应的孔压与大主应变的关系曲线预测对比结果. 由图可见,对应与沉积面的垂直加载以及顺层加载两种测试结果,孔压基本差异较小,表明孔压大小与加载方向基本无关. 所预测的结果差异也很小.
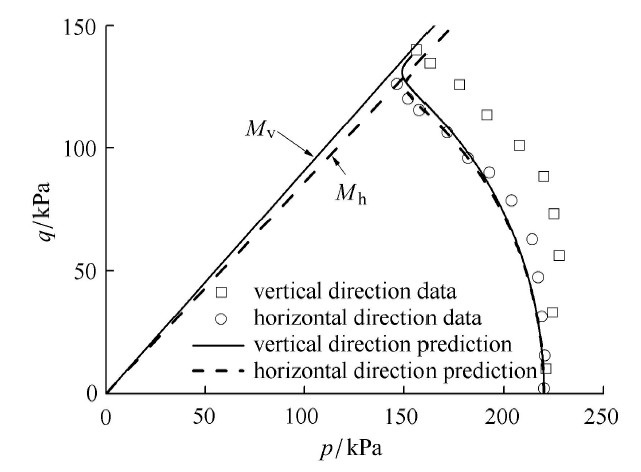
图26对应的有效应力路径预测对比结果. 从图中可观察,垂直沉积面的测试数据表明试样更硬,且最终的不排水强度更大,而顺沉积面加载结果表明试样较软,且最终不排水强度值较低. 图26中预测曲线体现了上述这种规律特点.
7 结 论
基于已提出的a强度准则,为反映岩土材料沉积面对于强度特性的影响,通过引入反映有效滑移面与沉积面夹角作为反映横观各向同性性质的状态参量,并利用上述夹角构建了反映横杆各向异性特性影响的偏平面强度应力比公式,结合子午面上幂函数强度公式,得到了能够反映岩土材料横观各向同性性质的强度一般表达式. 基于先变换各向异性因素再变换中主应力影响因素的思路,提出了反映横观各向同性性质的变换应力方程. 该方程描述了一般横观各向异性应力空间到各向同性应力空间的转换过程. 上述成果具有如下特点：(1)基于已有的a准则公式,通过只加入一个参数的情况下,将原a准则推广为可考虑横观各向同性性质的强度准则,且参数便于常规试验确定,物理意义明确.
(2)由于基于a准则,因而,所提的各向异性强度公式不仅仅适用于岩土材料,同时还可适用于金属、岩石、混凝土等具有一定凝聚力的材料. 上述材料都具有一定的原生各向异性性质.
(3)所建议的变换应力方程,可方便的将既有的以$p-q$为变量的二维模型推广为可考虑横观各向同性影响的一般应力应变关系模型.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . |
| [12] | . |
| [13] | . |
| [14] | . |
| [15] | . . |
| [16] | . |
| [17] | . |
| [18] | . . |
| [19] | . . |
| [20] | . . |
| [21] | . |
| [22] | . . |
| [23] | . . |
| [24] | . . |
| [25] | . |
| [26] | . . |
| [27] | . . |
| [28] | . . |
| [29] | . . |
| [30] | |
| [31] | . . |
| [32] | . |
| [33] | . |
| [34] | . |
| [35] | . |
| [36] | . |
| [37] | . |
| [38] | . |
| [39] | . |
| [40] | . |
| [41] | . |
